CURIE: a cellular automaton for concept drift detection

Abstract

Data stream mining extracts information from large quantities of data flowing fast and continuously (data streams). They are usually affected by changes in the data distribution, giving rise to a phenomenon referred to as concept drift. Thus, learning models must detect and adapt to such changes, so as to exhibit a good predictive performance after a drift has occurred. In this regard, the development of effective drift detection algorithms becomes a key factor in data stream mining. In this work we propose $\textit{CURIE}$, a drift detector relying on cellular automata. Specifically, in $\textit{CURIE}$ the distribution of the data stream is represented in the grid of a cellular automata, whose neighborhood rule can then be utilized to detect possible distribution changes over the stream. Computer simulations are presented and discussed to show that $\textit{CURIE}$, when hybridized with other base learners, renders a competitive behavior in terms of detection metrics and classification accuracy. $\textit{CURIE}$ is compared with well-established drift detectors over synthetic datasets with varying drift characteristics.

1 Introduction

Data Stream Mining (DSM) techniques are focused on extracting patterns from continuous (potentially infinite) and fast data. A data stream is the basis of machine learning techniques for this particular kind of data, which is composed of an ordered sequence of instances that arrive one by one or in batches. Depending on the constraints imposed by the application scenario at hand, such instances can be read only once or at most a reduced number of times, using limited computing and memory resources. These constraints require an incremental learning (or one-pass learning) procedure where past data cannot be stored for batch training in future time steps. Due to these challenging conditions under which learning must be done, DSM has acquired a notable relevance in recent years, mostly propelled by the advent of Big Data technologies and data-intensive practical use cases (Bifet et al. 2018).

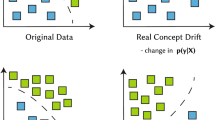
In this context, data streams are often generated by non-stationary phenomena, which may provoke a change in the distribution of the data instances (and/or their annotation). This phenomenon is often referred to as concept drift (Webb et al. 2016). These changes cause that predictive models trained over data streams become eventually obsolete, not adapting suitably to the new distribution (concept). The complexity of overcoming this issue, and its prevalence over many real scenarios, make concept drift detection and adaptation acknowledged challenges in DSM (Jie et al. 2018). Examples of data stream sources undergoing concept drift include computer network traffic, wireless sensor data, phone conversations, social media, marketing data, ATM transactions, web searches, and electricity consumption traces, among others (Žliobaitè 2016). Recently, several emerging paradigms such as the so-called Smart Dust (Ilyas and Mahgoub 2018), Utility Fog (Dastjerdi and Buyya 2016), Microelectromechanical Systems (MEMS or “motes”) (Judy 2001), or Swarm Intelligence and Robotics (Del Ser et al. 2019), are in need for efficient and scalable solutions in real-time scenarios. Here concept drift may be present, and thus making drift detection a necessity.

This complexity in the concept drift phenomenon manifests when researchers try to characterize it (Webb et al. 2016). Indeed, there are many different types of concept drifts, characterized by e.g. the speed or severity of change. Consequently, drift detection is a key factor for those active strategies that require triggering mechanisms for drift adaptation (Hu et al. 2019). A drift detector estimates the time instants at which changes occur over the stream, so that when a change is detected, an adaptation mechanism is applied to the base learner so as to avoid a degradation of its predictive performance. The design of a concept drift detector with high performance is not trivial, yet it is crucial to achieve more reliable DSM models. In fact, a general-purpose strategy for concept drift detection, handling and recovery still remains as an open research avenue, as foretold by the fulfillment of the No Free Lunch theorem in this field (Hu et al. 2019). This difficulty to achieve a universal best approach becomes evident in the most recent comparative among drift detectors made in Barros and Santos (2018). Analyzing its mean rank of methods, we observe how there is not a method with the best metrics, or even showing the best performance in the majority of them. In this regard, the design objective is to develop techniques that detect all existing drifts in the stream with low latency and as few false alarms and missed detections as possible. Thus, the most suitable drift detector depends on the characteristics of the DSM problem under study, giving more emphasis to some metrics than others. Regarding the detection metrics, we usually tend to put in value those drift detectors that are able to show a good classification performance while minimizing the distance of the true positive detections.

Cellular automata (CA), as low-bias and robust-to-noise pattern recognition methods with competitive classification performance, meet the requirements imposed by the aforementioned paradigms mainly due to their simplicity and parallel nature. In this work we present a Cellular aUtomaton for concept dRIft dEtection ($\textit{CURIE}$), capable of competitively identifying drifts over data streams. The proposed approach is based on CA, which became popular when Conway’s Game of Life appeared in 1970, and thereafter attracted attention when Stephen Wolfram published his CA study in 2002 (Wolfram 2002). Although CA are not very popular in the data mining field, Fawcett showed in Fawcett (2008) that they can become simple, low-bias methods. $\textit{CURIE}$, as any other CA-based technique, is computationally complete (able to perform any computation which can be done by digital computers) and can model complex systems from simple structures, which puts it in value to be considered in the DSM field. Moreover, $\textit{CURIE}$ is tractable, transparent and interpretable (Lobo et al. 2021), all ingredients that have lately attracted attention under the eXplainable Artificial Intelligence (XAI) paradigm (Arrieta et al. 2020), and not easy to achieve when designing new data mining techniques. The natural concordance between data and the internal structure of a cellular automaton makes $\textit{CURIE}$ to be closer to a transparent model by design, leaving aside any need for external algorithmic components (post-hoc explainability tools) to interpret its decisions (Rudin 2019). Next, we summarize the main contributions of $\textit{CURIE}$ to the drift detection field:

• It is capable of competitively detecting abrupt and gradual concept drifts.

• It does not require the output (class prediction) of the base learner. Instead, it extracts the required information for drift detection from its internal structure, looking at the changes occurring in the neighborhood of cells.

• It is transparent by design due to the fact that its cellular structure is a direct representation of the feature space and the labels to be predicted.

• It can be combined with any base learner.

Besides, $\textit{CURIE}$ offers another additional advantage in DSM:

• It is also able to act as an incremental learner and adapt to the change (Lobo et al. 2021), going one step further by embodying an all-in-one approach (learner and detector).

The rest of the manuscript is organized as follows: first, we provide the background of the field in Sect. 2. Next, we introduce the fundamentals of CA and their role in DSM in Sect. 3. Section 4 exposes the details of our proposed drift detector $\textit{CURIE}$, whereas Sects. 5 and 6 elaborate on experimental setup and analyze results with synthetic and real-world data stream respectively. Finally, Sect. 7 concludes the manuscript with an outlook towards future research derived from this work.

2 Related work

We now delve into the background literature related to the main topics of this work: drift detection (Sect. 2.1) and cellular automata for machine learning (Sect. 2.2).

2.1 Drift detection

DSM has attracted much attention from the machine learning community (Gomes et al. 2019). Researchers are now on the verge of moving out DSM methods from laboratory environments to real scenarios and applications, similarly to what occurred with traditional machine learning methods in the past. Most efforts in DSM have been focused on supervised learning (Bifet et al. 2018) (mainly on classification), addressing the concept drift problem (Webb et al. 2016). Generally, these efforts have been invested in the development of new methods and algorithms that maintain an accurate decision model with the capability of learning incrementally from data streams while forgetting concepts (Losing et al. 2018).

For this purpose, drift detection and adaptation mechanisms are needed (Jie et al. 2018). In contrast to passive (blind) approaches where the model is continuously updated every time new data instances are received (i.e., drift detection is not required), active strategies (where the model gets updated only when a drift is detected) are in need for effective drift detection mechanisms. Most active approaches usually utilize a specific classifier (base learner) and analyze its classification performance (e.g. accuracy or error rate) to indicate whether a drift has occurred or not. Then, the base learner is trained on the current instance within an incremental learning process repeated for each incoming instance of the data stream. Despite the most used input for the drift detectors are the accuracy or error rate, we can find other detectors that use other inputs such as diversity (Minku and Yao 2011) or structural changes stemming from the model itself (Lobo et al. 2018).

There is a large number of drift detectors in the literature, many of them compared in Gonçalves Jr et al. (2014). As previously mentioned, the conclusion of these and other works is that there is no a general-purpose strategy for concept drift. The selection of a good strategy depends on the type of drift and particularities of each data streaming scenario. Other more recent concept drift detection mechanisms have been presented and well described in Barros and Santos (2018).

2.2 Cellular automata for pattern recognition

CA are not popular in the pattern recognition community, but even so we can find recent studies and applications. In Collados-Lara et al. (2019), authors propose CA to simulate potential future impacts of climate change on snow covered areas, whereas in Gounaridis et al. (2019) an approach to explore future land use/cover change under different socio-economic realities and scales is presented. Scheduling is another field where CA has been profusely in use (Carvalho and Carneiro 2019). Another recent CA approach for classification is Uzun et al. (2018). CA have been also used with convolutional neural networks (Gilpin 2019) and reservoir computing (Nichele and Molund 2017).

Regarding DSM or concept drift detection fields, the presence of CA-based proposals is even scarcer. Although a series of contributions unveiled solid foundations for CA to be used for pattern recognition (Raghavan 1993), it was not until 2008 (Fawcett 2008) [departing from the seminal work in Ultsch (2002)] when CA was presented as a simple but competitive method for parallelism, with a low-bias, effective and competitive in terms of classification performance, and robust to noise. Regarding DSM and concept drift detection, timid efforts have been reported so far in Hashemi et al. (2007) and Pourkashani and Kangavari (2008), which must be considered as early attempts to deal with noise rather than with incremental learning and drift detection. They used a CA-based approach as a real-time instance selector to avoid noisy instances, while the classification task was performed in batch learning mode by non-CA-based learning algorithms. Thus, CA is proposed as a mere complement to select instances, and not as an incremental learner. Besides, their detection approach is simply based on the local class disagreements between neighboring cells, without considering relevant aspects such as the grid size, the radius of the neighborhood, or the moment of the disagreement, among other factors. Above all, they do not provide any evidence on how their solution learns incrementally, nor details on the real operation of the drift detection approach. Finally, in terms of drift detection evaluation, their approach is not compared to known detectors using reputed base learners and standard detection metrics.

More recently, the authors of Lobo et al. (2021) transform a cellular automaton into a real incremental learner with drift adaptation capabilities. In this work, we go one step further by proposing $\textit{CURIE}$, a cellular automaton featuring a set of novel ingredients that endow it with abilities for drift detection in DSM. As we will present in detail, $\textit{CURIE}$ is an interpretable CA-based drift detector, able to detect abrupt and gradual drifts, and providing very competitive classification performances and detection metrics.

3 Cellular automata

3.1 Foundations

Von Neumann described CA as discrete dynamical systems with a capacity of universal computability (Von Neumann and Burks 1966). Their simple local interaction and computation of cells result in a huge complex behavior when these cells act together, being able to describe complex systems in several scientific disciplines.

Following the notation of Kari in Kari (2005), a cellular automaton can be formally defined as: $A \doteq (d,{\mathcal {S}},f_{\boxplus },f_{\circlearrowright })$, with d denoting the dimension, ${\mathcal {S}}$ a group of discrete states, $f_{\boxplus }(\cdot )$ a function that receives as input the coordinates of the cell and returns the neighbors of the cell to be utilized by the update rule, and $f_{\circlearrowright }(\cdot )$ a function that updates the state of the cell at hand as per the states of its neighboring cells. Hence, for a radius $r=1$ von Neumann’s neighborhood defined over a $d=2$-dimensional grid, the set of neighboring cells and state of the cell with coordinates ${\mathbf {c}}=[i,j]$ are given by:

$$\begin{aligned}&f_{\boxplus }([i,j])=\{[i,j+1],[i-1,j],[i,j-1],[i+1,j]\}, \\&S({\mathbf {c}})=S([i,j])\\&\quad =f_{\circlearrowright }(S([i,j+1]),S([i-1,j]),S([i,j-1]),S([i+1,j])), \end{aligned}$$

i.e., the vector of states S([i, j]) of the [i, j] cell within the grid is updated according to the local rule $f_{\circlearrowright }(\cdot )$ when applied over its neighbors given by $f_{\boxplus }([i,j])$ (Fig. 1). For a d-dimensional space, a von Neumann’s neighborhood contains 2d cells.

A cellular automaton should present these three properties: i) parallelism or synchronicity (all of the updates to the cells compounding the grid are performed at the same time); ii) locality (when a cell [i, j] is updated, its state S[i, j] is based on the previous state of the cell and those of its nearest neighbors); and iii) homogeneity or properties-uniformity (the same update rule $f_{\circlearrowright }(\cdot )$ is applied to each cell).

Fig. 1

Neighborhood of CA in data mining: (a) a von Neumann’s neighborhood with radius $r=1$ and $r=2$ using the Manhattan distance; (b) the center cell inspects its von Neumann’s neighborhood ($r=1$) and applies the majority voting rule in a one-step update; (c) CURIE structure for $d\times {\mathcal {G}} = 6 \times 3$

3.2 Cellular automata for data stream mining

A DSM process that may evolve over time can be defined as follows: given a time period [0, t], the historical set of instances can be denoted as ${\mathbf {D}}_{0,t}={{\mathbf {d}}_{0},\ldots , {\mathbf {d}}_{t}}$, where ${\mathbf {d}}_{i}=({\mathbf {X}}_{i},y_{i})$ is an instance, ${\mathbf {X}}_{i}$ is the vector of features, and $y_{i}$ its label. Assuming that ${\mathbf {D}}_{0,t}$ follows a certain joint probability distribution $P_{t}({\mathbf {X}},y)$. As it has already been mentioned, data streams usually suffer from concept drift, which may change their data distribution, provoking that predictive models trained over them become obsolete. Thus, concept drift happens at timestamp $t+1$ when $P_{t}({\mathbf {X}},y) \ne P_{t+1}({\mathbf {X}},y)$, i.e. as a change of the joint probability distribution of ${\mathbf {X}}$ and y at time t.

In addition to the presence of concept drift, DSM also imposes by itself its own restrictions, which calls for a redefinition of the previous CA for data mining. Algorithms learning from data streams must operate under a set of restrictions:

• Each instance of the data stream must be processed only once.

• The time to process each instance must be low.

• Only a few data stream instances can be stored (limited memory).

• The trained model must provide a prediction at any time.

• The distribution of the data stream may evolve over time.

Therefore, when adapting a CA for DSM, the above restrictions must be taken into account to yield a CA capable of learning incrementally, and with drift detection and adaptation mechanisms. In order to use CA in DSM, data instances flowing over time must be mapped incrementally to the cells of the grid. Next, we analyze each of the mutually interdependent parts in CA for DSM:

• Grid: In a data mining problem with n features, the standard procedure adopted in the literature consists of assigning one grid dimension to each feature. After that, it is necessary to split each grid dimension by the values of the features, in a way that we obtain the same number of cells per dimension. To achieve that, “bins” must be created for every dimension (Fig. 2) by arranging evenly spaced intervals based on the maximum and minimum values of the features. These “bins” delimit the boundaries of the cells in the grid.

• States: We have to define a finite number of discrete states $|{\mathcal {S}}|$, which will correspond to the number of labels (classes) considered in the data mining problem.

• Local rule: In data mining the update rule $f_{\circlearrowright }(\cdot )$ can adopt several forms. One of the most accepted variants is a majority vote among neighbors’ states (labels). For example, for $d=2$:

  $$\begin{aligned} S([i,j])={{\,\mathrm{arg\,max}\,}}_{s\in {\mathcal {S}}}\sum _{[k,l]\in f_{\boxplus }([i,j])}{\mathbb {I}}(S([k,l])=s), \end{aligned}$$

  where the value of $f_{\boxplus }([i,j])$ will be the coordinates of neighboring cells of [i, j], and ${\mathbb {I}}(\cdot )$ is an auxiliary function taking value 0 when its argument is false and 1 if it is true.

• Neighborhood: a neighborhood and its radius must be specified. Even though a diversity of neighborhood relationships has been proposed in the related literature, the “von Neumann” (see Fig. 1) or “Moore” are arguably the most resorted definitions of neighborhood for CA.

• Initialization: the grid is seeded with the feature values of the instances that belong to the training dataset. In order to decide the state of each cell, we assign the label corresponding to the majority of training data instances with feature values falling within the range covered by the cell. After that, cells of the grid are organized into regions of similar labels (Fig. 2).

• Generations: when the initialization step finishes, some cells may remain unassigned, i.e. not all of them are assigned a state (label). In other words, the training dataset used to prepare the CA for online learning might not be large enough to “fill” all cells in the grid. In such a case, it becomes necessary to “evolve” the grid several times (generations) until all cells are assigned a state. In this evolving process, each cell calculates its new state by applying the update rule over the cells in its neighborhood. All cells apply the same update rule, being updated synchronously and at the same time. Here lies the most distinctive characteristic of CA: the update rule only inspects its neighboring cells, being the processing entirely local (Fig. 1).

Fig. 2

Data representation in CA: (a) a dataset with $d=2$ dimensions (features), $|{\mathcal {S}}|=\{0,1\}$, and ${\mathcal {G}}=2$ “bins”, where ${\mathbf {X}}_t=(X_t^1,X_t^2)$ falls between [3, 7] (min/max $X_t^1$) and $[-3,-3]$ (min/max $X_t^2$); (b) A different dataset whose instances initialize the grid of a bigger cellular automaton with $d=2$ and ${\mathcal {G}}=10$

4 Proposed approach: CURIE

We delve into the ingredients of $\textit{CURIE}$ to act as drift detector. As shown in Fig. 3, its detection mechanism hinges on the evidence that a recent number of mutations in the neighborhood of a cell that has just mutated, may serve as an symptomatic indicator of the occurrence of a drift.

$\textit{CURIE}$ builds upon this intuition to efficiently identify drifts in data streams by fulfilling the following methodological steps (Algorithm 1 for the initialization of $\textit{CURIE}$, and Algorithm 2 for the drift detection and DSM process):

• First, in Algorithm 1 the CA inside $\textit{CURIE}$ is created by setting the value of its parameters (detailed as inputs), and following the characteristics of the given dataset (lines 1–5).

• A reduced number of preparatory instances of the data stream $[({\mathbf {X}}_t,y_t)]_{t=0}^{P-1}$) is used to initialize the grid of $\textit{CURIE}$. This grid is seeded with these instances, and then $\textit{CURIE}$ is evolved for several iterations (generations) by applying the local rule until all cells are assigned a state i.e. the labels of the preparatory instances (lines 6–10).

• When the preparatory process is finished, we must ensure that several preparatory data instances have not seeded the same cell, because each cell must reflect only one single state. To this end, we must assign to each cell the most frequent state by inspecting the labels of all those instances that fell within its boundaries. Then, we must ensure that all cells have an assigned state by applying the local rule iteratively all over the grid. Since this last process can again seed a cell with several instances, we have to address this issue to ensure that the cell only reflects one single state (lines 11–13).

• Next in Algorithm 2, $\textit{CURIE}$ starts predicting the data instances coming from the stream in a test-then-train fashion (Gama et al. 2014) (lines 2–16). This process consists of first predicting the label of the incoming instance, and next updating the limits of the cells in the grid should any feature value of the processed instance fall beyond the prevailing boundaries of the grid (lines 4–6). Secondly, the label of the incoming instance is used for training, i.e. for updating the state of the corresponding cell (line 7).

• In line 3 $\textit{CURIE}$ stores the incoming instance in a sliding window W of size P, which is assumed, as in the related literature, to be small enough not to compromise the computational efficiency of the overall approach.

• During the test-then-train process, $\textit{CURIE}$ checks if a mutation of the cell states has occurred (line 9). If the previous state of the cell (before the arrival of the incoming instance) is different from the label of the incoming instance, a mutation has happened. When there is a mutation, we assign the current time step to the cell in the grid of time steps (line 10). Then, $\textit{CURIE}$ checks the state of the neighboring cells in a radius $r_{mut}$ (of a von Neumann’s neighborhood) in a specific period of time (line 11). If the number of neighboring mutants exceeds a threshold (line 12), $\textit{CURIE}$ considers that a drift has occurred.

• After drift detection, it is time to adapt $\textit{CURIE}$ to the detected change in the stream distribution. To this end, we reset the grid, the vector of states, and the vector of time steps in which a mutation was present (lines 13–15). Finally, the preparatory process is carried out by seeding the grid with the instances stored in the sliding window W (line 16).

Fig. 3

The interpretable adaptation mechanism of $\textit{CURIE}$ ($d\times {\mathcal {G}}=2 \times 10$) based on the mutations of its neighborhood: (a) before the drift. $\textit{CURIE}$ updates the time instants of each mutant cell, i.e. when the previous state of the cell (before the arriving of the incoming instance) is different from the label of the incoming instance itself; (b) drift occurs. $\textit{CURIE}$ checks the neighborhood of each cell, and when at least 2 neighboring cells (defined by $n\_muts\_allowed$ parameter) have mutated in the last 10 time steps (as per the $mutation\_period$ parameter), $\textit{CURIE}$ considers that a drift has occurred. This is what is declared at $t=1043$ with the cell [2, 6] and its neighborhood of $r=2$ (Manhattan distance), where 2 of its neighbors have mutated at time steps 1037 and 1039. The number in each cell represents the last time that has mutated. The neighborhood of the cell [2, 6] is darkened, and this cell (highlighted in white) and its neighbors which have mutated ([1, 6], [1, 7]) have been enlarged

Finally, after detailing the ingredients of $\textit{CURIE}$ to act as drift detector, we would like to highlight two improvements over (Lobo et al. 2021) that positively impact on the learning of data distribution:

• If the predicted and the true label do not equal each other, the cell state in $\textit{CURIE}$ is always changed to the class of the incoming instance. Otherwise, if the age of the cell state ($T_{age}$) was considered, this could impact on drift detection resulting in more detection delay.

• In $\textit{CURIE}$ there is always one state assigned to each cell, thus it is not necessary to check the state of the closest cell among those with assigned state to provide a prediction. The cost of assigning one state to all cells of the grid is insubstantial; it is just carried out at the preparatory process and when drift is detected. And so we achieve a more simple method that does not need to check the surroundings (neighborhood) of the cell when no state is assigned.

The source code of $\textit{CURIE}$ is available at https://github.com/TxusLopez/CURIE.

5 Experimental setup

In order to assess the performance of $CURIE$, we have designed several experiments with synthetic datasets configured with both abrupt and gradual drift versions.

Since drift detectors usually base their detection mechanisms on the prediction results of a base learner, both detection and classification are often set to work together. As it has been already mentioned, $\textit{CURIE}$ does not use the prediction of the base learner. Instead, it estimates the occurrence of the drift by looking at the changes that occur in the neighborhood of cells deployed over a grid that represents the distribution of data. In our experiments we have accordingly combined three well-known base learners (HT, NB and KNN) with five popular drift detectors including our proposed detector (corr. DDM, EDDM, PH, ADWIN, and CURIE). They form 15 different learning-detection schemes following the algorithmic template shown in Algorithm 3. Such base learners and drift detection methods have been selected due to their wide use by the DSM community, and the availability of their implementations in the scikit-multiflow¹ framework. For more information, we refer the reader to Gonçalves Jr et al. (2014) and Barros and Santos (2018). Please note that the inclusion of KNN is not only based on its frequent use, and it has also been considered due to its similarities with CA. While KNN is not strictly local (the neighborhood is not fixed beforehand and the nearest neighbor of an instance may change), CA has a fixed neighborhood. In CA the local interaction between cells affects the evolution of each cell. We would also like to underline that the size of the sliding window of KNN (max_window_size parameter in Table 1) is the same than the number of recent instances that CA uses to be initialized and seeded after a drift is detected.

The computer used in the experiments is based on a x86 64 architecture with 8 processors Intel(R) Core(TM) i7 at 2.70GHz, and 32GB DDR4 memory running at 2, 133 MHz. The source code for the experiments is publicly available at this GitHub repository: https://github.com/TxusLopez/CURIE.

5.1 Datasets

In order to assess the performance of a drift detector by measuring the different detection metrics, we need to know beforehand where a real drift occurs. This is only possible with synthetic datasets. The scikit-multiflow framework, as one of the most commonly accepted libraries in stream learning, allows generating a wide variety of synthetic data in order to simulate a realistic occurrence of drifts. The researcher can configure the number of features, type of features (numerical or categorical), the number of samples, the noise impact, the number of classes, etc. to get the synthetic data closer to a real scenario.

Concretely, we have generated 20 diverse synthetic datasets (10 abrupt and 10 gradual) by using several stream generators (Sine, Random Tree, Mixed, Sea, and Stagger) and functions. They have a different number of features, noise, and a balanced binary class. They exhibit 4 concepts and 3 drifts at time steps 10, 000, 20, 000, and 30, 000 in the case of abrupt datasets, and at time steps 9, 500, 20, 000, and 30, 500 in the case of gradual ones. In the latter case, the width of the drift is 1, 000 time steps. All generated data streams have 40, 000 instances in total.

Table 1 Configuration of detectors and CURIE

Finally, as it is explained in Sect. 3.2, it is necessary to create “bins” by splitting each grid dimension by the values of the features. For Sine and RT datasets we have used 20 “bins” per dimension, while for the rest of datasets we have used 10 “bins’. The values have been found experimentally, just knowing that a small grid is not capable of representing the data distribution (e.g. the grid of Fig. 1). Here, we would like to warn other researches by underlining that CURIE exhibits at this moment a drawback that should be considered. Due to its exponential complexity, we recommend the use of CURIE in datasets with a low number of features. This setback can be tackled by carrying out the search over the grid’s cells by parallelizing this process.

The datasets are available at this Harvard Dataverse repository: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/5OWRGB. And a more detailed description can be found at: https://github.com/TxusLopez/CURIE/blob/master/README.md

5.2 Methods and parameters

As for $\textit{CURIE}$ we have assigned one grid dimension to each feature of the dataset at hand. We also note that we have used a reduced number of instances to warm up the learning-detection schemes, and also $\textit{CURIE}$ (see Algorithms 1 and 2, and 3). The number of instances for this purpose usually depends on the memory or processing time restrictions. In our experiments we have considered a very low number of them in order to simulate a very restrictive real-time environment (see parameter P in Table 1). In all of them, $\textit{CURIE}$ has been configured with a von Neumann’s neighborhood rather than opting for its Moore alternative. A von Neumann’s neighborhood is linear in the number of dimensions of the instance space, and therefore scales well for problems of high dimensionality. In addition, a Moore’s neighborhood includes more neighbors, thus we would have to potentially apply the local rule over more cells. This would make the process computationally heavier and less suited for a DSM setting in the preparatory process and after the drift occurs.

The parameters configuration for the drift detectors under consideration was experimentally fixed, and is detailed in Table 1. The number of preparatory instances (P) and the sliding window (W) of size P are shared between $\textit{CURIE}$ and the base learners. Concretely, their values are $P=50$ and $w=P$. The values for the base learners parameters have been found through a hyper-parameter tuning process (Grid Search with 10 folds in a Stratified K-Folds cross-validator using a balanced accuracy metric) carried out with these preparatory instances (see Table 2). For more information about the meaning of the parameters and their values, we refer the reader to https://scikit-multiflow.readthedocs.io/en/stable/api/api.html. And to know more about the Grid Search process we refer to https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html. Finally, Algorithm 3 presents the details of the learning and detection scheme followed by the experiments.

Table 2 Grid Search parameters of the base learners

5.3 Performance metrics

Regarding the classification accuracy, we have adopted the so-called prequential accuracy (pACC) (Dawid and Vovk 1999), which is widely applied in streaming classification scenarios. This metric evaluates the base learner performance by quantifying the average accuracy obtained by the prediction of each test instance before its learning in an online test-then-train fashion. This accuracy metric can be defined as:

$$\begin{aligned} pACC(t)=\left\{ \begin{array}{ll} pACC_{ex}(t)\text{, } \text{ if } t= t_{ref}\text{; } \text{ otherwise } \\ \\ preACC_{ex}(t-1) + \dfrac{pACC_{ex}(t)-pACC_{ex}(t-1)}{t - t_{ref} + 1}, \end{array}\right. \end{aligned}$$

where $pACC_{ex}(t)=0$ if the prediction of the test instance at time t before its learning is wrong, and 1 when it is correct. The reference time $t_{ref}$ fixes the first time step used in the estimation, and allows isolating the computation of the prequential accuracy before and after a drift has occurred.

To know about the resources used by stream learners, we have adopted the measure RAM-Hours proposed in Bifet et al. (2010), based on rental cost options of cloud computing services. Here, 1 RAM-Hour equals 1 GB of RAM dispensed per hour of processing (GB-Hour). In order to analyze the concept drift identifications we have used the Matthews correlation coefficient (MCC) as detection metric. MCC it is a correlation coefficient between the current and predicted instances. It returns values in the $[-1,1]$ range, and it is defined as:

$$\begin{aligned} MCC=\dfrac{((TP \cdot TN)-(FP \cdot FN))}{\sqrt{(TP+FP)\cdot (TP+FN)\cdot (TN+FP)\cdot (TN+FN)}}. \end{aligned}$$

As the high variance may appear in MCC and ${\upmu }D$ when $TP=0$ in several datasets due to a) the very different behavior of detectors in such a diverse experimentation, and b) the period enabled to make detections ($2\%$ and $10\%$ of the concept size for abrupt and for gradual datasets respectively) is quite restricted and provokes that $TP=0$ frequently. Thus, we have included the non-detection rate (ND) as a new indicator to be considered. Therefore, ND shows clearly the detection performance without masking the behavior of those detectors which show a competitive MCC but with a high variance. The lower the rate is, the better this detection performance will be. It is defined as:

$$\begin{aligned} ND=\dfrac{\text {The}\ \text {number}\ \text {of}\ \text {experiments}\ \text {with}\ \text {TP=0}}{\text {The}\ \text {total}\ \text {number}\ \text {of}\ \text {experiments}\ \text {(30)}}. \end{aligned}$$

We have also measured the distance of the drift detection to the real drift occurrence (${\upmu }D$). Finally, it is worth mentioning that the drifts detected within $2\%$ and $10\%$ [for abrupt and gradual drifts) of the concept size after the real drift positions were computed as TP (as in Barros and Santos (2018)], e.g. $TP>3$ is possible, otherwise they are FP.

5.4 Statistical tests

We have statistically compared the detectors in all datasets by carrying out the Friedman non-parametric statistical test as described in Demšar (2006). This test is the first step to know whether any of the detectors have a performance statistically different (in prequential accuracy, RAM-Hours, ${\upmu }D$, MCC, and ND) from the others. The null hypothesis states that all detectors are statistically equal, and in all cases was rejected. Then it is necessary to use a post-hoc test to discover in what detectors there is a statistical difference (in prequential accuracy, RAM-Hours, ${\upmu }D$, and MCC), and we used the Nemenyi post-hoc test (Nemenyi 1963) with $95\%$ confidence to compare all the detectors against all the others. The results are graphically presented showing the critical difference (CD) represented by bars and detectors connected by a bar are not statistically different.

6 Results and discussion

In this section we present the mean results for all datasets in Table 3, and the mean results for abrupt and gradual datasets in Tables 4 and 5 respectively. The original results are given in Online Resource 1 and 2, which correspond to the original results for the order functions F1 and F2 respectively, as it was introduced in Sect. 5.1. At the beginning of these resources, a complete table compiles the results of the experiments. Each detector is hybridized with the base learners and tested over 20 datasets (10 in Online Resource 1 and 10 in Online Resource 2). The whole set of metrics is presented: prequential accuracy (pACC), $RAM-Hours$, true positives (TP), false positives (FP), true negatives (TN), false negatives (FN), distance to the drift (${\upmu }D$), precision, recall, MCC, and non-detection rate (ND). The ranking of pACC, $RAM-Hours$, ${\upmu }D$, MCC, and ND is provided for every experiment. At the end of the resources, 6 summarizing tables are shown. On the left, the “F global rank” shows the mean rank of detectors, while “F global results” shows the mean and standard deviation of the metrics. On the right, these tables (“F abrupt rank”, “F gradual rank”, “F abrupt results”, and “F gradual results”) detail the mean ranks and metrics for abrupt and gradual datasets. Finally, the Online Resource 3 correspond to Tables 3, 4, and 5. Online Resources 1, 2, and 3 can be found as $O\_R\_1.xlsx$, $O\_R\_2.xlsx$ and $O\_R\_3.xlsx$ respectively at https://github.com/TxusLopez/CURIE.

Table 3 Mean results and mean ranks of the detectors in each metric for all considered datasets

Table 4 Mean results and mean ranks of the detectors in each metric for abrupt datasets

Table 5 Mean results and mean ranks of the detectors in each metric for gradual datasets

In Table 3 we observe that CURIE achieves the second best pACC metric with $0.828\pm 0.08$, being ADWIN the best. However, CURIE is the worst in terms of $RAM-Hours$ with $9.55\cdot 10^{-4}\pm 12\cdot 10^{-4}$. Here, in favor of CURIE, it is worth mentioning that it is competing with well-established detectors whose code has been optimized and tested by the community in the scikit-multiflow framework. Probably, future versions of CURIE will be more competitive in terms of this metric. Regarding detection metrics, CURIE is the best with $303.45\pm 78.06$ for ${\upmu }D$, $0.37\pm 0.23$ for MCC, and 0.20 for ND.

Deepening the types of drifts, we see in Tables 4 and 5 how CURIE shows the best pACC metric (together with ADWIN) with $0.841\pm 0.09$, and the second best with $0.814\pm 0.07$ (with DDM immediately after) for abrupt and gradual datasets respectively. In terms of $RAM-Hours$ metric, CURIE exhibits the worst result for abrupt datasets and the second worst for gradual ones. However, CURIE is the best in ${\upmu }D$, MCC, and ND, with $118.90\pm 73.80$, $0.17\pm 0.15$, and 0.40 for abrupt datasets. In case of gradual datasets, CURIE is again the best in ${\upmu }D$ with $488.00\pm 82.32$, the second best in MCC (very close to ADWIN) with $0.57\pm 0.31$, and the best in ND with 0.00. Both for abrupt and gradual drifts, CURIE shows a very competitive behavior in pACC, and leads the ranking in ${\upmu }D$, MCC, and ND; although in $RAM-Hours$ has a poor performance.

We would like to devote particular attention to the results of the ND metric. As it has been already mentioned in Sect. 5.3, ND indicates how effective the detector is. Here, we see that CURIE achieves true detections ($TP>0$) in the majority of abrupt datasets ($ND=0.40$), while makes true detections in all gradual datasets ($ND=0.00$).

According to the mean ranks for all datasets of Fig. 4, ADWIN, CURIE and DDM are the best detectors in terms of pACC, yet no statistical differences between them. Regarding the $RAM-Hours$ metric, CURIE and DDM are the worst detectors, with no statistical differences between them. However, in what refers to ${\upmu }D$ and MCC, CURIE, ADWIN, and EDDM are the best detectors, yet again no statistical differences between them. We find the same results in the mean ranks for abrupt and gradual datasets depicted in Figs. 5 and 6 respectively.

Fig. 4

Comparison of mean ranks for all datasets in (a) pACC, (b) RAM-Hours, (c) ${\upmu }{D}$, (d) MCC, and (e) ND, using the Nemenyi test based on the results of Table 3 with a $95\%$ confidence interval. CD is 1.363887 for 5 detectors and 20 datasets

Fig. 5

Comparison of mean ranks for abrupt datasets in (a) pACC, (b) RAM-Hours, (c) ${\upmu }{D}$, (d) MCC, and (e) ND, using the Nemenyi test based on the results of Table 4 with a $95\%$ confidence interval. CD is 1.363887 for 5 detectors and 20 datasets

Fig. 6

Comparison of mean ranks for gradual datasets in (a) pACC, (b) RAM-Hours, (c) ${\upmu }{D}$, (d) MCC, and (e) ND, using the Nemenyi test based on the results of Table 5 with a $95\%$ confidence interval. CD is 1.363887 for 5 detectors and 20 datasets

The conditions of the Nemeneyi test have been very tight ($95\%$ confidence for 5 detectors in 20 datasets) and it is difficult to achieve statistical differences. Even so, CURIE has shown to be an interpretable drift detector competitive in terms of predictive performance (pACC) and detection metrics (${\upmu }D$, MCC, and ND), without depending on the output (class prediction) of the base learner. Moreover, CURIE provides competitive metrics for abrupt and gradual drifts, being this issue very controversial in the drift detection field, as it was shown in Gonçalves Jr et al. (2014).

Finally, we would like to discuss on the suitability of CA for high-dimensional datasets. When applying CA for streaming scenarios, we have to consider that since the number of cells is proportional to the number of dimensions, as many features in the dataset are, and as many cells per feature, as much computational cost and more processing time will be required. Concretely, in a problem with d dimensions, and with a size of the grid given by G, the worst-case complexity of predicting the class of a given test instance ${\mathbf {X}}_t$ will be ${\mathcal {O}}(G^d)$. This is the time required by a single processing thread to explore all cells of the d-dimensional grid and find the cell for the instance ${\mathbf {X}}_t$. Because of this exponential complexity, we recommend the use of CA for datasets with a low dimensionality. However, when the scenario imposes such conditions, the search process over the cells of the grid could be parallelized, allowing for faster prediction and cell updating processes.

7 Conclusion and outlook

This work has presented $\textit{CURIE}$, a competitive and interpretable drift detector based on cellular automata. Until now, cellular automata have shown to be suitable solutions for data mining tasks due to their simplicity to model complex systems, being robust to noise and a low-bias method. Besides, they are computationally complete with parallelism capacity, and they already showed competitive classification performances as data mining methods.

This time, we have focused on their capacity to detect concept drift. They have revealed themselves as suitable detectors that achieve competitive detection metrics. They have also allowed base learners to exhibit competitive classification accuracies in a diversity of datasets subject to abrupt and gradual concept drifts. They are suitable candidates to represent data distributions with a few instances, being this ability welcomed in data stream mining tasks where memory and computational resources are often severely constrained. Moreover, $\textit{CURIE}$ can act as an all-in-one approach, in contrast to many other drift detectors which are based on a combination of a base learner method with a detection mechanism.

As future work, we aim to extend the experimental benchmark to more synthetic and real datasets in order to extrapolate the findings and conclusions of this study to different types of drift and more realistic applications. Applying ensemble approaches or even networks of cellular automata are also among our subjects of further study. We also encourage other researchers to improve the performance of CA in high-dimensional datasets. Finally, we would like to underline the relevance of carrying out experiments on parallelized algorithms; they probably will show the way to overcome the high-dimensionality drawback.