Introducing time series snippets: a new primitive for summarizing long time series

Abstract

The first question a data analyst asks when confronting a new dataset is often, “Show me some representative/typical data.” Answering this question is simple in many domains, with random samples or aggregate statistics of some kind. Surprisingly, it is difficult for large time series datasets. The major difficulty is not time or space complexity, but defining what it means to be representative data for this data type. In this work, we show that the obvious candidate definitions: motifs, shapelets, cluster centers, random samples etc., are all poor choices. We introduce time series snippets, a novel representation of typical time series subsequences. Informally, time series snippets can be seen as the answer to the following question. If a user, which could be a human or a higher-level algorithm, only has resources (including human time) to inspect k subsequences of a long time series, which k subsequences should be chosen? Beyond their utility for visualizing and summarizing massive time series collections, we show that time series snippets have utility for high-level comparison of large time series collections.

1 Introduction

In many domains, a common analytical query is, “Show me some representative/typical data.” This query might be issued by a human, attempting to explore a massive archive, or it might be issued by an algorithm as a subroutine in some higher-level analytics. There are definitions and algorithms to answer this question for a plethora of datatypes, including images (Wang et al. 2012), sets (Pan et al. 2005), words (Salmenkivi 2006), graphs (Langohr and Toivonen 2012), videos (Elhamifar et al. 2012), tweets (Rosa et al. 2011), etc.

Surprisingly, to the best of our knowledge, the problems of finding representative time series subsequences have not been solved despite the ubiquity of time series in almost all human endeavors. Moreover, as we will show, the obvious candidates for this task: motifs, shapelets, cluster centers, and random samples, will not generally produce meaningful results. We propose an algorithm to discover such representative patterns, which we will call time series snippets, or just snippets, where there is no ambiguity.

We would like snippets to have the following properties:

• Scalable computability We wish to find snippets in datasets that defy rapid human inspection. Such datasets will be large. While we can often offload snippet discovery to offline batch preprocessing, we clearly cannot afford an algorithm that requires a large time or space overhead.

• Diversity The top-1 snippet should be the single most representative pattern. Clearly, the 2nd and subsequent snippets should not be redundant with previous snippets, and so on for the kth snippet.

• Diminishing returns As an implication of diversity, the earlier k-snippets have the greatest coverage, just as the dimensions in Multidimensional scaling are sorted by their rapidly diminishing ability to “explain” the variability of the original data.

• Quantifiability Suppose the top-1 snippet for a sleep study shows some typical healthy heartbeats. It may be that all the data looks like that, and if a clinician sees that snippet, they have effectively seen all the data. However, it may be that there were also regions of arrhythmias. Thus, we need some metadata to tell us how much of the data each snippet can explain/represent. A human or algorithm can use this metadata to decide how many snippets they need to see for the task at hand.

• Domain agnosticism For specialized domains it may be possible to leverage domain knowledge and/or training data to achieve all of the above; however, we wish to have a general-purpose algorithm to support data exploration.

• Coverage (allowing longer lengths) While the length of snippets is a user-defined parameter, we would like snippets to work well for longer lengths. For example, for many human aggregate activities (automobile traffic, web query volumes, transportation, electrical demand etc.), it is easy to find snippets that reflect a 24-h circadian cycle. However, there may be conserved structure at much longer lengths, of weeks, months or even years. We would like to be able to be able to represent such structure, if it exists.

In this work we introduce an algorithm, Snippet-Finder, which can discover snippets with all such properties. Figure 1 shows one potential use of snippets: integrating summarizations of files directly into an operating system.

Fig. 1

One use of time series snippets is to replace standard file icons with icons that show snippets reflecting the file’s content. This can allow an analyst to spot patterns and anomalies at a glance (Kolhoff et al.2008). This is real data; see Sect. 4.4 for more context for this example

Another potential use of snippets is in the production of automatically generated reports. For example, one could compactly summarize a sleep study (Alvarez-Estevez and Moret-Bonillo 2015) with a report like this:

Beyond the algorithm’s utility for visualization and summarization (Yu et al. 2007), snippets can be used to support a host of higher-level tasks, including the comparison of massive data collections.

The rest of this paper is organized as follows. In Sect. 2, we briefly review related work and background material, and then formally define time series snippets. We introduce an algorithm to compute time series snippets in Sect. 3. Section 4 shows the utility of time series snippet discovery. In Sect. 5, we show how we can find snippets in the face of continuously arriving data streams. Finally, in Sect. 6 we offer conclusions and directions for future work.

2 Background and related work

2.1 Dismissing apparent solutions

As noted above, the task at hand appears to invite many apparent solutions. Here we take the time to dismiss them.

Motif discovery At first glance, motif discovery seems like an obvious solution to our problem (Zhu et al. 2016; Yeh et al. 2016; Imani and Keogh 2019, 2020; Alaee et al. 2020; Imani et al. 2019; Abdoli et al. 2018). Consider Fig. 2, and imagine that we are tasked with finding the time series snippet of length 300, which we denote as snippet₃₀₀.

Fig. 2

A synthetic dataset. There are three repeated patterns embedded in a random walk; the best snippet₃₀₀ appears obvious to the naked eye

Surprisingly, even in the face of such an apparently simple dataset, motif discovery will not produce a satisfactory answer. Consider the clustering shown in Fig. 3.

Fig. 3

(Bottom) The dataset shown in Fig. 2 annotated by the subjectively correct answer. (Top) The dataset divided into seven equal length regions, and clustered using complete linkage hierarchical clustering

The three periodic elements are no more similar to each other under Euclidean distance than they are to random walks. One might imagine that the solution to this issue is to use a different distance measure, say Dynamic Time Warping (DTW). However, while DTW can be invariant to warping, and thus find A and C similar, it cannot warp eight periods to ten periods. Two periods must be “unexplained” and accumulate a large error. Thus, B is still no closer to A or C than it is to random walks under DTW.

There are additional reasons why motif discovery is not suitable to the task at hand. Consider the dataset shown in Fig. 4.top. At this scale, it is difficult to even guess its content. It is exactly the type of data that could benefit from snippet-based summarization. This dataset represents 55 min of Arterial Blood Pressure (ABP) collected during an experiment in which a volunteer strapped to a gimbal was subjected to sudden changes in orientation (Heldt et al. 2003). However, as Fig. 4.bottom shows, this dataset has an occasional sensor fault. When the sensor is not receiving true medical data, it instead sends a square wave calibration signal.

Fig. 4

(Top) Fifty-five minutes of APB data, taken from an individual experiencing occasional involuntary rapid changes in orientation (Papadimitriou and Yu 2006). (Bottom) A minute-long zoom-in starting at about the twelfth minute

If we defined snippets based on time series motifs, then the five identical regions corresponding to the sensor fault as shown in Fig. 4 would be the top snippet, even though such data only represents 0.14% of the dataset. However, there are snippets that are clearly much more representative of the data. For example, as the highlighted regions in Fig. 4.bottom suggest, normal ABP makes up the majority of this dataset, while a significant minority comprises of an ABP with an increased heartrate, induced by a change in gravity (Linnarsson et al. 1996).

The issue can be summarized as the following: while motifs reward fidelity of conservation, we need a measure that also rewards coverage. Informally, coverage is some measure of how much of the data is explained or represented by a given snippet. We will formalize this tradeoff between fidelity and coverage below.

Representative trends By title, the highly cited research effort on “Identifying Representative Trends in Massive Time Series Data Sets…” (Indyk et al. 2000), seems like it may offer a solution, or at least insight on the task at hand. However, the authors of this work are assuming that the time series has well-defined periods; for example, exactly 24 h, and a well-defined starting point, say midnight. However, choosing another starting point, such as 1:00 am, could produce arbitrarily different results. Moreover, while the assumption of well-defined periods might hold for traffic (both in the web and the automobile sense) and other quotidian human activities, it does not hold for most of the medical and scientific domains we are interested in. For example, the periodicity of heartbeats can vary by at least a factor of five, in just a few minutes. At a higher level, cardiac events clearly do not align themselves to midnight, 8:00 am, or any other arbitrary time frame.¹

Clustering In many cases, summarizing a dataset into the K best exemplars is as simple as running K-means clustering and reporting the K centers (or the K exemplars closest to the centers). However, it is well understood that one cannot meaningfully cluster time series subsequences, with any distance measure, or with any algorithm (Keogh and Lin 2005). This (at the time) surprising result was controversial a decade ago, but has since become universally accepted (see (Keogh and Lin 2005) and the references therein); we will avoid repeating the arguments here. In Sect. 4, we make a best faith effort to fix this issue, and compare to a K-means based algorithm.

Time series shapelets Time series shapelets are defined as subsequences that are maximally representative of a class (Yeh et al. 2016). This sounds superficially like time series snippets, however shapelets are supervised, and we require an unsupervised technique. Moreover, shapelets are generally biased to be as short as possible. In contrast, we want snippets to be longer, to intuitively capture the “flavor” of the time series. By analogy with text, to distinguish between English and Lithuanian chapters of J. K. Rowling’s famous septology, it is sufficient to see the letter “Č”, the equivalent of a shapelet. However, to summarize the latter with representative text, it would be much more informative to see something like “Haris Poteris”, the equivalent of a snippet.

Random sampling Simple random sampling (SRS) has many desirable properties that makes it useful and competitive in many domains. There are clearly cases in which it would be sufficient. For example, if a time series dataset consists solely of normal regular heartbeats, then any random two-beat region we extract would summarize the data (two beats because cardiologists are used to visualizing beats from a fixed starting point, and two beats will clearly include that point). However, as we shall see, even cardiological datasets can have surprising variability, and random sampling would have to be very lucky to hit one each of, say, three diverse regions. Nevertheless, we will include random sampling as a baseline in our experimental section.

2.2 Related work

Our review of related work is brief. To the best of our knowledge, there are simply no ideas closely related to domain agnostic representative pattern discovery in the time series domain, beyond our short paper on the topic (Imani et al. 2018), which is expanded here.

Recent work has demonstrated how to exploit representative electrocardiogram heartbeat morphologies based on the CUR matrix decomposition technique (Hendryx et al. 2018). Given a matrix A, CUR technique selects a subset of rows and columns of A to construct matrices C and R. Matrix U is computed in a way that makes the multiplication of C, U, and R the best approximation of A. However, this study is specific to a particular type of data and requires substantial human effort to align data.

There is a significant work on the automated extraction of music snippets (also called music thumbnails) (Lu and Zhang 2003). However, that literature addresses a specialized and limited form of time series data. Most songs are richly structured into some variant of intro, verse, chorus, bridge, and outro. Moreover, most songs are only a few minutes in length, or a few thousand time series data points in an MFCC representation. In contrast, we wish to consider unstructured datasets with tens of millions of data points.

2.3 Time series notation

Before we formally define time series snippets, we need to review some related definitions (Definitions 1 to 3) and create some new ones (Definitions 4 to 6).

The data type of interest is time series:

Definition 1

A time series T is a sequence of real-valued numbers t_i: T = t₁, t₂,…, t_n where n is the length of T.

A local region of time series is called a subsequence:

Definition 2

A subsequence T_i,m of a time series T is a continuous subset of the values from T of length m starting from position i. Formally, T_i,m= t_i, t_i+1,…, t_i+m−1, where 1 ≤ i ≤ n − m + 1.

If we “slide” a window of length m across T we produce n − m + 1 subsequences. However, we can also produce a set of non-overlapping subsequences:

Definition 3

Anon-overlapping subsequence S_i of a time series T is a continuous subset of the values from T of length m, starting from the position $\left( {i - 1} \right) \times m + 1$ and ending at the position $i \times m$, in which the value of i is an integer number chosen from $i = 1:n/m$. When $n/m$ is not an integer number, zeros are padded to the end of the time series until $n/m$ becomes an integer number.

Note that the number of non-overlapping subsequences is much smaller than the sliding windows, just ${ \lceil }n/m{ \rceil }$. For virtually any task, if working with Euclidean distance, you must use sliding windows. Otherwise, the higher-level algorithm would be brutally sensitive to the starting point (Keogh and Lin 2005). In contrast, as we will show in Sect. 3, using the much smaller set of non-overlapping subsequences is inconsequential if we use the MPdist, which we review in the next section.

We can now define time series snippets:

Definition 4

A time series snippet is a subsequence of T. Snippets are arranged in an ordered list C, with the ith snippet denoted as C_i.

We can access some useful metadata from the snippet, such as its location within T, and the fraction of T that it is said to represent, by C_i.index and C_i.frac respectively.

Note that our definition means that the snippets are actual subsequences of T. This need not have been the case. For example, consider the related problem of finding representative strings. The most common solution, variants of consensus strings (Schneider 2002), can produce a string that is optimal under some definition, but never actually appears in the data. This issue is somewhat like the question of how one reports a single exemplar from one of the clusters produced by K-means. We can report the cluster center, which is optimal in the sense that it minimizes the objective function, but in some cases that can lead to unintuitive results. For example, the cluster center of all Starbucks in South Africa might well be in a different country (Lesotho). For that reason, it makes more sense to report the item closest to the cluster center instead. Similarly, by insisting that the snippet is a real sequence that comes from the data, we can make claims such as, “The second week of July is the most typical summer month, in terms of electrical consumption, in Northern Italy.”

2.4 A brief review of MPdist

MPdist is a recently introduced distance measure that considers two time series to be similar if they share many similar subsequences, regardless of the order of matching subsequences (Gharghabi et al. 2018). It was demonstrated in (Gharghabi et al. 2018) that MPdist is robust to spikes, warping, linear trends, dropouts, wandering baseline and missing values, issues that are common in many real word datasets. For example, see Fig. 15 which shows a transportation dataset which has both a spike and missing data. The MPdist requires a single parameter called a subsequence length, $S$. We denote the value of this parameter with a subscript, as in MPdist₅₀. In the limit, when $S$ is equal to the full length of the query, the MPdist degenerates to the special case of the classic Euclidean distance.

Basically, author computes a matrix profile ($P_{AB}$) array in which the Euclidean distance between each pair in AB similarity join set is stored. The time complexity to compute $P_{AB}$ is $O\left( {\left( {n - S + 1} \right) \times n} \right)$, where $S$ the subsequence length. As $S$ approaches $n$, the time complexity approaches linear time, which in that case the $P_{AB}$ is the Euclidean distance between two time series. Note, the time complexity of MPdist in the worst case is ${\text{O}}\left( {n^{2} } \right)$.

Consider the small toy example of a time series shown in Fig. 5, which we will use as a running example.

Fig. 5

A toy time series. The highlighted section, from 201 to 400, will be used in subsequent examples

We can use the MPdist to create an MPdist-profile:

Definition 5

An MPdist-profile of time series T is a vector of the MPdist distances between a given query subsequence T_i,m, at position i, and each subsequence in time series T. Formally, MPD_i = [d_i,1, d_i,2,…, d_i,n−m+1], where d_i,j (1 ≤ i, j ≤ n − m + 1) is the distance between T_i,m and T_j,m, where j corresponds to any position in the time series 1 ≤ j ≤ n − m + 1.

When there is no ambiguity, we will refer to MPdist-profiles simply as profiles. Consider the profile for the time series shown in Fig. 5, using the highlighted region as the query. The subsequence length of this query is L = 200. The result is shown in Fig. 6. Notice that the length of the profile is shorter than the length of the time series by the length of query. Furthermore, note that the distance is exactly zero in the region from which the query was extracted, since the MPdist between an object and itself must be zero.

Fig. 6

The profile of the query highlighted in Fig. 5 using MPdist₇₀

As we shall show in the next section, our snippet discovery algorithm essentially reduces to “reasoning” about these profiles.

Our desired properties of diversity and diminishing returns suggest that we frame snippet discovery in a familiar “top-k” framework, much like k-itemsets or k-frequent items, etc. However, there is a caveat. It may be that there are as few as one snippet in a dataset, such as when the time series is comprised solely of a pure sine wave. Therefore, we will also need to provide some metadata for each snippet to quantify how well it represents the data.

3 Discovering time series snippets

We begin with a demonstration that both previews our method for discovering time series snippets and shows why the MPdist is critically needed for this task.

Consider again our running example time series shown in Fig. 7: this time series is annotated with two subsequences, which the reader will appreciate might serve as good snippets for this dataset.

Fig. 7

A toy time series that will be used as a running example. The two highlighted sections, from 201 to 400 and from 1201 to 1400, will be used in subsequent examples

Let us extract the two highlighted subsequences and then compute their profiles. The results are shown in Fig. 8.

Fig. 8

The profiles of the two queries highlighted in Fig. 7. Note their mutually exclusive nature, when one is high, the other is low

Note that these profiles offer strong clues to the locations of potential time series snippets. They are both approximately “step” functions with their respective low region corresponding to a region that contains subsequences that are similar to our two query patterns.

Furthermore, note that these profiles are “mutually exclusive”; that is to say, when the red one is low, the cyan one is high, and vice versa. This suggests that these two hand-chosen snippets would meet the diversity requirement listed in the introduction, as they both “explain” different and non-overlapping regions of the data.

Note that the shapes of these two profiles are very robust to both location, from which we extract the pattern, and to the query pattern’s length. To see this, in Fig. 9 we recomputed the profiles for both a shifted and a longer version of our query.

Fig. 9

The profiles of after: shifting the queries 50 points to the right and making the queries longer (extracted from 201 to 500, and from 1201 to 1500 respectively)

This result offers hope for an algorithm that is not too sensitive to the location or length of the candidate snippets. To see why this is a significant finding, Fig. 10 shows what happens if we computed these profiles with the Euclidean distance instead.

Fig. 10

The Euclidean Distance Profiles of after: shifting the queries 50 points to the right and making the queries longer (extracted from 201 to 500, and from 1201 to 1500 respectively). Contrast with Fig. 9

In contrast to the MPdist-Profile, the Euclidean distance Profiles are more sensitive to the length and offset of the subsequence. More importantly, they only have a low value when the matching pattern is exactly in phase. Thus, in contrast to the MPdist-Profile, it is difficult to “reason” about them, to understand how large a region they could represent as a prototype.

3.1 Snippet-finder: time series snippet discovery

We are finally in a position to explain our Snippet-Finder algorithm. Given a time series, a subsequence length, and the maximum number of snippets that the user wishes to find, the Snippet-Finder algorithm is to identify k snippets, and the fraction of data that each snippet covers. Note that the fraction of data covered by a single snippet is not necessarily contiguous. For example, an accelerometer dataset may consist of bouts of “walk-run-walk-cycle-walk”; a snippet of walking would represent all three regions of the slower gait.

We begin with the following intuition. Recall that Fig. 7 showed a time series with two subsequences highlighted. Those subsequences would clearly make intuitive snippets for that dataset. Recall also that Fig. 8 showed two profiles that offer strong clues that these subsequences would be excellent top-2 snippets. Together, their respective low-value regions cover almost the entire length of the time series, swapping over at about location 950.

In contrast, suppose instead that we had made a poor choice of two snippets for this dataset. As shown in Fig. 11, if we selected both snippets from the first half of the data, they would be highly redundant with each other, and this would be reflected in the high correlation of their profiles.

Fig. 11

(contrast with Figs. 7 and 8). (Top) Revisiting our running example, we extracted two similar snippets (highlighted). (Bottom) The redundancy of the snippets is revealed in the high correlation of the profiles

This observation immediately suggests an objective function that we can use to score choices of top-k snippets. Consider a non-empty set of profiles. Create a new curve, M, by taking the minimum value from all k profiles at each location. This new curve allows an objective function:

Definition 6

The area under the curve M is denoted as O, and is an objective function where 0 ≤ O. We will refer to the area under the curve of profile as the ProfileArea.

This function rewards a snippet’s fidelity and coverage exactly as required. Fidelity is rewarded by the snippet having a small distance to at least some of the T, lowering the profile and reducing the area under the curve in the corresponding region. Coverage is rewarded by the snippet representing large regions of T. Note that O has the intuitive property wherein if we used every non-overlapping subsequence as a snippet, its value would be exactly zero. Of course, we hope that in most cases, using just a few snippets will get us close to zero, achieving significant “compression” or more correctly, numerosity reduction.

In the simple example shown in Fig. 7, we found a low scoring value for O simply by using common sense to pick one snippet from each of the repeated patterns. More generally, if we had computed all of the non-overlapping profiles, we would have the “tangle” of profiles shown in Fig. 12.

Fig. 12

All the non-overlapping profiles for the time series shown in Fig. 7

For a more realistic dataset, finding the k profiles that minimize O from the P-choose-k possibilities $\left( {\begin{array}{*{20}c} P \\ k \\ \end{array} } \right)$ would be untenable. Here k is the user defined parameter for the number of snippets and P is the total number of snippets. This problem is related to the maximum coverage problem (Khuller et al. 1999). The classic maximum p-coverage problem is a well-known NP-hard problem in which, given a universal set of finite elements, the goal is to select p subsets such that their union covers the maximum set. In the snippet problem, we have N profiles and we want to select k of these profiles so that the total area under the cover of k profile has the minimum area. Thus, we frame the snippet discovery problem as a classic search problem. An exhaustive combinatorial search is infeasible, so below we outline a greedy search strategy.

The main algorithm for Snippet-Finder is outlined in Table 1, and its subroutine that computes profiles of each non-overlapping window is outlined in Table 2.

Table 1 Snippet-Finder: Snippets Selection Algorithm

Table 2 Calculating distance profiles

The main algorithm begins in line 1 by initializing the list of snippets C. In line 2, we calculate the profile of each non-overlapping window with the time series (see Table 2). At each iteration we calculate the minimum of each profile with the profiles within the snippet list C, and for each one, we find the area under the curve ProfileArea. For $k = 1$, the ProfileArea is simply equal to the area under the curve of each profile. The profile that has the minimum ProfileArea will be added to the snippet list C. We also add the location of each snippet within T. This is done in lines 4 to 15. We evaluate the terminal condition when we reach the number of snippets the user requested in line 16 to 18. After finding the top-k snippets, in line 20 we compute the minimum value from all k profiles totalmin. In line 21 to 24, we compare the top-k snippet profiles with totalmin. The number of points in which these two curves have the same value, f, gives us the fraction of data each snippet represents C_i.frac. Finally, when the algorithm terminates, the list of snippets C, the fraction of data that the ith snippet represents, the data C_i.frac and the location of the snippet within the time series C_i,index is returned.

To calculate the profile of each non-overlapping window, we use the subroutine outlined in Table 2.

The algorithm begins in line 1 by determining the length of the time series T, and initializes D to the empty list. From lines 2 to 4, we calculate all the profiles D, using each non-overlapping subsequence T [(i − 1) × m + 1:i × m] and the time series T. Finally, we return the result D in line 5.

3.2 Snippet MetaData

In addition to computing the snippets themselves, it is useful to compute some metadata that reflects how well the current snippet set is representing the dataset in question. More generally, metadata here is useful in the same way that metadata is useful in say factor analysis/principle component analysis. In that case, a user might say “keep enough factors to explain 90% of the variance”. For snippets, a user might say “keep enough snippets to explain 90% of the data”. In this sense we have a close analog to how K-means clustering is used. In some cases, say quantizing a color space, the number of clusters requested of K-means may be fixed in advance, regardless of the data itself. This is similar to our use of snippets for creating icon “thumbnails,” as shown in Fig. 1. Because the operating system limits us to 256 by 256 pixels, we hardcoded the number of snippets displayed to k = 2.

However, in other cases, we want the K-means clustering to reflect the “natural” clusters in the data. While the task of deciding what value of k best does that is outsourced to an external algorithm, K-means provides helpful information by reporting the objective function (sum of squares), a relative measure of how well the clustering reflects the data. We would like an analogous objective function for snippets.

We propose using the area under the curve ProfileArea as such a measure. As Fig. 13.left shows, for increasing values of k, this measure shows a classic diminishing returns behavior.

Fig. 13

(Left) The area under the curve ProfileArea for k = 1 to 9, for the running example shown in Fig. 7. (Right) For the same example we can also compute change_k for k = 1 to 9

This “scree-plot”-like curve suggests a heuristic that can be used to recommend a value for k. Similar to many suggested knee-finding algorithms in the literature, for each value of k we can compute change_k = (ProfileArea_k−1/ProfileArea _k) − 1. For a given value of k > 1, a small value for change_k suggests that adding the kth did not add much explanatory power; thus, we should use a value of k corresponding to a peak. As shown in Fig. 13.right, this heuristic suggests a value of k = 2 for our toy example, which is objectively correct. Unless otherwise stated, we use this simple heuristic in the rest of this work.

3.3 Complexity analysis

For the time series that has a length of $n$ and the subsequence length of $m$, the time complexity of our proposed Snippet-Finder is ${\text{O}}\left( {n^{2} \times \left( {n - m} \right)/m} \right)$. We need ${\text{O}}\left( {n^{2} } \right)$ for computing each profile, and the number of non-overlapping windows is ${\text{O}}\left( {\left( {n - m} \right)/m} \right)$. The pseudocode is optimized for simplicity, with an ${\text{O}}\left( {\left( {n - m} \right)^{2} /m} \right)$ space complexity. However, the space complexity in a slightly more sophisticated implementation is merely ${\text{O}}\left( {\left( {n - m} \right) \times k} \right).$ In addition, the ProfileArea curves only need to be represented with one-byte precision.

To concretely ground this analysis, consider the following. For typical datasets recorded at ~ 100 Hz (gait, ECG, insect telemetry, etc.), we can discover snippets many orders of magnitude faster than the data is actually collected. Moreover, even very large data collections can be processed using a small fraction of the main memory of a modern machine. Thus, computational resource limitations are not barriers to adoption.

3.4 Algorithms that exploit snippets

Up to this point we have presented snippets as tools to optimize the scarce resource of human time and attention. However, here we argue that snippets can be a useful primitive to provide information to be consumed by higher level algorithms. In a sense, this is almost tautological, given our argument that snippets are the best representatives of a data source. Below, we provide one such usage of snippets in clustering algorithm.

The city of Melbourne, Australia has developed an automated pedestrian counting system to better understand pedestrian activity within the municipality. The information can be used to examine how people use different city locations at different times of day to better inform decision-making and plan for future changes to transportation infrastructure.

From this archive we extracted data from eight different locations. In each case we extracted the pedestrian count for the entire year of 2017. To allow for some ground truth, we chose the data in two groupings that we felt might reflect similar behavior. The first four locations are geographically clustered in the Greek Precinct in Melbourne, Australia. The second set are locations that are relatively spread out but are all close to transportation hubs, and thus may be expected to have data that reflects some alignment to travel schedules. Figure 15.top shows one of the time series in its entirety and Fig. 15.bottom shows some examples of a zoomed in week of data.

It is clear that clustering using all the data might be problematic. The time series shown in Fig. 15.top has about 18 days of missing data around late August and a spike in July 29, which may confuse Euclidean distance, which attempts to “explain” all the data. We propose to address this by using a distance measure that considers only snippets, which we expect to ignore such spikes and missing data, since by definition they are not typical. There is one consideration we need to address in any snippet-based distance measurement: we should not naively compare snippet-1_WebbBridge to snippet-1_StateLibrary and compare snippet-2_WebbBridge to snippet-2_StateLibrary etc. To see this, consider the following analogy in the text space. Suppose we have the following two strings:

• A = sumsumsumsumsumsumwinwinwinwinwin

• B = sumsumsumsumsumwinwinwinwinwinwin

If we extracted “snippets” of length three from these strings, we would have snippet-1_A = ‘sum, snippet-2_A = ‘win, and we would have snippet-1_B = ‘win, snippet-2_B = ‘sum. Given that, if we naively defined the distance as the sum of distances between corresponding “snippets”, for 1 to k, then we would have OverallDist = dist(‘sum, ‘win) + dist(‘win, ‘sum). This means we would fail to find any similarity between the two strings, even though they are clearly highly related.

We should expect this issue in real time series data. For example, Fig. 26 shows the top-2 snippets taken from an electrical power demand dataset, which nicely correspond to winter/summer regimes. Suppose that we wish to compare two nearby cities based on such snippets. The top-1 snippet in one city might happen to correspond to winter months, which just beat out the slightly shorter summer months. However, in the adjacent city, the top-1 snippet in one city happens to correspond to summer months, which just beat out the slightly shorter winter month regime. It would be clearly wrong to compare snippets from different seasons. Fortunately, there is an easy fix. In essence, we compare each snippet to all other snippets from the other time series, and record only the minimum value, as in min[dist(‘sum, ‘win), dist(‘sum, ‘sum)].

Concretely, from each time series Tⁱ we extract two snippets, which we refer to as $s_{1}^{i} ,s_{2}^{i}$ where $i$ specifies the time series geographic location. (e.g. $T^{i}$ when $i$ = 1 is the time series for “State Library” location).

We define Snippet distance between two time series $T^{i}$ and $T^{j}$ as:

$$ Distance\left( {T^{i} ,T^{j} } \right) = min\left( {d\left( {s_{1}^{i} ,s_{1}^{j} } \right),d\left( {s_{2}^{i} ,s_{2}^{j} } \right),d\left( {s_{2}^{i} ,s_{1}^{j} } \right),d\left( {s_{1}^{i} ,s_{2}^{j} } \right)} \right) $$

where d is the Euclidean distance between two snippets. Since each snippet can start from any position, we use circular shift to align snippets.

Figure 14 shows the clustering of Euclidean distance and Snippet distance. Why does Euclidean distance fail here?

Fig. 14

The Euclidean distance and Snippet distance complete-linkage clustering for eight time series coming from two different locations: Greek precinct and transportation hubs

Figure 15.top offers a hint. Notice that the time series has a spike, and a region of zero data counts. Note that these “artifacts” might reflect reality. For example, the spike’s high count might reflect the route of a marathon race, or a protest march. Likewise, the missing data might reflect a temporary bridge closure for repairs. However, whether a true reflection of the behavior of Melbournians or a digital glitch, these atypical events (almost all the time series have them to some extent), offer difficulties for the Euclidean Distance.

Fig. 15

(Top) Pedestrian count time series where the sensor is located in Webb Bridge, Melbourne. (Bottom) examples of snippets extracted from time series. The red snippets belong to the Greek Precinct location, and the blue snippets belong to the transportation hubs

In contrast, the Snippet distance, which only considers the most typical weeks (by definition) has no problem correctly clustering the data. An additional advantage of Snippet distance is that it is defined for time series of different lengths. We can compare 1 year from one location, with just 6 months of a location that came online later.

4 Emprical evaluation

We begin by stating our experimental philosophy. We have designed all experiments such that they are easily reproducible. To this end, we have built a web page (Imani 2020) that contains all of the datasets and code used in this work, as well as the spreadsheets containing the raw numbers.

As we noted above, to the best of our knowledge there is no explicit strawman other than random sampling. However, we can create a simple strawman based on time series clustering, which is the most obvious, sensible “first thing to try.” For this algorithm, we randomly sample f% of the data subsequences. We then cluster the subsequences with K-means. For each cluster we find the subsequence that has the minimum distance to all other subsequences in the cluster (i.e. the medoid) and report these as the k-snippets. This leaves open the issue of finding a good value for f; for simplicity we allow this algorithm to “cheat” by testing all values in the range 1 to 20%, and reporting only the best result.

We also report the results of random sampling, which plays a role similar to the “default rate” for classification, setting a lower bound for performance.

4.1 Objective experiments

Our task at hand, to produce “typical” time series subsequences, seems hopelessly subjective and difficult to evaluate in an objective way. However, we can convert the problem to one for which objective truth is available. Suppose we have a dataset which is comprised of a minute of walking, followed by a minute of running. If we queried such a dataset for the top-2 snippets, we would surely hope to find one snippet from each gait type. This we count as a success, while any other result we count as a failure.

Of course, here there is a 50% chance of success with random sampling. More generally, if the two behaviors are different fractions of the length of the full-time series L and R, with L + R = 1, the probability of random sampling returning a satisfactory pair of snippets is 2 × L × R.

Thus the task is made more difficult by having an asymmetric length of behaviors. Nevertheless, a single successful experiment would not be very convincing. Thus, to stress test our algorithm, we created a diverse collection of one hundred time series that we call MixedBag. Figure 16 shows some representative examples.

Fig. 16

Five examples from the MixedBag archive, aligned such that the behavior change takes place at the center. Note that the examples are much longer, as data was truncated from both ends for visual clarity

Some of our examples are completely natural, and we are confident from some external knowledge that there are only two behaviors, and that we have correctly identified the transition point. For some datasets, we slightly contrived the data to give us an unambiguous ground truth. For example, we took two 1-min ECG traces of two different individuals and concatenated them. Our examples draw from robotics, human locomotion, ornithology (vocalizations), ornithology (flight), entomology, speech processing, pig physiology, etc.

The scoring function is simply the sum of all successes in our one-hundred experiments. Table 3 shows the result for the scoring function for three different algorithms.

Table 3 The performance of three algorithms in snippet discovery

While the results are impressive, we should point out that even the 16% of cases where we failed may not represent true failures. For example, consider a dataset that is labeled {walk|jog}, as in Fig. 16. If we reported two snippets that came from the walking section, our scoring function reports failure. However, it is possible that the walking section actually includes two distinct behaviors, say, walking upstairs and then walking downstairs, and those labels are not available to us. In such a case, a snippet from each of the two latent walking behaviors may actually represent a success.

4.2 Sensitivity tests

In the previous sections we have shown the Snippet-Finder algorithm’s accuracy for the MixedBag dataset, in which we chose the subsequence length of MPdist to be 50 percent of the total subsequence length. It is natural to ask how critically the good results depended on this user-defined parameter.

In this section, we evaluate empirically the sensitivity of subsequence length of MPdist. We repeat the same experiment using a different percentage of subsequence lengths of MPdist, and again computed the accuracy of the MixedBag data set. The results are shown in Table 4.

Table 4 The performance of the snippet-Finder over different subsequence length of MPdist

As shown in Table 4, choosing the percentage of subsequence length any value between 30 and 80 still gives us excellent results.

When the percentage of subsequence length get close to 100 we get poor results. This is not surprising because in this case MPdist degenerates to its special case which is Euclidean distance. As we explained in Fig. 10, using Euclidean distance is not suitable for summarization tasks. In summary, the Snippet-Finder algorithm is very robust to its only parameter choice.

4.3 Robustness tests

The experiments in the previous section could justifiably be criticized for being too contrived. All of the data belongs to exactly one of two behaviors, with no “distracting” subsequences. However, most real data has such sections. For example, the PAMAP dataset is comprised mostly of walk, run, cycle, etc. However, there are short regions of ill-defined and less structured data, such as when the user pauses at a stop light, or transitions from walking to cycling and spends a few ill-defined moments unlocking the bicycle and carrying it to the side of the road. It is natural to ask how our method fares when presented with such distracting regions.

To test this, we repeated the experiment above, this time after concatenating regions of distracting data to the original time series. To ensure that the distracting data itself does not have patterns worthy of being summarized by a snippet, we used both random data, and random walk data. We considered the cases where distracting data of 10% and 20% of the original time series length was appended to the original time series. Table 5 shows the result for the scoring function for three different algorithms in these more challenging scenarios.

Table 5 The performance of three algorithms in snippet discovery

We observed that our proposed algorithm is largely invariant to the reasonable amount of spurious distractor data. The performance does begin to suffer as we see large amounts (> 10%) of random walk data, as this data has the property that any two randomly selected subsequences tend to be closer than any random subsequences of structured data (i.e. gait, heartbeats etc.). In Batista et al. (2014) there is an explanation for this phenomenon, and a possible solution (a correction factor for the Euclidean distance). However, given the high performance of our simple algorithm, we leave such considerations for future work.

We have established that our snippet discovery algorithm can robustly find typical time series in diverse settings. In the following sections we show some case studies that demonstrate the utility of snippet discovery in real world applications.

4.4 Case study: human behavior

We consider a dataset collected as part of a large-scale five-year NIH-funded project at The University of Tennessee.

More than two hundred youths are being monitored in the free-living validation group. Also, the free-living is over 2 h periods in each location while another one hundred youths are being monitored during true free-living activities during an after-school program and at home (validation group). Figure 17 shows an example of the former data type. Note that for some data we have video, thus ground truth.

Fig. 17

(Left) A participant in The Tennessee study. He is wearing a portable indirect calorimeter, and sensors on each limb. (Right) A small sample of the data collected as the participant runs around a basketball court (The procedures were reviewed and approved by The University of Tennessee Institutional Review Board before the start of the study. A parent/legal guardian of each participant signed a written informed consent and filled out a health history questionnaire, and each child signed a written assent prior to participation in the study.)

Collecting and analyzing this massive dataset is a difficult task. For this experiment, we consider sensor data from a hip-mounted accelerometer, which is collected at 90 Hz. In Fig. 18 we show the snippets discovered.

Fig. 18

(Top) A five-minute region of behavior for the study participant. (Bottom) The top-2 snippets discovered in this dataset

With a quick glance at the output of Fig. 18, the study organizer can immediately tell that this data represents about 4 min of running followed about a minute of very slow “cool-down” walking. Note that this example was used in Fig. 1 as an example of the thumbnail icon summarization tool.

In Fig. 19 we show the profiles that were used to compute the top two snippets. Note that this is not a view that would be shown to an end-user; it is just an internal representation used by the snippet discovery algorithm. Here we show it to give context to the figures shown in Sect. 3 as we describe in our algorithm, and to explain how we compute the “regime bar”.

Fig. 19

(Top) The profiles that were used to compute the top two snippets. (Bottom) It is from these curves that we obtain the “regime bar,” which tells us which snippet explains which region of data

In this example, it happens that only one example of each regime is in the regime bar. However, that does not have to be the case. To see this, as shown in Fig. 20, we repeated the experiment with similar data from the PAMAP dataset, a widely used benchmark (Reiss and Stricker 2012).

Fig. 20

A 10-min region of behavior from the PAMAP dataset (Reiss and Stricker 2012). The data is the Y-axis acceleration from a chest-worn sensor. In this dataset the ground truth is available from careful annotations made at the time

As shown in Fig. 21, we extracted the top-4 snippets from this dataset. Note that one of the snippets, snippet-3, reflect two non-contiguous regions.

Fig. 21

(Top) The top-4 snippets from the PAMAP dataset. To someone with familiarly with this dataset/domain, it is easy to label the four behaviors. (Bottom) As an alternative to creating a regime bar, we can simply brush the colors of each snippet onto the original time series

Note that the skipping (rope-jumping) section has several discontinuities, presumably because the participant caught her foot in the rope and had to restart. In spite of these unstructured regions, the top-4 snippets perfectly summarize this data set.

4.5 Case study: medicine

Working with clinicians of the David Geffen School of Medicine at UCLA, we are creating a tool to summarize ICU (Intensive Care Unit) telemetry. In an ICU setting, for a Level-3 patient, a typical protocol requires a nurse or doctor to go physically bedside once an hour and examine both the patient and their vital signs, which are displayed on the bedside monitor (Drews 2008; Forde-Johnston 2014). The latter typically contains the most recent data in the sliding window for the last twelve seconds. However, it may be that this most recent data is atypical of the last hour. For example:

• If the patient recently sneezed, this will change her intrathoracic pressure, decreasing the flow of blood to the heart, which then is forced to compensate. This can change the ECG, arterial blood pressure (ABP), and respiration.

• The mere presence of medical staff may induce stress in a conscious patient and change their physiological readings.

Thus, we argue instead of (or in addition to), presenting the last 12 s, we should present the top-k snippets over the last hour.

We asked ICU clinicians to create datasets for which they know (or at least, strongly suspect) what a correct answer should look like, and to examine these datasets with Snippet-Finder. Figure 22 shows one such example.

Fig. 22

(Top) The ABP of a 54-year old female. (Bottom) The top-2 four-second snippets discovered in the APB data

Note that the two snippets reflect different heart rates, at about 70 and 84 BPM respectively. However, this is not the reason why they were reported as the top-2 snippets. If we rescale the data to make each beat the same length, we would get similar snippets. To make the difference between the two snippets clearer, in Fig. 23.left we show zoom-in sections of the individual beats.

Fig. 23

(Left) A zoom-into individual beats discovered in the top-2 snippets. (Right) A sensor failure in the original ABP dataset (see also Fig. 22)

Note that beyond differences in periodicity, these beats have very different shapes. We can now reveal the ground truth. This dataset was created by researchers interested in hyperemia, and the difference in the two regions was actually induced by clinicians who manipulated the patients by changing their orientation on a special bed. Thus, in this case, the researchers can confirm that the results of Snippet-Finder are objectively correct and medically meaningful.

Before moving on, there are two interesting observations for this case study. As shown in Fig. 23.right, the original data contains a small region in which the sensor failed to record physiological data, and instead reported a square-wave calibration signal (Samaniego et al. 2003). As noted in Sect. 2.1, any motif-based definition of a typical pattern would surely report this section. However, our definition rewards both coverage and fidelity, and while this section has perfect fidelity, it has very low coverage.

The second interesting observation is that most of the original dataset has the significant wandering baseline, while our top-2 snippets do not. This is a very desirable and sensible property. A snippet on a rising trend is a better fit with other rising trends, but a poorer fit with falling trends (and vice versa). However, if we only have one snippet per “behavior,” a neutral trend is clearly the best compromise and most representative.

4.6 Case study: electrical power demand

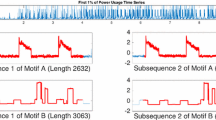
To demonstrate the versatility of snippets, we consider a dataset that is four orders of magnitude longer than the datasets considered in the previous examples. As shown in Fig. 24, the Italian power demand dataset represents the hourly electrical power demand of a small Italian city for 1220 days, beginning on Jan 1st1995.

Fig. 24

The Italian power demand dataset contains a little over 3 years of electrical demand for a small Italian city

To avoid “over polishing” our query with exact values query length, we search for the top-2 snippets of length 200. This was our quick “eyeballing” guess as to the length of a week, but it is actually about 8.3 days. As Fig. 25 shows, the returned snippets are not constrained by calendar conventions to start on a particular day. An HVAC engineer we consulted suggests that these profiles demonstrate that the respective households have high ownership rates and use of HVAC systems for cooling, but a low use of electrical equipment for heating in the winter.

Fig. 25

The top-2 snippets from the Italian power demand dataset. (Left) Snippet-1 runs from Monday to Monday (inclusive). (Right) Snippet-2 runs from Sunday to Sunday (inclusive)

However, in this case, the real power of these snippets comes from examining the regions they explain, as shown in Fig. 26. In this figure, it is clear that the snippets represent summer and winter regimes respectively.

Fig. 26

The Italian power demand dataset. The horizontal bar shows the colors of each snippet onto the original time series

Before finishing this section, we will take this opportunity to reiterate our discussion of what snippet discovery is not. As explained in Sect. 2.1, snippet discovery is a completely distinct task from clustering. Nevertheless, as a side effect, here we have produced an implicit clustering into seasons. Moreover, a brief survey of the research efforts to explicitly cluster the electrical profile into seasons (see Rhodes et al. 2014 and the references therein) suggests that the algorithms specialized for this task are more complex, and require more domain knowledge; for example, the subsequences must be exactly 1-week long.

Likewise, snippet discovery is a completely distinct task from segmentation (Gharghabi et al. 2019; Lin et al. 2016). Once again, it happens that in this case, snippet discovery incidentally provides an answer to the segmentation problem if we consider the boundaries between the snippets. However, recall that the segmentation problem, as it is typically defined, is tasked only with finding boundary locations, not in explaining them, or producing representative patterns (Lin et al. 2016).

4.7 Case study: biology

As a final example of the utility of snippets, we consider a problem for which our help was solicited by the team of biologists at UCR who recorded the feeding behaviors of sap-sucking insects with an electrical penetration graph (EPG). In Fig. 27 we show three examples of the data in question.

Fig. 27

Three examples of telemetry collected from the three individual Asian citrus psyllids (Diaphorina citri). Assume that the top example is an ideal specimen, and that the bottom two are alternative treatments. How could we quantify the differences (if any) caused by the treatments?

If they define the time series shown in the top of Fig. 27 as being ideal, and collect the two other examples under different environmental conditions, then they can ask: “How do T1 and T2 differ from the ideal specimen, if at all?” The answer does not appear to lay in any single number such as mean, max, variance, entropy, etc. We hypothesize that changes in behavior may show up in differences in local regions as changes in shape. However, given that the approximately 5 h of data shown in Fig. 27 represents less than one-thousandth of their archive, visual inspection of the full data archive is clearly intractable.

The reader will readily appreciate that snippets are a potential way to answer this question. As shown in Fig. 28, we can discover the top-2 snippets for each time series, and visually compare them.

Fig. 28

The top-2 snippets extracted from the datasets presented in Fig. 27. Note that the snippet-2 s are effectively identical, but while the snippet-1 for I and T1 are very similar, T2’s snippet-1 appears unique

For all three examples, the 2nd snippets are nearly identical and represent (to biologists) very familiar examples of “derailed stylet mechanics.” The 1st snippet from T1 and I appear to be “Xylem ingestion,” but the 1st snippet from T2 is a mystery. Its period is similar to that of Xylem ingestion, but the shape of the peaks are unfamiliarly sharp. Is this a biologically significant finding, or is there a more pedestrian explanation, such as a malfunctioning apparatus? This is currently under investigation. However, this experiment shows the utility of snippets in helping to explore and compare large datasets that would otherwise defy human inspection.

5 Online discovery of snippets

Thus far we have seen only a batch algorithm for snippet discovery. We have to wait to gather all the data and then start the discovery process. However, it is natural to ask if we can discover snippets in the face of streaming data.

In this section, we will introduce the online snippet discovery algorithm, which is computationally efficient, and can produce very similar results to the batch algorithm. The latter qualification is worth expanding on. Given infinite memory and CPU resources, we could simply rerun our batch algorithm from scratch for each datapoint’s arrival. This would guarantee that our batch and streaming algorithms would produce identical results. However, this is not tenable for arbitrarily long streams. With some care, we can cache previous computations, greatly reducing the CPU requirements, but clearly, we must eventually run out of memory.

The intuition of our streaming algorithm is as follows. We compare each subsequence of the incoming data with the current top-k snippets. If the fidelity and coverage of a new subsequence was better than the top-k snippets, then we update the top-k, otherwise the top-k remains the same.

We will illustrate the streaming version of snippet discovery by revisiting the example in Sect. 4.4, in which we have a time series of four behaviors: normal walking, Nordicwalking, running and skipping as shown in Fig. 29.

Fig. 29

A 10-min region of behavior from the PAMAP dataset (Reiss and Stricker 2012). The data is the Y-axis acceleration from a chest-worn sensor. In this dataset, the ground truth is available from careful annotations made at the time

Assume that instead of the full 10 min of the time series, we have just the first 3 min of the time series. We can calculate the snippets for this time series as shown in Fig. 30, using the algorithm outlined in Table 1.

Fig. 30

Three minutes of PAMAP data including Normal walking and Nordic walking behavior. Each snippet explains one type of behavior

Now assume we receive the remainder of the time series in a small batch of one subsequence per second. In this version, we update the profile of each snippet and calculate the arriving data’s profile with the time series. Then we choose the best k snippets based on these k profiles, in which k is the user-defined parameters for the number of snippets. The result after receiving the entire data is shown in Fig. 31.

Fig. 31

Online snippets after streaming the whole data

Table 6 shows online snippets algorithm.

Table 6 Online Snippets Algorithm

Considering the ground truth, the online snippets are the summary of all four activities, which suggests that this result is as comprehensive as the batch version. The benefit of online snippets is that we do not need to calculate the profile of the whole time series for each subsequence. Instead, we update the snippet’s profile and new incoming data’s profile as the data arrives. The time complexity of the online snippets algorithm is O(n + m) where n is the length of the current time series and m is the subsequence length. To concretely ground this, we answer the following question: “Given this arrival rate, how long can we maintain the profile before we can no longer update fast enough?”, for a typical scenario.

Consumer domestic electric power demand is often sampled at 1 Hz. On a standard desktop machine, with 1 GB of storage available for our problem (2³⁰ Bytes), if the frequency of data is 1 Hz (4 Bytes to store each data points), then we can update snippets for approximately 8 years until we run out of memory (we would not run out of CPU time for decades). This is fast enough for many practical deployments, however further optimizations would be needed to allow deployment on wearable devices or other resource constrained systems.

5.1 Objective evaluation of the online snippet algorithm

In this section, to evaluate the performance of online snippets algorithm, we create an experiment on our diverse collection of one-hundred time series, MixedBag. For each time series in the MixedBag collection, we give each time series as an input to our online snippets algorithm and compute the success rate. Recall the success rate as sum of all successes in our one-hundred experiments. Table 7 shows the result for the scoring function for two different algorithms.

Table 7 The performance of the Online Snippets Algorithm

As shown in Table 7, the online snippets algorithm performs slightly better that Snippet-Finder for the MixedBag dataset. This may be surprising, as we might have expected its streaming nature would have condemned it to do worse than the batch algorithm that can see all the data at once. However, recall that both Snippet-Finder and online snippets algorithm are greedy algorithms and they are not necessarily the optimal solution as we explained in Sect. 3.1. We can see this by running the online version again, after flipping the data backwards. That does not affect the results for the batch algorithm, but now the online version does do slightly worse than batch. In summary, these results are consistent with the idea that the online algorithm’s performance can approach that of the batch algorithm. However, it is clear that if we took an adversarial approach, we could create a synthetic dataset that would make the online version perform much worse than the batch case.

6 Conclusions and future work

We have introduced a novel primitive called top-k time series snippets. We have further shown an algorithm that can robustly find snippets in large datasets, even when corrupted by noise, dropouts, wandering baseline, etc. To handle the streaming setting, we have created an online version of our algorithm.

We have made all our data and code publicly available for the community to confirm and extend our work (Imani 2020), including a large archive of benchmark datasets that will allow the community to compare new approaches and gauge progress on this task. In ongoing work, we are optimizing our algorithms to allow them to work on severely resource-constrained devices. This will allow us to run our algorithms in the background on wearable devices.