Robust and sparse multigroup classification by the optimal scoring approach

Abstract

We propose a robust and sparse classification method based on the optimal scoring approach. It is also applicable if the number of variables exceeds the number of observations. The data are first projected into a low dimensional subspace according to an optimal scoring criterion. The projection only includes a subset of the original variables (sparse modeling) and is not distorted by outliers (robust modeling). In this low dimensional subspace classification is performed by minimizing a robust Mahalanobis distance to the group centers. The low dimensional representation of the data is also useful for visualization purposes. We discuss the algorithm for the proposed method in detail. A simulation study illustrates the properties of robust and sparse classification by optimal scoring compared to the non-robust and/or non-sparse alternative methods. Three real data applications are given.

1 Introduction

In linear discriminant analysis (LDA) the data originate from K different populations. The aim is to find linear decision boundaries to separate the observations from the K groups as good as possible and to predict the class membership of new, unlabeled observations. Several formulations for LDA exist. Fisher’s approach to LDA searches for directions that maximize the between group variance given the within group variance. Equivalently, one can take the conditional class densities as multivariate normal with the same covariance matrix, and apply the Bayes classification rule. The formulation for LDA considered in this paper is optimal scoring (Hastie et al. 1994). It recasts the classification problem into a regression framework and models the class-membership with a quantitative parameter for each class.

While these different approaches to LDA yield the same classification results (Johnson et al. 2002; Witten and Tibshirani 2011) they are all limited to settings with more observations n than variables p. Optimal scoring enables us to transfer new developments in high dimensional regression analysis to the classification context. In regression analysis the problem of high dimensional data, in particular data with more variables than observations, attracts a lot of attention. A variety of so-called sparse methods have been developed. The best known is the Lasso regression estimate (Tibshirani 2011). For a response $\varvec{y}\in \mathbb {R}^{n}$ and a column-wise centered and scaled predictor matrix $\varvec{X}\in \mathbb {R}^{n\times p}$, it is defined as

$$\begin{aligned} \min _{\varvec{\beta }}\frac{1}{n}\Vert \varvec{y} -\varvec{X}\varvec{\beta }\Vert ^2 + \lambda \Vert \varvec{\beta }\Vert _1 \end{aligned}$$

for regression coefficients $\varvec{\beta }$, where $\Vert \varvec{a}\Vert ^2 = \sum _{i=1}^p a_i^2$ is the squred Euclidean norm and $\Vert \varvec{a}\Vert _1 = \sum _{i=1}^p |a_i|$ the $L_1$ norm, for a vector $\varvec{a}=(a_1,\ldots ,a_p)^T$. Fast algorithms have been developed for Lasso regression (Efron et al. 2004; Wu and Lange 2008). The Lasso shrinks several of the estimated regression coefficients to zero, and is therefore said to be sparse. The zero coefficients correspond to the variables that are not selected into the model. Hence, the Lasso performs simultaneous model estimation and variable selection. The sparsity tuning parameter is $\lambda$, and increasing values of $\lambda$ will favor more coefficients equal to zero and sparser models. This is especially useful for data sets including uninformative variables which do not contribute information to predicting the response. When uninformative variables are excluded, the precision of the estimation increases and the models are easier to interpret. Recently, Clemmensen et al. (2012) proposed a sparse version of multigroup LDA, by adding an $L_1$ penalty to the objective function of the optimal scoring problem. This leads to a sparse discriminant analysis method applicable for $n<p$ as well.

In this paper we propose a robust version of sparse optimal scoring. It is robust because it is resistant to outliers. In linear discriminant analysis an observation is considered an outlier if it belongs to group k but differs from the majority of observations in group k, for $k=1,\dots ,K$. It is well known, that outliers may render a statistical method completely unreliable. The sample covariance matrix and the group average can be heavily distorted by single extreme observations and classification rules based on them will be unreliable. This will not happen if a robust method is used.

A variety of robust classification methods have been proposed (Hubert and Van Driessen 2004; Todorov and Pires 2007) but generally they are not applicable for data with $n<p$. Vanden Branden and Hubert (2005) proposed a robust classifier for high dimensions based on SIMCA, but it does not use sparse modeling, so all variables are included in the model. A sparse and robust classification method based on partial least squares was proposed by Hoffmann et al. (2016) but only for binary classification problems. Robust optimal scoring, even the non-sparse case, was not considered before in the literature.

The paper is structured as follows. In Sect. 2, we review the optimal scoring approach to linear discriminant analysis. In Sect. 3, we introduce the proposed method and present the algorithm in detail. In Sect. 4, a strategy is outlined to select the sparsity tuning parameter. A simulation study competing with existing alternative methods is presented in Sect. 5. Illustrations on real world examples are given in Sect. 6.

2 Optimal scoring for multigroup classification

We follow the notation of Clemmensen et al. (2012) to outline the optimal scoring method. Let $\varvec{X}$ be the $n\times p$ data matrix with the observations $\varvec{x}_1,\ldots ,\varvec{x}_n$ in its rows and $\varvec{Y}$ an $n\times K$ matrix of dummy variables coding the class membership of the observations, i.e. $y_{ik}=1$ if and only if observation $\varvec{x}_i$ belongs to group k, and zero otherwise. The rows of $\varvec{Y}$ are denoted by $\varvec{y}_1,\ldots ,\varvec{y}_n$. The columns of $\varvec{X}$ are centered to have mean zero and scaled to have unit variance. The aim of optimal scoring is to find projection vectors $\hat{\varvec{\beta }}_1,\ldots ,\hat{\varvec{\beta }}_H$, such that each $\varvec{X}\hat{\varvec{\beta }}_h$ is a good prediction of the corresponding vector $\varvec{Y}\hat{\varvec{\theta }}_h$, for $h=1,\dots ,H$, where the vector $\varvec{Y}\hat{\varvec{\theta }}_h$ contains the scores of the group each observation belongs to. The K components of the score vector $\hat{\varvec{\theta }}_h$ are the numeric scores assigned to each of the groups. One takes H smaller than the number of groups K, commonly $H=K-1$.

The projection vectors $\hat{\varvec{\beta }}_h$ and the score vectors $\hat{\varvec{\theta }}_h$ are obtained sequentially. Let $\varvec{D}=\frac{1}{n}\varvec{Y}^T\varvec{Y}$ be a $K\times K$ diagonal matrix of class proportions. Set $\hat{\varvec{\theta }}_0=\varvec{1}_K$, the K-vector of ones. Then solve for $h=1,\ldots ,H$

$$\begin{aligned} \min _{\varvec{\beta }_h,\varvec{\theta }_h} \frac{1}{n}\Vert \varvec{Y}\varvec{\theta }_h - \varvec{X}\varvec{\beta }_h\Vert ^2 \quad \text {s.t.} \quad \varvec{\theta }_h^T\varvec{D}\varvec{\theta }_h=1,\quad \varvec{Q}_h^T\varvec{D} \varvec{\theta }_h=\varvec{0}, \end{aligned}$$

where $\varvec{Q}_h=[\varvec{Q}_{h-1}, \hat{\varvec{\theta }}_{h-1}]$ is a $K\times h$ matrix.

The sparse optimal scoring method of Clemmensen et al. (2012) simply adds an $L_1$ penalty to the objective function.

$$\begin{aligned} \min _{\varvec{\beta }_h,\varvec{\theta }_h} \frac{1}{n}\Vert \varvec{Y}\varvec{\theta }_h - \varvec{X}\varvec{\beta }_h\Vert ^2+ \lambda \Vert \varvec{\beta }_h\Vert _1 \quad \text {s.t.} \quad \varvec{\theta }_h^T\varvec{D}\varvec{\theta }_h=1,\quad \varvec{Q}_h^T\varvec{D}\varvec{\theta }_h=0. \end{aligned}$$

(1)

Estimators $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$ that solve (1) can be obtained iteratively. Starting with a random vector for $\varvec{\theta }_h$ one computes the Lasso for $\varvec{\beta }_h$. For a given $\varvec{\beta }_h$ there exists an explicit solution of (1) for $\varvec{\theta }_h$. One iterates further until convergence. For details, see Clemmensen et al. (2012).

Once the projection vectors are obtained, a standard LDA is performed in a low dimensional space of dimension H. Let denote by $\varvec{z}_1,\dots , \varvec{z}_n$ the projected observations in the rows of $\varvec{Z}=\varvec{X}\varvec{B}$, $\varvec{B}=[\hat{\varvec{\beta }}_1,\ldots , \hat{\varvec{\beta }}_{H}]$. Denote the group averages of the projected observations by $\varvec{m}_k=\frac{1}{n_k}\sum _{i \in C_k} \varvec{z}_i$, where $C_k$ denotes the index set for observations from class k, and $n_k$ is the number of observations in class k, for $k=1,\ldots ,K$. The within group covariance matrix is

$$\begin{aligned} \varvec{S}= \frac{1}{n-K}\sum _{k=1}^K \sum _{i \in C_k} (\varvec{z}_i - \varvec{m}_k)(\varvec{z}_i - \varvec{m}_k)^T. \end{aligned}$$

The Mahalanobis distance of an observation $\varvec{z}$ to the center $\varvec{m}_k$ is given by

$$\begin{aligned} MD(\varvec{z}; \varvec{m}_k,\varvec{S})=\left( (\varvec{z} -\varvec{m}_k)^T \varvec{S}^{-1} (\varvec{z} -\varvec{m}_k)\right) ^{1/2}. \end{aligned}$$

An observation $\varvec{x}$, transformed to $\varvec{z}=\varvec{x}^T\varvec{B}$, is then assigned to the class k with smallest value of

$$\begin{aligned} MD(\varvec{z}; \varvec{m}_k, \varvec{S})^2 - 2 \log (\pi _k). \end{aligned}$$

Here, $\pi _k$ is the prior probability belonging to group k, with $\pi _1 + \dots + \pi _K=1$. In the following, $\pi _k$ is set to the class proportion of group k, so $\pi _k=n_k/n$.

3 Robust and sparse optimal scoring

We now propose an optimal scoring algorithm for data containing outliers and possibly more variables than observations. Furthermore, not all variables contribute information about the class membership of the observations, in the following referred to as uninformative variables, and therefore we aim at sparse estimation. To the best of our knowledge, sparse and robust classification methods for multiple groups have not been considered in literature so far. Even the non-sparse case, robust optimal scoring is a new approach to robust classification problems.

The aim of the algorithm is to reduce the influence of outlying observations on the model estimation. A common and powerful approach to achieve this in a regression model is the iteratively re-weighted least squares algorithm (Wolke and Schwetlick 1988). Given a robust initial estimator, the influence of observations with large residuals is down-weighted by case weights. The coefficient estimates and the case weights are iteratively re-estimated. Here we will take a related approach.

The data matrix $\varvec{X}$ is robustly centered by the coordinate-wise median and each column is scaled by the median absolute deviation (MAD) (Hampel 1974). The MAD is defined by $\text {MAD}(a_1,\ldots ,a_n)=1.48 \mathop {\text{ med }}_i|a_i - \mathop {\text{ med }}_j a_j|$ where $\mathop {\text{ med }}_i a_i$ denotes the median of $a_1,\ldots , a_n$ and 1.48 is a factor to get consistency at normal distribution.

3.1 Initial estimation

The vectors $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$ are estimated sequentially for $h=1,\dots , H$. As before, $\hat{\varvec{\theta }}_0=\varvec{1}_K$. First we obtain initial estimates for $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$. It is important that they are robust to outliers and can be computed in high dimensions. These initial estimates start up the iterative procedure to get the final $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$. “Appendix” provides full details for their computation.

3.2 Outlier weights

Residuals are computed as

$$\begin{aligned} r_i= \varvec{y}_i^T \hat{\varvec{\theta }}_h - \varvec{x}_i^T \hat{\varvec{\beta }}_h \quad \text {for } i=1,\ldots ,n. \end{aligned}$$

The observations will be weighted so that potential outliers receive less weight. The weights are computed from the residuals. Weights are calculated separately for each group. Denote $r_i^{(s)}$ the robustly standardized residuals where we center by the median and scale by the MAD.

Hampel’s re-descending weighting function (Hampel et al. 1986) is applied to the standardized residuals to obtain weights for each observation. This weighting function (plotted in Fig. 1) is given as

$$\begin{aligned} \omega _H(r) = \left\{ \begin{array}{ll} 1 &{} \quad |r| \le q_1 \\ \frac{q_1}{|r|} &{}\quad q_1< |r| \le q_2 \\ \frac{q_3 - r}{q_3 -q_2} \frac{q_1}{|r|} &{} \quad \text{ if } \,q_2< |r| \le q_3 \\ 0 &{}\quad q_3 < |r| \end{array} \right. \end{aligned}$$

where the parameters $q_1,q_2$ and $q_3$ are set to the 0.95, 0.975 and 0.999 quantiles of the standard normal distribution, respectively, i.e. $q_1=1.64, q_2=1.96$ and $q_3=3.09$. The case weights are then $\omega _i =\omega _H(r_i^{(s)})$ for $i=1,\ldots ,n$. Under the assumption of normality of the residuals, 90% of the observations will receive weight $\omega _i=1$ and 0.2% receive weight $\omega _i=0$.

Fig. 1

Hampel’s re-descending weighting function

3.3 Solving the weighted sparse optimal scoring problem

Let $\varvec{\varOmega }$ be a diagonal matrix with the case weights $\omega _1,\ldots ,\omega _n$ on the diagonal. Then define $\varvec{\tilde{Y}} = \varvec{\varOmega }^{1/2}\varvec{Y}$ and $\varvec{\tilde{X}} = \varvec{\varOmega }^{1/2}\varvec{X}$ the weighted data matrices. The diagonal matrix $\varvec{\tilde{D}} =\frac{1}{\sum \omega _i}\varvec{\tilde{Y}}^T\varvec{\tilde{Y}}$ contains on its diagonal the share of the total weight coming from each group’s observations. The weighted sparse optimal scoring problem is defined as

$$\begin{aligned} \min _{\varvec{\beta }_h,\varvec{\theta }_h}\frac{1}{\sum \omega _i}\Vert \tilde{\varvec{Y}}\varvec{\theta }_h - \tilde{\varvec{X}}\varvec{\beta }_h\Vert ^2+ \lambda \Vert \varvec{\beta }_h\Vert _1 \quad \text {s.t.} \quad \varvec{\theta }_h^T\tilde{\varvec{D}} \varvec{\theta }_h=1,\quad \varvec{Q}_h^T \tilde{\varvec{D}}\varvec{\theta }_l=\varvec{0}. \end{aligned}$$

(2)

If no outliers are detected, all weights are one, $\sum \omega _i=n$, $\varvec{\varOmega }$ is the identity matrix and Eq. (2) is the standard optimal scoring problem Eq. (1).

Equation (2) is solved by an alternating iterative scheme. For given $\hat{\varvec{\theta }}_h$ it reduces to the weighted Lasso regression problem

$$\begin{aligned} \hat{\varvec{\beta }}_h=\mathop {\text{ argmin }}_{\varvec{\beta }} \frac{1}{\sum \omega _i}\sum _{i=1}^n (\varvec{y}_i^T \hat{\varvec{\theta }}_h - \varvec{x}_i^T \varvec{\beta })^2 \omega _i+ \lambda \Vert \varvec{\beta }\Vert _1. \end{aligned}$$

(3)

which is equivalent to solving the Lasso for the weighted data, with sparsity parameter given by $\lambda \sum w_i /n$. For a given $\varvec{\hat{\beta }}_h$, the optimization problem Eq. (2) is solved by

$$\begin{aligned} \hat{\varvec{\theta }}_h=c\left\{ \varvec{I} - \varvec{Q}_h (\varvec{Q}_h^T \varvec{\tilde{D}} \varvec{Q}_h)^{-1} \varvec{Q}_h^T \varvec{\tilde{D}} \right\} (\varvec{\tilde{D}}^{-1} \varvec{\tilde{Y}}^T \varvec{\tilde{X}} \varvec{\hat{\beta }}_h) \end{aligned}$$

(4)

where c is a scalar so that $\hat{\varvec{\theta }}_h$ fulfills the side constraint $\hat{\varvec{\theta }}_h^T\varvec{\tilde{D}} \hat{\varvec{\theta }}_h=1$. The derivation of Eq. (4) is given in the “Appendix”. Notice that the last part in parentheses in Eq. (4) is proportional to $(\varvec{\tilde{Y}}^T\varvec{\tilde{Y}})^{-1} \varvec{\tilde{Y}}^T \varvec{\tilde{X}} \varvec{\hat{\beta }}_h$, the OLS estimate of $\varvec{\theta }_h$ when regressing $\tilde{\varvec{Y}}$ on $\tilde{\varvec{X}}\hat{\varvec{\beta }}_h$ without side constraints.

After computing $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$, new residuals $r_i$ and case weights $\omega _i$, for $i=1,\ldots ,n$, are calculated as described previously. New estimates of coefficient and score vectors are computed on the re-weighted data as in Eqs. (3) and (4).

The notation in Eq. (3) highlights the role of the weights $\omega _i$: for $\omega _i=0$ the term $(\varvec{y}_i^T \hat{\varvec{\theta }}_h - \varvec{x}_i^T \varvec{\beta })^2$ does not contribute to the parameter estimation, for $\omega _i=1$ the squared residual is fully considered in the objective function of Eq. (3). Intermediate values of the weights correspond to a reduced, but non-zero, influence of the observation on the estimators.

3.4 Convergence criterion

Let $\omega _1^j,\ldots ,\omega _n^j$ denote the case weights and $\hat{\varvec{\beta }}_h^j$ and $\hat{\varvec{\theta }}_h^j$ the estimates in the jth iteration step. Then the weighted mean residual sum of squares with Lasso penalty in the jth iteration step is

$$\begin{aligned} L^{j}_h=\sum _{i=1}^n (\varvec{y}_i^T \hat{\varvec{\theta }}_h^j - \varvec{x}_i^T \hat{\varvec{\beta }}_h^j)^2 \omega _i^j+ \sum _{i=1}^n\omega _i^j\lambda \Vert \hat{\varvec{\beta }}_h^j\Vert _1. \end{aligned}$$

The convergence criterion for stopping the iterative procedure is chosen as $|L^{j}_h-L^{j-1}_{h}|/L^{j}_h<10^{-4}$.

3.5 Classification rule

The iterative procedure outlined in Sects. 3.1–3.4 provides a projection matrix $\varvec{B}=[\hat{\varvec{\beta }}_1,\ldots , \hat{\varvec{\beta }}_{H}]$. We project the data into an H dimensional subspace, i.e. $\varvec{Z}=\varvec{X}\varvec{B}$, with the rows $\varvec{z}_1,\ldots ,\varvec{z}_n$. We observed that for a large sparsity parameter $\lambda$, the last column(s) of $\varvec{B}$ may consist of only zeros. Then the dimension of the classification problem on the projected data is reduced automatically.

Instead of computing sample averages and covariance matrices of the projected data, we compute a robust location and covariance matrix estimator. For this, we take the minimum covariance determinant (MCD) described in Rousseeuw and Van Driessen (1999). The robust group centers $\varvec{m}_k$, for $k=1,\ldots ,K$, are the MCD location estimates of the projected observations from the kth group, i.e. of $\varvec{z}_i$, $i\in C_k$. Then the projected observations are group-wise centered, $\tilde{\varvec{z}}_i=\varvec{z}_i - \varvec{m}_k$ for $i \in C_k$ and $k=1,\ldots ,K$. A robust covariance estimate $\varvec{S}$ from these pooled centered observations is obtained by the MCD covariance matrix estimate (Rousseeuw and Van Driessen 1999). The decision rule for a new observation $\varvec{x}$ is as follows. Project $\varvec{x}$ to the subspace, $\varvec{z}=\varvec{x}^T\varvec{B}$ and compute the Mahalanobis distances to the group centers $\varvec{m}_k$ with respect to $\varvec{S}$. Assign $\varvec{x}$ to group

$$\begin{aligned} \mathop {\text{ argmin }}_{k=1,\ldots ,K} (\varvec{z} -\varvec{m}_k)^T \varvec{S}^{-1} (\varvec{z} -\varvec{m}_k) -2\log (\pi _k). \end{aligned}$$

4 Model selection and evaluation

Two steps are necessary for the proper evaluation of the proposed method. First, a strategy to select an optimal sparsity parameter is needed, second, the prediction performance for new observations is evaluated. We split the data randomly into calibration data and test data.

To select the optimal sparsity parameter $\lambda ^*$, five-fold cross validation is performed on the calibration set. We split the calibration data randomly into $J=5$ blocks of approximately equal size such that the observations from each class are evenly spread across the blocks. Each of the five blocks is used in turn as validation set and the rest as training set. For a sequence of values for the sparsity parameter $\lambda _1,\ldots ,\lambda _L$ (covering the range between the full and the empty model) classification models are estimated on the training data and evaluated on the validation data. Since the decision for the optimal sparsity parameter $\lambda ^*$ should not be influenced by outliers, we propose to use a weighted misclassification rate (wmcr) for evaluation. For the jth validation set, which consists of $n_j$ observations $\varvec{x}_1^j, \ldots , \varvec{x}_{n_j}^j$ define

$$\begin{aligned} \text {wmcr}(\varvec{x}_1^j, \ldots , \varvec{x}_{n_j}^j, \lambda )=\frac{1}{K}\sum _{k = 1,\ldots ,K}\frac{\sum _{i \in M_k^j(\lambda )}w_i^j(\lambda )}{\sum _{i \in C_k^j}w_i^j(\lambda )}, \end{aligned}$$

(5)

where $C_k^j$ is the index set of all observations from the validation set belonging to group k, and $M_k^j(\lambda )$ is the subset of $C_k^j$ containing the indices of misclassified observations (for the model estimated with sparsity parameter $\lambda$). The weight $w_i^j(\lambda )$ of an observation $\varvec{x}_i^j$ is derived from the Mahalanobis distance to its closest center in the projected subspace, i.e.

$$\begin{aligned} MD_i^j(\lambda )=\min _{k=1,\ldots ,K} MD\left( \varvec{x}_i^{jT}\varvec{B}; \varvec{m}_k, \varvec{S} \right) , \end{aligned}$$

where $\varvec{B}$, $\varvec{m}_k$ and $\varvec{S}$ are estimated on the jth training set with sparsity parameter $\lambda$. Then the weight is defined as

$$\begin{aligned} w_i^j(\lambda ) = \left\{ \begin{array}{ll} 1 &{} \quad MD_i^{j}(\lambda )^2 \le \chi _{H}^2(0.975) \\ 1/MD_i^j(\lambda ) &{} \quad \text {else} \end{array} \right. , \end{aligned}$$

where $\chi _{H}^2(0.975)$ denotes the 97.5% quantile of the $\chi ^2$ distribution with H degrees of freedom. When all weights are equal to one, the wmcr is equivalent to the misclassification rate (mcr), the mean of the proportion of misclassified observations from each group.

The tuning parameter can now be selected such that the average wmcr over the $J=5$ validation sets is minimized, i.e.

$$\begin{aligned} \tilde{\lambda }=\mathop {\text{ argmin }}_{\lambda \in \{\lambda _1,\ldots ,\lambda _L\}} \frac{1}{J}\sum _j l^j(\lambda ), \end{aligned}$$

where, for easier notation, $l^j(\lambda )=\text {wmcr}(\varvec{x}_1^j, \ldots , \varvec{x}_{n_j}^j,\lambda )$, for $j=1,\ldots ,J$.

We then use the one-standard-error rule (Hastie et al. 2015): choose the model with largest sparsity parameter such that its average wmcr is still within one standard error of the minimum average wmcr. Thus, the optimal sparsity parameter with the one-standard-error rule is

$$\begin{aligned} \lambda ^*=\max \left\{ \lambda \in \{\lambda ,\ldots , \lambda _L\} \mid \frac{1}{J}\sum _{j=1}^J l^j(\lambda ) < \frac{1}{J}\sum _{j=1}^J l^j(\tilde{\lambda })+ \text {se} ( l^1(\tilde{\lambda }), \ldots ,l^J(\tilde{\lambda }))\right\} , \end{aligned}$$

where $\text {se}(a_1,\ldots ,a_J)=\sqrt{\text {var}(a_1,\ldots ,a_J)/J}$ denotes the standard error. This strategy favors more parsimonious models and is a safeguard against over-fitting. With the optimal sparsity parameter $\lambda ^*$ the final model is estimated on the whole calibration data and we obtain $\varvec{B}$, $\varvec{m}_k$ and $\varvec{S}$.

For the evaluation of the model, the class memberships of test data are predicted. Since the evaluation should not be distorted by outliers in the test data, we use the weighted misclassification rate Eq. (5). In the simulation study, since the test data are generated without outliers, we set the weights equal to one. In Sects. 5 and 6 we compare robust sparse optimal scoring (rSOS) with classical sparse optimal scoring (cSOS). The sparsity parameter for both methods is selected in the same way, but for cSOS the standard unweighted mcr is minimized.

5 Simulation study

Simulation schemes: The data are generated from $K=3$ different p-dimensional normal distributions representing three groups. The distributions have equal covariance structure, but different mean vectors. For group k ($k=1,2,3$) let the mean be a vector of length p with value 2 for the kth variable and zeros elsewhere. So the number of informative variables is $q=3$. The diagonal of the covariance matrix is a vector of ones. The covariance between the informative variables is 0.1 and zero between all others. The number of observations is $n=120$, where each group consists of $n_k=40$ observations.

In the first scenario of this simulation study the effect of increasing $p \in \{3,13,23,53,103,203\}$ is illustrated, i.e. of increasing the number of uninformative variables while the number of informative variables $q=3$ is fixed. The second scenario shows the effect of outliers on the methods, also for increasing $p \in \{3,13,23,53,103,203\}$. Outliers are included in the calibration data by taking 10% of the observations of the first group and replacing their values for the first variable by random values from $N(-10,1)$. Hence there are still two uncontaminated informative variables. In a third scenario the number of uninformative variables is fixed at 50 and the third informative variable is removed, i.e. $p=52$. Outliers are again only generated in the first group by replacing the values of the first variable by random values from $N(-20,1)$. This setting is more challenging because only one uncontaminated informative variable remains, and because the outliers take more extreme values. The percentage of outliers in the first group ranges from 0 to 45% by steps of 5%, allowing to observe the influence of increasing levels of contamination. Finally, simulation scenario four is used to study the effect of the sample size n on the performance of the algorithms. For this purpose, the second scenario is modified as follows. The number of variables is fixed with $p=53$ for an increasing number of observations $n \in \{120,600,1200, 120{,}000\}$.

Methods and evaluation: The results from robust sparse optimal scoring (rSOS) and classical sparse optimal scoring (cSOS) are compared. For settings where non-sparse classification methods can be applied (i.e. $n>p$), models are estimated with LDA and robust LDA (rLDA). The latter method uses the MCD of the pooled centered data as robust covariance matrix estimator, where the centers of each group are estimated by the location MCD estimator, see Hubert and Van Driessen (2004). Recall that LDA is equivalent to classical optimal scoring. As a benchmark, we first remove all uninformative variables and outliers from the calibration data and then apply LDA. This benchmark method cannot be applied in practice, since one does not know which variables are informative and which observations are outliers. We refer to this method as oracle; it gives an estimate of the lower bound for the best misclassification rate we can achieve with linear boundaries.

For rSOS the sparsity parameter $\lambda$ is selected with five-fold cross validation on the calibration data ($n=120$) from a grid of values between 0.1 and 2 with step size 0.05, as described in Sect. 4.

To evaluate the models, test data of size $n=120$ are generated in the same way as the calibration data, but without outliers for all scenarios. The predicted class membership of the test data is compared to the known, true class membership and the misclassification rate (mcr) is reported. Other criteria of the quality of the model concern the number of correctly selected variables. The false negative rate (FNR) is the fraction of informative variables not included in the model, the false positive rate (FPR) refers to the fraction of uninformative variables included in the model.

Fig. 2

Misclassification rate (mcr) averaged over 100 simulation runs as a function of p, the number of variables. a Scenario 1: models estimated on clean calibration data; b scenario 2: models estimated on calibration data with 10% outliers in one group

Simulation results: The results from the first scenario demonstrate the advantage of sparse modeling when the number of uninformative variables increases. Figure 2a shows the misclassification rate for test data, averaged over 100 simulation runs. The benchmark mcr for this simulation design is about 12.5%, as can be seen from the results of the oracle. Hardly any difference between the performance of cSOS and rSOS is visible in this setting. The mcr of both methods remains stable with increasing number of uninformative variables. In very low dimensions, for instance $p=3$, LDA and rLDA slightly outperform cSOS and rSOS, but with increasing p, LDA and rLDA quickly break down and give bad classification results, even for p still smaller than n. This shows that excluding uninformative variables is crucial for the quality of the prediction performance.

Table 1a shows the quality of the variable selection for cSOS and rSOS. The false negative rate is slightly higher for cSOS whereas the false positive rate is slightly higher for rSOS. Overall, both rates are low for both methods, which implies that the variable selection with the $L_1$ penalty achieves good results.

Table 1 Variable selection: the false negative rate (FNR) and the false positive rate (FPR) is averaged over 100 simulation runs for classical and for robust SOS for a scenario 1: models estimated on clean calibration data; b scenario 2: models estimated on calibration data with 10% outliers in one group

In the second scenario the effect of 10% outliers is investigated, see Fig. 2b. The benchmark given by the oracle is of course again about 12.5%. For $p=3$ the robust methods rLDA and rSOS outperform the classical methods LDA and cSOS. Increasing the number of variables heavily affects LDA, but also rLDA. The best performing method is rSOS, since it can cope with both increasing dimensions and outliers. Note that for cSOS the presence of outliers substantially increases the mcr but the number of uninformative variables has no further notable effect; for rSOS the mean mcr slightly increases when p tends to its highest value.

Table 1b shows that cSOS fails to identify the informative variables in presence of outliers. The FNR of cSOS is around 33% in this scenario, since the first of the three informative variables, the contaminated one, is not included anymore in the model. In this scenario the variables selected by cSOS do not contain any outliers, but since the information present in the first variable is lost, it still leads to an increased mcr. With rSOS this information can be recovered: rSOS down-weights the outliers and is able to reveal that this first variable contributes enough information to be selected. Comparing the FNR of rSOS in Table 1a and b shows an increase in the setting with outliers, but considerably smaller compared with cSOS. Finally, note that the FPR for rSOS is low, but slightly higher than for cSOS. In the second scenario, rSOS selects on average 4.7 variables, a bit more than the average of 2.2 variables for cSOS.

Fig. 3

Misclassification rate (mcr) averaged over 100 simulation runs, a scenario 3: as a function of increasing outlier proportion; $p=52$, $n=120$, b scenario 4: as a function of n, the number of observations (on log-scale); $p=53$, outlier proportion 10%

Scenario three illustrates how the percentage of outliers influences the classification performance of the different methods. Figure 3 pictures the mcr as a function of the proportion of outliers in the calibration data, for $p=52$. The benchmark given by the oracle is about 22.2%, and indicates a lower bound for the mcr. When there are no outliers, cSOS and rSOS are close to the oracle. However, already for only 5% outliers the cSOS is strongly affected in its prediction performance, whereas rSOS remains to give reasonable results for larger percentages of outliers. As expected, the mcr of LDA and rLDA is inflated due to the $p-q=50$ uninformative variables resulting in a high mean mcr, which increases slightly for higher percentages of contamination.

Figure 3b presents the results from scenario four and shows the best area of application as well as the limitations of the proposed algorithm. The number of variables is of moderate size and increasing the number of observations improves the performance of both non-sparse classifiers LDA and rLDA. Outliers in the simulation setting lead to heavy distortion of the classical methods LDA and cSOS. For small sample size ($n=120, n=600$) rSOS clearly outperforms all competitors whereas with sufficiently large sample size the robust covariance structure in rLDA can be properly estimated and slightly outperforms rSOS.

Computations are performed in R (R Core Team 2016). For classical sparse optimal scoring, R code is available in the package sparseLDA (Clemmensen and Kuhn 2012). The code for robust sparse optimal scoring is included in the package rrcovHD (Todorov 2016) in the function SosDiscRobust. The number of iteration steps for this algorithm depends on p with an average of 8.7 iterations for $p=3$ and 11.7 for $p=203$ in the simulation studies with $n=120$. Increasing n leads to fewer iterations.

Fig. 4

Fruit data: a visualization of 219 test observations in the projected subspace, b Mahalanobis distance of each projected test observation to its group center. Observations with weight smaller than one are colored in gray

Table 2 Fruit data: average (w)mcr is the (weighted) mcr averaged over the five test data sets

6 Examples

Fruit data: This data set consist of $n=1095$ measurements with $p=256$ wavelengths from $K=3$ different cultivars of the cantaloupe melon, named D, M and HA. We have 490 measurements from group D, 106 from group M and 499 from group HA. It is a well known benchmark data set to demonstrate the stability of robust classification methods (Hubert et al. 2008; Hubert and Van Driessen 2004; Vanden Branden and Hubert 2005). From former analyses it is known that the change of illumination led to outliers.

The data are 5 times split into calibration and test data (80% versus 20%), such that all observations are included in the test data once and the observations from each class are evenly spread across the test sets. For each calibration data set the optimal sparsity parameter $\lambda ^*$ is selected as described in Sect. 4 from a fine grid starting with $10^{-4}$ up to $10^{-1}$ with step size 0.002, covering model sizes from nearly full to empty.

The procedure is repeated for all calibration and test sets and results are summarized in Table 2. The weighted misclassification rate wmcr is calculated from the test data as in Eq. (5). The weights from the rSOS model are also used to calculate the wmcr for cSOS. Thereby observations which are detected as outliers by the rSOS model receive small influence on the wmcr of cSOS. Table 2 shows that the mcr of the cSOS is smaller than the mcr of the rSOS. On the other hand, the wmcr has a lower value for rSOS than for cSOS. The classical method tries to model the outliers and since outliers are present in the test data it achieves better results as well. The robust method, on the other hand, mainly models the non-outliers. So the weighted misclassification rate, which excludes the outliers, is lower for rSOS than for cSOS.

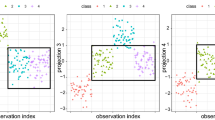
For visualization of the results we randomly select one of the five data splits and apply rSOS to the calibration data. Figure 4a shows the test observations projected into the subspace. The ellipses defined by the sets $\{\varvec{z} \in \mathbb {R}^2 | \mathrm {MD}\left( \varvec{z}; \varvec{m}_k, \varvec{S} \right) =\sqrt{\chi _{2}^2(0.975)} \}$, for $k=1,2,3$ enclose those observations which are considered non-outliers and which did receive weight one in the wmcr. The observations outside of the ellipses are colored in gray. Most outliers are from group HA which is in line with previous analyses (Vanden Branden and Hubert 2005). In Fig. 4b the Mahalanobis distances of each test observation to its group center are shown. The horizontal line represents the cut-off value $\sqrt{\chi _{2}^2(0.975)}$. Again we see that many observations of HA have a large Mahalanobis distance in the projected space. Figure 4b pinpoints other anomalous observations in all three groups.

Table 3 Olive oil data: average (w)mcr is the (weighted) mcr averaged over the five test data sets

Fig. 5

Olive oil data: Mahalanobis distances from rSOS of each projected observation to its group center. Observations with weight smaller than one are colored in gray

Olive oil data: The data set olitos (Armanino et al. 1989) available in the R package rrcovHD (Todorov 2016) contains $n=120$ measurements on olive oil samples with $p=25$ variables from fatty acids, sterols and triterpenic alcohols. The olive oils originate from Tuscany in Italy and are grouped into $K=4$ classes representing different regions of production with group size 50, 25, 34 and 11. In this example, the number of variables is quite low, but rSOS can still be an appropriate method. We will compare its results to cSOS as well as to LDA and rLDA. To estimate the models and to evaluate them, the same approach is taken as described previously for the fruit data. The optimal sparsity parameter is searched on a grid from 0.01 to 1 with step size 0.05, which covers various model sizes from the full model to the empty model.

Table 3 summarizes the quality of the resulting models. Our proposed method rSOS performs better on this data set than the other methods with an average wmcr of 13.3%. Interestingly, also the mcr is lowest for rSOS with 15.3%. This may happen if there is no pattern in the outlier configuration.

The classical sparse method cSOS outperforms LDA slightly, and robust LDA has a much lower prediction quality than all other methods. Figure 5 shows the Mahalanobis distances from the rSOS estimator of the projected test data. Especially region 3 and 4 have some observations with large distance to its group centers in the projected space. In Fig. 6 the projection of all observations into the subspace is visualized.

Fig. 6

Olive oil data: pairwise scatter plots of data projected into the 3-dimensional subspace derived from rSOS. Observations with weight smaller than one are colored in gray

Audio data: This database consists of more than 4000 audio samples with 679 features. The audio samples come from 12 different groups such as recordings from classical and electronic music, cats and whale sounds, the noise of crowds, speech recordings from men and women and others (Brodinova et al. 2015).

We construct 10 experimental data sets to demonstrate the performance under varying data structure. For each data set we randomly choose $K=4$ of the audio groups and randomly select 80, 70, 60 and 50 audio samples from the each of the groups, respectively. Further we add 23 observations from the remaining groups to the data set and assign them randomly to any of the four classes, thus generating outliers. Hence, each data set contains $n=283$ observations, of which approximately 8% are artificial outliers, and $p=679$ features.

The constructed data sets are randomly spit into calibration (80%) and test data (20%) such that the class proportions are preserved and the models are evaluated on the test data. Similar as in the simulation study the sparsity parameter is chosen from a grid of values between 0.1 and 2 with step size 0.05.

Table 4 Audio data: average (w)mcr is the (weighted) mcr averaged over the 10 experimental settings

The average mcr and wmcr computed from the 10 different data sets are reported in Table 4. We also report the results when the artificial outliers are removed from the data sets and cSOS is applied. First, note that the average mcr is not much different between cSOS and rSOS. To reduce the influence of outliers on the evaluation criterion, the wmcr should be used. Here rSOS clearly outperforms cSOS. Note that the average mcr calculated with cSOS from the data set without artificial outliers is 0.029 and close to the average wmcr calculated with rSOS. This shows, that the wmcr gives an approximation of the mcr without outliers.

7 Conclusion

This paper introduced a robust and sparse optimal scoring method for multigroup classification. It yields a new supervised classification method, applicable if the number of variables is large with respect to the sample size and with possible presence of outliers in the data. Using an iterative algorithm, it searches for an optimal projection into a subspace using only a subset of the original variables; the most informative ones. Potential outliers are down-weighted, reducing their influence in the search for this optimal projection. The final classification is then carried out in this ($K-1$)-dimensional subspace. As shown in the examples in Sect. 6, the resulting low-dimensional representation of the data is also useful for visualization and interpretation.

The algorithm we developed, see Sect. 3, is implemented and publicly available in the R-package rrcovHD (Todorov 2016). This package contains outlier detection methods and robust statistical procedures for high dimensions. A call to the function SosDiscrRobust, with the data matrix and the class memberships as input, returns the estimated model.

Only few proposals exist so far for robust classification in high dimensions. Our proposal has the important feature of being sparse, simultaneously performing variable selection and model estimation, by using a (robust) Lasso-type approach. The simulation study has shown the importance to consider both sparse modeling and robust estimation. If either of them is missing, the prediction performance may decrease drastically.

Appendix

1.1 Derivation of expression (4) for the score vector estimates

Let $\omega _1,\ldots ,\omega _n$ be case weights for each observation. $\varvec{\varOmega }$ is a diagonal matrix with these case weights in the diagonal. Then the weighted data matrices are $\varvec{\tilde{Y}}=\varvec{\varOmega }^{1/2}\varvec{Y}$ and $\varvec{\tilde{X}}=\varvec{\varOmega }^{1/2}\varvec{X}$. The diagonal matrix with weighted class proportions is $\varvec{\tilde{D}}=\frac{1}{\sum \omega _i}\varvec{\tilde{Y}}^T \varvec{\tilde{Y}}$. The optimization problem (2) in step h for a given $\varvec{\hat{\beta }}$ can be rewritten as

$$\begin{aligned} \min _{\varvec{\theta }}\Vert \varvec{\tilde{X}}\varvec{\hat{\beta }} - \varvec{\tilde{Y}}\varvec{\theta } \Vert ^2 \quad \text {s.t.} \quad \varvec{\theta }^T\varvec{\tilde{D}}\varvec{\theta }=1 \text { and } \varvec{C}\varvec{\theta }=\varvec{0} \in \mathbb {R}^h \end{aligned}$$

(6)

with $\varvec{C}=[\hat{\varvec{\theta }}_{1},\ldots , \hat{\varvec{\theta }}_{h-1}]^T\varvec{\tilde{D}}$, and we drop the depending on the index h for ease of notation.

We use the method of Lagrange multipliers. The Lagrangian associated to Eq. (6) is given by

$$\begin{aligned} L=(\varvec{\tilde{X}}\varvec{\hat{\beta }} - \varvec{\tilde{Y}}\varvec{\theta })^T (\varvec{\tilde{X}}\varvec{\hat{\beta }} - \varvec{\tilde{Y}}\varvec{\theta }) - \eta (\varvec{\theta }^T\varvec{\tilde{D}}\varvec{\theta } - 1) - 2\varvec{\gamma }^T\varvec{C}\varvec{\theta }. \end{aligned}$$

The partial derivative set to zero gives

$$\begin{aligned} \frac{\partial L}{\partial \varvec{\theta }}=-2\varvec{\tilde{Y}}^T(\varvec{\tilde{X}} \varvec{\hat{\beta }}-\varvec{\tilde{Y}}\varvec{\theta }) -2\eta \varvec{\tilde{D}}\varvec{\theta } -2\varvec{C}^T\varvec{\gamma }=\varvec{0}. \end{aligned}$$

Hence,

$$\begin{aligned} \varvec{\theta }=(\varvec{\tilde{Y}}^T\varvec{\tilde{Y}} -\eta \varvec{\tilde{D}})^{-1}(\varvec{\tilde{Y}}^T \varvec{\tilde{X}}\varvec{\hat{\beta }} +\varvec{C}^T\varvec{\gamma }). \end{aligned}$$

To solve for the Lagrange multipliers $\eta$ and $\varvec{\gamma }$, the side constraints are used.

$$\begin{aligned} 0=\varvec{C}\varvec{\theta }= \varvec{C}(\varvec{\tilde{Y}}^T\varvec{\tilde{Y}}-\eta \varvec{\tilde{D}})^{-1} \varvec{\tilde{Y}}^T\varvec{\tilde{X}}\varvec{\hat{\beta }}+ \varvec{C}(\varvec{\tilde{Y}}^T\varvec{\tilde{Y}}-\eta \varvec{\tilde{D}})^{-1} \varvec{C}^T\varvec{\gamma } \end{aligned}$$

So

$$\begin{aligned} \varvec{\gamma }=-\left( \varvec{C} (\varvec{\tilde{Y}}^T \varvec{\tilde{Y}}-\eta \varvec{\tilde{D}})^{-1} \varvec{C}^T \right) ^{-1} \varvec{C} (\varvec{\tilde{Y}}^T\varvec{\tilde{Y}}- \eta \varvec{\tilde{D}})^{-1} \varvec{\tilde{Y}}^T \varvec{\tilde{X}}\varvec{\hat{\beta }}. \end{aligned}$$

We conclude

$$\begin{aligned} \varvec{\theta }= & {} (\varvec{\tilde{Y}}^T \varvec{\tilde{Y}} -\eta \varvec{\tilde{D}})^{-1}\nonumber \\&\left\{ \varvec{I} - \varvec{C}^T(\varvec{C}(\varvec{\tilde{Y}}^T \varvec{\tilde{Y}}- \eta \varvec{\tilde{D}})^{-1}\varvec{C}^T)^{-1} \varvec{C} (\varvec{\tilde{Y}}^T\varvec{\tilde{Y}} - \eta \varvec{\tilde{D}})^{-1} \right\} (\varvec{\tilde{Y}}^T \varvec{\tilde{X}}\varvec{\hat{\beta }}). \end{aligned}$$

(7)

Since $\varvec{\tilde{Y}}^T\varvec{\tilde{Y}}$ is proportional to $\varvec{\tilde{D}}$, there exists a scalar c such that

$$\begin{aligned} (\varvec{\tilde{Y}}^T\varvec{\tilde{Y}} - \eta \varvec{\tilde{D}})^{-1}=c\varvec{\tilde{D}}^{-1}. \end{aligned}$$

Formula (7) can be simplified to

$$\begin{aligned} \varvec{\theta }=c\left\{ \varvec{I} - \varvec{\tilde{D}}^{-1} \varvec{C}^T (\varvec{C} \varvec{\tilde{D}}^{-1} \varvec{C}^T)^{-1} \varvec{C}\right\} \varvec{\tilde{D}}^{-1} \varvec{\tilde{Y}}^T \varvec{\tilde{X}} \varvec{\hat{\beta }}. \end{aligned}$$

Due to the symmetry of $\varvec{\tilde{D}}$ and with the definition of $\varvec{C}=\varvec{Q}^T\varvec{\tilde{D}}$ we obtain

$$\begin{aligned} \varvec{\theta }=c\left\{ \varvec{I} - \varvec{Q} (\varvec{Q}^T \varvec{\tilde{D}} \varvec{Q})^{-1} \varvec{Q}^T \varvec{\tilde{D}} \right\} \varvec{\tilde{D}}^{-1} \varvec{\tilde{Y}}^T \varvec{\tilde{X}} \varvec{\hat{\beta }}. \end{aligned}$$

The scalar c can then be scaled so that the side constraint $\varvec{\theta }^T\varvec{\tilde{D}}\varvec{\theta }=1$ is fulfilled.

1.2 Algorithm for the computation of the initial estimates for $\varvec{\beta }_h$ and $\varvec{\theta }_h$

Input: $h, \varvec{Q}_h, \varvec{X}, \varvec{Y}$, $\lambda$

• (i) Compute $\varvec{D}=\frac{1}{n}\varvec{Y}^T\varvec{Y}$.

• (ii) Generate $\varvec{\theta }_{*}$, a random vector from N(0, 1) of length K.

• (iii) Compute $\hat{\varvec{\theta }}_h=c\left\{ \varvec{I} - \varvec{Q}_h (\varvec{Q}_h^T \varvec{D} \varvec{Q}_h)^{-1} \varvec{Q}_h^T \varvec{D} \right\} \varvec{\theta }_{*}$, with c so that $\hat{\varvec{\theta }}_h^T\varvec{D}\hat{\varvec{\theta }}_h=1$.

Apply twice the following steps:

• 1. For fixed $\hat{\varvec{\theta }}_h$ apply sparse least trimmed squares (sparse LTS) regression (Alfons et al. 2013) to the response $\varvec{Y}\hat{\varvec{\theta }}_h$ and predictors $\varvec{X}$.

  Let $a=0.5n$ and $\Vert \varvec{r}\Vert ^2_{1:a}=\sum _{i=1}^a r_{(i)}^2$ denote the sum of the a smallest squared elements of the vector $\varvec{r}$. The sparse LTS estimator is a robust version of the Lasso and defined as

  $$\begin{aligned} \min _{\varvec{\beta }}\frac{1}{a}\Vert \varvec{Y} \varvec{\theta }_h-\varvec{X}\varvec{\beta }\Vert ^2_{(1):(a)} + \lambda \Vert \varvec{\beta }\Vert _1. \end{aligned}$$

  As in Alfons et al. (2013), a re-weighting step is carried out afterwards yielding $\hat{\varvec{\beta }}_h$.

• 2. For fixed $\hat{\varvec{\beta }}_h$ apply least absolute deviation (LAD) regression with response $\varvec{X}\hat{\varvec{\beta }}_h$ and predictor matrix $\varvec{Y}$:

  $$\begin{aligned} \varvec{\theta }^*=\mathop {\text{ argmin }}_{\varvec{\theta }}\Vert \varvec{Y}\varvec{\theta }-\varvec{X} \hat{\varvec{\beta }}_h\Vert _1. \end{aligned}$$

  The LDA estimator is robust to outliers in the dependent variable, but not to leverage points (i.e. outliers in the covariate space). Since the covariates are dummy variables here, leverage points cannot occur. Then we apply the transformation for satisfying the side constraints:

  $$\begin{aligned} \hat{\varvec{\theta }}_h=c\left\{ \varvec{I} - \varvec{Q}_h (\varvec{Q}_h^T \varvec{D} \varvec{Q}_h)^{-1} \varvec{Q}_h^T \varvec{D} \right\} \varvec{\theta }^*. \end{aligned}$$

Output: Initial estimators $\hat{\varvec{\beta }}_h$ and $\hat{\varvec{\theta }}_h$.