Sampling frequent and minimal boolean patterns: theory and application in classification

Abstract

We tackle the challenging problem of mining the simplest Boolean patterns from categorical datasets. Instead of complete enumeration, which is typically infeasible for this class of patterns, we develop effective sampling methods to extract a representative subset of the minimal Boolean patterns in disjunctive normal form (DNF). We propose a novel theoretical characterization of the minimal DNF expressions, which allows us to prune the pattern search space effectively. Our approach can provide a near-uniform sample of the minimal DNF patterns. We perform an extensive set of experiments to demonstrate the effectiveness of our sampling method. We also show that minimal DNF patterns make effective features for classification.

1 Introduction

Frequent pattern mining has long been a mainstay of data mining, with the focus of most existing work on complete enumeration methods. However, in many real-world problems the number of possible frequent patterns can be exponentially many, and in such cases it is important to develop approaches that can effectively sample the pattern space for the most interesting patterns. Whereas much research in the past has focused on itemset mining, i.e., conjunctive patterns, our focus is on the entire class of Boolean patterns in the disjunctive normal form (DNF), i.e., disjunctions over conjunctive patterns. Such Boolean patterns can help discover interesting relationships among attributes. As a simple example, consider the dataset shown in Fig. 1. It has 10 countries, described by four attributes: G—permanent members of the UN security council, R—countries with a history of communism, B—countries with land area over 3 million square miles, and Y—popular tourist destinations in North and South America. For instance there are five countries that are permanent members of the UN security council, namely China, France, Russia, UK and USA. Let us assume that we want to characterize the three countries China, Russia and USA. One of the simplest Boolean expressions that precisely describes them is (G and B), i.e., countries that are members of the UN security council with land are over 3 million square miles. However, there are two other Boolean expressions that also precisely characterize these three countries, namely (B and R) or ( G and Y) and (G and R) or ( G and Y). The former states that China, Russia and USA make up the exact set of countries that are either permanent members of UN security council that are popular tourist destinations in the Americas, or large landmass countries with history of communism. In fact, no sub-expression of these expression can describe the three countries of interest, and therefore they represent the set of simplest or minimal Boolean expressions for the chosen countries. If we allow negated attributes, we can get even richer Boolean expressions. For example, the minimal Boolean expression (not B) or (G and not R), i.e., countries that are not large or are UN security council members without history of communism, exactly describes Argentina, Brazil, Chile, Cuba, France, UK and USA.

Fig. 1

Countries dataset: four attributes ($G, R, B, Y$)

Boolean expressions play a prominent role in mining complex gene regulatory networks, which can be represented in a simplified form, as boolean networks (Akutsu et al. 1998). Consider the network involving 16 genes, taken from Akutsu et al. (1998), shown in Fig. 2. Here $\oplus$ and $\ominus$ denote gene activation and deactivation, respectively. For example, genes B, E, H, J, and M are expressed if their parents are not expressed. On the other hand G, L, and D express if all of their parents express. For example, D depends on C, F, X1 and X2. Note that F expresses if A does, but not L. Finally A, C, I, K, N, X1 and X2 do not depend on anyone, and can thus be considered as input variables for the boolean network.

Fig. 2

Gene network

We can model this network via a truth table corresponding to the seven input genes, but without explicit instruction about which are inputs and which are outputs. This yields a dataset with 128 rows and 16 items (genes). Some of the simple boolean expressions that all the rows satisfy include (not J) or A, (not F) or A, (not D) or A, H or A. Consider the first expression; which conveys an important fact about the gene network as follows: if J is present, then H cannot be present, which in turn implies that F is present. Finally, if F is expressed, then it implies that A must be present. This is precisely what the first expression states, since (not J) or A is logically equivalent to the implication J $\implies$ A. Another simple Boolean expression that is true for all the 128 rows is B or (not J) or (not L). Consider the input gene A. If B is present, it must mean that A is not there, which covers 64 out of the 128 rows. For the remaining 64 rows, we have A and not B. Among these consider gene C. If C is absent, then L cannot be present either. For the remaining 32 rows, we must have A and (not B) and C. Finally, consider when K is present, in this case M cannot be present and therefore neither can L be present. When K is not present, then M is present, and since C is also present, then L must be present, which in turn implies that F is not present, H is present, and J is not present. Thus, the 128 rows satisfy the condition that B or (not J) or (not L).

Boolean expression mining has many other applications, ranging from recommender systems (moving beyond purely conjunctive recommendations), to gene expression mining (Zhao et al. 2006). In general, given any binary-valued dataset, it allows one to mine the important logical relationships between the attributes. However, complete enumeration of all frequent Boolean patterns is prohibitive in most real-world datasets, and thus the main issue is how to effectively sample a representative subset. Such patterns can in turn be used as features to build classification models. To minimize the information overload problem, we focus on the problem of sampling only the most simple Boolean patterns that completely characterize a subset of the data, i.e., the minimal DNF expressions. Our work makes a number of novel contributions:

• (a) We propose the first approach to generate a near-uniform sample of the minimal Boolean expressions. Our method, based on Markov chain monte carlo (MCMC) sampling, yields a succinct subset of the simplest frequent Boolean patterns.

• (b) We propose a novel theoretical characterization of the minimal DNF expressions, which allows us to prune the pattern search space effectively. When combined with other optimization techniques, our approach is also practically effective. For instance, we are able to sample interesting “support-less” patterns, i.e., where the minimum frequency threshold is set to one. The pruning techniques can be applied by any method (even a complete one) for mining Boolean expressions.

• (c) We perform an extensive set of experiments to demonstrate the effectiveness of our method. In particular, we classify a variety of datasets from the UCI Machine Learning Repository (Frank and Asuncion 2010), and show that minimal DNF patterns make very effective features for classification. We also study the sample quality of our approach, as well as its scalability.

1.1 Preliminaries

Dataset: Let $\mathcal {Z}=\{z_1, z_2,\ldots , z_m \}$ be a set of binary-valued attributes or items, and let $\mathcal {T}=\{t_1, t_2, \ldots , t_n\}$ be a set of transactions identifiers or tids. A dataset $\mathcal {D}$ is a binary relation $\mathcal {D}\subseteq \mathcal {Z}\times \mathcal {T}$. The dataset $\mathcal {D}$ can also be considered as a set of tuples of the form $(t, t.X)$ where $t \in \mathcal {T}$ and $t.X \subseteq \mathcal {Z}$. Note that any categorical dataset can easily be converted into this format by assigning an item for each attribute-value pair.

Given dataset $\mathcal {D}$, we call $\mathcal {D}^T$ the vertical or transposed dataset comprising tuples of the form $(z, z.Y)$ where $z \in \mathcal {Z}$ and $z.Y \subseteq \mathcal {T}$. Table 1 shows an example dataset $\mathcal {D}$ and its transpose $\mathcal {D}^T$. The dataset has six items $\mathcal {Z}=\{A,B,C,D,E,F\}$ and five transactions $\mathcal {T}=\{1,2,3,4,5\}$. For example, the tuple $(2, ACDF) \in \mathcal {D}$ denotes the fact that tid $2$ has four items $A, C, D, F$, whereas the tuple $(E, 134) \in \mathcal {D}^T$ denotes the fact that item $E$ is contained in transactions $1, 3, 4$. For convenience, we write subsets without commas. Thus $\{A,C,D,F\}$ is written as ACDF, and so on.

Table 1 Dataset $\mathcal {D}$ (a) and its transpose $\mathcal {D}^T$ (b)

Boolean expressions: Let and, or, and not denote the logical operators. We denote a negated item $(\textsc {not}\ z)$ as $\bar{z}$. We also call $\bar{z}$ the complement of $z$. We use the symbols $\wedge$ and $\vee$ to denote $\textsc {and}$ and $\textsc {or}$, respectively. For example, $A \vee B$ and $A \wedge B$ denote logical expressions $A$ or $B, A$ and $B$, respectively. For conciseness we also use $|$ in place of $\vee$ and we usually omit the $\wedge$ operator. For example, $A|BC|D$ denotes the Boolean expression $A$ or ($B$ and $C$) or $D$.

A literal is either an item $z$ or its complement $\bar{z}$. A clause is either the logical $\textsc {and}$ or the logical $\textsc {or}$ of a set of literals. An AND-clause contains only the $\textsc {and}$ operator over all its literals, e.g., $BCD$. Likewise, an OR-clause contains only the $\textsc {or}$ operator over all its literals, e.g., $C|E|F$. We assume that a clause does not contain both a literal and its complement – e.g., $A \wedge \bar{A}$ leads to contradiction, and $\bar{A} \vee A$, to a tautology.

We adopt the DNF to represent Boolean expressions. A Boolean expression $Z$ is said to be in DNF if it consists of $\textsc {or}$ of AND-clauses, with the $\textsc {not}$ operator (if any) directly preceding only literals, written as:

$$\begin{aligned} Z = \bigvee _{i=1}^k Z_i = \bigvee _{i=1}^{k}\left( z_{i1} \wedge z_{i2} \wedge \ldots \wedge z_{i m_i} \right) \end{aligned}$$

Here each $z_{ik}$ is a literal and each $Z_i = (z_{i1}\wedge \ldots \wedge z_{i m_i})$ is an AND-clause. The size or length of a Boolean expression $Z$ is the number of literals in $Z$, denoted $|Z| = \sum _{i=1}^k m_i$.

Tidset and support: Given a tuple $(t, t.X) \in \mathcal {D}$, and a literal $l$, the truth value of $l$ in $t$ is $1$ if $l \in t.X$, and $0$ otherwise. Likewise, the truth value of $\bar{l}$ is $1$ if $l \not \in t.X$, and $0$ otherwise. We say $t$ satisfies a Boolean expression $Z$, if after replacing every literal in the Boolean expression with its truth value, the Boolean expression evaluates to true. The set of all satisfying transactions is called the tidset of $Z$, and is denoted as

$$\begin{aligned} T(Z) = \{t \in \mathcal {T}| t \text{ satisfies } Z\}. \end{aligned}$$

The number of satisfying transactions is called the support of $Z$ in $\mathcal {D}$, denoted $sup(Z) = |T(Z)|$. For the example database in Fig. 1, the tidset of the expression $AB|C$ is $t(AB|C) = 12$, and its support is therefore $sup(AB|C)=2$.

Minimal Boolean Expressions: Given DNF expressions $X = \bigvee _{i=1}^m X_i$ and $Y = \bigvee _{j=1}^n Y_j$, where $X_i$ and $Y_j$ are AND-clauses, we say that $X$ is a subset of $Y$, denoted $X \subseteq Y$, iff there exists an injective (or into) mapping $\phi : X \rightarrow Y$, that maps each clause $X_i$ to $\phi (X_i) = Y_{j_i}$, such that $X_i \subseteq Y_{j_i}$. If $X \subset Y$ and $|X| = |Y|-1$, we say that $X$ is a parent of $Y$, and $Y$ is a child of $X$.

Definition 1

A DNF expression $Z$ is said to be minimal or minDNF (with respect to support) if there does not exist any expression $Y \subset Z$, such that $T(Y) = T(Z)$. A minimal AND-clause is called minAND for short. A minimal Boolean expression is also called a minimal generator.

A minDNF expression $Z$ is thus the simplest DNF expression with tidset $T(Z)$. For example, the expression $AB|C$ is minDNF since its tidset is $T(AB|C) = 12$, but none of its subsets has the same tidset – we have $T(A|C) = 124, T(B|C) = 1235, T(AB)=1, T(A)=124, T(B)=135$, and $T(C)=2$. On the other hand, $A|C$ is not minimal since $T(A)=124$ which matches $T(A|C)$. Here $A$ is necessary and sufficient to characterize the tids $1, 2$, and $4$.

Frequent Boolean Expressions: Given a user-specified minimum support threshold ${\sigma _{\min }}$, we say that a DNF expression $Z$ is frequent if $sup(Z) \ge {\sigma _{\min }}$. However, note that the support of a minDNF expression is not monotonic, since the addition of an item to a clause causes the support to drop, whereas, the addition of an item as a new clause causes the support to increase. For example, $sup(A) = 3$, since $T(A) = 124$, but $sup(AB) = 1$ (since $T(AB)=1$) and $sup(A|E) = 4$ (since $T(A|E) = 1234$). Thus, the support of $Z$’s children can be higher or lower.

Let ${\sigma ^c_{\min }}={\sigma _{\min }}=1$. Table 2 shows the complete set of frequent minimal Boolean expressions, not allowing negated items, for the example dataset in Table 1. Given five transactions, there are 31 possible non-empty tidsets. Out of these there is no possible minDNF expression which precisely characterizes seven of the tidsets, namely 15, 25, 45, 125, 145, 245, and 1245 (again, disallowing negated items). For example, consider the tidset $15$. We might consider $ABE|BF$ as a possible boolean expression. However, $T(ABE|BF) = 135$. Put another way, since $BF \subset BEF$ the tid 5 cannot appear in isolation, it must always be accompanied by tid 3 in any tidset. For the remaining 24 tidsets, we have many possible minDNF expressions, as listed in Table 2. In total there are 43 frequent minDNF expressions in our example (discounting the empty expression). In general, given $n$ transactions and assuming that none is a subset of another, then each of $2^n - 1$ possible non-empty tidsets has at least one minDNF that characterizes it. Even if we restrict our attention to those tidsets with cardinality at least ${\sigma _{\min }}$, we still have an exponential search space, and it is typically not feasible to mine the complete set of frequent minDNF expressions. Thus, we focus on sampling a representative subset of frequent minDNF expressions and we also consider additional constraints to further reduce the search space.

Table 2 Complete set of frequent minimal Boolean expressions with ${\sigma _{\min }}=1$

Clause support and overlap constraints: We already noted that minDNF frequency is non-monotonic. Also note that any infrequent clause can be made frequent by adding additional clauses. For example, if ${\sigma _{\min }}=2$, then $C$ is infrequent for our example dataset in Table 1, but $C|B$ is frequent, since $T(C)=2$ and $T(C|B)=1235$. To prevent such “trivial” clauses, we also impose a minimum clause support threshold ${\sigma ^c_{\min }}$ on the clauses. That is, for any DNF expression $Z = \bigvee _{i=1}^m Z_i$, we require that $\sup (Z_i) \ge {\sigma ^c_{\min }}$ for all $i=1,\ldots ,m$. Clearly, clause support must satisfy ${\sigma ^c_{\min }}\le {\sigma _{\min }}$, since if a clause has support at least ${\sigma ^c_{\min }}$, then by definition the DNF expression must have support at least ${\sigma ^c_{\min }}$. For example, if ${\sigma _{\min }}=3$ and ${\sigma ^c_{\min }}=2$, then there are 12 minDNFs as shown in Table 3. Note that while $T(D|EF) = 234$ and thus $sup(D|EF)=3$, it fails the minimum clause support test, since $sup(EF)=1$. Also, whereas $E|C$ is also a minDNF with support $sup(E|C)=4$ (since $T(E|C)=1234$), it also fails the minimum clause support constraint because $sup(C)=2$, and therefore does not appear in Table 3.

Table 3 Frequent minDNF expressions with ${\sigma _{\min }}=3$ and ${\sigma ^c_{\min }}=2$

Since any clause’s support can be increased by adding another clause, we want to prevent unrelated additions, i.e., we impose a minimum clause overlap constraint on the tidsets. That is, for any DNF expression $Z = \bigvee _{i=1}^m Z_i$, we require that $|T(Z_i) \cap T(Z_j)| \ge {\sigma ^o_{\min }}$ for all $i \ne j$, where ${\sigma ^o_{\min }}$ is the number of common tids for the two clauses. For example, if ${\sigma _{\min }}=3, {\sigma ^c_{\min }}=2$ and ${\sigma ^o_{\min }}=2$, then $F|D$ is not a valid minDNF expression, since $|T(F) \cap T(D)| = |235 \cap 24| = 1$. In other words $F$ and $D$ are not sufficiently related. The minimum overlap constraint is a form of (pair-wise) minimum support check on the conjunctive clause $T(Z_i \cup Z_j)$, and it also serves to prune out trivial disjunctions.

Table 4 shows the set of minDNF expressions that satisfy the constraints ${\sigma _{\min }}=3, {\sigma ^c_{\min }}=2, {\sigma ^o_{\min }}=2$. We can observe that there is no satisfying minDNF for the tidset $12345$, since all the overlap among the tidsets for the corresponding pair-wise clauses shown in Table 3 fail the minimum overlap test.

Table 4 Frequent minDNF expressions with ${\sigma _{\min }}=3, {\sigma ^c_{\min }}=2$, and ${\sigma ^o_{\min }}=2$

Sampling frequent minDNF expressions: Combining all the constraints, we say that a DNF expression $Z = \bigvee _{i=1}^m Z_i$, is frequent iff $sup(Z) \ge {\sigma _{\min }}, \sup (Z_i) \ge {\sigma ^c_{\min }}$, and $|T(Z_i) \cap T(Z_j)| \ge {\sigma ^o_{\min }}$ for all $i,j=1,\ldots ,m$. As noted earlier, we are interested in sampling the frequent minDNF expressions, as opposed to complete mining, which is typically infeasible for many real-world datasets. For frequent minDNF sampling, we start from the empty expression. We then use the MCMC approach to sample the minimal expressions. The main challenges include efficiency and guaranteeing sampling quality. We address these questions below after reviewing some MCMC terminology and related work.

Markov chains: Let $\mathcal {S}= \{s_0, s_1, \ldots , s_N\}$ be the finite and discrete state space comprised of frequent Boolean expressions. Let $t \in {\mathord {\mathbb {N}}}$ denote the (discrete) time for an event, and let $X_t$ denote a random variable that represents the state at time $t$. A Markov chain over the finite state space $\mathcal {S}$ is a sequence of random variables $X_0, X_1, X_2, \ldots$, such that the current state $X_t$ depends only on the previous state $X_{t-1}$, i.e.,

$$\begin{aligned} P(X_{t+1}=s_{t+1}|X_t =s_t, X_{t-1}=s_{t-1}, \ldots , X_{0}= s_{0}) = P(X_{t+1}=s_{t+1}|X_t=s_t), \end{aligned}$$

for all $t \in {\mathord {\mathbb {N}}}$ and $s_t \in \mathcal {S}$. A homogeneous Markov chain is one where the transition probability between any two states is independent of time. That is, the transition from state $s_i$ to $s_j$ is governed by the transition probability $p(i,j) = P(X_t=j | X_{t-1}=i)$. Thus, the Markov chain is uniquely defined by the pair-wise transition probability matrix $\mathbf {P}= \{p(i,j)\}_{i,j \in 1,\ldots ,N}$.

Let $p^t(i,j)$ denote the $t$-step transition probability, i.e., $p^t(i,j)=P(X_{n+t}=s_{n+t}|X_{n}=s_{n})$. It is easy to show that the $t$-step transition probability matrix is simply $\mathbf {P}^t$, i.e., the $t$-th power of $\mathbf {P}$. Given two states $s_i$ and $s_j$, we say $s_j$ is reachable from $s_i$, if $\exists ~t, s.t.~ p^t(i,j)>0$, and we denote it as $s_i\rightarrow s_j$. If all state pairs are mutually reachable, we call the Markov chain irreducible. Let $R(i)$ denote the set of times when the chain returns to a starting state $s_i$, i.e., $R(i) = \{t > 0 |\; p^t(i,i) > 0\}$. The period of state $s_i$ is defined as the greatest common divisor of $R(i)$. The state is called aperiodic if its period is $1$. A Markov chain is called aperiodic if all states are aperiodic, i.e., have period $1$. If a Markov chain is irreducible and aperiodic, then for all states $s_i, s_j \in \mathcal {S}$, there $\exists ~t \in {\mathord {\mathbb {N}}}$, s.t. $p^t(i,j)>0$. Let $r^t(i,j)$ denote the probability that state $s_j$ is reachable from $s_i$ for the first time after $t$ steps, i.e.,

$$\begin{aligned} r^t(i,j) = \min \{p^t(i,j) > 0 |\; t > 0\}, \end{aligned}$$

A state $s_i$ is called recurrent if starting from $s_i$, the Markov chain will eventually return to $s_i$ with certainty, i.e., if $\sum _{t \ge 1} r^t(i,u) = 1$. Let $h(i,i) = \sum _{t \ge 1} t \cdot r^t(i,u)$ denote the expected time of return to state $s_i$ starting from $s_i$. A recurrent state $s_i$ is called positive recurrent if $h(i,i) < \infty$. An aperiodic, positive recurrent state is called an ergodic state, and a Markov chain is called ergodic if all its states are ergodic. It is known that any finite, aperiodic and irreducible Markov chain is an ergodic chain. An ergodic Markov chain has a unique stationary distribution $\pi =(\pi _{i}|s_i\in \mathcal {S})$, that satisfies the property

$$\begin{aligned} \pi \mathbf {P}= \pi , \qquad \text { i.e.,} \sum _{s_i \in \mathcal {S}} \pi _i p(i,j) = \pi _j \end{aligned}$$

Note that the distribution must also satisfy the conditions: (1) $\pi _{i}>0$ for all $s_i \in \mathcal {S}$ and (2) $\sum _{s_i \in \mathcal {S}} \pi _{i}= 1$. If the distribution $\pi$ satisfies the detailed balance equation

$$\begin{aligned} \pi _i p(i,j) = \pi _j p(j,i), \end{aligned}$$

(1)

for all $s_i, s_j \in \mathcal {S}$, then $\pi$ is the stationary distribution for the Markov chain; in this case it is also called a time reversible Markov chain.

2 Related work

Mining frequent itemsets (i.e., pure conjunctions or AND-clauses) has been extensively studied within the context of itemset mining (Agrawal et al. 1996). The closure operator for itemsets was proposed in Ganter and Wille (1999), and the notion of minimal generators for itemsets was introduced in Bastide et al. (2000). Many algorithms for mining closed itemsets [see Goethals and Zaki (2004)], and a few to mine minimal generators (Bastide et al. 2000; Zaki and Ramakrishnan 2005; Dong et al. 2005) have also been proposed in the past. The work in Dong et al. (2005) focuses on finding the succinct (or essential) minimal generators for itemsets, using a depth first approach for the local minimal generators and closed itemsets. CHARM-L (Zaki and Ramakrishnan 2005) modifies CHARM (Zaki and Hsiao 2005) to find the minimal generators for itemsets. It first mines the closed sets, builds a lattice, and then uses the lattice to extract the minimal generators.

The task of mining closed and minimal monotone DNF expressions was proposed in Shima et al. (2004). It gives a direct definition of the closed and minimal DNF expressions (i.e., a closed expression is one that doesn’t have a superset with the same support and a minimal expression is one that doesn’t have a subset with the same support). The authors further give a level-wise Apriori-style algorithm to extract closed monotone DNF formulas. Over previous work (Zhao et al. 2006, Zaki et al. 2010) proposed a complete framework, called BLOSOM, to extract the minimal DNF and pure AND-clauses, as well as the minimal CNF (conjunctive normal form – AND of OR-clauses) and pure OR-clauses. Blosom uses a two-step process to mine the minDNFs. It first mines all minimal AND-clauses, treats them as new items, as then extracts minimal OR-clauses over these composite AND-items. The BLOSOM framework can also mine the closed DNF and CNF expressions. The main contribution of our previous work was the structural characterization of the different classes of boolean expressions via the use of closure operators and minimal generators, as well as the framework for mining arbitrary Boolean expressions. However, the focus was on complete enumeration, which is typically not feasible for many real-world datasets. In contrast, the primary contribution of this paper is the novel theoretical characterization of the minDNF expressions, and using this theory to develop near-uniform sampling approaches to extract representative sample of the minDNF expressions. We note that a preliminary version of this paper appeared in Li and Zaki (2012).

Within the association rule context, there has been previous work on mining negative rules (Savasere et al. 1998; Yuan et al. 2002; Wu et al. 2004; Antonie et al. 2004), as well as disjunctive rules (Nanavati et al. 2001); the latter work first mines all frequent AND-clauses, and then greedily select good OR combinations. The notion of disjunctive emerging patterns (EPs) for classification was proposed in Loekito and Bailey (2006). Disjunctive EPs are Boolean expressions in CNF form, such that their support is high for the positive class and low for the negative class. However, they consider restricted CNF expressions that must contain a clause for each attribute. We mine general DNF expressions, without any constraints. On the other hand, our current sampling framework relies on a relatively straightforward approach to handle negated literals. Using more sophisticated methods, as suggested by some of the existing works on negative rules, can speed up the computation time. One can also use approaches that approximate the support of arbitrary boolean expressions (Calders and Goethals 2005; Jaroszewicz and Simovici 2002; Mannila and Toivonen 1996) to deliver further performance gains. The work in (Calders and Goethals 2005; Mannila and Toivonen 1996) proposed an algorithm based on the inclusion-exclusion principle, whereas Jaroszewicz and Simovici (2002) proposed a method that generalizes the Bonferroni inequalities to find frequent itemsets for estimating the bounds for support of database queries. Also related is the mining of optimal rules according to some constraints (Bayardo and Agrawal 1999), e.g., gini, entropy gain, lift, and conviction etc., since the boolean expressions can be considered as constraints on the patterns.

More general notions of itemsets (including negated items and disjunctions) have been considered in the context of concise representations (Calders et al. 2003; Kryszkiewicz 2001, 2005). Hamrouni and Ben (2009) proposed a closure operator that can be used to map disjunctive itemsets to a small unique disjunctive closed itemset. The work in (Vimieiro and Moscato 2012, 2014) proposes methods for mining disjunctive minimal generators, and also disjunctive closed patterns, inspired by Stumme et al. (2002), which described an algorithm called Titanic for computing (iceberg) concept lattices and finding conjunctive closed patterns using minimal generators. The work in Vreeken et al. (2011) uses a different approach to conciseness; it proposed the KRIMP method, which is based on the MDL principle that the optimal set of pattern is the one that gives the highest compression of the dataset. Another point of comparison is w.r.t. the work in Gunopulos et al. (2003) where the authors aim to find frequent and (maximally) interesting sentences w.r.t. a variety of criteria. Many data mining tasks, including inferring boolean functions, are instantiations of this problem.

Boolean expression mining is related to the task of mining redescriptions (Ramakrishnan et al. 2004) that seeks to find subsets of data affording multiple definitions. The input to redescription mining is a vocabulary of sets (or boolean propositions) over a domain and the goal is to construct two distinct expressions from this vocabulary or distinct attribute sets that induce the same subset over the domain. In essence, if there is more than one minDNF expression for a tidset, then we can obtain a minimal redescription, or logical equivalence between the two Boolean expressions. The CARTwheels algorithm (Ramakrishnan et al. 2004) mines redescriptions only between length-limited boolean expressions in DNF and CHARM-L (Zaki and Ramakrishnan 2005) is restricted to redescriptions between conjunctions. Approximate redescriptions correspond to the minimal non-redundant exact or inexact rules described in Zaki (2000). Our BLOSOM framework (Zhao et al. 2006; Zaki et al. 2010) can mine redescriptions between arbitrary boolean expressions.

The theoretical machine learning community has focused on learning boolean expressions in the presence of membership queries and equivalence queries (Bshouty 1995).  Mitchell (1982) proposed the concept of version spaces (which are basically a partial order over expressions) to organize the search for expressions consistent with a given set of data. However, these works conform to the classical supervised learning scenario where both positive and negative examples of the unknown function are supplied. In contrast, our work aims to find boolean expressions without explicit direction about the examples they cover.

As we shall see, complete mining is infeasible for all but very high support values. Thus, recent work has considered sampling based approaches. One of the earliest use of sampling was for mining maximal itemsets via randomization (Gunopulos et al. 1997). In the context of frequent graph mining, Chaoji et al. (2008) proposed a randomized sampling method to generate a small representative set of frequent maximal graph patterns; the method did not provide any sampling guarantee. The first method to sample maximal graph patterns with uniform sampling via MCMC was presented in Hasan et al. (2009). In Hasan and Zaki (2009), the authors introduced a generic sampling framework to sample the output space of frequent subgraphs, which is based on MCMC algorithm as well. In the context of itemset mining, Boley and Grosskreutz (2009) proposed a randomized approximation method for counting the number of frequent itemsets. In Boley et al. (2010) a Metropolis-Hastings algorithm for sampling closed itemsets is given. More recently, Boley et al. (2011) presented a direct sampling approach for mining AND-clauses. Unfortunately, direct sampling cannot be used for sampling minDNFs since the pattern space of minDNFs is not connected, as it is for closed AND-clauses. We thus focus on MCMC sampling, designing an appropriate transition probability matrix that ensures near-uniform sampling of the set of minDNF patterns.

3 Sampling minimal AND-clauses

To make the ideas on sampling via MCMC more concrete, we first consider the case of sampling minimal AND-clauses. Let us first characterize the state space $\mathcal {S}$ for the Markov chain.

Lemma 1

Any subset of a minimal AND-clause must also be minimal.

Proof

Let $X$ be a minAND expression, and let $Y \subset X$. Assume that $Y$ is not minimal. Then there exists a minAND expression $Z \subset Y$, such that $T(Z) = T(Y)$. However, in this case, $T( (X{\setminus } Y) \cup Z) = T(X)$, which contradicts the fact that $X$ is minimal. Thus, $Y$ must be a minAND expression. $\square$

Corollary 1

Any single item $z \in \mathcal {Z}$ is a minimal AND-clause provided $T(z) \ne \mathcal {T}$.

Proof

The empty expression $\emptyset$ satisfies all transactions by default, so that $T(\emptyset ) = \mathcal {T}$. Thus, it is the unique minimal expression for the universal set of tids $\mathcal {T}$. By definition, any other item $z \in \mathcal {Z}$ is minimal for its corresponding tidset $T(z)$, if $T(z) \ne \mathcal {T}$. $\square$

In our running example in Table 1, items $A, B, C, D, E$ and $F$ are all minAND clauses.

Consider the following Markov chain whose state space comprises the frequent and minimal AND-clauses. Start from an arbitrary state or minAND expression $X_0$. Typically $X_0 = \emptyset$, i.e., we start from the empty expression. Given $X_i$, the next state $X_{i+1}$ is obtained as follows:

• (a) Choose an item $z \in \mathcal {Z}$ uniformly at random.

• (b) If $z \in X_i$, then $X_{i+1} = X_i {\setminus } \{z\}$.

• (c) If $z \not \in X_i$, and if adding $z$ to $X_i$ results in a frequent and minimal AND-clause, then set $X_{i+1} = X_i \cup \{z\}$. Otherwise, let $X_{i+1}= X_i$.

Given a specific minAND expression $s_i$, let $N_i$ denote its frequent and minimal neighbors, i.e., those frequent minAND expressions that are reachable in one step from $s_i$ (excluding itself), i.e., by adding or deleting just one item. Let $d_i = |N_i|$ denote the degree of the state $s_i$. Note that if $s_i$ is a frequent minAND expression, then any expression obtained by deleting one item is also frequent and minimal. On the other hand, if we add an item to $s_i$ we do have to check whether the resulting expression is minimal and frequent. The above Markov chain is characterized by the following transition matrix

$$\begin{aligned} p(u,v) = {\left\{ \begin{array}{ll} 1/|\mathcal {Z}| &{} \text {if }\quad u \ne v \text { and } v \in N_u\\ 1 - d_u/|\mathcal {Z}| &{} \text {if }\quad u = v\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(2)

Lemma 2

The Markov chain defined by the transition probability matrix in Eq. (2) has the uniform distribution as its unique stationary distribution.

Proof

This Markov chain is clearly irreducible, since any subset of a minimal AND-clause is also a minimal AND-clause, and we can reach any minimal generator via the empty expression. Also, since every state has a self-loop, and thus the chain is aperiodic. The Markov chain is thus ergodic, since the state space is finite, and it thus has a unique stationary distribution.

Consider the uniform distribution $\pi$, which satisfies $\pi _u = \pi _v = 1/|\mathcal {S}|$, where $\mathcal {S}$ is the state space. For $u \ne v$, we have

$$\begin{aligned} \pi _u \; p(u,v) = \pi _u/|\mathcal {Z}| = \pi _v/|\mathcal {Z}| = \pi _v \; p(v,u). \end{aligned}$$

Thus, the uniform distribution satisfies the detailed balance condition in Eq. (1), and it must therefore be the unique stationary distribution for this chain. $\square$

One issue with the Markov chain above is that the probability of staying at the same state is relatively high, since many of the random items chosen to be added will result in infrequent or non-minimal expressions. We can reduce the probability of self-loops by first constructing the local neighborhood for each state visited by the chain. Let $X_t = s_i$; when we reach state $s_i$ for the first time, we determine its degree $d_i$ by computing each of its minimal and frequent neighbor $s_j$ obtained by deleting a single item from $s_i$, or by adding an item to it. Next, we allow transitions only between $s_i$ and a state $s_j \in N_i$. However, a simple random walk on this state space will be biased towards nodes with high degrees, i.e., the stationary probability of a state $s_i$ in a simple random walk is proportional to its degree $d_i$. We can fix this bias via the Metropolis method. Given that $X_i = s_i$, the next state $X_{i+1}$ is obtained as follows:

• (a) Choose a state $s_j \in N_i$ uniformly at random.

• (b) Set $X_{i+1} = s_j$ with probability $\min (1, d_i/d_j)$, otherwise set $X_{i+1} = X_i = s_i$.

The Markov chain is characterized by the following transition matrix, as we shall show in Lemma 3:

$$\begin{aligned} p(u,v) = {\left\{ \begin{array}{ll} \frac{1}{\max (d_u, d_v)} &{} \text {if }\quad u \ne v \text { and } v\in N_u \\ 1-\sum _{x\in N_u} p(u,v) &{} \text {if }\quad u=v\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(3)

Lemma 3

The Markov chain defined by the transition probability matrix in Eq. (3) has the uniform distribution as its unique stationary distribution.

Proof

The Markov chain is clearly irreducible, aperiodic and finite. It is thus ergodic and has a unique stationary distribution. We now show that its stationary probability distribution is the uniform distribution as follows. First, note that if $u \ne v$, then the transition probability is given as $p(u,v) = 1/d_u \min (1, d_u/d_v)$. If $d_u \ge d_v$, then $p(u,v) = 1/d_u$. On the other hand, it $d_v > d_u$, then $p(u,v) = 1/d_u \times d_u/d_v = 1/d_v$. In other words, $p(u, v) = 1/\max (d_u, d_v)$. Second, consider the uniform distribution with $\pi _u = \pi _v$; we have

$$\begin{aligned} \pi _u \; p(u,v) = \pi _u \frac{1}{\max (d_u, d_v)} = \pi _v \frac{1}{\max (d_u, d_v)} = \pi _v \; p(v,u). \end{aligned}$$

Thus, it follows that the uniform distribution is the unique stationary distribution for this Markov chain. $\square$

3.1 Computational complexity

In terms of the computational complexity of simulating a single step of the Markov chain, first consider Eq. (2). We assume that we have available the tidset $T(z)$ for each item $z \in \mathcal {Z}$, and also the tidset for state $X_i$, namely $T(X_i)$. Assume that $|\mathcal {Z}| = m$ and $|\mathcal {T}|=n$, and assume that $|X_i| = l$. Given state $X_i$, we randomly select an item $z \in \mathcal {Z}$. If $z \not \in X_i$, we compute the support of $X_i \cup \{z\}$, which takes $O(n)$ time for the intersection $T(X_i) \cap T(z)$. If $z \in X_i$ we have to compute the support of $X_i{\setminus } \{z\}$, which takes time $O(l\cdot n)$ for the intersection $\cap _{x_j \in X_i, x_j \ne z} T(x_i)$. For item addition, we also have to check if the resulting pattern is minimal, which takes time $O(l^2 \cdot n)$, since we have to delete each item in $X_i \cup \{z\}$ and we have to check that the support of the subset is not equal to the extended AND-clause. Since there are $l$ items, and support computation takes $O(l \cdot n)$ time, the total time is $O(l^2 \cdot n)$ for a single step.

Now consider the matrix in Eq. (3). Given $X_i$ we have to compute its degree. We already know by Lemma 1 that all its subsets obtained by deleting a single item must be minimal, so we only have to check item additions, which takes time $O(mn)$ over all items $z \in \mathcal {Z}$. In the worst case there are $O(m)$ frequent item additions and checking their minimality takes a total of $O(m |X_i|^2 n)$ time. Computing the degree and minimality of the selected neighbor also takes $O(m \cdot l^2\cdot n)$ time, so that the computational complexity of a single step is $O(m \cdot l^2\cdot n)$ in total. In practice, the minimality and frequency checking can be done much faster by memoizing the results of previous states, so that the full cost is incurred only when a state is seen for the first time, at which time we can compute its support and degree. Subsequent visits to or queries for the same state then incur only a $O(1)$ time for lookup.

3.2 Convergence rate

One important issue in using MCMC sampling is to determine when the initial distribution converges to the stationary distribution and how fast the convergence rate is. To measure the convergence rate we define the variation distance between two probability distributions on the same state space $\mathcal {S}$ after $t$ steps, as follows:

$$\begin{aligned} vd_s(t) = vd(p^t(s, .), \pi ) = {1\over 2}\sum _{q \in \mathcal {S}} |p^t(s, q) - \pi (q)|, \end{aligned}$$

(4)

where $s \in \mathcal {S}$ is the initial or starting state, $\mathbf {P}^t = \{p^t(i,j)\}_{i,j=1,\ldots ,|\mathcal {S}|}$ is the transition matrix at time $t$, and $\pi$ is the desired stationary distribution. Since we aim for a uniform sampling of the minimal expressions, the stationary distribution will be uniform, i.e.,

$$\begin{aligned} \pi = (\pi _1, \pi _2, \ldots , \pi _{|\mathcal {S}|}) = (1/|\mathcal {S}|, 1/|\mathcal {S}|, \dots , 1/|\mathcal {S}|). \end{aligned}$$

Let $vd(t) = \max _{s\in \mathcal {S}} vd_s(t)$ denote the maximum $t$-step variation distance over all states $s$. Define $\tau _s(\epsilon )$ as the minimum number of steps when the variation distance $vd_s(t)$ is less than $\epsilon > 0$, i.e.,

$$\begin{aligned} \tau _s(\epsilon ) = \min \{t |\; vd_s(t) \le \epsilon \}. \end{aligned}$$

Finally, the mixing time for the Markov chain is defined as the maximum value of $\tau _s(\epsilon )$ over all states, given as

$$\begin{aligned} \tau (\epsilon ) = \max _{s \in \mathcal {S}} \tau _s(\epsilon ). \end{aligned}$$

It is well known that the mixing time is closely related to the spectral gap, $\gamma = |\lambda _1 - \lambda _2| = |1-\lambda _2|$, which is defined as the absolute difference between the largest $\lambda _1 = 1$ and the second largest eigenvalue $\lambda _2$ of the transition matrix $\mathbf {P}$ (Cowles and Carlin 1996). The larger the spectral gap, the faster the walk converges.

Unfortunately, in practice, we typically cannot compute the entire transition matrix $\mathbf {P}$. The whole point of sampling is to avoid enumerating all the frequent minimal Boolean patterns. In these cases, if we know $|\mathcal {S}|$, we can estimate a lower bound on the variation distance by computing the transition probabilities from the empty expression, i.e., by computing $vd_\emptyset (t)$. In case we do not know the size of the state space $\mathcal {S}$, which is typical for many of the datasets, especially for lower values of ${\sigma _{\min }}$, we are limited to computing the variation distance only over the subset of the state space seen so far, say $\mathcal {S}' \subset \mathcal {S}$, which also gives a lower bound on the true variation distance. We study the convergence rate for the minAND sampling in Sect. 5.

4 Mining minimal boolean expressions

In this section we prove some properties of minDNF expressions, which will allow us to design effective pruning strategies while sampling. In fact, these properties can also be exploited for complete pattern enumeration.

Theorem 1

A DNF expression $Z = \bigvee _{i=1}^n Z_i$ is minDNF iff it satisfies the following two properties:

• (a) For any $Z_i$, ($i=1,\ldots ,n$), we have $T(Z_i) \nsubseteq \bigcup _{j \ne i} T(Z_j)$. In other words, for any tidset of a clause, it cannot be a subset of the unions of tidsets over the other clauses.

• (b) If we delete any item $z_{ja}$ from a clause $Z_j$ to yield a new clause $Z'_j = Z_j{\setminus } z_{ja}$, then for the resulting DNF expression $Z'=(\bigvee _{i \ne j} Z_i) \vee Z'_j$, we have $T(Z') \ne T(Z)$.

Proof

If (a) is violated, we can simply delete $Z_i$ without changing support, which would contradict the fact that $Z$ is minimal. Likewise, if (b) is violated, it would contradict $Z$’s minimality. For the reverse direction, suppose a DNF expression $Z=\bigvee _{i=1}^n Z_i$ satisfies properties (a) and (b). We have to show that $Z$ is a minDNF. Assume that $Z$ is not minimal. Then there exists a minDNF $Y = \bigvee _{j=1}^m Y_j$, such that $Y \subset Z$ and $T(Y) = T(Z)$, which implies that there exists an injective mapping $\phi$ that maps each $Y_j \in Y$ to $\phi (Y_j) = Z_i \in Z$, such that $Y_j \subseteq Z_i$ and $T(Y_j) \supseteq T(Z_i)$. There are two cases to consider:

• (1) If $\phi$ is a bijection, then $m=n$, and there exist a clause $Y_{j} \in Y$, such that $Y_j \subseteq \phi (Y_j)=Z_i \in Z$. However, in this case property (b) of $Z$ is violated, since we can delete some item from $(Z_i{\setminus } Y_j)$, and the resulting expression will still have the same support at $Z$.

• (2) If $\phi$ is not a bijection, then $m<n$, and there exists a clause $Z_k \in Z$, such that $\phi ^{-1}(Z_{k}) \notin Y$. However, in this case property (a) of $Z$ violated, since $T(Y) = T(Z)$ implies that $T(Z_{k}) \subseteq \bigcup _{i \ne k} T(Z_{i})$.

Therefore, $Z$ must be a minimal DNF expression. $\square$

Lemma 4

A minDNF consists of OR of minAND expressions, i.e., if $Z= \bigvee _{i=1}^n Z_i$ is minDNF, then each $Z_i$ must be a minimal AND-clause.

Proof

Assume some $Z_i$ is not a minimal AND-clause. Then there exists a literal $l \in Z_i$, such that $T(Z_i{\setminus } l)=T(Z)$. In this case we can delete $l$ from $Z_i$ without affecting $T(Z)$, which violates property (b) in Theorem 1. $\square$

Lemma 5

If $Z = \bigvee _{i=1}^n Z_i$ is minDNF, for any $Z_i, Z_j \in Z$, we have $Z_i\nsubseteq Z_j$. In other words, no clause is a subset of another clause.

Proof

Suppose $Z_i\subseteq Z_j$. Thus $T(Z_i)\supseteq T(Z_j)$ and property (a) in Theorem 1 is violated. $\square$

Please note that Theorem 1 is a sufficient condition for Lemmas 4 and 5 but not a necessary condition. As such a DNF expression that satisfies Lemmas 4 and 5, need not be a minimal generator. We use this observation to reduce the state space $\mathcal {S}$.

Corollary 2

Any clause-wise subset (obtained by deleting an entire clause) of a minDNF expression $Z$ is also minDNF.

Proof

The proof is similar to Lemma 1. Suppose a clause-wise subset $Z_s \subset Z$ is not minDNF. Then we can replace $Z_s$ with its equivalent minDNF, say $Z'_s$, in $Z$, without affecting the tidset of $Z$. This would contradict the minimality of $Z$. $\square$

For example, for the example in Table 1, $B|DF|E$ is a minimal DNF generator, with tidset $T(B|DF|E)=12{,}345$. Thus all clause-wise subsets, namely $B, DF, E, B|DF, B|E, DF|E$ are minDNF expressions.

4.1 Sampling minimal DNF expressions

Having characterized the minDNF expressions, we turn our focus on sampling them. We first consider sampling using a clause-wise state space. From Lemma 4, every minDNF consists of only minimal AND-clauses. Also by Corollary 2, any clause-wise subset is also a minDNF. Thus, the partial order over the clause-wise minDNF expressions or states is connected and all parents (immediate clause-wise subset) of a node will be minDNFs as shown in Fig. 3a. However, this approach requires that we first mine the complete set of minimal AND-clauses from the dataset, and then we sample over DNF expressions by considering their or. However, this approach is not practically feasible, since for typical support values mining all possible minimal AND-clauses is very expensive. It also defeats the main purpose of sampling.

Fig. 3

Clause- and item-wise state space.

Instead of sampling in the clause-wise space, we consider the space obtained by adding or deleting a single item from a DNF expression. The state space $\mathcal {S}$ for the Markov chain comprises DNF expressions linked by immediate subset-superset or parent-child relationships. Given a state $s_i \in \mathcal {S}$, its neighbors can be generated via the following three operations:

• (a) Add a new clause comprising a single item into the DNF.

• (b) Add an item to an existing clause.

• (c) Delete a single item from a clause in the DNF. If this results in an empty clause, delete the clause.

The added or deleted item can be either an item or its complement. Unfortunately, this state space has a problem—we cannot restrict the states to only the minDNF expressions.

Lemma 6

The state space over only the minimal DNF generators is disconnected.

Proof

We prove by counter-example. Consider the example in Table 1. Using ${\sigma _{\min }}=1$, all the minDNF expressions are listed in Table 2. The Boolean expression $AB|AF|EF$ is a minDNF with $T(AB|AF|EF)=123$. However, all its parents (obtained by deleting a single item) are not minimal DNFs. Take its parent $B|AF|EF$ as an example, $T(B)=135, T(AF)=2, T(EF)=3$, thus property $(a)$ in Theorem 1 is violated. Similarly, all its children (obtained by adding a single item to a clause, or as a clause) are not minimal DNF generators. For instance, $AB|ACF|EF$ is not a minimal DNF generator since property $(b)$ in Theorem 1 is violated. $\square$

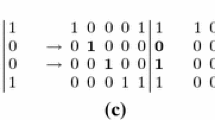
So, if we only keep only minDNF expressions in the state space, $AB|AF|EF$ would become an isolated point, and would never be reached! As another example, consider the minDNF expression $BF|DE$. All of its parents obtained by deleting a single item from a clause are not minimal, as shown in Fig. 3b. On the other hand $D|F$ is a minimal DNF generator, but it cannot reach $BF|DE$ via single item additions or deletions, as illustrated in Fig. 3b. The solid ovals in the figure are minimal DNF generators, and dashed ovals represent non-minimal DNFs.

4.1.1 Reducing the state space

Given that the item-wise state space is disconnected, in order to guarantee all minDNFs are reachable, we also need to keep non-minimal DNFs in the graph. However, the goal is to reduce the number of non-minimal DNF in the graph to as few as possible while retaining all possible minDNFs. The following lemmas helps in this direction.

Lemma 7

Let $Z$ be a DNF that violates Lemma 4. No extension of $Z$ (by adding an item) can result in a minDNF.

Proof

At least one of the clauses in $Z$ is not a minimal AND-clause. Any future extension by adding a literal to $Z$ cannot be a minDNF, since all its minimal AND-clause subsets must also be minimal by Lemma 1. $\square$

This lemma states that any DNF that violates Lemma 4 should be removed from the graph, which can greatly reduce the size of the search space. Furthermore, we also remove any DNF node that violates Lemma 5. Note that this pruning still keeps the graph connected since it is always possible to find other paths. As an example, for the data in Table 1, $DE|E$ should be removed since one of its parents $DE|EF$, which is a minimal generator, can be reached by another path, namely from $DE|F$. As mentioned earlier, Definition 1 is a sufficient condition for Lemma 4 and 5, but not a necessary condition. There still exist DNFs that satisfy Lemma 4 and 5 but are not minimal generators.

Lemma 8 and 9 mentioned below can help to quickly determine the minimality of a DNF expression without explicitly testing properties (a), (b) in Theorem 1, which can save a lot of computational overhead.

Lemma 8

Let $Z = \bigvee _{i=1}^m Z_i$, with $m\ge 2$, be a general DNF expression that violates property $(a)$ in Theorem 1. Let $T(Z_k) \subseteq \bigcup _{j \ne k} T(Z_j)$. By adding an item to clause $Z_k$ in $Z$, the resulting DNF cannot be minDNF.

Proof

The tidset of a clause is anti-monotonic. By adding an item $x$ to clause $Z_k$, resulting in clause $Z_k^{'}$, i.e., $Z_k^{'} = Z_k \wedge x$, we still have $T(Z_k^{'}) \subseteq \bigcup _{j \ne k} T(Z_j)$. Hence property (a) is violated. $\square$

However, note that adding an item to other clauses rather than $Z_k$ in $Z$ can result in a minDNF node.

Lemma 9

Let $Z = \bigvee _{i=1}^m Z_i$ be a general DNF expression, with $m\ge 2$, and let clause $Z_k \in Z$ violate property $(b)$ in Theorem 1. Adding an item to clause $Z_k$ cannot result in a minimal DNF expression.

Proof

Since $Z_k$ violates property (b) in Theorem 1, there exists item $x \in Z_k$, such that $T(Z_k) \cup (\bigcup _{j\ne k} T(Z_j)) = T(Z_k^{'})\cup (\bigcup _{j\ne k} T(Z_j))$, where $Z_k = Z'_k \wedge x$. Let $Z_k^{{''}}=Z_k \wedge y = Z'_k \wedge x \wedge y$ and consider the DNF expression $Z'' = Z_k^{{''}}\vee (\bigvee _{j\ne k} Z_j)$. Assume that $Z''$ is minDNF, which implies that $(Z_k^{'}\wedge x \wedge y)$ is minAND by Lemma 1. This in turn implies that the difference set $D_y = T(Z_k^{'}\wedge y)-T(Z_k^{'}\wedge x\wedge y)$ is non-empty. We consider three cases:

• (a) If $D_y \subseteq \bigcup _{j\ne k} T(Z_j)$, then $T(Z_k^{'}\wedge x \wedge y) \cup (\bigcup _{j\ne k} T(Z_j)) = T(Z_k^{'} \wedge y) \cup (\bigcup _{j\ne k} T(Z_j))$, which contradicts the assumption that $Z''$ is a minDNF.

• (b) If $D_y \cap \bigcup _{j\ne k} T(Z_j) = \emptyset$, then we have $D_y \subseteq T(Z_k^{'}) \subseteq T(Z_k^{'}) \cup (\bigcup _{j\ne k} T(Z_j)) = T(Z_k)\cup (\bigcup _{j\ne k} T(Z_j))$, which implies that $D_y \subseteq T(Z_k) = T(Z_k^{'}\wedge x)$. However, by definition, $D_y \subseteq T(Z_k^{'}\wedge y)$. Hence $D_y \subseteq T(Z_k^{'}\wedge x) \cap T(Z_k^{'}\wedge y) = T(Z_k^{'}\wedge x \wedge y)$. But thus implies that $D_y = \emptyset$, which contradicts the assumption that $Z_k^{'}\wedge x\wedge y$ is minAND.

• (c) If $D_y \nsubseteq \bigcup _{j\ne k} T(Z_j)$ and $D \cap \bigcup _{j\ne k} T(Z_j) \ne \emptyset$ then we can divide $D_y$ into two parts $D_y = D'_y \cup D''_y$, such that $D'_y \subseteq \bigcup _{j\ne k} T(Z_j), D''_y \cap \bigcup _{j\ne k} T(Z_j) = \emptyset$, and $D'_y\ne \emptyset , D''_y \ne \emptyset$. Similar to step (2), $D''_y \subseteq T(Z_k^{'}\wedge x \wedge y)$, which implies that $D_y = D'_y \cup D''_y = T(Z'_k \wedge y) - T(Z'_k \wedge x \wedge y) = D'_y$. However, this implies that $D''_y = \emptyset$, which is a contradiction.

From the three cases above, we conclude that $Z''$ is not minDNF. $\square$

4.1.2 Transition probability matrix

To sample the frequent minDNF expressions we can proceed as we did for the minAND case, by simply adding and deleting items, starting from the empty expression. Let $N_u$ denote the neighbors of $u$, that is, the set of states or expressions that can be obtained using item addition and deletions. Further, let the set of $u$’s neighbors that are minDNF be denoted as $N^m_u$, and those that are not minDNF be denoted as $N^n_u$, given as

$$\begin{aligned} N^m_u&= \left\{ v \in N_u | v \text { is a minDNF} \right\} \\ N^n_u&= \left\{ v \in N_u | v \text { is not a minDNF} \right\} \end{aligned}$$

Also, let $d^m_u = |N^m_u|$ and $d^n_u = |N^n_u|$ be the minDNF degree and non-minDNF degree of expression $u$. Clearly the degree of $u$ is given as $d_u = |N_u| = d^m_u + d^n_u$.

Just as for minAND sampling, we can obtain a uniform stationary distribution using the transition probability matrix defined in Eq. (3). However, there is one crucial difference when sampling minDNF expressions. This approach will uniformly sample the state space $\mathcal {S}$, which now comprises both minimal and non-minimal DNF expressions. It is true that the minDNF expressions will be sampled uniformly, but the probability of visiting a minDNF is minuscule, since the cardinality of frequent minDNF expressions is much smaller (exponentially smaller) compared to the set of all possible frequent DNF expressions! For example, consider our example dataset in Table 1, with ${\sigma _{\min }}=1$. It has 26 frequent AND clauses (itemsets), out of which only 14 are minAND, as shown in Table 2. Nevertheless, taking an or of any combination of these AND clauses will yield a frequent DNF expression, so there are $2^{26} = 67,108,864$ possible frequent DNF expressions. Granted that many of these frequent DNF expressions are redundant, and will be pruned by the application of the theorems/lemmas we outlined above, the size of the DNF space is still huge even for such a small toy dataset. On the other hand, there are only 43 frequent minDNF expressions, as shown in Table 2. We conclude that if we follow the same approach as for minAND, the Markov chain will mainly visit non-minDNF states and will rarely encounter minDNF expressions. In other words, the strategy used for minAND is basically infeasible for sampling minDNF expressions (a fact that we also experimentally verified). What we need is to bias the chain to prefer minDNFs over non-minDNFs, but at the same time guarantee uniform sampling of the frequent minDNFs, as described next.

To sample frequent minDNF expressions, we will simulate a Markov chain on the item-wise state space. We will ensure that the stationary distribution is the one that assigns uniform probability to all the minDNF expressions. Since we do not care about the distribution of the remaining non-minimal DNF expressions, the Markov chain is different from traditional MCMC methods like Metropolis or Metropolis-Hastings methods (Rubinstein and Kroese 2008). Consider the Markov chain on the state space with both minimal and non-minimal DNF generators, with the transition probability matrix $\mathbf {P}$ given as:

$$\begin{aligned} p(u,v) = {\left\{ \begin{array}{ll} (1-\beta ) \cdot \frac{w(u,v)}{\sum _{x\in N_u}w(u,x)} &{} \text {if }\quad u \ne v \text { and } v \in N_u \\ \beta &{} \text {if }\quad u=v\\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(5)

where the self-loop probability $\beta$ ensures aperiodicity of the Markov chain. We set $\beta = \frac{1}{d_u+1}$, so that the self-loop has a uniform probability of being chosen when we include all the neighbors of $u$. Further, we define the weight $w(u,v)$ as follows:

$$\begin{aligned} w(u,v) = {\left\{ \begin{array}{ll} \frac{(1-\alpha )c}{\max (d^m_u, d^m_v)} &{} \text { if }\quad u \text { and } v \text { are minDNFs }\\ \frac{\alpha c}{d^n_v} &{} \text { if }\quad v \text { is minDNF but } u \text { is not }\\ \frac{\alpha c}{d^n_u} &{} \text { if }\quad u \text { is minDNF but } v \text { is not }\\ 1 &{} \text { if }\quad u \text { and } v \text { are not minDNFs }.\\ \end{array}\right. } \end{aligned}$$

(6)

Note that if both $u$ and $v$ are minDNFs, then $d^m_u \ge 1$ and $d^m_v \ge 1$, since they both have each other as a minDNF neighbor. If $u$ is minDNF, but $v$ is not, then $d^n_u \ge 1$, since $u$ obviously has $v$ as a non-minDNF neighbor. Finally, if $u$ is not minDNF, but $v$ is, then $d_v^n \ge 1$, since $v$ has $u$ as a non-minDNF neighbor. Thus, $w(u,v)$ is always well defined.

Also $0 < \alpha < 1$ is a weighting term, and $c>0$ is a scaling constant. We shall see that $\alpha$ controls the degree of non-uniformity in the sampling, and along with $c$ also affects the convergence rate of the sampling method (it has no impact on the correctness). To better understand the role of $c$, if we divide each case (on the right hand side) in Eq. (6), we see that the term $c$ applies only to the last case, which turns into $1/c$, i.e., this ratio is proportional to the probability of a transition from $u$ to $v$ when both are non-minDNFs. A large value of $c$ disfavors these kinds of transitions. On the other hand, a large value of $\alpha$ favors transitions to minDNFs, as does a large value of $c$.

From the definition, one can verify that the edge weights in the graph are symmetric and the transition probability matrix is stochastic. Moreover, the weights favor transitions to minDNF nodes. We prove that the defined random walk converges to a stationary distribution.

Theorem 2

The Markov chain defined via Eq. (5) using the weights in Eq. (6) is reversible and converges to a stationary distribution.

Proof

The Markov chain is irreducible, aperiodic and finite. Let $w(u) \!=\! \sum _{v \in N_u} w(u,v)$ be the sum of the weights over all the neighbors of state $u$, and let $W = \sum _{u \in \mathcal {S}} w(u)$ denote the total weight over all the states in the Markov chain, which can be taken to be a constant. We show that the stationary distribution is given as $\pi (u) = w(u)/W$ for all $u \in \mathcal {S}$. Note that the weight function $w(u,v)$ is symmetric. If $u$ and $v$ are both minDNFs then $w(u,v) = (1-\alpha )c/\max (d^m_u, d^m_v) = w(v,u)$. If they are both non-minimal then $w(u,v) = w(v,u) = 1$. Finally, if either $u$ or $v$ is minimal and the other is not, we have $w(u,v) = \alpha c /d_x = w(v,u)$, where $d^n_x$ is the degree of the non-minimal expression ($x \in \{u,v\}$). Consider the detailed balance condition in Eq. (1). Let $u \ne v$; we have

$$\begin{aligned} \pi (u)p(u,v)&= \frac{w(u)}{W} \cdot (1-\beta )\frac{w(u,v)}{\sum _{x \in N_u} w(u, x)} = (1-\beta )\frac{w(u)}{W} \cdot \frac{w(u,v)}{w(u)}\\&= (1-\beta )\frac{w(u,v)}{W} \end{aligned}$$

On the other hand

$$\begin{aligned} \pi (v)p(v,u) = \frac{w(v)}{W} \cdot (1-\beta )\frac{w(v,u)}{w(v)} = (1-\beta )\frac{w(v,u)}{W} = (1-\beta )\frac{w(u,v)}{W} \end{aligned}$$

Thus, $\mathbf {P}$ satisfies the detailed balance condition, and therefore the Markov chain is reversible and converges to the stationary distribution $\pi (u) = w(u)/W$. $\square$

Definition 2

Let $\pi$ denote the stationary distribution for a Markov chain, where $\pi (u)$ denotes the probability of visiting node $u$. The non-uniformity of a random walk is defined as the ratio of the maximum to the minimum probability of visiting a minDNF node.

Theorem 3

The non-uniformity of minDNF sampling defined by Eq. (6) is bounded by the ratio $1/\alpha$.

Proof

From the proof of Theorem 2, the stationary distribution for any node $u$ is given as $\pi (u) = \frac{w(u)}{W}$, where $w(u)=\sum _{v \in N_u} w(u,v)$ is the total weight for node $u$, and $W=\sum _u w(u)$ is the sum of the weights over all nodes in the Markov chain. Thus, $\pi (u) \propto w(u)$. Let $u$ be a minDNF expression, with minDNF degree $d^m_u$ and non-minDNF degree $d^n_u$. The total weight for $u$ is given as

$$\begin{aligned} w(u) = \displaystyle \sum _{v \in {N_u}} w(u,v) = d^n_u \cdot \frac{\alpha c}{d^n_u} + (1-\alpha )c \sum _{v \in N^m_u} \frac{1}{\max (d^m_u,d^m_v)} \end{aligned}$$

Note that $\sum _{v \in N^m_u} \frac{1}{\max (d^m_u,d^m_v)}$ $\le d^m_u \cdot \frac{1}{d^m_u} = 1$. Equality is achieved only if $d^m_u \ge d^m_v$ for all $v \in N^m_u$, in which case $s(u) = \alpha c + (1-\alpha )c = c$. On the other hand, in the worst case we may assume that $d^m_v \gg d^m_u$ so that the second term vanishes in the limit, in which case we have $s(u) = \alpha c$. Thus the worst-case non-uniformity in sampling is $\frac{c}{\alpha c} = \frac{1}{\alpha }$. $\square$

We can see that the proposed weighting scheme in Eq. (6) allows for a near-uniform sampling of the frequent minDNF expressions. On the other hand, it does not give any guarantee on the sampling of the non-minDNF expressions. For example, if $u$ is non-minimal then its weight is given as

$$\begin{aligned} w(u) = \sum _{v \in N_u}w(u,v) = \sum _{v \in N^n_u}w(u,v) + \sum _{v \in N^m_u}w(u,v) = d^n_u + \alpha c \sum _{v \in N^m_u} 1/d^n_v \end{aligned}$$

Thus, the maximum weight value is $w(u) = d_u^n + \alpha c \;d_u^m$ and the minimum value is $w(u) = d^n_u$. The non-uniformity ratio for the non-minDNFs is therefore $1+\alpha c \; d^m_u/d^n_u$, which can be large.

We already mentioned that the weights in Eq. (6) have been chosen to favor minDNF expressions over non-minDNF ones, and to guarantee uniform sampling for minDNFs. For this we choose a large value for $c$ and also choose $\alpha$ close to one. One might be tempted to increase the transition probability between two minDNFs, $u$ and $v$, for instance by letting $w(u,v) = (1-\alpha )c$. However, doing so, the weight of a minDNF expression $u$ is given as:

$$\begin{aligned} w(u) = \sum _{v \in {N_u}} w(u,v) = \alpha c + (1-\alpha )c \; d^m_u \end{aligned}$$

which does not guarantee uniformity.

Computational complexity: Let us consider the Computational complexity of simulating a single step of the Markov chain that uses the weighting function in Eq. (6). Let $X_i = \bigvee _{j=1}^q Z_j$ be the current state of the Markov chain, i.e., a DNF expression with $q$ clauses, and let $|X_i| = l$ denote the total size in terms of the number of items over all clauses. Let $|\mathcal {Z}| = m$ and $|\mathcal {T}| = n$. We have to compute the minimal and non-minimal degrees of $X_i$ and each of its frequent neighbors. For item deletions, the cost for frequency computation is $O(l^2 \cdot n)$, since we have to delete each of the $l$ items and compute the support of the resulting DNF expression, which costs $O(l\cdot n)$. For item additions, the cost is $O(q\cdot m \cdot n)$, since we have to add each of the $m$ items in $\mathcal {Z}$ to each of the $q$ clauses, and support computation takes time $O(n)$. In both cases, minimality checking cost is $O(l^2 \cdot n)$. Thus, the cost for computing the frequent neighbors and their minimality is $O(n \cdot (l^2 + qm))$. However, we also have to determine the degree of each neighbor. Thus, the cost for a single step of the Markov chain is $O(d \cdot n \cdot (l^2 + qm))$, where $d$ is the degree for node $X_i$. In practice, we use the memoization approach to store the degree, support and minimality information of a state only the first time it is encountered, with subsequent queries resulting in an $O(1)$ time lookup. However, the memoization approach incurs higher memory overhead.

Fig. 4

minDNF sampling algorithm

4.1.3 minDNF sampling algorithm

The pseudo-code for the minDNF sampling algorithm is outlined in Fig. 4. The method always starts by picking a random frequent item (or its negation; we omit that here). Given the current node $B$, we first check if it minimal, and if so add it to the sampled set of patterns ${\mathcal {B}}$. If $k$ steps have been performed, we stop (line 4). Otherwise, in line 5, we determine all the immediate parents and children of the current node $B$ that satisfy support constraints, as given in the function Compute-Local-Neighborhood in lines 9–14. To get all possible parents and children of the current node $B$, the item addition or deletion operations are used in line 9. In Line 10 we test the support and prune out those patterns that do not satisfied the conditions. In line 11, we use Lemmas 4 and 5 to determine whether $f$ is qualified to be remain in the partial order graph. We further test property $(a)$ and $(b)$ in Theorem 1 for $f$ to determine its minimality. Returning back to line 6, we compute the transition probability ${\mathbf {P}}$ according to Eqs (5) and (6). Then we select a DNF expression $B_{next}$ proportional to $P$ to continue the walk in lines 7–8.

Sampling frequency: There is one detail missing in Algorithm 4. Assume that the Markov chain converges after a sufficiently large number of steps, say $r$. Starting from state $X_0$, the run of the chain is given as $X_0, X_1, X_2, \ldots , X_N$ over $N$ steps. After $r$ steps, the distribution of state $X_r$ will be close to the stationary distribution, so we can use the first minDNF after $r$ steps as a sample. Now, considering $X_r$ as the start state, $X_{2r}$ will also be close to the stationary distribution, and it can therefore be used as a sample. Thus, to sample $k$ minDNF patterns, the sample comprises the first minDNF expression after $r, 2r$, ..., $kr$ steps, and consequently the Markov chain should be run for $N \ge kr$ steps. In practice, we do not know $r$, which depends on the mixing rate of the Markov chain, so we simply use a user-specified parameter $r$ and output a minDNF expression after every $r$-th step, after a longer burn-in period.

AND- and OR-clause cache: To further improve execution time, we pre-compute the frequent AND-clauses and OR-Clauses of length 2, and store them in a hash table, so that they can be used to quickly test for the valid item addition operations. For example, when we add an item to a clause $Z_i$ in DNF $Z$, we first get all frequent candidate items $I_{ij}$ to be added for each literal $z_{ij} \in Z_i$. Then the candidate items to be added for the clause $Z_i$ are { $\bigcap _j I_{ij} | z_{ij} \in Z_i$ }. We can do so quickly by looking up the candidate items in the hash table. This step avoids searching the whole $\mathcal {Z}$ space when we apply item addition operations and thus improves the efficiency.

Random walks with jumps and restarts: Even after pruning, the state space for sampling minimal DNF generators is large. The walk may be thus get trapped in local regions, which consist of non-minimal DNFs. If this happens, our algorithm will not output minimal DNFs even after a long run, although the samples are guaranteed to be uniform. To avoid getting stuck in local parts, we use the following two strategies:

• (i) Random walks with random jumps (RWRJ): In case the algorithm outputs no minimal DNF generators even after $r$ consecutive steps, we abort the current path, and randomly jump to any earlier minimal DNF generator in the history as its new start. Any such node is then deleted, so that it will not again be chosen as a jump point.

• (ii) Random walks with restart (RWR): At each step in the random walk, we enable a certain probability $r$ that the walker jumps back to the root node (empty itemset). We confirm empirically that RWRJ is the better strategy.

4.1.4 Faster sampling

Whereas Eq. (6) gives a good guarantee on the sampling quality, it can be expensive to compute, since we have to determine the minDNF and non-minDNF degree for a node, as well as for all of its neighbors $N_u$. Instead, we propose another weighting scheme that leads to much faster sampling, without sacrificing the sampling quality too much:

$$\begin{aligned} w(u,v) = {\left\{ \begin{array}{ll} 1 &{} \text {if} \quad \text {u and v are minDNFs}\\ \frac{c}{d_v} &{} \text {if} \quad \text {v is minDNF but u is not}\\ \frac{c}{d_u} &{} \text {if} \quad \text {u is minDNF but v is not}\\ 0.5 &{} \text {if} \quad \text {u and v are not minDNFs}\\ \end{array}\right. } \end{aligned}$$

(7)

We note that if the nodes $u$ and $v$ are both either minDNFs or non-minDNFs then we do not need to compute their degrees. Only if one of the nodes is a minDNF, we have to compute its degree ($d_u$ or $d_v$), but we do not have to determine its minDNF or non-minDNF degrees. The theorem below, shows that sampling quality is still good:

Lemma 10

The sampling non-uniformity of weighting scheme in Eq. (7) is bounded by $1 + d^m/c$, where $d^m$ is maximum minDNF degree of a node.

Proof

Let $u$ be a minDNF node, with minDNF degree $d^m_u$ and non-minDNF degree $d^n_u$. The total weight for $u$ is given as $w(u) = \sum _{v \in {N_u}} w(u,v) = d^n_u \cdot \frac{c}{d_u} + d^m_u \le c + d^m_u$. The last step holds since $d^n_u \le d_u$. The least weight at any node occurs when $d^m_u=0$, and the most weight is when $d^m_u = \max _u\left\{ d^m_u \right\} = d^m$. Thus, the non-uniformity is given as $\frac{c + d^m}{c} = 1 + d^m/c$. $\square$

In practice, this weighting scheme works well. One reason for this is that the expected minDNF degree of a node is much better than the worst-case $d^m$ given above. Furthermore, for a large dataset, computing the degree for all neighboring nodes is an expensive process. From the edge weight definition 7, the degree of a neighbor is useful iff the current node is not a minDNF, but its neighbor is. Thus, we compute the neighbor’s degree only when necessary, which speeds up the execution time greatly.

5 Experiments

In this section, we evaluate the sampling quality of our proposed methods. We also evaluate the benefits of mining minDNF expressions by using them as features for categorical data classification task. We compare our results with Blosom (Zhao et al. 2006), which is the only current algorithm that can mine minDNF patterns (although it is a complete method). For pure AND-clauses, we also compare with CHARM-L (Zaki and Ramakrishnan 2005), a state-of-the-art method for mining minimal AND-clauses (i.e., minimal generators.) All experiments are performed on a quad-core Intel i7 3.5GHz CPU, with 16GB memory, and 2TB disk, running Linux (Ubuntu 11.10). The minDNF sampling code was implemented in C++. All datasets and source code are available at: http://www.cs.rpi.edu/~zaki/www-new/pmwiki.php/Software.

5.1 Sampling evaluation

We begin the MCMC sampling evaluation by considering minAND clauses first, and then we study general minDNF patterns. We use both small (first three) and large (last three) datasets shown in Table 5 for these experiments. The last four are taken from the FIMI repository (Goethals and Zaki 2004). The Gene dataset is from Zhao et al. (2006), and IBM100 is a synthetic dataset generated using the IBM itemset generator (Agrawal et al. 1996).

Table 5 Datasets

5.1.1 minAND sampling quality

Figure 5 shows minimal AND-clause sampling quality on the chess dataset using the transition probability matrix from Eq. 3. We set the support threshold $\sigma =2500$, for which the chess dataset has $f=6838$ frequent minAND patterns. We ran the MCMC chain for $k=683{,}800$ iterations so that each pattern can be sampled an average of $t=100$ times. Figure 5a shows the number of times each minAND expression is visited, with the x-axis arranged in lexicographic order and by length of the patterns (maximum minAND clause size was 10). We can see that there is no bias by length.

Fig. 5

minAND sampling: chess dataset

Figure 5b shows the histogram of the visit counts. We can observe that the histogram is very close to a binomial distribution with the peak at the mean value of 100. This is not surprising, since in the ideal case of sampling a pattern uniformly, the number of times a pattern is selected is described by the binomial distribution. To see this, consider a dataset that has $f$ minDNF patterns. If we perform a uniform sampling for $k=f\times t$ steps, the number of times $m$ a specific pattern will be sampled is described by the binomial distribution, $\mathcal{B}(m|k,p)$, where $p=\frac{1}{f}$. The expected number of times a minDNF pattern is visited is therefore given as

$$\begin{aligned} kp = f \cdot t \cdot {1\over f} = t, \end{aligned}$$

and the standard deviation is

$$\begin{aligned} \sqrt{kp(1-p)} = \sqrt{t(f-1) \over f}. \end{aligned}$$

(8)

In our experiment, we ran our minAND sampling algorithm $t=100$ times on chess. Thus, in the ideal case the mean (and median) is 100 and the standard deviation for the number of visits is given as $\sqrt{100\times \frac{6838-1}{6838}} = 10.0$. Table 6 shows the statistics for the number of visits for the minAND sampling and the ideal case. The least number of visits to a pattern was 58, and the maximum was 167 with the median We can see that the sampling quality for minAND-clauses is very good, with the median counts matching, and with the standard deviations also close to the ideal case.

Table 6 minAND sampling statistics: chess dataset

Figure 5c shows the variation distance between the probability of transitions from the empty expression $p^k(\emptyset ,.)$, and the uniform distribution $\pi$ over the 6838 minAND patterns, i.e., the figure plots $vd_\emptyset (k)$ using Eq. (4). The variation distance is plotted as a function of the number of iterations. We can see a very rapid decrease in the value from a variation distance of 0.999 to the final value of 0.0504. In fact, the variation distance drops to under 0.1 in just 177K iterations, even though the entire chain is run for 6838K iterations. Figure 5d shows the number of distinct minAND patterns seen versus the number of iterations. For instance, it took 161794 iterations to visit all 6838 minAND patterns, which gives an indication of the cover time of the Markov chain, i.e., the maximum expected number of steps to reach all states starting from a given state, with the maximum taken over all states. In fact it takes only 20697 iterations to visit 90 % of the states, with the remaining 10 % of the states taking the residual 141 K iterations, as seen from the sharp rise in the number of distinct patterns found followed by the leveling off after the knee of the curve.

Since each run of minAND sampling algorithm gives only one instance of the chain, we computed statistics from several runs. We run the chain 5 times and report the average statistics, and we perform total of $k=f\times 100$ iterations for each run. Table 7 shows the (complete) number of minAND patterns for the different support values, as well as the mean and standard deviations (avg$\pm$std) for the variation distance and the number of iterations it takes to cover all minAND states. For the support values shown it was possible to obtain the entire transition probability matrix $\mathbf {P}$, and thus we also show the spectral gap for the chain, i.e., the absolute difference between the largest ($\lambda _1=1$) and second largest ($\lambda _2$) eigenvalue of $\mathbf {P}$. Finally, we compare the results using the matrix $\mathbf {P}$ from Eq. (3) (the default), and the simpler one from Eq. (2). We can see that on average the simpler one takes many more iterations to cover all states. For example, for ${\sigma _{\min }}=2000$, Eq. (3) tool 1.6 millions steps (on average) to cover the states, whereas the simpler chain [Eq. (2)] took 3.9 million steps (more than twice as many steps). The simpler chain also had larger variation distance, and smaller spectral gap. These results confirm our earlier discussion that the transition matrix in Eq. (3) is more efficient.

Table 7 minAND sampling: average statistics

5.1.2 minDNF sampling quality

We now study the sampling quality for minDNF expressions and the sensitivity to various parameters. Before studying the Markov chain defined in Eq. 6, we compare it with the basic minAND type chain that adds and deletes items. We noted in the discussion at the beginning of Sect. 4.1.2 that given the large gap in the cardinalities of the minDNF and non-minDNF expressions, the probability of visiting minDNF nodes is much smaller than visiting non-minDNF nodes. This was confirmed experimentally. For example, on the chess dataset with ${\sigma _{\min }}=3100$, the minAND type chain took 12 min. and 14.4 s to sample 100 minDNF patterns, whereas our proposed weighting scheme (with $\alpha =0.9$ and $c=$avg. tlen) in Eq. 6 took only 8.7 s to sample the same number of minDNF expressions. Henceforth, we do not consider the minAND type sampling as a viable option, and discuss our proposed weighting schemes in Eq. 6.

Random walk type: We first show the effect of the type of random walk, i.e., (RWRJ, $j=50$ vs. RWR, $r=0.02$), as shown in Figs. 6 and 7. With ${\sigma _{\min }}=60$, on the IBM100 dataset, there are 654 distinct minDNF patterns (found using Blosom). We ran minDNF sampling for $k=654 \times 100$ iterations. We use $\alpha =0.25$ and $c$ is set to the avg. transaction length.

Fig. 6

Sampling quality (RWRJ): IBM100

Fig. 7

Sampling quality (RWR): IBM100

For the IBM100 dataset, we have $f=654$ and $t=100$, and thus in the ideal case we expect to see each pattern $100$ times, with standard deviation of $\sqrt{100 \cdot 653/654} = 9.99$ via Eq. 8. Figures 6 and 7 plot the number of times each pattern is visited (a), and the count histogram (b). The sampling statistics, namely the maximum, minimum, median, and standard deviation of visits counts for RWRJ and RWR are shown in Table 8. It is very clear that RWRJ is much superior to the RWR strategy; its median is closer to the ideal case, and the standard deviation is smaller. Whereas the RWRJ strategy jumps to a node in its history, RWR always restarts from the empty pattern. As such RWR is biased towards sampling patterns close to the origin, and this is reflected in the sampling quality.

Table 8 Sampling statistics: IBM100

Convergence rate: Figures 6c and 7c plot the variation distance for the RWRJ and RWR sampling methods. We compute the variation distance after every 1000 steps, using the probability of reaching a minDNF starting from the empty expression via the use of Eq. 4, i.e., the distance between $vd_\emptyset (k)$ and the uniform distribution $\pi$. We can see that the distance converges to slightly around 0.12 for RWRJ and to 0.36 for RWR, indicating that RWRJ is the better strategy. We also ran experiments on the Gene and Chess datasets, and obtained similar results (results not shown here).

Effect of $\alpha , c, j$: Table 9 shows the effect of these three parameters on the sampling quality on IBM100 with ${\sigma _{\min }}=60$. We set $k=10,000$ iterations. We run each experiment five times, and report the average number of distinct minDNFs sampled (npats), mean, standard deviation (std), maximum, minimum, and median (med) of the visit counts, and the average total time. Ideal sampling should yield a mean visit count of $k/f=15.3$, and a standard deviation of $\sqrt{k/f(1-1/f)} = 3.9$, since IBM100 has $f=654$ minDNF patterns for ${\sigma _{\min }}=60$. First, we look at the effect of $j$, fixing $c=avg$ and $\alpha =0.9$. Larger $j$ results in a smaller standard deviation, and ideally $j$ should not be constrained. However, for many of the classification datasets the random walk could get trapped in a local region, and therefore, we set $j=3$ in our earlier experiments. Next, we look at the effect of $\alpha$, setting $j=50$ and $c=avg$. We find that larger $\alpha$ takes more time, with a slight increase in std, most likely due to the constraint on $j$. Lastly, we fix $j=50, \alpha =0.9$ and vary $c$. Larger $c$ values take lesser time, but also result in higher deviation. The average $c$ value (9.3 for IBM100) offers an acceptable choice.

Table 9 Effect of parameters: IBM100

Table 10 Running time: minDNF and minDNF*

Scalability: Table 10 shows the time to sample the small (with $k=1000$) and large datasets (with $k=100$) for various support thresholds. In the table, results for minDNF sampling using the weight matrix in Eq. (6) are denoted as minDNF, whereas results using the faster weight computation in Eq. (7) are denoted as minDNF*. Blosom was unfortunately not able to mine the complete set of patterns for any of these datasets for the support levels shown even after 24 h for the smaller datasets, and 48 h for the large ones. We note that whereas minDNF provides better theoretical guarantee, minDNF* is significantly faster (by as much as an order of magnitude). We also compared minAND sampling time with Blosom-MA and CHARM-L, both of which can mine minimal AND-clauses. For example, for the Gene dataset with 10 % support, minAND took 0.7s to sample 1000 patterns, whereas CHARM-L took 40m54s and Blosom-MA took 2h58m56s. For lower support values, neither of these methods could finish within 24 h, whereas for 1 % support minAND finished in 1.3 s. These results confirm that complete mining is practically infeasible, whereas sampling provides a viable alternative.

5.2 Application of minDNF patterns for classification

Having studied the quality for the minAND and minDNF sampling, we now study an application of minDNF sampling for classification. The basic idea is to see whether minDNF pattern can be used as effective features for classification, and to compare and contrast with minAND features.

We experimented with a wide range of datasets from the UCI repository (Frank and Asuncion 2010) as shown in Table 11. First, each of the 34 datasets was converted into a categorical one using entropy-based discretization (Fayyad and Irani 1993), as implemented in the Orange data mining suite (Curk et al. 2005). The total number of transactions and items in each dataset, and the number of classes (ranging from 2 to 24) are shown in the table. These are denoted as trans, items, and cls, respectively. Next we ran a linear SVM, on the original (non-discretized) dataset, as well as on the discretized dataset, using fivefold cross-validation. For a given run of minDNF sampling, we converted each of the mined minDNF patterns into a binary attribute, that takes on the value 1 if a transaction satisfies the minDNF formula, and 0 otherwise. This binary-valued dataset is then classified using linear SVM with fivefold cross-validation, again using the Orange library [which in turn uses LIBSVM (Chang and Lin 2011)]. Since the sampling is randomized, we repeat the sampling 10 times, and report the averages.

Table 11 Classification performance: accuracy $\pm$ standard error. The column header cls denotes #classes, and trans and items denote the number of examples and attributes, respectively

For minDNF and minAND sampling the default parameters are as follows: We use the random walks with random jump approach, with $j=3$. We use $\alpha = 0.9$ and set $c$ to the average transaction length. The minimum support for the DNF and clause were both set to 1, i.e., ${\sigma _{\min }}= {\sigma ^c_{\min }}= 1$. Finally, we sampled $k=100$ minDNF patterns. Thus, for minDNF and minAND the number of “items” or features is at most $k$ for all datasets (it can be less after removing duplicates). Note also that by default we do not perform any feature selection; we study the effect of feature selection later.

Table 11 shows the fivefold cross-validation classification accuracy and standard-error for each algorithm, over each of the datasets, averaged over ten runs. The best results are shown in bold. In the table, results for minDNF sampling using the weight matrix in Eq. (6) are denoted as minDNF, whereas results using the faster weight computation in Eq. (7) are denoted as minDNF*. SVM-orig and SVMd denote the performance of SVM on the original and discretized dataset, respectively. Finally, non-default parameters are indicated in the table (third row), when we compare minAND with $k=500$, and minDNF/minAND with ${\sigma _{\min }}=5\,\%$.

5.2.1 minDNF versus SVM

minDNF time: The total times for minDNF and minDNF* for the various datasets are shown in Table 12. The running time is affected by the number of items, since the more the items, the more the number of neighbors, which affects the weight/transition probability computation time. However, note that these results are with support one, and substantial speedup is possible for higher support values. We can observe that minDNF* is typically over an order of magnitude faster than minDNF, though this comes at some penalty in classification performance, as we describe next.

Table 12 Time (in sec) for minDNF and minDNF*, and average number of clauses per DNF expression (with standard deviation)

minDNF versus SVMd: Our minDNF sampling algorithm yields a near-uniform sample and we can see from the classification accuracies in columns 7 and 8 in Table 11 that the sampled minDNF patterns make excellent features. In 24 out of the 34 datasets, they yield the best accuracy among all methods, including SVM-orig (on the original) and SVMd (on the discretized datasets). On three datasets, the differences between minDNF and the best method is not significant. On two datasets SVMs substantially outperform minDNF, namely, balancescale and postoperative, where the difference is more than 10 %.

minDNF* sampling: Since minDNF sampling using Eq. (6) does take more time, we also compared with minDNF* that uses the faster weight computation in Eq. (7). We can see from the results in column 9 in Table 11 that minDNF* sampling suffers in performance compared to minDNF. However, minDNF* still outperforms SVMd on 22, SVM-orig on 21, minAND patterns (with $k\!=\!100$) on 31, and minAND (with $k\!=\!500$) on 18 out of the 34 datasets.

5.2.2 minDNF versus minAND features

Comparing the Boolean expression features comprising minDNF patterns versus minAND patterns (both with $k\!=\!100$), we find that minDNF substantially outperforms minAND (see columns 7 and 10). Although initially unexpected, it is perhaps not that surprising, given the fact that minDNFs can be considered as disjunctive rules, and are much more informative than simple conjunctive rules. Over all the 34 datasets, minDNF sampling yields on average 2.69 clauses per DNF expression, with a standard deviation of 1, as shown in column 3 in Table 12. Therefore, for a fair comparison for minAND, we increased the number of sampled minAND expressions to $k\!=\!500$ features, so that minDNF (with $k\!=\!100$) and minAND (with $k\!=\!500$) have a comparable number of total clauses. The classification results are shown in column 11 in Table 11. We see that the larger number of features improves minAND in most cases. However, minDNF (with $k\!=\!100$) is still substantially better than minAND ($k=500$). Only on three datasets (lenses, monks1, and monks2) does minAND outperform minDNF.

Increasing $k$ for minAND: Table 13 records the classification accuracies obtained by increasing the number of sampled expressions ($k$) for minAND patterns. We see that a large number of clauses is clearly beneficial for minAND, since on 18 out of the 34 datasets, $k=10,000$ achieves the best accuracies. For example, on breastwisc2, the classification accuracy is $96.3$ with $k\!=\!10,000$, while it is $72.2$ with $k\!=\!500$. Comparing with minDNF with only $k\!=\!100$, we find that it is better than minAND with $k\!=\!10,000$ on 11 out of the 34 datasets. Even though minAND with $k\!=\!10,000$ has a slight edge, it is important to note that the differences are not really significant for 12 out of the 18 datasets where minAND performs better. We can observe that minAND outperforms significantly on the 6 datasets balancescale, car, monks1, monks2, promoters, and tictactoe. On the other hand, minDNF significantly outperforms minAND (with $k\!=\!10,000$) on 8 datasets like adultsample, anneal, audiology, brownselected, glass, lungcancer, yeastRPR and zoo. Particularly on adultsample, audiology and glass the accuracy difference is more than 30 percentage points (e.g., 79.8 vs. 46.7 % on adultsample).

Table 13 Classification performance with increasing $k$ for minAND: accuracy $\pm$ standard error

These results indicate that overall minDNF patterns are more effective than minAND patterns, for comparable model complexity in terms of the number of clauses.

5.2.3 Augmented experiments: effect of parameters and variants

Effect of support: To see the effect of minimum support on classification accuracy, we ran minDNF and minAND sampling with the minimum support set to 5 % of the number of transactions (see columns 8 and 12 in Table 11). Overall, we find that adding the frequency constraint is not that beneficial for minDNF sampling, since mining frequent minDNFs improves the accuracy only slightly in 9 datasets, when compared to the minDNFs with support one. On the other hand, frequent minANDs are better than support-one minANDs on 26 datasets. Mining frequent expressions obviously lowers running times.

$\alpha$ effect: Our default weighting parameter for the transition probability matrix is $\alpha = 0.9$. We also experimented $\alpha = 0.25$ and $\alpha = 0.5$. See the comparative results in columns 2–4 in Table 14. Note that column 2 contains the results from our default parameter settings. In 23 out of the 34 datasets, $\alpha = 0.9$ gave the best performance. This is because the random walk favors edges whose two ends are of different types, i.e., one end is a minDNF pattern and the other end is not a minDNF pattern (see Eq. 6). Thus, by setting $\alpha = 0.9$, and independence among the sampled minDNFs is increased and the redundancy is reduced, compared to both $\alpha = 0.25$ and $\alpha = 0.5$, which consequently yields more effective classifiers.

Alternative construction of minDNF features: Recall that each of the mined minDNF patterns comprises a binary feature for classification via SVMs. By default, a feature takes on the value $1$ if it is satisfied by an instance in the input dataset. We also experimented with some alternative approaches for feature construction. In particular, an input instance takes on the value $1$ if (1) the majority of clauses in the minDNF are satisfied (i.e., at least half of the clauses in the minDNF are true), and (2) the exclusive OR (XOR) of all the clauses in the minDNF is 1. The classification results are shown in columns 5 and 6, respectively, in Table 14. We can see that overall, these alternative approaches do not help. In essence, they negate the effect of satisfying the entire minDNF expression; the default binary minDNF features are the best among all the three approaches.

Table 14 Classification performance (augmented experiments) for minDNF: accuracy $\pm$ standard error

Effect of minimum overlap: In Table 14 columns 7–9 we look at the effect of increasing the minimum overlap parameter ${\sigma ^o_{\min }}$ between any two clauses. We range ${\sigma ^o_{\min }}$ from $0$ to $5\,\%$ similarity in terms of the total number of instances. When there is no overlap constraint the minDNF features achieve a better accuracy on 18 of the datasets compared to ${\sigma ^o_{\min }}=5\,\%$. On the other hand, a 5 % minimum overlap yields better accuracies on 15 of the datasets. Nevertheless, the differences are not that significant, except on a few cases (e.g., balancescale where ${\sigma ^o_{\min }}=0\,\%$ has an accuracy of 74.1 % whereas ${\sigma ^o_{\min }}=5\,\%$ has an accuracy of 92.2 %). Even though the benefits of the minimum overlap constraint may not appear in the classification results, it is a reasonable constraint that has its use in exploratory analysis applications.

Negated items: We also experimented with minDNF expressions containing negated items. However, in this case the accuracy was slightly better for the negated items in only 5 out of the 34 datasets, which unfortunately came at the expense of a significant increase in the runtime (sometimes by orders of magnitude). We conclude that negated items do not confer significant advantages in terms of classification (at least for the UCI datasets tested).

5.2.4 Effect of feature selection

So far we have not used any feature selection for the classification results. We wanted to see if careful selection of good features can improve accuracy results. For these experiments, we sampled $500$ Boolean expressions (minDNF or minAND) and used two criteria to select the top-$k$ for $k=100$ patterns that are useful for classification. Suppose that a dataset contains $l$ classes, then we can divide the dataset into $l$ parts as follows: $\mathcal {C}_i = \{t \in \mathcal {D}|\; t \text{ has } \text{ class } i\}$, with $i=1,\ldots ,l$. Let the dataset $\mathcal {D}$ have a total of $n$ transactions. For the $i$-th mined expression, we convert it into a new attribute $\mathcal {A}_i$ which is binary, $i \in \{1,2, \ldots , k\}$. Note that the new attribute $\mathcal {A}_i$ divides the dataset into two parts, $\mathcal {D}_{i1} = \{t \in \mathcal {D}|\; t \text { satisfies } \mathcal {A}_i \}$ and $\mathcal {D}_{i0} = \{t \in \mathcal {D}|\; t \text { does not satisfy } \mathcal {A}_i \}$. We rank the attribute $\mathcal {A}_i$ using the purity and entropy criteria, as follows:

• (a) Purity: For the $i$-th attribute $\mathcal {A}_i$, its purity is defined as

  $$\begin{aligned} purity(\mathcal {A}_i) = \frac{1}{n} \sum _{j=0}^{1} \max _{a} | \mathcal {D}_{ij} \cap \mathcal {C}_{a} |, \end{aligned}$$

  where $a \in [1,l]$. Purity lies in the range $[0, 1]$, and the higher the purity value, the better the discriminating power of $\mathcal {A}_i$. We ranked the mined expression in descending order of purity, and select the top $k$ as features for classification.

• (b) Entropy: For the $i$-th attribute $\mathcal {A}_i$, we first define the entropy of $\mathcal {D}_{ij}$, as follows:

  $$\begin{aligned} H_{ij} = - \sum _{a=1}^{l} P_{ij}(a) \log (P_{ij}(a)), \end{aligned}$$

  where $j \in \{0, 1\}$, and where $P_{ij}(a)$ is the probability of the transactions in the set $\mathcal {D}_{ij}$ having class label $a$, i.e., $P_{ij}(a) = \frac{|\mathcal {D}_{ij} \cap \mathcal {C}_a|}{|A_{ij}|}$. Finally, entropy of attribute $\mathcal {A}_i$ is defined as:

  $$\begin{aligned} H(\mathcal {A}_i) = \frac{|\mathcal {D}_{i0}|}{|\mathcal {D}_{i0}|+|\mathcal {D}_{i1}|} H_{i0} + \frac{|\mathcal {D}_{i1}|}{|\mathcal {D}_{i0}|+|\mathcal {D}_{i1}|} H_{i1}. \end{aligned}$$

  Entropy lies in the range $[0, 1]$, and the lower the entropy value, the better the discriminating power. We ranked the mined minDNF patterns by the ascending order of entropy and then select the top $k$ features.

In the experiments, we perform independent fold-based training (fivefold cross-validation classification) to selected the top $k=100$ expression. That is, the best patterns are selected using four of the folds as training and the remaining fold for testing, using the purity and entropy-based criteria. The results for both minDNF and minAND patterns is shown in Table 15. We find that adding the feature selection as a preprocessing step for minDNF classification is clearly beneficial. For example, using entropy for feature selection, 25 out of 34 datasets achieved better classification accuracies, compared to no feature selection. Using purity 20 datasets had better results. Comparing entropy and purity, entropy is slightly better on 21 datasets. For minAND, feature selection substantially improves the accuracies. For example, using entropy for minAND, 30 out of the 34 datasets had improvements, most of them very significantly.

Table 15 Classification performance (augmented experiments) for minDNF using top-$k$ feature ranking: accuracy $\pm$ standard error

minDNF versus rule-based classifiers: We wanted to evaluate the effectiveness of our minDNF features compared to rule-based classifiers. For this we select the lazy associative classifier (LAC; Veloso et al. 2006), which is a state-of-the-art exemplar of the rule-based approach. LAC is a lazy algorithm and it focuses on generating rules on testing instances that are useful for classification. It systematically enumerates itemsets (AND-clauses) that are the most discriminative, and classifies a test instance by combining/voting among all the rules that fire. Note that LAC is also able to deal with the small disjuncts problem (Holte et al. 1989). The last column in Table 15 shows the accuracy results for LAC. Comparing with column 4, i.e., minDNF with entropy-based feature selection, we find that minDNF features result in better accuracies in 18 out of the 34 datasets, whereas LAC is better on 14 datasets. Note that as expected, LAC is much better than minAND features, even with entropy-based selection. LAC is better than minAND with entropy on 25 datasets, whereas the opposite is true on 9 datasets. This is expected, since LAC mines AND-clauses and combines the most discriminative among them using various measures. On the other hand, minAND mines only minimal AND-clauses and uses entropy (or purity) for feature selection. It is interesting that even though LAC is specifically designed for classification, our minDNF features combined with feature selection, outperform LAC on 18 of the datasets. Notable examples are anneal (99.1 for minDNF vs. 85.6 for LAC), audiology (76.6 vs. 31.9), tictactoe (81.1 vs.67.6), and so on.

6 Conclusions

In this paper we presented the first approach to sample the simplest Boolean patterns, namely the minimal DNF expressions. We propose a novel weighting scheme to compute the transition probability matrix for the MCMC sampling algorithm, which bounds the amount of non-uniformity in the sampling. Since the method can be slow in practice, we also suggest a faster alternative, that yields effective sampling quality as well. We perform an extensive set of experiments to test various design parameters, and justify our choices. Finally, somewhat surprisingly, we found that the minimal DNF patterns make very effective features for classification. Via an extensive set of experiments on UCI datasets, we show that our method outperforms simple AND-clause based features, as well as the SVM method, typically by a wide margin, though it does suffer in the runtime comparison. However, the faster weight computation approach yields significantly faster running times, with some loss in the classification accuracy. The minDNF features still remain the effective across the different classifiers. Perhaps the most interesting aspect of the classification study is that using support-less patterns (with minimum support one) is already very effective for classification, and adding feature selection yields even more benefits. Our future work will target more effective feature selection by considering other interestingness criteria for the patterns while sampling, such as their discrimination power. Efficiency still remains an issue, which may be tackled by implementing the approach on multi-core processors, as well as utilizing graphics computing units, since the MCMC methods are inherently parallel.