Learning Bermudans

Abstract

American-type financial instruments are often priced with specific Monte Carlo techniques whose efficiency critically depends on the dimensionality of the problem and the available computational power. Our work proposes a novel approach for pricing Bermudan swaptions, well-known interest rate derivatives, using supervised learning algorithms. In particular, we link the price of a Bermudan swaption to its natural hedges, which include the underlying European swaptions, and other relevant financial quantities through supervised learning non-parametric regressions. We explore several algorithms, ranging from linear models to decision tree-based models and neural networks and compare their predictive performances. Our results indicate that all supervised learning algorithms are reliable and fast, with ridge regressor, neural networks, and gradient-boosted regression trees performing the best for the pricing problem. Furthermore, using feature importance techniques, we identify the most important driving factors of a Bermudan swaption price, confirming that the maximum underlying European swaption value is the dominant feature.

1 Introduction

In different scientific fields, the adoption of machine learning algorithms has shown significant promise to enhance the understanding and analysis of complex systems, as well as to improve the efficacy of current solutions. Specifically, a field that could greatly benefit from the study and application of these techniques is quantitative finance, particularly the pricing of financial instruments. Recently, a diverse range of machine learning techniques was effectively applied to this problem, as summarized by Bloch (2019). For example (Hernandez, 2017) applied neural networks to the market calibration of interest rate models; Masters and Luschi (2018), Ferguson and Green (2018), Cao et al. (2021) applied deep learning respectively to plain vanilla, basket and exotic options; Cao et al. (2019) employed neural networks to understand the option’s implied volatility; while (Huge & Savine, 2020) combined automatic adjoint differentiation (AAD) with modern machine learning for option pricing.

In the realm of financial instruments’ pricing, one crucial problem is determining the optimal stopping time; in general, it involves devising a strategy for determining when to take action to maximize an expected reward or minimize an expected cost. This issue is particularly relevant especially when pricing financial products such as American or Bermudan-type options, in which the purchaser can exercise their right at the most favourable time, making the determination of the optimal stopping time policy essential to achieve the highest expected value. Several studies explored optimal stopping time problems from a theoretical point of view, including works by Carriere (1996), Kobylanski et al. (2011). From a practical point of view, Monte Carlo simulations and dynamic programming are widely used; in fact, a number of algorithms were proposed in the literature, such as those presented by Barraquand and Martineau (1995), Longstaff and Schwartz (1998), Glasserman (2003), Egloff et al. (2007). However, the efficiency of Monte Carlo methods and, more importantly, the computational power available are critical factors affecting these techniques. Recently, researchers proposed the application of machine learning algorithms to solve or expedite the solution of optimal stopping time problems. For example, Becker et al. (2020a) and Becker et al. (2021) established a generalized framework and provided practical applications. Chen and Wan (2019), Lapeyre and Lelong (2020) utilized neural network regression to estimate continuation values, while (Becker et al., 2020b; Gaspar et al., 2020; Kohler et al., 2010) focused on pricing American/Bermudan options using deep learning. Hoencamp et al. (2022), Lokeshwar (2022) employed machine learning techniques for pricing and hedging American-type options. Additionally, Goudenège et al. (2019) proposed variance reduction techniques. These approaches are limited to a subset of machine learning algorithms that belong to the field of artificial neural networks to solve dynamic programming problems or approximate the optimal exercise boundary. Furthermore, they are still based on Monte Carlo numerical simulations, which may prove to be computationally intensive for path-dependent exotic options (Goldberg & Chen, 2018).

The present study contributes to this field by proposing an original approach based on a different perspective. We focus on supervised learning, a branch of machine learning, that facilitates the automation of decision-making processes by drawing generalizations from previously known examples. Specifically, we aim to establish a connection between the price of a Bermudan swaption, which is a well-known interest rate derivative used for hedging or speculation purposes in callable debt instruments or OTC trading, and the relevant financial quantities quoted on the market.

To achieve this goal, we employ different supervised algorithms and non-parametric regressions to obtain estimators for Bermudan swaption prices. Some, by nature, fit better to regression problems than others (e.g. regression models, k-nearest neighbours, etc), some are more suited to classification problems (e.g. decision trees, random forest, etc), some are more sensitive to hierarchical feature selection and assume some sort of feature independence (e.g. decision trees, etc) and some are more global models and treat the full feature vector together (e.g. kNN, MLP, etc). Since the selected machine learning algorithms differ profoundly in the way they interpret, process and represent the data, we carry out a comparative analysis in order to identify the algorithm with the best performance.

Moreover, as the actual market does not provide enough information and scenarios to build a sizeable dataset and, to make our models as general as possible, we generate a synthetic coherent price dataset through numerical simulations based on the Hull-White interest rate model (Hull & White, 1994). We consider two dimensions to increase the size of the dataset: the first consists of the contractual information of the Bermudan options, i.e. tenors, strikes and moneyness, that we select to cover a huge tradable domain. The second dimension consists of market scenarios. Typically the parameters of the pricing model are calibrated to the current market; instead in our approach, in order to consider a variety of market conditions, we select a large domain of feasible and market-consistent values of the model parameters. At this point, the synthetic option’s prices are derived using the Least Square Monte Carlo dynamic programming algorithm proposed by Longstaff and Schwartz (1998). Both the Hull-White model and the Least Square Monte Carlo technique are standard approaches widely used in the market.

Summarizing, the novelties introduced by our work range in several fields: first, to our knowledge, the paper is the first one to use machine learning to address the Bermudan swaption pricing problem, offering a viable solution to the computational challenges posed by Monte Carlo numerical simulations discussed above. Moreover, we do not the training of the models to a single market condition, but rather we have created a huge dataset with different feasible market scenarios trying to cover the research space in the most exhaustive and possible way. Furthermore, in order to maintain an agnostic view of the problem and to make our approach as general as possible, we implemented a heterogeneous set of machine learning algorithms with different peculiarities. Consequently, through feature importances analysis, we can obtain insights into the primary drivers of Bermudan swaption prices, a piece of information that cannot be obtained from traditional simulations. In addition, our approach is fully extendable to any other American-type instrument.

The remainder of the paper is structured as follows. In Sect. 2, we provide a concise overview of the various tools employed in this study. This includes a discussion of the Hull-White One Factor model, which we use to generate synthetic market data, and the description of the Least Square Monte Carlo algorithm, which we use to obtain target prices for Bermudan swaptions. Additionally, we provide a brief summary of the supervised learning algorithms used to estimate option prices. In Sect. 3, we provide a detailed description of the dataset creation process, including the specific market scenarios considered and the methodology used to generate synthetic data. In Sect. 4, we present the numerical results obtained from our analysis, including a comparative analysis of the performance of different supervised learning algorithms and an investigation of the relative importance of different input features. Finally, in Sect. 5, we summarize our findings and present some potential directions for future research.

2 Theoretical Setting

In this section, we give a short compendium of the tools implemented for this work. The first two sections briefly deal with the financial topics at the core of our research, while the last section introduces supervised learning and the algorithms considered.

2.1 Bermudan Swaptions

Swaptions are interest rate derivatives on an Interest Rate Swap (IRS) typically traded by large corporations, banks, financial institutions, and hedge funds. There are two main versions of swaptions, a payer and a receiver. A payer swaption is an option that gives the right, but no obligation, to enter a payer IRS at the maturity of the option; in other words, the buyer has the right to become the fixed rate payer in an IRS, which length is called the tenor of the swaption. Instead in the receiver version, the buyer has the right to become the receiver of the fixed leg. There are two standard market payoffs, that differ in the settlement convention: physical or cash. We will focus only on the first type, i.e. those once exercised, are transformed into the underlying swap. In general, three main styles define the exercise of derivative instruments and therefore also of a swaption: European, Bermudan and American. In this work, we will focus only on co-terminal Bermudan swaptions, i.e. exotic interest rate derivatives that allow the buyer to enter, at multiple exercise dates $\left\{ T_{1},\dots ,T_{N} \right\}$ into a swap starting at time $T_{i}$, $i=1,\dots ,N$ and maturing at $T_{M} > T_{N}$. If we indicate the valuation date as t the period $T_{1} - t > 0$ is defined as no call period. Notice that European swaptions can be seen as Bermudan with a single exercise date and in turn, the American type can be seen as the extension to the continuum of the Bermudan. There are no market quotations or broker pages available for Bermudan swaptions because they cannot be priced analytically; in fact, their value depends, at each exercise date, on the choice of the option holder whether it is more convenient to exercise it (retrieving the payoff) or to continue with the contract (continuation value).

2.2 Hull-White One-Factor Model and Least Square Monte Carlo

To analyze and price instruments described in the previous section we implemented two tools: the Hull-White One-Factor Model (G1++) (Hull & White, 1994) and the Least Square Monte Carlo (LSMC) (Longstaff & Schwartz, 1998).

The Hull-White One-Factor Model, also known as G1++, is a specific case of the Ornstein-Uhlenbeck process characterized by a single stochastic factor (see Appendix A). It is one of the major exogenous short rate models which is nowadays often used for pricing and risk management purposes and specifically, we used it for the simulation of the underlying stochastic dynamics and hence for the evolution of the interest rate curve. This model is analytically tractable, in fact, there are closed pricing formulas for some instruments, e.g. European swaptions (Brigo & Mercurio, 2006); this feature is decisive for us as European swaptions represent the natural hedges of Bermudan swaptions and they have a fundamental role in the pricing of these products (Hagan, 2002). Our aim is to probe different market scenarios, but since in recent years the rates and their correlations have always been low, these historical data do not allow us to have enough wealth in the dataset. For this reason, we have exploited the two G1++ parameters, i.e. speed of mean reversion (a) and volatility $(\sigma )$, to create many different market scenarios that differ in the global level of variances and covariances of the relevant stochastic processes, in order to increase the variability of our dataset, avoiding any type of calibration.

On the other hand, the Least Square Monte Carlo (LSMC) is one of the most widely used dynamic programming tools for the pricing of American-type options. It is one of the methods proposed to reduce the complexity of American option pricing avoiding nested Monte Carlo; it is a regression-based method that uses some specific function (basis function) to approximate the continuation values in the underlying optimal stopping time problem (Brigo & Mercurio, 2006). The success of this type of method, as well as depending on the computational power available, strongly relies on the choice of the basis functions and their number, making it still tied to the efficiency of the Monte Carlo simulation.

2.3 Supervised Learning Algorithms

The implementation of the tools explained in previous sections allowed us, starting from real market data (Appendix F) to obtain a synthetic price dataset used to train the supervised algorithms. To find out which supervised algorithm is best suited to our problem, we analysed a very heterogeneous set of models. Generally, since the problems faced with these techniques involve inferences on complex systems, it is a common choice to select several candidate models to which their predictive performance must be compared. Below we present the list of algorithms used in our work. For a more in-depth discussion of their main characteristics, strengths and weaknesses we refer to Appendix B, while for all mathematical details, we refer to Hastie et al. (2001), Géron (2017).

• k-Nearest Neighbour (k-NN);

• Linear Models;

• Support Vector Machine (SVM);

• Tree-based algorithms;

  • Random Forest (RF);

  • Gradient Boosted Regression Tree (GBRT).

• Artificial Neural Networks (ANN or MLP).

Although these algorithms are all different from each other in how they interpret and represent the features and the data, in order to define their predictive capabilities and to be able to compare them, we have adopted a similar approach for all. It can be divided into 3 steps:

• 1. The first focuses on the modelling of the input data in such a way as to present the dataset to the algorithms in the most effective way possible based on its intrinsic characteristics of the algorithm;

• 2. The second step concerned the optimization of the algorithms by modifying the respective hyperparameters to exploit their potential. This research on hyperparameters was carried out using exclusively the training set and the technique known as k-fold cross-validation; it consists of dividing the training set into k sets and in rotation using $k-1$ to the training and the remainder for validation. Once all the possible combinations have been completed, the average performance is used as a measure of the goodness of the model and as a comparison metric for the same algorithm with different values of the hyperparameters;

• 3. The third, and last step, consists of quantifying the errors of each algorithm in order to be able to compare them with each other. For this phase, we used exclusively the test set and different evaluation metrics with different characteristics. For definitions and their peculiarities, we refer to Appendix C.

3 Creation of the Dataset

Each supervised learning algorithm needs a dataset to start from and, given its importance, we will focus on its creation and exploration of it. Since our goal is to predict the price of Bermudan swaptions starting from some of their characteristics available to market participants, we need a dataset containing this information. Specifically, the prices of the Bermudan swaptions represent the dependent variable also known as the target, while all the information that we decide to use as independent variables, is known as features. Furthermore, it is well to underline that in our case the quantity to be predicted is a single real number (the Bermudan swaption price) and therefore the problem we face falls into the category of single output regression problems.

For the creation of the dataset, we selected a heterogeneous set of 434 Bermudan swaptions such as their terms cover the typical trading activity on the market. We report the entire set with their contractual specifications in Table 11 of Appendix G. The Bermudan swaptions considered have different characteristics like the side, i.e. the payer and receiver version, tenor, no call period and strike. Specifically, the tenor represents the duration (months) of the underlying swap contract, the no-call period is the period (months) until the first possible exercise date, and the strike is the distance in basis points from the ATM. Unlike pricing these instruments in a single market scenario, we considered different market scenarios to increase the number and variability of our dataset. This operation is possible considering multiple values of the parameters of the short-rate model implemented. Pricing the entire swaption set with different speed of mean reversion and volatility values allows us to consider different variance levels of the underlying stochastic processes, thus generating different market situations. In theory, these parameters could be chosen arbitrarily, but to obtain values that were reasonable with today’s market we acted differently: we calibrated the G1++ parameters (with the Nelder-Mead algorithm) for each of the Bermudan swaptions in the basket to their natural hedges, i.e. the underlying European swaption, not only using the market data available (Appendix F) but also other two scenarios obtained by modifying the implied Black volatility of those available. Specifically, we built high and low volatility scenarios by bumping the original volatility of $+25\%$ and $-25\%$ of its original value. In conclusion, this procedure allowed us to define reasonable ranges for the parameters of the Hull-White model:

$$\begin{aligned} a \in [ -2\%,30\% ], \qquad \sigma \in [ 0.1\%,9\% ]. \end{aligned}$$

(1)

within this parameter space, we identified two pathological areas that are not interesting to be explored, which are respectively the one with high speed of mean reversion and low volatility values and the opposite one, i.e. with high volatility and low speed of mean reversion. Specifically, the first combination returns an almost deterministic model as it does not have volatility while the second combination returns an explosive behaviour of the model. For these reasons, we have selected a central area in which to sample the parameters. We have selected 10 pairs of values which homogeneously cover the parameter space and we report them in Appendix E. Once these values were defined, it was possible to obtain the price, through the Least Square Monte Carlo, for each of the 434 Bermudan swaptions in the basket for a total of 4340 prices (10 different scenarios for each swaption). With the aim of speeding up the computation, we parallelized the simulations on a cluster; specifically, we used 25 CPU cores each of which is entrusted with $2 \times 10^{4}$ simulations for a total of $5 \times 10^{5}$ Monte Carlo paths for each sample.

Having defined the possible values of the G1++ parameters and obtained the corresponding prices, i.e. the target, we just have to identify the features. Since we want supervised learning algorithms to be independent of the underlying model, neither the speed of mean reversion nor the volatility will be used as a feature, but we have decided to designate as independent variables some parameters related to the distribution of underlying stochastic process (Cao et al., 2021). In particular, we choose the no-call period, the tenor, the strike, and the side. The first two are related to the variance of the underlying swap rate and the last two are linked to the moneyness of the swaption. This information uniquely identifies the 434 Bermudan swaptions that make up our basket. We have decided not to include maturity as a feature because, knowing the tenor and the no-call period, it is redundant information and we have also excluded the exercising frequency as for all swaptions it is the same (annual). To help supervised algorithms to distinguish the Bermudan swaptions in the different market scenarios, we decided to provide two additional elements that could be useful for characterising the target. First, the price of the underlying maximum European swaption, computed with the closed-form of G1++, since we know it to be the lower bound of the Bermudan swaption price. Second, once the Monte Carlo paths have been simulated we compute the correlations between the swap rates of the underlying European swaptions and used them as a feature. With such simplified dynamics, the speed of mean reversion is related to these statistical quantities. Specifically, we have calculated the correlation between the swap rates of the European swaption with the longest tenor and that with the shortest tenor. For example, if we consider a Bermudan swaption with a 10-years no-call period and a 5-years tenor, we have evaluated the correlation between the swap rates of the $11 \times 4$ European swaption and the $14 \times 1$ European swaption. We report in Fig. 1 the correlation obtained between the swap rates and the price of the maximum European swaption while in Fig. 2 we report the distributions of the target (Bermudan price).

Fig. 1

Distribution of the correlation between the swap rates (left) and the price of the maximum European swaption (right). It can be noted that the correlations obtained cover the space in a homogeneous way while the prices of European swaptions, obtained with the closed formula of G1++, vary on very different scales

Fig. 2

Distribution of the target (Bermudan price). The price of the Bermudan options is obtained through the Least Square Monte Carlo algorithm with $5 \times 10^{5}$ paths each. Note that the price obtained varies on very different scales

In conclusion, to summarize, we report in Table 1 all the features (independent variables) and their possible ranges and in Table 2 the target (dependent variable) and its domain.

Table 1 Features (independent variables) of the dataset

Table 2 Target (dependent variable) of the dataset; it is unique and is represented by the price of the Bermudan swaption obtained through the LSMC

As stated previously, in the development of supervised learning algorithms, it is fundamental how features are presented. The side feature in our dataset is the encoding of a categorical variable to distinguish the payer version from the receiver. The most common way to represent categorical variables is one-hot-encoding; since any of the possibilities excludes the other, we have decided to create a single feature that takes value 1 when it is payer and 0 otherwise.

At this point, before applying supervised algorithms it is necessary to separate our dataset into the training set, used to build our model, and the test set used to assess how well the model works. We decided to use 80% (3472 samples) of the dataset for training and the remaining 20% (868 samples) for testing. Since the data were collected sequentially before dividing the dataset it is necessary to shuffle it to make sure the test set contains data of all types. Moreover, a purely random sampling method is generally fine if the dataset is large enough, but if it is not, there is the risk of introducing a significant sampling bias. For this reason, we have performed what is referred to as stratified sampling (Géron, 2017): since we know that the price of the maximum European swaption is an important attribute to predict the price of Bermudan swaptions, we have divided the price range of the maximum European swaptions into subgroups and in order to guarantee that the test set is representative of the overall population the instances are sampled from each of them. The test set thus generated has been put aside and will be used only for the final evaluation of each model. The construction of the various models and the choice of hyperparameters was based exclusively on the training set.

4 Numerical Results

This section is devoted to the comparison of the predictive performance of all the algorithms analyzed. For simplicity, we will not report here the data preparation and optimization phase of the individual algorithms, but we report in Table 3 all of them with their respective pre-processing phase and the optimized hyperparameters on the training set. For more details, we described in Appendix D the hyperparameters tuning for all supervised algorithms. All the algorithms were implemented through Python open-source libraries like scikit-learn, Keras and Tensorflow on a MacBook Pro (MacOS version 10.15.7) with an Intel Quad-Core i5 2.3 GHz processor with a memory of 2133 MHz and 8GB of RAM.

Table 3 All models with their pre-processing phase and optimized hyperparameters

Fig. 3

Values of the different evaluation metrics on the test set for each algorithm. The graph above shows the comparison for the absolute metrics, that is, those that report the error in the unit of interest (euro). The graph below shows the comparison for relative metrics in which the relative error is expressed in percentage terms

An easy way to compare models and their predictive capabilities is to observe their performance on the test set. For this purpose, we report in Fig. 3 the comparison between all the values of the evaluation metrics (Appendix C), both absolute and relative, grouped by the algorithm. For completeness, we also report in Table 4 a comparison between all the indices of the relative error distribution for each of the algorithms and in Fig. 4 the respective error distributions. Furthermore, we have also reported in Table 5 the comparison between the training and pricing times for all the supervised algorithms. To compare these results with the standard method, we priced the same set with the Least Square Monte Carlo considering $5 \times 10^{4}$ paths for each Bermudan swaption obtaining a pricing time equal to 1086.6 s. Given these results, the first observation in Fig. 3 is purely statistical; as expected the RMSE values are always greater than the MAE ones for all the algorithms. Furthermore, the values of WAPE and RRMSE, introduced to reduce and limit some negative aspects of the MAPE and the RMSRE respectively, are in fact lower or equal to the latter. It can be observed that the model that can be considered the worst for this type of problem is undoubtedly the k-NN as it has the highest generalization error in almost all the metrics considered. We believe that this is due to the too-simple nature of the algorithm and above all to the lack of flexibility of its hyperparameters, which limit the reachable complexity. Among all the tree-based models, we can observe that the RF and GBRT perform better than the simple decision tree as we reasonably expect for ensemble methods. The best of this kind of model and the most promising is the GBRT that have the lowest generalization error of all and for all the metric considered. The great strength of this type of algorithm, which makes them very versatile, is the fact that they require practically no preprocessing of the data. For this reason, we consider the GBRT promising and usable even with a larger dataset above all as the first-entry algorithm. Instead, SVM has slightly worse performance than the GBRT for all the metrics considered; also note that it has the highest RMSRE value among all the analyzed models. Let us consider the two best algorithms obtained; the best performance of all belongs to the Ridge regressor. Moreover, note that it has the lowest generalization error whatever the metric considered. A slightly worse result than this, but still very promising, is obtained by MLP. However, we believe that with even more research on hyperparameters and especially with a greater amount of training data, ANN could improve its performance. The only downside to the Neural Network is the long time it takes to train the model (Table 5).

Table 4 Comparison for all relevant statistics of relative error for each algorithm

Fig. 4

Relative error distributions for each of the algorithms. To make them comparable, all the distributions were superimposed and the interval was reduced; for this reason, some of the distribution queues are not visible. The distributions were obtained with a Gaussian kernel density estimation

All these deductions are also supported by the information reported in Table 4 and Fig. 4. In fact, it can be noticed the algorithms that have been identified as the best, have the average values closest to zero with the lowest standard deviation. Furthermore, it can also be seen from the values of skewness, kurtosis and quantiles that these models are characterized by the most symmetrical distributions without outliers. All the others, on the other hand, are characterized by higher standard deviations and in some cases larger tails of the distributions.

Table 5 Comparison between training and pricing times of all supervised algorithms and Monte Carlo simulation.

In general, from Fig. 3 it can be seen, apart from a few exceptions, that the result of the comparison between two models does not change if we observe different metrics. In other words, if one model is better than another by considering the error reported by one metric, it will remain better even if they are compared using a different metric. Consequently, if the goal is the pure comparison between models, we can say that the use of a particular metric with respect to another is useless. The use of a particular metric becomes decisive if we consider the purpose of the work and what represents the generalization error. Since in our case the goal was to predict prices over an extended range with different scales, we believe a relative metric has more meanings than an absolute one, and among the relative metrics (on the bottom of Fig. 3), we prefer the RRMSE (green) for its intrinsic characteristics. Summarizing, we can say that the average price error of the Ridge equal to 1% is an excellent result in comparison to the 2% average of the standard deviation found from market data. In conclusion, we can state that the Ridge Regressor and the Neural Networks are the most reliable algorithms for this type of problem as they have shown the greatest pricing precision and represent valid alternatives to Monte Carlo simulations as their pricing time is at least 5 orders of magnitude fewer.

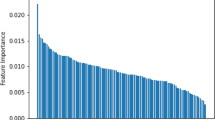
Typically, in supervised learning algorithms it is customary to ask what the relative weight of the independent variables in target prediction; this analysis is commonly known as feature importance. In other words, it gives a qualitative measure of the impact that each explanatory variable has in predicting the target. In Fig. 5 for each of the features, the importance assigned by each of the algorithms is reported together with their average value and the standard deviation.

Fig. 5

Feature importance for each of the algorithms grouped by feature. The values assigned by the algorithms to each of the features have been normalized so that sum up to 1. Note that all tree-based models have an endogenous method while for all the other models we used an indirect method, known as permutation importance. The last bar on the right for each feature represents the mean value and standard deviation of the feature importance assigned by each of the individual algorithms

Specifically, all methods based on decision trees have an endogenous method which is based on the reduction of the value of the metric used in the construction of the trees. For all the other models, however, we used an indirect method, known as permutation importance, which consists of evaluating the deterioration in performance when the values of a feature are randomly mixed and then using it as an indirect measure of the importance of a variable.

From Fig. 5 we can see a significant aspect: although with different weights, all the models developed indicate the price of the maximum underlying European swaption as the most explanatory variable. This outcome is reassuring as all models are able to recognize that the price of the Bermudan swaption is closely linked to the price of the maximum European swaption which constitutes its lower bound. Furthermore, except for the no-call period which is practically unused by all algorithms, the other features have comparable average values, with the only difference that the correlation between the swap rates has the lowest standard deviation, a sign that the returned weights by the individual algorithms are very similar to each other.

5 Conclusions and Perspective

In this paper we explored supervised learning techniques to address optimal stopping time problems in quantitative finance, focusing on the pricing of Bermudan swaptions. Our main goals were to assess the capability of these algorithms to correctly price these options overcoming the computational limitations of traditional Monte Carlo simulations, and identify the most important price drivers relying on feature selection analysis. To achieve these goals, we employed a heterogeneous set of different machine learning algorithms trained and tested on a synthetic dataset generated by means of the popular Hull and White short-rate model. By tuning its parameters we were able to explore different market conditions. Benchmark prices of Bermudan swaptions were obtained with a classic Least Square Monte Carlo simulation.

Our analysis demonstrates that the considered machine learning algorithms display high pricing precision yet being at least four orders of magnitude faster than the benchmark Monte Carlo simulation. In particular, the Neural Network and Ridge Regression are the most effective algorithms for this problem, with Ridge Regressor having a faster training phase. Gradient Boosted Regression Tree is also a promising algorithm due to its minimal data preparation requirements and intrinsic feature importance evaluation.

Furthermore, all the employed algorithms consistently highlight that the most relevant feature to explain Bermudan swaption prices is the maximum underlying European swaption premium. This result is coherent with the market knowledge that in order to price a Bermudan swaption it is essential to adopt pricing models capable of correctly pricing the underlying European swaptions quoted on the market. Finally, we emphasize that the approach developed in this work is easily generalizable to other American-type financial products.

The findings of this paper open new perspectives. For example, the set of features could be extended to include, for each Bermudan swaption, all the corresponding underlying European swaptions, leading to interesting analyses about optimal hedging strategies vega risk. Another interesting application of our approach regards co-terminal rate correlations, which are typically very difficult to imply from observed market prices. Instead to include their estimation with Hull and White model in the features set, one could use the machine learning algorithms to estimate them from historical Bermudan prices (i.e. swapping target and feature). Once available, these estimations could be used for pricing and correlation risk hedging purposes.

Appendices

Appendix A: Hull-White One Factor Model (G1++)

The G1++ model assumes that the instantaneous short-rate process evolves under the risk-neutral measure according to

$$\begin{aligned} dr(t)=[\vartheta (t)-a r(t)] d t+\sigma d W(t) \end{aligned}$$

(A1)

where a and $\sigma$ are positive constants and $\vartheta$ is chosen so as to exactly fit the term structure of interest rates being currently observed in the market.

For more details see Brigo and Mercurio (2006)

Appendix B: Supervised Learning Algorithms

We present a list of the supervised learning algorithms chosen in this work and their main characteristics and differences.

• k-Nearest Neighbour (k-NN) This algorithm is arguably the simplest, however being a non-parametric algorithm, i.e. it does not make assumptions regarding the dataset, it is widely used. The principle behind nearest neighbour methods is to find a predefined number k of training samples closest in distance to the new point and predict the label from these. As there is only a data storing phase, and no training phase, it is well suited for a small dataset (both in the number of features and in the number of samples) and it is known not to work well on sparse data¹ and features must have the same scale since absolute differences must weigh the same. The label assigned to a query point is computed based on the mean of the labels of its nearest neighbours. The model mainly presents three important hyperparameters: the number of neighbours k, the metric used to evaluate the distance and the weights assigned to the neighbours to define their importance.

• Linear Models Linear models are a class of models widely used in practice because they are very fast to train and predict; they make a prediction using a linear function of the input features, i.e. the target value is expected to be a linear weighted combination of the features. Notice that the linearity is a strong assumption and it is not always respected, but this gives them an easy interpretation. Training a model like that means setting its parameters so that the model best fits the training set. In general, linear models are very powerful with large datasets, especially if the number of features is huge (high-dimensional problem). There are many different linear models and the difference between them lies in how the parameters are learned and how the model complexity can be controlled. We have considered the Linear Regression and two of its regularised versions: Ridge and Lasso Regression where the regularization term is respectively the $L^{2}$ and the $L^{1}$ norm of the weight vector.

• Support Vector Machine (SVM) Conceptually the SVM, using some significant data points (support vector), try to define a corridor (or a hyper-volume in higher dimensions) within which the greatest number of data points fall. In general, SVMs are effective in the higher dimension, but they do not perform well when we have a large dataset due to the higher training time. They have a hyperparameter that performs the same task as the alpha of the linear models and therefore it limits the importance of each support vector. SVMs are efficient also for non-linear problems thanks to a mathematical technique called kernel trick; depending on the kernel used, additional hyperparameters are needed, but we must take that into account that one of the biggest drawbacks of these algorithms is the high sensitivity to hyperparameters.

• Tree-based algorithms As the name suggests, these algorithms are based on simple decision trees. Like SVMs, decision trees are versatile and very powerful and like k-NN, they are non-parametric algorithms. The goal of these algorithms is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features. To build a tree, the algorithm searches all over the possible tests (a subdivision of the training set) and finds the one that is most informative about the target variable. This recursive process yields a binary tree,² with each node containing a test and it is repeated until each region in the partition only contains a single target value. A prediction on a new data point is made by checking which partition of feature space the point lies in and the output is the mean target of the training point in this leaf. One of the main qualities of decision trees is that they require very little data preparation, moreover, they are very fast to predict and they are defined as white models because they are easily interpretable. Typically, building a tree and continuing until all leaves are pure leads to models that are very complex and highly overfit to the training data and therefore they provide poor generalization performance. The most common way to prevent overfitting is called pre-pruning and it consists of stopping the creation of the tree early. Possible criteria for pre-pruning include limiting the maximum depth of the tree, limiting the maximum number of leaves and others making the decision trees highly dependent on the numerous hyperparameters. Moreover, they have two main problems: the first is the inability to extrapolate or make predictions outside the training range, while the second is that they are unstable due to small variations in the training set. This last problem is solved with the decision tree ensembles: Random Forest (RF) and Gradient Boosted Regression Tree (GBRT).

  Ensembles are methods that combine multiple supervised models to create a more powerful one. They are based on the idea that the aggregation of the predictions of a group of models will often give better results than with the best individual predictor. One way to obtain a group of predictors is to use the same algorithm for every model and train them on different random subsets of the training set; when sampling is performed with replacement, this method is called bagging, otherwise, it is called pasting. Generally, the net result is that the ensemble has a similar bias but a lower variance than a single predictor trained on the original training set. Below we briefly describe the two ensemble methods considered.

  • A RF is an ensemble method of decision trees, generally trained via bagging method (Breiman, 2001). The idea behind random forests is that each decision tree will likely overfit on a specific part of the data, but if we build many trees that overfit in different ways, we can reduce the amount of overfitting by averaging their results. RF get its name from injecting randomness into the tree building in two ways: by the bagging method and by selecting a random subset of the features in each split test. In summary, the bootstrap sampling leads to each decision tree in the RF being built on a slightly different dataset and due to the selection of features in each node, each split in each tree operates on a different subset of features. Together, these two mechanisms ensure that all the trees in the RF are different. Essentially, RF shares all pros of the decision tree, while making up for some of their deficiencies; it also has practically all their hyperparameters with the addition of a new one that regulates the number of trees to consider whose greater values are always better, because averaging more trees will yield a more robust ensemble by reducing overfitting.

  • GBRT (Friedman, 2002) is part of the more general boosting method in which predictors are trained sequentially, each trying to correct its predecessor. By default there is no randomization in gradient-boosted decision trees instead, strong pre-pruning is used; it often uses very shallow trees which makes the model smaller in terms of memory and makes predictions faster. Each tree can only provide good predictions on part of the data, and so more and more trees are added to iteratively improve performance. This method shares the same hyperparameters as RF with the addition of the learning rate but, in contrast to RF, increasing the number of predictors leads to a more complex model. The learning rate and the number of estimators are highly interconnected, as a lower rate means more trees are needed to build a model of similar complexity and therefore there is a trade-off between them. Similar to other tree-based models, the GBRT works well without scaling and often does not works well on high-dimensional sparse data. Their main drawback is that they require careful tuning of hyperparameters and may take a long time to train.

• Artificial Neural Networks (ANN) or Multi-Layer Perceptron (MLP) They can be understood as a large set of simpler units, called neurons, connected in some way and organized in layers. An ANN is composed of one input layer, one or more hidden layers and one final output layer. In order to understand the entire functioning of the network, it is necessary to consider a single neuron: the inputs and the output are numbers and each input connection is associated with a weight. The artificial neuron computes a weighted sum of its inputs and then applies a non-linear transformation, called the activation function. In some way, ANNs can be viewed as generalizations of linear models that perform multiple stages of processing to come to a decision. The key point of ANN is the algorithm used to train them; it is called the back-propagation algorithm and in simple terms, it is a gradient descent using an efficient technique for computing the gradients automatically. In conclusion, ANNs are typically black box models defined by a set of weights; they take some variables as input and modify the values of the weights so that they return the desired target. Given enough computation time, data and careful tuning of the hyperparameters, ANN are the most powerful and scalable machine learning models. The real difficulty in implementing a suitable model is contained in the enormous amount of hyperparameters that regulate the complexity of the network. Both the number of hidden layers and the number of neurons in each layer can affect the performance of an ANN, but there is a large variety of hyperparameters that need to be optimized for acceptable results. In general, choosing the exact network architecture for an ANN remains an art that requires extensive numerical experimentation and intuition, and is often problem-specific.

Appendix C: Error Metrics

We present a list of the metrics implemented and their main characteristics and differences.

• MAE It measures the average magnitude of the errors in a set of predictions, without considering their direction. It’s the average over sample (n) of the absolute differences between the target ($y_{i}$) and prediction (${\hat{y}}_{i}$) where all individual differences have equal weight. In formula:

  $$\begin{aligned} MAE:= \frac{1}{n} \sum _{i=1}^{n}\left|y_{i}-{\hat{y}}_{i}\right|\end{aligned}$$

  (C2)

• MAPE Instead of using actual value, MAPE uses relative error to present the result. It is defined as

  $$\begin{aligned} MAPE:= \frac{1}{n} \sum _{i=1}^{n}\left|\frac{y_{i}-{\hat{y}}_{i}}{y_{i}}\right|\end{aligned}$$

  (C3)

  MAPE is also sometimes reported as a percentage, which is the above equation multiplied by 100.

• WAPE It is relative to what it would have been if a simple predictor had been used. More specifically, this simple predictor is just the average of the real values. Thus, it is defined as dividing the sum of absolute differences and normalising it by dividing the total absolute error of the simple predictor. In formula:

  $$\begin{aligned} WAPE:= \frac{\sum _{i=1}^{n}|y_{i}-{\hat{y}}_{i}\vert }{\sum _{i=1}^{n}|y_{i}|} \end{aligned}$$

  (C4)

  WAPE is also sometimes reported as a percentage, which is the above equation multiplied by 100.

• RMSE It represents the square root of the second sample moment of the differences between predicted values and real values. In formula:

  $$\begin{aligned} RMSE:=\sqrt{\frac{1}{n} \sum _{i=1}^{n} \left( y_{i}-{\hat{y}}_{i}\right) ^{2}} \end{aligned}$$

  (C5)

• RMRSE It is defined as

  $$\begin{aligned} RMSRE:= \sqrt{\frac{1}{n} \sum _{i=1}^{n} \left( \frac{y_{i}-{\hat{y}}_{i}}{y_{i}}\right) ^{2}} \end{aligned}$$

  (C6)

  RMRSE is also sometimes reported as a percentage, which is the above equation multiplied by 100.

• RRMSE Similarly to WAPE, it takes the total squared error and normalizes it by dividing it by the total squared error of a simple predictor. By taking the square root of the relative squared error one reduces the error to the same dimensions as the quantity being predicted. In formula:

  $$\begin{aligned} RRMSE:= \sqrt{ \frac{\sum _{i=1}^{n} \left( y_{i}-{\hat{y}}_{i}\right) ^{2}}{\sum _{i=1}^{n} \left( y_{i}\right) ^{2}}} \end{aligned}$$

  (C7)

  RRMSE is also sometimes reported as a percentage, which is the above equation multiplied by 100.

Both MAE and RMSE express average model prediction error in units of the variable of interest, they can range from 0 to $\infty$ and are indifferent to the direction of errors. They are negatively-oriented scores, which means lower values are better. Since the errors are squared before they are averaged, the RMSE gives a relatively high weight to large errors. This means the RMSE should be more useful when large errors are particularly undesirable and generally, RMSE will be higher than or equal to MAE. It can be noted that RMSRE and RRMSE are completely analogous to MAPE and WAPE where the absolute value is replaced with the square. RMSRE and MAPE are the relative versions of RMSE and MAE respectively and are taken into consideration in this context because, for example, an error of 100 EUR out of 200 EUR is worse than an error of the same amount out of 2000 EUR. However, they have some drawbacks: they are undefined for data points where the target value is 0 and they can grow unexpectedly large if the actual values are exceptionally small themselves. To avoid these problems, an arbitrarily small term is usually added to the denominator. Moreover, they are asymmetric and it puts a heavier penalty on negative errors (when forecasts are higher than target) than on positive errors. To solve these problems RRMSE and WAPE are introduced and they are particularly recommended when the number of samples is low or their values are on different scales.

Appendix D: Hyperparameters Tuning

We report the analysis for the selection of the best hyperparameters for all the algorithms implemented.

1.1 D.1 k-Nearest Neighbour

The model mainly presents three important hyperparameters: the number of neighbours k, the metric used to evaluate the distance and the weights assigned to the neighbours to define their importance. In the construction of this algorithm, we considered the Euclidean distance and we assigned uniform weights to all the neighbours as values other than these, which worsened the cross-validation performance considerably. The only hyperparameter that needs to be fixed is, therefore, the number of neighbours. Its value is strictly linked to the complexity of the model since by increasing the number of neighbours the prediction will be averaged over more data points, thus making the model less linked to the peculiarities of the training set and therefore simpler. Figure 6 shows the trend of the RMSE evaluated on the training and on the validation set as a function of the number of neighbours. Each point shown is the average value, with the respective error, of the RMSE obtained with 5-fold cross-validation. Considering a single neighbour the prediction on the training set is perfect, but when more neighbours are considered the model becomes simpler and the training error increases while the validation error drops. It can be easily seen that the optimal value of neighbours is 4 as the value of the validation error from that value onwards starts to increase and, since its distance with training error is low, we clearly avoid overfitting the training test.

Fig. 6

RMSE trend of training (blue) and validation (orange) of k-NN as a function of the number of neighbors (k). For each value of k the mean value of the 5-fold cross-validation is reported with the respective error

1.2 Linear Models

Among the linear models used, we found that the Ridge is the most promising for our problem. Therefore, considering the possibility of adding polynomial features, there are two hyperparameters of the algorithm: alpha, which is the magnitude of the regularization and degree, which is the maximum degree of the polynomial features. We report in Fig. 7 a grid search on the hyperparameters to find the optimal combination. The mean of the 5-fold cross-validation RMSE is reported for each pair of values. As can be deduced from Fig. 7, the hyperparameters that return the lowest value of the evaluation metric on the validation set are $\texttt{alpha} = 0.01$ and $\texttt{degree} = 6$ and consequently they were chosen as optimal parameters. It can be seen that increasing the maximum degree gives a great improvement in performance, but using one that is too high the model begins to generalize worse; this is due to the fact that polynomials of high degrees fit in an excellent way to the training set, but thus having a poor predictive power on the validation set.

Fig. 7

Heat-map of mean 5-fold cross-validation RMSE of Ridge Regression as a function of $\alpha$ and degree. Only the RMSE mean value on the validation set is reported

1.3 D.2 Support Vector Machines

The hyperparameter that performs the same task of alpha of the linear models is called C and therefore represents a regularizing parameter that has the task of limiting the importance of each support vector. The strength of the regularization is inversely proportional to C. In general, support vector machines are really effective in the higher dimension, but they do not perform well when we have a large dataset because the required training time is higher. SVMs are efficient also for non-linear problems thanks to a mathematical technique called kernel trick, which allows us to map our data into a higher-dimensional space. In our work, we implemented the Gaussian radial basis function kernel which considers all possible polynomials of all degrees, but the importance of the features decrees for a higher degree. Doing so, there is an additional hyperparameter, gamma, which is a regularizing hyperparameter. To obtain the best hyperparameters, we performed a grid search on C and gamma and we report in Fig. 8 the average values of the RMSE obtained from a 5-fold cross-validation for each pair. As can be deduced from Fig. 8, the hyperparameters that return the lowest value of the evaluation metric on the validation set are $\texttt{C}=100$ and $\texttt{gamma}=0.1$ and consequently, they were chosen as optimal parameters. In reality, the same value obtained for $\texttt{C}=100$ is also obtained with $\texttt{C}=1000$, but since the greater the value of C the more complex the model and the greater the probability of overfitting, the lower value has been chosen.

Fig. 8

Heat-map of mean 5-fold cross-validation RMSE of SVM with a radial basis function kernel as a function of C and gamma. Only the RMSE mean value on the validation set is reported

1.4 D.4 Tree

Since the decision tree works well on data with features that are on completely different scales, we have decided not to apply any transformations to our data, but as we would expect, if we apply this algorithm without pruning it, it tends to overfit; specifically, the algorithm builds a tree with a depth of 22 levels and with 3472 leaves, that is exactly the number of samples in our training set. After a phase of analysis and study of the various hyperparameters, we discovered that the parameters that most influenced the performance of our tree are respectively the maximum reachable depth (max_depth) and the minimum number of samples required to be at a leaf node (min_samples_leaf). We then carried out a grid search on these hyperparameters and in Fig. 9 we report the trend of the RMSE as a function of them. Each point shown is the average value, with the respective error, of the RMSE obtained with 5-fold cross-validation. As can be deduced from Fig. 9, the optimal values of the hyperparameters are respectively $\mathtt{min\_samples\_leaf} = 3$, as it returns the lowest value of the RMSE on the validation set and $\mathtt{max\_depth} = 11$ because for higher values the metric remains approximately constant, but having a greater error on the training set, the possibility of overfitting is lower.

Fig. 9

RMSE trend on training (blue) and validation (orange) set of the decision tree as a function of max_depth (left) and min_samples_leaf (right). For each of the hyperparameters, the average value of RMSE obtained with 5-fold cross-validation is reported with the respective error

1.5 D.5 Random Forest

Like decision trees, random forest works well with features that are on a completely different scale, therefore we have not applied any transformations to our data. It is known that the most important hyperparameters are max_features, i.e. the number of features to consider when looking for the best split and max_depth, i.e. the maximum depth of the trees. We have therefore decided to perform a grid search on these hyperparameters and we report in Fig. 10 the trend of the RMSE as a function of them. Each point shown is the average value, with the respective error, of the RMSE obtained with 5-fold cross-validation. As can be deduced from Fig. 10, the values of the optimal hyperparameters are respectively $\mathtt{max\_depth} = 17$, because for higher values the metric remains approximately constant, and $\mathtt{max\_features} = log2$. The term log2 means that max_features are equal to the logarithm to base 2 of the number of features. Once these values were set, we searched for the optimal value of trees to use. In Fig. 11 we report the trend of the RMSE as a function of the number of trees in the forest. A larger number of n_estimators is always better, but the training time increases considerably. As can be seen from Fig. 11, we have chosen to use 500 decision trees as increasing this number further does not provide any improvement in terms of performance.

Fig. 10

RMSE trend on training (blue) and validation (orange) set of the random forest as a function of the number of max_depth (left) and max_features (right). For each of the hyperparameters, the average value of RMSE obtained with 5-fold cross-validation is reported with the respective error. The term sqrt and log2 means that max_features are respectively equal to square root and logarithm to base 2 of the number of features; auto means that all features are used and therefore no randomness in selecting features

Fig. 11

RMSE trend on training (blue) and validation (orange) set of random forest with $\mathtt{max\_depth}= 17$ and $\mathtt{max\_features} = log2$ as a function of the number of n_estimators. For each of the hyperparameters the average value of RMSE obtained with 5-fold cross-validation is reported with the respective error

1.6 D.6 Gradient Boosted Regression Tree

This method shares the same hyperparameters as a random forest with the addition of the learning rate (learning_rate), which controls how strongly each tree tries to correct the mistakes of the previous trees; a higher learning rate means each tree can make stronger corrections, allowing for more complex models. In contrast to the random forest, where a higher number of predictors (n_estimators) is always better, increasing it in gradient boosting leads to a more complex model. The learning_rate and n_estimators are highly interconnected, as a lower rate means more trees are needed to build a model of similar complexity; generally, there is a trade-off between these two hyperparameters. Their main drawback is that they require careful tuning of hyperparameters and may take a long time to train. Furthermore, the number of hyperparameters to be set is high as each of them has a great influence on the performance. The first two hyperparameters studied are those considered most decisive and specifically, the learning rate and the number of trees. Figure 12 shows the heat map of the grid search on them where the average values of the RMSE obtained from 5-fold cross-validation for each pair are reported. From Fig. 12, it can be clearly seen that the learning rate has the greatest impact on performance and the pair $\mathtt{learning\_rate}=0.1$ and $\mathtt{n\_estimators}=1000$ has been selected as optimal hyperparameters. Like the random forest, the other two essential parameters to avoid overfitting our model are the maximum depth of the simple predictors (max_depth) and the number of features used for each split (max_features). In a totally similar way to before, we performed a grid search also on these hyperparameters in order to select the optimal ones. From Fig. 13, it can be noted that the factor that influences the performance the most is max_depth; the pair $\mathtt{max\_depth}=5$ and $\mathtt{max\_features}=log2$ are the optimal values. Although in a much lower way than all the previous ones, we have observed that the minimum number of samples required to be at a leaf node (min_samples_leaf) slightly influences the performance of gradient boosted regression tree. In Fig. 14 we report the trend of the RMSE as a function of it. Each point shown is the average value, with the respective error, of the RMSE obtained with 5-fold cross-validation. As can be seen from Fig. 14, as min_samples_leaf varies, the RMSE value on the validation set slightly decreases to a value of 6, while the training value increases. After this value, the evaluation metric on the validation set increases again. For this reason, we have fixed $\mathtt{min\_samples\_leaf} =6$.

Fig. 12

Heat-map of mean 5-fold cross-validation RMSE of GBRT as a function of learning_rate and n_estimators. Only the RMSE mean value on the validation set is reported

Fig. 13

Heat-map of mean 5-fold cross validation RMSE of GBRT with $\mathtt{learning\_rate}=0.1$ and $\mathtt{n\_estimators}=1000$ as a function of max_depth and max_features. Only the RMSE mean value on the validation set is reported

Fig. 14

RMSE trend on training (blue) and validation (orange) set of GBRT with $\mathtt{learning\_rate}=0.1$, $\mathtt{n\_estimators}=1000$, $\mathtt{max\_depth}=5$ and $\mathtt{max\_features}=log2$ as a function of min_samples_leaf. For each of the hyperparameter, the average value of RMSE obtained with 5-fold cross-validation is reported with the respective error

1.7 D.7 Artificial Neural Networks

In general, the design of the input and output layers in a network is often straightforward because they should adapt to the dataset and to the problem. In general, for multivariate regression, it is necessary one output neuron per output dimension. Consequently, since our aim is to produce a single value we will need only one output neuron. The number of neurons in the input layer is instead established by the number of inputs of our problems, that is, by the number of features; in our case, therefore we have an input layer composed of 7 neurons, i.e. one for each of the features of the dataset. These neurons have the sole task of passing the input values to the hidden layers without applying them to any transformations. Usually, in regression problems the activation function is the ReLU (or one of its variants); it is applied to all hidden neurons but not to the output ones, so they are free to output any range of values. The loss function to use during the training is typically the MSE. In order to make our training faster and more stable, we have scaled all the features and also the target by removing the mean and scaling to unit variance; centring and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. The back-propagation algorithm suffers from a problem called vanishing/exploding gradient, which consists of very unstable gradients. A way to alleviate that is to use the correct initialization of the weights for each activation function (Glorot & Bengio, 2010); for this reason, we select the He normal initialization in combination with ReLU. The random initialization of the weights is fundamental because breaks the symmetry and allows back-propagation to train a diverse team of neurons. Another fundamental element of neural networks is the batch size i.e. the size of the groups of instances used in the back-propagation algorithm; it can have a significant impact on the model performance and training time. Typically small batches are preferable because they led to better models in less training time (Masters & Luschi, 2018); for this reason, the batch size is set to 32. Moreover, in order to avoid overfitting, we have implemented early stopping. It is a regularization technique that consists of interrupt training when there is decreasing in the training loss function, but, at the same time, no progress on the validation set for a predefined number of epochs³; we set this limit to 30 epochs.

Once we have set these parameters and have adequately prepared the data to be processed by our neural networks we can concentrate on tuning the other hyperparameters. The most important are 4 mainly: the optimizer, the learning rate, the number of hidden layers and the number of neurons for each hidden layer. Training very large deep neural networks can be very slow. Some of the techniques already implemented and the choice of a good initialization strategy together with a good activation function, allow to speed up the training, but another huge speed boost comes from using a faster optimizer than the regular gradient descent. Our choice is to use Nadam algorithm (Dozat, 2016) that is an adaptive optimization method plus the Nesterov trick (Nesterov, 1983); it returns an excellent quality of convergence in a short time. A fundamental element for the convergence of the algorithm is the choice of the learning rate. Since the optimal learning rate depends on the other hyperparameter, we fix it after choosing the optimizer. Using too high learning rate values the training may diverge, but with values that are too low, training will eventually converge to the optimum, but it will take a very long time. One way to find a good learning rate (Muller & Guido, 2016) is to train the model for a few hundred iterations, exponentially increasing the learning rate from a very small value to a very large, and then looking at the learning curve and picking a learning rate slightly lower than the one at which the learning curves starts shooting back up; in this way, we set its value equal to 0.01.

Theoretically, neural networks with just one hidden layer can model even the most complex functions (Hornik, 1991), provided it has enough neurons. But for complex problems, deep networks have a much higher efficiency than shallow ones: they can model complex functions using exponentially fewer neurons than shallow nets allowing them to reach much better performance with the same amount of training data. Regarding the number of neurons in the hidden layers, it is common practice to use the same number of neurons in all hidden layers as in general performs well, plus, there is only one hyperparameter to tune, instead of one per layer. To obtain the optimal number of these two hyperparameters, we performed a grid search as in the previous cases. In Fig. 15 we report the heat-map of mean 5-fold cross-validation RMSE of the neural networks implemented as a function of the number of hidden layers (n_hidden) and the number of neurons per hidden layer (n_neurons). From Fig. 15, it would seem that increasing the number of layers has a greater impact on network performance than the number of neurons per layer. The hyperparameters that return the lowest value of the evaluation metric on the validation set are $\mathtt{n\_hidden} = 3$ and $\mathtt{n\_neurons}= 100$. Compared to the other similar cross-validation values we have chosen this configuration as it is the one with fewer weights to learn and consequently, the probability of overfitting is lower.

Fig. 15

Heat-map of mean 5-fold cross-validation RMSE of MLP as a function of n_hidden and n_neurons. Only the RMSE mean value on the validation set is reported

Appendix E: G1++ Parameters

We present the values of the G1 ++ parameters used for the creation of the dataset (Table 6).

Table 6 G1++ parameters chosen for the creation of the dataset

Appendix F: Market Data

See Tables 7, 8, 9, and 10.

Table 7 EONIA and EURIBOR 6 M zero rate yield curves as of 31st October 2019 (First part) in percentage values (continuous compounding, act/365 day-count convention)

Table 8 EONIA and EURIBOR 6 M zero rate yield curves as of 31st October 2019 (Second part) in percentage values (continuous compounding, act/365 day-count convention)

Table 9 EUR ATM swaption forward rates as of 31st October 2019

Table 10 EUR ATM European swaption straddles, forward premium, physical LCH settlement, notional 10,000 EUR

Appendix G: Bermudan Basket

See Table 11.

Table 11 Bermudan swaption selected for the dataset