1 Introduction

1.1 Production Networks and Risk

As highly complex and networked systems, the properties of economies are characterized by the behavior and interdependencies of their components (Kremer 1993; Bar-Yam 1997; Hidalgo et al. 2007; Barrat et al. 2008). Whether they arise from investments, trade or supply chains, interdependencies are increasingly important in contemporary economic systems, and fundamental for risk assessment and evaluation (Schweitzer et al. 2009). Interconnections enable the diversification of outputs, improve efficiency of economies, and increase the growth of economic complexity (Hidalgo et al. 2007). However, at the same time, they also introduce paths for risk contagion and generate large-scale vulnerabilities to systemic failure (Harmon et al. 2010, 2011). Strategic interdependencies, or complementarities, can generate aggregate volatility (Jovanovic 1987). Given the current context of increasing international trade, financialization and globalization in economies, it is crucial to understand the effects of connectivity on networked economies and its relationship to economic collapse.

Traditional economic studies focus on explaining collapse by the contribution of different factors such as bankruptcy (Battiston et al. 2007), bank loans (Stiglitz and Greenwald 2003), inter-bank credits (Allen and Gale 2000), and changes of asset prices (Kiyotaki and Moore 1997). Risk contagion in supply chains and production networks has seen important analyses on credit contagion (Jorion and Zhang 2009), default contagion in financial networks (Elliott et al. 2014), liquidity risk (Cifuentes et al. 2005), and development disruption (Brummitt et al. 2017). How idiosyncratic shocks propagate at the macroeconomic level, and the structure of production networks has been studied notably by Ciccone (2002), Levchenko (2007), Jones (2011) and Levine (2012), a literature surveyed by Carvalho (2014). Roukny et al. (2018) show that interconnections in bank systems through credit contracts and subject to correlated external shocks constitute a source of uncertainty in systemic risk assessment. Additional studies have indeed emphasized on the need for understanding the impact of network structure on the probability of collapse (Schweitzer et al. 2009; Iyer et al. 2013; Albert et al. 2000). Battiston et al. (2012b) emphasized the identification of important nodes through feedback centrality with debt ranking. Billio et al. (2012) established important econometric statistics to measure connectedness, and evaluate system risk in financial sectors. Recently, Elliott et al. (2020) linked supply network formation and fragility in this context. These studies show an inherent relationship between the structure of the network and its robustness and vulnerability to selected attacks and random errors independently of their nature. Stressing the systemic complexity of economic networks may contribute to the design and implementation of policies leading to higher diversity and efficiency without undermining the robustness of economic systems (Schweitzer et al. 2009; Battiston et al. 2012b).

In this paper we develop a model to show that while the creation of interdependencies among economic agents is fundamental for the growth of economic complexity, it also amplifies the risk of collapse during adverse conditions, and we characterize how the structure of the interdependencies shape the macroeconomic variables of the system. We show that the structure of interconnections among economic agents increases the fragility of economic systems despite an apparent improvement of their production complexity. We explore multiple ways in which systems can be interconnected. The first one is the density of the network, which refers to the number of connections that are drawn among agents independently. The second one is the network centralization, which refers to the emergence of highly connected nodes that bridge across large parts of the network. The third one is synthesized models of supply chain networks, which create instances of typical multilayer supply chains. Finally, we apply our models to international trade and supply chain networks created using real data. The results on realistic simulations and real data are consistent with the more generalized network framework. The networks based on density and centralization simplify and generalize previous literature specifications, focusing on a large variety of theoretical and empirical networks. Studying network density and centralization allows to account for this variety of structures in an unified framework. While different in nature, these directions show how nodes can become increasingly dependent on one another, either directly or indirectly (through secondary connections). We found that the transition to collapse is universal and independent of a specific network structure, including those that are built from real data. Instead the transition results from the accessibility of nodes one to another and the contagion of their failure.

We put an emphasis on the impact of network structure over systemic risk and aggregate productivity, across many different network structures, leaving out of this paper the question of network formation in the presence of shock. In the context of production webs, see Levine (2012), Rostek and Weretka (2015), Acemoglu and Azar (2017) in endogenous production networks, Brummitt et al. (2017); Baqaee (2018) for an influential model of cascading failures in production networks, Bimpikis et al. (2019), Yang et al. (2019). Cabrales et al. (2017), Elliott et al. (2018), Erol et al. (2018), Erol and Vohra (2018), Jackson and Pernoud (2019) studied network formation in finance. More specifically, Kranton and Minehart focused on buyer-seller networks, and Gale and Kariv (2009) on intermediation relationships. Link formation with contagion of risk was studied by Blume et al. (2011), who early identified the trade-off at the heart of our model: “each agent receives benefits from the direct links it forms to others, but these links expose it to the risk of being hit by a cascading failure that might spread over multi-step paths”, concluding that optimal networks were situated right beyond a phase transition in the behavior of cascading failure. In a related approach, we take a broader look at the impact of network structure on cascading failures, without restricting our results to the identification of optimal networks.

The architecture of economic networks is crucial to study their efficiency and vulnerabilities to systemic failure (Jackson et al. 2017), and full financial integration may not be desirable as it creates new risks (Stiglitz 2010). For example, if a vital firm within a supply chain suddenly ceases to exist, all producers linked to the failing element become unable to produce their output. The present analysis aims at quantifying both robustness and performance of production networks for various levels of individual node failure, and for various degrees of density and centralization in the network. Buldyrev et al. (2010), Tang et al. (2016) and Yang et al. (2019) studied different transmission mechanisms in supply chains, interdependent networks, giving rise to phase transitions. Interconnections may under certain conditions increase the complexity of production. However, as we introduce a non-zero probability of failure, the expected diversity and productivity decreases, leading the way to economic collapse. Even in most standard models of network production such as Acemoglu et al. (2012), such fragilities exist (Elliott et al. 2020), and motivated associations between physics of self-organized criticality and economics in the building of “sandpile” macroeconomic models (Scheinkman and Woodford 1994).

There is a large literature on network robustness to internal failure and external attacks on nodes or edges. Previous studies have mainly focused on two particular network topologies: the Erdos–Rényi random graph (Erdos and Rényi 1960) and Barabási’s scale-free network (Barabási and Albert 1999; Barabási and Bonabeau 2003). Albert et al. (2000) studied error tolerance and attack impact, notably testing both web robustness to targeted attacks on well connected nodes, and to removal of a given fraction of nodes. Crucitti et al. (2003) study network robustness to failure and targeted attacks. Iyer et al. (2013) likewise analyze how interconnections structure evolves with the removal of vertices, for a variety of networks types. Lorenz et al. (2009) developed a general framework to describe systemic risk with cascading failures processes in networks through node fragility. Pichler et al. (2018) investigated the issue of systemic risk in the context of efficient asset allocation in the form of a network optimization problem. Caccioli et al. (2018) recently provided a thorough review of research in network models of financial systemic risk. Buldyrev et al. (2010) extended the framework of network cascading failure analysis to the case of interconnected networks transmitting failure from one to another. In the spirit of Albert et al. (2000) who focused on two models: the Erdos–Rényi random network model (Erdos and Rényi 1960) and the scale-free web (Barabási and Albert 1999; Barabási and Bonabeau 2003), the present paper extends the investigation on the robustness of networks models to a more general framework, including the transition from random to scale-free networks and further centralization, as well as the effects of density of connections.

1.2 Production and Collapse

Various indicators of network robustness, and by consequence its fragility, have been extensively used in the literature. Identification of important nodes in contagion processes as occupied a central position in research on these topics (Billio et al. 2012; Battiston et al. 2012b; Thurner and Poledna 2013). The communication capacity of the network after nodes removal has been analyzed by Crucitti et al. (2003). Albert et al. (2000) used the average shortest path length among nodes in the network as a indicator of failure reachability. Iyer et al. (2013) and Callaway et al. (2000) analyzed robustness as percolation efficiency on networks. Lorenz et al. (2009) used the fraction of stable nodes after removing the failed ones as a measure of systemic risk. Rather than providing an indicator of fragility, we show the space of possible behaviors of networked production systems in terms of diversity of outcome and probability of collapse for different scenarios regarding conditions to failure and structure of interdependencies.

Collapse may be framed as a comparison of the current state of the system with respect to a reference one. We define the reference state as the situation of autarky or network-free environment, where agents have no interaction with each other. A production below such reference state could be considered as collapse, i.e. a systemic failure of the network to achieve the network-free production levels. Because the reference state is defined without knowledge of the networked structure of the system, collapse is interpreted in our model as the inability of the system to achieve the autarky production level. Our results can be generalized and are consistent with other definitions of collapse.

This article is organized as follows. Section 2 describes the network generation algorithms and the production model. Section 3 presents the results of model simulations in terms of productivity and collapse probability across multiple network topologies. Their discussion, implications and relations to previous literature are provided in Sect. 4. Section 5 concludes on the impact of network connectivity structure on global production and risk of failure in economic systems.

2 Model

We design a simple economic model of production, structured by a network of partnerships or supply chains. Nodes are represented as economic agents, such as individuals, firms or countries. Links indicate economic interdependencies. In order to produce goods, networked agents need the input from their connections. Each node has an individual error probability, analogous to the possibility of node removal in previous literature. Errors propagate through cascades across the network. We consider two network generation processes respectively based on the density or centralization of connections. Additionally, a multilayer structure is considered in the next sections. In this section we present the network generation processes, and define the mechanisms for production and collapse.

2.1 The Density Network Model

In order to analyze the impact of network density over production and risk of failure, we create a network generation model inspired from the network fragility literature (Crucitti et al. 2003; Albert et al. 2000; Lorenz et al. 2009. Nodes are randomly distributed in a torus space. Their connections depend on their distance to each other and a threshold denoted reach. Nodes first create a link with a randomly chosen node within the reach distance, denoted target, and second create links with all nodes linked to the target node. The probability of a node i to initially create a link to a node j at distance \(x_{ij}\) is as follows:

$$ p_{ij}(x_{ij}) = \left\{ \begin{array}{ll} \frac{1}{N(r)}&{}\quad {\text {if }}\,x_{ij} \le r \\ 0&{}\quad {\text {if }}\,x_{ij} > r \end{array}\right. $$
(1)

where r indicates the reach radius and N(r) represents the total number of nodes at reach from i. The number of potential target nodes N(r) increases proportionally to the reach parameter r. The density of the network (\(\delta \)) indicates the ratio between the number of existing edges divided by the total number of possible edges in the network. Low reach values yield only a few connections. As the reach parameter increases, so does the number of connections and the network density. Figure 1 illustrates networks that result from different model parameters. The density of the networks increase from left to right.

Fig. 1
figure 1

Visualization of network topologies from the density model. Panels show networks that result from different model parameters. The density of the networks increase from left to right. The node color is proportional to the degree (from black to green). Reach \( {r= 4} \) and density \(\delta = 0.028\) in the left panel. Reach \(r= 10\) and density \(\delta = 0.053\) in the middle panel. Reach \(r= 16\) and density \(\delta = 0.058\) in the right panel

Full size image

2.2 The Centralized Network Model

The centralized network model generates graphs with different levels of centralization. For this purpose, we generalize the preferential attachment mechanism (Barabási and Albert 1999) with an exponent that controls for the emergence and importance of hubs—ranging from no centralization (independently distributed edges) to perfectly centralized networks (in one or a couple hubs). In between the two extreme cases, we obtain a wide range of scale-free networks where several hubs are present with different relative importance in the graph.

The network generation process consists in creating edges as a function of the attachment probability. The probability of node i to create an edge with node j is as follows:

$$ p_{ij} \propto k_j ^ \alpha $$
(2)

where \(k_j\) is the number of connections of node j and \(\alpha \) is the exponent we use to control the influence of the preferential attachment mechanism. If \(\alpha = 0\), the attachment probability becomes equal among all nodes and we obtain a random network with no central hub similar to the Erdos–Ranyi model. If \(\alpha = 1\), we obtain the standard Barabási–Albert network with a few hubs. If \(\alpha = 2\), we create a network with full centralization where all nodes are linked to a single central one. This extension of the preferential attachment mechanism magnifies the degree heterogeneity among nodes for \(\alpha > 1\), and reduces such attractive force for any \(\alpha < 1\). An illustration of the model variants is shown in Fig. 2.

Fig. 2
figure 2

Visualization of network topologies from the centralized model. Panels show networks that result from different model parameters. From left to right the centralization of the network increases. The node color is proportional to the degree (from white to green). The left panel shows a decentralized network, similar to the Erdos–Rényi model (\(\alpha =0\)). The middle panel shows a scale-free network, similar to the Barabasi–Albert model (\(\alpha =1\)). The right panel shows a perfectly centralized network (\(\alpha =2\)). The number of edges and density is constant across all networks (\(\delta = 0.02\)). (Color figure online)

Full size image

2.3 Production and Collapse

The production mechanism is invariant across both network generation methods. In order to run simulations, we create 100 economic agents and interconnect them following the steps described in Sects. 2.1 and 2.2 respectively. Once the networks are created, we simulate both production and failure.

Agents produce goods with uniform and constant production technology. We consider production inputs as received endowments, without introducing stock constraints or resource extraction. Agents produce as many goods as possible, under the constrains imposed by the piece-wise production function described as follows:

$$ q_i = \left\{ \begin{array}{ll} 1 &{}\quad {\text {if }}\, k_i = 0 \\ 2n &{}\quad {\text {if }}\, k_i = n, n \in {\mathbb {N}}_{>0} \end{array}\right. $$
(3)

where \(q_i\) denotes production of node i, and \(k_i\) its degree (number of connections). A node without connections (\(k_i = 0\)) will only produce 1 good. We define this state as autarky. A node of n connections will be able to produce 2n goods (assuming no failure). The hypothesis behind introducing a production scaling parameter is derived from the view of production as a combinatorial process (Hidalgo et al. 2007). Economically speaking, it may account for increasing returns to scale, heterogeneity in marginal cost or differences in production efficiency. More generally, it corresponds to traditionally assumed positive gains from connections (Blume et al. 2011).

Agents have an identical and exogenous failure probability p. It conveys the individual probability of encountering issues in the production process and not providing any output at a given period. This modelling simplification can be related to error tolerance (Albert et al. 2000), discontinuous changes in asset values (Elliott et al. 2014), default probability (Jorion and Zhang 2009; Elliott et al. 2014) and removal probability (Crucitti et al. 2003). We define this phenomenon as individual failure. Individual failure may happen due to resource shortage, production tools dysfunction, or any other exogenous event leading to null production. Global failure arises as individual failures cascade across the network. Individual failure is denoted failure probability, while global failure is denoted collapse probability.

Individual failure spreads across the network through direct connections, i.e. to the economic partners directly linked to the failing node. We do not spread failure to neighbors of neighbors in this simple contagion mechanism. Our node-driven approach is closely related to Battiston et al. (2007, 2012a) who start from local interactions to study systemic failure, providing a new framework for understanding failure propagation. Our direct propagation framework enables the analysis of cascading failures, which is an essential phenomenon to be considered in the study of network robustness (Crucitti et al. 2013).

Accounting for failure probability p, and with \(k_i\) nodes directly linked to node i, the piece-wise conditional expected production function \(E(q_i|p)\) can be defined as follows:

$$ E(q_i|p) = \left\{ \begin{array}{ll} (1 -p) &{}\quad {\text {if }}\, k_i = 0 \\ 2n(1-p)^n &{}\quad {\text {if }}\, k_i = n, n \in {\mathbb {N}}_{>0} \end{array}\right. $$
(4)

If \(k_i = n > 0\), node i’s production is equal to 2n with probability \((1-p)^n\) and equal to 0 with probability \(1- (1-p)^n\). A sub network of n directly connected agents has a collective probability \((1-p)^n\) of not failing (i.e. all nodes produce). With probability \(1 - (1-p)^n\), at least one node fails and the entire sub network is not able to produce. Given that the production scales by a factor of 2n, the expected production function takes the value \(2n(1-p)^n\) for any \(n > 0\). For an autarkic node i, for which the number of neighbors \(k_i\) is null, the productivity is equal to 1, adjusted to the probability p of failing at each experiment. The expected production at each experiment for such node is thus equal to \((1 -p)\). This model specification simplifies greatly the economic structure present in the literature, aiming to illustrate the trade-off we examine between inter-connectivity and risk. It can however be related to these more sophisticated specifications as in Elliott et al. (2014) with the network value, and discontinuous changes in asset values. In their model, organizations held assets such as investments and factors of production, and mutual shares.

This production function specification illustrates the trade-off we examine between inter-connectivity and risk. In the density model, higher connectivity results in both better possible production, but also increased risk on the entire supply chains. In the centralized network, the central node has the potential to deliver a huge output, but is vulnerable to the failure of any other node it is connected to. The indicators developed in the next subsection allow us to measure these phenomena.

2.4 Measuring Collapse and Efficiency

The model is run for a given number of independent periods or experiments. We consider the failure and contagion processes as being transient. The failure of a node at a given experiment does not affect its state on the next experiment. This choice of simplicity identifies the impact of the network structure over systemic risk and productivity. We define the system’s total production T at each experiment t as the sum of the individual agent production levels \(q_i\) as follows:

$$ T_t = \sum _{i = 1}^Nq_i $$
(5)

where N is the total number of nodes in the network.

At a given experiment, we define collapse as the situation where the total production of the system \(T_t\) is below a reference level \(\lambda \), which is the expected production of the system in the autarky regime.

$$ \lambda (N,p) = N(1 - p) $$
(6)

The production level \(\lambda (N,p)\) does not depend on the network structure. It enables the performance analysis of any network topology with respect to the autarky case, and evaluate whether any particular system architecture is expected to yield higher or lower production. Through numerical simulations of the model, we apply Monte-Carlo to estimate the collapse probability over 10.000 independent experiments for each possible set of the model parameters, including different levels of failure probability and network topologies.

The model is implemented in the agent-based environment Netlogo (Wilensky 1999). We use the Pattern Space Exploration and Sampling algorithms from the OpenMole platform (Chérel et al. 2015; Reuillon et al. 2010, 2013) to identify areas of high variation in the model results and improve both tractability and validation. More details about the model implementation and simulation methodology can be found in the Supplement (Section S1).

3 Results

3.1 Mapping System Productivity

Fig. 3
figure 3

Network productivity as a function of model parameters. Color indicates average productivity (log unit) in units of the autarky level on logarithmic scale. The left panel shows the outcomes of the density model. The right panel shows the outcomes of the centralized model. The x-axis represents the probability of individual failure in both panels. The y-axis represents the network density (left panel) or centralization (right panel). Scale shown in Fig. 

Full size image

We define the system productivity level \(\pi \) as the ratio of the system average production (Eq. 4) and the reference autarky production level. A production level of \(\pi =2\) indicates that the system is able to double the autarky output level. Figure 3 shows the production levels (colored regions) of different network structures as a function of individual probability of failure (x-axis) and the parameters (y-axis) of the density (left) and centralized (right) models respectively. Red regions in Fig. 3 indicate high production, and green and blue regions indicate lower production. In the Supplement (subsection S2) we provide additional figures from the Pattern Space Exploration procedure used to determine areas of variation.

In both models, increasing the density or centralization of network connections results in higher production levels when the probability of failure is low (red regions near the vertical axis), given the possibility of agents to establish interdependencies and combine elements to create more complex products. However, as the probability of failure increases, the average output decreases with the density or centralization of connections. This effect is more abrupt in centralized systems (right panel). Therefore, increasing the number of interdependencies may increase the complexity of the economic systems but it also makes them more fragile to individuals’ failure.

3.2 Mapping the Collapse Probability

Fig. 4
figure 4

Probability of systemic collapse as a function of model parameters. Color indicates the collapse probability. The left panel shows the outcomes of the density model. The right panel shows the outcomes of the centralized model. The x-axis represents the probability of individual failure in both panels. The y-axis represents the network density (left panel) or centralization (right panel). Scale shown in figure

Full size image

While interconnections enable the creation of economic complexity, they also increase the probability of failure propagation and consequently the risk of global collapse. Figure 4 provides a precise mapping of system collapse probability as a function of network structure (given the parameters of the network density and centralization models) and probability of failure. Blue regions indicate very low risk of collapse. Red areas show very high risk of collapse. In both models, there is a region where the probability of collapse is low (blue). In these regions the productivity of the system is also high, as we previously noticed in Fig. 3. The probability of collapse increases when we either increase the probability of failure, for a given network setup, or when we increase the number of interdependencies, for probabilities of failure that are not close to zero.

The transition from robust (blue) to fragile (red) systems seems to be very sharp (yellow and green regions in Fig. 4). This indicates the existence of tipping points for each network setup. Moreover, the location of the tipping point changes as we modify the network structure or failure probability. It comes closer to the vertical axis as we increase the density or centralization of the network. Denser or more centralized networks are more sensitive (or fragile) to individual failure.

In Fig. 3 we showed that the highest levels of production take place when the density or centralization of connections is highest and the probability of failure lowest (upper left corner). In Fig. 4 we notice that such region is also the most fragile to an increase of the probability of failure. Notice that the number of links is constant in the centralized model and only the centralization of edges around hubs changes as we increase the parameter \(\alpha \). Therefore, two radically different network models present remarkable similarities in their behavior, which shows that centralizing interdependencies in a few nodes is just as potentially harmful as creating an excess of them in a distributed manner.

3.3 Productivity and Network Structure

Fig. 5
figure 5

System productivity and network properties. Productivity is measured in units of the reference level of production in the autarky regime (y-axis). The x-axis shows the network density (left panel) or centralization (right panel). Dots show the results of model simulations. Solid lines show the fitted curve using Polynomial Regression. Colors indicate distinct values of failure probability. Scale in figure. (Color figure online)

Full size image

Despite their similarities, the results presented in Figs. 3 and 4 also show differences between the two network models. These differences are manifested in the way system productivity changes as we vary failure probability. Figure 5 shows system productivity (Log unit) as a function of network density (left) and centralization (right) for various values of individual failure probability (color). The curves exhibit non linear behaviors.

In the density model (left panel in Fig. 5) there seem to be two distinct behaviors depending on the individual failure probability (color). If individual failure probability is below 0.4 (blue), the curves are concave downward and present a maximum value at density values that depend on the failure probability (for example at \(\delta =0.02\) for \(p=0.2\) or \(\delta =0.0175\) for \(p=0.2\)). The interval in which network density has a positive effect on productivity becomes narrower as individual failure probability increases. Above a failure probability of 0.4, the curves change their behavior and become concave upward (green, yellow and red). In this case, higher density results immediately in a decrease of productivity values regardless of the initial network density. On the other hand, in the network centralization model (right panel in Fig. 5), the curves are always concave downward and monotonically decreasing. In this case, an inflection point that accelerates the decrease of productivity appears when hubs start to gain more importance in the network (\(\alpha >1\)).

3.4 Collapse Probability and Network Structure

Fig. 6
figure 6

Collapse probability and network properties. The y-axis represents the collapse probability as explained in Sect. 2.4. The x-axis represents the probability of failure. Dots show the results of model simulations. Colors indicate distinct values of network density (left) and centralization (right). Scale in figure. (Color figure online)

Full size image

In Fig. 6, we analyze the behavior of the collapse probability as a function of individual failure probability by horizontally slicing the surface shown in Fig. 4 at different values of density (left panel) or centralization (right panel).

In both cases, the curves are monotonically increasing, showing that the risk of spreading failure is aligned with both network density and centralization. However, the behavior is non-linear. For small values of failure probability (dark blue curves) there is an interval of network density or centralization in which the system seems robust. In the case of the density model, the robust interval coincides with the location of maximum productivity points shown in Fig. 5a. As the networks get denser or more centralized (green, yellow and red curves in Fig. 6) the extent of the robust interval gets narrower, confirming that the excess of interdependencies increases the fragility of the system. Such decrease occurs more rapidly in the case of centralized networks.

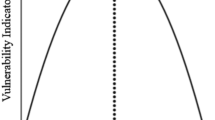
Using data from the Observatory of Economic Complexity, we apply the model to estimate the vulnerability of international trade networks from 1962 to 2012. Nodes represent countries and edges are present if they have traded on a given year above a significant threshold. Figure 7 shows that the the expansion of interconnections among countries has increased the global sensitivity to failure from 1962 to 2012, with a peak in 2007 just before the last major economic crisis. The figure outlines as well the fragility of trade networks. Certain systemic collapse is attained from a country failure probability of 0.02, i.e. 2%.

Fig. 7
figure 7

5-year evolution of systemic risk in trade networks computed using our model. Data from the Observatory of Economic Complexity

Full size image

3.5 Universality of Collapse

Fig. 8
figure 8

Universal behavior of collapse probability. The left panel shows the results for the density model. The right panel shows the results for the centralized model. Dots represent the resulting collapse probability (y-axis) of model simulations. The solid lines show the fit to the sigmoid function. Colors indicate the respective model parameters (scale inset). The x-axis represents the normalized failure probability (\(p^{*}\)), after subtracting the location parameter of the sigmoid curve

Full size image

The curves in Fig. 6 suggest that the relationship between collapse and interdependencies (either in the form of density or centralization) can be modeled by a sigmoid function, with the following form:

$$ f(x) = \frac{1}{1 + e^{-a(x-b)}} $$
(7)

where a determines the slope of the transition and b the location of the inflection point. In Fig. 8, we present the results of fitting the sigmoid function to the collapse probability as a function of failure probability for both network models, at various levels of density (left) and centralization (right) respectively. In order to collapse the curves we normalize the original failure probability (p) by subtracting the location parameter of the sigmoid function (b), such that \(p^{*}=p-b\).

The ubiquity of sigmoidal patterns in the transition to collapse on such different network models and various parameters suggests the existence of a universal behavior. As shown in Fig. 6, the sigmoid curves are present in both types of networks and increasing interdependencies simply moves the inflection point closer to the origin and yields steeper slopes, which indicates higher sensitivity to errors and system fragility. These results indicate that two radically different economic systems, such as centralized and decentralized economies, may fail because of one consistent reason which lies in the dynamics of failure propagation across networks and excess of direct or indirect interdependencies. Like in other complex systems, universalities represent the general structure in which phenomena take place. While individual instances may present different and heterogeneous details, i.e. prices, markets, bureaucracy, etc., there is an underlying structure that is common among them and in which they develop. In order to achieve effective solutions, we must understand and intervene in such structure. Otherwise, there is a risk of spending efforts in designing solutions based on the particularities of each case without considering the relevant variables.

4 Alternative Production Mechanisms with Lower Gains from Connections

The results on the trade-off between interconnections through network density and centralization, and productivity as well as stability, has been outlined in Figs. 3 and 4 for a production scaling of 2 in Eq. 4. That is, when connected and not affected by failure, a node connected to n neighbors will produce 2n goods. We here present simulation results when this value is lowered to 0.5 and 1 (Figs. 9, 10, 11).

Fig. 9
figure 9

Network productivity in the density model as a function of model parameters, with a production scaling of 0.5 (left) and 1 (right). Color indicates average productivity (log unit) in units of the autarky level on logarithmic scale. The x-axis represents the probability of individual failure in both panels. The y-axis represents density. Scale shown in figure

Full size image
Fig. 10
figure 10

Network productivity in the centrality model as a function of model parameters, with a production scaling of 0.5 (left) and 1 (right). Color indicates average productivity (log unit) in units of the autarky level on logarithmic scale. The x-axis represents the probability of individual failure in both panels. The y-axis represents centralization. Scale shown in figure. (Color figure online)

Full size image

As the gains from connections is reduced, so is the network productivity (see the supplementary material section S3). The trade-off and areas where the network structure offers improved productivity and robustness to failure shocks, are similar. Changing the values of the production scaling dramatically impacts the representation of collapse probability of the network. Lowering the gains from interconnections makes attaining the autarky level of production more difficult. Hence, intuitively, the blue region of low collapse risk is wider when gains from interconnections are higher than when they are lower (2 in Fig. 4b). This change appears of high magnitude between a production scaling of 0.5 and 1, showing high sensitivity of centralized production networks to the gains from connections in our model. When production scaling is as low as 0.5 in the centralization model, most leaves-nodes cannot meet their autarky level of production as in Fig. 12a. In Fig. 12b, when production scaling is equal to unity, these nodes when not affected by failure meet their autarky production, and provide positive externalities to central nodes, making robustness to production collapse less of a stretch in the parameters space.

Fig. 11
figure 11

Probability of systemic collapse in the density model as a function of model parameters, with a production scaling of 0.5 (left) and 1 (right). Color indicates the collapse probability. The x-axis represents the probability of individual failure in both panels. The y-axis represents density. Scale shown in figure. (Color figure online)

Full size image
Fig. 12
figure 12

Probability of systemic collapse in the centrality model as a function of model parameters, with a production scaling of 0.5 (left) and 1 (right). Color indicates the collapse probability. The x-axis represents the probability of individual failure in both panels. The y-axis represents centralization. Scale shown in figure. (Color figure online)

Full size image

5 Application to Empirical Supply Chain Multilayer Networks

As recently outlined by Elliott et al. (2020), and quite commonly before in the literature, production networks in the context of supply chains are not only defined by density, or centralization, but also by specific structure. We devote attention to the analysis of a typical supply chain network presented graphically in Fig. 13. We consider a production network with several layers. The green node (say primary good producer) supplies the blue nodes (intermediate producers), who supply the white nodes (final producers). Here, supply and demand relationships are accounted by undirected links, and our model applied in this structure. Figure 14 confirms that our previous results hold with such particular, and typical network architecture. The sigmoidal transition between node probability of failure and systemic outcomes (collapse probability and network productivity) we identified are visible. The production scaling parameter, i.e. the gains from interconnections, impact these curves. When gains from interconnections are low, the network hardly meets the autarky level of production, especially for higher chances of individual failure. When production scaling is higher, the parameter window in which the multilayer structure is both robust, and efficient from the production point of view, is larger.

Fig. 13
figure 13

An instance of a multilayer supply chain network. This network model is based on the work of Elliott et al. (2020)

Full size image
Fig. 14
figure 14

Probability of systemic collapse and Network productivity in the multilayer model as a function of model parameters. The x-axis represents the probability of individual failure in both panels. The y-axis represents collapse productivity (left) and average production in log unit (right). Scale shown in figure

Full size image

We move from abstract to empirical networks, by applying our model of cascading failures on 38 real-world supply chain networks. We use the data and networks originally published by Willems (2008) and notably studied by Fang et al. (2018). The data set is comprised of multiple multi-echelon supply chain networks, in a high variety of goods, services and economic sectors, ranging from cereals up to aircraft engines. The networks vary widely in size, spanning from a a couple dozens up to thousands of nodes. They have also various levels of complexity, in terms of the number of interconnections, and network features such as average path length. These networks allow to check the robustness of our theoretical insights on real-world webs of economic interdependencies among providers and producers. The results of applying the model to these networks are shown in Fig. 15. They are remarkably consistent with our theoretical findings, and replicate the sigmoidal relationship we identified before. Using the normalization technique previously applied in Fig. 16, we confirm the universality of the relationship between systemic risk, network structure and node probability of failure.

Fig. 15
figure 15

Collapse probability as a function of node probability of failure in the 38 empirical supply-chain networks (blue), with sigmoidal fits (red). Network 1, 2 and 3 giving identical results were collapsed to form subfigure 1 (top left). Networks are numbered from left to right, top to bottom. (Color figure online)

Full size image
Fig. 16
figure 16

Collapsed sigmoidal curves for the 38 empirical supply-chain networks. Collapse probability as a function of failure probability (normalized). (Color figure online)

Full size image

6 Discussion

6.1 Too Interconnected to Thrive?

Simulations show that production networks get increasingly sensitive to the propagation of individual failure as their topologies get denser and agents linked to each other. The resulting production may decrease faster than linearly with respect to failure probability. Sparser networks may have a lower productivity but are more resilient to probability of failure. Previous research has investigated the risks of creating agents “too big to fail”, or more recently “too central to fail” (Battiston et al. 2012b). In the continuity of this observation, our model emphasizes that without further hypotheses, economic agents may in some situations become too interconnected to thrive.

This observation from model results, notably drawing from Fig. 4a (density model), emphasizes the existence of positive returns to interconnections in system robustness below a given density tipping point. Above such a threshold, returns to interconnections play a negative role. Such a mapping of production performance and systemic risk in the sense of global failure appears relevant in tackling efficient asset allocation and minimization of systemic risk as a network optimization problem (Pichler et al. 2018).

These results on returns to interconnections also allow us to replicate in a more general context the findings of Albert et al. (2000) on error tolerance of scale-free networks. Their results indicate that systems exhibit strong robustness below a level of error of 5%. This is consistent with the results we obtain in the centralized model (\(\alpha =1\)) when the probability of individual failure \(p=0.05\) (Fig. 4b). In such networks the collapse probability is low and average production is satisfied. Our analysis thus successfully replicates their findings, while generalizing the study of network robustness to a larger range of organizations and organizing principles.

6.2 Risk Diversification or Containment?

As noted in the founding work of Schweitzer et al. (2009), traditional economic theory often concludes that dense networks enable risk diversification to counterbalance failure (Allen and Gale 2000). Risk diversification remains relevant in the context of production, as producers may prefer to protect themselves against the failure of suppliers or trade partners (Harmon et al. 2011). Battiston et al. (2007) identified instead that systemic risk may increase with network coupling strength between nodes in credit chains and production networks during bankruptcy propagation. Contrary to the more general policy implications of Allen and Gale (2000), Battiston et al. (2012c) identified that risk diversification not always reduces systemic risk.

Our model contributes to this debate extending the observations over a larger set of networks topologies. As illustrated in Fig. 4a, our model identifies parameter intervals in which increased density is not detrimental to systemic risk, here denoted as collapse probability of the production system, pointing back to the findings of Allen and Gale (2000). The dark blue region of collapse probability in the density model (Fig. 4a), show that the increasing network density through risk diversification, here understood as the creation of additional connections, is not harmful to system robustness if individual probabilities of failure are low. This extent, denoted ”density threshold”, differs according to network topologies.

Risk diversification through increased density may be beneficial for the expected productivity in certain intervals of network density and individual failure probabilities (Fig. 3a). However, in environments characterized by higher individual risks, increasing network density may lead to major changes in collapse probability, pushing the system towards unstable situations (red regions in Fig. 4a). These results are in line with previous research of Battiston et al. (2012a, (2012c). They show endogenous emergence of systemic risk because of feedback effects resulting from an excess of interdependencies. Our model shows that risk diversification improves global robustness only in an interval of individual risk of failure and outlines that systems may become sensitive too sensitive to individual failure if density and centralization are too high. We show that the transition is not smooth and instead it universally follows a sigmoid behavior. Analogue phase transition process are shown in the model of Lorenz et al. (2009). Our model extends this study with networks displaying centralization (Fig. 4b). In this case, the collapse probability increases more abruptly and is more sensitive to the risk of individual failure.

6.3 Policy Implications

Previous literature on systemic risk has raised important suggestions for policy actions. Protection measures have been pointed as necessary through identification of essential nodes (Battiston et al. 2012b). Others opted for a systemic risk tax (Leduc and Thurner 2017b), in order to make bank networks robust to insolvency cascades, or through an adequate credit default swap market, where CDS assets are taxed according to their contribution to systemic risk (Leduc et al. 2017a). Other scholars have emphasized on the importance of taking networks of interdependencies into account for improving systems’ resilience (Buldyrev et al. 2010) in the context of contagion (Marsiglio et al. 2019).

Barriers to contain risk contagion may improve global robustness, whether implemented around a centralized node, or distributed across the decentralized network. Further research on such implementation may shed new light on the impact of safety barriers on different network topologies. However, action in centralized networks cannot be reduced to protection on the central node, and may have less effect than expected, as expressed by Braha and Bar-Yam (2006).

7 Conclusion

In summary, we analyzed the effects of establishing interdependencies among economic agents on arising production complexity and systemic risk. We show that while interdependencies are beneficial for creating more complex products, they also create paths for failure propagation and amplify the fragility of the system–an effect often overlooked in the literature of economic complexity. Our results show that different network topologies, such as dense or centralized networks, show universal patterns of behavior, due to the common dynamics of cascading propagation through direct and indirect connections. Understanding universalities is critical in order to achieve effective solutions beyond the particular characteristics of individual cases. Further research accounting for additional policies such as the enforcement of new types of interdependencies, more sophisticated node behavior and strategic network formation mechanisms, may contribute to identify opportunities for improving the functioning and complexity of economic systems without compromising their robustness and resilience.