Possibilistic Moment Models for Multi-period Portfolio Selection with Fuzzy Returns

Abstract

The aim of this paper is to investigate the effects of higher moments on multi-period portfolio selection with fuzzy returns. This paper gives the definitions of possibilistic mean and variance about the product of multiple fuzzy numbers. Based on these definitions, three multi-period fuzzy portfolio optimization models are proposed. The proposed models aim to maximize terminal wealth and minimize terminal risk by taking into account some realistic constraints including higher moments, budget constraint, round-lot constraint, cardinality constraint and bound constraint. To ensure the selection of the best solutions, a novel fuzzy programming approach-based self-adaptive differential evolution algorithm is designed to solve the proposed models. A numerical example is given to demonstrate the application of the proposed models. Computational results show that the designed algorithm is effective for solving complex portfolio selection model with realistic constraints.

1 Introduction

Portfolio selection is one of the most hot topics in modern finance. The problem concerns about how to allocate investors’ wealth among a basket of securities by their investment intentions. Most of existing research works mainly concern about two main criteria, i.e., investment return and investment risk, see for instant in Kumar and Bhattacharya (2012), Hjalmarsson and Manchev (2012) and Shen (2015). In these models, they usually neglected the effects of higher moments on portfolio decision-making. Actually, numerous empirical evidences indicate that higher moments should be incorporated into portfolio selection models (Briec et al. 2007; Fang and Lai 1997). In particular, Díaz et al. (2009) addressed the importance of considering skewness and kurtosis when evaluated the performance of a portfolio. DiTraglia and Gerlach (2013) pointed out that lower tail dependence contained important information for risk averse investors. Fang and Lai (1997) used several empirical studies to illustrate the returns of risky assets with fat tails. Meanwhile, they pointed out that, when the mean, variance and skewness were the same, investors would prefer to select a portfolio with smaller kurtosis which indicates the fat-tails or thin-tails. Kim (2015) analyzed the return skewness of smaller portfolios using empirical returns from the Center for Research in Stock Prices database. Leung et al. (2001) found that excluding the factor of skewness may lead to an inefficient portfolio.

As stated above, the effects of higher moments on portfolio selection cannot be neglected. In the real world, investors must consider many factors to meet the requirements of real transactions. Meanwhile, different decision makers may have different preferences. To select a proper portfolio, investors should take multiple criteria and their own investment preferences into consideration. By probability theory, some researchers have investigated the portfolio selection problem by multiple criteria approaches. For example, Ballestero et al. (2007) proposed a multi-criteria methodology for selecting portfolios with respect to an investor’s individual preferences for risk and profitability. Leung et al. (2001) proposed a multi-objective approach to combine the forecasts obtained by different analysts.Liu et al. (2006) proposed a linear belief function (LBF) approach to evaluate portfolio performance by considering t market information and financial knowledge. Ge et al. (2014) presented an interactive portfolio decision analysis approach to to promote multistakeholder design negotiations on system portfolio selections. Utz et al. (2014) presented a tri-criterion inverse portfolio optimization model and applied it to socially responsible mutual funds. Yu and Lee (2011) presented five portfolio optimization models by using multiple criteria. Carli et al. (2016) focused on applying multicriteria decision making tools to determine an optimal energy retrofit plan for a portfolio of buildings. Liu et al. (2006) proposed a novel formula of characterizing robustness based on portfolio theory, and constructed a multiobjective optimization model of the robust learning to rank (LTR). Gong et al. (2017) designed an adaptive real coded genetic algorithm for solving portfolio selection problem based on cumulative prospect theory.

Notice that all the literatures mentioned above are proposed on the basis of probability theory. They often viewed a financial asset as a random variable with a probability distribution over its return. However, there are many non-stochastic factors that affect the real stock markets and they are improper to deal with stochastic approaches. With the widely use of fuzzy set theory in Zadeh (1965), numerous researchers have realized that they could use fuzzy set theory to handle the uncertainty in financial markets. Jalota et al. (2017) proposed four multi-objective portfolio optimization problems based on credibility measure to study the return and illiquidity of entire portfolio modelled using a L-R fuzzy number of power reference family. Li et al. (2016) proposed three mean–variance–skewness models for portfolio selection with fuzzy returns and used empirical studies to show the fact that portfolio returns were generally asymmetric, and investors would prefer a portfolio return with larger degree of asymmetry when the mean value and variance were same. Liu et al. (2006) discussed a multi-objective portfolio optimization problem for portfolio selection with fuzzy return rates and fuzzy turnover rates. Li et al. (2010) provided mean-variance-skewness model for portfolio selection with fuzzy returns. Zhang et al. (2010b) dealt with the portfolio selection problems with general transaction costs under the assumption that the returns of assets were characterized by LR-type possibility distributions. Mashayekhi and Omrani (2016) proposed an integrated multi-objective Markowitz-DEA cross-efficiency model for portfolio selection problem with fuzzy returns. Saborido et al. (2016) gave evolutionary multi-objective optimization algorithms for fuzzy portfolio selection. Chen (2015) designed a novel artificial bee colony algorithm for constrained possibilistic portfolio selection problem. Li et al. (2015) formulated a fuzzy mean–variance–skewness portfolio selection model and given its two variations. Notice that the studies on fuzzy portfolio selection are mainly in single period cases. However, in the real world, numerous investors’ investment behaviors are usually multi-period and they need to rebalance their positions from time to time. Thus, it is necessary to extend single-period portfolio selection models into multi-period cases. Recently, some researchers have discussed multi-period portfolio selection problems in fuzzy investment environment by using fuzzy set theory (Zhang et al. 2012; Guo et al. 2016; Mehlawat 2016).

Most of previously researches discussed portfolio selection in stochastic environment and single period portfolio selection in fuzzy environment have highlighted the effects of higher moments on portfolio selection cannot be neglect. However, so far, to the best of our knowledge, few studies have concerned about the effects of higher moments on multi-period fuzzy portfolio selection. The purpose of this paper is to investigate the effects of the higher moments on multi-period portfolio selection in fuzzy investment environment. The contributions of this paper are summarized as follows: (i) We define the possibilistic mean and variance about the product of fuzzy variables. And then, we discuss fuzzy portfolio selection problem by using them as measures of investment return and investment risk, respectively. (ii) We propose three multi-period portfolio selection models to take into account diverse decision criteria and investors’ different investment preferences, which can provide investors with additional choices. (iii) We design a fuzzy programming-based improved self-adaptive differential evolution (ISDE) algorithm to solve the proposed models.

The rest of this paper is organized as follows. In Sect. 2, we introduce some basic conceptions about fuzzy numbers. In Sect. 3, we formulate three possiblistic moment models for multi-period portfolio selection with fuzzy returns. In Sect. 4, we first employ fuzzy programming technique to transform our proposed models into single-objective programming models. And then, we design an improved self-adaptive differential evolution algorithm to solve them. In Sect. 5, we give a numerical example to demonstrate the application of the proposed models and illustrate the effectiveness of the designed algorithm. In Sect. 6, we conclude the paper. Finally, we give technical proofs in the “Appendix”.

2 Basic Conceptions

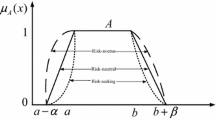
Let A be a fuzzy set of the real line $\mathbb {R}$ with a normal, convex and continuous membership function of bounded support. The family of fuzzy numbers is denoted by ${\mathcal {F}}$. The $\gamma$-level set of fuzzy number A is denoted by $[A]^{\gamma } = \{x\in \mathbb {R}| \mu _{A}(\gamma )\ge \gamma \}$ (the closure of the support of A) if $\gamma = 0$. The $\gamma$-level set of A is expressed as $[A]^{\gamma }=[\underline{a}(\gamma ),\overline{a}(\gamma )]\,(\gamma >0)$ (see Dubios and Prade 1980).

In Carlsson and Fullér (2001), the following results about the possibilistic mean, variance and covariance of fuzzy numbers can be obtained.

Definition 1

Let A be a fuzzy number with $\gamma$-level set $[A]^{\gamma }=[\underline{a}(\gamma ),\overline{a}(\gamma )]$. Then, the possibilistic mean of A is defined as

$$\begin{aligned} E(A)=\int _{0}^{1} \gamma \left( \underline{a}(\gamma )+\overline{a}(\gamma )\right) \text {d}\gamma =\tfrac{1}{2}(M^{-}(A)+ M^{+}(A)), \end{aligned}$$

(1)

where $M^{-}(A)={\int }_{0}^{1} 2\gamma \underline{a}(\gamma )\text {d}\gamma$ and $M^{+}(A)={\int }_{0}^{1} 2\gamma \overline{a}(\gamma )\text {d}\gamma$ represent the lower and upper possibilistic means of A.

Theorem 1

Let $A, B \in \mathcal {F}$ and let $\lambda ,\mu \in \mathbb {R}$. Then

$$\begin{aligned} E(\lambda A + \mu B) = \lambda E(A) + \mu E(B). \end{aligned}$$

(2)

Definition 2

Let A, B be two fuzzy numbers with $\gamma$-level sets $[A]^{\gamma }=[\underline{a}(\gamma ),\overline{a}(\gamma )]$ and $[B]^{\gamma }=[\underline{b}(\gamma ),\overline{b}(\gamma )]$. Then, the possibilistic covariance between A and B can be defined by

$$\begin{aligned} Cov(A,B)\!=\!\int _{0}^{1} \gamma \left[ \left( E(A)-\overline{a}(\gamma )\right) \left( E(B)-\overline{b}(\gamma )\right) +\left( E(A)-\underline{a}(\gamma )\right) (E(B)-\underline{b}(\gamma ))\right] \text {d} \gamma . \end{aligned}$$

In particular, if $A=B$, then the possibilistic variance of A can be expressed by

$$\begin{aligned} Var(A)=\int _{0}^{1} \gamma \left[ \left( E(A)-\overline{a}(\gamma )\right) ^{2}+\left( E(A)-\underline{a}(\gamma )\right) ^{2}\right] \text {d}\gamma . \end{aligned}$$

(3)

Theorem 2

Let $A_{1}, A_{2},\ldots , A_{n}$ be n fuzzy numbers, and let $\lambda _{1}, \lambda _{2},\ldots , \lambda _{n}$ be n positive numbers. Then, we have

$$\begin{aligned} Var\left( \sum \limits _{i = 1}^n \lambda _{i} A_{i}\right) =&\sum \limits _{i = 1}^n \lambda _{i}^{2} Var( A_{i})+2 \sum \limits _{i<j=1}^n \lambda _{i}\lambda _{j} Cov(A_{i},A_{j}). \end{aligned}$$

(4)

Definition 3

(Saeidifar and Pasha 2009). Let A be a fuzzy number with $\gamma$-level set $[A]^{\gamma }=[\underline{a}(\gamma ),\overline{a}(\gamma )]$. Then, the possibilistic skewness and kurtosis of A are, respectively, defined as

$$\begin{aligned} S(A)=\frac{M_{3}(A)}{\left( \sqrt{Var(A)}\right) ^{3}}, \end{aligned}$$

(5)

$$\begin{aligned} K(A)=\frac{M_{4}(A)}{\left( \sqrt{Var(A)}\right) ^{4}}, \end{aligned}$$

(6)

where $M_{3}(A)={\int }_{0}^{1}\gamma [(\underline{a}(\gamma )-E(A))^{3}+(\overline{a}(\gamma )-E(A))^{3}]\text {d}\gamma$ and $M_{4}(A)={\int }_{0}^{1}\gamma [(\underline{a}(\gamma )-E(A))^{4}+(\overline{a}(\gamma )-E(A))^{4}]\text {d}\gamma$ are the possibilistic third and forth moments of fuzzy number A about E(A).

Notice that S(A) measures the asymmetry degree of the possibility distribution of fuzzy number A. K(A) measures the peakedness of unimodal possibility distribution of fuzzy number A. For reducing computational burden, S(A) and K(A) are usually replaced by $M_{3}(A)$ and $M_{4}(A)$ in the practical application. In this paper, we denote $S(A)=M_{3}(A)$ and $K(A)=M_{4}(A)$.

Definition 4

(Chen and Tan 2009). Let A, B be two fuzzy numbers with $\gamma$-level sets $[A]^{\gamma }=[\underline{a}(\gamma ),\overline{a}(\gamma )]$ and $[B]^{\gamma }=[\underline{b}(\gamma ),\overline{b}(\gamma )]$. Then, the possibilistic mean and variance about the product of A and B (i.e., AB) are, respectively, defined as

$$\begin{aligned} E(AB)&=\int _{0}^{1}\int _{0}^{1}\gamma _{A}\gamma _{B}\left[ \underline{a}(\gamma _{A})\underline{b}(\gamma _{B})+\underline{a}(\gamma _{A})\overline{b}(\gamma _{B})+ \overline{a}(\gamma _{A})\underline{b}(\gamma _{B})+\overline{a}(\gamma _{A})\overline{b}(\gamma _{B})\right] \text {d}\gamma _{A}\text {d}\gamma _{B},\\ Var(AB)&=\int _{0}^{1}\int _{0}^{1}\gamma _{A}\gamma _{B}\big [(E(AB)-\underline{a}(\gamma _{A})\underline{b}(\gamma _{B}))^{2}+(\underline{a}(\gamma _{A})\overline{b}(\gamma _{B})-E(AB))^{2} \\ {}&\quad +\,(E(AB)-\overline{a}(\gamma _{A})\underline{b}(\gamma _{B}))^{2}+(E(AB)-\overline{a}(\gamma _{A})\overline{b}(\gamma _{B}))^{2}\big ]\text {d}\gamma _{A}\text {d}\gamma _{B}. \end{aligned}$$

Similar to Definition 4, we define the possibilistic mean and variance about the product of any given n fuzzy numbers as follows.

Definition 5

Let $A_{1}, A_{2},\ldots , A_{n}$ be any given n fuzzy numbers with $\gamma$-level sets $[A_{1}]^{\gamma }=[\underline{a}_{1}(\gamma ),\overline{a}_{1}(\gamma )],[A_{2}]^{\gamma }=[\underline{a}_{2}(\gamma ),\overline{a}_{2}(\gamma )],\ldots ,[A_{n}]^{\gamma }=[\underline{a}_{n}(\gamma ),\overline{a}_{n}(\gamma )]$. Then, the possibilistic mean and variance about the product of the n fuzzy numbers (i.e., $\prod \nolimits _{i = 1}^n A_{i}$) are, respectively, defined by

$$\begin{aligned} E\left[ \prod \limits _{i = 1}^n A_{i}\right]&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n}\left[ \prod \limits _{i = 1}^n\underline{a}_{i}(\gamma _{i})\right. \nonumber \\&\quad +\sum \limits _{k=1}^{n}\overline{a}_{k}(\gamma _{k})\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{i \ne k}^n\underline{a}_{i}(\gamma _{i})+\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}^{n}\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j})\mathop {\mathop {\mathop {\prod }\limits _{i=1}}\limits _{i\ne j}}\limits _{i \ne k }^n\underline{a}_{i}(\gamma _{i})\nonumber \\&\quad \left. +\sum \limits _{k=1}^{n}\underline{a}_{k}(\gamma _{k})\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}^n\overline{a}_{i}(\gamma _{i})+\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}, \end{aligned}$$

(7)

$$\begin{aligned} Var\left( \prod \limits _{i = 1}^n A_{i}\right)&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n}\left[ \left( \prod \limits _{i = 1}^n E(A_{i}\right) -\prod \limits _{i =1}^n\underline{a}_{i}(\gamma _{i}))^{2}\right. \nonumber \\&\quad +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k}(\gamma _{k})\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}\nonumber \\&\quad +\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}^{T}\left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j})\mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne j}} \limits _{i \ne k }^T\underline{a}_{i}(\gamma _{i})\right. )^{2}+\cdots \nonumber \\&\quad +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\underline{a}_{k}(\gamma _{k})\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})^{2}\right. \nonumber \\&\left. \quad +\left( \prod \limits _{i = 1}^n E(A_{i})-\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right) ^{2}\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}. \end{aligned}$$

(8)

Notice that the possibilsitic mean and variance about the product of n fuzzy numbers in Eqs. (7) and (8) satisfy the following relations (see the “Appendix” for proofs).

Theorem 3

Let $A_{1}, A_{2}, \ldots , A_{n}$ be n fuzzy numbers. Then

• (i) $E\left( \prod \limits _{i = 1}^n A_{i}\right) =\prod \limits _{i = 1}^n E(A_{i})$,

• (ii) $Var\left( \prod \limits _{i = 1}^n A_{i}\right) =\displaystyle \prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\sum \limits _{r = 1}^{n-2}\mathop {\mathop {\sum }\limits _{k_{j}=1}\;j\in \{1,\ldots ,r\}}^{n}\displaystyle \prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}} \times \mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\prod \limits _{i =1}^n\int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}-\left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}$.

3 Possibilistic Moment Models for Multi-period Fuzzy Portfolio Selection

In this section, we discuss a multi-period fuzzy portfolio selection problem based on possibility theory. To reflect investors’ different investment intention, we propose three multi-period fuzzy portfolio selection models.

3.1 Problem Description and Notations

Assume that there are n risky assets and a risk-free asset offering a fixed proceeds in financial markets for trading. An investor takes initial wealth $W_{0}$ into financial markets with the purpose of constructing T-period investment plan among the $n+1$ assets, and he can adjust his wealth at the beginning of the following $T-1$ consecutive periods. Due to the high volatility of financial markets, the proceeds per unit capital invested on any one of the n risky assets at each period is approximated by means of fuzzy number. For convenience, we let

$r_{t,i}$ :

the proceeds per unit capital invested on risky asset i at period t, where $r_{t,i}$ is a fuzzy number with the $\gamma$-level set $[r_{t,i}]^{\gamma }=[\underline{a}_{t,i}(\gamma ),\overline{a}_{t,i}(\gamma )]$;

$r_{t,n+1}$ :

the proceeds per unit capital invested on the risk-free asset at period t, where $r_{t,n+1}$ is a constant;

$x_{t,i}$ :

the investment proportion of risky asset i at period t for $i=1,2,\ldots ,n$;

$x_{t,n+1}$ :

the investment proportion of risk-free asset at period t;

$l_{t,i},u_{t,i}$ :

the lower and upper bounds of $x_{t,i}$ for $i=1,2,\ldots ,n+1$ and $t=1,2,\ldots ,T$;

$c_{t,i}$ :

the transaction cost of risky asset i at period t;

$R_{P,t}$ :

the proceeds per unit capital invested on the portfolio at period t;

$R_{N,t}$ :

the net proceeds per unit capital invested on the portfolio at period t;

r(t):

the preset minimum proceeds level about the portfolio at period t;

$\delta _{t}$ :

the given maximum risk tolerance level about the portfolio at period t;

$S_{t}$ :

the given minimum skewness level for the portfolio at period t;

$K_{t}$ :

the given maximum kurtosis level about the portfolio at period t;

$W_{t}$ :

the wealth obtained at the end of period t.

3.2 Possibilistic Moments for Fuzzy Portfolio Selection

Assume that the transaction cost at each period is a V-shape function in this paper. Then, the transaction cost of the portfolio $x_{t}=(x_{t,1},x_{t,2},\ldots ,x_{t,n+1})$ at period t can be expressed by

$$\begin{aligned} C_{t}=\sum \limits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|,\quad t=1,2,\ldots ,T. \end{aligned}$$

(9)

The proceeds per unit capital invested on the portfolio at period t is

$$\begin{aligned} R_{P,t}=\sum \limits _{i = 1}^{n+1} x_{t,i}r_{t,i},\quad t=1,2,\ldots ,T. \end{aligned}$$

(10)

After removing the transaction costs, the net proceeds per unit capital invested on the portfolio at period $t\,(t=1,2,\ldots ,T)$ is

$$\begin{aligned} R_{N,t}=\sum \limits _{i = 1}^{n+1} \left( x_{t,i}r_{t,i}- c_{t,i}|x_{t,i}-x_{t-1,i}|\right) . \end{aligned}$$

(11)

Thus, the wealth between the adjacent two periods satisfies the following relation

$$\begin{aligned} W_{t}=W_{t-1}R_{N,t},\quad t=1,2,\ldots ,T. \end{aligned}$$

(12)

It follows from Eq. (12) that

$$\begin{aligned} W_{T}=W_{0}\prod \limits _{t = 1}^T R_{N,t}. \end{aligned}$$

(13)

Since $r_{t,1},r_{t,2},\ldots , r_{t,n}$ are fuzzy numbers for all $t=1,2,\ldots ,T$, by using the fuzzy arithmetic operations in Zadeh (1965), we can find that $R_{P,t},R_{N,t}$ and $W_{T}$ are also fuzzy numbers. Then, the $\gamma$-level set of $R_{N,t}$ can be denoted by $[R_{N,t}]^{\gamma }=\big [\sum \nolimits _{i = 1}^{n} x_{t,i}\underline{a}_{t,i}(\gamma )+ x_{t,n+1}r_{t,n+1}-C_{t},\sum \nolimits _{i = 1}^{n} x_{t,i}\overline{a}_{t,i}(\gamma )+ x_{t,n+1}r_{t,n+1}-C_{t}\big ]$. For convenience, we denote $\underline{a}_{t}(\gamma )=\sum \nolimits _{i = 1}^{n} x_{t,i}\underline{a}_{t,i}(\gamma )+ x_{t,n+1}r_{t,n+1}-C_{t}$ and $\overline{a}_{t}(\gamma )=\sum \nolimits _{i = 1}^{n} x_{t,i}\overline{a}_{t,i}(\gamma )+ x_{t,n+1}r_{t,n+1}-C_{t}$ in the following sections. Using Theorem 1 and Eq. (11), the possibilistic mean of $R_{N,t}$ can be computed by

$$\begin{aligned} E(R_{N,t})=\sum \limits _{i = 1}^{n+1} \left( x_{t,i}E(r_{t,i})- c_{t,i}|x_{t,i}-x_{t-1,i}|\right) , \end{aligned}$$

(14)

where $E(r_{t,i})={\int }_{0}^{1}\gamma (\underline{a}_{_{t,i}}(\gamma )+\overline{a}_{_{t,i}}(\gamma ))\text {d}\gamma$ is the possibilistic mean of $r_{t,i}$ for $i=1, 2, \ldots , n+1$. Especially, when $i=n+1$, we have $E(r_{t,n+1})=r_{t,n+1}$.

Using Theorem 2 and Eq. (10), the possibilistic variance of $R_{P,t}$ can be expressed by

$$\begin{aligned} Var(R_{P,t})=\sum \limits _{i = 1}^n x_{t,i}^{2} Var( r_{t,i})+2 \sum \limits _{i<j=1}^n x_{t,i}x_{t,j} Cov(r_{t,i},r_{t,j}). \end{aligned}$$

(15)

From Eqs. (7) and (14), the crisp form of terminal wealth $W_{T}$ can be calculated by

$$\begin{aligned} E(W_{T})=W_{0} \prod \limits _{t = 1}^T \left[ \sum \limits _{i = 1}^{n+1} x_{t,i}E(r_{t,i})-\sum \limits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|\right] . \end{aligned}$$

(16)

Then, by Eqs. (8) and (11), the crisp form of terminal risk is

$$\begin{aligned} Var(W_{T})&=W_{0}^{2}Var\left( \prod \limits _{t = 1}^T R_{N,t}\right) \nonumber \\&=W_{0}^{2}\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{T}\left[ \left( \prod \limits _{t = 1}^T E(R_{N,t})-\prod \limits _{t = 1}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}\right. \nonumber \\&\quad +\sum \limits _{k=1}^{T}\left( \prod \limits _{t = 1}^T E( R_{N,t})-\overline{a}_{k}(\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{i \ne k}}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}\nonumber \\&\quad + \mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{T}\left( \prod \limits _{t = 1}^T E( R_{N,t})-\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j}) \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne j}}\limits _{i \ne k}}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}+\cdots \nonumber \\&\quad +\sum \limits _{k=1}^{T}\left( \prod \limits _{t = 1}^T E( R_{N,t})-\underline{a}_{k}(\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^T\overline{a}_{i}(\gamma _{i})\right) ^{2}\nonumber \\&\quad \left. +\left( \prod \limits _{t = 1}^T E(R_{N,t})-\prod \limits _{t = 1}^T\overline{a}_{t}(\gamma _{t})\right) ^{2}\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{T}. \end{aligned}$$

(17)

By Definition 3 and Eq. (10), the possibilistic skewness and kurtosis of $R_{P,t}$ can be, respectively, expressed as

$$\begin{aligned} S(R_{P,t})=&\int _{0}^{1}\gamma \left[ \left( \underline{a}_{t}(\gamma )-E(R_{P,t})\right) ^{3}+\left( \overline{a}_{t}(\gamma )-E(R_{P,t})\right) ^{3}\right] \text {d}\gamma , \end{aligned}$$

(18)

$$\begin{aligned} K(R_{P,t})=&\int _{0}^{1}\gamma \left[ \left( \underline{a}_{t}(\gamma )-E(R_{P,t})\right) ^{4}+\left( \overline{a}_{t}(\gamma )-E(R_{P,t})\right) ^{4}\right] \text {d}\gamma , \end{aligned}$$

(19)

where $\underline{a}_{t}(\gamma )=\sum \nolimits _{i = 1}^n x_{t,i}\underline{a}_{_{t,i}}(\gamma )$ and $\overline{a}_{t}(\gamma )=\sum \nolimits _{i = 1}^n x_{t,i}\overline{a}_{_{t,i}}(\gamma )$ represent the left- and right-hand endpoints of $[R_{P,t}]^{\gamma }$.

3.3 Modelling

Based on the discussion above, we use the posssibilistic mean and variance as the measures of return and risk, respectively. Then, we propose three possibilistic moment models for multi-period fuzzy portfolio selection.

As a first investment strategy, we assume that an investor wants to seek an investment strategy with two objectives, that is, maximizing terminal wealth and minimizing terminal risk. Then, we formulate the following posssibilistic mean–variance model $(P_{1})$:

$$\begin{aligned} ({P_1})\left\{ \begin{array}{l} \max E({W_T}) = {W_0}\prod \limits _{t = 1}^T {\left[ \sum \limits _{i = 1}^{n + 1} {{x_{t,i}}} E({r_{t,i}}) - \sum \limits _{i = 1}^n {{c_{t,i}}} |{x_{t,i}} - {x_{t - 1,i}}|\right] } \\ \min Var({W_T}) = W_0^2Var\left( \prod \limits _{t = 1}^T {{R_{N,t}}} \right) \\ s.t.\sum \limits _{i = 1}^n {{x_{t,i}}} E({r_{t,i}}) + {x_{t,n + 1}}{r_{t,n + 1}} - \sum \limits _{i = 1}^n {{c_{t,i}}} |{x_{t,i}} - {x_{t - 1,i}}| \ge r(t),\quad (a)\\ \sum \limits _{i = 1}^n x _{t,i}^2Var({r_{t,i}}) + 2\sum \limits _{i < j = 1}^n {{x_{t,i}}} {x_{t,j}}Cov({r_{t,i}},{r_{t,j}}) \le {\delta _t}, \quad (b)\\ \sum \limits _{i = 1}^{n + 1} {{x_{t,i}}} = 1,\quad {x_{t,i}} \ge 0, \quad (c)\\ {x_{t,i}} = {z_{t,i}}{\upsilon _{t,i}},\quad i = 1,2, \ldots ,n, \quad (d)\\ \sum \limits _{i = 1}^{n + 1} {\mathrm{{sign}}} ({x_{t,i}}) \le K, \quad (e)\\ {l_{t,i}} \le {x_{t,i}} \le {u_{t,i}},\quad i = 1,2, \ldots ,n + 1; \ t = 1,2, \ldots ,T.\quad (f) \\ \end{array} \right. \end{aligned}$$

(20)

Here, Constraint (20)a indicates that the net proceeds per unit capital invested on the portfolio at period t must be no less than the preset proceeds level r(t). Constraint (20)b means that the risk of the portfolio at period t must be not more than the given maximum risk tolerance level $\delta _{t}$. Constraint (20)c shows that the sum of the investment proportion of the portfolio at period t must be unit. Constraint (20)d is the round-lot constraint, in which $\upsilon _{t,i}$ is the smallest volume that can be purchased on each risky asset and $z_{t,i}$ is the transaction lots of risky asset i at period t. Constraint (20)e represents the cardinality constraint about the portfolio at period t, which means that the maximum holding number of assets in the portfolio at period t must be not more than K. Constraint (20)f is the bound constraint and it means that $x_{t,i}$ must be restricted in $[l_{t,i},u_{t,i}]$. Denote the feasible region of $(P_{1})$ as $x\in \varOmega _{1}$.

As a second investment strategy, we assume that the investor works with the two competing goals in $(P_{1})$. In addition, he also requires that the skewness of the portfolio at period t must be no less than the preset skewness level $S_{t}$ for all $t=1,2,\ldots ,T$. Then, we construct the following possibilistic mean–variance–skewness model $(P_{2})$:

$$\begin{aligned} (P_2)\left\{ \begin{array}{ll} \max &{}\quad W_{T}=W_{0} \prod \limits _{t = 1}^T \left[ \sum \limits _{i = 1}^{n+1} x_{t,i}E(r_{t,i})-\sum \limits _{i = 1}^n c_{t,i}|x_{t,i}-x_{t-1,i}|\right] \\ \min &{}\quad Var(W_{T})=W_{0}^{2}Var\left( \prod \limits _{t = 1}^T R_{N,t}\right) \\ s.t. &{}\quad S\left( \sum \limits _{i = 1}^{n} x_{t,i}r_{t,i}\right) \ge S_{t},\\ &{}\quad x\in \varOmega _{1}. \end{array}\right. \end{aligned}$$

For convenience, we denote the feasible region of $(P_{2})$ as $x\in \varOmega _{2}$.

As a third investment strategy, we assume that the investor considers all the investment constraints in the model $(P_{2})$. Meanwhile, he requires that the kurtosis of the portfolio at period $t\,(t=1,2,\ldots ,T)$ must be not more than the given maximum kurtosis level $K_{t}$ as an additional constraint. Then, we formulate the following possibilistic mean–variance–skewness–kurtosis model $(P_{3})$:

$$\begin{aligned} (P_3)\left\{ \begin{array}{ll} \max &{}\quad E(W_{T})=W_{0} \prod \limits _{t = 1}^T \left[ \sum \limits _{i = 1}^{n+1} x_{t,i}E(r_{t,i})-\sum \limits _{i = 1}^n c_{t,i}|x_{t,i}-x_{t-1,i}|\right] \\ \min &{}\quad Var(W_{T})=W_{0}^{2}Var\left( \prod \limits _{t = 1}^T R_{N,t}\right) \\ s.t. &{}\quad K\left( \sum \limits _{i = 1}^{n} x_{t,i}r_{t,i}\right) \le K_{t},\\ &{}\quad x\in \varOmega _{2}. \end{array}\right. \end{aligned}$$

3.4 Estimation Method for Fuzzy Return

To use the proposed models in previous subsection, it is necessary to estimate the distributions on the return rates of risky assets. Traditional portfolio models are proposed on the basis of the assumption that the probability distributions of the future return rates on risky assets can be accurately predicted by historical data. However, it is hard to keep this kind of assumption hold in the real ever-changing financial markets. Even though the probability distribution can be estimated, it is cannot guarantee that the future return rates of risky assets truly obey it. In the real world, financial markets are often affected by numerous subjective factors such as vagueness and ambiguity. As mentioned by Gupta et al. (2008), decision makers are usually provided with linguistic information such as high risk, low profit, high interest rate, etc. Thus, it is necessary to take the fuzzy nature of human subjective judgment on a financial decision into account. It is well-known that fuzzy set theory in Zadeh (1965) is a powerful tool for describing an uncertain environment with vagueness, ambiguity or some other type of fuzziness, which are always involved in not only the imperfect knowledge of the return rates on risky assets but also the human judgment for financial markets. By using fuzzy set theory, we need to determine the possibility distributions of the return rates on risky assets. In contrast to probability distributions, to determine the possibility distributions of the return rates on risky assets needs less information. What’s more, the unquantifiable factors such as experts’ knowledge and investors’ subjective opinions can be easily reflected. Thus, it is worthwhile to handle the uncertainty of financial markets by using fuzzy set theory.

As we know, several researchers presented different methods to estimate the possibility distributions on fuzzy variables. For example, Devi and Sarma (1985) gave a method to estimate the possibility distributions of fuzzy variables by using the histograms of a finite number of historical data. Cheng (2004) developed a group decision method for constructing triangular fuzzy numbers. Zhang et al. (2010a) proposed a frequency estimation method of the return rates on risky assets with triangular possibility distributions based on the frequency distributions of historical data. Triangular possibilistic distribution is commonly used to represent the fuzzy uncertainty on the return rate of a risky asset due to its simple to estimate and easy to generalize to the LR-type form with center point (Zhang et al. 2010b; Ammar and Khalifa 2003). In this paper, we also use the above-mentioned method to estimate the possibility distribution of the proceeds of a risky asset by using the historical data and human’s subjective judgement. To construct a triangular possibility distribution, we need to estimate three parameters, that is, the mode that represents the most possible value of the fuzzy number, the left and right spreads that denote the distance from the left and right endpoints to the mode of the fuzzy number. Here, we take the estimation of the possibility distribution of the proceeds per unit capital invested on risky asset i at period t (i.e., $r_{t,i}$) as an example to introduce the application of the above-mentioned method on multi-period portfolio selection. Let $a_{t,i}, \alpha _{t,i}>0$ and $\beta _{t,i}>0$ be the mode, the left and right spreads of $r_{t,i}$. It is well-known that, at the beginning of period t, the real return rates of risky assets at period $t-1$ are known. We use the proceeds of risky asset i at the past period to calculate its proceeds at current period. We select 5th percentile $P_{i}(5)$ and the 95th percentile $P_{i}(95)$ of its historical proceeds at period $t-1$ as the left endpoint $r_{\min }$ and the right endpoint $r_{\max }$ of its possibilistic return distribution at period t, respectively. Then, we determine the intervals $[d_{t-1,1}, d_{t-1,2}],[d_{t-1,2}, d_{t-1,3}],\ldots , [d_{t-1,m-1}, d_{t-1,m}]$ that contain the historical proceeds from $P_{i}(5)$ to $P_{i}(95)$ where $d_{t-1,1}=r_{\min }$, $d_{t-1,m}=r_{\max }$, and others $d_{t-1,j}$s are determined from $d_{t-1,j}=P_{i}(5+j\times k)\,(j=1, 2,\ldots , m)$ by selecting a reasonable $k\,(k>0)$. Assume that $n_{t-1,j}$ is the frequency of the jth interval $[d_{t-1,j}, d_{t-1,j+1}]$ for $j=1, 2,\ldots , m-1$. Then, we approximately calculate the mode of the proceeds per unit capital invested on risky asset i at period t by the following formula:

$$\begin{aligned} M_{t,i}=d_{t-1,k}+\frac{(n_{t-1,k}-n_{t-1,k+1})(d_{t-1,k+1}-d_{t-1,k})}{n_{t-1,k}-n_{t-1,k+1}+n_{t-1,k}-n_{t-1,k-1}}, \end{aligned}$$

where $n_{t-1,k}$ is the mode of $n_{t-1,1}, n_{t-1,2},\ldots ,n_{t-1,m}$. Here, we view $M_{t,i}$ as $a_{t,i}$. Then, we have $a_{t,i}-\alpha _{t,i}=r_{\min }$ and $a_{t,i}+\beta _{t,i}=r_{\max }$. The left and right spreads of $r_{t,i}$ can be estimated by $\alpha _{t,i}=M_{t,i}-r_{\min }$ and $\beta _{t,i}=r_{\max }-M_{t,i}$. It follows from $a_{t,i}$, $\alpha _{t,i}$ and $\beta _{t,i}$ that we can construct the triangular possibility distribution of $r_{t,i}$ as follows

$$\begin{aligned} \mu _{r_{t,i}}(x)= \left\{ \begin{array}{ll} 1-\frac{a_{t,i}-x}{\alpha _{t,i}}, &{}\quad \text {if} \quad a_{t,i}-\alpha _{t,i}\le x\le a_{t,i}, \\ 1-\frac{x-a_{t,i}}{\beta _{t,i}}, &{}\quad \text {if} \quad a_{t,i}\le x\le a_{t,i}+ \beta _{t,i}, \\ 0, &{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

Then, the $\gamma$-level set of $r_{t,i}=(a_{t,i}, \alpha _{t,i},\beta _{t,i})$ can be expressed by

$$\begin{aligned}{}[r_{t,i}]^{\gamma }=\left[ a_{t,i}-(1-\gamma )\alpha _{t,i}, a_{t,i}+(1-\gamma )\beta _{t,i}\right] . \end{aligned}$$

(21)

Repeat the procedure above, we can construct the triangular possibility distributions of the n risky assets at each period.

3.5 Crisp Forms of the Proposed Models

By Eqs. (2) and (14), the possibilistic mean of $R_{N,t}$ can be computed by

$$\begin{aligned} E(R_{N,t})=&\sum \limits _{i = 1}^n x_{t,i}\left( a_{t,i}+\tfrac{\beta _{t,i}-\alpha _{t,i}}{6}\right) +x_{t,n+1}r_{t,n+1}-\sum \limits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|. \end{aligned}$$

(22)

By Theorem 3, Eqs. (16) and (22), the crisp form of terminal wealth $W_{T}$ is

$$\begin{aligned} E(W_{T})\!=&W_{0} \prod \limits _{t = 1}^T \left[ \sum \limits _{i = 1}^{n} x_{t,i}\left( a_{t,i}+\tfrac{\beta _{t,i}-\alpha _{t,i}}{6}\right) +x_{t,n+1}r_{t,n+1}-\sum \limits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|\right] . \end{aligned}$$

(23)

From Eqs. (15) and (22), the possibilistic variance of $R_{N,t}$ can be calculated by

$$\begin{aligned} Var(R_{N,t})=&\frac{1}{18}\left[ \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{2}+\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{2}\right] +\frac{1}{18}\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) . \end{aligned}$$

(24)

By Theorem 3 and Eq. (17), the crisp form of terminal risk can be represented as

$$\begin{aligned}&Var(W_{T})=W_{0}^{2}\left[ \prod \limits _{i = 1}^T \left( \tfrac{1}{2}\overline{a}_{i}^{2}-\tfrac{1}{3}\overline{a}_{i}\overline{\alpha }_{i}+\tfrac{1}{12}\overline{\alpha }_{i}^{2}\right) +\sum \limits _{r = 1}^{T-2}\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2,\ldots ,r\}}}^{T}\prod \limits _{j = 1}^r\left( \tfrac{1}{2}\overline{a}_{k_{j}}^{2}+\tfrac{1}{3}\overline{a}_{k_{j}}\overline{\beta }_{k_{j}}+\tfrac{1}{12}\overline{\beta }_{k_{j}}^{2}\right) \right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^T\left( \tfrac{1}{2}\overline{a}_{i}^{2}-\tfrac{1}{3}\overline{a}_{i}\overline{\alpha }_{i}+\tfrac{1}{12}\overline{\alpha }_{i}^{2}\right) +\prod \limits _{i = 1}^T \left( \tfrac{1}{2}\overline{a}_{i}^{2}+\tfrac{1}{3}\overline{a}_{i}\overline{\beta }_{i}+\tfrac{1}{12}\overline{\beta }_{i}^{2}\right) -\prod \limits _{i = 1}^T\left( \overline{a}_{i}+\tfrac{\overline{\beta }_{i}-\overline{\alpha }_{i}}{6}\right) ^{2}\right] , \end{aligned}$$

(25)

where $\overline{a}_{t}=\sum \nolimits _{i = 1}^n x_{t,i}a_{t,i}+x_{t,n+1}r_{t,n+1}-\sum \nolimits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|$, $\overline{\alpha }_{t}=\sum \nolimits _{i = 1}^n x_{t,i}\alpha _{t,i}$ and $\overline{\beta }_{t}=\sum \nolimits _{i = 1}^n x_{t,i}\beta _{t,i}$ for all $t=1,2,\ldots ,T$.

According to Eqs. (18) and (19), the possibilistic skewness and kurtosis of $R_{P,t}$ can be, respectively, expressed by

$$\begin{aligned} S(R_{P,t})&=\frac{19}{1080}\left[ \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{3}-\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{3}\right] +\frac{1}{72}\left[ \left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{2}\right. \nonumber \\&\quad -\,\left. \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) \left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{2}\right] , \end{aligned}$$

(26)

$$\begin{aligned} K(R_{P,t})&=\frac{1}{72}\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{2}\left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{2}+\frac{5}{432}\left[ \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{4}+\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{4}\right] \nonumber \\&\quad +\,\frac{2}{135}\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) \left[ \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{2}+\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{2}\right] . \end{aligned}$$

(27)

If we substitute Eqs. (22)–(25) into the model $(P_{1})$, then we have

$$\begin{aligned} ({P_1})\left\{ \begin{array}{l} \max E({W_T}) = W_{0} \prod \limits _{t = 1}^T \left[ \sum \limits _{i = 1}^{n} x_{t,i}\left( a_{t,i}+\tfrac{\beta _{t,i}-\alpha _{t,i}}{6}\right) +x_{t,n+1}r_{t,n+1}-\sum \limits _{i = 1}^{n+1} c_{t,i}|x_{t,i}-x_{t-1,i}|\right] \\ \min Var(W_{T})=W_{0}^{2}\bigg (\prod \limits _{i = 1}^T \left( \tfrac{1}{2}\overline{a}_{i}^{2}-\tfrac{1}{3}\overline{a}_{i}\overline{\alpha }_{i}+\tfrac{1}{12}\overline{\alpha }_{i}^{2}\right) \\ \qquad \qquad +\sum \limits _{r = 1}^{T-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits {\;j\in \{1,2,\ldots ,r\}}}^{T}\prod \limits _{j = 1}^r\left( \tfrac{1}{2}\overline{a}_{k_{j}}^{2}+\tfrac{1}{3}\overline{a}_{k_{j}}\overline{\beta }_{k_{j}}+\tfrac{1}{12}\overline{\beta }_{k_{j}}^{2}\right) \\ \qquad \qquad \times \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits { i \ne k_{j}}}^T\left( \tfrac{1}{2}\overline{a}_{i}^{2}-\tfrac{1}{3}\overline{a}_{i}\overline{\alpha }_{i}+\tfrac{1}{12}\overline{\alpha }_{i}^{2}\right) \\ \qquad \qquad +\prod \limits _{i = 1}^T \left( \frac{1}{2}\overline{a}_{i}^{2}+\tfrac{1}{3}\overline{a}_{i}\overline{\beta }_{i}+\tfrac{1}{12}\overline{\beta }_{i}^{2}\right) -\prod \limits _{i = 1}^T\left( \overline{a}_{i}+\tfrac{\overline{\beta }_{i}-\overline{\alpha }_{i}}{6}\right) ^{2}\bigg )\\ s.t.\mathrm{{ }}\sum \limits _{i = 1}^n x_{t,i}\left( a_{t,i}+\tfrac{\beta _{t,i}-\alpha _{t,i}}{6}\right) +\quad x_{t,n+1}r_{t,n+1}-\sum \limits _{i = 1}^n c_{t,i}|x_{t,i}-x_{t-1,i}|\ge r(t), \\ \displaystyle \frac{1}{18}\left[ \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) ^{2}+ \left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) ^{2}\right] +\frac{1}{18}\left( \sum \limits _{i = 1}^n x_{t,i}\alpha _{t,i}\right) \left( \sum \limits _{i = 1}^n x_{t,i}\beta _{t,i}\right) \le \delta _{t},\\ \sum \limits _{i = 1}^{n+1} x_{t,i}=1,\quad x_{t,i}\ge 0,\\ x_{t,i}=z_{t,i}\upsilon _{t,i}, \quad i=1,2,\ldots ,n,\\ \sum \limits _{i = 1}^{n+1}\text {sign}(x_{t,i})\le K,\\ l_{t,i} \le x_{t,i} \le u_{t,i}, \quad \text {if}\quad x_{t,i}>0, \ i=1,2,\ldots ,n+1; \ t=1,2,\ldots ,T.\\ \end{array} \right. \end{aligned}$$

Similarly, if we substitute Eqs. (22)–(27) into $(P_{2})$ and $(P_{3})$, then the corresponding crisp form models can be also obtained.

4 Solution Algorithm

In this section, we design a fuzzy programming approach-based differential evolution algorithm to solve the proposed models. First, let us first introduce the fuzzy programming approach in Zimmermann (1978) for a general multi-objective optimization problem.

4.1 Fuzzy Programming Approach for General Multi-objective Optimization Problem

A general multi-objective optimization problem can be expressed as follows

$$\begin{aligned} (P)\left\{ \begin{array}{ll} \max &{}\quad Z(x)=\left[ Z_{1}(x),Z_{2}(x),\ldots ,Z_{k}(x)\right] \\ \min &{}\quad f(x)=\left[ f_{1}(x),f_{2}(x),\ldots ,f_{m}(x)\right] \\ s.t. &{}\quad x\in D, \end{array}\right. \end{aligned}$$

where $x\in D$ is the feasible region of the problem (P); $Z_{1}(x),Z_{2}(x),\ldots ,Z_{k}(x)$ are the profit forms of objectives; $f_{1}(x),f_{2}(x),\ldots ,f_{m}(x)$ are the cost forms of objectives.

To solve the problem (P), Zimmermann (1978) presented a fuzzy programming approach with the following procedures.

Step 1:

View (P) as a single-objective programming problem and obtain the ideal and anti-ideal solutions of each objective by solving the following problems

$$\begin{aligned} Z_{l}^{+}&=\max \limits _{x\in D}Z_{l}(x),\quad Z_{l}^{-}=\min \limits _{x\in D}Z_{l}(x), l=1,2,\ldots ,k;\\ f_{j}^{+}&=\min \limits _{x\in D}f_{j}(x),\quad f_{j}^{-}=\max \limits _{x\in D}f_{j}(x), j=1,2,\ldots ,m. \end{aligned}$$

Step 2:

Construct the membership function for each objective by using its ideal and anti-ideal solutions as follows:

$$\begin{aligned} \mu _{l}(Z_{l})&=\tfrac{Z_{1}(x)-Z_{l}^{-}}{Z_{l}^{+}-Z_{l}^{-}},\quad l=1,2,\ldots ,k, \end{aligned}$$

(28)

$$\begin{aligned} \mu _{j}(f_{j})&=\tfrac{f_{j}^{-}-f_{j}(x)}{f_{j}^{+}-f_{j}^{-}},\quad j=1,2,\ldots ,m. \end{aligned}$$

(29)

Step 3:

Use the maximization principle in Bellman and Zadeh (1970) to define the following function

$$\begin{aligned} \lambda =\min \{\mu _{1}(Z_{1}),\ldots ,\mu _{k}(Z_{k});\mu _{1}(f_{1}),\ldots ,\mu _{m}(f_{m})\}. \end{aligned}$$

(30)

Step 4:

Transform the problem (P) into the following single objective programming problem by Eqs. (28), (29) and (30). Then, we have

$$\begin{aligned} (P^{'})\left\{ \begin{array}{ll} \max &{}\quad \lambda \\ s.t. &{}\quad \mu _{l}(Z_{l})\ge \lambda ,\quad l=1,2,\ldots ,k,\\ &{}\quad \mu _{j}(f_{j})\ge \lambda ,\quad j=1,2,\ldots ,m,\\ &{}\quad x\in D. \end{array}\right. \end{aligned}$$

Using the approach above, the idea and anti-ideal solutions of the two objective functions in the model $(P_{1})$ can be obtained by solving the following problems

$$\begin{aligned} E(W_{T})^{+}&=\max \limits _{x\in X}E(W_{T}),\quad E(W_{T})^{-}=\min \limits _{x\in X}E(W_{T});\\ V^{+}&=\min \limits _{x\in X}Var(W_{T}),\quad V^{-}=\max \limits _{x\in X}Var(W_{T}). \end{aligned}$$

Here, $x\in X$ represents the feasible region of the model $(P_{1})$.

According to Step 2, the membership functions of the two objectives in the model $(P_{1}^{'})$ can be expressed as $\mu _{E}(x)=\tfrac{E(W_{T})-E(W_{T})^{-}}{E(W_{T})^{+}-E(W_{T})^{-}}$ and $\mu _{V}(x)=\tfrac{V^{-}-Var(W_{T})}{V^{+}-V^{-}}$. Then, the model $(P_{1})$ can be transformed into the following single-objective programming problem $(P_{1}^{'})$

$$\begin{aligned} (P_{1}^{'})\left\{ \begin{array}{ll} \max &{}\quad \lambda \\ s.t. &{}\quad \mu _{E}(x)\ge \lambda ,\\ &{}\quad \mu _{V}(x)\ge \lambda ,\\ &{}\quad x\in X. \end{array}\right. \end{aligned}$$

4.2 Differential Algorithm

Differential evolution algorithm (DE) is a simple yet powerful evolutionary algorithm (EA) for global optimization, which was originally introduced by Storn and Price (1995). DE is viewed as a reliable, efficient, robust and fast solution method. In DE, the suitable values of the control parameters affect its performance. Choosing suitable parameter values is often a problem dependent task and requires previous experience of the user. In this paper, we design an improved self-adaptive differential evolution (ISDE) algorithm to solve our proposed models. The designed ISDE algorithm is developed on the basis of the MDE algorithm in Mohamed and Sabry (2012) by introducing two novel control parameters. Without loss of generality, we take the model $(P_{1})$ as an example to introduce the designed algorithm. Now, let us introduce its parameter setting, initialization operation, evaluation function, mutation, crossover and selection operations.

4.2.1 Initialization Operation

Randomly generate a solution $x=(x_{1,1},x_{1,2},\ldots ,x_{1,n+1};\ldots ; x_{T,1},x_{T,2},\ldots ,x_{T,n+1})$ of the model $(P_{1}^{'})$ and represent it as a candidate individual of DE, where $x_{t,i}\in [0,u_{t,i}]$ for all $i=1,2,\ldots ,n+1$ and $t=1,2,\ldots ,T$. To satisfy Eq. (20)(c), we perform the following normalization technique

$$\begin{aligned} x_{t,i}^{'}=\frac{x_{t,i}}{x_{t,1}+x_{t,2}+\ldots +x_{t,n+1}}. \end{aligned}$$

Then, we check the feasibility of the individual. If it satisfies the constraints of the model $(P_{1})$, it will be accepted as an individual of the population. Otherwise, we perform the following repair mechanisms to guarantee it to satisfy the constraints of the model $(P_{1})$. For the sake of description, we rewrite $x=(x_{1,1},x_{1,2},\ldots ,x_{1,n+1};\ldots ; x_{T,1},x_{T,2},\ldots ,x_{T,n+1})$ into $x=(x_{1},x_{2},\ldots ,x_{D})$ with $D=(n+1)T$.

4.2.2 Handling the Constraints

To meet Eq. (20)a and c, we calculate the violation values of all chromosomes and keep the ones with violation values equal to zero. To satisfy Eq. (20)e, we select the K-largest values of $x_{t,1},x_{t,2},\ldots ,x_{t,n+1}$ and set all other $n+1-K$ elements as zero. To meet Eq. (20)d, similar to Liu and Zhang (2013), we round $x_{t,i}$ to the next transaction-lot level, $x_{t,i}^{'}= x_{t,i}-(x_{t,i}\mod \upsilon _{t,i})$, after cardinality repair and normalization are applied. The remainder of the rounding process, $(x_{t,i}\text {mod}\upsilon _{t,i})$, is expended in quantities of $\upsilon _{t,i}$ for those $x_{t,i}$ that had the largest values for $x_{t,i}$ mod $\upsilon _{t,i}$ until all of the remainder is disbursed. Then, we set an integer $pop_{-}size$ as the number of chromosomes. Repeating the above-mentioned process $pop_{-}size$ times, we can obtain $pop_{-}size$ initialized feasible chromosomes. Denote them as $ch_{1}, ch_{2}, \ldots ,ch_{pop_{-}size}$.

4.2.3 Evaluation Function

In this study, the evaluation function is defined as

$$\begin{aligned} f(x)=\min \{\mu _{E}(x),\mu _{V}(x)\}. \end{aligned}$$

(31)

4.2.4 Mutation Operation

For target vector $x_{i}^{G}$, a mutant vector $v_{i}^{G+1}$ is generated by

$$\begin{aligned} v_{i}^{G+1}= \left\{ \begin{array}{ll} x_{r}^{G}+F_{l}(G)(x_{b}^{G}-x_{w}^{G}), \quad \text {if} \quad r \text {and}[0,1]\le 0.5, \\ x_{r_{1}}^{G}+F_{g}(G)(x_{r_{2}}^{G}-x_{r_{3}}^{G}),\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(32)

Here, $r_{1}, r_{2},r_{3} \in \{1,2,\ldots ,pop_{-}size\}$ are randomly chosen indices with $r_{1}\ne r_{2}\ne r_{3} \ne i$; $x_{r}^{G}$ is a randomly chosen vector at iteration G; $x_{b}^{G}$ and $x_{w}^{G}$ represent the best and the worst individuals in the current population. $F_{l}(G)$ is a dynamic adaptive scale factor with the following form (see Wu and Wang 2007)

$$\begin{aligned} F_{l}(G)=\frac{F_{\text {min}}}{1+\left( \tfrac{F_{\text {min}}}{F_{\text {max}}}-1\right) e^{-\kappa G}}, \end{aligned}$$

(33)

where $\kappa \in [0,+\,\infty )$ is the initial decay rate, $F_{\text {min}}$ and $F_{\text {max}}$ are the minimum and maximum values of the scale factor $F_{l}$. In Eq. (33), if the value of $\kappa$ is dynamically adjusted, the decay rate will decrease with the increasing of iteration number G. When $F_{l}$ decreases to $F_{\text {min}}$, the decrease in the value of $F_{l}$ will stop. In other words, $\kappa =0$. To maintain the balance between the diversity and the convergence, the value of $F_{l}$ is often restricted in [0.5,1]. Here, the values of $\kappa$, $F_{\text {min}}$ and $F_{\text {max}}$ are set as 100, 0.5 and 1, respectively. In Eq. (32), $F_{g}(G)$ is a fitness-based adaptation scale factor as follows (see Ghosh et al. 2011)

$$\begin{aligned} F_{g}(G)=&\max \left\{ \frac{F_{g,\text {max}}|f\left( x_{i}^{G}\right) -f\left( x_{b}^{G}\right) |}{1.1\times |f\left( x_{i}^{G}\right) -f\left( x_{b}^{G}\right) |+10^{-14}},F_{g,\text {max}}\times \left( 1-e^{-|f\left( x_{i}^{G}\right) -f\left( x_{b}^{G}\right) |}\right) \right\} , \end{aligned}$$

where $F_{g,\text {max}}$ is the maximum value of $F_{g}$. Generally, $F_{g,\text {max}}$ is set as 0.8.

4.2.5 Crossover operation

The target vector $x_{i}^{G}$ is mixed with the mutated vector $v_{i}^{G}$ to generate a trial vector $u_{i}^{G+1}=(u_{1i}^{G+1},u_{2i}^{G+1},\ldots ,u_{Di}^{G+1})$ as follows

$$\begin{aligned} u_{ji}^{G+1}= \left\{ \begin{array}{ll} x_{ji}^{G+1},&{}\quad \text {rand}(j)\le CR \quad \text {or} \quad j=\text {randn}(i),\\ v_{ji}^{G},&{}\quad \text {rand}(j)> CR \quad \text {and} \quad j\ne \text {randn}(i), \end{array} \right. \end{aligned}$$

(34)

where $j = 1, 2,\ldots , D$; $\text {rand}(j)\in [0,1]$ is the jth evaluation of a uniform random generator number. $\text {randn}(i)\in \{1, 2,\ldots , D\}$ is a randomly chosen index which ensures that $u_{i}^{G+1}$ gets at least one element from $v_{i}^{G+1}$. Similar to Mohamed and Sabry (2012), CR is a dynamic non-linear increased crossover probability with the following form

$$\begin{aligned} CR=CR_{\text {max}}+(CR_{\text {min}}-CR_{\text {max}})(1-\tfrac{G}{G_{\text {max}}})^{k}, \end{aligned}$$

where $CR_{\text {max}}$ and $CR_{\text {min}}$ represent the maximum and the minimum values of CR; $G_{\text {max}}$ is the maximum number of iterations and k is a positive number. In this study, we set $CR_{\text {max}}=0.95$, $CR_{\text {min}}=0.5$ and $k=4$.

4.2.6 Selection operation

In this algorithm, we adapt a greedy selection strategy to perform selection operation. If and only if the trial vector $u_{i}^{G+1}$ yields a better fitness function value than $x_{i}^{G}$, then $u_{i}^{G+1}$ is set as $x_{i}^{G+1}$. Otherwise, the old value $x_{i}^{G}$ is retained. The selection scheme is summarized as follows

$$\begin{aligned} x_{i}^{G+1}= \left\{ \begin{array}{ll} u_{i}^{G+1},&{}\quad f(u_{i}^{G+1})> f(x_{i}^{G}), \\ x_{i}^{G}, &{}\quad f(u_{i}^{G+1})\le f(x_{i}^{G}). \end{array} \right. \end{aligned}$$

(35)

The concrete procedures of the designed algorithm are summarized as follows.

Step 1:

Initial parameters: Population size $pop_{-}size$, maximum crossover probability $CR_{\text {max}}$, minimum crossover probability $CR_{\text {min}}$ and maximum iteration number $G_{\text {max}}$;

Step 2:

Randomly generate $pop_{-}size$ candidate solutions and convert them into feasible ones;

Step 3:

Perform mutation and crossover operations by Eqs. (32) and (34);

Step 4:

Calculate the evaluation function value of each individual;

Step 5:

Perform selection operation by Eq. (35);

Step 6:

Check the stopping criterion. If the stopping criterion (maximum number of iterations $G_{\text {max}}$) is satisfied, then terminate the iterative operation and report the optimal solution. Otherwise, return to Steps 3.

4.2.7 Time complexity

Based on the discussion above, we can find that each individual of the designed algorithm has $(n+1)T$ elements. The population size and the maximum iteration number of our algorithm are $pop_{-}size$ and $G_{\text {max}}$, respectively. The required time complexity of the ISDE algorithm $\phi (n)$ is calculated by

$$\begin{aligned} \phi (n)&=O((n+1)T*pop_{-}size)+O(G_{\text {max}}*pop_{-}size)\\&=\left\{ \begin{array}{ll} O((n+1)T*pop_{-}size),&{}\quad \text {if}\quad (n+1)T> G_{\text {max}}, \\ O(G_{\text {max}}*pop_{-}size),&{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

4.2.8 Space complexity

Notice that the designed ISDE algorithm generates $pop_{-}size$ individuals at each generation and each individual has $(n+1)T$ elements. Thus, the space for storing the elements of the population at each generation of the ISDE algorithm is $O((n+1)T*pop_{-}size)$.

5 Numerical Example

Assume that there are 15 stocks from the Shanghai Stock Exchange and a risk-free asset (RFA) in a financial market for trading. The source data of the aforementioned 15 stocks are downloaded from choice east money “http://choice.eastmoney.com”. An investor with initial wealth 10,000 RMB intends to construct three consecutive periods investment among the 16 assets. The historical data of the 15 stocks are collected by their weekly closed prices from Jan. 2010 to Jan. 2013. We set each year as an observation period to handle these historical data. Suppose that the proceeds per unit capital invested on the 15 stocks at each period are triangular fuzzy numbers, i.e., $r_{t,i}=(a_{t,i},\alpha _{t,i},\beta _{t,i})\,(t=1,2,3; i=1,2,\ldots ,15)$. Here, $a_{t,i}, \alpha _{t,i}$ and $\beta _{t,i}$ are assumed to be the mode, 5th percentile and 95th percentile of the historical proceeds data on Stock i at period t. Table 1 shows the possibility distributions of the 15 stocks and the proceeds per unit capital invested on the RFA at each period.

Table 1 The possibility distributions of the 15 stocks and the proceeds per unit capital invested on the RFA at each period.

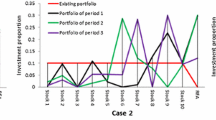
In this example, the maximum holding number of assets in the portfolio at each period is set as 10. The smallest volume that can be purchased on Stock i at period t is set as 0.0001, i.e., $\upsilon _{t,i}=0.0001\,(t=1,2,3;i=1,2,\ldots ,15)$. The proceeds demand levels of portfolios at the three periods are set as 1.090, 1.070 and 1.050, respectively. The risk tolerance levels of portfolios in the three periods are set as 0.0090, 0.0080 and 0.0070, respectively. The investment proportion of any asset at each period is restricted in the range of [0, 0.5], that is, $x_{t,i}\in [0,0.5]\,(t=1,2,3;i=1,2,\ldots ,16)$; The values of $u_{t,i}$ and $l_{t,i}\,(t=1,2,3;i=1,2,\ldots ,16)$ are set as 0.01 and 0.5, respectively. The given minimum skewness level of the portfolio at each period is set as 0.0002. The given minimum kurtosis level of the portfolio at each period is set as 0.00016. The parameters of the designed algorithm are set as follows. The population size is set as 100 and the maximum iteration number is set as 2000. After running the designed algorithm 2000 times on each one of the proposed models, the corresponding investment strategies can be obtained as shown in Table 2.

Table 2 The investment strategies (IS) of the 16 assets by using different models, where the unit of terminal wealth is RMB.

From Table 2, we can find that the higher moments do affect portfolio selection in fuzzy environment. If using the model $(P_{1})$, the investor should allocate his initial wealth among Stocks 2, 5, 6, 7, 9, 13 and the RFA at the beginning of period 1 by the proportions of 0.0660, 0.0166, 0.0389, 0.4905, 0.0127, 0.0998 and 0.2755. At the beginning of period 2, the investor should reallocate his wealth among Stocks 1, 2, 5, 6, 8, 11, 13 and the RFA by the proportions of 0.0172, 0.3876, 0.0113, 0.0147, 0.0350, 0.0173, 0.0395 and 0.4774, respectively. Then, at the beginning of period 3, the investor needs to reallocate his wealth. After adjustment, the investor will hold Stocks 2, 3, 5, 7, 12, 13, 15 and the RFA by the proportions of 0.0619, 0.0207, 0.0204, 0.0257, 0.0270, 0.2753, 0.0709 and 0.4981, respectively. In this decision case, at the end of period 3, the investor’s terminal wealth is 126,153.26 RMB. If using the model $(P_{2})$, the investor should follow the investment strategies listed in lines 9–16 of Table 2 to adjust his wealth at the beginning of each period. In this case, the investor’s terminal wealth is 126,827.63 RMB. If using the model $(P_{3})$, the investor should follow the investment strategies listed in lines 17–24 of Table 2 to adjust his wealth at the beginning of each period. In this case, the investor’s terminal wealth is 126,428.60 RMB. Note that, in the sense of terminal wealth, the models with higher moments (i.e., $(P_{2})$ and $(P_{3})$) perform better than the model $(P_{1})$ with no higher moments.

To illustrate the application of the proposed models, the numerical experiments about their investment metrics including annualized return, volatility, sharpe ratio and maximum drawdown of the portfolio at each period, which are obtained by solving different portfolio selection models, are performed on this example. The corresponding comparative results are shown in Table 3. In Table 3, the values of annualized return and volatility are, respectively, calculated by the possibilistic mean and variance of the fuzzy return of the portfolio at each period. The value of sharpe ratio is computed by the possibilistic return earned in excess of the risk-free generated by per unit of volatility. The value of maximum drawdown of the portfolio return at each period is calculated by (its upper possibilistic mean- its lower possibilistic mean)/its upper possibilistic mean $\times 100\%$. It can be seen from Table 3 that the values of the maximum drawdown with the portfolio returns in the three investment periods generated by the model $(P_{1})$ are 11.2655$\%$, 8.6740$\%$ and 9.0124 $\%$, respectively. From the comparative results in Table 3, we can find that higher risk accompanies an investment yielding a high return. Judged from the average sharpe ratio, we can conclude that the models $(P_{2})$ and $(P_{3})$ perform better than the model $(P_{1})$.

Table 3 Comparative results about investment metrics under different models.

Table 4 The sensitivity analysis of the model $(P_{1})$ under different parameters.

In the following, we take the model $(P_{1})$ as an example to make a sensitivity analysis about the results under different model parameters. We investigate the impact of the model parameters including the holding number of assets in each period portfolio K, return level r(t) and risk tolerance level $\delta _{t}$ at period t. The computational results under different cases are demonstrated in Table 4. It can be seen from the computational results listed in Table 4 that the model parameters pay important role in portfolio decision. For example, Lines 3–6 of Table 4 show the results of the model $(P_{1})$ by varying the value of K from 8 to 14 under the case that the other model parameter values are unchanged. It can be seen that, in the sense of terminal wealth, the optimal holding number of assets in the portfolio at each period is 10.

For comparison, we respectively perform thirty consecutive times running on the designed ISDE algorithm and the MDE algorithm in Mohamed and Sabry (2012) to highlight the performance of the designed ISDE algorithm. The corresponding comparative results about statistical tests of the objective values including mean, standard deviation and relative error obtained by the aforementioned two algorithms are listed in Table 5. In Table 5, we use the relative error index, which is calculated by (the best objective value- the real objective value)/the best objective value $\times 100\%$. Here, the best objective value is the maximum value of all the objective values obtained by the thirty consecutive times running, and the real objective value is computed by the objective value after running 2000 iterations.

Table 5 Comparative results about statistical tests of the objective values obtained by different solution algorithms.

From comparative results in Table 5, we can find out that the objective values obtained by the designed ISDE algorithm with higher mean and less relative error than the ones obtained by the MDE algorithm. Thus, we can conclude that our ISDE algorithm is more effective than the MDE algorithm for solving the proposed models.

6 Conclusions

In this paper, we discuss a multi-period portfolio selection problem in fuzzy environment, where the returns of risky assets at each period are represented by fuzzy numbers. We define the possibilistic mean and variance of the multiplication of multiple fuzzy numbers. Based on these definitions, we propose three multi-period fuzzy portfolio selection models by taking into account some realistic constraints including higher moment, budget, round-lot, cardinality and bound constraints. To solve the proposed models, we develop a fuzzy programming approach-based differential evolution algorithm. Besides, we use a numerical example to illustrate the application of the proposed models and demonstrate the effectiveness of the designed algorithm. The comparative results show that the higher moments associated with the fuzzy returns of risky assets do affect portfolio selection and the designed algorithm is suitable for complex portfolio selection models.

Appendix

Proof

(i) By Definition 1, we have $M^{-}(A_{i})={\int }_{0}^{1}\gamma \underline{a}_{i}(\gamma )\text {d}\gamma$, $M^{+}(A_{i})={\int }_{0}^{1}\gamma \overline{a}_{i}(\gamma )\text {d}\gamma$ and $E(A_{i})=\tfrac{1}{2}(M^{-}(A_{i})+M^{+}(A_{i}))$. Then, by Eq. (7), we have

$$\begin{aligned} E\left[ \prod \limits _{i = 1}^n A_{i}\right]&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n}\left[ \prod \limits _{i = 1}^n\underline{a}_{i}(\gamma _{i})+\sum \limits _{k=1}^{n}\overline{a}_{k}(\gamma _{k})\mathop {\mathop {\mathop {\prod }\limits _{i= 1}} \limits _{i \ne k}}^n\underline{a}_{i}(\gamma _{i})\right. \nonumber \\&\quad \left. +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{n}\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j}) \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne j}}\limits _{i \ne k}}^n\underline{a}_{i}(\gamma _{i})+\sum \limits _{k=1}^{n}\underline{a}_{k}(\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n\overline{a}_{i}(\gamma _{i})+\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}\\&= \prod \limits _{i = 1}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\sum \limits _{k=1}^{n}\int _{0}^{1}\gamma _{k}\overline{a}_{k}(\gamma _{k})\text {d}\gamma _{k}\mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{i \ne k}}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{n}\int _{0}^{1}\gamma _{k}\overline{a}_{k}(\gamma _{k})\text {d}\gamma _{k}\int _{0}^{1}\gamma _{j}\overline{a}_{j}(\gamma _{j})\text {d}\gamma _{j} \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne j}}\limits _{i \ne k }}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\cdots \nonumber \\&\quad \left. +\,\sum \limits _{k=1}^{n}\int _{0}^{1}\gamma _{k}\underline{a}_{k}(\gamma _{k})\text {d}\gamma _{k} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n\int _{0}^{1}\gamma _{i}\overline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\prod \limits _{i = 1}^n\int _{0}^{1}\gamma _{i}\overline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}\right] \\&= \frac{1}{2^{n}}M^{-}(A_{i})\left[ \prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{k=1}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n M^{-}(A_{i})+ \mathop {\mathop {\mathop {\sum }\limits _{k=1}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne j}}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=1}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i = 1}^n M^{+}(A_{i})\right] \\&= \frac{1}{2^{n-1}}E(A_{1})\left[ \prod \limits _{i =2}^n M^{-}(A_{i})+\sum \limits _{k=2}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =2}} \limits _{i \ne k}}^n M^{-}(A_{i})+ \mathop {\mathop {\mathop {\sum }\limits _{k=2}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i =2}}\limits _{ i \ne j}}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=2}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =2}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i =2}^n M^{+}(A_{i})\right] \\&\qquad \vdots \\&= \frac{1}{2^{n-l}}\prod \limits _{i =1}^l E(A_{i})\left[ \prod \limits _{i =l}^n M^{-}(A_{i})+\sum \limits _{k=l}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =l}} \limits _{i \ne k}}^n M^{-}(A_{i}) \mathop {+\mathop {\mathop {\sum }\limits _{k=l}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i =l}} \limits _{ i \ne j }}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=l}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =l}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i =l}^n M^{+}(A_{i})\right] \\&\qquad \vdots \\&=\prod \limits _{i = 1}^n E(A_{i}). \end{aligned}$$

(ii) According to Eq. (8), we have

$$\begin{aligned}&Var\left( \prod \limits _{i = 1}^n A_{i}\right) =\int _{0}^{1}\ldots \int _{0}^{1} \gamma _{1}\ldots \gamma _{n}\left[ \left( \prod \limits _{i = 1}^n E(A_{i})- \prod \limits _{i = 1}^n\underline{a}_{i}(\gamma _{i})\right) ^{2} \right. \nonumber \\&\quad +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k} (\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^T \underline{a}_{i}(\gamma _{i})\right) ^{2}\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{T} \left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j}) \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne j }}\limits _{i \ne k }}^T\underline{a}_{i} (\gamma _{i})\right) ^{2}+\cdots +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\underline{a}_{k}(\gamma _{k})\prod \limits _{i = 1}^n \overline{a}_{i}(\gamma _{i})^{2}\right. \nonumber \\&\quad +\,\left. \left( \prod \limits _{i = 1}^n E(A_{i})-\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right) ^{2}\right] \text {d}\gamma _{1} \ldots \text {d}\gamma _{n}. \end{aligned}$$

(36)

Notice that the rth item in Eq. (36) can be represented by

$$\begin{aligned}&\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{j\in \{1,2, \ldots ,r\}}}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\prod \limits _{j = 1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n \underline{a}_{i}(\gamma _{i})\right) ^{2}\text {d}\gamma _{1}\ldots \text {d} \gamma _{n}\nonumber \\&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2, \ldots ,r\}}}^{n}\left[ \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-2\prod \limits _{i = 1}^n E(A_{i})\prod \limits _{j = 1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n\underline{a}_{i}(\gamma _{i})\right. \nonumber \\&\quad +\,\left. \left( \prod \limits _{j =1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}\nonumber \\&= \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-2\prod \limits _{i = 1}^n \mathop {\mathop {E(A_{i})\mathop {\sum }\limits _{k_{j}=1}} \mathop {\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}\overline{a}_{k_{j}}(\gamma _{k_{j}}) \text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i}) \text {d}\gamma _{i}+\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2 \text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne k_{j}}}^T \int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i})\text {d} \gamma _{i})^{2}\nonumber \\&= \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\tfrac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i}) \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2, \ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}} (\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne k_{j}}}^T\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i} \end{aligned}$$

(37)

It follows that Eq. (37) can be rewritten as the following form

$$\begin{aligned}&Var\left( \prod \limits _{i = 1}^n A_{i}\right) =\frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\prod \limits _{i = 1}^n M^{-}(A_{i})+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}\nonumber \\&\quad +\,2^{n-2}\times \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\nonumber \\&\quad +\,\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}} (\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i}+\tfrac{1}{2^{n}}(\prod \limits _{i = 1}^n E(A_{i}))^{2}\nonumber \\&\quad -\,\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i}) \prod \limits _{i = 1}^n M^{+}(A_{i})+\prod \limits _{ i = 1}^n \int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2}\text {d} \gamma _{i}\nonumber \\&=\left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\left[ \prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\right. \nonumber \\&\quad +\,\left. \prod \limits _{i = 1}^n M^{+}(A_{i})\right] +\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i}+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r \int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2 \text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \,\mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2} \text {d}\gamma _{i}+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2} \text {d}\gamma _{i}. \end{aligned}$$

Notice that $\tfrac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})[\prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{r = 1}^{n-2}\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})+\prod \limits _{i = 1}^n M^{+}(A_{i})]=2(\prod \limits _{i = 1}^n E(A_{i}))^{2}$. Then, we have

$$\begin{aligned} Var\left( \prod \limits _{i = 1}^n A_{i}\right)&=\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}-\left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}. \end{aligned}$$

The theorem is proved. $\square$