1 Introduction

Traditional economic and finance theory is based on the assumptions of investor homogeneity and rational expectations. Recently, the literature has witnessed an increasing number of attempts to model financial markets by incorporating heterogeneous agents and bounded rationality. Both theoretically and computationally oriented heterogeneous-agent models are used to produce some common stylized facts regarding financial market time series in empirical investigations (see Pagan 1996), including excess volatility, some skewness and excess kurtosis, fat tails, and volatility clustering. There are two advantages to a computationally oriented model compared with a theoretically oriented one. Firstly, computer simulation can link many behavioral aspects at the micro level with the macro level. Secondly, more realistic market features, including budget or wealth constraints, and the irregular intraday trading of non-fractional shares, can be readily incorporated into the market microstructure of continuous double auctions and dealer and hybrid markets.

In this paper, we use a continuous double auction mechanism, which has become a widely used clearing device in many stock exchanges around the world. In the last few years, several order-driven microscopic models have been introduced to explain the statistical properties of asset prices (see Slanina 2008). Chiarella and Iori (2002) introduced a simple order-driven market model with heterogeneous agents to investigate how different trading strategies may affect the dynamics of price, bid-ask spreads, trading volume and volatility. Their results indicate that all three trader types are necessary in some form to generate realistic looking return dynamics. In addition, fundamentalist behavior can stabilize the market by reducing the amplitude of price excursions, whereas chartist behavior has the opposite effect and generates large price fluctuations and volatility clustering.

Although the microstructure model of Chiarella and Iori (2002) is very simple and can generate some properties in real asset prices, it does not consider the properties of the generated order flows or of the order book itself. Therefore, Chiarella et al. (2009) (CIP model, hereafter) built a model to incorporate the empirical findings of limit order data. These authors extend three main aspects of the previous model: different time horizons, more than one order submission, and heterogeneous risk aversion. Their model has a properly specified demand function and incorporates feedback from the ongoing evolution of the market. The CIP model has extended a number of the earlier models in this literature that only allowed the agents to place orders of unit size. They analyze the impact of the three trading strategy components on the statistical properties of prices and order flows and find that the chartist strategy is primarily responsible for fat tails and volatility clustering in the artificial price data generated by the model. Their analysis of the order book data has also added to the debate on what causes fat-tailed fluctuations in asset prices.

As we all know, the empirical distribution of asset price fluctuations is fat-tailed; that is, there is a higher probability of extreme events than in a Gaussian distribution. However, a consensus has not been achieved regarding the mechanism that causes fat-tailed fluctuations in asset prices. Gabaix et al. (2003) proposed that large price changes in stock market activity arise from large trading volumes. These authors presented empirical evidence for the shape of the price impact and found the ‘square root’ price impact of volume, emphasizing that the price impact of a trade size has an increasing functional form that applies to a large number of stocks. In contrast, Farmer et al. (2004) studied the distribution of price fluctuations generated by individual market orders. These authors show that the price fluctuations caused by individual market orders are essentially independent of the size of the orders. Gillemot et al. (2006) aggregated returns over a fixed number of transactions (or volume) and found that the return probability density function remains fat-tailed with properties very similar to those in a fixed interval of time. Their result also supports the idea that the heavy tail of the return distribution is not due to variations in the number of transactions because in this case, the number of transactions is held constant. Moreover, Farmer et al. have shown that large price fluctuations are driven by liquidity fluctuation, indicating that a large price change can be caused by a market order submission when a large gap is present between the best price and the price at the next best quote. The gap size is a measure of the liquidity available in the market as limit orders. Thus fluctuations of liquidity—that is, in the market’s ability to absorb new market orders—are the origin of large price fluctuations. The CIP model provides further evidence that large price changes are likely to be generated by the presence of large gaps in the book.

To further study the origin of large price fluctuations and the factors that generate the stylized facts, such as fat-tails and volatility clustering, this paper retains the continuous double auction trading mechanism and the restrictions on short selling and borrowing money and extends the CIP model in the following aspects.

Instead of blending three components (fundamentalist, chartist, noisy) in the strategy, the agent uses fully fundamental-value reversion or the trend following strategy at any given time in our model, specifically, using the fundamentalist or chartist behavior to represent these two types of strategy users, respectively. The fluctuation of supply and demand in the market may come from the response to information (such as the fundamentalists who keep the prices from deviating from the fundamental value too much and chartists who use the history trends of prices to forecast the price movement) or just from the liquidity requirement (such as the noise traders who trade randomly). The information hiding behind the supply and demand affects the order flow in the market, causing the change of orders stored in the limit order book, and then the market price changes. Therefore, the influence of market information on the price is directly reflected in the formation process of the market price.

Moreover, agents hold two specific individual strategies (fundamentalist strategy and chartist strategy) and can switch individually to another strategy depending on the relative performance of their personal strategy. Instead of randomly selecting the parameters for the fundamentalist and chartist expectation strategies, we choose parameters based on some fitness measure. In addition, we add a layer of intraday activity, as in Chiarella et al. (2012), that is missing from the CIP model and the closing price is formed after all of the agents enter the market.

We use some statistical tools such as cumulative distribution functions and the rescaled range statistic to analyze the time series simulated by the model. We find that, with the inclusion of the features mentioned, our model can reveal various types of price behaviors in intraday and daily horizon. The chartists’ behavior can lead to the price taking long excursions away from the fundamental value. Our model is able not only to obtain the essential features of the CIP model but also to characterize most of the stylized facts both in the daily price and the intraday price, such as volatility clustering, the insignificant autocorrelations of returns and the significant, slowly decaying autocorrelations of the absolute returns. We also discuss the statistical properties of spread, which describes the observed stylized facts of double auction markets such as the presentation of long-range correlations.

In addition, we also discuss what generates the large price changes in stock markets. At the daily trading horizon, trading volume is an influencing factor in generating larger price fluctuations, and traders’ expectations are also closely related to the daily price changes. Bubbles or crashes appear in the market as the market fraction of the chartist traders rises. Specifically, at the intraday trading horizon, we use the definition of liquidity from Farmer et al. (2004). The probability for larger returns conditioned on larger trading sizes is higher than that conditioned on smaller trading sizes, indicating that trading size is an influencing factor in generating larger price fluctuations. In the transactions with relatively smaller trading sizes, large price changes are driven by large gaps occurring in the price levels adjacent to the best bid and best ask, implying that liquidity plays a role in causing large price fluctuations.

The paper is structured as follows. In Sect. 2, we introduce the model. In Sect. 3, we show the simulation results of the model and compare them to the empirical studies. Furthermore, we discuss the origin of price fluctuations in different time intervals. Section 4 concludes the paper.

2 The Model

2.1 The Heterogeneous Agents

There are N agents in the market, who are initially endowed with a random amount of stock \(S_{i}^{0}\) and cash \(C_{i}^{0}\), with \(i=1,2,\ldots ,\mathsf{N}\). The difference between the agents’ endowments is not very large, although they are heterogeneous. The endowments \(S_{i}^{t}\) and \(C_{i}^{t}\) at time t are updated when a new transaction occurs. In our model, the agents are not allowed to short sell stocks or borrow money.

We use the subscript \(t=1,\ldots ,T\) to represent the calendar trading days where \(p_{t}\) represents the daily price or the closing price, referring to the transaction price of the last trade in the trading day on the \(t\hbox {th}\) trading day, whereas \(\tau \in R^{+}\) refers to intraday time. The daily price fluctuation, which is the return from \(t-1\) to t, is calculated as

$$\begin{aligned} r_{t} =\ln p_{t} -\ln p_{t-1} . \end{aligned}$$
(1)

We initialize the daily closing price \(p_{t}\) in the first \(\hat{{t}}\) days. All of the agents enter the market sequentially in a randomly selected instant \(t<\tau <t+1\) and trade with others during the trading day. At the beginning of each day, a random permutation \(\zeta _{\tau } \) of \(\{1,\ldots ,\mathsf{N}\}\) is drawn and the agents take action in the order dictated by \(\zeta _{\tau }\). In other words, the trading orders are issued sequentially in a random order that is independently sampled every day. The agents have only one chance to trade each day when it is their turn.

The CIP model assumes that all agents use a combination of fundamental value, chartist and noisy rules to form expectations on stock returns, and price is formed as an agent is randomly chosen to enter the market at any time t. We extend this rule in the following way. The agents make their investment choices based on their expectations for the closing price on the trading day, and they trade sequentially. Agents are either fundamentalists or chartists according to their expectation patterns. The agents switch individually depending on their personal performance for the two types of strategies.

The fundamentalists know the fundamental value \(p_{t}^{f}\) of the asset, which is fixed for day t. The fundamental value is exogenously given as

$$\begin{aligned} p_{t+1}^{f} =p_{t}^{f} \exp \left( \sigma _{f} \upsilon _{t} \right) , \end{aligned}$$
(2)

which is to say, \(\hbox {ln}p_{t+1}^{f} =\ln p_{t}^{f}+\sigma _{f} \upsilon _{t}\), where \(\sigma _{f}\) is the volatility of the fundamental returns. \(\upsilon _{t} \sim N(0,1)\) follows a standard normal distribution. The fundamentalist, i, believes that the closing price will reverse to the fundamental value \(p_{t}^{f}\), forming an expectation about the spot price at the end of the day:

$$\begin{aligned} E^{i}\left( \ln p_{t} \right) =\ln p_{t-1} + \kappa _{t}^{i} \left( E^{i}\left( \ln p_{t}^{f}\right) -\ln p_{t-1} \right) , \end{aligned}$$
(3)

where \(\kappa _{t}^{i}\) represents agent i’s expected speed of mean reversion. Because the fundamental price \(p_{t}^{f}\) is known to each agent in our model, we can obtain

$$\begin{aligned} E^{i}\left( \ln p_{t} -\ln p_{t-1} \right) =\kappa _{t}^{i} \left( \ln p_{t}^{f} -\ln p_{t-1} \right) . \end{aligned}$$
(4)

Moreover, we define

$$\begin{aligned} \kappa _{t}^{i} =\theta _{1} \beta _{t}^{i} \end{aligned}$$
(5)

in our model, where \(\beta _{t}^{i}\) is related to the historical performance of the fundamentalist strategy and \(\theta _{1}\) is some reference level for the mean reversion speed. Therefore, the expected spot return is estimated as

$$\begin{aligned} E^{i}\left( r_{t}\right) =\beta _{t}^{i} \theta _{1} \left( \ln p_{t}^{f} -\ln p_{t-1} \right) . \end{aligned}$$
(6)

The better the performance is, the bigger \(\beta _{t}^{i}\) is and the quicker the reversion speed to the fundamental value.

Chartists do not rely on their knowledge of the fundamental price but try to extrapolate the past price movements into the future and form expectations about the next period’s return according to an adaptive scheme. More precisely, the agents’ expectations for stock returns \(E^{i}(r_{t})\) are based on the observations of the spot daily returns over the last \({\tilde{t}}^{i}\) days. The expected return is given as

$$\begin{aligned} E^{i}\left( r_{t} \right) =\theta _{2} \left( \ln p_{t-1} -\ln p_{t-{\tilde{t}}^{i}-1}\right) , \end{aligned}$$
(7)

where \(r_{t} \;\mathrm{{and}}\;p_{t}\) are, respectively, the spot return and spot price at time t.\(\theta _{2}\) is a given parameter. We choose the time horizon \({\tilde{t}}^{i}\) of each chartist to form an expectation according to

$$\begin{aligned} {\tilde{t}}^{i}={\tilde{t}}\gamma _{t}^{i} , \end{aligned}$$
(8)

where \({\tilde{t}}\) is some reference time horizon. We assume that the chartists believe that the return change in a day can be forecast using the historical return change for several days, which is to say that the expected return \(E^{i}(r_{t})\) is similar to the historical return between the last \({\tilde{t}}^{i}\) days. Meanwhile, the agents use the historical performance of the chartist rules to calculate the parameter \(\gamma _{t}^{i}\).

In addition, we add a noise induced component \(\varepsilon _\mathrm{t}^{i}\), with zero mean and variance \(\sigma _{\varepsilon }\), to the agent’s expectation with weight \(g^{i}\) in the decision process. The expected closing price is given as

$$\begin{aligned} E^{i}\left( p_{t}\right) =p_{t-1} \exp \left( E^{i}\left( r_{t}\right) \right) \left( 1+g^{i}\varepsilon _{t}\right) . \end{aligned}$$
(9)

For agent i, the initial weights are uniformly chosen from the interval \(g^{i} \in [0,1]\) and remain constant.

To facilitate trading, we also introduce a small number of noise traders except for the agents using the trading strategies. The noisy agents enter the market with probability \({\tilde{\rho }}=0.1\) and issue a random order with the same probability to buy or sell.

2.2 The Order Placement Mechanism

Once the agent forms an expectation for the future return and price, he decides the order type and size to maximize his utility. We assume that the agents are risk averse and that the utility is an exponential function of wealth \(W_{t}^{i}\), which is given as

$$\begin{aligned} U\left( W_{t}^{i} ,\alpha ^{i}\right) =-e^{-\alpha ^{i}W_{t}^{i}}, \end{aligned}$$
(10)

where the coefficient \(\alpha ^{i}\) measures the absolute risk aversion of agent i. We assume that those agents using a fundamental strategy are more risk averse than those using a chartist strategy. This effect is captured by setting

$$\begin{aligned} \alpha ^{i}=\alpha \left( 1+\beta _{t}^{i} \right) \hbox { or } \alpha ^{i} =\alpha /\left( 1+\gamma _{t}^{i}\right) , \end{aligned}$$
(11)

where \(\alpha \) is some reference level of risk aversion.

Define the portfolio wealth of each agent as

$$\begin{aligned} W_{t}^{i} =S_{t}^{i} p_{t} +C_{t}^{i} , \end{aligned}$$
(12)

where \(S_{t}^{i}\) and \(C_{t}^{i}\), respectively, represent the stock and cash position of agent i at time t. The optimal composition of the agents’ portfolio is determined by trading off the expected return against the expected risk, which is how it is determined in the CIP model. The number of stocks that the agent wants to hold in his portfolio at a given price depends on the choice of the utility function. For the CARA utility function, the number of stocks that agent i wants to hold at a given price \({\tilde{p}}_{d}^{i}\) is given by

$$\begin{aligned} \pi ^{i}\left( {\tilde{p}}_{d}^{i}\right) = \frac{\ln \left( E^{i}\left( p_{t} \right) /{\tilde{p}}_{d}^{i} \right) }{\alpha ^{i}{ {Var}}_{t}^{i} {\tilde{p}}_{d}^{i}}, \end{aligned}$$
(13)

where \(\alpha ^{i}\) is the risk aversion coefficient and \({ {Var}}_{t}^{i}\) is the expected variance of returns. We use the historical variance of the market price as the expectation for the variance of the return in the future and define it as

$$\begin{aligned} { {Var}}_{t}^{i} =\frac{1}{\tilde{t}^{i}}\sum _{j=1}^{\tilde{t}^{i}} {\left[ {r_{t-j}-\bar{{r}}_{t}^{i} } \right] ^{2}} , \end{aligned}$$
(14)

where \({\tilde{t}}^{i}\) is the time horizon for observation, which we define it as

$$\begin{aligned} {\tilde{t}}^{i}={\tilde{t}}\beta _{t}^{i} \end{aligned}$$
(15)

and

$$\begin{aligned} \tilde{t}^{i}={\tilde{t}}\gamma _{t}^{i} \end{aligned}$$
(16)

for the fundamentalists and the chartists, respectively. From the formula, we can see that the optimal number of stocks is independent of wealth and related to the expected return and its variance.

The price that agent i submits is restricted in the range \({\tilde{p}}_{d}^{i} \in [p_{m}^{i} ,p_{M}^{i}]\) because of budget and stock constraints. We numerically estimate the price level \(p^{{*}}\) at which the agents are satisfied with the composition of their current portfolio and will not change the number of stocks that they hold, which is given by

$$\begin{aligned} \pi ^{i}\left( p^{{*}}\right) = \frac{\ln \left( E^{i}\left( p_{t} \right) /p^{{*}}\right) }{\alpha ^{i}{ {Var}}_{t}^{i} p^{{*}}}=S_{t}^{i} . \end{aligned}$$
(17)

Because the agents are not allowed to short sell, which is to say, \(S_{t}^{i} >0\), we ensure that \(\pi ^{i}({\tilde{p}}_{d}^{i} )\ge 0\) and this equation admits a unique solution \(0<{\tilde{p}}_{d}^{i} \le E^{i}(p_{t})\). Therefore, the upper price bound is given as \(p_{M}^{i} =E^{i}(p_{t})\). Furthermore, to ensure that an agent has sufficient cash to purchase the desired stocks, the smallest value \(p_{m}^{i}\) is determined by the agent’s cash position, which is given by the condition

$$\begin{aligned} p_{m}^{i} \left( \pi ^{i}\left( p_{m}^{i}\right) -S_{t}^{i} \right) = C_{t}^{i} \;or\;\pi ^{i}\left( p_{m}^{i}\right) ={C_{t}^{i} }/{p_{m}^{i} }+S_{t}^{i} . \end{aligned}$$
(18)

During the trading days, the agents use their own expectation \(\hbox {pattern } [F,C]\) to form the expected price \(E^{i}(p_{t})\), where F and C represent the fundamentalist and the chartist strategies, respectively. Then, the agents calculate the buy/sell price \(\hbox {interval } [p_{m}^{i} ,p_{M}^{i}]\) and choose the willingness to trade price \({\tilde{p}}_{d}^{i}\) with a uniform distribution. Bids, asks and prices need to be positive and agents can submit limit orders at any price on a prespecified grid, defined by tick size \(\Delta \). We next consider how the agent’s order is determined. When the agent’s willingness price is \(\tilde{p}_{d}^{i}\), taking the condition in the limit order book into consideration, his actual quote \(p_{d}^{i}\) and trading volume are given as follows, where \(a_{t}^{q}\) and \(b_{t}^{q}\) represent the current quoted best ask and bid, respectively (Table 1).

Table 1 Summary of the trading mechanism of a typical trader i with willingness price \({\tilde{p}}_{d}^{i}\) to trade, which is chosen from the buy/sell price interval \([p_m^{i} ,p_M^{i}]\)
Full size table

After the agent issues his order at each moment \(\tau \), all existing orders in the market match with each other to form the transaction price under the rule of price priority and time priority.

2.3 Switching Trading Strategies

In our model, we assume that each agent knows the fundamental value and holds two specific individual strategies \(J_{t}^{i}\)—the fundamentalist strategy and the chartist strategy; \(J_{t}^{i} \in \{F,C\}\). The agent i can calculate the performance measure of the expectation strategy used \(J_{t}^{i}\) at day t when the closing price becomes available and can choose which strategy to use the next day. We use the switching rules as defined in Chiarella et al. (2012). However, we emphasize the prediction accuracy of the strategy \(J_{t}^{i}\), which is to say, that the performance of strategy \(J_{t}^{i}\) is better if the expected price movement direction is the same as the daily price movement direction in the market. In this case, the agent will always update the performance of expectation strategy \(J_{t}^{i}\) at the end of the trading day. Agent i computes his performance index for the expectation strategy \(J_{t}^{i}\) used according to his quote \(p_{d}^{i}\) and the daily closing price \(p_{t}\). Specifically, the performance index \(\Omega _{t}^{i,J_{t}^{i}}\) of the used expectation strategy \(J_{t}^{i} \) is computed as follows:

$$\begin{aligned} \Omega _{t}^{i,J_{t}^{i} } =\left\{ {{\begin{array}{ll} p_{t} -p_{d}^{i}, \quad &{} i\;\mathrm{is\;a \;buyer}, \\ p_{d}^{i} -p_{t}, \quad &{} i\;\mathrm{is\;a \;seller}. \\ \end{array} }} \right. \end{aligned}$$
(19)

while for the other strategy that is not used, \(\Omega _{t}^{i,J_{t}^{i}} =0\).

Then, the agents adjust an individual smoothed performance index \(U_{t}^{i,J_{t}^{i}}\) for each expectation strategy \(J_{t}^{i} \in \{F,C\}\) as

$$\begin{aligned} U_{t}^{i,J_{t}^{i} } =\eta U_{t-1}^{i,J_{t}^{i} } +\Omega _{t}^{i,J_{t}^{i}} , \end{aligned}$$
(20)

where \(\eta \) is a memory parameter. On the \(\hbox {day }t+1\), the agents choose the fundamentalist strategy with the probability \(\rho _{t+1}^{i,F}\):

$$\begin{aligned} \rho _{t+1}^{i,F} =\frac{e^{U_{t}^{i,F} }}{e^{U_{t}^{i,F} } +e^{U_{t}^{i,C}}} \end{aligned}$$
(21)

Equivalently, the probability of choosing the chartist strategy is given by

$$\begin{aligned} \rho _{t+1}^{i,C} =1-\rho _{t+1}^{i,F} . \end{aligned}$$
(22)

As we have mentioned before, the weight coefficient for each expectation rule is related with its performance, which is given as

$$\begin{aligned} \beta _{t}^{i} =\frac{e^{U_{t}^{i,F} }}{e^{U_{t}^{i,F} } +e^{U_{t}^{i,C} }},\gamma _{t}^{i} =\frac{e^{U_{t}^{i,C} }}{e^{U_{t}^{i,F} }+e^{U_{t}^{i,C} }}. \end{aligned}$$
(23)

3 Simulation Results

In this section, we discuss the effect of the different strategies on the process of price formation and analyze the various properties of the returns such as fat-tails, volatility clustering and the long-memory of volatility. Moreover, we discuss the origin of the price fluctuations. In particular, we focus on trading volume, agents’ expectations and liquidity.

In the simulations, we set the number of agents at \(N=500\) with the initial stock uniformly distributed on the interval \(S_{i}^{0} \in [10,13]\) and an amount of cash \(C_{i}^0 \in [500,500+3{\times }P_{200}^{f} ]\). We choose an initial fundamental value \(P_{0}^{f} =30\) and volatility \(\sigma _{f} =0.005\). The transaction price for the initial periods is given as \(p_{t} \in [p_{t}^{f} -0.005,p_{t}^{f} +0.005]\), where \(t\in [1,200]\). We also fix \(\sigma _\varepsilon =10^{-6},{\tilde{t}}=100,\theta _{1} =1.5,{\theta _2} =0.58,\rho _{\varepsilon } =0.1,\Delta =0.001,\alpha =0.085\) and \(\eta =0.8\).

The results below are the outcome of 1,000,000 step simulations corresponding to 2000 trading days. We have also repeated the simulations varying the parameter set within a small neighborhood of the parameters used in the model and the qualitative features are robust to such variations.

3.1 The Effect of Trading Strategy on Price and Return

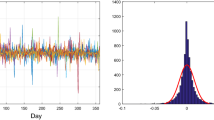
In this section, our aim is to gain some insight into the details of the price formation in the model, especially into the influence of the trading strategy on the process of price formation. Therefore, we display sample paths for the price under very different assumptions concerning the trading strategies used. Figure 1 depicts the time series in the market with fundamentalists only, setting the agents’ mean reversion speed between the interval [0.5, 1.5]. From Fig. 1a, we observe that the market price closely follows the fundamental value. The traders form the expectation for \(t+1\) according to the closing price at t and the new fundamental value, resulting in a closing price for \(t+1\) that converges to the fundamental value. Figure 1c, d show the autocorrelation function for \(r_{t}\) and \(|r_{t}|\), indicating that there is no evidence of a long memory in volatility. Therefore, the model with only fundamentalists cannot reflect the long memory phenomenon from the real market.

Fig. 1
figure 1

Representative time series for only the fundamentalists. The top figures show the relationship between price and the fundamental value (left) and the return time series (right). The bottom figures show the autocorrelation of raw (left) and absolute returns (right)

Full size image

Figure 2 displays sample paths for the price in the market with only chartists. In addition, we set the price interval over which the agents can submit orders to be [15, 45]. When the chartists occupy the market, the price will rise to the upper bound or fall to the lower bound due to the positive feedback. The chartist trading strategy, which means that traders follow the historical price tendency, will bring the persistent increase or decrease of prices.

Fig. 2
figure 2

Price and fundamental price for only the chartists. In addition, we set the price interval over which the agents can submit orders to be [15, 45]

Full size image

From the results, we can see that both the fundamentalists and the chartists need to be included in the model to characterize the real market. The fundamentalists can guarantee that the market operates around the fundamental value. The chartists bring extreme movements such as the bubble and the crash to force the price to deviate from the fundamental value and to intensify the price fluctuation, which may also cause volatility clustering and a long memory of volatility.

3.2 Stylized Facts in the Model

In this section, we discuss the price behavior in a model with fundamentalists, chartists and noise traders using the parameters previously provided, and we display the stylized facts obtained by the model’s simulation.

3.2.1 Fat-Tail and Volatility Clustering

Some representative time series are shown in Fig. 3. Figure 3a shows the time series of the market price and the fundamental value. We can see that the price is tracking the fundamental value, but deviations are persistent and sizable. For example, at \(t=500\), there is a sudden drop and at \(t=1200\), the price is fluctuating smoothly around the fundamental value. Figure 3b shows that the trading volume \(V_{t}\) fluctuates approximately 2000. The definition of the intraday price \(p_{\tau }\) in our model is consistent with the CIP model. At any time \(\tau \), the price is given by the price at which a transaction, if any, occurs. If no new transaction occurs, a proxy for the price is given by the average of the quoted ask \(a_{\tau }\) (the lowest ask listed in the book) and the quoted bid \(b_{\tau }\) (the highest bid listed in the book):

$$\begin{aligned} p_{\tau } =(a_{\tau }+b_{\tau } )/2, \end{aligned}$$
(24)

a value that we called mid-price, which is also used in Farmer et al. (2004). The price reflects the change in the best prices when a market or a limit order arrives. The daily return \(r_{t}\) and the intraday return \(r_{\tau }\) are represented in Fig. 3c, d, respectively, and exhibit episodes of large changes in price and some degree of volatility clustering.

Fig. 3
figure 3

Some representative time series with fundamentalists, chartists and noise traders. From the top, the panels show the price and the fundamental value (left) and the trading volume (right). The bottom figures show the daily returns (left) and the intraday returns (right)

Full size image

To provide a further description and a comparison of the daily returns and the intraday returns, Fig. 4 gives an example of the density of the intraday returns \(r_{\tau }\) and the daily returns \(r_{t}\). There are more extreme values in the intraday returns. We can see that the distributions tend to be non-Gaussian, sharp peaked and heavy tailed. The kurtosis for the depicted returns’ time series is 25.18 (left) and 99.68 (right), showing that these leptokurtic and fat-tailed properties are more pronounced for the intraday values, which are consistent with the empirical features. Moreover, for the longer time intervals, the tail behavior of the return distribution slowly becomes consistent with a Gaussian tail in accordance with the central limit theorem.

Fig. 4
figure 4

(Left) Daily return distribution compared with the normal distribution. (Right) Intraday return distribution compared with the normal distribution, using the same coordinate value as in the figure at left

Full size image

3.2.2 Long Memory of the Volatility

Aside from the fat-tailed price fluctuations and the volatility clustering, Fig. 5 illustrates the autocorrelation function of the returns \(r_{t}\) and the absolute returns \(|r_{t}|\), which we use as a proxy for volatility to check the long memory of the volatility. We can see the insignificant correlation between the returns for most of the time lags on the Fig. 5a, while the autocorrelation of absolute returns is slowly decaying to up to 100 lags on the figure at 5b. The linear predictability of returns is very weak, showing some form of efficiency for the market. The absolute return displays a positive autocorrelation over several days, which quantifies the fact that high-volatility events tend to cluster. Moreover, the slow decay of the autocorrelation of volatility reveals the sign of the long memory of volatility.

Fig. 5
figure 5

The autocorrelation function of the daily returns (left) and the absolute daily returns (right) as a function of lag

Full size image

To make a comparison with the CIP model, we also calculate the autocorrelation of the intraday returns. The intraday return is computed when a trader enters the market just as in the CIP model. We plot the autocorrelation function of the returns and the absolute returns of 10,000 simulations from \(t=901\) to \(t=1100\) in Fig. 6. The noise levels are computed as \(\pm 3/\sqrt{L}\) (Bouchaud and Potters 2000; Raberto et al. 2001), where L is the length of the time series. We can see that Fig. 6a also shares a common feature found in the CIP model, as the autocorrelation coefficients of returns are within the confidence band while those of the absolute returns are slowly decaying. From Fig. 6b, shown for a longer time length, we can see that autocorrelation coefficients of absolute returns decays slowly and displays pronounced peaks at multiples of 1 day (500 transactions). Furthermore, we implement the modified R/S, or rescaled range, analysis (see Lo 1991) to quantify the memory range. The modified R/S statistic of absolute returns is 0.7201, which is bigger than 0.5, showing that the series is positively correlated, while that of the raw returns is 0.4106. This result verifies the long memory property of the absolute return series. Therefore, some properties of the original model are retained at the intraday horizon in our model.

As Chiarella et al. (2012) mentioned, there must be occasional large returns and occurrences of ‘spikes,’ but not too frequent, to obtain the uncorrelated raw returns and a long memory in the absolute returns. In our model, the parameters in the expectation strategy affect the price movement indirectly because the agent’s quote depends on his expectations. Increasing the reference level of fundamentalist strategy \(\theta _{1}\) influences the statistical properties of returns because the market price quickly reverts to the fundamental value. Moreover, by decreasing the parameter of the chartist strategy \(\theta _{2}\), which is also related to the chartists’ expectations, the probability of the occasional large return tends to decrease. In addition, increasing the probability of the noise traders entering the market will frequently exaggerate the price fluctuations.

Fig. 6
figure 6

(Left) The black solid curve and the black dashed curve represent the autocorrelation function of the intraday returns and the absolute intraday returns for the time length of 100 transactions respectively. (Right) The fork and dot symbols represent the autocorrelation function of the intraday returns and the absolute intraday returns for the time length of 1000 transactions respectively

Full size image

3.2.3 Long Memory of the Spread

Moreover, we investigate the property of the market book shape. Spread is an important index of the order book and is defined as

$$\begin{aligned} s=\log p_{a} (t)-\log p_{b} (t) \end{aligned}$$
(25)

in Mike and Farmer (2008). In their empirical study, Plerou et al. (2005) find that the spread for a typical stock displays large fluctuations, and the cumulative distribution is consistent with a power law. The tail exponent is similar in value to the exponent describing the distribution of volatility. These authors’ analysis of the autocorrelation function of spread shows long-range power law correlations, similar to those previously found for volatility.

We consider temporal correlations in the bid-ask spread. Figure 7 shows the autocorrelation function of the spread from day 501 to day 1500. The figures give the autocorrelation function of the spread in the interval of transactions but at different time lengths. We find that the autocorrelation function of the spread decays slowly and displays pronounced peaks at multiples of 1 day (500 transactions), giving the same results as the empirical study of Plerou et al. (2005). Stanley’s study explains that the peaks originate from the U-shaped intraday pattern in the bid-ask spread, similar to the previously reported intraday patterns in volatility. The figure indicates the presence of long-range correlations with the feature that the autocorrelation function decays slowly.

Fig. 7
figure 7

The autocorrelation function of spread as a function of lag. We calculate the autocorrelation coefficient of spread in the interval of transactions at different time length

Full size image

In summary, this model characterizes the stylized facts in an empirical study, such as fat tails of the return distribution, volatility clustering, uncorrelated raw returns and a long memory in the absolute returns and spreads. The model can reflect the real market to some extent. Furthermore, we can see that the tail of the distribution of high frequency prices is heavier than that of low frequency prices, showing that the number of large price jumps in transactions is higher than that in days.

3.3 Origin of the Price Fluctuations

In this model, a fundamentalist uses the fundamental value information that is exogenously given while the chartist processes the information contained in the history of prices. Fundamental information entering the market will change the fundamental value, and then it is processed and incorporated into prices, influencing the agents’ expectations. The agent’s expectation affects the quote of the agent’s orders, which influences the transaction price. The fluctuations in liquidity during the day can also affect the transactions, leading to price jumps in each transaction. Therefore, in this subsection, we discuss the origin of price jumps in different time intervals.

3.3.1 Daily Fluctuations: Trading Volume or Agents’ Expectations

Firstly, we discuss the relationship between price fluctuations and trading volumes in days. Figure 8 shows the cumulative probability for volumes V conditioned on returns generated r, i.e.,

$$\begin{aligned} F(V>x|r)=\int _{x}^{\infty } {f(V|r)d V} , \end{aligned}$$
(26)

for different ranges of returns r. We sum up the orders in transactions during a day to obtain the daily trading data. Next, we sort the data by daily returns into five groups with roughly the same number of data in each group. We can see that the volume distributions for each range of \(r_{t}\) are roughly similar except for the group with the largest returns. The probability of a larger trading volume conditioned on larger returns generated is higher than that conditioned on smaller returns generated, illustrating that the trading volume is an influencing factor for generating larger price fluctuations. When the returns generated are relatively small, the distribution characteristics of the trading volumes are similar, showing that small price fluctuations are less likely to be initiated by trading volume.

Fig. 8
figure 8

The cumulative distribution of daily trading volume conditioned on returns generated. The daily returns are sorted by values into five groups with roughly the same number of data in each group. The black dashed curve represents the group with the largest returns. The other four groups, ranging from large returns to small returns, are indicated with successively lighter shades of grey

Full size image

Aside from the trading volume, the agents’ expectations for the closing price determine the orders that they submitted and the closing price is formed through a continuous double auction. So, we investigate the influence of different expectation strategies by considering the proportion of different types of traders. Figure 9 depicts the relationship between the trading strategy and the price, with grey and black lines representing the proportions of fundamentalists and chartists varying with time. The proportion value changes in the interval of [0.3, 0.75] without any observations of dramatic switching for all of the agents to either one of the expectation strategies. As traders enter the market in sequence, the performance of the two types of expectation strategies is different due to the different market conditions that the traders face. However, we can observe that the proportion of agents using a particular expectation strategy increases in a short time. A bubble or a crash appears in the market as the market fraction of chartists rises, while the price fluctuates around the fundamental value when the fundamentalists and chartists are at approximately the same proportion or when the fundamentalists dominate the market. Therefore, the traders’ expectations are closely related to the daily price changes.

Fig. 9
figure 9

Evolution of the fraction of fundamentalists (grey) and chartists (black). For convenience, the price and the fundamental value are shown as a black dashed line and a grey dashed line, respectively

Full size image

In summary, the traders’ expectations primarily influence the daily price fluctuations, and large trading volumes may bring the largest daily price fluctuations. If there are more fundamentalists in the market, they expect the price to converge to the fundamental value, issuing a quote near the fundamental value. If they submit market orders that can be transacted immediately, this behavior will push the temporal price toward the fundamental price. The limit orders submitted by the fundamentalists will offer liquidity for the other traders and will influence the price in the future. Therefore, the price will converge to the fundamental value in a market with more fundamentalists. The analysis of the conditions in a market with more chartists coincides with the analytical method described above, and the price will surge or crash.

3.3.2 Intraday Fluctuations: Order Size or Liquidity in Transactions

Next, we focus on the price fluctuations in transactions. During the trading day, a piece of news becomes available, and the market participants work out how this changes the fundamental value of the stock. The informed traders trade accordingly and the market price gradually converges to its new equilibrium value. In the empirical study, the liquidity as measured by the number of standing limit orders is always low. Because of the lack of liquidity, high frequency prices are not in equilibrium and the market needs some time to converge to the new equilibrium price. Here, we discuss the features in this process and assess whether large price fluctuations in transactions are due to large order sizes or to the presence of these large gaps.

Firstly, we discuss the relationship between the price fluctuation and the market order size. We compute the distribution of returns conditioned on the size of the incoming market orders. Just as in the CIP model, we split the orders into five groups with approximately the same number of orders in each. Figure 10 displays the conditional distribution of returns given orders of different sizes and shows that the distribution characteristics for each range of the four groups with smaller order sizes are similar, with the conditional distribution of the range for the group with the biggest order sizes being slightly fatter. Thus, for several different groups with a small order size value, there appears to be virtually the same curve independent of order size, meaning that the probability of large price fluctuations is similar. A relatively smaller order size does not play an important role in generating large price fluctuations while a large order size can cause larger price fluctuations.

Fig. 10
figure 10

Dependence of returns on order size. The figure shows the probability of an absolute return \({\vert }\hbox {r}{\vert }>\hbox {x}\) conditioned on the order size and on the fact that the price shift is nonzero. The orders are sorted by size into five groups with roughly the same number of orders in each group. Ranging from large orders to small orders, the curves are indicated with successively lighter shades of grey

Full size image

Secondly, we consider the relationship between the order book and the price series.

Figure 11 depicts the distributions of spreads and price fluctuations. The two curves are similar in shape and the probability of large spreads is bigger than that of large returns, indicating that the price fluctuation does not fully reflect the change in the spread.

Fig. 11
figure 11

The cumulative distribution of the size of the bid-ask spread (black dashed line) compared to the cumulative distribution of the returns generated by market orders (black)

Full size image

Next, we discuss the relationship between the liquidity as measured by the gap and the size of the price moves in transactions. We define the gap as it is defined in Farmer et al. (2004). The size of the first gap is denoted as the absolute difference between the best log price \(\xi _{best}\) and the log price of the next best quote \(\xi _{next}\), as

$$\begin{aligned} g=|\ln \xi _{best} -\ln \xi _{next} |. \end{aligned}$$
(27)

We assume that the behavior of the price increase is due to the execution of the best sell orders, in which condition we use

$$\begin{aligned} g_{a} =\ln a_{best} -\ln a_{next} \end{aligned}$$
(28)

to calculate the gap while the execution of the best buy orders cause the price to fall, in which condition equation

$$\begin{aligned} g_{b} =\ln b_{best} -\ln b_{next} \end{aligned}$$
(29)

is used.

In Fig. 12, we compare the distribution of the gaps to the distribution of price returns using the transaction data for the time interval [201, 2000]. The distributions are very similar, showing that the fluctuation of the gaps in the limit order book plays an important role in the price changes. Furthermore, the tail of the return distribution is slightly fatter than that of the gap distribution, indicating that large returns may be bigger than the gaps because of the large order sizes. In our model, the gaps reflect the price fluctuations, implying that newly arriving market orders can cover the volume at the best price with the resulting price changes.

Fig. 12
figure 12

The cumulative distribution of the size of the gap (black dashed) compared to the cumulative distribution of returns generated by the market orders (black). The two distributions are very similar

Full size image

In this subsection, we discuss the influential factors for large price fluctuations and find that they are related to large gaps and large order sizes. When the order size is relatively smaller, the return distributions are similar while the probability of extreme events is higher when the trading size is large. Thus, the larger transactions can cause relatively larger price fluctuations to some extent. Moreover, the distributions of the intraday gap and the returns are similar except in the tail, indicating that the gap is an influential factor.

Next, we further discuss the relationship between the gap and the return. Most large changes in the intraday price are due to fluctuations in liquidity, manifested by gaps in the filled price levels in the limit order book. Farmer et al. (2004) noted that the distribution of large price changes merely reflects the distribution of gap sizes in the order book at a microscopic time scale. In the empirical study, even for the most liquid stocks in the London Stock Exchange, the limit order book often contains large gaps that correspond to a block of adjacent price levels containing no quotes. When such a gap exists next to the best price, a new market order can remove the best quote and generate a large price change. A study of London Stock Exchange data indicates that 97 % of the trades having a nonzero price impact generate a price change equal to the first gap. As a consequence, even a small order can create a large price change, creating a very large spread. Therefore, the fluctuations of the gap sizes in the book are another key determinant of large price changes. The gap size is a measure of the liquidity available in the market as limit orders. Thus, fluctuations in liquidity—that is, in the market’s ability to absorb new market orders—are also the origin of large price changes.

4 Conclusion

In this paper, we established an order-driven market model with heterogeneous agents. We retain some points of the CIP model to allow the agent to determine his demand through the maximization of his expected utility of wealth; we also allow the agent to place orders of more than one size. We extend the original model in the following aspects. Each agent uses a fundamental-value reversion or trend following strategy and can switch individually to another strategy based on their personal performance. With the incorporation of a fitness measure to the agents’ strategy choice and expectation formation process, agents can adapt their beliefs over time and their expectations are closely related with the ongoing evolution of the market. In this way, we can investigate the role of agents’ behavioral traits on the property of the price series. The agents submit orders according to their expectations for future returns. We also add a layer of intraday activity. Therefore, we can analyze the statistical properties of the price series in both the intraday and the daily horizon.

The simulated return series exhibits many empirically observed features such as volatility clustering, fat tails and the long memory of returns and spreads, and we find that both fundamentalists and chartists should be included to reproduce theses stylized facts.

This model exhibits many empirically observed features in both the intraday and the daily horizon. In the CIP model, the price is given when a trader is chosen to enter the market, which is similar with the intraday price in our model. Our model can obtain the essential features of the CIP model such as the fat-tailed distribution of intraday returns, volatility clustering and significant slowly decaying autocorrelations of absolute returns in the intraday horizon. Furthermore, our model can reproduce more stylized facts. Besides of the features shown above, the autocorrelation coefficients of absolute intraday returns displays pronounced peaks at multiples of 1 day. The daily return series also shows volatility clustering, the fat-tailed distribution and long memory properties. And the tail of the intraday return distribution is heavier than that of daily return distribution. We also show the long memory property of daily volatility and bid-ask spread.

We also discuss the source of large price changes both in intraday trading and at the daily horizon. From the daily time series, we find that traders’ expectations are closely related to price changes, and the role of the trading volume is minor except for the largest returns. From the intraday time series, our simulation confirms the debate on different conditions. Large price changes are driven by large gaps when the price change values are relatively smaller while a larger transaction size can cause relatively larger price fluctuations.

Future research could add the interaction between the agents to the framework and analyze the influence of the information sharing process on the time series simulated by the model.