1 Introduction

A basic feature of an economical system is that markets constitute a dynamically evolving universe, comprising of individual components, which may compete or cooperate with each other, while often hidden relations are formed. Such relational knowledge can be crucial when investing in a market, where potential losses, for instance, due to a sudden fall of prices in a group of shares, affect all those interrelated components of the market. This behavior gave rise to the framework of market integration, which is of special interest to a broad range of markets, such as, foreign exchange, commodity, and derivative markets, to name a few, and appeared to be a key issue in distinct application areas, such as asset allocation and risk management.

The commonly accepted and intuitive definition of market integration states that “two financial markets are integrated when they evolve in a combined way”. In this context, several studies try to formalize this concept and provide numerical and analytic integration measures. On the other hand, the increasing demand for improved market integration measures is placing significant constraints on extracting highly accurate descriptors of the variability of the distinct markets.

In general, a high degree of integration among markets indicates that investors interested in well-diversified portfolios will concentrate on the available assets without taking into account the concrete markets. On the contrary, low integration implies entirely different pricing rules affecting the diversification process. Based on this consideration, numerous approaches have been proposed in the literature to quantify the degree of integration between distinct markets. The majority of existing measures of market integration can be distinguished in two general classes: (i) measures designed by exploiting the principles of asset pricing theory; (ii) measures implied by statistical and econometric methods.

The first class includes methods based on asset pricing models in order to verify that assets are correctly priced and assess market integration. Typical examples belonging in this class are methods based on cross-market arbitrage (Chen and Knez 1995; Balbás and Munoz 1998), or equilibrium models (Garbade and Silber 1983; Bessembinder 1992) just to name a few. However, the main disadvantage of the methods belonging to the second class is that their performance depends on the accuracy of the chosen pricing model.

On the other hand, the second class comprises of methods which quantify the degree of market integration based on the use of statistical and econometric concepts. The most commonly adopted, yet intuitive, method employs the computation of pairwise cross-correlations between the corresponding time series. In particular, Kempf and Korn (1998) suggested that the higher the correlation coefficient, the stronger the market integration is. In the same direction, several methods have been introduced recently exploiting time-varying cross-market correlations (Longin and Bruno 1995; Goetzmann et al. 2005; Baur 2006). Although all those works rely on the observation that increased integration may lead to increased correlations between markets, however, it has been shown that making inferences about market integration based on changes in cross-market or cross-asset correlations only may be hazardous (Forbes and Rigobon 2002). One reason is that correlations may increase simply due to more volatile common factors, rather than to increased market linkages.

For this purpose, alternative methods were proposed incorporating the framework of factor analysis, which rely on a factor decomposition of returns (Stock and Watson 1988). The motivation behind these methods stems from the APT literature (Burmeister and McElroy 1988), which states that markets are ruled by common factors and as comovements become stronger, specific risk and diversification potential get lower. However, a main disadvantage of factor analysis is the difficulty to interpret the factors, except for the first factor which has been interpreted as a market factor closely related to an equally weighted index (EWI) composed of all assets (Heston et al. 1995). To overcome this limitation, principal component analysis (PCA) was used as a proxy to factor analysis so as to yield a more meaningful interpretation of the extracted principal factors (Caicedo-Llano and Dionysopoulos 2008). Doing so, the first principal factor explains the average percentage of variance over all the available assets, and can be exploited to build “buy-and-hold” strategies. On the other hand, the second and third principal factors explain the degrees of volatility and dispersion, respectively, among the assets and can be employed in building “long-short” strategies.

A common characteristic of all the methods mentioned above is that the rely only on information across time. In particular, the goal of such time-domain approaches is to investigate the temporal behaviour of financial or economic variables. However, a market integration analysis should also account for the distinction between the short and long-term investor (Candelon et al. 2008). From a portfolio diversification perspective, a short-term investor is more interested in the integration of stock returns at higher frequencies, which represent short-term fluctuations, whereas a long-term investor focuses on identifying the relationship at lower frequencies, which are associated with long-term fluctuations. This motivates a natural extension of the previous time-domain methods, in order to incorporate information from the frequency domain, thus obtaining enhanced insights about the integration at the frequency level (A’Hearn and Woitek 2001; Pakko 2004).

Simultaneous analysis in both the time and frequency domain by employing efficient time-frequency representations has gained great interest in the financial practice (Gençay et al. 2002; Masset 2008). This is also impelled by the fact that different investors and agents view the markets at different time resolutions (e.g., hourly, daily, weekly or monthly), therefore, the dynamics of the potential interrelation between markets consist of distinct scales that possibly behave differently. To this end, especially wavelet decompositions (Daubechies 1992; Mallat 2008), which constitute a prominent family of time-frequency representations, have been applied on distinct economic and financial time series to decompose the data into time-scaleFootnote 1 components of varying granularity. Typical early applications include the analysis of foreign exchange data (Ramsey and Zhang 1997), the study of relationships between various economic and macroeconomic variables (Ramsey and Lampart 1998; Crowley 2007), and the investigation of the scaling properties of volatility (Gençay et al. 2001; Capobianco 2004). More recently, new integration measures were introduced, extending the methods proposed in A’Hearn and Woitek (2001) and Pakko (2004), for the characterization of international diversification benefits at different time horizons (Crowley and Lee 2005; Rua and Nunes 2009), based on the computation of cross-correlations between the wavelet spectra corresponding to the market time series.

Despite its recognized virtue, incorporation of frequency information for improving the efficiency of time-varying market integration measures has not received a great deal of attention. Motivated by the success of previous studies, where the inference accuracy about the degree of market integration is improved by exploiting time-frequency information, in this work, our goal is to advance these methods by proposing a novel market integration measure, which also exploits both temporal and frequency information. Doing so, we can assess simultaneously the degree of integration at multiple frequencies, thus accounting for both the short-run movements and long-run fluctuations, and how the integration strength evolves over time. In this way, it is also possible to distinguish between the diverse needs of short and long-term investors. The performance of our proposed measure is then evaluated in the framework of optimal portfolio construction based on the principles of the mean-variance portfolio theory. In particular, the values of our market integration measure are computed following a rolling time-frequency window approach, and are then used to estimate optimal weights adapting to the varying integration strength, so as to increase portfolio’s expected return.

We emphasize though that our proposed method should not be considered as an attempt to dominate the complex model-based techniques of mainstream econometrics, but rather it should be seen as an alternative useful analysis tool in the applied economist’s toolkit, which relies only on the available time series data without any prior assumption on the data generating model.

1.1 Contributions

The main contribution of this work concerns the design of a novel measure for quantifying the degree of integration among distinct markets. Specifically, similarly to recent methods mentioned above, our proposed method exploits both temporal and frequency information to enable adaptation not only across time, but also with respect to short and long-run fluctuations. However, our approach differs from the previous techniques in terms of two key points, which further affect the overall performance of the proposed integration measure.

The first key difference of the integration measure introduced herein, when compared with the previous works, is related to the form of the time-scale (time-frequency) information we use. In particular, in contrast to previous approaches, which employ directly the two-dimensional wavelet spectrum, that is, the magnitude of the wavelet coefficients associated with a given time series, our integration measure applies a feature extraction step to identify significant patterns in the two-dimensional (time-scale) wavelet decomposition.

For this purpose, motivated by its success in various digital image processing and computer vision tasks (Leavers 1992; Llebaria and Lamy 1999), a Hough transform (HT) (Hough 1962; Duda and Hart 1972) is applied to detect complex patterns in the corresponding wavelet decomposition. This is achieved by determining the values of specific parameters, which characterize these patterns. The use of Hough transform in our method is justified by two attributes: (i) it is very robust to outliers (points that are not on a line or a curvilinear pattern have little influence on the estimation); (ii) it detects accurately the linear (or curvilinear) structures in the time-scale domain, which correspond to specific oscillation patterns in the original time series. The first attribute is very important, since outliers in the time-scale domain, which may be due to a transient phenomenon or the occurrence of singularities in the original time series, are suppressed. This eliminates the possibility of yielding erroneous inference with respect to the degree of integration between a pair of time series by accounting for those isolated large-magnitude wavelet coefficients located near the singularities. The second attribute is also significant, since the Hough transform, when applied on the wavelet coefficients, enables a more compact and accurate extraction of the oscillation patterns that exist in the original series, which may not be possible by simply relying on the magnitudes of the wavelet coefficients. This subsequently affects the performance of a market integration measure, which aims exactly on distinguishing between short and long-run fluctuations.

The second key difference of our proposed integration measure against the previous approaches concerns the extraction of interrelations (correlations) among an ensemble of time series. More specifically, as mentioned above, making inference about market integration based on changes in cross-market correlations can be misleading (Forbes and Rigobon 2002), since correlations may increase simply due to increased volatility of the common factors, rather than to increased market linkages. Instead of adopting the typical cross-correlation between pairs of time series, as the majority of previous methods do, we employ the approach introduced in a recent study (Tzagkarakis et al. 2013). In particular, the integration strength is quantified by first extracting the main factors explaining the cross-market returns in terms of the average percentage of variance explained by the first significant principal factors. To this end, probabilistic principal component analysis (PPCA) (Tipping and Bishop 2002) is employed to extract the principal factors, yielding certain improvements when compared with the standard PCA, such as decreased sensitivity to outliers, as well as increased robustness to the presence of noise in the data. Having extracted the principal factors, the degree of integration is measured by computing the correlations between the ensemble of time series and the first principal factor, which explains the average percentage of variance over all the available series. As it will be analyzed in the subsequent sections, this PPCA-based approach for quantifying integration strength is coupled with a Hough transformed wavelet decomposition in order to extract more meaningful principal factors conveying information not only across time, but also across frequency.

To summarize, our major contribution in this work is threefold: (i) we illustrate that the detection of complex local patterns occurring in financial time series can be improved by combining appropriate time-scale decompositions with a Hough transform; (ii) we incorporate efficiently the two-dimensional patterns extracted by Hough transform to design an effective and robust market integration measure, which achieves improved adaptation across time and in multiple scales (short and long-run fluctuations); (iii) we demonstrate the enhanced performance of the proposed market integration measure, when compared against recently introduced and alternative measures, in terms of estimating optimal weights for maximizing the expected return of a constructed portfolio. An increased performance of the constructed portfolios is also revealed by applying the proposed measure on an ensemble of equity market indices, in terms of typical financial performance indicators (e.g., return, volatility, information ratio, and maximum drawdown).

The rest of the paper is organized as follows: Sect. 2 introduces the main mathematical properties of PPCA, time-scale wavelet decompositions, and the Hough transform, which constitute the building blocks of our proposed method. In Sect. 3, the proposed measure of market integration is described in detail, along with recently introduced and alternative market integration measures. A performance evaluation in the framework of portfolio optimization is carried out in Sect. 4. Finally, conclusions and further research directions are drawn in Sect. 5.

1.2 Notation

In the subsequent analysis, the following notation is employed. Let \(Y = \{y_1,\ldots ,y_N\}\) denote a time series consisting of N samples. Each sample \(y_i\in Y\) is a pair \((t_i,\,x_i)\), where \(t_i\) is a time instant and \(x_i\in {{\mathbb {R}}}\) is the observed value at time \(t_i\). Notice that the set of time instants \(T=\{t_1,\ldots ,t_N\}\) can be non-uniform (unequally spaced) in the general case. For convenience, we ignore the time instants and we work directly with the observed values \(x_i\), \(i=1,\ldots ,N\). Thus in the following, \(\mathbf{x} = [x_1,\ldots ,x_N]\) will denote the vector of time series observations, which can be also considered as a vector in the N-dimensional space, \(\mathbf{x}\in {\mathbb {R}}^N\). In the rest of the text, Y and \(\mathbf{x}\) will be used interchangeably to denote a time series. In addition, capital bold letters are reserved to denote matrices (e.g., \(\mathbf{A}\)), while lowercase bold letters are used to denote vectors.

We also emphasize that our proposed market integration measure, as well as the alternative integration measures introduced below, are designed and applied in rolling windows of length w, which slide with a step size equal to s samples across the given time series. Doing so, \(\mathbf{x}_{i,w} = [x_{i-w+1},\ldots ,x_i]\) denotes a window of length w whose ending point is the ith sample of the original time series \(\mathbf{x}\).

2 Building blocks of the proposed market integration measure

This section introduces the main mathematical tools constituting the core of our proposed market integration measure. In particular, the main properties of probabilistic principal component analysis (PPCA) are reviewed first, followed by a description of the basic characteristics of time-scale decompositions. Finally, the main attributes of the Hough transform are introduced, which is applied on the resulting time-scale representations yielding spatially compact features in an appropriate parameter space.

2.1 Extraction of probabilistic principal factors from a time series ensemble

A remarkable feature of the typical PCA is the absence of a probabilistic model for describing the observed data. A probabilistic formulation of PCA is obtained by means of a Gaussian latent-variable model, with the principal axes emerging as maximum-likelihood (ML) estimates, which can be computed via an iterative and computationally efficient expectation-maximization (EM) algorithm. Moreover, PPCA is characterized by some additional practical advantages: (a) the probabilistic model offers the potential to extend the scope of standard PCA. More specifically, multiple PPCA models can be combined as a probabilistic mixture, increasing the explanatory power of the principal factors, while also PPCA projections are robust to outliers and noise in the data; (b) along with its use as a dimensionality reduction technique, PPCA can be employed as a general Gaussian density model. The benefit of doing this is that ML estimates for the parameters associated with the covariance matrix can be computed efficiently from the data principal components.

Let \(\mathbf{X}^T=[\mathbf{x}_1,\ldots ,\mathbf{x}_M]\) be the \(N\times M\) data matrix whose columns are the observed time series. A latent-variable model aims to relate an M-dimensional observation vector (rows of \(\mathbf{X}^T\)) to a corresponding K-dimensional vector of latent (or unobserved) variables (rows of \(\mathbf{Y}^T\)) as follows,

$$\begin{aligned} \mathbf{X}^T = \mathbf{Y}^T\mathbf{W}^T + \mathbf{1}_{N\times 1}\varvec{\mu }^T + \mathbf{1}_{N\times 1}\varvec{\eta }^T \end{aligned}$$
(1)

where \(\mathbf{X}^T\) is the \(N\times M\) data matrix, \(\mathbf{Y}^T\) is the \(N\times K\) (\(K\le M\)) matrix of latent variables, \(\mathbf{W}^T\) denotes a \(K\times M\) linear mapping between the original space and the space of latent variables, \(\mathbf{1}_{N\times 1}\in {\mathbb {R}}^{N\times 1}\) is a vector of all 1’s, \(\varvec{\mu }^T\in {\mathbb {R}}^{1\times M}\) is a parameter vector permitting the model to have non-zero mean, and \(\varvec{\eta }^T\in {\mathbb {R}}^{1\times M}\) stands for the measurement error or the noise corrupting the observations.

In the subsequent analysis, \(\mathbf{x}^T\) and \(\mathbf{y}^T\) will denote an arbitrary row of the matrices \(\mathbf{X}^T\) and \(\mathbf{Y}^T\), respectively. In addition, we make the following assumptions for the parameters contained in (1):

  1. 1.

    The latent variables are independent and identically distributed (i.i.d.) Gaussians with unit variance, that is, \(\mathbf{y}^T\sim {\mathcal {N}}(\mathbf{0},\,\mathbf{I})\), where \(\mathbf{I}\) is the identity matrix. A statistical interpretation for the latent variables is that they explain correlations between the original variables.

  2. 2.

    The error (noise) model is isotropic Gaussian, that is, \(\varvec{\eta }^T\sim {\mathcal {N}}(\mathbf{0},\, \sigma ^2\mathbf{I})\). Notice also that the mth element of \(\varvec{\eta }^T\), \(\varvec{\eta }^T(m)\), represents the variability which is unique to the mth variable (column of \(\mathbf{X}^T\)).

  3. 3.

    By combining the above two assumptions with (1), a Gaussian distribution is also induced for the observations, namely, \(\mathbf{x}^T\sim {\mathcal {N}}(\varvec{\mu }^T,\,\mathbf{C})\), where the observation covariance model is given by \(\mathbf{C} = \mathbf{W}\mathbf{W}^T + \sigma ^2\mathbf{I}\).

From the above we deduce that the model parameters can be determined by ML via an iterative procedure. We also emphasize that the subspace defined by the ML estimates of the columns of \(\mathbf{W}\) will not correspond, in general, to the principal subspace of the observed data.

The isotropic Gaussian noise model (ref. (2) above), in conjunction with (1) yields that the conditional probability distribution of \(\mathbf{x}^T\) given \(\mathbf{y}^T\) is given by

$$\begin{aligned} \mathbf{x}^T|\mathbf{y}^T\sim {\mathcal {N}}(\mathbf{y}^T\mathbf{W}^T+\varvec{\mu }^T,\,\sigma ^2\mathbf{I}). \end{aligned}$$
(2)

Then, the associated log-likelihood function is expressed as follows,

$$\begin{aligned} {\mathcal {L}} = -\frac{N}{2}\Bigl (M\,\ln (2\pi ) + \ln (|\mathbf{C}|) + \mathrm {tr}\bigl (\mathbf{C}^{-1}\mathbf{\Sigma }_\mathbf{X}\bigr )\Bigr ), \end{aligned}$$
(3)

where \(|\mathbf{A}|\) and \(\mathrm {tr}(\mathbf{A})\) denote the determinant and the trace, respectively, of a matrix \(\mathbf{A}\), and

$$\begin{aligned} \mathbf{\Sigma }_\mathbf{X} = \frac{1}{N-1}\sum _{n=1}^N (\mathbf{x}_n^T-\varvec{\mu }^T)^T(\mathbf{x}_n^T-\varvec{\mu }^T), \end{aligned}$$
(4)

with \(\mathbf{x}_n^T\) denoting the nth observation (row of \(\mathbf{X}^T\)). Notice that the ML estimate for \(\varvec{\mu }^T\) is given by the sample mean of the data, in which case \(\mathbf{\Sigma }_\mathbf{X}\) is exactly the sample covariance matrix of the observations. Finally, estimates for \(\mathbf{W}\) and \(\sigma ^2\) are obtained by iterative maximization of \({\mathcal {L}}\) via an EM approach, resulting in

$$\begin{aligned} \sigma ^2_{\mathrm {ML}}= & {} \frac{1}{M-K}\sum _{j=K+1}^M\lambda _j \end{aligned}$$
(5)
$$\begin{aligned} \mathbf{W}_{\mathrm {ML}}= & {} \mathbf{E}_K\bigl ({\varvec{\Lambda }}_K - \sigma ^2_{\mathrm {ML}}\mathbf{I}\bigr )^{1/2}\mathbf{R}, \end{aligned}$$
(6)

where the K columns of \(\mathbf{E}_K\in {\mathbb {R}}^{M\times K}\) are the principal eigenvectors of \(\mathbf{\Sigma }_\mathbf{X}\), with corresponding eigenvalues \(\{\lambda _j\}_{j=1}^K\) constituting the diagonal matrix \({\varvec{\Lambda }}_K\in {\mathbb {R}}^{K\times K}\), and \(\mathbf{R}\) is an arbitrary \(K\times K\) orthogonal rotation matrix. In practice, \(\mathbf{R}\) could be ignored by simply setting \(\mathbf{R}=\mathbf{I}\). Finally, the \(N\times K\) matrix \(\mathbf{P}\), whose columns are the probabilistic principal factors of a given time series ensemble, is simply obtained by projecting the data matrix on the probabilistic principal components, that is,

$$\begin{aligned} \mathbf{P} = \mathbf{X}^T \mathbf{W}_{\mathrm {ML}}. \end{aligned}$$
(7)

2.2 Time-scale wavelet decompositions of time series

Several distinct transformations were introduced during the last decades for the analysis of signals, such as time series, in multiple scales (or frequencies). Typical examples include the wavelet transform (Mallat 2008) and the ridgelet transform (Do and Vetterli 2003), with the choice of the most appropriate representation depending on the specific characteristics of the given signal, as well as of the structures we are interested in identifying. For instance, wavelets are widely used to distinguish the smooth parts and detect singularities in one-dimensional (1-D) and two-dimensional (2-D) signals, while ridgelets are efficient in extracting curvilinear structures in 2-D signals.

In the following, we focus on the wavelet transform, given its wide and successful applicability in numerous distinct types of signals. Wavelet-based methods are among the most important ones in statistics, in areas such as regression, density and function estimation, factor analysis, modeling and forecasting of time series, in assessing self-similarity, as well as in characterizing spatial statistics.

The first theoretical results in wavelets had been concerned with the continuous wavelet transform (CWT) of functions in the early ’80s. CWT is used to divide a continuous-time function into wavelets providing a very redundant (2-D representation of an 1-D signal), but also very finely detailed description of a signal in terms of both time and frequency. Besides, CWT is particularly efficient in tackling problems involving signal identification and detection of hidden transients, that is, hard to detect, short-lived elements of a signal. Unlike Fourier transform, the CWT possesses the ability to construct a time-scale representation of a signal that offers increased time and frequency localization. The CWT of a continuous, square-integrable function x(t) at a scale \(a>0\) and translation \(b\in {\mathbb {R}}\) is given by the following integral

$$\begin{aligned} C_x(a,\,b) = \frac{1}{\sqrt{a}}\int _{-\infty }^{\infty }x(t)\bar{\psi } \Bigl (\frac{t-b}{a}\Bigr )\, \mathrm {d}t, \end{aligned}$$
(8)

where \(\psi (t)\) is a continuous function in both the time and scale (equivalently, frequency) domain, called the mother wavelet, and \(\bar{\psi }(t)\) denotes its complex conjugate. A wavelet associated with a time-scale decomposition is defined by two functions, namely, the wavelet function \(\psi (t)\), which is responsible to extract the localized details, and the scaling function \(\varphi (t)\), which is primarily responsible for improving the coverage of the wavelet spectrum. Typical examples of widely used wavelets include the Haar and Morlet wavelets, as well as the Daubechies’ (dbN) family, where the choice of the most suitable wavelet depends on the specific signal characteristics (Mallat 2008).

Fig. 1
figure 1

Difference of the interpretability between the DWT and CWT of a financial time series, analyzed using the db8 wavelet in 10 levels for the DWT or, equivalently, \(2^{10}=1024\) scales for the CWT

Full size image

The scale factor a either dilates or compresses a given time series. When the scale factor is relatively low, the time series is more contracted, which results in a more detailed representation. However, the drawback is that a low scale factor does not cover the entire duration of the time series. On the other hand, when the scale factor is high, the time series is stretched out, which means that the resulting representation will be less detailed, while it covers a larger duration of the time series. In other words,

  • low scale \(a \Rightarrow \) compressed wavelet \(\Rightarrow \) rapidly changing details \(\Rightarrow \) high frequency content,

  • high scale \(a \Rightarrow \) stretched wavelet \(\Rightarrow \) slowly changing, coarse features \(\Rightarrow \) low frequency content.

A feature that wavelets are very good at detecting is the presence of discontinuities, or singularities. More specifically, smooth time series features produce relatively large-magnitude wavelet coefficients at scales where the oscillation in the wavelet correlates best with the time series feature. On the other hand, abrupt transitions in the time series result in wavelet coefficients with large absolute values. Several signal processing tasks also employ the percentage of energy (or, equivalently, of squared magnitude) associated with each wavelet coefficient, the so-called scalogram, which is defined as follows

$$\begin{aligned} S_x(a,\,b) = \frac{\left| C_x(a,\,b)\right| ^2}{\sum _{a'}\sum _{b'}\left| C_x(a',\,b')\right| ^2},\quad \, a,\,a'\in [1,\,a_{\mathrm {max}}], b,\,b'\in [b_{\mathrm {min}},\,b_{\mathrm {max}}]. \end{aligned}$$
(9)

On the other hand, any processing task performed on real data should be carried out on a discrete time series, that is, on a time series that has been measured at discrete time. However, what distinguishes the CWT from its discrete analogue, the discrete wavelet transform (DWT), is the set of scales and positions (translations) at which it operates. In particular, unlike the DWT, the CWT can operate at every scale, from that of the original time series up to some maximum predetermined scale, which is set by trading-off the requirements for detailed analysis with the available computational resources. The CWT is also continuous in terms of shifting, namely, during computation, the analyzing wavelet is shifted smoothly over the full time domain of the analyzed time series.

Despite the decreased computational complexity of DWT, since the decomposition is performed in a set of usually dyadic scales and translations, it results in a less detailed visual interpretability when compared with CWT. Based on that, CWT is adopted in our proposed market integration measure. To illustrate the difference of the interpretability between the CWT and DWT, Fig. 1 shows the absolute wavelet coefficients corresponding to the DWT (upper plot) and CWT (bottom plot) of a financial time series from our dataset, analyzed using the db8 wavelet in 10 levels for the DWT or, equivalently, \(2^{10}=1024\) scales for the CWT.

2.3 Hough transform of time-scale decompositions

In the computed scalograms associated with CWT as described above, we are interested in extracting and describing the localized features expressing the energy concentration in the time-scale domain. In particular, we would like to represent the energy distribution over the time-scale domain in a more compact fashion, so as to simplify its further processing towards the design of an efficient market integration measure. The key idea is that such features can be represented as distributed patterns of peaks in a suitable parameter space.

The Hough transform (HT) (Duda and Hart 1972) is a technique, which can be used to isolate patterns of distinct shapes within a 2-D signal (i.e., image). In practice, we have to deal with complex patterns for which descriptions through analytic expressions are unavailable. For this purpose, the generalized HT (Ballard 1981) raised as an extension of the standard HT, enabling the detection of patterns with more complicated non-regular shapes. In our proposed approach, we exploit the power of HT to accumulate the energy in the time-scale domain, as expressed by the patterns in the scalograms of the given financial time series, as well as of their dominant probabilistic principal factor.

The use of (generalized) HT in our case is justified by two major attributes: (i) HT is very robust to outliers, that is, points that do not lie on a line or a curvilinear pattern have little influence on the estimation; (ii) HT detects accurately the linear (or curvilinear) structures in the time-scale domain, which correspond to specific oscillation patterns in the original time series. The first attribute is very important, since outliers in the time-scale domain, which may be due to a transient phenomenon or the occurrence of singularities in the original time series, are suppressed. This eliminates the possibility of yielding an erroneous inference with respect to the degree of integration between a pair of time series by accounting for those isolated large-magnitude wavelet coefficients located near the singularities. The second attribute is also significant, since the Hough transform, when applied on the scalogram, enables a more compact and accurate extraction of the oscillation patterns that exist in the original series, which may not be possible by simply relying on the magnitudes of the wavelet coefficients. This subsequently affects the performance of a market integration measure, which aims exactly on distinguishing between short and long-run fluctuations.

The generalized HT defines a set of parameters for an arbitrary shape, as follows,

$$\begin{aligned} \mathbf{a} = \{ \mathbf{o},\,\mathbf{s},\,\theta \}, \end{aligned}$$
(10)

where \(\mathbf{o} = (o_1,\,o_2)\) is a reference origin for the shape, \(\mathbf{s} = (s_1,\,s_2)\) denotes two orthogonal scale factors, and \(\theta \) is the orientation. For convenience, we overview the main principles of the standard HT, which are also the basis for its generalized counterpart, and we omit the details of the generalized extension for the interested reader (Ballard 1981).

In the following, we consider that the pixels, that is, the scalogram coefficients, whose magnitude exceeds some threshold are defined as edge pixels. Then, if a given pixel lies on a curve we are interested in estimating the locus of the parameters specifying this curve. At the core of HT is the following interesting result about this locus in the parameter space: if a set of edge pixels in an image (the scalograms in our case) are arranged on a curve with parameters \(\{ \mathbf{o},\,\mathbf{s},\,\theta \}\), the resultant loci of parameters for each such pixel will pass through the same point \(\{ \mathbf{o},\,\mathbf{s},\,\theta \}\) in the parameter space.

First, the reference origin \(\mathbf{o}\) is described in terms of a table of possible edge pixel orientations. The computation of the additional parameters \(\mathbf{s}\) and \(\theta \) is then accomplished by transformations applied on this table. Notice also that there is a correspondence between the choice of parameters \(\mathbf{a}\) and the analytic forms to which the standard HT is applied. For instance, for lines and circles this correspondence is given by

  • line: \(\{s,\,\theta \}\longrightarrow x\cos \theta +y\sin \theta = s\)

  • circle: \(\{\mathbf{o},\,s\}\longrightarrow (x-o_1)^2 + (y-o_2)^2 = s^2\)

The generalization of HT to arbitrary shapes is performed by using directional information, which improves greatly its accuracy. An accumulator array \(\mathbf{A}(\mathbf{a})\) is formed, whose entries are incremented for those \(\mathbf{a}\) such that \(\mathbf{a} = \mathbf{p}+\varvec{\epsilon }\), where \(\mathbf{p}\) is an edge pixel, and \(\varvec{\epsilon } = \mathbf{o}-\mathbf{p}_b\) is the difference between a reference point \(\mathbf{o}\) and a boundary point \(\mathbf{p}_b\). For each boundary point \(\mathbf{p}_b\) we also compute the gradient direction \(\varphi (\mathbf{p}_b)\) and we store \(\varvec{\epsilon }\) as a function of \(\varphi \). Finally, for each edge pixel \(\mathbf{p}\) in the scalogram we increment all the corresponding points \(\mathbf{p} + \varvec{\epsilon }\) in the accumulator array \(\mathbf{A}\). Doing so, local maxima in \(\mathbf{A}\) correspond to potential instances of a shape. We emphasize here that the resolution accuracy of both the standard and the generalized HT depends on the quantization level of the parameter space. In our case, we try to achieve a trade-off between an increased resolution of the obtained HT representations and the associated computational complexity by setting the quantization steps for the parameters neither to a very low nor to a very high value.

Fig. 2
figure 2

Scalogram and corresponding Hough transform for a financial time series (\(\rho \) and \(\theta \) are discretized in 512 bins, db8 is used)

Full size image

Figure 2 shows the Hough transform of the scalogram corresponding to the CWT shown in Fig. 1. We employ an \((\rho ,\,\theta )\) parameter space to represent the energy distribution, where \(\rho \ge 0\), \(\theta \in [0,\,2\pi ]\) denote the radius and angle, respectively. For both parameters, their range of values is discretized in 512 bins. We observe that the generalized Hough accumulator, which coincides with the standard Hough accumulator in this test case, presents a more compact representation of the energy distribution in the \((\rho ,\,\theta )\) space, when compared with the associated scalogram. This behavior enables a more concrete comparison between the Hough transformed scalograms, and subsequently, the design of a more efficient market integration measure, as we describe in the following sections. Notice also that, in our current implementation, the outputs of the standard and generalized HT coincide. However, without loss of generality, we keep using both terms (HT and generalized HT) in the rest of the text.

3 Design of time-frequency adapted market integration measure

As mentioned in Sect. 1, until recently, the most commonly adopted approach to extract correlations and quantify the integration strength among distinct markets was by means of the typical (squared) correlation coefficient computed for their corresponding time series. However, the main drawback of those approaches is that they rely solely on characteristics of the time series which vary only across time. Nevertheless, incorporating additional information related to the frequency content of the time series could provide enhanced insight for their inherent structures.

On the other hand, an efficient market integration analysis should account for the distinction between the short and long-term investors, who are focusing on distinct regions in the frequency domain. From a portfolio diversification perspective, a short-term investor is more interested in the integration of stock returns at higher frequencies, which represent short-term fluctuations, whereas a long-term investor focuses on identifying the relationship at lower frequencies, which are associated with long-term fluctuations. This requirement motivates a natural extension of the previous time-domain methods, in order to incorporate information from the frequency domain, thus obtaining enhanced insights about the joint integration at both the temporal and frequency levels.

In this section, we propose a novel market integration measure based on the enhanced capabilities of Hough transformed scalograms in localizing the energy distribution, which is related to the oscillating patterns across time and multiple frequencies in the original time series. More specifically, our proposed method quantifies the degree of integration between distinct markets by employing the time-scale energy distribution of a given ensemble of time series and their corresponding dominant probabilistic principal factor, \(\mathbf{p}_1\). In particular, the problem of computing the integration strength is reduced to measuring the statistical similarity between the associated Hough transformed scalograms of the CWT representations of the given time series ensemble and \(\mathbf{p}_1\). The improved performance of the proposed market integration measure is revealed by comparing against recently introduced and alternative integration measures, which we also propose in this work based on 1-D scale-by-scale similarity measurement. In the rest of the paper, a similarity function will be denoted by \(\mathcal {S}(\cdot ,\cdot )\).

3.1 Proposed time-frequency adapted market integration measure

In the following, let \(\mathbf{X}^T = [\mathbf{x}_1,\ldots ,\mathbf{x}_M]\) be the \(N\times M\) data matrix whose columns are the observed time series. First, in order to achieve adaptation across time, our proposed market integration measure is applied on a rolling window of length w, which slides with a step size equal to s samples across the given time series. Doing so, let \(\mathbf{X}_{i,w}^T = [\mathbf{x}_{1;i,w},\ldots ,\mathbf{x}_{M;i,w}]\) be the \(w\times M\) matrix whose columns are the current rolling windows associated with the time series, where the ending points are the ith samples of the original time series \(\mathbf{x}_m\), \(m=1,\ldots ,M\).

Moreover, in order to emphasize the short-run movements of the data, the relative change between consecutive time instants is employed. This can be measured by computing the returns series of the original time series, which is defined as the first difference of the natural logarithm (dlog). Specifically, the ith sample of the returns series, \(\mathbf{r}\in {\mathbb {R}}^{N-1}\), is given by

$$\begin{aligned} \mathbf{r}_{m;i} = \log (\mathbf{x}_{m;i}) - \log (\mathbf{x}_{m;i-1}), \quad m = 1,\ldots ,M,\, i = 2,\ldots ,N, \end{aligned}$$
(11)

where \(\mathbf{x}_{m;i}\) is the value of the mth market variable at the end of time (e.g., day) i, and \(\mathbf{r}_{m;i}\) defines the continuously compounded return during time i (between the end of time \(i-1\) and the end of time i). It is also noted that, for numerical reasons, we set \(\mathbf{r}_{m;1} = \mathtt NaN \), since for \(i = 1\) the sample \(\mathbf{x}_{m;i-1}\) does not exist. Besides, to overcome the limitation of significantly different variances or expression in different units (e.g., different currencies) between the distinct time series, a further normalization of the current (dlog) windows, \(\mathbf{r}_{m;i,w}\) (\(m=1,\ldots ,M\)), to zero mean and unit variance is performed, namely,

$$\begin{aligned} \hat{\mathbf{r}}_{m;i,w} = \frac{\mathbf{r}_{m;i,w}-\mu _{m;i,w}}{\sigma _{m;i,w}}, \quad m = 1, \ldots , M, \end{aligned}$$
(12)

where \(\mu _{m;i,w}\) and \(\sigma _{m;i,w}\) are the mean and standard deviation, respectively, of the current window of the mth returns series. Let \(\hat{\mathbf{R}}_{i,w}^T = [\hat{\mathbf{r}}_{1;i,w},\ldots ,\hat{\mathbf{r}}_{M;i,w}]\) be the \(w\times M\) matrix whose columns are the normalized windows of the returns series.

In contrast to Caicedo-Llano and Dionysopoulos (2008), Caicedo-Llano and Bruneau (2009), where the dominant principal factor is computed via the standard PCA, here we adopt the PPCA to extract the dominant probabilistic principal factor, \(\mathbf{p}_{1,i,w}\), for the ensemble of the current windows \(\hat{\mathbf{R}}_{i,w}^T\). As mentioned in Sect. 2.1, the probabilistic principal factors are characterized by an increased robustness to the presence of outliers and noise in the data, which is inherent to any real dataset, as well as by an increased explanatory power of the variance described by the first few significant probabilistic principal factors.

The next step towards the design of our proposed market integration measure involves the computation of the energy distribution in the time-scale domain. For this purpose, a CWT is applied first on each window \(\hat{\mathbf{r}}_{m;i,w}\) (\(m=1,\ldots ,M\)), as well as on the corresponding dominant probabilistic principal factor \(\mathbf{p}_{1,i,w}\) using the same parameter setting (that is, number of decomposition scales, and analyzing wavelet). Based on the computed CWTs, the associated energy distributions for the current windows and the dominant principal factor are expressed via the corresponding scalograms, namely, \(S_{\hat{\mathbf{r}}_{m;i,w}}\) (\(m=1,\ldots ,M\)) and \(S_{\mathbf{p}_{1,i,w}}\).

Then, the Hough transform is applied on the scalograms as a final step yielding a more compact representation of the energy distribution in an appropriate parameter space \((\rho ,\,\theta )\). In order to account for the contribution of all returns series (that is, of all the markets), the average Hough transform over all the returns series in the current window is computed as follows,

$$\begin{aligned} \mathbf{H}_{\text {avg};i,w} = \frac{1}{M}\sum _{m=1}^M \mathcal {H}\left( S_{\hat{\mathbf{r}}_{m;i,w}}\right) , \end{aligned}$$
(13)

where \(\mathcal {H}(\cdot )\) denotes the Hough transform operator, which maps the scalogram \(S_{\hat{\mathbf{r}}_{m;i,w}}\) to a \(P_{\text {bins}} \times \Theta _{\text {bins}}\) matrix, with \(P_{\text {bins}}\), \(\Theta _{\text {bins}}\) denoting the number of discretization bins for the \(\rho \) and \(\theta \) parameter, respectively. Let also \(\mathbf{H}_{\mathbf{p}_{1,i,w}}=\mathcal {H}\left( \mathbf{p}_{1,i,w}\right) \) denote the corresponding Hough transform of the scalogram associated with the dominant probabilistic principal factor.

The statistical similarity between \(\mathbf{H}_{\text {avg};i,w}\) and \(\mathbf{H}_{\mathbf{p}_{1,i,w}}\) is defined based on a 2-D correlation analysis, which increases the frequency resolution by spreading overlapping spectral peaks over two dimensions, resulting in a simplified, yet enhanced, interpretation of the individual 1-D spectra. Specifically, our proposed time-frequency adapted market integration measure at time instant i is defined in terms of the 2-D correlation coefficient between the average Hough transform of the windowed returns series and the Hough transform of the associated dominant probabilistic principal factor, as follows,

$$\begin{aligned} G_{\text {corr2d},i} = \text {corr2}\left( \mathbf{H}_{\text {avg};i,w},\,\mathbf{H}_{\mathbf{p}_{1,i,w}}\right) , \quad i=1,\ldots ,N, \end{aligned}$$
(14)

where

$$\begin{aligned} \text {corr2}\left( \mathbf{A},\,\mathbf{B}\right) =\frac{\sum _{\rho } \sum _{\theta } \left( \mathbf{A}(\rho ,\theta )-\overline{\mathbf{A}}\right) \left( \mathbf{B}(\rho ,\theta )-\overline{\mathbf{B}}\right) }{\sqrt{\left( \sum _{\rho } \sum _{\theta } \left( \mathbf{A}(\rho ,\theta )-\overline{\mathbf{A}}\right) ^2\right) \left( \sum _{\rho } \sum _{\theta } \left( \mathbf{B}(\rho ,\theta )-\overline{\mathbf{B}}\right) ^2\right) }}, \end{aligned}$$
(15)

denotes the 2-D correlation coefficient between two matrices \(\mathbf{A}\), \(\mathbf{B}\), with \(\overline{\mathbf{A}}\) and \(\overline{\mathbf{B}}\) being the overall mean of \(\mathbf{A}\) and \(\mathbf{B}\), respectively. Figure 3 shows the flow diagram for the design of our proposed market integration measure.

Fig. 3
figure 3

Flow diagram for the design of the proposed time-frequency adapted market integration measure

Full size image

3.2 Alternative market integration measures

In this section, we introduce recently proposed market integration measures, along with some alternative approaches by considering the CWT representation of a given time series in a (1-D) scale-by-scale fashion. In particular, each row of the associated scalogram can be represented in several distinct ways, for instance, (i) as a discrete-time series, (ii) by means of a probability density function (or a histogram), or (iii) via a model fitted on the data, whose parameters are estimated from the observations (transform coefficients). Based on that, geometric (norm-based) or probabilistic similarity functions can be exploited to define market integration measures, depending on the selected representation of the 1-D scalogram coefficients for each scale.

In the following, given a time series \(\mathbf{x}\in {\mathbb {R}}^N\), we assume that, for the CWT, the scale varies in \(a\in [1,\,a_{\mathrm {max}}]\), while the translation parameter b spans the whole discrete-time range, that is, \(b\in [1,\,N]\). In the previous section, we defined \(\hat{\mathbf{R}}_{i,w}^T = [\hat{\mathbf{r}}_{1;i,w},\ldots ,\hat{\mathbf{r}}_{M;i,w}]\) to be the \(w\times M\) matrix whose columns are the normalized windows of the returns series. As defined above, let \(S_{\hat{\mathbf{r}}_{m;i,w}}\) (\(m=1,\ldots ,M\), \(i=1,\ldots ,N\)) be the scalogram of the mth column of \(\hat{\mathbf{R}}_{i,w}^T\), while \(S_{\hat{\mathbf{r}}_{m;i,w,a}}\) (\(a\in [1,\,a_{\mathrm {max}}]\)) stands for the vector of scalogram coefficients of the mth returns series window at scale a. Accordingly, we define \(S_{\mathbf{p}_{1,i,w}}\) and \(S_{\mathbf{p}_{1,i,w,a}}\) to be the scalogram and the vector of scalogram coefficients at scale a, respectively, for the associated first probabilistic principal factor obtained by performing PPCA on \(\hat{\mathbf{R}}_{i,w}^T\).

To verify the enhanced performance of our proposed market integration measure, we compare it against the following alternative integration measures, which are defined either in the time domain or in the time-frequency domain. For convenience, we use the acronyms “TD” and “TFD” to indicate whether a given measure is applied in the time or the time-frequency domain, respectively.

  1. 1.

    PPCA-based Correlation Coefficient (Corr-TD) In order to illustrate the superiority of a time-frequency adaptive integration measure, we compare against the time-domain approach introduced in Tzagkarakis et al. (2013). More specifically, the integration measure proposed therein is defined as the average squared correlation coefficient between each windowed returns series and their first probabilistic principal factor, as follows,

    $$\begin{aligned} G_{\text {Corr-TD},i} = \frac{1}{M}\sum _{m=1}^M \text {corr}^2\left( \hat{\mathbf{r}}_{m;i,w},\mathbf{p}_{1,i,w}\right) , \end{aligned}$$
    (16)

    where \(\text {corr}^2\left( \cdot ,\cdot \right) \) denotes the squared sample (Pearson) correlation coefficient between two vectors. This measure improved the one introduced in Caicedo-Llano and Dionysopoulos (2008) by substituting the typical PCA with its probabilistic counterpart, while both were shown to outperform previous measures based on the computation of correlations between pairs of returns series directly.

  2. 2.

    Cosine Similarity (Cos-TFD) Cosine similarity is a measure of similarity between two vectors of an inner product space that measures the cosine of the angle between them. It is thus an assessment of angular (orientation) similarity and not magnitude. We use the cosine similarity function to define an integration measure in the time-frequency domain, which is applied on the returns series’ and the first probabilistic principal factor’s scalograms in a scale-by-scale fashion. The scale-by-scale cosine similarity is given by

    $$\begin{aligned} \mathcal {S}_\text {Cos-TFD}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}) = \frac{\sum _{t=1}^w S_{\hat{\mathbf{r}}_{m;i,w,a,t}}\,S_{\mathbf{p}_{1,i,w,a,t}}}{\sqrt{\sum _{t=1}^w S_{\hat{\mathbf{r}}_{m;i,w,a,t}}^2}\sqrt{\sum _{t=1}^w S_{\mathbf{p}_{1,i,w,a,t}}^2}}. \end{aligned}$$
    (17)

    Based on this similarity, the associated market integration measure is defined as follows,

    $$\begin{aligned} G_{\text {Cos-TFD},i} = \frac{1}{M}\frac{1}{a_{\mathrm {max}}} \sum _{m=1}^M \sum _{a=1}^{a_{\mathrm {max}}} \mathcal {S}_\text {Cos-TFD}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}), \end{aligned}$$
    (18)

    which is the average cosine similarity over all returns series and scales.

  3. 3.

    Peak-to-Correlation Energy (PCE-TFD) In the frequency (energy) domain, an alternative criterion is defined to extract pairwise correlations. Specifically, the peak-to-correlation energy (Kumar and Hassebrook 1990) is employed, which is defined as the energy of the peak correlation normalized to the total energy of the correlation plane:

    $$\begin{aligned}&\mathcal {S}_{\text {PCE-TFD}}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}) \nonumber \\&\quad = \frac{\sum _{t=1}^w S_{\hat{\mathbf{r}}_{m;i,w,a,t}}\,S_{\mathbf{p}_{1,i,w,a,t}}}{\sum _{t=1}^w S_{\hat{\mathbf{r}}_{m;i,w,a,t}}^2 + \sum _{t=1}^w S_{\mathbf{p}_{1,i,w,a,t}}^2 - \sum _{t=1}^w S_{\hat{\mathbf{r}}_{m;i,w,a,t}}\,S_{\mathbf{p}_{1,i,w,a,t}}}. \end{aligned}$$
    (19)

    In practice, \(\mathcal {S}_{\text {PCE-TFD}}\) measures similarity by measuring the sharpness of the peak in the cross-correlation plane defined between the scalograms of the returns series and the first probabilistic principal factor in a scale-by-scale fashion. Then, a market integration measure is defined as the average PCE over all returns series and scales as follows,

    $$\begin{aligned} G_{\text {PCE-TFD},i} = \frac{1}{M}\frac{1}{a_{\mathrm {max}}} \sum _{m=1}^M \sum _{a=1}^{a_{\mathrm {max}}} \mathcal {S}_\text {PCE-TFD}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}). \end{aligned}$$
    (20)
  4. 4.

    Spearman Rank Correlation Coefficient (SRCC-TFD) The Spearman rank correlation coefficient is defined as the Pearson correlation coefficient between the corresponding ranked variables (Myers et al. 2010), and assesses whether the relation between two random variables (time-scale coefficients in our case) can be described using a monotonic function:

    $$\begin{aligned}&\mathcal {S}_{\text {SRCC-TFD}}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}) \nonumber \\&\quad = \frac{\sum _{t=1}^w \left( S_{\hat{\mathbf{r}}^{r}_{m;i,w,a,t}} - \bar{S}_{\hat{\mathbf{r}}^{r}_{m;i,w,a}}\right) \left( S_{\mathbf{p}^{r}_{1,i,w,a,t}} - \bar{S}_{\mathbf{p}^{r}_{1,i,w,a}}\right) }{\sqrt{\sum _{t=1}^w \left( S_{\hat{\mathbf{r}}^{r}_{m;i,w,a,t}} - \bar{S}_{\hat{\mathbf{r}}^{r}_{m;i,w,a}}\right) ^2 \sum _{t=1}^w \left( S_{\mathbf{p}^{r}_{1,i,w,a,t}} - \bar{S}_{\mathbf{p}^{r}_{1,i,w,a}}\right) ^2}}, \end{aligned}$$
    (21)

    where \(S_{\hat{\mathbf{r}}^{r}_{m;i,w,a}}\) and \(S_{\mathbf{p}^{r}_{1,i,w,a}}\) denote the scalogram coefficients at scale a, for \(\hat{\mathbf{r}}_{m;i,w}\) and \(\mathbf{p}_{1,i,w}\), converted to ranks, while \(\bar{S}_{\hat{\mathbf{r}}^{r}_{m;i,w,a}}\) and \(\bar{S}_{\mathbf{p}^{r}_{1,i,w,a}}\) denote the corresponding mean values at scale a. \(\mathcal {S}_{\text {SRCC-TFD}}\) is a valid similarity function for defining a market integration measure, since its sign indicates the direction of association between \(S_{\hat{\mathbf{r}}_{m;i,w,a}}\) (the independent variable) and \(S_{\mathbf{p}_{1,i,w,a}}\) (the dependent variable). If \(S_{\mathbf{p}_{1,i,w,a}}\) tends to increase when \(S_{\hat{\mathbf{r}}_{m;i,w,a}}\) increases, the Spearman correlation coefficient is positive. If \(S_{\mathbf{p}_{1,i,w,a}}\) tends to decrease when \(S_{\hat{\mathbf{r}}_{m;i,w,a}}\) increases, the Spearman correlation coefficient is negative. A Spearman correlation equal to zero indicates that there is no tendency for \(S_{\mathbf{p}_{1,i,w,a}}\) to either increase or decrease when \(S_{\hat{\mathbf{r}}_{m;i,w,a}}\) increases. The associated market integration measure is defined as the average Spearman rank correlation coefficient over all returns series and scales, as follows,

    $$\begin{aligned} G_{\text {SRCC-TFD},i} = \frac{1}{M}\frac{1}{a_{\mathrm {max}}} \sum _{m=1}^M \sum _{a=1}^{a_{\mathrm {max}}} \mathcal {S}_\text {SRCC-TFD}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}). \end{aligned}$$
    (22)
  5. 5.

    Ultrametric Similarity (Ultra-TFD) The standard correlation coefficient varies in the interval \([-1,1]\), thus we rise to the power of two (ref. measure (1) above) to avoid negative values, so as to be a valid candidate for designing an integration measure. Another way to do so is to transform the correlation function in order to fulfill the distance axioms, resulting in the so-called ultrametric distance,

    $$\begin{aligned} \text {UltraDist}(X,Y) = \sqrt{\frac{1}{2}\left( 1-\text {corr}\left( X,Y\right) \right) }, \end{aligned}$$
    (23)

    which maps the linear space of the time series of length N onto the interval [0, 1]. Towards designing a market integration measure in the time-frequency domain, the distance function (23) can be re-written as a similarity function, as follows,

    $$\begin{aligned} \mathcal {S}_{\text {Ultra-TFD}}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}) = 1 - \sqrt{\frac{1}{2}\left( 1-\text {corr}\left( S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}\right) \right) }. \end{aligned}$$
    (24)

    Based on the above similarity function, a market integration measure is defined as the average ultrametric similarity over all returns series and scales, as follows,

    $$\begin{aligned} G_{\text {Ultra-TFD},i} = \frac{1}{M}\frac{1}{a_{\mathrm {max}}} \sum _{m=1}^M \sum _{a=1}^{a_{\mathrm {max}}} \mathcal {S}_\text {Ultra-TFD}(S_{\hat{\mathbf{r}}_{m;i,w,a}},S_{\mathbf{p}_{1,i,w,a}}). \end{aligned}$$
    (25)
  6. 6.

    2-D Correlation Coefficient between Scalograms (ScaloCorr2-TFD) To verify the efficiency of the Hough transform in extracting the effective time-frequency localized patterns of a given time series, our proposed market integration measure is compared with a measure defined on the scalograms directly, without applying a Hough transformation, as follows,

    $$\begin{aligned}&\mathcal {S}_\text {ScaloCorr2-TFD}(S_{\hat{\mathbf{r}}_{m;i,w}},S_{\mathbf{p}_{1,i,w}}) \nonumber \\&\quad = \frac{\sum _{a=1}^{a_{\mathrm {max}}} \sum _{b=1}^{b_{\mathrm {max}}} \left( S_{\hat{\mathbf{r}}_{m;i,w}}(a,b)-\bar{S}_{\hat{\mathbf{r}}_{m;i,w}}\right) \left( S_{\mathbf{p}_{1,i,w}}(a,b)-\bar{S}_{\mathbf{p}_{1,i,w}}\right) }{\sqrt{\left( \sum _{a=1}^{a_{\mathrm {max}}} \sum _{b=1}^{b_{\mathrm {max}}} \left( S_{\hat{\mathbf{r}}_{m;i,w}}(a,b)-\bar{S}_{\hat{\mathbf{r}}_{m;i,w}}\right) ^2\right) \left( \sum _{a=1}^{a_{\mathrm {max}}} \sum _{b=1}^{b_{\mathrm {max}}} \left( S_{\mathbf{p}_{1,i,w}}(a,b)-\bar{S}_{\mathbf{p}_{1,i,w}}\right) ^2\right) }}, \end{aligned}$$
    (26)

    where \(\bar{S}_{\hat{\mathbf{r}}_{m;i,w}}\), \(\bar{S}_{\mathbf{p}_{1,i,w}}\) denote the overall mean of the scalograms of \(\hat{\mathbf{r}}_{m;i,w}\) and \(\mathbf{p}_{1,i,w}\), respectively. Similarly to the previous measures, the market integration measure associated with the function (26) is given by averaging the pairwise 2-D correlation coefficients between the scalograms of the returns series and the scalogram of their corresponding first probabilistic principal factor, as follows,

    $$\begin{aligned} G_{\text {ScaloCorr2-TFD},i} = \frac{1}{M} \sum _{m=1}^M \mathcal {S}_\text {ScaloCorr2-TFD}(S_{\hat{\mathbf{r}}_{m;i,w}},S_{\mathbf{p}_{1,i,w}}). \end{aligned}$$
    (27)

We note here that, as it can be seen in (18)–(25), the corresponding market integration measures are defined as weighted sums of equally-weighted (with a weight equal to \(\frac{1}{M}\frac{1}{a_{\mathrm {max}}}\)) scale-by-scale sub-similarities, which may provide improved insight into their inherent regulatory relationship. Most importantly, by summing these pairwise sub-similarities only up to a scale \(a_K<a_{\mathrm {max}}\), we can ignore high-frequency components which may be due to noise, thus increasing the accuracy of the integration measures. However, the determination of the optimal subset of scales is by itself a very important topic, which is left for a future thorough study.

4 Performance evaluation

In this section, the performance of our proposed time-frequency adapted market integration measure, given by (14), is evaluated and compared against the performance of the market integration measures introduced in Sect. 3.2. More specifically, the efficiency of all the integration measures is examined in the framework of optimal mean-variance portfolio construction.

To this end, a set of 12 developed equity markets are employed (Australia (XP1), Canada (SPTSX), France (CF1), Germany (GX1), Hong Kong (HI1), Japan (TP1), Singapore (QZ1), Spain (IB1), Sweden (OMX), Switzerland (SM1), United Kingdom (Z1), and USA (ES1)), for which liquid index futures contracts are available in order to enable short positions in the portfolio strategies. Closing prices at a daily frequency for the main futures indices of each country have been gathered, expressed in local currency, covering the period between January 2001 and January 2013. During this time period, all markets had undergone through various financial crises, such as, the IT-bubble (or dot-com bubble), whose collapse took place by the end of 2001, the global subprimes/debt crisis, whose effects were perceived by the markets in 2007–2008, and the European sovereign crisis in 2010. All crises were followed by a recovery period, which might differ depending on the country and the continent, thus offering a good opportunity to study integration and long-term portfolio performance.

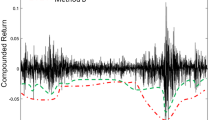
Besides, to overcome the limitation of significantly different variances and expression in different currencies between the distinct time series, a further normalization to zero mean and unit variance of their returns series is performed according to (12). Furthermore, to account for the time-varying dynamics of our data, the performance of all the market integration measures is evaluated in a rolling window of length \(w = 250\) with step size \(s = 25\). Figure 4 shows the original time series, along with their normalized returns.

Fig. 4
figure 4

Original and normalized returns series for the 12 equity markets

Full size image
Fig. 5
figure 5

Market integration measures evolution across time for the 12 equity markets

Full size image

In the subsequent evaluation, the CWTs, and thus the associated scalograms, are computed by decomposing the normalized returns series windows, as well as the extracted first probabilistic principal factor, using the db8 wavelet at \(a_{\mathrm {max}} = 75\) scales. For the Hough transform, the \((\rho ,\,\theta )\) (radial, angle) parameter space is discretized in a grid of size \(512\times 512\). The selected parameter values for both the CWT and the Hough transform were set empirically on a basis of keeping a trade-off between the achieved accuracy of the various market integration measures and their computational cost. However, the development of automatic rules for choosing the best wavelet, along with the optimal parameter values is of high importance and is left as a separate work.

Figure 5 shows the values of our proposed time-frequency adapted market integration measure across time, along with the alternative integration measures introduced above, for the 12 equity markets. As it can be seen, the proposed integration measure, as well as most of the alternative ones, achieve to track the important periods of interest, such as, the increased integration around 2001 and between 2007–2008, since the IT-bubble and the subprimes/debt crisis, respectively, affected all markets globally, and the decreased integration around 2010, since the European sovereign crisis affected mostly the European markets, thus leaving more opportunities for global markets diversification.

For the construction of the optimal portfolios we follow the approach described in Caicedo-Llano and Dionysopoulos (2008). More precisely, a two-stage process is adopted, by first estimating the optimal weights solving an optimization problem of the form shown in (28), and then by adapting these weights so as to keep a constant risk through the strategy or to achieve a time-varying risk allocation. The optimal weights are estimated by solving the following optimization problem:

$$\begin{aligned} \mathbf{w}^*= \arg \max _\mathbf{w} \left( \mathbb {E}\{r_p\}-\zeta \,\mathrm {Var}\{r_p\}\right) , \end{aligned}$$
(28)

where \(\mathbb {E}\{r_p\} = \mathbf{w}^T\mathbf{z}\) is the expected return of our portfolio, with \(\mathbf{z}\) being the vector of expected excess returns of the assets, \({\mathrm {Var}}\{r_p\} = \mathbf{w}^{T} \hat{\varvec{\Sigma }}\mathbf{w}\) is the portfolio’s variance, with \(\hat{\varvec{\Sigma }}\) being the estimated covariance matrix of the returns, and \(\zeta \) is a parameter representing the investor’s level of risk aversion. The adaptation of the estimated weights is performed by employing the values of the computed market integration measures \(G_{\cdot ,i}\).

More specifically, the estimated optimal weights are modified according to three different scaling rules: (i) (1-Gdet): a de-trending step is applied first on the computed values of each integration measure before adjusting the weights; (ii) H: the estimated optimal weights are smoothed. In particular, the optimal weights are modified linearly for integration values ranging in an interval \([G_{min}, G_{max}]\) using the rule,

$$\begin{aligned} \mathbf{w}_s^*= \left( 1-\frac{\bar{G_{i}}-G_{min}}{G_{max}}\right) \mathbf{w}^*, \end{aligned}$$
(29)

where \(\bar{G_{i}}\) is the integration value at time i after removing the mean computed over all the overlapping windows, so as to use the same thresholds for the whole time period of study. On the other hand, for integration values larger than \(G_{max}\) the weights are set equal to zero and for integration values smaller than \(G_{min}\) the optimal weights are left unchanged. In practice, the values of the two thresholds \(G_{min}\), \(G_{max}\) can be set based on the quantiles of the distribution of the historical values for each integration measure separately; (iii) (1-G): the integration measure values are subtracted from 1. The resulting risk-adjusted performance measures for each modified strategy ((1-Gdet), H, (1-G)) are presented in Table 1.

Table 1 Performance of the proposed time-frequency adapted market integration measure (2), compared with the Basic MV and alternative integration measures, for portfolio optimization using three scaling rules (db8 wavelet, 75 scales)
Full size table

The constructed portfolio’s optimality is defined in terms of the following typical financial performance metrics:

  • Return (Ret)

  • Volatility (Vol)

  • Information ratio (IR): measures the excess annualized return of a portfolio, \(r_p\), over the annualized returns of its benchmark, \(r_B\), divided by the volatility of these excess returns,

    $$\begin{aligned} \mathrm {IR} = \frac{\mathbb {E}\{r_p-r_B\}}{\sigma _{r_p-r_B}} \end{aligned}$$

  • Maximum drawdown (MDD): it is defined as the maximum cumulated continuous loss over a given period, measuring the degree of extreme losses

  • Maximum drawdown over Volatility (MDD/Vol): it is a normalization of the MDD for a fair comparison of portfolio optimization strategies resulting in different MDD and volatility values.

Table 1 compares the performance of all the market integration measures introduced in this work by adjusting accordingly the weights obtained as the solution of the mean-variance optimization problem. The comparison is also carried out among the three scaling rules mentioned above, which are used to adjust the optimal weights. For convenience, the enumeration of the market integration measures, as they appear in the following tables and figures, is as follows (Sect. 3): (1) Corr-TD; (2) Proposed market integration measure (corr2d); (3) Cos-TFD; (4) PCE-TFD; (5) SRCC-TFD; (6) Ultra-TFD; and (7) ScaloCorr2-TFD. For each market integration measure and each performance metric the optimal values are presented in italics, while the boldtype numbers correspond to the best values for each performance metric among all the compared market integration measures.

First, we observe that the PPCA-based method, Corr-TD, produces a portfolio with higher risk-adjusted performance metrics. The basic mean-variance (Basic MV) strategy, employing pairwise correlations among the time-domain returns series directly, has a ratio of average performance over risk equal to 0.19, while the portfolios composed of a risk scaling strategy based on PPCA have ratios of 0.54, 0.42 and 0.25, respectively. For the first two scaling rules the performance over the whole time period is improved from 1.94 to 2.16 and 2.43 %, whereas the volatility is reduced for the three scaling rules from 10.02 to 4.48 % on average. Moreover, the MDD over the monitored period is also reduced significantly from 44.3 to 15.7 % on average for the different scaling rules, as well as the ratio of MDD over volatility.

Concerning our proposed market integration measure (corr2d), we observe that, in general, it improves the performance, while the risk is reduced producing better risk-adjusted performance metrics than the basic strategy. Moreover, it also improves the majority of the main performance metrics for most of the scaling rules, when compared with the alternative integration measures, while for the rest of the metrics it achieves a performance which is close to the optimal one achieved by some of the alternative scale-by-scale integration measures (methods 3–7 in Table 1).

In particular, our proposed time-frequency adapted integration measure combined with the second scaling rule for the optimal weights, produces a strategy delivering 3.11 % return and 6.49 % volatility, which corresponds to a ratio of 0.49, significantly improved compared with the basic strategy, and close to the optimal PPCA result. The ratio of MDD over volatility is also improved significantly from \(-4.42\) to \(-2.15\), which is the optimal value achieved among all the integration measures. In general, our proposed integration measure is able to produce a portfolio construction strategy with better overall performance for the chosen set of market indices and the selected parameters values.

Furthermore, among the three scaling rules, the second one, H, corresponding to a transformation to very low risk when the integration is high and a smooth transition to high risk taking when the level of integration is low, is the one delivering the best results. From the three different scaling rules, two of them, namely, H and (1-G), considerably improve the results.

As an overall conclusion, the time-frequency adapted market integration measure proposed in this work achieves a significant reduction of the optimal portfolio’s volatility compared with the volatility of the basic strategy, which is also captured through the drawdown measures to focus on the negative side of the returns, while improving or maintaining the performance of the alternative integration measures. This is attributed to the efficiency of our proposed integration measure to better capture the localized patterns in the time-frequency domain, which are inherent in each time series, and correlate them accurately among distinct markets.

5 Conclusions and further work

In this paper, we proposed a novel market integration measure, which adapts to the time-frequency evolution of an ensemble of financial time series. The proposed integration measure was designed by exploiting the enhanced time-frequency representation provided by multi-scale wavelet decompositions, which are able to capture the inherent variability not only across time, but also in the frequency domain. A more compact and meaningful representation of the energy distribution was then obtained by applying a Hough transformation on the corresponding scalograms. The same procedure was applied on the dominant probabilistic principal factor of the time series ensemble, obtained via PPCA. Finally, the degree of market integration was measured by the 2-D correlation coefficient between the associated Hough transforms of the time series and the first principal factor.

An evaluation of the proposed integration measure in the framework of mean-variance portfolio optimization, and its comparison against several alternative integration measures performing either in the time-domain or in the time-frequency domain adopting a scale-by-scale approach, revealed an improved performance in terms of various distinct performance metrics. The results also revealed an increased capability of the proposed integration measure to deliver improved portfolio performance for the short and long-term investors, by accounting simultaneously for the inherent short and long-run fluctuations in the original time series.

The results presented in this work correspond to a specific selection of the window length, the selected wavelet (db8 was used in this study), and the number of scales. As a future extension, an automatic rule for making optimal choices of these parameter values, along with an adaptive selection of the most suitable wavelet according to the original time series characteristics, will be studied. In addition, the representative capability of the Hough transform can be enhanced by developing an appropriate peak detection method, which will extract the significant energy peaks, yielding potential improvements by easing the parameter space interpretation.

From a financial perspective, it could be of interest to extent the proposed market integration measure in order to allow the incorporation of single or multiple sources of risk. This stems from the fact that an omitted risk factor could potentially mask itself through evidence of time-varying integration. Furthermore, measuring and monitoring the degree of market integration could have implications beyond explaining why expected returns may differ across distinct countries. To this end, it is of high importance to develop models that relate capital market restrictions and the stage of financial market integration to economic growth, through the improvement of risk sharing, which is reflected in the measured integration strength.