Detecting Causality in Non-stationary Time Series Using Partial Symbolic Transfer Entropy: Evidence in Financial Data

Abstract

In this paper, a framework is developed for the identification of causal effects from non-stationary time series. Focusing on causality measures that make use of delay vectors from time series, the idea is to account for non-stationarity by considering the ranks of the components of the delay vectors rather than the components themselves. As an exemplary measure, we introduce the partial symbolic transfer entropy (PSTE), which is an extension of the bivariate symbolic transfer entropy quantifying only the direct causal effects among the variables of a multivariate system. Through Monte Carlo simulations it is shown that the PSTE is directly applicable to non-stationary in mean and variance time series and it is not affected by the existence of outliers and VAR filtering. For stationary time series, the PSTE is also compared to the linear conditional Granger causality index (CGCI). Finally, the causal effects among three financial variables are investigated. Computations of the PSTE and the CGCI on both the initial returns and the VAR filtered returns, and the PSTE on the original non-stationary time series, show consistency of the PSTE in estimating the causal effects.

1 Introduction

The investigation of interactions among the components of a multivariate system addresses three major issues: the detection of the couplings, their direction, and the quantification of the coupling strengths. When evaluating the causal influence between two variables from a multivariate time series, it is necessary to take the effects of the remaining variables into account. Multivariate analysis is required to distinguish between direct and indirect causal effects.

The concept of Granger causality is instrumental in the study of dynamic interactions in multivariate systems (Granger 1969). Linear Granger causality suggests that causes always precede their effects and it is implemented by fitting autoregressive models. However, the selected model should be appropriately matched to the underlying dynamics of the examined system, otherwise model misspecification may lead to spurious identification of causality.

Stationarity is not expected when examining real data possessing non-constant mean and variance. Preliminary data treatment (i.e. detrending, differencing, filtering) can be used to deal with non-stationarity, e.g. see Wei (2006) and Bossomaier et al. (2013).

In econometrics, causality in non-stationary time series in the mean is typically investigated through vector error correction models (VECM), and it is subdivided into short-run and long-run (Lee et al. 2002; Cheng et al. (2010)). In this respect, cointegration between two variables implies the existence of long-run causality in at least one direction and a cointegration test can be viewed as an indirect test of long-run dependence (Engle and Granger 1987). Testing for cointegration and causality are thus jointly applied to investigate long- and short-run relationships among variables. Regarding non-stationarity in variance, several methods have been proposed in the literature, e.g. model fitting allowing for a time-varying variance and heteroskedasticity tests (Xu and Phillips 2008; Kim and Park 2010), but we are not aware of any works treating the problem of causality and non-stationarity in variance jointly.

Most Granger causality measures are developed for stationary time series, e.g. conditional Granger causality (Geweke 1982), partial directed coherence (Baccala and Sameshima 2001), coarse-grained information rates (Paluš et al. 2001), extended Granger causality (Chen et al. 2004), and conditional mutual information (Vejmelka and Paluš 2008). Methods, such as transfer entropy (Schreiber 2000) from information theory and linear Granger causality, are theoretically invariant under a rather broad class of transformations (Barnett and Seth 2011). However, in practice, data transformations may have an impact on causal inference. Recently, many model-free causality measures have been developed to address nonlinear signal properties, as for example state space and information measures. On the other hand, these methods involve more free parameters and are more data demanding than linear model-based methods, such as linear Granger causality.

In financial applications, most causality tests are not applied to the raw data but to the (log) returns. For example, we can mention the modified test of nonlinear Granger causality that has been introduced by Hiemstra and Jones (1994), corrected by Diks and Panchenko (2006), and it is usually applied on the Vector Auroregressive (VAR) filtered residuals. It is, however, reported that linear filtering of the data before the application of a causality test can lead to serious distortions, e.g. see Kyrtsou (2005) and Karagianni and Kyrtsou (2011). On the other hand, it is claimed that the estimation of information-theoretical quantities is typically improved by diminishing long-range second-order temporal structure using VAR filters, provided that the interactions between time series are not purely linear (Gomez-Herrero 2010). The influence of filtering on the different causality tests remains open for further investigation, but it is not within the scope of the present work.

The developments above highlight the importance of building causality tests able to take into account causal effects directly in non-stationary time series. In this work, we propose a general framework to address non-stationarity when estimating causality which encompasses all causality measures that involve the delay vectors in their computation. Specifically, we suggest to formulate and utilize the rank vector of the corresponding sample vectors reconstructed from the time series, instead of the delay vectors themselves.

The idea of using ranks instead of the values of a vector variable dates back to Spearman (1904) and Kendall (1938) suggesting the estimation of the statistical dependence between two variables. This idea has been adopted for the estimation of correlation and causality measures. Along these lines, the symbolic transfer entropy (STE) (Staniek and Lehnertz 2008) and the generalized measure of association (Fadlallah et al. 2012) have been introduced.

To demonstrate the efficiency of the proposed framework based on rank vectors, we extend the bivariate information causality measure of STE (Staniek and Lehnertz 2008) to the multivariate case, called partial symbolic transfer entropy (PSTE), in order to account only for direct causal effects among the components of a complex system. The PSTE, as the STE, is estimated on rank vectors. It is evaluated on multivariate time series of known coupled and uncoupled systems, on stationary and non-stationary time series in mean and in variance, on time series with outliers, and on VAR filtered time series as well. Complementarily and for comparison reasons, the conditional Granger causality index (CGCI) is also considered.

A corrected version of the STE and PSTE (namely TERV and PTERV) have been recently introduced in Kugiumtzis (2012, 2013), but here we consider the initial definition of STE, as used in different applications (Kowalski et al. 2010; Ku et al. 2011; Martini et al. 2011). To get further insight on the performance of the suggested approach, besides an extensive simulation experiment, we look for causal relationships between three well-known financial time series, namely the 3-month Treasury Bill, the 10-year Treasury Bond and the volatility index VIX.

The structure of the paper is as follows. In Sect. 2, the multivariate causality measures of PSTE and conditional Granger causality index are presented, and their statistical significance is discussed. In Sect. 3, the two causality measures are evaluated in a simulation study, while their performance is also examined in three financial time series. Finally, conclusions are discussed in Sect. 4.

2 Materials and Methods

Let us consider the bivariate process ${(x_{1,t},x_{2,t})}$, i.e. two simultaneously observed time series $\{x_{1,t}\}$, $\{x_{2,t}\}$, $t=1,\ldots ,n$ derived from the dynamical systems $X_1$ and $X_2$, respectively. The delay vectors for $X_1$ and $X_2$ are defined as $\mathbf x _{1,t}$ $=(x_{1,t}$, $x_{1,t-\tau _1},\ldots$, $x_{1,t-(m_1-1)\tau _1})'$, $\mathbf x _{2,t}$ $=(x_{2,t}$, $x_{2,t-\tau _2},\ldots$ ,$x_{2,t-(m_2-1)\tau _2})'$, where $t=1,\ldots ,n^{\prime }$, $n^{\prime } = n-h-\max \{(m_1-1)\tau _1,(m_2-1)\tau _2\}$, $m_1$ and $m_2$ are the embedding dimensions, $\tau _1$ and $\tau _2$ are the time delays and $h$ is the step ahead to address for the interaction. The rank vectors are formed by ordering the amplitude values of the delay vectors. Considering the delay vector $\mathbf x _{1,i}$, the $m_1$ amplitude values are arranged in an ascending order so that $x_{1,t -(r_{i,1}-1)\tau _1} \le x_{1,t -(r_{i,2}-1)\tau _1} \le \ldots \le x_{1,t -(r_{i,m}-1)\tau _1}$, where $r_{i,j}$, $j=1,\ldots ,m$, are all different and $r_{i,j} \in \{1,\ldots ,m_1\}$. Therefore, every delay vector is uniquely mapped onto one of the $m_1!$ possible permutations. The rank vectors for $X_1$ are defined as $\hat{\mathbf{x }}_{1,i} = (r_{i,1}, r_{i,2},\ldots , r_{i,m_1})$ and accordingly for $\mathbf x _{2,i}$. The advantage of using ranks is that vectors formed by time series segments at different levels of magnitude can be compared in terms of distance, and thus similar data patterns can be searched regardless of their magnitude levels, accounting in this way for non-stationarity.

To indicate the suitability of this approach for non-stationary time series, we take the example of a stationary time series $\{x_{t}\}$, with outliers added to it, denoted as $\{y_{t}\}$ (see Fig. 1). We construct also the time series $\{z_{t}\}$ by adding a linear trend to $\{x_{t}\}$: $z_t = x_t + 0.1t$ (Fig. 1c). Further, we consider the embedding dimension $m=4$ and the time delay $\tau =1$, while we highlight all the delay vectors with corresponding rank vectors $\{2,1,4,3\}$. For $\{x_t\}$, we observe 8 delay vectors in total with corresponding rank vector $\{2,1,4,3\}$. In $\{y_t\}$ there are again 8 delay vectors, all of which are at the same time points as in $\{x_t\}$, while in $\{z_t\}$ there are 6 in total delay vectors all of which are at the same time points as in $\{x_t\}$. We note that all the highlighted delay vectors have identical rank vectors ($\{2,1,4,3\}$), whereas the corresponding sample vectors (delay vectors) are not necessarily close.

Fig. 1

a A realization of the Henon map and its corresponding time series after adding outliers (b) and after adding a linear trend (c). The delay vectors of the time series that correspond to rank vectors with the pattern $\{2,1,4,3\}$ are displayed with grey in the printed version and cyan in the online one

Thus one can base the distance measure on the relative magnitude ordering and not the sample values of the delay vectors of the time series. The estimation of the probability of occurrence of the rank vectors can be more robust than in the case of the delay vectors. The possible combinations of the rank vectors are $m!=4!$, while using a binning approach for the delay vectors with $b$ bins, there are $b^m$ possible vectors for each component.

Therefore, measures that make use of embedding point distances, e.g. interdependence measures (Arnhold et al. 1999; Romano et al. 2007; Chicharro and Andrzejak 2009)¹ and information measures can be modified to use ranks instead of samples. As an exemplary measure that uses rank vectors, we introduce here the PSTE.

2.1 Partial Symbolic Transfer Entropy

The transfer entropy (TE) is an information measure related to the concept of Granger causality, which has been utilized for the detection of the directional couplings and the asymmetry in the interaction of subsystems (Schreiber 2000). The TE and its multivariate extension, the partial transfer entropy (PTE), incorporate time dependence by relating previous values of two variables $X_1$ and $X_2$ in order to predict $X_1$ (or similarly $X_2$) $h$ steps ahead. The TE quantifies the deviation from the generalized Markov property, $p(x_{1,i+h}|\mathbf x _{1,i},\mathbf x _{2,i}) = p(x_{1,i+h}|\mathbf x _{1,i})$, where $p$ denotes the transition probability density. If the generalized Markov property holds, then $X_2$ does not drive $X_1$. Different techniques have been proposed to estimate the TE and PTE from observed data, e.g. binning, kernel methods and nearest neighbor estimators (Cover and Thomas 1991; Silverman 1986; Kraskov et al. 2004).

The STE has been introduced aiming to provide an alternative way of estimating the TE, i.e. in terms of rank vectors (Staniek and Lehnertz 2008). For each of $x_{1,i+h}$, $\mathbf x _{1,i}$ and $\mathbf x _{2,i}$ first the rank vectors are formed denoted $\hat{\mathbf{x }}_{1,i+h}$, $\hat{\mathbf{x }}_{1,i}$ and $\hat{\mathbf{x }}_{2,i}$. Note that the scalar future response $x_{1,i+h}$ is treated as an embedding vector $\mathbf x _{1,i+h}$. Then the STE is expressed similarly to TE as

$$\begin{aligned} \text{ STE }_{X_2 \rightarrow X_1} = \sum p(\hat{\mathbf{x }}_{1,t+h},\hat{\mathbf{x }}_{1,t},\hat{\mathbf{x }}_{2,t}) \log \frac{p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t}, \hat{\mathbf{x }}_{2,t})}{p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t})}, \end{aligned}$$

(1)

where $p(\hat{\mathbf{x }}_{1,t+h},\hat{\mathbf{x }}_{1,t},\hat{\mathbf{x }}_{2,t})$, $p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t},\hat{\mathbf{x }}_{2,t})$ and $p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t})$ are the joint and conditional distributions estimated on the rank vectors as relative frequencies, respectively.

The PSTE is the extension of the STE that accounts only for direct causal effects in multivariate systems. It is defined conditioning on the set of the remaining variables $Z=\{X_3, X_4,\ldots ,X_K\}$ of a multivariate system of $K$ observed variables

$$\begin{aligned} \text{ PSTE }_{X_2 \rightarrow X_1|Z} = \sum p(\hat{\mathbf{x }}_{1,t+h},\hat{\mathbf{x }}_{1,t},\hat{\mathbf{x }}_{2,t}, \hat{\mathbf{z }}_t) \log \frac{p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t}, \hat{\mathbf{x }}_{2,t},\hat{\mathbf{z }}_t)}{p(\hat{\mathbf{x }}_{1,t+h}|\hat{\mathbf{x }}_{1,t},\hat{\mathbf{z }}_t)}, \end{aligned}$$

(2)

where the rank vector $\hat{\mathbf{z }}_{t}$ is formulated as the concatenation of the rank vectors for each of the delay vectors of the variables in $Z$.

The PSTE is a measure formed on nonparametric estimators from information theoretical arguments. Its definition is built on the probability distributions or equivalently on conditional entropies, and quantifies the reduction in conditional uncertainty of $\hat{\mathbf{x }}_{1,t+h}$ when the conditioning changes from $\hat{\mathbf{x }}_{1,t},\hat{\mathbf{z }}_{t}$ to $\hat{\mathbf{x }}_{2,t},\hat{\mathbf{x }}_{1,t},\hat{\mathbf{z }}_{t}$. Causality is defined in terms of predictive power using an information theoretical statistic rather than linear modeling tools and thus it accounts for nonlinearity in the data. Similarly to PSTE, also other causality measures calculated using the delay vectors of the time series could be estimated on the corresponding rank vectors.

2.2 Conditional Granger Causality Index

For comparison reasons, the Conditional Granger Causality Index (CGCI) is also considered in this study (Geweke 1982). To define CGCI from $X_2$ to $X_1$ for a multivariate time series of the variables $\{X_1,X_2,\ldots ,X_K\}$, two vector autoregressive models (VAR) are considered, the unrestricted model

$$\begin{aligned} x_{1,t+1} = \sum _{j=0}^{P-1} a_{1,j}x_{1,t-j}+ \sum _{j=0}^{P-1} a_{2,j}x_{2,t-j} + \sum _{i=3}^K \sum _{j=0}^{P-1} a_{i,j}x_{i,t-j} + \epsilon _{U,t+1}, \end{aligned}$$

(3)

and the restricted model

$$\begin{aligned} x_{1,t+1} = \sum _{j=0}^{P-1} a_{1,j}x_{1,t-j}+ \sum _{i=3}^K \sum _{j=0}^{P-1} a_{i,j}x_{i,t-j} + \epsilon _{R,t+1}, \end{aligned}$$

(4)

where $a_{i,j}$ are coefficients and $\epsilon _{U,t}$ and $\epsilon _{R,t}$ are residual terms. If the variance $s_{U}^2$ of the residuals of the unrestricted model in Eq. 3 for $X_1$ is statistically significantly less than the residual variance $s_{R}^2$ of the restricted model for $X_1$ in Eq. 4 that does not include $X_2$, then there is statistical evidence that the variable $X_2$ Granger causes $X_1$. The magnitude of the effect of $X_2$ on $X_1$ in the presence of the other variables is given by the CGCI defined as

$$\begin{aligned} \text{ CGCI }_{X_2 \rightarrow X_1|Z} = \ln \left( s_{R}^2 / s_{U}^2\right) . \end{aligned}$$

(5)

The CGCI is a causality measure able to detect the direct causal effects in multivariate systems with linear couplings.

2.3 Statistical Significance of the PSTE and CGCI

Kugiumtzis (2013) discussed the parametric approximation of the null distribution $H_0$ of no coupling for PSTE (and the corrected version PTERV) was discussed but found it insufficient in general and always inferior to approximation based on resampling. Therefore, the statistical significance of the PSTE is assessed by a randomization test making use of time-shifted surrogates (Quian Quiroga et al. 2002). The surrogate time series are formed by time-shifting the time series of the driving variable by a random time step, while the other time series remain intact. By this, the driving and the response time series become independent to each other and the couplings are destroyed. Explaining further time-shifting, we draw a random integer $d$ (with $d$ less than the time series length $n$), and the first $d$ values of the driving time series are moved to the end, so that the new driving series is $\{x_{d+1},\ldots ,x_{n},x_{1},\ldots ,x_d\}$.

To test $H_0$, denote $q_0$ the PSTE value estimated from the original data and $q_1,\ldots ,q_M$ the PSTE values estimated from the $M$ surrogate multivariate time series. $H_0$ is rejected if $q_0$ lies at the tail of the distribution of $q_1,\ldots ,q_M$. The $p$-values for the two-sided test are derived by rank ordering. Letting the original value have rank $i$ in the ordered list of $M+1$ values, the $p$-value equals $2i/(M+1)$ if $i \le (M+1)/2$ and $2(M+1-i)/(M+1)$ if $i > (M+1)/2$ (the correction of the rank approximation of the cumulative density function in Yu and Huang (2001) is applied).

The statistical significance of the CGCI can be assessed by means of a parametric test, i.e. the $F$-test for the null hypothesis that the coefficients for the driving variable in the unrestricted model are zero (Brandt and Williams 2007). For example, applying the $F$-significance test for each of the $P$ coefficients $a_{2,j}$ in Eq. 3, constitutes the parametric significance test for CGCI to test the null hypothesis that variable $X_2$ is not driving $X_1$.

3 Results

The effectiveness of the PSTE in detecting direct nonlinear causal effects at different settings is assessed based on a simulation study. The PSTE and the CGCI are complementarily used, in order to determine both the linear and nonlinear couplings from the simulation systems. The two causality measures are estimated from 100 realizations of different simulation systems with linear and/or nonlinear couplings, for different coupling strengths and for all directions. However, the CGCI is only estimated on stationary data.

3.1 Simulation Study

The PSTE and CGCI are evaluated on multivariate time series from coupled and uncoupled systems of different types: stationary, non-stationary in mean and in variance, with outliers, with linear and / or nonlinear causal effects. We also apply the PSTE on VAR filtered time series in order to assess the ability to capture remaining nonlinear couplings. Specifically, the following simulation systems are examined:

• (1) A stationary system in three variables with one linear coupling ($X_2 \rightarrow X_3$) and two nonlinear ones ($X_1 \rightarrow X_2$, $X_1 \rightarrow X_3$) (Gourévitch et al. 2006, Model 7) (see Fig. 2a)

  $$\begin{aligned} x_{1,t}&= 3.4x_{1,t-1}(1-x_{1,t-1})^2 \exp {(-x_{1,t-1}^2)} + 0.4\epsilon _{1,t} \\ x_{2,t}&= 3.4x_{2,t-1}(1-x_{2,t-1})^2 \exp {(-x_{2,t-1}^2)} + 0.5x_{1,t-1}x_{2,t-1} +0.4\epsilon _{2,t} \\ x_{3,t}&= 3.4x_{3,t-1}(1-x_{3,t-1})^2 \exp {(-x_{3,t-1}^2)} + 0.3x_{2,t-1}+ 0.5x_{1,t-1}^2 + 0.4\epsilon _{3,t}, \end{aligned}$$

  where $\epsilon _{i,t}$, $i=1,2,3$, are Gaussian white noise terms with unit covariance matrix.

• (2) A stationary system in three variables, with only nonlinear couplings ($X_1 \rightarrow X_2$, $X_1 \rightarrow X_3$) (see Fig. 2b)

  $$\begin{aligned} x_{1,t}&= 0.7x_{1,t-1} + \epsilon _{1,t} \\ x_{2,t}&= 0.3x_{2,t-1} + 0.5x_{2,t-2} x_{1,t-1} + \epsilon _{2,t} \\ x_{3,t}&= 0.3x_{3,t-1} + 0.5x_{3,t-2} x_{1,t-1} + \epsilon _{3,t}. \end{aligned}$$

  The model restricted to the two first variables was introduced in Baghli (2006). The term product of the variables in the second and third equation causes the variables $X_2$ and $X_3$ to have marginal distributions with long tails.

• (3) A stationary system of three coupled Hénon maps with nonlinear couplings ($X_1 \rightarrow X_2$, $X_2 \rightarrow X_3$) (see Fig. 2c)

  $$\begin{aligned} x_{1,t}&= 1.4 - x_{1,t-1}^2 + 0.3x_{1,t-2} \\ x_{2,t}&= 1.4 - c x_{1,t-1} x_{2,t-1} - (1-c)x_{2,t-1}^2 + 0.3x_{2,t-2} \\ x_{3,t}&= 1.4 - c x_{2,t-1} x_{3,t-1} - (1-c)x_{3,t-1}^2 + 0.3x_{3,t-2}, \end{aligned}$$

  with equal coupling strengths $c$ for $X_1 \rightarrow X_2$ and $X_2 \rightarrow X_3$, with $c = 0$, 0.05, 0.3, 0.5. The time series of this system become completely synchronized for coupling strengths $c \ge 0.7$.

• (4) A system of four coupled Hénon maps with nonlinear couplings (two unidirectional $X_1 \rightarrow X_2$, $X_4 \rightarrow X_3$ and a bidirectional coupling $X_2 \leftrightarrow X_3$) (see Fig. 2d), defined as

  $$\begin{aligned} x_{i,t}&= 1.4 - x_{i,t-1}^2 + 0.3x_{i,t-2}, i=1,4 \\ x_{i,t}&= 1.4 - \left( 0.5c(x_{i-1,t-1}+x_{i+1,t-1})+(1-c)x_{i,t-1}\right) ^2 + 0.3x_{i,t-2}, i=2,3 \end{aligned}$$

  for coupling strengths $c=0$ (uncoupled case), $c=0.2$ (weak coupling) and $c=0.4$ (strong coupling).

• (5) A stationary system with outliers, from the three coupled Hénon maps (system 3), where outliers have been randomly added to each variable drawn from the standard uniform distribution. The number of outliers constitute $1~\%$ of the total number of data points.

• (6) A non-stationary system in level (mean), from the three coupled Hénon maps (system 3), where a stochastic trend $\eta _t = \eta _{t-1} + \epsilon _t$ is added to each variable; $\epsilon _t$ is Gaussian white noise with unit variance. The CGCI is estimated on the detrended time series.

• (7) A non-stationary system in level (mean), from the three coupled Hénon maps (system 3) where a deterministic trend $\eta _t = a \cdot t$ is added to each variable, and $a$ is a constant. The value of $a$ is randomly set for each realization of the system and normally distributed with mean $0.01$ and standard deviation $0.02$. The CGCI is estimated on the first differences of the data.

• (8) A system which is non-stationary in variance, resulting from the addition of an integrated generalized autoregressive conditional heteroskedasticity process of order (1,1), IGARCH (1,1), to system 2:

  $$\begin{aligned} z_t&= \sigma _t \epsilon _t \\ \sigma _{t}^2&= \alpha _0 + \alpha _1 \epsilon _{t-1}^2 + \beta _1 \sigma _{t-1}^2, \end{aligned}$$

  where $\epsilon _t$ is Gaussian white noise with unit variance, $\alpha _0 = 0.2$, $\alpha _1 = 0.9$ and $\beta _1 = 0.1$. The $z_{i,t}$ of IGARCH (1,1) is first multiplied by a factor $g$ and then added to each $x_i$, $i=1,2,3$ of system 2, so that the derived time series of $y_i$ is $y_{i,t}=x_{i,t} + g z_{i,t}$, $i=1,2,3$.

• (9) It is a common practice in financial applications, to estimate causality measures or apply causality tests to the VAR residuals of the data in order to specify the underlying nature of the couplings. However, the influence of the filtering on the different causality measures and tests has not been fully investigated so far. For this reason, we consider here the VAR filtered residuals of system 1. The order of the VAR filter is set from the Schwarz’s Bayesian Information Criterion (BIC) (Schwartz 1978), for each realization.

• (10) Finally, we consider a VAR(3) process in three variables with linear causal effects $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_1$, which is non-stationary in mean and there is one co-integrating relationship between the variables (see Sharp (2010), Model 8, p.78):

  $$\begin{aligned} x_{1,t}&= 0.4x_{1,t-1}+0.4x_{2,t-1}+0.5x_{3,t-1} \\&+\, 0.2x_{1,t-2}-0.2x_{2,t-2} \\&-\, 0.2x_{1,t-3}+0.15x_{2,t-3}+0.1x_{3,t-3}+\epsilon _{1,t} \\ x_{2,t}&= 0.6x_{2,t-1}+0.2x_{2,t-2} +0.2x_{2,t-3}+\epsilon _{2,t} \\ x_{3,t}&= 0.4x_{3,t-1}+0.3x_{3,t-2} +0.3x_{3,t-3}+\epsilon _{3,t}, \end{aligned}$$

  where $\epsilon _{i,t}, i = 1,\ldots ,3$ are independent to each other Gaussian white noise processes with unit standard deviation. Further, in order to generate a non-stationary system both in mean and variance, we add to this stochastic system an IGARCH(1,1) multiplied by the factor $g=0.2$, as for System 8.

Fig. 2

Couplings in a systems 1 and 9, b systems 2 and 8, c systems 3, 5, 6, 7, and d system 4

The time series lengths $n=512$ and 2048 are considered in the simulation study, to test the effectiveness of the measures on relatively small and large time series lengths. Larger time series lengths have not been considered due to the long calculation time that is required. For the PSTE, the time lag $\tau _i$ for all variables is set to $\tau =1$, as all the systems are discrete in time. The embedding dimension $m_i$ is identical for all variables (denoted as $m$) and for each system it is set according to its complexity. The number of time steps ahead $h$ equals 1, as in the original definition of transfer entropy (Schreiber 2000). For the estimation of the order $P$ of the VAR model used in CGCI, the Bayesian Information Criterion (BIC) (Schwartz 1978) is applied to model orders from 1 to 5 for all systems, taking into consideration that the true model order for each system lies within this range.

3.2 Results from Simulation Study

The performance of the PSTE and the CGCI is quantified by the percentage of statistically significant values in the 100 realizations for all the ordered couples of variables in the system, i.e. the percentage of rejections of the null hypothesis $H_0$ of no causal effects. For both measures, the causal effects are always regarded to be conditioned on the remaining variables. The true causal directions are appropriately highlighted in the respective Tables.

System 1 The optimal choice for the embedding dimension $m$ is 1, since the equations of system 1 are given only in terms of the first lag. By definition, however, we can only set $m \ge 2$ to estimate the PSTE. For $m=2$, the PSTE correctly detects the direct linear causal effect $X_2 \rightarrow X_3$ and, to a lesser extend, the nonlinear causal effect $X_1 \rightarrow X_2$. For these directions, the power of the test increases with $n$. Nevertheless, the PSTE fails to recognize the nonlinear causal effect $X_1 \rightarrow X_3$ (see Table 1). The percentages of significant PSTE values in the direction of no causal effects are low (between 1 and $8\,\%$). Its inability to detect the relationship $X_1 \rightarrow X_3$ is probably due to the fact that the effect of $X_2$ on $X_3$ is much larger than that of $X_1$ on $X_3$. The weak coupling of $X_1$ on $X_3$ might be arising from the small values of the variable $X_1$ that gets even smaller by squaring ($x_1^2$ is included in the equation of the system).

Table 1 Percentage of statistically significant PSTE ($m=2$) and CGCI ($P=2$) values for the simulation system 1

The CGCI cannot take into account the nonlinear causal effects of the first coupled system, for model order $P=1$, 2 and 3. It captures only the linear causal effect $X_2 \rightarrow X_3$ with high confidence (see Table 1 for $P=2$). The percentage of significant CGCI values at the direction of no causal effects are low (e.g. between 4 and $7~\%$ for $P=2$), as for the two nonlinear relationships.

System 1 is an example that shows the strength of the PSTE in detecting nonlinear couplings (as opposed to CGCI) and its shortcoming, i.e. that it cannot detect weak couplings (in the presence of other stronger causal effects to the same response).

System 2 It is a stationary system with long tails. Specifically, we consider the nonlinear couplings $X_1 \rightarrow X_2$ and $X_1 \rightarrow X_3$, whereas the variables $X_2$ and $X_3$ come from distributions with long tails. The maximum delay in the equations of this system is 2, and therefore we set $m=2$. One realization of system 2, for $n=512$ is displayed in Fig. 3a.

Fig. 3

a One realization of system 2, b the corresponding realization of system 8 (defined as a superimposition of the realization of system 2 and a realization of an IGARCH(1,1) model) for $g=1$

The PSTE correctly detects the nonlinear direct causality for $m=2$, giving low percentage of significant values for $n=512$ (see Table 2). Again, the power of the test increases with the time series length $n$. The percentage of significant PSTE values at the direction of no causal effects are between $1$ and $6~\%$.

Table 2 Percentage of statistically significant PSTE ($m=2$) and CGCI ($P=2$) values for the simulation system 2

The CGCI is not able to describe the two nonlinear interactions, but on the contrary, it indicates four spurious causal effects (see Table 2). The CGCI is estimated for orders $P$ from 1 to 10, nevertheless the results are similar for all $P$ values.

System 3 Here, we discuss a chaotic system, the coupled Hénon maps, first in its original form and then with outliers and drifts added to the generated time series. The PSTE is estimated for $m=2$ as there are two delays involved in the system equations. For the uncoupled case ($c=0$), the PSTE indicates no interactions, while for the weakly coupled case ($c=0.05$) it gives very low percentage of significant values. For coupling strength $c=0.3$ and for strongly coupled systems ($c=0.5$), it performs well. The power of the test increases with $n$. For $c=0.5$ and $n=2048$, along with $100\%$ significant PSTE for the true couplings, there is also a high percentage for false couplings, approximately $30\%$ for $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_2$ (see Table 3). For $m=3$, the PSTE shows the indirect causal effect $X_1 \rightarrow X_3$ and the spurious ones $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_2$, but only for $c=0.5$ and $n=2048$.

Table 3 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 3

Table 4 Percentage of statistically significant CGCI ($P=2$) values for the simulation system 3

The CGCI correctly finds the couplings for the coupled Hénon maps for $P=2$, but it also falsely detects at higher percentage than for the PSTE, the spurious causalities $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_2$ for strong coupling strengths (see Table 4). Results for $P=3$ seem to improve the performance of the CGCI, since it correctly captures the causal relationships for $c=0.3$ and $c=0.5$, while identifies only the indirect coupling $X_1 \rightarrow X_3$ for $c=0.5$ and $n=2,048$ ($52~\%$).

System 4 It is a coupled system in four variables with unidirectional ($X_1 \rightarrow X_2$, $X_4 \rightarrow X_3$) and bidirectional nonlinear causal effects ($X_2 \leftrightarrow X_3$). The PSTE is estimated for $m=2$. Regarding the uncoupled case ($c=0$), it correctly denotes the absence of causal effects giving low percentage of rejection of $H_0$ (see Table 5). In the case of weak couplings ($c=0.2$), it recognizes the true relationships but only for large time series lengths, i.e. the power of the test increases with $n$. High value of the coupling strength ($c=0.4$) does not affect the detection of the true couplings without avoiding however the presence of spurious results for $n=2,048$ ($X_2 \rightarrow X_1$, $X_2 \rightarrow X_4$, $X_3 \rightarrow X_4$).

Table 5 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 4

The CGCI is estimated for $P=2$ and 4 (based on BIC). Its performance is not significantly affected by the selection of $P$. For the uncoupled case ($c=0$), the CGCI indicates no causal effects, but the actual level of rejections can be substantially higher than the nominal level of $5~\%$, varying from $6$ to $17\,\,\%$ when $P=2$ and from $2$ to $11\%$ when $P=4$. Concerning the case of weak ($c=0.2$) and strong coupling strength ($c=0.4$), the CGCI correctly shows the true couplings for both time series lengths, however many spurious causal effects are also obtained (see Table 6).

Table 6 Percentage of statistically significant CGCI ($P=4$) values for the simulation system 4

System 5 For the coupled Hénon system with the addition of outliers ($1~\%$ of $n$), the PSTE performs similarly as without outliers. Indicative results are displayed in Table 7, for $c=0.3$ and $c=0.5$. We notice that the percentages of significant PSTE values at the directions $X_1 \rightarrow X_3$ and $X_3 \rightarrow X_1$ vary between $3$ and $10\,\%$.

Table 7 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 5

On the other hand, the CGCI is significantly affected by the existence of outliers, performing poorly for $P=2$ and $3$, failing to detect the direct causal effects for all but the case of strong coupling strength $c=0.5$ and $n=2,048$. The significance test with CGCI reveals the spurious causalities $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_2$ for the coupling strengths $c=0.3$ and 0.5.

System 6 The simulation systems 6 and 7 are non-stationary in mean, therefore only the PSTE can be directly applied to the data. One realization of system 6, the coupled Hénon maps with the addition of stochastic trends, for $n=512$ and $c=0$ is reported in Fig. 4a.

Fig. 4

a One realization of system 6 (three coupled Hénon maps with addition of stochastic trends), b one realization of system 7 (three coupled Hénon maps with addition of deterministic trends), for $n=512$

The sensitivity of the PSTE is reduced by the addition of the stochastic trend, but still it increases with $n$, indicating that the PSTE requires large time series lengths to effectively identify the couplings. Representative results are displayed in Table 8, for $c=0.3$ and 0.5.

Table 8 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 6

The CGCI is applied to the first differences of the data for $P=1$ and $P=2$. No causal effects are identified in the uncoupled case ($c=0$) for both $P$ (percentage of significant CGCI values range from $2$ to $13~\%$). For $c=0.3$ and $c=0.5$, the CGCI has a poor performance for $P=1$, failing to detect the coupling $X_1 \rightarrow X_2$, while indicating the spurious coupling $X_3 \rightarrow X_2$. On the other hand, for $P=2$, the CGCI indicates the true couplings for both $n$ (Table 9). The sensitivity of CGCI is reduced compared to that for system 3, but it increases with $n$, as for the PSTE. The percentage of significant CGCI values at the directions of no coupling are also lower compared to those for system 3.

Table 9 Percentage of statistically significant CGCI ($P=2$) values for the simulation system 6, after taking first differences

System 7 The seventh simulation system consists of 3 coupled Hénon maps (system 3) with the addition of deterministic trend. One realization for $n=512$ in the uncoupled case ($c=0$) is displayed in Fig. 4b. The addition of the deterministic trend does not affect the performance of the PSTE, and the results are very similar to those for system 3 (see Table 10). The CGCI is applied to the detrended time series using a polynomial fit of degree 1 (for higher degrees the fit reduces to linear). We estimate the CGCI from the smoothed time series for $P=2$, 3 and 4. When $P=2$ and $P=3$, the CGCI has the same performance as for system 3 (see Table 11). Spurious and indirect couplings are achieved when we set $P=4$ for the coupling strengths $c=0.3$ and $c=0.5$, e.g. for $c=0.3$ and $n=2048$, the percentage of significant CGCI values is $81\%$ at the direction $X_2 \rightarrow X_1$, and $21\%$ for $X_3 \rightarrow X_2$.

Table 10 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 7

Table 11 Percentage of statistically significant CGCI ($P=2$) values for the detrended time series of the simulation system 7

System 8 It is a non-stationary system in variance, superimposing an IGARCH(1,1) time series multiplied by a factor $g$ to the time series of system 2, which has two nonlinear causal effects ($X_1 \rightarrow X_2$ and $X_1 \rightarrow X_3$). One realization of the system 8 for $n=512$ and $g=1$ is displayed in Fig. 3b. The PSTE requires large time series lengths here in order to detect appropriately the couplings. The percentage of significant PSTE values for $X_1 \rightarrow X_2$ and $X_1 \rightarrow X_3$ increases with $n$ (see Table 12). At the directions of no causal effects, low percentages are obtained (between $2$ and $5~\%$). When $g=1$, the PSTE has the smallest power in detecting the direct causal effects, which steadily increases with $n$, e.g. from $n=2,048$ to $n=4,096$ the percentage of significant PSTE raised from $24$ and $17~\%$ to $38$ and $54~\%$ for $X_1 \rightarrow X_2$ and $X_1 \rightarrow X_3$, respectively.

Table 12 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 8 (standardized realizations of an IGARCH(1,1) multiplied by $g$ and added to the time series of system 2)

When $g=1$, the variance of input noise in the IGARCH term is at the same amplitude as the original system, and the effect of non-stationarity in variance turns out to be very strong. For smaller $g$ ($g=0.5$ and $g=0.2$), the PSTE provides much higher percentages in the case of direct causality, and still around the nominal significance level at the directions of no causal effects.

For comparison reasons, we also consider the results from the CGCI, directly applied to the non-stationary in variance time series. To estimate CGCI, we set $P=1$ and 2. It reveals the correct couplings but with low sensitivity for both $n$, and it produces spurious couplings in the opposite directions $X_2 \rightarrow X_1$ and $X_3 \rightarrow X_1$ (see Table 13). Similar results are observed for both $P$.

Table 13 Percentage of statistically significant CGCI ($P=2$) values for the simulation system 8

System 9 It is represented by the VAR filtered residuals of the simulation system 1. The PSTE has similar performance to system 1, revealing the nonlinear causal effect but for large time series lengths (see Table 14). The percentage of significant PSTE values remain low at the directions of no causal effects at all cases. As expected, the CGCI finds no couplings when estimated on the VAR filtered data.

Table 14 Percentage of statistically significant PSTE ($m=2$) values for the simulation system 9

System 10 Since only nonlinear and chaotic models have been considered so far, we will complete the simulation study displaying the performance of the PSTE on a stochastic system. The PSTE ($m=3$) is effective for system 10 and large $n$, therefore performs equivalently for the stochastic system as for the previous ones (see Table 15). The variables of this system are co-integrated. Moreover, the PSTE can be directly applied to the original signal without any detrending and manages to detect the true causal effects. In order to compute the CGCI, the time series of system 10 should be detrended to render stationary. As for System 7, a polynomial of order one is fitted prior to the estimation of the CGCI. The CGCI ($P=3$) correctly detects the couplings on the detrended data, for both time series lengths (see Table 15). The CGCI on the detrended data is more effective than the PSTE on the original data especially for small $n$, but it depends to the detrending.

Table 15 Percentage of statistically significant PSTE ($m=3$) values for the simulation system 10

Finally, we add a time series from an IGARCH(1,1) process (multiplied by $g=0.2$ as in the case of System 7) to the original time series of System 10 in order to obtain a signal which is non-stationary both in mean and variance. The PSTE is directly applied to the non-stationary signal, while detrending (using a polynomial fit of order one) is required for the estimation of the CGCI. The percentages of significant PSTE values are very low for both $n$ and all directions, however they increase with $n$ for the true couplings (see Table 16). Larger $n$ is required for an efficient implementation of the PSTE. The CGCI indicates spuriously the bidirectional coupling among all variables. The failure of the CGCI is due to the non-stationarity in variance. A different detrending process could be more appropriate and could improve the performance of the CGCI. Furthermore, the CGCI can be sensitive to the existence of co-integration between the variables; a vector error correction model (VECM) may be applied in such cases. The stationarity and the absence of co-integration are two requirements that should be tested before estimating the CGCI.

Table 16 Percentage of statistically significant PSTE ($m=3$) values for the simulation system 10 with an IGARCH(1,1) superimposed to it

Fig. 5

Time series of a original prices and b the returns of the studied economic variables

This example indicates the necessity of employing causality measures such as the PSTE that are directly applicable to the original time series and do not require detrending or filtering. Since most measures are sensitive to detrending and filtering, their performance may depend on the effectiveness of these procedures.

3.3 Application to Financial Time Series

In the aim to investigate any direct causal effect of financial uncertainty in both the short and long-term interest rates we apply our suggested methodology to the daily time series of the 3-month Treasury Bill of Secondary Market Rate (denoted as $X_1$), the 10-year Treasury Constant Maturity Rate ($X_2$) and the Chicago Board Options Exchange (CBOE) Volatility Index or VIX ($X_3$) (see Fig. 5). The data set spans the period from 05/01/2004 to 18/5/2012. The choice of the variables addresses two main issues: (1) how the short and long-term interest rates, determinant components of the spread, interact and (2) how uncertainty shocks can affect the term structure of interest rates. Financial uncertainty is taken into account by the well-known fear index VIX (option-implied expected volatility on the $S \& P 500$ index with an horizon of 30 calendar days) while the stance of monetary policy is represented by the 3-month Treasury Bill, taking into account its close positive relationship with the key-interest rate (FF) of the US central bank (Kyrtsou and Vorlow 2009). To the best of our knowledge, this application is the first attempt to investigate the impact of a fear index to interest rates of different maturities simultaneously, with means of either linear or nonlinear causality tests.

The fact that real data obey rich underlying structures, together with the significant power of the CGCI and PSTE in the presence of linear and nonlinear couplings respectively, underline the need of a joint implementation. Both the CGCI and PSTE are applied to the VAR-filtered and returns series in order to shed light on the nature of the causal effects. Since the PSTE is not affected by non-stationarity, it is applied directly to the original data (prices) as well, helping us gather additional information about the possible links in the long-run.

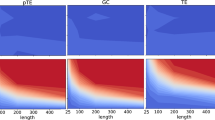
Regarding the estimation of the CGCI, the BIC suggests using $P = 1$ and 2. To examine also its sensitivity to the model order, we vary $P$ from 1 to 5. As expected, the CGCI indicates no causal effects after the VAR filtering. When the returns series are taken, the test recognizes the couplings $X_1 \rightarrow X_2$, $X_1 \rightarrow X_3$, $X_2 \rightarrow X_1$ for different $P$ values (see Table 17); while $P$ increases, fewer couplings are emerged i.e for $P$ = 6 to 10, only the coupling $X_1 \rightarrow X_3$ is significant.

Table 17 Direct causal effects based on the CGCI values for the financial application

As stated previously, the PSTE is estimated on the original prices, the returns and the VAR-filtered returns for $m = 2$ and 3, while the time delay is set to one. It consistently indicates that the 10-year Treasury Bond drives the short-term interest rate ($X_2 \rightarrow X_1$) for all data sets when $m = 2$. Only in the case of the VAR residuals, the additional coupling between the VIX and the 3-month Treasury Bill ($X_3 \rightarrow X_1$) is obtained. For $m = 3$, the estimated relationships for the VAR residuals do not change (see Table 18). It is more than evident that the dominant driving $X_2 \rightarrow X_1$ is not affected by the non-stationarity of data.

Table 18 Direct causal effects based on the PSTE values for the financial application

Combining the empirical findings confirms the nonlinear direct causality from both the VIX and the 10-year Treasury Bill to the short-term rate, emphasizing the significant impact of expectations on the design of monetary policy. The latter finding comes to validate the results of Bekaert et al. (2011) supporting the view that the uncertainty component of the VIX index determines the direction of the relationship.

On the other hand, the behavioral content of the long-term interest rate, which is strongly related to the agents’ expectations about the future inflation levels, in association with the specific character of factors affecting its evolution, explain the detected nonlinear coupling. Such factors include budget deficits (Laubach 2009), public debt (Ardagna et al. 2007), global shocks (Alper Emre and Forni 2011) and sovereign spreads (Favero et al. 2010). The reverse causality from the long to the short-term interest rate can find its source at the evolving connection between monetary policy actions and long-term rates. According to Roley and Sellon (1995) “while there is considerable evidence that monetary policy has a large impact on short-term interest rates, the connection between policy actions and long-term rates often appears weaker and less reliable”.

4 Conclusions

The PSTE is a nonlinear causality measure designed to detect only direct causal effects. It is not affected by the presence of outliers and non-stationarity, since it uses ranks from the delay vectors of the data and not the sample values. However, it requires large time series lengths in order to attain high power. The stability of the results based on the PSTE is expected to be lost by increasing $m$, unless large data sets are considered (see Papana et al. 2013). Besides, the PSTE is not effective when only linear couplings are present in the systems. Additional results for the performance of the PSTE in case of linear systems can be found in Papana et al. (2013).

In contrast, although the CGCI has proved to be efficient in different applications (e.g. Geweke (1984) and Chen et al. (2006)), it has a poorer performance compared to the PSTE when the causal couplings are nonlinear. The present simulation experiment showed also the inadequacy of the CGCI in the presence of long tails and outliers.

The PSTE is compared only with the CGCI, since this is the most common measure for the detection of causal effects in financial time series. If the signal is non-stationary, data are first transformed and the estimation of CGCI follows. Causality measures that require detrending or filtering of the original data are sensitive to this procedure. Since this is out of the scope of this paper, we do not consider alternative causality measures. A joint implementation of the PSTE and additional causality measures can be found in Papana et al. (2013) and Kugiumtzis (2013). Moreover, the VECM methodology together with the partial transfer entropy on rank vectors (PTERV), which is an extension of the PSTE are analytically presented and applied in economic data in a recent paper by Papana et al. (2014).

It is well documented that financial time series are prone to stylized facts such as non-stationarity in mean or in variance, heteroskedasticity, nonlinearity and outliers (Alexander 2008; Kyrtsou and Malliaris 2009). The sensitivity of the CGCI to nonlinear structures is revealed when real data are considered. On the contrary, the PSTE performs well, highlighting the interesting transmission mechanism between the 10-year Treasury Bond and the VIX to the 3-month Treasury Bill. It turns out that the PSTE remains robust with, either non-stationary or stationary in mean and variance, financial time series. As such, it constitutes a powerful tool when real data with complex underlying properties are studied.