Computational aspects of column generation for nonlinear and conic optimization: classical and linearized schemes

Abstract

Solving large scale nonlinear optimization problems requires either significant computing resources or the development of specialized algorithms. For Linear Programming (LP) problems, decomposition methods can take advantage of problem structure, gradually constructing the full problem by generating variables or constraints. We first present a direct adaptation of the Column Generation (CG) methodology for nonlinear optimization problems, such that when optimizing over a structured set ${\mathcal {X}}$ plus a moderate number of complicating constraints, we solve a succession of (1) restricted master problems on a smaller set ${\mathcal {S}}\subset {\mathcal {X}}$ and (2) pricing problems that are Lagrangean relaxations wrt the complicating constraints. The former provides feasible solutions and feeds dual information to the latter. In turn, the pricing problem identifies a variable of interest that is then taken into account into an updated subset ${\mathcal {S}}'\subset {\mathcal {X}}$. Our approach is valid whenever the master problem has zero Lagrangean duality gap wrt to the complicating constraints, and not only when ${\mathcal {S}}$ is the convex hull of the generated variables as in CG for LPs, but also with a variety of subsets such as the conic hull, the linear span, and a special variable aggregation set. We discuss how the structure of ${\mathcal {S}}$ and its update mechanism influence the number of iterations required to reach near-optimality and the difficulty of solving the restricted master problems, and present linearized schemes that alleviate the computational burden of solving the pricing problem. We test our methods on synthetic portfolio optimization instances with up to 5 million variables including nonlinear objective functions and second order cone constraints. We show that some CGs with linearized pricing are 2–3 times faster than solving the complete problem directly and are able to provide solutions within 1% of optimality in 6 h for the larger instances, whereas solving the complete problem runs out of memory.

1 Introduction

Decomposition methods are fundamental tools to solve difficult large scale problems. In this work, we focus on Column Generation (CG) algorithms, where the number of variables is too large to allow a direct solution with an off-the-shelf optimization software. More formally, we focus on solving the following problem:

$$\begin{aligned} \left( P\left( {\mathcal {X}}\right) \right) \quad \omega \left( {\mathcal {X}}\right) := \min \limits _{x,y}\quad&f(x,y)\\ \text {s.t.}\quad&x\in {\mathcal {X}},\, -g(x,y)\in {\mathcal {C}}, \end{aligned}$$

where ${\mathcal {C}}$ is a cone in some Euclidean space, ${\mathcal {X}}$ is a high-dimensional structured set and f and g are generic mappings¹. The feasibility set of the auxiliary variables y is fully defined by constraints $-g(x,y)\in {\mathcal {C}}$.

Defining n, $n_0$ and m as the respective dimensions of x, y and ${\mathcal {C}}$, we assume that the main issue with $P({\mathcal {X}})$ is the joint presence of the difficult (or coupling/side) constraints $-g(x,y)\in {\mathcal {C}}$ and the magnitude of $n\gg 1$. In other words, we consider a setting in which: (1) for some low-dimensional subset ${\mathcal {S}}\subseteq {\mathcal {X}}$, $P({\mathcal {S}})$ can be solved efficiently, and (2) $P({\mathcal {X}})$ without the constraints $-g(x,y)\in {\mathcal {C}}$ gives birth to an efficiently solvable problem. We propose to use these simpler optimization problems to build a computationally efficient solution method for $P({\mathcal {X}})$. For the sake of simplicity, we do not consider equalities in the complicating constraints (the generalization is straightforward).

1.1 Examples

We now show some examples of problems that have the structure we just described. For given integers $p,q>0$, we denote $[p]:=\{1,...,p\}$, $||\cdot ||_q$ is the q-norm in ${\mathbb {R}}^p$, the Lorentz cone of dimension $p+1$ is the set ${\mathcal {L}}^{p+1}_2:=\{ (u,u_0)\in {\mathbb {R}}^{p+1} : ||u||_2\leqslant u_0\}$. Finally, given symmetric matrices $M^1$ and $M^2$, $M^1\succeq M^2$ means that $M^1-M^2$ belongs to the cone of semidefinite positive matrices, i.e. the eigenvalues of $M^1-M^2$ are nonnegative.

Example 1

Partially separable Second-Order cone (SOC) Programming, where ${\mathcal {X}}:=\{x=(x^k)_{k\in [K]}:||A^k x^k-a^k||_2\leqslant (p^k)^\top x^k -p_0^k,\forall k\in [K]\}$, $g(x,y):=(b^l-X^{l}x-Y^l y;r_0^l-x^\top q^{l}-y^\top r^l)_{l\in [L]}$ and ${\mathcal {C}}:=\{(u^l,u^l_0)_{l\in [L]}:||u^l||_2\leqslant u^l_0, \forall l\in [L]\}$ with L reasonably small:

$$\begin{aligned} \min \limits _{x=(x^k)_{k},y}\quad&f(x,y):=c^\top x+d^\top y\\ \text {s.t.}\quad&\left| \left| A^k x^k-a^k\right| \right| _2\leqslant \left( p^k\right) ^\top x^k-p_0^k,&\forall k\in [K]\\&\left| \left| X^lx +Y^l y-b^l\right| \right| _2\leqslant x^\top q^{l}+y^\top r^l-r_0^l,&\forall l\in [L]. \end{aligned}$$

Notice that partially block-angular LPs are a particular case of Example 1 (i.e. when $A^k$, $a^k$, $X^l$, $Y^l$ and $b^l$ are all zero).

Example 2

Partially separable Semidefinite Programming (SDP) where $g(x,y):=B-\sum _{k=1}^K\sum _{j=1}^{n_k}x_j^k X^{kj}-\sum _{j=1}^{n_0}y_j Y^j$, ${\mathcal {X}}:=\{x=(x^k)_{k\in [K]}:\sum _{j=1}^{n_k}x_j^k A^{kj}\succeq B^k,\forall k\in [K]\}$ and ${\mathcal {C}}$ is a cone of SDP matrices of reasonable dimension:

$$\begin{aligned} \min \limits _{x=(x^k)_k,y}\quad&f(x,y):=c^\top x+d^\top y\\ \text {s.t.}\quad&\sum _{j=1}^{n_k}x_j^k A^{kj}\succeq B^k,&\forall k\in [K]\\&\sum \limits _{k=1}^K\sum \limits _{j=1}^{n_k}x_j^k X^{kj}+\sum \limits _{j=1}^{n_0}y_j Y^j\succeq B. \end{aligned}$$

Several existing works already use CG to tackle this kind of problem with e.g. polyhedral approximations of the cone of SDP matrices as their ${\mathcal {S}}$ sets [2]. CG could also be used to generate the block factor-width-2 cone of matrices that is used in [68] to inner approximate huge SDP cones. Example 1 and some inner approximations of high-dimensional SDP cones are a particular case of Example 2.

Example 3

Partially separable Nonlinear Programming (NLP). ${\mathcal {C}}:={\mathbb {R}}_+^m$ with m reasonably small and ${\mathcal {X}}:=\{x=(x^k)_{k\in [K]}:p_i^k\left( x^k\right) \leqslant 0,\forall i\in [m_k],\forall k \in [K]\}$:

$$\begin{aligned} \min \limits _{x=(x^k)_k,y}\quad&f(x,y):=\sum \limits _{k=1}^K c_k\left( x^k\right) +d(y)\\ \text {s.t.}\quad&p_i^k\left( x^k\right) \leqslant 0,&\forall i\in [m_k],\forall k \in [K]\\&g_i\left( x^1,...,x^K,y\right) \leqslant 0,&\forall i\in [m]. \end{aligned}$$

Examples 1 and 2 are particular cases of Example 3.

Finally, a vast majority of problems that are tractable computationally when their data is known become way harder when considering their stochastic counterpart, i.e. when their data—such as their objective function or constraints—are uncertain and considered random [5]. They can become highly nonlinear or too big when—to name a few—using risk measures or chance constraints. As we see later in our experimental setup, the risk-averse portfolio optimization problem that we consider allows our CG scheme to take advantage of the original (deterministic) features of the problem.

1.2 Preliminaries

We now introduce several definitions that are used through this paper. We call the dual cone of the cone ${\mathcal {C}}$, the set ${\mathcal {C}}^*$ defined as ${\mathcal {C}}^*:=\{ u: \langle u,v\rangle \geqslant 0, \forall v\in {\mathcal {C}} \}$. For any penalization vector $\lambda \in {\mathcal {C}}^*$, let us define the following Lagrangean relaxation:

$$\begin{aligned} \left( L\left( {\mathcal {X}},\lambda \right) \right) \quad \omega \left( {\mathcal {X}},\lambda \right) := \min \limits _{x\in {\mathcal {X}},y}\left\{ f(x,y)+ \left\langle \lambda , g(x,y)\right\rangle \right\} . \end{aligned}$$

For any $\lambda \in {\mathcal {C}}^*$ we have $\omega ({\mathcal {X}},\lambda )\leqslant \omega ({\mathcal {X}})$. The Lagrangean dual of $P({\mathcal {X}})$ is:

$$\begin{aligned} \left( D\left( {\mathcal {X}}\right) \right) \quad \max \limits _{\lambda \in {\mathcal {C}}^*} \left\{ \omega \left( {\mathcal {X}},\lambda \right) \right\} \leqslant \omega ({\mathcal {X}}). \end{aligned}$$

We say that $P({\mathcal {X}})$ has no Lagrangean duality gap if $P({\mathcal {X}})$ and $D({\mathcal {X}})$ share the same optimal value $\omega ({\mathcal {X}})$. Notice that the concept of Lagrangean dual is associated to the constraints that are relaxed, which in this work are the constraints $-g(x,y)\in {\mathcal {C}}$. On another hand, given a set ${\mathcal {S}}\subseteq {\mathcal {X}}$, we define the restricted problem as follows:

$$\begin{aligned} \left( P\left( {\mathcal {S}}\right) \right) \quad \omega \left( {\mathcal {S}}\right) :=\min \limits _{x\in {\mathcal {S}}, y }\left\{ f(x,y): -g(x,y)\in {\mathcal {C}}\right\} . \end{aligned}$$

Given that the original problem $P({\mathcal {X}})$ is a relaxation of $P({\mathcal {S}})$ for any ${\mathcal {S}}\subseteq {\mathcal {X}}$, we have $\omega ({\mathcal {X}})\leqslant \omega ({\mathcal {S}})$. If ${\mathcal {S}}$ contains the projection onto the x-components of an optimal solution of $P({\mathcal {X}})$, notice that we have $\omega ({\mathcal {X}})= \omega ({\mathcal {S}})$ and $P({\mathcal {S}})$ returns optimal solutions for $P({\mathcal {X}})$.

1.3 Main concept

In this paper, we extend the concept of CG beyond the scope of LPs and simplicial approximations of ${\mathcal {X}}$, while keeping a similar philosophy: in the LP case, at each iteration k we solve an approximation $P({\mathcal {S}}^k)$ of $P({\mathcal {X}})$ that uses ${\mathcal {S}}^k:=\text {conv}({{\bar{x}}}^l)_{l\in [k]}$, the convex hull of a family of columns ${{\bar{x}}}^l$, each belonging to ${\mathcal {X}}$. Doing so, we obtain an upper bound $\omega ({\mathcal {S}}^k)$ on $\omega ({\mathcal {X}})$ and retrieve the corresponding optimal dual multipliers $\lambda ^k$. These multipliers are fed to the pricing problem $L({\mathcal {X}},\lambda ^k)$ that returns an optimal solution $(\bar{x}^k,{{\bar{y}}}^k)$ and provides a lower bound $\omega ({\mathcal {X}},\lambda ^k)$ for $\omega ({\mathcal {X}})$.

Fig. 1

CG feedback: $({{\bar{x}}}^k,{{\bar{y}}}^k)$ is optimal for $L({\mathcal {X}},\lambda ^k)$, $\lambda ^k$ is dual-optimal for $P({\mathcal {S}}^k)$

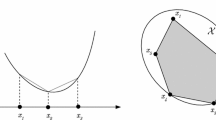
As pictured in Fig. 1, we iteratively refine both problems until the optimality gap $\omega ({\mathcal {X}},\lambda ^k) - \omega ({\mathcal {S}}^k)$ is under some tolerance. Our approach generalizes CG in several ways: under reasonable conditions (1) the approximating set ${\mathcal {S}}^k$ does not have to be a convex hull of previous columns, and (2) $P({\mathcal {X}})$ is not necessarily an LP but $P({\mathcal {S}}^k)$ must have zero Lagrangean duality gap wrt the complicating constraints $-g(x,y)\in {\mathcal {C}}$. Further, (1) depending on the structure of the approximations ${\mathcal {S}}^k$, the master problem can be greatly simplified and (2) under some convexity assumptions, it is possible to replace $L({\mathcal {X}},\lambda ^k)$ by a computationally easier pricing. We now present the assumptions used in this article.

1.4 Working hypothesis

We make two kinds of assumptions: the first ensures the validity of our framework and the remaining are necessary to make it computationally efficient:

Assumption 1

${\mathcal {S}}$ is such that $P({\mathcal {S}})$ can be solved by a Lagrangean algorithm that provides a multiplier $\lambda \in {\mathcal {C}}^*$ such that $\omega ({\mathcal {S}}) = \omega ({\mathcal {S}},\lambda )$.

Assumption 2

For any $\lambda \in {\mathcal {C}}^*$ we can solve efficiently $L({\mathcal {X}},\lambda )$ in practice.

Assumption 3

The choice of ${\mathcal {S}}$ makes $P({\mathcal {S}})$ efficiently solvable in practice.

Assumption 1 implies that $P({\mathcal {S}})$ has no Lagrangean duality gap and we have an algorithm to find an optimal primal-dual pair $((x,y),\lambda )$ for $P({\mathcal {S}})$; notice that (x, y) is also optimal for $L({\mathcal {S}},\lambda )$. Assumption 1 is satisfied by many optimization problems such as e.g. LPs or Linear Conic problems (LC) and Nonlinear optimization Problems (NLP) that satisfy a Constraint Qualification [43], which can be solved using an interior point method [41]. Slater’s condition is a popular constraint qualification that is satisfied if the problem at hand is convex and strictly feasible²: Although Assumption 1 may sound overly restrictive, we show in Proposition 1 that for a regular enough ${\mathcal {S}}$, $P({\mathcal {S}})$ satisfies Slater’s condition. Notice that we only need $P({\mathcal {S}})$ to satisfy Assumption 1, while $P({\mathcal {X}})$ may not, as we show in Example 4:

Example 4

Consider the following sets

$$\begin{aligned} {\mathcal {X}}:=&\left\{ x\in {\mathbb {R}}^6: \begin{pmatrix} x_1&{}x_4&{}x_5\\ x_4&{}x_2&{}x_6\\ x_5&{}x_6&{}x_3 \end{pmatrix}\succeq 0 \right\} ,\\ {\mathcal {S}}:=&\left\{ x\in {\mathbb {R}}^6 : \exists \theta \in [0,1]: \begin{pmatrix} x_1&{}x_4&{}x_5\\ x_4&{}x_2&{}x_6\\ x_5&{}x_6&{}x_3 \end{pmatrix} =\theta \begin{pmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0\\ \end{pmatrix}+(1-\theta ) \begin{pmatrix} 0&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0\\ \end{pmatrix} \right\} \subsetneq {\mathcal {X}} \end{aligned}$$

and the following SDP $P({\mathcal {X}})$:

$$\begin{aligned} \omega ({\mathcal {X}}):=\min _{x\in {\mathcal {X}},y}\left\{ y_2 : \begin{pmatrix} x_1&{}x_4&{}x_5\\ x_4&{}x_2&{}x_6\\ x_5&{}x_6&{}x_3 \end{pmatrix} = \begin{pmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}0 \end{pmatrix} -y_1 \begin{pmatrix} 1&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{pmatrix} -y_2 \begin{pmatrix} 0&{}0&{}1\\ 0&{}-1&{}0\\ 1&{}0&{}0 \end{pmatrix} \right\} . \end{aligned}$$

Because $P({\mathcal {S}})$ is an LP, it satisfies Assumption 1, while $P({\mathcal {X}})$ does not by having a nonzero duality gap (see Appendix A for the details). This example shows that our framework could possibly solve some problems having a nonzero duality gap.

Assumptions 2 and 3 are not needed from a theoretical point a view, however, they are essential for our methodology to be competitive computationally. Assumption 2 is the basic assumption for classical CG for LPs and means that the pricing problem $L({\mathcal {X}},\lambda )$ is either (1) block-decomposable thanks to the structure of ${\mathcal {X}}$ and can be solved in parallel, or (2) there is an efficient dedicated algorithm to solve it. Finally, Assumption 3 says that ${\mathcal {S}}$ is e.g. low dimensional and defined with a few constraints³. Both Assumptions 2 and 3 depend on the ability of the modeller to identify a set of constraints that are relaxed and choose a set ${\mathcal {S}}$ such that both $P({\mathcal {S}})$ and $L({\mathcal {X}},\lambda )$ are easy enough to solve in practice.

Our objective is to design an iterative search in terms of both $\lambda$ and ${\mathcal {S}}$ that successively improves the lower and upper bounds $\omega ({\mathcal {X}},\lambda )$ and $\omega ({\mathcal {S}})$, returning increasingly good feasible solutions as a byproduct. Our framework achieves this goal by feeding information from one problem to the other by updating respectively $\lambda$ from $P({\mathcal {S}})$ and ${\mathcal {S}}$ from $L({\mathcal {X}},\lambda )$, while choosing computationally efficient approximations ${\mathcal {S}}$ and pricing problems.

1.5 Dantzig–Wolfe for LPs

To illustrate our point, consider the following LP as a special (well known) case of $P({\mathcal {X}})$ - i.e. when ${\mathcal {X}}$ is a polyhedron, f and g are linear mappings and ${\mathcal {C}}:={\mathbb {R}}^m_+$:

$$\begin{aligned} \omega ({\mathcal {X}}):=\min \limits _{x,y}\quad&c^\top x+d^\top y \end{aligned}$$

(1a)

$$\begin{aligned} \quad\quad\quad\quad\quad\quad\quad\text {s.t.}\quad&x\in {\mathcal {X}}:=\left\{ x\geqslant 0: Ax=a\right\} \end{aligned}$$

(1b)

$$\begin{aligned}\quad\quad\quad\quad&Xx+Yy\geqslant b. \end{aligned}$$

(1c)

Because of the high dimensionality of the polyhedron ${\mathcal {X}}$ and the presence of (1c) breaking any eventual structure, even state-of-the art solvers cannot tackle directly this kind of problem. Suppose in our case that optimizing a linear objective over the (high-dimensional) polyhedron ${\mathcal {X}}$ is easy in practice and, as pointed out before, if we were to replace ${\mathcal {X}}$ by some wisely chosen subset ${\mathcal {S}}\subseteq {\mathcal {X}}$ in (1), we would obtain a computationally cheap upper bound for the optimal value of (1).

Master problem $P({\mathcal {S}})$ In this LP case, there is a natural choice for ${\mathcal {S}}$ readily available [7]: Letting ${\mathcal {V}}$ be the set of vertices of ${\mathcal {X}}$ and ${\mathcal {R}}$ a complete set of extreme rays of ${\mathcal {X}}$, we have ${\mathcal {X}}=\text {conv }{\mathcal {V}}+\text {cone } {\mathcal {R}}$, where $\text {cone } {\mathcal {R}}$ is the conic hull of ${\mathcal {R}}$:

$$\begin{aligned} {\mathcal {X}}= \left\{ x : x=\sum \limits _ {l:{{\bar{x}}}^l \in {\mathcal {V}}}\theta _l {{\bar{x}}}^l +\sum \limits _ {l:{{\bar{x}}}^l \in {\mathcal {R}}}\theta _l {{\bar{x}}}^l, \text { for some } \theta \geqslant 0 : \sum \limits _{l:{{\bar{x}}}^l \in {\mathcal {V}}} \theta _l =1 \right\} . \end{aligned}$$

Problem (1) can thus be rewritten as the following extensive formulation:

$$\begin{aligned} \omega ({\mathcal {X}})=\min \limits _{\theta \geqslant 0,y}\quad&\sum \limits _ {l:{{\bar{x}}}^l \in {\mathcal {V}}}\theta _l c^\top {{\bar{x}}}^l +\sum \limits _ {l:{{\bar{x}}}^l \in {\mathcal {R}}}\theta _l c^\top {{\bar{x}}}^l +d^\top y \end{aligned}$$

(2a)

$$\begin{aligned} \quad\quad\quad\text {s.t.}\quad&\!\sum \limits _ {l:\bar{x}^l \in {\mathcal {V}}}\theta _l X {{\bar{x}}}^l +\sum \limits _ {l:{{\bar{x}}}^l \in {\mathcal {R}}}\theta _l X{{\bar{x}}}^l +Yy\geqslant b \end{aligned}$$

(2b)

$$\begin{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sum \limits _{l:{{\bar{x}}}^l \in {\mathcal {V}}} \theta _l =1 \end{aligned}$$

(2c)

Because ${\mathcal {X}}:=\{x\geqslant 0: Ax=a\}$ is convex and each ${{\bar{x}}}^l$ belongs to ${\mathcal {X}}$, notice that the side constraints $Xx+Yy\geqslant b$ are the only remnants of the original problem. The LP dual of the extended formulation is the following problem:

$$\begin{aligned} \omega ({\mathcal {X}})=\max \limits _{\lambda \geqslant 0,\eta }\quad&b^\top \lambda +\eta \end{aligned}$$

(3a)

$$\begin{aligned} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\text {s.t.}\quad&\left( X {{\bar{x}}}^l\right) ^\top \lambda \leqslant c^\top {{\bar{x}}}^l-\eta ,&\forall l: {{\bar{x}}}^l\in {\mathcal {V}} \end{aligned}$$

(3b)

$$\begin{aligned}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad&\left( X {{\bar{x}}}^l\right) ^\top \lambda \leqslant c^\top {{\bar{x}}}^l,&\forall l: {{\bar{x}}}^l\in {\mathcal {R}} \end{aligned}$$

(3c)

$$\begin{aligned}\quad\quad\quad\quad&Y^\top \lambda =d. \end{aligned}$$

(3d)

A direct solution of problem (2) is in general impractical as its number of variables can be exponential in $(n,n_0,m)$. However, the Dantzig–Wolfe (DW) algorithm [16] offers a solution method successively generating vertices and extreme rays of the polyhedron ${\mathcal {X}}$. It starts with finite subsets $\overline{{\mathcal {V}}}\subset {\mathcal {V}}$ and $\overline{{\mathcal {R}}}\subset {\mathcal {R}}$ and solves a restricted master problem (2) with $\overline{{\mathcal {V}}}$ and $\overline{{\mathcal {R}}}$ instead of the full sets ${\mathcal {V}}$ and ${\mathcal {R}}$. With our notation, this restricted master problem is none other than $P({\mathcal {S}})$ with ${\mathcal {S}}:=\text {conv }\overline{{\mathcal {V}}}+\text {cone }\overline{{\mathcal {R}}}$. Making different choices for ${\mathcal {S}}$ and consider a broader class of optimization problems is one of the central ideas of this paper.

Pricing problem $L({\mathcal {X}},\lambda )$ Obtaining the optimal dual variables $\lambda$ associated with constraints (2b) in $P({\mathcal {S}})$, the Lagrangean relaxation $L({\mathcal {X}},\lambda )$ is solved:

$$\begin{aligned}&\min \limits _{x\in {\mathcal {X}},y}\left\{ c^\top x+d^\top y+\lambda ^\top \left( b-Xx-Yy\right) \right\} \\ =&\min \limits _{x\in {\mathcal {X}},y}\left\{ \left( c-X^\top \lambda \right) ^\top x + \left( d-Y^\top \lambda \right) ^\top y \right\} +\lambda ^\top b. \end{aligned}$$

By dual feasibility (3d) of $\lambda$, implying that $Y^\top \lambda = d$, it can be rewritten

$$\begin{aligned}&\lambda ^\top b+ \min \limits _{x\in {\mathcal {X}}}\left\{ \left( c-X^\top \lambda \right) ^\top x \right\} , \end{aligned}$$

(4)

thus eliminating the variables y from the pricing problem. Discarding this dependency in y is, however, not always possible in a nonlinear setting. Letting ${{\bar{x}}}$ be an optimal solution of the pricing problem (4), with a slight abuse of notation we refer to an optimal solution to either (1) a vertex of ${\mathcal {X}}$ if the pricing problem in x has a bounded optimal objective value, or (2) an extreme ray of ${\mathcal {X}}$ otherwise. In the latter case we increment $\bar{{\mathcal {R}}}\leftarrow \bar{{\mathcal {R}}}\cup \{{{\bar{x}}}\}$ and in the former $\bar{{\mathcal {V}}}\leftarrow \bar{{\mathcal {V}}}\cup \{{{\bar{x}}}\}$, which defines the particular update mechanism used by DW. We iterate until an optimality tolerance criterion is satisfied or until we generated the complete sets ${\mathcal {V}}$ and ${\mathcal {R}}$, thus solving the full, original problem $P({\mathcal {X}})$.

1.6 Decomposition methods and previous work

CG algorithms were studied in depth for LPs [16, 36] or Mixed Integer Linear Programming (MILP) problems [4, 55], where notoriously large MILPs could be solved by embedding DW in a branch-and-price framework [14, 18]. The main idea of DW is to exploit the structure of ${\mathcal {X}}$ and solve smaller problems: (1) the master problem, that works over a reduced subset ${\mathcal {S}}\subset {\mathcal {X}}$ while keeping the side constraints; and (2) a pricing problem that is still large but is computationally easy to solve thanks to the absence of side constraints.

In a nonlinear setting, several algorithms such as the Alternating Direction Method of Multipliers (ADMM) [64], the Douglas–Rachford splitting operator [21] or augmented Lagrangean algorithms [53] all make use of a special structure in ${\mathcal {X}}$. However, they all solve inexactly the Lagrangean dual $D({\mathcal {X}})$ and do not always provide feasible solutions for $P({\mathcal {X}})$. Further, proving optimality or near optimality can be tricky and a concrete stopping criterion is also not always available. Closer to a generalization of CG for NLPs, the convex simplex method [65] minimizes a nonlinear objective over a polyhedron. It can be seen as solving a master problem over a basis of variables and—similar to the simplex algorithm—selecting the entering variable by linearizing some penalization function. Akin to DW, the simplicial decomposition [61] solves a linearized master problem over a subset ${\mathcal {S}}$ that is the convex hull of a handful of points, and the pricing problem generating such columns is the original problem $P({\mathcal {X}})$ with an objective linearized at an incumbent point. [39] has the same master problem but the pricing problem uses a penalty function instead of a lagrangean relaxation and does not consider generic conic constraints.

Problem-dependent CG schemes for NLPs were presented in e.g. [42] for nonlinear facility location problems that are reformulated as set partitioning problems and solved with DW, whose pricing problem is an NLP with integer variables; [15] that uses a branch-and-price scheme for sibling groups reconstruction, which is reformulated as a set covering problem for which columns are generated with quadratic optimization pricing problems. A direct extension of DW for NLPs with ${\mathcal {C}}={\mathbb {R}}^m_+$ is introduced in [9]. DW is used in [40, 44] for mixed integer nonlinear-nonconvex optimization problems with polyhedral complicating constraints.

In an LC setting—i.e. f and g are linear mappings but ${\mathcal {C}}$ is a more general cone than ${\mathbb {R}}^m_+$—similar extensions of CG have been developed: [2] present a decomposition procedure for SDPs where ${\mathcal {S}}$ is an inner approximation of a matrix set ${\mathcal {X}}$, that are updated with the (matricial) “columns” generated by a separation problem tailored for SDPs. The approach has two drawbacks: (1) depending on the inner approximation chosen, the master problem can be slow to attain near optimality, and (2) the pricing problem is a handmade separation problem that uses problem-specific considerations and does not provide dual bounds. For SDPs, chordal sparsity patterns [59] are able to detect underlying substructures that can be exploited by ADMM [58, 66, 67], but no CG approach has been attempted so far. The presence of a special substructure being crucial for decomposition, automatic structure detection in LPs were developed in [6, 31, 63] so that a decomposition method can make use of it. Previous CG methods for LC have focused on gradually building the set of variables considered with problem specific algorithms that are difficult to generalize.

Other works use a different kind of set ${\mathcal {S}}$ for LPs. A subset ${\mathcal {S}}$ consisting on forcing clusters of variables to share the same value—thus aggregating the variables together—is used in [38] and [8]. This variable aggregation principle has been successfully applied to Freight routing [54], general extended formulations [55], open pit mining scheduling [8], pricing problems [3], quadratic binary knapsack problems [50], support vector machine problems [45] or in a column-and-row generation context where DW is used in combination with a constraint aggregation scheme to solve resource constrained covering problems [51]. Finally, [23, 24] introduce a CG scheme for almost generic sets ${\mathcal {S}}$ and pricing problems. However, they do not take into account generic conic side constraints and link their generic scheme with only a few special cases, whereas we take advantage of the structure of both the pricing and master problems.

1.7 Article outline

Section 2 presents a CG algorithm to solve the generic NLP $P({\mathcal {X}})$ with a large number of variables and nonlinear-conic side constraints. We show that it admits several existing schemes as special cases, all defined by different sets ${\mathcal {S}}$. We present sufficient conditions to (1) drop the optimization in the y variables for the pricing problem and (2) make sure that $P({\mathcal {S}})$ has no Lagrangean duality gap. As the Lagrangean relaxation of a nonlinear optimization problem can be as hard as the problem itself, under some convexity assumptions we present in Sect. 3 a linearized version of the methodology making the pricing problem easier to solve. Additionally, we also prove that $L({\mathcal {X}},\lambda )$ can always be independent of the secondary variables y in the linearized algorithm. In Sect. 4, we point out the relationships of our generic schemes to existing frameworks. In Sect. 5 we describe the risk-averse portfolio optimization problem on which we test our algorithms, and present several computational enhancements. In Sect. 6, we present numerical results on large scale synthetic instances and empirically prove the usefulness of our methodology. We conclude with some remarks and the description of several ongoing works in Sect. 7.

1.8 Background notations

Given a set ${\mathcal {U}}$, we call respectively $\text {conv } {\mathcal {U}}$, $\text {cone } {\mathcal {U}}$, $\text {lin } {\mathcal {U}}$, $\text {aff } {\mathcal {U}}$, $\text {relint } {\mathcal {U}}$ and $\text {dim } {\mathcal {U}}$, the convex hull, the conic hull, the linear span, the affine span, the relative interior and the dimension of ${\mathcal {U}}$. The adjoint $U^*$ of a linear mapping $U:{\mathcal {U}}\rightarrow {\mathcal {V}}$ is the linear operator such that $\langle Uu,v\rangle = \langle u, U^*v\rangle$ for any $(u,v)\in {\mathcal {U}}\times {\mathcal {V}}$. For any integer $p>0$, ${\mathcal {B}}({{\bar{u}}},\rho ):=\{u \in {\mathbb {R}}^p: ||{{\bar{u}}} - u||_2 < \rho \}$ is the open ball of radius $\rho >0$ centered at ${{\bar{u}}} \in {\mathbb {R}}^p$. A cone ${\mathcal {K}}$ is said to be proper if it is convex, closed, contains no line and $\text {relint } {\mathcal {K}}\ne \emptyset$. If ${\mathcal {K}}$ is a proper cone then $u\in \text {relint }{\mathcal {K}}$ and ${{\bar{u}}}\in {\mathcal {K}}$ imply that $u+{{\bar{u}}}\in \text {relint }{\mathcal {K}}$.

Consider some function $\varphi :{\mathcal {U}}\rightarrow {\mathcal {V}}$. For some $L>0$ and a norm $||\cdot ||$, we say that $\varphi$ is L-Lipschitz if for any $(u^1,u^2)\in {\mathcal {U}}\times {\mathcal {U}}$ we have $||\varphi (u^1)-\varphi (u^2)||\leqslant L ||u^1-u^2||$. For some cone ${\mathcal {K}}\subseteq {\mathcal {V}}$, $\varphi$ is said to be ${\mathcal {K}}$-convex [10] if for any $t\in [0,1]$ and any $(u^1,u^2)\in {\mathcal {U}}\times {\mathcal {U}}$, we have $t\varphi \left( u^1\right) +(1-t)\varphi \left( u^2\right) -\varphi \left( t u^1+(1-t)u^2\right) \in {\mathcal {K}}$. If $\varphi$ is real-valued and differentiable, we call its linear approximation at some ${{\bar{u}}}\in {\mathcal {U}}$ the function: $\bar{\varphi }\left[ {{\bar{u}}}\right] : u\rightarrow \varphi \left( {{\bar{u}}}\right) + \left\langle \nabla \varphi \left( {{\bar{u}}} \right) , u-\bar{u}\right\rangle$. Notice that ${{\bar{\varphi }}} [{{\bar{u}}}]$ is a global under estimator of $\varphi$ if $\varphi$ is convex. If $\varphi$ is vector valued, its linear approximation is the component-wise linear approximation ${{\bar{\varphi }}}\left[ {{\bar{u}}}\right] (u)=\varphi \left( \bar{u}\right) + D \varphi \left( {{\bar{u}}} \right) \left( u-{{\bar{u}}}\right) ,$ where $D \varphi ({{\bar{u}}} )$ is the Jacobian of $\varphi$ at ${{\bar{u}}}$. Given a linear mapping $\phi$ and a mapping $\gamma$, we say that ${\mathcal {U}}:=\{u:\phi (u) = 0,\, -\gamma (u)\in {\mathcal {K}}\}$ or $\min _{u\in {\mathcal {U}}}\varphi (u)$ is strictly feasible iff there exists u such that $\phi (u)=0$ and $-\gamma (u)\in \text {relint }{\mathcal {K}}$.

Unless otherwise specified, through this document $((x^k,y^k),\lambda ^k)$ is an optimal primal-dual pair for $P({\mathcal {S}}^k)$ and $({{\bar{x}}}^k,{{\bar{y}}}^k)$ is an optimal solution for $L({\mathcal {X}},\lambda ^k)$.

2 A generic column generation algorithm

Instead of using specific forms of feeding the pricing information to the restricted problem, we use a generic mechanism to update ${\mathcal {S}}$ at each iteration as described in Algorithm 1.

Fig. 2 summarizes the relationships between the bounds of the problems involved in Algorithm 1. In all the “bound relationship" figures of this paper, an edge $a\rightarrow b$ means that $a\leqslant b$, the gray edges are the nontrivial relationships that apply at a stopping criterion and the gray nodes are the optimal values of the problems solved by the algorithm.

Fig. 2

Relationships of the optimal values involved in Algorithm 1

Theorem 1

At termination, Algorithm 1 returns an optimal solution for $P({\mathcal {X}})$.

Proof

If Algorithm 1 terminates at line 8, we have ${{\bar{x}}}^k\in {\mathcal {S}}^{k}$. $({{\bar{x}}}^k,{{\bar{y}}}^k)$ is then feasible and optimal for the Lagrangean relaxation of $P({\mathcal {S}}^k)$ with $\lambda ^k$:

$$\begin{aligned} \left( L({\mathcal {S}}^{k},\lambda ^{k})\right) \quad \omega \left( {\mathcal {S}}^{k},\lambda ^{k}\right) = \min \limits _{x\in {\mathcal {S}}^{k},y}\left\{ f\left( x,y\right) + \left\langle \lambda ^{k} , g\left( x,y\right) \right\rangle \right\} . \end{aligned}$$

In consequence, we have that $\omega ({\mathcal {X}},\lambda ^{k})=\omega ({\mathcal {S}}^{k},\lambda ^{k})$. Recall that $(x^k,y^k)$ is optimal for $P({\mathcal {S}}^{k})$ and $\lambda ^{k}$ is an optimal dual vector associated to $-g(x,y)\in {\mathcal {C}}$ in $P({\mathcal {S}}^{k})$. From Assumption 1, $(x^k,y^k)$ is then also optimal for $L({\mathcal {S}}^{k},\lambda ^{k})$, and $\omega ({\mathcal {S}}^{k})=\omega ({\mathcal {S}}^{k},\lambda ^{k})$, thus proving the gray edges in Fig. 2. To summarize, we have:

$$\begin{aligned} \omega \left( {\mathcal {X}}\right) \leqslant \omega \left( {\mathcal {S}}^{k}\right) = \omega \left( {\mathcal {S}}^{k},\lambda ^{k}\right) = \omega \left( {\mathcal {X}},\lambda ^{k}\right) \leqslant \omega \left( {\mathcal {X}}\right) , \end{aligned}$$

making $(x^{k},y^{k})$ optimal for $P({\mathcal {X}})$. Now, if Algorithm 1 terminates at line 5, we can choose $({{\bar{x}}}^k,{{\bar{y}}}^k) = ({{\bar{x}}}^{k-1},{{\bar{y}}}^{k-1})$ and have ${{\bar{x}}}^{k}\in {\mathcal {S}}^k$, which is the first stopping condition at line 8. $\square$

2.1 General remarks

Algorithm 1 can be useful only if Assumptions 2 and 3 are satisfied, i.e. either $\text {dim }{\mathcal {S}}^k$ is significantly smaller than n, or $P({\mathcal {S}}^k)$ possesses a special structure or is sparser than in $P({\mathcal {X}})$. In Sects. 4 and 5, we show that the master problem can be considerably shrunk depending on the set ${\mathcal {S}}^k$ in use. Even though Assumption 1 must be satisfied in order to get the dual variables and make Theorem 1 hold, in presence of a nonzero duality gap Algorithm 1 can still be used as a heuristic that provides optimality bounds. Notice again that we do not need $P({\mathcal {X}})$ to have zero duality gap, but we do see in the next Subsection that it does help to make Assumption 1 hold.

We did not prove that Algorithm 1 always finishes but we did prove that if it were to stop, it would return an optimal solution. Its finite termination depends on the way the sets ${\mathcal {S}}^k$ are generated in combination with the structure of the original problem. More precisely, the sequence ${\mathcal {S}}^k$ should shift towards at least one optimal solution of $P({\mathcal {X}})$ by e.g. strictly growing in dimension until reaching ${\mathcal {X}}$ in the worst case (which can be achieved in some special cases that we describe later). Ideally, the sets ${\mathcal {S}}^k$ should contain increasingly good solutions for $P({\mathcal {X}})$ such that we can stop prematurely the algorithm and still obtain an approximately optimal solution. For example, by forcing ${\mathcal {S}}^{k+1}$ to contain ${\mathcal {S}}^{k}$ or $x^k$, we ensure that the primal bound $\omega ({\mathcal {S}}^k)$ is nonincreasing.

Because we maintain lower and upper bounds over the optimal value of $P({\mathcal {X}})$ at each iteration, early termination can be reasonably used and Algorithm 1 can provide a solution $(x^k,y^k)$ feasible for $P({\mathcal {X}})$ with an optimality gap $\omega ({\mathcal {S}}^k) - \omega ({\mathcal {X}},\lambda ^k)$. Because the algorithm is not guaranteed to converge, we set a maximum number of iterations and execution time that we can spend before forcing the algorithm to stop.

2.2 How can the restricted problem $P({\mathcal {S}})$ maintain a zero duality gap?

As we mentioned earlier, it is not clear when Assumption 1 can hold. We now show that whenever (1) the approximated sets ${\mathcal {S}}^k$ are described by convex constraints and are strictly feasible, and (2) $P({\mathcal {S}}^k)$ admits as a feasible solution some known, feasible solution for $P({\mathcal {X}})$ satisfying strictly the side constraints $-g(x,y)\in {\mathcal {C}}$, then Slater’s condition holds for $P({\mathcal {S}}^k)$ and thus satisfies Assumption 1:

Proposition 1

Suppose that ${\mathcal {C}}$ is proper, g is L-Lipschitz, f is convex, we know some $(\bar{x}, {{\bar{y}}})$ such that ${\bar{x}}\in {\mathcal {X}}$ and $-g({{\bar{x}}},\bar{y})\in \text {relint }{\mathcal {C}}$, and ${\mathcal {S}}$ is described as

$$\begin{aligned} {\mathcal {S}}:=\{x : \phi (x,\theta )=0,\, -\gamma (x,\theta )\in {\mathcal {K}}, \hbox { for some}\ \theta \}, \end{aligned}$$

for some proper cone ${\mathcal {K}}$, a linear mapping $\phi$ and a ${\mathcal {K}}$-convex mapping $\gamma$. If ${\mathcal {S}}\subseteq {\mathcal {X}}$ is strictly feasible and contains ${{\bar{x}}}$, then $P({\mathcal {S}})$ has no Lagrangean duality gap.

Proof

Appendix B. $\square$

In this work, we consider approximated sets ${\mathcal {S}}^k$ that are nonempty polyhedra⁴ that always contain the projection onto the variables x of a known, strictly feasible solution for $P({\mathcal {X}})$. In fact, it is enough to find some feasible solution $({{\bar{x}}}^0,{{\bar{y}}}^0)$ for $P({\mathcal {X}})$ such that $-g({{\bar{x}}}^0,{{\bar{y}}}^0)\in \text {relint }{\mathcal {C}}$, and set ${\mathcal {S}}^1 \ni {{\bar{x}}}^0$: In other words, we consider ${{\bar{x}}}^0$ as the first column generated.

2.3 y-independent pricing problems $L({\mathcal {X}},\lambda ^k)$

Notice that $L({\mathcal {X}},\lambda ^k)$ optimizes in both x and y and is still an NLP that can be as difficult to solve as $P({\mathcal {X}})$. We partially address the former issue in the next Proposition and both in the next Section. We now introduce an adaptation of the P-property⁵ [25]: Given a function $\varphi : {\mathcal {U}}\times {\mathcal {V}}\rightarrow {\mathbb {R}}$, consider the following NLP:

$$\begin{aligned} \min \limits _{(u,v)\in {\mathcal {U}}\times {\mathcal {V}}} \varphi (u,v). \end{aligned}$$

(5)

Problem (5) satisfies the P-property wrt v if $\min _{v\in {\mathcal {V}}}\varphi (u,v)$ can be solved independently of $u\in {\mathcal {U}}$. Even if this P-property appears to be overly restrictive, it holds if $\varphi (u,v)=\varphi _1(u,\varphi _2(v))$, for some $\varphi _2:{\mathcal {V}}\rightarrow {\mathbb {R}}$ and some $\varphi _1:{\mathcal {U}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ that is non-decreasing in its second argument. This structure can appear if e.g. (1) $\varphi$ is separable in u and v (i.e. $\varphi (u,v)=\varphi _1(u)+\varphi _2(v)$), or (2) $\varphi (u,v)=\varphi _1(u)\varphi _2(v)$ with $\varphi _1(u)\geqslant 0$ for any $u\in {\mathcal {U}}$. We are now ready to state a y-independency result for the Lagrangean relaxation $L({\mathcal {X}},\lambda ^k)$:

Proposition 2

If $L({\mathcal {X}},\lambda ^k)$ satisfies the P-property wrt y, then $y=y^k$ is always an optimal choice in $L({\mathcal {X}},\lambda ^k)$, which becomes an optimization problem in x only:

$$\begin{aligned} \left( L\left( {\mathcal {X}},\lambda ^k\right) \right) \quad \omega \left( {\mathcal {X}},\lambda ^k\right) := \min \limits _{x\in {\mathcal {X}}}\left\{ f\left( x,y^k\right) + \left\langle \lambda ^k , g\left( x,y^k\right) \right\rangle \right\} . \end{aligned}$$

Proof

Appendix C. $\square$

Proposition 2 allows to drop the optimization in y in the pricing problem if the P-property holds. We now show that using a linearized version of $L({\mathcal {X}},\lambda ^k)$, we can always drop the optimization in y in the pricing, regardless of the P-property.

3 A linearized column generation algorithm

In practice, it is common to face e.g. LPs with a nice structure that admit tailored algorithms to solve them, getting hardened by replacing their linear objective with a nonlinear objective function f and/or adding possibly nonlinear side constraints $-g(x,y)\in {\mathcal {C}}$ to their polyhedral feasible set ${\mathcal {X}}$. This can happen for e.g. robust optimization problems [5] that are no easier than their deterministic counterparts.

In this Section, we show that solving a pricing problem whose objective function is linearized at the current incumbent $(x^k,y^k)$ holds the same guarantees as Algorithm 1, while alleviating the difficulty of solving the pricing problem whenever optimizing a linear objective over ${\mathcal {X}}$ is an easy task. As we show in our experiments, this can be extremely useful whenever a linear objective pricing problem can be solved with a dedicated algorithm.

3.1 Additional assumptions and results

We now present several results that allow the use of a linearized version of $L({\mathcal {X}},\lambda ^k)$ as a pricing problem. In this Section, the following extra assumption is met:

Assumption 4

${\mathcal {S}}^k$, ${\mathcal {C}}$ and f are convex, g is ${\mathcal {C}}$-convex, f and g are differentiable.

Further, we assume that for any cost vector c, $\min _{x\in {\mathcal {X}}} \langle c, x\rangle$ can be solved efficiently (which is in fact equivalent to Assumption 2 if the objective function of $L({\mathcal {X}},\lambda ^k)$ is linear). We now present several technical Lemmas to prove our main result:

Lemma 1

Consider a cone ${\mathcal {K}}$, $\lambda \in {\mathcal {K}}^*$ and a ${\mathcal {K}}$-convex function $\varphi$. Then $\psi : u\rightarrow \left\langle \lambda , \varphi (u)\right\rangle \text { is convex.}$

Proof

Appendix D. $\square$

Lemma 2

Given $\lambda \in {\mathcal {V}}$, a differentiable function $\varphi :{\mathcal {U}}\rightarrow {\mathcal {V}}$ and ${{\bar{u}}}\in {\mathcal {U}}$, the linear approximation of $\psi :u\rightarrow \langle \lambda , \varphi (u)\rangle$ at ${{\bar{u}}}$ is ${{\bar{\psi }}}[{{\bar{u}}}] : u\rightarrow \langle \lambda , {{\bar{\varphi }}}[{{\bar{u}}}](u)\rangle$.

Proof

Appendix E. $\square$

Lemma 3

Consider the NLC $\omega ^*:=\min _{u\in {\mathcal {U}}} \varphi (u)$, where ${\mathcal {U}}$ is convex and $\varphi :{\mathcal {U}}\rightarrow {\mathbb {R}}$ is differentiable. If $u^*$ is one of its optimal solutions, it is also optimal for ${{\bar{\omega }}} [u^ *]:=\min _{u\in {\mathcal {U}}} \{\bar{\varphi }[u^*](u):=\varphi (u^ *) +\langle \nabla \varphi (u^*), u-u^*\rangle \}$ and we have $\omega ^ *={{\bar{\omega }}}[u^ *]$.

Proof

Appendix F. $\square$

Lemma 3 tells us that an optimal solution of a convex optimization problem is also optimal for the same problem with an objective function linearized at said solution. For any ${\mathcal {S}}\subseteq {\mathcal {X}}$, $\lambda \in {\mathcal {C}}^*$ and $({{\bar{x}}}, {{\bar{y}}})$, let us define the following problem:

$$\begin{aligned} \left( {\bar{L}}\left[ {{\bar{x}}},\bar{y}\right] \left( {\mathcal {S}},\lambda \right) \right) \quad \bar{\omega }\left[ {{\bar{x}}},{{\bar{y}}}\right] \left( {\mathcal {S}},\lambda \right) := \min \limits _{x\in {\mathcal {S}},y}&\left\{ {{\bar{f}}}\left[ {{\bar{x}}},\bar{y}\right] (x,y)+\left\langle \lambda ,{{\bar{g}}}\left[ {{\bar{x}}},\bar{y}\right] (x,y)\right\rangle \right\} , \end{aligned}$$

which is $L({\mathcal {S}},\lambda )$ with its objective function linearized at $({{\bar{x}}}, {{\bar{y}}})$.

3.2 A linearized algorithm

Now consider the following algorithm: (1) instead of solving $L({\mathcal {X}},\lambda ^{k})$, the pricing we solve is its linear approximation ${\bar{L}}[x^k,y^k]({\mathcal {X}},\lambda ^k)$ at the current incumbent $(x^k,y^k)$ of the restricted problem $P({\mathcal {S}}^k)$ and (2) the stopping criterion at line 5 of Algorithm 1 is replaced by a slightly more restrictive condition. We describe the changes applied to Algorithm 1 in Algorithm 2 and illustrate in Fig. 3 the relationships between the bounds of the problems involved in it.

Fig. 3

Relationships of the optimal values involved in Algorithm  2

Theorem 2

Algorithm 2 returns an optimal solution for $P({\mathcal {X}})$ at termination.

Proof

If Algorithm 2 terminates because $\bar{x}^k\in {\mathcal {S}}^k$, then $({{\bar{x}}}^k,{{\bar{y}}}^k)$ is feasible and optimal for ${\bar{L}}[x^ {k},y^k]({\mathcal {S}}^{k},\lambda ^{k})$ and we have:

$$\begin{aligned} {{\bar{\omega }}}\left[ x^ {k},y^k\right] \left( {\mathcal {S}}^{k},\lambda ^{k}\right) = \bar{\omega }\left[ x^{k},y^k\right] \left( {\mathcal {X}},\lambda ^{k}\right) . \end{aligned}$$

Because f is convex and g is ${\mathcal {C}}$-convex, Lemmas 1 and 2 imply that ${{\bar{f}}} [x^ {k},y^k]$ and $\langle \lambda ^k,{{\bar{g}}}[x^k,y^k](\cdot )\rangle$ are global under estimators of f and $\langle \lambda ^k,g(\cdot )\rangle$ respectively. In consequence we have that

$$\begin{aligned} {{\bar{\omega }}}\left[ x^ {k},y^k\right] \left( {\mathcal {X}},\lambda ^{k}\right) \leqslant \omega \left( {\mathcal {X}},\lambda ^ {k}\right) \leqslant \omega \left( {\mathcal {X}}\right) . \end{aligned}$$

On another hand, $(x^{k},y^k)$ is also an optimal solution for $L({\mathcal {S}}^{k},\lambda ^ {k})$ from Assumption  1. Finally, we can interpret ${\overline{L}}[x^ {k},y^k]({\mathcal {S}}^{k},\lambda ^ {k})$ as the linearization of $L({\mathcal {S}}^{k},\lambda ^ {k})$ at one of its optimal solutions $(x^{k},y^k)$. Recalling that:

$$\begin{aligned} \omega \left( {\mathcal {S}}^{k},\lambda ^{k}\right) =&\min \limits _{x\in {\mathcal {S}}^{k},y}\left\{ f(x,y) +\left\langle \lambda ^{k} , g(x,y)\right\rangle \right\} \\ \bar{\omega }\left[ x^{k},y^k\right] \left( {\mathcal {S}}^{k},\lambda ^{k}\right) =&\min \limits _{x\in {\mathcal {S}}^{k},y}\left\{ \bar{f}\left[ x^{k},y^k\right] (x,y) +\left\langle \lambda ^{k} , \bar{g}\left[ x^{k},y^k\right] (x,y)\right\rangle \right\} , \end{aligned}$$

Lemma 3 then tells us that $(x^ {k},y^k)$ is also an optimal solution for ${\bar{L}}[x^ {k},y^k]({\mathcal {S}}^{k},\lambda ^ {k})$, giving $\omega ({\mathcal {S}}^{k},\lambda ^ {k})= {{\bar{\omega }}}[x^ {k},y^k]({\mathcal {S}}^{k},\lambda ^{k})$. To summarize, we obtain

$$\begin{aligned} \omega \left( {\mathcal {X}}\right) \leqslant&\omega \left( {\mathcal {S}}^{k}\right) = \omega \left( {\mathcal {S}}^{k},\lambda ^ {k}\right) ={{\bar{\omega }}}\left[ x^ {k},y^k\right] \left( {\mathcal {S}}^{k},\lambda ^{k}\right) \\ =&{{\bar{\omega }}}\left[ x^ {k},y^k\right] \left( {\mathcal {X}},\lambda ^{k}\right) \leqslant \omega \left( {\mathcal {X}},\lambda ^k\right) \leqslant \omega \left( {\mathcal {X}}\right) , \end{aligned}$$

thus proving the optimality of $(x^{k},y^k)$ for $P({\mathcal {X}})$. If Algorithm 2 stops from its criterion at line  5, we can choose $({{\bar{x}}}^{k},\bar{y}^{k})=({{\bar{x}}}^{k-1},{{\bar{y}}}^{k-1})$, giving ${{\bar{x}}}^k \in {\mathcal {S}}^k$. $\square$

As in the nonlinearized case, there is no guarantee that Algorithm  2 terminates but if it does, an optimal solution for $P({\mathcal {X}})$ is returned.

3.3 y-independent pricing problems ${{\bar{L}}}[x^{k},y^k]({\mathcal {X}},\lambda ^{k})$

As opposed to Algorithm 1, we now show that regardless of the P-property, we can always get rid of the variables y in the linearized pricing ${\bar{L}}[x^ {k},y^k]({\mathcal {X}},\lambda ^ {k})$:

Proposition 3

Taking $y=y^k$ is always optimal for ${\bar{L}}[x^ {k},y^k]({\mathcal {X}},\lambda ^ {k})$, which becomes a linear objective minimization problem in x only:

$$\begin{aligned} {{\bar{\omega }}}\left[ x^k, y^k\right] \left( {\mathcal {X}},\lambda ^k\right) =&\min \limits _{x\in {\mathcal {X}}} \left\{ {{\bar{f}}}\left[ x^k,y^k\right] \left( x,y^k\right) +\left\langle \lambda ^k,\bar{g}\left[ x^k,y^k\right] \left( x,y^k\right) \right\rangle \right\} \end{aligned}$$

Proof

Appendix G. $\square$

3.4 “Reduced costs”

Recall that DW for LPs can stop whenever the reduced costs⁶ are zero: we now show that this is also true for the linearized scheme in our nonlinear setting.

Proposition 4

Let ${{\bar{c}}}^k:= \nabla _x f(x^k,y^k)+D^*g(x^k,y^k)\lambda ^k$ be the cost vector wrt x in ${\bar{L}}[x^ {k},y^k]({\mathcal {X}},\lambda ^ {k})$. If ${{\bar{c}}}^k = 0$ then $(x^k,y^k)$ is optimal for $P({\mathcal {X}})$.

Proof

The linearized pricing in x is $\min _{x\in {\mathcal {X}}} \langle {{\bar{c}}}^k , x\rangle$. If ${{\bar{c}}}^k = 0$, then any $\bar{x}^k\in {\mathcal {X}}$ is optimal: choosing any ${{\bar{x}}}^k \in {\mathcal {S}}^k\subseteq {\mathcal {X}}$ satisfies the stopping criterion. $\square$

This last result provides a computationally cheap stopping criterion for the non-linearized scheme as well, as the pricing problem—linearized or not—always provides a lower bound for $\omega ({\mathcal {X}})$: an all-zeroes reduced cost vector ensures that the master problem cannot be improved.

4 Relationship with existing schemes

4.1 Dantzig–Wolfe

Assume that ${\mathcal {X}}\subseteq {\mathbb {R}}^n$ is a polyhedron (that we consider bounded for simplicity), $f(x,y):=c^\top x+d^\top y$ and the conic inequality is defined by ${\mathcal {C}}:={\mathbb {R}}^m_+$ and $g(x,y):=b-Xx-Yy$. Using ${\mathcal {S}}^k:= \text {conv}({{\bar{x}}}^l)_{l\in \{0,...,k-1\}}$ we retrieve DW for LPs. Its finite convergence is ensured by the fact that ${\mathcal {X}}$ has a finite—although exponential in general—number of extreme points.

Extensions Notice that if ${\mathcal {C}}$ is a more general cone, our algorithm generalizes DW for LCs, where at each iteration $P({\mathcal {S}}^k)$ is an LC and $L({\mathcal {X}},\lambda ^k)$ is an LP. Applications of DW to LCs can be found in [2] and references therein. Further, there is a direct extension of DW to a special class of nonlinear problems: going back to the general case for ${\mathcal {C}}$, f and g but keeping ${\mathcal {X}}$ polyhedral, ${{\bar{L}}}[x^k,y^k]({\mathcal {X}},\lambda ^k)$ turns out to be an LP. Because ${\mathcal {X}}$ is finitely generated, the finite convergence of the linearized algorithm is also ensured with the same arguments.

Constraint redundancy If ${\mathcal {X}}$ is not convex, to enforce ${\mathcal {S}}^k\subseteq {\mathcal {X}}$, we must use

$$\begin{aligned} {\mathcal {S}}^k:= {\mathcal {X}}\cap \text {conv}\left( {{\bar{x}}}^l\right) _{l\in \{0,...,k-1\}}, \end{aligned}$$

thus potentially losing the advantage of dropping any ${\mathcal {X}}$-defining constraint in the master problem as in the LP/convex cases. Similarly, if the conic hull is used instead and ${\mathcal {X}}$ is a cone, it is sufficient to use ${\mathcal {S}}^k:= \text {cone}({{\bar{x}}}^l)_{l\in \{0,...,k-1\}}$ instead of ${\mathcal {S}}^k:= {\mathcal {X}}\cap \text {cone}(\bar{x}^l)_{l\in \{0,...,k-1\}}$.

4.2 Bienstock–Zuckerberg (BZ)

We now link our framework with a decomposition scheme for LPs [8] where the choice of ${\mathcal {S}}$ differs substantially from DW. Considering a partition ${\mathcal {J}}^k:=\{{\mathcal {J}}^k_1,...,{\mathcal {J}}^k_{L_k}\}$ of the indices [n], we force all the variables $x_j$ belonging to a same cluster ${\mathcal {J}}^k_l$ to yield the same value, ultimately aggregating all the variables into a single one. In other words, we use

$$\begin{aligned} {\mathcal {S}}^k:={\mathcal {P}}({\mathcal {J}}^k):= \left\{ x\in {\mathcal {X}}: x_j=\theta _l, \forall j\in {\mathcal {J}}^k_l, \forall l\in \left[ L_k\right] , \text { for some } \theta \in {\mathbb {R}}^{L_k} \right\} . \end{aligned}$$

Update mechanism The update mechanism in this case refines the partition ${\mathcal {J}}^k$ into a new partition ${\mathcal {J}}^{k+1}$, by splitting some of its clusters such that the new column ${{\bar{x}}}^k$ belongs to ${\mathcal {S}}^{k+1}:={\mathcal {P}}({\mathcal {J}}^{k+1})$. We call a partition induced by some $x\in {\mathbb {R}}^n$, a partition ${\mathcal {J}}(x)=\{{\mathcal {J}}_1(x),...,{\mathcal {J}}_{L}(x)\}$ of [n] such that for every $l\in [L]$ and any pair of indices $(j,j')\in {\mathcal {J}}_l(x)\times {\mathcal {J}}_l(x)$ we have $x_j=x_{j'}$. Given two partitions of [n], ${\mathcal {J}}=\{{\mathcal {J}}_1,...,{\mathcal {J}}_L\}$ and ${\mathcal {J}}'=\{{\mathcal {J}}'_1,...,{\mathcal {J}}'_{L'}\}$, their intersection ${\mathcal {J}}\Delta {\mathcal {J}}'$ is the partition of [n] defined as follows:

$$\begin{aligned} {\mathcal {J}}\Delta {\mathcal {J}}':=\left\{ {\mathcal {J}}_l\cap {\mathcal {J}}'_{l'}, \forall \left( l,l'\right) \in [L]\times [L']\right\} . \end{aligned}$$

Given a partition ${\mathcal {J}}^k$ and ${\mathcal {J}}^k({{\bar{x}}}^k)$ a partition induced by ${{\bar{x}}}^k$, we first compute the refined partition ${\mathcal {J}}^{k+1}:={\mathcal {J}}^{k}\Delta {\mathcal {J}}^k({{\bar{x}}}^k)$ and the new restricted set is given by ${\mathcal {S}}^{k+1}:={\mathcal {P}}({\mathcal {J}}^{k+1})$.

Extensions and convergence Such a scheme makes Algorithms 1 and 2 generalizations to nonlinear problems of the BZ algorithm [8]. This time the convergence is not ensured by some property of $P({\mathcal {X}})$, but rather thanks to the structure of the sets ${\mathcal {S}}^k$. In fact, either (1) the partition is refined until turning into $\{\{1\},...,\{n\}\}$, meaning we reached the original problem $P({\mathcal {X}})$, or (2) the partition is not refined, in which case ${\mathcal {J}}^{k+1}={\mathcal {J}}^{k}\Delta {\mathcal {J}}^k(\bar{x}^k)={\mathcal {J}}^{k}$. It is not difficult to see that the latter implies that ${{\bar{x}}}^k\in {\mathcal {S}}^k={\mathcal {P}}({\mathcal {J}}^{k})$, which is a stopping criterion for both Algorithms 1 and 2. The former implies that we are guaranteed to converge to an optimal solution in at most n iterations because the size of the partition increases by at least one (i.e. $|{\mathcal {J}}^{k+1}| > |{\mathcal {J}}^{k}|$). Motivating the scheme in the next Subsection, [38] show that given a sequence of columns $({{\bar{x}}}^l)_{l\in \{0,...,k-1\}}$, we have ${\mathcal {S}}^k\supseteq {\mathcal {X}}\cap \text {lin}(\bar{x}^l)_{l\in \{0,...,k-1\}}$.

Induced partition cardinality Notice that the pricing problem may provide a column ${{\bar{x}}}^k$ with a large number of different values, hence generating a high-cardinality induced partition ${\mathcal {J}}({{\bar{x}}}^k)$ and increasing rapidly the size of the partition ${\mathcal {J}}^{k+1}$ used in the next restricted problem $P({\mathcal {S}}^{k+1})$. This issue is partially addressed by the linearized Algorithm 2 and completely circumvented in the next scheme. For example, if ${\mathcal {X}}$ is polyhedral and possesses the integrality property [26], the pricing problems ${\bar{L}}[x^k,y^k]({\mathcal {X}},\lambda ^k)$ can return integer optimal solutions ${{\bar{x}}}^k$, thus increasing the probability of having a reduced number of different values.

Constraint redundancy Given that $\{ x: x_j=\theta _l, \forall j\in {\mathcal {J}}^k_l, \forall l\in [L_k], \text { for some }\theta \in {\mathbb {R}}^{L_k} \}$ is not necessarily contained in ${\mathcal {X}}$, we need to keep the ${\mathcal {X}}$-defining constraints in general. This issue can sometimes be avoided for e.g. bound constraints $\ell \leqslant x\leqslant u$ that are present in the definition of ${\mathcal {X}}$: they become equivalent to the following $L_k\ll n$ bound constraints in terms of $\theta$:

$$\begin{aligned} \max \limits _{j\in {\mathcal {J}}^k_l}\, \ell _j \leqslant \theta _l \leqslant \min \limits _{j\in {\mathcal {J}}^k_l}\, u_j \quad , \forall l \in \left\{ 1,...,L_k\right\} . \end{aligned}$$

(6)

4.3 Non-partitioned BZ

[38] link the last scheme for MILPs to another that uses at each iteration the subset of ${\mathcal {X}}$ spanned by $\text {lin}({{\bar{x}}}^l)_{l\in \{0,...,k-1\}}$, i.e.

$$\begin{aligned} {\mathcal {S}}^k:=\left\{ x\in {\mathcal {X}} : x=\sum \limits _{l=0}^{k-1} \theta _l {{\bar{x}}}^l, \text { for some } \theta \in {\mathbb {R}}^k \right\} ={\mathcal {X}}\cap \text {lin}(\bar{x}^l)_{l\in \{0,...,k-1\}}. \end{aligned}$$

Akin to the classical BZ, it converges in at most n iterations. What is not mentioned in [38] is that this is also true independently of the structure of $P({\mathcal {X}})$. Instead of using partitions of variables, it uses the raw directions ${{\bar{x}}}^l$, thus avoiding an explosive increase in the number of variables. This comes at the cost of a less structured $P({\mathcal {S}})$: in fact, variable aggregation is akin to a contraction operation in combinatorial optimization, which can eliminate a substantial amount of rows and columns when dealing with structured LPs.

Notice that even if we can maintain a reasonable number of variables in the master problem, the loss in structure in comparison to BZ prohibits in general the use of the trick we present in (6), and all the ${\mathcal {X}}$-defining constraints must be kept, including variables bounds.

4.4 How do we check if ${{\bar{x}}}^k \in {\mathcal {S}}^k$?

In our experimental design, we consider the four aforementioned sets ${\mathcal {S}}^k$. We now show how to determine if $\bar{x}^k\in {\mathcal {S}}^k$ efficiently in those special cases: For BZ, it is enough to check if the size of the partition after refinement increased or not; For the linear span case, it is enough to check if ${{\bar{x}}}^k$ is a linear combination of the previous columns, which is done by projection. In the convex and conic hull cases, we must check whether a small LP is feasible. Let the polyhedron $\Theta ^k$ be as follows:

$$\begin{aligned} \Theta ^k:= {\left\{ \begin{array}{ll} \left\{ \theta \in {\mathbb {R}}_+^k : \sum _{l = 0}^{k-1}\theta _{l}=1 \right\} &{}\text { If using the convex hull} \\ {\mathbb {R}}_+^k &{}\text { If using the conic hull} . \end{array}\right. } \end{aligned}$$

In these cases, we have that ${{\bar{x}}}^k\in {\mathcal {S}}^k$ iff $\{\theta \in \Theta ^k : \sum _{l=0}^{k-1} \theta _{l} {{\bar{x}}}^{l} = \bar{x}^k\}\ne \emptyset$, which can be done by solving an LP having k variables $\theta _k$ and $O(n)\gg O(1)$ linear constraints. To avoid this large number of constraints, we choose to solve the following problem instead:

$$\begin{aligned} \text {distance}^2_2\left( \bar{x}^k,{\mathcal {S}}^k\right) :=\min \limits _{\theta \in \Theta ^k} \left| \left| {{\bar{x}}}^k - \sum _{l=0}^{k-1}\theta _{l} {{\bar{x}}}^{l} \right| \right| _2^2. \end{aligned}$$

(7)

We can see that ${{\bar{x}}}^k\in {\mathcal {S}}^k$ iff $\text {distance}^2_2\left( {{\bar{x}}}^k,{\mathcal {S}}^k\right) =0$. There are two advantages to use (7): (1) we are able to monitor the distance of the current column ${{\bar{x}}}^k$ to ${\mathcal {S}}^k$, and (2) when solving (7) with an interior point method, the O(k) constraints that define $\Theta ^k$ are not a problem because $k\ll n$ and the gradient and Hessian of the penalized objective have dimensions k and $k\times k$ respectively.

4.5 x-free master problems $P({\mathcal {S}})$ and constraint redundancy

First, notice that all of the aforementioned schemes are of the form

$$\begin{aligned} {\mathcal {S}}^k:=\left\{ x\in {\mathcal {X}} : x=Q^k \theta \text { for some } \theta \in \Theta ^k \right\} , \end{aligned}$$

meaning that $P({\mathcal {S}}^k)$ is equivalent to the following problem in $\theta$ and y only:

$$\begin{aligned} \left( P({\mathcal {S}}^k\right) \quad \omega \left( {\mathcal {S}}^k\right) := \min \limits _{\theta \in \Theta ^k, y} \left\{ f(Q^k\theta ,y): Q^k\theta \in {\mathcal {X}}, -g\left( Q^k\theta ,y\right) \in {\mathcal {C}} \right\} . \end{aligned}$$

Further, we are sometimes able to shrink or make redundant some ${\mathcal {X}}$-defining constraints in $P({\mathcal {S}}^k)$. This is of crucial importance from a computational point of view, as we must make $P({\mathcal {S}}^k)$ as simple to solve as possible: Given a generic set ${\mathcal {G}}$, a convex set ${\mathcal {V}}$, a cone ${\mathcal {K}}$, a subspace ${\mathcal {E}}:=\{x:Ex=0\}$ and some variable bounds (if x is a vector) ${\mathcal {B}}:=\{x:\ell \leqslant x\leqslant u\}$, consider that

$$\begin{aligned} {\mathcal {X}}:={\mathcal {G}}\cap {\mathcal {V}}\cap {\mathcal {K}}\cap {\mathcal {E}}\cap {\mathcal {B}} . \end{aligned}$$

We summarize in Table 1 how each of these ${\mathcal {X}}$-defining constraints can be simplified depending of the scheme used:

Table 1 Master constraints redundancy

5 Risk-averse portfolio optimization problem

We now describe the NLP we test our algorithms on. We consider the portfolio optimization problem of determining which assets to buy—with uncertain returns—such that (1) some risk of being rewarded a poor outcome is minimized, and (2) the variance of the return is kept under some threshold. As opposed to a classical expected value maximization model, using the variance and nonlinear risk measures makes the resulting optimization problem a large scale, nonlinear objective, SOC constrained optimization problem (See e.g. [1, 17, 33, 34, 60] for non expected value portfolio optimization).

5.1 Problem description

An administrator must allocate the resources of $T+1$ different clients interested in disjoint subsets of stocks. The administrator must minimize some client-dependant risk measures while keeping the variance of some returns under some threshold $\sigma ^2$. The clients have budgets $b_t$ and are interested in $n_t$ assets each. We purposefully separate the 0th client from the T others as its associated decision variables are only a handful that we model with the y variables. Client t has to pay a unitary cost $a^t_j$ per asset j. Each asset j has an uncertain future value $c^t_j$ and at most $u^t_j$ units can be purchased . The variables $x^t_j$ ($y_j$) represent the amount of each asset j purchased by client t (0). We enforce that $x^t\in {\mathcal {X}}_t$ and $y\in {\mathcal {X}}_0$ where

$$\begin{aligned} {\mathcal {X}}_t:=\left\{ z \in \left[ 0,u^t\right] : \left( a^t\right) ^\top z\leqslant b_t\right\} , \forall t\in \{0,...,T\}. \end{aligned}$$

$y\in {\mathcal {X}}_0$ is considered to be part of the side constraints $-g(x,y)\in {\mathcal {C}}$. We define $d^t$ as the vector of returns $c^t$, where many components are zero except for some vital assets. Upper bounding the variance of the returns of these assets is equivalent to:

$$\begin{aligned} {\mathbb {V}}\left( y^\top d^0+\sum \limits _{t=1}^T \left( d^t\right) ^\top x^t \right) \leqslant \sigma ^2. \end{aligned}$$

(8)

Each client minimizes a risk measure $f_t$ that depends on its uncertain returns. They each minimize an entropic risk [52] of parameter $\alpha _t$, $f_t(z):={\mathcal {E}}_{\alpha _t}(-(c^t)^\top z)$, where⁷${\mathcal {E}}_{\alpha }(Z):=\alpha \ln {\mathbb {E}}(e^{Z/\alpha } )$. The general problem can be cast as follows:

$$\begin{aligned} \min \limits _{x,y}\left\{ f_0(y)+\sum \limits _{t=1}^T f_t\left( x^t\right) \, : \, x^t\in {\mathcal {X}}_t,\forall t \in [T], \, y\in {\mathcal {X}}_0,\, (8) \right\} . \end{aligned}$$

5.2 Sample average approximation (SAA)

The last problem is approximated by using S samples $c^{ts}$ of respective probabilities $p_s$ with SAA [32]. The approximations of the variance and expectations are summarized in Table 2. For simplicity, we use the same names for the functions and their respective SAAs.

Table 2 Sample average approximations

Defining V, $V^t$ and $V^0$ such that $V^t_{sj}:=\sqrt{p_s}(d^{ts}_j - d^t_j)$ and $Vx := \sum _{t=1}^T V^tx^t$, the variance constraint can be expressed as a classic nonlinear quadratic (CLA) convex constraint $||V^0 y+Vx ||^2_2\leqslant \sigma ^2$, or the SOC constraint $(V^0 y+Vx ,\sigma )\in {\mathcal {L}}^{S+1}_2$. The full approximated problem becomes:

$$\begin{aligned} \omega \left( {\mathcal {X}}\right) = \min \limits _{ x ,y} \quad&\alpha _0\ln \sum \limits _{s=1}^S p_s e^{-\left( c^{0s}\right) ^\top y/\alpha _0} + \sum \limits _{t=1}^T \alpha _t\ln \sum \limits _{s=1}^S p_s e^{-\left( c^{ts}\right) ^\top x^t/\alpha _t} \\ \text {s.t.:}\quad&x^t\in {\mathcal {X}}_t\quad ,\forall t \in [T]\\&y\in {\mathcal {X}}_0\\&{\left\{ \begin{array}{ll} \left| \left| V^0y+Vx \right| \right| _2^2\leqslant \sigma ^2 &{}\text { If (8) is seen as a CLA}\\ \left( V^0 y+Vx ,\sigma \right) \in {\mathcal {L}}^{S+1}_2 &{}\text { If (8) is seen as a SOC.} \end{array}\right. } \end{aligned}$$

Notice that Assumption 1 is satisfied from Proposition 1, as $P({\mathcal {X}})$ is a convex NLP that for some small $\epsilon >0$, admits the all-$\epsilon$’s vector of ${\mathbb {R}}^{n+n_0}$, $\epsilon _{n+n_0}$ , as a strictly feasible point and we can use $\epsilon _n$ as a starting column for ${\mathcal {S}}^1\subset {\mathcal {S}}^2\subset {\mathcal {S}}^3...$

5.3 Pricing problem

The structure of the pricing problem depends on the coupling constraint considered: Given any dual vector $(\lambda ^{1,0}, \lambda ^{2,0},\lambda ^{3,0}) \in {\mathbb {R}}^{n_0}_+\times {\mathbb {R}}^{n_0}_+\times {\mathbb {R}}_+$ corresponding to the y-specific constraints $y\geqslant 0$, $y\leqslant u^0$ and $(a^0)^\top y\leqslant b_0$, the pricing problem is:

$$\begin{aligned} \omega \left( {\mathcal {X}},\lambda \right) = \min \limits _{ x ,y} \quad&\alpha _0\ln \sum \limits _{s=1}^S p_s e^{-\left( c^{0s}\right) ^\top y/\alpha _0} + \sum \limits _{t=1}^T \alpha _t\ln \sum \limits _{s=1}^S p_s e^{-\left( c^{ts}\right) ^\top x^t/\alpha _t} \\&-\left( \lambda ^{1,0} \right) ^\top y +\left( \lambda ^{2,0} \right) ^\top \left( y- u^0 \right) + \lambda ^{3,0} \left( \left( a^0\right) ^\top y-b_0 \right) \\&+ {\left\{ \begin{array}{ll} \lambda ^4\left( \left| \left| V^0y+Vx \right| \right| _2^2-\sigma ^2 \right) &{}\text { If (8) is seen as a CLA,}\\ &{}(\lambda ^4\in {\mathbb {R}}_+)\\ -\left( \lambda ^4\right) ^\top \left( V^0y+Vx \right) -\lambda ^4_0\sigma &{}\text { If (8) is seen as SOC,}\\ &{}\left( \left( \lambda ^4,\lambda ^4_0\right) \in {\mathcal {L}}_2^{S+1}\right) \end{array}\right. } \\ \text {s.t.}\quad&x^t\in {\mathcal {X}}_t,\,\forall t \in [T]. \end{aligned}$$

Notice that considering (8) as a SOC makes the pricing problem separable in each $x^t$ and y and also allows the use of the y-independency result in Proposition 2. More importantly, using the linearized pricing each problem in $x^t$ is solvable in $O(n_t \ln n_t)$ time: the objective function becomes linear and every problem in $x^t$ can be solved with a dedicated algorithm (see Proposition 5).

Proposition 5

The following LP with p variables can be reduced to a continuous knapsack problem, for which an optimal solution can be found in $O( p\ln p)$ time:

$$\begin{aligned} \omega ^*:=\min \limits _{z\in [0,\mu ]} \left\{ \gamma ^\top z : \alpha ^\top z\leqslant \beta \right\} . \end{aligned}$$

Proof

Appendix H. $\square$

We summarize In Table 3 the types of pricing problem we encounter with our framework, and how to solve them.

Table 3 Types of pricing problems

5.4 Master problem

Table 4 Master constraints ($y\in {\mathcal {X}}_0$ and the variance constraint are always present)

From Table 1, we summarize in Table 4 the types of sets ${\mathcal {S}}^k$ we use in our experiments and their implications for the master problems $P({\mathcal {S}}^k)$. Notice that the convex hull and the partitioning schemes hold a clear advantage wrt the others, as their number of constraints is way lower than the rest.

Chasing the conic dual variables If we consider the variance constraint as a SOC we must be able to retrieve conic dual variables for the master problem $P({\mathcal {S}})$. Even though nonlinear or linear conic solvers do exist, we could not find any general purpose package for problems having both features and returning conic multipliers. To circumvent this issue, we solve the master with an off the shelf nonlinear solver by considering the quadratic constraint as a CLA, then use the following result to obtain conic multipliers:

Proposition 6

For some $\gamma _0<0$, consider the following optimization problem:

$$\begin{aligned} \omega ^*:=\min \limits _{u}\left\{ \varphi (u): \phi (u)\leqslant 0, -\left( \gamma (u),\gamma _0\right) \in {\mathcal {L}}_2 \right\} , \end{aligned}$$

(9)

and its equivalent representation as a classic nonlinear optimization problem:

$$\begin{aligned} \omega ^*:=\min \limits _{u}\left\{ \varphi (u): \phi (u)\leqslant 0, \left| \left| \gamma (u)\right| \right| _2^2-\gamma _0^2\leqslant 0 \right\} , \end{aligned}$$

(10)

where their objective functions and constraints are convex and neither has a Lagrangean duality gap. Given an optimal primal-dual pair $(u^*,(\pi ^*,\lambda ^*))$ for (10) then $(u^*,(\pi ^*,\hat{\lambda },{\hat{\lambda }}_0))$ is an optimal pair for (9), where: $({{\hat{\lambda }}},{\hat{\lambda }}_0):= 2 \lambda ^*( \gamma (u^*), -\gamma _0)$.

Proof

Appendix I. $\square$

Proposition 6 indicates that we can always derivate SOC multipliers from the multipliers of the constraint in nonlinear quadratic convex form.

5.5 Numerical enhancement

In preliminary experiments, solving the convex optimization problems at hand as they are with an interior point method rapidly exceeds the capabilities of an average workstation. This is due to the fact that the Hessian matrix of the penalized objective can have many nonzero coefficients because of the entropic risk measures and the variance constraint. This observation implies that the linear system that is solved during each Newton step of the interior point method can be overly demanding both in terms of memory and running time. Introducing new variables and constraints, notice that we have the following identity: for any $t\in \{0,...,T\}$ and any z ($x^t$ or y) we have

$$\begin{aligned} \alpha _t \ln \sum \limits _{s=1}^S p_s e^{\left( -c^{ts}\right) ^\top z / \alpha _t}= \min \limits _{v^t}\left\{ \alpha _t \ln \sum \limits _{s=1}^S p_s e^{v^t_s / \alpha _t} : v^t_s = -\left( c^{ts}\right) ^\top z, \forall s \in [S] \right\} . \end{aligned}$$

In the same fashion, we can replace the variance constraint with

$$\begin{aligned} ||w||_2^2 \leqslant \sigma ^2 \quad \text { and }\quad w = V^0 y+Vx . \end{aligned}$$

By using this transformation, the objective function eliminates the variables z from the objective function and involves only the S variables $v^t_s$. This way, the Hessian of the Lagrangean function is a slightly larger matrix with $(T+1)S$ extra columns and rows having way less nonzero coefficients: at most $(T+1)S^2$ of them come from the entropies, and S from the variance constraint. For this reason and the fact that CG is typically useful when there are only a few side constraints, we purposefully kept S moderately small for our experiments.

In Appendix J, we briefly recall the mechanics of an iteration of a primal-dual interior point scheme and showcase the sparsity patterns of the Newton step for the pricing problem and the master problem in their original and enhanced forms. We also show that on our testbed, we can divide at least by a factor 100 the number of nonzero coefficients in the Newton system at the cost of having less than a percent of additional unknowns.

Chasing the dual variables for the enhanced model We must now be able to catch the dual variables associated to the original constraints (depending only of x and y) from the dual variables of the constraints in the enhanced formulation (now also including v and w). We address this in a general setting in the next Proposition, by showing that we can ignore the extra constraints and use the multipliers as is:

Proposition 7

Given a proper cone ${\mathcal {K}}$, consider:

$$\begin{aligned} \omega ^*:=\min \limits _{u}\left\{ \varphi (u): \phi (u)\leqslant 0, -\gamma (u)\in {\mathcal {K}} \right\} . \end{aligned}$$

(11)

Suppose there is a transformation with extra variables v and w such that for any $v=Vu$, $\varphi (u)={{\tilde{\varphi }}}(v)$ and for any $w=Wu$, $\gamma (u)={{\tilde{\gamma }}}(w)$, so that (11) can be rewritten as:

$$\begin{aligned} \omega ^*:=\min \limits _{u,v,w}\left\{ {{\tilde{\varphi }}}(v)\,:\, \phi (u)\leqslant 0,\, -{{\tilde{\gamma }}}(w)\in {\mathcal {K}},\, v=Vu,\, w = Wu \right\} . \end{aligned}$$

(12)

If both are convex and neither has a Lagrangean duality gap, given an optimal primal-dual pair $(({{\tilde{u}}},{{\tilde{v}}},{{\tilde{w}}}),(\tilde{\pi },{{\tilde{\lambda }}},{{\tilde{\alpha }}},{{\tilde{\beta }}}))$ for (12) then $({{\tilde{u}}},({{\tilde{\pi }}},\tilde{\lambda }))$ is optimal for (11).

Proof

Appendix K. $\square$

6 Computational experience

The algorithms presented in this paper were coded in C programming language and run over Dell PowerEdge C6420 cluster nodes with Intel Xeon Gold 6152 CPUs at 2.10GHz with 32Gb RAM each. All the convex NLPs are solved using the callable library of IPOPT [49, 62], using as a subroutine the linear solver Pardiso [47, 48].

6.1 Methods tested and nomenclature

We test our methods (1) on different sets ${\mathcal {S}}$ that use the convex hull (V), the conic hull (C), the linear span (LR) or the partition-based linear span (LP), (2) using a linearized pricing problem (L) or without (NL), (3) considering the variance constraint as a conic (SOC) or as a classical nonlinear quadratic (CLA). The y-independency result or the tailored algorithm for knapsack problems are always used whenever it applies. For example, the scheme using the convex hull with linearized pricing and considering the variance constraint as a SOC will be named L-SOC-V. We summarize the different options tested in Table 5.

Table 5 Algorithms tested

We do not test any non-linearized scheme if the variance constraint is considered CLA, as the pricing problem is still not separable and can be as hard as $P({\mathcal {X}})$.

6.2 Instances generated

In order to push our frameworks to their limits, we generate synthetic instances of variable sizes. We consider $T\in \{1,50\}$ blocks of equal sizes $n_t=N\in \{10^4,10^5\}$. There are $n_0 = 50$ auxiliary variables and we generate $S=20$ scenarios. The supplies $u^t_j$ are uniformly drawn from $\{1,...,5\}$, and the costs and weights $c^{ts}_j$ and $a^t$ are uniformly drawn from [1, 2]. The budgets are $b_t=0.05 \cdot (u^t)^\top a^t$, i.e. such that each client can buy 5% of the assets. For some scenario $s\in [S]$, letting ${{\hat{x}}}^t\in \arg \max _{x^t}\{(c^{ts})^\top x^t: x^t\in {\mathcal {X}}_t\}$ and ${{\hat{y}}}\in \arg \max _{y}\{(c^{0s})^\top y : y\in {\mathcal {X}}_0\}$, we set $\sigma ^2:=0.1 \cdot ||V^0{{\hat{y}}} + V{{\hat{x}}}||_2^2$ so that the variance constraint is binding.

Remark that for any value z and any utility random variable Z we have ${\mathcal {E}}_\alpha (-Z)={\mathcal {E}}_\alpha (z-Z) -z$, meaning that minimizing the entropic risk measure means to avoid outcomes of Z such that $z-Z$ is greater than $\alpha$. Given a reference random variable ${{\hat{Z}}}$, by setting $z={\mathbb {E}}({{\hat{Z}}})$ and $\alpha =\beta \cdot ({\mathbb {V}}({{\hat{Z}}}))^{1/2}$, the clients wish to avoid asset selections whose outcomes can make you lose more than $\beta$ standard deviations, compared to the expected return of the reference solution. With this observation in mind, we set $\alpha _t:=0.7 \cdot ||V^t{{\hat{x}}}^t||_2 \text { and } \alpha _0:=0.7 \cdot ||V^0{{\hat{y}}}||_2.$ The vectors $d^t$ are the returns $c^t$ where all the components are zero, except for 60% of the assets bought in the referent $({{\hat{y}}}, {{\hat{x}}})$ (i.e. only these are considered in the variance constraint), and the initial column ${{\bar{x}}}^0\in {\mathcal {S}}^1$—that is feasible for $P({\mathcal {X}})$—is:

$$\begin{aligned} \left( {{\bar{x}}}^0\right) ^t_j = {\left\{ \begin{array}{ll} 0&{}\text { If } d_j^t\ne 0\\ {{\hat{x}}}_j^t&{}\text { Otherwise.} \end{array}\right. } \end{aligned}$$

Absolute and relative tolerances are respectively set to $10^{-6}$ and $0.1\%$ and the runs are stopped after 6 h.

6.3 Computational results

In Tables 6, 7, 8 and 9, we report the number of iterations (it), the total execution time (t), the master time (tmas), the pricing time (tpri), the best lower bound given by a pricing problem at any time (LB), the best upper bound given by the objective value of the last master (UB), the optimality gap (gap), and the number of variables $\theta$ defined by the last set ${\mathcal {S}}^k$ ($|{\mathcal {S}}|$). The execution times are in seconds, the gaps in % and LB and UB are scaled wrt to the upper bound of L-CLA-V. The entries in bold font are the best of each column, except for the “t” column where it means that the associated scheme went faster than solving the monolithic problem. If the time limit is hit during the last iteration, we report the execution time at the end of the previous one. If an algorithm stalls before giving any partial result, we mark the entry with “*”.

Table 6 Aggregated results for $T=1$, $N=10.000$

Table 7 Aggregated results for $T=1$, $N=100.000$

Table 8 Aggregated results for $T=50$, $N=10.000$

Table 9 Aggregated results for $T=50$, $N=100.000$

Overall, every scheme is shown to always converge to solutions within the optimality tolerance for the small and mid-sized instances (10K–500K main variables: Tables 6, 7 and 8). Further, the execution time is mostly used to solve the master problems for the linearized schemes but more evenly split with the pricing time for the non-linearized schemes. We can see that using the convex hull with a linearized pricing (L-SOC-V and L-CLA-V) performs 2–3 times faster than the monolithic model. Along with using the partitioned linear span with a linearized pricing (L-SOC-LP and L-CLA-LP), they are the only algorithms that were able to terminate successfully or return a good quality solution in the allotted time for the largest instance (Table 9, $T=50$, $N=100K$) with 5 million variables. This is due to the fact that these schemes are the only ones that reduce substantially the size of our master problem, be it by making the ${\mathcal {X}}$ constraints redundant for the convex hull, or by shrinking the variable bounds into a small number of other variable bounds for the partitioned linear span (See Table 4 in Subsection 5.4).

We can see that—in our case—a linearized pricing is a crucial ingredient for a successful scheme as we can use a tailored algorithm to solve it. Also, considering the main side constraint as a SOC or a CLA does not make any difference when linearizing the pricing. Even though the non-linearized schemes are not competitive for large instances, we can see that their pricing problems provide excellent quality columns and bounds and make the schemes converge in a few iterations. This phenomenon is probably due to the reliability of the pricing problem on giving a “good” column: By linearizing the objective function of the pricing problem, we somehow lose some of the information that the nonlinearity of the pricing’s objective would have carried along. One could make a parallel with bundle/proximal methods [11] and stabilization techniques for CG [20, 46] where the objective function of the pricing problem is penalized with a nonlinear term enforcing that the new column does not make the dual variables stray too much away from the current dual incumbent. Notice that using the variable aggregation scheme, the master problems are significantly bigger than the others, thus making their solution slower, although the bounds they return are also significantly better.

Fig. 4

Bounds vs. Time for $T=50$, $N=10.000$

Fig. 5

Gap vs. Time for $T=50$, $N=10.000$

In Figs. 4 and 5, we show examples of progression of respectively the bounds and gaps over time of the schemes associated to V and LP on the mid-sized instance ($T=50$, $N=10K$). We can see that the bound/gap improvement is quite progressive for the linearized schemes, whereas it takes only a few large steps in the nonlinearized schemes.

Fig. 6

Column distance to ${\mathcal {S}}$ vs. Time for $T=50$, $N=10.000$

Fig. 7

Reduced Cost vs. Time for $T=50$, $N=10.000$

In Figs. 6 and 7, we show examples of progression of respectively the distance between ${{\bar{x}}}^k$ and ${\mathcal {S}}^k$, and the largest “reduced costs” (see Subsection 3.4) in absolute value over time of the schemes associated to V and LP on the mid-sized instance ($T=50$, $N=10K$). This empirically confirms the theoretical results about the stopping criterion ${{\bar{x}}}^k\in {\mathcal {S}}^k$ and the zero-reduced cost one presented in Proposition 4. Interestingly, to some extent these values can be used to estimate the proximity of the current solution from being optimal. We can make the same observation as for the bounds/gap, where the evolution is more progressive for the linearized schemes than the nonlinearized ones.

7 Conclusions and future work

We propose a generic primal decomposition method that unifies a broad range of existing schemes and opens the door for new exotic algorithmic frameworks. The convergence rate of the algorithms we present is not studied but can be heavily problem dependent. Several special cases of our methods have been proved to converge under mild assumptions but more work is required to prove the convergence of broader classes of algorithms. Extensive computational experiments should be conducted on benchmark instances to gauge the advantages and inconvenients of each of those schemes.

Delayed column generation We assumed here that some structure ${\mathcal {X}}$ is exploitable: in an ongoing work, we explore the same kind of algorithm but relaxing all the constraints. It leads to algorithms sharing similarities with delayed column generation [7] and a simplex for nonlinear problems [65]. The pricing boils down to check if the reduced costs are zero and pick as an entering column a variable whose reduced cost is nonzero, while hardening significantly the master problem.

Non Lagrangean relaxations as pricing problems Instead of relying on Lagrangean duality, be it in the information we have access to when solving the master problem or the kind of pricing problem we solve, different relaxations can be used to provide stronger bounds and attenuate unstable behaviors [36, 46]. We can use e.g. surrogate relaxations [27, 30] where instead of relaxing the side constraints in the objective, they are bundled into a single constraint $\langle \lambda ,g(x,y)\rangle \leqslant 0$. The pricing problem becomes harder, but provides stronger dual bounds with weaker working hypothesis. The master problems must be solved with a surrogate algorithm [37] that returns optimal surrogate multipliers $\lambda$ .

Non-convex problems $P({\mathcal {X}})$ ${\mathcal {X}}$ can be a tractable relaxation of a combinatorial problem $P(\widetilde{{\mathcal {X}}})$: a choice of ${\mathcal {S}}$ defines the relaxation ${\mathcal {X}}$ of $\widetilde{{\mathcal {X}}}$ we work on. The strength of the bounds and the difficulty to solve the subproblems in our algorithms can vary greatly from one choice of ${\mathcal {S}}$ to another [12, 19, 28, 29, 35, 57, 68].

Dual decomposition In an ongoing work, we provide Dual decomposition schemes where—using the tight relationship between DW and the Benders decomposition method—we present a constraint generation methodology where the dual variables are decomposed and generated on the fly. Again, a variety of sets ${\mathcal {S}}$ can be used, yielding different master problems e.g. the generalized Benders decomposition [25] or constraint aggregation schemes [13, 22, 56].

Appendices

Appendix A: Proof of Example 4

We necessarily have $y_2=x_3=x_4=x_5=x_6=0$, $y_1=1-x_1$ and $x_2=1$, which turns the SDP constraint into $x_1\geqslant 0$ and we have $\omega ({\mathcal {X}})=0$. The conic dual of the latter problem is

$$\begin{aligned} \omega ':=\max _{\lambda }\left\{ -\lambda _1-\lambda _2 : \begin{pmatrix} \lambda _1&{}\lambda _4&{}\lambda _5\\ \lambda _4&{}\lambda _2&{}\lambda _6\\ \lambda _5&{}\lambda _6&{}\lambda _3 \end{pmatrix} \succeq 0,\quad 1-\lambda _2+2\lambda _5=0,\quad \lambda _1=0 \right\} . \end{aligned}$$

We necessarily have $\lambda _1=\lambda _4=\lambda _5=0$, $\lambda _2=1$, which turns the SDP constraint into $\lambda _3\geqslant \lambda _6^2$ and we have $\omega '=-1<0=\omega ({\mathcal {X}})$, proving that $P({\mathcal {X}})$ does not satisfy Assumption 1.

Now, by construction ${\mathcal {S}}\subset {\mathcal {X}}$ and $P({\mathcal {S}})$ is a feasible LP that always satisfies Assumption 1. $\square$

Appendix B: Proof of Proposition 1

We prove that some $({{\tilde{x}}}, {{\tilde{y}}})$ is strictly feasible for $P({\mathcal {S}})$. Because $-g({{\bar{x}}},{{\bar{y}}})\in \text {relint }{\mathcal {C}}$ and ${\mathcal {C}}$ is proper, there is $\rho >0$ such that ${\mathcal {B}}(-g({{\bar{x}}},\bar{y}),\rho )\subset \text {relint }{\mathcal {C}}$. Consider $({{\hat{x}}},\hat{\theta })$ strictly feasible for ${\mathcal {S}}$ and $\epsilon >0$ and ${\tilde{x}}$ as follows:

$$\begin{aligned} \epsilon = \min \left\{ 1, \frac{\rho }{L || {{\hat{x}}} - {{\bar{x}}} ||}\right\} ,&\quad {{\tilde{x}}} = {{\bar{x}}} + \epsilon ({{\hat{x}}} - {{\bar{x}}}). \end{aligned}$$

Because ${{\bar{x}}}\in {\mathcal {S}}$ and $({{\hat{x}}},{{\hat{\theta }}})$ is strictly feasible for ${\mathcal {S}}$, there exists ${{\bar{\theta }}}$ such that $\phi ({{\bar{x}}}, {{\bar{\theta }}})=0$, $-\gamma ({{\bar{x}}}, {{\bar{\theta }}})\in {\mathcal {K}}$, $\phi ({{\hat{x}}}, {{\hat{\theta }}})=0$ and $-\gamma ({{\hat{x}}}, {{\hat{\theta }}})\in \text {relint }{\mathcal {K}}$. $\phi$ being linear, defining ${{\tilde{\theta }}} = {{\bar{\theta }}}+\epsilon ({{\hat{\theta }}} - \bar{\theta })$, we immediately have $\phi ({{\tilde{x}}},{{\tilde{\theta }}})=0$. Further, $\epsilon >0$, ${\mathcal {K}}$ is proper, $-\gamma ({{\bar{x}}},\bar{\theta }) \in {\mathcal {K}}$ and $-\gamma ({{\hat{x}}},{{\hat{\theta }}}) \in \text {relint }{\mathcal {K}}$ so we obtain $-\epsilon \gamma ({{\hat{x}}},{{\hat{\theta }}})-(1-\epsilon ) \gamma ({{\bar{x}}},\bar{\theta })\in \text {relint }{\mathcal {K}}$. Because $\gamma$ is ${\mathcal {K}}$-convex and $\epsilon \in ]0,1]$ we obtain $-\gamma ({{\tilde{x}}},{{\tilde{\theta }}})\in \text {relint }{\mathcal {K}}$. We just proved that $({{\tilde{x}}},{{\tilde{\theta }}})$ is strictly feasible for ${\mathcal {S}}$. We finish by proving that $({{\tilde{x}}}, {\bar{y}})$ is strictly feasible for $P({\mathcal {S}})$: By definition we have $\rho \geqslant L\epsilon || {{\hat{x}}} - {{\bar{x}}} ||=L||{{\tilde{x}}}- {{\bar{x}}}|| =L||({{\tilde{x}}}- {{\bar{x}}};{{\bar{y}}}- {{\bar{y}}})||$. Because g is L-Lipschitz, we obtain that $\rho \geqslant ||g({{\tilde{x}}},{{\bar{y}}}) - g({{\bar{x}}},{{\bar{y}}})||$, meaning that $-g({{\tilde{x}}},{{\bar{y}}}) \in {\mathcal {B}}(-g({\bar{x}}, {{\bar{y}}}),\rho )\subset \text {relint }{\mathcal {C}}$. Because $P({\mathcal {S}})$ is convex, Slater’s condition holds, thus finishing the proof. $\square$

Appendix C: Proof of Proposition 2

If $L({\mathcal {X}},\lambda ^k)$ satisfies the P-property wrt y, the problem in y given some $x\in {\mathcal {X}}$ is equivalent to the problem in y given $x=x^k$, i.e. for any $x\in {\mathcal {X}}$ we have

$$\begin{aligned}&\arg \min \limits _{y}\left\{ f\left( x,y\right) +\left\langle \lambda ^k , g\left( x,y\right) \right\rangle \right\} \\ \nonumber =&\arg \min \limits _{y}\left\{ f\left( x^k,y\right) + \left\langle \lambda ^k , g\left( x^k,y\right) \right\rangle \right\} . \end{aligned}$$

(13)

Because $P({\mathcal {S}}^k)$ satisfies Assumption 1, $(x^k,y^k)$ is optimal for $L({\mathcal {S}}^k,\lambda ^k)$, i.e.

$$\begin{aligned} \omega ({\mathcal {S}}^k,\lambda ^k)= \min _{x\in {\mathcal {S}}^k,y}\left\{ f\left( x,y\right) +\left\langle \lambda ^k , g\left( x,y\right) \right\rangle \right\} =f\left( x^k,y^k\right) +\left\langle \lambda ^k , g\left( x^k,y^k\right) \right\rangle . \end{aligned}$$

In consequence, $y^k\in \arg \min _{y}\{f(x^k,y)+\langle \lambda ^k , g(x^k,y)\rangle \}$. Using equality (13) finishes the proof. $\square$

Appendix D: Proof of Lemma 1

First, for any $t\in [0,1]$ and any pair $(u^1,u^2)\in {\mathcal {U}}\times {\mathcal {U}}$ we have: $t\varphi (u^1) +(1-t)\varphi (u^2) -\varphi (t u^1+(1-t)u^2) \in {\mathcal {K}}$. Given that $\lambda \in {\mathcal {K}}^*$ we have $\langle \lambda , t\varphi (u^1) +(1-t)\varphi (u^2) -\varphi (t u^1+(1-t)u^2) \rangle \geqslant 0$, meaning that

$$\begin{aligned}&t \underbrace{ \left\langle \lambda , \varphi \left( u^1\right) \right\rangle }_{ \psi \left( u^1\right) } +(1-t) \underbrace{ \left\langle \lambda , \varphi \left( u^2\right) \right\rangle }_{ \psi \left( u^2\right) } \geqslant \underbrace{ \left\langle \lambda , \varphi \left( t u^1+(1-t)u^2\right) \right\rangle }_{ \psi \left( t u^1+(1-t)u^2\right) } \quad .\square \end{aligned}$$

Appendix E: Proof of Lemma 2

The linear approximation of $\psi$ at ${{\bar{u}}}$ is ${{\bar{\psi }}}[\bar{u}](u):= \psi ({{\bar{u}}})+ \langle \nabla \psi [{{\bar{u}}} ],u-{{\bar{u}}}\rangle$. By definition, for every $u\in {\mathcal {U}}$:

$$\begin{aligned} \left\langle \nabla \psi \left[ {{\bar{u}}} \right] ,u-{{\bar{u}}}\right\rangle =&\lim \limits _{\epsilon \rightarrow 0} \frac{\psi \left( {{\bar{u}}} +\epsilon \left( u-{{\bar{u}}}\right) \right) -\psi \left( {{\bar{u}}}\right) }{\epsilon }\\ =&\lim \limits _{\epsilon \rightarrow 0} \frac{ \left\langle \lambda , \varphi \left( {{\bar{u}}} +\epsilon \left( u-\bar{u}\right) \right) \right\rangle -\left\langle \lambda , \varphi \left( {{\bar{u}}}\right) \right\rangle }{\epsilon }\\&= \left\langle \lambda , \lim \limits _{\epsilon \rightarrow 0} \frac{ \varphi \left( {{\bar{u}}} +\epsilon \left( u-{{\bar{u}}}\right) \right) -\varphi \left( {{\bar{u}}}\right) }{\epsilon } \right\rangle = \left\langle \lambda , D\varphi \left( {{\bar{u}}} \right) \left( u-{{\bar{u}}}\right) \right\rangle , \end{aligned}$$

implying that ${{\bar{\psi }}}[{{\bar{u}}}](u)= \langle \lambda , \varphi (\bar{u})\rangle + \langle \lambda , D\varphi ({{\bar{u}}} ) (u-{{\bar{u}}}) \rangle =\langle \lambda , {{\bar{\varphi }}}[{{\bar{u}}}](u)\rangle$. $\square$

Appendix F: Proof of Lemma 3

By convexity of ${\mathcal {U}}$ and optimality of $u^*$, for any $\epsilon \in ]0,1]$ and any $u\in {\mathcal {U}}$ we have $\varphi (u^ *)\leqslant \varphi (u^ *+\epsilon (u-u^ *))$, i.e.

$$\begin{aligned} \frac{\varphi \left( u^ *+\epsilon \left( u-u^*\right) \right) -\varphi \left( u^*\right) }{\epsilon }\geqslant 0,&\quad \forall \epsilon \in ]0,1], \forall u \in {\mathcal {U}}, \end{aligned}$$

which implies that when $\epsilon \rightarrow 0$, for any $u \in {\mathcal {U}}$ we have $\left\langle \nabla \varphi \left( u^ *\right) ,u-u^ *\right\rangle \geqslant 0$, i.e.

$$\begin{aligned} \underbrace{ \varphi \left( u^*\right) +\left\langle \nabla \varphi \left( u^ *\right) ,u-u^ *\right\rangle }_{ \bar{\varphi }\left[ u^*\right] (u) } \geqslant \underbrace{ \varphi \left( u^*\right) +\left\langle \nabla \varphi \left( u^ *\right) ,u^*-u^ *\right\rangle }_{ \bar{\varphi }\left[ u^*\right] \left( u^*\right) },&\quad \forall u \in {\mathcal {U}}, \end{aligned}$$

meaning that $u^*$ is optimal for $\min _{u\in {\mathcal {U}}} \bar{\varphi }[u^*](u)$ and implying $\omega ^ *= {{\bar{\omega }}}[u^ *]$. $\square$

Appendix G: Proof of Proposition 3

First, notice that the following holds:

$$\begin{aligned} {{\bar{f}}} \left[ x^k,y^k\right] (x,y)=&f\left( x^k,y^k\right) +\left\langle \nabla _x f\left( x^k,y^k\right) ,x-x^k\right\rangle +\left\langle \nabla _y f\left( x^k,y^k\right) ,y-y^k\right\rangle \\ {{\bar{g}}} \left[ x^k,y^k\right] (x,y)=&g\left( x^k,y^k\right) +D_x g\left( x^k,y^k\right) \left( x-x^k\right) +D_y g\left( x^k,y^k\right) \left( y-y^k\right) \end{aligned}$$

In consequence, we have that:

$$\begin{aligned} \nonumber \bar{\omega }\left[ x^{k},y^k\right] \left( {\mathcal {X}},\lambda ^{k}\right) =&f\left( x^k,y^k\right) -\left\langle \nabla _x f\left( x^k,y^k\right) ,x^k\right\rangle -\left\langle \nabla _y f\left( x^k,y^k\right) ,y^k\right\rangle \\ \nonumber&+\left\langle \lambda ^{k} , g\left( x^k,y^k\right) -D_x g\left( x^k,y^k\right) x^k -D_y g\left( x^k,y^k\right) y^k\right\rangle \\ \nonumber&+\min \limits _{x\in {\mathcal {X}}} \left\{ \left\langle \nabla _x f\left( x^k,y^k\right) ,x\right\rangle +\left\langle \lambda ^{k} , D_x g\left( x^k,y^k\right) x\right\rangle \right\} \\&+\min \limits _{y} \left\{ \left\langle \nabla _y f\left( x^k,y^k\right) ,y\right\rangle +\left\langle \lambda ^{k} , D_y g\left( x^k,y^k\right) y\right\rangle \right\} , \end{aligned}$$

(14)

which is separable in x and y. Wlog we can assume that (14) attains its minimum, otherwise the master problem is unbounded and we can stop. Under this assumption, the first order optimality conditions in y for the master problem $P({\mathcal {S}}^k)$ are $\nabla _y f(x^k,y^k)+D_y g ( x^k,y^k)^*\lambda ^k =0$, in turn implying that for any y: $\langle \nabla _y f(x^k,y^k),y\rangle +\langle \lambda ^k,D_y g ( x^k,y^k) y\rangle =0$, meaning that the objective function of (14) is identically zero. $\square$

Appendix H: Proof of Proposition 5

Let us define the following subsets of [p]:

$$\begin{aligned} {\mathcal {J}}_+:=\left\{ j\in [p]: \gamma _j<0, \alpha _j>0 \right\} ,&\quad {\mathcal {J}}_-:=\left\{ j\in [p]: \gamma _j>0, \alpha _j<0 \right\} ,\\ {\mathcal {J}}_0:=\left\{ j\in [p]: \gamma _j, \alpha _j\geqslant 0 \right\} ,&\quad {\mathcal {J}}_\mu :=\left\{ j\in [p]: \gamma _j, \alpha _j\leqslant 0 \right\} . \end{aligned}$$

First notice that we can fix beforehand the following variables:

$$\begin{aligned} z^*_j = {\left\{ \begin{array}{ll} \mu _j&{}\text { If } j\in {\mathcal {J}}_\mu \\ 0&{}\text { If } j\in {\mathcal {J}}_0. \end{array}\right. } \end{aligned}$$

Next, for every $j\in {\mathcal {J}}_-$, we use the change of variable $z_j\leftarrow \mu _j-z_j$, obtaining the following problem:

$$\begin{aligned} \omega ^*:= \sum \limits _{j\in {\mathcal {J}}_-\cup {\mathcal {J}}_\mu } \gamma _j\mu _j + \min \limits _{z}\quad&\sum \limits _{j\in {\mathcal {J}}_+\cup {\mathcal {J}}_-} {{\hat{\gamma }}}_jz_j \\ \text {s.t.:}\quad&\sum \limits _{j\in {\mathcal {J}}_+\cup {\mathcal {J}}_-} {{\hat{\alpha }}}_jz_j \leqslant {{\hat{\beta }}} \\&z_j\in \left[ 0,\mu _j\right] ,&\forall j \in {\mathcal {J}}_+\cup {\mathcal {J}}_- \end{aligned}$$

where ${{\hat{\beta }}}:= \beta -\sum _{j\in {\mathcal {J}}_-\cup {\mathcal {J}}_\mu } \alpha _j \mu _j$ and:

$$\begin{aligned} {{\hat{\alpha }}}_j:= {\left\{ \begin{array}{ll} \alpha _j&{} \text { if } j\in {\mathcal {J}}_+\\ -\alpha _j&{} \text { if } j\in {\mathcal {J}}_- \end{array}\right. }{} & {\quad\quad\quad} {{\hat{\gamma }}}_j:= {\left\{ \begin{array}{ll} \gamma _j &{}\text { if } j\in {\mathcal {J}}_+\\ -\gamma _j&{}\text { if } j\in {\mathcal {J}}_-. \end{array}\right. } \end{aligned}$$

The latter is a knapsack problem with positive capacity ${{\hat{\beta }}}$ and weights ${{\hat{\alpha }}}_j$ that can be solved by sorting the remaining indices $j\in {\mathcal {J}}_+\cup {\mathcal {J}}_-$ in increasing disutility ${{\hat{\gamma }}}_j/{{\hat{\alpha }}}_j$ and filling the capacity constraint until no variable is available or the capacity constraint is tight. $\square$

Appendix I: Proof of Proposition 6

It is enough to show that $(u^*,( \pi ^*,\hat{\lambda },{\hat{\lambda }}_0))$ satisfies the KKT conditions for (9):

$$\begin{aligned} \phi \left( u^*\right) \leqslant 0,\quad -\left( \gamma \left( u^*\right) ,\gamma _0\right) \in {\mathcal {L}}_2 \end{aligned}$$

(15a)

$$\begin{aligned} \pi ^*\geqslant 0,\quad \phi \left( u^*\right) ^\top \pi ^*= 0 \end{aligned}$$

(15b)

$$\begin{aligned} \left( {{\hat{\lambda }}},{\hat{\lambda }}_0\right) \in {\mathcal {L}}_2 \end{aligned}$$

(15c)

$$\begin{aligned} \gamma \left( u^*\right) ^\top \hat{\lambda }+\gamma _0 {{\hat{\lambda }}}_0 = 0 \end{aligned}$$

(15d)

$$\begin{aligned} \nabla \varphi \left( u^*\right) + D\phi \left( u^*\right) ^\top \pi ^*+ D\gamma \left( u^*\right) ^\top {{\hat{\lambda }}} = 0. \end{aligned}$$

(15e)

(15a) and (15b) are trivially satisfied. Given that $-\gamma _0,\lambda ^*\geqslant 0$, the remaining conditions are equivalent to:

$$\begin{aligned} \left( \lambda ^*\right) ^2\left( \left| \left| \gamma \left( u^*\right) \right| \right| _2^2 -\gamma ^2_0\right) \leqslant 0\\ \lambda ^*\left( \left| \left| \gamma \left( u^*\right) \right| \right| _2^2 -\gamma ^2_0\right) = 0\\ \nabla \varphi \left( u^*\right) + D\phi \left( u^*\right) ^\top \pi ^*+ 2\lambda ^*D\gamma \left( u^*\right) ^\top \gamma \left( u^*\right) = 0, \end{aligned}$$

which are all implied by the KKT conditions for (10) at $(u^*,(\pi ^*,\lambda ^*))$. $\square$

Appendix J: Sparsity patterns for the enhanced models

Primal-dual interior point and Newton step Given a barrier parameter $\mu >0$ and an optimization problem $\min _{u}\{\varphi (u):\phi (u)\leqslant 0,\,Ru=s\}$, the barrier problem is defined as $\min _{u}\{\varphi (u)-\mu \sum _{i=1}^p\ln (-\phi _i(u)):Ru=s\}$. The first order optimality conditions for the barrier problem are the following perturbed conditions:

$$\begin{aligned} \nabla \varphi (u)+R^\top \pi +\beta ^\top D\phi (u)=0\\ \mu +\beta _i\phi _i(u)=0\\ Ru=s. \end{aligned}$$

The heavy works at each iteration of a primal-dual interior point algorithm occur during the Newton step, which consists in approximately solve the latter system of equations by solving in $(\Delta u,\Delta \beta , \Delta \pi )$ its following first-order approximation:

$$\begin{aligned} \begin{pmatrix} \!\nabla ^2 \varphi (u) \!+\!\sum \limits _{i=1}^p\beta _i\nabla ^2\phi (u) &{}\!\!\!\!D\phi (u)^\top &{}\!\!R^\top \\ \!\!\!\!\!\!-\text {diag}(\beta )D\phi (u) &{}\!\!\!-\text {diag}(\phi (u)) &{}\!\!\!0\\ \!\!R&{}\!\!\!\!\!\!\!0&{}\!\!\!0 \end{pmatrix} \begin{pmatrix} \Delta u\\ \Delta \beta \\ \Delta \pi \end{pmatrix} \!+\! \begin{pmatrix} \nabla \varphi (u)\!+\!R^\top \pi \!+\!\beta ^\top D\phi (u)\\ \left( \mu \!+\!\beta _i\phi _i(u)\right) _{i\in [p]}\\ Ru-s \end{pmatrix} \!=\!0 \end{aligned}$$

Monolithic formulation After the sparsity patterns in Figs. 8, 9, Figure 10 summarizes the number of nonzero coefficients present in the Newton step’s system.

Fig. 8

Number of nonzeroes per block: Non-enhanced model vs. enhanced

The non-enhanced version has $n^2+10n+T+2$ nonzeroes, with $3n+T+2$ unknowns, while the enhanced version sums $n(4S+8)+S(S(T+1)+2T+7)+2+T$ nonzeroes, with $3n+2ST+4S+T+2$ unknowns. We summarize these results in Table 10 to illustrate the benefits of using the enhanced version instead of the original version (recall that we used $S=20$):

Table 10 Benefits of enhancing the master problem on our instances

We can see that we can divide at least by a factor 100 the number of nonzero coefficients in our instances at the cost of having less than a percent of additional unknowns.

Fig. 9

Sparsity pattern of the Newton step’s matrix for P without numerical enhancement

Fig. 10

Sparsity pattern of the Newton step’s matrix for P with numerical enhancement

Pricing problems We only cover here the pricing problem when the variance constraint is considered as conic because the pricing when considering it as a single nonlinear constraint becomes very similar to the monolithic formulation. Given that the problem is splittable in each $x^t$ (and $x^0=y$), we successively solve the pricing for each $t\in \{0,...,T\}$, which is the problem for which we study the sparsity pattern. As per Fig. 11, Fig. 12 summarizes the number of nonzero coefficients present in the Newton step’s system.

Fig. 11

Number of nonzeroes per block: Non-enhanced model vs. enhanced

The non-enhanced version has $n_t^2+8n_t+1$ nonzeroes, with $3n_t+1$ unknowns, while the enhanced version sums $n_t(8+2S)+S(S+2)+1$ nonzeroes, with $3n_t+2S+1$ unknowns. We summarize these results in Table 11 to illustrate the benefits of using the enhanced version instead of the original version, where we can see again that we can divide at least by a factor 100 the number of nonzero coefficients in our instances at the cost of having less than a percent of additional unknowns.

Fig. 12

Sparsity patterns for the t-th pricing problem

Table 11 Benefits of enhancing the pricing problems on our instances

Appendix K: Proof of Proposition 7

The KKT conditions for (12) are

$$\begin{aligned} \phi \left( {{\tilde{u}}}\right) \leqslant 0,\quad -{{\tilde{\gamma }}}\left( {{\tilde{w}}}\right) \in {\mathcal {K}},\quad {{\tilde{v}}}=V{{\tilde{u}}},\quad {{\tilde{w}}}= W{{\tilde{u}}} \end{aligned}$$

(16a)

$$\begin{aligned} {{\tilde{\pi }}}\geqslant 0,\quad {{\tilde{\lambda }}}\in {\mathcal {K}}^*\end{aligned}$$

(16b)

$$\begin{aligned} \phi \left( {{\tilde{u}}}\right) ^\top {{\tilde{\pi }}} = 0,\quad \left\langle {{\tilde{\gamma }}}\left( {{\tilde{w}}}\right) ,{{\tilde{\lambda }}}\right\rangle = 0 \end{aligned}$$

(16c)

$$\begin{aligned} \nabla {{\tilde{\varphi }}}\left( \tilde{v}\right) - {{\tilde{\alpha }}} = 0,\quad D{{\tilde{\gamma }}}\left( {{\tilde{w}}}\right) ^*{{\tilde{\lambda }}} - {{\tilde{\beta }}} = 0 \end{aligned}$$

(16d)

$$\begin{aligned} D\phi \left( {{\tilde{u}}}\right) ^\top \tilde{\pi }+V^*{{\tilde{\alpha }}} +W^*{{\tilde{\beta }}} = 0. \end{aligned}$$

(16e)

Conditions (16a)–(16b)–(16c) represent respectively primal and dual feasibility and complementary slackness for (11) at $({{\tilde{u}}},(\tilde{\pi },{{\tilde{\lambda }}}))$. We now prove that (16d)–(16e) imply the last remaining KKT condition for (11): stationarity. Replacing (16d) in (16e) we obtain:

$$\begin{aligned} D\phi \left( {{\tilde{u}}}\right) ^\top \tilde{\pi }+V^*\nabla {{\tilde{\varphi }}}\left( {{\tilde{v}}}\right) +W^*D{{\tilde{\gamma }}}\left( {{\tilde{w}}}\right) ^*{{\tilde{\lambda }}} = 0. \end{aligned}$$

(17)

For any (u, v, w) such that $Vu=v$ and $Wu = w$, we have $\varphi (u) = {{\tilde{\varphi }}}(Vu)$ and $\gamma (u) = {{\tilde{\gamma }}}(Wu)$, implying that

$$\begin{aligned} \nabla \varphi (u)&= V^*\nabla {{\tilde{\varphi }}} \left( Vu\right) =V^*\nabla {{\tilde{\varphi }}} \left( v\right) \end{aligned}$$

(18a)

$$\begin{aligned} D\gamma (u)&= D{{\tilde{\gamma }}}\left( Wu\right) W = D\tilde{\gamma }\left( w\right) W. \end{aligned}$$

(18b)

Using (18) at $(u,v,w)=(\tilde{u},{{\tilde{v}}},{{\tilde{w}}})$ and replacing in (17) we get $D\phi ({{\tilde{u}}})^\top {{\tilde{\pi }}} +\nabla \varphi ({{\tilde{u}}}) +D\gamma ({{\tilde{u}}})^*{{\tilde{\lambda }}} = 0$. $\square$