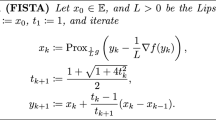Some modified fast iterative shrinkage thresholding algorithms with a new adaptive non-monotone stepsize strategy for nonsmooth and convex minimization problems

Abstract

The “ fast iterative shrinkage-thresholding algorithm " (FISTA) is one of the most famous first order optimization schemes, and the stepsize, which plays an important role in theoretical analysis and numerical experiment, is always determined by a constant relating to the Lipschitz constant or by a backtracking strategy. In this paper, we design a new adaptive non-monotone stepsize strategy (NMS), which allows the stepsize to increase monotonically after finite iterations. It is remarkable that NMS can be successfully implemented without knowing the Lipschitz constant or without backtracking. And the additional cost of NMS is less than the cost of some existing backtracking strategies. For using NMS to the original FISTA (FISTA_NMS) and the modified FISTA (MFISTA_NMS), we show that the convergence results stay the same. Moreover, under the error bound condition, we show that FISTA_NMS achieves the rate of convergence to $o\left( {\frac{1}{{{k^6}}}} \right)$ and MFISTA_NMS enjoys the convergence rate related to the value of parameter of $t_k$, that is $o\left( {\frac{1}{{{k^{2\left( {a + 1} \right) }}}}} \right) ;$ and the iterates generated by the above two algorithms are convergent. In addition, by taking advantage of the restart technique to accelerate the above two methods, we establish the linear convergences of the function values and iterates under the error bound condition. We conduct some numerical experiments to examine the effectiveness of the proposed algorithms.

1 Introduction

We consider the nonsmooth optimization problem:

(P)$\mathop {\min }\limits _{x \in {R^n}} F\left( x \right) = f\left( x \right) + g\left( x \right).$

The following assumptions are made throughout the paper:

• (A) $g:{R^n} \rightarrow ] { - \infty , + \infty } ]$ is a proper, convex, “ proximal-friendly ” [11] and lower semi-continuous function.

• (B) $f:{R^n} \rightarrow ] { - \infty , + \infty } [$ is a smooth convex function and continuously differentiable with Lipschitz continuous gradient, i.e., there exists a Lipschitz constant ${L_f}$ such that for every $x,y \in {R^n},$ $\left\| {\nabla f\left( x \right) - \nabla f\left( y \right) } \right\| \le {L_f}\left\| {x - y} \right\|$ and $\left\| \cdot \right\|$ denotes the standard Euclidean norm.

• (C) Problem (P) is solvable, i.e., ${X^*}: = \arg \min F \ne \emptyset ,$ and for ${x^ * } \in {X^ * }$ we set ${F^ * }: = F\left( {{x^ * }} \right) .$

Problem (P) arises in many contemporary applications such as machine learning [24], compressed sensing [13], and image processing [8]. And due to the importance and the popularity of the problem (P), various attempts have been made to solve it efficiently, especially when the problem instances are of large scale. One popular class of methods for solving problem (P) are first-order methods due to their cheap iteration cost and good convergence properties. Among them, the proximal gradient (PG) method [14, 17, 22] is arguably the most fundamental one, in which the basic iteration is

$$\begin{aligned} {x_{k + 1}} = {\mathrm{pro}}{{\mathrm{x}}_{{\lambda _k}g}}\left( {{x_k} - {\lambda _k}\nabla f\left( {{x_k}} \right) } \right) ,\;{\lambda _k} \in ] {0,{1 \big / {{L_f}}}} ], \end{aligned}$$

(1)

where ${\mathrm{pro}}{{\mathrm{x}}_{\lambda g}}\left( \cdot \right) \mathop { = \arg \min }\limits _x \left\{ {g\left( x \right) + \frac{1}{{2\lambda }}{{\left\| {x - \cdot } \right\| }^2}} \right\}$ denotes the proximal operator of $\lambda g$, and $\lambda _k$ indicates the stepsize and has an upper bound relating to Lipschitz constant. The convergence of PG has been well studied in the literature under various contexts and frameworks (The detailed information can be referred to [7, 9, 18, 20]). However, PG can be slow in practice, see, for example, [23].

Various ways have thus been made to accelerate the proximal gradient algorithm. By performing the extrapolation technique, a prototypical algorithm takes the following form:

$$\begin{aligned} \begin{array}{c} {y_{k + 1}} = {x_k} + {\gamma _k}\left( {{x_k} - {x_{k - 1}}} \right) ,\\ {x_{k + 1}} = {p_{{\lambda _{k + 1} g}}}\left( {{y_{k + 1}}} \right) , \end{array} \end{aligned}$$

(2)

where $\gamma _k$ is the extrapolation parameter satisfying $0 \le \gamma _k \le 1$, ${\lambda _{k + 1}} \in ] {0,{1 \big / {{L_f}}}} ],$ and

$$\begin{aligned} {p_{\lambda g} }\left( y \right) \mathop { = \arg \min }\limits _x \left\{ {{Q_\lambda }(x,y)} \right\} {\mathrm{= pro}}{{\mathrm{x}}_{\lambda g}}\left( {y - \lambda \nabla f\left( y \right) } \right) . \end{aligned}$$

(3)

Here Q(x, y) is the approximation function of F(x) at the given point y, where

$$\begin{aligned} {Q_\lambda }\left( {x,y} \right) = g\left( x \right) + f\left( y \right) + \left\langle {\nabla f\left( y \right) ,x - y} \right\rangle + \frac{1}{{2\lambda }}{\left\| {x - y} \right\| ^2},\quad \forall x \in {R^n}. \end{aligned}$$

(4)

One representative algorithm that takes the form of (2) and with the extrapolation parameter

$$\begin{aligned} {\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k + 1}}}},\;{\mathrm{where}}\; {t_1} = 1, {t_{k + 1}}{\mathrm{= }}\frac{{{\mathrm{1 + }}\sqrt{{\mathrm{1 + 4}}t_k^2} }}{2}{\mathrm{}} \end{aligned}$$

(5)

is the fast iterative shrinkage-thresholding algorithm (FISTA), which was proposed by Beck and Teboulle [5] and was based on the idea that was introduced and developed by Nesterov [21] for minimizing a smooth convex function. The stepsize $\lambda _k$ can be dynamically updated to estimate the Lipschitz constant $L_f$ by a backtracking stepsize rule. FISTA is a very effective algorithm that keeps the simplicity of schemes like PG and improves the convergence rate of objective function value to $O\left( {{k^{ - 2}}} \right)$ for solving the problem (P), hence, it has become a standard algorithm [17] and motivates subsequent studies on the extrapolation scheme (2), see, for example, [6, 19, 22, 23, 29, 32]. Though FISTA is surprisingly efficient, the convergence of the whole iterative sequence generated by FISTA is still unclear [12, 30]. Chambolle and Dossal [12] established the convergence of the sequence generated by FISTA with the new parameter ${\gamma _k} = \frac{{k - 1}}{{k + a}}$ for a fixed $a > 2$ and the assumption $\lambda _k \in ] {0,{\textstyle {1 \over {{L_f}}}}} ],$ for problem (P). Furthermore, Attouch and Peypouquet [1] proved that the convergence rate of function values generated by the algorithm in [12] is $o\left( {{k^{ - 2}}} \right)$ and they considered the convergence of iterates and the rate of convergence of function values for the scheme of (2) with various options of extrapolation parameter $\gamma _k$ in [2]. In addition, in [3], the authors showed that the algorithm in [12] with $a \in \left( {0,2} \right)$ enjoys the convergence rates of function value as $O\left( {{k^{ - \frac{{2\left( {a - 1} \right) }}{3}}}} \right)$. Under the convex setting, Wen, Chen and Pong [30] established the R-linear convergence of the sequences generated by (2) with a parameter $\sup {\gamma _k} < 1$ based on the error bound condition. However, the stepsize in these algorithms such as [1,2,3, 12, 30] is directly related to the Lipschitz constant, which results in that the algorithm implementation as well as the theoretical analysis rely heavily on the Lipschitz constant.

Backtracking for estimating Lipschitz constant works well in practice but the principal drawback is that the stepsize ${\lambda _k}$ generated by the backtracking strategy in FISTA is non-increasing. This non-increasing property can substantially limit the performance of FISTA when a small stepsize is encountered early in the algorithm since this causes the stepsize taken at that point, and at all subsequent iterates, to be very small. Scheinberg, Goldfarb and Bai [27] developed a new backtracking strategy, which allows stepsize to increase. This new backtracking strategy [27] starts with a new initial value at the beginning of each iteration, rather than the stepsize of last iteration like the backtracking in FISTA, and estimates the local Lipschitz constant $L_k,$ which is often smaller than $L_f.$ Hence, $\frac{1}{{{L_k}}}$ may be a better estimate for the stepsize than $\frac{1}{{{L_f}}}.$ With this new backtracking strategy, they proposed a new version of accelerated FISTA (FISTA_BKTR), which reduces the number of iteration greatly and the calculating cost is much less than the one in backtracking rule of original FISTA, and the convergence result is still $O\left( {{1 \big / {{k^2}}}} \right) .$

It is natural that each time the backtracking step operates, the calculating cost of algorithm will increase. Although both of the mentioned backtracking strategies work well, we still pursue to develop a stepsize strategy, which does not use the backtracking procedure and can bring some numerical improvements and some new theoretical results. In this paper, we exploit a new adaptive non-monotone stepsize technique (NMS) to determine $\lambda _k$ in (2), where the stepsize increases monotonically after finite iterations. We prove that FISTA with NMS keeps $O\left( {{1 \big /{{k^2}}}} \right)$ convergence rate of the objective function values, which is similar to original FISTA and FISTA_BKTR. By using the new choice of $t_k$ in [12] and the new adaptive non-monotone technique, we present a modified FISTA (MFISTA) with NMS which also achieves $o\left( {\frac{1}{{{k^2}}}} \right)$ convergence rate of the objective function values. Also, the convergence of the iterative sequence is established without depending on the Lipschitz constant $L_f$ unlike the analysis in [12]. Meanwhile, we prove that both of those two algorithms with NMS enjoy $o\left( {\frac{1}{k}} \right)$ convergent rates of the norm of subdifferential of the objective function. Furthermore, under the error bound condition, we prove that FISTA and MFISTA with NMS can achieve some improved convergence rates for objective function values and the sequence of iterates is convergent; we also take advantage of the restart technique in [23] to accelerate the above FISTA methods with NMS, and establish the linear convergences of the function values and iterative sequence under the error bound condition.

The reminder of the paper is organized as follows. In Sect. 2, we provide a new adaptive non-monotone stepsize strategy. In Sect. 3, we propose an algorithm FISTA_NMS by combining FISTA with the new adaptive non-monotone technique, which ensures the similar convergence rate of the objective function values with FISTA, and a faster convergence rate of the norm of subdifferential of function value than FISTA (See Sect. 3.1 for details). Also, with a small modification, we present a MFISTA_NMS which has similar theoretical results like [1, 12, 26] (See Sect. 3.2 for details). In Sect. 3.3, under the error bound condtion, we show that FISTA_NMS and MFISTA_NMS enjoy improved convergence results. In Sect. 4, we use the restart technique in [23] to accelerate the above methods and establish the linear convergences of the function values and iterates under the error bound condition. Numerical results are reported in Sect. 5. In the last section, conclusions and discussions are presented.

2 Adaptive non-monotone stepsize strategy

In this section, we present a new adaptive non-monotone stepsize strategy.

We first state the algorithm of FISTA with backtracking [5] and the detailed algorithm of FISTA_BKTR [27] as follows.

Denote the computations of ${t_{k + 1}}:= \frac{{1 + \sqrt{1 + 4{\theta _k}t_k^2} }}{2}$ and ${y_{k + 1}}:= {x_k} + \frac{{{t_k} - 1}}{{{t_{k + 1}}}}\left( {{x_k} - {x_{k - 1}}} \right)$ by $({t_{k + 1}},{y_{k + 1}}) = FistaStep\left( {{x_k},{x_{k - 1}},{t_k},{\theta _k}} \right)$. And in following two algorithms, ${p_{{\lambda _k}g}}\left( {{y_k}} \right)$ is defined in (3) with $\lambda : = {\lambda _k}, y: = {y_k}$ and ${Q_{{\lambda _k}}}\left( {{p_{{\lambda _k g}}}\left( {{y_k}} \right) ,{y_k}} \right)$ is defined in (4) with $\lambda : = {\lambda _k}, y: = {y_k}$ and $x: = {p_{{\lambda _k}g}}\left( {{y_k}} \right) .$

Since that (6) holds if ${\lambda _k} \le \frac{1}{{{L_f}}}$, we have that ${\lambda _k} > \frac{\eta }{{{L_f}}},$ which means that the lower bound of stepsize is related to $L_f$, and $\lambda _k$ in Algorithm 1 can be seen as an estimate for the global Lipschitz constant. It is easy to obtain that there are at most ${\log _{\frac{1}{\eta }}}\left( {{\lambda _0}{L_f}} \right) + 1$ backtracking steps at each iteration [27]. Each time the backtracking performs, ${p_{{\lambda _k}g}}\left( {{y_k}} \right)$ and $f\left( {{p_{{\lambda _k}g}}\left( {{y_k}} \right) } \right)$ must be recomputed, that is the main cost of FISTA_backtracking.

To obtain larger stepsize than Algorithm 1, The following Algorithm 2 proposes a new backtracking step rule, which starts with a new initial value at the beginning of each iteration and can be reduced to Algorithm 1 if we set ${\lambda _k^0 = {\lambda _{k - 1}}}.$

We see that the updating rule of $\theta _k$ is equivalent to ${\theta _k} = \frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}}$ and $\lambda _k$ in Algorithm 2 is an estimate for the local Lipschitz constant, while the $\lambda _k$ in Algorithm 1 is an estimate of the global Lipschitz constant. Similar to the analysis of Algorithm 1, the lower bound of stepsize is related to the local Lipschitz constant $L_k$ for $\nabla f\left( x \right)$ restricted to the interval $\left[ {{p_{{\lambda _k}g}}\left( {{y_k}} \right) ,{y_k}} \right]$ for any ${\lambda _k} \le \frac{1}{{{L_k}}},$ which is less than or equal to $L_f$. If the backtracking step is performed, the values of $f\left( {{y_k}} \right)$, $\nabla f\left( {{y_k}} \right)$, ${p_{{\lambda _k}g}}\left( {{y_k}} \right)$ and $f\left( {{p_{{\lambda _k}g}}\left( {{y_k}} \right) } \right)$ must be recomputed. Here, we can see that computation of $f\left( {{y_k}} \right)$ and $\nabla f\left( {{y_k}} \right)$ will be additional costs over against Algorithm 1 for the case that $\nabla f$ is non-linear; otherwise, those computation can be negligible. Since the option of initial stepsize is related to the number of backtracking steps closely, based on the idea of Nesterov [22], the author chose $\lambda _k^0 = \frac{{{\lambda _{k-1}}}}{\sigma }\left( {\sigma \ge \beta } \right)$ to reduce the total number of backtracking steps to $[1 + \frac{{\ln \sigma }}{{\ln \beta }}]\left( {Iter + 1} \right) + \frac{1}{{\ln \beta }}{[{\mathrm{ln}}\frac{{\sigma {\lambda _0}}}{{\beta /{L_f}}}]_ + },$ where Iter means the total number of iterations of Algorithm 2.

Although Algorithm 2 greatly reduces the number of cycle of the internal loop, and generates better stepsize, it still may have additional costs per backtracking step, especially, when the function f is non-linear, the computations of $f\left( {{y_k}} \right)$, $\nabla f\left( {{y_k}} \right)$, ${p_{{\lambda _k}g}}\left( {{y_k}} \right)$ and $f\left( {{p_{{\lambda _k}g}}\left( {{y_k}} \right) } \right)$ will occupy the CPU time. Hence, we design a stepsize strategy that directly gives the stepsize at each iteration, which avoids any extra computations due to line search. We present the adaptive non-monotone stepsize strategy as follows.

In Algorithm 3, we use the condition

$$\begin{aligned} \left\langle {\nabla f\left( x \right) - \nabla f\left( y \right) ,x - y} \right\rangle \le \frac{{{\mu _0}}}{\lambda }{\left\| {x - y} \right\| ^2} \; \mathrm{where} \; {\mu _0} \in ] {0,1} [ \end{aligned}$$

(9)

to control the increase or decrease of the stepsize $\lambda _ k$. When the condition (9) does not holds, the stepsize ${\lambda _k}$ is determined by (7), which implies that ${\lambda _{k + 1}} < {\lambda _k}.$ Conversely, ${\lambda _{k + 1}} \ge {\lambda _k}$. The $\sum \limits _{k = 1}^\infty {E_k}$ is called control series, which can be corrected adaptively for better control of stepsize growth. For the choice of $E_k,$ we will discuss later in this section.

It is remarkable that it is not required to know the Lipschitz constant or use a line search procedure when one uses Algorithm 3 to determine the stepsize $\lambda _k.$ Now we study some important properties of the stepsize $\left\{ {{\lambda _k}} \right\}$ generated by Algorithm 3.

Lemma 2.1

Let $\left\{ {{\lambda _k}} \right\}$ be the sequence generated by Algorithm 3. We have that the sequence $\left\{ {{\lambda _k}} \right\}$ is convergent, and

$$\begin{aligned} \quad \quad {\lambda _k} \ge {\lambda _{min}} := \min \left\{ {{\lambda _1},\frac{{{\mu _1}}}{{{L_f}}}} \right\} , \;\; {\forall }k \ge 1. \end{aligned}$$

(10)

Proof

First, we prove that $\forall k \ge 1$, ${\lambda _k} \ge \min \left\{ {{\lambda _1},\frac{{{\mu _1}}}{{{L_f}}}} \right\}$ holds by induction.

For $k=1,$ the conclusion is obvious. Suppose that the conclusion holds true for some $k = p \ge 1.$ Then, for $k=p+1,$ there are two situations:

• (1) ${\lambda _{p + 1}}$ is generated by (7). We obtain

  $$\begin{aligned} {\lambda _{p + 1}} = {\mu _1}\frac{{{{\left\| {{x_p} - {y_p}} \right\| }^2}}}{{\left\langle {\nabla f\left( {{x_p}} \right) - \nabla f\left( {{y_p}} \right) ,{x_p} - {y_p}} \right\rangle }} \ge \frac{{{\mu _1}}}{{{L_f}}}, \end{aligned}$$

  (11)

  the inequality follows from the fact that f is Lipschitz continuous gradient.

• (2) ${\lambda _{p + 1}}$ is generated by (8). We obtain

  $$\begin{aligned} {\lambda _{p + 1}} \ge {\lambda _p} \ge \min \left({\lambda _1},\frac{{{\mu _1}}}{{{L_f}}}\right). \end{aligned}$$

  (12)

  From (11) and (12), we conclude that $\forall k \ge 1$, ${\lambda _k} \ge \min \left\{ {{\lambda _1},\frac{{{\mu _1}}}{{{L_f}}}} \right\}$ holds for $\forall k \ge 1.$

Denote that

$$\begin{aligned} \ln {\lambda _{i + 1}} - \ln {\lambda _i} = {\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) ^ + } - {\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) ^ - }, \end{aligned}$$

(13)

where ${\left( \cdot \right) ^ + } = \max \{ 0, \cdot \},{\left( \cdot \right) ^ - } = - \min \{ 0, \cdot \}.$ Following the fact that

$$\begin{aligned} \ln {\lambda _{i + 1}} - \ln {\lambda _i} \le \ln \left( {1 + {E_i}} \right) \le {E_i},\forall i \ge 1, \end{aligned}$$

(14)

we have

$$\begin{aligned} {\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) ^ + } \le {E_i},\forall i = 1,2, \cdots , \end{aligned}$$

(15)

which implies that $\sum \nolimits _{i = 1}^\infty {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ + }}$ is convergent from the fact that $\sum \nolimits _{i = 1}^\infty {{E_i}}$ is a convergent nonnegative series.

The convergence of $\sum \nolimits _{i = 1}^\infty {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ - }}$ also can be proved as follows.

Assume by contradiction that $\sum \nolimits _{i = 1}^\infty {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ - }} {\mathrm{= + }}\infty$. Based on the convergence of $\sum \nolimits _{i = 1}^\infty {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ + }}$ and the equality

$$\begin{aligned} \ln {\lambda _{k + 1}} - \ln {\lambda _1} &= \sum \limits _{i = 1}^k {\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) } \\ &= \sum \limits _{i = 1}^k {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ + }} - \sum \limits _{i = 1}^k {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ - }}\end{aligned}$$

(16)

we can easily deduce $\mathop {\lim }\limits _{k \rightarrow \infty } {\ln \lambda _k} = - \infty$, which is a contradiction with ${\lambda _k} \ge \min \left\{ {{\lambda _1},\frac{{{\mu _1}}}{{{L_f}}}} \right\} > 0$. As a result, $\sum \nolimits _{i = 1}^\infty {{{\left( {\ln {\lambda _{i + 1}} - \ln {\lambda _i}} \right) }^ - }}$ is a convergent series. Then, in view of (16), we obtain the sequence $\left\{ {{\lambda _k}} \right\}$ is convergent. $\square$

Lemma 2.2

For the sequence $\left\{ {{\lambda _k}} \right\}$ generated by Algorithm 3, there exists a positive integer${\hat{k}} \ge 1$ such that condition (9) holds constantly for every $k > {\hat{k}}.$

Proof

Suppose the conclusion is not true, i.e. there exists a sequence $\left\{ {{k_j}} \right\} ,$ where ${k_j} \rightarrow \infty ,$ such that

$$\begin{aligned} {{\left\| {{x_{{k_j}}} - {y_{{k_j}}}} \right\| }^2}&< \frac{{{\lambda _{{k_j}}}}}{{{\mu _0}}}\left\langle {\nabla f\left( {{x_{{k_j}}}} \right) - \nabla f\left( {{y_{{k_j}}}} \right) ,{x_{{k_j}}} - {y_{{k_j}}}} \right\rangle \\ \nonumber&= \frac{{{\lambda _{{k_j}}}}}{{{\lambda _{{k_j} + 1}}}}\frac{1}{{{\mu _0}}}{\lambda _{{k_j} + 1}}\left\langle {\nabla f\left( {{x_{{k_j}}}} \right) - \nabla f\left( {{y_{{k_j}}}} \right) ,{x_{{k_j}}} - {y_{{k_j}}}} \right\rangle \\ \nonumber&= \frac{{{\lambda _{{k_j}}}}}{{{\lambda _{{k_j} + 1}}}}\frac{{{\mu _1}}}{{{\mu _0}}}{{\left\| {{x_{{k_j}}} - {y_{{k_j}}}} \right\| }^2}. \end{aligned}$$

(17)

Combining this with the fact

$$\begin{aligned} \mathop {\lim }\limits _{j \rightarrow \infty } \frac{{{\lambda _{{k_j}}}}}{{{\lambda _{{k_j} + 1}}}}\frac{{{\mu _1}}}{{{\mu _0}}} = \frac{{{\mu _1}}}{{{\mu _0}}} < 1, \end{aligned}$$

(18)

which follows from Lemma 2.1, we obtain

$$\begin{aligned} {\left\| {{x_{{{ k}_j}}} - {y_{{{ k}_j}}}} \right\| ^2} < {\left\| {{x_{{{ k}_j}}} - {y_{{{ k}_j}}}} \right\| ^2}, \;\; {\mathrm{for}} \; j \; {\mathrm{is \; sufficiently \; large,}} \end{aligned}$$

(19)

which is a contradiction. Therefore, (9) will hold constantly after finite iterations ${\hat{k}}.$ $\square$

For the rest of this article, we always denote that $k_0 = {\hat{k}} +1$ is the first positive integer such that ${\lambda _{k}}$ satisfies the condition (9), which means that condition (9) holds for any $k \ge k_0.$ It follows from Lemma 2.2 that the stepsize $\left\{ {{\lambda _k}} \right\}$ generated by Algorithm 3 increases monotonically after ${\hat{k}}$ steps.

According to Lemmas 2.1 and 2.2, we can easily obtain the following conclusion.

Corollary 2.1

For the sequence $\left\{ {{\lambda _k}} \right\}$ generated by Algorithm 3, denote that $\mathop {\lim }\limits _{k \rightarrow \infty } {\lambda _k} = {\lambda ^ * }.$ Then, for any $k \ge 1,$ we have ${\lambda _k} \le {\lambda _{\max }}:= \max \left\{ {{\lambda _1}, \cdots ,{\lambda _{{\hat{k}}}},{\lambda ^*}} \right\} .$

Now, we discuss the choice of $E_k.$ In Algorithm 3, we set ${E_k}:= \frac{w_k}{{{k^p}}}\left( {p > 1} \right) ,$ where $\left\{ {{w_i}} \right\}$ is a nonnegative bounded sequence. Generally, we set the value of p close to 1. For the choice of $w_k,$ we can adjust the value of $w_k$ based on the angle between the vectors ${x_k} - {x_{k - 1}}$ and ${x_{k - 1}} - {x_{k - 2}}.$ If the value $\frac{{\left\langle {{x_k} - {x_{k - 1}},{x_{k - 1}} - {x_{k - 2}}} \right\rangle }}{{\left\| {{x_k} - {x_{k - 1}}} \right\| \left\| {{x_{k - 1}} - {x_{k - 2}}} \right\| }}$ is close to 1, it may be caused by a small stepsize, then, we may want to use a larger stepsize in the next iteration. Hence, we can set the value of $w_k$ adaptively. In the following, we give the details for setting $w_k.$

Set $w_k=\eta _1,$ if $\left\langle {{x_k} - {x_{k - 1}},{x_{k - 1}} - {x_{k - 2}}} \right\rangle \le 0.9\left\| {{x_k} - {x_{k - 1}}} \right\| \left\| {{x_{k - 1}} - {x_{k - 2}}} \right\| ;$

set $w_k=\eta _3,$ if $\left\langle {{x_k} - {x_{k - 1}},{x_{k - 1}} - {x_{k - 2}}} \right\rangle \ge 0.98\left\| {{x_k} - {x_{k - 1}}} \right\| \left\| {{x_{k - 1}} - {x_{k - 2}}} \right\| ;$

set $w_k=\eta _2,$ otherwise, where $0< \eta _1< \eta _2 <\eta _3.$ In the numerical experiment, $\eta _1 = 1, \eta _2 = 2, \eta _3 = 10.$

3 FISTA-type algorithm with the adaptive non-monotone stepsize

Based on the adaptive non-monotone stepsize strategy, we present a class of FISTA-type algorithms with non-monotone stepsize (FISTA-type_NMS) and show its convergence results under different inertial terms. The algorithm scheme is as follows:

We first show some key results and the theoretical analysis of the algorithms proposed in this paper relies heavily on it. For ease of description, we define the following sequences.

Notation 3.1

Let $\left\{ {{x_k}} \right\}$ and $\left\{ {{y_k}} \right\}$ be generated by the Algorithm 4 and ${x^*}$ be a fixed minimizer of F. Then, for the convergence of objective function values holds, the sequence $\left\{ {{\upsilon _k}} \right\}$ tends to zero when k goes to infinity

$$\begin{aligned} {v_k} := F\left( {{x_k}} \right) - F\left( {{x^*}} \right) . \end{aligned}$$

(20)

The sequence $\left\{ {{\delta _k}} \right\}$ means the local variation of the sequence $\left\{ {{x_k}} \right\}$

$$\begin{aligned} {\delta _k} := \frac{1}{2}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2}, \end{aligned}$$

(21)

and the sequence $\left\{ {{\varGamma _k}} \right\} ,$ denoting the distance between $\left\{ {{y_k}} \right\}$ and $\left\{ {{p_{{\lambda _k}g}}\left( {{y_k}} \right) } \right\} ,$ is

$$\begin{aligned} {\varGamma _k} := \frac{1}{2}{\left\| {{x_k} - {y_k}} \right\| ^2}, \end{aligned}$$

(22)

and we define ${\varPhi _k}$ as the distance between $\left\{ {{x_k}} \right\}$ and a fixed minimizer $\left\{ {{x^*}} \right\}$

$$\begin{aligned} {\varPhi _k} := \frac{1}{2}{\left\| {{x_k} - {x^*}} \right\| ^2}. \end{aligned}$$

(23)

Lemma 3.1

[5] For any $y \in {R^n},$ one has $z = {p_{\lambda g}}\left( y \right)$ if and only if there exists $\sigma \left( y \right) \in \partial g\left( z \right)$ the subdifferential of $g\left( \cdot \right) ,$ such that

$$\begin{aligned} \nabla f\left( y \right) + \frac{1}{\lambda }\left( {z - y} \right) + \sigma \left( y \right) = 0.\end{aligned}$$

Lemma 3.2

For any $y \in {R^n},{\mu _0} \in ] {0,1} ],$ if y and ${p_{\lambda g} }\left( y \right)$ satisfy the condition (9), then, for any $x \in {R^n},$

$$\begin{aligned} F\left( x \right) - F\left( {{p_{\lambda g} }\left( y \right) } \right) \ge \frac{{{\bar{\mu }} }}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2} + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle , \end{aligned}$$

(24)

where ${\bar{\mu }} = 1 - \frac{{{\mu _0}}}{2},$ if f is a quadratic function; ${\bar{\mu }} = 1 - {\mu _0},$ if f is a non-quadratic function.

Proof

Since f, g are convex, we have

$$\begin{aligned} \begin{array}{l} f\left( x \right) \ge f\left( y \right) + \left\langle {x - y,\nabla f\left( y \right) } \right\rangle ,\\ g\left( x \right) \ge g\left( {{p_{\lambda g} }\left( y \right) } \right) + \left\langle {x - {p_{\lambda g} }\left( y \right) ,\gamma \left( y \right) } \right\rangle , \end{array} \end{aligned}$$

(25)

where $\gamma \left( y \right) = - \nabla f\left( y \right) - \frac{1}{\lambda }\left( {{p_{\lambda g} }\left( y \right) - y} \right) \in \partial g\left( {{p_{\lambda g} }\left( y \right) } \right) ,$ and $\partial g\left( \cdot \right)$ denotes the subdifferential of $g\left( \cdot \right) .$ Then,

$$\begin{aligned}&F\left( x \right) - F\left( {{p_{\lambda g} }\left( y \right) } \right) \\ \nonumber&= f\left( x \right) + g\left( x \right) - f\left( {{p_{\lambda g} }\left( y \right) } \right) - g\left( {{p_{\lambda g} }\left( y \right) } \right) \\ \nonumber&\ge f\left( y \right) + \left\langle {x - y,\nabla f\left( y \right) } \right\rangle + \left\langle {{p_{\lambda g} }\left( y \right) - x,\nabla f\left( y \right) + \frac{1}{\lambda }\left( {{p_{\lambda g} }\left( y \right) - y} \right) } \right\rangle \\ \nonumber&\quad - f\left( {{p_{\lambda g} }\left( y \right) } \right) \\ \nonumber&= f\left( y \right) - f\left( {{p_{\lambda g} }\left( y \right) } \right) + \left\langle {{p_{\lambda g} }\left( y \right) - y,\nabla f\left( y \right) } \right\rangle + \frac{1}{\lambda }\left\langle {{p_{\lambda g} }\left( y \right) - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \nonumber&= f\left( y \right) - f\left( {{p_{\lambda g} }\left( y \right) } \right) + \left\langle {{p_{\lambda g} }\left( y \right) - y,\nabla f\left( y \right) } \right\rangle + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \nonumber&\quad + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}. \end{aligned}$$

(26)

Denote

$$\begin{aligned} \varDelta&= f\left( y \right) - f\left( {{p_{\lambda g} }\left( y \right) } \right) + \left\langle {{p_{\lambda g} }\left( y \right) - y,\nabla f\left( y \right) } \right\rangle + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle \nonumber \\&\quad + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}. \end{aligned}$$

(27)

The proof is derived by dividing into two cases.

• (1) In the case that f is a quadratic function, without loss of generality, assume that

  $$\begin{aligned} f\left( x \right) = \frac{1}{2}{x^T}Ax + {b^T}x,\nabla f\left( x \right) = Ax + b. \end{aligned}$$

  (28)

  It is easy to obtain that

  $$\begin{aligned} f\left( x \right) - f\left( y \right) = \frac{1}{2}\left\langle {\nabla f\left( x \right) + \nabla f\left( y \right) ,x - y} \right\rangle . \end{aligned}$$

  (29)

  Then,

  $$\begin{aligned} \begin{array}{l} \varDelta = \frac{1}{2}\left\langle {\nabla f\left( y \right) + \nabla f\left( {{p_{\lambda g} }\left( y \right) } \right) ,y - {p_{\lambda g} }\left( y \right) } \right\rangle + \left\langle {\nabla f\left( y \right) ,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \qquad + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}\\ \quad = \frac{1}{2}\left\langle {\nabla f\left( y \right) - \nabla f\left( {{p_{\lambda g} }\left( y \right) } \right) ,{p_{\lambda g} }\left( y \right) - y} \right\rangle + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \qquad + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}\\ \quad \ge \frac{1}{\lambda }\left( {1 - \frac{{{\mu _0}}}{2}} \right) {\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2} + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle . \end{array} \end{aligned}$$

  (30)

• (2) In the case that f is a non-quadratic function,

  $$\begin{aligned} \begin{array}{l} \varDelta \ge \left\langle {\nabla f\left( {{p_{\lambda g} }\left( y \right) } \right) ,y - {p_{\lambda g} }\left( y \right) } \right\rangle + \left\langle {\nabla f\left( y \right) ,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \qquad + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}\\ \quad = \left\langle {\nabla f\left( y \right) - \nabla f\left( {{p_{\lambda g} }\left( y \right) } \right) ,{p_{\lambda g} }\left( y \right) - y} \right\rangle + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle \\ \qquad + \frac{1}{\lambda }{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2}\\ \quad \ge \frac{1}{\lambda }\left( {1 - {\mu _0}} \right) {\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2} + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle . \end{array} \end{aligned}$$

  (31)

  The last inequalities of (30) and (31) are from the condition (9).

By combining (26), (27), (30) and (31), we can easily obtain (24). $\square$

Remark 3.1

when ${\bar{\mu }} \ge \frac{1}{2},$ the result (24) of Lemma 3.2 reduces to the Lemma 2.3 in [5]

$$\begin{aligned} F\left( x \right) - F\left( {{p_{\lambda g} }\left( y \right) } \right) \ge \frac{1}{{2\lambda }}{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| ^2} + \frac{1}{\lambda }\left\langle {y - x,{p_{\lambda g} }\left( y \right) - y} \right\rangle , \end{aligned}$$

(32)

which plays a crucial role for the analysis of FISTA.

We always choose the value range of ${\mu _0} \in ] {0,1} [$ for the quadratic function and ${\mu _0} \in ] {0,\frac{1}{2}} [$ for the non-quadratic function, i.e. ${\bar{\mu }} > \frac{1}{2},$ which means that Lemma 3.2 is a result stronger than Lemma 2.3 of [5].

Further, it follows from the identity

$$\begin{aligned} \left\langle {a - b,a - c} \right\rangle = \frac{1}{2}{\left\| {a - b} \right\| ^2} + \frac{1}{2}{\left\| {a - c} \right\| ^2} - \frac{1}{2}{\left\| {b - c} \right\| ^2} \end{aligned}$$

(33)

and (24) that

$$\begin{aligned} F\left( {{p_{\lambda g} }\left( y \right) } \right) + \frac{{{{\left\| {{p_{\lambda g} }\left( y \right) - x} \right\| }^2}}}{{2\lambda }}&\le F\left( x \right) + \frac{{{{\left\| {y - x} \right\| }^2}}}{{2\lambda }} - \left( {\frac{{2{\bar{\mu }} - 1}}{{2\lambda }}} \right) {{\left\| {{p_{\lambda g} }\left( y \right) - y} \right\| }^2} \\ \nonumber&\le F\left( x \right) + \frac{{{{\left\| {x - y} \right\| }^2}}}{{2\lambda }},\;\forall x \in {R^n},{\bar{\mu }} > \frac{1}{2}. \end{aligned}$$

(34)

Independent of the inertial term, we can obtain the following inequality:

Lemma 3.3

Let $\left\{ {{x_k}} \right\} ,\left\{ {{y_k}} \right\}$ be generated by the Algorithm 4. Then, for any $k \ge k_0:= {\hat{k}}+1,$ where ${\hat{k}}$ is defined in Lemma 2.2, we have

$$\begin{aligned}&{\lambda _k}t_k^2{v_k} - {\lambda _{k + 1}}t_{k + 1}^2{v_{k + 1}} - {\rho _k}{v_k} \\&\quad \ge \frac{1}{2}\left( {{{\left\| {{u_{k + 1}}} \right\| }^2} - {{\left\| {{u_k}} \right\| }^2}} \right) {\mathrm{+ }}\left( {{\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2},\end{aligned}$$

where ${\rho _k} = {\lambda _k}t_k^2 - {\lambda _{k + 1}}{t_{k + 1}}\left( {{t_{k + 1}} - 1} \right) ,$ ${u_k} = {t_k}{x_k} - \left( {{t_k} - 1} \right) {x_{k - 1}} - {x^ * }$ and $v_k$ is defined in (20).

Proof

Invoking Lemmas 2.2 and 3.2, we obtain that (24) holds for every $k \ge k_0:= {\hat{k}} + 1,$ where ${\hat{k}}$ is defined in Lemma 2.2.

Denote that ${u_k} = {t_k}{x_k} - \left( {{t_k} - 1} \right) {x_{k - 1}} - {x^ * }.$ We apply the inequality (24) at the points $\left( {x: = {x_k},y: = {y_{k + 1}}} \right)$ with $\lambda : = {\lambda _{k + 1}},$ and likewise at the points $\left( {x: = {x^ * },y: = {y_{k + 1}}} \right) ,$ to get

$$\begin{aligned} {\lambda _{k{\mathrm{+ }}1}}\left( {{v_k} - {v_{k + 1}}} \right) \ge {\bar{\mu }} {\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2} + \left\langle {{x_{k + 1}} - {y_{k + 1}},{y_{k + 1}} - {x_k}} \right\rangle ,\\ - {\lambda _{k{\mathrm{+ }}1}}{v_{k + 1}} \ge {\bar{\mu }} {\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2} + \left\langle {{x_{k + 1}} - {y_{k + 1}},{y_{k + 1}} - {x^ * }} \right\rangle , \end{aligned}$$

(35)

where ${\left\{ {{v_k}} \right\} }$ is defined in (20). Multiplying the first inequality above by $\left( {{t_{k + 1}} - 1} \right)$ and adding it to the second inequality, we have

$$\begin{aligned}&{\lambda _{k{\mathrm{+ }}1}}\left( {\left( {{t_{k + 1}} - 1} \right) {v_k} - {t_{k + 1}}{v_{k + 1}}} \right) \nonumber \\&\quad \ge {\bar{\mu }} {t_{k + 1}}{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2} + \left\langle {{x_{k + 1}} - {y_{k + 1}},{t_{k + 1}}{y_{k + 1}} - \left( {{t_{k + 1}} - 1} \right) {x_k} - {x^*}} \right\rangle . \end{aligned}$$

(36)

Further, multiplying (37) by ${t_{k + 1}},$ we obtain

$$\begin{aligned}&{\lambda _k}t_k^2{v_k} - {\lambda _{k + 1}}t_{k + 1}^2{v_{k + 1}} - \left( {{\lambda _k}t_k^2 - {\lambda _{k + 1}}{t_{k + 1}}\left( {{t_{k + 1}} - 1} \right) } \right) {v_k}\\ \nonumber&\ge {\bar{\mu }} {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2} + \left\langle {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) ,{t_{k + 1}}{y_{k + 1}} - \left( {{t_{k + 1}} - 1} \right) {x_k} - {x^*}} \right\rangle \\ \nonumber&\begin{array}{l} {\mathrm{= }}\frac{1}{2}{\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2} + \left\langle {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) ,{t_{k + 1}}{y_{k + 1}} - \left( {{t_{k + 1}} - 1} \right) {x_k} - {x^*}} \right\rangle \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {{\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2} \end{array}\\ \nonumber&= \frac{1}{2}\left( {{{\left\| {{u_{k + 1}}} \right\| }^2} - {{\left\| {{u_k}} \right\| }^2}} \right) {\mathrm{+ }}\left( {{\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2}. \end{aligned}$$

(37)

$\square$

3.1 FISTA algorithm with the adaptive non-monotone stepsize

In this subsection, we consider the parameter

$$\begin{aligned} {t_1} = 1 \; {\mathrm{and}} \; {t_{k + 1}} = \frac{{1 + \sqrt{1 + 4\left( {{{{\lambda _k}} \big / {{\lambda _{k + 1}}}}} \right) t_k^2} }}{2} \end{aligned}$$

(38)

in the setting of Algorithm 4, which will be called the FISTA algorithm with the adaptive non-monotone stepsize (FISTA_NMS).

Since

$$\begin{aligned} {t_{k + 1}} - {t_k} &= \frac{{1 + \sqrt{1 + 4\frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}}t_k^2} }}{2} - {t_k}\\ &= \frac{{ - 4\left( {1 - \frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}}} \right) t_k^2 + 4{t_k}}}{{2\left( {\sqrt{1 + 4\frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}}t_k^2} + 2{t_k} - 1} \right) }} \ge \frac{{ - 4{t_k} + 4{t_k}}}{{2\left( {\sqrt{1 + 4\frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}}t_k^2} + 2{t_k} - 1} \right) }} = 0, \end{aligned}$$

it’s easy to show that

$$\begin{aligned} {\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k + 1}}}} \le \frac{{{t_k} - 1}}{{{t_k}}} = 1 - \frac{1}{{{t_k}}} \le 1. \end{aligned}$$

(39)

Hence, (39) is an appropriate parameter option for Algorithm 4. In the following, we firstly prove a trivial fact about this $\left\{ {{t_k}} \right\} .$

Lemma 3.4

Let $\left\{ {{t_k}} \right\}$ be generated by FISTA_NMS. Then, we obtain that ${1 \big /{{t_k}}} = {\varTheta }\left( {{1 \big / k}} \right) .$

Proof

Rearranging the expression of ${t_{k+1}}$, we have $2\sqrt{{\lambda _{k + 1}}} {t_{k + 1}} = \sqrt{{\lambda _{k + 1}}} + \sqrt{{\lambda _{k + 1}} + 4{\lambda _k}t_k^2}.$ Denote that ${w_k} = \sqrt{{\lambda _k}} {t_k},$ then

$$\begin{aligned} 2{w_{k + 1}} = \sqrt{{\lambda _{k + 1}}} + \sqrt{{\lambda _{k + 1}} + 4w_k^2} , \end{aligned}$$

(40)

it is easy to get that $\left\{ {{w_{k}}} \right\}$ increasing monotonically.

The following proves that $\mathop {\lim }\limits _{k \rightarrow \infty } {w_k} = {\mathrm{+ }}\infty .$ Suppose that $\mathop {\lim }\limits _{k \rightarrow \infty } {w_k} = w < {\mathrm{+ }}\infty .$ Using Lemmas 2.1 and 2.2, denoted $\mathop {\lim }\limits _{k \rightarrow \infty } {\lambda _k} = {\lambda ^ * } > 0,$ we have $2w = \sqrt{{\lambda ^*}} + \sqrt{{\lambda ^*} + 4{w^2}},$ which implies a contradiction that $4{w^2} - 4w\sqrt{{\lambda ^ * }} = 4{w^2}.$ Therefore, $\mathop {\lim }\limits _{k \rightarrow \infty } {w_k} = {\mathrm{+ }}\infty .$

Using the Stolz theorem, we deduce

$$\begin{aligned} \mathop {\lim }\limits _{k \rightarrow \infty } \frac{{{t_k}}}{k}&= \mathop {\lim }\limits _{k \rightarrow \infty } \frac{{{w_k}}}{{\sqrt{{\lambda _k}} k}} = \frac{1}{{\sqrt{{\lambda ^*}} }}\mathop {\lim }\limits _{k \rightarrow \infty } \left( {{w_{k + 1}} - {w_k}} \right) \\ \nonumber&{\overset{(41)}{=}} \frac{1}{{\sqrt{{\lambda ^*}} }}\mathop {\lim }\limits _{k \rightarrow \infty } {\frac{1}{2}\left( {\sqrt{{\lambda _{k + 1}}} + \sqrt{{\lambda _{k + 1}} + 4w_k^2} } \right) - {w_k}} \\ \nonumber&= \frac{1}{{\sqrt{{\lambda ^*}} }}\mathop {\lim }\limits _{k \rightarrow \infty } \frac{1}{2}\left( {\sqrt{{\lambda _{k + 1}} + 4w_k^2} - \left( {2{w_k} - \sqrt{{\lambda _{k + 1}}} } \right) } \right) \\ \nonumber&= \frac{1}{{\sqrt{{\lambda ^*}} }}\mathop {\lim }\limits _{k \rightarrow \infty } \frac{1}{2}\left( {\frac{{4{w_k}\sqrt{{\lambda _{k + 1}}} }}{{\sqrt{{\lambda _{k + 1}} + 4w_k^2} + \left( {2{w_k} - \sqrt{{\lambda _{k + 1}}} } \right) }}} \right) \\ \nonumber&= \frac{1}{{\sqrt{{\lambda ^*}} }}\mathop {\lim }\limits _{k \rightarrow \infty } \left( {\frac{{2\sqrt{{\lambda _{k + 1}}} }}{{\sqrt{{{{\lambda _{k + 1}}} \big /{w_k^2}} + 4} + 2 - \sqrt{{{{\lambda _{k + 1}}} \mathord \big / {w_k^2}}} }}} \right) = \frac{1}{2}. \end{aligned}$$

(41)

Hence, we have ${1 \big / {{t_k}}} = {\varTheta }\left( {{1 \big / k}} \right) .$ $\square$

Next, we will show that FISTA_NMS enjoys the $O\left( {{1 \big / {{k^2}}}} \right)$ convergence rate of the objective function values and $o\left( {\frac{1}{k}} \right)$ convergence rate of the norm of subdifferential of function value.

Theorem 3.1

(Convergence rate) Let $\left\{ {{x_k}} \right\} ,\left\{ {{y_k}} \right\}$ be generated by FISTA_NMS. Then,

(a)

$$\begin{aligned} F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) \le O\left( {{1 \big /{{k^2}}}} \right) ,\;\;\;\;\forall {x^*} \in {X^*}\,{\mathrm{and}}\,\,\forall k \ge 1. \end{aligned}$$

(42)

(b) The series $\sum \nolimits _{k = 1}^\infty {{k^2}{{\left\| {{x_{k}} - {y_{k}}} \right\| }^2}}$ is convergent and $\mathop {\lim {} \inf }\nolimits _{k \rightarrow \infty } {k^{1.5}}\left\| {{x_k} - {y_k}} \right\| = 0.$

Proof

Define the quantities ${a_k} = {\lambda _k}t_k^2{v_k},{b_k} = \frac{1}{2}{\left\| {{u_k}} \right\| ^2},$ where $v_k$ was defined in (20) and $u_k$ was defined in the statement of Lemma 3.3. Since ${t_{k + 1}} = \frac{{1 + \sqrt{1 + 4\left( {{{{\lambda _k}} \big / {{\lambda _{k + 1}}}}} \right) t_k^2} }}{2}$, one have that ${\rho _k} = {\lambda _k}t_k^2 - {\lambda _{k + 1}}\left( {t_{k + 1}^2 - {t_{k + 1}}} \right) = 0.$ Then, the inequality in Lemma 3.3 can be rewritten as

$$\begin{aligned} {a_k} - {a_{k + 1}} \ge \left( {{b_{k + 1}} - {b_k}} \right) {\mathrm{+ }}\left( { {\bar{\mu }} - \frac{1}{2} } \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2} \ge {b_{k + 1}} - {b_k}, \;\; \forall k \ge k_0. \end{aligned}$$

(43)

It is not difficult to show that there exists a constant $c > 0$ such that

$$\begin{aligned} {a_k} + {b_k} \le {a_{{k_0}}} + {b_{{k_0}}} \le c, \end{aligned}$$

(44)

which implies that ${\lambda _k}t_k^2{v_k} \le c.$ Applying (10), we have

$$\begin{aligned} {v_k}{\mathrm{= }}F\left( {{x_k}} \right) - F\left( {{x^*}} \right) \le \frac{c}{{{\lambda _k}t_k^2}} \le \frac{c}{{{\lambda _{\min }}t_k^2}}, \end{aligned}$$

(45)

then, Lemma 3.4 yields the result that $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) \le O\left( {{1 \big / {{k^2}}}} \right) .$

Rearranging (44) we see that

$$\begin{aligned}\left( {{a_k} + {b_k}} \right) - \left( {{a_{k + 1}} + {b_{k + 1}}} \right) \ge \left( { {\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2}, \;\; \forall k \ge k_0.\end{aligned}$$

Summing the inequality from $k = k_0$ to $k = N,$ we obtain that

$$\begin{aligned} \left( {{a_{k_0}} + {b_{k_0}}} \right) - \left( {{a_{N + 1}} + {b_{N + 1}}} \right) \ge \left( { {\bar{\mu }} - \frac{1}{2}} \right) \sum \limits _{k = k_0}^N {{{\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| }^2}}, \end{aligned}$$

(46)

where ${\bar{\mu }} - \frac{1}{2} > 0$ based on the choice of ${\mu _0}.$ Then, from ${a_k} + {b_k} > 0$ and Lemma 3.4 we have $\sum \limits _{k = 1}^\infty {{k^2}{{\left\| {{x_{k }} - {y_{k }}} \right\| }^2}}$ is convergent.

Further, we can obtain that $\mathop {\lim {} \inf }\limits _{k \rightarrow \infty } {k^{1.5}}\left\| {{x_k} - {y_k}} \right\| = 0.$ Suppose that there exists a constant c such that $\mathop {\lim \inf }\limits _{k \rightarrow \infty } {k^3}{\left\| {{x_k} - {y_k}} \right\| ^2} = c > 0,$ then for k is sufficiently large, we have ${k^3}{\left\| {{x_k} - {y_k}} \right\| ^2} > \frac{c}{2},$ which means that ${k^2}{\left\| {{x_k} - {y_k}} \right\| ^2} > \frac{c}{{2k}}.$ Summing the inequality from $k=1$ to $k=\infty ,$ we obtain that $\sum \nolimits _{k = 1}^{ + \infty } {{k^2}{{\left\| {{x_k} - {y_k}} \right\| }^2}} > \sum \nolimits _{k = 1}^{ + \infty } {\frac{c}{{2k}}},$ which is a contradiction since the left side of the inequality is a convergent series, but the right side is a divergent series. $\square$

Remark 3.2

Denote ${\psi _k} = \nabla f\left( {{x_k}} \right) - \frac{1}{{{\lambda _k}}}\left( {{x_k} - {y_k} + {\lambda _k}\nabla f\left( {{y_k}} \right) } \right) .$ Based on Lemma 3.1, we have ${\psi _k} \in \partial F\left( {{x_k}} \right) .$ It follows from Lemmas 2.1, 3.4, the conclusion $\mathop {\lim }\limits _{k \rightarrow \infty } k^2{\left\| {{x_k} - {y_k}} \right\| ^2} = 0$ and the fact that $\left\| {{\psi _k}} \right\| \le \left( {{L_f} + {1 \big /{{\lambda _{\min }}}}} \right) \left\| {{x_k} - {y_k}} \right\|$ that $\mathop {\lim }\limits _{k \rightarrow \infty } k\left\| {{\psi _k}} \right\| = 0,$ which implies that $\left\| {{\psi _k}} \right\| = o\left( {\frac{1}{k}} \right) .$ However, for the FISTA, we deduce that $t_k^2{\left\| {{x_k} - {y_k}} \right\| ^2}$ is bounded from the proof of Lemma 4.1 in [5], i.e. $\left\| {{\psi _k}} \right\| = O\left( {\frac{1}{k}} \right) .$ Hence, it seems that the sequence $\left\{ {\left\| {{\psi _k}} \right\| } \right\}$ generated by FISTA_NMS converges to zero faster than the one generated by FISTA. In Sect. 5, the numerical performances can verify this.

In following theorem, we will show that the sequence $\left\{ {{x_k}} \right\}$ has at least one accumulation point, and any accumulation point belongs to ${X^ * }.$

Theorem 3.2

For $\forall k \ge 1,$ we have the sequence $\left\{ {{x_k}} \right\}$ generated from FISTA_NMS is bounded, and all the accumulation points of $\left\{ {{x_k}} \right\}$ belong to ${X^ * }.$

Proof

From (45), we have that $b_k \le c$ for any $k \ge k_0$.

With the definition of $b_k$ and triangle inequality, we see that

$$\begin{aligned} \left\| {{x_k} - {x^*}} \right\| \le \frac{{\sqrt{2{b_k}} }}{{{t_k}}} + \left( {1 - \frac{1}{{{t_k}}}} \right) \left\| {{x_{k - 1}} - {x^*}} \right\| \le \frac{{\sqrt{2c} }}{{{t_k}}} + \left( {1 - \frac{1}{{{t_k}}}} \right) \left\| {{x_{k - 1}} - {x^*}} \right\| . \end{aligned}$$

(47)

Let $M_0 = \max \left( {2c,\left\| {{x_{k_0}} - {x^ * }} \right\| } \right) .$ Then, we can easily prove that $\left\| {{x_k} - {x^ * }} \right\| \le M_0$ by induction, which implies $\left\{ {{x_k}} \right\}$ is bounded. Assume that $\left\{ {{x_{{k_j}}}} \right\}$ is a convergent subsequence of $\left\{ {{x_k}} \right\}$ and $\mathop {\lim }\limits _{j \rightarrow \infty } {x_{{k_j}}} = {\bar{x}}.$

In view of (43) and F is lower semi-continuous, we see that

$$\begin{aligned} F\left( {{\bar{x}}} \right) \le \mathop {\lim \inf }\limits _{j \rightarrow \infty } F\left( {{x_{{k_j}}}} \right) = \mathop {\lim }\limits _{j \rightarrow \infty } F\left( {{x_{{k_j}}}} \right) = F\left( {{x^*}} \right) . \end{aligned}$$

(48)

Combining this with the fact that $F\left( {{\bar{x}}} \right) \ge F\left( {{x^ * }} \right) ,$ we have $F\left( {{\bar{x}}} \right) = F\left( {{x^ * }} \right) ,$ which means that ${\bar{x}} \in {X^*}.$ $\square$

3.2 Modified FISTA algorithm with the adaptive non-monotone stepsize

In the previous subsection, for the FISTA Algorithm with adaptive non-monontone stepsize strategy (FISTA_NMS), we proved that convergence rate of the function values remains $O\left( {\frac{1}{k^2}} \right) ,$ however, same as the original FISTA algorithm, the convergence of iterates generated by FISTA_NMS is still unknown. As mentioned in Sect. 1, Chambolle and Dossal [12] exploited a new ${\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k{\mathrm{+ }}1}}}}$ with ${t_k} = \frac{{k + a - 1}}{a},\;a > 2$ for original FISTA, and established the convergence of the iterates generated by FISTA with this new parameter $\gamma _k$ and a constant stepsize $\lambda _k \equiv \frac{1}{{{L_f}}}$ (MFISTA). Attouch and Peypouquet [1] proved that the convergence rate of function values of MFISTA is actually $o\left( {\frac{1}{{{k^2}}}} \right) ,$ better than $O\left( {\frac{1}{{{k^2}}}} \right)$ of FISTA. Moreover, MFISTA has a better numerical performance than FISTA.

In order to establish the convergence of iterates generated by FISTA_NMS, and accelerate its convergence speed, we consider the parameter

$$\begin{aligned} {t_k} = \frac{{k + a - 1}}{a},\;a > 2, \end{aligned}$$

(49)

which satisfies that ${\gamma _k} = \left( {k - 1} \right) /\left( {k + a} \right) \le 1.$ Hence, (50) is a good parameter option for Algorithm 4, which will be called the modified FISTA algorithm with the new adaptive non-monotone stepsize (MFISTA_NMS).

From Theorem 3.1, we can see that if the sequence $\left\{ {{t_k}} \right\}$ satisfies

$$\begin{aligned} {\rho _k} = {\lambda _k}t_k^2 - {\lambda _{k + 1}}\left( {t_{k + 1}^2 - {t_{k + 1}}} \right) \ge 0, \end{aligned}$$

(50)

where ${t_1} = 1$ and $\left\{ {{\lambda _k}} \right\}$ is generated by the Algorithm 3, then the objective function values generated by Algorithm 4 has the $O\left( {{1 \big /{{k^2}}}} \right)$ convergence rate. Particularly, ${\rho _k} = 0$ for ${t_{k + 1}} = \frac{{1 + \sqrt{1 + 4\left( {{{{\lambda _k}} \big / {{\lambda _{k + 1}}}}} \right) t_k^2} }}{2}.$ The following result is based on the analysis of ${\rho _k}.$

Lemma 3.5

Let $\left\{ {{x_k},{y_k}} \right\}$ be the sequences generated via MFISTA_NMS. Assume that $\sum \limits _{k = 1}^\infty {E_k}$ is a convergent nonnegative series and $\left\{ {E_k} \right\}$ is decreasing monotonically. We obtain the following conclusions.

• (a) The series $\sum \limits _{k = 1}^\infty {k\left( {F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) } \right) }$ is convergent.

• (b) The series $\sum \limits _{k = 1}^\infty {{k^2}{{\left\| {{x_k} - {y_k}} \right\| }^2}}$ is convergent and $\mathop {\lim {} \inf }\limits _{k \rightarrow \infty } {k^{1.5}}\left\| {{x_k} - {y_k}} \right\| = 0.$

Proof

Based on the assumption that $\sum \limits _{k = 1}^\infty {E_k}$ is a convergent nonnegative series and $\left\{ {E_k} \right\}$ is decreasing monotonically, we can easily obtain that $\mathop {\lim }\limits _{k \rightarrow \infty } kE_k = 0.$ Then, for any $k > {\hat{k}},$ the following equality

$$\begin{aligned} \nonumber {\rho _{k - 1}}&= \frac{1}{{{a^2}}}\left( {{\lambda _{k - 1}}{{\left( {k + a - 2} \right) }^2} - {\lambda _k}\left( {k - 1} \right) \left( {k + a - 1} \right) } \right) \\ \nonumber&= \frac{1}{{{a^2}}}\left( {{\lambda _{k - 1}}{{\left( {k + a - 2} \right) }^2} - {\lambda _k}\left( {{{\left( {k + a - 2} \right) }^2} + \left( {2 - a} \right) \left( {k + a - 2} \right) + 1 - a} \right) } \right) \\ \nonumber&= \frac{1}{{{a^2}}}\left( {\left( {{\lambda _{k - 1}} - {\lambda _k}} \right) {{\left( {k + a - 2} \right) }^2} + {\lambda _k}\left( {\left( {a - 2} \right) \left( {k + a - 2} \right) + a - 1} \right) } \right) \\ \nonumber&= \frac{1}{{{a^2}}}\left( { - \left| {{\lambda _{k - 1}} - {\lambda _k}} \right| {{\left( {k + a - 2} \right) }^2} + {\lambda _k}\left( {\left( {a - 2} \right) \left( {k + a - 2} \right) + a - 1} \right) } \right) \\ \nonumber&= \frac{1}{{{a^2}}}\left( { - {\lambda _{k - 1}} \cdot {E_{k - 1}} \cdot {{\left( {k + a - 2} \right) }^2} + {\lambda _k}\left( {\left( {a - 2} \right) \left( {k + a - 2} \right) + a - 1} \right) } \right) \end{aligned}$$

(51)

yields that $\mathop {\lim }\limits _{k \rightarrow \infty } \frac{{{\rho _k}}}{k} = \frac{{a - 2}}{{{a^2}}}{\lambda ^ * } \ge {\omega _3},$ where ${\omega _3} = \frac{{\left( {a - 2} \right) }}{{{a^2}}}{\lambda _{\min }}.$ Note the fourth equality follows from the fact that the stepsize $\left\{ {{\lambda _k}} \right\}$ increases monotonically after ${\hat{k}}$ step.

Invoking the inequality in Lemma 3.3 and combining $\mathop {\lim }\limits _{k \rightarrow \infty } \frac{{{\rho _k}}}{k} \ge {\omega _3},$ then, for all k is sufficiently large, we have $\frac{{{\rho _k}}}{k} \ge \frac{{{\omega _3}}}{2}$ and

$$\begin{aligned}&{\lambda _k}t_k^2{v_k} - {\lambda _{k + 1}}t_{k + 1}^2{v_{k + 1}} \nonumber \\&\quad \ge \frac{1}{2}\left( {{{\left\| {{u_{k + 1}}} \right\| }^2} - {{\left\| {{u_k}} \right\| }^2}} \right) {\mathrm{+ }}\left( {{\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2} + \frac{{{\omega _3}}}{2}k{v_k}, \end{aligned}$$

(52)

where ${u_k} = {t_k}{x_k} - \left( {{t_k} - 1} \right) {x_{k - 1}} - {x^ * }$ and ${v_k}$ is defined in (20). We rearrange (52) into

$$\begin{aligned} \left( {{\lambda _k}t_k^2{v_k} + \frac{1}{2}{{\left\| {{u_k}} \right\| }^2}} \right) - \left( {{\lambda _{k + 1}}t_{k + 1}^2{v_{k + 1}} + \frac{1}{2}{{\left\| {{u_{k + 1}}} \right\| }^2}} \right) \ge \frac{{{\omega _3}}}{2}k{v_k},\end{aligned}$$

and

$$\begin{aligned}\begin{array}{l} \left( {{\lambda _k}t_k^2{v_k} + \frac{1}{2}{{\left\| {{u_k}} \right\| }^2}} \right) - \left( {{\lambda _{k + 1}}t_{k + 1}^2{v_{k + 1}} + \frac{1}{2}{{\left\| {{u_{k + 1}}} \right\| }^2}} \right) \ge \left( {{\bar{\mu }} - \frac{1}{2}} \right) {\left\| {{t_{k + 1}}\left( {{x_{k + 1}} - {y_{k + 1}}} \right) } \right\| ^2}. \end{array}\end{aligned}$$

Summing the above two inequalities from $k = N_s$ to $k = N,$ where $N_s$ is sufficiently large, yields that $\sum \limits _{k = 1}^\infty {k\left( {F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) } \right) }$ and $\sum \limits _{k = 1}^\infty {t_k^2{{\left\| {{x_k} - {y_k}} \right\| }^2}}$ are convergent. With the definition of ${t_k} = \frac{{k + a - 1}}{a}\left( {a > 2} \right) ,$ we can further obtain that $\sum \limits _{k = 1}^\infty {{k^2}{{\left\| {{x_k} - {y_k}} \right\| }^2}}$ is convergent. In addition, we can also show that $\mathop {\lim {} \inf }\limits _{k \rightarrow \infty } {k^{1.5}}\left\| {{x_k} - {y_k}} \right\| = 0.$ $\square$

Remark 3.3

Recalling that $\partial F\left( {{x_k}} \right) \ni {\psi _k} = \nabla f\left( {{x_k}} \right) - \frac{1}{{{\lambda _k}}}\left( {{x_k} - {y_k} + {\lambda _k}\nabla f\left( {{y_k}} \right) } \right) .$ It follows that $\sum \limits _{k = 1}^\infty {{k^2}{{\left\| {{\psi _k}} \right\| }^2}}$ is convergent from Lemma 3.5 (b), which is stronger than the fact in [1] that $\left\| {{\psi _k}} \right\| = o\left( {\frac{1}{k}} \right)$ for MFISTA.

Lemma 3.6

Let $\left\{ {{x_k}} \right\}$ be generated by MFISTA_NMS. Then, the series $\sum \limits _{k = 1}^\infty {k{\delta _k}}$ is convergent, where $\delta _k$ is defined in (21).

Proof

From (34) with $x: = {x_k},y: = {y_{k + 1}},$ we have that

$$\begin{aligned} \frac{{{\delta _{k + 1}}}}{{{\lambda _{k + 1}}}} - \gamma _k^2\frac{{{\delta _k}}}{{{\lambda _k}}} \le {v_k} - {v_{k + 1}}, \forall k \ge k_0, \end{aligned}$$

(53)

where ${\gamma _k} = \left( {k - 1} \right) /\left( {k + a} \right) ,$ ${v_k}: = F\left( {{x_k}} \right) - F\left( {{x^ * }} \right)$ is defined in (20) and ${\delta _k}: = \frac{1}{2}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2}$ is defined in (21).

Multiplying this inequality by ${\left( {k + a} \right) ^2}$ and summing from $k = {N_s}$ to $k = N,$ where $N_s$ is sufficiently large, leads to

$$\begin{aligned} \begin{array}{l} - {\left( {{N_s} - 1} \right) ^2}\frac{{{\delta _{{N_s}}}}}{{{\lambda _{{N_s}}}}} + \left[ {{{\left( {{N_s} + a} \right) }^2} - {{\left( {{N_s} + 1 - 1} \right) }^2}} \right] \frac{{{\delta _{{N_s} + 1}}}}{{{\lambda _{{N_s} + 1}}}} \\ \qquad + \left[ {{{\left( {{N_s} + 1 + a} \right) }^2} - {{\left( {{N_s} + 2 - 1} \right) }^2}} \right] \frac{{{\delta _{{N_s} + 2}}}}{{{\lambda _{{N_s} + 2}}}}\\ \qquad + \cdots + \left[ {{{\left( {N - 1 + a} \right) }^2} - {{\left( {N - 1} \right) }^2}} \right] \frac{{{\delta _N}}}{{{\lambda _N}}} + {\left( {N + a} \right) ^2}\frac{{{\delta _{N{\mathrm{+ }}1}}}}{{{\lambda _{N{\mathrm{+ }}1}}}}\\ \quad \le {\left( {{N_s} + a} \right) ^2}{v_{{N_s}}} + \left[ {{{\left( {{N_s}{\mathrm{+ }}1 + a} \right) }^2} - {{\left( {{N_s} + a} \right) }^2}} \right] {v_{{N_s} + 1}} \\ \qquad + \left[ {{{\left( {{N_s}{\mathrm{+ }}2 + a} \right) }^2} - {{\left( {{N_s} + 1 + a} \right) }^2}} \right] {v_{{N_s} + 2}}\\ \qquad + \cdots + \left[ {{{\left( {N + a} \right) }^2} - {{\left( {N - 1 + a} \right) }^2}} \right] {v_N} - {\left( {N + a} \right) ^2}{v_{N + 1}}, \end{array} \end{aligned}$$

(54)

i.e.,

$$\begin{aligned} \begin{array}{*{20}{l}} {{{\left( {N + a} \right) }^2}\frac{{{\delta _{N + 1}}}}{{{\lambda _{N + 1}}}} - {{\left( {{N_s} - 1} \right) }^2}\frac{{{\delta _{{N_s}}}}}{{{\lambda _{{N_s}}}}} + \sum \limits _{k = {N_s} + 1}^N {a\left( {2k - 2 + a} \right) \frac{{{\delta _k}}}{{{\lambda _k}}}} }\\ {\quad \quad \quad \quad \quad \le {{\left( {{N_s} + a} \right) }^2}{v_{N_s}} - {{\left( {N + a} \right) }^2}{v_{_{N + 1}}} + \sum \limits _{k = {N_s} + 1}^N {\left( {2k + 2a - 1} \right) {v_k}} .} \end{array} \end{aligned}$$

(55)

From Lemma 3.5 (a) and $a > 2,$ the series $\sum \limits _{k = 1}^\infty {k\frac{{{\delta _k}}}{{{\lambda _k}}}}$ is convergent. Further, we obtain that $\sum \limits _{k = 1}^\infty {k{\delta _k}}$ is convergent by using $\mathop {\lim }\limits _{k \rightarrow \infty } {\lambda _k} = {\lambda ^ * } > 0.$ $\square$

Next, we construct the convergence rate of function values generated by MFISTA_NMS.

Theorem 3.3

For the sequence $\left\{ {{x_k}} \right\}$ generated by MFISTA_NMS, we have $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) = o\left( {\frac{1}{{{k^2}}}} \right)$ and $\left\| {{x_k} - {x_{k - 1}}} \right\| = o\left( {\frac{1}{k}} \right) .$

Proof

Recalling the definitions of $\left\{ {{v_k}} \right\}$ in (20) and $\left\{ {{\delta _k}} \right\}$ in (21). Denote ${\phi _k} = {v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}.$

From (53) and $\gamma _k \le 1$, we can easily deduce that ${\phi _{k + 1}} \le {\phi _k}$ for $k \ge k_0$. Multiplying by ${\left( {k + 1} \right) ^2}$ we have

$$\begin{aligned} {\left( {k + 1} \right) ^2}{\phi _{k + 1}} \le {\left( {k + 1} \right) ^2}{\phi _k} = {k^2}{\phi _k} + \left( {2k + 1} \right) {\phi _k}. \end{aligned}$$

(56)

Then, we have

$$\begin{aligned} {\left( {{{\left( {k + 1} \right) }^2}{\phi _{k + 1}} - {k^2}{\phi _k}} \right) ^ + } \le \left( {2k + 1} \right) {\phi _k}. \end{aligned}$$

(57)

Since $\sum \limits _{k = 1}^\infty {k{\phi _k}}$ is convergent from Lemma 3.5 (a) and Lemma 3.6, we get that

$$\begin{aligned} \sum \nolimits _{k = 1}^{ + \infty } {{{\left( {{{\left( {k + 1} \right) }^2}{\phi _{k + 1}} - {k^2}{\phi _k}} \right) }^ + }} < + \infty . \end{aligned}$$

(58)

We also can prove that $\sum \nolimits _{k = 1}^{ + \infty } {{{\left( {{{\left( {k + 1} \right) }^2}{\phi _{k + 1}} - {k^2}{\phi _k}} \right) }^ - }} < + \infty .$ Otherwise, based on (58) and the equality

$$\begin{aligned}&{\left( {k + 1} \right) ^2}{\phi _{k + 1}} - {\phi _1} \nonumber \\&\quad = \sum \nolimits _{i = 1}^{ k } {{{\left( {{{\left( {i + 1} \right) }^2}{\phi _{i + 1}} - {i^2}{\phi _i}} \right) }^ + }} - \sum \nolimits _{i = 1}^{ k } {{{\left( {{{\left( {i + 1} \right) }^2}{\phi _{i + 1}} - {i^2}{\phi _i}} \right) }^ - }}, \end{aligned}$$

(59)

we can get that $\mathop {\lim }\limits _{k \rightarrow \infty } {\left( {k + 1} \right) ^2}{\phi _{k + 1}} = - \infty ,$ which is a contradiction with the fact that ${{k^2}{\phi _k} \ge 0}.$ Hence, in view of (59), we have that $\left\{ {{k^2}{\phi _k}} \right\}$ is convergent. Further, we have $\mathop {\lim \inf }\limits _{k \rightarrow \infty } {k^2}{\phi _k} = 0$ by using the convergence of $\sum\nolimits_{k = 1}^\infty {k{\phi _k}}.$ Hence, $\mathop {\lim }\limits _{k \rightarrow \infty } {k^2}{\phi _k} = 0,$ which implies $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) = o\left( {\frac{1}{{{k^2}}}} \right)$ and $\left\| {{x_k} - {x_{k - 1}}} \right\| = o\left( {\frac{1}{k}} \right)$ by Lemma 2.1. $\square$

Now, we give the proof of convergence of the sequence $\left\{ {{x_k}} \right\}$ generated by MFISTA_NMS. Before that, we give some auxiliary results.

Lemma 3.7

For $\forall k \ge 1,$ we have the sequence $\left\{ {{x_k}} \right\}$ generated from MFISTA_NMS is bounded, and all the accumulation points of $\left\{ {{x_k}} \right\}$ belong to ${X^ * }.$

Proof

The proof is similar to the Theorem 3.2.

Lemma 3.8

For any ${x^ * } \in {X^ * },$ and the sequence $\left\{ {{x_k}} \right\}$ generated by MFISTA_NMS, we have ${\varPhi _k} = \frac{1}{2}{\left\| {{x_k} - {x^ * }} \right\| ^2}$ is convergent.

Proof

Recalling (52) in the proof of Lemma 3.5, we have ${a_k} + {b_k} \ge {a_{k + 1}} + {b_{k + 1}}$ for all $k \ge k_0,$ where ${a_k}:= {\lambda _k}t_k^2{v_k} \; {\mathrm{and}} \; {b_k}:= \frac{1}{2}{\left\| {\left( {{t_k} - 1} \right) \left( {{x_k} - {x_{k - 1}}} \right) + \left( {{x_k} - {x^ * }} \right) } \right\| ^2}.$ Combining this and the fact that ${a_k} + {b_k} \ge 0,$ we can easily deduce that the sequence $\left\{ {{a_k} + {b_k}} \right\}$ is convergent.

With Lemma 2.1, the definition of $t_k$ in (50) and $\mathop {\lim }\limits _{k \rightarrow \infty } {k^2}\left( {F\left( {{x_k}} \right) - F\left( {{x^*}} \right) } \right) = 0$ from Theorem 3.3, we obtain that $\mathop {\lim }\limits _{k \rightarrow \infty } {a_k} = 0,$ which implies that $\left\{ {{b_k}} \right\}$ is convergent. From the definition of $\left\{ {{b_k}} \right\} ,$ we see that

$$\begin{aligned} {b_k}&= \frac{1}{2}{{\left\| {\left( {{t_k} - 1} \right) \left( {{x_k} - {x_{k - 1}}} \right) + \left( {{x_k} - {x^*}} \right) } \right\| }^2} \\ \nonumber&= \frac{1}{2}{{\left( {{t_k} - 1} \right) }^2}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2} + \left\langle {\left( {{t_k} - 1} \right) \left( {{x_k} - {x_{k - 1}}} \right) ,\left( {{x_k} - {x^*}} \right) } \right\rangle + \frac{1}{2}{{\left\| {{x_k} - {x^*}} \right\| }^2}. \end{aligned}$$

(60)

It follows from (50) and Theorem 3.3 that the first item of (60) converges to zero, i.e.,

$$\begin{aligned} \mathop {\lim }\limits _{k \rightarrow \infty } \frac{1}{2}{\left( {{t_k} - 1} \right) ^2}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2} = 0. \end{aligned}$$

(61)

In addition, from (50), Theorem 3.3 and the fact from Lemma 3.7 that $\left\| {{x_k} - {x^ * }} \right\|$ is bounded, we have

$$\begin{aligned} \mathop {\lim }\limits _{k \rightarrow \infty } \left\langle {\left( {{t_k} - 1} \right) \left( {{x_k} - {x_{k - 1}}} \right) ,\left( {{x_k} - {x^ * }} \right) } \right\rangle = 0. \end{aligned}$$

(62)

With (60), (61), (62) and the fact that $\left\{ {{b_k}} \right\}$ is convergent, we can obtain that ${\varPhi _k} = \frac{1}{2}{\left\| {{x_k} - {x^ * }} \right\| ^2}$ is convergent.

Theorem 3.4

The sequence $\left\{ {{x_k}} \right\}$ generated by MFISTA_NMS converges to a minimizer of F.

Proof

From Lemma 3.7, we have $\mathop {\lim }\limits _{j \rightarrow \infty } {x_{{k_j}}} = {\bar{x}} \in {X^ * }.$ And with the result of Lemma 3.8, we have ${\left\| {{x_k} - {\bar{x}}} \right\| ^2}$ is convergent by using ${\bar{x}}$ to replace $x^*.$ Then one can easily deduce that the sequence $\left\{ {{{\left\| {{x_k} - {\bar{x}}} \right\| }^2}} \right\}$ converges to zero, which implies $\left\{ {{x_k}} \right\}$ converges to a minimizer of F. $\square$

It is worth mentioning that the biggest difference between MFISTA_NMS and MFISTA is that MFISTA_NMS is not required to do any assumption relating to the $L_f$, while the condition $\lambda \in ] {0,\frac{1}{{{L_f}}}} ]$ in MFISTA plays an important role in algorithm implementation and theoretical analysis.

Meanwhile, it is unclear that whether the iterative sequence generated by MFISTA with the backtracking stepsize converges. However, MFISTA_NMS keeps the similar theoretical results with MFISTA and guarantees in addition the convergence rate of objective function values and the convergence of iterative sequence.

3.3 The convergence results for FISTA_NMS and MFISTA_NMS under the error bound condition

In the above analysis, we proved that for the FISTA_NMS and MFISTA_NMS, function values keep similar convergence rates with FISTA and MFISTA, however, the convergence of the iterates generated by FISTA or FISTA_NMS has not been established so far. Note that the convergence of the iterates generated by FISTA is a puzzling question in the study of numerical optimization methods, meanwhile, the linear convergence rate of function values always be expected, but there is no effective way to prove it. Recently, in [19], under the error bound condition, the authors proposed a comparison method to prove the convergence of iterates generated by FISTA and $o\left( {\frac{1}{{{k^6}}}} \right)$ rate of convergence for the function values. Moreover, the convergence rate of function values generated by MFISTA can be improved to $o\left( {\frac{1}{{{k^{2\left( {1 + a} \right) }}}}} \right) .$

In this subsection, based on the idea of the proof in [19], we will derive that FISTA_NMS and MFISTA_NMS enjoy similar results (See Corollary 3.1 and Corollary 3.2). It is worth emphasizing that the main difference between our setting and the setting of [19] is that we use the adaptive non-monotone stepsize strategy but a constant stepsize was used in [19]. Although there are large overlaps with Theorem 2.6, Corollary 3.5 and Corollary 3.6 in [19], there are some subtle differences. Here, we present the detailed proofs for self-containedness and the convenience of the readers.

Now, we recall the error bound condition which is a key ingredient in proving convergence of iterative methods.

Assumption 3.1

(Error bound condition) For any $\xi \ge {F^ * }: = \mathop {\inf }\limits _{x \in {R^n}} F\left( x \right) ,$ there exist $\varepsilon > 0$ and ${{\bar{\tau }} } > 0$ such that

$$\begin{aligned} {\mathrm{dist}}\left( {x,{X^*}} \right) \le {\bar{\tau }} \left\| {{p_{\frac{1}{{{L_f}}}g}}\left( x \right) - x} \right\| \end{aligned}$$

(63)

whenever $\left\| {{p_{\frac{1}{{{L_f}}}g}}\left( x \right) - x} \right\| < \varepsilon$ and $F\left( x \right) \le \xi .$

Major contributions on developing and using error bound condition to derive convergence rate of iterative descent algorithms have been developed in a series of papers [4, 15, 16, 28, 30].

Lemma 3.9

[22, Lemma 2] For ${\lambda _1} \ge {\lambda _2} > 0,$ we have

$$\begin{aligned} \left\| {{p_{{\lambda _1}g}}\left( x \right) - x} \right\| \ge \left\| {{p_{{\lambda _2}g}}\left( x \right) - x} \right\| \quad {\mathrm{and}}\quad \frac{{\left\| {{p_{{\lambda _1}g}}\left( x \right) - x} \right\| }}{{{\lambda _1}}} \le \frac{{\left\| {{p_{{\lambda _2}g}}\left( x \right) - x} \right\| }}{{{\lambda _2}}}, \end{aligned}$$

(64)

where ${p_{\lambda g}}\left( \cdot \right)$ is defined in (3).

Lemma 3.10

Suppose that Assumption 3.1 holds. Let $\left\{ {{x_k}} \right\}$ be generated by Algorithm 4 and ${x^ * } \in {X^ * }.$ Then, for k is sufficiently large, there exists $\tau _1 >0$ such that

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right) \le {\tau _1}{\left\| {{y_{k + 1}} - {x_{k + 1}}} \right\| ^2}.\end{aligned}$$

Proof

Setting ${\xi _0} = F\left( {{x_{{k_0} + 1}}} \right) + \frac{1}{{2\lambda _{k_0 +1} }}{\left\| {{x_{{k_0} + 1}} - {x_{{k_0}}}} \right\| ^2}.$ From Lemma 2.1, we obtain that $\frac{1}{{{L_f}}} \ge \frac{{{\lambda _{\min }}}}{{{\mu _1}}},$ $\frac{{{\lambda _{\min }}}}{{{\mu _1}}} \le \frac{{{\lambda _k}}}{{{\mu _1}}}$ and $\frac{{{\lambda _k}}}{{{\mu _1}}} \ge {\lambda _k},$ then, combining with Lemma 3.9, the nonexpansiveness property of the proximal operator and the fact that $\nabla f$ is Lipschitz continuous, we obtain that

$$\begin{aligned} \left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\|&\le \frac{{{\mu _1}}}{{{L_f}{\lambda _{\min }}}}\left\| {{p_{\frac{{{\lambda _{\min }}}}{{{\mu _1}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| \le \frac{{{\mu _1}}}{{{L_f}{\lambda _{\min }}}}\left\| {{p_{\frac{{{\lambda _k}}}{{{\mu _1}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| \\ \nonumber&\le \frac{1}{{{L_f}{\lambda _{\min }}}}\left\| {{p_{{\lambda _k}g}}\left( {{x_k}} \right) - {x_k}} \right\| = \frac{1}{{{L_f}{\lambda _{\min }}}}\left\| {{p_{{\lambda _k}g}}\left( {{x_k}} \right) - {p_{{\lambda _k}g}}\left( {{y_k}} \right) } \right\| \\ \nonumber&\le \frac{1}{{{L_f}{\lambda _{\min }}}}\left( {1 + {\lambda _k}{L_f}} \right) \left\| {{x_k} - {y_k}} \right\| . \end{aligned}$$

(65)

Applying the inequality (34) at the point $x:={x_k},\;y:={y_{k + 1}}$ and $\lambda := \lambda _{k+1},$ we obtain that for $k \ge k_0,$

$$\begin{aligned}&\frac{{2{\bar{\mu }} - 1}}{{2{\lambda _{k + 1}}}}{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2} \\ \nonumber&\le \left( {F\left( {{x_k}} \right) + \frac{{\gamma _k^2}}{{2{\lambda _{k + 1}}}}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2}} \right) - \left( {F\left( {{x_{k + 1}}} \right) + \frac{1}{{2{\lambda _{k + 1}}}}{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right) \\ \nonumber&\le \left( {F\left( {{x_k}} \right) + \frac{1}{{2{\lambda _k}}}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2}} \right) - \left( {F\left( {{x_{k + 1}}} \right) + \frac{1}{{2{\lambda _{k + 1}}}}{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right) , \end{aligned}$$

(66)

where the second inequality follows the facts that ${\gamma _k} \le 1$ and ${\lambda _k} \le {\lambda _{k + 1}},$ the latter relation was proved in Lemma 2.2.

It follows from (66) that for $k \ge k_0,$ $\left\{ {F\left( {{x_{k + 1}}} \right) + \frac{1}{{2\lambda }}{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right\}$ is non-increasing, and $\sum \nolimits _{k = {k_0}}^{ + \infty } {{{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}} < + \infty$ due to the convergence of $\left\{ {{\lambda _k}} \right\} .$ Then, we get that for k is sufficiently large, $F\left( {{x_k}} \right) \le {\xi _0}$ and there exists a ${\varepsilon _0} > 0$ such that $\left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| < {\varepsilon _0}$ by (65). Hence, combining with Assumption 3.1, we have for ${\xi _0} = F\left( {{x_{{k_0} + 1}}} \right) + \frac{1}{{2\lambda _{k_0+1} }}{\left\| {{x_{{k_0} + 1}} - {x_{{k_0}}}} \right\| ^2},$ there exists ${ \tau _0 } > 0,$ for k is sufficiently large, such that

$$\begin{aligned} {\mathrm{dist}}\left( {{x_k},{X^*}} \right) \le {\tau _0}\left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| . \end{aligned}$$

(67)

In addition, applying the inequality (34) at the point $y:= {y_{k + 1}},$ $\lambda := \lambda _{k+1}$ with $x_{k+1}^* \in {X^ * }$ satisfying ${\mathrm{dist}}\left( {{x_{k+1}},{X^ * }} \right) = \left\| {{x_{k+1}} - x_{k+1}^*} \right\| ,$ we obtain

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right)&\le \frac{1}{{2\lambda _{k+1} }}{\left\| {{y_{k + 1}} - x_{k + 1}^*} \right\| ^2} - \frac{1}{{2\lambda _{k+1} }}{\left\| {{x_{k + 1}} - x_{k + 1}^*} \right\| ^2} \\&= \frac{1}{{2\lambda _{k+1} }}{\left\| {{y_{k + 1}} - {x_{k + 1}}} \right\| ^2} + \frac{1}{\lambda _{k+1} }\left\langle {{y_{k + 1}} - {x_{k + 1}},{x_{k + 1}} - x_{k + 1}^*} \right\rangle \\&\le \frac{1}{{2\lambda _{k+1} }}{\left\| {{y_{k + 1}} - {x_{k + 1}}} \right\| ^2} + \frac{1}{\lambda _{k+1} }\left\| {{y_{k + 1}} - {x_{k + 1}}} \right\| {\mathrm{dist}}\left( {{x_{k + 1}},{X^*}} \right) . \end{aligned}$$

Then, combining (67), (65) and Corollary 2.1, we have for k is sufficiently large,

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right) \le {\tau _1}{\left\| {{y_{k + 1}} - {x_{k + 1}}} \right\| ^2}, \end{aligned}$$

(68)

where ${\tau _1} = \frac{1}{{{\lambda _{\min }}}}\left( {\frac{1}{2} + \frac{{{\tau _0}}}{{{\lambda _{\min }}{L_f}}}\left( {1 + {\lambda ^ * }{L_f}} \right) } \right) .$ ${} \Box$ $\square$

Lemma 3.11

Suppose that there exists a nonnegative sequence $\left\{ {{s_k}} \right\}$ such that for k is sufficiently large, ${\alpha _k} = \frac{{{s_k} - 1}}{{{s_{k + 1}}}} \ge {\gamma _k},$ where ${\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k + 1}}}}$ and $\mathop {\lim }\limits _{k \rightarrow + \infty } {\gamma _k} = 1.$ Then, we have $\mathop {\lim }\limits _{k \rightarrow \infty } {s_k} = + \infty$ and $\mathop {\lim \sup }\limits _{k \rightarrow \infty } \frac{{s_{k + 1}^2 - s_k^2}}{{s_k^2}} \le 0.$

Proof

The proof is similar to Lemma 2.5 in [19]. $\square$

The following theorem is largely similar to [19, Theorem 2.6], here, we still give a complete proof since our setting is equipped with the adaptive non-monotone stepsize, which is different from constant stepsize be used in [19].

Theorem 3.5

Suppose that Assumption 3.1 holds and there exists a nonnegative sequence $\left\{ {{s_k}} \right\}$ such that for k is sufficiently large, ${\alpha _k} = \frac{{{s_k} - 1}}{{{s_{k + 1}}}} \ge {\gamma _k},$ where ${\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k + 1}}}}$ and $\mathop {\lim }\limits _{k \rightarrow + \infty } {\gamma _k} = 1.$ Then, we have that $F\left( {{x_{k + 1}}} \right) - F\left( {{x^ * }} \right) = o\left( {\frac{1}{{s_{k + 1}^2}}} \right)$ and ${\left\| {{x_{k + 1}} - {x_k}} \right\| } = O\left( {\frac{1}{{s_{k + 1}}}} \right) .$

Proof

Denote that ${E_k} = s_{k + 1}^2\left( {F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) } \right) + \frac{{s_k^2}}{{2\lambda _k }}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2}.$ Applying inequality (34) at the point $x:={x_k},\;y:={y_{k + 1}}$ and $\lambda := \lambda _{k+1},$ we have for $k \ge k_0,$

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^ * }} \right) + \frac{{2{\bar{\mu }} - 1 }}{{2\lambda _{k+1} }}{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2}&+ \frac{1}{{2\lambda _{k+1} }}{\left\| {{x_{k + 1}} - {x_k}} \right\| ^2} \\ \nonumber&\le F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) + \frac{{\gamma _k^2}}{{2\lambda _k }}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2}. \end{aligned}$$

(69)

By the supposed condition, we have $\gamma _k^2 \le \alpha _k^2$ for any $k \ge {k_1},$ where $k_1$ is sufficiently large, then,

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^ * }} \right) + \frac{{2{\bar{\mu }} - 1 }}{{2\lambda _{k+1} }}{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| ^2}&+ \frac{1}{{2\lambda _{k+1} }}{\left\| {{x_{k + 1}} - {x_k}} \right\| ^2} \\ \nonumber&\le F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) + \frac{{\alpha _k^2}}{{2\lambda _k }}{\left\| {{x_k} - {x_{k - 1}}} \right\| ^2}. \end{aligned}$$

(70)

Multiplying by $s_{k + 1}^2,$ we have

$$\begin{aligned}&{E_{k + 1}} + \left( {s_{k + 1}^2 - s_{k + 2}^2} \right) \left( {F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right) } \right) + \frac{{2{\bar{\mu }} -1 }}{{2\lambda _{k+1} }}s_{k + 1}^2{{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2} \\&\le s_{k + 1}^2\left( {F\left( {{x_k}} \right) - F\left( {{x^*}} \right) } \right) + \frac{{{{\left( {{s_k} - 1} \right) }^2}}}{{2\lambda _k }}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2} \\&= s_{k + 1}^2\left( {F\left( {{x_k}} \right) - F\left( {{x^*}} \right) } \right) + \frac{{s_k^2}}{{2\lambda _k }}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2} \\&\quad - \frac{{2{s_k} - 1}}{{2\lambda _k }}{{\left\| {{x_k} - {x_{k - 1}}} \right\| }^2} \le {E_k},\;\forall k \ge {k_1}. \end{aligned}$$

Then, combining with the inequality in Lemma 3.10 and Corollary 2.1, we have

$$\begin{aligned} {E_{k + 1}} + \left( {\frac{{\left( {s_{k + 1}^2 - s_{k + 2}^2} \right) }}{{s_{k + 1}^2}} + \frac{{2{\bar{\mu }} - 1}}{{2{\tau _1}{\lambda _{\max } }}}} \right) s_{k + 1}^2\left( {F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right) } \right) \le {E_k}. \end{aligned}$$

(71)

Since $\mathop {\lim \sup }\limits _{k \rightarrow \infty } \frac{{s_{k + 2}^2 - s_{k + 1}^2}}{{s_{k + 1}^2}} \le 0$ from Lemma 3.11, we have $\frac{{\left( {s_{k + 1}^2 - s_{k + 2}^2} \right) }}{{s_{k + 1}^2}} \ge - \frac{{2{\bar{\mu }} - 1}}{{4{\tau _1}{\lambda _{\max } }}}$ for k is sufficiently large, then, (71) implies that, for k is sufficiently large,

$$\begin{aligned} {E_{k + 1}} + \frac{{2{\bar{\mu }} - 1}}{{4{\tau _1}{\lambda _{\max } }}}s_{k + 1}^2\left( {F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right) } \right) \le {E_k}, \end{aligned}$$

(72)

which means that $\left\{ {{E_k}} \right\}$ is nonincreasing and convergent and $\sum \limits _{k = 1}^\infty {s_{k + 1}^2\left( {F\left( {{x_{k + 1}}} \right) - F\left( {{x^ * }} \right) } \right) }$ is convergent. Hence, $F\left( {{x_{k + 1}}} \right) - F\left( {{x^ * }} \right) = o\left( {\frac{1}{{s_{k + 1}^2}}} \right)$ holds ture.

Further, since the convergence of $\left\{ {{E_k}} \right\} ,$ we have $\left\{ {s_{k + 1}^2{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right\}$ is bounded, which means that ${\left\| {{x_{k + 1}} - {x_k}} \right\| } \le O\left( {\frac{1}{{s_{k + 1}}}} \right) ,$ i.e., there exists a constant $c_1 >0$ such that for k is sufficiently large, $\left\| {{x_{k+1}} - {x_{k}}} \right\| \le \frac{c_1}{{{s_{k+1}}}}.$ ${} \Box$ $\square$

Corollary 3.1

Suppose that Assumption 3.1 holds. Let $\left\{ {{x_k}} \right\}$ be generated by FISTA_NMS and ${x^ * } \in {X^ * }.$ Then,

• (1) $F\left( {{x_k}} \right) - F\left( {{x^*}} \right) = o\left( {\frac{1}{{{k^6}}}} \right)$ and $\left\| {{x_k} - {x_{k - 1}}} \right\| = O\left( {\frac{1}{{{k^3}}}} \right)$.

• (2) $\left\{ {{x_k}} \right\}$ converges to ${\bar{x}} \in {X^ * }$ at the $O\left( {\frac{1}{{{k^2}}}} \right)$ rate of convergence.

Proof

Denote that ${s_1} = {s_2} = 1$ and ${s_k} = \frac{{{{\left( {k - 1} \right) }^3}}}{{{{\left( {\int _1^{k - 1} {\frac{{\ln x}}{{{x^2}}}dx} } \right) }^2}}},\; \forall k \ge 3.$ Based on the proof of Corollary 3.5 in [19], we have $\alpha _k \ge \gamma _k$ for k is sufficiently large and ${s_k} \sim {k^3}.$ Then, By Theorem 3.5, we can get that $F\left( {{x_k}} \right) - F\left( {{x^*}} \right) = o\left( {\frac{1}{{{k^6}}}} \right)$ and there exists a $c' > 0$ such that for sufficiently large k, $\left\| {{x_{k + 1}} - {x_k}} \right\| \le \frac{{c'}}{{{k^3}}}.$ Then, we can deduce that

$$\begin{aligned} \forall p > 1,\quad \left\| {{x_{k + p}} - {x_k}} \right\| &\le \sum \nolimits _{i = k + 1}^{k + p} {\left\| {{x_i} - {x_{i - 1}}} \right\| } \\ &\le c'\sum \nolimits _{i = k + 1}^{k + p} {\frac{1}{{{i^3}}}} \le c'\int _k^{k + p} {\frac{1}{{{x^3}}}dx}.\end{aligned}$$

Then,

$$\begin{aligned}\left\| {{x_k} - {\bar{x}}} \right\| \le \frac{c'}{{2{k^2}}}.\end{aligned}$$

$\square$

Corollary 3.2

Suppose that Assumption 3.1 holds. Let $\left\{ {{x_k}} \right\}$ be generated by MFISTA_NMS and ${x^ * } \in {X^ * }.$ Then,

• (1) $F\left( {{x_k}} \right) - F\left( {{x^*}} \right) = o\left( {\frac{1}{{{k^{2\left( {a + 1} \right) }}}}} \right)$ and $\left\| {{x_k} - {x_{k - 1}}} \right\| = O\left( {\frac{1}{{{k^{a + 1}}}}} \right)$.

• (2) $\left\{ {{x_k}} \right\}$ converges to ${\bar{x}} \in {X^ * }$ at the $O\left( {\frac{1}{{{k^a}}}} \right)$ rate of convergence.

Proof

For $a \ge 1,$ denote ${s_k} = {\left( {k + a - 1} \right) ^{a + 1}};$ otherwise, denote ${s_1} = {s_2} = 1,$ and ${s_k} = \frac{{{{\left( {k + a - 1} \right) }^{a + 1}}}}{{\int _1^{k - 1} {\frac{{\ln x}}{{{x^{1 + a}}}}dx} }},\; \forall k \ge 3.$ Based on the proof of Corollary 3.6 in [19], we have $\gamma _k \le \alpha _k$ for k is sufficiently large and ${s_k} = O\left( {{k^{a + 1}}} \right) .$ Then, By Theorem 3.5, we can get that $F\left( {{x_k}} \right) - F\left( {{x^*}} \right) = o\left( {\frac{1}{{{k^{2\left( {a + 1} \right) }}}}} \right)$ and there exists a $c'' > 0$ such that for sufficiently large k, $\left\| {{x_{k + 1}} - {x_k}} \right\| \le \frac{{c''}}{{{k^{a+1}}}}.$ Then, we can deduce that

$$\begin{aligned}&\forall p > 1,\quad \left\| {{x_{k + p}} - {x_k}} \right\| \le \sum \nolimits _{i = k + 1}^{k + p} {\left\| {{x_i} - {x_{i - 1}}} \right\| } \\&\quad \le c''\sum \nolimits _{i = k + 1}^{k + p} {\frac{1}{{{i^{a+1}}}}} \le c''\int _k^{k + p} {\frac{1}{{{x^{a+1}}}}dx}. \end{aligned}$$

Then,

$$\begin{aligned} \left\| {{x_k} - {\bar{x}}} \right\| \le \frac{c''}{{a{k^a}}}. \end{aligned}$$

$\square$

It is noted that the stepsize $\lambda _k$ generated by Algorithm 3 increases monotonically after finite iterations, while the stepsize $\lambda _k$ generated by backtracking of FISTA_BKTR may increases or decreases in the backtracking process. Meanwhile, we cannot obtain a similar inequality with (34) based on FISTA_BKTR. Hence, using the same idea of proof in [19], backtracking of FISTA_BKTR can not obtain the results in Corollaries 3.1 and 3.2, and to our knowledge, there aren’t similar results in the literature. From this point of view, FISTA with $\lambda _k$ generated by the new stepsize strategy (Algorithm 3) enjoys better theoretical properties than Algorithm 2 (FISTA_BKTR).

To further illustrate this point, we consider a restart technique, which is crucially important in improving the theoretical results and accelerating the numerical performance of the algorithm, to improve our algorithms in next section.

4 Restart FISTA algorithm with the adaptive non-monotone stepsize strategy

O’Donoghue and Candès [23] introduced two simple heuristic adaptive restart techniques that can improve the convergence rate of accelerated gradient schemes. One restart technique is fixed restarting, that restarts the algorithm every K iterations and takes the last point generated by the algorithm as the starting point. Another is the adaptive restart, which restarts the algorithm based on the following schemes: 1) function scheme: $F\left( {{x_k}} \right) > F\left( {{x_{k - 1}}} \right) ;$ 2)gradient scheme: ${\left( {{y_{k}} - {x_{k}}} \right) ^T}\left( {{x_{k }} - {x_{k-1}}} \right) > 0.$

O’Donoghue and Candès pointed out that both of the two adaptive restart schemes perform similarly well. But when the iteration point is close to the minimum, the algorithm with the gradient restart technique is more numerically stable. Therefore, we combine the fixed restarting with the gradient restart technique to improve the performance of FISTA_NMS and MFISTA_NMS in this section.

We present algorithms as follows.

The schemes of FISTA_BKTR and MFISTA_BKTR combining the restart strategy separately, namely FISTA_BKTR_restart and MFISTA_BKTR_restart, are similar to the above two algorithms, here we omit the unnecessary details. In the following, we prove that under the error bound condition, the sequences generated by Algorithm 6 and Algorithm 7 are R-linearly convergent; Moreover, the corresponding sequences of objective function values are also R-linearly convergent. Note that whether the FISTA_BKTR with restart strategy enjoys similar convergence results is unknown.

Before proceeding with the convergence results, we give some auxiliary conclusions as follows.

Definition 4.1

[25] Let the iterative sequence $\left\{ {{x_k}} \right\}$ generated by an algorithm converges to $x^*$ in some norm. If there is a positive constant $\beta \in \left( {0,1} \right)$ which is independent of the iterative number k, such that

$$\begin{aligned} \mathop {\lim }\limits _{k \rightarrow \infty } \frac{{\left\| {{x_{k + 1}} - {x^ * }} \right\| }}{{\left\| {{x_k} - {x^ * }} \right\| }} = \beta ,\end{aligned}$$

then the sequence $\left\{ {{x_k}} \right\}$ is said to be Q-linear convergence. If there is a positive constant $\alpha \in \left( {0,1} \right)$ such that

$$\begin{aligned} \mathop {\lim \sup }\limits _{k \rightarrow \infty } {\left\| {{x_k} - {x^ * }} \right\| ^{\frac{1}{k}}} = \alpha ,\end{aligned}$$

then the sequence $\left\{ {{x_k}} \right\}$ is said to be R-linear convergence.

Lemma 4.1

[25] The sequence $\left\{ {{x_k}} \right\}$ is said to be R-linear convergence if there is a sequence of nonnegative scalars $\left\{ {{q_k}} \right\}$ such that

$$\begin{aligned} \left\| {{x_k} - {x^ * }} \right\| \le {q_k}\;for\;all\;k,\;and\;\left\{ {{q_k}} \right\} \;converges\;Q\mathrm{-}linearly\;to\;zero.\end{aligned}$$

Lemma 4.2

Let $\left\{ {{A_k}} \right\} ,$ $\left\{ {{B_k}} \right\}$ and $\left\{ {{C_k}} \right\}$ be three nonnegative sequences. Suppose that there exist $0< \tau < 1, l > 0$ and $k_l > 0$ such that ${A_{k + 1}} + {B_{k + 1}} + {C_{k + 1}} \le {A_k} + \tau {B_k}$ and ${A_{k}} \le l {C_k}$ hold for any $k>k_l$, we have $\left\{ {{A_{k + 1}} + \alpha {B_{k + 1}}} \right\}$ converges Q-linearly to zero, where $\alpha = \min \left( {\frac{1}{{1 + \frac{1}{l}}},\tau } \right)$. And both of $\left\{ {{A_k}} \right\}$ and $\left\{ {{B_k}} \right\}$ converges Q-linearly to zero.

Proof

We can easy to deduce that for any $k>k_l$,

$$\begin{aligned} \left( {1 + \frac{1}{l}} \right) {A_{k + 1}} + {B_{k + 1}} \le {A_k} + \tau {B_k}. \end{aligned}$$

(74)

Denote $\alpha = \min \left( {\frac{1}{{1 + \frac{1}{l}}},\tau } \right)$ and $\beta = \max \left( {\frac{1}{{1 + \frac{1}{l}}},\tau } \right) .$ Using the definitions of $\alpha$ and $\beta$ and (74), we obtain

$$\begin{aligned}&{A_{k + 1}} + \alpha {B_{k + 1}} \le {A_{k + 1}} + \left( {\frac{1}{{1 + \frac{1}{l}}}} \right) {B_{k + 1}} \le \left( {\frac{1}{{1 + \frac{1}{l}}}} \right) {A_k} \nonumber \\&\quad + \left( {\frac{\tau }{{1 + \frac{1}{l}}}} \right) {B_k} \le \beta \left( {{A_k} + \alpha {B_k}} \right) , \end{aligned}$$

(75)

which means that $\left\{ {{A_{k}} + \alpha {B_{k}}} \right\}$ converges Q-linearly to zero.

Further, we can deduce that $\left\{ {{A_k}} \right\}$ and $\left\{ {{B_k}} \right\}$ converge R-linearly to zeros using Lemma 4.1. ${} \Box$ $\square$

Notation 4.1

Since Algorithm 5 and Algorithm 6 are special instances of Algorithm 4, then, similar to the Notation 3.1 in Sect. 3, we define the similar sequences $\left\{ {{v_k}} \right\} ,\left\{ {{\delta _k}} \right\}$ and $\left\{ {{\varGamma _k}} \right\} ,$ which are defined in (20),(21) and (22) respectively, for $\left\{ {{x_k}} \right\}$ and $\left\{ {{y_k}} \right\}$ generated by Algorithm 5 and Algorithm 6.

Theorem 4.1

Suppose that Assumption 3.1 holds. Then, both of the sequences $\left\{ {{x_k}} \right\}$ generated by the Algorithm 6 and Algorithm 7 are convergent and converges R-linearly to their limits. Also, $\left\{ {F\left( {{x_k}} \right) } \right\}$ converges R-linearly to $F\left( {{x^ * }} \right) .$

Proof

For the $t_k$ generated by Algorithm 6, it follows from

$$\begin{aligned} {t_{k + 1}} - 1 = \frac{{\sqrt{1 + 4\left( {\frac{{{\lambda _k}}}{{{\lambda _{k{\mathrm{+ }}1}}}}} \right) t_k^2} - 1}}{2} \le \frac{{\sqrt{1 + 4t_k^2} - 1}}{2} < {t_k},\;\forall \; k\; {\mathrm{is \; sufficiently}}{}\; {\mathrm{large}} \end{aligned}$$

(76)

that there exists a ${{\hat{M}}}$ such that ${t_k} \le {{\hat{M}}}.$ Based on Lemma 2.1 and Corollary 2.1, we have

$$\begin{aligned} 0 \le 1 - \frac{{{\lambda _k}}}{{{\lambda _{k + 1}}}} \le \frac{1}{{\hat{M}}} \le \frac{1}{{{t_k}}},\end{aligned}$$

holds for k is sufficiently large. Then, similar with (40), it’s easy to show that

$$\begin{aligned} {\gamma _k} = \frac{{{t_k} - 1}}{{{t_{k + 1}}}} \le \frac{{{t_k} - 1}}{{{t_k}}} = 1 - \frac{1}{{{t_k}}} \le \frac{{{\hat{M}} - 1}}{{{\hat{M}}}} < 1.\end{aligned}$$

From Algorithm 7, it is obvious that ${\gamma _k} = \frac{{k - 1}}{{k + a}} \le \frac{{K - 1}}{{K + a}} < 1.$ Thus, for Algorithm 6 or Algorithm 7, there exists a ${{\bar{\gamma }}}$ such that ${\gamma _k} \le {\bar{\gamma }} < 1.$

Denote $N_s$ is a sufficiently large positive integer. Recalling the definitions of $\left\{ v_k \right\}$ and $\left\{ \delta _k \right\}$ in (20) and (21). Let $\xi = {v_{{N_s}}} + \frac{{{\delta _{{N_s}}}}}{{{\lambda _{{N_s}}}}} + F\left( {{x^ * }} \right) .$ From the Assumption 3.1, we can deduce that for this $\xi ,$ there exist $\varepsilon > 0$ and ${\bar{\tau }} > 0$ such that ${\mathrm{dist}}\left( {{x},{X^ * }} \right) \le {\bar{\tau }} \left\| {{p_{\frac{1}{{{L_f}}}g}}\left( x \right) - x} \right\|$ holds for $\left\| {{p_{\frac{1}{{{L_f}}}g}}\left( x \right) - x} \right\| < \varepsilon$ and $F\left( x \right) \le \xi .$

Recalling the definition of $\left\{ {{\varGamma _{k + 1}}} \right\}$ in (22). From (34), we obtain that

$$\begin{aligned} {v_{k + 1}} + \frac{{{\delta _{k + 1}}}}{{{\lambda _{k + 1}}}} + \frac{{2{\bar{\mu }} - 1}}{{{\lambda _{k + 1}}}}{\varGamma _{k + 1}} \le {v_k} + {{{\bar{\gamma }} }^2}\frac{{{\delta _k}}}{{{\lambda _k}}}, \end{aligned}$$

(77)

it is easy to get

$$\begin{aligned} {v_{k + 1}} + \frac{{{\delta _{k + 1}}}}{{{\lambda _{k + 1}}}} \le {v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}, \end{aligned}$$

(78)

which means that for k is sufficiently large, $\left\{ {{v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}} \right\}$ is nonincreasing. This together with the fact that $\left\{ {{v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}} \right\}$ is bounded below deduce that $\left\{ {{v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}} \right\}$ is convergent. Moreover, it follows from (78) that

$$\begin{aligned}{v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}} \le {v_{{N_s}}} + \frac{{{\delta _{{N_s}}}}}{{{\lambda _{{N_s}}}}}\end{aligned}$$

which implies that for $k \ge N_s$

$$\begin{aligned} F\left( {{x_k}} \right) \le \xi . \end{aligned}$$

(79)

Based on Lemma 3.9, the nonexpansiveness property of the proximal operator [9], $\nabla f$ is Lipschitz continuous and ${\lambda _{\min }} \le {\lambda _k} \le {\lambda ^*}$ for k is sufficiently large, we deduce that

$$\begin{aligned} \left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| \le \frac{{{\mu _1}}}{{{\lambda _{\min }}{L_f}}}\left( {1 + {\lambda ^ * }{L_f}} \right) \left\| {{x_k} - {y_k}} \right\| . \end{aligned}$$

(80)

See the detailed proof in (65).

Recalling (77), for $k \ge N_s$ we have

$$\begin{aligned}\left( {\frac{{2{\bar{\mu }} - 1}}{{{\lambda _{k + 1}}}}} \right) {\varGamma _{k + 1}} \le \left( {{v_k} + \frac{{{\delta _k}}}{{{\lambda _k}}}} \right) - \left( {{v_{k + 1}} + \frac{{{\delta _{k + 1}}}}{{{\lambda _{k + 1}}}}} \right) .\end{aligned}$$

Summing from $k = N_s$ to $k = N$ and letting $N \rightarrow \infty ,$ we obtain that $\sum \limits _{k = 1}^\infty {{\varGamma _k}},$ i.e. $\sum \limits _{k = 1}^\infty {{{\left\| {{x_k} - {y_k}} \right\| }^2}}$ is convergent from Lemma 2.1. Then, combining with (80), we have

$$\begin{aligned} \mathop {\lim }\limits _{k \rightarrow \infty } \left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| = 0. \end{aligned}$$

(81)

Following (79) and (81), we have $F\left( x_k \right) \le \xi$ and $\left\| {{p_{\frac{1}{{{L_f}}}g}}\left( {{x_k}} \right) - {x_k}} \right\| < \varepsilon$ hold for k is sufficiently large. Then, combining with (63), there exists ${\tau _2} >0$ for k is sufficiently large,

$$\begin{aligned} {\mathrm{dist}}\left( {{x_k},{X^*}} \right) \le \tau _2 \left\| {{x_k} - {y_k}} \right\| . \end{aligned}$$

(82)

From (34) with $y: = {y_{k + 1}}$ and $\lambda : = {\lambda _{k + 1}},$ we have

$$\begin{aligned} \begin{array}{l} F\left( {{x_{k + 1}}} \right) \le F\left( x \right) + \frac{{{{\left\| {x - {y_{k + 1}}} \right\| }^2}}}{{2{\lambda _{k + 1}}}} = F\left( x \right) + \frac{{{{\left\| {x - {x_{k{\mathrm{+ }}1}}{\mathrm{+ }}{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}}}{{2{\lambda _{k + 1}}}}\\ \quad \quad \quad \;\;\;\; \le F\left( x \right) + \frac{1}{{{\lambda _{k + 1}}}}\left( {{{\left\| {x - {x_{k{\mathrm{+ }}1}}} \right\| }^2} + {{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}} \right) . \end{array} \end{aligned}$$

(83)

Choose x to be an $x_{k + 1}^* \in {X^ * }$ satisfying $\left\| {{x_{k + 1}^ * } - {x_{k{\mathrm{+ }}1}}} \right\| = {\mathrm{dist}}\left( {{x_{k + 1}},{X^ * }} \right) ,$ then,

$$\begin{aligned} F\left( {{x_{k + 1}}} \right) - F\left( {{x^*}} \right)&\le \frac{1}{{{\lambda _{k + 1}}}}\left( {{{\left\| {x_{k + 1}^* - {x_{k{\mathrm{+ }}1}}} \right\| }^2} + {{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}} \right) \\ \nonumber&= \frac{1}{{{\lambda _{k + 1}}}}\left( {{\mathrm{dist}}^2\left( {{x_{k{\mathrm{+ }}1}},{X^*}} \right) + {{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}} \right) \\ \nonumber&\le {\tau _3}{{\left\| {{x_{k + 1}} - {y_{k + 1}}} \right\| }^2}, \end{aligned}$$

(84)

where ${\tau _3}{\mathrm{= }}\frac{{1 + {{\left( {{\tau _2}} \right) }^2}}}{{{\lambda _{\min }}}}$ and the last inequality is from (82) and Lemma 2.1, i.e.,

$$\begin{aligned} {\upsilon _{k + 1}} \le 2{\tau _3}{\varGamma _{k + 1}} \end{aligned}$$

(85)

holds.

It follows from (77) and (85) and Lemma 4.2 that $\left\{ {{v _k} + \alpha \frac{{{\delta _k}}}{{{\lambda _k}}}} \right\}$ converges Q-linearly to zero. And ${F(x_k)}$ converges R-linearly to ${F(x^*)},$ $\left\{ {{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right\}$ converges R-linearly to zero.

With the R-linear convergence of $\left\{ {{{\left\| {{x_{k + 1}} - {x_k}} \right\| }^2}} \right\} ,$ we obtain that there exist $0< {\bar{c}} < 1$ and ${M_1} > 0,$ such that

$$\begin{aligned}{\left\| {{x_k} - {x_{k - 1}}} \right\| } \le {M_1}{{\bar{c}}^k}.\end{aligned}$$

Consequently, for any ${m_2}> {m_1} >0,$ we have

$$\begin{aligned}\left\| {{x_{{m_2}}} - {x_{{m_1}}}} \right\| \le \sum \limits _{k = {m_1 +1}}^{{m_2}} {\left\| {{x_k} - {x_{k - 1}}} \right\| } \le {M_1} \cdot \frac{{{{{{\bar{c}}} }^{{m_1}}}}}{{1 - {{\bar{c}}} }}\end{aligned}$$

showing that $\left\{ {{x_k}} \right\}$ is a Cauchy sequence and hence convergent. Denoting its limit by $x^*$and passing to the limit as ${m_2} \rightarrow \infty$ in the above relation, we see further that

$$\begin{aligned}\left\| {{x_{{m_1}}} - {x^*}} \right\| \le {{M_1}} \cdot \frac{{{{ {{\bar{c}}} }^{{m_1}}}}}{{1 - {{\bar{c}}} }}\end{aligned}$$

that means that the sequence $\left\{ {{x_k}} \right\}$ converges R-linearly to its limit. $\square$

Remark 4.1

Under the error bound condition, Wen et al. [30] proved that for FISTA equipping with the restart scheme and the constant stepsize $\frac{1}{{{L_f}}},$ the sequences $\left\{ {{x_k} - {x^ * }} \right\}$ and $\left\{ {F\left( {{x_k}} \right) - F\left( {{x^ * }} \right) } \right\}$ converge R-linearly to zero. In Theorem 4.1, we show similar results hold for FISTA and MFISTA with stepsize generated by Algorithm 3 based on the error bound condition and restart scheme. The proposed algorithm implementations are independent of $L_f.$ In the proof of Theorem 4.1, the main contribution of Algorithm 3 is that it generates a stepsize sequence which is convergent and increases monotonically after finite iterations. We see that backtracking strategy in FISTA_BKTR does not have this property, hence, it is not clear whether FISTA_BKTR can obtain the linear convergence.

5 Numerical experiments

5.1 Performance comparison of FISTA algorithms based on different stepsize strategies

We conduct numerical experiments to demonstrate effectiveness of our algorithms by testing the following six algorithms:

• FISTA_NMS

• MFISTA_NMS($a=4$)

• FISTA_BKTR

• MFISTA_BKTR($a=4$)

• FISTA_backtracking

• SpaRSA: This algorithm is a non-monotone proximal gradient method, whose description can be found in [31].

Termination condition: The inequality $\left\| {{\psi _k}} \right\| \le \varepsilon$ is often used to be the termination condition for all comparison algorithms, where ${\psi _k} = \nabla f\left( {{x_k}} \right) - \frac{1}{{{\lambda _k}}}\left( {{x_k} - {y_k} + {\lambda _k}\nabla f\left( {{y_k}} \right) } \right) \in \partial F\left( {{x_k}} \right) .$ However, we notice that if F is flat, the distance between two iterates will be very far but the value of $\left\| {{\psi _k}} \right\|$ is close to 0; and vice versa. Hence, we terminate the test algorithms when $\min \left( {\left\| {{\psi _k}} \right\| ,\left\| {{x_k} - {x_{k - 1}}} \right\| } \right) \le \varepsilon .$

Test Function: The numerical experiments are conducted on the following two types of test functions: (1) the $l_1$-regularized least squares problem; (2) the ${l_1-}$regularized logistic regression. It’s obvious that the first problem is the case that f is a quadratic function, thus we need to restrict the parameter $\mu _1< \mu _0 < 1;$ for the latter that f is a non-quadratic function, $\mu _1< \mu _0 < 1/2.$ In the numerical experiment, we set ${E_k} = \frac{{{w_k}}}{{{k^{1.1}}}},$ $\forall k \ge 1$ be the control series for the new adaptive non-monotone stepsize strategy, parameter $w_k$ same as the setting we introduced in Sect. 2; ${\mu _0} = 0.99,{\mu _1} = 0.95$ for the test function (1), ${\mu _0} = 0.49,{\mu _1} = 0.45$ for the test function (2); $\varepsilon = 1e-5.$ For the backtracking scheme, we set $\eta = 0.5;$ For the BKTR scheme, we set $\beta =0.5$ and $\lambda _k^0 = \frac{{{\lambda _{k - 1}}}}{0.8 }.$

5.1.1 $l_1$-regularized least squares problem

$l_1$-regularized least squares problem is described as follows:

$$\begin{aligned} \mathop {\min }\limits _x F\left( x \right) = \frac{1}{2}{\left\| {Ax - b} \right\| ^2} + \sigma {\left\| x \right\| _1}, \end{aligned}$$

(86)

where the linear operator A and observation b is generated by the following scheme:

• $\begin{array}{c} {\mathrm{A = randn(n,m);}}\; \end{array}$

• $\begin{array}{c} {\mathrm{xstar = ones(m,1);}}\;\; \end{array}$

• $\begin{array}{c} \mathrm{Set} \;s:{\mathrm{The\;number\;of\;non-zero\;elements\;of\;xstar}} \end{array}$

• $\begin{array}{c} {\mathrm{I = randperm(m);}}\;{\mathrm{xstar(I(1:m - s)) = 0;}} \end{array}$

• $\begin{array}{c} {\mathrm{b = A}} * {\mathrm{xstar + }} 0.1 * {\mathrm{randn(n,1);}} \end{array}$

In the numerical experiments, we take $n = 800,m = 8000.$

Note that in this linear inverse problem, $\nabla f(x) = {A^T}\left( {Ax - b} \right) ,$ which is linear, hence, we can directly compute $\nabla f\left( {y_{k }} \right)$ by linear relationship between $\nabla f\left( {{x_{k - 1}}} \right)$ and $\nabla f\left( {{x_{k - 2}}} \right) ;$ since $A{y_{k}} - b$ can be computed by linear relationship between $A{x_{k - 1}} - b$ and $A{x_{k - 2}} - b,$ so the computation of $f\left( {{y_k}} \right) {\mathrm{= }}\frac{1}{2}{\left\| {A{y_k} - b} \right\| ^2}$ can be almost negligible. Through numerical experiments, we find that for FISTA_backtracking and FISTA_BKTR, the condition $F\left( {{p_{{\lambda _k g}}}\left( {{y_k}} \right) } \right) \le {Q_{{\lambda _k}}}\left( {{p_{{\lambda _k g}}}\left( {{y_k}} \right) ,{y_k}} \right)$ is difficult to distinguish if we set $\varepsilon$ too small, which means that these two backtracking schemes are not suitable for applications with high precision requirements like medical imaging. We consider the influence of such factors like sparsity $\left( {\frac{s}{m}} \right)$ and regularization parameter $\sigma$ on the algorithms. The selection of regularization parameter is separately $\sigma = 1$ and $\sigma = 0.1.$ Iter denotes the total number of iterations and Mult denotes the number of matrix–vector product for compute $Ax-b$ and Time denotes the CPU time.

From Table 1, 2, 3, we see that under the setting of different parameters and different sparsity, our algorithms FISTA_NMS and MFISTA_NMS hava significant improvment over FISTA_backtracking and SpaRSA, and comparing with FISTA_BKTR and MFISTA_BKTR, we see that FISTA_BKTR is a little better than FISTA_NMS for the total number of iterations, but much more than FISTA_NMS for the number of matrix–vector product, the comparison with other two algorithms MFISTA_NMS and MFISTA_BKTR shows similar results. In order to more intuitively show the effectiveness of our algorithms, we plot how $\left\| {{\psi _k}} \right\|$ and $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right)$ change during the progress of the six algorithms, where $F^*$ be the smallest terminating $F\left( {{x_k}} \right)$ among all methods.

Table 1 Comparison of algorithms for solving (86) with $n=800, m=8000, s=80,\sigma = 1$

Fig. 1

Performance profile for the convergences of $\left\| {{\psi _k}} \right\|$ and $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right)$ with $\sigma = 1$

Table 2 Comparison of algorithms for solving (86) with $n=800, m=8000, s=80,\sigma = 0.1$

Fig. 2

Performance profile for the convergences of $\left\| {{\psi _k}} \right\|$ and $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right)$ with $\sigma = 0.1$

Table 3 Comparison of algorithms for solving (86) with $n=800,m=8000,s=200,\sigma = 1$

Fig. 3

Performance profile for the convergences of $\left\| {{\psi _k}} \right\|$ and $F\left( {{x_k}} \right) - F\left( {{x^ * }} \right)$ with $\sigma = 1$

From Figs. 1, 2, 3, we can see that even if regularization parameter selection and sparsity are different, FISTA_NMS has a significant improvement over the FISTA_BKTR, FISTA_backtracking and SpaRSA for the given test problems. In particular, at the maximum iteration point, SpaRSA is far from the optimal value, it needs more iterations to meet the termination condition, and the corresponding Mult and Time will increase. Moreover, we can see that MFISTA_NMS is more efficient than MFISTA_BKTR, which means that our stepsize strategy is also effective for the modified algorithm MFISTA. Numerical experiments show that the new adaptive nonmonotone stepsize strategy is very useful for improving algorithm performances and our algorithms are very suitable for practical application problems such as sparse signal processing.

Since numerical performance of BKTR is better than backtracking and BB stepsize, in the following computational experiments, we just compare NMS and BKTR strategies with same algorithm schemes like FISTA and MFISTA for solving the sparse logistic regression problem to better illustrate the efficiency of NMS.

5.1.2 Sparse logistic regression

Consider the question

$$\begin{aligned} \mathop {\min }\limits _x F\left( x \right) : = \frac{1}{n}\sum \limits _{i = 1}^n {\log \left( {1 + \exp \left( { - {l_i}\left\langle {{h_i},x} \right\rangle } \right) } \right) } + \sigma {\left\| x \right\| _1}, \end{aligned}$$

(87)

where $x \in {R^m},{h_i} \in {R^m}, {l_i} \in \left\{ { - 1,1} \right\} ,i = 1, \cdots ,n,$ and $\sigma = 1e - 2.$ The problem sparse logistic regression is a popular problem in machine learning applications, where $f(x) = \frac{1}{n}\sum \limits _{i = 1}^n {\log \left( {1 + \exp \left( { - {l_i}\left\langle {{h_i},x} \right\rangle } \right) } \right) }$ is non-linear. Define ${K_{ij}} = - {l_i}{h_{ij}},$ and set ${\tilde{f}}\left( y \right) = \sum \limits _{i = 1}^m {\log \left( {1 + \exp \left( {{y_i}} \right) } \right) }.$ Then $f\left( x \right) = {\tilde{f}}\left( {Kx} \right) ,$ and ${L_f} = \frac{4}{n}\left\| {{K^T}K} \right\| .$ Initial point ${{\mathrm{x}}_{\mathrm{0}}}{\mathrm{= zeros(m,1).}}$ We take three datasets ‘heart_test’, ‘sonar_test’ and ‘mushroom’ from LIBSVM [10]. We report the number of iterations (Iter), calculation of function value (Fval), calculation of gradient value (Gval) and CPU time (Time) (Tables 4, 5, 6).

Table 4 Comparison of algorithms for solving “heart_test”

Fig. 4

Performance profile for solving “heart_test”

Table 5 Comparison of algorithms for solving “sonar_test”

Fig. 5

Performance profile for solving “sonar_test”

Table 6 Comparison of algorithms for solving “mushroom”

Fig. 6

Performance profile for solving “mushroom”

The algorithms for solving the Sparse logistic regression problem obtain similar results, i.e., though the number of iterations of algorithms with NMS is slightly worse than algorithms with BKTR, we can see that the algorithms with NMS are obviously better from the calculation times of function and gradient values and CPU time. Hence, FISTA_NMS outperforms the FISTA_BKTR, and meanwhile, MFISTA_NMS is more efficient than the MFISTA_BKTR. Observe that sometimes FISTA_NMS is faster than MFISTA_BKTR for some test problems, like the Sparse logistic regression with "mushroom" dataset (Figs. 4, 5, 6).

5.2 Performance comparison of FISTA algorithms with restart based on different stepsize strategies

The main goal of our experiments in this subsection is to test that our algorithms combining with the Restart scheme are still effective. The test functions and the related parameter settings are same as Sect. 5.1.

Table 7 Comparison of algorithms with restart scheme and without restart scheme for solving (86) with $n=800, m=8000$

Table 8 Comparison of algorithms with restart scheme and without restart scheme for solving (87)

First, we compare the following four algorithms: FISTA_NMS; FISTA_NMS_restart; MFISTA_NMS and MFISTA_NMS_restart. We can see that using the restart strategy, both of our algorithms’ performances can be greatly improved, which shows from Table 7 that Iter, Mult and Time for solving the $l_1$-regularized least squares problem be greatly reduced; and from Table 8 that Iter, Fval, Gval and Time for solving the Sparse logistic regression be greatly reduced. Further, by comparing FISTA_BKTR_restart, MFISTA_BKTR_restart, FISTA_NMS_restart and MFISTA_NMS_restart, the numerical results elaborate that: after incorporating restart strategy into all the comparison algorithms, our algorithms are still superior to the other two comparison algorithms, which shows the stability of our algorithms.

6 Conclusion

In this paper, we introduce a new adaptive non-monotone stepsize strategy (NMS), which does not execute line search and is independent of the Lipschitz constant. Based on NMS, we propose FISTA_NMS that has $O\left( {\frac{1}{{{k^2}}}} \right)$ convergence rate of the objective function values, which is similar to FISTA. We construct the convergence of iterates generated by MFISTA_NMS based on the new adaptive non-monotone stepsize without depending on the Lipschitz constant. Also, the convergence rate of objective function values shares $o\left( {\frac{1}{{{k^2}}}} \right)$. Further, our algorithms FISTA_NMS and MFISTA_NMS achieve similar convergence rates in the norm of subdifferential of objective function. Under error bound condition, we prove that FISTA_NMS and MFISTA_NMS have improved convergence results, i.e., for FISTA_NMS, convergence rates of function values and iterates can be achieved to $o\left( {\frac{1}{{{k^6}}}} \right)$ and $O\left( {\frac{1}{{{k^2}}}} \right) ;$ for MFISTA_NMS, that are $o\left( {\frac{1}{{{k^{2\left( {a + 1} \right) }}}}} \right)$ and $o\left( {\frac{1}{{{k^a}}}} \right) .$ In addition, we improve our algorithms and give the proof of the linear convergence of function values and iterates by combining our algorithms with the restart strategy. Note that FISTA and MFISTA with backtracking schemes can not achieve the same results, which means that NMS has theoretical advantages. We demonstrate the performances of our schemes on some numerical examples to show that our stepsize strategy outperforms the backtracking.