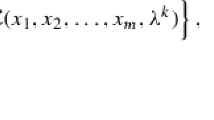1 Introduction

Our discussion starts with the following canonical convex minimization problem with linear equality constraints:

$$\begin{aligned} \min \left\{ \theta (x) \;|\; {\mathcal {A}}x=b, \; x\in {{{\mathcal {X}}}} \right\} , \end{aligned}$$
(1.1)

where \(\theta : \mathfrak {R}^{n}\rightarrow \mathfrak {R}\cup \{+\infty \}\) is a closed proper convex but not necessarily smooth function; \({{{\mathcal {X}}}}\subseteq \mathfrak {R}^{n}\) is a closed convex set; \({\mathcal {A}}\in \mathfrak {R}^{l\times n} \;\hbox {and} \; b\in \mathfrak {R}^{l}\). Among algorithms for solving (1.1), the augmented Lagrangian method (ALM) introduced in [24, 29] turns out to be a fundamental tool in both theoretical and algorithmic aspects, and its associated iterative scheme reads as

$$\begin{aligned} \hbox {(ALM)}\left\{ \begin{array}{l} x^{k+1}=\arg \min \left\{ {\mathcal {L}}_{\beta }(x, \lambda ^k) \;|\; x\in {\mathcal {X}}\right\} ,\\ \lambda ^{k+1}=\lambda ^k-\beta ({\mathcal {A}}x^{k+1}-b), \end{array} \right. \end{aligned}$$
(1.2)

where

$$\begin{aligned} {\mathcal {L}}_{\beta }(x, \lambda ):=\theta (x)-\lambda ^T({\mathcal {A}}x-b)+\frac{\beta }{2}\Vert {\mathcal {A}}x-b\Vert _2^2 \end{aligned}$$

denotes the augmented Lagrangian function of (1.1); \(\lambda \in \mathfrak {R}^l\) is the Lagrange multiplier and \(\beta >0\) is a penalty parameter for the linear constraints. As analyzed in [30], the classic ALM is indeed an application of the proximal point algorithm (PPA) in [26] to the dual of (1.1). Throughout our discussion, the penalty parameter \(\beta\) is assumed to be fixed for simplification.

In this paper, we focus on a special case of (1.1), where its objective function is the sum of m subfunctions without coupled variables:

$$\begin{aligned} \min \left\{ \sum _{i=1}^m\theta _i(x_i)\; \left| \; \sum _{i=1}^m A_ix_i=b; \; x_i\in {{{\mathcal {X}}}}_i,\; i=1,2,\ldots ,m\right. \right\} . \end{aligned}$$
(1.3)

Here, \(\theta _i: \mathfrak {R}^{n_i}\rightarrow \mathfrak {R}\cup \{+\infty \} \;(i=1,\ldots ,m)\) are closed proper convex functions and they are not necessarily smooth; \({{{\mathcal {X}}}}_i\subseteq \mathfrak {R}^{n_i} \;(i=1,\ldots ,m)\) are closed convex sets; \(\sum _{i=1}^mn_i=n\); \(A_i\in \mathfrak {R}^{l\times n_i} \;(i=1,\ldots ,m)\;\hbox {and} \; b\in \mathfrak {R}^{l}\). Obviously, the model (1.3) corresponds to (1.1) with \(x=(x_1;\ldots ;x_m)\), \({\mathcal {A}}=(A_1,\ldots ,A_m)\) and \(\theta (x)=\sum _{i=1}^m\theta _i(x_i)\). In practice, the generic model (1.3) finds a multitude of applications in, e.g., [4, 31] for some image reconstruction problems, [32, 35] for the matrix recovery model and the Potts based image segmentation problem, and [5, 6, 33] for a number of problems arising in distributed optimization and statistical learning. We also refer to, e.g., [25, 34], for more applications in other communities. Throughout our discussion, the solution set of (1.3) is assumed to be nonempty and the matrices \(A_i\;(i=1,\ldots ,m)\) are assumed to be full column-rank. In addition, we assume each \(x_i\)-subproblem

$$\begin{aligned} x_i^{*}=\arg \min \left\{ \theta _i(x_i)+\frac{\beta }{2}\Vert A_ix_i-q_i\Vert _2^2 \;\;|\;\; x_i\in {\mathcal {X}}_i\right\} , \end{aligned}$$
(1.4)

with any given \(q_i\in \mathfrak {R}^l\) and \(\beta >0\), has a closed-form solution or can be easily solved with a high precision (see, e.g., [27], for specific supported examples).

Applying the classical ALM (1.2) straightforwardly to (1.3), the resulting scheme then reads as

$$\begin{aligned} \left\{ \begin{array}{l} (x_1^{k+1},\ldots ,x_m^{k+1})=\arg \min \left\{ {\mathcal {L}}_{\beta }(x_1,x_2,\ldots , x_m, \lambda ^k)\,|\,x_i\in {\mathcal {X}}_i,\;i=1,\ldots ,m\right\} ,\\ \lambda ^{k+1}=\lambda ^k-\beta \left( \sum _{i=1}^m A_ix_i^{k+1}-b\right) , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}_{\beta }(x_1,x_2,\ldots , x_m, \lambda )=\sum _{i=1}^m\theta _i(x_i)-\lambda ^T\left( \sum _{i=1}^mA_ix_i-b\right) +\frac{\beta }{2}\left\| \sum _{i=1}^mA_ix_i-b\right\| _2^2. \end{aligned}$$
(1.5)

However, note there are coupled terms in the quadratic term \(\Vert \sum _{i=1}^mA_ix_i-b\Vert _2^2\). The \(x_i\)-subproblems (\(i=1,\ldots ,m\)) generally can not be tackled simultaneously. Exploiting the separable structure of the objective function \(\theta\), a common-used separable strategy for x-subproblem is the following Gaussian decomposition iterative scheme:

$$\begin{aligned} \left\{ \begin{array}{ll} \left\{ \begin{array}{l} x_1^{k+1} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1,x_2^k,\ldots , x_{m-1}^k, x_m^k, \lambda ^k) \;|\; x_1\in {\mathcal {X}}_1\right\} ,\\ x_2^{k+1} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k+1},x_2,\ldots , x_{m-1}^k, x_m^k, \lambda ^k) \;|\; x_2\in {\mathcal {X}}_2\right\} ,\\ \qquad \quad \vdots \\ x_m^{k+1} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k+1},x_2^{k+1},\ldots , x_{m-1}^{k+1},x_m, \lambda ^k) \;|\; x_m\in {\mathcal {X}}_m\right\} ,\\ \end{array} \right. &{} \\ \quad \lambda ^{k+1}= \lambda ^k-\beta \left( \sum _{i=1}^m A_ix_i^{k+1}-b\right) .&{} \end{array} \right. \end{aligned}$$
(1.6)

Clearly, each \(x_i\)-subproblem in (1.6) possesses the favorable composition (1.4) and can be treated individually. In particular, for the case \(m=2\), the method (1.6) corresponds to the classical alternating direction method of multipliers (ADMM) proposed in [9, 10], which is indeed an application of the Douglas-Rachford splitting method (see [8]). The generic scheme (1.6) is thus named the direct extension of ADMM (D-ADMM) in [7, 10]. For the case \(m\ge 3\), the D-ADMM has been shown to be empirically efficient for various applications, see, e.g., [28, 32] and references cited therein. However, a counterexample in [7] reveals that the D-ADMM (1.6) is not necessarily convergent. It has immediately inspired a number of works such as [11, 13, 17,18,19, 23, 25, 31,32,33]. Especially, the ADMM with Gaussian back substitution in [12, 17, 19], which needs only an additional back substitution step based on the D-ADMM, turns out to be a convergent yet numerically well-preforming method.

We now turn our attention to another common-used splitting strategy for the x-subproblem in the generic ALM scheme (1.2). Applying the full Jacobian-decomposition of x-subproblem to (1.2), it immediately leads to the following so-named direct extension of ALM (abbreviated as D-ALM):

$$\begin{aligned} \hbox {(D-ALM)} \left\{ \begin{array}{ll} \left\{ \begin{array}{l} x_1^{k+1} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1,x_2^k,\ldots , x_{m-1}^k, x_m^k, \lambda ^k) \;|\; x_1\in {\mathcal {X}}_1\right\} ,\\ x_2^{k+1} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k},x_2,\ldots , x_{m-1}^k, x_m^k, \lambda ^k) \;|\; x_2\in {\mathcal {X}}_2\right\} ,\\ \qquad \quad \vdots \\ x_m^{k+1} =\arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k},x_2^{k},\ldots , x_{m-1}^{k},x_m, \lambda ^k) \;|\; x_m\in {\mathcal {X}}_m\right\} ,\\ \end{array} \right. &{}\\ \quad \lambda ^{k+1}\; =\;\lambda ^k-\beta \left( \sum _{i=1}^m A_ix_i^{k+1}-b\right) . &{} \end{array} \right. \end{aligned}$$

It is obvious that each \(x_i\)-subproblem in the above D-ALM can be solved in a parallel way. In practice, there are many applications (see [36]) in the medical image processing field such as the Potts-model based image segmentation problem and its variants, can be solved efficiently by using the D-ALM. However, as analyzed in [14], the D-ALM is proved to be not necessarily convergent in theory. Let \(w:=(x_1;\ldots ;x_m;\lambda )\). To ensure the convergence, in [14], the authors regard first the output of the D-ALM as a predictor \({\tilde{w}}^k\) (i.e., \(({\tilde{x}}_1^k;\ldots ;{\tilde{x}}_m^k;{\tilde{\lambda }}^k):=(x_1^{k+1};\ldots ;x_m^{k+1};\lambda ^{k+1})\)), then the new iterate \(w^{k+1}\) is updated via

$$\begin{aligned} w^{k+1}=w^k-\alpha (w^k-{\tilde{w}}^{k})\quad \hbox {with} \quad \alpha \in (0,\;2(1-\sqrt{m/(m+1)})). \end{aligned}$$

Since the modification is simple, the variant is also named the parallel splitting ALM (denoted by P-ALM) in [14]. It is easy to verify that, as the increase of m, the step size \(\alpha\) would be tiny (for example, if \(m=3\), then \(\alpha \in (0,0.268)\)), which would adversely affect the convergence efficiency in the real computations. In [18], by adding extra regularization terms to the D-ALM, it directly leads to the following parallel splitting ADMM-like scheme (denoted by PS-ADMM):

$$\begin{aligned} \left\{ \begin{array}{l} \quad \, x_1^{k+1}\; = \;\arg \min \left\{ {\mathcal {L}}_{\beta }(x_1,x_2^k,\ldots , x_{m-1}^k, x_m^k, \lambda ^k) \;|\; x_1\in {\mathcal {X}}_1\right\} ,\\ \left\{ \begin{array}{l} \begin{aligned} x_2^{k+1} &{}= \arg \min \{ {\mathcal {L}}_{\beta }(x_1^{k+1},x_2,\ldots , x_{m-1}^k, x_m^k, \lambda ^k)\\ &{} \quad +\frac{\tau }{2}\beta \Vert A_2(x_2-x_2^k)\Vert _2^2 \;|\; x_2\in {\mathcal {X}}_2\}, \end{aligned}\\ \qquad \qquad \qquad \vdots \\ \begin{aligned} x_m^{k+1} &{}\;= \;\arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k+1},x_2^{k},\ldots , x_{m-1}^{k},x_m, \lambda ^k)\right. \\ &{} \left. \quad +\frac{\tau }{2}\beta \Vert A_m(x_m-x_m^k)\Vert _2^2 \;|\; x_m\in {\mathcal {X}}_m\right\} , \end{aligned} \end{array}\right. \\ \quad \lambda ^{k+1}\;\; =\;\;\lambda ^k-\beta (\sum _{i=1}^m A_ix_i^{k+1}-b), \end{array} \right. \end{aligned}$$

in which \(\tau >m-2\). Clearly, it would correspond to a huge regularization term (or equivalently, a tiny step size) as the increase of m. Recent works such as [15, 16, 20] have demonstrated that relaxation of regularization term allows a bigger step size to potentially accelerate the convergence. Hence, it is necessary to reduce such a regularization factor \(\tau\).

The primary purpose of the paper is to present a novel parallel splitting ALM-based algorithm for the multiple-block separable convex programming problem (1.3). More concretely, our new method begins with the following fully parallel regularized ALM-based scheme:

$$\begin{aligned} \left\{ \begin{array}{ll} \left\{ \begin{array}{ll} \begin{aligned} {\tilde{x}}_1^{k}&{} = \arg \min \{ {\mathcal {L}}_{\beta }(x_1,x_2^k,\ldots , x_{m-1}^k, x_m^k, \lambda ^k)\\ &{} \quad +\frac{\tau }{2}\beta \Vert A_1(x_1-x_1^k)\Vert _2^2 \;|\; x_1\in {\mathcal {X}}_1\}, \end{aligned}\\ \begin{aligned} {\tilde{x}}_2^{k}&{} = \arg \min \{ {\mathcal {L}}_{\beta }(x_1^k,x_2,\ldots , x_{m-1}^k, x_m^k, \lambda ^k)\\ &{} \quad +\frac{\tau }{2}\beta \Vert A_2(x_2-x_2^k)\Vert _2^2 \;|\; x_2\in {\mathcal {X}}_2\}, \end{aligned}\\ \qquad \qquad \qquad \vdots \\ \begin{aligned} {\tilde{x}}_m^{k} &{}= \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^k,x_2^{k},\ldots , x_{m-1}^{k},x_m, \lambda ^k)\right. \\ &{} \left. \quad +\frac{\tau }{2}\beta \Vert A_m(x_m-x_m^k)\Vert _2^2 \;|\; x_m\in {\mathcal {X}}_m\right\} , \end{aligned} \end{array} \right. \\ \quad {\tilde{\lambda }}^{k} \; = \;\lambda ^k - \beta \left( \sum _{i=1}^mA_ix_i^{k} -b\right) , \end{array} \right. \end{aligned}$$
(1.7)

where \(\tau >(m-4)/4\). As can be seen easily, the scheme (1.7) possesses a fully parallel splitting structure for both \(x_i\)-subproblems (\(i=1,\ldots ,m\)) and \(\lambda\)-subproblem. It thus belongs to the category of parallel operator splitting schemes. Furthermore, as will be shown in Sect. 3.1, the scheme (1.7) can provide a descent direction yielding the contraction of proximity to the solution set of (1.3). It is thus inspired to generate the new iterate \(w^{k+1}\) via

$$\begin{aligned} w^{k+1}=w^k+\alpha d(w^k,{\tilde{w}}^k):=w^k-\alpha M(w^k-{\tilde{w}}^k), \end{aligned}$$
(1.8)

where \(\alpha \in (0,1)\) and the correction matrix M will be defined in (2.11). Note that the step size \(\alpha\) is a constant. The correction step (1.8), as the initialization of next iteration, could be handled easily. Moreover, we give a more practical and succinct scheme (3.7) to replace the method (1.7)–(1.8) in Sect. 3.3.

The novel algorithm (1.7)–(1.8) enjoys great advantages in mainly two folds: first, compared with the P-ALM, the constant step size \(\alpha \in (0,1)\) can be taken more broadly; second, it reduces the regularization factor \(\tau\) from \((m-2)\) to \((m-4)/4\) compared with the PS-ADMM, so it provides a wider choice of the regularization term to potentially accelerate the convergence. Also, we show the global convergence of the proposed method, and then illustrate its efficiency by extensive numerical experiments.

The rest of the paper is organized as follows. In Sect. 2, we summarize some preliminaries and fundamental matrices, which will be useful for further analysis. Then, we propose the novel method in Sect. 3 and establish its convergence analysis in Sect. 4. The numerical efficiency of the proposed method is further demonstrated in Sect. 5. Some conclusions are drawn in Sect. 6.

2 Preliminaries

In this section, we summarize some preliminary results that will be used frequently throughout our discussion. The analysis of the paper is based on the following elementary lemma (its proof can be found in, e.g., [2]).

Lemma 1

Let \({{{\mathcal {X}}}} \subseteq \mathfrak {R}^n\) be a closed convex set, \(\theta (x)\) and \(\varphi (x)\) be convex functions. If \(\varphi (x)\) is differentiable on an open set which contains \({{{\mathcal {X}}}}\), and the solution set of the convex minimization problem \(\min \{\theta (x)+\varphi (x) \; | \; x\in {\mathcal {X}} \}\) is nonempty, then we have

$$\begin{aligned} x^*\in \arg \min \left\{ \theta (x) +\varphi (x) \; | \; x\in {{{\mathcal {X}}}}\right\} \end{aligned}$$

if and only if

$$\begin{aligned} {x^*} \in {{{\mathcal {X}}}}, \quad \theta (x) -\theta (x^*) + (x-x^*)^T\nabla \varphi (x^*) \ge 0, \quad \forall \; x\in {{{\mathcal {X}}}}. \end{aligned}$$

2.1 A variational characterization of (1.3)

To begin with, using the similar techniques in, e.g., [22], we show first how to stand for the optimality condition of (1.3) in the variational inequality context. By attaching the Lagrange multiplier \(\lambda \in \mathfrak {R}^l\) to the linear constraints, the Lagrange function of (1.3) reads as

$$\begin{aligned} L(x_1,x_2,\ldots , x_m, \lambda )=\sum _{i=1}^m\theta _i(x_i)-\lambda ^T\left( \sum _{i=1}^mA_ix_i-b\right) , \end{aligned}$$
(2.1)

and it is defined on the set \(\Omega :={\mathcal {X}}_1\times {\mathcal {X}}_2\times \cdots \times {\mathcal {X}}_m\times \mathfrak {R}^l\). Suppose the pair \((x_1^*,x_2^*,\ldots ,x_m^*,\lambda ^*)\in \Omega\) is a saddle point of (2.1). Then, for any \(\lambda \in \mathfrak {R}^l\) and \(x_i\in {\mathcal {X}}_i\,(i=1,\ldots ,m)\), we have

$$\begin{aligned} L(x_1^*,x_2^*,\ldots ,x_m^*,\lambda ) \le L(x_1^*,x_2^*,\ldots ,x_m^*,\lambda ^*) \le L(x_1,x_2,\ldots ,x_m,\lambda ^*). \end{aligned}$$

In view of Lemma 1, it is equivalent to finding \((x_1^*,\ldots ,x_m^*,\lambda ^*)\) such that

$$\begin{aligned} \left\{ \begin{array}{ll} \theta _1(x_1) - \theta _1(x_1^*) + (x_1-x_1^*)^T(- A_1^T\lambda ^*) \ge 0, &{} \qquad \forall \; x_1\in {{{\mathcal {X}}}}_1, \\ \qquad \quad \qquad \qquad \qquad \vdots &{}\\ \theta _m(x_m) - \theta _m(x_m^*) + (x_m-x_m^*)^T(- A_m^T\lambda ^*) \ge 0, &{} \qquad \forall \; x_m\in {{{\mathcal {X}}}}_m, \\ (\lambda -\lambda ^*)^T\left( \sum _{i=1}^mA_ix_i^*-b\right) \ge 0, &{} \qquad \forall \; \lambda \in \mathfrak {R}^l. \end{array} \right. \end{aligned}$$
(2.2)

Furthermore, if we set

$$\begin{aligned} \begin{array}{c} x= \left( \!\begin{array}{c} x_1\\ \vdots \\ x_m \end{array} \!\right) ,\quad \theta (x)=\sum _{i=1}^m\theta _i(x_i),\quad {\mathcal {A}}=(A_1, A_2, \ldots , A_m),\\ \\ w= \left( \!\begin{array}{c} x_1\\ \vdots \\ x_m\\ \lambda \end{array}\! \right) \quad \hbox {and}\quad F(w)=\left( \begin{array}{c} -A_1^T\lambda \\ \vdots \\ -A_m^T\lambda \\ \sum _{i=1}^m A_ix_i-b \\ \end{array} \right) , \qquad \qquad \quad \end{array} \end{aligned}$$
(2.3)

the inequalities (2.2) can be compactly rewritten as

$$\begin{aligned} \hbox {VI}(\Omega ,F,\theta ): \;\; w^*\in \Omega , \;\; \theta (x) -\theta (x^*) + (w-w^*)^T F(w^*) \ge 0, \;\; \forall \; w\in \Omega . \end{aligned}$$
(2.4)

In the later sections, we denote by \(\Omega ^*\) the solution set of (2.4), which is assumed to be nonempty. On the one hand, since the operator F(w) in (2.3) is affine with a skew-symmetric matrix, we obtain

$$\begin{aligned} (w-{\bar{w}})^T(F(w)-F({\bar{w}}))\equiv 0, \quad \forall \; w,\;{\bar{w}}\in \Omega , \end{aligned}$$
(2.5)

which means F is monotone. On the other hand, the objective function \(\theta (x)\) is not necessarily differentiable. With this regard, we also name (2.4) the mixed monotone variational inequality. In the following, we say (2.4) the variational inequality (VI) for short.

2.2 A variational characterization of (1.7)

The associated VI-structure of the introduced parallel splitting scheme (1.7) can be deduced by the following fundamental lemma.

Lemma 2

Let \(\{{\tilde{w}}^{k}\}\) be the sequence generated by (1.7) for solving (1.3). Then, we have

$$\begin{aligned} \theta (x)-\theta ({\tilde{x}}^k)+(w-{\tilde{w}}^k)^TF({\tilde{w}}^k)\ge (w-{\tilde{w}}^k)^TQ(w^k-{\tilde{w}}^k),\quad \forall \; w\in \Omega , \end{aligned}$$
(2.6)

where

$$\begin{aligned} Q=\left( \begin{array}{cccc} (1+\tau )\beta A_1^TA_1 &{} \cdots &{} 0 &{} 0 \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} \cdots &{} (1+\tau )\beta A_m^TA_m &{} 0 \\ -A_1 &{} \cdots &{} -A_m &{} \frac{1}{\beta }I_l \\ \end{array} \right) . \end{aligned}$$
(2.7)

Proof

To begin with, for each \(x_i\)-subproblem in (1.7), it follows from the fundamental Lemma 1 that \({\tilde{x}}_i^k\in {\mathcal {X}}_i\), and \({\tilde{x}}_i^k\) satisfies

$$\begin{aligned} \begin{aligned}&\theta _i(x_i)-\theta _i({\tilde{x}}_i^k)+(x_i-{\tilde{x}}_i^k)^T\\&\quad \left\{ -A_i^T\left( \lambda ^k-\beta \left( A_i{\tilde{x}}_i^k+\sum _{j\ne i}A_jx_j^k-b\right) \right) +\tau \beta A_i^TA_i({\tilde{x}}_i^k-x_i^k)\right\} \ge 0,\; \forall \; x_i\in {\mathcal {X}}_i. \end{aligned} \end{aligned}$$

Since \({\tilde{\lambda }}^{k} = \lambda ^k - \beta ({\mathcal {A}}x^{k} -b)\) in (1.7), we obtain

$$\begin{aligned} \begin{aligned}&-A_i^T\left( \lambda ^k-\beta \left( A_i{\tilde{x}}_i^k+\sum _{j\ne i}A_jx_j^k-b\right) \right) +\tau \beta A_i^TA_i({\tilde{x}}_i^k-x_i^k)\\&\qquad =-A_i^T[\lambda ^k-\beta ({\mathcal {A}}x^k-b)]+\beta A_i^TA_i({\tilde{x}}_i^k-x_i^k)+\tau \beta A_i^TA_i({\tilde{x}}_i^k-x_i^k)\\&\qquad =-A_i^T{\tilde{\lambda }}^k+(1+\tau )\beta A_i^TA_i({\tilde{x}}_i^k-x_i^k). \end{aligned} \end{aligned}$$

Therefore, the \(x_i\)-subproblem in (1.7) satisfies

$$\begin{aligned} \begin{aligned}&\theta _i(x_i)-\theta _i({\tilde{x}}_i^k)\\&\quad +(x_i-{\tilde{x}}_i^k)^T\left\{ \!-A_i^T{\tilde{\lambda }}^k+(1+\tau )\beta A_i^TA_i({\tilde{x}}_i^k-x_i^k)\right\} \ge 0,\quad \forall \; x_i\in {\mathcal {X}}_i. \end{aligned} \end{aligned}$$
(2.8)

For the \(\lambda\)-subproblem in (1.7), it is easy to see that \({\mathcal {A}}x^k-b+\frac{1}{\beta }({\tilde{\lambda }}^k-\lambda ^k)=0\), which is also equivalent to

$$\begin{aligned} (\lambda -{\tilde{\lambda }}^k)^T\{{\mathcal {A}}{\tilde{x}}^k-b-{\mathcal {A}}({\tilde{x}}^k-x^k)+\frac{1}{\beta }({\tilde{\lambda }}^k-\lambda ^k)\}=0,\quad \forall \;\lambda \in \mathfrak {R}^l. \end{aligned}$$
(2.9)

Using the notations in (2.3), the assertion of the lemma follows immediately by adding (2.8) and (2.9). \(\square\)

2.3 Some basic matrices

We list some fundamental matrices which will be useful for further discussion. Recall the matrix Q defined in (2.7). Setting \(S=Q^T+Q\), we get

$$\begin{aligned} \begin{aligned} S&=Q^T+Q=\left( \begin{array}{cccc} 2(1+\tau )\beta A_1^TA_1 &{} \cdots &{} 0 &{} -A_1^T \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} \cdots &{} 2(1+\tau )\beta A_m^TA_m &{} -A_m^T \\ -A_1 &{} \cdots &{} -A_m &{} \frac{2}{\beta }I_l \\ \end{array} \right) \\&=\hbox {diag}\left( \left( \begin{array}{c} A_1^T \\ \vdots \\ A_m^T \\ I_l \\ \end{array} \right) \right) \left( \begin{array}{cccc} 2(1+\tau )\beta I_l &{} \cdots &{} 0 &{} -I_l \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} \cdots &{} 2(1+\tau )\beta I_l &{} -I_l \\ -I_l &{} \cdots &{} -I_l &{} \frac{2}{\beta }I_l \\ \end{array} \right) \hbox {diag}\left( \left( \begin{array}{c} A_1 \\ \vdots \\ A_m \\ I_l \\ \end{array} \right) \right) . \end{aligned} \end{aligned}$$
(2.10)

Note that the matrices \(A_i\;(i=1,\ldots ,m)\) are assumed to be full column-rank. Clearly, the matrix S is symmetric, and \(S\succ 0\) provided \(\tau >(m-4)/4\). Throughout, \(\tau >(m-4)/4\) is required to guarantee the positive definiteness of the matrix S. Furthermore, we define \(M=Q^{-T}S\), and thus

$$\begin{aligned} \begin{aligned} M&=\frac{1}{1+\tau }\hbox {diag}((A_1^TA_1)^{-1},\ldots ,\; (A_m^TA_m)^{-1},\; I_l )\\&\quad \left( \begin{array}{ccccc} (2\tau +1)A_1^TA_1 &{} -A_1^TA_2 &{} \cdots &{} -A_1^TA_m &{} \frac{1}{\beta }A_1^T \\ -A_2^TA_1 &{} (2\tau +1)A_2^TA_2 &{} \cdots &{} -A_2^TA_m &{} \frac{1}{\beta }A_2^T \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ -A_m^TA_1 &{} -A_m^TA_2 &{} \cdots &{} (2\tau +1)A_m^TA_m &{} \frac{1}{\beta }A_m^T \\ -(1+\tau )\beta A_1 &{} -(1+\tau )\beta A_2 &{} \cdots &{} -(1+\tau )\beta A_m &{} 2(1+\tau )I_l \\ \end{array} \right) . \end{aligned} \end{aligned}$$
(2.11)

Note that these inverses \((A_i^TA_i)^{-1}\;(i=1,\ldots ,m)\) are just for algebraically showing the correction step explicitly, and they can be completely avoided (see Sect. 3.3). We also set

$$\begin{aligned} H=QS^{-1}Q^T, \end{aligned}$$
(2.12)

and

$$\begin{aligned} {\bar{M}}= \left( \begin{array}{ccccc} \frac{2\tau +1}{1+\tau }I_l &{} -\frac{1}{1+\tau }I_l &{} \cdots &{} -\frac{1}{1+\tau }I_l &{} \frac{1}{(1+\tau )\beta }I_l \\ -\frac{1}{1+\tau }I_l &{} \frac{2\tau +1}{1+\tau }I_l &{} \cdots &{} -\frac{1}{1+\tau }I_l &{} \frac{1}{(1+\tau )\beta }I_l \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ -\frac{1}{1+\tau }I_l &{} -\frac{1}{1+\tau }I_l &{} \cdots &{} \frac{2\tau +1}{1+\tau }I_l &{} \frac{1}{(1+\tau )\beta }I_l \\ -\beta I_l &{} -\beta I_l &{} \cdots &{} -\beta I_l &{} 2I_l \\ \end{array} \right) . \end{aligned}$$
(2.13)

3 Algorithm

Based on the framework of contraction method (see, e.g., [3]), we present the novel parallel algorithm (1.7)–(1.8) in this section.

3.1 A descent direction of the distance function induced by (1.7)

Recall the VI-structure of (1.7). The predictor \({\tilde{w}}^{k}\) generated by (1.7) satisfies

$$\begin{aligned} \theta (x)-\theta ({\tilde{x}}^k)+(w-{\tilde{w}}^k)^TF({\tilde{w}}^k)\ge (w-{\tilde{w}}^k)^TQ(w^k-{\tilde{w}}^k), \;\; \forall \; w\in \Omega . \end{aligned}$$
(3.1)

Without loss of generality, we assume \(w^k\ne {\tilde{w}}^k\) throughout our discussion. Otherwise, it follows from (2.4) that \({\tilde{w}}^k\) would be an optimal solution. Let \(w^*\) be an arbitrary solution of (2.4). Setting \(w=w^*\) in (3.1), we have

$$\begin{aligned} \begin{aligned}&({\tilde{w}}^k-w^*)^TQ(w^k-{\tilde{w}}^k)\ge \theta ({\tilde{x}}^k)-\theta (x^*)+({\tilde{w}}^k-w^*)^TF({\tilde{w}}^k)\\&\qquad \overset{(2.5)}{=}\theta ({\tilde{x}}^k)-\theta (x^*)+({\tilde{w}}^k-w^*)^TF(w^*)\ge 0. \end{aligned} \end{aligned}$$

Using \({\tilde{w}}^k-w^*=({\tilde{w}}^k-w^k)+(w^k-w^*)\) and \(w^TQw=\frac{1}{2}w^T(Q^T+Q)w\), the above inequality can be rewritten as

$$\begin{aligned} (w^k-w^*)^TQ(w^k-{\tilde{w}}^k)\ge (w^k-{\tilde{w}}^k)^TQ(w^k-{\tilde{w}}^k)\overset{(2.10)}{=}\frac{1}{2}\Vert w^k-{\tilde{w}}^k\Vert _{S}^2. \end{aligned}$$
(3.2)

Taking the nonsingularity of the matrices Q and H (see (2.7) and (2.12)) into consideration, the inequality (3.2) can be further reformulated as

$$\begin{aligned} \begin{aligned}&\left\langle \nabla \left( \frac{1}{2}\Vert w-w^*\Vert _H^2\right) \left| _{w=w^k}\;,\; -H^{-1}Q(w^k-{\tilde{w}}^k)\right. \right\rangle \\&\qquad = -(w^k-w^*)^TQ(w^k-{\tilde{w}}^k)\le -\frac{1}{2}\Vert w^k-{\tilde{w}}^k\Vert _{S}^2. \end{aligned} \end{aligned}$$

Therefore, for any fixed \(w^*\in \Omega ^*\),

$$\begin{aligned} d(w^k,{\tilde{w}}^k):=-H^{-1}Q(w^k-{\tilde{w}}^k)=-Q^{-T}S(w^k-{\tilde{w}}^k)=-M(w^k-{\tilde{w}}^k) \end{aligned}$$

is a descent direction of the unknown distance function \(\Vert w-w^*\Vert _H^2\) at the point \(w^k\). According to the same analysis in [21], such a direction is able to yield the contraction of proximity to the solution set of (1.3) if an appropriate step size is taken. Hence, we generate the new iterate \(w^{k+1}\) via

$$\begin{aligned} w^{k+1}=w^k+\alpha _k d(w^k,{\tilde{w}}^k)=w^k-\alpha _kM(w^k-{\tilde{w}}^k). \end{aligned}$$
(3.3)

It remains to find a step size \(\alpha _k\) to make the update \(w^{k+1}\) closer to \(\Omega ^*\).

3.2 A befitting step size \(\alpha _k\) in the correction step (3.3)

We now turn to choose an appropriate step size \(\alpha _k\) in the correction step (3.3). Since

$$\begin{aligned} \begin{aligned}&\Vert w^{k+1}-w^*\Vert _{H}^2\\&\quad =\Vert w^k-\alpha Q^{-T}S(w^k-{\tilde{w}}^k)-w^*\Vert _{H}^2\\&\quad =\Vert w^k-w^*\Vert _{H}^2-2\alpha (w^k-w^*)^TQ(w^k-{\tilde{w}}^k)+\alpha ^2\Vert w^k-{\tilde{w}}^k\Vert _S^2\\&\;\;\overset{(3.2)}{\le }\Vert w^k-w^*\Vert _{H}^2-\alpha \Vert w^k-{\tilde{w}}^k\Vert _{S}^2+\alpha ^2\Vert w^k-{\tilde{w}}^k\Vert _S^2, \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} \Vert w^k-w^*\Vert _{H}^2-\Vert w^{k+1}-w^*\Vert _{H}^2\ge \alpha \Vert w^k-{\tilde{w}}^k\Vert _{S}^2-\alpha ^2\Vert w^k-{\tilde{w}}^k\Vert _S^2=:q(\alpha ). \end{aligned} \end{aligned}$$

Maximizing the quadratic term \(q(\alpha )\), it follows that

$$\begin{aligned} \alpha _k^*=\frac{\Vert w^k-{\tilde{w}}^k\Vert _{S}^2}{2\Vert w^k-{\tilde{w}}^k\Vert _S^2}=\frac{1}{2}. \end{aligned}$$

Meanwhile, note that \(q(\alpha )\) is a lower bounded quadratic contraction function. Refer to the similar technique in [14], we can introduce a relaxation factor \(\gamma \in (0,2)\) and thus \(\alpha _k:=\gamma \alpha _k^*\in (0,1)\), which means a fixed step size \(\alpha _k\in (0,1)\) can be taken in (3.3). Consequently, the correction step (3.3), as an update process, can be tackled easily.

3.3 The practical computing scheme for the new method (1.7)–(1.8)

Since the matrix M defined in (2.11) contains some inverses \((A_i^TA_i)^{-1}\;(i=1,\ldots ,m)\), the corrector (3.3) is relatively complicated. Refer to the similar analysis in [23], these inverses are just for algebraically showing the correction step explicitly, and they can be completely avoided in computation empirically. More concretely, note that the variables \((A_1x_1^{k},\ldots ,A_mx_m^{k},\lambda ^{k})\) is essentially required in each iteration of (1.7). Using the same technique in, e.g., [19, 23], the correction step (3.3) can be replaced with

$$\begin{aligned} \left( \begin{array}{c} A_1x_1^{k+1} \\ \vdots \\ A_mx_m^{k+1} \\ \lambda ^{k+1} \\ \end{array} \right) =\left( \begin{array}{c} A_1x_1^{k} \\ \vdots \\ A_mx_m^{k} \\ \lambda ^{k} \\ \end{array} \right) -\alpha {\bar{M}}\left( \begin{array}{c} A_1x_1^{k}- A_1{\tilde{x}}_1^{k}\\ \vdots \\ A_mx_m^{k}- A_m{\tilde{x}}_m^{k} \\ \lambda ^{k}-{\tilde{\lambda }}^k \\ \end{array} \right) , \end{aligned}$$
(3.4)

where the matrix \({\bar{M}}\) is defined in (2.13), and it can be concretely written as

$$\begin{aligned} \left\{ \begin{array}{ll} A_ix_i^{k+1} &=A_ix_i^{k}-\alpha \left\{ \frac{2\tau +1}{1+\tau }A_i(x_i^k-{\tilde{x}}_i^k)-\frac{1}{1+\tau } \left[ \sum _{j\ne i}A_j(x_j^k-{\tilde{x}}_j^k)\right. \right. \\ &{}\left. \left. \quad -\frac{1}{\beta }(\lambda ^k-{\tilde{\lambda }}^k)\right] \right\} ,\quad i=1,\ldots ,m,\\ \lambda ^{k+1} &{}= \lambda ^k - \alpha \left\{ -\beta {\mathcal {A}}(x^{k}-{\tilde{x}}^k )+2(\lambda ^k-{\tilde{\lambda }}^k)\right\} . \end{array} \right. \end{aligned}$$
(3.5)

We now give a succinct representation of (3.5) for easy-implementation. Recall \({\tilde{\lambda }}^{k} = \lambda ^k - \beta ({\mathcal {A}}x^{k} -b)\) in (1.7). By substituting it into (3.5), it follows that

$$\begin{aligned} \begin{aligned}&A_ix_i^{k+1} \\&= A_ix_i^{k}-\alpha \left\{ \frac{2\tau +1}{1+\tau }A_i(x_i^k-{\tilde{x}}_i^k)-\frac{1}{1+\tau }\left[ \displaystyle \sum _{j\ne i}A_j(x_j^k-{\tilde{x}}_j^k)-\frac{1}{\beta }(\lambda ^k-{\tilde{\lambda }}^k)\right] \right\} \\&= A_ix_i^{k}-\alpha \left\{ \frac{2\tau +1}{1+\tau }A_i(x_i^k-{\tilde{x}}_i^k)-\frac{1}{1+\tau }\left[ \displaystyle \sum _{j\ne i}A_j(x_j^k-{\tilde{x}}_j^k)-({\mathcal {A}}x^k -b)\right] \right\} \\&= A_ix_i^{k}-\alpha \left\{ 2A_i(x_i^k-{\tilde{x}}_i^k)+\frac{1}{1+\tau }\left( {\mathcal {A}}{\tilde{x}}^{k} -b\right) \right\} , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \lambda ^{k+1}&= \lambda ^k - \alpha \left\{ -\beta {\mathcal {A}}(x^{k}-{\tilde{x}}^k )+2(\lambda ^k-{\tilde{\lambda }}^k)\right\} \\&= \lambda ^k - \alpha \left\{ -\beta {\mathcal {A}}(x^{k}-{\tilde{x}}^k )+2\beta ({\mathcal {A}}x^{k} -b)\right\} \\&=\lambda ^k - \alpha \beta \left\{ {\mathcal {A}}x^k+{\mathcal {A}}{\tilde{x}}^k-2b\right\} . \end{aligned} \end{aligned}$$

Therefore, the practical correction step (3.5) can be reformulated concisely as

$$\begin{aligned} \left\{ \begin{array}{ll} \left\{ \begin{array}{ll} \hbox {for} \quad i=1,\ldots ,m,\quad \hbox {do:}\\ A_ix_i^{k+1} \;\; = \;\; A_ix_i^{k}-\alpha \left\{ 2A_i(x_i^k-{\tilde{x}}_i^k)+\frac{1}{1+\tau }({\mathcal {A}}{\tilde{x}}^{k}-b)\right\} ,\\ \end{array} \right. \\ \quad \lambda ^{k+1} \;\; = \;\; \lambda ^k - \alpha \beta ({\mathcal {A}}x^k+{\mathcal {A}}{\tilde{x}}^k-2b). \end{array} \right. \end{aligned}$$
(3.6)
Fig. 1
figure 1

An ideal parallel implementation mechanism of the proposed algorithm (3.7)

Full size image

It further leads to the following more practical and succinct scheme to replace the proposed algorithm (1.7)–(1.8):

$$\begin{aligned} \left\{ \begin{array}{ll} \hbox {(Parallel)} \left\{ \begin{array}{ll} \begin{aligned} {\tilde{x}}_1^{k}&{} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1,x_2^k,\ldots , x_{m-1}^k, x_m^k, \lambda ^k)\right. \\ &{}\left. \quad +\frac{\tau }{2}\beta \Vert A_1(x_1-x_1^k)\Vert _2^2 \;|\; x_1\in {\mathcal {X}}_1\right\} , \end{aligned}\\ \begin{aligned} {\tilde{x}}_2^{k}&{} = \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^k,x_2,\ldots , x_{m-1}^k, x_m^k, \lambda ^k)\right. \\ &{} \left. \quad +\frac{\tau }{2}\beta \Vert A_2(x_2-x_2^k)\Vert _2^2 \;|\; x_2\in {\mathcal {X}}_2\right\} , \end{aligned}\\ \quad\quad\quad\quad\vdots \\\begin{aligned} {\tilde{x}}_m^{k}\, &{}= \arg \min \left\{ {\mathcal {L}}_{\beta }(x_1^{k},x_2^{k},\ldots , x_{m-1}^{k},x_m, \lambda ^k)\right. \\ &{}\left. \quad +\frac{\tau }{2}\beta \Vert A_m(x_m-x_m^k)\Vert _2^2 \;|\; x_m\in {\mathcal {X}}_m\right\} , \end{aligned}\\ \end{array} \right. \\ \hbox {(Update)} \left\{ \begin{array}{l} \hbox {for} i=1,\ldots ,m,\quad \hbox {do:}\\ A_ix_i^{k+1} = \; A_ix_i^{k}-\alpha \left\{ 2A_i(x_i^k-{\tilde{x}}_i^k)+\frac{1}{1+\tau }({\mathcal {A}}{\tilde{x}}^{k}-b)\right\} ,\\ \lambda ^{k+1} = \; \lambda ^k - \alpha \beta ({\mathcal {A}}x^k+{\mathcal {A}}{\tilde{x}}^k-2b), \end{array} \right. \end{array} \right. \end{aligned}$$
(3.7)

in which \(\alpha \in (0,1)\) and \(\tau >(m-4)/4\). Figure 1 shows an ideal parallel implementation mechanism of the proposed algorithm (3.7) for the case where each \(x_i\)-subproblem needs a high computational cost. In such a case, every \(x_i\)-subproblem can be solved in an independent CPU platform.

4 Convergence

We establish the convergence analysis of the proposed method (1.7)–(1.8) in this section. The technique of analysis is motivated by the work in [19, 23]. As we have mentioned, \(\tau >(m-4)/4\) is required to guarantee the positive definiteness of the matrices S and H. To show the global convergence of the novel algorithm (1.7)–(1.8), we first prove a lemma, followed by a theorem.

Lemma 3

Let \(\{{\tilde{w}}^k\}\) and \(\{w^k\}\) be the sequences generated by the algorithm (1.7)–(1.8) for (1.3). Then, for any constant \(\alpha \in (0,1),\) we have

$$\begin{aligned} \Vert w^k-w^*\Vert _{H}^2-\Vert w^{k+1}-w^*\Vert _{H}^2\;\ge \;\alpha (1-\alpha )\Vert w^k-{\tilde{w}}^k\Vert _{S}^2. \end{aligned}$$
(4.1)

Proof

It follows from (3.3) that

$$\begin{aligned} \begin{aligned}&\Vert w^{k+1}-w^*\Vert _{H}^2\\&\;=\Vert w^k-\alpha Q^{-T}S(w^k-{\tilde{w}}^k)-w^*\Vert _{H}^2\\&\;=\Vert w^k-w^*\Vert _{H}^2-2\alpha (w^k-w^*)^TQ(w^k-{\tilde{w}}^k)+\alpha ^2\Vert w^k-{\tilde{w}}^k\Vert _S^2\\&\overset{(3.2)}{\le }\Vert w^k-w^*\Vert _{H}^2-\alpha (1-\alpha )\Vert w^k-{\tilde{w}}^k\Vert _{S}^2, \end{aligned} \end{aligned}$$

and the proof is complete. \(\square\)

Theorem 1

Let \(\{{\tilde{w}}^k\}\) and \(\{w^k\}\) be the sequences generated by the method (1.7)–(1.8) for solving (1.3). Then, for any \(\alpha \in (0,1),\) we obtain \(\lim _{k\rightarrow \infty }w^k=w^\infty\) where \(w^\infty\) belongs to \(\Omega ^*.\)

Proof

First of all, it follows from (4.1) that the generated sequence \(\{w^k\}\) satisfies

$$\begin{aligned} \begin{aligned} \Vert w^{k+1}-w^*\Vert _{H}^2&\le \Vert w^k-w^*\Vert _{H}^2-\alpha (1-\alpha )\Vert w^k-{\tilde{w}}^k\Vert _{S}^2\\&\le \Vert w^k-w^*\Vert _{H}^2\le \cdots \le \Vert w^0-w^*\Vert _{H}^2, \end{aligned} \end{aligned}$$

which means the sequence \(\{w^k\}\) is bounded. Furthermore, summing (4.1) over \(k=0,1,\ldots ,\infty\), we obtain

$$\begin{aligned} \begin{aligned}\sum _{k=0}^{\infty }\alpha (1-\alpha )\Vert w^k-{\tilde{w}}^k\Vert _{S}^2&\le \sum _{k=0}^{\infty }(\Vert w^k-w^*\Vert _{H}^2-\Vert w^{k+1}-w^*\Vert _{H}^2)\\&\le \Vert w^0-w^*\Vert _{H}^2, \end{aligned} \end{aligned}$$

and thus

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert w^k-{\tilde{w}}^k\Vert _{S}^2=0. \end{aligned}$$
(4.2)

This indicates the sequence \(\{{\tilde{w}}^k\}\) is also bounded. Let \(w^\infty\) be a cluster point of \(\{{\tilde{w}}^k\}\), where \(\{{\tilde{w}}^{k_j}\}\) is a subsequence which converges to \(w^\infty\). Then, it follows from (2.6) that

$$\begin{aligned} \theta (x)-\theta ({\tilde{x}}^{k_j})+(w-{\tilde{w}}^{k_j})^TF({\tilde{w}}^{k_j})\ge (w-{\tilde{w}}^{k_j})^TQ(w^{k_j}-{\tilde{w}}^{k_j}),\quad \forall \; w\in \Omega . \end{aligned}$$

Note the matrix Q is nonsingular. It follows from the continuity of \(\theta (x)\) and F(w) that

$$\begin{aligned} w^\infty \in \Omega ,\quad \theta (x) -\theta (x^\infty ) +(w-w^{\infty })^T F(w^{\infty }) \ge 0, \quad \forall \, w\in \Omega , \end{aligned}$$

which means \(w^\infty\) is a solution of the VI(\(\Omega ,F,\theta\)) (2.4). On the one hand, according to (4.2), we have \(\lim _{k\rightarrow \infty }w^{k_j}=w^\infty\). On the other hand, it follows from (4.1) that

$$\begin{aligned} \begin{aligned} \Vert w^{k+1}-w^\infty \Vert _{H}^2\le \Vert w^k-w^\infty \Vert _{H}^2, \end{aligned} \end{aligned}$$
(4.3)

which means it is impossible that the sequence \(\{w^k\}\) has more than one cluster point. Therefore, we have \(\lim _{k\rightarrow \infty }w^k=w^\infty\) and the proof is complete. \(\square\)

Remark 1

Refer to the same techniques in, e.g., [19, 23], we can easily show a worst-case \({\mathcal {O}}(1/N)\) convergence rate measured by iteration complexity for the novel method (1.7)–(1.8) by using the essential Lemma 2. Since the techniques are completely similar, the analysis of the convergence rate is omitted here.

5 Numerical experiments

We report the numerical results of the proposed algorithm (1.7)–(1.8) (practical scheme is indeed (3.7)) in this section. All codes are written in a Python 3.9 and implemented in a laptop with Intel Core CPU 2.20 GHz (i7-8750H) and 16 GB memory. The preliminary numerical results affirmatively demonstrate that the proposed method can perform more efficiently than some known parallel spitting algorithms.

5.1 The test model

The latent variable Gaussian graphical model selection (LVGGMS) problem in [6] is a typical three-block separable convex minimization model arising in statistical learning. As stated in [1], the mathematical form of the LVGGMS model reads as

$$\begin{aligned} \begin{aligned} \min&\;\; F(X,Y,Z):=\langle X,C\rangle -\log \det (X)+\nu \Vert Y\Vert _1+\mu \hbox {tr}(Z)\\ \hbox {s.t.}&\;\;\;X-Y+Z=0,\;\;Z\succeq 0, \end{aligned} \end{aligned}$$
(5.1)

where \(C\in \mathfrak {R}^{n\times n}\) is the covariance matrix obtained from the observation, \(\nu\) and \(\mu\) stand for two given positive weight parameters, \(\Vert Y\Vert _1=\sum _{i,j}|Y_{i,j}|\) and \(\hbox {tr}(\cdot )\) represents the trace of a matrix.

We first show the implementation of the proposed scheme (3.7) for tackling the LVGGMS model (5.1). Since the update (3.6) is simple, we only focus on the detail of the resulting \(x_i\)-subproblems (\(i=1,2,3\)). Let

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_{\beta }(X,Y,Z, \Lambda )=&\langle X,C\rangle -\log \det (X)+\nu \Vert Y\Vert _1+\mu \hbox {tr}(Z)\\&-\langle \Lambda ,X-Y+Z\rangle +\frac{\beta }{2}\Vert X-Y+Z\Vert _F^2 \end{aligned} \end{aligned}$$

be the augmented Lagrangian function of (5.1). The corresponding scheme of the x-subproblem in (3.7) then reads as

$$\begin{aligned} \left\{ \begin{array}{ll} {\tilde{X}}^{k}=\,\displaystyle \arg \min \left\{ {\mathcal {L}}_{\beta }(X,Y^k,Z^k, \Lambda ^k)+\frac{\tau \beta }{2}\Vert X-X^k\Vert _F^2\;\left| \;X\in \mathfrak {R}^{n\times n}\right. \right\} ,\\ {\tilde{Y}}^{k}\,=\,\displaystyle \arg \min \left\{ {\mathcal {L}}_{\beta }(X^k,Y,Z^k, \Lambda ^k)+\frac{\tau \beta }{2}\Vert Y-Y^k\Vert _F^2\;\left| \;Y \in \mathfrak {R}^{n\times n}\right. \right\} ,\\ {\tilde{Z}}^{k}\,=\,\displaystyle \arg \min \left\{ {\mathcal {L}}_{\beta }(X^k,Y^k,Z, \Lambda ^k)+\frac{\tau \beta }{2}\Vert Z-Z^k\Vert _2^2\;\left| \;Z\succeq 0,\,Z\in \mathfrak {R}^{n\times n} \right. \right\} . \end{array} \right. \end{aligned}$$
(5.2)

For the X-subproblem in (5.2), according to the first-order optimal condition, it is equivalent to solving the nonlinear equation system

$$\begin{aligned} C-X^{-1}+\beta \left( X-Y^k+Z^k-\frac{1}{\beta }\Lambda ^k\right) +\tau \beta (X-X^k)=0. \end{aligned}$$

Multiplying X to both sides, it follows that

$$\begin{aligned} (1+\tau )\beta X^2+(C-\tau \beta X^k-\beta Y^k+\beta Z^k-\Lambda ^k)X-I=0. \end{aligned}$$
(5.3)

Let \(UDU^T=C-\tau \beta X^k-\beta Y^k+\beta Z^k-\Lambda ^k\) be an eigenvalue decomposition. Plugging it back into (5.3) and setting \(P=U^TXU\), we have

$$\begin{aligned} (1+\tau )\beta PP+D P-I=0, \end{aligned}$$

and thus obtain

$$\begin{aligned} P_{ii}=\frac{1}{2\beta (1+\tau )}\left( -D_{ii}+\sqrt{D_{ii}^2+4(1+\tau )\beta }\;\right) . \end{aligned}$$

Therefore, we can derive that \({\tilde{X}}^k=U\,\hbox {diag}(P)\, U^T\) is a solution of (5.3). For the Y-subproblem in (5.2), since

$$\begin{aligned} \begin{aligned} {\tilde{Y}}^k&=\arg \min _{Y}\left\{ \nu \Vert Y\Vert _1+\frac{\beta }{2}\Vert X^k-Y+Z^k-\frac{1}{\beta }\Lambda ^k\Vert _F^2+\frac{\tau }{2}\beta \Vert Y-Y^k\Vert _F^2\right\} \\&=\arg \min _{Y}\left\{ \Vert Y\Vert _1+\frac{\beta (1+\tau )}{2\nu }\left\| Y-\frac{1}{1+\tau }(X^k+\tau Y^k+Z^k-\frac{1}{\beta }\Lambda ^k)\right\| _F^2\right\} ,\\ \end{aligned} \end{aligned}$$

the Y-subproblem can be solved via the soft shrinkage operator (see [32]) immediately. Finally, for the Z-subproblem in (5.2), note that

$$\begin{aligned} \begin{aligned} {\tilde{Z}}^{k}&=\arg \min _{Z\succeq 0}\left\{ \mu \hbox {tr}(Z)+\frac{\beta }{2}\left\| X^k-Y^k+Z-\frac{1}{\beta }\Lambda ^k\right\| _F^2+\frac{\tau }{2}\beta \Vert Z-Z^k\Vert _2^2\right\} \\&=\arg \min _{Z\succeq 0}\left\{ \left\| Z-\frac{1}{1+\tau }\left( -X^k+Y^k+\tau Z^k+\frac{1}{\beta }(\Lambda ^k-\mu I)\right) \right\| _2^2\right\} . \end{aligned} \end{aligned}$$

Let \(VD_1V^T=\frac{1}{1+\tau }(-X^k+Y^k+\tau Z^k+\frac{1}{\beta }\Lambda ^k-\frac{\mu }{\beta }I)\) be an eigenvalue decomposition. Then, we can easily verify that \({\tilde{Z}}^k=V\max (D_1,0)\, V^T\) is a solution of the Z-subproblem (where \(\max (D_1,0)\) is taken component-wisely).

5.2 Numerical results

We evaluate the numerical performance of the proposed method (3.7) in this subsection. Some parallel splitting algorithms including the parallel augmented Lagrangian method (denoted by P-ALM) proposed in [14] and the parallel splitting ADMM-like method (denoted by PS-ADMM) proposed in [18] are compared. In addition, as a reference, the numerical results of the direct extension of ADMM (denoted by D-ADMM) is also listed.

In our experiments, we take \(\nu =0.005\) and \(\mu =0.05\) (refer to [1]), and the covariance matrix C is randomly generated according to S. Boyd’s Homepage (see http://web.stanford.edu/~boyd/papers/admm/covsel/covsel_example.html). Moreover, refer to [1], the following two stopping conditions are taken:

$$\begin{aligned} \begin{array}{ll} \hbox {IER}(k) &{}:=\max \left\{ \Vert X^k-X^{k+1}\Vert _\infty ,\Vert Y^k-Y^{k+1}\Vert _\infty ,\Vert Z^k-Z^{k+1}\Vert _\infty \right\}<\hbox {Tol},\\ \hbox {CER}(k) &{}:=\Vert X^k-Y^k+Z^k\Vert _F<\hbox {Tol}. \end{array} \end{aligned}$$

Clearly, the feasibility errors IER and CER can be regarded as the primal and dual errors of the mentioned algorithms, respectively. When the proposed method (3.7) is applied for solving (5.1), it is convergent provided \(\tau >(3-4)/4\), and we consider three special cases: \(\tau =0\), \(\tau =1/3\) and \(\tau =1\). Moreover, the initial values are chosen as \((X_0,Y_0,Z_0,\Lambda _0)=(I_{n},2I_{n},I_{n},\mathbf {0}_{n\times n})\) in our experiments. Meanwhile, taking the high communication cost between different CPU platforms into consideration, what we emphasize here is that the tested algorithms are implemented by a serial way, rather than a parallel way. In the following tables and figures, the numerical performance of the tested methods is evaluated by the following parameters:

  • Iter: the required iteration number;

  • Time: the total computing time in seconds;

  • CPU: the maximum total running time of subproblems in seconds.

Note that the D-ADMM enjoys a Gaussian decomposition structure. The CPU time is indeed the total computing time for the D-ADMM.

In Table 1, we report the numerical results of the proposed method (3.7) for solving the LVGGMS model (5.1) with \(n=100\) when various stop stopping conditions are adopted. As can be seen easily, both the feasibility errors IER and CER have a similar changing pattern with the change of \(\beta\) for the various regularization parameters \(\tau\). In particular, the cases where \(\tau =1/3\) and \(\beta \in (0,12,0.14)\) perform more stably and efficiently, and they need only a reduced iterations and computational time (both Time and CPU) in terms of the feasibility errors IER and CER.

To show the comparisons between the novel method (3.7) and other operator spitting methods, we list first some efficient parameters for the above mentioned splitting algorithms. Using the same parameter adjustment strategy (trial-and-error) as the novel method (3.7), the toned parameters of the mentioned methods for solving the LVGGMS problem are given in Table 2.

In Table 3, we report the numerical results of the above tested algorithms for the LVGGMS problem (5.1) with various settings of n. As shown in Table 3, it is clear that the D-ADMM needs less required iterations and the proposed method (3.7) needs less CPU time than other algorithms. Compared with P-ALM and PS-ADMM, the novel method needs also fewer required iterations to reach different stopping criteria, which verifies empirically our theoretical motivation of this study (our purpose is to present a more efficient parallel spitting method). In addition, it can be seen easily from Table 3 that the D-ALM is divergent for the LVGGMS model (5.1), which can be further numerically illustrated that the direct extension of ALM is not necessarily convergent.

Table 1 Numerical results of the novel method (3.7) for solving the LVGGMS model (5.1) with \(n=100\)
Full size table
Table 2 Toned values of parameters of the above mentioned operator spiting methods for the LVGGMS model (5.1)
Full size table
Fig. 2
figure 2

First column: convergence curves of the IER and CER with iteration numbers; second column: convergence curves of the IER and CER with CPU time (\(n=100\))

Full size image

To further visualize the numerical comparison between the new method and the other splitting algorithms, in Fig. 2, we plot their respective feasibility errors with respect to iterations and CPU time for the case \(n=100\). Computational results in Fig. 2 demonstrate that the proposed method has steeper convergence curves than PS-ADMM and P-ALM both in iterations and CPU time. In particular, it can bee seen from Fig. 2 that the new method is faster than D-ADMM, even though the latter needs a less required iterations. For other settings of n, since their convergence curves are similar as the case \(n=100\), we opt to skip them for succinctness.

Table 3 Numerical results of the tested algorithms for solving the LVGGMS problem (5.1) with various n
Full size table

6 Conclusions

We propose a novel parallel splitting ALM-based algorithm for solving the multiple-block separable convex programming problem with linear equality constraints, where the objective function can be expressed as the sum of some individual subfunctions without coupled variables. By adding a simple update (1.8) to the fully parallel regularized ALM (1.7), convergence of the novel method can be guaranteed provided a reduced parameter of the regularization terms, which allows bigger step sizes and thus potentially results in fewer required iterations in the real computations. The numerical results on the LVGGMS problem affirmatively illustrates that the proposed method has an acceleration effect compared with some known parallel splitting algorithms.