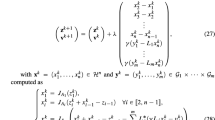Strengthened splitting methods for computing resolvents

Abstract

In this work, we develop a systematic framework for computing the resolvent of the sum of two or more monotone operators which only activates each operator in the sum individually. The key tool in the development of this framework is the notion of the “strengthening” of a set-valued operator, which can be viewed as a type of regularisation that preserves computational tractability. After deriving a number of iterative schemes through this framework, we demonstrate their application to best approximation problems, image denoising and elliptic PDEs.

1 Introduction

The resolvent of a monotone operator, as studied by Minty [41] and others [13, 15, 33, 50], is an integral building block of many iterative algorithms. By specialising to the subdifferentials of convex functions, the notion includes the commonly encountered proximity operator in the sense of Moreau [42] as a special case, as well as the nearest point/orthogonal projector onto a set. In general, evaluating the resolvent at a point is not a straightforward task and involves solving a non-trivial monotone inclusion. Fortunately however, a number of special cases of practice importance have closed form expressions which lend themselves to efficient evaluation, such as the soft-thresholding operator [38, Example 4.1], which arises from $\ell _1$-regularisation, the proximity operator of the logarithmic barrier used in interior point approaches [17], as well as many nearest point projectors onto convex sets [9]. For an extensive list of such examples, the reader is referred to [27, 44].

While it is often possible to decompose a monotone operator into a sum of simpler monotone operators, each having easy to compute resolvents, this additive structure does not generally ensure ease of computing its resolvent, except in certain restrictive settings (such as [10, Proposition 23.32]) which have limited applicability. A concrete example requiring computation of the resolvents of a sum arises in fractional programming problems as we show next.

Example 1

(Fractional programming) Let $\mathcal {H}$ be a real Hilbert space. Consider the fractional programming problem

$$\begin{aligned} \bar{\theta } := \inf _{x\in S}\frac{f(x)}{g(x)}, \end{aligned}$$

(1)

where $S\subseteq \mathcal {H}$ is nonempty, closed and convex, $f:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ is proper, lower semicontinous and convex with $f(x)\ge 0$ for all $x\in S$ and $S\cap {\mathrm{dom}}f\ne \emptyset$, and $g:\mathcal {H}\rightarrow \mathbb {R}$ is either convex or concave, differentiable and satisfies $g(S)\subseteq {]0,M]}$ for some $M>0$. To solve this problem, a proximal-gradient-type algorithm of the following form was proposed in [18] (see also [19]).

Note that the subproblem (2) in Step 2 of Algorithm 1 amounts to evaluating the proximity operator of $\eta _k(f+\iota _S)$ at the point $q:=x_{k-1}-\theta _k\eta _k\nabla g(x_{k-1})$ where $\iota _S$ denotes the indicator function of the set S. If the subdifferential sum rule holds for f and $\iota _S$, then $\partial (f+\iota _S)=\partial f+N_S$, where $\partial f$ denotes the subdifferential of a function f and $N_S$ denotes the normal cone to S. In this case, evaluating the aforementioned proximity operator requires the computation of the resolvent of the sum $\eta _k(\partial f+N_S)$ at q, where both $A:=\partial f$ and $B:=\partial \iota _S=N_S$ are set-valued maximally monotone operators.

To overcome these difficulties, it is natural to consider iterative algorithms for computing the resolvent of the sum of monotone operators whose iteration uses the resolvents of the individual monotone operators. To this end, Combettes [28] considered algorithms based on the Douglas–Rachford method and a Dykstra-type method in the product space (in the sense of Pierra [45]). More recently, Aragón and Campoy [7] developed a method based on a modification of the Douglas–Rachford method for two operators which does not necessarily require a product space, which was further studied in [3, 31]. Building on the work of Moudafi [43], Chen and Tang [26] devised an algorithm for computing the resolvent of sum of a monotone and a composite operator. A different approach based on a composition formula involving generalised resolvents has also been considered in works by Adly and Bourdin [1], and Adly, Bourdin and Caubet [2].

In most of the aforementioned works, the main focus of the analysis has been on specific algorithms. In this work, our approach is different. We instead focus on the interplay between properties of the operators themselves and the underlying problem formulations. By doing so, we unify many of the existing algorithms for computing resolvents in the literature within a framework based on strengthenings of monotone operators. This notion can be viewed as a regularisation of an operator which preserves certain computationally favourable properties. Moreover, this framework has the advantage of providing transparency and insight into the mechanism of existing methods as well as providing a way to systematically develop new algorithms.

The remainder of this work is structured as follows. We begin in Sect. 2 by recalling preliminaries for use in the sequel. In Sect. 3, we introduce and study the notion of strengthenings of set-valued operators, including establishing relationships between the resolvents, continuity properties and zeros of operators and their strengthenings. Next we turn to iterative algorithms, with Sect. 4 focusing on methods which incorporate forward steps and Sect. 5 focusing on methods which incorporate only backward steps. Finally, in Sect. 6, we apply our results to devise algorithms for three different applications: best approximation with three sets, ROF-type imaging denoising, and elliptic PDEs with partially blinded Laplacians. In addition, we also provide an alternative proof of Ryu’s three operator splitting method [52, Section 4] in the Appendix, which also covers convergence of its shadow sequence in the infinite dimensional setting.

2 Preliminaries

Throughout this paper, $\mathcal {H}$ is a real Hilbert space equipped with inner product $\langle \cdot , \cdot \rangle$ and induced norm $\Vert \cdot \Vert$. We abbreviate norm convergence of sequences in $\mathcal {H}$ with $\rightarrow$ and we use $\rightharpoonup$ for weak convergence. We denote the closed ball centered at $x\in \mathcal {H}$ of radius $\delta >0$ by $\mathbb {B}(x,\delta )$.

2.1 Operators

Given a non-empty set $D\subseteq \mathcal {H}$, $A:D\rightrightarrows \mathcal {H}$ denotes a set-valued operator that maps any point from D to a subset of $\mathcal {H}$, i.e., $A(x)\subseteq \mathcal {H}$ for all $x\in D$. In the case when A always maps to singletons, i.e., $A(x)=\{u\}$ for all $x\in D$, A is said to be a single-valued mapping and it is denoted by $A:D\rightarrow \mathcal {H}$. In an abuse of notation, we may write $A(x)=u$ when $A(x)=\{u\}$. Note that one can always write $A:\mathcal {H}\rightrightarrows \mathcal {H}$ by setting $A(x):=\emptyset$ for all $x\not \in D$. The domain, the range, the graph, the set of fixed points and the set of zeros of A, are denoted, respectively, by ${\mathrm{dom}}\,A$, ${\mathrm{ran}}\,A$, ${\mathrm{gra}}\,A$, ${\mathrm{Fix}}\,A$ and ${\mathrm{zer}}\,A$; i.e.,

$$\begin{aligned} {\mathrm{dom}}A&:=\left\{ x\in \mathcal {H}: A(x)\ne \emptyset \right\} ,&{\mathrm{ran}}A&:=\left\{ u\in \mathcal {H}: \exists x\in \mathcal {H}: u\in A(x) \right\} ,&\\ {\mathrm{gra}}A&:=\left\{ (x,u)\in \mathcal {H}\times \mathcal {H}: u\in A(x)\right\} ,&{\mathrm{Fix}}A&:=\left\{ x\in \mathcal {H}: x\in A(x)\right\} , \end{aligned}$$

and    

$${\mathrm{zer}}A:=\left\{ x\in \mathcal {H}: 0\in A(x)\right\} .$$

The identity operator is the mapping ${\mathrm{Id}}:\mathcal {H}\rightarrow \mathcal {H}$ that maps every point to itself. The inverse operator of A, denoted by $A^{-1}$, is defined through $x\in A^{-1}(u) \iff u\in A(x).$

Definition 1

($\alpha$-monotonicity) Let $\alpha \in \mathbb {R}$. An operator $A:\mathcal {H}\rightrightarrows \mathcal {H}$ is $\alpha$-monotone if

$$\begin{aligned} \langle x-y,u-v\rangle \ge \alpha \Vert x-y\Vert ^2\quad \forall (x,u),(y,v)\in {\mathrm{gra}}\,A. \end{aligned}$$

Furthermore, an $\alpha$-monotone operator A is said to be maximally $\alpha$-monotone if there exists no $\alpha$-monotone operator $B:\mathcal {H}\rightrightarrows \mathcal {H}$ such that ${\mathrm{gra}}\,B$ properly contains ${\mathrm{gra}}\,A$.

Depending on the sign of $\alpha$, Definition 1 captures three important classes of operators in the literature. Firstly, an operator is monotone (in the classical sense) if it is 0-monotone. Secondly, an operator is $\alpha$-strongly monotone (in the classical sense) if it is $\alpha$-monotone for $\alpha >0$. And, finally, an operator is $\alpha$-weakly monotone (or $\alpha$-hypomonotone) if it is $\alpha$-monotone for $\alpha <0$.

Definition 2

(Resolvent operator) Given an operator $A:\mathcal {H}\rightrightarrows \mathcal {H}$, the resolvent of A with parameter $\gamma >0$ is the operator $J_{\gamma A}:\mathcal {H}\rightrightarrows \mathcal {H}$ defined by $J_{\gamma A}:=({\mathrm{Id}}+\gamma A)^{-1}$.

Proposition 1

(Resolvents of $\alpha$-monotone operators) Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$ be $\alpha$-monotone and let $\gamma >0$ such that $1+\gamma \alpha >0$. Then

• (i) $J_{\gamma A}$ is single-valued,

• (ii) ${\mathrm{dom}}J_{\gamma A}=\mathcal {H}$ if and only if A is maximally $\alpha$-monotone.

Proof

See [30, Proposition 3.4]. $\square$

Definition 3

Let D be a nonempty subset of $\mathcal {H}$ and let $T:D\rightarrow \mathcal {H}$. The operator T is said to be

• (i) $\kappa$ -Lipschitz continuous for $\kappa >0$ if

  $$\begin{aligned} \Vert T(x)-T(y)\Vert \le \kappa \Vert x-y\Vert \quad \forall x,y\in D; \end{aligned}$$

• (ii) locally Lipschitz continuous if, for all $x_0\in D$, there exist $\delta ,\kappa >0$ such that

  $$\begin{aligned} \Vert T(y)-T(z)\Vert \le \kappa \Vert y-z\Vert \quad \forall z,y\in \mathbb {B}(x_0,\delta )\cap D; \end{aligned}$$

• (iii) nonexpansive if it is Lipschitz continuous with constant 1;

• (iv) $\alpha$-averaged for $\alpha \in \,]0,1[$ if there exists a nonexpansive operator $R:D\mapsto \mathcal {H}$ such that

  $$\begin{aligned} T=(1-\alpha )I+\alpha R; \end{aligned}$$

• (v) $\alpha$-negatively averaged for $\alpha \in {]0,1[}$ if $-T$ is $\alpha$-averaged;

• (vi) $\beta$-cocoercive for $\beta >0$ if

  $$\begin{aligned} \langle x-y,T(x)-T(y)\rangle \ge \beta \Vert T(x)-T(y)\Vert ^2\quad \forall x,y\in D. \end{aligned}$$

Remark 1

(Lipschitz continuity versus cocoercivity) By the Cauchy–Schwarz inequality, any $\beta$-cocoercive mapping is $\frac{1}{\beta }$-Lipschitz continuous. In general, cocoercivity of an operator is a stronger condition than Lipschitz continuity, except when the operator is the gradient of a differentiable convex function: in this case the Baillon–Haddad theorem states that both notions are equivalent (see, e.g., [10, Corollary 18.17]).

2.2 Functions and subdifferentials

An extended real-valued function ${f:\mathcal {H}\rightarrow ]-\infty ,+\infty ]}$ is said to be proper if its domain, ${\mathrm{dom}}\,f:=\{x\in \mathcal {H}: f(x)<+\infty \}$, is nonempty. We say f is lower semicontinuous (lsc) if, at any $\bar{x}\in \mathcal {H}$,

$$\begin{aligned} f(\bar{x})\le \liminf _{x\rightarrow \bar{x}} f(x). \end{aligned}$$

A function f is said to be $\alpha$-convex, for $\alpha \in \mathbb {R}$, if $f-\frac{\alpha }{2}\Vert \cdot \Vert ^2$ is convex; i.e, for all $x,y\in \mathcal {H}$,

$$\begin{aligned} f((1-\lambda )x+\lambda y)\le \lambda f(x)+(1-\lambda )f(y)-\frac{\alpha }{2}\lambda (1-\lambda )\Vert x-y\Vert ^2, \quad \forall \lambda \in [0,1]. \end{aligned}$$

Clearly, 0-convexity coincides with classical convexity. We say f is strongly convex when $\alpha >0$ and weakly convex (or hypoconvex) when $\alpha <0$.

For any extended real valued function f, the Fenchel conjugate of f is denoted by $f^*(\phi ):=\sup _{x\in \mathcal {H}}\{\langle x,\phi \rangle -f(x)\}$ for all $\phi \in \mathcal {H}$. The Fréchet subdifferential of f at $x\in {\mathrm{dom}}\,f$ is given by

$$\begin{aligned} \partial f(x):=\left\{ u\in \mathcal {H}: \liminf _{\begin{array}{c} y\rightarrow x\\ y\ne x \end{array}} \frac{f(y)-f(x)-\langle u,y-x\rangle }{\Vert y-x\Vert }\ge 0\right\} \end{aligned}$$

and $\partial f(x):=\emptyset$ at $x\not \in {\mathrm{dom}}\,f$. When f is differentiable at $x\in {\mathrm{dom}}\,f$, then $\partial f(x)=\{\nabla f(x)\}$ where $\nabla f(x)$ denotes the gradient of f at x. When f is convex, then $\partial f(x)$ coincides with the classical (convex) subdifferential of f at x, which is the set

$$\begin{aligned} \{u\in \mathcal {H}: f(x)+\langle u,y-x\rangle \le f(y),\,\forall y\in \mathcal {H}\}. \end{aligned}$$

Given a nonempty set $C\subseteq \mathcal {H}$, the indicator function of C, $\iota _C:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$, is defined as

$$\begin{aligned} \iota _C(x):=\left\{ \begin{array}{cl} 0, &{} \text {if } x\in C,\\ +\infty , &{} \text {if } x\not \in C.\end{array}\right. \end{aligned}$$

When C is a convex set, $\iota _C$ is a convex function whose subdifferential becomes the (convex) normal cone to C, $N_C:\mathcal {H}\rightrightarrows \mathcal {H}$, given by

$$\begin{aligned} \partial \iota _C(x)=N_C(x):=\left\{ \begin{array}{ll}\{u\in \mathcal {H}: \langle u, c-x \rangle \le 0, \, \forall c\in C \}, &{}\text {if }x\in C,\\ \emptyset , &{} \text {otherwise.}\end{array}\right. \end{aligned}$$

Example 2

(Monotonicity of subdifferentials and normal cones) The subdifferential and the normal cone are well-known examples of maximally monotone operators.

• (i) Let $f:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and $\alpha$-convex for $\alpha \in \mathbb {R}$. Then, $\partial f$ is a maximally $\alpha$-monotone operator. Furthermore, given $\gamma >0$ such that $1+\gamma \alpha >0$, it holds that $J_{\gamma \partial f}={\mathrm{prox}}_{\gamma f}$, where ${\mathrm{prox}}_{\gamma f}:\mathcal {H}\rightrightarrows \mathcal {H}$ is the proximity operator of f (with parameter $\gamma$) defined at $x\in \mathcal {H}$ by

  $$\begin{aligned} {\mathrm{prox}}_{\gamma f}(x):={\mathrm{argmin}}_{u\in \mathcal {H}} \left( f(u)+\frac{1}{2\gamma }\Vert x-u\Vert ^2\right) , \end{aligned}$$

  see, e.g., [30, Lemma 5.2].

• (ii) Let $C\subseteq \mathcal {H}$ be a nonempty, closed and convex set. Then, the normal cone $N_C$ is maximally monotone. Furthermore, $J_{N_C}=P_C$, where $P_C:\mathcal {H}\rightrightarrows \mathcal {H}$ denotes the projector onto C defined at $x\in \mathcal {H}$ by

  $$\begin{aligned} P_C(x):={\mathrm{argmin}}_{c\in C} \Vert x-c\Vert , \end{aligned}$$

  see, e.g., [10, Example 20.26 and Example 23.4].

$\square$

3 Strengthenings of set-valued operators

In this section, we introduce the notion of the strengthening of a set-valued operator and study its properties. This idea appears without name in [31] which, in turn, builds on the special cases considered in [7]. This concept was motivated by the ideas of [28], where a particular case of the strengthening was employed in algorithm analysis.

Definition 4

($(\theta ,\sigma )$-strengthening) Let $\theta >0$ and $\sigma \in \mathbb {R}$. Given $A:\mathcal {H}\rightrightarrows \mathcal {H}$, the $(\theta ,\sigma )$-strengthening of A is the operator $A^{(\theta ,\sigma )}:\mathcal {H}\rightrightarrows \mathcal {H}$ defined by

$$\begin{aligned} A^{(\theta ,\sigma )}:=A\circ (\theta {\mathrm{Id}})+\sigma {\mathrm{Id}}. \end{aligned}$$

(3)

Remark 2

In [7, Definition 3.2], the authors define the $\beta$-strengthening of an operator A for $\beta \in {]0,1[}$ as the operator $A^{(\beta )}:=A^{(\theta ,\sigma )}$ with $\theta :=\frac{1}{\beta }$ and $\sigma :=\frac{1-\beta }{\beta }$.

We recall next the concept of perturbation of an operator, which was studied in [11]. We follow the notation used in [12].

Definition 5

(Inner perturbation) Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$ and let $w\in \mathcal {H}$. The inner w-perturbation of A is the operator $A_w:\mathcal {H}\rightrightarrows \mathcal {H}$ defined at $x\in \mathcal {H}$ by

$$\begin{aligned} A_w(x) := A(x-w). \end{aligned}$$

Of particular interest in this work, will be the strengthenings of inner perturbations. In other words, given an operator $A:\mathcal {H}\rightrightarrows \mathcal {H}$ and a point $q\in \mathcal {H}$, we shall study the operator $(A_{-q})^{(\theta ,\sigma )}$ which is given by

$$\begin{aligned} (A_{-q})^{(\theta ,\sigma )}=A_{-q}\circ (\theta {\mathrm{Id}})+\sigma {\mathrm{Id}}=A\circ (\theta {\mathrm{Id}}+q)+\sigma {\mathrm{Id}}. \end{aligned}$$

Remark 3

Suppose $f:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ is a proper, lsc and $\alpha$-convex function for $\alpha \in \mathbb {R}$. Then the subdifferential sum rule ensures

$$\begin{aligned} ((\partial f)_{-q})^{(\theta ,\sigma )} = \partial f\circ (\theta {\mathrm{Id}}+q)+\sigma {\mathrm{Id}}= \partial \left( \frac{1}{\theta }f\circ (\theta {\mathrm{Id}}+q) +\frac{\sigma }{2}\Vert \cdot \Vert ^2\right) . \end{aligned}$$

In other words, the strengthening of the inner perturbation of a subdifferential coincides with the subdifferential of the proper, lsc and $(\theta \alpha +\sigma )$-convex function $x\mapsto \frac{1}{\theta }f(\theta x+q) +\frac{\sigma }{2}\Vert x\Vert ^2$.

The following property shows that the resolvent of a strengthening can be computed using the resolvent of the original operator, and vice versa.

Proposition 2

Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$, let $q\in \mathcal {H}$, let $\theta ,\gamma >0$ and let $\sigma \in \mathbb {R}$. Then the following assertions hold.

• (i) A is (maximally) $\alpha$-monotone if and only if $(A_{-q})^{(\theta ,\sigma )}$ is (maximally) $(\theta \alpha +\sigma )$-monotone.

• (ii) If $1+\gamma \sigma \ne 0$, then

  $$\begin{aligned} J_{\gamma (A_{-q})^{(\theta ,\sigma )}}=\frac{1}{\theta }\left( J_{\frac{\gamma \theta }{1+\gamma \sigma }A}\circ \left( \frac{\theta }{1+\gamma \sigma }{\mathrm{Id}}+q\right) -q\right) . \end{aligned}$$

  If, in addition, A is maximally $\alpha$-monotone and $1+\gamma (\theta \alpha +\sigma )>0$, then both $J_{\gamma (A_{-q})^{(\theta ,\sigma )}}$ and $J_{\frac{\gamma \theta }{1+\gamma \sigma }A}$ are single-valued with full domain.

Proof

See [31, Proposition 2.1]. $\square$

Using the expression (3), it can be seen that the strengthening of an operator can be evaluated whenever the original operator can be evaluated. Next, we investigate how other properties are preserved under taking strengthenings.

Theorem 1

Let $B:\mathcal {H}\rightarrow \mathcal {H}$, let $q\in \mathcal {H}$, let $\theta >0$, let $\sigma \in \mathbb {R}$, and let $\kappa >0$. Then the following assertions hold.

• (i) B is $\kappa$-Lipschitz continuous if and only if $(B_{-q})^{(\theta ,0)}$ is $\kappa \theta$-Lipschitz continuous. Consequently, $(B_{-q})^{(\theta ,\sigma )}$ is $(\kappa \theta +|\sigma |)$-Lipschitz continuous.

• (ii) B is locally Lipschitz if and only if $(B_{-q})^{(\theta ,\sigma )}$ is locally Lipschitz.

• (iii) B is $\beta$-cocoercive if and only if $(B_{-q})^{(\theta ,0)}$ is $\frac{\beta }{\theta }$-cocoercive. Consequently, if $\sigma >0$, then $(B_{-q})^{(\theta ,\sigma )}$ is $\mu$-cocoercive with

  $$\begin{aligned} \mu := \left( \frac{\theta }{\beta }+\sigma \right) ^{-1}. \end{aligned}$$

Proof

First note that since Lipschitz continuity and cocoercivity are preserved undertaking inner perturbations, it suffices to prove the result for $q=0$.

(i): The equivalence follows immediately from definition the $(\theta ,0)$-strengthening. Using the identity $B^{(\theta ,\sigma )}=B^{(\theta ,0)}+\sigma {\mathrm{Id}}$, we then deduce

$$\begin{aligned} \Vert B^{(\theta ,\sigma )}(x)-B^{(\theta ,\sigma )}(y)\Vert&\le \Vert B^{(\theta ,0)}(x)-B^{(\theta ,0)}(y)\Vert +|\sigma |\Vert x-y\Vert \\&\le \kappa \theta \Vert x-y\Vert +|\sigma |\Vert x-y\Vert , \end{aligned}$$

from which the result follows. (ii): The proof is similar to (i). (iii): The equivalence follows immediately from definition of the $(\theta ,0)$-strengthening. Next, note that

$$\begin{aligned} \begin{aligned} \frac{\alpha _1\alpha _2}{\alpha _1+\alpha _2}\Vert u+v\Vert ^2&\le \frac{\alpha _1\alpha _2}{\alpha _1+\alpha _2}\left( \Vert u\Vert ^2+\Vert v\Vert ^2+2\Vert u\Vert \Vert v\Vert \right) \\&\le \frac{\alpha _1\alpha _2}{\alpha _1+\alpha _2}\left( \Vert u\Vert ^2+\Vert v\Vert ^2+\frac{\alpha _1}{\alpha _2}\Vert u\Vert ^2+\frac{\alpha _2}{\alpha _1}\Vert v\Vert ^2\right) \\&= \alpha _1\Vert u\Vert ^2 + \alpha _2\Vert v\Vert ^2, \end{aligned} \end{aligned}$$

(4)

for all weights $\alpha _1,\alpha _2>0$ and $u,v\in \mathcal {H}$. Using the identity $B^{(\theta ,\sigma )}=B^{(\theta ,0)}+\sigma {\mathrm{Id}}$ and the $\frac{\beta }{\theta }$-cocoercivity of $B^{(\theta ,0)}$, followed by an application of (4) with weights $\alpha _1=\frac{\beta }{\theta }$ and $\alpha _2=\frac{1}{\sigma }$ we obtain

$$\begin{aligned} \langle x-y,B^{(\theta ,\sigma )}(x)-B^{(\theta ,\sigma )}(y)\rangle&= \langle x-y, B^{(\theta ,0)}(x)-B^{(\theta ,0)}(y)\rangle + \frac{1}{\sigma }\Vert \sigma x-\sigma y\Vert ^2 \\&\ge \frac{\beta }{\theta }\Vert B^{(\theta ,0)}(x)-B^{(\theta ,0)}(y)\Vert ^2 + \frac{1}{\sigma }\Vert \sigma x-\sigma y\Vert ^2\\&\ge \left( \frac{\theta }{\beta }+\sigma \right) ^{-1}\Vert B^{(\theta ,\sigma )}(x)-B^{(\theta ,\sigma )}(y)\Vert ^2, \end{aligned}$$

which establishes the result. $\square$

The following proposition characterises the structures of the zeros of the sum of strengthenings of operators in terms of resolvents. It will be key in the development of algorithms in subsequent sections.

Proposition 3

Let $A_i:\mathcal {H}\rightrightarrows \mathcal {H}$ and $\sigma _i\in \mathbb {R}$ for $i\in \{1,\dots ,n\}$ with $\sigma :=\sum _{i=1}^n\sigma _i>0$. Let $q\in \mathcal {H}$ and $\theta >0$. Then

$$\begin{aligned} J_{\frac{\theta }{\sigma }\left( \sum _{i=1}^nA_i\right) }(q) = \left\{ \theta x +q: x\in {\mathrm{zer}}\left( \sum _{i=1}^n((A_i)_{-q})^{(\theta ,\sigma _i)}\right) \right\} . \end{aligned}$$

(5)

Consequently, if each $A_i$ is $\alpha _i$-monotone, $\sum _{i=1}^n(\theta \alpha _i+\sigma _i)>0$ and $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\theta }{\sigma }\sum _{i=1}^nA_i\right)$, then $J_{\frac{\theta }{\sigma }\left( \sum _{i=1}^nA_i\right) }(q)$ is a singleton and $\frac{1}{\theta }\left( J_{\frac{\theta }{\sigma }\left( \sum _{i=1}^nA_i\right) }(q)-q\right)$ is the unique element of ${\mathrm{zer}}\left( \sum _{i=1}^n((A_i)_{-q})^{(\theta ,\sigma _i)}\right) .$

Proof

For convenience, denote $A:=\sum _{i=1}^nA_i$. Then we have

$$\begin{aligned} x\in {\mathrm{zer}}\left( \sum _{i=1}^n((A_i)_{-q})^{(\theta ,\sigma _i)}\right)&\iff 0 \in \sum _{i=1}^n\left( A_i(\theta x+q)+\sigma _ix\right) = A(\theta x+q) + \sigma x \\&\iff q \in \left( {\mathrm{Id}}+ \frac{\theta }{\sigma }A\right) (\theta x+q) \\&\iff \theta x+q \in J_{\frac{\theta }{\sigma } A}(q), \end{aligned}$$

which establishes (5). Now suppose that $A_i$ is $\alpha _i$-monotone for $i=1,\dots ,n$. Then $((A_i)_{-q})^{(\theta ,\sigma _i)}$ is $(\theta \alpha _i+\sigma _i)$-monotone by Proposition 2 (i) and hence $\sum _{i=1}^n((A_i)_{-q})^{(\theta ,\sigma _i)}$ is $\alpha$-strongly monotone for $\alpha :=\sum _{i=1}^n(\theta \alpha _i+\sigma _i)>0$. The result follows by noting that a strongly monotone operator has at most one zero (see, e.g., [10, Proposition 23.35]) and that $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\theta }{\sigma }\sum _{i=1}^nA_i\right)$ if and only if $J_{\frac{\theta }{\sigma }\sum _{i=1}^nA_i}(q)\ne \emptyset$. $\square$

Remark 4

Proposition 3 formalises and extends a number of formulations which can be found in the literature.

• (i) If $\beta =\frac{1}{\theta }\in {]0,1[}$ and $\sigma _1=\dots =\sigma _n=\frac{1-\beta }{\beta }$, then

  $$\begin{aligned} {\mathrm{zer}}\left( \sum _{i=1}^nA_i^{(\beta )}\right) = \beta J_{\frac{1}{n(1-\beta )}\sum _{i=1}^nA_i}(0). \end{aligned}$$

This recovers [7, Proposition 4.2]. Moreover, this result can be generalised in the following way. Let $k\in \{1,\dots ,n-1\}$. If $\beta =\frac{1}{\theta }\in {]0,1[}$, $\sigma _1=\dots =\sigma _k=\frac{1-\beta }{\beta }$ and $\sigma _{k+1}=\dots =\sigma _n=0$, then

$$\begin{aligned} {\mathrm{zer}}\left( \sum _{i=1}^k A_i^{(\beta )}+\sum _{i=k+1}^nA_i(\cdot /\beta )\right) = \beta J_{\frac{1}{k(1-\beta )}\sum _{i=1}^nA_i}(0). \end{aligned}$$

• (ii) Consider weights $\omega _1,\dots ,\omega _n>0$ with $\sum _{i=1}^n\omega _i=1$. If $\theta =1$ and $\sigma _1,\ldots ,\sigma _n>0$ with $\sum _{i=1}^n\sigma _i=1$, then

  $$\begin{aligned} J_{\sum _{i=1}^n\omega _iA_i}(q) = {\mathrm{zer}}\left( \sum _{i=1}^n\left( (\omega _iA_i)_{-q}\right) ^{(1,\sigma _i)}\right) + q = {\mathrm{zer}}\left( -q+{\mathrm{Id}}+ \sum _{i=1}^n\omega _iA_i\right) . \end{aligned}$$

  This fact is used in [28, Theorem 2.8].

• (iii) Consider $n=2$, $\theta >0$, $\omega >0$, $\vartheta ,\tau \in \mathbb {R}$ and $q,r,r_A,r_B\in \mathcal {H}$ satisfying

  $$\begin{aligned} \vartheta +\tau =\frac{\theta }{\omega }\quad \text {and}\quad r_A+r_B=\frac{1}{\omega }(q+r). \end{aligned}$$

  Let $A:=A_1$ and $B:=A_2$. Take $\sigma _1=\sigma _2=\frac{\theta }{2\omega }$. Then

  $$\begin{aligned} J_{\omega (A+B)}(r)&=\theta {\mathrm{zer}}\left( ((A)_{-r})^{(\theta ,\sigma _1)}+((B)_{-r})^{(\theta ,\sigma _2)}\right) +r\\&=\theta {\mathrm{zer}}\left( A\circ (\theta {\mathrm{Id}}+r)+B\circ (\theta {\mathrm{Id}}+r)+\frac{\theta }{\omega }{\mathrm{Id}}\right) +r\\&=\theta {\mathrm{zer}}\left( A\circ (\theta {\mathrm{Id}}-q){+}\vartheta {\mathrm{Id}}{+}B\circ (\theta {\mathrm{Id}}{-}q){+}\tau {\mathrm{Id}}{-}\frac{1}{\omega }(q{+}r)\right) {-}q\\&=\theta {\mathrm{zer}}\left( A\circ (\theta {\mathrm{Id}}-q){+}\vartheta {\mathrm{Id}}{-}r_A{+}B\circ (\theta {\mathrm{Id}}{-}q){+}\tau {\mathrm{Id}}{-}r_B\right) {-}q, \end{aligned}$$

  which recovers [31, Proposition 3.1].

$\square$

Corollary 1

For each $i\in \{1,\ldots ,n\}$, let $f_i:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and $\alpha _i$-convex, with $\alpha _i\in \mathbb {R}$. Let $\sigma _1,\ldots ,\sigma _n\in \mathbb {R}$ such that $\sigma :=\sum _{i=1}^n\sigma _i> 0$. Let $q\in \mathcal {H}$ and $\theta >0$, and suppose that $\sum _{i=1}^n(\theta \alpha _i+\sigma _i)>0.$ Then $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\theta }{\sigma }\sum _{i=1}^n\partial f_i\right)$ if and only if

$$\begin{aligned} q-{\mathrm{prox}}_{\frac{\theta }{\sigma }\sum _{i=1}^n f_i}(q) \in \left( \frac{\theta }{\sigma }\sum _{i=1}^n \partial f_i\right) \left( {\mathrm{prox}}_{\frac{\theta }{\sigma }\sum _{i=1}^n f_i}(q)\right) . \end{aligned}$$

(6)

In this case, $\frac{1}{\theta }\left( {\mathrm{prox}}_{\frac{\theta }{\sigma }\sum _{i=1}^n f_i}(q)-q\right)$ is the unique element of ${\mathrm{zer}}\left( \sum _{i=1}^n((\partial f_i)_{-q})^{(\theta ,\sigma _i)}\right)$.

Proof

The reverse implication is immediate. To prove the forward implication, consider $x\in \mathcal {H}$ such that $q\in x+\frac{\theta }{\sigma }\sum _{i=1}^n\partial f_i(x)$. Combining this with the inclusion $\sum _{i=1}^n\partial f_i(x)\subseteq \partial (\sum _{i=1}^n f_i)(x)$ gives

$$\begin{aligned} q\in \left( {\mathrm{Id}}+\frac{\theta }{\sigma }\partial \left( \sum _{i=1}^n f_i\right) \right) (x) \iff x=J_{\frac{\theta }{\sigma }\partial \left( \sum _{i=1}^n f_i\right) }(q). \end{aligned}$$

Since $f_i$ is proper, lsc and $\alpha _i$-convex, then $\sum _{i=1}^nf_i$ is proper, lsc and $\alpha$-convex with $\alpha :=\sum _{i=1}^n\alpha _i$. By assumption on the parameters, it holds that $1+\alpha \frac{\theta }{\sigma }>0$. Then, by Example 2(i), we get that

$$\begin{aligned} J_{\frac{\theta }{\sigma }\partial \left( \sum _{i=1}^n f_i\right) }(q)={\mathrm{prox}}_{\frac{\theta }{\sigma }\sum _{i=1}^n f_i}(q), \end{aligned}$$

and, thus, (6) holds. The last assertion follows from Proposition 3 combined with the fact that $\partial f_i$ is $\alpha _i$-monotone, for $i=1,\ldots ,n$, by Example 2(i). $\square$

Corollary 2

Let $C_i\subseteq \mathcal {H}$ be a nonempty, closed and convex set and $\sigma _i\in \mathbb {R}$ for $i\in \{1,\ldots ,n\}$ such that $\sigma :=\sum _{i=1}^n\sigma _i>0$. Let $q\in \mathcal {H}$ and let $\theta >0$. Then $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\sum _{i=1}^n N_{C_i}\right)$ if and only if

$$\begin{aligned} q-P_{\cap _{i=1}^n C_i}(q) \in \left( \sum _{i=1}^n N_{C_i}\right) \left( P_{\cap _{i=1}^n C_i}(q)\right) . \end{aligned}$$

In this case, $\frac{1}{\theta }\left( P_{\cap _{i=1}^n C_i}(q)-q\right)$ is the unique element of ${\mathrm{zer}}\left( \sum _{i=1}^n((N_{C_i})_{-q})^{(\theta ,\sigma _i)}\right)$.

Proof

Apply Corollary 1 with $f_i=\iota _{C_i}$, for $i\in \{1,\ldots ,n\}$. $\square$

Remark 5

(Sum rule and strong CHIP) In the setting of Corollary 1, a sufficient condition for (6) is

$$\begin{aligned} \sum _{i=1}^n\partial f_i(x) = \partial \left( \sum _{i=1}^n f_i\right) (x),\quad \forall x\in \mathcal {H}, \end{aligned}$$

(7)

which is referred to as the subdifferential sum rule. In fact, using an argument analogous to [6, Proposition 4.1], it can be easily shown that the sum rule (7) is equivalent to having condition (6) to hold for all $q\in \mathcal {H}$. Sufficient conditions for (7) can be expressed in terms of the domains of the functions (see, e.g., [10, Corollary 16.50]). Specialising to the indicator functions to sets, that is, in the framework of Corollary 2, the sum rule becomes

$$\begin{aligned} \sum _{i=1}^n N_{C_i}(x) = N_{\cap _{i=1}^nC_i}(x),\quad \forall x\in \mathcal {H}, \end{aligned}$$

(8)

which is known as the strong conical hull intersection (strong CHIP) property. Specific sufficient conditions for (8) can be found in [22].

4 Forward-backward-type methods

In this section, we focus on the problem of computing

$$\begin{aligned} J_{\omega (A+B)}(q), \end{aligned}$$

(9)

for some given $q\in \mathcal {H}$ and $\omega >0$, where $A:\mathcal {H}\rightrightarrows \mathcal {H}$ is $\alpha _A$-maximally monotone and $B:\mathcal {H}\rightarrow \mathcal {H}$ is $\alpha _B$-monotone, single-valued and continuous.

In this situation, we can perform direct evaluations (forward steps) of B and resolvent evaluations (backward steps) of A. For simplicity of exposition, the operator B is assumed to have full domain which ensures maximality of $A+B$.

Assumption 1

Let $\alpha _A,\alpha _B\in \mathbb {R}$ denote the monotonicity constants associated with the operators A and B in (9), respectively. Suppose $\theta >0$ and $\sigma =(\sigma _A,\sigma _B)\in \mathbb {R}_{++}^2$ satisfy

$$\begin{aligned} \theta \alpha _A+\sigma _A>0\quad \text {and}\quad \theta \alpha _B+\sigma _B>0. \end{aligned}$$

Remark 6

For any $\alpha _A,\alpha _B\in \mathbb {R}$, there always exist $\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$ satisfying Assumption 1. Thus, Assumption 1 does not induce any restrictions on the operators A and B in (9), but it may restrict the values of $\omega$ for which the resolvent in (9) can be computed if $\alpha _A$ or $\alpha _B$ is negative. When A and B are monotone (i.e., $\alpha =(\alpha _A,\alpha _B)\in \mathbb {R}^2_+$), Assumption 1 is trivially satisfied.

In some circumstances, it may suffice to assume that $\theta >0$ and $(\sigma _A,\sigma _B)\in \mathbb {R}^2$ satisfy the weaker assumption

$$\begin{aligned} \sigma _A+\sigma _B>0, \quad \theta \alpha _A+\sigma _A\ge 0\quad \text {and} \quad \theta \alpha _B+\sigma _B\ge 0. \end{aligned}$$

(10)

In this case, Proposition 2(i) yields maximal monotonicity of the strengthenings, whereas Proposition 3 is still applicable. Thus, (10) may be sufficient for the convergence of some algorithms (see, e.g., Remark 8). However, we shall develop our analysis under Assumption 1 since it significantly improves our results and simplifies our presentation.

In the following result we establish the maximality of the sum $A+B$ within the framework of this section. Thus, under Assumption 1, condition $q\in {\mathrm{ran}}({\mathrm{Id}}+\frac{\theta }{\sigma _A+\sigma _B}(A+B))$ in Proposition 3 holds for every point $q\in \mathcal {H}$.

Lemma 1

Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally $\alpha _A$-monotone and let $B:\mathcal {H}\rightarrow \mathcal {H}$ be $\alpha _B$-monotone and continuous. Then $A+B$ is maximally $(\alpha _A+\alpha _B)$-monotone. Consequently, if $\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$ satisfy Assumption 1, the resolvent $J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}$ has full domain.

Proof

Consider the operators $\widetilde{A}:=A-\alpha _A{\mathrm{Id}}$ and $\widetilde{B}:=B-\alpha _B{\mathrm{Id}}$. Then $\widetilde{A}$ is maximally monotone and $\widetilde{B}:\mathcal {H}\rightarrow \mathcal {H}$ is monotone and continuous. Thus, by [10, Corollary 20.28] we get that $\widetilde{B}$ is maximally monotone and ${\mathrm{dom}}\widetilde{B}=\mathcal {H}$. It then follows from [10, Corollary 25.5] that

$$\begin{aligned} \widetilde{A}+\widetilde{B}= A+B-(\alpha _A+\alpha _B){\mathrm{Id}}, \end{aligned}$$

is maximally monotone. Hence, $A+B$ is maximally $(\alpha _A+\alpha _B)$-monotone. The remaining assertion follows from Proposition 1, since

$$\begin{aligned} 1+\frac{\theta }{\sigma _A+\sigma _B}(\alpha _A+\alpha _B)>0, \end{aligned}$$

by Assumption 1. $\square$

Recall that a sequence $(x_k)\subseteq \mathcal {H}$ converges linearly to $x\in \mathcal {H}$ if $\limsup _{k\rightarrow \infty }\frac{\Vert x_{k+1}-x\Vert }{\Vert x_k-x\Vert }<1$.

Theorem 2

(Forward-backward method) Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally $\alpha _A$-monotone and let $\gamma ,\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$. Suppose one of the following holds:

• (i) $B:\mathcal {H}\rightarrow \mathcal {H}$ is $\alpha _B$-monotone and $\kappa$-Lipschitz and $\gamma \in {\bigl ]0,\frac{2(\theta \alpha _B+\sigma _B)}{(\theta \kappa +\sigma _B)^2}\bigr [}$.

• (ii) $B:\mathcal {H}\rightarrow \mathcal {H}$ is $\beta$-cocoercive for $\beta >0$ and $\gamma \in {\bigl ]0,\frac{2\beta }{\theta +\beta \sigma _B}\bigr [}$. In this case, set $\alpha _B:=0$.

Suppose that Assumption 1 holds. For any initial point $x_0\in \mathcal {H}$, consider the sequence $(x_k)$ given by

$$\begin{aligned} x_{k+1} = J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A}\left( (1-\gamma \sigma _B)x_k-\gamma \theta B(x_k)+\gamma (\sigma _A+\sigma _B)q\right) \right) ,\quad \forall k\in \mathbb {N}. \end{aligned}$$

(11)

Then $(x_k)$ converges linearly to $J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)$.

Proof

According to Proposition 2, $(A_{-q})^{(\theta ,\sigma _A)}$ is maximally $(\theta \alpha _A+\sigma _A)$-strongly monotone and $J_{\gamma A_{-q}^{(\theta ,\sigma _A)}}$ is single-valued with full domain. For the operator $(B_{-q})^{(\theta ,\sigma _B)}$, we distinguish two cases which correspond to (i) and (ii), respectively.

• (i) By Proposition 2(i), $(B_{-q})^{(\theta ,\sigma _B)}$ is $(\theta \alpha _B+\sigma _B)$-strongly monotone. Since B is $\kappa$-Lipschitz, Theorem 1(i) implies that $(B_{-q})^{(\theta ,\sigma _B)}$ is $(\kappa \theta +\sigma _B)$-Lipschitz. In this setting, we assume that $\gamma < \frac{2(\theta \alpha _B+\sigma _B)}{(\kappa \theta +\sigma _B)^2}$.

• (ii) Since B is $\beta$-cocoercive, it is monotone; i.e., $\alpha _B$-monotone for $\alpha _B=0$. Moreover, since $\sigma _B>0$, Theorem 1(iii) shows that $(B_{-q})^{(\theta ,\sigma _B)}$ is $\mu$-cocoercive for $\mu :=(\theta /\beta +\sigma _B)^{-1}$. In this setting, we assume that $\gamma <2\mu =\frac{2\beta }{\theta +\beta \sigma _B}$.

Now, let $y_0:=\frac{1}{\theta }(x_0-q)$ and let $(y_k)$ be the sequence generated according to

$$\begin{aligned} y_{k+1} = J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}\left( y_k-\gamma (B_{-q})^{(\theta ,\sigma _B)}(y_k)\right) ,\quad \forall k\in \mathbb {N}. \end{aligned}$$

(12)

In both of the above settings, [10, Proposition 26.16] shows that $(y_k)$ converges linearly to the unique element in ${\mathrm{zer}}\left( (A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}\right)$ which, by Proposition 3, is equal to $\frac{1}{\theta }(J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)-q)$. By setting $x_k:=\theta y_k+q$ for all $k\in \mathbb {N}$ and using Proposition 2(ii), one obtains (11) from (12). It follows that $(x_k)$ is given by (11) and converges linearly to $J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)$. $\square$

Remark 7

Consider the setting of Theorem 2(i). $B^{(\theta ,-\theta \alpha _B)}=B^{(\theta ,\sigma _B)}-(\theta \alpha _B+\sigma _B){\mathrm{Id}}$ is $\theta (\kappa +|\alpha _B|)$-Lipschitz continuous by Theorem 1(i). In this setting, Chen and Rockafellar [25, Theorem 2.4] proved that $(x_k)$ converges linearly when $\gamma >0$ satisfies

$$\begin{aligned} \gamma ^{-1} > \frac{\theta (\alpha _B-\alpha _A)+\sigma _B-\sigma _A}{2}+\frac{\theta (\kappa +|\alpha _B|)}{2}\max \left\{ 1,\frac{\theta (\kappa +|\alpha _B|)}{\theta (\alpha _B+\alpha _A)+\sigma _B+\sigma _A}\right\} . \end{aligned}$$

Theorem 3

(Forward-backward-forward method) Let $A:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally $\alpha _A$-monotone, and let $B:\mathcal {H}\rightarrow \mathcal {H}$ be $\alpha _B$-monotone and $\kappa$-Lipschitz. Let $\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$ be such that Assumption 1 holds and let $\gamma \in {]0,\frac{1}{\theta \kappa +\sigma _B}[}$. For any initial point $x_0\in \mathcal {H}$, consider the sequence $(x_k)$ given by

$$\begin{aligned} \left\{ \begin{aligned} y_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A}\left( (1-\gamma \sigma _B)x_k-\gamma \theta B(x_k)+\gamma (\sigma _A+\sigma _B)q\right) \right) \\ x_{k+1}&= (1-\gamma \sigma _B)y_k +\gamma \sigma _Bx_k -\gamma \theta B(y_k) + \gamma \theta B(x_k). \end{aligned}\right. \end{aligned}$$

(13)

Then $(x_k)$ converges linearly to $J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)$.

Proof

The proof is similar to Theorem 2(i) but uses [55, Theorem 3.4(c)] in place of [10, Proposition 26.16]. Indeed, let $u_0:=\frac{1}{\theta }(x_0-q)$ and consider the sequence $(u_k)$ given by

$$\begin{aligned} \left\{ \begin{aligned} v_{k}&= J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}\left( u_k-\gamma (B_{-q})^{(\theta ,\sigma _B)}(u_k)\right) \\ u_{k+1}&= v_k -\gamma (B_{-q})^{(\theta ,\sigma _B)}(v_k) + \gamma (B_{-q})^{(\theta ,\sigma _B)}(u_k). \end{aligned}\right. \end{aligned}$$

(14)

Since $(B_{-q})^{(\theta ,\sigma _B)}$ is $(\theta \kappa +\sigma _B)$-Lipschitz, applying [55, Theorem 3.4(c)] (or [10, Theorem 26.17]) shows that $(u_k)$ converges linearly to the unique element of ${\mathrm{zer}}\left( (A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}\right)$ which is equal to $\frac{1}{\theta }(J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)-q)$. By Proposition 2(ii), we deduce that

$$\begin{aligned} \left\{ \begin{aligned} \theta v_{k} +q&= J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A}\left( (1-\gamma \sigma _B)(\theta u_k+q)-\gamma \theta B(\theta u_k+q)+\gamma (\sigma _A+\sigma _B)q\right) \right) \\ \theta u_{k+1} +q&= (1-\gamma \sigma _B)(\theta v_k+q)+\gamma \sigma _B(\theta u_k+q) -\gamma \theta B(\theta v_k+q) + \gamma \theta B(\theta u_k+q). \end{aligned}\right. \end{aligned}$$

By setting $(x_k,y_k):=(\theta u_k+q,\theta v_k+q)$, we obtain (13) and deduce that $(x_k)$ converges linearly to $J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)$. $\square$

Remark 8

Weak converge of the algorithm in Theorem 3 can still be obtained if we assume the restrictions on the parameters in (10) instead of Assumption 1. Indeed, as stated in Remark 6, $(A_{-q})^{(\theta ,\sigma _A)}$ is maximally monotone, while $(B_{-q})^{(\theta ,\sigma _B)}$ remains $(\theta \kappa +\sigma _B)$-Lipschitz. Therefore, by applying [10, Theorem 26.17(ii)], we obtain that the sequence $(u_k)$ generated by (14) converges weakly to a zero of $(A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}$, provided that this set of zeros is nonempty, or equivalently, if $q\in {\mathrm{ran}}({\mathrm{Id}}+\frac{\theta }{\sigma _A+\sigma _B}(A+B))$. Observe that the latter automatically holds under Assumption 1, in view of Lemma 1.

The following result concerns a strengthened version of the adaptive Golden Ratio Algorithm (GRAAL) for variational inequalities.

Theorem 4

(Adaptive GRAAL) Suppose $\dim \mathcal {H}<+\infty$. Let $g:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and $\alpha _A$-convex, and let $B:\mathcal {H}\rightarrow \mathcal {H}$ be $\alpha _B$-monotone and locally Lipschitz continuous. Let $\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$ be such that Assumption 1 holds. Choose $x_0,x_1\in \mathcal {H}$, $\gamma _0,\overline{\gamma }\in \mathbb {R}_{++}$, $\phi \in \bigl ]1,\frac{1+\sqrt{5}}{2}\bigr ]$. Set $\bar{x}_0=x_1$, $\gamma _{-1}=\phi \gamma _0$ and $\rho =\frac{1}{\phi }+\frac{1}{\phi ^2}$. For $k\ge 1$, consider

$$\begin{aligned} \left\{ \begin{aligned} \gamma _k&= \min \left\{ \rho \gamma _{k-1},\frac{\phi ^2}{4\gamma _{k-2}}\frac{\Vert x_k-x_{k-1}\Vert ^2}{\Vert \theta \bigl (B(x_k)-B(x_{k-1})\bigr )+\sigma _B(x_k-x_{k-1})\Vert ^2},\overline{\gamma }\right\} \\ \bar{x}_k&= \frac{(\phi -1)x_k+\bar{x}_{k-1}}{\phi } \\ x_{k+1}&={\mathrm{prox}}_{\frac{\gamma _k\theta }{1+\gamma _k\sigma _A}g}\left( \frac{1}{1+\gamma _k\sigma _A}\left( \bar{x}_k-\gamma _k\sigma _B x_k-\gamma _k \theta B(x_k)+\gamma _k(\sigma _A+\sigma _B)q\right) \right) . \end{aligned}\right. \end{aligned}$$

(15)

Then $(x_k)$ and $(\bar{x}_k)$ converge to $J_{\frac{\theta }{\sigma _A+\sigma _B}(\partial g+B)}(q)$.

Proof

The proof is similar to Theorem 2(i) with [39, Theorem 2] applied. To this end, set $\bar{g}(z):=\frac{1}{\theta }g(\theta z+q)+\frac{\sigma _A}{2}\Vert z\Vert ^2$ and $F:=(B_{-q})^{(\theta ,\sigma _B)}$. Since g is proper, lsc and $\alpha _A$-convex, $\partial \bar{g}=((\partial g)_{-q})^{(\theta ,\sigma _A)}$ is maximally $(\theta \alpha _A+\sigma _A)$-monotone by Proposition 2(i) (see also Example 2(i) and Remark 3). Note also that since B is locally Lipschitz, so is F by Theorem 1(ii). Now, consider the variational inequality

$$\begin{aligned} \text {find }z^*\in \mathcal {H}\text { such that }\langle F(z),z-z^*\rangle +\bar{g}(z)-\bar{g}(z^*)\ge 0\quad \forall z\in \mathcal {H}, \end{aligned}$$

which is equivalent to finding a point $z^*\in {\mathrm{zer}}(\partial \bar{g}+F)$ (which is nonempty by Proposition 3 and Lemma 1). Set $(z_0,z_1):=\frac{1}{\theta }(x_0-q,x_1-q)$ and $\bar{z}_0=z_1$. Consider the sequences generated by

$$\begin{aligned} \left\{ \begin{aligned} \gamma _k&= \min \left\{ \rho \gamma _{k-1},\frac{\phi ^2}{4\gamma _{k-2}}\frac{\Vert z_k-z_{k-1}\Vert ^2}{\Vert F(z_k)-F(z_{k-1})\Vert ^2},\overline{\gamma }\right\} \\ \bar{z}_k&= \frac{(\phi -1)z_k+\bar{z}_{k-1}}{\phi } \\ z_{k+1}&= {\mathrm{prox}}_{\gamma _k\bar{g}}\bigl ( \bar{z}_k-\gamma _kF(z_k) \bigr ). \end{aligned}\right. \end{aligned}$$

(16)

Then, according to [39, Theorem 2], $(z_k)$ and $(\bar{z}_k)$ converge to a point $z^*\in {\mathrm{zer}}(\partial \bar{g}+F)$. Since ${\mathrm{prox}}_{\gamma _k\bar{g}}=J_{\gamma _k\partial \bar{g}}$ by Example 2(i), Proposition 2(ii) gives

$$\begin{aligned} z_{k+1}&=\frac{1}{\theta }\left( {\mathrm{prox}}_{\frac{\gamma _k\theta }{1+\gamma _k\sigma _A}g}\left( \frac{\theta }{1+\gamma _k\sigma _A}\left( \bar{z}_k-\gamma _k B(\theta z_k+q)-\gamma _k\sigma _Bz_k\right) +q\right) -q\right) . \end{aligned}$$

Setting $(x_k,\bar{x}_k):=(\theta z_k+q,\theta \bar{z}_k+q)$ in (16) gives (15). It follows that $(x_k)$ and $(\bar{x}_k)$ converge to $x^*:=\theta z^*+q$ and $x^*=J_{\frac{\theta }{\sigma _A+\sigma _B}(\partial g+B)}(q)$, by Proposition 3. $\square$

Theorem 5

(Primal-dual method) Suppose $\dim \mathcal {H}<+\infty$ and $\dim \mathcal {H}'<+\infty$. Let $\sigma >0$, $g:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and $(-\sigma )$-convex, $\phi :\mathcal {H}'\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and convex, and $K:\mathcal {H}\rightarrow \mathcal {H}'$ be a linear operator. Suppose $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{1}{\sigma }(\partial g+K^*\circ \partial \phi \circ K)\right)$. Choose $(x_0,y_0)\in \mathcal {H}\times \mathcal {H}', \lambda \in [0,1]$ and $\gamma ,\tau >0$ such that $\gamma \tau \Vert K\Vert ^2<1$. Set $\bar{x}_0:=x_0$ and, for $k\ge 1$, consider

$$\begin{aligned} \left\{ \begin{aligned} y_{k+1}&= {\mathrm{prox}}_{\gamma \phi ^*}\bigl (y_k+\gamma K\bar{x}_k\bigr ) \\ x_{k+1}&= {\mathrm{prox}}_{\frac{\tau }{1+\tau \sigma }g}\left( \frac{1}{1+\tau \sigma }(x_k-\tau K^*y_{k+1}+\tau \sigma q)\right) \\ \bar{x}_{k+1}&= x_{k+1}+\lambda \bigl (x_{k+1}-x_k\bigr ). \\ \end{aligned}\right. \end{aligned}$$

(17)

Then $(x_k)$ and $(\bar{x}_k)$ converge to ${\mathrm{prox}}_{\frac{1}{\sigma }(g+\phi \circ K)}(q)$.

Proof

Denote $\bar{g}(x):=g(x)+\frac{\sigma }{2}\Vert x-q\Vert ^2$. Then $\bar{g}$ is convex and

$$\begin{aligned} \partial \bar{g} = \partial g+\sigma ({\mathrm{Id}}-q) = (\partial g_{-q})^{(1,\sigma )}\circ ({\mathrm{Id}}-q). \end{aligned}$$

Since $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{1}{\sigma }(\partial g+K^*\circ \partial \phi \circ K)\right)$, there exist points $(x,y)\in \mathcal {H}\times \mathcal {H}'$ such that

$$\begin{aligned} \left\{ \begin{array}{rl} 0 &{}\in \partial \bar{g}(x)+K^*y \\ y &{}\in \partial \phi (Kx) \\ \end{array}\right. \iff \left\{ \begin{array}{rl} -K^*y &{}\in \partial \bar{g}(x) \\ Kx &{}\in (\partial \phi )^{-1}(y)=\partial \phi ^*(y). \\ \end{array}\right. \end{aligned}$$

(18)

Using [24, Theorem 1], we deduce that the sequences $(x_k)$ and $(y_k)$ given by

$$\begin{aligned} \left\{ \begin{aligned} y_{k+1}&= {\mathrm{prox}}_{\gamma \phi ^*}\bigl (y_k+\gamma K\bar{x}_k\bigr ) \\ x_{k+1}&= {\mathrm{prox}}_{\tau \bar{g}}\bigl (x_k-\tau K^*y_{k+1}\bigr ) \\ \bar{x}_{k+1}&= x_{k+1}+\lambda \bigl (x_{k+1}-x_k\bigr ) \\ \end{aligned}\right. \end{aligned}$$

(19)

converge to points $x\in \mathcal {H}$ and $y\in \mathcal {H}'$, respectively, which satisfy (18). Moreover, we also have $x=J_{\frac{1}{\sigma }(\partial g+K^*\circ \partial \phi \circ K)}(q)={\mathrm{prox}}_{\frac{1}{\sigma }(g+\phi \circ K)}(q).$ By applying [10, Proposition 23.17(iii)] followed by Proposition 2(ii), we obtain

$$\begin{aligned} {\mathrm{prox}}_{\tau \bar{g}}=J_{\tau (\partial g_{-q})^{(1,\sigma )}\circ ({\mathrm{Id}}-q)}&= q+J_{\tau (\partial g_{-q})^{(1,\sigma )}}\circ ({\mathrm{Id}}-q) \\&= q+J_{\frac{\tau }{1+\tau \sigma }\partial g}\circ \left( \frac{1}{1+\tau \sigma }{\mathrm{Id}}+q\right) \circ ({\mathrm{Id}}-q)-q \\&={\mathrm{prox}}_{\frac{\tau }{1+\tau \sigma }g}\circ \left( \frac{1}{1+\tau \sigma }\left( {\mathrm{Id}}+\tau \sigma q\right) \right) . \end{aligned}$$

Substituting this expression into (19) gives (17), and the claimed result follows. $\square$

Remark 9

The assumption $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{1}{\sigma }(\partial g+K^*\circ \partial \phi \circ K)\right)$ in Theorem 5 holds under standard constraint qualifications (e.g., $K{\mathrm{dom}}g\cap {\text {cont}}\phi \ne \emptyset$, where ${\text {cont}}\phi$ denotes set of points where $\phi$ is continuous). Indeed, we have $x={\mathrm{prox}}_{\frac{1}{\sigma }(g+\phi \circ K)}(q) \iff 0\in x-q+\frac{1}{\sigma }\partial (g+\phi \circ K)(x).$ When the subdifferential sum-rule holds, the latter is equivalent to $0\in x-q+\frac{1}{\sigma }\bigl (\partial g(x)+K^*\circ \partial \phi (Kx)\bigr )$, which implies $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{1}{\sigma }(\partial g+K^*\circ \partial \phi \circ K)\right)$.

Remark 10

Using the framework devised in this section, several other algorithms of forward-backward-type for finding the resolvent of the sum of two monotone operators can be derived. Examples of addition algorithms for general monotone operators include those based on shadow Douglas–Rachford splitting [29], forward reflected backward splitting [40], reflected forward-backward splitting [23], projective splitting with forward steps [36], three-operator splitting [32], the forward-Douglas–Rachford method [53], and the backward-forward-reflected-backward method [47]. Furthermore, in the special case where the operator A is the normal cone to a convex set, algorithms based on Korpelevich’s and on Popov’s extragradient methods [37, 46], respectively, can also be derived.

5 Resolvent iterations

In this section, we focus on the problem of computing

$$\begin{aligned} J_{\omega (A+B)}(q), \end{aligned}$$

(20)

for some given $q\in \mathcal {H}$ and $\omega >0$, where $A:\mathcal {H}\rightrightarrows \mathcal {H}$ is maximally $\alpha _A$-monotone and $B:\mathcal {H}\rightrightarrows \mathcal {H}$ is maximally $\alpha _B$-monotone. In this situation, we will assume that we have access to the resolvents of both A and B. We will also consider the extension to three operators, that is, the problem of computing

$$\begin{aligned} J_{\omega (A+B+C)}(q), \end{aligned}$$

(21)

where, in addition, $C:\mathcal {H}\rightrightarrows \mathcal {H}$ is maximally $\alpha _C$-monotone.

The following assumption is a variant of Assumption 1 with operator B (potentially) set-valued, rather than single-valued.

Assumption 2

Let $\alpha _A,\alpha _B\in \mathbb {R}$ denote the monotonicity constants associated with the operators A and B in (20), respectively. Suppose $\theta >0$ and $\sigma =(\sigma _A,\sigma _B)\in \mathbb {R}_{++}^2$ satisfy

$$\begin{aligned} \theta \alpha _A+\sigma _A>0\quad \text {and}\quad \theta \alpha _B+\sigma _B>0. \end{aligned}$$

Theorem 6

(Douglas/Peaceman–Rachford algorithm) Let $A,B:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally $\alpha _A$-monotone and maximally $\alpha _B$-monotone, respectively. Let $\theta ,\sigma _A,\sigma _B\in \mathbb {R}_{++}$ be such that Assumption 2 holds, let $\gamma >0$, let $\lambda \in {]0,2]}$ and let $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\theta }{\sigma _A+\sigma _B}(A+B)\right)$. Given any arbitrary $x_0\in \mathcal {H}$, consider the sequences generated by

$$\begin{aligned} \left\{ \begin{aligned} u_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A}(x_k+\gamma \sigma _Aq)\right) \\ v_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _B}B}\left( \frac{1}{1+\gamma \sigma _B}(2u_k- x_k+\gamma \sigma _Bq)\right) \\ x_{k+1}&= x_k + \lambda (v_k-u_k). \\ \end{aligned}\right. \end{aligned}$$

(22)

Then $u_k\rightarrow J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)$ and $x_k\rightharpoonup x$ with

$$\begin{aligned} J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A}(x+\gamma \sigma _Aq)\right) =J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q). \end{aligned}$$

Proof

Set $\bar{x}_0:=\frac{1}{\theta }(x_0-q)$ and consider the sequences

$$\begin{aligned} \left\{ \begin{aligned} \bar{u}_k&= J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}(\bar{x}_k) \\ \bar{v}_k&= J_{\gamma (B_{-q})^{(\theta ,\sigma _B)}}(2\bar{u}_k-\bar{x}_k) \\ \bar{x}_{k+1}&= \bar{x}_k + \lambda (\bar{v}_k-\bar{u}_k). \\ \end{aligned}\right. \end{aligned}$$

(23)

We distinguish two cases based on the value of $\lambda$. First, suppose that $\lambda \in {]0,2[}$. By combining [10, Theorem 26.11] with Proposition 3, we get that $\bar{x}_k\rightharpoonup \bar{x}$ and $\bar{u}_k\rightarrow \bar{u}$ with

$$\begin{aligned} \bar{u}= & {} J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}(\bar{x})\in {\mathrm{zer}}\left( (A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}\right) \\= & {} \left\{ \frac{1}{\theta }\left( J_{\frac{\theta }{\sigma _A+\sigma _B}(A+B)}(q)-q\right) \right\} . \end{aligned}$$

Here the strong convergence of $(\bar{u}_k)$ comes from [10, Theorem 26.11(vi)] and the fact that both $(A_{-q})^{(\theta ,\sigma _A)}$ and $(B_{-q})^{(\theta ,\sigma _B)}$ are strongly monotone by Proposition 2(i). Now, using Proposition 2(ii) and making the change of variables $(x_k,u_k,v_k):=(\theta \bar{x}_k+q,\theta \bar{u}_k+q,\theta \bar{v}_k+q)$, $u:=\theta {\bar{u}}+q$ and $x:=\theta \bar{x}+q$ the iteration in (23) reduces to (22) and the result follows.

Next, consider the limiting case where $\lambda =2$. Observe that (23) can be expressed as

$$\begin{aligned} \bar{x}_{k+1} = \left( 2J_{\gamma (B_{-q})^{(\theta ,\sigma _B)}}-{\mathrm{Id}}\right) \circ \left( 2J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}} -{\mathrm{Id}}\right) (\bar{x}_k). \end{aligned}$$

(24)

Since $(A_{-q})^{(\theta ,\sigma _A)}$ and $(B_{-q})^{(\theta ,\sigma _B)}$ are maximally strongly monotone, their reflected resolvents,

$$\begin{aligned} 2J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}-{\mathrm{Id}}\quad \text {and}\quad 2J_{\gamma (B_{-q})^{(\theta ,\sigma _B)}}-{\mathrm{Id}}, \end{aligned}$$

are negatively averaged by [34, Proposition 5.4]. Their composition is therefore averaged by [34, Proposition 3.12 and Remark 3.13]. Thus, according to [10, Proposition 5.16], the sequence $(\bar{x}_k)$ generated by (24) weakly converges to a fixed point of the composition of the reflected resolvents. The strong convergence of the shadow sequence $(\bar{u}_k)$ is a consequence of [10, Proposition 26.13]. Finally, by making a change of variables as in the case $\lambda \in {]0,2[}$, the result follows. $\square$

Remark 11

Theorem 6 was established in [31, Theorem 3.2], with the exception of the weak convergence of $(x_k)$ in the case $\lambda =2$. As we now explain, it covers the following two schemes from the literature as special cases. In both settings, we assume that A and B are maximally monotone operators and that $\alpha _A=\alpha _B=0$.

• (i) Set $\theta :=\frac{1}{\beta }$ and $\sigma _A=\sigma _B:=\frac{1-\beta }{\gamma \beta }$ for any $\beta \in {]0,1[}$. Then (22) becomes

  $$\begin{aligned} \left\{ \begin{aligned} u_k&= J_{\gamma A}\left( \beta x_k + (1-\beta )q\right) \\ v_k&= J_{\gamma B}\left( \beta (2u_k-x_k)+(1-\beta )q\right) \\ x_{k+1}&= \left( 1-\frac{\lambda }{2}\right) x_k + \frac{\lambda }{2}(2v_k-2u_k+x_k). \\ \end{aligned}\right. \end{aligned}$$

  By taking $y_k:=\beta (x_k-q)$ and $\kappa :=\frac{\lambda }{2}\in {]0,1[}$, this can be rewritten as

  $$\begin{aligned} y_{k+1}=(1-\kappa )y_k+\kappa (2\beta J_{(\gamma B_{-q})}-{\mathrm{Id}})(2\beta J_{(\gamma A_{-q})}-{\mathrm{Id}})(y_k), \end{aligned}$$

  which coincides with the Averaged Alternating Modified Reflections (AAMR) algorithm developed in [7].

• (ii) Let $\lambda =2$, $\sigma _A=\sigma _B$, $\gamma =\frac{1}{\sigma _A}$, and $\theta =2\sigma _A$. By denoting $z_k:=\frac{1}{2}(x_k+q)$, (22) can be written as

  $$\begin{aligned} x_{k+1}&=x_k-2J_A(z_k)+2J_B\left( J_A(z_k)-\frac{1}{2}x_k+\frac{1}{2}q\right) \\&=2z_k-q-2J_A(z_k)+2J_B\left( J_A(z_k)-z_k+q\right) , \end{aligned}$$

  which is equivalent to

  $$\begin{aligned} z_{k+1}=z_k-J_A(z_k)+J_B\left( J_A(z_k)-z_k+q\right) . \end{aligned}$$

  This coincides with the variant of the Douglas–Rachford algorithm proposed in [1], where it is referred to as “Algorithm $(\mathcal {A})$”. While Adly and Bourdin proved weak convergence of $(z_k)$ to a point $z\in ({\mathrm{Id}}+B\circ J_A)^{-1}(q)$, they only established weak convergence of $(J_A(z_k))$ to $J_A(z)\in J_{A+B}(q)$ (see [1, Theorem 3]). In addition to weak convergence of $(z_k)$, Theorem 6 shows that $(J_A(z_k))$ is actually strongly convergent to $J_{A+B}(q)$.

$\square$

We now derive a splitting method for computing the resolvent of the sum of three operators based on the scheme proposed by Ryu in [52, Section 4] for finding a zero of the sum. We provide a direct proof of its convergence in the infinite dimensional setting in the Appendix, which also provides new conditions ensuring the convergence of the limiting case $\lambda =1$.

The following assumption is the three operator analogue of Assumption 2.

Assumption 3

Let $\alpha _A,\alpha _B,\alpha _C\in \mathbb {R}$ denote the monotonicity constants associated with the operators A, B and C in (21), respectively. Suppose $\theta >0$ and $\sigma =(\sigma _A,\sigma _B,\sigma _C)\in \mathbb {R}_{+}^3$ satisfy

$$\begin{aligned} \theta \alpha _A+\sigma _A>0,\quad \theta \alpha _B+\sigma _B>0,\quad \theta \alpha _C+\sigma _C>0. \end{aligned}$$

Remark 12

As was the case in Remark 6, for any $\alpha _A,\alpha _B,\alpha _C\in \mathbb {R}$, there always exist $\theta ,\sigma _A,\sigma _B,\sigma _C\in \mathbb {R}_{++}$ satisfying Assumption 3. Thus, Assumption 3 does not induce any restrictions on the operators A, B and C in (21), but it may restrict the values of $\omega$ for which the resolvent in (21) can be computed if $\alpha _A$, $\alpha _B$ or $\alpha _C$ is negative. When A, B and C are monotone (i.e., when $\alpha =(\alpha _A,\alpha _B,\alpha _C)\in \mathbb {R}^3_{+})$, Assumption 3 trivially holds.

Theorem 7

(Ryu splitting) Let $A,B,C:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally $\alpha _A$-monotone, maximally $\alpha _B$-monotone, and maximally $\alpha _C$-monotone, respectively. Let $\theta ,\sigma _A,\sigma _B,\sigma _C\in \mathbb {R}_{++}$ be such that Assumption 3 holds, let $\gamma >0$, and let $\lambda \in {]0,1]}$. Suppose $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\gamma \theta }{\sigma _A+\sigma _B+\sigma _C}(A+B+C)\right)$. Given any $x_0,y_0\in \mathcal {H}$, consider the sequences

$$\begin{aligned} \left\{ \begin{aligned} u_k&= J_{\frac{\gamma \theta }{1+\sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A} x_k+\frac{\gamma \sigma _A}{1+\gamma \sigma _A}q \right) \\ v_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _B}B}\left( \frac{1}{1+\gamma \sigma _B}(u_k+y_k)-\frac{1-\gamma \sigma _B}{1+\gamma \sigma _B}q\right) \\ w_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _C}C}\left( \frac{1}{1+\gamma \sigma _C}(u_k-x_k+v_k-y_k)+q \right) \\ x_{k+1}&= x_k + \lambda (w_k-u_k) \\ y_{k+1}&= y_k + \lambda (w_k-v_k). \end{aligned}\right. \end{aligned}$$

(25)

Then $u_k\rightarrow J_{\frac{\theta }{\sigma _A+\sigma _B+\sigma _C}(A+B+C)}(q)$ as $k\rightarrow +\infty$. Further, if $\lambda \ne 1$, then $x_k\rightharpoonup x$ with

$$\begin{aligned} J_{\frac{\gamma }{1+\gamma \sigma _A}A} \left( \frac{1}{1+\gamma \sigma _A}x+\frac{\gamma \sigma _A}{1+\gamma \sigma _A}q\right) =J_{\frac{\theta }{\sigma _A+\sigma _B+\sigma _C}(A+B+C)}(q). \end{aligned}$$

Proof

Set $(\bar{x}_0,\bar{y}_0):=\frac{1}{\theta }(x_0-q,y_0-q)$ and consider the sequences

$$\begin{aligned} \left\{ \begin{aligned} \bar{u}_k&= J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}(\bar{x}_k) \\ \bar{v}_k&= J_{\gamma (B_{-q})^{(\theta ,\sigma _B)}}(\bar{u}_k+\bar{y}_k) \\ \bar{w}_k&= J_{\gamma (C_{-q})^{(\theta ,\sigma _C)}}(\bar{u}_k-\bar{x}_k+\bar{v}_k-\bar{y}_k) \\ \bar{x}_{k+1}&= \bar{x}_k + \lambda (\bar{w}_k-\bar{u}_k) \\ \bar{y}_{k+1}&= \bar{y}_k + \lambda (\bar{w}_k-\bar{v}_k). \end{aligned}\right. \end{aligned}$$

(26)

By Assumption 3, the sum $(A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}+ (C_{-q})^{(\theta ,\sigma _C)}$ is $\alpha$-strongly monotone for $\alpha := \bigl (\theta \alpha _A+\sigma _A\bigr )+\bigl (\theta \alpha _B+\sigma _B\bigr )+\bigl (\theta \alpha _C+\sigma _C\bigr )>0$. By assumption $q\in {\mathrm{ran}}\left( {\mathrm{Id}}+\frac{\gamma \theta }{\sigma _A+\sigma _B+\sigma _C}(A+B+C)\right)$ and hence Proposition 3 implies

$$\begin{aligned} {\mathrm{zer}}\left( (A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}+(C_{-q})^{(\theta ,\sigma _C)}\right) =\left\{ \frac{1}{\theta }\left( J_{\frac{\theta }{\sigma _A+\sigma _B+\sigma _C}(A+B+C)}(q)-q\right) \right\} . \end{aligned}$$

Appealing to Theorem 8(ii) gives $u_k\rightarrow \bar{u}$, where

$$\begin{aligned} \bar{u}\in {\mathrm{zer}}\left( ( A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}+(C_{-q})^{(\theta ,\sigma _C)}\right) . \end{aligned}$$

Further, if $\lambda \in {]0,1[}$, then Theorem 8(i) gives $(\bar{x}_k,\bar{y}_k)\rightharpoonup (\bar{x},\bar{y})$ where $\bar{x}$ satisfies

$$\begin{aligned} \bar{u}:=J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}(\bar{x})\in {\mathrm{zer}}\left( ( A_{-q})^{(\theta ,\sigma _A)}+(B_{-q})^{(\theta ,\sigma _B)}+(C_{-q})^{(\theta ,\sigma _C)}\right) . \end{aligned}$$

Finally, by applying Proposition 2(ii), we may write (26) as

$$\begin{aligned} \left\{ \begin{aligned} \theta \bar{u}_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _A}A}\left( \frac{\theta }{1+\gamma \sigma _A} \bar{x}_k + q\right) -q \\ \theta \bar{v}_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _B}B}\left( \frac{\theta }{1+\gamma \sigma _B}(\bar{u}_k+\bar{y}_k)+q\right) -q \\ \theta \bar{w}_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _C}C}\left( \frac{\theta }{1+\gamma \sigma _C}(\bar{u}_k-\bar{x}_k+\bar{v}_k-\bar{y}_k)+q\right) -q \end{aligned}\right. \end{aligned}$$

and $\theta J_{\gamma (A_{-q})^{(\theta ,\sigma _A)}}(\bar{x})=J_{\frac{\gamma }{1+\gamma \sigma _A}A} \left( \frac{\theta }{1+\gamma \sigma _A}\bar{x}+q\right) -q$. The claimed result follows by making the change of variables $(x_k,y_k,u_k,v_k,w_k):=(\theta \bar{x}_k+q,\theta \bar{y}_k+q,\theta \bar{u}_k+q,\theta \bar{v}_k+q,\theta \bar{w}_k+q)$ for all $k\in \mathbb {N}$ and $(x,u):=(\theta \bar{x}+q,\theta \bar{u}+q)$. $\square$

Remark 13

Consider the case with $B=0$ and $\sigma _B=0$. Although this setting is not covered by Assumption 3 as $\sigma _B\not >0$, it is easily covered by an extension analogous to the one described in Remark 6. In such a case, the sequence $(v_k)$ in (25) simplifies to

$$\begin{aligned} v_k = u_k+y_k-q. \end{aligned}$$

Using this identity to eliminate $(v_k)$ and $(y_k)$ from (25) gives

$$\begin{aligned}\left\{ \begin{aligned} u_k&= J_{\frac{\gamma \theta }{1+\sigma _A}A}\left( \frac{1}{1+\gamma \sigma _A} x_k+\frac{\gamma \sigma _A}{1+\gamma \sigma _A}q \right) \\ w_k&= J_{\frac{\gamma \theta }{1+\gamma \sigma _C}C}\left( \frac{1}{1+\gamma \sigma _C}(2u_k-x_k)+\frac{\gamma \sigma _C}{1+\gamma \sigma _C}q \right) \\ x_{k+1}&= x_k + \lambda (w_k-u_k), \end{aligned}\right. \end{aligned}$$

which coincides with (22) applied to the operators A and C.

6 Applications

In this section, we consider three applications of the framework developed in the previous sections. All computations were run on a machine running Ubuntu 18.04.5 LTS with an Intel Core i7-8665U CPU and 16GB of memory.

6.1 Best approximation problems

Let $C_1,\dots ,C_m\subseteq \mathcal {H}$ be closed and convex sets with $\cap _{i=1}^mC_i\ne \emptyset$. Given a point $q\in \mathcal {H}$, the best approximation problem is

$$\begin{aligned} \min _{x\in \mathcal {H}}\frac{1}{2}\Vert x-q\Vert ^2\text { such that }x\in \bigcap _{i=1}^mC_i, \end{aligned}$$

(27)

which is equivalent to the formally unconstrained problem

$$\begin{aligned} \min _{x\in \mathcal {H}}\frac{1}{2}\Vert x-q\Vert ^2+\sum _{i=1}^m\iota _{C_i}(x). \end{aligned}$$

We therefore see that solving (27) is equivalent to computing the proximity operator of $\sum _{i=1}^m\iota _{C_i}$. Thus, assuming the strong CHIP holds (see Remark 5), the solution x of (27) is given by

$$\begin{aligned} x = J_{\sum _{i=1}^mN_{C_i}}(q)={\mathrm{prox}}_{\sum _{i=1}^m\iota _{C_i}}(q). \end{aligned}$$

Using results from Sect. 5, we obtain the following projection algorithm for best approximation which appears to be new. It will be referred to as S-Ryu (which stands for strengthened-Ryu).

Corollary 3

(Best approximation with three sets – S-Ryu) Let $C_1,C_2,C_3\subseteq \mathcal {H}$ be closed and convex sets with nonempty intersection, and suppose that $q\in {\mathrm{ran}}(I+N_{C_1}+N_{C_2}+N_{C_3})$. Let $\beta \in {]0,1[}$ and $\lambda \in {]0,1]}$. Given any $x_0,y_0\in \mathcal {H}$, consider the sequences

$$\begin{aligned} \left\{ \begin{aligned} u_k&= P_{C_1}\left( \beta x_k+(1-\beta )q \right) \\ v_k&= P_{C_2}\left( \beta (u_k+y_k)-(2\beta -1)q\right) \\ w_k&= P_{C_3}\left( \beta (u_k-x_k+v_k-y_k)+q \right) \\ x_{k+1}&= x_k + \lambda (w_k-u_k) \\ y_{k+1}&= y_k + \lambda (w_k-v_k). \end{aligned}\right. \end{aligned}$$

(28)

Then $u_k\rightarrow u=P_{C_1\cap C_2\cap C_3}(q)$ as $k\rightarrow +\infty$. Furthermore, if $\lambda \ne 1$, then $x_k\rightharpoonup x$ with $P_{C_1}\left( \beta x+(1-\beta )q\right) =u.$

Proof

Set $A=N_{C_1}, B=N_{C_2}, C=N_{C_3}$, $\sigma _A=\sigma _B=\sigma _C=\frac{1-\beta }{\beta }$ and $\gamma =1$ in Theorem 7. $\square$

In order to examine the performance of the algorithm (28) and the effect of the parameters $\beta$ and $\lambda$, we considered the problem of finding the nearest positive semidefinite doubly stochastic matrix with prescribed entries. Denoting by $\varOmega$ the location of the entries that are prescribed and by M the matrix with its values, this problem can be described in terms of three sets:

$$\begin{aligned} C_1&:=\{X\in \mathbb {R}^{n\times n}: Xe=X^Te=e\},\\ C_2&:=\{X\in \mathbb {R}^{n\times n}: X_{ij}\ge 0\text { for }i,j=1,\ldots ,n\text { and }X_{ij}=M_{ij} \text { for all }(i,j)\in \varOmega \},\\ C_3&:=\{X\in \mathbb {R}^{n\times n}: X\text { is positive semidefinite}\}, \end{aligned}$$

where $e=[1,1,\ldots ,1]^T\in \mathbb {R}^n$. The projectors onto these sets have a closed form:

$$\begin{aligned} P_{C_1}(X)&=(I-J)X(I-J)+J,\text { where }J=ee^T/n,\\ P_{C_2}(X)_{ij}&=\left\{ \begin{array}{ll} M_{ij} &{}\text {if }(i,j)\in \varOmega ,\\ \max \{X_{ij},0\}&{}\text {otherwise,} \end{array}\right. \\ P_{C_3}(X)&=\frac{Y+P}{2},\text { where }Y=\frac{X+X^T}{2}\text { and } Y=UP\text { is a polar decomposition}, \end{aligned}$$

for $X=(X_{ij})\in \mathbb {R}^{n\times n}$; see [54, Proposition 4.4] for the formula for $P_{C_1}$ and [35, Theorem 2.1] for the formula $P_{C_3}$. For further details and extensions, see [5, Section 3] and [14].

In our test, we took $\varOmega =\{(1,1)\}$ with $M_{11}=0.25$ (that is, we prescribed the first entry to 0.25). We compared the performance of S-Ryu against Dykstra’s method [20] and AAMR [6]. To this aim, we computed the nearest matrix satisfying the constraints to a symmetric matrix with random entries uniformly distributed in $(-2,2)$. In order to apply Corollary 3, for S-Ryu, or [6, Theorem 5.1], for AAMR, we need to check that the strong CHIP condition holds for $C_1$, $C_2$ and $C_3$ (see Remark 5). A sufficient condition is the nonempty intersection of the relative interiors of the three sets (see, e.g., [49, Corollary 23.8.1]). Since $C_1$ and $C_2$ are affine subspaces, and the relative interior of $C_3$ consists of the positive definite matrices in X (see, e.g., [16, Exercise 5.12]), it suffices to find a positive definite matrix in $C_1\cap C_2$. A possible choice is the matrix

$$\begin{aligned} M:=\frac{0.25n-1}{n-1}I+\frac{0.75}{n-1}ee^T\in C_1\cap C_2. \end{aligned}$$

The matrix M is clearly symmetric and it can be readily checked that its eigenvalues are 1 and $\frac{0.25n-1}{n-1}$ (with multiplicity $n-1$). Hence, M is positive definite as long as $n\ge 5$, which holds for the instances considered here.

For the algorithm implementations in our first test, we took 10 values of $\lambda$ equispaced in [0.7, 1] and $\beta \in \{0.85,0.9,0.95,0.99,0.999\}$. For each pair of values and each $n\in \{25,50,75,100\}$ we generated 20 random matrices in $\mathbb {R}^{n\times n}$. We have represented in Fig. 1 the average time required by each of the algorithms to achieve $\sum _{i=1}^3\Vert U_k-P_{C_i}(U_k)\Vert \le 10^{-5}$ for each pair of parameters. For brevity, we do not include the figures with the iteration count because they produce a similar result. In these numerical results, the fastest algorithm was S-Ryu with parameters $(\beta ,\lambda )=(.99,1)$.

Fig. 1

Comparison of the performance of Dykstra [20], AAMR [6] and S-Ryu (28) for finding the nearest positive semidefinite doubly stochastic matrix with a prescribed entry. For each pair of parameters $(\beta ,\lambda )$ we represent the average time of 20 random instances

We performed a second test for larger matrices, where we fixed the value of $(\beta ,\lambda )$ to (0.99, 1) for S-Ryu and (0.99, 0.95) for AAMR. The results are summarised in Fig. 2. We observe that S-Ryu was consistently 10 times faster than Dykstra and more than 2 times faster than AAMR.

Fig. 2

Comparison of the performance of Dykstra [20], AAMR [6] and S-Ryu (28) for finding the nearest positive semidefinite doubly stochastic matrix with a prescribed entry on 20 random instances. We represent the time and the iterations required by each algorithm with respect to the size, as well as the ratios. (a) Time, (b) Iterations, (c) Time ratio (log. scale), (d) Iterations ratio (in log. scale)

6.2 ROF-type models for image denoising

Let $\phi :\mathcal {H}'\rightarrow {]-\infty ,+\infty ]}$ and $g:\mathcal {H}\rightarrow {]-\infty ,+\infty ]}$ be proper, lsc and convex and let $K:\mathcal {H}\rightarrow \mathcal {H}'$ be a bounded linear operator. Given $q\in \mathcal {H}$ and $\eta >0$, consider the problem

$$\begin{aligned} \min _{x\in \mathcal {H}}\frac{\eta }{2}\Vert x-q\Vert ^2+\phi (Kx)+g(x), \end{aligned}$$

(29)

which is equivalent to computing the proximity operator of $\phi \circ K+g$ (with parameter $1/\eta$) at q. Using the identity $\phi (Kx)=\phi ^{**}(Kx)=\sup _{y\in \mathcal {H}'}\{\langle Kx,y\rangle -\phi ^*(y)\}$, problem (29) may be expressed in saddle-point form as

$$\begin{aligned} \min _{x\in \mathcal {H}}\sup _{y\in \mathcal {H}'}\frac{\eta }{2}\Vert x-q\Vert ^2+\langle Kx,y\rangle -\phi ^*(y)+g(x). \end{aligned}$$

Solutions to this problem (in the sense of saddle-points [48, p. 244]) can be characterised by the operator inclusion

$$\begin{aligned} \left( {\begin{array}{c}q\\ 0\end{array}}\right) \in \left( \begin{pmatrix}{\mathrm{Id}}&{}0\\ 0&{}{\mathrm{Id}}\\ \end{pmatrix} +\left( {\begin{array}{c}\frac{1}{\eta }\partial g\\ \partial \bigl (\frac{1}{\eta }\phi ^*-\frac{1}{2}\Vert \cdot \Vert ^2\bigr )\end{array}}\right) +\frac{1}{\eta }\begin{pmatrix} 0 &{} K^* \\ -K &{} 0 \\ \end{pmatrix}\right) \left( {\begin{array}{c}x\\ y\end{array}}\right) \end{aligned}$$

which is equivalent to $\left( {\begin{array}{c}x\\ y\end{array}}\right) \in J_{A+B}\left( \left( {\begin{array}{c}q\\ 0\end{array}}\right) \right)$ where the operators A and B are given by

$$\begin{aligned} A:=\left( {\begin{array}{c}\frac{1}{\eta }\partial g\\ \partial \bigl (\frac{1}{\eta }\phi ^*-\frac{1}{2}\Vert \cdot \Vert ^2\bigr )\end{array}}\right) ,\quad B:=\frac{1}{\eta }\begin{pmatrix} 0 &{} K^* \\ -K &{} 0 \\ \end{pmatrix}. \end{aligned}$$

(30)

Here we note that the operator A is maximally $\alpha _A$-monotone and B is $\alpha _B$-monotone with $\alpha =(-1,0)$. Thus, by choosing $\sigma _B=0$ and $\theta =\sigma _A>0$, we have $\theta \alpha _A+\sigma _A=\theta \alpha _B+\sigma _B=0$ and so we can ensure that conditions in (10) are satisfied. Hence, in view of Remark 8, the strengthened Tseng’s method (S-Teng) in Theorem 3 converges weakly assuming that a saddle-point for the problem exists.

Let $\mathcal {H}=\mathbb {R}^{n\times n}$ represent the $n\times n$ pixel grayscale images (with pixel values in [0, 1]) and let $\mathcal {H}'=\mathbb {R}^{n\times n}\times \mathbb {R}^{n\times n}$. Then the Rudin–Osher–Fatemi (ROF) model [51] for image denoising can be understood as a particular case of (29) where $\phi (Kx)$ represents the discrete version of the isotropic TV-norm and $g=0$. In this setting, the $K:\mathcal {H}\rightarrow \mathcal {H}'$ denotes the discrete gradient with Lipschitz constant $\sqrt{8}$ and $\phi \bigl (\left( {\begin{array}{c}y^1\\ y^2\end{array}}\right) \bigr )=\sum _{i,j=1}^n\sqrt{ (y^1_{i,j})^2+(y^2_{i,j})^2 }$. For further details, see [24]. A setting with $g\ne 0$ was considered in [26] where it was taken as $g=\iota _C$ for a convex constraint set C. The addition of this constraint set allows a priori information about the image to be incorporated. In this work, we take $C = \{x\in \mathbb {R}^{n\times n}:0\le x\le 1\}$ to encode the bounds on legal pixel values. Also note that, since $\phi$ is continuous on $\mathcal {H}'$, the assumptions of Theorem 5 hold (see also Remark 9).

In order to examine the effect of the varying algorithm parameters on performance, we applied the algorithms presented in Theorems 3 and 5 to the ROF-denoising model with the constraint C via the operator formulation provided by (30) and (29), respectively. The regularisation parameter was chosen by trial and error to be $\eta =12$ (see Fig. 3). The noisy image to be denoised is given by $q\in \mathcal {H}$. For all tests, $\left( {\begin{array}{c}q\\ 0\end{array}}\right) \in \mathcal {H}\times \mathcal {H}'$ was used as the initial point (i.e., the noisy image was used as the initialisation).

Fig. 3

The effect of $\eta$ on the solution of (29)

Figure 4 shows the effect on the signal to noise ratio (SNR) and objective function value after 100 iterations. For the strengthened primal-dual method (S-PD), we examined the effect of changing the dual stepsize, denoted by $\gamma$, with the primal stepsize chosen as $\tau =\frac{0.99}{\gamma \Vert K\Vert ^2}=\frac{0.12375}{\gamma }$ so that the condition $\gamma \tau \Vert K\Vert ^2<1$ holds. The figure suggests $\gamma =15$ as a good choice for S-PD. For the strengthened Tseng’s method (S-Tseng), the stepsize $\gamma$ was chosen to satisfy $\gamma =\frac{0.99}{\theta \kappa +\sigma _B}$ where $\kappa =\sqrt{8}/\eta$ denotes the Lipschitz constant of the operator B. This is equivalent to asserting that $\gamma \sigma _A=\frac{11.88}{\sqrt{8}}$.

Fig. 4

The effect of the dual stepsize, $\gamma$, for S-PD after 100 iterations with the primal stepsize taken to be $\tau =\frac{0.99}{8\gamma }$

Figure 5 also suggests that the strengthened primal-dual method (S-PD) performs slightly better than the strengthened Tseng’s method (S-Tseng). Further computational results for the strengthened primal-dual method applied to four square test images with $n\in \{250,500,750,1000\}$ are shown in Fig. 6. The final change iterates (i.e., $\Vert \left( {\begin{array}{c}x_k\\ y_k\end{array}}\right) -\left( {\begin{array}{c}x_{k-1}\\ y_{k-1}\end{array}}\right) \Vert$), signal-to-noise ratio (SNR), final objective function value, and CPU after $k=100$ iterations can be found in Table 1. Figure 6 also shows a comparison with Chen & Tang’s method using the best performing algorithms parameters as described in [26, Section 5]. The results suggest that the performance of both methods is similar.

Fig. 5

Results after 10, 100, 1000 iterations for the algorithms from Sect. 4 with $\eta =12$, $\gamma =15$, $\tau =\frac{33}{4000}$, $\theta =10.1$ and $\sigma =(10.0,0.1)$. The image (cameraman), with and without additive Gaussian noise, is shown on the right

Fig. 6

Original, noisy and typical de-noised images for the results reported in Table 1

6.3 PDEs with partially blinded laplacians

In this subsection, we consider a problem in elliptic PDEs previously studied in [1, Section 5.2]. To this end, let $\mathcal {H}=\mathcal {L}^2(\varOmega )$ denote the Hilbert space of real (Lebesgue) square-integrable functions defined on a nonempty open subset $\varOmega \subset \mathbb {R}^d$ with a nonempty, bounded and Lipschitz boundary denoted by $\partial \varOmega$. Let $L_+^2(\varOmega )=\{v\in L^2(\varOmega ):v\ge 0\text { a.e. on }\varOmega \}$ and $L^2_\varDelta =\{v\in L^2(\varOmega ):\varDelta v\in L^2(\varOmega )\}$, where $\varDelta$ denotes the Laplace operator. Further, let $H^1_0(\varOmega ):=\{v\in H^1(\varOmega ):v_{|_{\partial \varOmega }}=0\}$, where $H^1(\varOmega )$ denotes the standard Sobolev space of functions having first order distribution derivatives in $L^2(\varOmega )$ and $v_{|_{\partial \varOmega }}$ denotes the trace of v on $\partial \varOmega$ (see, for instance, [4, 21]). Given $u\in \mathcal {H}$, we denote $u^+:=\max \{u,0\}$ and $u^-:=\min \{u,0\}$ which are understood in the pointwise sense.

Let $f\in L^2(\varOmega )$ be fixed. In this subsection, we consider the partially blinded problem with homogeneous Dirichlet boundary condition

$$\begin{aligned} \text {find }u\in L^2(\varOmega )\text { such that }u^+\in H^1_0(\varOmega )\cap L^2_\varDelta (\varOmega )\text { and }-\varDelta (u^+)+u=f, \end{aligned}$$

(31)

as well as the corresponding obstacle problem given by

Table 1 Results for $\eta =12$ after 100 iterations of (left values) S-PD with $\gamma =15$ and (right values) Chen and Tang’s method from [26]. Time is reported as the average from ten replications

$$\begin{aligned} \text {find }v\in L^2(\varOmega )\text { such that }v\in H^1_0(\varOmega )\cap L^2_\varDelta (\varOmega )\text { and }0\le (-\varDelta v+v-f)\perp v\ge 0. \qquad \end{aligned}$$

(32)

As explained in [1], (31) derives its name from the fact that the Laplacian operator is partially blinded in the sense that diffusion only occurs on the nonnegative part of the unknown function u.

The following proposition collects results useful for solving these two problems.

Proposition 4

Let $A:=N_{L^2_+(\varOmega )}$ and let $B:=-\varDelta :H^1_0(\varOmega )\cap L^2_{\varDelta }(\varOmega )\rightarrow L^2(\varOmega )$. Then:

• (i) A, B and $A+B$ are maximally monotone on $L^2(\varOmega )$.

• (ii) Let $g\in L^2(\varOmega )$ and let $\gamma >0$. Then $J_{\gamma A}(g)=g^+$ and $J_{\gamma B}(g)$ is the (unique) solution of linear boundary value problem given by

  $$\begin{aligned} \text {find }w\in L^2(\varOmega )\text { such that }w\in H^1_0(\varOmega )\cap L^2_\varDelta (\varOmega )\text { and }-\varDelta w+\frac{1}{\gamma }w=\frac{1}{\gamma }g. \qquad \qquad \end{aligned}$$

  (33)

• (iii) The unique solution of (31) is given by $u:=\bigl ({\mathrm{Id}}-B\circ J_{A+B}\bigr )(f)$.

• (iv) The unique solution of (32) is given by $v:=J_{A+B}(f)$.

• (v) The functions u and v satisfy $v=u^+$.

Proof

Items (i), (ii), (iv) and (v) appear in the proof of [1, Proposition 5] as well as the claimed uniqueness of the solution to (31) in (iii). The formula for u follows by combining (iv), (v) and (31). $\square$

Proposition 4 shows that to solve either (31) or (32) it suffices to compute the resolvent of $A+B$ at f. Since the resolvent of A and B are both accessible, according to Proposition 4(ii), the strengthened Douglas–Rachford method (S-DR, see Theorem 6) can be applied with $\theta =\sigma _A+\sigma _B$. Observe that the assumption $f\in {\mathrm{ran}}({\mathrm{Id}}+A+B)$ in Theorem 6 is automatically guaranteed, thanks to Proposition 4(i). Note also that, as a simple linear boundary value problem, can be easily implemented using standard finite element method solvers. Following [1], we used the finite element library FreeFem++ with a P1 finite element discretisation.

In our computational tests we set the parameter $\lambda =2$, which appears to be optimal for this problem. This empirical observation is in accordance with [8, Theorem 3.2], which proves that the optimal rate of linear convergence of AAMR when it is applied to two subspaces is attained at $\kappa =\frac{\lambda }{2}=1$ (see also Remark 11). The second pair of parameters we set was $\sigma _A=\sigma _B=0.25$. Observe that the behaviour of the iterative process (22) when $\sigma _A=\sigma _B$ is driven by the parameter $\gamma \sigma _A$, so in order to evaluate the variation of the algorithm’s performance with respect to the parameters, one can either fix $\gamma$ or $\sigma _A$. We did not observe any apparent advantage of choosing $\sigma _A\ne \sigma _B$ in the current setting.

We compared the performance of S-DR for $\gamma \in \{0.1,0.2,\ldots ,4.9,5.0\}$. Recall that for $\gamma =4$ the algorithm coincides with the one proposed by Adly–Bourdin (AB in short) in [1, Proposition 5]), see Remark 11(ii). In our first experiment we used the data function $f(x,y)=xe^{-x^2-y^2}$ with $\varOmega$ the open disk of centre (0, 0) and radius $\frac{3\pi }{2}$, which was tested in [1]. We began by computing with AB an approximate solution $v_{AB}$ to $J_{A+B}(f)$ by running the algorithm for 10000 iterations with a mesh constructed by FreeFem++ with 200 points in the boundary, see Fig. 8a, and b. Then, we ran S-DR for each $\gamma \in \{0.1,0.2,\ldots ,4.9,5\}$. The algorithm was stopped when the norm of the difference between $v_{AB}$ and the current iterate was smaller than a given precision of $10^{-p}$, with $p\in \{5,6,\ldots ,10\}$. The results are summarised in Fig. 7. A value of $\gamma$ between 0.4 and 0.6 appears to be optimal for all tested values of p. In particular, for $\gamma =0.5$ and $p=10$, S-DR was 8 times faster than AB.

Fig. 7

(Left) For each precision $10^{-p}$, we computed the minimum number of iterations among AB and S-DR for each $\gamma \in \{0.1,0.2,\ldots ,4.9,5\}$. The figure is coloured according to the ratio between the number of iterations of each of the methods and that minimum number. (Right) The number of iterations of AB and S-DR for different values of $\gamma$

In our second experiment we used the function

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} -2\left( (10y\pi -5y^2+1)\cos (x)^2-4y\pi +2y^2-1\right) \sin (x), &{} x\le \pi ,\\ (2\pi -y)y\cos (x)^2\sin (x)^3, &{} x>\pi ; \end{array}\right. \end{aligned}$$

(34)

with $\varOmega =(0,2\pi )\times (0,2\pi )$. In this case, the unique solution of (PBP$_{0})$ can be analytically computed and is given by $u(x,y):=(2\pi -y)y\sin (x)^3$, see Fig. 8c and d. Therefore, it is possible to test how good the approximate solution given by each of the algorithm settings is. In Fig. 9 we show the result of running the algorithms for 10000 iterations, again with a mesh with 200 points in the boundary.

Fig. 8

Representation of the data (left) and the solution (right) of two (32) problems. (a) Plot of the data $f(x,y)=xe^{-x^2-y^2}$, (b) For $f(x,y)=xe^{-x^2-y^2}$, plot of the solution of (32) computed with AB, (c) Plot of the data (34), (d) For the data (34), plot of the solution of (32) $v(x)={\text {max}}\{0, (2\pi -y)u\sin (x)^3\}$

Fig. 9

(Left) The error in the solution of AB and S-DR with parameter $\gamma \in \{0.1,0.2,\ldots ,4.9,5\}$ after running the algorithms for 10000 iterations. (Right) The error (in log. scale) as a function of iterations for different values of $\gamma$

Therefore, when $\sigma _A=\sigma _B$, the results in these experiments suggest that the value of $\gamma \sigma _A$ has a considerable effect on the performance of S-DR. If this value is chosen too small, the solution found may be more inaccurate, while a large value can slow down the algorithm. A value of $\gamma \sigma _A=0.125$ appeared to be optimal in terms of the number of iterations and the error for both of the function data considered.

Appendix: Proof of convergence for Ryu splitting

In this appendix, we offer a direct proof for convergence of the method proposed in [52, Section 4]. In doing so, we also extend the result to the infinite dimensional setting as well as establishing weak convergence of the shadow sequence, which is required to prove Theorem 7.

Let $A,B,C:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally monotone operators. Consider the problem

$$\begin{aligned} \text {find }x\in \mathcal {H}\text { such that }0\in (A+B+C)(x). \end{aligned}$$

Note that $u\in {\mathrm{zer}}(A+B+C)$ if and only if there exist points $x,y\in \mathcal {H}$ such that

$$\begin{aligned} x-u\in \gamma A(u),\qquad y\in \gamma B(u),\qquad u-x-y\in \gamma C(u). \end{aligned}$$

Using the definition of the resolvent, the latter is equivalent to

$$\begin{aligned} u = J_{\gamma A}(x),\qquad u = J_{\gamma B}(u+y), \qquad u = J_{\gamma C}(2u-x-y). \end{aligned}$$

(35)

Consequently, we have ${\mathrm{zer}}(A+B+C)\ne \emptyset$ if and only if $\varOmega \ne \emptyset$, where

$$\begin{aligned} \varOmega := \bigl \{(x,y)\in \mathcal {H}\times \mathcal {H}: J_{\gamma A}(x)=J_{\gamma B}(J_{\gamma A}(x)+y)= J_{\gamma C}(2J_{\gamma A}(x)-x-y)\bigr \}. \end{aligned}$$

Recall that an operator $A:\mathcal {H}\rightrightarrows \mathcal {H}$ is said to be uniformly monotone with modulus $\phi :\mathbb {R}_+\rightarrow {[0,+\infty [}$ if $\phi$ is increasing, vanishes only at 0 and

$$\begin{aligned} \langle x-y,u-v\rangle \ge \phi (\Vert x-y\Vert )\quad \forall (x,u),(y,v)\in {\mathrm{gra}}\,A. \end{aligned}$$

Theorem 8

(Ryu splitting) Let $A,B,C:\mathcal {H}\rightrightarrows \mathcal {H}$ be maximally monotone operators with ${\mathrm{zer}}(A+B+C)\ne \emptyset$. Let $\gamma >0$ and $\lambda >0$. Given some initial points $x_0,y_0\in \mathcal {H}$, consider the sequences given by

$$\begin{aligned} \left\{ \begin{aligned} u_k&= J_{\gamma A}(x_k) \\ v_k&= J_{\gamma B}(u_k+y_k) \\ w_k&= J_{\gamma C}(u_k-x_k+v_k-y_k) \\ x_{k+1}&= x_k + \lambda (w_k-u_k) \\ y_{k+1}&= y_k + \lambda (w_k-v_k). \end{aligned}\right. \end{aligned}$$

(36)

The following assertions hold.

• (i) If $\lambda \in {]0,1[}$, then $(x_k,y_k)\rightharpoonup (x,y)\in \varOmega$, $u_k\rightharpoonup u, v_k\rightharpoonup u$ and $w_k\rightharpoonup u$ with

  $$\begin{aligned} u=J_A(x)=J_{\gamma B}(J_{\gamma A}(x)+y)= J_{\gamma C}(2J_{\gamma A}(x)-x-y)\in {\mathrm{zer}}(A+B+C). \end{aligned}$$

  (37)

• (ii) If $\lambda \in {]0,1]}$ and any of A, B or C is uniformly monotone, then $(u_k), (v_k)$ and $(w_k)$ converge strongly.

Proof

(i): Let $(x,y)\in \varOmega$ and denote $u:=J_{\gamma A}(x)$. Since $x-u\in \gamma A(u)$ and $x_k-u_k\in \gamma A(u_k)$, monotonicity of $\gamma A$ implies

$$\begin{aligned} \begin{aligned} 0&\le \langle (x-u)-(x_k-u_k),u-u_k \rangle \\&= \langle (x-u)-(x_k-u_k),u-w_k \rangle + \langle (x-u)-(x_k-u_k),w_k-u_k \rangle . \end{aligned} \end{aligned}$$

(38)

Since $y\in \gamma B(u)$ and $u_k+y_k-v_k\in \gamma B(v_k)$, monotonicity of $\gamma B$ implies

$$\begin{aligned} \begin{aligned} 0&\le \langle y-(u_k+y_k-v_k),u-v_k\rangle \\&= \langle y-(u_k+y_k-v_k),u-w_k\rangle + \langle y-(u_k+y_k-v_k),w_k-v_k\rangle . \end{aligned} \end{aligned}$$

(39)

Since $u-x-y\in \gamma C(u)$ and $u_k-x_k+v_k-y_k-w_k\in \gamma C(w_k)$, monotonicity of $\gamma C$ implies

$$\begin{aligned} \begin{aligned} 0&\le \langle (u-x-y)-(u_k-x_k+v_k-y_k-w_k),u-w_k\rangle \\&= \langle w_k-u_k,u-w_k\rangle - \langle (x-u)-(x_k-u_k),u-w_k\rangle \\&\quad -\langle y -(u_k+y_k-v_k),u-w_k\rangle . \end{aligned} \end{aligned}$$

(40)

Summing together (38), (39) and (40) yields

$$\begin{aligned} \begin{aligned} 0&\le \langle (x-u)-(x_k-u_k),w_k-u_k \rangle + \langle y-(u_k+y_k-v_k),w_k-v_k\rangle \\&\quad + \langle w_k-u_k,u-w_k\rangle \\&= \langle x-x_k,w_k-u_k\rangle - \Vert w_k-u_k\Vert ^2 + \langle y-y_k,w_k-v_k\rangle -\Vert w_k-v_k\Vert ^2\\&\quad + \langle w_k-u_k,w_k-v_k\rangle . \end{aligned} \end{aligned}$$

(41)

The first and second terms in (41) can be expressed as

$$\begin{aligned}&2\lambda \left( \langle x-x_k,w_k-u_k\rangle - \Vert w_k-u_k\Vert ^2\right) = 2\langle x-x_k,x_{k+1}-x_k\rangle - \frac{2}{\lambda }\Vert x_{k+1}-x_k\Vert ^2 \\&\quad = \Vert x_k-x\Vert ^2 - \Vert x_{k+1}-x\Vert ^2 - \left( \frac{2}{\lambda }-1\right) \Vert x_{k+1}-x_k\Vert ^2. \end{aligned}$$

Similarly, the third and fourth terms in (41) can be written as

$$\begin{aligned} 2\lambda \left( \langle y-y_k,w_k-v_k\rangle -\Vert w_k-v_k\Vert ^2 \right)&= \Vert y_k-y\Vert ^2 - \Vert y_{k+1}-y\Vert ^2\\&\quad - \left( \frac{2}{\lambda }-1\right) \Vert y_{k+1}-y_k\Vert ^2. \end{aligned}$$

The last term in (41) can be estimated as

$$\begin{aligned} 2\lambda \langle w_k-u_k,w_k-v_k\rangle= & {} \frac{2}{\lambda }\langle x_{k+1}-x_k,y_{k+1}-y_k \rangle \\\le & {} \frac{1}{\lambda }\Vert x_{k+1}-x_k\Vert ^2 + \frac{1}{\lambda }\Vert y_{k+1}-y_k\Vert ^2. \end{aligned}$$

Altogether, we have

$$\begin{aligned}&\Vert x_{k+1}-x\Vert ^2 +\Vert y_{k+1}-y\Vert ^2 + \left( \frac{1-\lambda }{\lambda }\right) \left( \Vert x_{k+1}-x_k\Vert ^2+\Vert y_{k+1}-y_k\Vert ^2\right) \nonumber \\&\quad \le \Vert x_k-x\Vert ^2 + \Vert y_k-y\Vert ^2, \end{aligned}$$

(42)

where we note that $\frac{1-\lambda }{\lambda }>0$ since $\lambda \in {]0,1[}$. For convenience, denote $z_k=(x_k,y_k)$ and $z=(x,y)$. Then (42) implies that $(z_k)$ is Fejér monotone with respect to $\varOmega$ (so in particular, $(\Vert z_k-z\Vert )$ is nonincreasing and convergent, see e.g. [10, Proposition 5.4]), and that $z_{k+1}-z_k\rightarrow (0,0)$. Since resolvents are nonexpansive, it follows that $(u_k)$, $(v_k)$ and $(w_k)$ are bounded, and that $w_k-u_k\rightarrow 0$ and $w_k-v_k\rightarrow 0$.

Let $\bar{z}=(\bar{x},\bar{y})$ be a weak sequential cluster point of the bounded sequence $(z_k)$. Then there exists a weak sequential cluster cluster point $\bar{u}$ of $(u_k)$ such that there exists a subsequence of $(z_{k},u_{k})$ which converges weakly to $(\bar{z},\bar{u})$. Now, from (36), it follows that

$$\begin{aligned}&\begin{pmatrix}u_k-w_k\\ v_k-w_k\\ u_k-w_k\end{pmatrix} \in T\begin{pmatrix}x_k-u_k\\ u_k+y_k-v_k\\ w_k\end{pmatrix}\\&\quad := \left( \begin{pmatrix}(\gamma A)^{-1}\\ (\gamma B)^{-1}\\ \gamma C\end{pmatrix}+\begin{pmatrix}0&{}0&{}-{\mathrm{Id}}\\ 0&{}0&{}-{\mathrm{Id}}\\ {\mathrm{Id}}&{}{\mathrm{Id}}&{}0\end{pmatrix}\right) \begin{pmatrix}x_k-u_k\\ u_k+y_k-v_k\\ w_k\end{pmatrix} \end{aligned}$$

where we note that the operator $T:\mathcal {H}^3\rightrightarrows \mathcal {H}^3$ is maximally monotone as the sum of a maximally monotone operator and a skew-symmetric matrix (see, e.g., [10, Example 20.35 & Corollary 25.5(i)]). Since the graph of a maximally monotone operator is sequentially closed in the weak-strong topology [10, Proposition 20.38], taking the limit along a subsequence of $(z_k,u_k)$ which converges weakly to $(\bar{z},\bar{u})$ (and noting that $w_k-u_k\rightarrow 0$ and $w_k-v_k\rightarrow 0$, which imply $u_k-v_k\rightarrow 0$ and $w_k\rightharpoonup \bar{u}$) yields

$$\begin{aligned} \begin{pmatrix}0\\ 0\\ 0\end{pmatrix} \in \left( \begin{pmatrix}(\gamma A)^{-1}\\ (\gamma B)^{-1}\\ \gamma C\end{pmatrix}+\begin{pmatrix}0&{}0&{}-{\mathrm{Id}}\\ 0&{}0&{}-{\mathrm{Id}}\\ {\mathrm{Id}}&{}{\mathrm{Id}}&{}0\end{pmatrix}\right) \begin{pmatrix}\bar{x}-\bar{u}\\ \bar{y}\\ \bar{u}\end{pmatrix} \implies \left\{ \begin{array}{l}\bar{z}=(\bar{x},\bar{y})\in \varOmega \\ \bar{u}=J_{\gamma A}(\bar{x}).\end{array} \right. \end{aligned}$$

(43)

In particular, this shows that every weak sequential cluster point of $(z_k)$ is contained in $\varOmega$, and so [10, Theorem 5.5] implies that $(z_k)$ converges weakly to a point $\bar{z}\in \varOmega$. Then (43) shows that $\bar{u}=J_{\gamma A}(\bar{x})$ is necessarily the unique cluster point of $(u_k)$, and hence $u_k\rightharpoonup \bar{u}$. It follows that $v_k\rightharpoonup \bar{u}$ and $w_k\rightharpoonup \bar{u}$. The fact that $\bar{u}$ satisfies (37) follows by the argued in after (35).

(ii): Suppose A is uniformly monotone with modulus $\phi$. Then, using uniform monotoncity of A in place of monotonicity in (38), yields the stronger inequality

$$\begin{aligned} \gamma \phi \big (\Vert u_k-u\Vert \bigl ) \le \langle (x-u)-(x_k-u_k),u-w_k \rangle + \langle (x-u)-(x_k-u_k),w_k-u_k \rangle . \end{aligned}$$

By propagating this inequality through the remainder of the proof, noting that $\lambda \in {]0,1]}$, (42) becomes

$$\begin{aligned} \Vert x_{k+1}-x\Vert ^2 +\Vert y_{k+1}-y\Vert ^2 + 2\lambda \gamma \phi \bigl (\Vert u_k-u\Vert \bigr ) \le \Vert x_k-x\Vert ^2 + \Vert y_k-y\Vert ^2. \end{aligned}$$

From this it follows that $\phi \bigl (\Vert u_k-u\Vert \bigr )\rightarrow 0$ and hence that $u_k\rightarrow u$. When B (resp. C) is uniformly monotone, the result follows by an analogous argument by modifying (39) (resp. (40)). $\square$