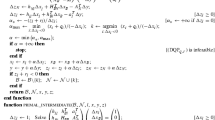Abstract
In this paper, we are concerned with efficient algorithms for solving the least squares semidefinite programming which contains many equalities and inequalities constraints. Our proposed method is built upon its dual formulation and is a type of active-set approach. In particular, by exploiting the nonnegative constraints in the dual form, our method first uses the information from the Barzlai–Borwein step to estimate the active/inactive sets, and within an adaptive framework, it then accelerates the convergence by switching the L-BFGS iteration and the semi-smooth Newton iteration dynamically. We show the global convergence under mild conditions, and furthermore, the local quadratic convergence under the additional nondegeneracy condition. Various types of synthetic as well as real-world examples are tested, and preliminary but promising numerical experiments are reported.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({{\mathcal {S}}}_+^n\) be the cone of positive semidefinite matrices in the space \({{{\mathcal {S}}}}^n\) of \(n\times n\) symmetric matrices, and \(\langle A,B\rangle :=\mathrm{tr}(A^TB)\) with \(A,B\in {{{\mathcal {S}}}}^n\). In this paper, we consider the least squares semidefinite programming (LSSDP) [2, 10, 12, 17, 27] of the following form
where \(b=(b_1,\ldots ,b_m)^T\in {\mathbb {R}}^m\), and \(G, A_i\in {{{\mathcal {S}}}}^n\) for \(i=1,\ldots ,m\) are all given.
To solve the problem (1.1) numerically, in the literature, a couple of methods have been proposed and can be used in different situations. For instance, for small- to medium-size n and m, interior point methods implemented in, for example, SeDuMi [31] and SDPT3 [34], can solve efficiently the dual problem (1.2)
which is just to minimize a simple linear function subject to the constraints of linear equalities/inequalities, the second order cone, and the positive semidefinite cone. However, since a linear system associated with a dense Schur complement matrix of the size \((m+1+ {\bar{n}})\times (m+1+ {\bar{n}})\) with \({\bar{n}} := \frac{1}{2}n(n + 1)\) needs to be solved at each iteration, the efficiency of interior point methods decreases as n gets moderately larger (say, 2000). In the literature, therefore, methods other than interior point methods have been proposed and applied. For example, Malick [17], Boyd and Xiao [2], and Gao and Sun [10] proposed the BFGS method, the projected gradient method, and semi-smooth Newton method respectively, to solve the Lagrangian dual problem of (1.1). Along the dual framework, Li and Li [15] introduced a projected semi-smooth Newton method. Unlike [2, 10, 17], He, Xu and Yuan [12] suggested the augmented Lagrangian function with an auxiliary matrix variable and then applied the alternating direction methods (ADM) [8, 9, 35] to (1.1). Very recently, Sun and Vandenberghe [33] considered decomposition methods for matrix nearness problems with some sparsity pattern.
We remark that each of the previously mentioned methods handles either the computational and memory costs per step or the fast local convergence. For example, the projected gradient method [2] and the ADM methods [12] usually are of economic computational costs at each step, but they have relatively slow convergence, especially when the iterates reach in the vicinity of a minimizer. The BFGS method [17] and the semi-smooth Newton method [10] locally converge fast, but the approximate Hessian matrix in the BFGS method has to be stored at each step, while the generalized Newton equation has to be solved in the semi-smooth Newton method, which degrades the efficiency of the related method when m gets very large.
In this paper, relying on the dual technique, we attempt to handle both the computational and memory costs per step and the local fast convergence. In particular, we combine the advantages of limited-BFGS (L-BFGS) and the semi-smooth Newton method to propose an accelerated active-set method for the dual problem. In our first stage, the Barzlai–Borwein (BB) step is used to draw information of the index of the final active/inactive sets. These active/inactive sets correspond to free/fixed variables. The second stage employs the L-BFGS method and the semi-smooth Newton method to accelerate the convergence of these free variables. For a practical implementation, we propose an adaptive strategy to smoothly switch them so that it adaptively refines the estimated index of the final active/inactive sets, and also is able to use the full-power of the semi-smooth Newton method whenever the iterates are close to the minimizer. We establish the global convergence and the fast local convergence under some mild conditions.
The rest of this paper is organized as follows. In Sect. 2, we state the dual problem and give the first-order/second-order optimality conditions. In Sect. 3, we present the details of our accelerated active-set method by describing four main ingredients: identification of active/inactive sets, the L-BFGS acceleration, the semi-smooth Newton acceleration, and an adaptive acceleration strategy. The global convergence of the proposed algorithm is proved under some mild conditions in Sect. 4, and fast local convergence is established in Sect. 5. Numerical evaluation of the proposed method is conducted in Sect. 6, where LSSDP instances on both real and synthetic data are tested, and the performance of other solvers [10, 12, 14, 35] are reported and compared. Final remarks are drawn in Sect. 7.
2 The dual problem and optimality conditions
We first rewrite (1.1) into the following general form:
where \({\mathcal {Q}}=\{0\}\times {\mathbb {R}}_+^{m-p}\), \({{{\mathcal {K}}}}\) is a closed and convex cone, and \({\mathcal {A}}(X)\) is defined as
Note that the primal form (2.1) is convex and the associated Lagrangian function is given by
where \(\langle {x,y}\rangle :=x^Ty\) with \(x,y\in {\mathbb {R}}^n\).
2.1 The dual problem
The Lagrangian dual of (2.1) (see [10]) is
where \({\mathcal {Q}}^*={\mathbb {R}}^p\times {\mathbb {R}}_+^{m-p}\) is the dual cone of \({\mathcal {Q}}\), \({{{\mathcal {A}}}}^*\) is the adjoint operator of \({{{\mathcal {A}}}}\) defined by \({{{\mathcal {A}}}}^*(y)=\sum _{i=1}^my_iA_i\), and \(\Pi _{{{\mathcal {K}}}}[Y]\) denotes the metric projection of \(Y\in {{{\mathcal {S}}}}^n\) onto \({{{\mathcal {K}}}}\), i.e.,
Denote
Obviously, the dual problem (2.2) is equivalent to the problem
For \(Y\in {{{\mathcal {S}}}}^n\), let the spectral decomposition be \(Y=P\Lambda P^T\) with \(\Lambda :=\mathrm{diag}(\lambda _1,\ldots ,\lambda _n)\), where \(\lambda _1\ge \cdots \ge \lambda _n\) are the eigenvalues of Y and P is a corresponding orthogonal matrix of orthonormal eigenvectors of Y. Note that this decomposition needs \(9n^3\) multiplications or so. From [26], we have
Hence, for (1.1), \({{{\mathcal {K}}}}={{{\mathcal {S}}}}_+^n\), \({{{\mathcal {A}}}}^*(y)=\sum _{i=1}^my_iA_i\), and
where \([\cdot ]_+=\Pi _{{{{\mathcal {S}}}}_+^n}[\cdot ]\). The function f(y) is convex, continuously differentiable and coercive (i.e., \(f(y)\rightarrow \infty\) as \(\Vert y\Vert \rightarrow \infty\)) [25] under the Slater condition. The gradient is given by
which is also Lipschitz continuous. Moreover, under the Slater constraint qualification, it has zero duality gap between the primal problem (1.1) and its dual (2.3), which provides a possibility to solve (1.1) from the dual. We point out that, due to the projection \(\Pi _{{{{\mathcal {S}}}}_+^n}[\cdot ]\), \(\nabla f(y)\) generally is not differentiable, and thus, the classical Newton method is not applicable for (2.3).
2.2 Optimality conditions
For convenience, we denote the index sets of equalities and inequalities of (1.1) by \({{{\mathcal {E}}}}:=\{1,\ldots ,p\}\) and \({{{\mathcal {I}}}}:=\{p+1,\ldots ,m\}\), respectively. Also, we denote \(\nabla f(y)\) by g(y) and the subvector of g(y) with components \(g_i(y), i\in { {{\mathcal {E}}}}\) by \(g_{\scriptscriptstyle {{\mathcal {E}}}}(y)\). The meanings of \(g_{\scriptscriptstyle {{\mathcal {I}}}}(y)\) and \(y_{\scriptscriptstyle {{\mathcal {I}}}}\) follow similarly.
Due to the special structure of the constraints \(y_i\ge 0\) with \(i\in {{{\mathcal {I}}}}\), the Mangasarian-Fromovitz constraint qualification (MFCQ) is satisfied at any feasible point of (2.3). The first-order condition (i.e., the KKT condition) of (2.3) is
where \(\mu =(\mu _1,\ldots ,\mu _{m-p})^T\in {\mathbb {R}}^{m-p}\) is the multiplier vector corresponding to the constraints \(y_i\ge 0, i\in {{{\mathcal {I}}}}\). If a pair \((y,\mu )\) satisfies (2.5), we call it a KKT pair. One way to measure the KKT error is the KKT residual
where \(\min (y_{\scriptscriptstyle {{\mathcal {I}}}},\mu )\) is the componentwise minimum function of the vectors \(\mu\) and \(y_{\scriptscriptstyle {{\mathcal {I}}}}\). It is easy to verify that \(\Psi (y^*,\mu ^*)=0\) if and only if \((y^*,\mu ^*)\) is a KKT pair for (2.3).
We now suppose \(\Psi (y^*,\mu ^*)=0\), and let
and
The (strong) second-order sufficient condition holds at \(y^*\) if \(h^TVh>0\) for all nonzero vectors \(h\in {{{\mathcal {H}}}}_{\theta }(y^*)\) \((h\in \bar{{{{\mathcal {H}}}}}_{\theta }(y^*))\) and all matrices \(V\in \partial _{B}(\nabla f(y^*))\), where \(\partial _{B}(\nabla f(y^*))\) denotes the B-subdifferential of \(\nabla f(y)\) at \(y^*\) in the sense of Qi [21]. In [22, Theorem 2.2], it is shown that \(y^*\) is a strict local minimum of (2.3) if the (strong) second-order sufficient condition holds.
3 Algorithm
In this section, we will present our accelerated active set algorithm for solving the dual problem (2.3). Our approach consists of a procedure of active set detection by the BB step [1], and a smoothly-switching search direction procedure between L-BFGS and the semi-smooth Newton methods. The BB step aims at estimating the index of the active/inactive sets (free/fixed variables), and whenever this stage is fulfilled, the L-BFGS method or the semi-smooth Newton method will be triggered to accelerate the convergence of the free variables.
3.1 The BB step
Originated by Barzlai and Borwein [1], the BB method has been discussed by many other researchers and applied in a broad area of applications. In our case, at the current iterate \(y^k\), we first use the BB step to generate a trial iterate \({\tilde{y}}^k\) which is called a BB point. There are two commonly used formula of the stepsize (see [1]), namely,
where \(s^{k-1}=y^k-y^{k-1},\ w^{k-1}=g(y^k)-g(y^{k-1})\). It has been proved in theory that the long stepsize \(\alpha _{l}^k\) can guarantee the reduction of the objective function, and the short stepsize \(\alpha _{s}^k\) can induce a good descent direction for the next iteration. Based on this fact, Zhou, Gao and Dai [37] present an adaptive stepsize selection strategy and report numerical results for its efficiency. Specifically, such adaptive stepsize with some safeguards is defined as
where \(\kappa \in (0,1)\), and \(\alpha _{\max }>\alpha _{\min }>0\). The adaptive stepsize can be viewed as a combination of the long BB stepsize and the short BB stepsize, and the parameter \(\kappa\) determines the trade-off between \(\alpha _{l}^k\) and \(\alpha _{s}^k\). Generally, \(\kappa\) is around 0.5. Other adaptive strategies are discussed in [5, 37].
In our case, we use the strategy in [37] to generate the BB point. In particular, for the dual problem (2.3), we generate the trial BB point as
where \(g^k:=g(y^k)\), and the stepsize is determined by the adaptive stepsize \(\alpha _B^k\) in (3.1).
3.2 Identification of the active set
In this subsection, we will discuss how to detect the active/inactive sets at the trial BB point \({\tilde{y}}^k\). Assume that \(y^*\) is a minimizer of the problem (2.3). As the linear independence constraint qualification (LICQ) holds at \(y^*\), the uniqueness of the associated multiplier \(\mu ^*\) is ensured. Moreover, when the second-order sufficient condition holds, \(y^*\) is isolated (see [22, Theorem 2.2]). According to [7, Theorem 3.6], we have the following theorem.
Theorem 3.1
Assume that the second-order sufficient condition holds at \(y^*\). Then there exist two scalars \(\kappa _1,\kappa _2>0\) such that
for any pair \((y,\mu )\) sufficiently close to \((y^*,\mu ^*)\).
Using [7, Theorems 3.7 and 2.2], the index set
correctly identifies all active constraints if \((y,\mu )\) is sufficiently close to \((y^*,\mu ^*)\). To apply this fact, by canceling the multiplier \(\mu\) in (2.5), we rewrite the KKT condition (2.5) as
and by \(\mu =g_{\scriptscriptstyle {{\mathcal {I}}}}(y)\), we have
Here \(\Pi _{\scriptscriptstyle {{\mathcal {Q}}}}[x]\) denotes the metric projection of \(x\in {\mathbb {R}}^m\) onto \({{{\mathcal {Q}}}}\), which can be easily calculated as
In our algorithm, at the BB point \({\tilde{y}}^k\) in (3.2), we define two index sets \({\mathcal {B}}^k\) and \({\mathcal {F}}^k\) associated with the point \(y^k\) as
where \(\nu ^k=\min {\lbrace \epsilon _0,\sqrt{\varrho ^k}\rbrace }\), \(\epsilon _0\in (0,0.1)\) (generally, \(\epsilon _0\) is a small parameter of order, e.g., \(10^{-6}\)), and \(\varrho ^k=\varrho (y^k)\). One can see from the definition of \({{{\mathcal {B}}}}^k\) that components of \({\tilde{y}}^k\) and \(y^k\) that approach the boundary are taken as the potential fix variables, and therefore, the corresponding indices are put in \({{{\mathcal {B}}}}^k\). More explanations will be stated in Sect. 4.
As \({\mathcal {B}}^k\) differs slightly from \(\bar{{{\mathcal {B}}}}(y^k,\mu ^k)\), we find that [7, Theorems 3.7, 2.2] is not directly applicable to \({\mathcal {B}}^k\) to detect the active set correctly. However, such a desired conclusion still holds as shown in the following theorem.
Theorem 3.2
Assume that the second-order sufficient condition holds at \(y^*\). Then \({\mathcal {B}}^k\) and \({{{\mathcal {F}}}}^k\) can correctly identify all active/inactive constraints respectively if \(y^k\) is sufficiently close to \(y^*\).
Proof
It suffices to prove that \({\mathcal {B}}^k\) can correctly identifies all active/inactive constraints if \(y^k\) is close to \(y^*\) enough. By the definition of \(\varrho ^k\) and (3.5),
From (3.2) and (3.5), we obtain that for \(i\in {{{\mathcal {I}}}}\),
Suppose \(y_i^*=0\) for some \(i\in {{{\mathcal {I}}}}\). Due to Theorem 3.1 and \(\varrho (y)=\Psi (y,\mu )\), it holds
It follows with the definition of \(\nu ^k\) that \(y_i^k\le \Vert y^k-y^*\Vert \le \nu ^k/2\) for \(y^k\) close to \(y^*\) enough. By (3.7) and the definition of \(\nu ^k\), it holds \(|\min (y_i^k,\alpha _B^kg_i^k)|\le \nu ^k/2\). This together with (3.8) and \(y_i^k\le \nu ^k/2\) yields \({\tilde{y}}_i^k \le \nu ^k\). So \(i\in {{{\mathcal {B}}}}^k\).
On the other hand, if \(y_i^*>0\) for some \(i\in { {{\mathcal {I}}}}\), then \(g_i(y^*)=0\) due to the KKT condition (3.3). By (3.8), \({\tilde{y}}_i^k>\nu ^k\) if \(y^k\) is sufficiently close to \(y^*\). By (3.9) and the definition of \(\nu ^k\), we have
for \(y^k\) sufficiently close to \(y^*\), where \(\alpha _B^k\in [\alpha _{\min },\alpha _{\max }]\) is the BB stepsize from (3.1) and \(L_g>0\) is the Lipschitz constant of g(y). This combining with the Lipschitz continuity of g(y) gives
Thus, \(-g_i^k< \nu ^k/(2\alpha _B^k)\) for any \(y^k\) sufficiently close to \(y^*\). So, \(i\notin { {{\mathcal {B}}}}^k\) and consequently, \({\mathcal {B}}^k\) identifies all active constraints accurately. \(\square\)
Theorem 3.2 reveals that the problem (2.3), with the second-order sufficient condition (not the strict complementarity condition), locally can be reduced to an unconstrained minimization problem. This provides an important foundation for establishing the fast local convergence in Sect. 5.
3.3 The search direction
With the BB point \({\tilde{y}}^k\) computed by (3.2) at hand, we can determine the working sets \({{{\mathcal {B}}}}^k\) and \({{{\mathcal {F}}}}^k\) by (3.6). Let \(J^k\) be a generalized Hessian matrix of f(y) at \(y^k\). Without loss of generality, we assume \({\mathcal {F}}^k=\{1,2,\ldots ,|{{{\mathcal {F}}}}^k|\}\) with \(|{{{\mathcal {F}}}}^k|\) being the cardinality of \({{{\mathcal {F}}}}^k\), and then partition \(J^k\) and \(g^k\) as
As a result, we present the entry \(d^k_i\) of the search direction \(d^k=d(y^k)\) associated with \(y^k\) as
where Z is a matrix of columns consisting of \(\lbrace e_i|i\in {\mathcal {F}}^k \rbrace\) with \(e_i\) being the ith column of the identity matrix \(I_{n}\) (i.e., \(Z=(I_{|{{{\mathcal {F}}}}^k|},0)^T\in {\mathbb {R}}^{n\times |{{{\mathcal {F}}}}^k|}\) when \({\mathcal {F}}^k=\{1,2,\ldots ,|{{{\mathcal {F}}}}^k|\}\)), and \({\bar{H}}^k\) is \((J^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k})^{-1}\) or a certain approximation of \((J^k)^{-1}_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}\); here \((J^k)^{-1}_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}\) denotes the top-left block of \((J^k)^{-1}\) with \((J^k)^{-1}\) being partitioned similar as \(J^k\).
The matrix \({\bar{H}}^k\) is a key to define the search direction in (3.11). In the next subsection, we will specify two ways to compute \({\bar{H}}^k\): the way based on the L-BFGS formula and the one based on the semi-smooth Newton method. Here, we only mention that if the approximation \(H^k\) of \((J^k)^{-1}\) is updated by the L-BFGS formula implicitly, then its top-left block \(H^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}\) can be considered as an approximation of \((J^k)^{-1}_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}\), and thus \({\bar{H}}^k=H^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}=Z^TH^kZ\), whereas if the semi-smooth Newton acceleration is applied, then \({\bar{H}}^k=(J^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k})^{-1}\). The detailed information on computation of \(Z{\bar{H}}^kZ^Tg^k\) will be given in the next subsection.
3.4 The L-BFGS and semi-smooth Newton search direction
3.4.1 The L-BFGS direction
The BFGS method [20, Chapter 7] is a well-known quasi-Newton method for the unconstrained minimization \(\min f(y)\). A basic iteration of BFGS is
where \(\alpha ^k\) is a stepsize, and \(H^k\) is the inverse Hessian approximation updated by
where \(\rho ^k=1/(w^k)^Ts^k\), \(V^k=I-\rho ^kw^k(s^k)^T\), and \(s^k=y^{k+1}-y^k\), \(w^k=g^{k+1}-g^{k}\).
The L-BFGS algorithm (see [16, 20]) is an improvement of BFGS for large-scale problems which alleviates the memory requirement in storing \(H^k\) in each step. In particular, the matrix \(H^k\) in the L-BFGS algorithm is formed implicitly by the l most recent vectors pairs \(\{s^i,w^i\}\), \(i=k-l,\ldots ,k-1\). Starting from an initial Hessian approximationFootnote 1\((H^k)^0\), at the kth iteration, it uses the l most recent vector pairs \(\{s^i,w^i\}\), \(i=k-l,\ldots ,k-1\) to have
According to this formula, an efficient recursive procedure (see [20, Algorithm 7.4]) can be derived to compute \(H^kg^{k}\). In the case of the L-BFGS acceleration, the term \(Z{\bar{H}}^kZ^Tg^k\) in (3.11) is
With the partition \(H^k=\begin{pmatrix} H^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k} &{}H^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {B}}}}^k}\\ H^k_{{\scriptscriptstyle {{\mathcal {B}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k} &{} H^k_{{\scriptscriptstyle {{\mathcal {B}}}}^k{\scriptscriptstyle {{\mathcal {B}}}}^k} \end{pmatrix}\), we know that the first sub-vector \(H^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}g^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\) is the same as that of \(H^k \begin{pmatrix} g^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\\ 0 \end{pmatrix}\), and therefore, the part of search direction of \(d^k\) in (3.11) for the variables in \({{{\mathcal {F}}}}^k\) can be calculated by the recursive procedure with (3.12) (see [20, Algorithm 7.4]). Note that this recursive procedure requires about 4ml multiplications.
3.4.2 The semi-smooth Newton direction
Qi and Sun [24] introduced a semi-smooth Newton method to solve the correlation matrix approximation problem, and further extended it to the problem with general linear equality constraints. Numerical experiments show that the semi-smooth Newton method has better performance than methods using first-order information (for example, the projected gradient method and BFGS method).
For our case, we find that the semi-smooth Newton method can serve as a good acceleration for the solution of the dual problem. Let \(\partial g(y^k)\) denote the generalized Jacobian of g(y) at \(y^k\) in the sense of Clarke [4]. It is also the convex hull of \(\partial _B g(y^k)\) [21]. For (2.4), let \(G(y^k)=G+{{{\mathcal {A}}}}^*(y^k)\) and its spectral decomposition be \(G(y^k)=P\Lambda (y^k) P^T\), where \(\Lambda (y^k):=\mathrm{diag}(\lambda _1(y^k),\ldots ,\lambda _n(y^k))\), \(\lambda _1(y^k)\ge \cdots \ge \lambda _n(y^k)\) are the eigenvalues and \(P\in {\mathbb {O}}_{G(y^k)}:=\{P\in {\mathbb {R}}^{n\times n}|G(y^k)=P\Lambda (y^k)P^T, P^TP=I_n\}\) is a corresponding orthogonal matrix. Define three index sets associated with \(\lambda _i(y^k)\), \(i=1,\ldots ,n\) as follows:
and define
Then we have the following results.
Lemma 3.1
For any \(h\in {\mathbb {R}}^m\),
where \(T={\mathcal {A}}^*(h)\), \({\mathcal {W}}\) is a set of operators given by
and \(\circ\) is the Hadamard product.
Proof
The proof follows similarly to that of [24, Lemma 3.5]. \(\square\)
At \(y^k\), let \(J^{k}\in \partial _B(g(y^k))\) be partitioned as (3.10) assuming, w.l.g., \({\mathcal {F}}^k=\{1,2,\ldots ,|{{{\mathcal {F}}}}^k|\}\). Our choice of semi-smooth Newton search direction \(d_{{\scriptscriptstyle {{\mathcal {F}}}}^k}^k\) in \(d^{k}\) for the variables in \({{{\mathcal {F}}}}^k\) satisfies the linear system
Thus, for the semi-smooth Newton acceleration, we can compute the part of search direction \(-Z{\bar{H}}^kZ^Tg^k\) in (3.11) as
where \(d_{{\scriptscriptstyle {{\mathcal {F}}}}^k}^k\) is from (3.15). Practically, by taking advantage of the convexity of the problem, we invoke a certain Krylov subspace method (for example CG) for this system to obtain approximations of \(d_{{\scriptscriptstyle {{\mathcal {F}}}}^k}^k\), in which the main costs lie in the matrix-vector products of the form \(J^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\) for \(h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\in {\mathbb {R}}^{|{{{\mathcal {F}}}}^k|}\). If \(N_{CG}\) CG steps are used to solve for \(d_{{{{\mathcal {F}}}}^k}^k\), excluding the multiplications in \({{{\mathcal {A}}}}(X)\) and \({{{\mathcal {A}}}}^*(y)\), we require \((4n^3+n^2+2|{{{{\mathcal {F}}}}^k}|)N_{CG}\) multiplications.
Note the matrix-vector product \(J^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\) is indeed the first sub-vector of length \(|{{{\mathcal {F}}}}^k|\) of
and thus, \(J^k_{{\scriptscriptstyle {{\mathcal {F}}}}^k{\scriptscriptstyle {{\mathcal {F}}}}^k}h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\in \{{\mathcal {A}}_{{\scriptscriptstyle {{\mathcal {F}}}}^k}(WH):\ W\in {\mathcal {W}} \}\), where the linear mapping \({{{\mathcal {A}}}}_{{{{\mathcal {F}}}}^k}\): \({{{\mathcal {S}}}}^n\rightarrow {\mathbb {R}}^{|{{{{\mathcal {F}}}}^k}|}\) is given by \({{{\mathcal {A}}}}_{{{{\mathcal {F}}}}^k}(X)=[{{{\mathcal {A}}}}(X)]_{{{{\mathcal {F}}}}^k}\) and \(H={\mathcal {A}}^*\left( \left( \begin{array}{c}h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\\ 0\end{array}\right) \right) =\sum _{i\in { {{\mathcal {F}}}}^k}h_iA_i\). This leads to the following corollary.
Corollary 3.1
For the index set \({{{\mathcal {F}}}}^k\), define the linear mapping \({{{\mathcal {A}}}}_{{{{\mathcal {F}}}}^k}\): \({{{\mathcal {S}}}}^n\rightarrow {\mathbb {R}}^{|{{{{\mathcal {F}}}}^k}|}\) by \({{{\mathcal {A}}}}_{{{{\mathcal {F}}}}^k}(X)=[{{{\mathcal {A}}}}(X)]_{{{{\mathcal {F}}}}^k}\), and the function \(F(y_{{\scriptscriptstyle {{\mathcal {F}}}}^k}):{\mathbb {R}}^{|{{{\mathcal {F}}}}^k|}\rightarrow {\mathbb {R}}^{|{{{\mathcal {F}}}}^k|}\) by \(F(y_{{\scriptscriptstyle {{\mathcal {F}}}}^k})=g_{{\scriptscriptstyle {{\mathcal {F}}}}^k}(y)\) in which the elements of y in \({{{\mathcal {B}}}}^k\) are fixed at \(y_{{\scriptscriptstyle {{\mathcal {B}}}}^k}^k\), i.e., \(y_{{\scriptscriptstyle {{\mathcal {B}}}}^k}=y_{{\scriptscriptstyle {{\mathcal {B}}}}^k}^k\), where \({{{\mathcal {B}}}}^k=({{{\mathcal {E}}}}\cup {{{\mathcal {I}}}})\backslash {{{\mathcal {F}}}}^k\). Then for any \(h_{{\scriptscriptstyle {{\mathcal {F}}}}^k}\in {\mathbb {R}}^{|{\scriptscriptstyle {{\mathcal {F}}}}^k|}\), it follows
where \(H={\mathcal {A}}^*(Zh_{{\scriptscriptstyle {{\mathcal {F}}}}^k})\), the columns of \(Z\in {\mathbb {R}}^{n\times |{{{\mathcal {F}}}}^k|}\) are \(\lbrace e_i|i\in {\mathcal {F}}^k \rbrace\), and \({{{\mathcal {W}}}}\) is defined in (3.14).
3.5 Algorithm
With the previous preparation, we now can summarize the procedure of our algorithm. Let \(y^k\) be the current iteration for (2.3). After computing the search direction \(d^k\) in (3.11), we determine a stepsize \(\alpha ^k\) by the backtracking line search technique to fulfill the following nonmonotone reduction condition on f(y) [36]:
where \(f_p^k\) is a weighted average of the past function values that is no less than \(f(y^k)\), and \(\delta \in (0,\frac{1}{2})\). We mention that such condition (3.16) is more relaxable than the standard Armijo condition. The framework of our proposed algorithm is as follows:

Note that the generated sequence \(\{f(y^k)\}\) by Algorithm 1 is nonmonotonically descent (see Lemma 4.2 and (4.24)) and the objective function f(y) is coercive, \(\{y^k\}\) is bounded, and thereby, it has a convergent subsequence.
The final execution of Algorithm 1 needs the specification of the search direction \(d^{k+1}\) in step 9 of Algorithm 1. There are several possible ways for adaptively switching the directions (indexed by variable switch) between the one of L-BFGS (denoted by switch=“Q") and the semi-smooth Newton (denoted by switch=“N"). In the next subsection, we shall present an adaptive strategy.
3.6 An adaptive acceleration strategy
This subsection is to specify step 9 of Algorithm 1. In particular, we introduce a two-stage adaptive acceleration strategy: “A-stage acceleration" (triggered by \(\varrho ^{k+1}\le \epsilon _a\)) and “B-stage acceleration" (triggered by \(\varrho ^{k+1}\le \epsilon _b\)).
For “A-stage acceleration", we adaptively use the generalized Newton step to accelerate the inactive part of \(d^{k+1}\) while the active part of \(d^{k+1}\) still goes a BB step. For convenience, we use “N" (or N-step) and “Q" (or Q-step) to represent the generalized Newton acceleration step (denoted by \(d_N^{k+1}\)) and the L-BFGS acceleration step (denoted by \(d_Q^{k+1}\)), respectively. Generally, computing \(d_N^{k+1}\) is more expensive than \(d_Q^{k+1}\), but \(d_N^{k+1}\) can usually bring more improvements on reduction of the residual \(\varrho ^k\) in (3.4). To measure the improvement at kth iteration, if the previous two steps, i.e., \((k-1)\)th and kth are both the generalized Newton steps, we introduce the 3-N-step improvement factor as
where the generalized Newton steps are used for \(\varrho ^{k-1}, \varrho ^{k}\) and \(\varrho ^{k+1}\). The reason behind our 3-N-step improvement rate is that the generalized Newton step may not provide great reductions on the residual \(\varrho ^{k}\) at each iteration, but it usually is able to reduce the residual in several successive steps. Our numerical experiments show that using three successive steps turns out a good choice in general. The “A-stage acceleration" of the adaptive acceleration strategy is stated in Lines 16–27 of Algorithm 2.
To achieve the fast local convergence speed, we introduce “B-stage acceleration" of the adaptive acceleration strategy. Notice from (3.11) that \(d_i^k,i\in {{{\mathcal {B}}}}^k\) only involves the gradient information, and the stepsize can be cut to be very small in order to meet the nonmonotone reduction condition (3.16) on f. This implies that the fast local convergence may not be generally ensured in “A-stage acceleration". Fortunately, Theorem 3.2 shows that \({\mathcal {B}}^k\) and \({{{\mathcal {F}}}}^k\) can correctly identify all active/inactive constraints respectively in the final stage under the constraint nondegeneracy condition [10]. Thus, in “B-stage acceleration", we force \(y_i^{k+1},i\in {{{\mathcal {B}}}}^{k+1}\) to be zero, i.e., restrict the fix variables to the boundary. To distinguish the iterate \(y^{k+1}\) in Algorithm 1, we denote the full successive generalized Newton iterates by \(z^{j}\) for \(j=1,2,\ldots\) with \(z^1=y^{ {k+1}}\) used in this adaptive strategy. This means that the semi-smooth Newton acceleration is a first try at the \((k {+1})\)th iteration. Whenever the acceleration fails to meet our criterion to be specified, we shrink \(\epsilon _b\) and go back to \(y^{ {k+1}}\), and then apply the L-BFGS acceleration to Algorithm 1 instead. The “B-stage acceleration" of the adaptive acceleration strategy is described in Lines 2–14 of Algorithm 2.

Remark 3.1
The condition in Line 6 of Algorithm 2 means that during iterations the sufficient decrease condition
holds and the working set \({{{\mathcal {F}}}}(z^j)\) keeps unchanged.
Remark 3.2
The statement of ‘3-N-step fails to be accepted’ in Line 19 of Algorithm 2 means that one of the following conditions holds:
-
(i)
\(f(\Pi _{{{\mathcal {Q}}}}(y^{k+1}+d_N^{k+1}))> f^{k+1}_p+\delta (g^{k+1})^Td_N^{k+1}\); that is, the generalized Newton step \(d_N^{k+1}\) is not sufficiently descent for f in the sense of (3.16) with \(\alpha ^{k+1}=1\);
-
(ii)
in case that the previous two steps \((k-1)\)th and kth are both the generalized Newton steps, the 3-N-step improvement factor \(\chi _N^{k+1}\le \epsilon _\chi\). (In our numerical testing, \(\epsilon _\chi =0.3\))
Remark 3.3
For the computational costs of Algorithm 1 with Algorithm 2 embedded at each iteration, we first note that about \(9n^3\) multiplications are required to compute the spectral decomposition of an n-by-n matrix; second, for the search direction, about 4lm multiplications are used in L-BFGS for computing \(d_Q^k\), while \((4n^3+n^2+2|{{{\mathcal {F}}}}^k|)N_{CG}\) multiplications for the generalized Newton step \(d_N^k\) (or \({\bar{d}}_N^j\)). Therefore, by excluding the multiplications in computing \({{{\mathcal {A}}}}(X)\) and \({{{\mathcal {A}}}}^*(y)\), the total computational amount is about \(9n^3+4lm\) multiplications for \(d_Q^k\) and \((4n^3+n^2+2|{{{\mathcal {F}}}}^k|)N_{CG}\) multiplications for \(d_N^k\) (or \({\bar{d}}_N^j\)). The cost in computing \({{{\mathcal {A}}}}(X)\) and \({{{\mathcal {A}}}}^*(y)\) is depend on the structure of the matrices \(A_i\), \(i=1,\ldots ,m\), and in particular, in our numerical experiments, \({{{\mathcal {A}}}}(X)\) and \({{{\mathcal {A}}}}^*(y)\) can be calculated efficiently due to the special structure of the matrices \(A_i\), \(i=1,\ldots ,m\).
4 Convergence analysis
We now turn to the issue of the global convergence of Algorithm 1. Define four subsets for the index set \({{{\mathcal {I}}}}=\{p+1,\ldots ,m\}\):
Remark 4.1
The index sets \({\mathcal {C}}_i^k, i=1,2,3,4\) are mutually exclusive and \({\mathcal {B}}^k = \bigcup _{i=1}^4{\mathcal {C}}_i^k\). By (4.1), \({\mathcal {C}}_1^k\) indeed represents the set corresponding to variables on the constraint boundary. The index set \({\mathcal {C}}_2^k\) contains indices associated with variables that are within the boundary but will get to the boundary after the BB step. The index set \({\mathcal {C}}_3^k\) points to the indices corresponding to variables that do not reach the boundary after the BB step. The variables \(y_i^k\) associated with \({{{\mathcal {C}}}}_4^k\) are very close to the boundary but might not be good “active" candidates due to \(g_i^k\le - \nu ^k/(2\alpha _B^k)\le 0\); nevertheless, in the limit, \({\mathcal {C}}_4^k\) might reduce to be empty or identify a part of active set which is said be degenerate (i.e., both \(g_i^k\) and \(y_i^k\) vanish in the limit).
The index \({{{\mathcal {F}}}}^k\) in (3.6) of the estimated inactive set now can be expressed as
where
and
Here, \({\mathcal {D}}^k\) is actually the complementary set of \(\bigcup _{i=1}^3{ {{\mathcal {C}}}}_i^k\) in \({{{\mathcal {I}}}}\). Recalling \({\tilde{y}}^k=\Pi _{{\mathcal {Q}}}[y^k-\alpha _B^kg^k]\), we can rewrite \(d^k\) in (3.11) equivalently as
This expression of \(d^k\) facilitates our convergence analysis.
Our global convergence is based on the following assumption.
Assumption 4.1
There exist two scalars \(\gamma _1,\gamma _2>0\) such that
are satisfied for all k.
Remark 4.2
We remark that Assumption 4.1 holds when \(\lambda _{\min }({\bar{H}}^k)\ge \gamma _1\) and \(\Vert {\bar{H}}^k\Vert \le \gamma _2\) for all k, where \(\lambda _{\min }({\bar{H}}^k)\) denotes the minimum eigenvalue of \({\bar{H}}^k\). Note that if the strong second-order sufficient condition for the problem (2.3) holds at a minimizer \(y^*\), then \(h^TVh>0\) for all nonzero vectors \(h\in \bar{{{{\mathcal {H}}}}}_{\theta }(y^*)\) and all matrices \(V\in \partial _{B}(\nabla f(y^*))\). Equivalently, for all \(V\in \partial _{B}(\nabla f(y^*))\), all matrices \(({{{\mathcal {A}}}}V{{{\mathcal {A}}}}^*)_{\scriptscriptstyle {{{\mathcal {F}}}}{{{\mathcal {F}}}}}\) are positive definite, where \({{{\mathcal {F}}}}=({{{\mathcal {E}}}}\cup {{{\mathcal {I}}}})\backslash {{{\mathcal {I}}}}_0(y^*)\). Therefore, if \({\bar{H}}^k\) is approaching \(({{{\mathcal {A}}}}V{{{\mathcal {A}}}}^*)_{\scriptscriptstyle {{{\mathcal {F}}}}{{{\mathcal {F}}}}}^{-1}\), then Assumption 4.1 holds for some scalars \(\gamma _1, \gamma _2>0\). We will prove in Sect. 5 (refer to Theorem 5.2) that if the constraint nondegenercy condition [10] for the problem (1.1) holds at \(X^*\) (\(X^*\) is associated with \(y^*\)), then the strong second-order sufficient condition for the problem (2.3) holds at a minimizer \(y^*\). In this sense, Assumption 4.1 is consistent with the constraint nondegenercy condition for the problem (1.1).
Lemma 4.1
Suppose that Assumption 4.1holds. Then
Furthermore, equality holds if and only if \(d^k=0\).
Proof
According to (4.5),
For \(i\in {{{\mathcal {C}}}}_2^k\), due to (4.1b) and (3.2), \(y_i^k-\alpha _B^kg_i^k\le 0\) and then \(\alpha _B^kg_i^k\ge y_i^k> 0\), and therefore \(y_i^kg_i^k\ge (y_i^k)^2/\alpha _B^k> 0\) for \(i\in {{{\mathcal {C}}}}_2^k\). Thus, the first term in the right hand side of (4.9) is no greater than 0. The second term is obviously non-positive. Also, the third term is also non-positive by (4.6). Consequently, (4.8) is true. From (4.9), we know that \(d^k=0\) if and only if all the terms in the right-hand side of (4.9) vanish. \(\square\)
Lemma 4.2
Let \(\{d^k\}\) and \(\{y^k\}\) be generated by Algorithm 1. If Assumption 4.1holds, then
where \(\ f^k_p=(\xi Q^k f_p^{k-1}+f(y^k))/Q^k\), and \(\chi ^k=\frac{1}{k+1}\sum _{i=0}^{k}f(y^i)\).
Proof
The proof follows analogously from [36, Lemma 1.1]. \(\square\)
Proposition 4.1
Given \(d^k\) defined in (4.5), we have
where \(y^k \in {{{\mathcal {Q}}}}\).
Proof
Since \(\bigcup _{i=1}^4{\mathcal {C}}_i^k={\mathcal {B}}^k\), the conclusion follows from (3.11) and (3.2).\(\square\)
Proposition 4.2
The index sets \({\mathcal {C}}_i^k, i=1,2,3\) can be described as follows
Proof
According to (4.1a), if \(i\in {\mathcal {C}}_1^k\), then \({\tilde{y}}_i^k=\max (0,y_i^k-\alpha _B^k g_i^k)=\max (0,-\alpha _B^k g_i^k)=0\) and therefore (4.12a) is true. If \(i\in {\mathcal {C}}_2^k\), then
because of (3.2) and (4.1b). Thus, \(g_i^k\ge y_i^k/\alpha _B^k>0\) which together with (4.1b) implies (4.12b). By (3.2) and (4.1c), \(0<y^k_i-\alpha _B^kg_i^k={\tilde{y}}^k_i\le \nu ^k\) for \(i\in {\mathcal {C}}_3^k\) and \(\alpha _B^kg_i^k<y_i^k\le \nu ^k+\alpha ^k_B{g^k_i}\). Use (4.1c) to have (4.12c). Finally, by (4.3), if \(i\in {\mathcal {D}}^k\), then \({\tilde{y}}^k_i=y^k_i-\alpha _B^kg_i^k>\nu ^k\) which yields (4.12d). \(\square\)
The reformulation of \({\mathcal {C}}_i^k,i=1,2,3\) in (4.12) facilitates our subsequent characterization of optimality conditions.
Lemma 4.3
Let Assumption 4.1hold, and \(\{d^k\}\) and \(\{y^k\}\) be generated by Algorithm 1. Then \(y^k\) is a KKT point of the problem (2.3) if and only if \(d^k=0\).
Proof
If \(y^k\) is a KKT point of the problem (2.3), then \(\nu ^k=\min {\lbrace \epsilon _0,\sqrt{\varrho ^k}\rbrace }=\sqrt{\varrho ^k}=0\) which implies
By (4.2), (4.3) and (4.4), if \(-g_i^k<\nu ^k/(2\alpha _B^k)\) with \(i\in {\mathcal {F}}^k \cap {{{\mathcal {I}}}}\) (\(={{{\mathcal {D}}}}^k\cap ({\mathcal {C}}_4^k)^0\)), then
and therefore \(y^k_i>\nu ^k/2=0, i\in {\mathcal {F}}^k \cap {{{\mathcal {I}}}}\). Thus use (4.14) to get \(g_i^k=0, i\in {\mathcal {F}}^k\) and \(d_i^k=0,i\in {\mathcal {F}}^k\). If \({\mathcal {C}}_3^k\ne \emptyset\), from (4.12c) and \(\nu ^k=0\), we have \(0<{\tilde{y}}_i^k\le \nu ^k=0,i\in {\mathcal {C}}_3^k\), which is a contradiction. Therefore \({\mathcal {C}}_3^k=\emptyset\). In view of \(\nu _k=0\), (4.1d) and (4.14), \(y_i^k=g_i^k=0\) and \({\tilde{y}}_i^k>0\) for \(i\in {\mathcal {C}}_4^k\). Using (4.5) gives \(d_i^k=0\) and \({\tilde{y}}_i^k=0\) for \(i\in {\mathcal {C}}_4^k\), which contradicts \({\tilde{y}}_i^k>0\). So \({\mathcal {C}}_4^k\) is empty. By (4.12b) and (4.14), the index set \({\mathcal {C}}_2^k\) is empty, too. Hence, \(d^k= 0\).
Conversely, assume \(d^k=0\). From (4.5) and (4.12a), we have \(y_i^k=0,g_i^k\ge 0,i\in {{{\mathcal {C}}}}_1^k\). By (4.5) and (4.12b), we know \(y_i^k=d_i^k=0\) indicating that \({\mathcal {C}}_2^k\) is empty. For \(i\in {{{\mathcal {C}}}}_3^k\), due to (4.5) and (4.12c), it is true that \(y_i^k>0,g_i^k=0\). Also, based on (4.5) and (4.1d), it holds that \({\mathcal {C}}_4^k=\emptyset\) or \(\nu ^k=0\), where the latter implies that \(y^k\) is a KKT point of the problem (2.3). For the case \({\mathcal {C}}_4^k=\emptyset\), from (4.5), we have \((Z{\bar{H}}^kZ^Tg^k)_i=0,i\in {\mathcal {F}}^k\) which together with (4.6) gives \(g^k_i= 0\), \(i\in {\mathcal {F}}^k\). Overall, by (3.3), \(y^k\) is a KKT point of the problem (2.3). \(\square\)
Lemma 4.4
Let \(\{d^k\}\) and \(\{y^k\}\) be generated by Algorithm 1. If \(d^k\ne 0\), then
where \({{{\mathcal {Q}}}}\) is defined in (2.1).
Before proving Lemma 4.4, we make some comments on the implication of this lemma. From the current iterate \(y^k\), the trial point \(y^k+\alpha d^k\) is searched along \(d^k\). It can be seen that the largest step size that makes this trial point remain in the feasible region \({\mathcal {Q}}\) must be equal or greater than \(\bar{\beta ^k}:=\min \{1,\frac{\nu ^k}{2\Vert {d^k}\Vert _\infty }\}\). Therefore, Lemma 4.4 says that if \(\alpha \le \bar{\beta ^k} \le \beta ^k\), by (4.15), we have \(y^k+\alpha d^k\in {\mathcal {Q}}\), and
Proof
It suffices to prove that \(y_i^k+\bar{\beta ^k} d_i^k\ge 0\) for all \(i\in {{{\mathcal {I}}}}\). For \(i\in {{{\mathcal {B}}}}^k\) and \(0<\alpha \le 1\), \(y_i^k+\alpha d_i^k=(1-\alpha )y_i^k+\alpha (y_i^k+d_i^k)\ge 0\) due to \(y_i^k\ge 0\) and Proposition 4.1. Hence, \(y_i^k+\bar{\beta ^k} d_i^k\ge 0,i\in { {{\mathcal {B}}}}^k\). For \(i\in {\mathcal {F}}^k\cap {{{\mathcal {I}}}}\) (\(={{{\mathcal {D}}}}^k\cap ({\mathcal {C}}_4^k)^0\)), \(y^k_i>\nu ^k+\alpha ^k_B{g^k_i}\) due to (4.12d). This combining with (4.4) gives \(y^k_i>\nu ^k/2, i\in {\mathcal {F}}^k \cap {{{\mathcal {I}}}}\). Recall \(\bar{\beta ^k} \le \frac{\nu ^k}{2\Vert d^k\Vert _\infty }\). Thus, \(y^k_i+ \bar{\beta ^k}d^k_i\ge \frac{\nu ^k}{2}-\frac{\nu ^k}{2\Vert d^k\Vert _\infty }|d^k_i|\ge 0,\) \(i\in {\mathcal {F}}^k \cap {{{\mathcal {I}}}}\). \(\square\)
Lemma 4.5
Suppose that Assumption 4.1holds. Let \(\{d^k\}\) and \(\{y^k\}\) be generated by Algorithm 1. Then there exists a scalar \(u_d>0\) such that
for all k, i.e., the sequence \(\{d^k\}\) is bounded.
Proof
From (4.5), we have
and together with (4.7) and (4.13), it follows
Since g(y) is continuous and \(\{y^k\}\) is bounded, inequality (4.18) with \(\alpha _B^k\le \alpha _{\max }\) implies \(\{\Vert d^k\Vert ^2\}\) is bounded. Hence, there exists a scalar \(u_d>0\) such that \(\Vert d^k\Vert _{\infty }\le u_d\) for all k. \(\square\)
The boundedness of \(\{d^k\}\) and Lemma 4.4 lead to
The next lemma gives a lower bound of the step size \(\alpha ^k\), which also implies that Algorithm 1 is well-defined (i.e., the inner loop (from Line 5 to Line 7) terminates finitely).
Lemma 4.6
Suppose that Assumption 4.1holds. Let \(\{\alpha ^k\}\) be generated by Algorithm 1. Then there exists a scalar \({\bar{\alpha }}>0\) such that
where \(\bar{\beta ^k}\) is defined after Lemma 4.4, and \(\sigma \in (0,1)\) is from Algorithm 1.
Proof
From (4.17), (4.7) and (4.13), we obtain
where the last inequality follows from (4.9) and \(\alpha _B^k\le \alpha _{\max }\). We now prove that the step size \(\alpha ^k\) generated by Algorithm 1 is no less than either \(\sigma \bar{\beta ^k}\) or some constant \({\bar{\alpha }}>0\). If \(\alpha ^k<\sigma \bar{\beta ^k}\), then the trial step size \(\alpha _t^k:=\frac{\alpha ^k}{\sigma }\) cannot be accepted in Algorithm 1. As \(\alpha _t^k<\bar{\beta ^k}\),
where the first equality follows from (4.16). By the mean value theorem,
where \(L_g\) is the Lipschitz constant of g(y). By (4.10), (4.21) and (4.22),
and together with (4.20), we get
As \(\alpha ^k=\sigma \alpha _t^k\), it is true that \(\alpha ^k\ge {\bar{\alpha }}\) in the case \(\alpha ^k<\sigma \bar{\beta ^k}\), where \({\bar{\alpha }}=\frac{2\sigma (1-\delta )}{L_g\max (\alpha _{\max },\gamma _2)}\). Therefore,
holds in all cases. \(\square\)
Theorem 4.1
Suppose that Assumption 4.1holds. Let \(\{y^k\}\) be generated by Algorithm 1. Then any accumulation point of the sequence \(\{ y^k \}\) is a KKT point of the problem (2.3).
Proof
The update rule of \(Q^{k+1}\) given by Algorithm 1 yields
By the nonmonotone reduction condition of f and (4.10), we have
where the last inequality follows from (4.8) and (4.23). Since \(\{y^k\}\) is bounded, \(\{f(y^k)\}\) and \(\{f^k_p\}\) are bounded below by (4.10). Combine with (4.24) to have
Using (4.8), we obtain that
We now prove that any accumulation point of \(\{y^k\}\) is a KKT point of the problem (2.3). Let \(y^*\) be an accumulation point of \(\{y^k\}\), and the subsequence \(\{y^{k_i}\}\) of \(\{y^k\}\) converges to \(y^*\). It follows from the continuity of \(\nabla f(y)\) that \(g^{k_i}\rightarrow g^*:=\nabla f(y^*)\) as \(k_i\rightarrow \infty\). Similarly, due to (3.4) of the KKT error \(\varrho ^{k_i}\), we can assume, without loss of generality, that \(\{\varrho ^{k_i}\}\) converges to some limit point \(\varrho ^*\). If \(\varrho ^*=0\), then \(y^*\) is already a KKT point. Otherwise, for all sufficiently large \(k_i\), \(\varrho ^{k_i}\ge \frac{\varrho ^*}{2}\). By (4.19) and Lemmas 4.5 and 4.6, \(\alpha ^{k_i}\) is bounded away from zero, and according to (4.25),
As k increases, we can assume without loss of generality that \({{{\mathcal {C}}}}_i^k,i=1,2,3,4\) and \({{{\mathcal {F}}}}^k\) are constants for all sufficiently large \(k=k_i\), and thereby, we drop the superscripts k by simply denoting \({{{\mathcal {C}}}}_i,i=1,2,3,4\) and \({{{\mathcal {F}}}}\). Using (4.9) and (4.6), we have that
Recall the definitions of \(d^k\) and \({{{\mathcal {C}}}}_i^k,i=1,2\) to have
Putting above equalities and inequalities together, we conclude that \(y^*\) is a KKT point of the problem (2.3). \(\square\)
5 Local quadratic convergence
We now investigate the convergence behavior of Algorithm 1 with Algorithm 2 embedded in Line 9 for adaptively computing the search direction. For simplicity, we call such an implementation of Algorithm 1 as AASA(Adaptive), for which the sequences \(\{y^k\}\) and \(\{z^j\}\) are called the outer-loop and inner-loop sequence, respectively. It should be noticed from Algorithm 2 that a particular inner-loop sequence \(\{z^j\}\) starts from a certain outer-loop iterate \(y^{k+1}\), and has one of the two mutually exclusive scenarios: (a) \(\{z^j\}\) stops at some \(z^{j_k}\) and then the iteration of AASA(Adaptive) enters back to \(y^{k+1}\), and continuously produces \(y^{k+2}\), and (b) \(\{z^j\}\) is an infinite sequence satisfying \({\varrho (z^{j})}\rightarrow 0\) as \(j\rightarrow \infty\). For the former case (a), the intermediate \(\{z^j\}_{j=1}^{j_k}\) are only trials which do not change current outer \(y^{k+1}\), whereas for (b), AASA(Adaptive) converges. Therefore, one and only one of the following situations occurs in AASA(Adaptive):
-
(i)
an infinite outer-loop sequence \(\{y^{k}\}_{k=1}^{\infty }\) is generated, or
-
(ii)
from some \(y^{k+1}\), a sequence \(\{z^{j}\}_{j=1}^{\infty }\) is generated by Algorithm 2 and AASA(Adaptive) converges.
Theorem 5.1
Suppose that Assumption 4.1holds, then any accumulation point of the sequence \(\{ y^k \}\) from case (i) or \(\{z^j\}\) from case (ii) is a KKT point of the problem (2.3).
Proof
If case (i) occurs, we know that all the inner-loop sequences \(\{z^j\}\) are finite sequences, and the convergence analysis of Theorem 4.1 is true for the outer-loop sequence \(\{y^k\}_{k=1}^\infty\). Indeed, for a \(y^{k+1}\), if AASA(Adaptive) generates a finite sequence \(\{z^j\}_{j=1}^{j_k}\), the search direction at \(y^{k+1}\) will be reset as the L-BFGS direction \(d_Q^{k+1}\) (cf. Line 14 of Algorithm 2), and thus Theorem 4.1 applies for this case.
For the case of (ii), the condition in Line 6 of Algorithm 2 ensures that
By Assumption 4.1 and Lemma 4.1,
and use (5.1) to conclude \(\{f(z^j)\}\) is monotonically decreasing. The coercivity of f ensures the boundedness of \(\{f(z^j)\}\) and further the convergence of \(\{f(z^j)\}\). Thus by (5.1) and Lemma 4.1, \(\lim \limits _{j\rightarrow \infty }\nabla f(z^j)^Td_N(z^{j})=0,\) a result similar to (4.26). With this and following analogously the proof of Theorem 4.1, we know any accumulation point of the sequence \(\{ z^j \}\) is a KKT point of (2.3). \(\square\)
Let \(y^*\) be an accumulation point of the sequence \(\{y^k\}\) (or \(\{z^j\}\)) generated by AASA(Adaptive). According to the convexity of (2.3), \(y^*\) is also a minimizer. From [22, Theorem 2.2], we know that a minimizer \(y^*\) is isolated under the second-order sufficient condition, which, by Theorem 5.2 below, is true under the constraint nondegeneracy condition for the primal problem (1.1). Therefore, we can assume that the sequence \(\{y^k\}\) (or \(\{z^j\}\)) converges to a minimizer \(y^*\) with the constraint nondegeneracy condition, and define accordingly
The constraint nondegenercy condition holds at \(X^*\) if
where \(T_{{{\mathcal {K}}}}(X)\) denotes the tangent cone of \({{{\mathcal {K}}}}\) at \(X\in {{{\mathcal {K}}}}\), \(\mathrm{lin}T_{{{\mathcal {K}}}}(X)\) denotes the largest linear space contained in \(T_{{{\mathcal {K}}}}(X)\), and \({{{\mathcal {I}}}}_e\) is the identity mapping from \({{{\mathcal {S}}}}^n\) to \({{{\mathcal {S}}}}^n\). Let the primal index set of active constraints at \(X^*\) be
Then the linear mapping \({{{\mathcal {A}}}}_{\bar{{{\mathcal {F}}}}}\): \({{{\mathcal {S}}}}^n\rightarrow {\mathbb {R}}^{p+{\bar{s}}}\) given by \({{{\mathcal {A}}}}_{\bar{{{\mathcal {F}}}}}(X)=[{{{\mathcal {A}}}}(X)]_{\bar{{{\mathcal {F}}}}}\) has its adjoint \({{{\mathcal {A}}}}^*_{\bar{{{\mathcal {F}}}}}\), where \({\bar{{{\mathcal {F}}}}}={{{\mathcal {E}}}}\cup {{{\mathcal {I}}}}^p(X^*)\), and \({\bar{s}}\) denotes the cardinality of \({{{\mathcal {I}}}}^p(X^*)\).
Theorem 5.2
If the constraint nondegeneracy condition for the problem (1.1) holds at \(X^*\) given in (5.2), then the strong second-order sufficient condition for the dual problem (2.3) holds at \(y^*\).
Proof
By [10, Lemma 4.3], for any \(V\in \partial _B(\Pi _{{{{\mathcal {S}}}}_+^n}[X^*])\),
for any \(h_{\bar{{{\mathcal {F}}}}}\ne 0\) with \(h\in {\mathbb {R}}^m\). Because of the complementarity between \(\langle A_i,X^*\rangle =b_i,i\in {{{\mathcal {I}}}}\) and \(y^*_{\scriptscriptstyle {{\mathcal {I}}}}\), \({\bar{{{\mathcal {F}}}}}\cup {{{\mathcal {I}}}}_0(y^*)\) equals \({{{\mathcal {E}}}}\cup {{{\mathcal {I}}}}\), but \({\bar{{{\mathcal {F}}}}}\cap {{{\mathcal {I}}}}_0(y^*)\) may not be empty. So, if \(i\notin {\bar{{{\mathcal {F}}}}}\), then \(i\in {{{\mathcal {I}}}}_0(y^*)\). For any \(h\in \bar{{{{\mathcal {H}}}}}_{\theta }(y^*)\backslash \{0\}\), \(h_i=0,i\in {{{\mathcal {I}}}}_0(y^*)\), and then \({{{\mathcal {A}}}}^*(h)=\sum _{i\in {\bar{{{\mathcal {F}}}}}} h_iA_i+\sum _{i\notin {\bar{{{\mathcal {F}}}}}}h_iA_i={{{\mathcal {A}}}}_{\bar{{{\mathcal {F}}}}}^*(h_{\bar{{{\mathcal {F}}}}})\). Therefore, for any \(h\in \bar{{{{\mathcal {H}}}}}_{\theta }(y^*)\backslash \{0\}\) and any \(V\in \partial _B(\Pi _{{{{\mathcal {S}}}}_+^n}[X^*])\),
which implies the strong second-order sufficient condition. \(\square\)
Under the constraint nondegeneracy condition for the primal problem (1.1), the following theorem shows that our algorithm converges to a minimizer of the dual problem (2.3) quadratically.
Theorem 5.3
Let \(y^*\) be any limit point from case (i) or (ii) of AASA(Adaptive). If the strict complementarity condition for the dual problem (2.3) holds at \(y^*\) and the constraint nondegeneracy condition holds at \(X^*\) given by (5.2), then \(y^*\) must be a limit point from case (ii); that is, \(y^*\) is a limit point of \(\{z^{j}\}_{j=1}^\infty\) generated at Line 7 of Algorithm 2 from some outer iterate \(y^{k+1}\). Moreover, \(\{z^{j}\}_{j=1}^\infty\) converges to \(y^*\) quadratically.
Proof
By assumption, Theorem 5.2 ensures that the strong second-order sufficient condition holds at the KKT point \(y^*\), which is a minimizer by the convexity. Using Theorem 3.2, for sufficiently large k, \({{{\mathcal {F}}}}(y^k)\) (or \({{{\mathcal {F}}}}(z^j)\)) and \({{{\mathcal {B}}}}(y^k)\) (or \({{{\mathcal {B}}}}(z^j)\)) can correctly identify the inactive and active sets \({{{\mathcal {F}}}}\) and \({{{\mathcal {B}}}}\), respectively.
Let \(X^*\) and \({{{\mathcal {I}}}}^p(X^*)\) be defined by (5.2) and (5.3), respectively. Then the strict complementarity condition ensures \({{{\mathcal {F}}}}=\bar{{{\mathcal {F}}}}:={{{\mathcal {E}}}}\cup {{{\mathcal {I}}}}^p(X^*)\). Therefore, with the active (inactive) set identified by \(y^k\) which is sufficiently close to \(y^*\), solving (2.3) is equivalent to \(\min _{z\in {{\mathcal {Z}}}} f(z)\), where \({{{\mathcal {Z}}}}=\{z|z_i=0,i\in {{{\mathcal {B}}}}\}\). At such \(y^k\), define an auxiliary function \({\hat{f}}(z_{\scriptscriptstyle {{\mathcal {F}}}})\) with the variables \(z_{\scriptscriptstyle {{\mathcal {F}}}}\) extracted from z by \({{\mathcal {F}}}\) and \(z_{\scriptscriptstyle {{\mathcal {B}}}}=0\) fixed, and \({\hat{f}}(z_{\scriptscriptstyle {{\mathcal {F}}}})=f_{|_{z\in {{{\mathcal {Z}}}}}}(z)\). Thus
Due to the convexity of \({\hat{f}}(z_{\scriptscriptstyle {{\mathcal {F}}}})\), (5.4) can be solved from
where \(\nabla f(z)\) is given by (2.4).
Let \(\{{\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^j\}_{j=1}^{\infty }\) be the sequence from the generalized Newton iteration for \(F(z_{\scriptscriptstyle {{\mathcal {F}}}})=0\) via
where \({\hat{J}}^j{\hat{d}}_{\scriptscriptstyle {{\mathcal {F}}}}^j=-F({\hat{z}}^j_{\scriptscriptstyle {{\mathcal {F}}}})\) and \({\hat{J}}^j\in \partial _B F({\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^j)\). For the index set \({{{\mathcal {F}}}}\), define the linear mapping \({{{\mathcal {A}}}}_{{\scriptscriptstyle {{\mathcal {F}}}}}\): \({{{\mathcal {S}}}}^n\rightarrow {\mathbb {R}}^{|{{{{\mathcal {F}}}}}|}\) by \({{{\mathcal {A}}}}_{\scriptscriptstyle {{\mathcal {F}}}}(X)=[{{{\mathcal {A}}}}(X)]_{\scriptscriptstyle {{\mathcal {F}}}}\), whose adjoin mapping \({{{\mathcal {A}}}}_{{\scriptscriptstyle {{\mathcal {F}}}}}^*\): \({\mathbb {R}}^{|{{{{\mathcal {F}}}}}|}\rightarrow {{{\mathcal {S}}}}^n\) is given by \({{{\mathcal {A}}}}_{\scriptscriptstyle {{\mathcal {F}}}}^*(h_{\scriptscriptstyle {{\mathcal {F}}}})=\sum _{i\in {\scriptscriptstyle {{\mathcal {F}}}}} h_iA_i\). By (2.4),
is locally Lipschitz continuous and also strongly semi-smooth on \({\mathbb {R}}^{|{{{\mathcal {F}}}}|}\) [3, 32]. From [10, Lemma 4.3], for all \(V\in \partial _B(\Pi _{{{{\mathcal {S}}}}_+^n}[G+{{{\mathcal {A}}}}_{\scriptscriptstyle {{\mathcal {F}}}}^*(y_{{\scriptscriptstyle {{\mathcal {F}}}}}^*)])\), every \({{{\mathcal {A}}}}_{\scriptscriptstyle {{\mathcal {F}}}}V{{{\mathcal {A}}}}_{\scriptscriptstyle {{\mathcal {F}}}}^*\in \partial _B F(y_{\scriptscriptstyle {{\mathcal {F}}}}^*)\) is positive definite. Consequently, by [23, Theorems 3.2 and 3.3], \(\{{\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^{j}\}\) converges to \(y_{\scriptscriptstyle {{\mathcal {F}}}}^*\) globally and quadratically provided that \({\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^1\) is sufficiently close to \(y_{\scriptscriptstyle {{\mathcal {F}}}}^*\).
Recall \(y^*\) is a limit point from case (i) or (ii). By Theorem 5.1, we can assume, without loss of generality, that \(z^1\) (see Line 3 of Algorithm 2) is sufficiently close to the limit point \(y^*\) of either case (i) or (ii). Let \({z}_{{{\mathcal {F}}}}^1\) be the subvector of \(z^{1}\) indexed by \({{\mathcal {F}}}\). Starting from \({\hat{z}}_{{{\mathcal {F}}}}^1={z}_{{{\mathcal {F}}}}^1\), the sequence \(\{{\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^{j}\}\) generated by (5.5) converges to \(y_{\scriptscriptstyle {{\mathcal {F}}}}^*\) globally and quadratically. Augment \({\hat{z}}_{\scriptscriptstyle {{\mathcal {F}}}}^{j}\) to \({\hat{z}}^{j}\) by setting \({\hat{z}}_{\scriptscriptstyle {{\mathcal {B}}}}^j=0\) accordingly to have an auxiliary sequence \(\{{\hat{z}}^{j}\}\), and we know it converges to \(y^*\) globally and quadratically. Our final task is to show \(\{{\hat{z}}^j\}\) is the same as that generated by Algorithm 2 (cf. Line 7).
The proof is by induction on j. First, \(z^1={\hat{z}}^1\). Suppose the conclusion holds for \(j>0\) and we will show \(z^{j+1}={\hat{z}}^{j+1}\). In fact, as \(\{{\hat{z}}^j\}\) converges to \(y^*\) and \({\hat{z}}^1(=z^1)\) is sufficiently close to \(y^*\), by the inductive hypothesis, we know \({{{\mathcal {F}}}}(z^j)={{{\mathcal {F}}}}\) and \({{{\mathcal {B}}}}(z^j)={{{\mathcal {B}}}}\). This ensures that the later condition in Line 6 of Algorithm 2 is fulfilled. By (3.11) and (3.15), \([{\bar{d}}_N^j]_{\scriptscriptstyle {{\mathcal {F}}}}(=[d_N(z^j)]_{\scriptscriptstyle {{\mathcal {F}}}})\) is exactly \({\hat{d}}^j_{\scriptscriptstyle {{\mathcal {F}}}}\) in (5.5). Because of \({\hat{z}}^j\rightarrow y^*\) and \([{\bar{d}}_N^j]_{\scriptscriptstyle {{\mathcal {B}}}}=0\) (see Lines 5 and 12 of Algorithm 2), \(d_N({\hat{z}}^j)\rightarrow 0\). Second, due to \(y_{\scriptscriptstyle {{{\mathcal {F}}}}\cap {{{\mathcal {I}}}}}^*>0\), assume, without loss of generality, \({\hat{z}}_{\scriptscriptstyle {{{\mathcal {F}}}}\cap {{{\mathcal {I}}}}}^j>0\). By induction, we further have \(\Pi _{{{\mathcal {Q}}}}(z^{j}+{\bar{d}}_N^{j})=\Pi _{{{\mathcal {Q}}}}({\hat{z}}^{j}+{\bar{d}}_N^{j})={\hat{z}}^{j}+{\bar{d}}_N^{j}={z}^{j}+{\bar{d}}_N^{j}\). Note that the strict complementarity condition implies \(y_{{\scriptscriptstyle {{\mathcal {B}}}}}^*=0\) and \(g_{{\scriptscriptstyle {{\mathcal {B}}}}}^*>0\). Assume \(g_{{\scriptscriptstyle {{\mathcal {B}}}}}({\hat{z}}^j)>0\), and thus \(g_{{\scriptscriptstyle {{\mathcal {B}}}}}(z^j)>0\). By (3.11) and (3.2),
Hence, \(z_{{\scriptscriptstyle {{\mathcal {B}}}}}^j=0\) and \(g_{{\scriptscriptstyle {{\mathcal {B}}}}}(z^j)>0\) imply \([d_N(z^j)]_{\scriptscriptstyle {{\mathcal {B}}}}=0\). Due to the generalized Newton equation \(J_{\scriptscriptstyle {{\mathcal {F}}} F}^j[{\bar{d}}_N^{j}]_{\scriptscriptstyle {{\mathcal {F}}}}=-g_{\scriptscriptstyle {{\mathcal {F}}}}(z^j)\) with \(J_{\scriptscriptstyle {{\mathcal {F}}} F}^j\in \partial _B F(z_{\scriptscriptstyle {{\mathcal {F}}}}^j)\), it holds that
and \(\Vert z_{\scriptscriptstyle {{\mathcal {F}}}}^j+[{\bar{d}}_N^{j}]_{\scriptscriptstyle {{\mathcal {F}}}}-y_{\scriptscriptstyle {{\mathcal {F}}}}^*\Vert ={{{\mathcal {O}}}}(\Vert z_{\scriptscriptstyle {{\mathcal {F}}}}^j-y_{\scriptscriptstyle {{\mathcal {F}}}}^*\Vert ^2)\). By [10, Lemma 4.3], \(J_{\scriptscriptstyle {{\mathcal {F}}} F}^j\) is uniformly positive definite for all \(z_{\scriptscriptstyle {{\mathcal {F}}}}^j\), i.e., \(\exists {\bar{\rho }}>0\) such that
Applying [6, Lemma 3.2 and Theorem 3.3], we have
As \(z_{{\scriptscriptstyle {{\mathcal {B}}}}}^j=0\) and \([d_N(z^j)]_{\scriptscriptstyle {{\mathcal {B}}}}=0\), it holds that
which together with (5.6) yields that
Consequently, the sufficient decrease condition (3.17) is true due to \(\Pi _{{{\mathcal {Q}}}}(z^{j}+{\bar{d}}_N^{j})=z^{j}+{\bar{d}}_N^{j}\). According to Algorithm 2 (see Lines 6-7), the new iterate is
where the last equality follows from \([d_N(z^j)]_{\scriptscriptstyle {{\mathcal {F}}}}={\hat{d}}^j_{{\scriptscriptstyle {{\mathcal {F}}}}}\), \([d_N(z^j)]_{\scriptscriptstyle {{\mathcal {B}}}}=0\), and the inductive hypothesis. This completes the proof. \(\square\)
6 Numerical experiments
In this section, we conduct numerical evaluation of Algorithm 1 with the adaptive acceleration of Algorithm 2 (denoted by AASA(Adaptive)) on various problems. Our numerical experiments are obtained by comparing with several other approaches or implementations, including the inexact smoothing Newton method (denoted by ISNM) [10], the projected BFGS method (denoted by P-BFGS) [14], Algorithm 1 accelerated by the pure limited memory BFGS (denoted by AASA(L-BFGS)), and the alternating direction method (ADM) [12, 35]. The codes of ISNM and P-BFGS are available online,Footnote 2 while the ADM is coded by ourselves. For comparison purpose, we report the number of iterations, CPU time and the KKT residuals \(\varrho ^k\). The numerical comparison was carried out on a PC under Windows 8 (64bits) system with Inter(R) Core(TM) i5-4590 CPU @ 2.4GHz and 4GB memory, in the Matlab environment (R2019a).
For the parameters involved, we terminate our algorithm whenever \(\varrho ^k\le \varepsilon =10^{-6}\); other parameters in our implementation are given as follows:
All the parameters for AASA(L-BFGS) are the same as AASA(Adaptive). For ISNM, P-BFGS and ADM, we set \(\varepsilon =10^{-6}\) as tolerance and use default values for other parameters. We remark that the stopping conditions for AASA(Adaptive), ISNM, P-BFGS and ADM are not completely the same, due to their different optimality measures involved.
Our numerical examples are in the following form:
where \({{{\mathcal {B}}}}_e\), \({{{\mathcal {B}}}}_l\) and \({{{\mathcal {B}}}}_u\) are three index subsets of \(\{(i,j)|1\le i\le j\le n\}\); in particular, the values of \(l_{ij}\) for \((i,j)\in {{{\mathcal {B}}}}_l\) and \(u_{ij}\) for \((i,j)\in {{{\mathcal {B}}}}_u\) are lower and upper bounds, respectively, satisfying \(l_{ij}<u_{ij}\) for all \((i,j)\in {{{\mathcal {B}}}}_l\cap {{{\mathcal {B}}}}_u\).
We choose various specific problems for testing. The set of test problems includes synthetic data as well as real world data. Numerical results from synthetic problems are reported in Sect. 6.1, where the data matrix G is generated randomly with medium size problems (\(n<1000\)) and large-scale problems (\(1000\le n \le 2000\)). Numerical results from real world data are shown in Sect. 6.2, where two data matrices are from financial markets (Shenzhen Stock Exchange and Shanghai Stock Exchange in China) and constraint positions and constraint levels are specified to simulate some stress testing scenarios in financial risk management.
6.1 Synthetic examples
Similar to [10, 12], we randomly generate six synthetic examples (denoted by E1–E6) as follows:
E1: The matrix G is generated by Matlab built-in command rand via
G=2.0*rand(n,n)-ones(n,n); G=triu(G)*triu(G,1)’; for i=1:n; G(i,i)=1; end; The index sets are
where \(n_r\le n\) is an positive integer. Moreover, \(b_{ii}=1\) for \((i,i)\in {{{\mathcal {B}}}}_e\), \(l_{i {j}}=-0.1\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{i {j}}=0.1\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
E2: G and \({{{\mathcal {B}}}}_e\) are the same as in E1. The index sets \({{{\mathcal {B}}}}_l, {{{\mathcal {B}}}}_u\subset \{(i,j)|1\le i<j\le n\}\) consist of \(\min (n_r,n-i)\) pairs (i, j) with j randomly generated at the ith row of X, \(i=1,\ldots ,n\). Similar to E1, \(b_{ii}=1\) for \((i,i)\in {{{\mathcal {B}}}}_e\), \(l_{ij}=-0.1\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{ij}=0.1\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
E3: The settings are the same as in E1 except that \(l_{i {j}}=-0.5\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{ij}=0.5\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
E4: The settings are the same as in E2 except that \(l_{i {j}}=-0.5\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{ij}=0.5\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
E5: The settings are the same as in E1 except that \(l_{i {j}}=-0.5*\texttt {rand}\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{ij}=0.5*\texttt {rand}\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
E6: The settings are the same as in E2 except that \(l_{i {j}}=-0.5*\texttt {rand}\) for \((i,j)\in {{{\mathcal {B}}}}_l\), and \(u_{ij}=0.5*\texttt {rand}\) for \((i,j)\in {{{\mathcal {B}}}}_u\).
6.1.1 Choice of the parameter l
Generally, the performance of the L-BFGS method is dependent on the parameter l in (3.12). Also, since AASA(Adaptive) and AASA(L-BFGS) both involve the L-BFGS update, a good choice l is desired practically. For that purpose, we particularly test AASA(L-BFGS) using various \(l=2,3,5,8\) on E3 with \(n=1000,1500,2000\) and \(n_r=300,600,800,1200\). The numerical results are listed in Table 1, where the label ‘Iter’ stands for the number of iterations, and \(m=2(n-1-n_r)n_r+(1+n_r)n_r +n\) is the number of constraints.
From Table 1, overall, we observed that \(l=3\) turns out to be a good choice for AASA(L-BFGS). In particular, the algorithm with \(l=3\) converges (in CPU time) fastest in general. Since AASA(Adaptive) generates the same iteration in the earlier stage as AASA(L-BFGS), we also set \(l=3\) for both AASA(Adaptive) and AASA(L-BFGS) in the following numerical experiments.
6.1.2 Fast local convergence
We now demonstrate the fast local convergence of AASA(Adaptive) in practice. For illustration, we run AASA (Adaptive) on two instances of E2: one is a medium instance with \(n=500\), \(n_r=200\) and \(m=90{,}400\), and the other is a large-scale instance with \(n=2000\), \(n_r=500\) and \(m=1{,}751{,}500\). The toleranceFootnote 3\(\varepsilon\) is set to be \(10^{-8}\) in order to observe the quadratic convergence.
In this experiment, AASA(Adaptive) solves the first instance within 160 iterations, where the generalized Newton steps \(d_N^k\) and \({\bar{d}}_N^{j}\) are used 15 times (\({\bar{d}}_N^{j}\) is rejected for once time, accepted 3 times, and \(d_N^k\) is used for the remaining 11 times). For the second instance, it takes 311 iterations, where the generalized Newton steps \(d_N^k\) and \({\bar{d}}_N^{j}\) are used 17 times (\({\bar{d}}_N^{j}\) is rejected for 2 times, accepted 2 times, and \(d_N^k\) is used for the remaining 13 times). The detailed information of iterations on the two instances is given in Tables 2 and 3, where the label ‘Res’ represents the KKT residual. The column of ‘Step \(d^k\)’ gives information about the search direction, and ‘Active set’ tells if the true active set is detected or not; moreover, the column labeled by ‘Full step \({\bar{d}}_N^{j}\)’ shows if the full semi-smooth Newton step \({\bar{d}}_N^{j}\) (in Algorithm 2) is accepted or not. From Tables 2 and 3, we know that the residuals in the last 3 or 2 iterations drop very rapidly as long as the active set is identified. The semi-Newton direction \({\bar{d}}_N^{j}\) is used at the final several iterations and fast local convergence is observed.Footnote 4
6.1.3 Results from medium size problems
We test E1–E6 with n varying from 400 to 900 and \(n_r\) from 100 to 500. In this testing, the maximum number of iterations for ISNM, AASA(L-BFGS), AASA(Adaptive), P-BFGS and ADM are set to be 1000, 2000, 2000, 2000 and 3000, respectively, and the maximal allowed CPU consuming time is 1500 seconds for all solvers. The numerical results on E1 and E2 are listed in Tables 4 and 5, respectively, where the labels ‘t’, ‘N’ and ‘\(N_u\)’ represent CPU time (in seconds), the number of generalized Newton steps (both \(d_N^k\) and \({\bar{d}}_N^{j}\)), the number of rejected generalized Newton steps (\({\bar{d}}_N^{j}\)), respectively. It should be pointed out that the KKT residuals associated with each solver are recalculated by (3.4) for measuring the accuracy of the computed solutions; moreover, since ADM only gives the primal solution, which cannot be used to calculate the KKT residual \(\varrho ^k\) directly, we omit the final residuals associated with ADM in Tables 4 and 5.
We observed from Tables 4 and 5 that ISNM, AASA(L-BFGS) and AASA(Adaptive) succeed in solving all the instances of E1 and E2, while the other two solvers fail (labeled by \(^\dagger\)) in some instances. Particularly, ADM fails on all the cases as it cannot find approximate solutions within the prescribed accuracy in 3000 iterations. P-BFGS fails in almost all the instances due to either exceeding the maximum number (2000) of iterations. Also, we can see that the number \(N_u\) in Tables 4 and 5 is no more than 5, i.e., no more than 5 generalized Newton steps are rejected for each instance. The number N in Tables 4 and 5 is less than 40, which means that no more than 40 generalized Newton equations are solved for each instance. The numerical results in Tables 4 and 5 show the efficiency of AASA(Adaptive) in terms of CPU time.
The numerical results on E3–E6 are presented on Table 6. Again, we can see that ASSA(adaptive) successfully solves all the problems efficiently, while P-BFGS and ADM both fail in most cases. ISNM generally terminates in a reasonable number of iterations but needs more CPU consuming times comparing with ASSA(adaptive) and ASSA(L-BFGS). Also, the magnitudes of N and \(N_u\) here are similar to those in Tables 4 and 5.
6.1.4 Results from large-scale problems
Next, we increase n and \(n_r\) to use various n ranging from 1000 to 2000, and \(n_r\) from 300 to 800. In this case, we also extend the maximum CPU time to 3600 seconds. The numerical results for E1 and E2 are omitted due to its similarity to those of E3–E6 in Table 7. Also, results from ADM and P-BFGS are exclusive due to their poor performance. It can be seen from Table 7 that, as n and \(n_r\) increase, the efficiency of AASA(Adaptive) gets more manifest.
Without the restriction on the consuming CPU time and the number of iterations, we provide two cases for medium-scale problems on E5 and E6: one (called case (i)) is \((n,n_r)=(1000,500)\) and the other (called case (ii)) is \((n,n_r)=(2000,500)\). Figures 1 and 2 demonstrate the performances of three solvers in terms of the number of iterations, the residuals and the CPU time.
It can be seen from Fig. 1a that the residual corresponding to AASA(Adaptive) gradually decreases as the number of iterations increases from 1 to 240 (the L-BFGS acceleration works in this phase), and then rapidly drops to the preset tolerance (the semi-smooth Newton acceleration works at that stage). The residual corresponding to ISNM declines slowly at the beginning, and drops rapidly in the last period. This also verifies the fast convergence of the semi-smooth Newton method numerically. From Fig. 1b, the three curves of CPU time are nearly linear. Similar observation can be seen from Fig. 1c and d and from Fig. 2 for case (ii). Again, the comparison also indicates that AASA(Adaptive) is the most efficient one.
6.2 Real examples
In this subsection, we test two real world instances whose data are obtained from financial markets.
In calculating value at risk in financial markets, the correlation matrix [28] is a critical factor. For example, it is noticed that the market correlation structure serves as a reflection of the Great Crash, which changes around the Great Crash in several aspects [11] like abrupt regime changes [29, 30] or periodic economic cycle. In particular, the average correlation coefficient after the critical point of crash usually gets higher than that before the crash [18, 19] and will approach to a steady state gradually. Moreover, the correlation coefficients can be used in the stress testing: the correlation coefficients between certain underlying assets and others are adjusted largely to simulate the stress scenarios [28]; in financial industry, people usually try to find an approximation of the restricted correlation matrix in stress testing scenario in order to recover the adjusted matrix back to a correlation matrix. Such task can be mathematically formulated as the model (6.1).
In our numerical verification, the correlation matrices to be approximated are calculated from the sample data in the Shenzhen Stock Exchange and the Shanghai Stock Exchange in China. For the constraints of (6.1), we notice that particular restrictions may be associated with a historical stressful event (such as the 1987 stock market crash and 2008 economic crisis), or can be a set of hypothetical changes related with same possible future stressful market event [13]. Generally, identifying accurately the stress events set and restricting the correlation coefficients between stress events and other underlying events [13] are very difficult, and therefore, following [27], in our experiments, we just randomly generate the constraints and their positions to imitate the stress testing scenarios.
Precisely, for the first real world example (denoted by E7), we follow the way in [27] and calculate the data matrix using the daily closing price of 792 stocks listed in Shanghai Stock Exchange (from September 2016 to September 2018). For the constraints, we restrict all entries of the correlation matrix to be no less than \(\texttt {-0.1*rand+0.6}\) and there are no restrictions on the upper bounds, which can mimic some sort of scenarios in the period of economic depression or economic crisis.
For the second real world example (denoted by E8), the data matrix is obtained from 1187 stocks in Shenzhen Stocks Exchange (from September 2016 to September 2018). Again, we follow the way in [27] to generate the correlation matrix. For the constraints, here, we choose 400 random positions at each row of the matrix X, and set \(\texttt {-0.3*rand+0.1}\) and \(\texttt {0.3*rand+0.1}\) as the lower and upper bounds corresponding to the selected positions, respectively.
We plotted Fig. 3 to show how the residual changes against the number of iterations when applying the five solvers to solve E7 and E8. It can be seen that all the solvers succeed in solving the two real data examples within the maximum number of iterations. We remark that the residual used in ADM is different from others but it is a default option in [12]. Figure 3 (both left and right) shows that the residuals corresponding to AASA(Adaptive) and ISNM drop very fast as the number of iterations increases. This is explainable because AASA(Adaptive) and ISNM both make use of the second-order information, while the other three solvers (AASA(L-BFGS), P-BFGS and ADM) are based on the first-order information which generally need less computational effort per iteration but converges (in the sense of the residuals) slower. Besides the behavior of the residual against the number of iterations, we also reported the consuming CPU times in Fig. 3 for the overall performance of these algorithms. One can see that AASA(Adaptive) in general is one of the best and can be an efficient and robust approach for solving the problem (6.1).
7 Conclusion
In this paper, we have presented a type of active-set algorithm for solving a generalization of least squares semidefinite programming. Treating it from its equivalent dual form, our algorithm begins with estimating the active/inactive sets using the BB step information, and then adaptively applies the L-BFGS and the semi-smooth Newton methods to accelerate the convergence of the free variables. Under some mild conditions, the proposed algorithm is proved to be globally convergent, and fast local convergence is guaranteed in a refined adaptive strategy. Numerical experiments on both synthetic and real world data problems are conducted. The reported numerical results are preliminary but very promising, indicating our proposed AASA(Adaptive) algorithm is an efficient and robust approach for this programming.
Notes
The initial inverse Hessian approximation in L-BFGS is generally set to be \(\zeta ^k I\) with \(\zeta ^k=\frac{(s^{k-1})^Tw^{k-1}}{(w^{k-1})^Tw^{k-1}}\).
Codes of the approaches of ISNM and P-BFGS are available online at http://www.math.nus.edu.sg/~matsundf/, and https://ctk.math.ncsu.edu/matlab_darts.html, respectively.
We remark that \(\varepsilon\) is set to be \(10^{-8}\) only in this subsubsection because it is beneficial to observe the quadratic convergence rate from numerical results. In the rest numerical experiments, \(\varepsilon\) is still set to be \(10^{-6}\).
References
Barzilai, J., Borwein, J.M.: Two point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988)
Boyd, S., Xiao, L.: Least squares covariance matrix adjustment. SIAM J. Matrix Anal. Appl. 27, 532–546 (2005)
Chen, X., Qi, H., Tseng, P.: Analysis of nonsmooth symmetric-matrix-valued functions with applications to semidefinite complementarity problems. SIAM J. Optim. 13, 960–985 (2003)
Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)
Dai, Y.H.: Alternate step gradient method. Optimization 52, 395–415 (2003)
Facchinei, F.: Minimization of SC\(^1\) functions and the Maratos effect. Oper. Res. Lett. 17(3), 131–137 (1995)
Facchinei, F., Fischer, A., Kanzow, C.: On the accurate identification of active constraints. SIAM J. Optim. 9(1), 14–32 (1998)
Gabay, D.: Application of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrangian Methods: Application to the Numerical Solution of Boundary-Value Problems, pp. 299–331. North-Holland, Amsterdam (1983)
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Comput. Math. Appl. 2, 17–40 (1976)
Gao, Y., Sun, D.F.: Calibrating least squares semidefinite programming with equality and inequality constraints. SIAM J. Matrix Anal. Appl. 31, 1432–1457 (2009)
Han, R.Q., Xie, W.J., Xiong, X.: Market correlation structure changes around the great crash: a random matrix theory analysis of the Chinese stock market. Fluct. Noise Lett. 16(02), 1750018 (2017)
He, B.S., Xu, M.H., Yuan, X.M.: Solving large-scale least squares covariance matrix problems by alternating direction methods. SIAM J. Matrix Anal. Appl. 32, 136–152 (2011)
Kupiec, P.H.: Stress testing in a value-at-risk framework. J. Deriv. 6, 7–24 (1998)
Kelley, C.T.: Iterative Methods for Optimization, pp. 102–104. SIAM, Philadelphia (1999)
Li, Q.N., Li, D.H.: A projected semi-smooth Newton method for problems of calibrating least squares covariance matrix. Oper. Res. Lett. 39, 103–108 (2011)
Liu, D.C., Nocedal, J.: On the limited memory BFGS method for large-scale optimization. Math. Program. 45, 503–528 (1989)
Malick, J.: A dual approach to semidefinite least squares problems. SIAM J. Matrix Anal. Appl. 26, 272–284 (2004)
Nobi, A., Maeng, S.E., Ha, G.G., Lee, J.W.: Random matrix theory and cross-correlations in global financial indices and local stock market indices. J. Korean Phys. Soc. 62(4), 569–574 (2013)
Nobi, A., Maeng, S.E., Ha, G.G., Lee, J.W.: Effects of global financial crisis on network structure in a local stock market. Phys. A 407, 135–143 (2014)
Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, Berlin (2006)
Qi, L.Q.: Convergence analysis of some algorithms for solving nonsmooth equations. Math. Oper. Res. 18, 227–244 (1993)
Qi, L.Q.: Superlinearly convergent approximate Newton methods for LC\(^1\) optimization problems. Math. Program. 64(1–3), 277–294 (1994)
Qi, L.Q., Sun, J.: A nonsmooth version of Newton’s method. Math. Program. 58, 353–367 (1993)
Qi, H.D., Sun, D.F.: A quadratically convergent Newton method for computing the nearest correlation matrix. SIAM J. Matrix Anal. Appl. 28, 360–385 (2006)
Rockafellar, R.T.: Conjugate Duality and Optimization. SIAM, Philadelphia (1974)
Schwertman, N.C., Allen, D.M.: Smoothing an indefinite variance–covariance matrix. J. Stat. Comput. Simul. 9, 183–194 (1979)
Shen, C.G., Fan, C.X., Wang, Y.L., Xue, W.J.: Limited memory BFGS algorithm for the matrix approximation problem in Frobenius norm. Comput. Appl. Math. 39, 43 (2020)
So, M.K.P., Wang, J., Asai, M.: Stress testing correlation matrices for risk management. North Am. J. Econ. Finance 26, 310–322 (2013)
Sornette, D.: Critical market crashes. Phys. Rep. 378(1), 1–98 (2003)
Sornette, D.: Why Stock Markets Crash: Critical Events in Complex Financial Systems. Princeton University Press, Princeton (2017)
Sturm, J.F.: Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 11, 625–653 (1999)
Sun, D.F., Sun, J.: Semi-smooth matrix valued functions. Math. Oper. Res. 27, 150–169 (2002)
Sun, Y.F., Vandenberghe, L.: Decomposition methods for sparse matrix nearness problems. SIAM J. Matrix Anal. Appl. 36, 1691–1717 (2015)
Tütüncü, R.H., Toh, K.C., Todd, M.J.: Solving semidefinite-quadratic-linear programs using SDPT3. Math. Program. 95, 189–217 (2003)
Ye, C.H., Yuan, X.M.: A descent method for structured monotone variational inequalities. Optim. Methods Softw. 22, 329–338 (2007)
Zhang, H., Hager, W.W.: A nonmonotone line search technique and its application to unconstrained optimization. SIAM J. Optim. 14, 1043–1056 (2004)
Zhou, B., Gao, L., Dai, Y.H.: Gradient methods with adaptive step-sizes. Comput. Optim. Appl. 35, 69–86 (2006)
Acknowledgements
The authors would like to thank the Associate Editor and anonymous referees for their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Wenjuan Xue: The work of this author was supported in part by the National Natural Science Foundation of China NSFC-11601318. Lei-Hong Zhang: The work of this author was supported in part by the National Natural Science Foundation of China (NSFC-11671246, NSFC-12071332), the National Key R&D Program of China (No. 2018YFB0204404) and Double Innovation Program of Jiangsu Province, Year 2018.
Rights and permissions
About this article
Cite this article
Shen, C., Wang, Y., Xue, W. et al. An accelerated active-set algorithm for a quadratic semidefinite program with general constraints. Comput Optim Appl 78, 1–42 (2021). https://doi.org/10.1007/s10589-020-00228-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-020-00228-5