1 Introduction

Tensors (a.k.a. hypermatrices) are natural generalizations of vectors and matrices, serving as much more apparent and convenient tools to encode, analyze, as well as represent data and information in diverse disciplines of applied science. As one of the two sides of a coin, opposite to their capability over matrices, computations with tensors are subject to the curse of dimensionality [29, 32]. A vector can be represented as an array indexed by one subscript, a matrix by two, whereas a higher order tensor by several. Usually, we refer to order as the number of subscripts needed to express a tensor, each subscript represents one mode, whereas the range of each subscript is the dimension in that mode. As is well-known, almost all computations of tensors have complexity exponential with respect to their orders and dimensions [29]. This brings a heavy obstacle to warrant tensors in many real applications. This tough situation dramatically improves if the tensor has a rank one decomposition with few rank one components, since in which case the computational complexity becomes linear with respect to either the order, the dimensions, or the rank of this tensor. Therefore, there is a natural invitation to the study of tensor rank one decompositions. As a result, the focus of research on tensors has been putting on both theoretical and computational properties of tensor rank one decompositions. This article falls into this main stream as well, and will be devoted to a particular rank one decomposition of tensors—the strongly orthogonal (rank) decomposition.

The conception of strongly orthogonal rank and the corresponding decomposition were proposed in the thesis of Franc in 1992 [17]. It is a natural generalization of SVD for matrices from a restricted perspective (cf. Sect. 2.4). In [33], “free orthogonal rank” and “free rank decomposition” were employed instead of “strong orthogonal rank” and “strong orthogonal rank decomposition” respectively by Leibovici and Sabatier. We will follow the terminologies of [17, 27]. The number of rank one tensors in a strongly orthogonal decomposition is referred as the length of this decomposition.

In the following, we want outline three aspects that motivate this work. The first one is the wide range applications of strongly orthogonal (rank) decompositions of tensors, please refer to [3, 12, 13, 27, 29, 30, 33] and references therein. Particularly, in statistical modelings for learning latent variables [3] and blind source separations [12, 13], orthogonality is a reasonable requirement. Unlike the second order case in which a complete orthogonality (a.k.a. diagonalization) can be assumed (guaranteed by SVD of matrices, cf. Sect. 2.4), complete orthogonality for higher order tensors is impossible in general [27, 32, 41]. Therefore, strong orthogonality becomes an appropriate tradeoff between orthogonality and diagonality—it preserves the orthogonality and seeks the most sparsity on the representation. As a result, strongly orthogonal decompositions as well as general orthogonal decompositions have being adopted in diverse applications [6, 10, 13, 14, 24, 28, 29, 36].

The second one is the appealing theoretical and computational benefits by considering strong orthogonality over the general rank one decompositions. The most general tensor rank one decomposition is decomposing a tensor with rank one components without further requirements on the structures of these rank one tensors. The smallest number of rank one tensors in such a decomposition is the rank of that tensor. It is well-known that determining the rank, computing a rank decomposition of a tensor is very difficulty [32]. From the computational complexity perspective, they are respectively NP-complete and NP-hard problems [15, 19]. Given the freedom on the structures of the decomposed rank one tensors, the tensor rank one decomposition and approximation problems suffer from many numerical difficulties as well, such as the component matrices of the iteration become unbounded, etc, please see [15, 29] and references therein. However, whenever strong orthogonality is imposed on the decomposed rank one tensors, both the decomposition and the approximation become well-possed (cf. Sect. 2.3). Thus, from the computational point of view, the strongly orthogonal decomposition is a good candidate for tensor decomposition.

The strongly orthogonal (rank) decomposition has a geometric meaning as well. One widely admitted rule of science is simplification. A tensor (hypermatrix) is actually the coordinate representation of an element in a certain tensor space under a chosen coordinate system. A representation with simple coordinates should be the goal in many tasks. SVD for matrices and principal component analysis are both ruled by this principle, and it can represent a matrix with the simplest coordinates (i.e., a diagonal matrix). With the matrix-tensor multiplication, it is easy to see that a strongly orthogonal rank decomposition of a tensor also falls into this principle (cf. Proposition 2.1). Thus, geometrically, computing a strongly orthogonal rank decomposition is equivalent to finding a coordinate system such that the representation of this tensor is the simplest in the sense of having the fewest nonzero coordinates. This concise mathematical interpretation will provide insights on investigations of strongly orthogonal rank decompositions.

The last but not the least is a direct motivation for this article—computing out a strongly orthogonal (rank) decomposition for a given tensor. There lacks a systematic study on this issue in the literature, since the works [17, 27, 33]. To compute a strongly orthogonal decomposition for a given tensor, in [27], a greedy tensor decomposition is proposed. In each step of this algorithm, a best rank one approximation problem subject to orthogonality constraints must be solved. As observed already by Kolda [27], solving such a sequence of optimization problems is a very challenging task. Moreover, it is pointed out that the difficulty with this approach is in enforcing the constraints [27, Page 252]. A purpose of this article is providing a numerical method enforcing the orthogonality constraints during the iteration and computing a strongly orthogonal decomposition with the rank one tensors all at once.

At present, there has no computational complexity of computing a strongly orthogonal rank decomposition for a given tensor [27,28,29]. However, it is suspected to be NP-hard, in viewing of the NP-hardness of some related problems [11, 20, 34]. Thus, it would be difficult and impossible (if this problem is indeed NP-hard and P\(\ne \)NP) to compute out a strongly orthogonal rank decomposition of a general tensor in polynomial time. Therefore, the primary purpose of this article is presenting a heuristic approach for computing a strongly orthogonal decomposition of a given tensor with length as short as possible and a numerical method to realize it. Hopefully, this heuristic approach could give a strongly orthogonal rank decomposition in several cases as well.

The main contributions of this article are

  1. (1)

    With \(l_0\)-norm and matrix-tensor multiplication, the strongly orthogonal rank decomposition is reformulated as an optimization problem over the matrix manifolds (cf. (9)) the first time (Proposition 2.1). This should serve as a standard tool and accumulate a step towards a systematic way for analyzing strongly orthogonal rank decompositions.

  2. (2)

    A heuristic optimization problem (cf. (12)) is proposed to approximate the hard problem (9) which has a discontinuous objective function. An inexact augmented Lagrangian method is proposed to solve (12), i.e., Algorithm 3.1. With a careful design, all the subproblems have closed formula solutions, all the iterations fulfill the orthogonality constraints, and thus this algorithm always give a strongly orthogonal decomposition (Algorithm 4.1). Global convergence to a critical point of (12) is established without any further hypothesis (Proposition 3.3). Extensive numerical experiments show that this approach is quite promising (Sect. 5), and in several cases strongly orthogonal rank decompositions can be found.

The equivalent reformulation (9) actually reflects the difficulty in the sense that the task is minimizing a discontinuous (letting alone differentiable) function over a system of a large number of highly nonlinear equations and a manifold constraint. Note that even the optimization of a differentiable function over a smooth manifold is a hard computational problem in general [2]. Therefore, there is no guarantee that an algorithm can always return a global optimizer for (9). Actually, advances on manifold optimization are more focused on smooth functions for finding critical points, see [2, 25] and references therein; a call for study on nonsmooth manifold optimization is given by Absil and Hosseini very recently [1]. This gives a motivation for the particularly designed inexact augmented Lagrangian method to problem (12).

With the discontinuous objective function in (9), a common strategy is replacing it with a heuristic continuous surrogate [1, 16]. The \(l_1\)-norm is applied in this article (cf. (12)). It is a reasonable choice, which can be viewed as a penalty approach (cf. Sect. 2.5). Although (12) belongs to the class of optimization problems with continuous objective function over a compact feasible set, there is no theoretical guarantee for a numerical optimization method on finding their global optimizers for such problems [2, 7], since the constraints are highly nonlinear and nonconvex. Usually, a wisely designed optimization method could converge to a critical point [2, 7].

The \(l_1\)-norm is a nonsmooth function. The nonsmoothness of (12) and the particular structure that the variables of the manifold constraints are not related directly to the objective function (cf. (12)) motivate us to a particularly designed algorithm. A general thought is employing the penalty technique. The augmented Lagrangian method is a modification of the penalty method in a wise way to avoid the penalty parameter being forced to going infinite. Thus, the augmented Lagrangian method has more stable numerical performance over the penalty method [7]. The general picture in this article is applying the augmented Lagrangian method to (12) and keeping the orthogonality of the iterations with a careful design. On the other hand, the “inexact version” is studied as (i) subproblems cannot always be guaranteed to be solved exactly and (ii) the subproblem can be solved only inexactly within appropriate required precision to improve the overall efficiency.

The rest paper is organized as follows. For the convenience of reading, several technical details are put in Appendixes. Preliminaries on matrix-tensor multiplication (Sect. 2.1), the orthogonal group and related optimization properties (Sect. 2.2), strongly orthogonal decompositions of a tensor (Sect. 2.3), some optimization techniques (Sect. 2.6) will be given in Sect. 2. In Sect. 2.5, the problem of computing a strongly orthogonal rank decomposition of a tensor is equivalently reformulated as a nonlinear optimization problem with orthogonality constraints and \(l_0\)-norm objective function. Replacing the \(l_0\)-norm by the \(l_1\)-norm surrogate, we get a heuristic of the problem, i.e., (12). In Sect. 3, an inexact augmented Lagrangian method (ALM) is proposed to solve this optimization problem. Critical points of the augmented Lagrangian function (Sect. 3.1), KKT points of the problem (12) (Sect. 3.2) are investigated. In order to study the KKT points, a nonsmooth version of the standard Lagrange multiplier theory is reviewed in Appendix B, since the \(l_1\)-norm is a nonsmooth function. Global convergence of the algorithm is established without any further hypothesis in Sect. 3.3, whose proof is put in Appendix C. The augmented Lagrangian subproblem is discussed in Sect. 4. Section 4.1 presents more details on implementing the ALM algorithm. The augmented Lagrangian subproblem is solved by a proximal alternating minimization (PAM) method, whose global convergence is also established without any further hypothesis in Sect. 4.2 and the proof is put in Appendix D. To this end, the convergence theory for a general PAM method is reviewed in Appendix A. Extensive numerical experiments are reported in Sect. 5. Sect. 5.1 is for concrete examples taken from literatures, Sect. 5.2 is for completely orthogonal decomposable tensors, in which a kind of condition numbers for tensors are discussed, Sect. 5.3 is for random examples, whereas Sect. 5.4 draws some conclusions for the numerical computations. Some final conclusions are given in Sect. 6.

2 Preliminaries

In this section, we will review some basic notions on tensors and preliminaries on strongly orthogonal (rank) decompositions of a tensor, as well as those of optimization theory which will be conducted in this article.

Given a positive integer \(k\ge 2\), and positive integers \(n_1,\dots ,n_k\), the tensor space consisting of real tensors of dimension \(n_1\times \dots \times n_k\) is denoted as \(\mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\). In this Euclidean space, inner product and the induced norm can be defined. The Hilbert–Schmidt inner product of two given tensors \(\mathcal {A}, \mathcal {B}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) is defined as

$$\begin{aligned} \langle \mathcal {A},\mathcal {B}\rangle :=\sum _{i_1=1}^{n_1}\dots \sum _{i_k=1}^{n_k}a_{i_1\dots i_k}b_{i_1\dots i_k}. \end{aligned}$$

The Hilbert–Schmidt norm \(\Vert \mathcal {A}\Vert \) is then defined as

$$\begin{aligned} \Vert \mathcal {A}\Vert :=\sqrt{\langle \mathcal {A},\mathcal {A}\rangle }. \end{aligned}$$

2.1 Matrix-tensor multiplication

Given a tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) and k matrices \(B^{(i)}\in \mathbb {R}^{n_i\times n_i}\) for \(i\in \{1,\dots ,k\}\), the matrix-tensor multiplication\((B^{(1)},\dots ,B^{(k)})\cdot \mathcal {A}\) results in a tensor in \(\mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), defined entry-wisely as

$$\begin{aligned} \big [(B^{(1)},\dots ,B^{(k)})\cdot \mathcal {A}\big ]_{i_1\dots i_k}:=\sum _{j_1=1}^{n_1}\dots \sum _{j_k=1}^{n_k}b^{(1)}_{i_1j_1}\dots b^{(k)}_{i_kj_k}a_{j_1\dots j_k} \end{aligned}$$
(1)

for all \(i_t\in \{1,\dots ,n_t\}\) and \(t\in \{1,\dots ,k\}\).

Let \(n^*:=\prod _{i=1}^kn_i\). The mode-jmatrix flattening of \(\mathcal {A}\) is a matrix \(A^{(j)}\in \mathbb {R}^{n_j\times \frac{n^*}{n_j}}\) defined entry-wisely as

$$\begin{aligned} a^{(j)}_{i_ji_j^*}=a_{i_1\dots i_k}\ \text {for all }i_j\in \{1,\dots ,n_j\}\ \text {and }i_j^*\in \left\{ 1,\dots ,\frac{n^*}{n_j}\right\} \end{aligned}$$
(2)

with

$$\begin{aligned} i_j^*=(i_1-1)\frac{n^*}{n_1n_j}+\dots +(i_{j-1}-1)\frac{n^*}{n_1\cdots n_{j}}+(i_{j+1}-1)\frac{n^*}{n_1\cdots n_{j+1}}+\dots +i_k. \end{aligned}$$

We will denote by \(\mathcal {A}^{({\text {f}},i)}=A^{(i)}\) the mode-i matrix flattening of \(\mathcal {A}\). Let I be the identity matrix of appropriate size. It follows that

$$\begin{aligned} \big [(B^{(1)},\dots ,B^{(k)})\cdot \mathcal {A}\big ]^{({\text {f}},i)} =B^{(i)}\big [(B^{(1)},\dots ,B^{(i-1)},I,B^{(i+1)},\dots ,B^{(k)})\cdot \mathcal {A}\big ]^{({\text {f}},i)} \end{aligned}$$

for all \(i\in \{1,\dots ,k\}\).

It follows from the Hilbert–Schmidt inner product that

$$\begin{aligned} \langle \mathcal {A},\mathcal {B}\rangle =\langle \mathcal {A}^{({\text {f}},i)},\mathcal {B}^{({\text {f}},i)}\rangle \end{aligned}$$

for any pair \(\mathcal {A},\mathcal {B}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) and any \(i\in \{1,\dots ,k\}\).

Let \(\mathbb {O}(n)\subset \mathbb {R}^{n\times n}\) be the group of \(n\times n\) orthogonal matrices. Whenever \(B^{(i)}\in \mathbb {O}(n_i)\) for each \(i\in \{1,\dots ,k\}\), it is a direct calculation to see that

$$\begin{aligned} \Vert (B^{(1)},\dots ,B^{(k)})\cdot \mathcal {A}\Vert =\Vert \mathcal {A}\Vert . \end{aligned}$$

2.2 Orthogonal group and its normal cone

For any \(A\in \mathbb {O}(n)\), the Fréchet normal cone to \(\mathbb {O}(n)\) at A is defined as

$$\begin{aligned} \hat{N}_{\mathbb {O}(n)}(A):=\{B\in \mathbb {R}^{n\times n}\mid \langle B,C-A\rangle \le o(\Vert C-A\Vert )\ \text {for all }C\in \mathbb {O}(n)\}. \end{aligned}$$

Usually, we set \(\hat{N}_{\mathbb {O}(n)}(A)=\emptyset \) whenever \(A\notin \mathbb {O}(n)\). The (limiting) normal cone to \(\mathbb {O}(n)\) at \(A\in \mathbb {O}(n)\) is denoted by \(N_{\mathbb {O}(n)}(A)\) and is defined as

$$\begin{aligned} B\in N_{\mathbb {O}(n)}(A)\ \iff \ \exists A_k\in \mathbb {O}(n),\ A_k\rightarrow A,\ \exists B_k\in \hat{N}_{\mathbb {O}(n)}(A_k),\ \text {such that }B_k\rightarrow B. \end{aligned}$$

It is easily seen from the definition that the normal cone \(N_{\mathbb {O}(n)}(A)\) is always closed. The indicator function \(\delta _{\mathbb {O}(n)}\) of \(\mathbb {O}(n)\) is defined as

$$\begin{aligned} \delta _{\mathbb {O}(n)}(X):={\left\{ \begin{array}{ll}0&{}\text {if }X\in \mathbb {O}(n),\\ +\infty &{}\text {otherwise}.\end{array}\right. } \end{aligned}$$

Given a function \(f : \mathbb {R}^n\rightarrow \mathbb {R}\cup \{\infty \}\), the regular subdifferential of f at \(\mathbf {x}\in \mathbb {R}^n\) is defined as

$$\begin{aligned} \hat{\partial }f(\mathbf {x}):=\Bigg \{\mathbf {h}\in \mathbb {R}^n:\liminf _{\mathbf {x}\ne \mathbf {y}\rightarrow \mathbf {x}}\frac{f(\mathbf {y})-f(\mathbf {x})-\langle \mathbf {h},\mathbf {y}-\mathbf {x}\rangle }{\Vert \mathbf {y}-\mathbf {x}\Vert }\ge 0\Bigg \} \end{aligned}$$

and the (limiting) subdifferential of f at \(\mathbf {x}\) is defined as

$$\begin{aligned} \partial f(\mathbf {x}):=\Big \{\mathbf {h}\in \mathbb {R}^n:\exists \{\mathbf {x}^k\}\rightarrow \mathbf {x}\ \text {and }\{\mathbf {h}^k\}\rightarrow \mathbf {h}\ \text {satisfying }\mathbf {h}^k\in \hat{\partial }f(\mathbf {x}^k)\ \text {for all }k\Big \}. \end{aligned}$$

We refer to [40] for more details on variational analysis concepts. An important fact about normal cone \(N_{\mathbb {O}(n)}(A)\) and the subdifferential of the indicator function \(\delta _{\mathbb {O}(n)}\) of \(\mathbb {O}(n)\) at A is (cf. [40])

$$\begin{aligned} \partial \delta _{\mathbb {O}(n)}=N_{\mathbb {O}(n)}. \end{aligned}$$
(3)

Note that the group \(\mathbb {O}(n)\) of orthogonal matrices of size \(n\times n\) is a smooth manifold of dimension \(\frac{n(n-1)}{2}\). It follows from [40, Chapter 6.C] that

$$\begin{aligned} N_{\mathbb {O}(n)}(A)=\hat{N}_{\mathbb {O}(n)}(A)=\{AS\mid S\in {\text {S}}^{n\times n}\}, \end{aligned}$$

where \({\text {S}}^{n\times n}\subset \mathbb {R}^{n\times n}\) is the subspace of \(n\times n\) symmetric matrices.

Given a matrix \(B\in \mathbb {R}^{n\times n}\), the projection of B onto the normal cone of \(\mathbb {O}(n)\) at A is

$$\begin{aligned} \pi _{N_{\mathbb {O}(n)}(A)}(B)=A\left( \frac{A^\mathsf {T}B+B^\mathsf {T}A}{2}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned}&B\in N_{\mathbb {O}(n)}(A)\ \iff \ B-A\left( \frac{A^\mathsf {T}B+B^\mathsf {T}A}{2}\right) =O\nonumber \\&\quad \iff \, B-AB^\mathsf {T}A=O\ \iff \ A^{\mathsf {T}}B-B^{\mathsf {T}}A=O, \end{aligned}$$
(4)

since

$$\begin{aligned} \left( I-\frac{1}{2}AA^\mathsf {T}\right) AB^\mathsf {T}A=\frac{1}{2}AB^\mathsf {T}A \end{aligned}$$

and

$$\begin{aligned} I-\frac{1}{2}AA^\mathsf {T} \end{aligned}$$

is an invertible matrix. The invertibility follows from the fact that \(\mathbf {x}^\mathsf {T}(I-\frac{1}{2}AA^\mathsf {T})\mathbf {x}=\frac{1}{2}\Vert \mathbf {x}\Vert ^2\).

2.3 Strongly orthogonal decomposition

Two rank one tensors

$$\begin{aligned} \mathcal {U}=\mathbf {u}^{(1)}\otimes \dots \otimes \mathbf {u}^{(k)}\ \text {and } \mathcal {V}=\mathbf {v}^{(1)}\otimes \dots \otimes \mathbf {v}^{(k)} \end{aligned}$$

with unit component vectors \(\mathbf {u}^{(i)}\)’s and \(\mathbf {v}^{(i)}\)’s are strongly orthogonal, denoted as \(\mathcal {U}\perp _{\text {s}} \mathcal {V}\), if \(\mathcal {U}\perp \mathcal {V}\), i.e.,

$$\begin{aligned} \langle \mathcal {U},\mathcal {V}\rangle =\prod _{i=1}^k\langle \mathbf {u}^{(i)},\mathbf {v}^{(i)}\rangle =0, \end{aligned}$$

and

$$\begin{aligned} \mathbf {u}^{(i)}=\pm \mathbf {v}^{(i)}\ \text {or }\mathbf {u}^{(i)}\perp \mathbf {v}^{(i)}\ \text {for all }i=1,\dots ,k. \end{aligned}$$

Given a tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), a strongly orthogonal decomposition means a rank one decomposition of \(\mathcal {A}\)

$$\begin{aligned} \mathcal {A}=\sum _{i=1}^r\lambda _i\mathbf {u}^{(1)}_i\otimes \dots \otimes \mathbf {u}^{(k)}_i \end{aligned}$$
(5)

such that the set of rank one tensors \(\{\mathbf {u}^{(1)}_i\otimes \dots \otimes \mathbf {u}^{(k)}_i\}_{i=1}^r\) is a set of mutually strongly orthogonal rank one tensors. For each given tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), there is a natural strongly orthogonal decomposition as

$$\begin{aligned} \mathcal {A}=\sum _{i_1=1}^{n_1}\cdots \sum _{i_k=1}^{n_k}a_{i_1\dots i_k}\mathbf {e}^{(1)}_{i_1}\otimes \dots \otimes \mathbf {e}^{(k)}_{i_k}, \end{aligned}$$

where \(\{\mathbf {e}^{(s)}_1,\dots ,\mathbf {e}^{(s)}_{n_s}\}\) is the standard basis of \(\mathbb {R}^{n_s}\) for all \(s\in \{1,\dots ,k\}\). It is immediate to see that this can be done for any given orthogonal basis of \(\mathbb {R}^{n_s}\) for all \(s\in \{1,\dots ,k\}\).

A strongly orthogonal decomposition of \(\mathcal {A}\) with the minimum r is called a strongly orthogonal rank decomposition of \(\mathcal {A}\) and the corresponding r is the strongly orthogonal rank of \(\mathcal {A}\), denoted as \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\) [27]. It is called free orthogonal rank by Leibovici and Sabatier [33]. Some properties on strongly orthogonal rank of a tensor are investigated in [22], including an upper bound of the strongly orthogonal ranks and expected strongly orthogonal rank for a given tensor space.

2.4 An SVD perspective of strongly orthogonal rank decomposition

Given a matrix \(A\in \mathbb {R}^{n_1\times n_2}\), the classical singular value decomposition (SVD) of A reads that there exist orthogonal matrices \(U\in \mathbb {O}(n_1)\), \(V\in \mathbb {O}(n_2)\) and a diagonal matrix \(\Lambda \in \mathbb {R}^{n_1\times n_2}\) such that (cf. [21])

$$\begin{aligned} A=U\Lambda V^\mathsf {T}=(U,V)\cdot \Lambda . \end{aligned}$$
(6)

The diagonality of the matrix \(\Lambda \) ensures that we can take a nonnegative diagonal of \(\Lambda \), and define these diagonals as singular values of the matrix A. Arrange these singular values in nonincreasing order along the diagonals. Suppose without loss of generality that \(n_1\le n_2\), and the columns of U and V are denoted as \(\mathbf {u}_i\)’s and \(\mathbf {v}_j\)’s. Then the SVD (6) can be expanded as

$$\begin{aligned} A=\sum _{i=1}^{n_1}\lambda _i\mathbf {u}_i\mathbf {v}_i^\mathsf {T}=:\sum _{i=1}^{n_1}\lambda _i\mathbf {u}_i\otimes \mathbf {v}_i=\sum _{i=1}^{r}\lambda _i\mathbf {u}_i\otimes \mathbf {v}_i, \end{aligned}$$
(7)

where \(r={\text {rank}}(A)\) is the rank of the matrix A. Obviously, (7) is a strongly orthogonal rank decomposition of A. The importance of SVD for matrices and its fundamental influence are widely known [18].

The beautiful nature of the matrix case makes many essential features of orthogonal decompositions simple and vague to picture their higher order counterparts, i.e., tensors (a.k.a. hypermatrices). There exist various attempts to generalize this fundamental singular value decomposition of a matrix to tensors. As the philosophy suggests, each generalization has its own advantages with the sacrifice of losing some attracting properties of their matrix counterpart [14].

Perhaps the most important fact that people unwilling to see is the missing of diagonalization for a tensor. It is a commonly admitted fact that for a given tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) there cannot always exist a set of orthogonal matrices \(U_i\in \mathbb {O}(n_i)\) for all \(i\in \{1,\dots ,k\}\) and a diagonal tensor \(\Lambda \in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) (i.e., the only possible nonzero entries of \(\Lambda \) are \(\lambda _{i_1\dots i_k}\) with \(i_1=\dots =i_k=i\) for \(i\in \{1,\dots ,\min \{n_1,\dots , n_k\}\}\)) such that (cf. [32])

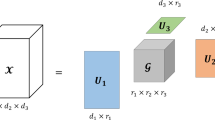
$$\begin{aligned} \mathcal {A}=(U_1,\dots ,U_k)\cdot \Lambda . \end{aligned}$$
(8)

Therefore, searching a decomposition of the form (8) keeping the orthogonality of \(U_i\)’s and allowing possible a non-diagonal tensor \(\Lambda \) should be the main task in decomposing a tensor and a reasonable alternative orthogonal decomposition scheme for a tensor. Compared with the other decompositions of a tensor, the decomposition (8) has the advantage of interpolation with orthogonal coordinates change, parallelling to the discussion on geometry of vector spaces in the matrix case by Jordan [26].

2.5 Optimization reformulation for the strongly orthogonal rank decomposition

Given a tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), we consider the following optimization problem

$$\begin{aligned} \begin{array}{rl} \min &{}\Vert \mathcal {B}\Vert _0\\ \text {s.t.}&{}(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}=\mathcal {B},\\ &{} U^{(i)}\in \mathbb {O}(n_i)\ \text {for all }i=1,\dots ,k, \end{array} \end{aligned}$$
(9)

where \(\Vert \mathcal {B}\Vert _0\) is the zero norm of \(\mathcal {B}\), i.e., counting the number of nonzero entries of \(\mathcal {B}\).

Proposition 2.1

(Optimization Reformulation) For any given tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), the minimization problem (9) has an optimizer \((\mathcal {B},U^{(1)},\dots ,U^{(k)})\) with optimal value being \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\), and a strongly orthogonal rank decomposition of \(\mathcal {A}\) is given by

$$\begin{aligned} \mathcal {A}=\sum _{i_1=1}^{n_1}\cdots \sum _{i_k=1}^{n_k}b_{i_1\dots i_k}\mathbf {u}^{(1)}_{i_1}\otimes \dots \otimes \mathbf {u}^{(k)}_{i_k}, \end{aligned}$$
(10)

where \(\mathbf {u}^{(s)}_i\) is the i-th row of \(U^{(s)}\) for all \(i\in \{1,\dots ,n_s\}\) and \(s\in \{1,\dots ,k\}\).

Proof

We first show that the optimization problem (9) always has an optimizer. Note that each \(\mathbb {O}(n_i)\) is a compact set. By the matrix-tensor multiplication, we have that

$$\begin{aligned} \Vert \mathcal {B}\Vert =\Vert (U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}\Vert =\Vert \mathcal {A}\Vert . \end{aligned}$$

Thus, the feasible set of (9) is compact. Since the zero norm is lower semi-continuous, we conclude that the minimum in (9) is always attainable by an optimizer \((\mathcal {B},U^{(1)},\dots ,U^{(k)})\).

In the following, we assume that \((\mathcal {B},U^{(1)},\dots ,U^{(k)})\) is such an optimizer. It follows from the matrix-tensor multiplication that

$$\begin{aligned} \mathcal {A}&=\big ((U^{(1)})^\mathsf {T}U^{(1)},\dots ,(U^{(k)})^\mathsf {T}U^{(k)}\big )\cdot \mathcal {A}\\&=\big ((U^{(1)})^\mathsf {T},\dots ,(U^{(k)})^\mathsf {T}\big )\cdot \big ((U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}\big )\\&=\big ((U^{(1)})^\mathsf {T},\dots ,(U^{(k)})^\mathsf {T}\big )\cdot \mathcal {B}\\&=\sum _{i_1=1}^{n_1}\cdots \sum _{i_k=1}^{n_k}b_{i_1\dots i_k}\mathbf {u}^{(1)}_{i_1}\otimes \dots \otimes \mathbf {u}^{(k)}_{i_k}, \end{aligned}$$

where \(\mathbf {u}^{(s)}_i\) is the i-th row of \(U^{(s)}\) for all \(i\in \{1,\dots ,n_s\}\) and \(s\in \{1,\dots ,k\}\). Thus, each optimizer \((\mathcal {B},U^{(1)},\dots ,U^{(k)})\) of (9) gives a strongly orthogonal decomposition of \(\mathcal {A}\), and the number of strongly orthogonal rank one tensors in this decomposition is exactly the number of nonzero entries of \(\mathcal {B}\), i.e., \(\Vert \mathcal {B}\Vert _0\). Consequently, we must have \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\le \Vert \mathcal {B}\Vert _0\) and hence the optimal value of (9) is lower bounded by \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\).

In the following, we complete the proof by constructing a feasible solution of (9) from a strongly orthogonal rank decomposition of \(\mathcal {A}\). Suppose that (5) gives such a decomposition, i.e.,

$$\begin{aligned} \mathcal {A}=\sum _{i=1}^r\lambda _i\mathbf {u}^{(1)}_i\otimes \dots \otimes \mathbf {u}^{(k)}_i. \end{aligned}$$
(11)

By the definition of strong orthogonality, we have that each pair of the vectors \(\mathbf {u}^{(s)}_1,\dots ,\mathbf {u}^{(s)}_r\) consists of either orthogonal or equal or two opposite vectors, for all \(s\in \{1,\dots ,k\}\). Thus, without loss of generality (changing \(\lambda _i\) to \(-\lambda _i\) if necessary), we can assume that the set \(\{\mathbf {u}^{(s)}_1,\dots ,\mathbf {u}^{(s)}_r\}\) forms an orthnormal set of vectors for all \(s\in \{1,\dots ,k\}\). Let \(p_s\) be the cardinality of the set \(\{\mathbf {u}^{(s)}_1,\dots ,\mathbf {u}^{(s)}_r\}\) for all \(s\in \{1,\dots ,k\}\). Note that \(p_s\le \min \{r,n_s\}\) and strict inequality can happen for all \(s\in \{1,\dots ,k\}\). Let \(U^{(s)}\in \mathbb {O}(n_s)\) with the first \(p_s\) columns being these of \(\{\mathbf {u}^{(s)}_1,\dots ,\mathbf {u}^{(s)}_r\}\) for all \(s\in \{1,\dots ,k\}\), and tensor \(\mathcal {B}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) with entries

$$\begin{aligned} b_{i_1\dots i_k}:={\left\{ \begin{array}{ll}\lambda _i&{}\text {if }\mathbf {u}^{(s)}_i\ \text {is the }i_s\text {-th column of }U^{(s)}\ \text {for all }s=1,\dots ,k,\\ 0&{}\text {otherwise}.\end{array}\right. } \end{aligned}$$

Immediately, we see that \(\Vert \mathcal {B}\Vert _0=r\) and

$$\begin{aligned} \mathcal {A}=(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {B}. \end{aligned}$$

Therefore, the above constructed \((\mathcal {B}, U^{(1)},\dots ,U^{(k)})\) is a feasible solution to (9) with objective function value \(\Vert \mathcal {B}\Vert _0=r={\text {rank}}_{{\text {SO}}}(\mathcal {A})\). As a result, the optimal value of (9) is upper bounded by \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\).

Hence, an optimizer \((\mathcal {B}, U^{(1)},\dots ,U^{(k)})\) of (9) exists with \(\Vert \mathcal {B}\Vert _0={\text {rank}}_{{\text {SO}}}(\mathcal {A})\) and a strongly orthogonal rank decomposition of \(\mathcal {A}\) is given as (10) with this optimizer. The proof is then complete. \(\square \)

With Proposition 2.1, computing a strongly orthogonal rank decomposition of a given tensor \(\mathcal {A}\) can be done, if one can solve the optimization problem (9). Moreover, optimizers of (9) will give such decompositions. Therefore, we will concentrate on solving the problem (9) in the rest article.

The constraint is nonlinear in \(U^{(i)}\)’s and linear in \(\mathcal {B}\). However, the objective function is not even continuous. In order to resolve this, we would like to use a continuous sparsity measure \(\Vert \mathcal {B}\Vert _1\) (i.e., the absolute sum of all the entries of \(\mathcal {B}\)) as a surrogate for \(\Vert \mathcal {B}\Vert _0\).

$$\begin{aligned} \begin{array}{rl}\min &{}\Vert \mathcal {B}\Vert _1\\ \text {s.t.}&{}(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}=\mathcal {B},\\ &{} U^{(i)}\in \mathbb {O}(n_i)\ \text {for all }i=1,\dots ,k. \end{array} \end{aligned}$$
(12)

The heuristic of employing \(l_1\)-norm \(\Vert \mathcal {B}\Vert _1\) for \(l_0\)-norm \(\Vert \mathcal {B}\Vert _0\) is quite popular and useful in compressive sensing as well as in convex mathematical optimization models [16]. Theoretical justification for this convex relaxation has been established in the literature. For our problem (9), (12) is still nonconvex, and hence it is hard to give a theoretical guarantee on exactness of the relaxation. However, this heuristic is quite reasonable: If \(\mathcal {B}\) is an optimizer of (9) such that \(b_{i_1\dots i_k}=0\) for \((i_1,\dots ,i_k)\in S\) with a subset \(S\subseteq \{1,\dots ,n_1\}\times \dots \times \{1,\dots ,n_k\}\), then the constraint \(b_{i_1\dots i_k}=0\) for \((i_1,\dots ,i_k)\in S\) can be added into (9). The objective function value is then constant and irrelevant to the optimization, and hence it can be removed. On the other hand, \(|b_{i_1\dots i_k}|\) is a nonsmooth penalty for the constraint \(b_{i_1\dots i_k}=0\). By adding \(\sum _{(i_1,\dots ,i_k)\in S}|b_{i_1\dots i_k}|\) into the objective function, we get a penalized problem with equal penalty weights. \(\Vert \mathcal {B}\Vert _1-\sum _{(i_1,\dots ,i_k)\in S}|b_{i_1\dots i_k}|\) can be added into the objective function as a regularizer for selecting an optimizer with the minimum absolute sum from the set of optimizers with \(b_{i_1\dots i_k}=0\) for \((i_1,\dots ,i_k)\in S\).

2.6 Optimization techniques

In this section, we give some basic optimization techniques that will be used in the sequel.

For a given \(\alpha \in \mathbb {R}\), \(\text {sign}(\alpha )\) is the sign of \(\alpha \), defined as

$$\begin{aligned} \text {sign}(\alpha ):={\left\{ \begin{array}{ll}1&{}\text {if }\alpha >0,\\ 0&{}\text {if }\alpha =0,\\ -1&{}\text {if }\alpha <0.\end{array}\right. } \end{aligned}$$

Given a vector \(\tilde{\mathbf {x}}\in \mathbb {R}^n\) and parameter \(\gamma >0\), the optimizer of the following optimization problem

$$\begin{aligned} \min _{\mathbf {x}\in \mathbb {R}^n} \Vert \mathbf {x}\Vert _1+\frac{\gamma }{2}\Vert \mathbf {x}-\tilde{\mathbf {x}}\Vert ^2 \end{aligned}$$

is given by

$$\begin{aligned} \mathbf {x}^*={\text {T}}_{\frac{1}{\gamma }}(\tilde{\mathbf {x}}):=\Bigg (\text {sign}((\tilde{\mathbf {x}})_1)\max \big \{0,|(\tilde{\mathbf {x}})_1|-\frac{1}{\gamma }\big \},\dots ,\text {sign}((\tilde{\mathbf {x}})_n)\max \big \{0,|(\tilde{\mathbf {x}})_n|-\frac{1}{\gamma }\big \}\Bigg )^\mathsf {T}. \end{aligned}$$

It is known as the soft-thresholding, and \({\text {T}}_{\alpha }\) is the soft-thresholding operator for a given \(\alpha >0\).

Given a matrix \(A\in \mathbb {R}^{n\times n}\), an optimizer of the following optimization problem

$$\begin{aligned} \min _{X\in \mathbb {O}(n)} \Vert X-A\Vert ^2 \end{aligned}$$

is given by \(X^*=UV^\mathsf {T}\) [18], where \(U,V\in \mathbb {O}(n)\) are taken from the full singular value decomposition of A, i.e., \(U\Sigma V^\mathsf {T}=A\) for some nonnegative diagonal matrix \(\Sigma \in \mathbb {R}^{n\times n}\).

3 Augmented Lagrangian method

In this section, we apply the classical augmented Lagrangian method (ALM) for solving problem (12).

A standard reformulation of (12) by putting the orthogonality constraints into the objective function is

$$\begin{aligned} \begin{array}{rl}\min &{}\Vert \mathcal {B}\Vert _1+\sum \nolimits _{i=1}^k\delta _{\mathbb {O}(n_i)}(U^{(i)})\\ \text {s.t.}&{}(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}=\mathcal {B}. \end{array} \end{aligned}$$
(13)

With Lagrangian multiplier \(\mathcal {X}\) and penalty parameter \(\rho \), the augmented Lagrangian function of problem (13) is (cf. [7])

$$\begin{aligned} L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X})= & {} \Vert \mathcal {B}\Vert _1+\sum _{i=1}^k\delta _{\mathbb {O}(n_i)}(U^{(i)}) +\langle \mathcal {X},(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}\rangle \nonumber \\&+\frac{\rho }{2}\Vert (U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}\Vert ^2. \end{aligned}$$
(14)

For given matrices \(U^{(i)}_s\in \mathbb {O}(n_i)\) for all \(i\in \{1,\dots ,k\}\) and \(s=1,2,\dots \), let

$$\begin{aligned} \mathbb {U}_{s}:=(U^{(1)}_s,\dots ,U^{(k)}_s). \end{aligned}$$

For convenience, we define

$$\begin{aligned} \Vert \mathbb {U}_s\Vert :=\Vert U^{(1)}_s\Vert +\dots +\Vert U^{(k)}_s\Vert . \end{aligned}$$

Note that minimization problem (13) is an equality constrained nonlinear optimization problem with nonsmooth objective function. The classical inexact augmented Lagrangian method for solving (13) is

Algorithm 3.1

inexact ALM

figure a

Several problems should be addressed for Algorithm 3.1: (i) Step 1 is well-defined, i.e., there exists a solution for (15), (16) and (17); and (ii) efficient computation of such a solution as \(\epsilon _s\downarrow 0\). For a succinct representation, these algorithmic implementations will be discussed later. Convergence properties will be established first, assuming Algorithm 3.1 is well-defined.

To that end, critical points of the augmented Lagrangian function and KKT points of the original optimization problem (12) will be discussed.

3.1 Critical points

In the following, we study the critical points of the augmented Lagrangian. For a given multiplier \(\mathcal {X}\), we can split \(L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X})\) as

$$\begin{aligned} L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X}):=f(\mathbb {U})+Q(\mathbb {U},\mathcal {B})+g(\mathcal {B}), \end{aligned}$$
(20)

where

$$\begin{aligned} f(\mathbb {U}):=\sum _{i=1}^k\delta _{\mathbb {O}(n_i)}(U^{(i)}),\ g(\mathcal {B}):=\Vert \mathcal {B}\Vert _1, \end{aligned}$$

and

$$\begin{aligned} Q(\mathbb {U},\mathcal {B}):=\langle \mathcal {X},(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}\rangle +\frac{\rho }{2}\Vert (U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}\Vert ^2 \end{aligned}$$

with

$$\begin{aligned} \mathbb {U}:=(U^{(1)},\dots ,U^{(k)})\in \mathbb {R}^{n_1\times n_1}\times \dots \times \mathbb {R}^{n_k\times n_k}. \end{aligned}$$

With the natural structure of the variables, we can partition the subdifferentials or gradients of the functions involved so far accordingly. The subdifferentials and gradients are kept aligned as the variables without vectorizing, e.g., the partial derivatives of \(Q(\mathbb {U},\mathcal {B})\) are collected in the same tensor format as \(\mathcal {B}\) and the block matrix structure of \(\mathbb {U}\). This notation can be easily understood from the linear operator perspective of subdifferentials and gradients. In particular,

$$\begin{aligned} \partial f(\mathbb {U})=\left\{ \begin{bmatrix}B_1\\ \vdots \\ B_k\end{bmatrix}\Bigg | B_i\in \partial \delta _{\mathbb {O}(n_i)}(U^{(i)})\right\} =\left\{ \begin{bmatrix}B_1\\ \vdots \\ B_k\end{bmatrix}\Bigg | B_i\in N_{\mathbb {O}(n_i)}(U^{(i)})\right\} , \end{aligned}$$

and

$$\begin{aligned} \nabla _{\mathbb {U}} Q(\mathbb {U},\mathcal {B})=\rho \begin{bmatrix}U^{(1)}V^{(1)}\big [V^{(1)}\big ]^\mathsf {T}-\mathcal {B}^{({\text {f}},1)}\big [V^{(1)}\big ]^\mathsf {T}+\frac{1}{\rho }\mathcal {X}^{({\text {f}},1)}\big [V^{(1)}\big ]^\mathsf {T}\\ \vdots \\ U^{(k)}V^{(k)}\big [V^{(k)}\big ]^\mathsf {T}-\mathcal {B}^{({\text {f}},k)}\big [V^{(k)}\big ]^\mathsf {T}+\frac{1}{\rho }\mathcal {X}^{({\text {f}},k)}\big [V^{(k)}\big ]^\mathsf {T}\end{bmatrix} \end{aligned}$$

where

$$\begin{aligned} V^{(i)}:=\big [(U^{(1)},\dots ,U^{(i-1)},I,U^{(i+1)},\dots ,U^{(k)})\cdot \mathcal {A}\big ]^{({\text {f}},i)}\ \text {for all }i\in \{1,\dots ,k\}. \end{aligned}$$
(21)

Likewise,

$$\begin{aligned} \nabla _{\mathcal {B}}Q(\mathbb {U},\mathcal {B}) =\rho \left( \mathcal {B}-(U^{(1)},\dots ,U^{(k)}) \cdot \mathcal {A}-\frac{1}{\rho }\mathcal {X}\right) . \end{aligned}$$

We also have that

(22)

for all \(i_j\in \{1,\dots ,n_j\}\) and \(j\in \{1,\dots ,k\}\).

Given a lower semicontinuous function f, a critical point of f is a point \(\mathbf {x}\) such that \(0\in \partial f(\mathbf {x})\).

Proposition 3.2

(Critical Points) With notation as above, a point \((\mathbb {U},\mathcal {B})\in (\mathbb {R}^{n_1\times n_1}\times \dots \times \mathbb {R}^{n_k\times n_k})\times (\mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k})\) is a critical point of the minimization problem

$$\begin{aligned} \min _{\mathbb {U},\mathcal {B}}L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X}) \end{aligned}$$

if and only if

$$\begin{aligned} \big (U^{(i)}\big )^\mathsf {T}\big (\mathcal {B}^{({\text {f}},i)}-\frac{1}{\rho }\mathcal {X}^{({\text {f}},i)}\big )\big [V^{(i)}\big ]^\mathsf {T}- V^{(i)} \big (\mathcal {B}^{({\text {f}},i)}-\frac{1}{\rho }\mathcal {X}^{({\text {f}},i)}\big )^\mathsf {T}U^{(i)}=O\ \text {for all }i\in \{1,\dots ,k\} \end{aligned}$$

and

$$\begin{aligned} \rho ((U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B})+\mathcal {X}\in \partial g(\mathcal {B}). \end{aligned}$$

Proof

By the structure of the augmented Lagrangian (cf. (20)), we have that

$$\begin{aligned} \partial _{\mathbb {U}} L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X})=\partial f(\mathbb {U})+\nabla _{\mathbb {U}}Q(\mathbb {U},\mathcal {B})\ \text {and }\partial _{\mathcal {B}} L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X})=\nabla _{\mathcal {B}}Q(\mathbb {U},\mathcal {B})+\partial g(\mathcal {B}). \end{aligned}$$

The rest then follows from (4). \(\square \)

3.2 KKT points

In this section, we study KKT points of the optimization problem (12). A general theory on Lagrange multiplier rule for optimization problems with nonsmooth objective functions is presented in Appendix B, for more details, we refer to [40].

In the following, we first rewrite (12) in the form (43) asFootnote 1

$$\begin{aligned} \begin{array}{rl}\min &{}\Vert \mathcal {B}\Vert _1\\ \text {s.t.}&{}(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}=\mathcal {O},\\ &{} (U^{(1)},\dots ,U^{(k)},\mathcal {B})\in \mathbb {O}(n_1)\times \dots \times \mathbb {O}(n_k)\times \big (\mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\big ), \end{array} \end{aligned}$$
(23)

where \(\mathcal {O}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) is the zero tensor. Note that all requirements in Appendix B for the objective and constraint functions and abstract set X are satisfied. In the following, we will show that the constraint qualification (44) is satisfied at each feasible point of (23).

Note that in this case

$$\begin{aligned} X=\mathbb {O}(n_1)\times \dots \times \mathbb {O}(n_k)\times \big (\mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\big ), \end{aligned}$$

and

$$\begin{aligned} N_X(U^{(1)},\dots ,U^{(k)},\mathcal {B})=N_{\mathbb {O}(n_1)}(U^{(1)})\times \dots \times N_{\mathbb {O}(n_k)}(U^{(k)})\times \{\mathcal {O}\}. \end{aligned}$$

Let matrices \(V^{(i)}\in \mathbb {R}^{n_i\times \frac{n^*}{n_i}}\) be defined as (21) for all \(i\in \{1,\dots ,k\}\). Let \(\mathcal {X}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\). With a direct calculation, the system (44) for problem (23) becomes

$$\begin{aligned} \nabla (\langle \mathcal {X},(U^{(1)},\dots ,U^{(k)})\cdot \mathcal {A}-\mathcal {B}\rangle )= \begin{bmatrix}\mathcal {X}^{({\text {f}},1)}\big (V^{(1)}\big )^\mathsf {T}\\ \vdots \\ \mathcal {X}^{({\text {f}},k)}\big (V^{(k)}\big )^\mathsf {T}\\ -\mathcal {X}\end{bmatrix} \in N_X(U^{(1)},\dots ,U^{(k)},\mathcal {B}), \end{aligned}$$
(24)

which implies directly \(\mathcal {X}=\mathcal {O}\) from the last relation. Therefore, the constraint qualification (44) is satisfied at each feasible, and hence local minimum, solution of (23).

Next, we present the KKT system of (23) in an explicit form. With (24) and the fact that each \(N_{\mathbb {O}(n_i)}(U^{(i)})\) is a linear space (cf. Sect. 2.2), it is easy to see that a feasible point \((\mathbb {U},\mathcal {B})=(U^{(1)},\dots ,U^{(k)},\mathcal {B})\) is a KKT point of (23) (as well as (12)) if and only if the following system is fulfilled

$$\begin{aligned} \mathcal {X}\in \partial \Vert \mathcal {B}\Vert _1,\ \text {and } \mathcal {X}^{({\text {f}},i)}\big (V^{(i)}\big )^\mathsf {T}\in N_{\mathbb {O}(n_i)}(U^{(i)})\ \text {for all }i\in \{1,\dots ,k\}. \end{aligned}$$
(25)

3.3 Global convergence

Suppose that \(\{(\mathbb {U}_s,\mathcal {B}_s,\mathcal {X}_s)\}\) is a sequence generated by Algorithm 3.1. We will show first that the sequence \(\{(\mathbb {U}_s,\mathcal {B}_s,\mathcal {X}_s)\}\) is bounded. Then, suppose that \((\mathbb {U}_*,\mathcal {B}_*,\mathcal {X}_*)\) is one of its limit points. We will next show that \((\mathbb {U}_*,\mathcal {B}_*,\mathcal {X}_*)\) is a KKT point of (12), i.e., the system (25) is satisfied.

Proposition 3.3

Let \(\{(\mathbb {U}_s,\mathcal {B}_s,\mathcal {X}_s)\}\) be the iteration sequence generated by Algorithm 3.1. Then it is a bounded sequence, every limit point \((\mathbb {U}_*,\mathcal {B}_*,\mathcal {X}_*)\) of this sequence satisfies the feasibility of problem (12), i.e.,

$$\begin{aligned} (U^{(1)}_*,\dots ,U^{(k)}_*)\cdot \mathcal {A}=\mathcal {B}_*\ \text {and }U^{(i)}_*\in \mathbb {O}(n_i)\ \text {for all }i\in \{1,\dots ,k\}, \end{aligned}$$

and \((\mathbb {U}_*,\mathcal {B}_*)\) is a KKT point of problem (12).

The proof of Proposition 3.3 is given in Appendix C. Proposition 3.3 gives the global convergence result for Algorithm 3.1. In the following Sect. 4, we will address the well-definiteness and computation issues.

4 Augmented Lagrangian subproblem

In this section, we apply a proximal alternating minimization (PAM) method to solve the augmented Lagrangian subproblem (15), (16) and (17). For the sake of notational simplicity, we will omit the outer iteration indices of Algorithm 3.1 and present the algorithm for the problem

$$\begin{aligned} (\mathbb {U}_*,\mathcal {B}_*)\approx {\text {argmin}}_{\mathbb {U}, \mathcal {B}}L_{\rho }(\mathbb {U},\mathcal {B};\mathcal {X}) \end{aligned}$$

for given multiplier \(\mathcal {X}\) and penalty parameter \(\rho \). The initial guess for this problem is denoted as \((\mathbb {U}_0,\mathcal {B}_0)\), which can be taken as the previous outer iteration of Algorithm 3.1.

4.1 Proximal alternating minimization algorithm

The algorithm is a regularized proximal multi-block nonlinear Gauss–Seidel method: starting from \(s=1\), iteratively solve the following problems

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {B}_s={\text {argmin}}_{\mathcal {B}}L_{\rho }(\mathbb {U}_{s-1},\mathcal {B};\mathcal {X})+\frac{c^{(0)}_s}{2}\Vert \mathcal {B}-\mathcal {B}_{s-1}\Vert ^2,\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {and for }j=1,\dots ,k,\ \text {solve }\\ U^{(j)}_s\in {\text {argmin}}_{U^{(j)}}L_{\rho }\big ((U^{(1)}_s,\dots ,U^{(j-1)}_s,U^{(j)},U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1}),\mathcal {B}_s;\mathcal {X}\big )\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \frac{c^{(j)}_s}{2}\Vert U^{(j)}-U^{(j)}_{s-1}\Vert ^2, \end{array}\right. } \end{aligned}$$
(26)

in which \(c^{(j)}_s\ge 0\) for all \(j\in \{0,\dots ,k\}\) and \(s=1,2,\dots \) are proximal parameters chosen by the user. There are \(k+1\) subproblems in (26), whereas the last k subproblems are of the same structure. A good news is that all the subproblems have optimal solutions in closed formulae. In the sequel, we will derive these closed formulae.

The first subproblem is equivalent to

$$\begin{aligned}&\min _{\mathcal {B}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}} \Vert \mathcal {B}\Vert _1+\frac{\rho }{2}\Vert \mathcal {B}-(U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}-\frac{1}{\rho }\mathcal {X}\Vert ^2+\frac{c^{(0)}_s}{2}\Vert \mathcal {B}-\mathcal {B}_{s-1}\Vert ^2\\&\quad \simeq \min _{\mathcal {B}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}} \Vert \mathcal {B}\Vert _1+\frac{\rho +c^{(0)}_s}{2}\bigg \Vert \mathcal {B}-\frac{\rho (U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}+\mathcal {X}+c^{(0)}_s\mathcal {B}_{s-1}}{\rho +c^{(0)}_s}\bigg \Vert ^2 \end{aligned}$$

whose solution is analytic and obtained by the soft-thresholding (cf. Sect. 2.6)

$$\begin{aligned} \mathcal {B}_s={\text {T}}_{\frac{1}{\rho +c^{(0)}_s}}\bigg (\frac{\rho (U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}+\mathcal {X}+c^{(0)}_s\mathcal {B}_{s-1}}{\rho +c^{(0)}_s}\bigg ). \end{aligned}$$

In the next, we derive optimal solutions for the rest subproblems. Let \(j\in \{1,\dots ,k\}\), and

$$\begin{aligned} V^{(j)}_s:=\big [(U^{(1)}_s,\dots ,U^{(j-1)}_s,I,U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}\big ]^{({\text {f}},j)}. \end{aligned}$$

Then the subproblem for computing \(U^{(j)}_s\) is

$$\begin{aligned}&\min _{U^{(j)}\in \mathbb {O}(n_j)}\langle \mathcal {X},(U^{(1)}_s,\dots ,U^{(j-1)}_s,U^{(j)},U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}\rangle \nonumber \\&\quad +\frac{\rho }{2}\Vert (U^{(1)}_s,\dots ,U^{(j-1)}_s,U^{(j)},U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}-\mathcal {B}_s\Vert ^2+ \frac{c^{(j)}_s}{2}\Vert U^{(j)}-U^{(j)}_{s-1}\Vert ^2.\nonumber \\ \end{aligned}$$
(27)

Note that

$$\begin{aligned}&\langle \mathcal {X},(U^{(1)}_s,\dots ,U^{(j-1)}_s,U^{(j)},U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}\rangle \\&\quad =\langle \mathcal {X}^{({\text {f}},j)},U^{(j)}V^{(j)}_s\rangle =\langle \mathcal {X}^{({\text {f}},j)}(V^{(j)}_s)^\mathsf {T},U^{(j)}\rangle . \end{aligned}$$

Likewise,

$$\begin{aligned} \langle \mathcal {B}_s,(U^{(1)}_s,\dots ,U^{(j-1)}_s,U^{(j)},U^{(j+1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}\rangle =\langle \mathcal {B}_s^{({\text {f}},j)}(V^{(j)}_s)^\mathsf {T},U^{(j)}\rangle . \end{aligned}$$

With these facts and \(U^{(j)}\in \mathbb {O}(n_j)\), the subproblem (27) is equivalent to

$$\begin{aligned} \min _{U^{(j)}\in \mathbb {O}(n_j)}\Vert U^{(j)}-c^{(j)}_sU^{(j)}_{s-1}+\big (\mathcal {X}^{({\text {f}},j)}-\rho \mathcal {B}_s^{({\text {f}},j)}\big )(V^{(j)}_s)^\mathsf {T}\Vert ^2, \end{aligned}$$

which in turn can be solved by singular value decomposition (SVD) or polar decomposition [18] (cf. Sect. 2.6).

We are now in the position to present the proximal alternating minimization algorithm for the augmented Lagrangian subproblem.

Algorithm 4.1

PAM

figure b

4.2 Convergence analysis

In this section, we will establish the global convergence of Algorithm 4.1. To that end, optimality conditions of problem (26) will be derived first.

A direct calculation shows that the optimality conditions for the subproblem (26) are the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll}\rho \Bigg (\mathcal {B}_s-(U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}-\frac{1}{\rho }\mathcal {X}\Bigg )+c^{(0)}_s\big (\mathcal {B}_s-\mathcal {B}_{s-1}\big )\in -\partial \Vert \mathcal {B}_s\Vert _1,\\ \mathcal {X}^{({\text {f}},j)}(V^{(j)}_s)^\mathsf {T}+\rho \big (U^{(j)}_sV^{(j)}_s-\mathcal {B}_s^{({\text {f}},j)}\big )(V^{(j)}_s)^\mathsf {T}+ c^{(j)}_s(U^{(j)}_s-U^{(j)}_{s-1})\in -\partial _{\mathbb {O}(n_j)}(U^{(j)}_s)\\ \quad \quad \quad \quad \text {for all }j=1,\dots ,k. \end{array}\right. } \end{aligned}$$

With the fact that the normal cones of the orthogonal groups are linear subspaces, the above system can be simplified as

$$\begin{aligned} {\left\{ \begin{array}{ll}\rho \Bigg (\mathcal {B}_s-(U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}-\frac{1}{\rho }\mathcal {X}\Bigg )+c^{(0)}_s\big (\mathcal {B}_s-\mathcal {B}_{s-1}\big )\in -\partial \Vert \mathcal {B}_s\Vert _1,\\ \mathcal {X}^{({\text {f}},j)}(V^{(j)}_s)^\mathsf {T}-\rho \mathcal {B}_s^{({\text {f}},j)}(V^{(j)}_s)^\mathsf {T}+ c^{(j)}_s(U^{(j)}_s-U^{(j)}_{s-1})\in -\partial _{\mathbb {O}(n_j)}(U^{(j)}_s)\ \text {for all }j=1,\dots ,k. \end{array}\right. } \end{aligned}$$

Let

$$\begin{aligned} \Theta _s:=\begin{bmatrix}\mathcal {X}^{({\text {f}},1)}(V^{(1)}_s-\tilde{V}^{(1)}_s)^\mathsf {T}-\rho \mathcal {B}_s^{({\text {f}},1)}(V^{(1)}_s-\tilde{V}^{(1)}_s)^\mathsf {T}+ c^{(1)}_s(U^{(1)}_s-U^{(1)}_{s-1})\\ \vdots \\ \mathcal {X}^{({\text {f}},k)}(V^{(k)}_s-\tilde{V}^{(k)}_s)^\mathsf {T}-\rho \mathcal {B}_s^{({\text {f}},k)}(V^{(k)}_s-\tilde{V}^{(k)}_s)^\mathsf {T}+ c^{(k)}_s(U^{(k)}_s-U^{(k)}_{s-1})\\ \rho \Big ((U^{(1)}_{s-1},\dots ,U^{(k)}_{s-1})\cdot \mathcal {A}-(U^{(1)}_{s},\dots ,U^{(k)}_{s})\cdot \mathcal {A}\Big )-c^{(0)}_s\big (\mathcal {B}_s-\mathcal {B}_{s-1}\big )\end{bmatrix}, \end{aligned}$$
(30)

where for \(j\in \{1,\dots ,k\}\)

$$\begin{aligned} \tilde{V}^{(j)}_s:=\big [(U^{(1)}_s,\dots ,U^{(j-1)}_s,I,U^{(j+1)}_{s},\dots ,U^{(k)}_{s})\cdot \mathcal {A}\big ]^{({\text {f}},j)}. \end{aligned}$$

Compared with the critical points of the augmented Lagrangian function (cf. Sect. 3.1), we have that

$$\begin{aligned} \Theta _s\in \partial L_{\rho }(\mathbb {U}_s,\mathcal {B}_s,\mathcal {X}). \end{aligned}$$
(31)

We will show that Algorithm 4.1 converges. It is based on a general result established in [4, Theorem 6.2]. We summarized the convergence theory for this general PAM in Appendix A.

Proposition 4.2

For any given tensors \(\mathcal {A}, \mathcal {X}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\), and parameters \(\rho >0\), \(\epsilon >0\), \(0<\underline{c}<\overline{c}\), we have that the sequence \(\{(\mathbb {U}_s,\mathcal {B}_s)\}\) produced by Algorithm 4.1 converges and

$$\begin{aligned} \Vert \Theta _s\Vert \rightarrow 0\ \text {as }s\rightarrow \infty \end{aligned}$$

for the sequence \(\{\Theta _s\}\) generated by (28), (29) and (30). Then Algorithm 4.1 is finite termination.

The proof of Proposition 4.2 is given in Appendix D.

5 Numerical experiments

In this section, we test Algorithm 3.1 for several classes of tensors. All the tests were conducted on a Dell PC with RAM 4GB and 3.2GHz CPU in 64bt Windows operation system. All codes were written in MatLab with Tensor ToolBox by Bader and Kolda [5]. Some default parameters were chosen as \(\gamma =1.05\), \(\tau =0.8\), and

$$\begin{aligned} \epsilon _s = \max \{10^{-10}*\max \{n_i\mid 1\le i\le k\},\min \{0.8^s,0.8*\hat{\epsilon }_{s-1}\}\}\ \text {with }\hat{\epsilon }_0=0.8, \end{aligned}$$

with \(\hat{\epsilon }_{s-1}:=\Vert \Theta _{s-1}\Vert \le \epsilon _{s-1}\) for \(s\ge 2\). The initial guess \(\mathcal {X}_1=\mathcal {O}\), and \(\mathcal {B}_1=((U^{(1)}_1)^\mathsf {T},\dots ,(U^{(k)}_1)^\mathsf {T})\cdot \mathcal {A}\) with each \(U^{(i)}_1\in \mathbb {O}(n_i)\) randomly chosen for all \(i\in \{1,\dots ,k\}\) (unless otherwise stated). The other parameters are given concretely. The maximum outer iteration number (i.e., the maximum iteration number allowed for Algorithm 3.1) is 1000. The termination rule is

$$\begin{aligned} \begin{array}{c} \frac{\Vert (U^{(1)}_s,\dots ,U^{(k)}_s)\cdot \mathcal {A}-\mathcal {B}_s\Vert }{\Vert \mathcal {A}\Vert \sqrt{\prod _{i=1}^kn_i}}<10^{-8}\ \text {and }\\ \sqrt{\frac{\Vert {\text {max}}\{|\mathcal {X}_s|-1,0\}\Vert ^2+\frac{1}{\Vert \mathcal {A}\Vert ^2}\sum _{i=1}^k\Vert (U^{(i)}_s)^\mathsf {T}\mathcal {X}_s^{({\text {f}},i)}(V^{(i)}_s)^\mathsf {T}-V^{(i)}_s(\mathcal {X}_s^{({\text {f}},i)})^\mathsf {T}(U^{(i)}_s)^\mathsf {T}\Vert ^2}{\prod _{i=1}^kn_i}}<10^{-8}, \end{array} \end{aligned}$$
(32)

representing the relative feasibility and optimality residuals. Unless otherwise stated, the inner iteration Algorithm 4.1 is terminated whenever either the optimality condition (17) is satisfied or the number of iterations exceeds 1000. If the number of the outer iteration exceeds 1000 and (32) is not satisfied, then the algorithm fails for this test; otherwise the problem is solved successfully.

As problem (12) is nonlinear and nonconvex, the solution found heavily depends on the initial point. Thus, each instance is tested 10 times (unless otherwise stated) with randomly generated initializations. In the tables, the column \(\mathbf sucp \) indicates the probability of successful computations in the 10 simulations; \(\mathbf max(len) \) is the maximum length of the strongly orthogonal decomposition computed among the simulations, and \(\mathbf min(len) \) for the minimum; prob is the probability the algorithm computes out a strongly orthogonal decomposition with length \(\mathbf min(len) \). All the other columns are the mean of the successfully solved simulations: len is the length of the strongly orthogonal decomposition, \(\mathbf out-it \) and \(\mathbf inner-it \) are respectively the numbers of the outer and inner iterations, \(\mathbf cpu \) is the cpu time consumed, \(\mathbf in (10^{-9})\) and \(\mathbf op (10^{-9})\) are respectively the final infeasibility and optimality residuals in the magnitude \(10^{-9}\).

5.1 Examples

In the following, we test several classes of examples from known literatures.

Example 5.1

This example is taken from Kolda [28, Section 3]. Let \(\mathbf {a},\hat{\mathbf {a}}\in \mathbb {R}^n\) be two unit vectors and orthogonal to each other, and \(\sigma _1>\sigma _2>0\). The tensor \(\mathcal {A}\in \mathbb {R}^{n}\otimes \mathbb {R}^{n}\otimes \mathbb {R}^n\) is given by

$$\begin{aligned} \mathcal {A}=\sigma _1\mathbf {a}^{\otimes 3}+\sigma _2\mathbf {b}\otimes \mathbf {b}\otimes \hat{\mathbf {a}}, \end{aligned}$$
(33)

where \(\mathbf {b} = \frac{1}{\sqrt{2}}(\mathbf {a}+\hat{\mathbf {a}})\). The rank of \(\mathcal {A}\) is two, and (33) is a rank decomposition, while it is not a strongly orthogonal decomposition. Obviously, \({\text {rank}}_{{\text {SO}}}(\mathcal {A})\le 5\), by expanding \(\mathbf {b}\) into \(\mathbf {a}\) and \(\hat{\mathbf {a}}\).

We tested sampled examples with the dimensions n varying from 2 to 8. Usually, we get a strongly orthogonal decomposition with length 5; sometimes we get 4. The starting penalty parameter is 10 and the maximum inner iteration number is \((n-1)*100\). For each case, 10 simulations were generated with random \([\mathbf {a},\hat{\mathbf {a}}]\in {\text {St}}(n,2)\), and random \(\sigma _2<\sigma _1\in (0,1)\). The results are collected in Table 1.

Table 1 Computational results for Example 5.1
Full size table

Example 5.2

This example is taken from Ishteva et al. [24, Section 4.1]. Let \(\mathbf {a},\mathbf {b},\mathbf {c}\in \mathbb {R}^n\) be three unit vectors and orthogonal to each other. The tensor \(\mathcal {A}\in \mathbb {R}^{n}\otimes \mathbb {R}^{n}\otimes \mathbb {R}^n\) is given by

$$\begin{aligned} \mathcal {A}=\mathbf {a}\otimes \mathbf {b}\otimes \mathbf {c}+\mathbf {b}\otimes \mathbf {c}\otimes \mathbf {a}+\mathbf {c}\otimes \mathbf {a}\otimes \mathbf {b}. \end{aligned}$$

Obviously, this already gives a strongly orthogonal rank decomposition of \(\mathcal {A}\).

For each case, 10 simulations were generated with random \([\mathbf {a},\mathbf {b},\mathbf {c}]\in {\text {St}}(n,3)\). The penalty parameter is chosen as 10. The computational results are listed in Table 2. All simulations were solved by the algorithm successfully. Thus the column sucp is omitted. It is easily seen from Table 2 that in most cases the algorithm can find out a strongly orthogonal rank decomposition.

Table 2 Computational results for Example 5.2
Full size table

Example 5.3

This example is taken from Kolda [27, Example 3.3]. Let \(\mathbf {a},\mathbf {b}\in \mathbb {R}^n\) be two unit vectors and orthogonal to each other, and \(\sigma _1>\sigma _2>\sigma _3>0\). The tensor \(\mathcal {A}\in \mathbb {R}^{n}\otimes \mathbb {R}^{n}\otimes \mathbb {R}^n\) is given by

$$\begin{aligned} \mathcal {A}=\sigma _1\mathbf {a}\otimes \mathbf {b}\otimes \mathbf {b}+\sigma _2\mathbf {b}\otimes \mathbf {b}\otimes \mathbf {b}+\sigma _3\mathbf {a}\otimes \mathbf {a}\otimes \mathbf {a}. \end{aligned}$$

The definition of \(\mathcal {A}\) gives a strongly orthogonal rank decomposition already. The parameters are chosen the same as Example 5.2. The initialization for the orthogonal matrices is by the factor matrices of the higher order singular value decomposition (HOSVD) of the underlying tensor [14]. Computational results are shown in Table 3.

Table 3 Computational results for Example 5.3
Full size table

Example 5.4

This example is taken from Kolda [27, Example 3.6]. Let \(\mathcal {U}_1,\mathcal {U}_2\in \mathbb {R}^{n_1}\otimes \mathbb {R}^{n_2}\otimes \mathbb {R}^{n_3}\) be two unit rank one tensors that are not orthogonal to each other, and \(\sigma _1\ge \sigma _2\). The tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \mathbb {R}^{n_2}\otimes \mathbb {R}^{n_3}\) is given by

$$\begin{aligned} \mathcal {A}=\sigma _1\mathcal {U}_1+\sigma _2\mathcal {U}_2. \end{aligned}$$

The penalty parameter is chosen as 10. The computational results are given in Table 4.

Table 4 Computational results for Example 5.4
Full size table

Example 5.5

This example is taken from Kolda [27, Example 5.1]. Let \(\mathbf {a},\mathbf {b},\mathbf {c},\mathbf {d} \in \mathbb {R}^n\) be four unit vectors and orthogonal to each other,

$$\begin{aligned} \sigma _1=1,\ \sigma _2=0.75,\ \sigma _3=\sigma _4=0.7,\ \sigma _5=\sigma _6=0.65, \end{aligned}$$

and

$$\begin{aligned}&\mathcal {U}_1=\mathbf {a}^{\otimes 3},\ \mathcal {U}_2=\mathbf {b}^{\otimes 3},\ \mathcal {U}_3=\mathbf {a}\otimes \mathbf {c}\otimes \mathbf {d},\ \mathcal {U}_4=\mathbf {a}\otimes \mathbf {d}\otimes \mathbf {c},\\&\mathcal {U}_5=\mathbf {b}\otimes \mathbf {c}\otimes \mathbf {d},\ \mathcal {U}_6=\mathbf {b}\otimes \mathbf {d}\otimes \mathbf {c}. \end{aligned}$$

The tensor \(\mathcal {A}\in \mathbb {R}^{n}\otimes \mathbb {R}^{n}\otimes \mathbb {R}^n\) is given by

$$\begin{aligned} \mathcal {A}=\sum _{i=1}^6\sigma _i\mathcal {U}_i. \end{aligned}$$

The definition of \(\mathcal {A}\) gives a strongly orthogonal rank decomposition already. The penalty parameter is chosen as 10. The computational results are given in Table 5.

Table 5 Computational results for Example 5.5
Full size table

Example 5.6

This example is taken from Nie [37, Example 5.6]. The tensor \(\mathcal {A}\in \otimes ^5\mathbb {R}^3\) is given by

$$\begin{aligned} \mathcal {A}=\begin{bmatrix}1\\ 2\\ 3\end{bmatrix}^{\otimes 5}+\begin{bmatrix}1\\ -2\\ 3\end{bmatrix}^{\otimes 5}+\frac{1}{3}\begin{bmatrix}1\\ -12\\ -3\end{bmatrix}^{\otimes 5}+\frac{1}{5}\begin{bmatrix}1\\ 12\\ -13\end{bmatrix}^{\otimes 5}. \end{aligned}$$

This tensor is a hard one, since the entries of the tensor varies from \(\frac{38}{15}\) to \(-\frac{369268}{5}=-7.38\times 10^{4}\). The computed orthogonal decomposition has rank 213, slightly smaller than the upper bound \(3^5-15=228\) (cf. [22]). We take the penalty parameter 10, and run 100 simulations. Each simulation finds a decomposition with length 213. The average outer iteration number is 83.15, the inner iteration number is 5435.59, the cpu time is 78.771, the infeasibility is \(1.7597\times 10^{-11}\), and the optimality residual is \(3.6463\times 10^{-9}\).

Example 5.7

This example is taken from Nie [37, Example 5.8]. The tensor \(\mathcal {A}\in {\text {S}}^3(\mathbb {R}^n)\), the subspace of symmetric tensors in \(\otimes ^3\mathbb {R}^n\), is given by

$$\begin{aligned} a_{ijk}=ijk-i-j-k,\ \text {for all }i,j,k\in \{1,\dots ,n\}. \end{aligned}$$

The penalty parameter is chosen as 10. The computational results are given in Table 6.

Table 6 Computational results for Example 5.7
Full size table

Example 5.8

This example is taken from Nie[37, Example 5.9]. The tensor \(\mathcal {A}\in {\text {S}}^4(\mathbb {R}^n)\) is given by

$$\begin{aligned} a_{ijkl}={\text {tan}}(ijkl),\ \text {for all }i,j,k,l\in \{1,\dots ,n\}. \end{aligned}$$

This example is also not easy to solve, since the entries of the tensor vary with large magnitudes. The penalty parameter is chosen as 10. The computational results are given in Table 7.

Table 7 Computational results for Example 5.8
Full size table

Example 5.9

This example is taken from Nie [37, Example 5.10]. The tensor \(\mathcal {A}\in {\text {S}}^4(\mathbb {R}^n)\) is given by

$$\begin{aligned} a_{ijkl}={\text {sin}}(i+j+k+l)+{\text {cos}}(ijkl),\ \text {for all }i,j,k,l\in \{1,\dots ,n\}. \end{aligned}$$

The penalty parameter is chosen as 10. The computational results are given in Table 8.

Table 8 Computational results for Example 5.9
Full size table

Example 5.10

The last concrete example is taken from Batselier et al. [6, Example 6]. The tensor \(\mathcal {A}\in \otimes ^3\mathbb {R}^n\) is given by

$$\begin{aligned} a_{ijk}=\frac{1}{i+j+k},\ \text {for all }i,j,k\in \{1,\dots ,n\}. \end{aligned}$$

Similar reason as that in Example 5.8, this class of tensors is hard. The penalty parameter is 100. The computational results are given in Table 9.

Table 9 Computational results for Example 5.10
Full size table

5.2 Completely orthogonally decomposable tensors

We would like to separate a section for the class of completely orthogonally decomposable tensors (CODT), as it is of particular interest [3, 23]. For this class of tensors, we can consider an analogue condition number for tensors.

A tensor \(\mathcal {A}\in \mathbb {R}^{n_1}\otimes \dots \otimes \mathbb {R}^{n_k}\) is called completely orthogonally decomposable (cf. [27, 38, 41]) if there exist orthogonal matrices

$$\begin{aligned} A_i=[\mathbf {a}_{i,1},\dots ,\mathbf {a}_{i,n_i}]\in \mathbb {R}^{n_i\times n_i}\ \text {for all }i=1,\dots ,k \end{aligned}$$

and numbers \(\lambda _d\in \mathbb {R}_+\) for \(d=1,\dots ,D_0:=\min \{n_1,\dots ,n_k\}\) such that

$$\begin{aligned} \mathcal {A}=\sum _{d=1}^{D_0}\lambda _d\mathbf {a}_{1,d}\otimes \dots \otimes \mathbf {a}_{k,d}. \end{aligned}$$
(34)

Note that some of the \(\lambda _d\)’s can be zeros. By eliminating the zeros, we can further assume that a nonzero completely orthogonally decomposable tensor takes the form

$$\begin{aligned} \mathcal {A}=\sum _{d=1}^D \lambda _d\mathbf {a}_{1,d}\otimes \dots \otimes \mathbf {a}_{k,d}. \end{aligned}$$

with \(D \le D_0:=\min \{n_1,\dots ,n_k\}\) and \(\lambda _d>0\), \(d=1,\ldots ,D\). It is easy to see that D is then the strongly orthogonal rank of \(\mathcal {A}\).

Unlike the matrix case (i.e., \(k=2\)), the rank one decomposition of a completely orthogonally decomposable tensor is always unique [41], regardless of the possibility of equal \(\lambda _i\)’s. It can be derived from Kruskal’s uniqueness theorem [31] as well, in which the prerequisity is the trivial inequality \(k-1\le (k-2)D\) when \(D\ge 2\) and the case \(D=1\) is obvious. Therefore, in this case, problem (13) has an optimizer with a diagonal tensor \(\mathcal {B}\).

For this class of tensors, we implement two tests for stability of the algorithm. The first test is on tensors with respectively small, medium, and large strongly orthogonal ranks. All the tensors are third order, and the dimensions are listed in Table 10 case by case. In this table, \({\text {rk}}\) indicates the rank of the generated tensor. In each case, 10 simulations were generated with the factor orthogonal matrices being the orthogonalization of the columns of randomly generated matrices. The penalty parameter for tensors with dimensions 30, 50, 80, and 100 are chosen respectively as 10, 20, 30, and 40.

Denote by \(\lambda _{\max }:=\max \{\lambda _d\mid 1\le d\le D\}\), and \(\lambda _{\min }:=\min \{\lambda _d\mid 1\le d\le D\}\). Then

$$\begin{aligned} \kappa :=\frac{\lambda _{\max }}{\lambda _{\min }} \end{aligned}$$
(35)

will serve as the role of condition number in the tensor case. The other test is on third order tensors of strongly orthogonal rank 3 and dimension 30 with different levels of condition numbers, which are indicated as cond in Table 11. Computational tests are given in Table 11 for the performance. The penalties for these nine cases are respectively ranging from 20 to 100 with equi-gap 10.

Table 10 Computational results for third order CODTs with different ranks
Full size table
Table 11 Computational results for third order CODTs with different condition numbers
Full size table

5.3 Random examples

In this section, we test random examples to see the performance of Algorithm 3.1.

We generate two sets of random examples, the first one is generated with each entry being drawn randomly in \([-1,1]\). The second one is generated as the sum of rk rank one tensors, with each component vector in the rank one tensor being drawn componentwisely in \([-1,1]\). In this set, we also generate symmetric tensors. The penalty parameter is chosen as 100 for all simulations, and the results are listed in Tables 12, 13 and 14. In Table 14, sym indicates the symmetry of the tensors; it is symmetric when it takes value 1, and nonsymmetric otherwise.

Table 12 Computational results for randomly generated nonsymmetric third order tensors
Full size table
Table 13 Computational results for randomly generated symmetric third order tensors
Full size table
Table 14 Performance for randomly generated higher order tensor examples: symmetric and nonsymmetric
Full size table

5.4 Conclusions

We see that problem (13) is highly nonlinear, especially when the tensor size is large, thus solutions of Algorithm 3.1 depend on the initializations heavily. While, for most cases, the convergence is fast with high accuracy. These can be seen from Tables 1, 2,  10, 11, 12,  13 and 14. We can also see from these computations that when the strongly orthogonal ranks are small relative to the tensor sizes or the tensor sizes are small, the computational performance is very well, which can be seen from Tables 3, 4, 5,  6 and 11. On the other hand, when the tensor components have a large deviation in magnitude or the strongly orthogonal ranks are large, the performance is reduced, which can be seen from Tables 7, 8, 9,  10, 12 and 13.

We want to emphasize Table 11, from which we can see that the condition number defined as (35) plays a key role in the performance of the algorithm. We think this is an intrinsic property of the underlying tensor, which will domonstrate the efficiency of most computations. Since the rank one decomposition for CODT is unique, and then the condition number as (35) for CODTs is well-defined. More sophisticated definition and investigation for general tensors should be carried out in the future. Also, theoretical justification of the dependence of the efficiency of an algorithm on the condition number should be investigated in the next.

6 Conclusions

In this article, computing the strongly orthogonal rank decomposition of a given tensor is formulated as solving an optimization problem with the help of matrix-tensor multiplication. This optimization problem has discrete-valued objective function (the \(l_0\)-norm of the tensor) subject to a system of nonlinear equality constraints and a set of orthogonal constraints. As the number of components of a tensor increases exponentially with respect to the tensor size, the number of nonlinear equality constraints becomes huge for tensors with large sizes. For example, it is one million for a sixth order ten dimensional tensor. As we can image, this class of problem is very difficult to solve in general, partly due to (i) the huge number of equality constraints, (ii) the orthogonality constraints, and (iii) the discrete-valued objective function.

Nevertheless, we propose to replace the objective function by a widely used surrogate–the \(l_1\)-norm of the tensor. Then, we apply an inexact augmented Lagrangian multiplier method to solve the resulting optimization problem. During the iterations, the orthogonality requirements are always guaranteed. Thus, the algorithm will always return a strongly orthogonal decomposition whatever the termination situations were met. Moreover, the augmented Lagrangian subproblem is solved by a proximal alternating minimization method with the benefit being that each subproblem has a closed formula solution. This is one key ingredient to keep the orthogonality constraints. Global convergence of the ALM algorithm is established without any further assumptions. Surprisingly, though as simple this algorithm as it sounds, the performance of the proposed algorithm is quite well. Extensive numerical computations were conducted with quite sounding efficiency as well as high accuracy. Note that in Table 14, the number of nonlinear equality constraints is 3,200,000 for the case \((n,k)=(20,5)\).

It follows from the computations that several issues need further investigation. The first is the exactness of the \(l_1\)-norm surrogate with respect to the original \(l_0\)-norm. It can be seen from the computations that quite often, \(l_1\)-norm can realize the strongly orthogonal rank decomposition. Thus, theoretical justifications should be established. The second would be a more efficient method to deal with tensors with larger strongly orthogonal ranks, which are the hard ones in the present computations. Another is that various other surrogates for the \(l_0\)-norm should be studied.