1 Introduction

Let \(G = (\mathcal{{V}}, \mathcal{{E}})\) be a graph on vertex set \(\mathcal{{V}} = \{1,2,\ldots ,n\}\) and edge set \(\mathcal{{E}} \subseteq \mathcal{{V}} \times \mathcal{{V}}\). We assume G is simple and undirected; that is for any vertices i and j we have \((i,i) \notin \mathcal{{E}}\) and \((i,j) \in \mathcal{{E}}\) if and only if \((j,i) \in \mathcal{{E}}\) (note that this implies that \(|\mathcal{{E}}|\), the number of elements in \(\mathcal{{E}}\), is twice the total number of edges in G). For each \(i \in \mathcal{{V}}\), let \(c_i\in \mathbb {R}\) denote the cost and \(w_i > 0\) denote the weight of vertex i. If \(\mathcal{{Z}} \subseteq \mathcal{{V}}\), then

$$\begin{aligned} \mathcal{{C}}(\mathcal{{Z}}) = \sum _{i \in \mathcal{{Z}}} c_i \quad \text{ and } \quad \mathcal{{W}}(\mathcal{{Z}}) = \sum _{i \in \mathcal{{Z}}} w_i \end{aligned}$$

denote the total cost and weight of the vertices in \(\mathcal{{Z}}\), respectively.

If the vertices \(\mathcal{{V}}\) are partitioned into three disjoint sets \(\mathcal{{A}}\), \(\mathcal{{B}}\), and \(\mathcal{{S}}\), then \(\mathcal{{S}}\) separates \(\mathcal{{A}}\) and \(\mathcal{{B}}\) if there is no edge \((i,j)\in \mathcal{{E}}\) with \(i\in \mathcal{{A}}\) and \(j\in \mathcal{{B}}\). The Vertex Separator Problem (VSP) is to minimize the cost of \(\mathcal{{S}}\) while requiring that \(\mathcal{{A}}\) and \(\mathcal{{B}}\) have approximately the same weight. We formally state the VSP as follows:

$$\begin{aligned}&\displaystyle {\min _{\mathcal{{A}},\mathcal{{S}},\mathcal{{B}} \subseteq \mathcal{{V}}} \quad \mathcal{{C}}(\mathcal{{S}})} \nonumber \\&\quad \displaystyle {\text{ subject } \text{ to } \quad \mathcal{{S}} = \mathcal{{V}} \setminus (\mathcal{{A}}\cup \mathcal{{B}}), \quad \mathcal{{A}} \cap \mathcal{{B}} = \emptyset , \quad (\mathcal{{A}} \times \mathcal{{B}}) \cap \mathcal{{E}} = \emptyset , } \nonumber \\&\quad \displaystyle {\ell _a \le \mathcal{{W}}(\mathcal{{A}}) \le u_a, \;\; \text{ and } \;\; \ell _b \le \mathcal{{W}}(\mathcal{{B}}) \le u_b}, \end{aligned}$$
(1)

where \(\ell _a\), \(\ell _b\), \(u_a\), and \(u_b\) are given nonnegative real numbers less than or equal to \(\mathcal{{W}}(\mathcal{{V}})\). The constraints \(\mathcal{{S}} = \mathcal{{V}} \setminus (\mathcal{{A}}\cup \mathcal{{B}})\) and \(\mathcal{{A}} \cap \mathcal{{B}} = \emptyset \) ensure that \(\mathcal{{V}}\) is partitioned into disjoint sets \(\mathcal{{A}}\), \(\mathcal{{B}}\), and \(\mathcal{{S}}\), while the constraint \((\mathcal{{A}} \times \mathcal{{B}}) \cap \mathcal{{E}} = \emptyset \) ensures that there are no edges between the sets \(\mathcal{{A}}\) and \(\mathcal{{B}}\). Throughout the paper, we assume (1) is feasible. In particular, if \(\ell _a, \ell _b \ge 1\), then there exist at least two distinct vertices i and j such that \((i,j)\notin \mathcal{{E}}\); that is, G is not a complete graph.

Vertex separators have applications in VLSI design [26, 30, 39], finite element methods [32], parallel processing [12], sparse matrix factorizations ([9, Sect. 7.6], [16, Chapter 8], and [34]), hypergraph partitioning [25], and network security [7, 27, 31]. The VSP is NP-hard [5, 15]. However, due to its practical significance, many heuristics have been developed for obtaining approximate solutions, including node-swapping heuristics [29], spectral methods [34], semidefinite programming methods [13], and recently a breakout local search algorithm [3].

Early methods [17, 34], for computing vertex separators were based on computing edge separators (bipartitions of \(\mathcal{{V}}\) with low cost edge-cuts). In these algorithms, vertex separators are obtained from edge separators by selecting vertices incident to the edges in the cut. More recently, [1] gave a method for computing vertex separators in a graph by finding low cost net-cuts in an associated hypergraph. Some of the most widely used heuristics for computing edge separators are the node swapping heuristics of Fiduccia–Mattheyses [14] and Kernighan–Lin [26], in which vertices are exchanged between sets until the current partition is considered to be locally optimal.

It has been demonstrated repeatedly that for problems on large-scale graphs, such as finding minimum k-partitionings [6, 20, 24] or minimum linear arrangements [36, 38], optimization algorithms can be much more effective when carried out in a multilevel framework. In a multilevel framework, a hierarchy of increasingly smaller graphs is generated which approximate the original graph, but with fewer degrees of freedom. The problem is solved for the coarsest graph in the hierarchy, and the solution is gradually uncoarsened and refined to obtain a solution for the original graph. During the uncoarsening phase, optimization algorithms are commonly employed locally to make fast improvements to the solution at each level in the algorithm. Although multilevel algorithms are inexact for most NP-hard problems on graphs, they typically produce very high quality solutions and are very fast (often linear in the number of vertices plus the number of edges with no hidden coefficients). Many multilevel edge separator algorithms have been developed and incorporated into graph partitioning packages (see survey in [6]). In [2], a Fiduccia–Mattheyses type heuristic is used to find vertex separators directly. Variants of this algorithm have been incorporated into the multilevel graph partitioners METIS [23, 24] and BEND [21].

In [19], the authors make a departure from traditional discrete-based heuristics for solving the VSP, and present the first formulation of the problem as a continuous optimization problem. In particular, when the vertex weights are identically one, conditions are given under which the VSP is equivalent to solving a continuous bilinear quadratic program.

The preliminary numerical results of [19] indicate that the bilinear programming formulation can serve as an effective tool for making local improvements to a solution in a multilevel context. The current work makes the following contributions:

  1. 1.

    The bilinear programming model of [19] is extended to the case where vertex weights are possibly greater than one. This generalization is important since each vertex in a multilevel compression corresponds to a collection of vertices in the original graph. The bilinear formulation of the compressed graph is not exactly equivalent to the VSP for the compressed graph, but it very closely approximates the VSP as we show.

  2. 2.

    We develop an approach to improve upon a given vertex separator by applying a Mountain Climbing Algorithm to the bilinear program using the incidence vector for the separator as a starting guess. Sufficient conditions are developed under which the algorithm can improve upon the separator after at most two iterations.

  3. 3.

    We investigate a technique for escaping local optima encountered by the Mountain Climbing Algorithm based on relaxing the constraint that there are no edges between the sets in the partition. Since this constraint is enforced by a penalty in the objective, we determine the smallest possible relaxation of the penalty for which a gradient descent step moves the iterate to a new location where the separator could be smaller.

  4. 4.

    A multilevel algorithm is developed which incorporates the weighted bilinear program in the refinement phase along with the perturbation technique. Computational results are given to compare the quality of the solutions obtained with the bilinear programming approach to a multilevel vertex separator routine in the METIS package. The algorithm is shown to be especially effective on communication and collaboration networks.

The outline of the paper is as follows. Section 3 reviews the bilinear programming formulation of the VSP in [19] and develops the weighted formulation which is suitable for the coarser levels in the algorithm. In Sect. 4 we develop the Mountain Climbing Algorithm and examine some sufficient conditions under which a separator can be improved by the algorithm. The conditions are derived in the appendix. In addition, a perturbation technique is developed for escaping local optima. Section 5 summarizes the multilevel framework, while Sect. 6 gives numerical results comparing our algorithm to METIS. Conclusions are drawn in Sect. 7.

2 Notation

Vectors or matrices whose entries are all 0 or all 1 are denoted by \(\mathbf{{0}}\) or \(\mathbf{{1}}\) respectively, where the dimension will be clear from the context. The set of integers is \(\mathbb {Z}\), while \(\mathbb {Z}^+\) is the set of strictly positive integers. If \(\mathbf{{x}} \in \mathbb {R}^n\) and \(f:\mathbb {R}^n\rightarrow \mathbb {R}\), then \(\nabla f (\mathbf{{x}})\) denotes the gradient of f at \(\mathbf{{x}}\), a row vector, and \(\nabla ^2 f (\mathbf{{x}})\) is the Hessian. If \(f : \mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {R}\), then \(\nabla _{\mathbf{{x}}} f (\mathbf{{x}},\mathbf{{y}})\) is the row vector corresponding to the first n entries of \(\nabla f (\mathbf{{x}},\mathbf{{y}})\), while \(\nabla _{\mathbf{{y}}} f (\mathbf{{x}},\mathbf{{y}})\) is the row vector corresponding to the last n entries. If \(\mathbf{{A}}\) is a matrix, then \(\mathbf{{A}}_i\) denotes the i-th row of \(\mathbf{{A}}\). If \(\mathbf{{x}}\in \mathbb {R}^n\), then \(\mathbf{{x}}\ge \mathbf{{0}}\) means \(x_i \ge 0\) for all i, and \(\mathbf{{x}}^\mathsf{T}\) denotes the transpose, a row vector. Let \(\mathbf{{I}}\in \mathbb {R}^{n\times n}\) denote the \(n\times n\) identity matrix, let \(\mathbf{{e}}_i\) denote the i-th column of \(\mathbf{{I}}\), and let \(|\mathcal{{A}}|\) denote the number of elements in the set \(\mathcal{{A}}\). If \(\mathcal{{Z}}\subseteq \mathcal{{V}}\), then

$$\begin{aligned} \mathcal{{N}} (\mathcal{{Z}}) = \{j \in \mathcal{{V}}\backslash \mathcal{{Z}}\; :\;\exists \;i\in \mathcal{{Z}} \text{ s.t. } (i,j)\in \mathcal{{E}}\} \end{aligned}$$

is the set of neighbors of \(\mathcal{{Z}}\) and \(\overline{\mathcal{{N}}} (\mathcal{{Z}}) = \mathcal{{N}} (\mathcal{{Z}}) \cup \mathcal{{Z}}\). Let \(\mathbb {B} = \{ 0, 1\}\) denote the binary numbers. If \(\mathbf{{x}} \in \mathbb {B}^n\), then the support of \(\mathbf{{x}}\) is defined by

$$\begin{aligned} \mathrm{supp}(\mathbf{{x}}) = \{i \in \mathcal{{V}} : x_i = 1 \}, \end{aligned}$$

and if \(\mathcal{{A}} \subseteq \mathcal{{V}}\), then \(\mathrm{supp}^{-1}(\mathcal{{A}})\) is the vector \(\mathbf{{x}} \in \mathbb {B}^n\) whose support is \(\mathcal{{A}}\). Hence, \(\mathrm{supp}^{-1}(\mathrm{supp}(\mathbf{{x}} )) = \mathbf{{x}}\).

3 Bilinear programming formulation

Since minimizing \(\mathcal{{C}}(\mathcal{{S}})\) in (1) is equivalent to maximizing \(\mathcal{{C}}(\mathcal{{A}} \cup \mathcal{{B}})\), we may view the VSP as the following maximization problem:

$$\begin{aligned}&\displaystyle {\max _{\mathcal{{A}},\mathcal{{B}} \subseteq \mathcal{{V}}} \quad \mathcal{{C}}(\mathcal{{A}}\cup \mathcal{{B}})} \nonumber \\&\quad \displaystyle {\text{ subject } \text{ to } \quad \mathcal{{A}} \cap \mathcal{{B}} = \emptyset , \quad (\mathcal{{A}} \times \mathcal{{B}}) \cap \mathcal{{E}} = \emptyset , } \nonumber \\&\quad \displaystyle {\ell _a \le \mathcal{{W}}(\mathcal{{A}}) \le u_a, \;\; \text{ and } \;\; \ell _b \le \mathcal{{W}}(\mathcal{{B}}) \le u_b}. \end{aligned}$$
(2)

Let \(\mathbf{{A}}\) be the \(n \times n\) adjacency matrix for the graph G defined by \(a_{ij} = 1\) if \((i,j) \in \mathcal{{E}}\) and \(a_{ij} = 0\) otherwise, and let \(\mathbf{{I}}\) be the \(n\times n\) identity matrix. For any pair of subsets \(\mathcal{{A}}, \mathcal{{B}} \subseteq \mathcal{{V}}\), let \(\mathbf{{x}} = \mathrm{supp}^{-1}(\mathcal{{A}})\) and \(\mathbf{{y}} = \mathrm{supp}^{-1}(\mathcal{{B}})\) be the associated binary support vectors. Observe that

$$\begin{aligned} {\mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}} \quad = \quad {\sum _{i = 1}^n\sum _{j = 1}^n x_i a_{ij} y_j} + {\sum _{i = 1}^n x_i y_i} \quad = \quad {\sum _{x_i = 1}\sum _{y_j = 1} a_{ij}} + {\sum _{x_i = y_i= 1} 1} . \end{aligned}$$

By definition, \(x_i = 1\) or \(y_j = 1\) if and only if \(i \in \mathcal{{A}}\) or \(j \in \mathcal{{B}}\) respectively, and \(a_{ij} = 1\) if and only \((i, j) \in \mathcal{{E}}\). Consequently, we have

$$\begin{aligned} {\mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}}\quad = \quad {\sum _{i \in \mathcal{{A}}}\sum _{j\in \mathcal{{B}}} a_{ij}} + {\sum _{i \in \mathcal{{A}} \cap \mathcal{{B}}} 1} \quad = \quad {|(\mathcal{{A}}\times \mathcal{{B}})\cap \mathcal{{E}}|} + {|\mathcal{{A}} \cap \mathcal{{B}}|}. \end{aligned}$$

So, the constraints \(\mathcal{{A}} \cap \mathcal{{B}} = \emptyset \) and \((\mathcal{{A}} \times \mathcal{{B}}) \cap \mathcal{{E}} = \emptyset \) in (2) hold if and only if

$$\begin{aligned} \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} = 0, \quad \text{ where } \mathbf{{x}} = \mathrm{supp}(\mathcal{{A}}) \text{ and } \mathbf{{y}} = \mathrm{supp}(\mathcal{{B}}) . \end{aligned}$$
(3)

Moreover, for these support vectors, we have \(\mathcal{{C}}(\mathcal{{A}} \cup \mathcal{{B}}) = \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}})\) and \(\mathcal{{W}}(\mathcal{{A}}) = \mathbf{{w}}^\mathsf{T}\mathbf{{x}}\), where \(\mathbf{{c}}\) and \(\mathbf{{w}}\) are the n-dimensional vectors which store the costs \(c_i\) and weights \(w_i\) of vertices, respectively. Hence, a binary formulation of (2) is

$$\begin{aligned}&\displaystyle {\max _{\mathbf{{x}}, \mathbf{{y}} \in \mathbb {B}^n } \;\; \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}})} \nonumber \\&\quad \displaystyle {\text{ subject } \text{ to }} \,\, \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} = 0,\nonumber \\&\quad \ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a, \;\; \text{ and } \;\; \ell _b \le \mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_b. \end{aligned}$$
(4)

Now, consider the following problem in which the quadratic constraint of (4) has been relaxed:

$$\begin{aligned}&\displaystyle {\max _{\mathbf{{x}}, \mathbf{{y}} \in \mathbb {B}^n} \;\; f (\mathbf{{x}}, \mathbf{{y}}) := \; \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) - \gamma \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}} \nonumber \\&\quad \begin{array}{cl} \text{ subject } \text{ to } \quad \ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a\;\; \text{ and } \;\; \ell _b \le \mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_b. \end{array} \end{aligned}$$
(5)

Here, \(\gamma \in \mathbb {R}\). Notice that \(\gamma \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}\) acts as a penalty term in (5) when \(\gamma \ge 0\), since \(\mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} \ge 0\) for every \(\mathbf{{x}},\mathbf{{y}} \in \mathbb {B}^n\). Moreover, (5) gives a relaxation of (4), since the constraint (3) is not enforced. Problem (5) is feasible since the VSP (2) is feasible by assumption. The following proposition gives conditions under which (5) is essentially equivalent to (4) and (2).

Proposition 1

If \(\mathbf{{w}} \ge \mathbf{{1}}\) and \(\gamma > 0\) with \(\gamma \ge \max \{c_i : i\in \mathcal{{V}}\}\), then for any feasible point \((\mathbf{{x}},\mathbf{{y}})\) in (5) satisfying

$$\begin{aligned} f (\mathbf{{x}}, \mathbf{{y}}) \ge \gamma (\ell _a + \ell _b), \end{aligned}$$
(6)

there is a feasible point \((\overline{\mathbf{{x}}},\overline{\mathbf{{y}}})\) in (5) such that

$$\begin{aligned} f(\overline{\mathbf{{x}}}, \overline{\mathbf{{y}}}) \ge f(\mathbf{{x}}, \mathbf{{y}})\quad \text{ and }\quad \overline{\mathbf{{x}}}^\mathsf{T}\mathbf{{(A+I)}}\overline{\mathbf{{y}}} = 0. \end{aligned}$$
(7)

Hence, if the optimal objective value in (5) is at least \(\gamma (\ell _a + \ell _b)\), then there exists an optimal solution \((\mathbf{{x}}^*, \mathbf{{y}}^*)\) to (5) such that an optimal solution to (2) is given by

$$\begin{aligned} \mathcal{{A}} = \mathrm{supp}(\mathbf{{x}}^*), \;\; \mathcal{{B}} = \mathrm{supp}(\mathbf{{y}}^*), \;\;\text{ and } \;\; \mathcal{{S}} = \mathcal{{V}} \setminus \mathcal{{A}} \cup \mathcal{{B}}. \end{aligned}$$
(8)

Proof

Let \((\mathbf{{x}},\mathbf{{y}})\) be a feasible point in (5) satisfying (6). Since \(\mathbf{{x}}\), \(\mathbf{{y}}\), and \(\mathbf{{(A+I)}}\) are nonnegative, we have \(\mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} \ge 0\). If \(\mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} = 0\), then we simply take \(\overline{\mathbf{{x}}} = \mathbf{{x}}\) and \(\overline{\mathbf{{y}}} = \mathbf{{y}}\), and (7) is satisfied. Now suppose instead that

$$\begin{aligned} \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} > 0. \end{aligned}$$
(9)

Then,

$$\begin{aligned} \gamma (\ell _a + \ell _b) \le f(\mathbf{{x}}, \mathbf{{y}})= & {} \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) - \gamma \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}} \end{aligned}$$
(10)
$$\begin{aligned}< & {} \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) \end{aligned}$$
(11)
$$\begin{aligned}\le & {} \gamma \mathbf{{1}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) . \end{aligned}$$
(12)

Here, (10) is due to (6), (11) is due to (9) and the assumption that \(\gamma > 0\), and (12) holds by the assumption that \(\gamma \ge \max \{c_i : i\in \mathcal{{V}}\}\). It follows that either \(\mathbf{{1}}^\mathsf{T}\mathbf{{x}} > \ell _a\) or \(\mathbf{{1}}^\mathsf{T}\mathbf{{y}} > \ell _b\).

Assume without loss of generality that \(\mathbf{{1}}^\mathsf{T}\mathbf{{x}} > \ell _a\). Since \(\mathbf{{x}}\) is binary and \(\ell _a\) is an integer, we have

$$\begin{aligned} \mathbf{{1}}^\mathsf{T}\mathbf{{x}} \ge \ell _a + 1. \end{aligned}$$

Since the entries in \(\mathbf{{x}}\), \(\mathbf{{y}}\), and \(\mathbf{{(A+I)}}\) are all non-negative integers, (9) implies that there exists an index i such that \(\mathbf{{(A+I)}}_i \mathbf{{y}} \ge 1\) and \(x_i = 1\) (recall that subscripts on a matrix correspond to the rows). If \(\hat{\mathbf{{x}}} = \mathbf{{x}} - \mathbf{{e}}_i\), then \((\hat{\mathbf{{x}}},\mathbf{{y}})\) is feasible in problem (5) since \(u_a \ge \mathbf{{w}}^\mathsf{T}\mathbf{{x}} > \mathbf{{w}}^\mathsf{T}\hat{\mathbf{{x}}}\) and

$$\begin{aligned} \mathbf{{w}}^\mathsf{T}\hat{\mathbf{{x}}} \ge \mathbf{{1}}^\mathsf{T}\hat{\mathbf{{x}}} = \mathbf{{1}}^\mathsf{T}\mathbf{{x}} - 1 \ge \ell _a. \end{aligned}$$

Here the first inequality is due to the assumption that \(\mathbf{{w}}\ge \mathbf{{1}}\). Furthermore,

$$\begin{aligned} f(\hat{\mathbf{{x}}},\mathbf{{y}}) = f(\mathbf{{x}},\mathbf{{y}}) - c_i + \gamma \mathbf{{(A+I)}}_i \mathbf{{y}} \ge f(\mathbf{{x}},\mathbf{{y}}) - c_i + \gamma \ge f(\mathbf{{x}},\mathbf{{y}}), \end{aligned}$$
(13)

since \(\mathbf{{(A+I)}}_i\mathbf{{y}} \ge 1\), \(\gamma \ge 0\), and \(\gamma \ge c_i\). We can continue to set components of \(\mathbf{{x}}\) and \(\mathbf{{y}}\) to 0 until reaching a binary feasible point \((\overline{\mathbf{{x}}}, \overline{\mathbf{{y}}})\) for which \(\overline{\mathbf{{x}}}^\mathsf{T}\mathbf{{(A+I)}}\overline{\mathbf{{y}}} = 0\) and \(f(\overline{\mathbf{{x}}}, \overline{\mathbf{{y}}}) \ge f(\mathbf{{x}}, \mathbf{{y}})\). This completes the proof of the first claim in the proposition.

Now, if the optimal objective value in (5) is at least \(\gamma (\ell _a + \ell _b)\), then by the first part of the proposition, we may find an optimal solution \((\mathbf{{x}}^*,\mathbf{{y}}^*)\) satisfying (3); hence, \((\mathbf{{x}}^*,\mathbf{{y}}^*)\) is feasible in (4). Since (5) is a relaxation of (4), \((\mathbf{{x}}^*,\mathbf{{y}}^*)\) is optimal in (4). Hence, the partition \((\mathcal{{A}},\mathcal{{S}},\mathcal{{B}})\) defined by (8) is optimal in (2). This completes the proof. \(\square \)

Algorithm 1 represents the procedure used in the proof of Proposition 1 to move from a feasible point in (5) to a feasible point \((\overline{\mathbf{{x}}},\overline{\mathbf{{y}}})\) satisfying (7).

figure a

Remark 1

There is typically an abundance of feasible points in (5) satisfying (6). For example, in the common case where \(\gamma = c_i = w_i = 1\) for each i, (6) is satisfied whenever \(\mathbf{{x}} = \mathrm{supp}^{-1}(\mathcal{{A}})\) and \(\mathbf{{y}} = \mathrm{supp}^{-1}(\mathcal{{B}})\) for a pair of feasible sets \(\mathcal{{A}}\) and \(\mathcal{{B}}\) in (2), since in this case

$$\begin{aligned} f (\mathbf{{x}},\mathbf{{y}}) = \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) = \mathbf{{w}}^\mathsf{T}\mathbf{{x}} + \mathbf{{w}}^\mathsf{T}\mathbf{{y}} = \mathcal{{W}}(\mathcal{{A}}) + \mathcal{{W}}(\mathcal{{B}}) \ge \ell _a + \ell _b = \gamma (\ell _a + \ell _b). \end{aligned}$$

The algorithms developed in the next section find and improve upon vertex separators by generating approximate solutions to the binary program (5). A key step towards generating these solutions is in solving the following continuous relaxation, which provides an upper bound on the optimal objective value of (5):

$$\begin{aligned}&\displaystyle {\max _{\mathbf{{x}}, \mathbf{{y}} \in \mathbb {R}^n} \;\; f (\mathbf{{x}}, \mathbf{{y}}) := \; \mathbf{{c}}^\mathsf{T}(\mathbf{{x}} + \mathbf{{y}}) - \gamma \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}} \nonumber \\&\quad \begin{array}{cl} \text{ subject } \text{ to } \,\, \mathbf{{0}}\le \mathbf{{x}}\le \mathbf{{1}}, \quad \mathbf{{0}}\le \mathbf{{y}}\le \mathbf{{1}}, \quad \ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a,\;\; \text{ and } \;\; \ell _b \le \mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_b. \end{array}\nonumber \\ \end{aligned}$$
(14)

The upper bound provided by (14) is typically very tight in practice. In fact, in [19] the authors showed that (14) is in a sense equivalent to (5) in the case where \(\mathbf{{c}} \ge \mathbf{{0}}\), \(\mathbf{{w}} = \mathbf{{1}}\), and the upper and lower bounds on \(\mathcal{{A}}\) and \(\mathcal{{B}}\) are integers. In particular, the following result was proved:

Theorem 1

(see [19, Theorem 2.1, Part 1]) Suppose that \(u_a,\ell _a,u_b,\ell _b\in \mathbb {Z}\), \(\mathbf{{w}} = \mathbf{{1}}\), \(\mathbf{{c}} \ge \mathbf{{0}}\), and \(\gamma \ge \max \{c_i : i \in \mathcal{{V}} \} > 0\). If (2) is feasible and the optimal objective value in (2) is at least \(\gamma (\ell _a + \ell _b)\), then (14) has a binary optimal solution \((\mathbf{{x}},\mathbf{{y}})\in \mathbb {B}^{2n}\) satisfying (3).

In the proof of Theorem 1, a step-by-step procedure is given for moving from any feasible point \((\mathbf{{x}},\mathbf{{y}})\) in (14) to a binary point \((\overline{\mathbf{{x}}},\overline{\mathbf{{y}}})\) satisfying \(f (\overline{\mathbf{{x}}},\overline{\mathbf{{y}}}) \ge f (\mathbf{{x}},\mathbf{{y}})\). Thus, when the assumptions of Theorem 1 are satisfied the VSP may be solved with a 4-step procedure:

  1. 1.

    Obtain an optimal solution to the continuous bilinear program (14).

  2. 2.

    Move to a binary optimal solution using the algorithm of [19, Theorem 2.1, Part 1].

  3. 3.

    Convert the binary solution of (14) to a separator using Algorithm 1.

  4. 4.

    Construct an optimal partition via (8).

When G has a small number of vertices, the dimension of the bilinear program (14) is small, and the above approach may be effective, depending mainly on the continuous optimization algorithm one chooses for Step 1. However, since the objective function in (14) is non-concave, the number of local maximizers in (14) grows quickly as \(|\mathcal{{V}}|\) becomes large and solving the bilinear program becomes increasingly difficult.

In order to find good approximate solutions to (14) when G is large, we will incorporate the 4-step procedure (with some modifications) into a multilevel framework (see Sect. 5). The basic idea is to coarsen the graph into a smaller graph having a similar structure to the original graph; the VSP is then solved for the coarse graph via a procedure similar to the one above, and the solution is uncoarsened to give a solution for the original graph.

At the coarser levels of our algorithm, each vertex represents an aggregate of vertices from the original graph. Hence, in order to keep track of the sizes of the aggregates, weights must be assigned to the vertices in the coarse graphs, which means the assumption of Theorem 1 that \(\mathbf{{w}} = \mathbf{{1}}\) does not hold at the coarser levels. However, in the general case where \(\mathbf{{w}} > \mathbf{{0}}\) and \(\mathbf{{c}}\in \mathbb {R}^n\), the following weaker result is obtained:

Definition 1

A point \((\mathbf{{x}},\mathbf{{y}}) \in \mathbb {R}^{2n}\) is called mostly binary if \(\mathbf{{x}}\) and \(\mathbf{{y}}\) each have at most one non-binary component.

Proposition 2

If the VSP (2) is feasible and \(\gamma \in \mathbb {R}\), then (14) has a mostly binary optimal solution.

Proof

We show that the following stronger property holds:

  1. (P)

    For any \((\mathbf{{x}}, \mathbf{{y}})\) feasible in (14), there exists a piecewise linear path to a feasible point \((\overline{\mathbf{{x}}}, \overline{\mathbf{{y}}}) \in \mathbb {R}^{2n}\) which is mostly binary and satisfies \(f(\overline{\mathbf{{x}}}, \overline{\mathbf{{y}}}) \ge f(\mathbf{{x}}, \mathbf{{y}})\).

Let \((\mathbf{{x}},\mathbf{{y}})\) be any feasible point of (14). If \(\mathbf{{x}}\) and \(\mathbf{{y}}\) each have at most one non-binary component, then we are done. Otherwise, assume without loss of generality there exist indices \(k \ne l\) such that

$$\begin{aligned} 0< x_k \le x_l < 1. \end{aligned}$$

Since \(\mathbf{{w}} > \mathbf{{0}}\), we can define

$$\begin{aligned} \mathbf{{x}}(t) := \mathbf{{x}} + t\left( \frac{1}{w_k}\mathbf{{e}}_k - \frac{1}{w_l}\mathbf{{e}}_l\right) \end{aligned}$$

for \(t\in \mathbb {R}\). Substituting \(\mathbf{{x}} = \mathbf{{x}}(t)\) in the objective function yields

$$\begin{aligned} f(\mathbf{{x}}(t), \mathbf{{y}}) = f(\mathbf{{x}}, \mathbf{{y}}) + t d, \quad \text{ where } d = \nabla _{\mathbf{{x}}} f(\mathbf{{x}},\mathbf{{y}}) \left( \frac{1}{w_k}\mathbf{{e}}_k - \frac{1}{w_l}\mathbf{{e}}_l \right) . \end{aligned}$$

If \(d \ge 0\), then we may increase t from zero until either \(x_k(t) = 1\) or \(x_l(t) = 0\). In the case where \(d < 0\), we may decrease t until either \(x_k(t) = 0\) or \(x_l(t) = 1\). In either case, the number of non-binary components in \(\mathbf{{x}}\) is reduced by at least one, while the objective value does not decrease by the choice of the sign of t. Feasibility is maintained since \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}}(t) = \mathbf{{w}}^\mathsf{T}\mathbf{{x}}\). We may continue moving components to bounds in this manner until \(\mathbf{{x}}\) has at most one non-binary component. The same procedure may be applied to \(\mathbf{{y}}\). In this way, we will arrive at a feasible point \((\overline{\mathbf{{x}}},\overline{\mathbf{{y}}})\) such that \(\overline{\mathbf{{x}}}\) and \(\overline{\mathbf{{y}}}\) each have at most one non-binary component and \(f(\overline{\mathbf{{x}}},\overline{\mathbf{{y}}})\ge f(\mathbf{{x}},\mathbf{{y}})\). This proves (P), which completes the proof. \(\square \)

The proof of Proposition 2 was constructive. A nonconstructive proof goes as follows: Since the quadratic program (14) is bilinear, there exists an optimal solution lying at an extreme point [28]. At an extreme point of the feasible set of (14), exactly 2n linearly independent constraints are active. Since there can be at most n linearly independent constraints which are active at \(\mathbf{{x}}\), and similarly for \(\mathbf{{y}}\), there must exist exactly n linearly independent constraints which are active at \(\mathbf{{x}}\); in particular, at least \(n - 1\) components of \(\mathbf{{x}}\) must lie at a bound, and similarly for \(\mathbf{{y}}\). Therefore, \((\mathbf{{x}},\mathbf{{y}})\) is mostly binary. In the case where \(\mathbf{{w}} \ne \mathbf{{1}}\), there may exist extreme points of the feasible set which are not binary; for example, consider \(n=3\), \(\ell _a = \ell _b = 1\), \(u_a = u_b = 2\), \(\mathbf{{w}} = (1,1,2)\), \(\mathbf{{x}} = (1, 0, 0.5)\), and \(\mathbf{{y}} = (0, 1, 0.5)\).

Often, the conclusion of Proposition 2 can be further strengthened to assert the existence of a solution \((\mathbf{{x}}, \mathbf{{y}})\) of (14) for which either \(\mathbf{{x}}\) or \(\mathbf{{y}}\) is completely binary, while the other variable has at most one nonbinary component. The rationale is the following: Suppose that \((\mathbf{{x}},\mathbf{{y}})\) is a mostly binary optimal solution and without loss of generality \(x_i\) is a nonbinary component of \(\mathbf{{x}}\). Substituting \(\mathbf{{x}}(t) = \mathbf{{x}} + t\mathbf{{e}}_i\) in the objective function we obtain

$$\begin{aligned} f(\mathbf{{x}}(t), \mathbf{{y}}) = f(\mathbf{{x}}, \mathbf{{y}}) + td, \quad d = \nabla _{\mathbf{{x}}} f(\mathbf{{x}}, \mathbf{{y}})\mathbf{{e}}_i. \end{aligned}$$

If \(d \ge 0\), we increase t, while if \(d < 0\), we decrease t; in either case, the objective function \(f(\mathbf{{x}}(t), \mathbf{{y}})\) cannot decrease. If

$$\begin{aligned} \ell _a + w_i \le \mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a - w_i, \end{aligned}$$
(15)

then we can let t grow in magnitude until either \(x_i(t) = 0\) or \(x_i(t) = 1\), while complying with the bounds \(\ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{x}}(t) \le u_a\). In applications, either the inequality (15) holds, or an analogous inequality \(\ell _b + w_j \le \mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_a - w_j\) holds for \(\mathbf{{y}}\), where \(y_j\) is a nonbinary component of \(\mathbf{{y}}\). The reason that one of these inequalities holds is that we typically have \(u_a = u_b > \mathcal{{W}}(\mathcal{{V}})/2\), which implies that the upper bounds \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a\) and \(\mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_b\) cannot be simultaneously active. On the other hand, the lower bounds \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} \ge \ell _a\) and \(\mathbf{{w}}^\mathsf{T}\mathbf{{y}} \ge \ell _b\) are often trivially satisfied when \(\ell _a\) and \(\ell _b\) are small numbers like one.

Algorithm 2 represents the procedure used in the proof of Proposition 2 to convert a given feasible point for (14) into a mostly binary feasible point without decreasing the objective function value. In the case where \(\mathbf{{w}} = \mathbf{{1}}\), the final point returned by Algorithm 2 is binary.

figure b

Although the continuous bilinear problem (14) is not necessarily equivalent to the discrete VSP (2) when \(\mathbf{{w}} \ne \mathbf{{1}}\), it closely approximates (2) in the sense that it has a mostly binary optimal solution. Since (14) is a relaxation of (4), the objective value at an optimal solution to (14) gives an upper bound on the optimal objective value in (4), and therefore on the optimal objective value in (2). On the other hand, given a mostly binary solution to (14), we can typically push the remaining fractional components to bounds without violating the constraints on \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}}\) and \(\mathbf{{w}}^\mathsf{T}\mathbf{{y}}\). Then we apply Algorithm 1 to this binary point to obtain a feasible point in (4), giving a lower bound on the optimal objective value in (4) and (2). In the case where \(\mathbf{{w}} = \mathbf{{1}}\), the upper and lower bounds are equal.

4 Finding and improving upon vertex separators

Due to the bilinear structure of the objective in (14), one strategy for generating an approximate solution is to start from any feasible point and successively optimize over \(\mathbf{{x}}\) and then over \(\mathbf{{y}}\) while leaving the other variable fixed. This is a specific instance of the general Mountain Climbing Algorithm of Konno [28] for solving bilinear programs. Let \(\mathcal{{P}}_a\) and \(\mathcal{{P}}_b\) denote the feasible sets (polyhedra) associated with \(\mathbf{{x}}\) and \(\mathbf{{y}}\) in (14); that is,

$$\begin{aligned} \mathcal{{P}}_{i} = \{ \mathbf{{z}} \in \mathbb {R}^n : \mathbf{{0}} \le \mathbf{{z}} \le \mathbf{{1}} \;\; \text{ and } \;\; \ell _i \le \mathbf{{w}}^\mathsf{T}\mathbf{{z}} \le u_i \}, \quad i = a, b\;. \end{aligned}$$
(16)

In Algorithm 3, we employ a variant of the Mountain Climbing Algorithm (MCA) that includes a diagonal step. For a given \((\mathbf{{x}}, \mathbf{{y}})\), let \(\hat{\mathbf{{x}}}\) denote the maximizer of \(f(\mathbf{{x}}, \mathbf{{y}})\) over \(\mathbf{{x}} \in \mathcal{{P}}_a\), and let \(\hat{\mathbf{{y}}}\) denote the maximizer over \(\mathbf{{y}} \in \mathcal{{P}}_b\). The diagonal steps to \((\hat{\mathbf{{x}}}, \hat{\mathbf{{y}}})\) are only taken during the initial iterations when they provide an improvement at least \(1+ \eta \) times better than either an individual \(\hat{\mathbf{{x}}}\) or \(\hat{\mathbf{{y}}}\) step, where \(\eta \) is a small constant (\(10^{-10}\) in our experiments). After an \(\hat{\mathbf{{x}}}\) or \(\hat{\mathbf{{y}}}\) step is taken, the iterates alternate between \((\hat{\mathbf{{x}}}, \mathbf{{y}})\) and \((\mathbf{{x}},\hat{\mathbf{{y}}})\), and hence only one linear program is solved at each iteration.

figure c

At each iteration of MCA, computing \(\hat{\mathbf{{x}}}\) or \(\hat{\mathbf{{y}}}\) amounts to solving a linear program where the feasible set is of the form (16). For example, the computation of \(\hat{\mathbf{{x}}}\) in MCA amounts to solving the linear program

$$\begin{aligned} \max \{ \mathbf{{g}}^\mathsf{T}\mathbf{{z}} : \mathbf{{0}} \le \mathbf{{z}} \le \mathbf{{1}}, \; \ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{z}} \le u_a \}, \end{aligned}$$
(17)

where \(\mathbf{{g}}\) corresponds to the gradient of the objective \(f(\mathbf{{x}}, \mathbf{{y}})\) with respect to \(\mathbf{{y}}\). We note that (17) is a special case of the convex quadratic knapsack problem studied in [11]. In most VSP applications, the constraint \(\ell _a \le \mathbf{{w}}^\mathsf{T}\mathbf{{z}}\) is satisfied trivially. In this case, the algorithm in [11] for solving (17) introduces a Lagrange multiplier \(\lambda \) for the constraint \(\mathbf{{w}}^\mathsf{T}\mathbf{{z}} \le u_a\) and defines

$$\begin{aligned} z_i (\lambda ) = \left\{ \begin{array}{ll} 1 &{} \quad \text{ if } g_i + \lambda w_i > 0, \\ 0 &{} \quad \text{ if } g_i + \lambda w_i < 0, \end{array} \right. \end{aligned}$$

where \(z_i (\lambda )\) can be chosen arbitrarily in the interval [0, 1] when \(g_i + \lambda w_i = 0\). To solve (17), we start from \(\lambda = 0\) and decrease \(\lambda \) until reaching the first \(\mathbf{{z}}({\lambda })\) for which \(\mathbf{{w}}^\mathsf{T}\mathbf{{z}}(\lambda ) \le u_a\). Since the set \(\mathcal{{Z}} =\) \(\{i: g_i + \lambda w_i = 0\}\) could have more than one element, there could be multiple solutions to (17). In order to explore a larger swath of the solution space, we make at most one component \(z_i (\lambda )\) fractional for \(i \in \mathcal{{Z}}\), and make the remaining components of \(z_i (\lambda )\) for \(i \in \mathcal{{Z}}\) binary; the ones in these remaining binary components are assigned randomly. MCA will typically converge to a stationary point of (14) in a small number of iterations. Moreover, using the implementation described above, the stationary point is almost binary.

Fig. 1
figure 4

Examples of the cases (J1)–(J5) in the Appendix where MCA is guaranteed to strictly improve the objective value. The initial partition \(\mathcal{{A}}\), \(\mathcal{{S}}\), \(\mathcal{{B}}\), appears on the left, followed by the next one or two iterates of MCA

Full size image

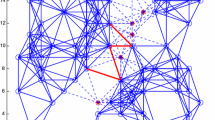
In the Appendix, we develop 5 different cases, (J1)–(J5), where MCA is guaranteed to strictly improve the objective value. Specific instances of these cases are shown in Fig. 1, where \(\mathbf{{c}} = \mathbf{{w}} = \mathbf{{1}}\), \(\ell _a = \ell _b = 1\), and \(u_a\) and \(u_b\) are sufficiently large. The figure gives for each case the initial partition in the order \(\mathcal{{A}}\), \(\mathcal{{S}}\), \(\mathcal{{B}}\), followed by the next one or two iterations of MCA obtained by maximizing (14) first with respect to \(\mathbf{{y}}\) and then possibly with respect to \(\mathbf{{x}}\) while holding the other variable fixed. In two of these cases, MCA leads to iterates for which one or two vertices satisfy \(x_i = y_i = 1\), so the disjointness condition \(\mathbf{{x}}^\mathsf{T}\mathbf{{y}} = 0\) does not hold. Dotted lines connect vertices that appear in both \(\mathcal{{A}}\) and \(\mathcal{{B}}\). In this case, Proposition 1 and Algorithm 1 can be used to obtain a feasible partition for (1) where \(\mathcal{{A}}\) and \(\mathcal{{B}}\) are disjoint. The objective value in (14) appears above each partition. In the cases (J2), (J4), and (J5) a traditional Fidducia-Matheyses type algorithm based on iteratively moving vertices from \(\mathcal{{S}}\) to one of the two shores and then moving the neighbors in the opposite shore into \(\mathcal{{S}}\) would fail to find an improvement in the initial partition. Indeed, applying the routine METISRefine (from METIS 5.1.0 [24]) to these partitions fails to reduce the size of the separator. Observe that in cases (J4) and (J5), MCA is able to reduce the size of \(\mathcal{{S}}\) by essentially removing “false hub” vertices from the separator and replacing them with a single better vertex. One of the mechanisms by which MCA finds these improvement opportunities (eg. (J4)) is by temporarily violating the disjointness condition, effectively delaying the assignment of a vertex to a particular set until the “optimal” choice can be determined. We remark that the structures described in (J4) and (J5) often arise in communication networks and in networks having a centralized hub of vertices. This suggests that MCA may be particularly effective on graphs coming from communication applications. As we will see, this hypothesis is supported by our computational results in Sect. 6.

There are also many cases in which a vertex separator cannot be improved by MCA, but can be improved by a Fidduccia-Mattheyses type algorithm. In order to improve the performance of MCA in these cases, we enhance it to include a technique which we call \(\gamma \)-perturbations. Let us also denote the objective function in (14) as \(f_\gamma \) to emphasize its dependence on the penalty parameter \(\gamma \).

According to our theory, we need to take \(\gamma \ge \max \{c_i : i \in \mathcal{{V}}\}\) to ensure an (approximate) equivalence between the discrete (2) and the continuous VSP (14). The penalty term \(-\gamma \mathbf{{x}}^\mathsf{T}\mathbf{{(A+I)}}\mathbf{{y}}\) in the objective function of (14) enforces the constraints \(\mathcal{{A}} \cap \mathcal{{B}} = \emptyset \) and \((\mathcal{{A}}\times \mathcal{{B}}) \cap \mathcal{{E}} = \emptyset \) of (2). Thus, by decreasing \(\gamma \), we relax our enforcement of these constraints and place greater emphasis on the cost of the separator. The next proposition will determine the amount by which we must decrease \(\gamma \) in order to ensure that a first-order optimal point \((\mathbf{{x}}, \mathbf{{y}})\) of \(f_\gamma \) no longer satisfies the first-order optimality conditions for the perturbed problem \(f_{\tilde{\gamma }}\). A standard statement of the first-order optimality conditions for non-linear programs is given in [33]. The following theorem is a special case [18, Proposition 3.1].

Theorem 2

If \(\gamma \in \mathbb {R}\) and \((\mathbf{{x}}, \mathbf{{y}})\) is feasible in (14), then \((\mathbf{{x}}, \mathbf{{y}})\) satisfies the first-order optimal condition if and only if the following hold:

(C1):

\(\nabla _{\mathbf{{x}}} f (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{d}} \le 0\) for every \(\mathbf{{d}} \in \mathcal{{F}}_a(\mathbf{{x}}) \cap \mathcal{{D}}\),

(C2):

\(\nabla _{\mathbf{{y}}} f (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{d}} \le 0\) for every \(\mathbf{{d}} \in \mathcal{{F}}_b(\mathbf{{y}}) \cap \mathcal{{D}}\),

where

$$\begin{aligned} \mathcal{{F}}_i (\mathbf{{z}})= & {} \left\{ \mathbf{{d}} \in \mathbb {R}^n : \begin{array}{l} {d_j \le 0 \text{ for } \text{ all } j \text{ such } \text{ that } z_j = 1}\\ {d_j \ge 0 \text{ for } \text{ all } j \text{ such } \text{ that } z_j = 0}\\ \mathbf{{w}}^\mathsf{T}\mathbf{{d}} \le 0 \text{ if } \mathbf{{w}}^\mathsf{T}\mathbf{{z}} = u_i\\ \mathbf{{w}}^\mathsf{T}\mathbf{{d}} \ge 0 \text{ if } \mathbf{{w}}^\mathsf{T}\mathbf{{z}} = l_i \end{array} \right\} , \quad i = a, b, \; \mathbf{{z}} \in \mathbb {R}^n,\nonumber \\ \text{ and }\nonumber \\ \mathcal{{D}}= & {} \bigcup _{i,j = 1}^n\left\{ \mathbf{{e}}_i, -\mathbf{{e}}_i, {w_j}\mathbf{{e}}_i - {w_i}\mathbf{{e}}_j\right\} . \end{aligned}$$
(18)

The sets \(\mathcal{{F}}_a\) and \(\mathcal{{F}}_b\) are the cones of first-order feasible directions at \(\mathbf{{x}}\) and \(\mathbf{{y}}\). The set \(\mathcal{{D}}\) is a reflective edge description (introduced in [18]) of each of the sets \(\mathcal{{P}}_a\) and \(\mathcal{{P}}_b\); that is, each edge of \(\mathcal{{P}}_a\) is parallel to an element of \(\mathcal{{D}}\). Since \(\mathcal{{D}}\) is a finite set, checking the first-order optimality conditions reduces to testing the conditions (C1) and (C2) for the finite collection of elements from \(\mathcal{{D}}\) that are in the cone of first-order feasible directions.

Proposition 3

Let \(\gamma \in \mathbb {R}\), let \((\mathbf{{x}}, \mathbf{{y}})\) be a feasible point in (14) which satisfies the first-order optimality condition (C1) for \(f=f_{\gamma }\), and let \(\tilde{\gamma }\le \gamma \). Suppose that \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} > \ell _a\). Then (C1) holds at \((\mathbf{{x}}, \mathbf{{y}})\) for \(f = f_{\tilde{\gamma }}\) if and only if

$$\begin{aligned} \tilde{\gamma }\;\ge \; \alpha \; :=\; \left\{ \begin{array}{rl} \alpha _1, &{} \text{ if }\;\;\;\mathbf{{w}}^\mathsf{T}\mathbf{{x}} < u_a,\\ \alpha _2, &{} \text{ if }\;\;\;\mathbf{{w}}^\mathsf{T}\mathbf{{x}} = u_a , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} \alpha _1= & {} \max \;\left\{ \frac{c_j}{\mathbf{{(A+I)}}_j\mathbf{{y}}} : \;x_j< 1 \text{ and } \mathbf{{(A+I)}}_j \mathbf{{y}}> 0\right\} \;,\;\;\text{ and }\\ \alpha _2= & {} \inf \; \left\{ \alpha \in \mathbb {R} : \frac{1}{w_i}\frac{\partial f_{\alpha }}{\partial x_i}(\mathbf{{x}},\mathbf{{y}}) \le \frac{1}{w_j}\frac{\partial f_{\alpha }}{\partial x_j}(\mathbf{{x}},\mathbf{{y}})\; \forall \;x_i < 1 \text{ and } x_j > 0 \right\} \;. \end{aligned}$$

Proof

First, we consider the case where \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} < u_a\). In this case, the cone of first-order feasible directions at \(\mathbf{{x}}\) is given by

$$\begin{aligned} \mathcal{{F}}_a (\mathbf{{x}}) = \left\{ \mathbf{{d}} \in \mathbb {R}^n: d_i \ge 0 \text{ when } x_i = 0 \text{ and } d_i \le 0 \text{ when } x_i = 1, \; i = 1, \ldots , n \right\} . \end{aligned}$$

It follows that for each \(i = 1,\ldots ,n\),

$$\begin{aligned} \begin{array}{ccl} \mathbf{{e}}_i &{} \in &{} \mathcal{{F}}_a (\mathbf{{x}}) \; \text{ if } \text{ and } \text{ only } \text{ if } \; x_i< 1, \\ -\mathbf{{e}}_i &{} \in &{} \mathcal{{F}}_a (\mathbf{{x}}) \; \text{ if } \text{ and } \text{ only } \text{ if } \; x_i> 0, \\ (w_j\mathbf{{e}}_i -w_i\mathbf{{e}}_j) &{} \in &{} \mathcal{{F}}_a (\mathbf{{x}}) \; \text{ if } \text{ and } \text{ only } \text{ if } \;x_i < 1 \text{ and } x_j > 0. \end{array} \end{aligned}$$

Hence, the first-order optimality condition (C1) for \(f_{\tilde{\gamma }}\) can be expressed as follows:

$$\begin{aligned} \nabla _{\mathbf{{x}}} f_{\tilde{\gamma }} (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{e}}_i \le 0&\; \text{ when } \;&x_i < 1, \end{aligned}$$
(19)
$$\begin{aligned} \nabla _{\mathbf{{x}}} f_{\tilde{\gamma }} (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{e}}_i \ge 0&\; \text{ when } \;&x_i > 0, \end{aligned}$$
(20)
$$\begin{aligned} \nabla _{\mathbf{{x}}} f_{\tilde{\gamma }} (\mathbf{{x}}, \mathbf{{y}}) (w_j\mathbf{{e}}_i - w_i\mathbf{{e}}_j) \le 0&\; \text{ when } \;&x_i < 1 \text{ and } x_j > 0. \end{aligned}$$
(21)

Since (21) is implied by (19) and (20), it follows that (C1) holds if and only if (19) and (20) hold. Since (C1) holds for \(f_\gamma \), we know that

$$\begin{aligned} \nabla _{\mathbf{{x}}} f_{{\gamma }} (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{e}}_i = c_i - \gamma \mathbf{{(A+I)}}_i\mathbf{{y}} \ge 0 \;\; \text{ when }\;\; x_i > 0. \end{aligned}$$

Hence, since \(\tilde{\gamma } \le \gamma \) and \(\mathbf{{(A+I)}}_i\mathbf{{y}} \ge 0\),

$$\begin{aligned} \nabla _{\mathbf{{x}}} f_{\tilde{\gamma }} (\mathbf{{x}}, \mathbf{{y}}) \mathbf{{e}}_i = c_i - \tilde{\gamma } \mathbf{{(A+I)}}_i\mathbf{{y}} \ge 0 \quad \text{ when } x_i > 0. \end{aligned}$$

Hence, (C1) holds with respect to \(\tilde{\gamma }\) if and only if (19) holds. Since (C1) holds for \(f = f_{\gamma }\), we have

$$\begin{aligned} c_j - \gamma \mathbf{{(A+I)}}_j \mathbf{{y}} \le 0 \text{ when } x_j < 1. \end{aligned}$$
(22)

Hence, for every j such that \(x_j < 1\) and \(\mathbf{{(A+I)}}_j\mathbf{{y}} = 0\), we have

$$\begin{aligned} c_j - \tilde{\gamma }\mathbf{{(A+I)}}_j\mathbf{{y}} = c_j = c_j - \gamma \mathbf{{(A+I)}}_j\mathbf{{y}} \le 0. \end{aligned}$$

So, (19) holds if and only if \(c_j - \tilde{\gamma }\mathbf{{(A+I)}}_j\mathbf{{y}} \le 0\) for every \(j \in \mathcal{{J}}\); that is, if and only if \(\tilde{\gamma } \ge \alpha _1\).

Next, suppose that \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} = u_a\). Then, the cone of first-order feasible directions at \(\mathbf{{x}}\) has the constraint \(\mathbf{{w}}^\mathsf{T}\mathbf{{d}} \le 0\). Consequently, \(\mathbf{{e}}_i \not \in \mathcal{{F}}_a (\mathbf{{x}}) \cap \mathcal{{D}}\) for any i, and the first-order optimality condition (C1) for \(f_{\tilde{\gamma }}\) reduces to (20)–(21). As in Part 1, (20) holds, since \(\tilde{\gamma } \le \gamma \). Condition (21) is equivalent to \(\tilde{\gamma } \in \varGamma \), where \(\varGamma \) is the set on the right hand side of the definition of \(\alpha _2\). Since (21) holds for \(f = f_{\gamma }\), we have \(\gamma \in \varGamma \). Since \(\nabla _{\mathbf{{x}}} f_{\tilde{\gamma }} (\mathbf{{x}}, \mathbf{{y}})\) is a affine function of \(\tilde{\gamma }\), the set of \(\tilde{\gamma }\) satisfying (21) for some i and j such that \(x_j > 0\) and \(x_i < 1\) is a closed interval, and the intersection of the intervals over all i and j for which \(x_j > 0\) and \(x_i < 1\) is also a closed interval. Hence, since \(\tilde{\gamma } \le \gamma \in \varGamma \), we have \(\tilde{\gamma } \in \varGamma \) if and only if \(\tilde{\gamma } \ge \alpha _2\), which completes the proof. \(\square \)

Remark 4.1 Of course, Proposition 3 also holds when the variables \(\mathbf{{x}}\) and \(\mathbf{{y}}\) and the bounds \((\ell _a, u_a)\) and \((\ell _b, u_b)\) are interchanged. Hence, to ensure that the current iterate is not a stationary point of of \(f_\gamma \), we only need to choose \(\gamma \) strictly smaller than the largest of the two lower bounds gotten from Proposition 3. Given a stationary point \((\mathbf{{x}}, \mathbf{{y}})\) for (14), let the function minreduce\(\;(\mathbf{{x}}, \mathbf{{y}})\) denote the smallest \(\gamma \) for which \((\mathbf{{x}}, \mathbf{{y}})\) remains a stationary point of \(f_\gamma \). In most applications, \(u_a\) and \(u_b > {\mathcal{{W}}(\mathcal{{V}})}/{2}\), \(\ell _a = \ell _b = 1\), which implies that at most one of the constraints \(\mathbf{{w}}^\mathsf{T}\mathbf{{x}} \le u_a\) or \(\mathbf{{w}}^\mathsf{T}\mathbf{{y}} \le u_b\) is active. Note that the bound given by \(\alpha _2\) in Proposition 3 often provides no useful information in the following sense: In a multilevel implementation, the vertex costs (and weights) are often 1 at the finest level, and at coarser levels, the vertex costs may not differ greatly. When the vertex costs are equal, (21) holds when \(\tilde{\gamma }\) has the same sign as \(\gamma \); that is, as long as \(\tilde{\gamma } \ge 0\), which implies that \(\alpha _2 = 0\). Since \(\alpha _1\) is typically positive, minreduce\(\;(\mathbf{{x}}, \mathbf{{y}})\) often corresponds to \(\alpha _1\).

Algorithm 5, denoted MCA_GR, approximately solves (14), using MCA in conjunction with \(\gamma \)-refinements. Here, the notation MCA\((\mathbf{{x}},\mathbf{{y}},\tilde{\gamma })\) indicates that the MCA algorithm is applied to the point \((\mathbf{{x}},\mathbf{{y}})\) using \(\tilde{\gamma }\) in place of \(\gamma \) as the penalty parameter. In our implementation of MCA_GR, we used the function reduce which was defined as follows:

$$\begin{aligned} \text{ reduce }\; (\tilde{\gamma }, k) = \left\{ \begin{array}{ll} \tilde{\gamma } - 10^{-6} &{} \text{ when } k = 1, \\ \tilde{\gamma }/2 &{} \text{ when } k > 1. \end{array} \right. \end{aligned}$$
figure d

5 Multilevel algorithm

We now give an overview of a multilevel algorithm, which we call BLP, based on the bilinear programming formulation of the vertex separator problem. The algorithm consists of three phases: coarsening, solving, and uncoarsening.

Coarsening Vertices are visited one by one and each vertex is matched with an unmatched adjacent vertex, whenever one exists. Matched vertices are merged together to form a single vertex having a cost and weight equal to the sum of the costs and weights of the constituent vertices. This coarsening process repeats until the graph has fewer than 75 vertices or fewer than 10 edges.

The goal of the coarsening phase is to reduce the number of degrees of freedom in the problem, while preserving its structure so that the solutions obtained for the coarse problems give a good approximation to the solution for the original problem. We consider two matching rules: random and heavy-edge. In random matching, we randomly combine pairs of vertices in the graph. To implement heavy-edge matching, we associated weights with each edge in the graph. When two edges are combined during the coarsening process, the new edge weight is the sum of the weights of the combined edges. In the coarsening, each vertex is matched with an unmatched neighbor such that the edge between them has the greatest weight over all unmatched neighbors. Heavy edge matching rules have been used in multilevel algorithms such as [20, 24], and were originally developed for edge-cut problems. In our initial experiments, we also considered a third rule based on an algebraic distance [8] between vertices. However, the results were not significantly different from heavy-edge matching, which is not surprising, since (like heavy-edge rules) the algebraic distance was originally developed for minimizing edge-cuts.

Solving For each of the graphs in the multilevel hierarchy, we approximately solve (14) using MCA_GR. For the coarsest graph, the starting guess is \(x_i = u_a/\mathcal{{W}}(\mathcal{{V}})\) and \(y_i = u_b/\mathcal{{W}}(\mathcal{{V}})\), \(i = 1,2,\ldots ,n\). For the finer graphs, a starting guess is obtained from the next coarser level using the uncoarsening process described below. After MCA_GR terminates, Algorithm 3.2 along with the modification discussed after Proposition 2 are used to obtain a mostly binary approximation to a solution of (14). Algorithm 3.1 is then used to convert the binary solution into a vertex separator.

Uncoarsening We use the solution for the vertex separator problem computed at any level in the multilevel hierarchy as a starting guess for the solution at the next finer level. Sophisticated cycling techniques like the W- or F-cycle [4] were not implemented. A starting guess for the next finer graph is obtained by unmatching vertices in the coarser graph. Suppose that we are uncoarsening from level l to \(l-1\) and \((\mathbf{{x}}^l, \mathbf{{y}}^l)\) denotes the solution computed at level l. If vertex i at level l is obtained by matching vertices j and k at level \(l-1\), then our starting guess for \((\mathbf{{x}}^{l-1}, \mathbf{{y}}^{l-1})\) is simply \((x_{j}^{l-1}, y_{j}^{l-1}) = (x_{i}^{l}, y_{i}^{l})\) and \((x_{k}^{l-1}, y_{k}^{l-1}) = (x_{i}^{l}, y_{i}^{l})\).

6 Numerical results

The multilevel algorithm BLP was programmed in C++ and compiled using g++ with optimization O3 on a Dell Precision T7610 Workstation with a Dual Intel Xeon Processor E5-2687W v2 (16 physical cores, 3.4GHz, 25.6MB cache, 192GB memory). When solving the linear programs (17) arising in MCA, it was convenient to sort the ratios \(g_i/w_i\); the sorting phase was carried out by calling std :  : sort, the (\(O (n\log n)\)) sorting routine implemented in the C++ standard library. The number of iterations of the main loop in MCA_GR was capped at \(K = 10\). On each level in the multilevel hierarchy, after the uncoarsening phase, MCA_GR was called repeatedly until the solution failed to improve, but at most 10 times. We used the parameters \(\eta = 10^{-10}\) and \(\delta = 10^{-13}\) for MCA and MCA_GR, respectively.

We evaluated the performance of BLP by making comparisons with the routine

figure e

which is an implementation of a multilevel Fidduccia-Mattheyses-like algorithm for the VSP available from METIS 5.1.0 [24]. The following options were used:

figure f

In a preliminary experiment, we also considered the refinement option

figure g

but the results obtained were not significantly different. On average, the option

figure h

provided slightly better results.

For our experiments, we compiled a test set of 52 sparse graphs with n ranging from \(n = 1,000\) to \(n = 139,752\) and with sparsities ranging from \(1.32\times 10^{-2}\) to \(5.65\times 10^{-5}\), where sparsity is defined as the ratio \(\frac{|\mathcal{{E}}|}{n(n-1)}\) (recall that \(|\mathcal{{E}}|\) is equal to twice the number of edges). Our graphs were taken from the Stanford SNAP database [22], the University of Florida Sparse Matrix Library [10], and from a test set from [37] consisting of graphs which were specifically designed to be challenging for graph partitioning. Nine of the graphs from our test set represent 2D or 3D meshes, 15 represent either a communication, collaboration, or social network, and the remaining 31 come from miscellaneous applications. We label these groups with the letters M (mesh), C (communication), and O (other), respectively. In order to enable future comparisons with our solver, we have made this benchmark set available at http://people.cs.clemson.edu/~isafro/data.html as well as in the supplementary material for this paper.

After our experiments, we found that it was useful to further subdivide the O instances into two groups based on the frequency of structures of the form (J4) (see Appendix) in the final partition. We considered (J4), and not (J5), only because the structure appearing in (J5) seemed more difficult to detect. One necessary condition for the structure (J4) to arise is for there to exist a vertex \(i\in \mathcal{{A}}\) such that \(\mathcal{{N}} (i)\cap \mathcal{{A}} = \emptyset \) or a vertex \(j \in \mathcal{{B}}\) such that \(\mathcal{{N}} (j)\cap \mathcal{{B}} = \emptyset \). Hence, we (upper-)estimated the number of (J4) structures in each graph by finding an approximate vertex separator (via a call to METIS_ComputeVertexSeparator), and calculating the percentage p(G) of vertices i lying in \(\mathcal{{A}}\cup \mathcal{{B}}\) for which the containment \(\mathcal{{N}} (i) \subseteq \mathcal{{S}}\) held. A graph G in group O was moved to OC if \(p (G)\ge 5\%\) and to OO otherwise. Table 1 gives the statistics for each graph: number of vertices, number of edges, sparsity, min/max/average degree, and p(G). Note that \(p (G) \ge 5\%\) for all but two C graphs, and \(p (G) < 5\%\) for all but two of the M graphs.

Table 1 Test set graphs with their statistics
Full size table

Vertex costs \(c_i\) and weights \(w_i\) were assumed to be 1 at the finest level for all graphs. For the bounds on the shores of the separator, we took \(\ell _a = \ell _b = 1\) and \(u_a = u_b = \lfloor 0.6 n \rfloor \), which are the default bounds used by METIS. (Here \(\lfloor r \rfloor \) denotes the largest integer not greater than r.) We considered both random matching and heavy-edge matching schemes for both algorithms. Since both algorithms contain random elements, the algorithms were run using 100 different random seeds for each instance.

Tables 2, 3, 4 and 5 give the average, minimum, and maximum cardinalities of the separators obtained by the algorithms for the 100 different random seeds. For each test problem, the smallest separator size obtained across all four algorithms (METIS or BLP with random or heavy edge matching) is highlighted in bold. Here, METIS_HE and METIS_RM refer to the METIS algorithm with heavy-edge matching and with random matching, respectively. Tables 6 and 7 compare the average separator sizes obtained by the algorithms for 100 different random seeds. The column labeled “Wins” gives the percentage of problems where the average separator size for BLP was strictly smaller than the average separator size for METIS. The column labeled “Ave” takes these average separator sizes, forms the relative ratio \(\frac{|\mathcal{{S}}_{METIS}| - |\mathcal{{S}}_{BLP}|}{|\mathcal{{V}}|}\) of the average separator sizes, and then computes the average over a test set. The columns labeled “Min” and “Max” replace the average over a test set by either the minimum or maximum. Regardless of the matching scheme used, the average separator size obtained by BLP was smaller than that of METIS for all of the C graphs, with an average improvement of almost \(3\%\), with similar (though slightly worse) results for the OC graphs. We believe that the strong performance of BLP on these graphs is likely due to the relatively large p(G) values, which suggest that improvement opportunities of type (J4) may arise frequently. Likely for the same reason, the performance of BLP was much poorer on the M and OO graphs.

Table 2 Comparison of sizes of separators obtained by METIS and BLP on M graphs
Full size table
Table 3 Comparison of sizes of separators obtained by METIS and BLP on C graphs
Full size table
Table 4 Comparison of sizes of separators obtained by METIS and BLP on OO graphs
Full size table
Table 5 Comparison of sizes of separators obtained by METIS and BLP on OC graphs
Full size table
Table 6 Improvement of BLP over METIS when random matching was used
Full size table
Table 7 Improvement of BLP over METIS when heavy-edge matching was used
Full size table

METIS exhibited a clear favorability towards the heavy-edge-based matching scheme (which out-performed the random matching scheme in approximately 82% of the instances). On the other hand, BLP was relatively indifferent to the choice of the matching scheme (the heavy-edge-based scheme performed better in approximately 48% of the instances). However, when each algorithm was run with its optimal matching scheme, BLP still out-performed METIS in approximately 58% of the instances. Figure 2 gives a performance profile comparing the separator sizes obtained by each algorithm with its optimal matching scheme. The profile gives the percentage P of graphs in which each algorithm produced a solution which was within a factor of \(\tau \) of the best solution (between the two algorithms). The left hand side of the plot gives the percentage of instances for which each algorithm obtained the best solution, while the center and right hand sides of the plot give an indication of the relative robustness of the algorithms. In terms of overall robustness, we conclude that the algorithms are comparable, though for about 5% of the instances the BLP solution was within a factor of between 2 and 2.25 of the METIS solution.

Fig. 2
figure 6

Performance profile comparing BLP and METIS with their optimal matching schemes on all graphs

Full size image

Since each iteration of MCA requires the solution of an LP (which is often more computationally intensive than performing swaps), the running time of BLP is considerably slower than METIS. CPU times for BLP_RM ranged from 0.02 (s) to 66.92 (s), with an average of 6.77 (s), while CPU times for METIS_RM ranged from less than 0.01 (s) to 0.84 (s), with an average of 0.13 (s).

Figure 3 gives a log–log plot of \(n = |\mathcal{{V}}|\) versus CPU time for all 52 instances. The best fit line through the data in the log–log plot has a slope of approximately 1.62, which indicates that the CPU time of BLP is between a linear and a quadratic function of the number of vertices.

Fig. 3
figure 7

Number of vertices n versus CPU time for BLP_RM

Full size image

In order to close the gap in running time between BLP and METIS, the BLP code needs further development to take into account the sparse change in successive iterates. The current code takes into account the sparsity of \(\mathbf{{A}}\) when computing a matrix vector product \(\mathbf{{Ax}}\), but it does not take into account the fact the change \(\mathbf{{x}}_k - \mathbf{{x}}_{k-1}\) and \(\mathbf{{y}}_k - \mathbf{{y}}_{k-1}\) in successive iterates is often sparse. Instead of computing the product \(\mathbf{{Ax}}_k\) from scratch in each iteration, we could store the prior product \(\mathbf{{Ax}}_{k-1}\) and update it with the very sparse change \(\mathbf{{A}}(\mathbf{{x}}_k - \mathbf{{x}}_{k-1})\) to obtain \(\mathbf{{Ax}}_k\). Similarly, when solving the linear programs in MCA, a solution obtained at iteration \(k-1\) could be updated to get a solution at iteration k. There are many potential enhancements of this nature that should provide a much faster running time for BLP.

In [35], the authors developed a semi-definite programming method for computing tight upper and lower bounds on the cardinality of an optimal vertex separator in a graph, where the cardinalities of the two shores are approximately the same. Tests were run on a set of 11 graphs having between 93 and 343 vertices. Table 8 gives the dimensions of the test graphs, the upper and lower bounds on the cardinality of an optimal separator, and the average, minimum, and maximum cardinality of the vertex separator found by BLP_HE across 100 random trials using \(\ell _a = \ell _b = 1\) and \(u_a = u_b = \lfloor 0.5 n\rfloor \). The results for BLP_RM were similar. For all graphs, the minimum cardinality separator obtained by BLP was always less than or equal to the upper bound of [35]. The average cardinality was less than or equal to the upper bound in 5 out of the 11 instances. Due to slight differences in the way the bounds on the shores are enforced in the SDP method of [35], the BLP solution is below the lower bound in 3 of the instances.

Table 8 Results for BLP_HE on test graphs from [35]
Full size table

7 Conclusion

We have developed a new algorithm (BLP) for solving large-scale instances of the Vertex Separator Problem (1). The algorithm incorporates a multilevel framework; that is, the original graph is coarsened several times; the problem is solved for the coarsest graph; and the solution to the coarse graph is gradually uncoarsened and refined to obtain a solution to the original graph. A key feature of the algorithm is the use of the continuous bilinear program (14) in both the solution and refinement phases. In the case where vertex weights are all equal to one (or a constant), (14) is an exact formulation of the VSP in the sense that there exists a binary solution satisfying (3), from which an optimal solution to the VSP can be recovered using (8). When vertex weights are not all equal, we showed that (14) still approximates the VSP in the sense that there exists a mostly binary solution.

During the solution and refinement phases of BLP, the bilinear program is solved approximately by applying the algorithm MCA_GR, a mountain climbing algorithm which incorporates a technique which we call \(\gamma \)-perturbations to escape from stationary points and explore more of the search space. The \(\gamma \)-perturbations improve the separator by relaxing the requirement that there are no edges between the sets in the partition. We determined the smallest relaxation that will generate a new partition. To our knowledge, this is the first multilevel algorithm to make use of a continuous optimization based refinement method for the family of graph partitioning problems. The numerical results of Sect. 6 indicate that BLP is capable of locating vertex separators of high quality (comparing against METIS); the algorithm is particularly effective on communication and collaboration networks, while being less effective on graphs arising in mesh applications.