On the update of constraint preconditioners for regularized KKT systems

Abstract

We address the problem of preconditioning sequences of regularized KKT systems, such as those arising in interior point methods for convex quadratic programming. In this case, constraint preconditioners (CPs) are very effective and widely used; however, when solving large-scale problems, the computational cost for their factorization may be high, and techniques for approximating them appear as a convenient alternative. Here, given a block $LDL^T$ factorization of the CP associated with a KKT matrix of the sequence, called seed matrix, we present a technique for updating the factorization and building inexact CPs for subsequent matrices of the sequence. We have recently proposed an updating procedure that performs a low-rank correction of the Schur complement of the (1,1) block of the CP for the seed matrix. Now we focus on KKT sequences with nonzero (2,2) blocks and make a step further, by enriching the low-rank correction of the Schur complement by an additional cheap update. The latter update takes into account information not included in the former one and expressed as a diagonal modification of the low-rank correction. Theoretical results and numerical experiments show that the new strategy can be more effective than the procedure based on the low-rank modification alone.

1 Introduction

We consider the problem of preconditioning a sequence of regularized KKT systems of the following form:

$$\begin{aligned} \left[ \begin{array}{cc} B_k &{}\quad A^T \\ A &{}\quad -\varTheta _k \end{array} \right] \left[ \begin{array}{l} \Delta x_k\\ \Delta y_k\\ \end{array} \right] =\left[ \begin{array}{l} f_k\\ g_k\\ \end{array} \right] , \quad k=1,2,\ldots , \end{aligned}$$

(1)

where $B_k \in {\mathbb {R}}^{n\times n}$ is symmetric positive definite, $A\in {\mathbb {R}}^{m\times n}$ is full rank, $m\le n$, and $\varTheta _k \in {\mathbb {R}}^{m \times m}$ is diagonal positive semidefinite. We focus on problems where $\varTheta _k \ne 0$ and its sparsity pattern does not change throughout the sequence. We further assume that the above linear systems are large and possibly sparse. Linear systems of this form arise, e.g. in interior point (IP) methods for convex quadratic programming problems [25, 34]:

$$\begin{aligned} \begin{array}{cc} \text {Minimize} &{} \displaystyle \frac{1}{2} x^T Q x + c^Tx , \\ \text {Subject to} &{} A_1 x - s = b_1, \quad A_2 x = b_2, \quad x + v = u, \quad (x,s,v) \ge 0, \end{array} \end{aligned}$$

(2)

where $A_1\in {\mathbb {R}}^{m_1\times n}$, $A_2\in {\mathbb {R}}^{m_2\times n}$, and s and v are slack variables, used to transform the inequality constraints $A_1 x \ge b_1$ and $x \le u$ into equality constraints.

In this case we have

$$\begin{aligned} B_k = Q + \varPhi _k, \quad \begin{array}{l} \varPhi _k = X_k^{-1}W_k + V_k^{-1} T_k, \quad \varTheta _k = \left[ \begin{array}{cc} Y_k^{-1}S_k &{}\quad 0 \\ 0 &{}\quad 0 \end{array} \right] , \quad A = \left[ \begin{array}{l} A_1 \\ A_2 \end{array} \right] , \end{array} \end{aligned}$$

where $X_k$, $W_k$, $S_k$, $Y_k$, $V_k$ and $T_k$ are suitable diagonal matrices and $m=m_1+m_2$. More precisely, letting $(x_k, w_k), \; (s_k,y_k)$ and $( v_k, t_k)$ be the pairs of complementary variables of problem (2) evaluated at the k-th iteration, we have that $X_k$, $W_k$, $S_k$, $Y_k$, $V_k$ and $T_k$ are the diagonal matrices where the diagonal is equal to the corresponding lowercase vector, according to the usual IP notation. A nonzero block $\varTheta _k$ arises whenever the problem has linear inequality constraints, i.e., $m_1\ne 0$, as in this case $\varTheta _k$ admits $m_1$ positive diagonal entries corresponding to the slack variables for the linear inequality constraints; furthermore, the number and the position of the nonzero entries of $\varTheta _k$ does not change throughout the IP iterations. It is well known that the nonzero entries of $\varPhi _k$ and $\varTheta _k$ usually display a drastic difference of magnitude: some of them tend to zero while others go to infinity. The nonzero matrix $\varTheta _k$ may also arise when regularized IP methods are applied to quadratic programming problems with no linear inequality constraints. In this case $\varTheta _k$ is diagonal positive definite and its form depends on the dual regularization adopted (see, e.g. [23, 26] and the references therein).

Typically, the solution of sequence (1) represents the major computational burden of the IP procedure. Therefore, if the linear systems are solved iteratively, the effectiveness and the efficiency of the preconditioners used affect the overall performance of the IP method. Here we address the case where the systems are solved by an iterative linear solver and constraint preconditioners (CPs) are employed (see, e.g. [10, 11, 15, 19, 20, 24, 28, 31]).

Whenever the computational cost for building a CP for each system of the sequence is high, a preconditioner updating strategy can offer a tradeoff between cost and efficiency and can enhance the overall procedure for the solution of problem (1). Given a factorization of the preconditioner for a matrix of the sequence, such a strategy builds the preconditioners for some successive systems of the sequence by suitably modifying the available factorization to take into account the matrix changes. The aim is to form a preconditioner that is computationally cheaper than the one computed from scratch, though preserving efficiency in the solution of the linear systems.

A first proposal for an updating strategy for CP preconditioners has been presented in [5]. It relies on a low-rank modification of the factorized Schur complement of the (1,1) block, which has been designed by exploiting results from [1, 33]. Clearly, to keep the computational cost low, only small-rank changes are allowed. In this paper, in order to partially recover the information discarded by the low-rank correction, we propose to perform a further update. We note that a part of the discarded information can be seen as a diagonal positive semidefinite modification of the matrix resulting from the low-rank modification. Then we compute an approximate Cholesky factorization of the diagonally modified matrix by updating the Cholesky factorization of the preconditioner resulting from the low-rank correction. This step is accomplished by using a procedure in the framework given in [4]. Theoretical and numerical results show that the latter procedure can improve the preconditioner updating strategy in [5].

The paper is organized as follows. In Sect. 2 we provide the basis for describing our preconditioner updating procedure along with some theoretical results which will be exploited to analyze it. In Sect. 3 we first recall the updating procedure based on the low-rank correction of the Schur complement and then we present the new updating step, aimed at recovering part of the information discarded by the low-rank approach. In Sect. 4 we show some numerical results illustrating the behavior of the overall updating approach. We give some conclusions in Sect. 5.

Henceforth we use the following notations. We denote by $\Vert \cdot \Vert$ the matrix 2-norm. For any symmetric matrix M, we denote by $\lambda (M)$ any eigenvalue of M, and by $\lambda _{\min }(M)$ and $\lambda _{\max }(M)$ the minimum and maximum of these eigenvalues; furthermore, we use $\mathrm{diag }(M)$ to indicate the diagonal matrix with the same diagonal entries as M. Finally, for any complex number z, we denote by ${\mathcal {R}}(z)$ and ${\mathcal {I}}(z)$ the real and imaginary parts of z.

2 Preliminaries

The updating strategy presented in this paper builds a preconditioner for a generic matrix of the sequence (1),

$$\begin{aligned} {\mathcal {A}}_k=\left[ \begin{array}{cc} B_k &{}\quad A^T \\ A &{}\quad -\varTheta _k \end{array} \right] , \end{aligned}$$

exploiting information from a preconditioner built for a previous matrix of the sequence, which is denoted by

$$\begin{aligned} {\mathcal {A}}_{seed}= \left[ \begin{array}{cc} B_{seed}&{}\quad A^T \\ A &{}\quad -\varTheta _{seed}\end{array} \right] . \end{aligned}$$

(3)

We assume that a CP ${\mathcal {P}}_{seed}$ is available for ${\mathcal {A}}_{seed}$, having the following form:

$$\begin{aligned} {\mathcal {P}}_{seed}=\left[ \begin{array}{cc} H_{seed}&{}\quad A^T \\ A &{}\quad -\varTheta _{seed}\end{array} \right] , \end{aligned}$$

(4)

where $H_{seed}$ is the following approximation to $B_{seed}$:

$$\begin{aligned} H_{seed}=\mathrm{diag }(B_{seed}). \end{aligned}$$

The effectiveness of this preconditioner in the context of IP methods is widely recognized by the optimization community, see, e.g. [6, 10, 11, 21, 28].

In order to simplify the notations, henceforth we denote $H_{seed}$ by H. The application of ${\mathcal {P}}_{seed}$ requires its factorization. We consider the following block $LDL^T$ factorization:

$$\begin{aligned} {\mathcal {P}}_{seed}= \left[ \begin{array}{cc} I_n &{}\quad 0 \\ AH^{-1} &{}\quad I_m \end{array} \right] \left[ \begin{array}{cc} H &{}\quad 0 \\ 0 &{}\quad -S_{seed}\end{array} \right] \left[ \begin{array}{cc} I_n &{}\quad H^{-1}A^T \\ 0 &{}\quad I_m \end{array} \right] , \end{aligned}$$

(5)

where $I_j$ is the identity matrix of dimension j and $S_{seed}$ is the negative Schur complement of H in ${\mathcal {P}}_{seed}$, i.e.,

$$\begin{aligned} S_{seed}=AH^{-1}A^T+\varTheta _{seed}. \end{aligned}$$

(6)

We also assume that a Cholesky factorization of $S_{seed}$ has been computed:

$$\begin{aligned} S_{seed}= L_{seed}D_{seed}L_{seed}^T, \end{aligned}$$

(7)

where $L_{seed}$ is unit lower triangular.

Now we consider a generic system of the sequence and we drop the iteration index k from ${\mathcal {A}}_k$, $B_k$ and $\varTheta _k$ in order to simplify the notation. Then, as with the previous definition of ${\mathcal {P}}_{seed}$, the CP for

$$\begin{aligned} {\mathcal {A}}=\left[ \begin{array}{cc} B &{}\quad A^T \\ A &{}\quad -\varTheta \end{array} \right] , \end{aligned}$$

(8)

is given by

$$\begin{aligned} {\mathcal {P}}_{ex}=\left[ \begin{array}{cc} G &{}\quad A^T \\ A &{}\quad -\varTheta \end{array} \right] = \left[ \begin{array}{cc} I_n &{}\quad 0 \\ AG^{-1} &{}\quad I_m \end{array} \right] \left[ \begin{array}{cc} G &{}\quad 0 \\ 0 &{}\quad -S \end{array} \right] \left[ \begin{array}{cc} I_n &{}\quad G^{-1}A^T \\ 0 &{}\quad I_m \end{array} \right] , \end{aligned}$$

(9)

where

$$\begin{aligned} G=\mathrm{diag }(B), \quad S = AG^{-1}A^T +\varTheta . \end{aligned}$$

Concerning the eigenvalue distribution of ${\mathcal {P}}_{ex}^{-1}{\mathcal {A}}$, there exists an eigenvalue at 1 with multiplicity $2m-p$, with $p = \mathrm{rank }(\varTheta )$, and $n-m+p$ real positive eigenvalues such that the better G approximates B the more clustered around 1 they are [18]. On the other hand, computing a Cholesky factorization of S may account for a large part of the computational cost for solving the KKT system, and hence replacing S with a computationally cheaper approximation of it, $S_{inex}$, may be convenient [5, 21, 29, 31].

The resulting inexact CP has the following form:

$$\begin{aligned} {\mathcal {P}}_{inex}=\left[ \begin{array}{cc} I_n &{}\quad 0 \\ AG^{-1} &{}\quad I_m \end{array} \right] \left[ \begin{array}{cc} G &{}\quad 0 \\ 0 &{}\quad -S_{inex}\end{array} \right] \left[ \begin{array}{cc} I_n &{}\quad G^{-1}A^T \\ 0 &{}\quad I_m \end{array} \right] . \end{aligned}$$

(10)

Approximations of CPs may be also obtained by replacing the constraint matrix A in (9) with a sparse approximations of it [9].

In our work we focus on ${\mathcal {P}}_{inex}$. The spectral analysis of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ has been addressed in [7, 8, 32] and further refined in [5]. Here we report some results from [5], which will be exploited to design and analyse our updating procedure. We note that, although the convergence of Krylov solvers for systems with coefficient matrix ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ is not fully characterized by the spectrum of the matrix, in many practical cases it depends on the distribution of the eigenvalues. Therefore we are interested in providing bounds on the eigenvalues of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$. The bounds given in the next theorem highlight the dependence of the spectrum of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ on that of $S_{inex}^{-1}S$ (see [5, Theorem 2.1]).

Theorem 1

Let ${\mathcal {A}}$ and ${\mathcal {P}}_{inex}$ be the matrices in (8) and (10), and let $\lambda$ and $[x^T, y^T]^T$ be an eigenvalue of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ and a corresponding eigenvector. Let

$$\begin{aligned} X = G^{-\frac{1}{2}} B G^{-\frac{1}{2}} \end{aligned}$$

(11)

and suppose that $2I_n-X$ is positive definite. Let

$$\begin{aligned} \bar{\lambda }= & {} \lambda _{\max }\big (S_{inex}^{-1}S\big )\, \max \big \{ 2-\lambda _{\min }(X),\, 1 \big \}, \end{aligned}$$

(12)

$$\begin{aligned} \underline{\lambda }= & {} \lambda _{\min }\big (S_{inex}^{-1}S\big )\, \min \big \{ 2-\lambda _{\max }(X) ,\, 1 \big \}. \end{aligned}$$

(13)

Then, ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ has at most 2m eigenvalues with nonzero imaginary part, counting conjugates. Furthermore, if $\lambda$ has nonzero imaginary part, then

$$\begin{aligned} \frac{1}{2}\big (\lambda _{\min }(X)+\underline{\lambda } \big ) \le {\mathcal {R}}(\lambda ) \le \frac{1}{2}\big (\lambda _{\max }(X)+\bar{\lambda }\big ) ; \end{aligned}$$

(14)

otherwise,

$$\begin{aligned} \min \big \{\lambda _{\min }(X),\, \underline{\lambda }\big \}\le & {} \lambda \le \max \big \{\lambda _{\max }(X),\, \bar{ \lambda }\big \}, \quad \text {for } y \ne 0, \end{aligned}$$

(15)

$$\begin{aligned} \lambda _{\min }(X)\le & {} \lambda \le \lambda _{\max }(X), \quad \text {for } y=0. \end{aligned}$$

(16)

Finally, the imaginary part of $\lambda$ satisfies

$$\begin{aligned} |{\mathcal {I}}(\lambda )| \le \sqrt{\lambda _{\max }\big (S_{inex}^{-1}AG^{-1}A^T\big )} \Vert I_n-X\Vert . \end{aligned}$$

(17)

We note that $2I_n-X$ can be made positive semidefinite by scaling X in (11) so that its eigenvalues are not greater than 2. Furthermore, if B is diagonal, then $X=I_n$ and all the eigenvalues of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ are real. In this case ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ has at least n unit eigenvalues, with n associated independent eigenvectors of the form $[x^T, 0^T]^T$, and the remaining eigenvalues lie in the interval $[\lambda _{\min }(S_{inex}^{-1} S), \, \lambda _{\max } (S_{inex}^{-1} \, S)]$ (see also [21]).

Finally, from the analysis carried out in [32, Sect. 5] it follows that the number of unit eigenvalues of ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ depends also on the number of zero eigenvalues of $S-S_{inex}$. In particular, when $S-S_{inex}$ has l zero eigenvalues, if $S^{-1/2} AA^T S^{-1/2}$ has no unit eigenvalues then ${\mathcal {P}}_{inex}^{-1}{\mathcal {A}}$ has l unit eigenvalues with geometric multiplicity l.

3 The preconditioner updating strategy

Our preconditioner updating strategy is based on building $S_{inex}$ by a suitable update of the seed Schur complement $S_{seed}$. In [5] we presented an updated preconditioner of the form (10), where $S_{inex}$ is a low-rank modification, $S_{ lr}$, of $S_{seed}$. Here we make a step further, improving the approximation of S provided by $S_{ lr}$, in the case where $\varTheta$ is a nonzero matrix. Therefore, our approach for building $S_{inex}$ consists of two steps: the first computes $S_{ lr}$ through the procedure discussed in [5]; the second employs updating techniques discussed in [3, 4] to form an approximate factorization of $S_{ lr}+ \Delta$, where $\Delta$ is a suitable diagonal positive semidefinite matrix containing information not included in the previous step. The latter factorization provides the matrix $S_{inex}$, henceforth denoted by $S_{cu}$ because it is the result of the combination of two updates. The corresponding inexact preconditioner is

$$\begin{aligned} {\mathcal {P}}_{cu}= & {} \left[ \begin{array}{cc} I_n &{}\quad 0 \\ AG^{-1} &{}\quad I_m \end{array} \right] \left[ \begin{array}{cc} G &{}\quad 0 \\ 0 &{}\quad -S_{cu}\end{array} \right] \left[ \begin{array}{cc} I_n &{}\quad G^{-1}A^T \\ 0 &{}\quad I_m \end{array} \right] . \end{aligned}$$

(18)

Next we provide a detailed description of our procedure and analyze the quality of the resulting preconditioner. First, we describe how to perform the low-rank update of ${\mathcal {P}}_{seed}$ and summarize related theoretical results given in [5]. Second, we present the subsequent updating step and provide new bounds on the eigenvalues of the preconditioned matrix.

3.1 First step: building $S_{ lr}$

Let ${\mathcal L}=\{i \, : \, \varTheta _{ii}\ne 0\}$ and let $m_1$ be its cardinality. We recall that the set ${\mathcal L}$ does not change throughout the sequence. Furthermore, let $\widetilde{\varTheta }_{seed}$ and $\widetilde{\varTheta }$ be the $m_1 \times m_1$ diagonal submatrices containing the nonzero diagonal entries of $\varTheta _{seed}$ and $\varTheta$, respectively, and let $\widetilde{I}_m$ be the rectangular matrix consisting of the columns of $I_m$ with indices in ${\mathcal L}$. Then, the Schur complements $S_{seed}$ and S, corresponding to ${\mathcal {P}}_{seed}$ and ${\mathcal {P}}_{ex}$, respectively, can be written as follows:

$$\begin{aligned} S_{seed}= \widetilde{A} \widetilde{H}^{-1} \widetilde{A}^T, \quad S = \widetilde{A} \widetilde{G}^{-1} \widetilde{A}^T, \end{aligned}$$

where

$$\begin{aligned} \widetilde{A} = \left[ \begin{array}{cc} A&\quad \, \widetilde{I}_m \end{array} \right] , \quad \widetilde{H}^{-1} = \left[ \begin{array}{cc} H^{-1} &{}\quad 0\\ 0 &{}\quad \widetilde{\varTheta }_{seed}\end{array} \right] , \quad \widetilde{G}^{-1} = \left[ \begin{array}{cc} G^{-1} &{}\quad 0\\ 0 &{}\quad \widetilde{\varTheta }\end{array} \right] . \end{aligned}$$

(19)

Trivially,

$$\begin{aligned} S=S_{seed}+ \widetilde{A} \left( \widetilde{G}^{-1} - \widetilde{H}^{-1} \right) \widetilde{A}^T. \end{aligned}$$

(20)

The updating procedure described in [5] consists in finding a low-rank correction of $S_{seed}$ of the form

$$\begin{aligned} S_{ lr}= S_{seed}+ \widetilde{A} \widetilde{K} \widetilde{A}^T = \widetilde{A} \left( \widetilde{H}^{-1} + \widetilde{K} \right) \widetilde{A}^T = \widetilde{A} \widetilde{J}^{-1} \widetilde{A}^T, \end{aligned}$$

(21)

where $\widetilde{K}$, and hence $\widetilde{J}$, is a suitable diagonal matrix. The matrix $\widetilde{J}$ (or, equivalently, $\widetilde{K}$) is chosen with a double goal: tightening the bounds on the eigenvalues provided by Theorem 1 and limiting the cost for computing the Cholesky factorization of $S_{ lr}$ as a modification of the Cholesky factorization (7). A key role in achieving the first goal is played by a result in [1], reported next for completeness.

Lemma 2

Let $U\in {\mathbb {R}}^{r\times s}$ be full rank and let $E, \, F\in {\mathbb {R}}^{s\times s}$ be symmetric positive definite. Then

$$\begin{aligned} \lambda _{\min }\left( E^{-1}F\right) \le \lambda \big (\left( UEU^T\right) ^{-1} \, UFU^T \big ) \le \lambda _{\max }\big (E^{-1}F\big ) . \end{aligned}$$

For any diagonal positive definite matrix $C \in {\mathbb {R}}^{(n+m_1)\times (n+m_1)}$, let $\gamma (C)$ be the vector of dimension $n+m_1$ with entries $\gamma _i (C)$ equal to the diagonal entries of $C \widetilde{G}^{-1}$ sorted in nondecreasing order, i.e.,

$$\begin{aligned} \min _{1\le i\le n+m_1} \frac{C_{ii} }{\widetilde{G}_{ii}} = \gamma _1(C) \le \gamma _2(C) \le \cdots \le \gamma _{n+m_1}(C) = \max _{1\le i\le n+m_1} \frac{C_{ii} }{\widetilde{G}_{ii}}. \end{aligned}$$

(22)

Lemma 2 yields the bounds

$$\begin{aligned} \gamma _1(\widetilde{J}) \le \lambda \big (S_{ lr}^{-1} S\big ) \le \gamma _{n+m_1}(\widetilde{J}). \end{aligned}$$

(23)

We now give some definitions useful to specify $\widetilde{J}$. Let $l = (l_1,l_2,\ldots ,l_{n+m_1})^T$ be the vector of indices such that

$$\begin{aligned} \gamma _{l_i}(\widetilde{H}) =\frac{\widetilde{H}_{ii}}{\widetilde{G}_{ii}}. \end{aligned}$$

Given two real constants $\mu _{\gamma } \ge 1$ and $\nu _{\gamma } \in (0,1]$, and two nonnegative integers $q_1$ and $q_2$ such that $q=q_1+q_2 \le n+m_1$, we define $\widetilde{\varGamma }$ as

$$\begin{aligned} \widetilde{\varGamma } = \widetilde{\varGamma }_1 \cup \widetilde{\varGamma }_2, \end{aligned}$$

(24)

where

$$\begin{aligned} \begin{array}{l} \displaystyle \widetilde{\varGamma }_1 = \left\{ i : n+m_1-q_1+1 \le l_i \le n+m_1 \text { and } \gamma _{l_i}(\widetilde{H}) > \mu _{\gamma }\right\} , \\ \displaystyle \widetilde{\varGamma }_2 = \left\{ i : 1 \le l_i \le q_2 \text { and } \gamma _{l_i}(\widetilde{H}) < \nu _{\gamma } \right\} . \end{array} \end{aligned}$$

(25)

Then we define the matrix $\widetilde{K}$ in (21) by setting

$$\begin{aligned} \widetilde{K}_{ii}= \left\{ \begin{array}{cc} \widetilde{G}^{-1}_{ii}-\widetilde{H}^{-1}_{ii} &{}\quad \text { if } i \in \widetilde{\varGamma } ,\\ 0 &{}\quad \text { otherwise}. \end{array} \right. \end{aligned}$$

(26)

As a consequence, the diagonal entries of $\widetilde{J}$ take the following form:

$$\begin{aligned} \widetilde{J}_{ii}=\left\{ \begin{array}{cc} \widetilde{G}_{ii} &{}\quad \text { if } \ i \in \widetilde{\varGamma }, \\ \widetilde{H}_{ii} &{}\quad \text { otherwise}. \end{array}\right. \end{aligned}$$

(27)

We also note that $\widetilde{J}^{-1}$ can be written as follows:

$$\begin{aligned} \widetilde{J}^{-1}= \left[ \begin{array}{cc} J^{-1} &{}\quad 0\\ 0 &{}\quad \widetilde{\varTheta }_{lr} \end{array} \right] , \end{aligned}$$

(28)

where $J \in {\mathbb {R}}^{n \times n}$ accounts for the changes from H to G, and $\widetilde{\varTheta }_{lr} \in {\mathbb {R}}^{m_1 \times m_1}$ for those from $\widetilde{\varTheta }_{seed}$ to $\widetilde{\varTheta }$.

Suppose that the sets $\widetilde{\varGamma }_1$ and $\widetilde{\varGamma }_2$ in (25) have cardinality equal to $q_1^*\le q_1$ and $q_2^*\le q_2$, respectively. Then, from (21), $S_{ lr}-S_{seed}$ is a correction of rank $q^*=q_1^*+q_2^*$ equal to the cardinality of $\widetilde{\varGamma }$. Once $S_{ lr}$ is defined, the low-rank update preconditioner ${\mathcal {P}}_{ lr}$ is simply obtained by setting $S_{inex}= S_{ lr}$ in (10), i.e.,

$$\begin{aligned} {\mathcal {P}}_{ lr}=\left[ \begin{array}{cc} I_n &{}\quad 0 \\ AG^{-1} &{}\quad I_m \end{array} \right] \left[ \begin{array}{cc} G &{}\quad 0 \\ 0 &{}\quad -S_{ lr}\end{array} \right] \left[ \begin{array}{cc} I_n &{}\quad G^{-1}A^T \\ 0 &{}\quad I_m \end{array} \right] . \end{aligned}$$

(29)

By combining Theorem 1 with (23) and (27), we get the following bounds on the eigenvalues of ${\mathcal {P}}_{ lr}^{-1}{\mathcal {A}}$, (see [5, Corollary 3.3]).

Corollary 3

Let ${\mathcal {A}}$, ${\mathcal {P}}_{ lr}$ and X be the matrices in (8), (29) and (11), and let $\lambda$ be an eigenvalue of ${\mathcal {P}}_{ lr}^{-1}{\mathcal {A}}$. Let $\gamma (\widetilde{H})$ and $\gamma (\widetilde{J})$ be defined as in (22), and let $q_1^*$ and $q_2^*$ be the cardinality of the sets $\widetilde{\varGamma }_1$ and $\widetilde{\varGamma }_2$ in (25), respectively. If $2I_n-X$ is positive definite, then $\lambda$ satisfies either (14) or (15)–(16) with

$$\begin{aligned} \bar{\lambda }\le & {} \gamma _{n+m_1}(\widetilde{J})\, \max \big \{ 2-\lambda _{\min } (X) ,\, 1 \big \} , \end{aligned}$$

(30)

$$\begin{aligned} \underline{\lambda }\ge & {} \gamma _1(\widetilde{J}) \, \min \big \{ 2-\lambda _{\max } (X) ,\, 1 \big \} , \end{aligned}$$

(31)

where

$$\begin{aligned} \gamma _1(\widetilde{J})= & {} \min \big \{1, \min _{i \notin \widetilde{\varGamma }} \gamma _{l_i}(\widetilde{H}) \big \}= \min \big \{1, \gamma _{q_2^*+1}(\widetilde{H})\big \}, \nonumber \\ \gamma _{n+m_1}(\widetilde{J})= & {} \max \big \{1, \max _{i\notin \widetilde{\varGamma }} \gamma _{l_i}(\widetilde{H}) \big \}= \max \big \{1, \gamma _{n+m_1-q_1^*}(\widetilde{H})\big \}. \end{aligned}$$

(32)

Furthermore,

$$\begin{aligned} |{\mathcal {I}}(\lambda )| \le \sqrt{\gamma _{n+m_1}(\widetilde{J})} \, \Vert I_n-X\Vert . \end{aligned}$$

(33)

It is clear that the bounds provided by the previous corollary are expected to improve as the set $\widetilde{\varGamma }$ is enlarged, i.e., q is increased. Likewise, smaller (larger) values of $\mu _{\gamma }$ ($\nu _{\gamma }$) may generally improve these bounds. However, the choice of the previous values must take into account the cost for computing the Cholesky factorization of $S_{ lr}$ by updating the factorization available for $S_{seed}$. From (7), (21) and (26) it follows that

$$\begin{aligned} S_{ lr}= L_{seed}D_{seed}L_{seed}^T+ \bar{A} \bar{K}\bar{A}^T, \end{aligned}$$

where $\bar{A} \in {\mathbb {R}}^{m\times q^*}$ consists of the columns of $\widetilde{A}$ with indices in $\widetilde{\varGamma }$, and $\bar{K} \in {\mathbb {R}}^{ q^*\times q^*}$ is the diagonal matrix having on the diagonal the nonzero entries of $\widetilde{K}$ corresponding to those indices. Therefore, the Cholesky factorization

$$\begin{aligned} S_{ lr}= L_{lr}D_{lr}L_{lr}^T, \end{aligned}$$

(34)

is a rank-$q^*$ modification of the factorization (7) and can be computed, e.g. through the update and downdate procedures in [17]. Note that an update is required if $\widetilde{H}_{ii} > \widetilde{G}_{ii}$ and a downdate is required if $\widetilde{H}_{ii} < \widetilde{G}_{ii}$.

The computational cost for building $S_{ lr}$ depends on the value of q, and for practical purposes the updating strategy is more convenient than computing the exact preconditioner as long as q is kept fairly small (see [5]). Similarly, values of $\mu _{\gamma }$ and $\nu _{\gamma }$ not too close to 1 are used in practice; thus, indices that do not bring significant improvement in the eigenvalue bounds while increasing the cost for the updating strategy (see again [5]) are excluded from $\widetilde{\varGamma }$. Since a large number of entries in $\widetilde{G}-\widetilde{H}$ must be discarded, we now propose a second step of our updating approach for recovering part of the discarded information.

3.2 Second step: updating $S_{ lr}$ to get $S_{cu}$

In order to recover information not included in $S_{ lr}$, we observe that part of this information can be regarded as a positive semidefinite diagonal modification, $\Delta$, of $S_{ lr}$. Therefore, we can compute a low-cost approximate $LDL^T$ factorization of the matrix $S_{ lr}+ \Delta$ by exploiting the procedures in [3, 4, 30] to update the factorization (34) of $S_{ lr}$. Furthermore, by expressing $S_{ lr}+ \Delta$ as $\widetilde{A} \widetilde{J}_\Delta ^{-1} \widetilde{A}^T$, with $\widetilde{J}_\Delta$ diagonal positive definite, we can exploit Lemma 2 to derive new eigenvalue bounds.

We consider the diagonal matrix $\widetilde{\Delta } \in {\mathbb {R}}^{m_1\times m_1}$ defined by

$$\begin{aligned} \widetilde{\Delta }_{ii} = \left\{ \begin{array}{cc} \widetilde{\varTheta }_{ii}- (\widetilde{\varTheta }_{seed})_{ii} &{}\quad \text { if } \ i+n \notin \widetilde{\varGamma } \text { and } \widetilde{\varTheta }_{ii}- (\widetilde{\varTheta }_{seed})_{ii}>0, \\ 0 &{}\quad \text { otherwise} , \end{array}\right. \end{aligned}$$

(35)

whose nonzero entries correspond to the ratios $\widetilde{\varTheta }_{ii}/(\widetilde{\varTheta }_{seed})_{ii}$ that are greater than 1 and have been discarded in the construction of $S_{ lr}$. Then, recalling the definition of $\widetilde{I}_m$ in Sect. 3.1, we set $\Delta \in {\mathbb {R}}^{m\times m}$ as follows:

$$\begin{aligned} \Delta =\widetilde{I}_m \, \widetilde{\Delta } \;\, \widetilde{I}_m^T, \end{aligned}$$

(36)

and define the matrix

$$\begin{aligned} S_\Delta = S_{ lr}+\Delta . \end{aligned}$$

(37)

Using $S_\Delta$ instead of $S_{ lr}$ generally improves the quality of the preconditioner ${\mathcal {P}}_{cu}$, as shown next. Let

$$\begin{aligned} \widetilde{\varGamma }_\Delta = \widetilde{\varGamma } \, \cup \, \left\{ j : \, j=i+n, \text { with } 1 \le i \le m_1 \text { and } \gamma _{l_j}(\widetilde{H}) = \frac{\widetilde{\varTheta }_{ii}}{(\widetilde{\varTheta }_{seed})_{ii}} >1 \right\} , \end{aligned}$$

and let $\widetilde{\varTheta }_\Delta \in {\mathbb {R}}^{m_1 \times m_1}$ the diagonal matrix defined by

$$\begin{aligned} ( \widetilde{\varTheta }_\Delta )_{ii} = \left\{ \begin{array}{cc} \widetilde{\varTheta }_{ii} &{}\quad \text { if } \ i+n \in \widetilde{\varGamma }_\Delta , \\ (\widetilde{\varTheta }_{seed})_{ii} &{}\quad \text { otherwise}. \end{array}\right. \end{aligned}$$

Then we have

$$\begin{aligned} S_\Delta = \widetilde{A} \widetilde{J}_\Delta ^{-1} \widetilde{A}^T, \quad \widetilde{J}_\Delta ^{-1} = \left[ \begin{array}{cc} J^{-1} &{} \\ &{} \widetilde{\varTheta }_\Delta \end{array} \right] , \end{aligned}$$

where $\widetilde{A}$ and J are the matrices in (19) and (28), respectively. By reasoning as in Sect. 3.1, we get the following bounds on the eigenvalues of $S_{\Delta }^{-1} S$:

$$\begin{aligned} \hat{\gamma }_1 \le \lambda \left( S_{\Delta }^{-1} S\right) \le \hat{\gamma }_{n+m_1}, \end{aligned}$$

(38)

where

$$\begin{aligned} \hat{\gamma }_1= & {} \gamma _{1}(\widetilde{J})= \min \big \{1, \gamma _{q_2^*+1}(\widetilde{H})\big \}, \end{aligned}$$

(39)

$$\begin{aligned} \hat{\gamma }_{n+m_1}= & {} \max \left\{ 1, \max _{i \notin \widetilde{\varGamma }_\Delta } \gamma _{l_i}(\widetilde{H}) \right\} . \end{aligned}$$

(40)

Trivially, $\hat{\gamma }_{n+m_1} \le \gamma _{n+m_1}(\widetilde{J})$, with $\gamma _{n+m_1}(\widetilde{J})$ given in (32), and the benefit of using $S_\Delta$ depends on the size of $\hat{\gamma }_{n+m_1}$ with respect to $\gamma _{n+m_1}(\widetilde{J})$.

On the other hand, using $S_{\Delta }$ in place of $S_{ lr}$ requires its factorization. In order to limit the computational cost of the preconditioner, we can compute an approximation to the Cholesky factorization of $S_\Delta$,

$$\begin{aligned} S_{cu}= L_{cu}D_{cu}L_{cu}^T\simeq S_\Delta , \end{aligned}$$

(41)

by using the updating procedures mentioned at the beginning of this section. The procedure considered here updates the matrices $L_{lr}$ and $D_{lr}$ in (34) as follows (see [4] for details). Let W be the diagonal matrix with diagonal entries defined by

$$\begin{aligned} W_{ii}=\frac{(D_{lr})_{ii}}{(D_{lr})_{ii}+\Delta _{ii}}, \quad i=1, \ldots , m ; \end{aligned}$$

we define the matrices $L_{cu}$ and $D_{cu}$ as

$$\begin{aligned} \begin{array}{l} D_{cu}= D_{lr}+\Delta , \\ (L_{cu})_{jj} = 1, \quad j=1,\ldots ,m, \\ L_{cu}(j+1:m,j) = W_{jj} L_{lr}(j+1:m,j), \quad j=1,\ldots ,m-1, \end{array} \end{aligned}$$

(42)

where, using the Matlab notation, $L_{lr}(j+1:n,j)$ denotes the strictly lower triangular part of the j-th column of $L_{lr}$. Note that the sparsity pattern of the factors of $S_{ lr}$ is preserved; furthermore, the cost of forming $S_{cu}$ is low, since the cost of $D_{cu}$ is negligible, and the computation of $L_{cu}$ consists in scaling only the nonzero entries of the columns of $L_{lr}$ corresponding to the nonzero entries of $\Delta$. Obviously, if $\Delta$ is the zero matrix, the update is not performed and $S_{cu}= S_{ lr}$, i.e., ${\mathcal {P}}_{cu}={\mathcal {P}}_{ lr}$. This limit case occurs if $\widetilde{\varTheta }_{ii}\le (\widetilde{\varTheta }_{seed})_{ii}$ for $i=1,\ldots ,m_1$, or if all the indices $i+n$ associated with the ratios $\widetilde{\varTheta }_{ii}/ (\widetilde{\varTheta }_{seed})_{ii}$ that are greater than 1 belong to $\widetilde{\varGamma }$.

We refer to [3, 4] for theoretical results and computational experiences motivating the previous updating approach. Here we report only some results concerning the eigenvalues of $S_{cu}^{-1}S$ (see [4, Theorems 2.2 and 2.4]), which are useful in the spectral analysis of ${\mathcal {P}}_{cu}^{-1}{\mathcal {A}}$.

Theorem 4

Let $S_\Delta$ and $S_{cu}$ be the matrices in (37) and (41). For all $\varepsilon > 0$ there exists $\eta > 0$ such that if $\Vert \Delta \Vert < \eta$, then

$$\begin{aligned} \left| \lambda (S_{cu}^{-1} \, S_\Delta ) - 1 \right| < \varepsilon \end{aligned}$$

for all the eigenvalues of $S_{cu}^{-1} \, S_\Delta$. Furthermore, if $S_\Delta - S_{cu}$ has rank $m-l$, then l eigenvalues of $S_{cu}^{-1} \, S_\Delta$ are equal to 1.

Theorem 5

Let $S_\Delta$ and $S_{cu}$ be the matrices in (37) and (41). For all $\varepsilon > 0$ there exists $\eta > 0$ such that if $\Delta _{ii} > \eta$ for r diagonal entries of $\Delta$, then

$$\begin{aligned} \left| \lambda (S_{cu}^{-1} \, S_\Delta ) - 1 \right| < \varepsilon \end{aligned}$$

for r eigenvalues of $S_{cu}^{-1} \, S_\Delta$.

The next theorem provides bounds on the eigenvalues of ${\mathcal {P}}_{cu}^{-1}{\mathcal {A}}$ in terms of $\hat{\gamma }_1$ and $\hat{\gamma }_{n+m_1}$ and of the minimum and maximum eigenvalues of $S_{cu}^{-1}\, S_\Delta$.

Theorem 6

Let ${\mathcal {A}}$, ${\mathcal {P}}_{cu}$, $S_{\Delta }$, $S_{cu}$ and X be the matrices in (8), (18), (37), (41) and (11), and let $\lambda$ be an eigenvalue of ${\mathcal {P}}_{cu}^{-1}{\mathcal {A}}$. Let $\hat{\gamma }_1$ and $\hat{\gamma }_{n+m_1}$ be the scalars in (39) and (40). If $2I_n-X$ is positive definite, then $\lambda$ satisfies either (14) or (15)–(16) with

$$\begin{aligned} \bar{\lambda }\le & {} \hat{\gamma }_{n+m_1} \lambda _{\max }(S_{cu}^{-1} S_\Delta )\max \big \{ 2-\lambda _{\min }(X) ,\, 1 \big \} , \end{aligned}$$

(43)

$$\begin{aligned} \underline{\lambda }\ge & {} \hat{\gamma }_1 \lambda _{\min }(S_{cu}^{-1} S_\Delta ) \min \big \{ 2-\lambda _{\max }(X) ,\, 1 \big \} . \end{aligned}$$

(44)

Furthermore,

$$\begin{aligned} |{\mathcal {I}}(\lambda )| \le \sqrt{\hat{\gamma }_{n+m_1} \lambda _{\max }(S_{cu}^{-1} S_\Delta )} \, \Vert I_n-X\Vert . \end{aligned}$$

(45)

Proof

The eigenvalue problem $S_{cu}^{-1} S w= \lambda w$ is equivalent to

$$\begin{aligned} S_\Delta ^{-\frac{1}{2}} S \, S_\Delta ^{-\frac{1}{2}} \bar{w}=\lambda \ S_\Delta ^{-\frac{1}{2}}\, S_{cu}\, S_\Delta ^{-\frac{1}{2}} \ \bar{w} , \end{aligned}$$

with $\bar{w}= S_\Delta ^{\frac{1}{2}} \, w$. Hence, for any eigenvalue of $S_{cu}^{-1} S$ and any corresponding eigenvector w we have

$$\begin{aligned} \lambda \big (S_{cu}^{-1} S\big ) = \frac{\bar{w}^T S_\Delta ^{-\frac{1}{2}} S \, S_\Delta ^{-\frac{1}{2}} \bar{w}}{\bar{w}^T S_\Delta ^{-\frac{1}{2}}\, S_{cu}\, S_\Delta ^{-\frac{1}{2}} \ \bar{w}} . \end{aligned}$$

Then, by exploiting (38) we get

$$\begin{aligned} \lambda \big ( S_{cu}^{-1} S \big ) \le \frac{\lambda _{\max }\big (S_\Delta ^{-1} S\big ) }{ \lambda _{\min }\big ( S_\Delta ^{-1} S_{cu}\big ) } \le \hat{\gamma }_{n+m_1}\, \lambda _{\max }\big ( S_{cu}^{-1} S_\Delta \big ) \end{aligned}$$

and

$$\begin{aligned} \lambda \big ( S_{cu}^{-1}S \big ) \ge \frac{\lambda _{\min }\big ( S_\Delta ^{-1}\, S\big )}{ \lambda _{\max }\big ( S_\Delta ^{-1} S_{cu}\big ) } \ge \hat{\gamma }_{1} \lambda _{\min }\big ( S_{cu}^{-1} S_\Delta \big ) . \end{aligned}$$

Inequalities (43) and (44) follow by recalling (12) and (13).

It remains to prove (45). The eigenvalue problem $S_{cu}^{-1} A \,G^{-1} A^T w = \lambda \, w$ is equivalent to

$$\begin{aligned} S_\Delta ^{-\frac{1}{2}} A \, G^{-1} A^T S_\Delta ^{-\frac{1}{2}} \bar{w} = \lambda S_\Delta ^{-\frac{1}{2}} S_{cu}S_\Delta ^{-\frac{1}{2}} \bar{w} . \end{aligned}$$

Furthermore, since $\varTheta$ is positive definite, for any vector $v \in {\mathbb {R}}^m$

$$\begin{aligned} v^T S_\Delta ^{-\frac{1}{2}} A \, G^{-1}A^T S_\Delta ^{-\frac{1}{2}} v \le v^T S_\Delta ^{-\frac{1}{2}} \big (A \, G^{-1}A^T +\varTheta \big ) S_\Delta ^{-\frac{1}{2}} v, \end{aligned}$$

and by matrix similarity

$$\begin{aligned} \lambda _{\max }\big (S_\Delta ^{-1} A \, G^{-1} A^T\big ) \le \lambda _{\max }\big (S_\Delta ^{-1} S\big ). \end{aligned}$$

By reasoning as in the first part of the proof and exploiting the previous inequality we get

$$\begin{aligned} \lambda \big ( S_{cu}^{-1} AG^{-1}A^T \big )\le & {} \frac{\lambda _{\max }\big (S_\Delta ^{-1} S\big ) }{ \lambda _{\min }\big ( S_\Delta ^{-1} \, S_{cu}\big ) } \\= & {} \hat{\gamma }_{n+m_1} \, \lambda _{\max }\big ( S_{cu}^{-1}\, S_\Delta \big ) , \end{aligned}$$

and (45) follows from (17). $\square$

The following result is a straightforward consequence of Theorem 6.

Corollary 7

Let ${\mathcal {A}}$, ${\mathcal {P}}_{cu}$, $S_{\Delta }$, $S_{cu}$ and X be the matrices in (8), (18), (37), (41) and (11), and let $\lambda$ be an eigenvalue of ${\mathcal {P}}_{cu}^{-1}{\mathcal {A}}$. Let $\hat{\gamma }_1$ and $\hat{\gamma }_{n+m_1}$ be the scalars in (39) and (40). If $2I_n-X$ is positive definite and, for all the eigenvalues of $S_{cu}^{-1}\, S_\Delta$,

$$\begin{aligned} \left| \lambda (S_{cu}^{-1}\, S_\Delta ) -1\right| \le \varepsilon \end{aligned}$$

for some $\varepsilon > 0$, then $\lambda$ satisfies either (14) or (15)–(16) with

$$\begin{aligned} \bar{\lambda }\le & {} (1+\varepsilon ) \hat{\gamma }_{n+m_1} \max \big \{ 2-\lambda _{\min }(X) ,\, 1 \big \} , \\ \underline{\lambda }\ge & {} (1-\varepsilon ) \hat{\gamma }_1 \min \big \{ 2-\lambda _{\max }(X) ,\, 1 \big \} . \end{aligned}$$

Furthermore,

$$\begin{aligned} |{\mathcal {I}}(\lambda )| \le \sqrt{(1+\varepsilon ) \hat{\gamma }_{n+m_1}} \, \Vert I_n-X\Vert . \end{aligned}$$

The previous results show that the bounds (30) and (33) can be effectively improved if $\lambda _{\max }( S_{cu}^{-1} S_\Delta )$ is not too far from 1. Furthermore, $\lambda _{\min }( S_{cu}^{-1} S_\Delta )$ must not be too far from 1, in order to avoid a significant deterioration of the bound (31). By Theorems 4 and 5, this happens when the entries of $\Delta$ are either all sufficiently small or all sufficiently large. In general, we cannot expect that all the eigenvalues of $S_{cu}^{-1} S_\Delta$ are close to 1; nevertheless, the ability of $S_{cu}$ of clustering around 1 some eigenvalues of $S_\Delta$ when $\Delta$ has large entries, provides a way to tighten the bounds on the spectrum of ${\mathcal {P}}_{cu}^{-1} {\mathcal {A}}$, as confirmed by numerical experiments.

We conclude this section by summarizing in Algorithm 1 the main steps of the overall updating procedure.

4 Numerical results

We provide some illustrative examples of the behavior of the preconditioner ${\mathcal {P}}_{cu}$ built with Algorithm 1, compared with the exact CP preconditioner ${\mathcal {P}}_{ex}$ in (9) and the updated preconditioner ${\mathcal {P}}_{ lr}$ in (29).

We consider five sequences of KKT systems that arise in the solution, by an IP method, of convex quadratic programming problems with linear inequality constraints. These problems have been obtained by modifying the CUTEst [27] problems CVXQP1, CVXQP3 and MOSARQP1. The modifications have been made because large or variable-size CUTEst convex quadratic programming problems with inequality constraints have Schur complements that are very inexpensive to factorize and thus are useless for our experiments. More precisely, CVXQP1 and CVXQP3, which have non-banded Schur complements, have been modified by changing their original equality constraint $Ax=b$ into $Ax \ge b$ (the modified problems have been identified by appending “-M” to the original names). Furthermore, in order to increase the density of their Schur complements, four nonzero entries per row have been added to the matrix A of CVXQP1-M, and one nonzero entry per row to the matrix A of CVXQP3-M (the denser problems have been identified by appending “-D” and “-D2” to their names, respectively, according to the notation used in [5]). Finally, nonzeros in the positions (i, n), with $mod(i,10)=1$, have been added to the matrix A of MOSARQP1, obtaining problem MOSARQP1-D (note that the original problem has a narrow-banded Schur complement). The dimensions n and m of the five problems and the number nnz(S) of nonzero entries of their Schur complements are reported in the second column of Table 1.

Table 1 Comparison of ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$: total number of SQMR iterations, refreshes of the preconditioners and execution times

The sequences of KKT systems have been obtained by running the Fortran 90 PRQP code, which implements an infeasible inexact potential reduction IP method [11, 13, 15], and extracting the KKT matrices arising at each IP iteration and the corresponding right-hand sides. Afterwards these sequences have been solved offline, applying ${\mathcal {P}}_{ex}$, ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$. The starting point for the IP procedure in PRQP has been built with the STP2 strategy described in [16] and the tolerances on the relative duality gap and the relative infeasibilities have been set to $10^{-6}$ and $10^{-7}$, respectively. Within PRQP the KKT systems have been solved by the SQMR method coupled with the exact CP, using an adaptive tolerance in the stopping criterion, which relates the accuracy in the solution of the KKT system to the quality of the current IP iterate, in the spirit of inexact IP methods [2, 12]. Specifically, in PRQP the SQMR iterations were stopped as soon as the norm of the unpreconditioned residual was below a tolerance of the form $\tau = \min \{\max \{\tau _1, 10^{-8}\}, 10^{-2} \Vert r_0\Vert \}$, where $\tau _1$ depends on the duality gap value at the current IP iteration and $r_0$ is the initial unpreconditioned residual (see [12] for more details). The values of $\tau$ corresponding to all the systems of each sequence were saved to be used in our experiments.

The numerical experiments have been performed in the Matlab environment, exploiting C code for the construction of ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$. More precisely, the CHOLMOD package [14] has been called, through its MEX interface, to compute the sparse $LDL^T$ factorization of $S_{seed}$ and the low-rank updates and downdates required to build ${\mathcal {P}}_{ lr}$. The updates (42) needed to form ${\mathcal {P}}_{cu}$ have been implemented in C as Matlab MEX-files too. The preconditioners have been built using $q_1=q_2=q/2=25$, in order to keep low the overhead of the updating/downdating phase; furthermore, $\mu _{\gamma } = 10$ and $\nu _{\gamma }=0.1$ have been used to select the indices to be put in $\widetilde{\varGamma }$. These choices agree with the results of the experiments with ${\mathcal {P}}_{ lr}$ discussed in [5]. When less than $q_1$ ratios $\gamma _{l_i}(\widetilde{H}) \ge \mu _{\gamma }$ (or less than $q_2$ ratios $\gamma _{l_i}(\widetilde{H}) \le \nu _{\gamma }$) were available, the number of ratios $\gamma _{l_i}(\widetilde{H}) \le \nu _{\gamma }$ (or $\gamma _{l_i}(\widetilde{H}) \ge \mu _{\gamma }$) was increased to have a total number of ratios in $\widetilde{\varGamma }$ as close as possible to q. We note that we have not applied any scaling to the matrix X in (11) to ensure positive definiteness of $2I_n - X$, although this is assumed in our theory. Nevertheless, the results generally appear to be in agreement with the theory (see also [5]). The linear systems have been solved using a Matlab implementation of the SQMR method without look-ahead [22], stopping the iterations when the norm of the residual had become smaller than the associated tolerance, as in the solution of the KKT systems within the IP code. A maximum number of 500 iterations has been considered too.

Table 2 CVXQP1-M: SQMR iterations and execution times obtained with ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$

Table 3 CVXQP3-M-D2: SQMR iterations and execution times obtained with ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$

Table 4 MOSARQP1-D: SQMR iterations and execution times obtained with ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$

Following [5], the preconditioners have been “refreshed” as explained next. When, for a system of the sequence, the time for computing ${\mathcal {P}}_{ lr}$ or ${\mathcal {P}}_{cu}$ and solving the preconditioned linear system exceeded 90 % of the time for building the last exact preconditioner and solving the corresponding system, the next system of the sequence was solved using the exact CP in (9). Furthermore, a maximum number of consecutive updates, $k_{\max }$, was also considered; here $k_{\max }=4$. This strategy aims at avoiding deterioration of the quality of the updated preconditioner and hence excessive increase of the number of SQMR iterations, which may make the updating strategy useless. We note that, by using a refreshing criterion based on the execution time, both the problem and the computing environment are taken into account to get an efficient preconditioning strategy.

The tests have been performed on a six-core Xeon processor with clock frequency of 2.4 GHz, 24 GB of RAM and 12 MB of cache memory, running Ubuntu/Linux 12.04.5 (kernel version 3.2.0_83_generic). CHOLMOD and the C code for the updates (42) have been compiled with gcc 4.6.3, and Matlab R2015a (v. 8.5, 64-bit) has been employed. The tic and toc Matlab commands have been used to measure the execution times.

We start the description of our numerical results comparing ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$. For the problems from the CVXQP family, we observe that the the number of elements used for the second step of the update, namely $nnz(\Delta )$ with $\Delta$ defined in (35) and (36), is zero or negligible (at most twenty) in the first systems of the sequence (first nine systems for CVXQP1-M-D, and first ten systems for CVXQP1-M, CVXQP3-M and CVXQP3-M-D2). Since no significant benefit can be obtained from the update strategy (42) with such a small number of elements, we exclude these first systems from the following analysis.

Table 5 CVXQP1-M: minimum and maximum eigenvalues of $S_{ lr}^{-1} S$ and $S_{cu}^{-1} S$

The results obtained with ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$ are shown in Table 1. We report the range ${ IPits}$ of IP iterations considered for each sequence and, for each preconditioner, the total number ${ nit}$ of SQMR iterations performed, the number ${ nref}$ of times the preconditioner has been refreshed, the total time $T_{prec}$ for building the preconditioner, the total time $T_{solve}$ for solving the preconditioned system, and the sum $T_{tot}$ of the two times. The times are expressed in seconds. We see that all the runs with ${\mathcal {P}}_{cu}$ are faster than those with ${\mathcal {P}}_{ lr}$. The gain, in terms of total execution time, varies between 6 and $23\,\%$. Furthermore, for two sequences, the savings obtained in the number of SQMR iterations reduce the number of preconditioner refreshes with respect to the use of ${\mathcal {P}}_{ lr}$.

Table 6 Comparison of ${\mathcal {P}}_{ex}$ and ${\mathcal {P}}_{cu}$: total number of SQMR iterations, refreshes for ${\mathcal {P}}_{cu}$ and execution times

Details on the solution of the sequences of KKT systems by using ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$ are shown in Tables 2, 3 and 4 for CVXQP1-M, CVXQP3-M-D2 and MOSARQP1-D, respectively. The IP iteration number corresponding to each system of a sequence is indicated by IP#. For each system and for both preconditioners, we report the number ${ nit}$ of SQMR iterations, the time $T_{prec}$ for building the preconditioner for that system, the time $T_{solve}$ for solving the preconditioned system, and $T_{sum}=T_{prec}+T_{solve}$. For ${\mathcal {P}}_{ lr}$ we also display the size $q^*$ of the low-rank update performed, i.e., the cardinality of the set $\widetilde{\varGamma }$ in (24), while for ${\mathcal {P}}_{cu}$ we display both $q^*$ and the number of elements used for the second step of the update, i.e., $nnz(\Delta )$. The data corresponding to refreshes are in bold and the times are expressed in seconds.

We observe that, in general, forming ${\mathcal {P}}_{cu}$ is inexpensive although $nnz(\Delta )$ is large. Using ${\mathcal {P}}_{cu}$ may significantly reduce the number of SQMR iterations, especially in the last runs before a refresh. In fact, the performance of both ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$ tends to deteriorate progressively after a refresh, but the use of the diagonal modification in ${\mathcal {P}}_{cu}$ may considerably improve the effectiveness of ${\mathcal {P}}_{cu}$ with respect to ${\mathcal {P}}_{ lr}$. This behavior is clearly illustrated, e.g. by the data of the $15\hbox {th}$, $19\hbox {th}$ and $22\hbox {nd}$ system of CVXQP1-M (Table 2); a similar behavior can be recognized in Tables 3 and 4. Taking into account this numerical evidence and the fact that forming ${\mathcal {P}}_{cu}$ is simple and inexpensive, the second phase of the update appears worthy to be coupled with the low-rank correction in the update of CP preconditioners for KKT systems.

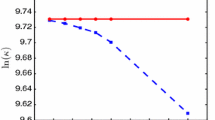
To provide further insight into the behavior of ${\mathcal {P}}_{cu}$, in Table 5 we report the maximum and minimum eigenvalues of $S_{ lr}^{-1} S$ and $S_{cu}^{-1} S$ from the 12th to the 25th iteration of CVXQP1-M. Note that at the 25th iteration $S_{ lr}$ is the matrix which $S_{cu}$ is built from, and not the matrix associated with the preconditioner ${\mathcal {P}}_{ lr}$ considered in Table 2 (with ${\mathcal {P}}_{ lr}$ and ${\mathcal {P}}_{cu}$ the refresh occurs at different IP iterations). We see that the updating strategy used to build $S_{cu}$ practically does not change the smallest eigenvalue, while it reduces the largest one, according to the decrease observed in the number of iterations (see Table 2).

We conclude this section by comparing the preconditioners ${\mathcal {P}}_{cu}$ and ${\mathcal {P}}_{ex}$. In Table 6 we summarize the total number of SQMR iterations and execution times for ${\mathcal {P}}_{ex}$; the same data for ${\mathcal {P}}_{cu}$, available in Table 1, are repeated for the sake of readability. The reduction of the total time obtained with ${\mathcal {P}}_{cu}$ over ${\mathcal {P}}_{ex}$ varies between 9 and $25\,\%$ although, as expected, the number of SQMR iterations performed is larger than with ${\mathcal {P}}_{ex}$. It is noteworthy that ${\mathcal {P}}_{cu}$ speeds up the solution of the sequences associated with CVXQP1-M, CVXQP1-M-D and MOSARQP1, where the use of ${\mathcal {P}}_{ lr}$ is not beneficial with respect to ${\mathcal {P}}_{ex}$. We also report briefly on experiments with inexact CPs obtained by approximating the exact Schur complement S with an inexact Cholesky factorization of it. These experiments have been performed to further assess the reliability of our updating approach. Unmodified and modified incomplete Cholesky factorizations of S have been computed using the Matlab function ichol and drop tolerances ranging from $10^{-1}$ to $10^{-5}$. However, the resulting inexact CPs seem to lack robustness on our sequences, as SQMR failed in the solution of at least one system of each sequence.

5 Conclusions

We have presented a procedure for updating CPs for sequences of regularized KKT systems with the nonzero (2,2) block having a fixed sparsity pattern. This procedure combines a recently proposed technique for updating a block $LDL^T$ factorization of a given seed CP, relying on a low-rank correction of its Schur complement, with a further update of the Schur complement. The latter update is performed to introduce into the preconditioner some information that has been discarded in the low-rank correction. It is based on a low-cost technique for approximating the Cholesky factorization when the matrix undergoes a diagonal positive semidefinite modification.

Theoretical results show that the procedure proposed here provides the possibility of tightening the bounds on the eigenvalues of the preconditioned matrix with respect to the procedure based on the low-rank correction alone, and that its effectiveness depends on the accuracy of the approximate Cholesky factorization computed in the second updating step. Numerical experiments confirm this behavior and show that the new approach can enhance the low-rank strategy.