1 Introduction

In recent years, the computation capability and energy efficiency of mobile devices have become extremely important with the emergence of new mobile applications (e.g., augmented reality and 3D games) [1,2,3]. Mobile edge computing (MEC) can effectively relieve the pressure of increasing computing demands on mobile devices, reduce task execution latency, and extend the battery life of terminals by offloading the computationally intensive tasks to neighboring edge servers [4,5,6]. However, although task offloading to edge servers can effectively utilize computational resources at the server side, the experience quality of users varies significantly under different task offloading strategies and network resource allocation states. The reason for this is that both the computation resources of the edge server and the radio resources in the network are limited. The computation offloading strategy is not always practical, and a poor computation offloading decision may even worsen task processing delay and increase energy consumption. Therefore, designing a reasonable task offloading strategy and allocating computational and radio resources in MEC systems are vital challenges that must be addressed [7,8,9,10,11].

Many studies deal with optimization problems related to computation offloading decisions and resource allocation in MEC systems [7, 12,13,14,15,16,17]. Considering the presence of binary offloading variables in these problems, they are typically categorized as mixed integer nonlinear programming (MINP) problems. Currently, exact approaches such as branch-and-bound algorithms [18] and dynamic programming [19] can be utilized to solve MINP problems; however, when the problem scales up, these algorithms will consume massive computation time and are difficult to scale. In addition, there are approximate approaches, such as heuristic local search [13, 20, 21] and relaxation algorithms [22, 23]. Compared to the exact approaches, the approximate approaches can search for a solution within an acceptable computation time. However, when the problem becomes complicated, a large number of iterations still lead to a considerable computation time. Hence, approximation methods are difficult to be applied to online, real-time computation offloading optimization problems.

In recent years, with the development of artificial intelligence technology, deep learning has been widely used in various fields [24, 25]. In this paper, to solve task offloading decisions and resource allocation in MEC systems online, we propose a deep reinforcement learning (DRL)-based offloading framework that works as an adaptive scheduler to learn binary offloading decisions. Edge servers can provide computing services to users, reducing task execution latency and energy consumption of mobile devices. Therefore, we use processing latency and energy consumption as evaluation metrics to analyze the performance of an MEC system. We define the user’s utility function as the weighted sum of the improvement ratios on delay and energy consumption via edge computing compared with local computing. Our study aims to maximize the system utility, which is defined as the weighted sum of the utility functions of all users in the system. The significant contributions of this study are as follows.

  1. 1.

    We construct a joint optimization problem of computation offloading, communication, and computational resource allocation in a time-varying MEC network to maximize system utility, which is a mixed integer nonlinear programming (MINP) problem.

  2. 2.

    We propose a DRL-based joint optimization approach (DRJOA) for each user in a time-varying MEC system to obtain an optimal offloading strategy and the corresponding resource allocation. DRJOA converts the original optimization problem into two subproblems: wireless and computational resource allocation and computation offloading decision problems. The proposed DRJOA learns the offloading generation strategy from past offloading experiences under the different wireless channels. The computation offloading decision problem uses a deep neural network (DNN) and K nearest neighbor (KNN) methods to generate offloading decisions efficiently. Thus, DRJOA selects the best offloading decision from a limited decision space, and its computational complexity does not grow dramatically with the size of the problem.

  3. 3.

    We conduct extensive simulations to evaluate the performance of our proposed DRJOA algorithm. The simulation results demonstrate that the system utility of the proposed solution is near-optimal, and the proposed DRJOA algorithm significantly improves system offloading utility compared with benchmark approaches.

The remainder of this paper is organized as follows. The related work is introduced in Sect. 2. Sections 3 and 4 describe the system model and problem formulation, respectively. Section 5 elaborates on the working principle of DRJOA to solve the optimal resource allocation and computation offloading problems. Finally, the experimental results are analyzed in Sect. 6, and conclusions are provided in Sect. 7.

2 Related work

In MEC networks, jointly optimizing computation offloading decisions and resource allocation have been extensively studied in academia and industry [14]. Many related studies [12, 13, 22, 23, 26, 27] have defined it as an MINP problem. For example, [26] presents a branch-and-bound method based on a reconstruction linearization technique to obtain optimal or suboptimal results by setting the accuracy of the solution. Considering that the complexity of this method was not guaranteed, the authors further designed a greedy heuristic algorithm to solve the MINP problem by reducing it into a convex problem. In [12], the authors decomposed the original MINP problem in a single-cell multi-user scenario into a resource allocation subproblem and a task offloading decision subproblem. The closed-form solution of the resource allocation subproblem was obtained via convex and quasi-convex optimization techniques, transforming the MINP problem into an integer programming problem; the offloading solution was obtained via a heuristic algorithm. In [13], the authors studied a joint optimization problem of resource allocation and computational offloading in a multi-cell multi-user system and solved the problem using a heuristic algorithm. In [27], the authors focused on optimizing the offloading decisions of all users, computing access points, and communication and computation resource allocation to minimize the weighted sum of energy costs, computation, and maximum delay among all users. They proposed a heuristic algorithm based on semi-definite relaxation and a novel randomization mapping method to solve the problem. However, applying these algorithms to real-time MEC systems still faces many challenges. The primary reason is that MEC systems are highly real-time systems wherein the channel changes rapidly. The heuristic algorithms mentioned above require numerous iterations to obtain the local optimum; thus, they do not meet real-time requirements.

To solve this problem, we introduce the DRL algorithm in the MEC system, which can use DNNs to learn the best mapping of state space to action space. At present, studies have been conducted on computation offloading methods based on DRL in MEC systems [28,29,30,31,32,33]. In order to minimize the overall cost in terms of time and energy for all users, a scheme based on Deep Q-Networks (DQN) is proposed in [28] to optimize computation offloading and resource allocation jointly. Without prior knowledge of the network dynamics, [29] presents a computation offloading algorithm based on a dual DQN that learns the optimal strategy. To address the problem of DQN-based methods for selecting actions by exhaustive search, [30] proposed a new DRL framework that maximizes the weighted sum of computation rates in wirelessly powered MEC networks. Specifically, in each iteration, only a tiny fraction of candidate offloading actions are considered in [30], leading to near-optimal offloading actions. Based on the advantages and disadvantages of the prior studies, the current work considers a DRL-based scheme with an action space that contains just a limited quantity of offloading decisions to solve the joint optimization problem of computation offloading and wireless and computational resource allocation in single-cell MEC networks.

3 System model

In this section, we introduce the system model. For easy reading and understanding, some notations frequently used in this paper and their corresponding descriptions are listed in Table 1.

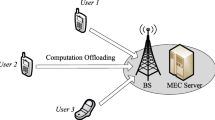
Table 1 Description of Key Notations
Full size table

We consider a single-cell MEC system, as shown in Fig. 1. The system is composed of a base station s and multiple mobile users \({\mathcal {N}}=\{1,\ldots ,N\}\), and users communicate with the base station through wireless channels. The base station is equipped with an edge server, which uses its powerful computing resources to provide computing services to mobile users. Mobile devices have different computing capabilities due to various limitations, such as physical size, battery capacity, and functionality. Each mobile device is assumed to have computational tasks that must be processed, and these tasks can be handled locally by the device or offloaded to the edge server.

Fig. 1
figure 1

A single-cell multi-user MEC system

Full size image

3.1 Task model

We assume that each user \(D_i\) has a computationally intensive task \({\mathcal {J}}_{i} \triangleq \left( d_{i}, w_{i}\right)\) to be processed. Here, \(d_{i}\) is the size of the input data of task \({\mathcal {J}}_{i}\), and \(w_{i}\) indicates the number of CPU cycles required to complete the task. Information about \(d_{i}\) and \(w_{i}\) can be obtained using the program analysis methods presented in [34, 35].

Tasks are supposed to be indivisible and cannot be decomposed into multiple subtasks. When user \(D_i\) has a task to perform, it first sends a message to the base station containing information about that task. Then, it waits for an offloading decision from the base station. There are two offloading decisions in total, one is offloading to the edge server, and the other is local processing. Due to their varying computing capabilities, the energy and time required to process the same task differ between mobile devices and the edge server. The base station considers the computation task requirements of all users and ultimately determines the offloading policies for all users. The offloading decision of user \(D_i\) is denoted as \(a_{i} \in \{0,1\}\). If the base station determines that the computational tasks of user \(D_i\) are processed locally at the user’s device, then \(a_{i}=0\); conversely, \(a_{i}=1\).

3.2 Communication model

The base station s manages users’ uplink and downlink communications in the network. Mobile devices are assumed to access the network via orthogonal frequency division multiplexing. The channel is divided into several orthogonal sub-channels for communication between a mobile device and the base station s. Various devices occupy different communication sub-channels for their respective transmission to eliminate intra-cell interference [36]. If the offloading decision of user \(D_i\) is \(a_{i}=1\), then the uplink rate \(r_{i}\left( p_{i}\right)\) at which user \(D_i\) transmits data at power \(p_{i}\) can be expressed as

$$\begin{aligned} r_{i}\left( p_{i}\right) =B \log _{2}\left( 1+\frac{p_{i} g_{i}}{B N_{0}}\right) , \end{aligned}$$
(1)

where B is the bandwidth for each orthogonal sub-channel, \(g_i\) represents the wireless channel gain of user \(D_i\), and \(N_{0}\) denotes the Gaussian noise power spectral density at the receiver of base station s. The total system bandwidth is W. Therefore, the total number of mobile users in the network that can simultaneously access base station s cannot exceed \(M=\lfloor W/B \rfloor\). In accordance with (1), mobile user \(D_i\) can change the uplink transmission rate \(r_{i}\left( p_{i}\right)\) by adjusting its upload power \(p_{i}\). Assuming that the maximum value of the upload power \(p_{i}\) is \(p_\text {max}\), the uplink transmission rate \(r_{i}\left( p_{i}\right)\) varies within the range of \((0,B \log _{2}\left( 1+{p_\text {max}g_{i}}/{B N_{0}}\right) ]\).

3.3 Computation model

This section analyzes the computational overhead of completing a task using both local and edge computing approaches. The computational overhead is mainly related to the time and energy consumed to complete the task.

3.3.1 Local computing

For the local computing method, mobile user \(D_i\) processes its task \({\mathcal {J}}_{i}\) by using its computational resources. Let \(c_i^{l}\) be the local computation capability of mobile user \(D_i\). Then, the time required to process the task locally for user \(D_i\) is

$$\begin{aligned} t_{i}^{l}=\frac{w_{i}}{c_{i}^{l}}. \end{aligned}$$
(2)

The energy consumption of user \(D_i\) is

$$\begin{aligned} e_{i}^{l}=\varepsilon _{i} w_{i}, \end{aligned}$$
(3)

where \(\varepsilon _{i}\) is the energy consumption factor that represents the energy consumed per CPU cycle. In accordance with [37, 38], \(\varepsilon _{i}\) is a superlinear function of computation capability and denoted as

$$\begin{aligned} \varepsilon _{i}=z \cdot \left( c_{i}^{l}\right) ^{\beta }, \end{aligned}$$
(4)

where z denotes the parameter related to the device chip architecture, and \(\beta\) is typically set to 2.

3.3.2 Edge computing

The tasks are processed on the edge servers for the edge computing method. The complete offloading process consists of the following three parts.

  • Device \(D_i\) sends task-related data to the base station over a wireless channel. Then, the base station forwards this information to the edge server.

  • The edge server allocates appropriate computation resources to execute the task.

  • After the task is processed, the output is returned to device \(D_i\).

Similar to [12, 39], for many applications (e.g., face recognition), the output data size of the task is much smaller than the input data size, so we ignore the overhead incurred by transmitting the output data back to the user.

The transmission time \(t_{i}^{e s, t}\left( p_{i}\right)\) and energy consumption \(e_{i}^{e s}\left( p_{i}\right)\) of user \(D_i\) for offloading input data \(d_{i}\) to the edge server can be computed as

$$\begin{aligned} t_{i}^\text {es,t}\left( p_{i}\right) =\frac{d_{i}}{r_{i}\left( p_{i}\right) }=\frac{d_{i}}{B \log _{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) } \end{aligned}$$
(5)

and

$$\begin{aligned} \begin{aligned} e_{i}^{e s}\left( p_{i}\right) =&p_{i} \cdot t_{i}^\text {es,t}\left( p_{i}\right) =p_{i} \cdot \frac{d_{i}}{r_{i}\left( p_{i}\right) }\\=&p_{i} \cdot \frac{d_{i}}{B{\text {log}}_{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) }. \end{aligned} \end{aligned}$$
(6)

After the task \({\mathcal {J}}_{i}\) of device \(D_i\) is offloaded to the edge server, the edge server will handle this task. Let \(c_{s}\) represent the computational capacity of the edge server and \(\rho _{i}\) be a percentage indicating the computational resources assigned to task \({\mathcal {J}}_{i}\) by edge server s. The processing time \(t_{i}^{e s, e}\left( \rho _{i}\right)\) for task \({\mathcal {J}}_{i}\) of device \(D_i\) by edge computing is given by:

$$\begin{aligned} t_{i}^\text {es,e}\left( \rho _{i}\right) =\frac{w_{i}}{\rho _{i} c_{s}}. \end{aligned}$$
(7)

Hence, the total time overhead \(t_{i}^{e s}\left( p_{i}, \rho _{i}\right)\) of processing task \({\mathcal {J}}_{i}\) using edge computing method consists of transmission time and edge processing time, which can be expressed as

$$\begin{aligned} \begin{aligned} t_{i}^{es}\left( p_{i}, \rho _{i}\right) =&t_{i}^\text {es,t}\left( p_{i}\right) +t_{i}^\text {es,e}\left( \rho _{i}\right) \\=&\frac{d_{i}}{{\text {Blog}}_{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) }+\frac{w_{i}}{\rho _{i} c_{s}}. \end{aligned} \end{aligned}$$
(8)

4 Problem formulation

In an MEC system, regardless of whether the task is processed locally (\(a_{i}=0\)) or at the edge server (\(a_{i}=1\)), the execution delay of task \({\mathcal {J}}_{i}\) can be written as

$$\begin{aligned} \begin{aligned} t_{i}=&\left( 1-a_{i}\right) t_{i}^{l}+a_{i} t_{i}^{e s}\\=&\left( 1-a_{i}\right) \frac{w_{i}}{c_{i}^{l}}+a_{i}\left( \frac{d_{i}}{r_{i}\left( p_{i}\right) }+\frac{w_{i}}{\rho _{i} c_{s}}\right) . \end{aligned} \end{aligned}$$
(9)

Similarly, the energy consumption for task \({\mathcal {J}}_{i}\) can be expressed as

$$\begin{aligned} \begin{aligned} e_{i}=&\left( 1-a_{i}\right) e_{i}^{l}+a_{i} e_{i}^{e s}\\=&\left( 1-a_{i}\right) \varepsilon _{i} w_{i}+a_{i} p_{i} \cdot \frac{d_{i}}{r_{i}\left( p_{i}\right) }. \end{aligned} \end{aligned}$$
(10)

We define the utility of user \(D_i\), \(u_{i}\left( a_{i}, p_{i}, \rho _{i}\right)\) as

$$\begin{aligned} \begin{aligned} u_{i}\left( a_{i}, p_{i}, \rho _{i}\right) =&\lambda _{i}^{t} \frac{t_{i}^{l}-t_{i}}{t_{i}^{l}}+\lambda _{i}^{e} \frac{e_{i}^{l}-e_{i}}{e_{i}^{l}}\\=&a_{i}\left( \lambda _{i}^{t} \frac{t_{i}^{l}-t_{i}^{es}}{t_{i}^{l}}+\lambda _{i}^{e}\frac{e_{i}^{l}-e_{i}^{e s}}{e_{i}^{l}}\right) , \end{aligned} \end{aligned}$$
(11)

where \(\lambda _{i}^{e} \in [0,1]\) and \(\lambda _{i}^{t} \in [0,1]\) denote mobile device user \(D_i\)’s preferences for energy consumption and computation time, respectively. Considering that the time and energy metrics differ, we need to perform a normalization operation. Furthermore, since we need to compare the performance of local and edge computing, we use \({(t_{i}^{l}-t_{i})}/{t_{i}^{l}}\) and \(({e_{i}^{l}-e_{i}})/{e_{i}^{l}}\) to eliminate the effect of different metrics. \({(t_{i}^{l}-t_{i})}/{t_{i}^{l}}\) and \(({e_{i}^{l}-e_{i}})/{e_{i}^{l}}\) represent the performance improvement in the time and energy consumption of task \({\mathcal {J}}_{i}\) executed via edge computing compared with that by local computing. The higher the utility function of mobile device user \(D_i\) is, the lower the cost of completing task \({\mathcal {J}}_{i}\) is; moreover, the better service user \(D_i\) receives from the MEC system. To analyze the computing services provided by the system to all mobile device users, we define the system utility as

$$\begin{aligned} \begin{aligned} R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })=&\sum _{i=1}^{N} \kappa _{i} u_{i}\left( a_{i}, p_{i}, \rho _{i}\right) \\=&\sum _{i=1}^{N} \kappa _{i} a_{i}\left( \lambda _{i}^{t} \frac{t_{i}^{l}-t_{i}^{e s}}{t_{i}^{l}}+\lambda _{i}^{e} \frac{e_{i}^{l}-e_{i}^{e s}}{e_{i}^{l}}\right) , \end{aligned} \end{aligned}$$
(12)

where \(\kappa _{i}\) denotes the system preference for mobile device user \(D_i\). \(\kappa _{i}\) can be set based on user type and the urgency of the computing task (e.g., tasks of first responders and police officers should be set higher priority with a high \(\kappa _{i}\)). In addition, \(\kappa _{i}\) is related to the price users pay for computing services.

All users’ offloading decisions and allocating communication and computational resources to the users for the MEC system are defined as a joint optimization problem. The optimization goal is to maximize the system utility so that the computing resources of the edge server can be fully utilized. Taking the constraints of offloading decision, transmission power, server computing capability, and wireless channel into consideration, we formulate this optimization problem as follows:

$$\begin{aligned} \begin{aligned}&\mathop {\text {max}}\limits _{{\varvec{a}}, {\mathbf {p}}, \varvec{\rho }} \quad R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t. &{}C_{1}&{}: a_{i}\in \{0,1\}, \forall i\in {\mathcal {N}},\\ &{}C_{2}&{}: 0<p_{i} \le p_{\max },\forall i \in {\mathcal {N}}_{s},\\ &{}C_{3}&{}: \rho _{i}>0, \forall i \in {\mathcal {N}}_{s},\\ &{}C_{4}&{}: \sum _{i \in {\mathcal {N}}_{s}} \rho _{i} \le 1,\\ &{}C_{5}&{}: \sum _{i \in {\mathcal {N}}} a_{i} \le M, \end{array} \end{aligned} \end{aligned}$$
(13)

where \({\varvec{a}}\), \({\mathbf {p}}\), and \(\varvec{\rho }\) denote the computation offloading decision vector, transmission power vector, and resource allocation percentage vector of all users, respectively. \({\mathcal {N}}_{s}\) is the set of users who choose edge computing.

Constraint \(C_{1}\) states that each user can choose only one between local computing or edge computing. Constraint \(C_{2}\) specifies the valid transmission power range for each user. Constraint \(C_{3}\) ensures that the edge server must allocate computing resources to the users who choose edge computing. Constraint \(C_{4}\) ensures that the total computing resources provided by the edge server to the users who choose edge computing cannot exceed its maximum available computing resources. Constraint \(C_{5}\) guarantees that the total number of users choosing edge computing simultaneously cannot be larger than the maximum number of subchannels M.

5 DRL-based approach: DRJOA

Since there are three variables that need to be determined in Problem (13) defined above, namely, \({\varvec{a}}\), \({\mathbf {p}}\) and \(\varvec{\rho }\), where \({\varvec{a}}\) is a binary vector, \({\mathbf {p}}\) and \(\varvec{\rho }\) are continuous vectors. Besides, the objective function \(R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) in (13) is nonlinear. Therefore, Problem (13) is a MINP problem, which is NP-hard. It is known that there is no efficient way to solve NP-hard problems. To solve Problem (13), we first rewrite Problem (13) as P:

$$\begin{aligned} \begin{aligned} P:&\mathop {\text {max}}\limits _{{\varvec{a}}}\mathop {\text {max}}\limits _{{\varvec{p}},\varvec{\rho }} R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{1},C_{2},C_{3},C_{4}, \text{ and } C_{5}. \end{array} \end{aligned} \end{aligned}$$
(14)

Suppose that offloading decision \({\varvec{a}}\) is fixed, Problem P can be rewritten as:

$$\begin{aligned} \begin{aligned} P_1:&\mathop {\text {max}}\limits _{{\varvec{p}},\varvec{\rho }} R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{2},C_{3}, \text{ and } C_{4}. \end{array} \end{aligned} \end{aligned}$$
(15)

Hence, we decompose Problem P into two subproblems.

  1. 1.

    Optimal resource allocation subproblem. This subproblem is Subproblem \(P_1\), which involves optimization variables \({\mathbf {p}}\) and \(\varvec{\rho }\) and can be solved by convex and quasiconvex optimization methods [12].

  2. 2.

    Computation offloading subproblem. The computational offloading subproblem is a combinatorial optimization problem. Due to the fast-changing wireless channel, a fast policy response is required, and the traditional numerical optimization methods are difficult to achieve online offloading decisions. Thus, we use a DRL-based method to address the online optimization problem of computation offloading.

5.1 Optimal resource allocation subproblem

Substituting (12) into (15), the objective function of \(P_1\) can be written as

$$\begin{aligned} \mathop {\text {max}}\limits _{{\varvec{p}},\varvec{\rho }} \sum _{i \in {\mathcal {N}}_{s}} \kappa _{i}\left( \lambda _{i}^{t}+\lambda _{i}^{e}\right) -\sum _{i \in {\mathcal {N}}_{s}} \kappa _{i}\left( \lambda _{i}^{t} t_{i}^{e s} / t_{i}^{l}+\lambda _{i}^{e} e_{i}^{e s} / e_{i}^{l}\right) . \end{aligned}$$
(16)

The first term of (16) is constant for a particular offloading decision and independent of the resource allocation variables \({\mathbf {p}}\) and \(\mathbf {\rho }\). Therefore, we can transform objective function (16) into  \(\mathop {\text {min}}\limits _{{\varvec{p}},\varvec{\rho }} \sum _{i \in {\mathcal {N}}_{s}} \kappa _{i}\left( \lambda _{i}^{t} t_{i}^{e s} / t_{i}^{l}+\lambda _{i}^{e} e_{i}^{e s} / e_{i}^{l}\right)\) .

Based on the above analysis and (1)-(8), we can transform Problem P1 into its equivalent problem as follows:

$$\begin{aligned} \begin{aligned} P_{1}^{'}:&\mathop {\text {min}}\limits _{{\mathbf {p}}, \varvec{\rho }} \quad \sum _{i \in {\mathcal {N}}_{S}} \frac{\varphi _{i} c_{i}^{l}}{\rho _{i}}+\frac{\delta _{i}+\xi _{i} p_{i}}{\log _{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) }\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{2},C_{3}, \text{ and } C_{4}, \end{array} \end{aligned} \end{aligned}$$
(17)

where \(\varphi _{i}=\kappa _{i} \lambda _{i}^{t} / c_{s}\), \(\delta _{i}=\kappa _{i} \lambda _{i}^{t} d_{i} /\left( B t_{i}^{l}\right)\), and \(\xi _{i}=\kappa _{i} \lambda _{i}^{e} d_{i} /\left( B e_{i}^{l}\right)\). Following Problem \(P_{1}^{'}\), we notice that the power assignment \(p_i\) and computational resource allocation \(\rho _i\) are mutually independent in terms of both the objective function and the constraints. We transform the original Problem \(P_{1}^{'}\) into two subproblems: optimal computational resource allocation and transmission power allocation. In the following, we solve these two subproblems separately.

5.1.1 Computational resource allocation

Using the first term of the objective function in (17) as the new objective function, the computational resource allocation problem is decoupled from Problem \(P_{1}^{'}\) and can be expressed as:

$$\begin{aligned} \begin{aligned} P_{2}:&\mathop {\text {min}}\limits _{\varvec{\rho }} \quad \sum _{i \in {\mathcal {N}}_{S}} \frac{\varphi _{i} c_{i}^{l}}{\rho _{i}}\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{3} \text{ and } C_{4}. \end{array} \end{aligned} \end{aligned}$$
(18)

Let \(f(\varvec{\rho })=\sum _{i \in {\mathcal {N}}_{S}} {\varphi _{i} c_{i}^{l}}/{\rho _{i}}\). Each term in the Hessian matrix of \(f(\varvec{\rho })\) can be written as

$$\begin{aligned} \frac{\partial ^{2} f}{\partial \rho _{i} \partial \rho _{j}}=\left\{ \begin{array}{ll} 2 \varphi _{i} c_{i}^{l}/\rho _{i}^{3}, & \quad \text{ if } i=j, \\ 0, & \quad \text{ otherwise } . \end{array}\right. \end{aligned}$$
(19)

From (19), we observe that all the diagonal elements of the Hessian matrix are positive, and the other elements are zero. Thus, the Hessian matrix of \(f(\varvec{\rho })\) is positive definite. In addition, the domain of \(f(\varvec{\rho })\) is convex. Therefore, \(f(\varvec{\rho })\) is a convex function.

Problem \(P_2\) can be addressed by applying Lagrange multiplier approaches. We define the Lagrange function \(L(\varvec{\rho }, \mu , \tau )\) related to Problem \(P_2\) as

$$\begin{aligned} L(\varvec{\rho }, \mu , \tau )=\sum _{i \in {\mathcal {N}}_{S}} \frac{\varphi _{i} c_{i}^{l}}{\rho _{i}}+\mu \left( \sum _{i \in {\mathcal {N}}_{S}} \rho _{i}-1\right) -\sum _{i \in {\mathcal {N}}_{S}} \rho _{i} \tau _{i}, \end{aligned}$$
(20)

where \(\mu\) and \(\tau _{i}\) are the Lagrange multipliers for Constraints \(C_4\) and \(C_3\). Based on the Karush-Kuhn-Tucker conditions, the optimal \(\rho _{i}^{*}\), \(\mu ^{*}\), and \(\tau _{i}^{*}\) need to satisfy the conditions below:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial L}{\partial \rho _{i}^{*}}=-\frac{\varphi _{i} c_{i}^{l}}{\rho _{i}^{*}{ }^{2}}+\mu ^{*}-\tau _{i}^{*}=0, \forall i \in {\mathcal {N}}_{S}; \\ \mu ^{*}\left( \sum _{i \in {\mathcal {N}}_{s}} \rho _{i}^{*}-1\right) =0; \\ \rho _{i}^{*} \tau _{i}^{*}=0, i \in {\mathcal {N}}_{S}; \\ \tau _{i}^{*} \ge 0, \rho _{i}^{*}>0, i \in {\mathcal {N}}_{S} ; \mu \ge 0, \end{array}\right. \end{aligned}$$
(21)

By solving (21), we derive an optimal \(\rho _{i}^{*}\) in closed form, and it is formulated as

$$\begin{aligned} \rho _{i}^{*}=\frac{\sqrt{\varphi _{i} c_{i}^{l}}}{\sum _{i \in {\mathcal {N}}_{s}} \sqrt{\varphi _{i} c_{i}}^{l}}. \end{aligned}$$
(22)

5.1.2 Transmission power allocation

The transmission power allocation problem is defined by

$$\begin{aligned} \begin{aligned} P_{3}:&\mathop {\text {min}}\limits _{{\mathbf {p}}} \quad \sum _{i \in {\mathcal {N}}_{s}} \frac{\delta _{i}+\xi _{i} p_{i}}{\log _{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) } \\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{2}&:0<p_{i} \le p_{\max },\forall i \in {\mathcal {N}}_{S}. \end{array} \end{aligned} \end{aligned}$$
(23)

Each term in the objective function of Problem \(P_3\) (i.e., \(\frac{\delta _{i}+\xi _{i} p_{i}}{\log _{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) }\)) is positive and independent of one another. Thus, Problem \(P_3\) can be transformed into a set of Problem \(P_4\), which is defined as follows:

$$\begin{aligned} \begin{aligned} P_{4}:&\mathop {\text {min}}\limits _{p_{i}} \quad \frac{\delta _{i}+\xi _{i} p_{i}}{\log _{2}\left( 1+{p_{i} g_{i}}/{B N_{0}}\right) } \\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{2}&:0<p_{i} \le p_{\max },\forall i \in {\mathcal {N}}_{S}. \end{array} \end{aligned} \end{aligned}$$
(24)

Problem \(P_4\) is quasi-convex and can be addressed utilizing a bisection method [12].

5.2 Computation offloading subproblem

Based on the analysis in the previous sections, we know that given an offloading decision \({\varvec{a}}\), the optimal uplink power \({\mathbf {p}}^{*}\) and computational resource allocation \(\varvec{\rho }^{*}\) can be obtained. We also get the optimal system utility with respect to the offloading decision \({\varvec{a}}\), denoted as

$$\begin{aligned} \begin{aligned} {\mathcal {F}}^{*}({\varvec{a}})=&\mathop {\text {max}}\limits _{{\varvec{p}},\varvec{\rho }} R({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\\=&\sum _{i \in {\mathcal {N}}_{s}} \kappa _{i}\left( \lambda _{i}^{t}+\lambda _{i}^{e}\right) -h(\varvec{\rho }^{*})-\sum _{i \in {\mathcal {N}}_{s}}g(p_{i}^{*}), \end{aligned} \end{aligned}$$
(25)

where \(h(\varvec{\rho }^{*})=\sum _{i \in {\mathcal {N}}_{S}} \frac{\varphi _{i} c_{i}^{l}}{\rho _{i}^{*}}\) can be calculated by substituting (22) into (18), and \(g(p_{i}^{*})=\frac{\delta _{i}+\xi _{i} p_{i}^{*}}{\log _{2}\left( 1+{p_{i}^{*} g_{i}}/{B N_{0}}\right) }\). Subsequently, we need to search for the optimal computation offloading decision via solving the following problem:

$$\begin{aligned} \begin{aligned}&\mathop {\text {max}}\limits _{{\varvec{a}}}\sum _{i \in {\mathcal {N}}_{s}} \kappa _{i}\left( \lambda _{i}^{t}+\lambda _{i}^{e}\right) -h(\varvec{\rho }^{*})-\sum _{i \in {\mathcal {N}}_{s}}g(p_{i}^{*})\\&\begin{array}{r@{\quad }r@{}l@{\quad }l} s.t.&C_{1}, \text{ and } C_{5}. \end{array} \end{aligned} \end{aligned}$$
(26)

Problem (26) is a combinatorial optimization problem. We use a DRL-based method to solve Problem (26) to obtain real-time offloading decisions.

Combined with the above analysis on the resource allocation subproblem, we propose a DRL-based online offloading optimization framework called DRJOA, as shown in Fig. 2. In the framework, DRJOA comprises four modules: DNN, KNN, offloading decision selection (ODS), and data caching module. The proposed DRJOA aims to approximate a function h that yields an output \(\{{\varvec{a}}^{*},{\varvec{p}}^{*},\varvec{\rho }^{*}\}\) when the system takes the channel gain \({\varvec{g}}\) as the input. System utility \(R^{*}({\varvec{a}}^{*}, {\mathbf {p}}^{*}, \varvec{\rho }^{*})\) acts as the reward. For simplicity, function h can be given by:

$$\begin{aligned} h: {\varvec{g}} \mapsto {\varvec{a}}^{*}. \end{aligned}$$
(27)
Fig. 2
figure 2

DRJOA framework

Full size image

In the following, we will introduce the DNN, KNN, ODS, and data caching modules.

5.2.1 DNN module

DNN has a powerful feature representation capability. Taking advantage of this feature, DRJOA adopts DNN to adapt to offloading decisions. DNN in DRJOA is used to generate an N-dimensional vector \({\varvec{a}}_{c}^{'}\), which can be represented by function \(h_1\), as follows:

$$\begin{aligned} h_1: {\varvec{g}} \mapsto {\varvec{a}}_{c}^{'}. \end{aligned}$$
(28)

The input of this DNN is a vector \({\varvec{g}}\) composed of the channel gains of N users, and its output is an N-dimensional vector \({\varvec{a}}_{c}^{'}\). Besides, there are also two hidden layers in the DNN module. Therefore, the number of both input and output neurons is N. For the two hidden layers, the number of neurons is specified as 120 and 80, and the rectified linear unit (ReLU) is employed as the activation function, wherein the relationship between the output y of a neuron and its input x is \(y=\max \{x,0\}\). For the output layer, we use the sigmoid function \(y=1 /\left( 1+e^{-x}\right)\) as the activation function, such that each element \({a_{c,i}}^{'}\) in the output vector \({\varvec{a}}_{c}^{'}\) satisfies \({a_{c,i}}^{'}\in (0,1)\).

5.2.2 KNN module

We use the KNN method to transform \({\varvec{a}}_{c}^{'}\) into K binary offloading decisions. The function of the KNN module can be represented in mathematical terms as

$$\begin{aligned} h_2: {\varvec{a}}_{c}^{'} \mapsto \left\{ {\varvec{a}}_{k} \mid {\varvec{a}}_{k} \in \{0,1\}^{N}, k=1, \cdots , K\right\} , \end{aligned}$$
(29)

where K is an integer within the interval \([1,2^N]\). With larger K, the higher the computational complexity of the DRJOA algorithm, the closer the solution is to the optimal one, and vice versa. Here, we set the value of K to N.

In DRJOA, KNN selects K nearest binary vectors to vector \({\varvec{a}}_{c}^{'}\) by calculating the distance between \({\varvec{a}}_{c}^{'}\) and each binary vector from the \(2^N\) N-dimensional binary vectors. A simple example is provided below to help understand how the KNN module works. Assume that \({\varvec{a}}_{c}^{'} = [0.1,0.2,0.3,0.4]\) and \(K = 4\). The distance between binary vectors [0, 0, 0, 0], [0, 0, 0, 1], ..., [1, 1, 1, 1] and vector \({\varvec{a}}_{c}^{'}\) (\({\varvec{a}}_{c}^{'} = [0.1,0.2,0.3,0.4]\)) is computed. The distances are 0.5477, 0.7071, 0.8367, 0.9487, 0.9487, 1.0488, 1.1402, 1.2247, 1.0488, 1.1402, 1.2247, 1.3038, 1.3038, 1.3784, 1.4491, and 1.5166. Therefore, the four nearest vectors to vector \({\varvec{a}}_{c}^{'}\) are \({\varvec{a}}_{1}=[0,0,0,0]\), \({\varvec{a}}_{2}=[0,0,0,1]\), \({\varvec{a}}_{3}=[0,0,1,0]\), and \({\varvec{a}}_{4}=[0,0,1,1]\).

5.2.3 ODS module

In the ODS module, the optimal resource allocation \({\mathbf {p}}\), \(\varvec{\rho }\) for each offloading decision is analyzed in detail above, and the corresponding reward \(R^{*}({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) can be computed. Then, the offloading decision that corresponds to the maximum value from these rewards is selected as the optimal offloading decision \({\varvec{a}}^{*}\) when the input is \({\mathbf {g}}\), that is, \({\varvec{a}}^{*}={\text {argmax}}R({\varvec{a}}_{k},{\mathbf {p}}^{*},\varvec{\rho }^{*})\). Finally, the optimal offloading decision \({\varvec{a}}^{*}\) and the corresponding resource allocation policies \({\mathbf {p}}^{*}\), \(\varvec{\rho }^{*}\) obtained via the ODS module constitute the output of the system. The optimal resource allocation scheme is described in detail in Sect. 5.1.

5.2.4 Data caching module

The data is collected to train the DNN module to enable DRJOA to make better offloading decisions. The network stores the input \({\mathbf {g}}\) and the output offloading decision \({\varvec{a}}^{*}\) for each time slot t as data samples in the data memory. Suppose the data memory size is L. If the memory is complete, the freshly obtained state-action pair \(\{{\mathbf {g}},{\varvec{a}}^{*}\}\) will be added to replace the oldest stored data. A batch of data is used to train the DNN by extracting data from the data storage every \(\Delta\) time slot. During the training process, we use the Adam algorithm [40] to update the parameters of the DNN to decrease the average cross-entropy loss, as

$$\begin{aligned} \begin{aligned}&L\left( \theta _{t}\right) = \\&\quad -\frac{1}{\left| {\mathcal {S}}_{t}\right| } \sum _{\tau \in {\mathcal {S}}_{t}}\left( \left( {\mathbf {a}}_{\tau }^{*}\right) ^{\top } \log f_{\theta _{t}}\left( {\mathbf {g}}_{\tau }\right) +\left( 1-{\mathbf {a}}_{\tau }^{*}\right) ^{\top } \log \left( 1-f_{\theta _{t}}\left( {\mathbf {g}}_{\tau }\right) \right) \right) , \end{aligned} \end{aligned}$$

where \({\mathcal {S}}_{t}\) is the training data set extracted from the data storage, and \(\left| {\mathcal {S}}_{t}\right|\) is the number of samples in the set. The Adam algorithm is an improved type of gradient descent method that adaptively adjusts the learning rate of gradient descent. Thus, it can converge more efficiently and avoids manual adjustment of the learning rate.

The proposed DRJOA algorithm is provided in Algorithm 1. Initially, the parameters \(\theta _{1}\) in the DNN are set randomly, and the data memory is empty. Then, the algorithm goes through the KNN, ODS, and data caching modules. The DNN parameters are continuously improved through learning, thus improving the offloading strategy.

figure f

6 Simulations

In this section, to analyze the performance of DRJOA, we compare DRJOA with the following benchmark schemes.

\(\bullet\) Local computing (LC): The tasks of all mobile device users are processed locally on their own devices.

\(\bullet\) Enumeration (Enum): We enumerate all task offloading policies to find the global optimal solution.

\(\bullet\) All edge computing (AEC): The offload decisions for all users are \(a_{i}=1, \forall i\in {\mathcal {N}}\). However, considering the limited bandwidth of the system, users who do not have acquired bandwidth resources can only handle their tasks on their devices.

\(\bullet\) Random computing (RC): Offloading decisions are made randomly.

6.1 Experiment setup

All simulation experiments are performed in a network with a hexagonal region whose side length is 288 m. In the center of the region, there is a base station equipped with an edge server. Users are randomly distributed in the network. For wireless communication, the system bandwidth is assumed to be \(W=8\) MHz, and user bandwidth is set to \(B=1\) MHz. As a result, at most eight users are allowed to send data simultaneously. According to the wireless channel interference model in [41], the channel gain is \(g_i=d_{i,s}^{-\alpha }\), where \(d_{i,s}\) denotes the distance between user \(D_i\) and base station s, and \(\alpha\) denotes the path loss exponent. During the simulation, we consider face detection and recognition as tasks. The size of the input data is \(d_i=420\) KB. The total amount of CPU cycles required to process this computational task is \(w_i=1000\) MCycles. The parameters employed in the simulation are summarized, as shown in Table 2.

Table 2 Simulation data parameter
Full size table

The proposed DRJOA algorithm is implemented in python based on TensorFlow. In the DRJOA algorithm, we use a fully connected DNN with one input layer, two hidden layers, and one output layer, where the number of neurons in two hidden layers is 120 and 80, respectively. We set the training interval to 10, the batch size of training data to 128, the size of data memory L = 1024, and the learning rate of the Adam optimizer to 0.01.

6.2 Convergence performance

We assume that the system time is divided into several consecutive time frames of equal length, which are set to be less than the channel coherence time. Also, the channel is assumed to remain unchanged within a time frame but may differ in different time frames. Figure 3 shows the variation of the training loss with the time frame for the DRJOA algorithm. The DRJOA algorithm has a much higher training loss in the initial training phase than in the later training phase. In order to be able to show the variation of training loss in one figure, we replace the training loss greater than 1 with 1 in the plotting process. During the initial phase of training, the training loss fluctuates significantly. As the number of iterations increases, the training loss gradually decreases. Consequently, the training loss curve tends to be smooth, and the model converges to the optimal offloading strategy.

Fig. 3
figure 3

Training loss of the DRJOA algorithm varies with the time frame

Full size image
Fig. 4
figure 4

Normalized utility vs. time frame

Full size image

Figure 4 shows how the normalized utility changes as the time frame increases. The normalized utility \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) is defined as

$$\begin{aligned} {R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })=\frac{R^{*}({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })}{\max _{{\varvec{a}}^{\prime } \in \{0,1\}^{N}} R^{*}\left( {\varvec{a}}^{\prime }, {\mathbf {p}}, \varvec{\rho }\right) }, \end{aligned}$$
(30)

where the denominator in (30) denotes the optimal utility obtained by finding the optimal policy by searching the entire offloading space and computing the corresponding optimal resource allocation policy, the numerator denotes the utility obtained by the DRJOA algorithm. Evidently, \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\in [0,1]\); and the larger the value of \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) is, the closer the policy obtained by the DRJOA algorithm is to the optimal one.

In Fig. 4, the blue curves indicate the average of the normalized utility \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) over the last 50 time frames, while the light blue shade indicates the maximum and minimum values of \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) over the last 50 time frames. As the time frame increases, the normalized utility \({R}_n({\varvec{a}}, {\mathbf {p}}, \varvec{\rho })\) obtained by the DRJOA algorithm gradually converges to the optimal solution.

6.3 Offloading decision

In this subsection, we evaluate the offloading decision accuracy of different algorithms through simulation experiments. Offloading decision accuracy is measured as the ratio of correctly predicted samples to the total amount of samples tested. Obviously, the higher the ratio, the more accurate the algorithm prediction is and the closer it is to the system’s best performance.

Fig. 5
figure 5

Comparison of offloading decision accuracy

Full size image

Figure 5 shows the offloading decision accuracy obtained by different offloading schemes. Accuracy varies widely among different methods. Thus, we present two different scales, as shown in Fig. 5. We observe that the left Y-axis in Fig. 5 indicates an accuracy interval from 0 to 1.1, and the right Y-axis indicates an accuracy interval from 0 to 0.005, with a minimum scale of 0.0005. The offloading policy obtained by the Enum algorithm is optimal; hence, accuracy is set to 1. The offloading decision accuracy of algorithms LC, RC, AEC, and our proposed DRJOA is 0.00, 0.0011, 0.0016, and 0.8870, respectively. The offloading decision accuracy of our proposed DRJOA algorithm outperforms those of other offloading schemes.

6.4 System utility

Figure 6 compares the average normalized utility obtained by different offloading schemes. The average normalized utility results from averaging the normalized utility obtained during the testing phase. Given that the Enum algorithm obtains the optimal utility, the average normalized utility value is set as 1. From Fig. 6, the average normalized utility obtained by algorithms LC, RC, AEC, and our proposed DRJOA are 0.00, 0.2988, 0.2479, and 0.9800, respectively. The average normalized utility of our proposed DRJOA is considerably better than those of the other methods.

Fig. 6
figure 6

Comparison of the average normalized utility obtained using different offloading schemes

Full size image

7 Conclusion

This study proposes a DRL-based online optimization approach DRJOA for computation offloading and resource allocation in single-cell networks. In particular, we first introduce the system model, which includes the task, communication, and computation models. Then, we establish the optimization problem to maximize system utility by jointly considering computation offloading and wireless and computational resource allocation. After that, we propose a DRL-based algorithm, i.e., DRJOA, to obtain a near-optimal solution rapidly for the optimization problem. In DRJOA, we use convex and quasi-convex optimization techniques to solve the wireless and computational resource allocation problem and construct a DRL method to handle the computation offloading problem. The results confirm that DRJOA outperforms other benchmark algorithms under the evaluation metrics of offloading decision accuracy and system utility. The results also demonstrate that the algorithm converges.