Weighted spatial skyline queries with distributed dominance tests

Abstract

In this paper, we study the retrieval of desired or relevant points of interest, a set of spatial skyline points, related to a set of query points to establish distance restrictions. Note that each point of interest has different importance, assigned to each of them as weight, and the weighted Euclidean distance is used. In order to efficiently handle the weighted spatial skyline queries, this research presents a novel MapReduce-based solution for the first time. The proposed method prevents the bottleneck of centrally finding the global skyline from the local skylines and reduces the dominance test by performing the necessary dominance tests in parallel. Finally, the experimental results show that the proposed method obtains significant performance improvement.

1 Introduction

Despite an increasing amount of data, the process of retrieving high-relevance information efficiently about a given query and separating irrelevant information is becoming increasingly important. The study of the problem of maximum vectors in the database context led to the proposal of several efficient algorithms for skyline queries [1]. Methods using indexing techniques [2,3,4,5,6] perform better because they can access the data through the index instead of the entire data set, although their applicability is limited due to collecting index data. Other approaches [1, 7,8,9,10,11] are more common because no specialized access structure is required to calculate the skyline set.

There are several types of skyline queries. Each of them maintains the main idea and notation of the skyline query and solves different aspects of the problem. Spatial skyline query is a novel type of skyline query that prioritizes both static and dynamic object attributes in multi-criteria decision-making applications [12]. In spatial skyline query, the distance between objects is a dynamic object attribute different from skyline query, which considers only static object attributes.

In particular, a set of data points of interest and a set of query points are the two main elements of a spatial skyline query. Query points define distance constraints on the set of points of interest. The spatial skyline query returns a subset of points of interest not spatially dominated by other points of interest.

Spatial skyline query applies to many applications such as facility location, crisis management, trips, or event planning. Take trip planning applications as an example. Spatial skyline queries help to select the desired set of hotels based on their distance from attractions of interest. Assume that some residential buildings must be evacuated because of several explosions or fires. The spatial skyline query helps to identify the first buildings to be evacuated.

The suitable hotels were selected by the traditional spatial skyline points, which only consider their distance to the query points. But this scenery is not realistic. When choosing a hotel, users also take into account several other aspects of the hotel, such as prices or opinions given by previous users. These aspects combine to obtain an attraction value to the hotel. Each hotel receives the obtained attraction value as a weight. The larger the weight associated with a hotel, the more attractive it is.

Notably, the Euclidean distance may not be able to model realistic scenery. Therefore, we assign a weight to each point of interest (for example, hotels and residential buildings) to reflect their importance. The weighted Euclidean distance is the product of the Euclidean distance and the inverse of the facility weight [13]. It is notable that the higher the weight, the smaller the weighted distance for the Euclidean distance. Although there are practical applications in spatial skyline query considering weighted Euclidean distance, it has not received much attention at present.

Note that many of the features used to solve spatial skyline query become incorrect in the weighted case [13]. For instance, the convex hull and Voronoi diagram accelerate the calculation of spatial skylines. However, they are not practical for weighted spatial skylines. Some efficient index structures [14] relying on the triangular inequality are used in spatial skylines to reduce the dominance tests. When considering weights, they are not correct. Therefore, most spatial features that reduce computation are generally not applicable to weighted spatial skylines. Consequently, we have to use strategies that require several scans of the entire data set.

The mentioned problems motivate us to use a parallel solution for weighted spatial skyline queries. An increasing number of methods have been proposed for skyline queries in parallel and distributed environments [2, 15,16,17,18,19,20,21,22,23]. There is only one parallel solution for spatial skyline queries using the MapReduce framework [24]. It uses the convex hull of the query points to define the independent regions. We know that the properties of the convex hull cannot be used for weighted spatial skyline queries. The only existing parallel solution for weighted spatial skyline queries is [13] using the GPU. It is notable that GPU hardware has limited memory, and the MapReduce scheme can efficiently handle large-scale data sets.

For the first time, this paper proposes a novel one-phase MapReduce-based solution for weighted spatial skyline queries called MR-WSS considering the weighted Euclidean distance. Our proposed method divides a MapReduce job into two phases: Phase 1: mapping data points, computing local weighted skyline points. Phase 2: verifying and reducing local weighted skyline points. As we all know, MapReduce is a divide-and-conquer model. Furthermore, obtaining a weighted spatial skyline set is not a decomposable problem. That means that the union of the results of reducers is not the final result for the weighted spatial skyline set. Hence, it is difficult to process a weighted spatial skyline query on large-scale data points in MapReduce. To address this deficiency, each reducer receives a dominatee set and several dominator sets in the second phase from mappers. Then, it verifies the data points in the dominatee set to be dominated by at least a data point in dominator sets. Finally, the results of all reducers create the final weighted spatial skyline points set.

The main contributions of this paper can be summarized as follows:

• We propose an effective one-phase MapReduce algorithm to evaluate the weighted spatial skyline queries on large data sets. To the best of our knowledge, it is possibly the first of this work.

• We introduce an adaptation of traditional methods to compute the local set of weighted spatial skyline points in the mappers for decreasing the computation overhead.

• We propose a distributed dominance test to calculate the final set of weighted spatial skyline points in the reducers.

• We theoretically and experimentally analyze our method and show the efficiency and effectiveness of our proposed algorithm.

The rest of this paper is organized as follows. Section 2 introduces related works, including the traditional skyline problems. We study the basic concepts of general spatial skyline query in Sect. 3. We also describe weighted Euclidean distance and the properties of the spatial skyline query under this distance. Section 4 presents the proposed solution based on MapReduce to handle weighted spatial skyline queries and theoretical analysis. The experimental validation of the proposed algorithm is shown in Sect. 5. Section 6 concludes this paper.

2 Related works

There are many studies on skyline computation. Skyline queries were first studied as maximal vectors and then introduced in database context [1]. Then, different algorithms were proposed to compute the skyline [5, 9, 25, 26]. Some studies solve the dimensionality problem of skyline queries due to the dimensional growth of data [27,28,29]. Some papers have introduced the dynamic skylines queries [5, 12, 30, 31]. They survey a moving point of interest that changes the distance to the candidate points. The reverse skylines queries are another research topic studying the changes in the skyline points when finding a new candidate. The approaches proposed to this problem are based on the dynamic skylines [3, 32].

As a specific case of dynamic skyline query, in [12], spatial skyline query was first proposed. Two efficient algorithms, Branch and Bound Spatial Skyline (B²S²) and Voronoi based Spatial Skyline (VS²), are introduced for the static query points. The set of data points of interest uses a data partitioning method, such as R-tree in the B²S² algorithm for indexing. This method constructs a convex hull on the query points Then, it uses the properties of the convex hull to reduce the check of all pairs of data points in the interest points and the query points. The B²S² algorithm scans space by traversing the R-tree from its root to leaves. In this algorithm, the mindist is the sum of distances between a point and the set of data points. When discovering the first spatial skyline, the R-tree expands with the node with the least mindist. Next, it performs the dominance test between the found node and all the candidates of the spatial skyline identified so far. This process continues until all intermediate nodes, including spatial skylines, have been visited. Another method, VS², generates a Voronoi diagram of the points of interest. Then, it considers the closest data points to the query points and traverses the space to access the neighborhood of the data points visited on the Voronoi diagram. Each visited data point is compared to all spatial skyline points identified earlier for the spatial dominance test. This procedure repeats until the algorithm finds all Voronoi cells involving spatial skyline points. The experiments in [12] show that the VS² algorithm performs better than the B²S² algorithm, but [33] demonstrates that the proposed VS² algorithm is not correct and accurate. The improvement algorithm identifies some spatial skyline points without a dominance test. The basic idea is that a spatial skyline point is each point of interest whose Voronoi cell intersects the interior of the convex hull of query points. Although error correction decreased the performance, it was still the best algorithm at that moment.

A faster method is represented in [34], which reduces the number of tests done. First, it reduces the query points to the set of points that constructs the smallest convex hull. Then, the algorithm selects an arbitrary query point q and sorts the set of interest points according to the increasing distance up to that point. It chooses the closest data point to q as the spatial skyline point and evaluates the remaining data points by increasing the distance to q. Furthermore, this method uses the transitivity of the dominance property to reduce the number of tests. A fast approximate algorithm is also introduced in [34] using the Voronoi diagram of points of interest and the convex hull of query points. This algorithm approximates the spatial skyline points by the points of interest whose Voronoi cell intersects the interior of the convex hull.

Notably, none of the mentioned approaches can solve the problem of the spatial skyline in parallel. It is non-trivial to extend them to a distributed and parallel system. Due to the high cost of skyline evaluation, various advanced solutions have been introduced in [2, 15,16,17,18,19,20,21,22,23] to analyze general skyline queries in distributed and parallel environments. None of the computation methods mentioned could address the spatial skyline problem. There is just a parallel method for calculating the spatial skyline introduced in [24] using the MapReduce technique. The basic idea is to define several independent regions into the search region. The spatial skyline points of each independent region do not depend on external data points. Therefore, the problem is divided into several subproblems and solved in parallel. This method consists of three MapReduce phases. The first phase partitions query points and constructs several local convex hulls in the map step. Then, it produces the global convex hull by merging the local convex hulls in the reduce step. The second phase determines the independent regions based on points of interest and the global convex hull. It calculates the pivots of the local independent region in the map step and then estimates the optimal pivot of the independent region in the reduce step. It is a point with equal distance from all convex points that can subdivide data points of the same size. The third phase selects an independent region for each point of interest in the map step. Then, it groups the points of interest by independent regions and sends them to reducers. Each reducer computes the spatial skyline points, and the global spatial skyline points are the union of the output of reducers. This method removes the repeated skyline points using an elimination algorithm. The reason is that some data points may be sent to two or more independent regions and produced duplicates into the result set.

As mentioned before, many properties such as convex hull and Voronoi diagram are not practical for calculating weighted spatial skylines. The only existent method that evaluates the spatial skyline queries under the weighted Euclidean distances is in [13]. Their authors introduce a sequential algorithm called the weighted distance sorting algorithm, WDS.

The WDS algorithm selects an arbitrary query point at first. Then, it sorts the points of interest according to their weighted distance and chooses the closest point of interest as the weighted spatial skyline query point. In the next step, the algorithm evaluates other points of interest in increasing distance order. It checks whether currently detected spatial skyline points dominate the data point. If the data point is not dominated, it is a point on the spatial skyline and added to the set of spatial skylines. Another algorithm is proposed in [13], which is called PWBF. This algorithm takes advantage of the capabilities of the GPU to accelerate the process and compute the weighted spatial skylines in parallel.

Our proposed solution targets weighted spatial skyline queries, which are different from the other skyline queries. None of the above computational algorithms except one could address the weighted spatial skyline problem. The only existing parallel solution for weighted spatial skyline queries cannot efficiently deal with large-scale data sets. Therefore, a novel MapReduce-based solution is proposed, including a parallel approach for computing the global weighted spatial skyline points from the local weighted spatial skyline points into multiple reducers.

3 Preliminaries

This section presents some fundamental concepts of general spatial skyline queries. Then, the weighted Euclidean distance is defined, and the properties of the spatial skyline queries under this distance are studied. Finally, the problem tackled in this paper is formalized which deals with the weighted spatial skyline queries. All notations used in this paper are summerized in Table 1.

Table 1 Overview of the symbols used in the paper

3.1 Skyline query

Let P be a data set in a d-dimensional space R^d. We represent a point p ∈ P as $p = \left\{ {x_{1} , x_{2} , \ldots , x_{d} } \right\}$ where $p.x_{i}$ is the value of the point on the ith dimension. Without loss of generality in this paper, assume that smaller values are preferable to larger ones in all dimensions. Given two points $p, p^{\prime} \in P$, p dominates $p^{\prime}$ ($p \prec p^{\prime}$) if and only if for every dimension $i \in \left\{ {1, \ldots , d} \right\}$, $p.x_{i} \le p^{\prime}.x_{i}$ and there is at least one dimension j such that $p.x_{j} < p^{\prime}.x_{j}$, i.e.

$$ \forall i \in \left\{ {1, \ldots , d} \right\}, p.x_{i} \le p^{\prime}.x_{i} \wedge \exists j \in \left\{ {1, \ldots , d} \right\}, p.x_{j} < p^{\prime}.x_{j} $$

(1)

A point p ∈ P is a skyline point if and only if no other point $p^{\prime} \in P$ dominates p in the data set. A skyline query retrieves the data points of P, called skyline points (S_skyline), over which no other data point dominates, i.e.

$$ S_{skyline} \left( P \right) = {\text{\{ }}p \in P{|} {\nexists } p^{\prime} \in P - \left\{ p \right\}, p^{\prime} \prec p\} $$

(2)

The skyline query returns the points in the data set that are better than other points in the data set. Based on the situation, “better” means lower or higher coordinate values.

3.2 Spatial skyline query

Assume that P is a set of n points of interest and Q is a set of m query points in a d-dimensional space. Assume $p.x_{i}$ is the value of the point in the ith dimension. The distance function d_E(p, q) computes the Euclidean distance between points p and q, and Eq. (3) represents it:

$$ d_{E} \left( {p, q} \right) = \sqrt {\mathop \sum \limits_{i = 1}^{d} \left( {p.x_{i} - q.x_{i} } \right)^{2} } $$

(3)

Given two points $p, p^{\prime} \in P$, p spatially dominates $p^{\prime}$ with respect to Q, denoted $p \prec_{Q} p^{\prime}$, if and only if $d_{E} \left( {p, q} \right) \le d_{E} \left( {p^{\prime}, q} \right)$ for every $q \in Q$ and there is at least one query point $q^{\prime} \in Q$ such that $d_{E} \left( {p,q^{\prime}} \right) < d_{E} \left( {p^{\prime},q^{^{\prime}} } \right)$, i.e.

$$ \begin{aligned} &p \prec_{Q} p^{\prime} \Leftrightarrow \forall q \in Q, d_{E} \left( {p, q} \right) \le d_{E} \left( {p^{\prime}, q} \right) \wedge \exists q^{\prime} \in Q, \hfill \\ &d_{E} \left( {p, q^{\prime}} \right) < d_{E} \left( {p^{\prime}, q^{\prime}} \right) \hfill \\ \end{aligned} $$

(4)

Let S_{spatialskyline} be the set of spatial skyline points of P with respect to Q in the Euclidean plane. The point $p \in P$ is a spatial skyline point with respect to Q ($p \in S_{spatialskyline}$) if and only if there is no other point in P that spatially dominates it, i.e.

$$ S_{spatialskyline} \left( {P, Q} \right) = {\text{\{ }}p \in P{|} {\nexists } p^{\prime} \in P - \left\{ p \right\}, p^{\prime} \prec_{Q} p\} $$

(5)

To obtain spatial skyline points, we require investigating each point in P whether it is spatially dominated by any other point in P with respect to Q. However, several geometric features of the spatial skyline can reduce the region where the spatial skyline point can be found. Some algorithms use these features to decrease dominance tests. We summarize the most important definitions and properties of the spatial skyline points in the following.

• The perpendicular bisector of two points $PB\left( {p, p^{\prime}} \right)$ is the locus of the points of equal distance of p and p′ in space. It is a straight line perpendicular to the line passing through the midpoint of the points p and p′.

• Closest region to p with respect to p′ $CR\left( {p, p^{\prime}} \right)$ is the locus of points closer to p than to $p^{\prime}$ in Euclidean space. The perpendicular bisector of two points p and p′ is $PB\left( {p, p^{\prime}} \right)$ and the half-plane including p.

• The convex hull of the query points CH (Q) is the smallest convex polytope that contains all points in Q. Its vertices are called convex points and define the set CP (Q).

• The voronoi diagram of the points of interest VD (P) divides the space into |P| regions. Each region contains a point of $p \in P$ and the points of the plane that are closer to p than any other point in P. Each partition is called the Voronoi cell.

• Independent Region IR (p, q) is a sphere centered at q with radius d (p, q). The union of the independent regions is IRG (Independent Region Group) of p with respect to Q [24].

• Dominator Region DR(p, Q) is the region where p is spatially dominated by any point within it [24]. Defined as Eq. (6):

  $$ \forall p \in P, \quad DR\left( {p, Q} \right) = \mathop {\bigcap }\limits_{{q_{i} \in Q}} IR\left( {p, q_{i} } \right) $$

  (6)

We can use these definitions to limit the search region to find the spatial skyline points. Based on these definitions, some properties are extracted in [12, 13, 24, 33,34,35], as shown in the following.

Property 1

If $p \in P$ is a spatial skyline point for $Q^{\prime} \subset Q$, then p is also a spatial skyline point for Q [12].

Property 2

The set of spatial skyline points of P with respect to Q depends only on the convex points which define the convex hull of Q [12], i.e.

$$ S_{spatialskyline} \left( {P, Q} \right) = S_{spatialskyline} \left( {P, CP\left( Q \right)} \right) $$

(7)

Property 3

Each point of P inside the convex hull of Q is a spatial skyline point of P with respect to Q [12].

Property 4

Each point of P whose Voronoi cell intersects the inside of the convex hull of Q is a spatial skyline point [33, 35].

Property 5

Let p, p′, and p″ be three data points of P. If p spatially dominates p′ with respect to Q and p′ spatially dominates p″ with respect to Q, then p spatially dominates p″ with respect to Q [34].

Property 6

Let $p,{ }p^{\prime}{ } \in {\text{P}}$ and $PB\left( {p, p^{\prime}} \right)$ be the perpendicular bisector of two points in the plane, and CH (Q) is the convex hull of Q. Two points do not spatially dominate each other if and only if $PB\left( {p, p^{\prime}} \right)$ intersects the interior of CH(Q) [34].

Property 7

Assume that p is the data point of P and DR(p, Q) is the dominator region of p with respect to Q. The p is a spatial skyline if and only if it is the only point of P in its dominator region [24]. Equation (8) represents it:

$$ \forall p \in P, p \in S_{spatialskyline} \left( {P, Q} \right) \Leftrightarrow P \cap DR\left( {p, Q} \right) = \left\{ p \right\} $$

(8)

Property 8

Given $p \in {\text{P}}$ and $q \in Q$, each point $p^{\prime} \in P \cap DR\left( {p, q} \right)$ can only be dominated by a data point of $P \cap DR\left( {p, q} \right)$ [24].

3.3 Weighted Euclidean distance

Let P be a set of points of interest and Q be a set of query points in the space. The d_E(p, q) denotes the Euclidean distance between points $p \in P$, and $q \in Q$. Assume that each point $p \in P$ is assigned a positive real number as the weight w(p) > 0 to consider its importance. The weighted Euclidean distance between two points $p \in P$ and $q \in Q$ is defined as:

$$ d_{WE} \left( {p, q} \right) = \frac{1}{w\left( p \right)}d_{E} \left( {p, q} \right) $$

(9)

The weighted Euclidean distance is a non-metric parameter. Because the weights are point-dependent, triangle inequality is not maintained.

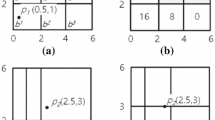
For instance, Fig. 1 shows a set of eight points P = {p1, p2, …, p8} and a query point Q = {q}. The Euclidean distance is considered for each point of P with respect to the query point q in Fig. 1a. Based on the point weight, the weighted Euclidean distance is computed for each point of P concerning q in Fig. 1b, while the weight of each point is shown in parentheses. It is notable that some points place near point q in the Euclidean distance (e.g., p1, p2, and p3 in Fig. 1a), containing a greater weighted Euclidean distance (in Fig. 1b). Since these points weigh less than other points, their weighted Euclidean distance is more. On the other hand, the more weight the points are than the other points (e.g., p5, p6, p7, and p8), the less their weighted Euclidean distance.

Fig. 1

An example of a set of points of interest and a query point: a Euclidean distances b weighted Euclidean distances

3.4 Bisector between two points with weighted Euclidean distance

Assume that P is a set of points, and each point $p \in P$ is also given a weight w(p) > 0. For each pair $p,{ }p^{\prime} \in {\text{P}}$, the set of all points that have equal weighted Euclidean distance between two points p and p′, with weights w(p) and w(p′) is called the bisector of p and p′ and is denoted B(p,p′) where

$$ \begin{aligned} B\left( {p,p^{\prime}} \right) & = {\text{\{ }}x{|} d_{WE} \left( {p, x} \right) &= d_{WE} \left( {p^{\prime},x} \right)\} \\ = \{ x| d_{E} \left( {p, x} \right)/d_{E} \left( {p^{\prime}, x} \right) = w\left( p \right)/w\left( {p^{\prime}} \right)\} \\ \end{aligned} $$

(10)

Bisectors generate two different types. If w(p) = w(p′) then, B(p, p′) is the hyperplane being orthogonal to the line between p and p′ and bisecting it. In the special case ($x \in R^{2}$ in Eq. 10), the hyperplane is a straight line. If w(p) ≠ w(p′) then B(p, p′) is a sphere that has the following center and radius:

$$ c = \frac{{w\left( p \right)^{2} p^{\prime} - w\left( {p^{\prime}} \right)^{2} p}}{{w\left( p \right)^{2} - w\left( {p^{\prime}} \right)^{2} }} \,\, and \,\, r = \frac{{w\left( p \right)w\left( {p^{\prime}} \right) d_{E} \left( {p, p^{\prime}} \right)}}{{\left| {w\left( p \right)^{2} - w\left( {p^{\prime}} \right)^{2} } \right|}} $$

(11)

In the special case ($x \in R^{2}$ in Eq. 10), the sphere is a circle. If w(p) < w(p′), B(p, p′) is a circle containing p in its interior [36]. Let WR be the weight ratio of two points, WR(p, p′) = w(p)/w(p′), Fig. 2 represents three examples of bisector B(p, p′) for fixed points p and p′ corresponding to WR(p, p′) = 1, 2, 1/3 values. The bisector becomes a straight line in the particular situation WR(p, p′) = 1 (w(p) = w(p′)). The bisector is a circle surrounding point p′ in the special case of WR(p, p′) = 2, and it is a circle surrounding point p in the case of WR(p, p′) = 1/3. Notably, the circle radius decreases as WR increases, and the center becomes closer to the surrounded point.

Fig. 2

The bisectors of p and p′ corresponding to three ratios WR(p, p′)

The definition of the closest region to p with respect to p′, $CR\left( {p, p^{\prime}} \right)$ should be re-evaluated according to the denotation of $B\left( {p,p^{\prime}} \right)$. The closest region to the point p may be the interior or the exterior of the circle specified by $B\left( {p,p^{\prime}} \right)$. For instance, in the case of WR(p, p′) = 2 in Fig. 2, the closest region to the point p with respect to p′ is the outer region of the circle.

3.5 Weighted spatial skyline queries

Let P be a set of n weighted points and Q be a set of m query points in a d-dimensional space. Assume that p and p′ are two weighted points of P, p spatially dominates $p^{\prime}$ with respect to Q in weighted Euclidean distance, denoted $p \prec_{Q}^{W} p^{\prime}$, if and only if $d_{WE} \left( {p, q} \right) \le d_{WE} \left( {p^{\prime}, q} \right)$ for every $q \in Q$ and there is at least one query point $q^{\prime} \in Q$ such that $d_{WE} \left( {p,q^{\prime}} \right) < d_{WE} \left( {p^{\prime},q^{^{\prime}} } \right)$, i.e.

$$ \begin{aligned} & p \prec_{Q}^{W} p^{\prime} \Leftrightarrow \forall q \in Q, d_{WE} \left( {p, q} \right) \le d_{WE} \left( {p^{\prime}, q} \right) \wedge \exists q^{\prime} \in \hfill \\ & Q,\, d_{WE} \left( {p, q^{\prime}} \right) < d_{WE} \left( {p^{\prime}, q^{\prime}} \right) \hfill \\ \end{aligned} $$

(12)

Assume that S_WSS is the set of weighted spatial skyline points of P with respect to Q in weighted Euclidean distance. The weighted point $p \in P$ is a weighted spatial skyline point with respect to Q ($p \in S_{WSS}$) if and only if there is no other weighted point in P that spatially dominates it, i.e.

$$ S_{WSS} \left( {P, Q} \right) = {\text{\{ }}p \in P{|} {\nexists } p^{\prime} \in P - \left\{ p \right\}, p^{\prime} \prec_{Q}^{W} p\} $$

(13)

In other words, $S_{WSS} \left( {P, Q} \right)$ contains the weighted points of the set P with respect to Q:

$$ S_{WSS} \left( {P, Q} \right) = {\text{\{ }}p \in P{|} \forall p^{\prime} \in P - \left\{ p \right\},\exists q \in Q, q \in CR\left( {p, p^{\prime}} \right)\} $$

(14)

We obtain different results in the spatial skyline query with the weights for the points of interest.

Some of the well-known properties of the spatial skyline points presented in Sect. 3.2 still hold in the weighted spatial skyline points, but most of them turn to be not true. Several statements related to the geometric properties of the weighted spatial skyline queries have been provided to demonstrate the difference between the weighted and the unweighted spatial skyline queries.

• 1. Assume that $Q^{\prime} \subset Q$ and $p \in P$ for Q′ is a weighted spatial skyline point. It may happen that p for Q is not a weighted spatial skyline point. For example, in Fig. 3, Q′ = {q₂, q₃, q₄} and p is a weighted spatial skyline point. The point p is not a weighted spatial skyline point for Q because p′ spatially dominates it with respect to q₁.

• 2. Let CP (Q) denote the convex points of Q, the points defining the convex hull of Q (see Sect. 3.2 for further details). The set of spatial skyline points of P may not depend only on CP (Q) in weighted Euclidean distance. For example, in Fig. 3, the point p spatially dominates p′ with respect to CP (Q) = {q₂, q₃, q₄}. The point p is not a weighted spatial skyline point with respect to Q because the point p′ spatially dominates it with respect to Q = {q_1, q₂, q₃, q₄}.

• 3. A point $p \in P$ inside the convex hull of Q (CH (Q)) may not be a spatial skyline point of P concerning Q in weighted Euclidean distance. For instance, in Fig. 4, the point p′ inside CH (Q) is not a weighted spatial skyline point because point p dominates it.

• 4. Two points $p, p^{\prime} \in P$ may dominate each other, while the bisector between two points ($B\left( {p, p^{\prime}} \right))$ intersects the interior of the convex hull of Q (CH (Q)). For example, in Fig. 3, even though $B\left( {p, p^{\prime}} \right)$ intersects with the interior of CH (Q), p′ dominates p. This statement can be seen again in Fig. 4. The bisector between p and p′ intersects with the interior of the convex hull of Q, but the point p dominates the point p′.

• 5. Each point $p \in P$ whose Voronoi cell overlaps the inside of the convex hull of Q may not be a weighted spatial skyline point. For example, in Fig. 4, the Voronoi cell of p′ overlaps the inside of CH (Q), but it is not a weighted spatial skyline point.

• 6. Assume that the independent region $p \in P$ and $q \in Q$ is a sphere centered at q with radius $d_{WE} \left( {p, q} \right)$. Dominator Region of p with respect to Q may not be created because the independent regions of p with respect to Q do not overlap. For instance, the independent regions of point p with w(p) = 2 with respect to Q = {q_1, q₂, q₃} are shown in Fig. 5. DR (p, Q) is the intersection of the regions of point p with respect to Q according to Eq. (6). It is empty in Fig. 5.

Fig. 3

An example of two weighted point P = {p, p′} with WR(p, p′) = 2 and Q = {q₁, q₂, q₃, q₄}

Fig. 4

An example of two weighted point P = {p, p′} with WR(p, p′) = 2 and Q = {q₁, q₂, q₃}

Fig. 5

The independent regions of p with w(p) = 2 and Q = {q₁, q₂, q₃} in 2-dimensional space

As it can be seen, many of the properties used to solve spatial skyline queries do not match the weighted spatial skyline queries. The convex hull or the Voronoi diagram does not reduce the number of tests performed. It is also not possible to use the Dominator Region to accelerate the discovery of the weighted spatial skylines. The weight cannot be selected randomly, and its value significantly affects the results. The weight causes |Q| virtual points to be extracted from each point $p \in P$. Each point p is virtually placed in a different place for each query point $q \in Q$. Figure 6 shows a transformation of the points of P according to each query point. Therefore, many of the techniques used in the unweighted case do not extend to the weighted one.

Fig. 6

Virtual transformation of P = {p₁, p₂} according to Q = {q₁, q₂}

4 Parallel processing of weighted spatial skyline queries

This section introduces a new MapReduce-based solution for processing weighted spatial skyline queries (MR-WSS). As described in the previous sections, many properties of spatial skylines cannot be used to reduce the number of tests done on weighted spatial skylines. Hence, this section proposes a parallel computing approach to accelerate the process.

4.1 Theoretical foundation

Consider a set of weighted data points P and a set of query points Q. The first property for the weighted spatial skyline set is as follows:

Lemma 1

Assume that $p \in P$ is a unique point and the point closest to $q \in Q$. The point p is a weighted spatial skyline point.

Proof

We have $p \in P$ is a unique point and the closest point to $q \in Q$, which means:

$$ \forall p^{\prime} \in P, d_{WE} \left( {p, q} \right) < d_{WE} \left( {p^{\prime}, q} \right) $$

(15)

Therefore, there is not a weighted point in P that spatially dominates p with respect to Q. Equation (13) implies that point p is a weighted spatial skyline point.□

In particular, if the point p is not unique. There is more than one weighted point with the same minimum distance to the point q. At least one of them is a weighted spatial skyline point, and others are spatially dominated. Therefore, we assume that the closest weighted point to each query point is unique in the remainder of this paper, without loss of generality.

Lemma 1 demonstrates that the presence of some points in the set of weighted spatial skyline points is independent of the position of any other data points. The following Lemma shows the transitivity rule in weighted spatial skyline points.

Lemma 2

For three weighted points $p, p^{\prime}, p^{\prime\prime} \in P$, if p spatially dominates p′ concerning Q and p′ spatially dominates p″ with respect to Q, then p spatially dominates p″ with respect to Q.

Proof

If p spatially dominates p′ with respect to Q i.e.

$$ \forall {\text{q}} \in {\text{Q}},{\text{ d}}_{{{\text{WE}}}} \left( {\text{p}},{\text{ q}} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}} \right){ } \wedge { }\exists {\text{q}}^{\prime} \in {\text{Q}},{\text{ d}}_{{{\text{WE}}}} \left( {\text{p}},{\text{q}}^{\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime} \right) $$

(16)

If p′ spatially dominates p″ with respect to Q i.e.

$$ \begin{gathered} \forall {\text{q}} \in {\text{Q}},{\text{ d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}} \right){ } \wedge { }\exists {\text{q}}^{\prime\prime} \in {\text{Q}},{ } \hfill \\ {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}}^{\prime\prime} \right) \hfill \\ \end{gathered} $$

(17)

Consider two cases (i) $q^{\prime} = q^{\prime\prime}$ (ii) $q^{\prime} \ne q^{\prime\prime}$.

• (i) $q^{\prime} = q^{\prime\prime}$: According to Eqs. (16) and (17):

  $$ \forall {\text{q}} \in {\text{Q}},{\text{ d}}_{{{\text{WE}}}} \left( {\text{p}},{\text{ q}} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}} \right) and $$
  $$ \exists {\text{ q}}^{\prime} = q^{\prime\prime} \in {\text{Q}},{\text{ d}}_{{{\text{WE}}}} \left( {{\text{p}}},{\text{ q}}^{\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}}^{\prime} \right) $$

  Therefore, p spatially dominates p″ with respect to Q ($p \prec_{Q}^{W} p^{\prime\prime}$).

• (ii) $q^{\prime} \ne q^{\prime\prime}$: According to Eq. (16), there is a query point ${\text{q}}^{\prime} \in {\text{Q}}$ that ${\text{ d}}_{{{\text{WE}}}} \left( {{\text{p}}},{\text{q}}^{\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left({\text{p}}^{\prime},{\text{q}}^{\prime} \right)$ and according to Eq. (17), for all query points ${\text{q}}^{\prime} \in {\text{Q }}$ except ${\text{q}}^{\prime\prime} \in {\text{Q}},$ ${\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}}^{\prime} \right)$. Therefore,

  $$ {\text{d}}_{{{\text{WE}}}} \left( {{\text{p}}},{\text{q}}^{\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{q}}^{\prime} \right) $$

  (18)

On the other hand, for all query points except ${\text{q}}^{\prime} \in {\text{Q}}$, we have ${\text{d}}_{{{\text{WE}}}} \left( {{\text{p}},{\text{ q}}} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {{\text{p}}^{\prime},{\text{ q}}} \right)$ or ${\text{d}}_{{{\text{WE}}}} \left( {\text{p}},{\text{q}}^{\prime\prime} \right) \le {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime\prime} \right)$ according to Eq. (16) and ${\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime},{\text{ q}}^{\prime\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}}^{\prime\prime} \right)$ according to Eq. (17). It is clear that:

$$ {\text{d}}_{{{\text{WE}}}} \left( {\text{p}},{\text{ q}}^{\prime\prime} \right) < {\text{d}}_{{{\text{WE}}}} \left( {\text{p}}^{\prime\prime},{\text{ q}}^{\prime\prime} \right) $$

(19)

Therefore, by Eqs. (18) and (19), p spatially dominates p″ with respect to Q ($p \prec_{Q}^{W} p^{\prime\prime}$).□

The typical method of calculating weighted spatial skyline is to check the spatial dominance between each pair of data points. We want to exploit the distributed environment to accelerate the computation process. The basic idea is to partition the data points first. Then, it assigns that data to different nodes to compute the weighted spatial skyline points locally. It is notable that according to the role of the query points set in the problem, its cardinality has to be much smaller than the cardinality of the data points set. Hence, each partition receives all query points. Finally, a central site collects the local weighted spatial skyline points to compute the global weighted spatial skyline points.

To solve the problem in a distributed environment, the problem must be decomposable. Assume that op₁ is a query operator on the data points set P and divide P into n subsets. The op₁ is a decomposable operator since it can be computed by another operator (for example, op₂) as given in Eq. (21):

$$ {\text{P}} = \mathop {\bigcup }\limits_{i = 1}^{n} P_{i} $$

(20)

$$ op_{1} \left( {\mathop {\bigcup }\limits_{i = 1}^{n} P_{i} } \right) = op_{2} \left( {\mathop {\bigcup }\limits_{i = 1}^{n} op_{1} \left( {P_{i} } \right)} \right) $$

(21)

Unfortunately, weighted spatial skyline computation is not a decomposable problem. According to Eq. (13), the weighted point $p \in P$ is a weighted spatial skyline point with respect to Q if and only if there is no other weighted point in P that spatially dominates it. Therefore, we have to check each point with the others, while some are in other partitions.

Lemma 3

The weighted spatial skyline query is not decomposable.

Lemma 3 shows that a set of data points cannot be divided into multiple partitions and, then the results of each partition are combined as the final results of a weighted spatial skyline query. Therefore, we need more operation to obtain the final result.

The proposed method computes the set of weighted spatial skyline points in one phase of MapReduce. It obtains the local weighted spatial skyline points in mappers and then distributes the tasks of computing the global weighted spatial skyline points into reducers.

4.1.1 Distributed dominance tests

Let p and p′ be two weighted data points in P and d_test(p, p′, Q) denote a function to evaluate whether p spatially dominates p′ with respect to Q. If $p \prec_{Q}^{W} p^{\prime}$, d_test(p, p′, Q) returns ‘True’ else returns ‘False’. A dominance test is to perform this function once. The intuitive method to find the weighted spatial skyline points of a set of data points P with respect to Q is to perform a dominance test on each data point pair (p, p′) with p ≠ p′. Let S_WSS be the set of weighted spatial skyline points of P with respect to Q and first S_WSS = P. The data point p′ is removed from S_WSS if d_test(p, p′, Q) is true for every other data point p in S_WSS.

We introduce a dominated subset operation on two sets of data points to design a distributed method to perform the dominance tests on the local weighted spatial skyline points. Let P1 and P2 denote two nonempty subsets of P. A dominated subset operation on P1 and P2 with respect to Q, denoted DS_Q(P1, P2), is as follows:

$$ DS_{Q} \left( {P1,{ }P2} \right) = {\text{\{ }}p_{j} { |}p_{j} \in P2{ } \wedge { }\exists { }p_{i} \in P1,{ }p_{i} \prec_{Q}^{W} p_{j} \} $$

(22)

where P1 as dominator set and P2 as dominatee set are known.

The result of DS_Q(P1, P2) is a spatially dominated subset of P2 with regard to P1. The P2—DS_Q(P1, P2) is the undominated subset of P2 with regard to P1. DS_Q(P, P) represents the data points in P spatially dominated by at least one point in P. In other words, DS_Q(P, P) consists of the data points which are not in S_WSS(P, Q).Therefore,

$$ S_{WSS} \left( {P,Q} \right) = P - DS_{Q} \left( {P,{ }P} \right) $$

(23)

Assume that P1, P2, …, Pm are m partitions of a set of data points P ($P = \mathop {\bigcup }\limits_{i = 1}^{m} Pi$). The main objective is to find S_WSS(P, Q) from the S_WSS(Pi, Q) for i = 1, …, m by performing the dominated subset operations among S_WSS(Pi, Q) for i = 1, …, m.

Lemma 4

Let P1, P2, …, Pm are m partitions of a set of data points P ($P = \mathop {\bigcup }\limits_{i = 1}^{m} Pi$). Let.

$$ local\_ S_{WSS} \left( {P, Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} S_{WSS} \left( {Pi, Q} \right) $$

(24)

For each partition Pi,

$$ DS_{Q} \left( {P,{ }Pi} \right) = DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), Pi} \right) $$

(25)

Proof

For each data point p belongs to $DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), Pi} \right)$, it also belongs to Pi ($p \in Pi$) and it is dominated by a point in $local_{ - } S_{WSS} \left( {P, Q} \right)$. Because the $local_{ - } S_{WSS} \left( {P, Q} \right)$ is a subset of P, p is dominated by a point in P, i.e., $p \in DS_{Q} \left( {P,{ }Pi} \right)$.

For each data point p in DS_Q (P, Pi), there is a data point in P (e.g., $p^{\prime} \in P$) that dominates p. Let Pj be the partition containing p′. Consider two cases:

• (i) p′ is in S_WSS(Pj, Q): p is dominated by a data point in $local_{ - } S_{WSS} \left( {P, Q} \right)$ because, according to Eq. (24), S_WSS(Pj, Q) is a subset of $local_{ - } S_{WSS} \left( {P, Q} \right)$.

• (ii) p′ is not in S_WSS(Pj, Q): there is a data point p″ in S_WSS(Pj, Q) which dominates p′ and p (Lemma 2.). Therefore, the data point p is dominated by a point in S_WSS(Pj, Q), a subset of $local_{ - } S_{WSS} \left( {P, Q} \right)$.

In both cases, the data point p is in $DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), Pi} \right)$.□

Lemma 5

Let P1, P2, …, Pm are m partitions of a set of data points P ($P = \mathop {\bigcup }\limits_{i = 1}^{m} Pi$). Then,

$$ S_{WSS} \left( {P, Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} (S_{WSS} \left( {Pi, Q} \right) - \mathop {\bigcup }\limits_{{\begin{array}{*{20}c} {j = 1..m} \\ {j \ne i} \\ \end{array} }} DS_{Q} \left( {S_{WSS} \left( {Pj, Q} \right),S_{WSS} \left( {Pi, Q} \right)} \right)) $$

(26)

Proof

According to Eq. (23): $S_{WSS} \left( {P,Q} \right) = P - DS_{Q} \left( {P,{ }P} \right)$

$$ S_{WSS} \left( {P,Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} Pi - DS_{Q} \left( {P,{ }\mathop {\bigcup }\limits_{i = 1}^{m} Pi} \right) $$

(27)

$$ = \mathop {\bigcup }\limits_{i = 1}^{m} Pi - \mathop {\bigcup }\limits_{i = 1}^{m} DS_{Q} \left( {P,{ }Pi} \right) $$

(28)

$$ = \mathop {\bigcup }\limits_{i = 1}^{m} \left( {Pi - DS_{Q} \left( {P,Pi} \right)} \right) $$

(29)

□

from Lemma 4:

$$ = \mathop {\bigcup }\limits_{i = 1}^{m} \left( {Pi - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), Pi} \right)} \right) $$

(30)

Each Pi consists of the points of the skyline and the points of non-skyline. The points dominated by the points in the skyline are the points of non-skyline. According to Eq. (13), Let S_WSS (Pi, Q) be the set of weighted spatial skyline points of the set Pi with respect to Q, and then nonS_WSS (Pi, Q) be the set of weighted spatial non-skyline points of the set Pi with respect to Q. Therefore, S_WSS(P, Q) is:

$$ \begin{aligned} & S_{WSS} \left( {P,Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} \left( {\left( {S_{WSS} \left( {Pi,{ }Q} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) \hfill \\ & - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), \left( {S_{WSS} \left( {Pi,{ }Q} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) \hfill \\ \end{aligned} $$

(31)

For any universe U and subsets A, B and C of U, the following identity holds:

$$ \left( {A \cup B} \right) - C = \left( {A - C} \right) \cup \left( {B - C} \right) $$

(32)

By Eqs. (31) and (32):

$$ \begin{gathered} S_{WSS} \left( {P,Q} \right) = \hfill \\ \mathop {\bigcup }\limits_{i = 1}^{m} \left( {(S_{WSS} \left( {Pi,{ }Q} \right) - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), \left( {S_{WSS} \left( {Pi,{ }Q} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right)} \right) \hfill \\ \cup \left( {nonS_{WSS} \left( {Pi,{ }Q} \right) - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), \left( {S_{WSS} \left( {Pi,{ }Q} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right))} \right)} \right)} \right) \hfill \\ \end{gathered} $$

(33)

We could consider:

$$ \begin{gathered} DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), \left( {S_{WSS} \left( {Pi,{ }Q} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) = \hfill \\ DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), S_{WSS} \left( {Pi,{ }Q} \right)} \right) \cup DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), nonS_{WSS} \left( {Pi,{ }Q} \right)} \right) \hfill \\ \end{gathered} $$

(34)

By Eq. (24), $S_{WSS} \left( {Pi, Q} \right) \subset local_{ - } S_{WSS} \left( {P, Q} \right) then:$

$$ DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), nonS_{WSS} \left( {Pi,{ }Q} \right)} \right) = nonS_{WSS} \left( {Pi,{ }Q} \right) $$

(35)

We substitute Eqs. (35) into (33):

$$ S_{WSS} \left( {P,Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} \left( {\left( {S_{WSS} \left( {Pi,{ }Q} \right) - (DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), S_{WSS} \left( {Pi,{ }Q} \right)} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) \cup \left( {nonS_{WSS} \left( {Pi,{ }Q} \right) - (DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), S_{WSS} \left( {Pi,{ }Q} \right)} \right) \cup nonS_{WSS} \left( {Pi,{ }Q} \right)))} \right) $$

(36)

Finally,

$$ S_{WSS} \left( {P,Q} \right) = \mathop {\bigcup }\limits_{i = 1}^{m} \left( {S_{WSS} \left( {Pi,{ }Q} \right) - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right), S_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) $$

(37)

The S_WSS (Pi, Q) from local_ S_WSS (P, Q) must be removed to solve the problem properly. Therefore,

$$ \begin{gathered} S_{WSS} \left( {P,Q} \right) = \hfill \\ \mathop {\bigcup }\limits_{i = 1}^{m} \left( {S_{WSS} \left( {Pi,{ }Q} \right) - DS_{Q} \left( {local_{ - } S_{WSS} \left( {P, Q} \right) - S_{WSS} \left( {Pi,{ }Q} \right), S_{WSS} \left( {Pi,{ }Q} \right)} \right)} \right) \hfill \\ \end{gathered} $$

(38)

$$ = \mathop {\bigcup }\limits_{i = 1}^{m} (S_{WSS} \left( {Pi, Q} \right) - \mathop {\bigcup }\limits_{{\begin{array}{*{20}c} {j = 1..m} \\ {j \ne i} \\ \end{array} }} DS_{Q} \left( {S_{WSS} \left( {Pj, Q} \right),S_{WSS} \left( {Pi, Q} \right)} \right)) $$

(39)

We design a distributed algorithm to compute the weighted spatial skyline points according to Lemma 5.

4.2 The proposed strategy

Our approach MR-WSS consists of one MapReduce phase, which receives a set of weighted data points P and query points Q and outputs a set of weighted spatial skyline points of P with respect to Q.

Initially, all data points are divided into m splits, and each split is assigned to a mapper. The cardinality of the set of query points is much less than that of the set of data points, so each mapper receives the set of query points. Each mapper (mapper_i) computes the set of weighted spatial skyline points of each split Pi with respect to Q (S_WSS (Pi, Q)) and then sends the result to the reducers.

Each reducer (reducer_i) uses the set of weighted spatial skyline points of split Pi (S_WSS(Pi, Q)) as the dominatee and the set of weighted spatial skyline points of split Pj ( S_WSS(Pj, Q)) as the dominator (for j = 1, 2, …, m, j ≠ i). Then, it removes the data points in S_WSS (Pi, Q) dominated by at least a data point in S_WSS (Pj, Q).

Finally, the results of all the reducers create the final set of weighted spatial skyline points (S_WSS (P, Q)). Figure 7 demonstrates the framework of the MR-WSS method.

Fig. 7

The framework of the proposed method MR-WSS

Each mapper should compute the set of weighted spatial skyline points for a split of data points concerning a set of query points in the proposed method. The main idea is to perform a dominance test on each pair of data points. An adaptation of the traditional methods of computing the local set of weighted spatial skyline points in the mappers is introduced.

An arbitrary point of query points is initially selected (e.g., $q \in Q$), and then the data points of P are sorted according to their weighted distance to the query point q. The closest data point of P to the query point q is chosen (e.g., $p^{\prime} \in P$) as the first data point of P in the weighted spatial skyline set (due to Lemma 1) and stored in the weighted spatial skyline set (S_WSS (P, Q)). Then, each data point $p \in P$ is analyzed in increasing distance order by checking whether it is dominated by any of the weighted spatial skyline points currently detected. If not dominated, it is a weighted spatial skyline point and is added to the weighted spatial skyline set (S_WSS (P, Q)). According to lemma 2, each non-skyline point will be dominated by one of the skyline points already detected. Therefore, the final set contains all points of the weighted spatial skyline. Algorithm 1 describes the details of the proposed method.

A dominance test determines whether the point $p \in P$ is dominated by a point of the currently detected weighted spatial skyline set ($p^{\prime} \in S_{WSS}$). If a point $q \in Q$ is closer to point p′ than to point p, then point p′ dominates point p. The algorithm traverses query points Q to compute and compare the weighted distances d_WE (p′,q) and d_WE (p,q). Once a point $q \in Q$ is found with d_WE (p′,q) < d_WE (p,q), it indicates that p′ dominates p and the dominance test returns the ‘True’ value. If for all $q \in Q$ the inequality d_WE (p′,q) ≥ d_WE (p,q) holds, p′ does not dominate p. If this process is repeated for all $p^{\prime} \in S_{WSS}$ and none dominates p, then point p is a weighted spatial skyline point. Algorithm 2 shows the dominance test pseudocode.

The proposed method MR-WSS first finds the local skyline points by mappers. Each mapper uses Algorithms 1 and 2 to compute the local skyline points from the assigned split (see the pseudocode in Algorithm 3). The global skyline computation from the local skyline points is done by the dominated subset operations distributed to multiple reducers for parallel processing. Algorithm 4 shows this process.

Complexity analysis Assume that n =|P|, m =|Q| and all data points are divided into k splits, and each mapper receives a split. First, the memory and then the execution time requirements of the MR-WSS are analyzed. Each mapper gets the same share of data points and whole query points and computes local weighted spatial skyline points (LS_WSS). Suppose that l =|LS_WSS| and in the best case l = m and the worst case l = n/k. Therefore, the memory requirements are O(n/k + m + l) = O(n/k + m) for each mapper. Each reducer receives local weighted spatial skyline points from the mappers and computes the fraction of global weighted spatial skyline points. The number of global weighted spatial skyline points is much less than the number of data points. Hence, the total memory requirement is O(n + m). In terms of time complexity, the algorithm requires O($n/k\log \left( {n/k)} \right)$ to sort the data points according to the distance to an arbitrary query point q in each mapper. It performs at most O(nl/k) dominance tests takes O(m) time each in the worst case. This process leads to the worst-case time complexity of O($n/k\log (n/k) + nml/k)$ for each mapper. Each reducer performs at most O(l²k) dominance tests taking O(m) time in the worst case. It leads to the worst-case time complexity of O(l²mk) for each reducer. There are cases the number of local skylines is l = O(m) in the best cases. The algorithm could run in O($n/k\log (n/k))$ time. On the other hand, there exist cases where l = O(n/k), in the worst case, and the time complexity of this algorithm is O(n²m/k).

Concerning the previous sections, most of the properties and techniques used in spatial skyline queries cannot be used to the weighted spatial skyline query because the nature of the problems is quite different. Therefore, this strategy is introduced to accelerate computations by taking advantage of the benefits of parallel implementation.

5 Experimental results

In this section, the two subsections introduce the experimental settings and the effectiveness evaluations on the strategies applied in the proposed algorithm MR-WSS, respectively.

5.1 Experimental settings

All experiments were performed by an Intel Xeon E7-8890 v4 processor, with a total speed of 2.2 GHz, 28 cores (48 threads) in total, and 512 GB of memory. We executed all the implementations in Spark 2.4.7 and Scala 2.11.12 on Linux 3.10.0.

The actual weighted data sets are not easy to obtain, so experiments have been performed with synthetic data. We consider several data sets P with different cardinalities from 2 to 100 K, and three data sets Q with 50, 100, and 150 queries as synthetic data sets. Because of the role of query points in the problem, their cardinality is much smaller than the cardinality of P. The sets P and Q were generated randomly in the squared domain [0, 1] × [0, 1], and the weights of data points were also generated within [1, 10]. Figure 8 shows a set P with 100 weighted points and a set Q with 5 query points that the weighted points are blue, the query points are red, and the obtained weighted skyline points are green. We label the skyline points obtained with their weights in the image. This figure reflects that the weighted spatial skyline points tend to be too close to the query points and, in most cases, have a significant weight.

Fig. 8

In blue 50 weighted points, in red 5 query points and in green all the weighted skyline points

5.2 Performance analysis

In this section, we evaluate the performance of the proposed MapReduce-based algorithm on several synthetic data sets. The following comparison algorithms were selected to be implemented in the same experimental environment to assess our proposed algorithm MR-WSS.

DEFT is a serial and base algorithm to obtain weighted spatial skyline points. WDS [13] is another serial algorithm that is an adaptation of [34]. It sorts the interest points according to their distance to an arbitrary query point. Then, it selects the closest point of interest as the first weighted spatial skyline point and checks other points of interest to add to the set of the weighted spatial skyline points. There is no parallel algorithm for weighted spatial skyline points based on the MapReduce framework. PWBF [13] is the only existing parallel solution that uses GPU for weighted spatial skyline queries. Due to the different implementation environments, we only used it to compare speedup.

Figures 9, 10, and 11 provide the information related to the performance of the mentioned algorithms when considering several sets of interest points and query points. We ran the algorithms with 21 pairs of P and Q sets, repeated ten times for each experimental group, and reported the average value to obtain more reliable results.

Fig. 9

Output size for different cardinalities of P and Q

Fig. 10

Execution time at different data sizes of P when a |Q| = 50, b |Q| = 100, c |Q| = 150

Fig. 11

Speedup MR-WSS vs WDS and PWBF at different data sizes of P when a |Q| = 50, b |Q| = 100, c |Q| = 150

We can see the number of weighted spatial skyline points for the different cardinalities of P and Q in Fig. 9. The output size increases as the number of interest points and query points increases. Based on the results obtained with different sets, between 8 and 31% of the points of P are skyline points. Figure 10 shows the execution times of the presented algorithms. We observe that the proposed algorithm MR-WSS is faster than the DEFT and WDS in all cases. When the number of points of interest is small, the execution time of the three algorithms is almost the same. The reason is that the number of dominance tests performed by the algorithm is small. The execution time of DEFT increases dramatically as the number of points of interest increases because this algorithm performs the dominance test for all pairs of points of interest. According to the experiment results, WDS has a shorter execution time than DEFT in all test cases because it performs less dominance test than DEFT. The proposed algorithm MR-WSS has the least execution time among these algorithms, and its execution time does not increase much as the number of points of interest increases. The reason is that it performs fewer dominance tests based on Lemma 2, similar to WDS. MR-WSS is faster than WDS because WDS sorts all data points serially, but MR-WSS sorts them in parallel by mappers. In addition, WDS does the dominance tests to obtain weighted spatial skyline points in serial, but MR-WSS first computes the local skylines by mappers and then obtains the global skylines by reducers. MR-WSS takes advantage of the benefits of parallel performing of the dominance tests.

To easily visualize how many times MR-WSS is faster than WDS and PWBF, in Fig. 11, we present the speedup of three methods related to DEFT. These speedups vary from 3.3 to 52.8 for |Q| = 50, 2.9 to 50.6 for |Q| = 100, and 2.7 to 52.9 for |Q| = 150. We can see that PWBF always has a higher speedup than WDS, although it does more operations as the number of points of interest increases. The reason is that PWBF exploits the parallel capabilities of the GPU. According to the experiment results, MR-WSS has the highest speedup among these algorithms. By comparing the complexities of PWBF and MR-WSS, they theoretically have the same time complexity. PWBF has the O(n²m/k) time complexity when O(n) threads are considered [13]. It is not possible in the real world. Therefore, GPU hardware has memory limitations, and the MapReduce scheme can efficiently deal with large-scale data sets. Finally, the experiment results demonstrate that the proposed method is a scalable and fast algorithm.

6 Conclusions and future work

We have theoretically studied and proposed a novel solution for the weighted spatial skyline query, namely MR-WSS, which can be applied to different decision-making applications. Traditional methods cannot efficiently process the weighted spatial skyline queries because most of their properties are useless for the weighted spatial skyline queries. Therefore, we design a parallel algorithm utilizing the MapReduce framework to improve the performance of the weighted spatial skyline queries. The proposed algorithm MR-WSS prevents the bottleneck of centrally finding the global spatial skyline from the local spatial skylines. It uses an adaptation of the traditional methods to compute the local set of weighted spatial skyline points in the mappers. Then, it distributes a set of dominated subset operations to reducers to find the global weighted spatial skyline points. The experimental results show that MR-WSS is a scalable and fast algorithm because the execution time increases much slower than other algorithms while the data points size increases. In addition, MR-WSS outperforms WDS and PWBF algorithms by a factor between 4 and 13 in most analyzed settings.

In the future, to further improve the performance, we are interested in controlling the load balance of the tasks assigned to the mappers and reducers. Another future work is to extend the proposed method to support the weighted spatial skyline queries over data streams. The proposed algorithm will be adapted to manage resources for virtual machine migration in cloud computing. The expanded solution can improve the performance to cases where more intelligence is required to improve the performance of fog or edge computing in task scheduling based on different parameters such as response time, quality of results, and energy.