Symmetric periodic orbits in the Moulton–Copenhagen problem

Abstract

We consider the planar restricted four-body problem proposed by Moulton. One infinitesimal mass moves under the attraction of three mass points in collinear Euler’s configuration, namely $P_0 (m_0 = \mu \,m)$ is placed at the origin, and other two identical points $P_1 (m)$ and $P_2 (m)$ are placed at the same distance from the origin. The problem is an extension of the well-known Copenhagen problem, in which $P_0$ does not exist, and therefore, the name is chosen for the considered problem. We perform a study on the evolution of families of symmetric periodic orbits (characteristic curves) as the mass parameter $\mu$ evolves. Compared with the Copenhagen problem, we find new families of periodic orbits and how the classical ones change. We also analyse the number and evolution of spiral points, which represent the heteroclinic orbits connecting equilibrium points.

1 Introduction

The so-called Copenhagen problem is a particular case of the restricted three-body problem (RTBP). It studies the motion of a massless particle under the attraction of two identical masses which move on circular orbits around their mutual centre of mass. This problem received its name after the huge work carried out by astronomers of the Copenhagen Observatory under the direction of Dr. Elis Strömgren. To have an idea of the work done there, the reader is addressed to the interesting review Strömgren (1933), in which he presented most of the work done by this observatory on this topic. Although simpler than the classical restricted three-body problem, it has been deeply analysed because too the many properties in periodic orbits related with its symmetry and the behaviour of asymptotic branches associated with the equilibria.

Periodic orbits are the most important objects in the study of dynamical systems. It is well known that Poincaré (1892) pointed out that periodic orbits form the skeleton of any dynamical system. In the cases of autonomous Hamiltonian systems, the periodic orbits appear in families. A family of periodic orbits is represented by a smooth one-parameter continuous curve (characteristic curve) in the space of initial conditions of parameters. A detailed study of periodic orbits of different types, their classification and evolution can be found in the excellent book written by Hénon (2003). The existence of periodic orbits in the three-body problem has been extensively studied, in particular, Strömgren (1933), Hénon (1965a), Hénon (1965b), Szebehely (1967), Danby (1984), Hénon (2003) found families of symmetric simple periodic orbits for this problem.

Extensions to more realistic problems appeared at the end of last century by considering the primaries oblate planets (Bhatnagar and Chawla 1977; Bhatnagar and Hallan 1983; Sharma 1981), radiation sources (Schuerman 1980; Simmons et al. 1985; Papadakis 1996; Papadakis et al. 2009; Papadouris and Papadakis 2014; Papadakis 2016) or both effects (Elipe and Ferrer 1985; Elipe 1992; Elipe and Lara 1997; Ishwar and Elipe 2001).

To our knowledge, Moulton (1900) was the first one in considering the “problem of four bodies, three of which are finite, moving in circles according to one or the other of the solutions of Lagrange.” For this problem, Moulton focused on its equilibria. In the present article, we extend the Copenhagen problem by placing a third mass $P_0$ on the origin of coordinates, in such a way that the primaries are in a collinear Euler configuration, as in Moulton’s case. Following Moulton, one century later, Maranhão and Llibre (1999) discovered transversal-collision orbits and proved the existence of invariant punctured tori. Michalodimitrakis (1981) studied the evolution of the system in terms of the mass of the central body $P_0$. More analyses of this problem have been made; for instance, Kalvouridis et al. (2006, 2007) studied the families of periodic orbits in terms of the radiation parameter, Arribas et al. (2016a, b) made a complete analysis of the existence and stability of the equilibrium points in the photo-gravitational collinear restricted four-body problem, Barrabés et al. (2017) studied the same problem by adding a repulsive Manev potential to the central mass.

The discovery of exoplanets gave a new impulse to these problems, since the celestial bodies are not only limited to the physical dimensions and configurations of those found in the Solar System, there are giant planets near the central star, planets under the attraction of two nearby binaries and, even, the movement of planets without sun is possible. Indeed, Chenciner and Montgomery (2000) published their article on a special periodic solution of the three-body problem originally discovered by Moore (1993). In this special orbit, the three bodies chase each other on the same path, a type of a Fig. 8 curve (Broucke et al. 2006). Hence, this scenario favours a series of recent studies which are not only interesting from the theoretical point of view, but also from their practical aspects, like the determination of habitability zones of these new solar systems (Érdi et al. 2004; Funk et al. 2015; Burgos-García et al. 2019).

In this work, we are interested in finding periodic orbits when only gravitational forces are considered. In order to find periodic orbits, we use the grid search method (Markellos et al. 1974); it is simple, and it is very efficient in finding symmetric periodic orbits for dynamical system of two degrees of freedom. The method can also take advantage from the mirror configurations that present these systems when they satisfy certain conditions of symmetry (Barrio and Blesa 2009).

Since Strömgren (1933), it is known that some families of periodic orbits of the restricted three-body problem end at an orbit formed by a pair of heteroclinic orbits connecting the two triangular equilibrium points. Henrard (1972) proved the Strömgren’s conjecture according to which a class of doubly asymptotic orbits are limit members of families of periodic orbits. These families end in what is known as a spiral point around the Lagrange’s equilibria. Strömgren (1933), Hénon (1965a, b) showed (graphically) four of these spiral points in the Copenhagen problem. Later, Gómez et al. (1988) developed a numerical method to find the heteroclinic orbits, which was applied to prove numerically the existence of the four asymptotic orbits in the Copenhagen problem and extended the result to find the exact number of this kind of orbits for different values of the mass parameter $\mu$ in the three-body problem.

In this paper, we deal with the gravitational collinear four-body problem in which the three primaries form a collinear central configuration. After formulating the problem, we show a brief description of the classical results for the symmetric periodic orbits in the three-body problem: twenty-two characteristic curves of three different classes and four spiral points. By using the grid search method, we find a huge amount of symmetric periodic orbits for a large number of values of mass of the central body in order to analyse the evolution of the characteristic curves from the three-body problem to the collinear restricted four-body problem with increasing values of the central mass. Finally, we use the method of Gómez et al. (1988) to find the number and location of spiral points in this problem in terms of the mass of the central primary.

2 Formulation of the problem

We consider the motion of an infinitesimal mass P under the action of three finite bodies $P_0$, $P_1$, $P_2$, which are located at the collinear Lagrange points of the three-body problem. Primaries $P_1$ and $P_2$ have equal masses $m_1 = m_2 = m$ and $P_0$ has mass $m_0 = \mu \, m$, where $\mu$ is called mass parameter. $P_1$ and $P_2$ are located symmetrically with respect to $P_0$, which is placed at the origin of an inertial reference frame. In this frame, $P_1$ and $P_2$ describe circular orbits around $P_0$ with angular velocity $\omega$ given by Eq. (1). Note that in this manuscript we will restrict the problem to planar motion. Besides, we consider a planar synodic reference frame with the same origin, the Ox axis the line joining the primaries towards $P_1$, and the axis Oy to complete the direct frame. Our problem consists in finding the planar motion (on the Oxy plane) of an infinitesimal mass P under the gravitational force of the three primaries. This is what we call Moulton–Copenhagen problem (M–C problem).

We choose the units of distance, mass and time in such a way that $\Vert P_1 P_2\Vert = 1$, and the gravitation constant $\mathcal {G} m = 1$. Hence, the coordinates of the primaries $P_0$, $P_1$, $P_2$ in the synodic frame are, respectively, $(0,0), \, (1/2,0)$ and $(-1/2, 0)$, and $\mathcal {G} m_0 = \mu$.

Since the primaries are at the collinear Lagrange equilibria, the sum of the gravity forces exerted by $P_0$ and $P_2$ on $P_1$ must be equal to the centrifugal force, that is,

$$\begin{aligned} m_1 \omega ^2 \Vert P_0 P_1 \Vert = \mathcal {G} m_0 m_1/\Vert P_0 P_1 \Vert ^2 + \mathcal {G} m_2 m_1/\Vert P_1 P_2 \Vert ^2; \end{aligned}$$

hence, the angular velocity of the synodic frame is

$$\begin{aligned} \omega ^2 = \Delta = 2 (1 + 4 \mu ). \end{aligned}$$

(1)

Then, the equations of motion for the infinitesimal particle P, after the change of time $ds = \omega \,dt$, are given by

$$\begin{aligned} \ddot{x} - 2 \, \dot{y} = \frac{\partial U}{\partial x}, \qquad \ddot{y} + 2\, \dot{x} = \frac{\partial U}{\partial y}, \end{aligned}$$

(2)

where the effective potential U is

$$\begin{aligned} U(x,y) = \frac{1}{2}\,(x^2 + y^2) + \frac{1}{\Delta }\left( \frac{\mu }{r_0}+\frac{1}{r_1}+\frac{1}{r_2}\right) , \end{aligned}$$

(3)

with

$$\begin{aligned} r_0 = \sqrt{x^2+y^2}, \quad r_1 = \sqrt{\left( x-1/2\right) ^2+y^2}, \quad r_2 =\sqrt{\left( x+1/2\right) ^2+y^2}. \end{aligned}$$

Furthermore, and when dealing with rotating frames, there exists the Jacobi constant C,

$$\begin{aligned} C = 2 \,U(x,y) - (\dot{x}^2 + \dot{y}^2). \end{aligned}$$

(4)

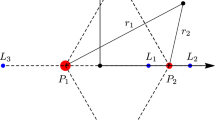
For $\mu = 0$ ($\not \exists P_0$), we have the classical Copenhagen problem, where there are five equilibrium points, $L_j, j=1,2,3,4,5$.

Fig. 1

Evolution of the six Lagrangian points in the collinear restricted four-body problem as $\mu$ increases

When $\mu \ne 0$ (see Fig. 1), the origin is occupied by a central body $P_0$ and the collinear point $L_1$ splits into two symmetric points $L_1^{+}$ and $L_1^{-}$ that move towards the primaries $P_1$, $P_2$, respectively, as $\mu$ increases. Simultaneously, $L_2$ and $L_3$ move towards $P_1$ and $P_2$, and $L_4$, $L_5$ go towards $P_0$. Hence, the problem has six equilibria (Arribas et al. 2016a).

3 Symmetric periodic orbits in the Copenhagen and in M–C

The system (2) is invariant under the symmetry $(x, y, \dot{x}, \dot{y}; t) \longrightarrow (x, -y, -\dot{x}, \dot{y}; -t)$. Because of this symmetry, in this paper we are interested in finding periodic orbits that are symmetric with respect to the Ox-axis. In such cases, the orbit will orthogonally cross the abscissas axis twice per period. Hence, if the initial conditions at $t_0 = 0$ for such an orbit are

$$\begin{aligned} (x_0, y_0, \dot{x}_0, \dot{y}_0; t_0=0) = (x_0, 0, 0,\dot{y}_0), \end{aligned}$$

at the instant $t= T/2$ (half period), the solution of (2) with the above initial conditions must be

$$\begin{aligned} (x_{T/2}, y_{T/2}, \dot{x}_{T/2}, \dot{y}_{T/2}; t_0=T/2) =(x_{T/2}, 0, 0,\dot{y}_{T/2}). \end{aligned}$$

That is, we need to check the first perpendicular crossing of the x-axis:

$$\begin{aligned} y(x_0, 0, 0 ,\dot{y}_0; \,T/2) = 0, \end{aligned}$$

(5)

$$\begin{aligned} \dot{x}(x_0, 0, 0 ,\dot{y}_0; \,T/2) = 0. \end{aligned}$$

(6)

and then, $(x_0, 0, 0 ,\dot{y}_0)$ will be initial conditions of a symmetric periodic orbit of period T.

Due to the existence of the Jacobi constant Eq. (4), we can express $\dot{y}_0^2 = 2 \,U(x_0,0) - C$; hence, we use the (x, C) plane to graphically represent the initial conditions of families of symmetric periodic orbits and to find them.

In order to find the initial conditions, we use here the grid search method (Markellos et al. 1974; Elipe et al. 2007; Barrio and Blesa 2009). Firstly, we build a regular mesh $(x_j,C_j), \, i=0, \ldots N$ of initial conditions. Then, we take from it two consecutive points, namely $(x_i,C_k)$ and $(x_{i+1},C_k)$, and integrate Eq. (2) for the initial conditions up to the instant (T / 2) at which the orbit crosses again the x-axis [Eq. (5)], i.e.,

$$\begin{aligned} \begin{array}{c} (x_i, 0, 0, \dot{y}_i)[t=0] \longmapsto (x_i, 0, \dot{x}_{i}, \dot{y}_{i})[t=T_i/2],\\ (x_{i+1}, 0, 0, \dot{y}_{i+1})[t=0] \longmapsto (x_{i+1}, 0, \dot{x}_{i+1}, \dot{y}_{i+1})[t=T_{i+1}/2]. \end{array} \end{aligned}$$

Then, we must check whether the product $\dot{x}_{i}[t=T_{i}/2] \,\cdot \, \dot{x}_{i+1}[t=T_{i+1}/2] < 0$ or not, that is, we have to determine if they have opposite signs. If that is not the case, we take the next point on the grid. If the condition is true, however, and due to continuity, there is value $(x^*_i,C_k)$ with $x^*_i \in (x_i,x_{i+1})$ such that $\dot{x}^*_i[t= T_i/2] = 0$, that is, the orbit crosses perpendicularly again the x-axis, thus, is a symmetric periodic orbit. Therefore, we keep this value and proceed with the next point of the mesh. Once we complete the row $C_k$, we repeat the procedure for the next row $C_{k+1}$ until every point of the grid is completed.

To solve this, a root-finding process combined with a numerical integrator is necessary. We used Brent’s method (Brent 1971) since it is an appropriate choice for this step of the grid search method. Once the convergence is reached, we have a set of initial conditions that satisfy the symmetric periodic conditions.

3.1 Copenhagen problem ($\mu = 0$)

To study the evolution of the families of symmetric periodic orbits in terms of the parameter $\mu$, we begin with the case $\mu = 0$, which coincides with the well-known Copenhagen three-body problem (Strömgren 1933; Hénon 1965a, b; Papadakis 1996).

Fig. 2

Families of symmetric periodic orbits in the Copenhagen problem and zoom of the three encircled areas. Each point on the plane (x, C) corresponds to a periodic orbit

Figure 2 shows the characteristic curves of the three-body problem with the same notation used by Hénon. There are 22 families of periodic orbits, named: a, b, c, f, g, h, i, j, k, l, m, n, o, r, s, t, u, v, w, x, y, z. In that sense, and in order to group families, we consider several regions of the plane (x, C) where families of periodic orbits appear, namely, $Z_1 = (-\infty , -0.5) \times [0, \infty )$, $Z_{23}$ = $Z_{2}$ $\cup$ $Z_{3}$, with $Z_2 = (-0.5, 0) \times [0, \infty )$ and $Z_3 = (0, 0.5) \times [0, \infty )$, $Z_4 = (0.5, \infty ) \times [0, \infty )$, $Z_5 = (-\infty , -0.5) \times ( -\infty , 0)$. $Z_1$ contains the families: b, h, l, u, w. $Z_{23}$ contains the families: c, f, i, n, o, r, s, x, y. $Z_4$ contains the families: a, g, j, k, t, v, z and, lastly, $Z_5$ contains only the family m.

Because of the symmetry of the problem, for each periodic orbit with initial conditions $(x_0, 0, 0, \dot{y}_0)$ at $t = 0$, there exists another periodic orbit, symmetric with respect to the Oy axis, with initial conditions $(-x_0, 0, 0, -\dot{y}_0)$ at $t = T/2$. This fact can be used to group the families of periodic orbits into three classes:

• First class (c, k, l, m and r): all the orbits are symmetric with respect to both axes.

• Second class (j, n and o): for each orbit in the family, its symmetric one also belongs to the family.

• Third class (a, b, f, g, h, i, s, t, u, v, w, x, y and z): for each orbit in the family, its symmetric ones does not belong to the family.

The continuous transition from orbits of the second class to their symmetric counterparts requires that a double symmetric orbit belongs to the family; thus, each second class curve must intersect with a curve of the first class. In this problem, we have the following intersections: j–k, n–c and o–r.

Since third class families do not contain the symmetric orbit of each of their members, this symmetric orbit must belong to another family. Therefore, third class families appear in pairs in such a way that each one contains the symmetric orbits of their paired family. In the three-body problem, the pairs are: a–b, f–h, g–i, s–t, u–v, w–x, y–z.

At the bottom of Fig. 2, a zoom of the different encircled regions near the spiral points is presented. We name these points $S_1$, $\hbox {S}'_2$, $\hbox {S}_2$, $\hbox {S}_4$, according to the zone $(Z_1, Z_2, Z_4)$ that they belong to. These are the end of several families (Henrard 1972) and represent asymptotic orbits, i.e., heteroclinic orbits that connect the two triangular Lagrangian points $L_4$, $L_5$. All these points have the same value of the Jacobi constant, $C = 11/4$, and the x coordinate is equal to $x_1 = -1.90, x_2 = -0.48, x_3 = -0.32, x_4 = 0.51$, respectively.

Fig. 3

Evolution of characteristic curves in the M–C problem as $\mu$ increases ($\mu = 0.001,\, 0.01, 0.1, \, 1, \, 10, \, 1000$)

3.2 Moulton–Copenhagen problem ($\mu \ne 0$)

When a fourth central body is considered, the characteristic curves of the restricted three-body problem change depending on the parameter $\mu$. See Fig. 3.

In what follows, we will focus on three different aspects of the evolution of the characteristic curves:

• The change in the number and position of spiral points with the value of $\mu$ and the appearance of a new spiral point $S_3$ in zone $Z_3$.

• In the collinear restricted four-body problem, a mass occupies the origin, so there can be no periodic orbit passing through the origin. This produces direct changes in the families f and h, because both families contain a periodic orbit with this property.

• New families of curves appear and some old families disappear. In Fig. 3, we show the characteristic curves of the four-body problem for different increasing values of $\mu > 0$. Each of these curves belongs to one of the three classes of families above mentioned.

4 Asymptotic orbits (spiral points)

4.1 Existence of asymptotic orbits

Asymptotic orbits in the restricted three-body problem (RTBP) appear when triangular Lagrangian points become unstable, i.e., when the mass parameter $\tilde{\mu }> 0.00385$ (see Szebehely 1967, Section 5.4.2).

N. B. The symbol $\tilde{\mu }$ stands for the mass parameter of the RTBP.

In Arribas et al. (2016a, b), we presented a detailed study on the existence and stability of the symmetric collinear restricted four-body photo-gravitational problem equilibria in terms of three parameters $\mu$, $q_0, q_1$ (mass and radiation parameters). The gravitational case presented here is a particular case of the former work, where $q_0 = q_1 = 1$, and $\mu$ is the only the mass parameter that varies. The problem has two triangular equilibria on the Oy axis which move towards the origin as $\mu$ increases (see Fig. 1). The stability of these points depends on the roots of the characteristic polynomial

$$\begin{aligned} \lambda ^4 + \lambda ^2 + b(\mu ) =0,\quad \text{ with } \quad b(\mu ) = \frac{\partial ^2 U}{\partial x^2}\Big |_{(0,y_L)} \, \frac{\partial ^2 U}{\partial y^2}\Big |_{(0,y_L)}, \end{aligned}$$

(7)

where $(0,y_L(\mu ))$ is the position of the Lagrange point. This point is stable when $0< b(\mu ) < 1/4$ and unstable otherwise. It is easy to show numerically that the triangular equilibria are unstable when $\mu < 11.72$ (Arribas et al. 2016a). Hence, and for these values, the collinear four-body problem can have asymptotic orbits.

Moreover, and in order to reach the equilibrium point, the asymptotic orbit must have a Jacobi constant equal to the value given by Eq. (4) and evaluated at the Lagrange triangular point with zero velocity: $C(\mu ) = 2 \,U(0,y_L(\mu ))$. This means that all the spiral points are on the same horizontal line on the plane (x, C).

Fig. 4

Jacobi constant of the spiral points versus $\mu$

Figure 4 shows the value of the Jacobi constant for the asymptotic orbits versus the parameter $\mu$, i.e., the curve $C=C(\mu )$. For the case of the RTBP, $C(0) = 11/4$. Furthermore, it can be seen that the ordinate of this point decreases when $\mu$ increases, reaching the limit $\lim _{\mu \rightarrow \infty }C(\mu ) = 3/4$.

4.2 Coordinate x of spiral points

In order to find the heteroclinic (asymptotic) orbits that connect both Lagrangian triangular points, we use the method developed by Gómez et al. (1988).

Let $L_4$, $L_5$ be the triangular equilibrium points of a vector field X on a certain manifold M; then, the stable and unstable manifolds of $L_i$ are defined, respectively, by

$$\begin{aligned} W^s(L_i) =\left\{ x \in M, \,\,\phi (t,x) \xrightarrow {t\rightarrow \infty } L_i\right\} \end{aligned}$$

and

$$\begin{aligned} W^u(L_i) = \left\{ x \in M, \,\,\phi (t,x) \xrightarrow {t\rightarrow -\infty } L_i \right\} , \end{aligned}$$

where $\phi$ is the flow of the field. Due to the symmetry of the problem, an orbit of the unstable manifold $W^u(L_4)$ that cuts orthogonally the Ox-axis ($\dot{x} = 0$) continues with an orbit of the stable manifold $W^s(L_5)$, creating a heteroclinic orbit.

Let us first study the motion near the equilibrium points $L_{4(5)}$ $= (0, y_L)$. Following Szebehely (1967, p. 241), if we change the coordinates to

$$\begin{aligned} \xi = x , \quad \eta = y - y_L \end{aligned}$$

(8)

and expand the effective potential U(x, y) around the point $L_i$, taking into account that $U_{xy}(0,y_L)=0$, and naming $\Gamma = U_{xx}(0,y_L), \Lambda = U_{yy}(0,y_L)$, the variational Eq. (2) becomes

$$\begin{aligned} \ddot{\xi } - 2 \dot{\eta }= & {} \Gamma \,\xi , \nonumber \\ \ddot{\eta } + 2 \dot{\xi }= & {} \Lambda \,\eta . \end{aligned}$$

(9)

In this case, the characteristic equation becomes expression (7). Thus, and for the values of the parameter $0 \le \mu \le 11.72$, the roots of this equation are $\pm \lambda _r \pm i \lambda _i$, where $\lambda _r, \lambda _i >0$ are functions of $\mu$. Then, the solution of (9) may be written as

$$\begin{aligned} \xi (t)= & {} e^{\lambda _r t} (A_1 \cos \lambda _i t + A_2 \sin \lambda _i t ) +e^{-\lambda _r t} (A_3 \cos \lambda _i t + A_4 \sin \lambda _i t ),\nonumber \\ \eta (t)= & {} e^{\lambda _r t} (B_1 \cos \lambda _i t + B_2 \sin \lambda _i t ) +e^{-\lambda _r t} (B_3 \cos \lambda _i t + B_4 \sin \lambda _i t ), \end{aligned}$$

(10)

where the constants $A_i, B_i,\, (i = 1,2,3,4)$ are related by the expressions

$$\begin{aligned} \begin{array}{l@{\quad }l} B_1 = k_1 A_1 + k_2 A_2, &{} B_2 = -k_2 A_1 + k_1 A_2,\\ B_3 = -k_1 A_3 + k_2 A_4, &{} B_4 = -k_2 A_3 - k_1 A_4, \end{array} \end{aligned}$$

with

$$\begin{aligned} k_1=\frac{\lambda _r}{2} (1 -K), \quad k_2 = \frac{\lambda _i}{2}(1 +K), \quad \text{ and } \quad K= \frac{\Gamma }{\lambda _r^2 + \lambda _i^2}. \end{aligned}$$

(11)

If we take the constants $A_3 = A_4 = B_3 = B_4 = 0$, we obtain an approximation of $W^u(L_4)$, then. Therefore, the linear approximation to $W^u(L_4)$ can be given by

$$\begin{aligned} \xi (t)= & {} e^{\lambda _r t} (A_1 \cos \lambda _i t + A_2 \sin \lambda _i t ), \nonumber \\ \eta (t)= & {} e^{\lambda _r t} (B_1 \cos \lambda _i t + B_2 \sin \lambda _i t ) . \end{aligned}$$

(12)

The method proposed by Gómez et al. (1988) benefits from expression (12) and gives an approximation of the solution of Eq. (2) only near $L_4$. However, we can assume that the point $(\xi (0), \eta (0))$ is sufficiently close to $L_4$ to take it as an initial condition in the integration of Eq. (2) and thus to obtain a good estimation of an orbit from the unstable manifold.

These initial conditions expressed in terms of the variables (x, y) are given by

$$\begin{aligned} \begin{array}{ll} x(0) = A_1, &{} y(0) = y_L + k_1A_1 + k_2 A_2, \\ \dot{x}(0) = A_1 \lambda _r + A_2 \lambda _i,\quad &{} \dot{y}(0) =\displaystyle \frac{A_1 }{2}\left[ (\lambda _r^2 - \lambda _i^2) - \Gamma \right] +\frac{A_2 }{2} \lambda _r \lambda _i. \end{array} \end{aligned}$$

(13)

Integrating (2) for a great number of initial conditions (by changing the constants $A_1, A_2$) and stopping the integration at the instant T, when $y(T) =0$, we can plot the points $(x(T), \dot{x}(T))$ to obtain curves that represent the manifold. The intersections of these curves with the x-axis provide the initial conditions for heteroclinic orbits.

In order to be more systematic, Gómez et al. (1988) proposed to take the initial conditions (x(0), y(0)) on a circle $(r \cos \theta , y_L + r \sin \theta )$ small enough (r small) around the equilibrium. This can be obtained by taking

$$\begin{aligned} A_1 = r \cos \theta , \quad A_2 = \frac{r \sin \theta - k_1 r \cos \theta }{k_2}, \quad \theta \in [0, 2 \pi ]. \end{aligned}$$

(14)

Fixing $r = 10^{-4}$ and integrating with a large number of values of the angle $\theta$, Gómez et al. (1988) proved the existence and found the position of the four asymptotic (spiral) points shown in Fig. 2 for the RTBP.

In order to study the existence of these asymptotic points in the C–M problem, we successively apply the same method for different values of the parameter $\mu$ and we obtain the following conclusions:

• For $\mu = 0$, we obtain exactly the same four asymptotic orbits as in the RTBP.

• For $\mu$ sufficiently small ($\mu \lesssim 10^{-3}$), we obtain the same number of spiral points as in the three-body problem, distributed in the same regions.

• When $\mu \approx 10^{-3}$, a fifth spiral point $S_3$ appears in $\hbox {Z}_3$.

• When $\mu \approx 0.23$, $S'_2$ disappears and there are four spiral points.

• When $\mu \approx 3$, $S_3$ disappears and there are three spiral points.

• When $\mu \approx 10$, $S_4$ disappears and we have only two spiral points.

Table 1 provides the values of the x-coordinate of the spiral points for different values of the parameter $\mu < 11.72$.

Table 1 Value of the coordinate x of the spiral points for different values of $\mu$

5 Effects of the central body on families h and f

To understand how the central body affects the families of symmetric periodic orbits, we analyse the paired families h and f.

Fig. 5

Left: characteristic curve h in restricted three-body problem. Right: three periodic orbits corresponding to three points in the figure

Figure 5(left) shows the family h of the RTBP, and three points representing three different periodic orbits, $O_1$, $O_2$, $O_3$ from the family. The same figure (right) shows these three orbits. Orbits from family h are retrograde and move around $P_2$. When $t = T/2$, these orbits cut the Ox axis at a point between $P_1$ and $P_2$. Additionally, the orbit $O_2$ crosses the origin. Note that in the collinear restricted four-body problem a central mass occupies the origin; therefore, the previous orbit $O_2$ is not possible. This fact splits the family h into two subfamilies $h_1$ and $h_2$ (see Fig. 6) in such a way that the intersection with the Ox axis at $t=T/2$ of the $h_1$ orbits is between $P_0$ and $P_1$, while the same point from $h_2$ orbits is between $P_2$ and $P_0$.

Fig. 6

Left: Characteristic curves $h_1$ and $h_2$ in the collinear restricted four-body problem. Right: Orbits that belong to $h_1$ (thinner) and $h_2$ (thicker)

On the other hand, the family f is paired with h, and thus, its behaviour must be similar. In the restricted three-body problem, family f crosses the axis $x=0$. Therefore this point represents the periodic orbit that passes through the origin. Obviously, when a mass is at the origin, no periodic orbit can pass through this point. Figure 7 shows how f splits in two subfamilies $f_1$ in $Z_2$, paired with $h_1$, and $f_2$ in $Z_3$ paired with $h_2$, where family $f_1$ tends asymptotically to the axis $x=0$, while $f_2$ tends to the new asymptotic point $S_3$.

Fig. 7

Top: characteristic curve $f_1$ and $f_2$ in the collinear restricted four-body problem. Bottom: orbits that belong to $f_1$ (thinner) and $f_2$ (thicker)

6 Evolution with $\mu$ of the other families

6.1 Region $Z_1$

Besides what is happening for h curve, a second change is happening around the spiral point $S_1$. The curve w is a closed curve up to $\mu \approx 0.1$, but after that value, the curve opens and moves towards the $h_1$ curve. For a value of $\mu \approx 0.86$, there is a bifurcation and two new curves appear: $h_1$, that ends at the spiral point, and $w_1$, a short characteristic curve that is close but does not tend to that point. This evolution is shown in Fig. 8.

Orbits from family $w_1$ are retrograde and surround the three primaries as well as the equilibria except the collinear $L_2$. For $\mu = 1$, the retrograde orbits from family $h_1$ are shown in Fig. 9.

Fig. 8

Evolution of the characteristic curves w and $h_1$ around $S_1$ in zone $Z_1$

6.2 Region $Z_2$

In addition to new families arising from family $f_1$, we found that family c disappears and two new families, $c_1$ and $c_2$, appear. The first one goes asymptotically between the forbidden area and the C-axis, while family $c_2$ moves from the equilibrium point $L_1^-$ to the spiral point $S_2$ (see top of Fig. 7). Moreover, a very short curve $\alpha$ can be seen close to the spiral point $S'_2$ (see top-left of Fig. 10 with a close look at regions around $S_2$, $S'_2$ in $Z_2$).

Fig. 9

Orbits of the family $h_1$ for $\mu =1$ in zone $Z_1$

On the other hand, these families evolve with $\mu$ (see Fig. 10). Family r merges with $c_1$ and two families are obtained: One of them moves towards the spiral point $S_2$, and the other one towards the point $S'_2$. For $\mu \in (0.03, 0.04)$, the new family closest to $S'_2$ intersects with families n and o, and then, two new families are created, each one tending towards a spiral point. The orbits involved in this process are retrograde and enclose $P_0$ as well as the two collinear equilibria close to it and the triangular equilibria.

The new family that ends at $S_2$ approaches the family $f_1$ and, finally, both create one family. Meanwhile, for $\mu \approx 0.23$ the spiral point $S'_2$ disappears as well as some of the families. These facts can be observed in Fig. 11.

Fig. 10

Evolution of characteristics close to $S'_2$ and $S_2$ in $Z_2$

Fig. 11

New family o–n–$f_{1}$ in $Z_2$

6.3 Region $Z_3$

In addition to the new spiral point $S_3$, new characteristic curves are obtained. In Fig. 12, all the new curves for the particular value $\mu = 0.1$ are presented.

A characteristic curve $c_2^p$ is found, that is paired with $c_2$ family, leaving $S_3$ and ending at the collinear equilibrium point $L_1^+$. Paired with $\alpha$ we find a short curve, $\alpha ^p$, very close to $S_3$.

A new curve $\beta$ leaves the point $S_3$. It is composed by direct orbits that enclose $P_0$ and $P_2$ creating loops around the triangular equilibria. As the orbits move away from $S_3$, loops disappear and the triangular equilibria are left outside the orbit (see Fig. 14 left).

Fig. 12

Orbits $O_\delta$ belong to characteristic $\delta$ and $O_\gamma$ belong to characteristic $\gamma$. The orbit named $O_{\gamma \delta }$ belongs to both characteristic curves

New characteristic curves $\gamma$ and $\delta$ cross each other. Curve $\gamma$ moves towards the equilibrium point with values of C varying very little. Curve $\delta$ leaves the space between the forbidden area and the C-axis, crosses $\gamma$ and ends at the spiral point $S_3$. These curves have self-symmetric orbits and they are not paired with others.

Orbits in $\gamma$ are direct orbits surrounding $P_0$ with a very small period. The orbits corresponding to $\delta$ are small direct orbits, too. For the largest value of C the orbits encompass $P_0$. When C decreases, there is an orbit with two cusp points on the Oy axis that tend to the origin creating loops. When we consider an orbit near $S_3$ the loops enclose the triangular equilibria and the inner loop encompasses $P_0$.

6.4 Region $Z_4$

In this area, we find the new family $\beta ^p$ that is paired with $\beta$ (in zone $Z_3$) and is located between the two g families of Hénon, as we can see in Fig. 13.

As $\mu$ increases, family j goes to the upper part of k; the rest of curves do not have a qualitative change, for instance, the new family $\beta ^p$.

Fig. 13

Characteristic curve $\beta ^p$ in $Z_4$ for $\mu = 0.1$

Fig. 14

Orbits of the families $\beta$ and $\beta ^p$

Figure 14(right) shows orbits from family $\beta ^p$, symmetric to others from family $\beta$.

7 Conclusions

We studied the motion of a small mass under the action of three primaries in a collinear central configuration, a problem that was proposed by Moulton and that is an extension of the Copenhagen problem. There are two peripheral equal masses (m) at the same distance from another mass ($m_0 = \mu \, m$) placed at the origin. An analysis of the evolution of the families of symmetric simple periodic orbits for this system, in terms of the parameter $\mu$, has been made.

We begin with a review of the results for the case $\mu =0$, (Copenhagen problem). This system has twenty-two characteristic curves of three different classes and four spiral points that represent heteroclinic orbits connecting the two triangular Lagrangian points $L_4$, $L_5$. Next, we proceed to compute the characteristic curves for the Moulton–Copenhagen problem in a similar way as we did for the Copenhagen problem, and we characterized them in terms of the new mass parameter.

Besides, we can conclude that the number of spiral points change: This number increases from four to five when the ${0.001} \le \mu < {0.23}$ and it decreases for ${0.23 \le \mu < \mu _{max} = 11.7}$; after this value, there is no longer any spiral point. The existence of these spiral points, that is to say, heteroclinic curves which points correspond to periodic orbits, shows a kind of accumulation periodic orbits on zones close to the spiral points, which could provide some clues in the formation of planets or asteroids.