Time distributions in satellite constellation design

Abstract

The aim of the time distribution methodology presented in this paper is to generate constellations whose satellites share a set of relative trajectories in a given time, and maintain that property over time without orbit corrections. The model takes into account a series of orbital perturbations such as the gravitational potential of the Earth, the atmospheric drag, the Sun and the Moon as disturbing third bodies and the solar radiation pressure. These perturbations are included in the design process of the constellation. Moreover, the whole methodology allows to design constellations with multiple relative trajectories that can be distributed in a minimum number of inertial orbits.

1 Introduction

Space has become a strategic resource that offers an unlimited number of possibilities. Scientific and military missions, telecommunications or Earth observation are some of its most important applications and have led the sector to a quick expansion with an increasing number of satellites orbiting the Earth.

Satellites lie in a very advantageous position that allows the observation of vast regions of the Earth in short periods of time, an objective which is difficult to achieve with human and technical means in ground. This advantage can be improved even further with the concept of satellite constellations. Satellite constellations are groups of satellites that, having the same mission, work cooperatively to achieve it. This concept increases the complexity of the Celestial Mechanics problem to solve, but opens new and interesting possibilities for future missions.

Satellite constellation design has been since its beginning a process that required a high number of iterations due to the lack of established models for the generation and study of constellations. This situation resulted in the necessity of specific studies for each particular mission, being unable to extrapolate the results from one mission to another. Fortunately, in the last decades, new theoretical models have been developed that include in their formulation all the former configurations. Examples of that are the Walker Constellations (Walker 1984) for circular orbits or the design of Draim (1987) for elliptic orbits. Afterwards, a new design theory was introduced, which included all the former designs and allowed more possibilities of configuration for circular and elliptic orbits: the Flower Constellations Theory.

Flower Constellations were introduced for the first time by Mortari et al. (2004) in the year 2004. The most relevant feature of this model consists of the visualization and study of the constellations using a rotating frame of reference instead of an inertial frame of reference. That way, a relative orbit whose geometry reminds the shape of the petals of a flower is obtained.

The initial Flower Constellations model was reformulated in the 2-D Lattice (Avendaño et al. 2013) and 3-D Lattice (Avendaño et al. 2013) models which improved the parametrization of the problem. However, due to the strictly Keplerian formulation of the model, the inclusion of orbital perturbations is required to enhance the precision. In Casanova et al. (2014) the perturbation created by the $J_2$ term of the gravitational potential of the Earth was introduced in the model. Nevertheless, other orbital perturbations are also significantly modifying the orbits, so it is important to include them in the design process of the constellation (Arnas et al. 2016).

The goal of the methodology presented in this paper is to generate satellite constellations that include the effects of orbital perturbations such as the gravitational potential of the Earth, the atmospheric drag, the Sun and the Moon as disturbing third bodies or the solar radiation pressure (Arnas et al. 2016). The proposed constellation design allows to generate a configuration in which a number of different relative trajectories is defined, each of these containing a number of satellites that present the same instantaneous relative trajectory over time. Moreover, in order to decrease the number of orbital launches to build the constellation, another constraint will be set: satellites from different relative trajectories have to share the same inertial orbit, allowing a decrease in the number of inertial orbits.

The time distribution methodology introduced is able to generate all kinds of satellite configurations including equally spaced in time distributions (as the Flower Constellations Theory does), but also formation flying (or cluster fight Mazal and Gurfil 2013). Examples of these are presented in this paper for both Keplerian formulation and perturbed models using the time distribution methodology introduced in this work.

2 Keplerian model for constellation design

Throughout this paper, the so called classical orbital elements will be used, namely: a the semi-major axis, e the eccentricity, i the inclination, $\omega$ the argument of perigee, $\varOmega$ the right ascension of the ascending node and M the mean anomaly. Other common parameters used are: f the true anomaly, $\omega _{\oplus }$ the angular velocity of the Earth, $\mu$ the Earth gravitational constant, $R_{\oplus }$ the Equatorial Earth radius and $J_2$ the second order term of the gravitational potential of the Earth.

In an unperturbed dynamic model, the classical orbital parameters (a, e, i, $\omega$, $\varOmega$) are constant whilst the mean anomaly (M) varies through time. This property will be used to show in a clear way the analytical model behind the constellation design proposed in this paper.

Along this section, three different constellation designs will be shown, each one expanding the possibilities of the former one with a new concept. First, a constellation design model in which satellites share the same relative trajectory with respect a rotating reference frame will be presented. Second, this model will be expanded with the possibility of distribution of the satellites in several different relative trajectories. And finally, a constraint will be set in order to reduce the number of inertial orbits to a minimum. That way, the costs of building the constellation in orbit are considerably reduced.

All these constellation designs share the mean values of the semi-major axis, the eccentricity, the inclination and the argument of perigee. This is done in order to achieve the sharing of the relative trajectories.

One important thing to notice is that the definition of the relative trajectory done throughout this paper can be established in whatever rotating frame of reference that rotates at a constant speed respect to the inertial frame of reference, and thus, it does not have to be the one fixed with the movement of the Earth. This has two important implications. The first one is that the methodology can be used in constellations orbiting any celestial body. The second one is that even if the satellites rotate a particular celestial body, the definition of the constellation does not have to be made in the reference frame fixed to the central body, it can be made in other reference systems, increasing the freedom in the design. However, in most applications, it is more practical the use of the ECEF (Earth Centered - Earth Fixed) frame of reference as it defines the constellation in a relative to Earth position, so during this paper, it is assumed that the design of the constellation is done in the ECEF frame of reference.

2.1 Constellation design with a common relative trajectory

The objective of this design model is to generate a constellation whose satellites share the same relative trajectory over time. The first thing required to achieve this condition is to define that particular relative trajectory. It is worth noting that the relative trajectory is not required to be closed in the proposed methodology.

The position of a satellite along its trajectory in the perifocal frame of reference is:

$$\begin{aligned} \mathbf {x} = \left( r\cos f, \, r\sin f, \, 0\right) , \end{aligned}$$

(1)

where r is the radius of the orbit in each instant of time:

$$\begin{aligned} r=\displaystyle \frac{a\left( 1-e^2\right) }{1+e\cos f}. \end{aligned}$$

(2)

These positions can be expressed in the inertial frame of reference (ECI: Earth Centered Inertial) using rotational matrices ($\mathcal {R}_3$ and $\mathcal {R}_1$):

$$\begin{aligned} \mathbf {x}\arrowvert _{ECI} = \mathcal {R}_3\left( \varOmega \right) \mathcal {R}_1 \left( i\right) \mathcal {R}_3\left( \omega \right) \mathbf {x}, \end{aligned}$$

(3)

and it can also be expressed in the ECEF (Earth Centered - Earth Fixed) frame of reference:

$$\begin{aligned} \mathbf {x}\arrowvert _{ECEF} = \mathcal {R}_3\left( -\psi _{G0} - \omega _{\oplus }t\right) \mathbf {x}\arrowvert _{ECI}, \end{aligned}$$

(4)

where $\psi _{G0}$ is the longitude of Greenwich at the time of reference $t=0$ and $\omega _{\oplus }$ is the angular velocity of rotation of the Earth.

Thus, using Eqs. (1), (3) and (4), the position of a certain satellite is obtained in the ECEF frame of reference:

$$\begin{aligned} \mathbf {x}\arrowvert _{ECEF} = \mathcal {R}_3\left( -\psi _{G0} - \omega _{\oplus }t\right) \mathcal {R}_3\left( \varOmega \right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) , \end{aligned}$$

(5)

where combining the first two matrices, the following expression is obtained:

$$\begin{aligned} \mathbf {x}\arrowvert _{ECEF} = \mathcal {R}_3\left( \varOmega -\psi _{G0} - \omega _{\oplus }t\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) . \end{aligned}$$

(6)

The aim now is to create a constellation of satellites whose trajectories in the ECEF frame of reference are the same. To be able to do that, the orbital elements a, e, i and $\omega$ must be equal for all the satellites of the constellation. Let a, e, i, $\omega$, $\varOmega _0$ be the orbital parameters of the reference trajectory and let $t_0$ be the reference time of the constellation which is associated with a reference satellite of the constellation (which can be an actual satellite or a fictitious position). This reference trajectory (named $\mathbf {x_0}$) can be expressed in the relative frame of reference as:

$$\begin{aligned} \mathbf {x_0}\arrowvert _{ECEF} = \mathcal {R}_3\left( \varOmega _0-\psi _{G0} - \omega _{\oplus }t\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) , \end{aligned}$$

(7)

where r and f are a function of t. This relative trajectory must be fulfilled by every satellite in the constellation, so it is fixed in the design of the constellation. If another point of this relative trajectory is considered, a satellite that shares the same relative trajectory can be obtained. If the value of $t_0$ is modified, this relative trajectory remains the same. Let $t_1$ be the changed value of $t_0$, then, the right ascension of the ascending node suffers a variation of $\varDelta \varOmega =-\omega _{\oplus }(t_1-t_0)$. Thus, the relative trajectory of the satellite ($\mathbf {x_1}$) when $t_1$ is considered is:

$$\begin{aligned} \mathbf {x_1}\arrowvert _{ECEF} = \mathcal {R}_3\left( \varOmega _0-\psi _{G0} - \omega _{\oplus }(t_1-t_0+t)\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) , \end{aligned}$$

(8)

where r and f are now a function of ($t_1+t$). From Eq. (8) and using the inverse relation of Eq. (4), the inertial orbit of this second satellite can be obtained through:

$$\begin{aligned} \mathbf {x_1}\arrowvert _{ECI} = \mathcal {R}_3\left( \psi _{G0} + \omega _{\oplus }t\right) \mathbf {x_1}\arrowvert _{ECEF}, \end{aligned}$$

(9)

so the inertial orbit is:

$$\begin{aligned} \mathbf {x_1}\arrowvert _{ECI} = \mathcal {R}_3\left( \varOmega _0- \omega _{\oplus }(t_1-t_0)\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) . \end{aligned}$$

(10)

In other words, let $\{a,e,i,\omega ,\varOmega _0,M_0\}$ and $\{a,e,i,\omega ,\varOmega _1,M_1\}$ be the classical orbital elements of two satellites where $M_0$ and $M_1$ are given for the initial time. We impose that both satellites lay in the same relative trajectory:

$$\begin{aligned} \mathbf {x_0}\arrowvert _{ECEF}(t + (t_1-t_0)) = \mathbf {x_1}\arrowvert _{ECEF}(t) \quad \forall t \in \mathbb {R}, \end{aligned}$$

(11)

where $t_1 - t_0$ is the time that satellite 0 requires to reach the same position of satellite 1 in the relative trajectory. Then, in the inertial frame of reference and following Eq. (10), a relation between both right ascensions of the ascending nodes can be obtained:

$$\begin{aligned} \varOmega _1 = \varOmega _0-\omega _{\oplus }(t_1-t_0). \end{aligned}$$

(12)

On the other hand, the mean anomaly of the reference satellite can be defined as:

$$\begin{aligned} M = n(t + t_0 -\tau ), \end{aligned}$$

(13)

where $\tau$ is the time of pass for the perigee, $t_0$ is the time of reference of the constellation and n is the mean motion of the satellite, which, for a Keplerian movement is:

$$\begin{aligned} n = \sqrt{\frac{\mu }{a^3}}, \end{aligned}$$

(14)

being $\mu$ the standard gravitational constant of the Earth. As all the inertial orbits are identical except for a rotation and a time of reference, we can define $\tau$ as the time of pass for the perigee of the leading satellite of the constellation, that is, satellite 0. It is important to notice that with this definition, $\tau$ becomes independent of the satellite of study. Thus, the mean anomaly of satellite 1 can be expressed as:

$$\begin{aligned} M_1 = n(t + t_1 - \tau ), \end{aligned}$$

(15)

where $t_1$ is the reference time of satellite 1. Then, a relation between both mean anomalies can be obtained:

$$\begin{aligned} M_1 = M_0 + n(t_1 - t_0). \end{aligned}$$

(16)

As it can be seen, combining Eqs. (12) and (16), a function between $M_1$ and $\varOmega _1$ can be established:

$$\begin{aligned} M_1 = \left( M_0 + \frac{n}{\omega _{\oplus }}\varOmega _0\right) - \frac{n}{\omega _{\oplus }}\varOmega _1, \end{aligned}$$

(17)

which represents a straight line ($M_1(\varOmega _1)$ with a slope of $n/\omega _{\oplus }$) as it can be seen in the $(\varOmega , \, M)$-space (Avendaño and Mortari 2012) representation of the relative trajectory shown in Fig. 1, where each vertical line represents the inertial orbit and the diagonal represents the relative trajectory of the satellite for a particular instant.

Fig. 1

$(\varOmega , \, M)$-space representation of a relative trajectory

If instead of only one satellite, a certain number of them are taken, it is possible to generate a constellation whose satellites share the same relative trajectory. Let $t_q$ be the temporal positions in the relative trajectory (in the same sense as $t_1$ worked) and let $N_{st}$ be the number of satellites in the relative trajectory, where $q\in \left[ 1, N_{st}\right]$ represents each particular satellite of the constellation. Then, for each q:

$$\begin{aligned} M_q = \left( M_0 + \frac{n}{\omega _{\oplus }} \varOmega _0\right) - \frac{n}{\omega _{\oplus }}\varOmega _q \end{aligned}$$

(18)

and the inertial orbits can be expressed as:

$$\begin{aligned} \mathbf {x_q}\arrowvert _{ECI} = \mathcal {R}_3\left( \varOmega _0- \omega _{\oplus }(t_q-t_0)\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) . \end{aligned}$$

(19)

As Eq. (19) shows, the first matrix corresponds to a rotation in a modified right ascension of the ascending node for each satellite. Let $\varOmega _q$ be the right ascension of the ascending node of the satellite q, then:

$$\begin{aligned} \varOmega _q = \varOmega _0 - \omega _{\oplus }(t_q-t_0). \end{aligned}$$

(20)

Note that ($t_q-t_0$) represents a distribution over time with respect to the reference trajectory defined in the beginning, and as such, it does not depend on the time (t) used in the propagation, that is, it remains constant. Moreover, $t_q$ and $\omega _{\oplus }$ are also constant in time, so it can be concluded that $\varOmega _q$ is fixed for each satellite of the constellation. On the other hand, the initial value of the true anomaly of each satellite of the constellation ($f_q$) only depends on $t_q$. Then, it is possible to generate the full constellation by the only use of the parameter of distribution $t_q$. Each inertial orbit of the constellation is obtained by:

$$\begin{aligned} \mathbf {x_q}\arrowvert _{ECI} = \mathcal {R}_3\left( \varOmega _0- \omega _{\oplus }(t_q-t_0)\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} \displaystyle \frac{a\left( 1-e^2\right) }{1+e\cos f_q}\cos f_q \\ \displaystyle \frac{a\left( 1-e^2\right) }{1+e\cos f_q}\sin f_q \\ 0 \end{array}\right) . \end{aligned}$$

(21)

Equation (21) allows to design a distribution of satellites in which all have the same relative trajectory (and thus, they share the same ground-track). This distribution is done over time, with no constraints in the selection of the different values of $t_q$ which is the parameter of distribution in the configuration.

A more compact representation of the distribution can be done combining Eqs. (18) and (20), which lead to:

$$\begin{aligned} \varOmega _q= & {} \varOmega _0-\omega _{\oplus }(t_q-t_0), \nonumber \\ M_q= & {} M_0 + n(t_q-t_0), \end{aligned}$$

(22)

where $t_q$ is the parameter of distribution of the configuration, and $\varOmega _0$, $t_0$ and $M_0$ are the parameters related to the leading satellite.

2.1.1 Example of constellation defined in a single relative trajectory

As an example of application, a constellation consisting on five satellites is selected. The semi-major axis of the constellation is $a=14{,}420$ km, the eccentricity is $e=0.4$ and the inclination is $i=63.435^\circ$. Suppose that a distribution of satellites is required in such a way that once the first satellite has observed a particular region, the rest of the satellites have to pass over the same region but with a delay of 5 min between them.

Without losing generality, let $\varOmega _0 = 0$, $M_0 = 0$ and $t_0=0$ be the parameters of the leading satellite. Then, the time distribution of the constellation is defined by the following relation:

$$\begin{aligned} t_q = 300(q-1), \end{aligned}$$

(23)

where $q\in \left[ 1,5\right]$ defines the parameter of distribution for each particular satellite and 300 represents the delay in seconds between satellites. From Eq. (22), the following distribution is obtained:

$$\begin{aligned} \varOmega _q= & {} -\omega _{\oplus }t_q, \nonumber \\ M_q= & {} nt_q, \end{aligned}$$

(24)

which leads to the configuration shown in Table 1.

Table 1 Initial distribution of the constellation

Fig. 2

Inertial (left) and relative (right) trajectories of the constellation

Figure 2 shows the inertial and relative trajectories of the constellation. As it can be seen, the relative trajectory is common for all the satellites in the constellation whilst they have five different inertial orbits. One important property of this design is that, even if we decrease the distances between satellites, it is not possible for the satellites to collide because they are moving in the same relative trajectory which does not have self intersections.

2.2 Constellation design with multiple relative trajectories

The objective now is to distribute the satellites in more than one relative trajectory. The methodology is similar to the previous one (see Sect. 2.1), but in this case, other degrees of freedom are added in the spacing of the relative trajectories in the ECEF frame of reference. Let $N_t$ be the number of relative trajectories in which the constellation is distributed and let $k\in \left[ 1, N_t\right]$ be the parameter that names each one of this trajectories. Therefore, the total number of satellites in the constellation $N_s$ is:

$$\begin{aligned} N_s = N_{st}N_t, \end{aligned}$$

(25)

where $N_{st}$ is the number of satellites in each relative trajectory.

Furthermore, the satellites named with the sub-index k0 are the leading satellites of each k relative trajectory, that is, the reference satellites that define the trajectories in the ECEF frame of reference. Moreover, the leading satellite, named with the sub-index 00, represents the reference origin of the whole constellation. Thus, as seen before, the relative trajectories can be defined as:

$$\begin{aligned} \mathbf {x_{kq}}\arrowvert _{ECEF} = \mathcal {R}_3\left( \sigma \right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} r\cos f \\ r\sin f \\ 0 \end{array}\right) , \end{aligned}$$

(26)

where:

$$\begin{aligned} \sigma = \varOmega _0 + \varDelta \varOmega _k - \psi _{G0} - \omega _{\oplus }(t_{kq}-t_0+t), \end{aligned}$$

(27)

$\varDelta \varOmega _k$ is the space distribution of the relative trajectories in the ECEF frame of reference and $t_{kq}$ represents the distribution parameter of the constellation. Note that r and f are now functions of $t_{kq}$. The parameter $t_{kq}$ distributes the satellites in a k relative trajectory and the q position in that relative trajectory. As it can be seen, two degrees of freedom control the distribution of the constellation: $\varDelta \varOmega _k$ and $t_{kq}$.

Transforming those coordinates to the ECI frame of reference, and naming $f_{kq}$ the true anomaly of the satellite q of the k relative trajectory at the initial time, the following inertial orbits for each satellite of the constellation are obtained:

$$\begin{aligned} \mathbf {x_{kq}}\arrowvert _{ECI} = \mathcal {R}_3\left( \varOmega _{kq}\right) \mathcal {R}_1\left( i\right) \mathcal {R}_3\left( \omega \right) \left( \begin{array}{c} \displaystyle \frac{a\left( 1-e^2\right) }{1+e\cos f_{kq}}\cos f_{kq} \\ \displaystyle \frac{a\left( 1-e^2\right) }{1+e\cos f_{kq}} \sin f_{kq} \\ 0 \end{array}\right) , \end{aligned}$$

(28)

where the right ascension of the ascending node of each satellite is:

$$\begin{aligned} \varOmega _{kq} = \varOmega _0+\varDelta \varOmega _k- \omega _{\oplus }(t_{kq}-t_0), \end{aligned}$$

(29)

which means that, in general, each satellite presents a different inertial orbit.

This distribution can also be represented in the $(\varOmega , \, M)$-space. As done before:

$$\begin{aligned} \varOmega _{kq}= & {} \varOmega _0 + \varDelta \varOmega _k - \omega _{\oplus }(t_{kq}-t_0), \nonumber \\ M_{kq}= & {} M_0 + n(t_{kq}-t_0), \end{aligned}$$

(30)

and the relation between $\varOmega _{kq}$ and $M_{kq}$ is:

$$\begin{aligned} M_{kq} = \left( M_0 + \frac{n}{\omega _{\oplus }}\varOmega _0\right) + \frac{n}{\omega _{\oplus }}\varDelta \varOmega _k - \frac{n}{\omega _{\oplus }}\varOmega _{kq}, \end{aligned}$$

(31)

which is a distribution of points over a family of straight lines that have the same slope. Figure 3 shows a particular case of a satellite with respect to the reference trajectory (named 0). There, the satellite 11 ($k=1,q=1$) is located in the relative trajectory 1 which presents a rotation of $\varDelta \varOmega _1$ with respect to the reference trajectory.

Fig. 3

$(\varOmega , \, M)$-space representation of the configuration for multiple relative trajectories

2.2.1 Example of constellation defined in various relative trajectories

As an example of this section, we present a sun synchronous constellation based on 15 satellites distributed in three relative trajectories and circular orbits. The constellation has an altitude of 880 km, and thus, a = 7260 km and $i=98.95^\circ$. Now, we choose a distribution of the constellation such that the relative trajectories are equally spaced and the satellites in each orbital plane are equally spaced in time. That way, this distribution can be expressed as:

$$\begin{aligned} \varDelta \varOmega _k= & {} 2\pi \frac{k-1}{N_t}, \nonumber \\ t_{kq}= & {} 2\pi \frac{q-1}{N_{st}}, \end{aligned}$$

(32)

where $N_t = 3$ is the number of relative trajectories and $N_{st}=5$ is the number of satellites per relative trajectory. Using Eq. (30) this initial distribution leads to the following configuration:

$$\begin{aligned} \varOmega _{kq}= & {} 2\pi \frac{k-1}{N_t} - \frac{2\pi \omega _{\oplus }}{n}\frac{q-1}{N_{st}}, \nonumber \\ M_{kq}= & {} 2\pi \frac{q-1}{N_{st}}, \end{aligned}$$

(33)

where $k\in \left[ 1,N_t\right]$ and $q\in \left[ 1,N_{st}\right]$. The distribution is shown in the $(\varOmega , \, M)$-space in Fig. 4, where it can be observed how the satellites are positioned in three different lines that represent the relative trajectories of the constellation.

Fig. 4

$(\varOmega , \, M)$-space, where each point represents a satellite in the constellation

Figure 5 shows the inertial and relative trajectories of the constellation. As it can be seen, there are 15 different orbits, one for each satellite, however there are only three different relative trajectories (a solid line, a dashed line and a dotted line), which was the objective sought.

Fig. 5

Inertial (left) and relative (right) trajectories of the constellation

As it can be seen from Figs. 4 and 5, this distribution generates too many different orbital planes, one per satellite, a fact that increases the expenses of building the constellation in orbit. Therefore, in the next subsection the constraint of minimum number of inertial orbits will be set in order to correct this situation.

2.3 Constellation design with minimum number of inertial orbits

Once a distribution over different relative trajectories is done, it is interesting to impose the restriction that the constellation has to be built in the least number of inertial orbits due to costs reduction. As seen before, the procedure places the satellites in different relative trajectories. Nevertheless, there is no constraint with respect to the inertial frame of reference, and in fact, each $\varOmega _{kq}$ is in general different. The aim now is to impose that the values of $\varOmega _{kq}$ are shared between relative trajectories.

The parameter $t_{kq}$ is a time distribution of the satellites in the constellation, but in reality, there exist two effects provoked by this parameter, the movement along the relative trajectory and the spacing of the inertial orbits. On the other hand, the spacing of the relative trajectories is controlled by the parameter $\varDelta \varOmega _k$. As we require to reduce the number of inertial orbits to a minimum, a relation between $t_{kq}$ and $\varDelta \varOmega _k$ has to be found in order to achieve this condition. As $t_{kq}$ is a distribution, we can separate it in two different parameters $t_k$ and $t_q$ such that:

$$\begin{aligned} t_{kq} = t_k + t_q, \end{aligned}$$

(34)

where $t_q$ is related to the distribution of satellites in the same relative trajectory as done in Sect. 2.1, and we want $t_k$ to be related with the inertial orbits. In order to achieve that, we impose the right ascension of the ascending node to be independent of the parameter k, in the form of $t_k$ or $\varDelta \varOmega _k$. That way, the number of inertial orbits only depends on $t_q$, which is related with the number of points per relative trajectory.

Thus, applying Eqs. (34) in  (29), we obtain:

$$\begin{aligned} \varOmega _{kq} = \varOmega _0+\varDelta \varOmega _k- \omega _{\oplus }(t_{k}+t_{q}-t_0), \end{aligned}$$

(35)

where it is possible to eliminate the dependence on k imposing:

$$\begin{aligned} t_k=\displaystyle \frac{\varDelta \varOmega _k}{\omega _{\oplus }}, \end{aligned}$$

(36)

and thus, introducing this value for $t_k$ in Eq. (35) the following expression for the right ascension of the ascending node is obtained:

$$\begin{aligned} \varOmega _{kq}=\varOmega _0- \omega _{\oplus }(t_q-t_0). \end{aligned}$$

(37)

Note that now, $\varOmega _{kq}$ does not depend on the terms in k, and as such, is the same for every satellite that shares the value of $t_q$, one for each relative trajectory. That leads to a distribution in which the satellites with the same q are distributed in the same inertial orbit whilst the satellites with the same k are distributed in the same relative trajectory (remember that $f_{kq}$ is a function of $t_q+t_k$). Figure 6 shows how the distribution works in the ECEF and the ECI frames of reference for two generic relative trajectories.

Fig. 6

Constellation distribution in the ECEF (left) and ECI (right) frames of reference

The $(\varOmega , \, M)$-space representation can be defined as before:

$$\begin{aligned} \varOmega _{kq}= & {} \varOmega _0 - \omega _{\oplus }(t_{q}-t_0), \nonumber \\ M_{kq}= & {} M_0 + n\left( \frac{\varDelta \varOmega _k}{\omega _{\oplus }}+t_q-t_0\right) , \end{aligned}$$

(38)

obtaining the same expression as in Eq. (31):

$$\begin{aligned} M_{kq} = \left( M_0 + \frac{n}{\omega _{\oplus }}\varOmega _0\right) + \frac{n}{\omega _{\oplus }}\varDelta \varOmega _k - \frac{n}{\omega _{\oplus }}\varOmega _{kq}. \end{aligned}$$

(39)

The difference now is that the right ascension of the ascending node is shared by one satellite of each relative trajectory as seen in Fig. 7. In fact this is a particular case of the one presented in Sect. 2.2.

Fig. 7

$(\varOmega , \, M)$-space representation of the configuration with minimum number of inertial orbits

Using the two time distributions $t_q$ and $t_k$, it is possible to achieve the configuration desired with no constraints in the distribution, generating constellation configurations distributed in a reduced number of orbital planes.

2.3.1 Example of constellation defined in various relative trajectories with minimum number of inertial orbits

As an example of application, a constellation of five satellites is chosen. This time we impose as a requirement of the mission that the satellites have to be distributed forming a “+” shape during their movement around the Earth. Let $a = 26{,}562$ km, $e=0$ and $i=50^\circ$ be the orbital parameters of the constellation, and let $\varOmega _0 = 0$, $M_0 = 0$ and $t_0=0$ be the parameters of the leading satellite.

In order to design the constellation, three relative trajectories and three inertial orbits are required to be able to obtain that shape. So three different values of $t_q$ (inertial orbits) and three different values of $\varDelta \varOmega _k$ (relative trajectories) must be taken. We define the first relative trajectory as the one that contains the central point of the “+” ($k=1$), being the upper and lower points also contained in this relative trajectory (see Fig. 8). On the other hand, the left and right points are contained in two different relative trajectories, $k=2$ and $k=3$ respectively. Moreover, the left and right points of the “+” are defined in the same inertial orbits as the upper and lower points, more precisely, the left and the upper points have the same inertial orbit $q=2$, whilst the right and lower point are contained in the same inertial orbit $q=3$. The central point has its own inertial orbit $q=1$.

If the delay between satellites in the same relative trajectory is taken as 10 min, the values of $t_q$ can be defined as: $t_1 = 0$ s, $t_2=600$ s and $t_3=-600$ s. Regarding the values of $\varDelta \varOmega _k$ and for the sake of simplicity, we choose $\varDelta \varOmega _1 = 0$, $\varDelta \varOmega _2 = -\omega _{\oplus }t_2$ and $\varDelta \varOmega _3 = -\omega _{\oplus }t_3$. With those parameters, the distribution of the constellation is shown in Table 2, where Sat. (k, q) represents the satellite contained in the inertial orbit q and the relative trajectory k.

Fig. 8

Inertial (left) and relative (right) trajectories of the constellation

Table 2 Initial distribution of the constellation

Figure 8 shows the inertial orbits and relative trajectories of the constellation. As it can be seen, the constellation is built in three different inertial orbits and three relative trajectories generating the “+” shape that we were aiming for.

3 Perturbed model for constellation design

It has been previously seen how to generate the constellation design in a Keplerian model. The objective now is to apply this methodology to the case of orbital perturbations. Orbital perturbations such as the gravitational potential of the Earth, the solar radiation pressure, the Sun and Moon as disturbing third bodies or the atmospheric drag, will destroy the Keplerian configuration proposed in a short period of time, so other complementary model has to be developed to solve this problem. The perturbed model proposed in this paper achieves the sharing of the relative trajectories despite of being the satellites subjected to certain known orbital perturbations. This methodology can be applied with any kind of orbital propagators (analytical, semi-analytical or numerical) not having any constraint in that respect.

As done in the latter section, three different constellation designs will be presented, corresponding to the ones studied previously in the Keplerian model. That way, a clearer exposition of the methodology is presented.

3.1 Constellation design with a common relative-trajectory

The objective is to generate a constellation whose satellites share the same relative trajectory despite of being subjected to several known orbital perturbations. Note that sharing the same relative trajectory does not mean that it has to be closed, in fact, the model is independent of this property.

The idea behind the perturbed model is to propagate first a reference satellite $\mathbf {x_0}$, which will be called the leading satellite, taking into account all the perturbations of the dynamical model chosen, and keeping the results of times, positions and velocities of the propagation in certain moments to generate the positions and velocities of the satellites of the constellation. The information that is kept corresponds to the moments when:

$$\begin{aligned} t=t_q-t_0, \end{aligned}$$

(40)

where $t_0$ is the reference time of the leading satellite, and $t_q$ represents the parameter of distribution of each particular satellite. Moreover, using the nomenclature introduced in the Keplerian model, $q\in [1, N_{st}]$.

Then, a transformation of these positions and velocities, given in the ECI frame of reference, will be performed in order to define the initial positions and velocities of the satellites of the constellation. Therefore, two transformations will be required: the first one to define the relative trajectory, and the second one to obtain the inertial orbits that have generated that relative trajectory and correspond to satellites of the constellation.

Let ${{\tilde{\mathbf{x}}}_\mathbf{q}}\arrowvert _{ECI}$ and ${{\tilde{\mathbf{v}}}_\mathbf{q}}\arrowvert _{ECI}$ be the positions and velocities of the leading satellite in the inertial frame of reference. The relative positions (${\mathbf {x}_\mathbf {q}}\arrowvert _{ECEF}$) and velocities (${\mathbf {v}_\mathbf {q}}\arrowvert _{ECEF}$) are obtained from the inertial ones by using the following expressions:

$$\begin{aligned} \mathbf {x_q}\arrowvert _{ECEF}= & {} \mathcal {R}_3\left( -\psi _{G0} -\omega _{\oplus }(t_q-t_0)\right) {\tilde{\mathbf{x}}_q}\arrowvert _{ECI}, \end{aligned}$$

(41)

$$\begin{aligned} \mathbf {v_q}\arrowvert _{ECEF}= & {} \mathcal {R}_ 3\left( -\psi _{G0}-\omega _{\oplus }(t_q-t_0)\right) {\tilde{\mathbf{v}}_q}\arrowvert _{ECI}- \varvec{\omega _{\oplus }}\times \mathbf {x_q}\arrowvert _{ECEF}. \end{aligned}$$

(42)

However, the initial inertial positions $\mathbf {x_q}\arrowvert _{ECI}$ and velocities $\mathbf {v_q}\arrowvert _{ECI}$ are required in order to define the constellation, thus, the second transformation of frames of reference is needed:

$$\begin{aligned}&\displaystyle \mathbf {x_q}\arrowvert _{ECI}=\mathcal {R}_3\left( \psi _{G0}\right) \mathbf {x_q}\arrowvert _{ECEF}, \end{aligned}$$

(43)

$$\begin{aligned}&\displaystyle \mathbf {v_q}\arrowvert _{ECI}=\mathcal {R}_3\left( \psi _{G0}\right) \mathbf {v_q}\arrowvert _{ECEF}+\varvec{\omega _{\oplus }}\times \mathbf {x_q}\arrowvert _{ECI}. \end{aligned}$$

(44)

One important thing to notice is that, having included the perturbations in the initial orbit propagation, all the satellites follow the same relative trajectory for the perturbations considered in the constellation design. Thus, the more realistic the orbital perturbation model is, the better the constellation will perform in the reality.

3.2 Constellation design with multiple relative trajectories

The next step in complexity in the design of a constellation is to include multiple relative trajectories in the configuration. The process is similar as before, but now, several leading satellites are required in order to define the different relative trajectories, one leading satellite for each relative trajectory. Furthermore, the distribution of the satellites is done using two parameters: the time distribution over the different relative trajectories $t_{kq}$ and the angular distribution of the relative trajectories in the ECEF frame of reference $\varDelta \varOmega _k$.

As it has been said, each relative trajectory requires a leading satellite. Those satellites have the same values of $a_0$, $e_0$, $i_0$ and $w_0$, whilst the right ascension of the ascending node follows:

$$\begin{aligned} \varOmega _{k0}=\varOmega _0 + \varDelta \varOmega _k - \omega _{\oplus }\left( t_{k0}-t_0\right) , \end{aligned}$$

(45)

where $\varOmega _{k0}$ are the right ascension of the ascending nodes of the leading satellites and each relative trajectory is named as $k\in [1, N_t]$. Moreover, each one can present a different reference with respect to the global reference time of the constellation $t_0$, that means that in general, each leading satellite defines a time of reference for each relative trajectory $t_{k0}$.

Once the leading satellites are defined, each one of them is propagated for a time equal to at least the maximum value of ($t_{kq}-t_{k0}$), that is, the maximum distance in time between the leading satellite and the satellites in the constellation related to it. This generates a number of relative trajectories equal to $N_t$, the number of different relative trajectories of the constellation. As previously, the values of the positions and velocities of each relative trajectory for the moments when ($t = t_{kq} - t_0$) are kept, which represent the distribution of the constellation, and two transformations are performed:

$$\begin{aligned}&\mathbf {x_{kq}}\arrowvert _{ECEF} = \mathcal {R}_3\left( -\psi _{G0}-\omega _{\oplus }(t_{kq}-t_0)\right) {\tilde{\mathbf{x}}_\mathbf{kq}}\arrowvert _{ECI},&\nonumber \\&\mathbf {v_{kq}}\arrowvert _{ECEF} = \mathcal {R}_3\left( -\psi _{G0}-\omega _{\oplus }(t_{kq}-t_0)\right) {\tilde{\mathbf{v}}_\mathbf{kq}}\arrowvert _{ECI} -\varvec{\omega _{\oplus }}\times \mathbf {x_{kq}}\arrowvert _{ECEF};&\nonumber \\&\mathbf {x_{kq}}\arrowvert _{ECI} = \mathcal {R}_3\left( \psi _{G0}\right) \mathbf {x_{kq}}\arrowvert _{ECEF},&\nonumber \\&\mathbf {v_{kq}}\arrowvert _{ECI} = \mathcal {R}_3\left( \psi _{G0}\right) \mathbf {v_{kq}}\arrowvert _{ECEF}+{\varvec{\omega }_{\oplus }}\times \mathbf {x_{kq}}\arrowvert _{ECI}. \end{aligned}$$

(46)

The values of the inertial positions $\mathbf {x_{kq}}\arrowvert _{ECI}$ and velocities $\mathbf {v_{kq}}\arrowvert _{ECI}$ of each satellite determine the initial configuration of the constellation. This configuration distributes the constellation in $N_t$ different relative trajectories and a number of inertial orbits equal to the number of satellites (in general). This is the same case as the one seen in Sect. 2.2 but for a non Keplerian model. Having too many different orbital planes in the constellation increases the costs of the mission, therefore, it is required to include the constraint of minimum number of inertial orbits which is presented in the next section.

3.3 Constellation design with minimum number of inertial orbits

The latter configuration distributes the constellation in $N_s$ different inertial orbits, which is a design decision that carries a lot of expenses to build the constellation in orbit. In order to solve that, and as done Sect. 2.3, the distribution parameter can be separated in two different distribution parameters $t_k$ and $t_q$ where $t_{kq} = t_k + t_q$. Then, a relation can be established between $t_k$ and $\varOmega _k$ using Eq. (36). However, the orbital perturbations make the right ascension of the ascending node to shift and therefore, the configuration obtained from the Keplerian procedure does not generate orbits in the same inertial planes.

In order to solve that, we introduce a modification in the distribution of $t_k$ from Eq. (36) that allows to include the effects of the shifting of the right ascension of the ascending node in the formulation. If we fix a frame of reference in the orbit, we observe that the Earth does not rotate at $\omega _{\oplus }$ due to the shifting in the right ascension of the ascending node. In this frame of reference, the Earth rotates respect to the orbit at $\omega _{\oplus }-\dot{\varOmega }$, where $\dot{\varOmega }$ is the derivative of the right ascension of the ascending node. Thus, applying this modification to Eq. (36), we obtain:

$$\begin{aligned} t_k = \displaystyle \frac{\varDelta \varOmega _k}{\omega _{\oplus }-\dot{\varOmega }_{k0}}, \end{aligned}$$

(47)

where $\dot{\varOmega }_{k0}$ is the derivative of the right ascension of the ascending node for the leading satellite of the relative trajectory k, which can be obtained using the secular value of the perturbation. The value of $t_k$ is introduced in Eq. (46) leading to a constellation based on $N_s$ satellites distributed in $N_t$ relative trajectories and $N_{st}$ inertial orbits. All this design includes the orbital perturbations considered in the propagations that were made.

4 Constellation design based on equally spaced in time distributions

The aim of this section is to define a constellation distribution that is equally spaced in time, basing the design in the case of multiple relative trajectories and minimum number of inertial orbits. In order to do this kind of distribution, it is required to have a closed relative track, which defines a repeating cycle that allows to define the distribution.

Let a cycle be the time that a satellite requires to repeat its ground-track, and let $T_c$ be the period of this cycle. In order to achieve the repeating ground-track property, the orbital parameters have to fulfill a relation with the rotation of the Earth, given by:

$$\begin{aligned} T_c=N_pT_{\varOmega }=N_dT_{\varOmega G}, \end{aligned}$$

(48)

where $N_p$ is the number of orbital revolutions to cycle repetition, $N_d$ is the number of revolutions of the ECEF frame with respect the orbital plane to cycle repetition, $T_{\varOmega }$ is the nodal period of the orbit and $T_{\varOmega G}$ is the nodal period of Greenwich.

Let $N_{st}$ be the number of satellites in each different relative trajectory, and let $q\in [1, N_{st}]$ be the integer that names each satellite of each relative trajectory of the constellation. In order to obtain an equally spaced time distribution in each relative trajectory, we distribute the values of $t_q$ over the period of the cycle $T_c$, where $t_q<T_c$, generating the following configuration:

$$\begin{aligned} t_q = (q-1)\frac{T_c}{N_{st}}. \end{aligned}$$

(49)

Furthermore, let $N_t$ be the number of different relative trajectories, and let $k\in [1,N_{t}]$ be the integer that names each different relative trajectory of the constellation. The right ascension of the ascending nodes of the leading satellites of each relative trajectory are expressed as:

$$\begin{aligned} \varOmega _k = \varOmega _0 + (k-1)\frac{2\pi }{N_t}, \end{aligned}$$

(50)

where:

$$\begin{aligned} \varDelta \varOmega _k = \varOmega _k - \varOmega _0 = (k-1)\frac{2\pi }{N_t}. \end{aligned}$$

(51)

Note that the right ascension of the ascending node of the leading satellites is not shared in general with the rest of the satellites situated in the same relative trajectory (see Eq. 20).

Using Eq. (47), the distribution of $t_k$ is obtained:

$$\begin{aligned} t_k = \displaystyle \frac{(k-1)\displaystyle \frac{2\pi }{N_t}}{\omega _{\oplus }-\dot{\varOmega }_{k0}}, \end{aligned}$$

(52)

thus, the distribution of each satellite ($t_{kq}=t_k+t_q$) for an equally spaced in time configuration is:

$$\begin{aligned} t_{kq} = (q-1)\frac{T_c}{N_{st}} + (k-1)\frac{2\pi }{N_t\left( \omega _{\oplus }-\dot{\varOmega }_{k0}\right) }. \end{aligned}$$

(53)

One thing to notice is that due to the possible symmetries in the configuration, two conditions have to be assured by the designer. The first one is that the parameters $N_d$ and $N_p$ must be relatively primes in order to avoid duplicities in the formulation (for example $N_p=2$ and $N_d=3$ is equivalent to $N_p=4$ and $N_d=6$).

The second condition is related to avoiding the overlapping of satellites in the configuration. This may occur if the distribution is uniform with symmetries in time and space, a condition that appears when the parameters $N_p$ and $N_t$ are relatively primes between them. Let $N_f$ be the maximum common divisor between $N_p$ and $N_t$. Then, the distribution over space is:

$$\begin{aligned} \varOmega _k = \varOmega _0 + (k-1)\frac{2\pi }{N_tN_f}, \end{aligned}$$

(54)

and therefore, the distribution over time is:

$$\begin{aligned} t_{kq} = (q-1)\frac{T_c}{N_{st}} + (k-1)\frac{2\pi }{N_tN_f\left( \omega _{\oplus }-\dot{\varOmega }_{k0}\right) }, \end{aligned}$$

(55)

where Eqs. (54) and (55) substitute Eqs. (50) and (53) in order to avoid the overlapping of satellites.

5 Examples of application

In this section, two examples of application are shown. In particular, a Medium Earth Orbit Constellation and a Low Earth Orbit Constellation are presented. In these designs, constellations whose satellites are equally spaced in time are defined (see Sect. 4). Moreover, the satellites will present the repeating ground-track property and will be distributed in the least number of inertial orbits using the perturbed model (see Sect. 3.3).

During these examples the following perturbations have been taken into account: the gravitational potential of the Earth (National Imagery and Mapping Agency 2000) up to 4th order terms (including tesserals), the Sun and Moon as disturbing third bodies (Abad 2012), the solar radiation pressure (Fortescue et al. 2003) and the atmospheric drag (Harris and Priester 1962, 1963 model). In addition, it has been supposed that all the satellites are identical in each constellation.

Table 3 Initial positions and velocities of the constellation

5.1 Example of Medium Earth Orbit Constellation

First, it is supposed, as part of the mission requirements, that the parameters $N_p$, $N_d$, $N_{st}$ and $N_t$ are known, as well as the inclination and eccentricity of the orbits. Moreover, as a mission requirement, the pass of the constellation over a certain point of the Earth with coordinates in longitude and latitude $(\psi _r, \, \phi _r)$ is imposed, and we choose $f=\pi$ over that point to maximize the time of coverage of the constellation in these coordinates.

On the other hand, we impose that the semi-major axis of all the satellites of the constellation present the repeating ground-track property. This condition is achieved by the use of osculating elements in the constellation for each satellite, having considered the orbital perturbations mentioned before. This is performed by the use of a numerical method to find the semi-major axis that is able to achieve the ground-track repetition for each satellite.

The basis of the numerical method is to correct the value of the semi-major axis by adjusting the orbit of the satellite in the ECEF frame of reference. This correction is achieved by using a basic property in celestial mechanics: if the semi-major axis of an orbit increases, its period also increases and vice versa. Therefore, the goal of the correction is to find the value of the semi-major axis that allows the closing of the ground-track in a period of time equal to a cycle: $T_c=TN_p$ (being T the orbital period and $N_p$ the number of orbital periods to complete a cycle). This is done by a series of iterations in which the secant method and the intermediate value theorem are used to find the value of the semi-major axis that allows the closing of the ground-track for the orbital perturbations considered.

Once the orbital parameters are established for one satellite, it is time to generate the initial configuration of a constellation with minimum number of inertial orbits, that is, the methodology presented in Sect. 3.3 is used. However, in order to do that, the constellation distribution must be chosen firstly. For the sake of simplicity, the value of $t_0$ is fixed as $t_0=0$ and Eqs. (49) and (55) are used in order to define the equally spaced in time configuration.

Using this equally spaced in time distribution, we apply it to a constellation consisting of 24 satellites and show the results. The constellation repeats its ground-track each two orbital revolutions ($N_p=2$) and each day ($N_d=1$). Furthermore, all satellites have an inclination of $i=63.435^\circ$ and an eccentricity of $e=0.5$. A high eccentricity orbit has been selected in order to show the possibilities of the constellation design model. The constellation is distributed in 6 different relative trajectories ($N_t=6$) and 4 inertial orbits ($N_{st}=4$), thus $N_s=N_tN_{st}=24$.

Note that $N_t=6$ and $N_p=2$ have a maximum common divisor of $N_f=2$, so, Eqs. (54) and (55) must be used to perform the distribution. As a further requirement, it has been imposed that one ground-track of the constellation passes over the city of Zaragoza (Spain) with coordinates ($\phi _r=41.698169^\circ$ and $\psi _r=-0.874295^\circ$).

With these conditions, the constellation is designed following the perturbed model proposed in this work obtaining the initial positions and velocities shown in Table 3. These results are given in the inertial frame of reference and generate a constellation whose satellites are distributed in 4 different inertial orbits and 6 relative trajectories. The satellites are subjected to the orbital perturbations named at the beginning of this section: the gravitational potential of the Earth, the Sun and Moon as disturbing third bodies, the solar radiation pressure and the atmospheric drag.

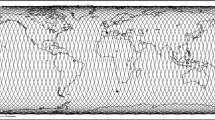
This configuration can be seen in Fig. 9, where the ground-track of the whole constellation is presented. There, it can be observed that the constellation is distributed in 6 different ground-tracks, being them completely closed and shared by 4 satellites each.

Fig. 9

Ground-track of the constellation

Figure 10 shows the inertial (left) and relative (right) trajectories of all the satellites in the constellation. There, it can be seen how the constellation is distributed in only 4 different inertial orbits, and how the relative trajectory is shared by groups of satellites (4 for each relative trajectory). The figure allows also to see the possibilities that the definition of the constellation in the relative frame of reference brings, generalizing the orbits from a conic shape in the inertial frame of reference into a more diverse group of configurations in the relative frame of reference.

Fig. 10

Inertial (left) and relative (right) trajectories of the constellation

Finally, in Fig. 11, the polar view of the constellation in the ECEF frame of reference can be observed. It can be concluded that the satellites are able to share their relative trajectories (4 satellites in each trajectory) despite of being subjected to orbital perturbations.

Fig. 11

Polar view of the constellation in the ECEF frame of reference

5.2 Example of Low Earth Orbit Constellation

For this second example, we choose a constellation composed by 16 satellites that has as main mission Earth observation. The constellation is distributed in circular orbits and in the same relative trajectory in the ECEF frame of reference using the uniform in time distribution seen in Sect. 4. As in the former example, the repeating ground-track property is imposed following the methodology explained for orbital perturbations. However, due to the nature of the mission, two new requirements are included, the sun-synchrony of the orbits and the ability to scan all the Earth surface in the minimum time considering a sensor with a field of view of $7.5^\circ$ that requires to work at $705\pm 5$ km over the Earth surface.

With these conditions, we obtain a constellation whose satellites have $a=7978.61$ km, $e = 0$, $i = 98.21^\circ$ and that repeat a cycle of their ground-tracks in 233 orbital revolutions or 16 days. The initial positions and velocities of the satellites of the constellation can be seen in Table 4.

Table 4 Initial positions and velocities of the constellation

On the other hand, in Fig. 12, the inertial orbits of the constellation in the initial time (left) and during a propagation of 16 days (right) are presented. As it can be seen, all the satellites of the constellation lay in the same inertial orbit that, due to the orbital perturbations considered, is modified during the time of propagation as seen clearly in the figure. Nevertheless, although the inertial orbits are greatly perturbed, we can observe in Fig. 13 that the ground-track of the constellation for 16 days of propagation remains fixed for all the satellites of the constellation.

Fig. 12

Inertial orbits of the constellation for the initial time (left) and 16 days of propagation (right)

Fig. 13

Coverage and ground-track of the constellation for 16 days of propagation

The property of ground-track repetition (or the sharing of the same relative trajectory) can be maintained over time without orbital maneuvers using the design methodology proposed in this work. However, due to the non periodic perturbations such as the atmospheric drag or the solar radiation pressure, the constellation will be modified and thus, orbital maneuvers will be required in the long term. One important thing to notice is that although in orbit maneuvers are always needed, the use of this methodology reduces the effects of orbital perturbations over the constellation (specially periodic perturbations such as the non-uniformity of the Earth gravitational field) and thus, this perturbed design model allows the reduction of the fuel required for the station-keeping of the constellation.

6 Conclusions

This paper has shown a new design model to create constellations whose satellites share one or several relative trajectories using time as parameter of distribution in the configuration. This design allows to distribute satellites in several relative trajectories without no restrictions at all in their distribution, a property that can be used to configure missions in which the satellites have to pass consecutively over a certain point of the Earth’s surface.

This design model opens a wide variety of possibilities in the configuration of satellite constellations, and it is able to handle any combination of orbital parameters, being the model applicable even with constellations based on high eccentricity orbits.

Furthermore, two different approaches have been presented for this design model, a Keplerian model in which no orbital perturbation was considered, and a perturbed model that can handle orbital perturbations. These two methodologies represent the same idea, but each one has its own peculiarities and uses. Specifically, the perturbed model allows to include the orbital perturbations inside the design process, improving the results obtained.

Moreover, this constellation design model allows to include orbital properties to the basic design. In that respect, a semi-major axis correction has been applied to the example presented in the paper in order to achieve the repeating ground-track property in the constellation despite of being the satellites subjected to certain known orbital perturbations. The ability to include other properties such as the sun-synchrony or the frozen character will be studied in a future work.

Finally the decrease on the number of inertial orbits to a minimum, represents a big design advantage, due to the fact that the reduction of inertial orbits allows to group satellites in their launches, therefore reducing the costs of the mission.