On the exactness of estimates for irregularly structured bodies of the general term of Laplace series

Abstract

The main form of the representation of a gravitational potential V for a celestial body T in outer space is the Laplace series in solid spherical harmonics $(R/r)^{n+1}Y_n(\theta ,\lambda )$ with R being the radius of the enveloping T sphere. The surface harmonic $Y_n$ satisfies the inequality

$$\begin{aligned} \langle Y_n\rangle < Cn^{-\sigma }. \end{aligned}$$

The angular brackets mark the maximum of a function’s modulus over a unit sphere. For bodies with an irregular structure $\sigma = 5/2$, and this value cannot be increased generally. However, a class of irregular bodies (smooth bodies with peaked mountains) has been found recently in which $\sigma = 3$. In this paper, we will prove the exactness of this estimate, showing that a body belonging to the above class does exist and

$$\begin{aligned} 0<\varlimsup n^3\langle Y_n\rangle <\infty \end{aligned}$$

for it.

1 Introduction

The main form of the representation of a gravitational potential V for a celestial body T in outer space is the Laplace series, which can be written in spherical coordinates $r,\theta ,\lambda$ as

$$\begin{aligned} V(r,\theta ,\lambda )=\frac{M}{R}\sum _{n=0}^{\infty } \left( \frac{R}{r}\right) ^{n+1}Y_n(\theta ,\lambda ). \end{aligned}$$

(1)

Here M is the mass of T, $Y_n$ is a dimensionless spherical harmonic; gravitational constant is set equal to unity. The radius R of the enveloping sphere ${\mathbb {S}}$ (Brillouin sphere) is taken as the scale factor. By definition, its centre O lies at the origin of the coordinate system; it contains T inside and possesses at least one common point with T. Generally, a spherical harmonic depends on $2n+1$ parameters (Stokes coefficients). Below we consider compact bodies with a finite positive integrable density $\varrho (r,\theta ,\lambda )$ only. As $Y_0\equiv 1$, we put $n\geqslant 1$ below.

Since the beginning of the space era, the problem of estimation of the series (1) general term becomes actual. Several qualitative estimates of the decreasing rate of $\langle Y_n\rangle$ were proposed by Chuikova (1980), Moritz (1978), Petrovskaya (1982) and others. Kaula (1968) proposed an empirical quantitative rule

$$\begin{aligned} \langle Y_n\rangle =\frac{C_n}{n^\sigma }\,,\qquad C_n\leqslant C \end{aligned}$$

(2)

with $\sigma =2$. Diverse quantities depending on properties of the density $\varrho$ are labeled as $C_n,\,C$; $\langle \cdot \rangle$ is the Chebyshevian norm, maximum modulus of a function on the sphere. Yarov-Yarovoi (1963) deduced the same estimation (2) with the same value $\sigma =2$ theoretically.

Most general theoretic results were obtained by K.V.Kholshevnikov, improved by V.A.Antonov, and accumulated in the book (Antonov et al. 1988). They were refined in Kholshevnikov and Shaidulin (2015a). Three classes of irregularly structured bodies were introduced there, and two of them are pertinent to this paper:

${\mathcal {T}}_3$ containing bodies with a density possessing a uniformly bounded variation along any circumference with the centre at the origin;

${\mathcal {T}}_5$ containing bodies having a finite number of points on ${\mathbb {S}}$. For any such a point $Q_k$ there exists a circular cone $K_k$ with the vertex $Q_k$, axis $OQ_k$, and the semivertex angle $\alpha _k<\pi /2$, provided that the intersection of some neighborhood of the point $Q_k$ and the body T lies entirely in $K_k$. It can be readily illustrated as a planet with peaked mountains, with their summits lying on ${\mathbb {S}}$.

According to Kholshevnikov and Shaidulin (2015a) $\sigma =5/2$ for $T\in {\mathcal {T}}_3$, $\sigma =3$ for $T\in {\mathcal {T}}_5$.

After an estimate is established, a question on its exactness arises. The last notion may have different meanings, so it is better to define it rigorously.

Let us consider a sequence $F_n(T)$ of non-negative numbers defined for any T belonging to a set ${\mathcal {T}}$. Let $F_n(T)$ for each $T\in {\mathcal {T}}$ satisfies the inequality

$$\begin{aligned} F_n(T)\leqslant \frac{C}{n^\sigma } \end{aligned}$$

(3)

with a fixed $\sigma \in {\mathbb {R}}$, $C>0$. We call this inequality exact with respect to $\sigma$ if there exists $T_0\in {\mathcal {T}}$ such that

$$\begin{aligned} 0<\varlimsup n^{\sigma }F_n(T_0)<\infty . \end{aligned}$$

(4)

In other words, the element $T_0$ of the set ${\mathcal {T}}$ possesses 2 properties.

• 1. There exists a constant $C_0$ such that $F_n(T_0)\leqslant C_0 n^{-\sigma }$.

• 2. For any $\sigma _1>\sigma$, and any $C_1>0$ there exists a number $n_1$ such that $F_{n_1}(T_0)>C_1 n_1^{-\sigma _1}$.

So exactness means that it is impossible to improve (3) replacing $\sigma$ by a certain $\sigma _1>\sigma$.

Remark

Usually ${\mathcal {T}}$ contains elements T for which $F_n(T)$ decrease much faster, so the left inequality (4) holds true not for all $T\in {\mathcal {T}}$. For example, the classes $\mathcal T_3$, ${\mathcal {T}}_5$ contain balls, and $Y_n=0$ for them.

Later we shall write simply exact instead of exact with respect to $\sigma$.

It is known (Kholshevnikov 1977; Antonov et al. 1988) that the estimate (2) is exact for $T\in {\mathcal {T}}_3$ with $\sigma =5/2$: examples of bodies are constructed for which

$$\begin{aligned} 0<\varlimsup n^{5/2}\langle Y_n\rangle <\infty . \end{aligned}$$

(5)

Exactness of the estimate (2) under $\sigma =3$ is established in Shaidulin (2010) for $T\in {\mathcal {T}}_5$ via an example of a spherical sector, but the proof is cumbersome. Here we consider this model in detail and affirm the exactness of the estimate. As a by-product an amazing property is revealed: different values of $\sigma$, and even $\sigma =\infty$, can correspond to the same body in diverse frames of reference. The equality $\sigma =\infty$ means

$$\begin{aligned} \lim n^\sigma \langle Y_n\rangle =0 \end{aligned}$$

(6)

for any $\sigma$. In our example (see Sect. 3.3) $Y_n$ satisfies the condition

$$\begin{aligned} \langle Y_n\rangle =\frac{C_n}{n^\sigma }\,p^n \qquad \text {with} \qquad 0<p<1,\qquad C_n \leqslant C \end{aligned}$$

(7)

instead of (2). It is obvious that (7) implies (5). The estimate (7) was established earlier (Kholchevnikov 1971; Antonov et al. 1988) for bodies with analytical structure. Now it is extended to bodies with analytical structure of their part only, namely the part nearest to the enveloping sphere. This fact illustrates the principle of the surface layer (Kholshevnikov and Shaidulin 2015a) once more.

Relations (1), (2) are simplified for bodies of revolution (the one examined in this paper belongs to them) as zonal harmonic coefficient only remains:

$$\begin{aligned} Y_n(\theta ,\lambda )\equiv Y_n(\theta )= c_nP_n(\cos \theta ),\qquad \langle Y_n\rangle =|c_n|, \end{aligned}$$

(8)

$P_n$ being Legendre polynomial with standard normalization $P_n(1)=1$.

If the body is homogeneous, then $Y_n$ does not depend on the density. Let us consider the density as unitary and the mass equal to the volume.

We have postponed proofs of several mathematical propositions to the “Appendix” for ease of treatment.

2 Potential of a spherical sector

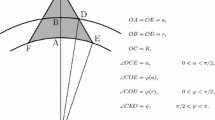
Let us consider a spherical sector T with unitary density, the radius a, and the semivertex angle $\alpha$ choosing the reference frame ${\mathcal {O}}$ with the origin O at the sector’s vertex, and z-axis directed along the axis of sector’s symmetry away from it, see Fig. 1. Let us suppose $0<\alpha <\pi$, sometime allowing limiting cases $\alpha =0$ (a rod), and $\alpha =\pi$ (a ball). Let ${\mathcal {S}}$ be the sphere bounding the ball from which the sector is cut off.

Fig. 1

Section of a spherical sector T by the plane passing through the symmetry axis z; $OA_1=OA_2=OA_3=a$, $\angle A_1OA_2=\alpha$; $\angle QOQ'=\theta$; $Q'$ represents a variable point of integration over T; the circumference represents a section of the enveloping sphere ${\mathbb {S}}=\mathcal S$

Sector’s mass equals to

$$\begin{aligned} M=2\pi \int _{0}^a w^2\,dw\int _{\pi -\alpha }^{\pi }\sin \theta \,d\theta =\frac{2\pi (1-\cos \alpha )}{3}\,a^3. \end{aligned}$$

(9)

We designate the variable radius via w in order to avoid confusion with the distance r from the origin O to the test point Q.

Let us use the following scheme to determine Stokes coefficients (Hobson 1931). We seek the potential on the axis of rotation at the point Q(0, 0, r) for $r>R$ and expand it into a Laurent series in negative powers of r, or equally into a Maclaurin series in powers of $u=1/r$

$$\begin{aligned} V(r)=\sum _{n=0}^{\infty }\frac{c_n^*}{r^{n+1}}=\sum _{n=0}^{\infty }c_n^* u^{n+1}. \end{aligned}$$

(10)

Hence, according to (1), (8) with $\theta =0$ we have

$$\begin{aligned} c_n^*=MR^{n}c_n. \end{aligned}$$

(11)

The potential of the sector at the point Q(0, 0, z) equals to

$$\begin{aligned} V(z)=2\pi \int _{0}^a w^2\,dw\int _{\pi -\alpha }^{\pi } \frac{\sin \theta \,d\theta }{\sqrt{w^2-2wz\cos \theta +z^2}}. \end{aligned}$$

(12)

The internal integral is elementary, so

$$\begin{aligned} V(z)=\frac{2\pi }{z}\int _{0}^aw\left[ w+z-g(w,z)\right] \,dw \end{aligned}$$

(13)

with $g(w,z)=\sqrt{w^2+2wz\cos \alpha +z^2}$. The integral (13) is evaluated in elementary functions (Shaidulin 2010; Kholshevnikov and Shaidulin 2011):

$$\begin{aligned} V=\frac{\pi }{3}\left[ g_1(z)+g_2(z)+g_3(z)+g_4(z)\right] , \end{aligned}$$

(14)

where

$$\begin{aligned} g_1(z)= & {} 3a^2+(2-3c^2)z^2,\qquad g_2(z)= -\left[ ac+(2-3c^2)z\right] g(a,z), \\ g_3(z)= & {} 2a^2\frac{a-g(a,z)}{z}\,,\qquad g_4(z)=3cs^2z^2 g_5(z), \\ g_5(z)= & {} \ln [a+cz+g(a,z)]- \ln (cz+z). \end{aligned}$$

We use the notations

$$\begin{aligned} c=\cos \alpha ,\qquad s=\sin \alpha ,\qquad g(a,z)=\sqrt{a^2+2acz+z^2}. \end{aligned}$$

We shall consider the sector not only in the frame ${\mathcal {O}}$, but also in the frame ${\mathcal {O}}(b)$, with its origin placed at the point $O_1(0,0,-b)$, and the directions of axes are the same. If $b>0$, the point $O_1$ displaces downwards, whereas if $b<0$ it goes upwards. In all cases coordinates of a test point Q referred to the frame ${\mathcal {O}}(b)$ are (0, 0, r), and $z=r-b$. The formula (14) holds valid under

$$\begin{aligned} g_1= & {} 3a^2+(2-3c^2)\eta ^2\frac{(1-\beta v)^2}{v^2}\,,\qquad g_2= -\left[ \frac{ac}{v}+(2-3c^2)\eta \,\frac{1-\beta v}{v^2}\right] \eta g_0, \nonumber \\ g_3= & {} 2a^2\frac{av-\eta g_0}{\eta (1-\beta v)}\,,\qquad g_4=3cs^2\eta ^2\frac{(1-\beta v)^2}{v^2}\,g_5, \nonumber \\ g_5= & {} \ln \left[ c+\frac{a-bc}{\eta }\,v+g_0\right] -\ln [(1+c) (1-\beta v)], \nonumber \\ g= & {} \frac{\eta }{v}\,g_0,\qquad g_0=\sqrt{1-2\xi v+v^2}. \end{aligned}$$

(15)

We use the notations

$$\begin{aligned} \eta= & {} \sqrt{a^2-2abc+b^2},\qquad \xi =\frac{b-ac}{\eta }\,,\qquad u=\frac{1}{r}\,, \qquad v=\eta u,\nonumber \\ \beta= & {} \frac{b}{\eta }\,, \qquad z=\frac{1-bu}{u}=\frac{\eta (1-\beta v)}{v}. \end{aligned}$$

(16)

It is important that $|\xi |<1$ irrespective of arbitrary parameters of the sector $a>0, 0<\alpha <\pi$, or of an arbitrary shift parameter b.

Let us find the closest to zero $u=v=0$ singular points of V as an analytical function of u (or, equally, of v). The point $u=0$ itself is an ordinary one in virtue of the convergence of the series (10) if $|u|<1/R$. Hence, we do not pay attention to the presence of v in the denominators of several $g_k$.

2.1 Potential’s singularities under a shift down, $b>0$

Let $b>0$.

• 1. $g_1$. No singularities.

• 2. $g_0$, $g_2$. Two complex singular points $v_{1,2}=\xi \pm \sqrt{\xi ^2-1}$ with a common modulus $|v_{1,2}|:=\varrho _0=1$.

• 3. $g_3$. The denominator of $g_3$ vanishes at $v=v_3:=1/\beta$. At the same time $g_0|_{v=v_3}=a/b$, so the numerator vanishes too. Let us put $v=v_3+\varepsilon$. Then

  $$\begin{aligned} g_0=\frac{a}{b}\left[ 1+\frac{\beta }{a}(a-bc)\varepsilon +\cdots \right] ,\quad av-\eta g_0=bc\varepsilon +\cdots ,\quad 1-\beta v=-\beta \varepsilon +\cdots , \end{aligned}$$

  so $g_3$ is regular at $v=v_3$, and singularities of $g_3$ and $g_0$ coincide.

• 4. $g_5$. Let us transform $g_5$ to a more convenient form. The derivatives with respect to v are

  $$\begin{aligned} \frac{dg_0}{dv}= & {} \frac{v-\xi }{g_0}\,,\qquad \frac{dg_5}{dv}=g_6+g_7\,, \nonumber \\ g_6= & {} \frac{(a-bc)g_0+\eta (v-\xi )}{g_0[\eta g_0+\eta c+(a-bc)v]}\,,\qquad g_7=\frac{\beta }{1-\beta v}. \end{aligned}$$

  (17)

  Multiplying the numerator and denominator of $g_6$ by $\eta g_0-\eta c-(a-bc)v$ we obtain after manipulations

  $$\begin{aligned} g_6=\frac{a-bg_0}{\eta g_0(1-\beta v)}\,, \end{aligned}$$

  hence

  $$\begin{aligned} \frac{dg_5}{dv}=\frac{a}{\eta g_0(1-\beta v)}. \end{aligned}$$

  (18)

  Taking into account $g_5\left| _{v=0}=0\right.$ we find

  $$\begin{aligned} g_5=\frac{a}{\eta }\int _0^v\frac{dv'}{(1-\beta v')g_0(v')}. \end{aligned}$$

  (19)

  The function $g_5$ is singular at $v=v_{1,2}$, $|v_{1,2}|=\varrho _0=1$, and at $v=v_3=1/\beta$.

• 5. $g_4$. Evidently

  $$\begin{aligned} g_4=\frac{3acs^2\eta }{v^2}(1-\beta v)^2\int _0^v\frac{dv'}{(1-\beta v')g_0(v')}. \end{aligned}$$

  (20)

  Singularities of $g_5$ and $g_4$ coincide.

2.2 Potential’s singularities under a shift up, $b<0$

Let $b<0$. The sign of b only plays a role for the property 3. So we discuss this case in short.

• 1. $g_1$. No singularities.

• 2. $g_0$, $g_2$. Two complex singular points $v_{1,2}$ with a common modulus $\varrho _0=1$.

• 3. $g_3$. At $v=v_3=1/\beta$ we have $g_0=-a/b$, $av-\eta g_0=2a\eta /b$. So $g_3$ is singular at $v=v_{1,2}$ and $v=v_{3}$.

• 4. $g_4$, $g_5$. Both functions are singular at $v=v_{1,2}$ and $v=v_{3}$.

3 Laplace series for the spherical sector

3.1 Laplace series for the spherical sector in the frame ${\mathcal {O}}$

In this frame, $z=r$. The Laplace series for the body T can be more easily found from (13) than from (14). Using expansion (61) from the “Appendix 2” we represent g(w, z) by a series

$$\begin{aligned} g(w,z)=r\left[ 1+\frac{cw}{r}-\sum _{n=1}^{\infty }P_{n1}(-c) \frac{w^{n+1}}{r^{n+1}}\right] . \end{aligned}$$

(21)

Polynomials $P_{n1}(x)$ are introduced in the “Appendix 2”, p. 18. The integral (13) can be calculated easily:

$$\begin{aligned} V(r)=\frac{2\pi }{r}\left[ \frac{1}{3}\,a^3(1-c)-\sum _{n=1}^{\infty } \frac{(-1)^{n}a^{n+3}}{(n+3)r^{n}}\,P_{n1}(c)\right] , \end{aligned}$$

where the rule of parity $P_{n1}(-x)=(-1)^{n+1}P_{n1}(x)$ is used. Taking into account (9) we have

$$\begin{aligned} V(r)=\frac{M}{r}\left[ 1-\sum _{n=1}^{\infty } \frac{3(-1)^{n}a^{n}}{(n+3)(1-c)r^{n}}\,P_{n1}(c)\right] . \end{aligned}$$

The section of the enveloping sphere ${\mathbb {S}}={\mathcal {S}}$ passes through the arc $A_1A_2A_3$ in the frame ${\mathcal {O}}$, its radius $R=a$, see Fig. 1. We obtain an exact expression for harmonic coefficients:

$$\begin{aligned} c_n=\frac{3(-1)^{n+1}}{(n+3)(1-c)}\,P_{n1}(c). \end{aligned}$$

(22)

It remains to use the asymptotics (62) of the polynomial $P_{n1}$ under great n. As the remainder depends on $\alpha$ singularly, we should examine several cases.

• 1. $\alpha =0$. The sector is changed into a rod of zero-mass, and $V=0$. For a non-trivial result we send the density to infinity in such a way that the mass M remains finite and positive. At the limit we see a heterogeneous rod $-a\leqslant z\leqslant 0$ with a linear density ${{\tilde{\varrho }}}(z)=(3M/a^3)z^2$. The zonal coefficient arises from (22) by the passage to the limit. By L’Hospital rule we find

  $$\begin{aligned} \lim _{\alpha \rightarrow 0}\frac{P_{n1}(c)}{1-c}=\lim _{\alpha \rightarrow 0} \frac{-\sin \alpha P_{n}(\cos \alpha )}{\sin \alpha }=-P_{n}(1)=-1. \end{aligned}$$

  Hence,

  $$\begin{aligned} c_n=\frac{3(-1)^{n}}{(n+3)}. \end{aligned}$$

  (23)

  It is at first disturbing that we reach an estimate (2) with exact exponent $\sigma =1$ instead of $\sigma =5/2$. However, the Newtonian potential of one-dimensional bodies possesses worse differential properties.

• 2. $\alpha =\pi$. As $P_{n1}(-1)=0$, then $c_n=0$. It is not surprising: if $\alpha =\pi$ the sector becomes a ball.

• 3. $0<\alpha <\pi$. According to (22), (62)

  $$\begin{aligned} c_n\sim \frac{(-1)^{n+1}B}{n^{5/2}} \cos \left[ \left( n+\frac{1}{2}\right) \alpha +\frac{\pi }{4}\right] ,\quad B=\frac{3}{1-c}\sqrt{\frac{2s}{\pi }}. \end{aligned}$$

  (24)

  The sequence of cosines contains a subsequence bounded away from zero. Hence, relations (2), (5) are valid with the exponent $\sigma =5/2$.

• 4. $\alpha =\pi /2$. Though this case is contained in the previous one, it is worth emphasizing due to its exclusive simplicity. The body T represents a semi-ball. According to (22)

  $$\begin{aligned} c_n=\frac{3(-1)^{n+1}}{n+3}\,P_{n1}(0). \end{aligned}$$

  (25)

  Values $P_{n1}(0)$ vanish for even $n>0$. For odd n a simple asymptotics (63) is valid. Finally, for the odd n

  $$\begin{aligned} c_n\sim \frac{3(-1)^{\frac{n+1}{2}}\sqrt{2/\pi }}{n^{5/2}}. \end{aligned}$$

  (26)

Below we suppose $0<\alpha <\pi$ eliminating degenerate cases.

3.2 Laplace series for the spherical sector in the frame ${\mathcal {O}}(b)$, $b>0$

Let us pass to the frame ${\mathcal {O}}(b)$ while shifting down, $b>0$. We ought to consider three cases.

• 1. $a-2bc>0$, which always takes place in a right or obtuse angle $\alpha$; $R=\eta >b$, $0<\beta <1$, see Fig. 2.

• 2. $a-2bc=0$, which is possible in case of an acute angle $\alpha$ only; $R=\eta =b$, $\beta =1$, see Fig. 3.

• 3. $a-2bc<0$, which is possible in case of an acute angle $\alpha$ only; $R=b>\eta$, $\beta >1$, see Fig. 4.

Fig. 2

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b)$, $b>0$; $a-2bc>0$, $R=O_1A_1=\eta >b$; left $c>0$, right $c<0$. Enveloping sphere ${\mathbb {S}}$ passes through the points $A_1,A_3$

Fig. 3

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b)$, $b>0$; $a-2bc=0$, $R=O_1O=O_1A_1=O_1A_3=\eta =b$. Enveloping sphere ${\mathbb {S}}$ passes through the points $A_1,A_3,O$

Fig. 4

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b)$, $b>0$; $a-2bc<0$, $R=O_1O=b>\eta$. Enveloping sphere ${\mathbb {S}}$ passes through the point O

Combersome calculations have allowed us to prove relations (2) with $\sigma =5/2$ in cases 1, 2, but we did not succed to prove (5). We have omitted these computations as the validity of (2) is ascertained in the general case.

Let us turn to the case 3. We examine the behaviour of entering in (14) functions $g_s$ in the neighborhood of singular points which are nearest to the origin, see Sect. 2.1. The formulae (15) represent $g_s$ via functions of v. The singularities nearest to the origin are situated on the circumference $|v|=\varrho _1=1/\beta <1=\varrho _0$. So the quantities $g_1,g_2$, and $g_3$ in (14) can be disregarded because they do not influence the asymptotics of $c_n$. Further, let us use an expansion of $1/g_0(v)$ in Legendre polynomials

$$\begin{aligned} \frac{1}{g_0(v)}=1+\sum _{n=0}^{\infty }a_nv^{n+1},\qquad a_n=P_{n+1}(\xi ). \end{aligned}$$

According to the “Appendix 1d”

$$\begin{aligned} \frac{1}{(1-\beta v)g_0(v)}=1+\sum _{n=0}^{\infty }b_nv^{n+1},\quad b_n=\beta ^nB_{n}\,, \quad B_n=\beta +\sum _{k=0}^{n}\frac{a_k}{\beta ^k}. \end{aligned}$$

After integration

$$\begin{aligned} \int _0^v\frac{dv'}{(1-\beta v')g_0(v')}=v+\sum _{n=0}^{\infty }\frac{b_n}{n+2}\,v^{n+2}. \end{aligned}$$

As suggested by (20)

$$\begin{aligned} g_4(v)=\frac{3acs^2\eta }{v^2}\left[ \left( v-2\beta v^2+\beta ^2v^3\right) +\sum _{n=-1}^{\infty } e_n\beta ^{n+1}v^{n+3}\right] . \end{aligned}$$

(27)

Here

$$\begin{aligned} e_n=\frac{B_{n+1}}{n+3}-\frac{2B_{n}}{n+2}+\frac{B_{n-1}}{n+1}= \frac{\alpha _0+\alpha _1 n+\alpha _2 n^2}{(n+1)(n+2)(n+3)} \end{aligned}$$

with

$$\begin{aligned} \alpha _0= & {} 2B_{n+1}-6B_{n}+6B_{n-1}=2\beta +2\, \frac{a_{n+1}}{\beta ^{n+1}}- 4\,\frac{a_n}{\beta ^{n}}+2\sum _{k=0}^{n-1}\frac{a_k}{\beta ^{k}}\,, \\ \alpha _1= & {} 3B_{n+1}-8B_{n}+5B_{n-1}=3\,\frac{a_{n+1}}{\beta ^{n+1}}-5\,\frac{a_n}{\beta ^{n}}\,, \\ \alpha _2= & {} B_{n+1}-2B_{n}+B_{n-1}=\frac{a_{n+1}}{\beta ^{n+1}}-\frac{a_n}{\beta ^{n}}. \end{aligned}$$

Let us calculate the limits

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _0= & {} 2\beta +2\sum _{k=0}^{\infty }\frac{P_{k+1}(\xi )}{\beta ^{k}}= 2\beta +2\beta \left[ -1+1+\sum _{k=0}^{\infty }\frac{P_{k+1} (\xi )}{\beta ^{k+1}}\right] \\= & {} \frac{2\beta }{\sqrt{1-2\xi /\beta +1/\beta ^2}}=\frac{2b^2}{a\eta }\,, \\ \lim _{n\rightarrow \infty }n\alpha _1= & {} \lim _{n\rightarrow \infty }n^2\alpha _2=0. \end{aligned}$$

As a result

$$\begin{aligned} e_n\sim \frac{2b^2}{a\eta n^{3}}. \end{aligned}$$

(28)

Passing in (27) from v to u in agreement with (16), and using relations (11), (14), (27), (28), we obtain

$$\begin{aligned} Mb^n c_n\sim 2\pi cs^2b^{n+3}n^{-3}. \end{aligned}$$

Taking into account (9) we reach

$$\begin{aligned} c_n\sim \frac{3cs^2b^3}{(1-c)a^3n^{\sigma }}\,,\qquad \sigma =3. \end{aligned}$$

(29)

Asymptotics (29) demonstrate the exactness of the estimate (2) with $\sigma =3$ for bodies from the family $\mathcal T_5$.

3.3 Laplace series for the spherical sector in the frame ${\mathcal {O}}(b)$, $b<0$

Let us pass to the frame ${\mathcal {O}}(b)$ while shifting up, $b<0$. Now $R=a+|b|=a-b$. Let us use the integral representation of the potential as in the Sect. 3.1 and put

$$\begin{aligned} R= & {} a-b,\quad u=\frac{1}{r}\,,\quad z=\frac{1-bu}{u}\,,\quad {{\tilde{\eta }}}(w)=\sqrt{w^2-2bcw+b^2}\,,\nonumber \\ {{\tilde{\xi }}}(w)= & {} \frac{b-cw}{{{\tilde{\eta }}}(w)}\,,\quad \tilde{v}(w)={{\tilde{\eta }}} u, \quad g(w,z)=\frac{1}{u} \sqrt{1-2{{\tilde{\xi }}}\tilde{v}+{{\tilde{v}}}^2}. \end{aligned}$$

(30)

When examining the behaviour of ${{\tilde{\eta }}}$, ${{\tilde{\xi }}}$ we calculate derivatives

$$\begin{aligned} \frac{d({{\tilde{\eta }}}^2)}{dw}=2(w-bc),\qquad \frac{d{{\tilde{\xi }}}}{dw}=-\frac{bs^2w}{{{\tilde{\eta }}}^3}>0. \end{aligned}$$

(31)

Evidently, ${{\tilde{\eta }}}$ takes on the greatest value at one of the endpoints of the segment [0, a]. Simple algebra leads to

$$\begin{aligned} {{\tilde{\eta }}}(0)=|b|,\qquad {{\tilde{\eta }}}(a)=\eta , \end{aligned}$$

(32)

whereas ${{\tilde{\xi }}}$ increases from ${{\tilde{\xi }}}(0)=-1$ to ${{\tilde{\xi }}}(a)=\xi$, $|\xi |<1$. Substituting (30) in (13) with due regard to (9) we obtain

$$\begin{aligned} V= & {} \frac{3M}{a^3(1-c)}\,g_8(u),\qquad g_8(u)=\frac{g_9(u)}{1-bu}\,,\qquad g_9(u)=\int _{0}^a wg_{10}(w,u)\,dw, \nonumber \\ g_{10}(w,u)= & {} 1+(w-b)u-\sqrt{1-2{{\tilde{\xi }}} {{\tilde{v}}}+{{\tilde{v}}}^2}. \end{aligned}$$

(33)

Using (61) we can represent $g_{10}$ by a series

$$\begin{aligned} g_{10}= & {} \sum _{n=0}^\infty h_n u^{n+1}, \end{aligned}$$

(34)

$$\begin{aligned} h_0= & {} w(1-c),\qquad h_n=P_{n1}({{\tilde{\xi }}}) {{\tilde{\eta }}}^{n+1},\quad n\geqslant 1. \end{aligned}$$

(35)

After integrating $wg_{10}$ term by term we obtain

$$\begin{aligned} g_9(u)=\sum _{n=0}^\infty h_{n1} u^{n+1}. \end{aligned}$$

(36)

Here

$$\begin{aligned} h_{01}=\frac{a^3(1-c)}{3}\,,\qquad h_{n1}=\int _{0}^aP_{n1}({{\tilde{\xi }}}){{\tilde{\eta }}}^{n+1}w\,dw. \end{aligned}$$

(37)

Further we ought to investigate 3 cases as in Sect. 3.2.

• 1. $a-2bc>0$ which takes place always under an acute angle $\alpha$; $R=a+|b|=a-b>\eta >|b|$, see Fig. 5.

  From the mean value theorem it follows from (37) that

  $$\begin{aligned} h_{n1}=P_{n1}({{\bar{\xi }}}_n)\int _{0}^a{{\tilde{\eta }}}^{n+1}w\,dw,\qquad -1<{{\bar{\xi }}}_n<\xi <1. \end{aligned}$$

  (38)

  An estimate of factors in the right hand side of (38) is given by the formulae (62) and (68):

  $$\begin{aligned} |h_{n1}|<\frac{H_1}{n^{5/2}}\,\eta ^{n+1},\qquad H_{1}=\frac{a\eta ^2\sqrt{2/\pi }}{a-bc}. \end{aligned}$$

  (39)

  As $|b|<\eta$, the formula (49) holds true, hence

  $$\begin{aligned} g_8(u)=\sum _{n=0}^\infty h_{n2}u^{n+1},\qquad |h_{n2}|<\frac{H_2}{n^{5/2}}\,\eta ^{n+1} \end{aligned}$$

  (40)

  with

  $$\begin{aligned} H_2=\frac{H_1}{1-\delta }\left\{ 2^{5/2}+\frac{1-\delta }{2\sqrt{\delta }} \left[ \frac{7}{e\ln (1/\delta )}\right] ^{7/2}\right\} ,\qquad \delta =\frac{|b|}{\eta }<1. \end{aligned}$$

  Finally, we obtain the estimate (7) with

  $$\begin{aligned} p=\frac{\eta }{R}=\frac{\sqrt{a^2-2abc+b^2}}{a+|b|}<1, \qquad \sigma =\frac{5}{2}\,,\qquad C=\frac{3H_2\eta }{a^3(1-c)}. \end{aligned}$$

  (41)

  It will be observed that $pR=\eta =O_1A_1$, see Fig. 5. Note that 2-dimensional sections of the sectors and spheres are pictured on the figures. In the 3-dimensional space an angular point O corresponds to a conic point of the sector, whereas angular points $A_1,A_3$ correspond to an edge of the sector; so the sector and the sphere have a common circumference.

• 2. $a-2bc=0$, which is only possible under an obtuse angle $\alpha$; $R=a+|b|=a-b>\eta =|b|$, see Fig. 6.

• 3. $a-2bc<0$, which is only possible under an obtuse angle $\alpha$; $R=O_1A_2=a+|b|=a-b>|b|>\eta$, see Fig. 7.

Combining the last two cases, we suppose $a-2bc\leqslant 0$.

Fig. 5

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b)$, $b<0$; $a-2bc>0$, enveloping sphere ${\mathbb {S}}$ touches ${\mathcal {S}}$ at the point $A_2$, $R=O_1A_2=a+|b|>\eta >|b|$; convergence sphere ${\mathbb {S}}^*$ passes through points $A_1, A_3$; left $c>0$, right $c<0$

Fig. 6

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b)$, $b<0$; $a-2bc=0$, enveloping sphere ${\mathbb {S}}$ touches ${\mathcal {S}}$ at the point $A_2$, $R=O_1A_2=a+|b|>\eta =|b|$; convergence sphere ${\mathbb {S}}^*$ passes through points $A_1, A_3, O$

Fig. 7

Section of a spherical sector T by the plane in the frame ${\mathcal {O}}(b), b<0$; $a-2bc<0$, enveloping sphere ${\mathbb {S}}$ touches ${\mathcal {S}}$ at the point $A_2$, $R=O_1A_2=a+|b|>|b|>\eta$; convergence sphere ${\mathbb {S}}^*$ passes through the point O

Direct calculations show

$$\begin{aligned} \left. \sqrt{1-2{{\tilde{\xi }}}{{\tilde{v}}}+{{\tilde{v}}}^2}\right| _{u=1/b} =\frac{w}{|b|}\,,\quad g_{10}\left( w,\frac{1}{b}\right) =\frac{2w}{b}\,,\quad D:= g_{9}\left( \frac{1}{b}\right) = \frac{2a^3}{3b}. \end{aligned}$$

The general term of the series (36) under summation in powers of u equals $h_{n-1,1}u^n$ and can be evaluated easily

$$\begin{aligned} |h_{n-1,1}|<\frac{a^2\sqrt{2/\pi }}{2(n-1)^{3/2}}\,|b|^{n}, \qquad n\geqslant 2. \end{aligned}$$

Hence, the series (36) converges absolutely if $|u|\geqslant 1/|b|$. Conditions of the “Appendix 1b” are fulfilled, and

$$\begin{aligned} \frac{g_{9}(u)-D}{1-bu}=\sum _{n=0}^\infty h_{n-1,3}u^n, \end{aligned}$$

(42)

where

$$\begin{aligned} \frac{h_{n-1,3}}{b^n}= & {} -\sum _{m=n+1}^\infty \frac{h_{m-1,1}}{b^m}=- \sum _{m=n}^\infty \frac{h_{m1}}{b^{m+1}}\,,\\ \frac{h_{n3}}{b^n}= & {} -\sum _{m=n+1}^\infty \frac{h_{m1}}{b^m}\,, \end{aligned}$$

or

$$\begin{aligned} \frac{h_{n3}}{b^n}=-\int _0^a{{\tilde{\eta }}} w\,dw\sum _{m=n+1}^\infty P_{m1}({{\tilde{\xi }}}) \left( \frac{{{\tilde{\eta }}}}{|b|}\right) ^m. \end{aligned}$$

(43)

Using inequalities ${{\tilde{\eta }}}\leqslant |b|$ and (62) we obtain

$$\begin{aligned} \left| \frac{h_{n3}}{b^n}\right|<|b|\int _0^a w\,dw\sum _{m=n+1}^\infty \frac{\sqrt{2/\pi }}{m^{3/2}}<\frac{C}{\sqrt{n}} \end{aligned}$$

(44)

with a certain constant C.

On the other hand,

$$\begin{aligned} \frac{D}{1-bu}=D+\sum _{n=0}^\infty Db^{n+1}u^{n+1}. \end{aligned}$$

A comparison with (42), (43) shows that

$$\begin{aligned} h_{n2} \sim Db^{n+1}. \end{aligned}$$

(45)

Finally, we arrive at a more informative estimate than the one given in (7):

$$\begin{aligned} c_n \sim \frac{2(-1)^np^n}{(1-c)n^\sigma }\,,\qquad p=\frac{|b|}{R}<1,\qquad \sigma =0. \end{aligned}$$

(46)

Remark

If $a-2bc=0$ (see Fig. 6), then $pR=\eta =|b|=O_1A_1=O_1A_3=O_1O$. If $a-2bc<0$ (see Fig. 7), then $pR=|b|=O_1O$.

4 Conclusion

We have examined the convergence rate of the Laplace series (1) for a certain body (spherical sector) in diverse reference frames, distinguished by a variety of origins. The compiled results can be found in the table below. Different variants we have described above are given in the first column. The class of the body’s structure is given in the second column. Parameters p and $\sigma$ are given in the third column. Comments are given in the last column.

We have settled on the following properties.

Let $\partial T$ be the surface of a compact body T, and ${\mathfrak {S}}$ be the intersection of $\partial T$ with the enveloping sphere ${\mathbb {S}}$.

• Let ${\mathfrak {S}}$ consist of a single point, and $\partial T$ be analytic in its neighbourhood. Then $\langle Y_n\rangle$ decreases in a geometrical progression according to (7), and pR equals the distance between the origin O and the nearest angular point of $\partial T$. However, the exponent $\sigma$ can vary from 0 to 5 / 2. In the general case the presence of an angular point is not necessary. The homogeneous ellipsoid of revolution (unimportant oblate or prolate) serves as an example. It was found by Laplace that p is equal to the eccentricity of the meridional section, whereas $\sigma =2$ (Antonov et al. 1988, section 4.10). Another example represents an equipotential ellipsoid of revolution with the same p and $\sigma =1$ (Caputo 1967, section 14).

• Let ${\mathfrak {S}}$ consist of a part of the sphere ${\mathbb {S}}$ with a positive area, and its boundary represent an edge of the surface $\partial T$. Then $\langle Y_n\rangle$ decreases in a power law (2) with the exact exponent $\sigma =5/2$.

• Let ${\mathfrak {S}}$ consists of a conic point of $\partial T$ with no curve beginning at this point and lying on $\partial T$ which touches the enveloping sphere. Then $\langle Y_n\rangle$ decreases as a power law (2) with the exact exponent $\sigma =3$. That is the main result of the present paper.

One may note that a spherical sector is a poor resemblence of real celestial bodies. But we can present bodies similar to real ones. Indeed, in Kholshevnikov and Shaidulin (2015a) we show that the class ${\mathcal {T}}_5$ contains smooth bodies with mountains. It is easy to choose a body $T\in {\mathcal {T}}_5$ satisfying (4) with $\sigma =3$ among them. It is sufficient to take a ball (or an ellipsoid) with a finite number of mountains. To exclude the possibility that inputs of different mountains in $Y_n$ annihilate, it is sufficient to choose one of them as a predominate one.

Variant	Class	p, $\sigma$	Comments
$b=0$	${\mathcal {T}}_3$	$p=1$, $\sigma =5/2$	Spherical part of sector’s surface lies on the enveloping sphere
$b>0$			Sector’s vertex lies inside the enveloping sphere
$a-2bc>0$	${\mathcal {T}}_3$	$p=1$, $\sigma =5/2$	Sector’s edge lies on the enveloping sphere
$b>0$			Sector’s vertex lies on the enveloping sphere
$a-2bc=0$	${\mathcal {T}}_3$	$p=1$, $\sigma =5/2$	Sector’s edge lies on the enveloping sphere
$b>0$			Sector’s vertex lies on the enveloping sphere
$a-2bc<0$	${\mathcal {T}}_5$, ${\mathcal {T}}_3$	$p=1$, $\sigma =3$	Sector’s edge lies inside the enveloping sphere
$b<0$			Sector’s edge and vertex lie inside the enveloping sphere
$a-2bc>0$	${\mathcal {T}}_3$	$p<1$, $\sigma =5/2$	The enveloping sphere is tangent to the sector
$b<0$			Sector’s edge and vertex lie inside the enveloping sphere
$a-2bc\leqslant 0$	${\mathcal {T}}_3$	$p<1$, $\sigma =0$	The enveloping sphere is tangent to the sector

Appendices

Appendix 1: Connection between Maclaurin coefficients of two functions

• 1a. Let

  $$\begin{aligned} f(z)= & {} \sum _{n=0}^{\infty } a_nz^{n+1},\qquad a_n=\frac{A_n}{(n+1)^\sigma }\gamma ^n, \qquad |A_n|\leqslant A, \nonumber \\ g(z)= & {} \frac{f(z)}{1-\beta z}=\sum _{n=0}^{\infty } b_nz^{n+1},\qquad b_n=\sum _{k=0}^{n} a_k\beta ^{n-k} :=\frac{B_n}{(n+1)^\sigma }\gamma ^n, \nonumber \\ \sigma\in & {} {\mathbb {R}},\quad 0<\beta <\gamma . \end{aligned}$$

  (47)

  Then

  $$\begin{aligned} -\infty<A_*=\varliminf A_n\leqslant \varlimsup A_n=A^*< \infty , \end{aligned}$$

  (48)

  the sequence $B_n$ is bounded

  $$\begin{aligned} |B_n|<\frac{A}{1-\delta }\times \left\{ \begin{array}{ll} 1,&{}\quad \text {if}\quad \sigma \leqslant 0,\\ 2^\sigma +\frac{1-\delta }{2\sqrt{\delta }} \left[ \frac{2(\sigma +1)}{e\ln (1/\delta )}\right] ^{\sigma +1}, &{}\quad \text {if}\quad \sigma > 0, \end{array}\right. \end{aligned}$$

  (49)

  and relations

  $$\begin{aligned} B_*=\varliminf B_n\geqslant \frac{A_*}{1-\delta }\,,\quad B^*=\varlimsup B_n\leqslant \frac{A^*}{1-\delta } \quad \text {with} \quad \delta =\frac{\beta }{\gamma }<1 \end{aligned}$$

  (50)

  are fulfilled. In particular, if the limit $\lim A_n=A^*$ exists, then the limit $\lim B_n=B^*$ exists also, and

  $$\begin{aligned} B^*=\frac{A^*}{1-\delta }. \end{aligned}$$

  (51)

  Proof Relations (48) represent a trivial corollary of the boundedness of $A_n$. It follows from (47) that

  $$\begin{aligned} B_n=\sum _{k=0}^{n} \left( \frac{n+1}{k+1}\right) ^\sigma \delta ^{n-k}A_k\,, \qquad \frac{|B_n|}{A}\leqslant \sum _{k=0}^{n} \left( \frac{n+1}{k+1}\right) ^\sigma \delta ^{n-k}:=u_n. \end{aligned}$$

  (52)

  If $\sigma \leqslant 0$, then $|B_n|< A(1-\delta )^{-1}$. Let $\sigma >0$. The last sum can be decomposed as

  $$\begin{aligned} u_n=u_{1n}+u_{2n} \end{aligned}$$

  with

  $$\begin{aligned}&u_{1n}:=\sum _{k=0}^{\lfloor n/2 \rfloor }\left( \frac{n+1}{k+1}\right) ^\sigma \delta ^{n-k}< (n+1)^\sigma \delta ^{\lceil n/2 \rceil } u_{3n}\,,\qquad u_{3n}=\sum _{k=0}^{\lfloor n/2 \rfloor } \frac{1}{(k+1)^\sigma }\,; \\&u_{2n}:= \sum _{k=\lfloor n/2 \rfloor +1}^n\left( \frac{n+1}{k+1}\right) ^\sigma \delta ^{n-k}< 2^\sigma \sum _{m=0}^{\infty }\delta ^{m}=\frac{2^\sigma }{1-\delta }. \end{aligned}$$

  If n is even and positive, then

  $$\begin{aligned} u_{3n}=1+\frac{1}{2^\sigma }+\cdots +\frac{1}{(1+n/2)^\sigma }<\frac{n+1}{2}. \end{aligned}$$

  It can be shown by induction. If n is odd, then the number of terms in the sum equals to $(n+1)/2$, and we arrive to the same inequality. Hence,

  $$\begin{aligned} 2u_{1n}<(n+1)^{\sigma +1} \delta ^{n/2}. \end{aligned}$$

  The right hand side has a maximum at

  $$\begin{aligned} n=\frac{2(\sigma +1)}{\ln (1/\delta )}-1. \end{aligned}$$

  So

  $$\begin{aligned} 2u_{1n}<\frac{1}{\sqrt{\delta }}\left[ \frac{2(\sigma +1)}{e\ln (1/\delta )}\right] ^{\sigma +1}. \end{aligned}$$

  The validity of (49) is proved for $n>0$. At $n=0$ the inequality (49) is trivial. Equalities

  $$\begin{aligned} b_{n+1}=a_{n+1}+\beta b_{n}\,,\qquad B_{n+1}=A_{n+1}+\delta \left( \frac{n+2}{n+1}\right) ^\sigma B_n \end{aligned}$$

  (53)

  follow from (47). The second formula (53) implies (Nikolsky 1977, section 3.7) that

  $$\begin{aligned} B_*\geqslant A_* +\delta B_*\,,\qquad B^*\leqslant A^* +\delta B^*. \end{aligned}$$

  (54)

  Relations (50) arise from (54). In case $A_*=A^*$ the equality (51) follows from (50).

• 1b. Let relations (47) be true except the last one, and now $\beta <0$, $|\beta |<\gamma$.

  Then inequalities (49) remain valid after replacing $\delta$ by $|\delta |$. Relations (53) are valid too. However, we get

  $$\begin{aligned} B_*\geqslant \frac{A_*-|\delta | A^*}{1-\delta ^2}\,,\qquad B^*\leqslant \frac{A^*-|\delta | A_*}{1-\delta ^2} \end{aligned}$$

  (55)

  instead of (50). If the limit $\lim A_n=A^*$ exists, then the limit $\lim B_n=B^*$ exists also, and the equality (51) holds true.

  Inequality (55) only needs a proof. Negativeness of $\delta$ implies $\varliminf \{\delta B_n\}=\delta \varlimsup B_n$, $\varlimsup \{\delta B_n\}=\delta \varliminf B_n$, see (Nikolsky 1977, section 3.7). We have now

  $$\begin{aligned} B_*\geqslant A_* -|\delta | B^*\,,\qquad B^*\leqslant A^* -|\delta | B_*\,, \end{aligned}$$

  (56)

  instead of (54). Inequalities (55) arise from (56).

• 1c. Let f(z) be holomorphic in the circle $|z|<1/|\beta |$, $\beta \ne 0$, and the series

  $$\begin{aligned} f(z)=\sum _{n=0}^{\infty } a_n\beta ^nz^n \end{aligned}$$

  converge (perhaps conditionally) at $z=1/\beta$.

  Then Maclaurin coefficients of the function

  $$\begin{aligned} g(z)=\frac{f(1/\beta )-f(z)}{1-\beta z}=\sum _{n=0}^{\infty } b_n\beta ^nz^n \end{aligned}$$

  are equal to

  $$\begin{aligned} b_n=f(1/\beta )-\sum _{m=0}^{n} a_m=\sum _{m=n+1}^{\infty } a_m. \end{aligned}$$

  (57)

  Proof Evidently,

  $$\begin{aligned} g(z)=\sum _{k=0}^{\infty }\beta ^kz^k\left[ f(1/\beta )- \sum _{m=0}^{\infty }a_m\beta ^mz^m\right] \end{aligned}$$

  in the circle $|z|<1/|\beta |$. The left equality (57) follows from it. The right equality (57) arises from the left one taking into account the convergence of the last series.

• 1d. Let

  $$\begin{aligned} f(z)= & {} \sum _{n=0}^{\infty } a_nz^{n+1},\qquad a_n=A_n\gamma ^n, \end{aligned}$$

  (58)
  $$\begin{aligned} g(z)= & {} \frac{f(z)}{1-\beta z}=\sum _{n=0}^{\infty } b_nz^{n+1},\qquad b_n=\sum _{k=0}^{n} a_k\beta ^{n-k}. \end{aligned}$$

  (59)

  Suppose

  $$\begin{aligned} \gamma>0,\qquad |\beta |>\gamma ,\qquad |A_n|\leqslant A, \qquad A>0. \end{aligned}$$

  Then

  $$\begin{aligned} b_n=B_n\beta ^n,\qquad B_n=\sum _{k=0}^{n} A_k\left( \frac{\gamma }{\beta }\right) ^{k}, \qquad |B_n|<B=\frac{A}{1-\gamma /|\beta |}. \end{aligned}$$

  (60)

  We omit an elementary proof.

Appendix 2: Representation of a certain standard function

The formula

$$\begin{aligned} \sqrt{1-2xz+z^2}=1-xz-\sum _{n=1}^{\infty }P_{n1}(x)z^{n+1} \end{aligned}$$

(61)

is valid (Antonov et al. 2010; Kholshevnikov and Shaidulin 2014) on the product of a segment $-1\leqslant x\leqslant 1$ and a circle $|z|\leqslant 1$. Here

$$\begin{aligned} P_{n1}(x)=\int _{-1}^xP_{n}(y)\,dy, \end{aligned}$$

$P_{n}$ being Legendre polynomial with the standard normalization $P_{n}(1)=1$.

Functions $P_{n1}$ have the following properties (Kholshevnikov and Shaidulin 2014, 2015b):

$$\begin{aligned} P_{n1}(\cos \theta )= & {} \sqrt{\frac{2\sin \theta }{\pi n^3}}\left\{ \cos \left[ \left( n+\frac{1}{2}\right) \theta +\frac{\pi }{4}\right] +\frac{r(n,\theta )}{n\sin \theta }\right\} ,\nonumber \\ |P_{n1}(\cos \theta )|< & {} \frac{\sqrt{2/\pi }}{n^{3/2}}. \end{aligned}$$

(62)

Here $r(n,\theta )$ is bounded under $n\geqslant 1$, $0\leqslant \theta \leqslant \pi$; the exponent 3 / 2 in the estimate of $|P_{n1}|$ is exact. Moreover, $P_{n1}(0)=0$ if n is even, and

$$\begin{aligned} P_{n1}(0)=(-1)^{(n+1)/2}\frac{(n-2)!!}{(n+1)!!}\sim (-1)^{(n+1)/2} \frac{\sqrt{2/\pi }}{n^{3/2}} \end{aligned}$$

(63)

if n is odd.

Appendix 3: Asymptotics of a certain integral

An asymptotic representation (under $\nu \rightarrow \infty$) with a remainder

$$\begin{aligned} \int y^\nu \,dx=\sum _{n=0}^{k}c_n\frac{y^{\nu +n+1}}{(x-bc)^{2n+1}}+(2k+1)c_k\int \frac{y^{\nu +k+1}\,dx}{(x-bc)^{2k+2}} \end{aligned}$$

(64)

is true. Here

$$\begin{aligned} y=x^2-2bcx+b^2,\qquad c_n=\frac{(2n-1)!!}{2^{n+1}(\nu +1)^{\overline{n+1}}}, \end{aligned}$$

the point $x_0=bc$ must not belong to the segment of integration.

To prove (64) it is sufficient to differentiate it.

Limiting ourselves to the first two terms in the right hand side of (64) we obtain

$$\begin{aligned} \int y^\nu \,dx\asymp \frac{y^{\nu +1}}{2(\nu +1)(x-bc)}+ \frac{y^{\nu +2}}{4(\nu +1)(\nu +2)(x-bc)^3}+\cdots \end{aligned}$$

(65)

As a consequence of (64) it is easy to establish, that

$$\begin{aligned} \int xy^\nu \,dx= & {} \frac{xy^{\nu +1}}{2(\nu +1)(x-bc)}+bc\sum _{n=1}^{k}c_n \frac{y^{\nu +n+1}}{(x-bc)^{2n+1}}+ \nonumber \\&+(2k+1)bcc_k\int \frac{y^{\nu +k+1}\,dx}{(x-bc)^{2k+2}}. \end{aligned}$$

(66)

Limiting ourselves to the first two terms in the right hand side we receive

$$\begin{aligned} \int xy^\nu \,dx\asymp \frac{xy^{\nu +1}}{2(\nu +1)(x-bc)}+ \frac{bc y^{\nu +2}}{4(\nu +1)(\nu +2)(x-bc)^3}+\cdots \end{aligned}$$

(67)

Let I be the integral (67) taken between 0 and a, $a>0$. We assume the possibility that $x_0\in [0,a]$. Let us prove the asymptotic representation:

$$\begin{aligned} I=\left\{ \begin{array}{ll} \frac{y^{\nu +2}(0)}{4(\nu +1)(\nu +2)(bc)^2}+\cdots ,&{}\quad \text {if}\quad a-2bc<0,\\ \frac{y^{\nu +1}(a)}{\nu +1}+\frac{2y^{\nu +2}(a)}{(\nu +1)(\nu +2)a^2}+\cdots ,&{}\quad \text {if}\quad a-2bc=0,\\ \frac{ay^{\nu +1}(a)}{2(\nu +1)(a-bc)}+\frac{bc y^{\nu +2}(a)}{4(\nu +1)(\nu +2)(a-bc)^3}+\cdots ,&{}\quad \text {if}\quad a-2bc>0. \end{array}\right. \end{aligned}$$

(68)

The variable y(x) is a downward-convex function, and takes the maximum at one of the endpoints of the segment [0, a]. We consider three cases depending on the sign of the difference $y(a)-y(0)=a(a-2bc)$.

• (a) $a-2bc<0$, $\max y(x)=y(0)>y(a)$, $bc>a/2$. If $bc>a$, then we may use (67) straightforwardly. If $a/2<bc\leqslant a$ we may restrict ourselves to an integration over the segment [0, a / 2]. Indeed,

  $$\begin{aligned}&\int _{0}^{a/2} xy^\nu \,dx\sim \frac{bc y^{\nu +2}(0)}{4(\nu +1)(\nu +2)(bc)^3}\,, \\&\int _{a/2}^{a} xy^\nu \,dx<\frac{a^2}{2}{{\bar{y}}}^\nu ,\quad \bar{y}=\max \{y(a/2),\,y(a)\}<y(0). \end{aligned}$$

• (b) $a-2bc=0$, $\max y(x)=y(a)=y(0)$. The function y(x) is symmetric with respect to the point $x_0=bc=a/2$. After the substitution $x=x_0+z$ we have

  $$\begin{aligned} I=\frac{a}{2}\int _{-a/2}^{a/2} y^\nu \,dz+\int _{-a/2}^{a/2} zy^\nu \,dz= a\int _{0}^{a/2} y^\nu \,dz=a\int _{a/2}^{a} y^\nu \,dx. \end{aligned}$$

  The last integral over the segment from a / 2 to 3a / 4 may be thrown off. For the integral from 3a / 4 to a we may use (65).

• (c) $a-2bc>0$, $\max y(x)=y(a)>y(0)$. If $bc<0$, then $x_0$ lies out of the segment of integration, and (68) follows from (67). Let $bc\geqslant 0$. Then $bc<a/2$, $a-bc>a/2$, so

  $$\begin{aligned} \int _{0}^{a/2} xy^\nu \,dx<\frac{a^2}{8}{{\bar{y}}}^\nu ,\quad \bar{y}=\max \{y(0),\,y(a/2)\}<y(a). \end{aligned}$$

  For the integral between a / 2 and a we may use the formula (67).