First-order analytic propagation of satellites in the exponential atmosphere of an oblate planet

Abstract

The paper offers the fully analytic solution to the motion of a satellite orbiting under the influence of the two major perturbations, due to the oblateness and the atmospheric drag. The solution is presented in a time-explicit form, and takes into account an exponential distribution of the atmospheric density, an assumption that is reasonably close to reality. The approach involves two essential steps. The first one concerns a new approximate mathematical model that admits a closed-form solution with respect to a set of new variables. The second step is the determination of an infinitesimal contact transformation that allows to navigate between the new and the original variables. This contact transformation is obtained in exact form, and afterwards a Taylor series approximation is proposed in order to make all the computations explicit. The aforementioned transformation accommodates both perturbations, improving the accuracy of the orbit predictions by one order of magnitude with respect to the case when the atmospheric drag is absent from the transformation. Numerical simulations are performed for a low Earth orbit starting at an altitude of 350 km, and they show that the incorporation of drag terms into the contact transformation generates an error reduction by a factor of 7 in the position vector. The proposed method aims at improving the accuracy of analytic orbit propagation and transforming it into a viable alternative to the computationally intensive numerical methods.

1 Introduction

The accurate orbit prediction for satellites in low Earth orbit (LEO) is vital for space missions, from the design phase until the satellite decommissioning and beyond. The growing number of space debris catalogued objects (expected to increase tenfold in the near future, reaching about 200,000 tracked objects¹) poses a real threat to LEO satellites, and therefore the ability to simultaneously propagate a large number of orbits becomes essential to mission safety. Today, there are three main paradigms of realistic orbit prediction: analytic, numeric and semi-analytic. Analytic approaches involve the replacement of the original equations of motion with a new set, that is integrable and captures the essential character of the motion. Their prediction accuracy decreases with time, but they offer a fast and computationally light method to evaluate the position and the velocity on short time scales, that is enough for low Earth orbit (LEO) satellites.² We propose the convention to address an orbit propagation technique by “analytic” if it involves no iterative methods, but only algebraic explicit equations. Some authors address the aforementioned paradigm with the term “entirely analytic” (Vallado 2001). If a propagator is based solely on numerical integration schemes, it is addressed with the term “numeric”, and any combination of the two aforementioned paradigms is called semi-analytic.

The main drawback of numerical methods is that they are very slow and require considerable computational capabilities. In addition, onboard propagation needs to accommodate very low computational resources, that are shared between several mission control algorithms. In this context, the replacement of numerical methods by analytic propagators represents an interesting alternative. On the other hand, although there are several analytic propagation methods available in the literature, very few come with a full documentation package and only a small part of them exhibit ellasticity with regard to the perturbing forces. For example, the widely used Simplified General Perturbations (SGP) propagator family, initially introduced by Hilton and Kuhlman (1966), improved by Lane et al. (1969) and available today as SGP4/8 (LEO) and SDP4/8 (deep space) (full documentation available in Vallado et al. 2006), uses an atmospheric model based on power density functions and it is not adaptable for other atmospheric models.

The main challenge for the analytic propagation of space orbits is brought by the perturbations that act upon satellites. The two dominant perturbations for LEO satellites are the Earth oblateness (modeled by the $J_{2}$ zonal harmonic coefficient) and the atmospheric drag. A smaller contribution is made by the solar radiation pressure, but its effect for short-term propagation (up to a few days) is negligible. Long-term accurate propagation for LEO satellites is non-realistic, given the presence of large amounts of uncertainties (see Dell’Elce and Kerschen 2014).

The Main Problem in Artificial Satellite Theory deals with the realistic analytic or semi-analytic propagation of satellites under the combined effect of the aforementioned perturbations, which are of different nature. The oblateness perturbation is conservative (although it exhibits a weakly-chaotic behaviour, see Irigoyen and Simo 1993; Celletti and Negrini 1995), and may be approached (if considered separately) by classic canonical perturbation methods, as in Brouwer (1959), Deprit (1981), Cid and Lahulla (1969). The atmospheric drag is a dissipative perturbation, and therefore it cannot be tackled by the aforementioned methods.

The first and perhaps most widely used analytic solution to the $J_{2}$ problem was proposed by Brouwer (1959), although several other methods were previously proposed by Sterne (1958) and Garfinkel (1959). Brouwer’s original solution is obtained through the Poincaré–von Zeipel approach (see Zeipel 1916) and contains several singularities (for circular, equatorial and critically inclined orbits). The first two were removed by Lyddane (1963), while the singularity at the critical inclination was avoided (but not removed³), under very restrictive assumptions, by Vinti (1960). One major drawback of the von Zeipel method is that it involves non-explicit canonical transformations (a feature exhibited by all conventional approaches, see Goldtsein et al. 2002). This inconvenient was overcome by Deprit (1969), who proposed a method based on Lie transforms,⁴ that are fundamentally involved in his orbit propagation approach through the natural intermediaries paradigm introduced in Deprit (1981). In the quest for orbit propagators that may be implemented onboard small satellites, Deprit’s method saw a recent revival, as in Lara and Gurfil (2012), Gurfil and Lara (2014).

The combined effect of oblateness and atmospheric drag complicates the development of an analytic solution. Brouwer and Hori (1961) proposed the same Poincaré–von Zeipel method for the treatment of both perturbations, but their solution is not fully analytic since it requires numerical manipulations. Barrio and Palacián (2003) propose an analytic approach to the combined effect of oblateness and the drag produced by an exponentially distributed atmospheric density on very eccentric orbits (like the geostationary transfer ones), but without reaching explicit equations of motion.

A recent successful attempt to provide an approximate time-explicit solution for the combined effect of the Earth’s oblateness and atmospheric drag was recently published in Martinusi et al. (2015). However, these developments were carried out under the relatively strong assumption of constant atmospheric density, and therefore the model’s validity is limited to orbits with very low eccentricities (${\mathcal {O}} \left( e^{2}\right) \simeq 0$).

The present paper considers the motion of a LEO satellite under the influence of the $J_2$ perturbation and of an exponential atmosphere. It follows a similar propagation paradigm as the one proposed by Deprit. The original mathematical model—a non-integrable system of nonlinear ordinary differential equations (ODE)—is transformed into an integrable one, that admits a time-explicit solution. This time-explicit solution represents the first contribution of the paper. This solution is then expressed with respect to a new set of variables, that are linked to the original variables by a so-called contact transformation. Unlike the Brouwer–Hori approach from Brouwer and Hori (1961) and adopting the method proposed by Barrio and Palácian (1997), we propose to include the drag terms in the contact transformation, which is the second contribution of this research. The major improvement with respect to the work of Barrio and Palacián (2003) is that both the solution to the approximate equations of motion and the infinitesimal contact transformation are first given in closed-form and then they are made explicit by using standard numerical approximations techniques.

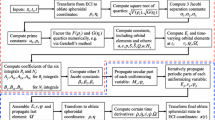
The paper is organized as follows. Section 2 offers the analytic solution to the new ODE system (obtained through a classic averaging method) in Delaunay variables. The solution involves the inverse of the complex error function ${{\mathrm{erfi}}}$, and therefore a numeric implementation scheme by using series expansions is proposed in the Appendix. The final expressions are given in the non-singular Poincaré canonical variables. Section 3 presents the contact transformation, that is determined by using both Poincaré and polar-nodal variables, and exhibits no singularities. The transformation is built in two stages, one for the conservative part (by using the simplification proposed by Lara 2015a) and one for the non-conservative part. Again, a numerical scheme for the explicit series approximation of the contact transformation is developed in the Appendix. In this way, the proposed model is fully reproducible and easily implementable by using only elementary standard library functions. Section 4 provides a comparison between the method introduced herein and the drag-free contact transformation approach (while keeping the analytic solution for the new system). Section 5 summarizes the main findings of this paper.

2 The analytic solution

2.1 Problem formulation

Denote by ${\mathbf {f}}_{J_{2}}$and ${\mathbf {f}}_{drag}$ the perturbing accelerations due to the oblateness and the atmospheric drag, respectively. The mathematical model for a satellite orbiting in the atmosphere of an oblate planet is the initial value problem (IVP):

$$\begin{aligned} \ddot{{\mathbf {r}}}+\frac{\mu }{r^{3}}{\mathbf {r}}={\mathbf {f}}_{J_{2}}+{\mathbf {f}} _{drag},\quad {\mathbf {r}}\left( t_{0}\right) ={\mathbf {r}}_{0},\quad \dot{{\mathbf {r}}} \left( t_{0}\right) ={\mathbf {v}}_{0} \end{aligned}$$

(1)

where $\mu$ is Earth’s gravitational parameter, $t_{0}\ge 0$ the initial moment of time. Consider the Keplerian classical orbital elements ${\mathcal {O}}_{K}=\left( a,e,i,\omega ,\varOmega ,M\right) ,$ let f be the true anomaly and denote:

$$\begin{aligned} n=\sqrt{\frac{\mu }{a^{3}}},\eta =\sqrt{1-e^{2}},\kappa =e\cos f,\sigma =e\sin f,\quad p=a\eta ^{2},c=\cos i,s=\sin i \end{aligned}$$

Assume an exponential distribution of the atmospheric density, expressed at an altitude H as:

$$\begin{aligned} \rho \left( H\right) =\frac{1}{2}C_{D}\frac{S_{ref}}{m}\rho _{0}\exp \left( - \frac{H-H_{0}}{\alpha }\right) \end{aligned}$$

(2)

where the constants involved in Eq. (2) are defined as follows: $H_{0}$ is a reference altitude, $\rho _{0}$ is the density associated at this altitude, $\alpha$ is a constant (the density scale factor), $C_{D}$ is the drag coefficient, m the mass of the satellite and $S_{ref}$ its cross-sectional area, orthogonal to the velocity direction. Denote by ${\mathbf {i}}_{z}$ the unit vector of Earth’s rotation axis, pointing North, and let $J_{2}$ be the second zonal harmonic coefficient. Denote by $r_{eq}$ the Earth’s mean equatorial radius and by $\widehat{{\mathbf {r}}}={\mathbf {r}} /\left\| {\mathbf {r}}\right\|$ the unit vector associated to ${\mathbf {r}}$ and by $r=\left\| {\mathbf {r}}\right\|$ its magnitude. Let $r_{0}$ be the magnitude of the initial position vector. Denote:

$$\begin{aligned} k_{2}=\frac{\mu J_{2}r_{eq}^{2}}{4};\quad C_{0}=\frac{1}{2}C_{D}\frac{S_{ref}}{ m}\rho _{0};\quad C_{u}=\mu C_{0}\sqrt{1+\left( \frac{\sigma }{1+\kappa } \right) ^{2}}\exp \left( -\frac{r-r_{0}}{\alpha }\right) \end{aligned}$$

(3)

In Eq. (3), the link between the satellite’s latitude and altitude, due to the Earth’s oblateness, is ignored. The expressions of the peturbing accelerations, in an Earth-centerd inertial frame (ECI), are:

$$\begin{aligned} {\mathbf {f}}_{J_{2}}= & {} -\frac{3k_{2}}{2r^{4}}\left\{ \left[ 1-5\left( \frac{ {\mathbf {r}}\cdot {\mathbf {i}}_{z}}{r}\right) ^{2}\right] \widehat{{\mathbf {r}}} +2\left( \frac{{\mathbf {r}}\cdot {\mathbf {i}}_{z}}{r}\right) {\mathbf {i}} _{z}\right\} \\ {\mathbf {f}}_{drag}= & {} -C_{0}\exp \left( -\frac{r-r_{0}}{\alpha }\right) \left\| \dot{{\mathbf {r}}}\right\| \dot{{\mathbf {r}}} \end{aligned}$$

Let ${\mathbf {h}}={\mathbf {r}}\times \dot{{\mathbf {r}}}$ denote the instantaneous angular momentum vector. Introduce the Local–Vertical–Local–Horizontal (LVLH) frame associated to the satellite, defined by its unit vectors

$$\begin{aligned} {\mathbf {i}}_{1}=\widehat{{\mathbf {r}}};\quad {\mathbf {i}}_{2}=\widehat{{\mathbf {h}}} \times \widehat{{\mathbf {r}}};\quad {\mathbf {i}}_{3}=\widehat{{\mathbf {h}}} \end{aligned}$$

In this frame, vectors ${\mathbf {r,v}}$ and ${\mathbf {i}}_{z}$ have the Cartesian components:

$$\begin{aligned} {\mathbf {r}}=\left[ \begin{array}{c} r \\ 0 \\ 0 \end{array} \right] ;\quad {\mathbf {v}}=\left[ \begin{array}{c} \dot{r} \\ G/r \\ 0 \end{array} \right] ;\quad {\mathbf {i}}_{z}={\mathbf {R}}\left( {\mathbf {i}}_{3},\varOmega \right) {\mathbf {R}}\left( {\mathbf {i}}_{1},i\right) {\mathbf {R}}\left( {\mathbf {i}} _{3},\theta \right) \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] , \end{aligned}$$

where the rotation matrices ${\mathbf {R}}\left( {\mathbf {i}}_{1,3},\beta \right)$ are defined as:

$$\begin{aligned} {\mathbf {R}}\left( {\mathbf {i}}_{1},\beta \right) =\left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos \beta &{} -\sin \beta \\ 0 &{} \sin \beta &{} \cos \beta \end{array} \right] ;\quad {\mathbf {R}}\left( {\mathbf {i}}_{3},\beta \right) =\left[ \begin{array}{ccc} \cos \beta &{} -\sin \beta &{} 0 \\ \sin \beta &{} \cos \beta &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] ,\;\beta \in {\mathbb {R}} \end{aligned}$$

With respect to the LVLH frame, the perturbing accelerations have the expressions:

$$\begin{aligned} {\mathbf {f}}_{J_{2}}^{LVLH}=-\frac{3k_{2}}{r^{4}}\left[ \begin{array}{c} 1-3\sin ^{2}i\sin ^{2}\theta \\ \sin ^{2}i\sin 2\theta \\ \sin 2i\sin \theta \end{array} \right] ;\quad {\mathbf {f}}_{drag}^{LVLH}=-\frac{C_{u}}{r}\left[ \begin{array}{c} \sigma \\ 1+\kappa \\ 0 \end{array} \right] \end{aligned}$$

Denote:

$$\begin{aligned} {\mathbf {f}}={\mathbf {f}}_{J_{2}}^{LVLH}+{\mathbf {f}}_{drag}^{LVLH},\quad f_{r}= {\mathbf {f}}\cdot {\mathbf {i}}_{1},\quad f_{\theta }={\mathbf {f}}\cdot {\mathbf {i}} _{2},\quad f_{h}={\mathbf {f}}\cdot {\mathbf {i}}_{3} \end{aligned}$$

Equation (1) is now transformed into classical orbital elements and expressed with respect to $f_{r,\theta ,h},$ leading to Gauss’ variational equations (GVE) Battin (1999):

$$\begin{aligned} \frac{\text {d}a}{\text {d}t}= & {} \frac{2p^{2}}{\eta ^{4}G}\left[ \sigma f_{r}+\left( 1+\kappa \right) f_{\theta }\right] \end{aligned}$$

(4a)

$$\begin{aligned} \frac{\text {d}e}{\text {d}t}= & {} \frac{p}{G}\left[ f_{r}\sin f+\frac{\left( 2+\kappa \right) \cos f+e}{1+\kappa }f_{\theta }\right] \end{aligned}$$

(4b)

$$\begin{aligned} \frac{\text {d}i}{\text {d}t}= & {} \frac{r\cos \theta }{G}f_{h} \end{aligned}$$

(4c)

$$\begin{aligned} \frac{\text {d}\omega }{\text {d}t}= & {} \frac{p}{Ge^{2}}\left[ -\kappa f_{r}+\sigma \frac{2+\kappa }{1+\kappa }f_{\theta }\right] -\frac{cr\sin \theta }{sG}f_{h} \end{aligned}$$

(4d)

$$\begin{aligned} \frac{\text {d}\varOmega }{\text {d}t}= & {} \frac{r\sin \theta }{sG}f_{h} \end{aligned}$$

(4e)

$$\begin{aligned} \frac{\text {d}M}{\text {d}t}= & {} \frac{\eta ^{3}G}{p^{2}}+\frac{p\eta }{Ge^{2}} \left[ \frac{\kappa -\kappa ^{2}-2\sigma ^{2}}{1+\kappa }f_{r}-\sigma \frac{ 2+\kappa }{1+\kappa }f_{\theta }\right] \\ a\left( t_{0}\right)= & {} a_{0};\;e\left( t_{0}\right) =e_{0};\;i\left( t_{0}\right) =i_{0};\;\omega \left( t_{0}\right) =\omega _{0};\;\varOmega \left( t_{0}\right) =\varOmega _{0};\;M\left( t_{0}\right) =M_{0}\nonumber \end{aligned}$$

(4f)

In order to apply the proposed perturbation method, Eq. (4) are transformed in action-angle variables. To this end, the Delaunay variables $\left( l,g,h,L,G,H\right)$ are defined as:

$$\begin{aligned} l=M,\quad g=\omega ,\quad h=\varOmega ,\quad L=\sqrt{\mu a},\quad G=\eta \sqrt{\mu a} ,\quad H=\eta \sqrt{\mu a}\cos i \end{aligned}$$

The counterparts of Eq. (4) in Delaunay variables are:

$$\begin{aligned} \frac{\text {d}l}{\text {d}t}= & {} n+\frac{\eta p}{Ge^{2}}\left[ \frac{\kappa -\kappa ^{2}-2\sigma ^{2}}{1+\kappa }f_{r}-\sigma \frac{2+\kappa }{1+\kappa } f_{\theta }\right] \end{aligned}$$

(5a)

$$\begin{aligned} \frac{\text {d}g}{\text {d}t}= & {} \frac{p}{Ge^{2}}\left[ -\kappa f_{r}+\sigma \frac{2+\kappa }{1+\kappa }f_{\theta }-\frac{e^{2}c\sin \theta }{s\left( 1+\kappa \right) }f_{h}\right] \end{aligned}$$

(5b)

$$\begin{aligned} \frac{\text {d}h}{\text {d}t}= & {} \frac{r\sin \theta }{Gs}f_{h} \end{aligned}$$

(5c)

$$\begin{aligned} \frac{\text {d}L}{\text {d}t}= & {} \frac{p}{\eta ^{3}}\left[ \sigma f_{r}+\left( 1+\kappa \right) f_{\theta }\right] \end{aligned}$$

(5d)

$$\begin{aligned} \frac{\text {d}G}{\text {d}t}= & {} rf_{\theta } \end{aligned}$$

(5e)

$$\begin{aligned} \frac{\text {d}H}{\text {d}t}= & {} r\left[ cf_{\theta }-s\left( \cos \theta \right) f_{h}\right] \end{aligned}$$

(5f)

with the initial conditions:

$$\begin{aligned} l\left( t_{0}\right) =l_{0};\quad g\left( t_{0}\right) =g_{0};\quad h\left( t_{0}\right) =h_{0};\quad L\left( t_{0}\right) =L_{0};\quad G\left( t_{0}\right) =G_{0};\quad H\left( t_{0}\right) =H_{0} \end{aligned}$$

2.2 Averaging and explicit solution

Since on average the atmospheric drag has no effect on the angle variables l, g, h,  their averaged equations will be identical to those from the $J_{2}$-only model. On the other hand, the averaged variation of the action variables L, G, H depends only on the atmospheric drag, and their Taylor series expansions are:

$$\begin{aligned} \frac{\text {d}L}{\text {d}t}= & {} -\frac{1}{2\pi \alpha }C_{0}\left( \kappa L^{2}+\mu \alpha \right) \exp \left( -\frac{\overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) +{\mathcal {O}}\left( e^{2}\right) \end{aligned}$$

(6a)

$$\begin{aligned} \frac{\text {d}G}{\text {d}t}= & {} -\frac{1}{2\pi \alpha }C_{0}\left[ \kappa \left( L^{2}-2\mu \alpha \right) +\mu \alpha \right] \exp \left( -\frac{ \overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) +{\mathcal {O}}\left( e^{2}\right) \end{aligned}$$

(6b)

$$\begin{aligned} \frac{\text {d}H}{\text {d}t}= & {} -\frac{c}{2\pi \alpha }C_{0}\left[ \kappa \left( L^{2}-2\mu \alpha \right) +\mu \alpha \right] \exp \left( -\frac{ \overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) +{\mathcal {O}}\left( e^{2}\right) \end{aligned}$$

(6c)

Introduce the new variables $\overline{{\mathbf {X}}}=\left[ \overline{l},\overline{g},\overline{h},\overline{L},\overline{G},\overline{H}\right] ^{T}$, satisfying the IVP:

$$\begin{aligned} \frac{\text {d}\overline{{\mathbf {X}}}}{\text {d}t}=\frac{1}{T}\int _{0}^{T}\frac{ \text {d}{\mathbf {X}}}{\text {d}t}\text {d}t,\quad \overline{{\mathbf {X}}}\left( t_{0}\right) =\overline{{\mathbf {X}}}_{0} \end{aligned}$$

(7)

Denote $\overline{c}=\overline{H}/\overline{G},\;\overline{\eta }=\overline{G }/\overline{L}.$ Equation (7) yields:

$$\begin{aligned} \frac{\text {d}\overline{l}}{\text {d}t}= & {} \frac{\mu ^{2}}{\overline{L}^{3}}+ \frac{3k_{2}\mu ^{3}}{\overline{\eta }^{3}\overline{L}^{7}}\left( -1+3 \overline{c}^{2}\right) \end{aligned}$$

(8a)

$$\begin{aligned} \frac{\text {d}\overline{g}}{\text {d}t}= & {} \frac{3k_{2}\mu ^{3}}{\overline{ \eta }^{4}\overline{L}^{7}}\left( -1+5\overline{c}^{2}\right) \end{aligned}$$

(8b)

$$\begin{aligned} \frac{\text {d}\overline{h}}{\text {d}t}= & {} -\frac{6k_{2}\mu ^{3}}{\overline{ \eta }^{4}\overline{L}^{7}}\overline{c} \end{aligned}$$

(8c)

$$\begin{aligned} \frac{\text {d}\overline{L}}{\text {d}t}= & {} -\mu C_{0}\exp \left( -\frac{ \overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) \end{aligned}$$

(8d)

$$\begin{aligned} \frac{\text {d}\overline{G}}{\text {d}t}= & {} -\mu C_{0}\exp \left( -\frac{ \overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) \end{aligned}$$

(8e)

$$\begin{aligned} \frac{\text {d}\overline{H}}{\text {d}t}= & {} -\overline{c}\mu C_{0}\exp \left( - \frac{\overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) \\ \overline{l}\left( t_{0}\right)= & {} \overline{l}_{0};\quad \overline{g}\left( t_{0}\right) =\overline{g}_{0};\quad \overline{h}\left( t_{0}\right) =\overline{h }_{0};\quad \overline{L}\left( t_{0}\right) =\overline{L}_{0};\quad \overline{G} \left( t_{0}\right) =\overline{G}_{0};\quad \overline{H}\left( t_{0}\right) = \overline{H}_{0}\nonumber \end{aligned}$$

(8f)

An essential remark needs to be made at this point. Conceptually, regardless the method by which Eqs. (8d–8f) were obtained, we choose these equations to be the analytic approximation of the original equations of motion, and the contribution of higher-order eccentricity terms will display in the contact transformation (presented further in the paper). Because of the Taylor series truncation, Eqs. (8d–8f) do not obey the “optimality” condition to be the exact average of the equations of motion, since they differ from this value by terms of order ${\mathcal {O}}\left( e^{2}\right) .$ This choice has been made in order to make the determination of a closed-form solution possible. Obviously, this choice introduces a trade between accuracy and speed, but the comprehensive analysis of the error injection due to this manipulation is beyond the scope of this paper.

Note that $\overline{c}=\cos \overline{i}$ remains constant. This will significantly simplify the path towards the closed-form solution to Eqs. (8a)–(8c). These equations are decoupled from the full system and solved first. Eq. (8d) is straightforwardly integrated, yielding:

$$\begin{aligned} \frac{1}{2}\sqrt{\pi }\sqrt{\mu \alpha }\exp \left( -\frac{r_{0}}{\alpha } \right) \left[ {{\mathrm{erfi}}}\left( \frac{\overline{L}}{\sqrt{\mu \alpha }}\right) - {{\mathrm{erfi}}}\left( \frac{\overline{L}_{0}}{\sqrt{\mu \alpha }}\right) \right] =-\mu C_{0}\left( t-t_{0}\right) , \end{aligned}$$

(9)

where ${{\mathrm{erfi}}}\left( \cdot \right)$ is the complex error function, defined as:

$$\begin{aligned} {{\mathrm{erfi}}}\left( x\right) =\frac{2}{\sqrt{\pi }}\int \limits _{0}^{x}\exp \left( u^{2}\right) \text {d}u,\quad \left( \forall \right) x\in {\mathbb {R}} \end{aligned}$$

The explicit expression of $\overline{L}$ is obtained from Eq. (9), yielding the explicit solution for Eqs. (8e, 8f):

$$\begin{aligned} \overline{L}\left( t\right)= & {} \sqrt{\mu \alpha }{{\mathrm{erfi}}}^{-1}\left[ {{\mathrm{erfi}}}\left( \frac{\overline{L}_{0}}{\sqrt{\mu \alpha }}\right) -\frac{2}{\sqrt{ \pi }}\sqrt{\frac{\mu }{\alpha }}C_{0}\left( t-t_{0}\right) \exp \left( \frac{r_{0}}{\alpha }\right) \right] \end{aligned}$$

(10a)

$$\begin{aligned} \overline{G}\left( t\right)= & {} \overline{L}\left( t\right) +\overline{G}_{0}- \overline{L}_{0} \end{aligned}$$

(10b)

$$\begin{aligned} \overline{H}\left( t\right)= & {} \overline{c}\overline{G}\left( t\right) \end{aligned}$$

(10c)

To obtain the solution to Eqs. (8a)–(8c), a change of variable is performed. From Eq. (8d) it follows that d$\overline{L} /$d$t<0,$ making $\overline{L}$ a good candidate for the new independent variable. Equations (8a)–(8c) are recast into:

$$\begin{aligned} \frac{\text {d}\overline{l}}{\text {d}\overline{L}}= & {} -C_{0}\left[ \frac{\mu ^{3}}{\overline{L}^{3}}+\frac{3k_{2}\mu ^{4}}{\overline{\eta }^{3}\overline{L }^{7}}\left( -1+3\overline{c}^{2}\right) \right] \exp \left( \frac{\overline{ L}^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \end{aligned}$$

(11a)

$$\begin{aligned} \frac{\text {d}\overline{g}}{\text {d}\overline{L}}= & {} -C_{0}\frac{3k_{2}\mu ^{4}}{\overline{\eta }^{4}\overline{L}^{7}}\left( -1+5\overline{c} ^{2}\right) \exp \left( \frac{\overline{L}^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \end{aligned}$$

(11b)

$$\begin{aligned} \frac{\text {d}\overline{h}}{\text {d}\overline{L}}= & {} C_{0}\frac{6k_{2}\mu ^{4}}{\overline{\eta }^{4}\overline{L}^{7}}\overline{c}\exp \left( \frac{ \overline{L}^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \end{aligned}$$

(11c)

The integration of Eq. (11) yields:

$$\begin{aligned} \overline{l}\left( \overline{L}\right)= & {} \overline{l}_{0}-\mu ^{3}C_{0}I_{1}-3\mu ^{4}k_{2}C_{0}\left( -1+3\overline{c}^{2}\right) I_{2} \end{aligned}$$

(12a)

$$\begin{aligned} \overline{g}\left( \overline{L}\right)= & {} \overline{g}_{0}-3\mu ^{4}k_{2}C_{0}\left( -1+5\overline{c}^{2}\right) I_{3} \end{aligned}$$

(12b)

$$\begin{aligned} \overline{h}\left( \overline{L}\right)= & {} \overline{h}_{0}+6\mu ^{4}k_{2}C_{0}I_{3}\overline{c} \end{aligned}$$

(12c)

with $I_{1,2,3}$ defined as:

$$\begin{aligned} I_{1}= & {} \int \limits _{\overline{L}_{0}}^{\overline{L}}\frac{1}{u^{3}}\exp \left( \frac{u^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \text {d}u \end{aligned}$$

(13a)

$$\begin{aligned} I_{2}= & {} \int \limits _{\overline{L}_{0}}^{\overline{L}}\frac{1}{\left( u+ \overline{G}_{0}-\overline{L}_{0}\right) ^{3}u^{4}}\exp \left( \frac{ u^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \text {d}u \end{aligned}$$

(13b)

$$\begin{aligned} I_{3}= & {} \int \limits _{\overline{L}_{0}}^{\overline{L}}\frac{1}{\left( u+ \overline{G}_{0}-\overline{L}_{0}\right) ^{4}u^{3}}\exp \left( \frac{ u^{2}-\mu \overline{r}_{0}}{\mu \alpha }\right) \text {d}u \end{aligned}$$

(13c)

Equations (10) and (12) represent the closed-form solution for the truncated averaged equations of motion (8) of a LEO satellite under the combined influence of the $J_{2}$ perturbation and of an exponential atmosphere.

Although the solution to the approximate model was determined in closed-form, owing to the presence of the inverse of the complex error function, its practical usage is bounded to numerical errors, because small differences between very large numbers have to be evaluated. In addition, only $I_{1}$ can be explicitly expressed with the help of elementary functions:

$$\begin{aligned} I_{1}=\left. -\frac{1}{2}\left[ \frac{1}{u^{2}}\exp \left( \frac{u^{2}}{\mu \alpha }\right) +\frac{1}{\mu \alpha }{{\mathrm{Ei}}}\left( 1,-\frac{u^{2}}{\mu \alpha } \right) \right] \exp \left( -\frac{r_{0}}{\alpha }\right) \right| _{u= \overline{L}_{0}}^{u=\overline{L}} \end{aligned}$$

(14)

where ${{\mathrm{Ei}}}\left( \cdot \right)$ denotes the exponential integral:

$$\begin{aligned} {{\mathrm{Ei}}}\left( m,z\right) =\int \limits _{1}^{\infty }u^{-m}\exp \left( -zu\right) \text {d}u,\;\left( \forall \right) \left( m,z\right) \in {\mathbb {R}} \times {\mathbb {C}} \end{aligned}$$

The presence of the exponential integral function adds more complexity to the practical implementation of the equations of motion. For these reasons, the solution through Lie series expansion of Eq. (8d) will be used instead of Eq. (10a), while integrals $I_{1,2,3}$ are evaluated through regular Taylor series expansions of the exponential function. The approximate expressions of $\overline{L}\left( t\right)$ and $I_{1,2,3}$ are derived in “Lie series approximation for $\overline{L}$” and “Evaluation of $I_{1,2,3}$ integrals” sections in Appendix, respectively, and are validated by comparison with the numerical integration of IVP (8).

Although singular for equatorial or circular orbits, the explicit expressions of the averaged classical orbital elements are displayed here for the sake of tradition:

$$\begin{aligned} \bar{a}\left( t\right)= & {} \alpha \left\{ {{\mathrm{erfi}}}^{-1}\left[ {{\mathrm{erfi}}}\left( \sqrt{ \frac{\overline{a}_{0}}{\alpha }}\right) -\frac{2K_{0}}{\sqrt{\pi }}\sqrt{ \frac{\mu }{\alpha }}\left( t-t_{0}\right) \right] \right\} ^{2} \end{aligned}$$

(15a)

$$\begin{aligned} \bar{e}\left( t\right)= & {} \left\{ \dfrac{\bar{a}\left( t\right) }{\bar{a}_{0} }\left( 1-\overline{\eta }_{0}\right) \left[ 2\sqrt{\dfrac{\bar{a}\left( t\right) }{\bar{a}_{0}}}-1+\overline{\eta }_{0}\right] \right\} ^{\frac{1}{2} } \end{aligned}$$

(15b)

$$\begin{aligned} \overline{i}\left( t\right)= & {} \overline{i}_{0} \end{aligned}$$

(15c)

$$\begin{aligned} \overline{\omega }\left( t\right)= & {} \overline{\omega }_{0}-3\mu ^{4}k_{2}C_{0}\left( -1+5\cos ^{2}\overline{i}\right) I_{3} \end{aligned}$$

(15d)

$$\begin{aligned} \overline{\varOmega }\left( t\right)= & {} \overline{\varOmega }_{0}+6\mu ^{4}k_{2}C_{0}I_{3}\cos \overline{i} \end{aligned}$$

(15e)

$$\begin{aligned} \overline{M}\left( t\right)= & {} \overline{M}_{0}-\mu ^{3}C_{0}I_{1}-3\mu ^{4}k_{2}C_{0}\left( -1+3\cos ^{2}\overline{i}\right) I_{2} \end{aligned}$$

(15f)

where $\overline{\eta }_{0},K_{0}$ are defined as:

$$\begin{aligned} \overline{\eta }_{0}=\sqrt{1-\overline{e}_{0}^{2}},\quad K_{0}=C_{0}\exp \left( \frac{r_{0}}{\alpha }\right) \end{aligned}$$

2.3 Singularity removal

Delaunay variables were the simplest choice for determining the equations of motion in closed-form. However, they are singular for zero eccentricity and for equatorial orbits. Introduce the Poincaré canonical coordinates $\left( Q_{1},Q_{2},Q_{3},P_{1},P_{2},P_{3}\right)$:

$$\begin{aligned} \begin{array}{lllll} Q_{1}=l+g+h, &{} \quad Q_{2}=-\sqrt{2\left( L-G\right) }\sin \left( g+h\right) , &{} \quad Q_{3}=-\sqrt{2\left( G-H\right) }\sin h \\ &{} &{} &{} &{} \\ P_{1}=L, &{} \quad P_{2}=\sqrt{2\left( L-G\right) }\cos \left( g+h\right) , &{} \quad P_{3}=\sqrt{2\left( G-H\right) }\cos h \end{array} \end{aligned}$$

(16)

By using the Jacobian of the transformation from Delaunay to Poincaré variables (developed in “Jacobian for coordinate transformations” section in Appendix), as well as the equations of motion (10) and (12), the solution is expressed as:

$$\begin{aligned} \overline{Q}_{1}= & {} \overline{Q}_{1}\left( t_{0}\right) +C_{0}\mu ^{3}\left\{ -I_{1}+3\mu k_{2}\left[ \left( 1-3\overline{c}^{2}\right) I_{2}+\left( 5c^{2}-2c-1\right) I_{3}\right] \right\} \end{aligned}$$

(17a)

$$\begin{aligned} \overline{Q}_{2}= & {} \sqrt{\overline{Q}_{2}^{2}\left( t_{0}\right) +\overline{ P}_{2}^{2}\left( t_{0}\right) }\sin \left[ \overline{g}_{0}+\overline{h} _{0}+3\mu ^{4}C_{0}k_{2}\left( 5c^{2}-2c-1\right) I_{3}\right] \end{aligned}$$

(17b)

$$\begin{aligned} \overline{Q}_{3}= & {} -\sqrt{\left[ 2\overline{L}+\overline{Q}_{2}^{2}\left( t_{0}\right) +\overline{P}_{2}^{2}\left( t_{0}\right) \right] \left( 1- \overline{c}_{0}\right) }\sin \left( \overline{h}_{0}+6\overline{c}\mu ^{4}C_{0}k_{2}I_{3}\right) \end{aligned}$$

(17c)

$$\begin{aligned} \overline{P}_{1}= & {} \overline{L} \end{aligned}$$

(17d)

$$\begin{aligned} \overline{P}_{2}= & {} \sqrt{\overline{Q}_{2}^{2}\left( t_{0}\right) +\overline{ P}_{2}^{2}\left( t_{0}\right) }\cos \left[ \overline{g}_{0}+\overline{h} _{0}+3\mu ^{4}C_{0}k_{2}\left( 5\overline{c}^{2}-2\overline{c}-1\right) I_{3} \right] \end{aligned}$$

(17e)

$$\begin{aligned} \overline{P}_{3}= & {} \sqrt{2\left( \overline{L}+\overline{G}_{0}-\overline{L} _{0}\right) \left( 1-\overline{c}_{0}\right) }\cos \left( \overline{h}_{0}+6 \overline{c}\mu ^{4}C_{0}k_{2}I_{3}\right) \end{aligned}$$

(17f)

where $\overline{L}=\overline{L}\left( t\right)$ is expressed in Eq. (10a). The quantities $\overline{h}_{0}$ and $\overline{g}_{0}+\overline{ h}_{0}$ might pose problems for equatorial or circular orbits. Assuming that the approach was made from the beginning in Poincaré variables, these potential singularities are removed as follows. Consider $\overline{Q} _{k}^{0},$ $\overline{P}_{k}^{0}$ the initial values of the variables at $t=t_{0},$ $k=1,2,3,$ assumed to be known. The quantities $\overline{h}_{0}$ and $\overline{g}_{0}+\overline{h}_{0}$ may be defined, in any situation,⁵ as follows:

If $\left( \overline{Q}_{3}^{0}\right) ^{2}+\left( \overline{P} _{3}^{0}\right) ^{2}\not =0,$ then:

$$\begin{aligned} \cos \overline{h}_{0}=\dfrac{\overline{P}_{3}^{0}}{\sqrt{\left( \overline{Q} _{3}^{0}\right) ^{2}+\left( \overline{P}_{3}^{0}\right) ^{2}}},\quad \sin \overline{h}_{0}=\dfrac{-\overline{Q}_{3}^{0}}{\sqrt{\left( \overline{Q} _{3}^{0}\right) ^{2}+\left( \overline{P}_{3}^{0}\right) ^{2}}} \end{aligned}$$

and$\;\overline{h}_{0}=0$ if $\left( \overline{Q}_{3}^{0}\right) ^{2}+\left( \overline{P}_{3}^{0}\right) ^{2}=0.$ Similarly, if $\left( \overline{Q} _{2}^{0}\right) ^{2}+\left( \overline{P}_{2}^{0}\right) ^{2}\not =0$ then:

$$\begin{aligned} \cos \left( \overline{g}_{0}+\overline{h}_{0}\right) =\dfrac{\overline{P} _{2}^{0}}{\sqrt{\left( \overline{Q}_{2}^{0}\right) ^{2}+\left( \overline{P} _{2}^{0}\right) ^{2}}},\quad \sin \left( \overline{g}_{0}+\overline{h} _{0}\right) =\dfrac{-\overline{Q}_{2}^{0}}{\sqrt{\left( \overline{Q} _{2}^{0}\right) ^{2}+\left( \overline{P}_{2}^{0}\right) ^{2}}} \end{aligned}$$

and$\;\overline{g}_{0}+\overline{h}_{0}=0$ if $\left( \overline{Q} _{2}^{0}\right) ^{2}+\left( \overline{P}_{2}^{0}\right) ^{2}=0.$

The transformation from Poincaré to Cartesian variables is given in “Transformation from Poincaré to Cartesian coordinates” section in Appendix.

3 The infinitesimal contact transformation

3.1 Quasi-Hamiltonian formalism for nonconservative systems

Although canonical coordinates are used for conservative systems only, or for systems where a (non-constant) Hamiltonian may still exist, it is possible to express the mathematical model of a single particle perturbed by nonconservative forces (even if they are not derived from a potential function) by making use of the (modified) Hamilton’s equations.

In what follows, the entire set of canonical variables, generally denoted by $\left( {\mathbf {q}},{\mathbf {p}}\right) ,$ with ${\mathbf {q}}$ being the generalized coordinates and ${\mathbf {p}}$ their conjugate momenta, will be denoted by a 6-dimensional vector ${\mathbf {X=}}\left[ {\mathbf {q}}^{T},{\mathbf {p}}^{T}\right] ^{T},$ and the convention that the generalized coordinates are on the first three places is made. Consider ${\mathbf {O}}_{3}$ and ${\mathbf {I}} _{3}$ the zero and the identity matrices, respectively. Denote by ${\mathcal {I}}$ the $6\times 6$ symplectic matrix:

$$\begin{aligned} \mathcal {I}=\left[ \begin{array}{cc} {\mathbf {O}}_{3} &{} {\mathbf {I}}_{3} \\ -{\mathbf {I}}_{3} &{} {\mathbf {O}}_{3} \end{array} \right] \end{aligned}$$

Consider a single-particle dynamical system such that there exists a scalar function ${\mathcal {H}}={\mathcal {H}}\left( {\mathbf {X}}\right)$ and a vector function ${\mathbf {f}}_{\mathbf {NH}}={\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}} ,t\right)$ such that the motion is modeled by the initial value problem (IVP):

$$\begin{aligned} \frac{\text {d}{\mathbf {X}}}{\text {d}t}=\mathcal {I}\frac{\partial {\mathcal {H}}}{ \partial {\mathbf {X}}}+\delta {\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}} ,t\right) ,\;{\mathbf {X}}\left( t_{0}\right) ={\mathbf {X}}_{0} \end{aligned}$$

(18)

where $\delta >0$ is a small parameter. If ${\mathbf {f}}_{\mathbf {NH}}\equiv {\mathbf {0}},$ then the system is Hamiltonian and Eq. (18) gives the canonical equations of Hamilton. When ${\mathbf {f}}_{\mathbf {NH}}\not \equiv \mathbf {0,}$ Eq. (18) models a conservative system perturbed by a nonconservative force, expressed in canonical variables ${\mathbf {X}}.$

A change of variables ${\mathbf {X\rightarrow Y}}$ is said to be canonical if it preserves Hamilton’s equations (if dissipative terms like ${\mathbf {f}}_{{\mathbf {NH}}}$ are neglected). In our case, it is more useful to use its mathematical equivalent, that is independent of the Hamiltonian formulation, namely:⁶

$$\begin{aligned} \frac{\partial {\mathbf {Y}}}{\partial {\mathbf {X}}}{\mathcal {I=I}}\left[ \frac{ \partial {\mathbf {X}}}{\partial {\mathbf {Y}}}\right] ^{T}, \end{aligned}$$

(19)

where $\partial \mathbf {Y}/\partial {\mathbf {X}}$ denotes the Jacobian of the transformation, while $\partial {\mathbf {X}}/\partial \mathbf {Y}$ is its inverse. Such change of variable will act upon Eq. (18) as follows:

$$\begin{aligned} \frac{\text {d}{\mathbf {Y}}}{\text {d}t}= & {} \frac{\partial {\mathbf {Y}}}{\partial {\mathbf {X}}}\frac{\text {d}{\mathbf {X}}}{\text {d}t}=\frac{\partial {\mathbf {Y}}}{\partial {\mathbf {X}}}\left[ {\mathcal {I}}\frac{\partial {\mathcal {H}}}{\partial {\mathbf {X}}}+\delta {\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}},t\right) \right] \\= & {} \mathcal {I}\left[ \frac{\partial {\mathbf {X}}}{\partial {\mathbf {Y}}}\right] ^{T}\frac{\partial {\mathcal {H}}}{\partial {\mathbf {X}}}+\delta \frac{\partial {\mathbf {Y}}}{\partial {\mathbf {X}}}{\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}} ,t\right) \\= & {} \mathcal {I}\frac{\partial {\mathcal {K}}}{\partial {\mathbf {Y}}}+\delta {\mathbf {g}}_{\mathbf {NH}}\left( {\mathbf {Y}},t\right) \end{aligned}$$

where the new Hamiltonian ${\mathcal {K}}$ is the old one ${\mathcal {H}}$ expressed with respect to the new variables ${\mathbf {Y}},$ while ${\mathbf {g}}_{ \mathbf {NH}}\left( {\mathbf {Y}},t\right) =\left[ \partial {\mathbf {Y}}/\partial {\mathbf {X}}\right] {\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}}\left( {\mathbf {Y}} \right) ,t\right) .$

3.2 Choosing the best variables

Although there is no ideal set of canonical coordinates, since each set has its own singularities, each situation requires the use of one particular set, and usually it is the one that leads to the least amount of symbolic computations. In the present case, there are several challenges that need to be overcome: (i) the derivation of the conservative part ${\mathbf {W}}^{{\mathbf {I}}}$ of the transformation is nonsingular only for Whittaker⁷ (see Lara 2015a) and Poincaré (see Lyddane 1963) variables; if Delaunay’s variables are used, singularities for zero eccentricity and zero inclinations are injected; (ii) in order to obtain the non-conservative part of the transformation ${\mathbf {W}}^{\mathbf {II}}$, it would be ideal to choose a set of coordinates ${\mathbf {X}}$ where the gradient $\partial {\mathcal {H}}_{0}/\partial {\mathbf {X}}$ has most coordinates 0; a good candidate are the Delaunay set of canonical variables, but they interfere with the first part of the transformation; the other choice is the Poincaré variables; (iii) indeed the same set of coordinates should be used for both parts of the transformation; (iv) written in Poincaré variables, the conservative part of the transformation (that is the equivalent of the Lyddane transformation) yields quite intricate expressions.

The non-singular Poincaré variables are chosen for the non-conservative part of the transformation, since the Hamiltonian of the unperturbed Keplerian motion is cyclic in 5 variables (i.e. only one component of the gradient $\partial {\mathcal {H}}_{0}/\partial {\mathbf {X}}$ is different from 0 ), simplifying the approach to Eq. (28). The conservative part of the transformation is solved in two steps: (i) determine the generating function ${\mathcal {W}}^{\mathbf {I}}$ by using Delaunay variables in Eq. (25); (ii) compute the gradient $\left( \partial {\mathcal {W}}^{\mathbf {I} }/\partial {\mathbf {X}}\right)$ by using Whittaker variables, and multiply this gradient with the jacobian of the transformation between the Poincar é and Whittaker coordinates, deducible based on the considerations made in “Jacobian for coordinate transformations” section in Appendix; the resulting conservative part of contact transformation will be expressed in Poincaré variables, in order to match the variables used for the non-conservative part.

3.3 Lie-deprit approach to non-conservative perturbations

The perturbation method used by Deprit enables the possibility to include nonconservative perturbations. An approach where the Hamiltonian part of the perturbation is used in order to simplify the computations was described by Barrio and Palácian (1997), and will be used in the current work. For the sake of clarity and self-consistency, a brief description of the transformation algorithm is presented below. Since the aim of the current approach is a first-order solution, the approach to higher-order terms is ommitted.

Consider the mathematical model of the motion of a particle subject to a main conservative force (with the associated unperturbed Hamiltonian denoted by ${\mathcal {H}}_{0}$) and two different perturbations, one conservative—potential denoted by $\epsilon {\mathcal {H}}_{1}$—and one non-conservative—force denoted by $\delta {\mathbf {f}}_{\mathbf {NH}}\left( {\mathbf {X}},t\right) ,$ where $\epsilon ,\delta >0$ are small constant parameters:

$$\begin{aligned} \frac{\text {d}{\mathbf {X}}}{\text {d}t}=\mathcal {I}\frac{\partial \left[ {\mathcal {H}}_{0}\left( {\mathbf {X}}\right) +\epsilon {\mathcal {H}}_{1}\left( {\mathbf {X}}\right) \right] }{\partial {\mathbf {X}}}+\delta {\mathbf {f}}_{\mathbf { NH}}\left( {\mathbf {X}},t\right) ,\quad {\mathbf {X}}\left( t_{0}\right) ={\mathbf {X}} _{0} \end{aligned}$$

(20)

Assume that by means of some perturbation method (in the present case, averaging), the original system (20) is transformed into:

$$\begin{aligned} \frac{\text {d}{\mathbf {X}}^{*}}{\text {d}t}={\mathcal {I}}\frac{\partial \left[ {\mathcal {H}}_{0}\left( {\mathbf {X}}^{*}\right) +\epsilon {\mathcal {H}} _{1}^{*}\left( {\mathbf {X}}^{*}\right) \right] }{\partial {\mathbf {X}} ^{*}}+\delta {\mathbf {f}}_{\mathbf {NH}}^{*}\left( {\mathbf {X}}^{*},t\right) ,\quad {\mathbf {X}}^{*}\left( t_{0}\right) ={\mathbf {X}}_{0}^{*} \end{aligned}$$

(21)

Then the connection between the new variables ${\mathbf {X}}^{*}$ and the old variables ${\mathbf {X}}$ is made via a transformation that is a Lie series, and at first order it has a simple expression:

$$\begin{aligned} {\mathbf {X}}={\mathbf {W}}^{\mathbf {I}}\left( {\mathbf {X}}^{*},\epsilon \right) +\delta {\mathbf {W}}^{\mathbf {II}}\left( {\mathbf {X}}^{*}\right) \end{aligned}$$

(22)

One key feature in Eq. (22) is that ${\mathbf {W}}^{\mathbf {I}}\left( {\mathbf {X}}^{*},\epsilon \right)$ emanates exclusively from the conservative parts of the perturbations in Eqs. (20) and (21), and it is a (truncated) infinitesimal canonical transformation that is derived from a generating function ${\mathcal {W}}^{\mathbf {I}}= {\mathcal {W}}^{\mathbf {I}}\left( {\mathbf {X}}^{*}\right)$ as follows:

$$\begin{aligned} {\mathbf {W}}^{\mathbf {I}}\left( {\mathbf {X}}^{*},\epsilon \right) ={\mathbf {X}} ^{*}+\epsilon \mathcal {I}\frac{\partial {\mathcal {W}}^{\mathbf {I}}\left( {\mathbf {X}}^{*}\right) }{\partial {\mathbf {X}}^{*}} \end{aligned}$$

(23)

Consider $\mathbf {X}$ an arbitrary set of canonical coordinates. Denote by $\left\{ \cdot ,\cdot \right\}$ the Lie bracket of two scalar functions, defined as:

$$\begin{aligned} \left\{ U,V\right\} =\frac{\partial U}{\partial {\mathbf {X}}}\cdot \left[ \mathcal {I}\frac{\partial V}{\partial {\mathbf {X}}}\right] \end{aligned}$$

(24)

The generating function ${\mathcal {W}}^{\mathbf {I}}$ is determined with the help of the Lie triangle (Barrio and Palácian 1997; Deprit 1981) as follows:

$$\begin{aligned} \left\{ {\mathcal {H}}_{0};{\mathcal {W}}^{\mathbf {I}}\right\} ={\mathcal {H}} _{1}^{*}-{\mathcal {H}}_{1} \end{aligned}$$

(25)

Denote by ${\mathcal {L}}_{{\mathbf {W}}}{\mathbf {s}}$ the action of the Lie differential operator over the vector field ${\mathbf {s}}$ (evaluated with respect to the flow generated by ${\mathbf {W}}$). Its expression is:

$$\begin{aligned} {\mathcal {L}}_{{\mathbf {W}}}{\mathbf {s}}=\frac{\partial {\mathbf {s}}}{\partial {\mathbf {X}}}{\mathbf {W}}-\frac{\partial {\mathbf {W}}}{\partial {\mathbf {X}}}{\mathbf {s}} \end{aligned}$$

(26)

Then the second term of the right-hand side of Eq. (22) is evaluated based on the extended Lie triangle (Barrio and Palácian 1997) starting from:

$$\begin{aligned} {\mathcal {L}}_{{\mathbf {W}}^{\mathbf {II}}}\left( \frac{\partial {\mathcal {H}}_{0}}{ \partial {\mathbf {X}}}\right) ={\mathbf {f}}_{\mathbf {NH}}^{*}-{\mathbf {f}}_{ \mathbf {NH}}, \end{aligned}$$

(27)

By taking Eq. (26) into account, Eq. (27) becomes:

$$\begin{aligned} \frac{\partial ^{2}{\mathcal {H}}_{0}}{\partial {\mathbf {X}}^{2}}{\mathbf {W}}^{ \mathbf {II}}-\frac{\partial {\mathbf {W}}^{\mathbf {II}}}{\partial {\mathbf {X}}} \frac{\partial {\mathcal {H}}_{0}}{\partial {\mathbf {X}}}={\mathbf {f}}_{\mathbf {NH} }^{*}-{\mathbf {f}}_{\mathbf {NH}} \end{aligned}$$

(28)

Remark 1

The Lie bracket of two scalar fields defined in Eq. (24) is independent of the choice of the canonical coordinates ${\mathbf {X}}$; the proof is straightforward and is based on the symplectic nature of the Jacobian of a canonical transformation, expressed in Eq. (19). Unlike the scalar field case, when the Lie bracket produces a scalar output, care should be taken regarding the second part of the transformation ${\mathbf {W}}^{\mathbf {II}}$, since the same variables should be used in both sides of Eq. (28).

The construction of the transformation between the coordinates explicitly expressed in Eq. (17) and the ones associated to the original mathematical model is made by following the approach in Barrio and Palácian (1997). To this end, the osculating state vector will be denoted by ${\mathbf {X}}_{\mathcal {D},{\mathcal {W}},{\mathcal {P}}},$ and its averaged counterpart by ${\mathbf {X}}_{\mathcal {D},{\mathcal {W}},{\mathcal {P}}}^{*},$ where subscripts ${\mathcal {D}},{\mathcal {W}},{\mathcal {P}}$ depict the set of canonical variables that is used, namely Delaunay, Whittaker and Poincaré, respectively. As stated before, the transformation is determined by a two-step procedure, each step concerning the conservative and non-conservative parts of the perturbation, taken in this precise order.

In order to comply with the desired features of the transformation (explicit & singularity-free), all three sets of the aforementioned variables are used.

Start with the original model for the motion of a satellite in the atmosphere of an oblate planet, expressed in Delaunay canonical variables, that is:

$$\begin{aligned} \frac{\text {d}{\mathbf {X}}_{\mathcal {D}}}{\text {d}t}=\mathcal {I}\frac{\partial \left[ {\mathcal {H}}_{\mathcal {D},0}\left( {\mathbf {X}}_{\mathcal {D}}\right) +\epsilon {\mathcal {H}}_{\mathcal {D},1}\left( {\mathbf {X}}_{\mathcal {D}}\right) \right] }{\partial {\mathbf {X}}_{\mathcal {D}}}+\delta {\mathbf {f}}_{\mathbf {NH}_{ \mathcal {D}}}\left( {\mathbf {X}}_{\mathcal {D}},t\right) ,\;{\mathbf {X}}_{ \mathcal {D}}\left( t_{0}\right) ={\mathbf {X}}_{\mathcal {D},0} \end{aligned}$$

(29)

$$\begin{aligned} {\mathcal {H}}_{\mathcal {D},0}\left( {\mathbf {X}}_{\mathcal {D}}\right)= & {} -\frac{ \mu ^{2}}{2L^{2}} \end{aligned}$$

(30a)

$$\begin{aligned} \epsilon {\mathcal {H}}_{\mathcal {D},1}\left( {\mathbf {X}}_{\mathcal {D}}\right)= & {} -\frac{k_{2}}{r^{3}}\left[ -\left( 1-\frac{3H^{2}}{G^{2}}\right) +3\left( 1-\frac{H^{2}}{G^{2}}\right) \cos \left( 2f+2g\right) \right] \end{aligned}$$

(30b)

$$\begin{aligned} \delta {\mathbf {f}}_{\mathbf {NH}_{\mathcal {D}}}\left( {\mathbf {X}}_{\mathcal {D} },t\right) =\left( 1+\kappa \right) C_{u}\left[ \begin{array}{cccccc} -\dfrac{2\eta \sigma }{Ge^{2}}\dfrac{e^{2}+\kappa +1}{1+\kappa };&-\dfrac{ 2\sigma }{Ge^{2}};&0;&-\dfrac{e^{2}+2\kappa +1}{\eta ^{3}};&-1;&-c \end{array} \right] ^{T} \end{aligned}$$

(31)

Equation (29) is just a reformulation of Eq. (5), aimed at separating the conservative and non-conservative parts. The averaged model described by Eq. (8) is recast into:

$$\begin{aligned} \frac{\text {d}{\mathbf {X}}_{\mathcal {D}}^{*}}{\text {d}t}=\mathcal {I}\frac{ \partial \left[ {\mathcal {H}}_{\mathcal {D},0}\left( {\mathbf {X}}_{\mathcal {D} }^{*}\right) +\epsilon {\mathcal {H}}_{\mathcal {D},1}^{*}\left( \mathbf { X}_{\mathcal {D}}^{*}\right) \right] }{\partial {\mathbf {X}}_{\mathcal {D} }^{*}}+\delta {\mathbf {f}}_{\mathbf {NH}_{\mathcal {D}}}^{*}\left( {\mathbf {X}}_{\mathcal {D}}^{*},t\right) ,\;{\mathbf {X}}_{\mathcal {D}}^{*}\left( t_{0}\right) ={\mathbf {X}}_{\mathcal {D},0}^{*} \end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {H}}_{\mathcal {D},0}\left( {\mathbf {X}}_{\mathcal {D}}^{*}\right)= & {} -\frac{\mu ^{2}}{2\overline{L}^{2}} \end{aligned}$$

(33a)

$$\begin{aligned} \epsilon {\mathcal {H}}_{\mathcal {D},1}^{*}\left( {\mathbf {X}}_{\mathcal {D} }^{*}\right)= & {} \frac{\mu ^{3}k_{2}}{\overline{L}^{3}G^{3}}\left( 1-3 \frac{\overline{H}^{2}}{\overline{G}^{2}}\right) \end{aligned}$$

(33b)

$$\begin{aligned} \delta {\mathbf {f}}_{\mathbf {NH}_{\mathcal {D}}}\left( {\mathbf {X}}_{\mathcal {D} },t\right) =-\mu C_{0}\exp \left( -\frac{\overline{L}^{2}-\mu r_{0}}{\mu \alpha }\right) \left[ \begin{array}{cccccc} 0&0&0&1&1&\dfrac{\overline{H}}{\overline{G}} \end{array} \right] ^{T} \end{aligned}$$

(34)

3.3.1 The conservative part

The generating function ${\mathcal {W}}^{\mathbf {I}}$ associated to the canonical conservative part of the transformation is determined from the homological equation (25), written in this particular case as:

$$\begin{aligned} \left\{ {\mathcal {H}}_{\mathcal {D},0};{\mathcal {W}}^{\mathbf {I}}\right\} = {\mathcal {H}}_{\mathcal {D},1}^{*}-{\mathcal {H}}_{\mathcal {D},1} \end{aligned}$$

(35)

Eq. (35) leads to:

$$\begin{aligned} -\frac{\mu ^{2}}{L^{3}}\frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial l}= \frac{\mu ^{3}k_{2}}{L^{3}G^{3}}\left( 1-3\frac{H^{2}}{G^{2}}\right) +\frac{ k_{2}}{r^{3}}\left[ -\left( 1-\frac{3H^{2}}{G^{2}}\right) +3\left( 1-\frac{ H^{2}}{G^{2}}\right) \cos \left( 2f+2g\right) \right] , \end{aligned}$$

that is solved through the quadrature:

$$\begin{aligned} {\mathcal {W}}^{\mathbf {I}}=-k_{2}\frac{L^{3}}{\mu ^{2}}\int \left\{ \frac{\mu ^{3}}{\overline{L}^{3}G^{3}}\left( 1-3c^{2}\right) +\frac{1}{r^{3}}\left[ -\left( 1-3c^{2}\right) +3\overline{s}^{2}\cos \left( 2f+2g\right) \right] \right\} \text {d}l \end{aligned}$$

Take into account:

$$\begin{aligned} r=\frac{p}{1+e\cos f},\quad \frac{L^{3}}{\mu ^{2}}\text {d}l=\frac{r^{2}}{G} \text {d}f \end{aligned}$$

The generating function is determined as:

$$\begin{aligned} {\mathcal {W}}^{\mathbf {I}}=\frac{\mu k_{2}}{G^{3}}\left[ \left( 2-3s^{2}\right) \left( f-l+\sigma \right) +s^{2}\left( -\sigma \cos 2\theta + \frac{4\kappa +3}{2}\sin 2\theta \right) \right] \end{aligned}$$

(36)

Since the computations need to be performed in Poincaré canonical variables (the reason why is presented in the next paragraph), and the partial derivatives of ${\mathcal {W}}^{\mathbf {I}}$ with respect to these variables involve intricate expressions, the following simplifying approach is chosen. Introduce the polar-nodal canonical variables $\left( r,\theta ,\nu ,R,\varTheta ,N\right)$:

$$\begin{aligned} r=\frac{p}{1+\kappa },\quad \theta =\omega +f,\quad \nu =\varOmega ,\quad R=\sqrt{ \frac{\mu }{a}}\frac{\sigma }{\eta },\quad \varTheta =G,\;\;N=H \end{aligned}$$

The partial derivatives of ${\mathcal {W}}^{\mathbf {I}}$ with respect to the Whittaker variables are (see Lara 2015a):

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial r}= & {} \frac{k_{2}}{\varTheta p^{2}}\left\{ -2s^{2}\left( 1+\kappa \right) \sin 2\theta +\sigma \left( 2-3s^{2}\right) \left[ \eta +\frac{\left( 1+\kappa \right) ^{2}}{1+\eta } \right] \right\} \end{aligned}$$

(37a)

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial \theta }= & {} -\frac{k_{2}}{ \varTheta p}s^{2}\left[ \left( 3+4\kappa \right) \cos 2\theta +2\sigma \sin 2\theta \right] \end{aligned}$$

(37b)

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial \nu }= & {} 0 \end{aligned}$$

(37c)

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial R}= & {} \frac{k_{2}}{\varTheta ^{2}}\left[ \left( 2-3s^{2}\right) \left( \frac{\kappa }{1+\eta }+\frac{ 2\eta }{1+\kappa }+1\right) -s^{2}\cos 2\theta \right] \end{aligned}$$

(37d)

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial \varTheta }= & {} \frac{k_{2}}{ \varTheta p^{2}}\left\{ -3\left( 4-5s^{2}\right) \left( f-l\right) +\frac{1}{6} \left[ \left( 12\kappa +7\right) \left( 2-3s^{2}\right) +4\right] \sin 2\theta \right. \nonumber \\&\left. +2\sigma \left[ 1+\frac{2-3s^{2}}{2}u+\left( 1-2s^{2}\right) \cos 2\theta \right] \right\} \end{aligned}$$

(37e)

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial N}= & {} \frac{k_{2}c}{\varTheta p^{2}}\left[ 6\left( f-l\right) -\left( 4\kappa +3\right) \sin 2\theta +2\sigma \sin 2\theta \right] \end{aligned}$$

(37f)

The partial derivatives of ${\mathcal {W}}^{\mathbf {I}}$ with respect to the Poincaré variables may now be expressed as:

$$\begin{aligned} \frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial \left( Q_{1},Q_{2},Q_{3},P_{1},P_{2},P_{3}\right) }={\mathcal {J}}_{\mathcal {P}}^{ {\mathcal {W}}}\frac{\partial {\mathcal {W}}^{\mathbf {I}}}{\partial \left( r,\theta ,\nu ,R,\varTheta ,N\right) } \end{aligned}$$

(38)

where the evaluation of ${\mathcal {J}}_{\mathcal {P}}^{{\mathcal {W}}}$ is given in “Jacobian for coordinate transformations” section in Appendix.

3.3.2 The non-conservative part

Equation (28) provides the non-conservative part ${\mathbf {W}}^{ \mathbf {II}}$ of the contact transformation. In order to reduce the number of computations, the unperturbed Hamiltonian is expressed in one set of variables where most elements in the Hessian matrix are 0. Although Delaunay variables are a good candidate, they exhibit singularities, so the Poincaré canonical variables are used instead. The unperturbed Hamiltonian ${\mathcal {H}}_{0}$ is cyclic with respect to 5 of these variables, its expression being:

$$\begin{aligned} {\mathcal {H}}_{0}=\frac{-\mu ^{2}}{2P_{1}^{2}} \end{aligned}$$

Equation (28) becomes:

$$\begin{aligned} \frac{\mu ^{2}}{P_{1}^{3}}\left[ -\dfrac{3}{P_{1}}\left( {\mathbf {W}}^{\mathbf { II}}\cdot \mathbf {e}_{4}\right) \mathbf {e}_{1}-\frac{\partial {\mathbf {W}}^{ \mathbf {II}}}{\partial Q_{1}}\right] =\delta \left( {\mathbf {f}}_{\mathbf {NH}_{ \mathcal {P}}}^{*}-{\mathbf {f}}_{\mathbf {NH}_{\mathcal {P}}}\right) \end{aligned}$$

(39)

where $\left\{ \mathbf {e}_{k}\right\} _{k=\overline{1,6}}$ is a canonical base in ${\mathbb {R}} ^{6}.$ The expressions in Poincaré variables for the non-conservative terms of the perturbations are determined by left-multiplying Eq. (29) and (32) with the Jacobian ${\mathcal {J}}_{\mathcal {P}}^{ \mathcal {D}}$ of the transformation from Delaunay to Poincaré. The components of the right-hand side of Eq. (39) are evaluated as follows:

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 1\right) }= & {} C_{u}\frac{ 2\sigma }{G}\left( \eta -\frac{1+\kappa }{1+\eta }\right) \end{aligned}$$

(40a)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 2\right) }= & {} C_{u}\frac{\left( 1+\kappa \right) ^{2}}{\eta ^{2}\sqrt{2L\left( 1+\eta \right) }}\left\{ 4\sin E\cos \left( g+h\right) \right. \nonumber \\&\left. +\left[ \frac{2\left( 1+\eta \right) \left( \cos E-e\right) }{\eta ^{2}}+e\left( 2+2\eta +\eta ^{2}\right) \right] \frac{\sin \left( g+h\right) }{\eta }\right\} \end{aligned}$$

(40b)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 3\right) }= & {} C_{u}\frac{\left( 1+\kappa \right) \sqrt{1-c}}{\sqrt{2G}}\sin h \end{aligned}$$

(40c)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 4\right) }= & {} -C_{u}\frac{ \left( 1+\kappa \right) \left( e^{2}+2\kappa +1\right) }{\eta ^{3}} \end{aligned}$$

(40d)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 5\right) }= & {} C_{u}\frac{\left( 1+\kappa \right) ^{2}}{\eta ^{2}\sqrt{2L\left( 1+\eta \right) }}\left\{ 4\sin \left( g+h\right) \sin E{\frac{1}{1}}\right. \end{aligned}$$

(40e)

$$\begin{aligned}&\left. -\left[ e\frac{2+2\eta +\eta ^{2}}{1+\kappa }+2\frac{1+\eta }{\eta ^{2}}\left( \cos E-e\right) \right] \frac{\cos \left( g+h\right) }{\eta } \right\} \nonumber \\ \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 6\right) }= & {} -C_{u}\frac{ \left( 1+\kappa \right) \sqrt{1-c}}{\sqrt{2G}}\cos h \end{aligned}$$

(40f)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 1\right) *}= & {} 0 \end{aligned}$$

(41a)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 2\right) *}= & {} 0 \end{aligned}$$

(41b)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 3\right) *}= & {} \frac{1}{4} C_{0}\exp \left( -\frac{a-r_{0}}{\alpha }\right) \frac{\left( 2G\right) ^{3/2}}{p}\sqrt{1-c}\sin h \end{aligned}$$

(41c)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 4\right) *}= & {} K0 \end{aligned}$$

(41d)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 5\right) *}= & {} 0 \end{aligned}$$

(41e)

$$\begin{aligned} \delta f_{\mathbf {NH}_{\mathcal {P}}}^{\left( 6\right) *}= & {} -\frac{1}{4} C_{0}\exp \left( -\frac{a-r_{0}}{\alpha }\right) \frac{\left( 2G\right) ^{3/2}}{p}\sqrt{1-c}\cos h \end{aligned}$$

(41f)

Denote by $W_{k}^{\mathbf {II}},$ $k=\overline{1,6},$ the components of the column matrix ${\mathbf {W}}^{\mathbf {II}}.$ Equation (39) leads to:

$$\begin{aligned} -\frac{\partial W_{k}^{\mathbf {II}}}{\partial Q_{1}}= & {} \frac{P_{1}^{3}}{\mu ^{2}}\left[ \delta \left( f_{\mathbf {NH}_{\mathcal {P}}}^{\left( k\right) *}-f_{\mathbf {NH}_{\mathcal {P}}}^{\left( k\right) }\right) \right] ,\;\;k=\overline{2,6} \end{aligned}$$

(42a)

$$\begin{aligned} -\frac{3}{P_{1}}W_{4}^{\mathbf {II}}-\frac{\partial W_{1}^{\mathbf {II}}}{ \partial Q_{1}}= & {} \frac{P_{1}^{3}}{\mu ^{2}}\left[ \delta \left( f_{\mathbf { NH}_{\mathcal {P}}}^{\left( 1\right) *}-f_{\mathbf {NH}_{\mathcal {P} }}^{\left( 1\right) }\right) \right] \end{aligned}$$

(42b)

The component ${\mathbf {W}}_{1}^{\mathbf {II}}$ is determined by straightforward integration, by taking into account that $W_{4}^{\mathbf {II} }$ should be computed before:

$$\begin{aligned} W_{k}^{\mathbf {II}}= & {} -\frac{P_{1}^{3}}{\mu ^{2}}\int \left( f_{\mathbf {NH} _{\mathcal {P}}}^{\left( k\right) *}-f_{\mathbf {NH}_{\mathcal {P} }}^{\left( k\right) }\right) \text {d}Q_{1},\;\;k=\overline{2,6} \end{aligned}$$

(43a)

$$\begin{aligned} W_{1}^{\mathbf {II}}= & {} -\frac{P_{1}^{3}}{\mu ^{2}}\int \left( f_{\mathbf {NH} _{\mathcal {P}}}^{\left( 1\right) *}-f_{\mathbf {NH}_{\mathcal {P} }}^{\left( 1\right) }\right) \text {d}Q_{1}+\frac{3}{P_{1}}\int W_{4}^{ \mathbf {II}}\text {d}Q_{1} \end{aligned}$$

(43b)

In this case, it is simpler to use the eccentric anomaly substitution, and this is made by taking into account:

$$\begin{aligned} \frac{P_{1}^{3}}{\mu ^{2}}\text {d}Q_{1}=\frac{p^{2}}{\left( 1+\kappa \right) \eta P_{1}}\text {d}E \end{aligned}$$

(44)

The evaluation of the integrals in Eq. (43) is not possible with the help of elementary functions, and therefore series expansions about $e\simeq 0$ should be performed. Note that the truncation of these series may be made such that ${\mathcal {O}}\left( e^{n}\right) \simeq 0$ for any natural $n\ge 1.$

For the sake of simplicity, the expressions are given in classical orbital elements mixed with Delaunay. Denote:

$$\begin{aligned} n= & {} \sqrt{\mu ^{2}/P_{1}^{3}};\;\;K_{0}=-\mu C_{0}\exp \left( -\frac{a-r_{0} }{\alpha }\right) ;\;\;q=\frac{a}{\alpha };\;\;\varpi =g+h \\ p_{1}= & {} \left( 1+q\right) \left( 3+q\right) \\ p_{2}= & {} q^{3}+6q^{2}+9q+6 \\ \lambda _{1}= & {} 27\left( 3p_{1}+2p_{2}\right) \eta +18\left( q^{2}-2q-5\right) \\ \lambda _{2}= & {} -3\left( q^{2}-9\right) \eta -4\left( q-1\right) \\ \lambda _{3}= & {} 6\left( 1+q\right) \left( q-3\right) -\left( 9p_{1}-2p_{2}\right) \eta \\ \gamma _{1}= & {} \frac{1}{2}\left( q^{2}+2q-4\right) \cos \left( E+\varpi \right) +\frac{1}{6}\left( 1+q\right) ^{2}\cos \left( 3E+\varpi \right) -\left( 1+q\right) \left( 2+q\right) \sin E\sin \varpi \\ \gamma _{2}= & {} \frac{1}{2}\left( q^{2}+2q-4\right) \sin \left( E+\varpi \right) +\frac{1}{6}\left( 1+q\right) ^{2}\sin \left( 3E+\varpi \right) +\left( 1+q\right) \left( 2+q\right) \sin E\cos \varpi \end{aligned}$$

The truncated series for ${\mathcal {O}}\left( e^{5}\right) \simeq 0$ of the non-conservative part of the transformation are expressed as follows:

$$\begin{aligned} W_{1}^{\mathbf {II}}= & {} K_{0}\frac{e}{nG}\left[ \left( \frac{3\eta p_{1}}{1+q} +1\right) \cos E-\frac{e}{2}\left( 12\eta p_{1}E^{2}+2\lambda _{2}\cos 2E\right) \right. \nonumber \\&+\frac{e^{2}}{144}\left( 108\eta p_{1}E\sin E+\lambda _{1}\cos E+\lambda _{3}\cos 3E\right) \nonumber \\&\left. -\frac{e^{3}}{192}\eta p_{2}\left( 20\cos 2E+\cos 4E\right) \right] \end{aligned}$$

(45a)

$$\begin{aligned} W_{2}^{\mathbf {II}}= & {} K_{0}\frac{1}{2n\sqrt{G}}\left\{ 4\cos \left( E{+}\varpi \right) {-}e\left[ \left( 2q+3\right) E\sin \varpi {-}\left( q+1\right) \cos \left( 2E+\varpi \right) \right] +e^{2}\gamma _{1}\right\} \nonumber \\ \end{aligned}$$

(45b)

$$\begin{aligned} W_{3}^{\mathbf {II}}= & {} -K_{0}\frac{e}{4n\sqrt{G}}\sin h\sin \dfrac{i}{2} \left\{ 4\left( 1+q\right) \sin E+\frac{e}{2}\left[ 2\left( q^{2}-3\right) E+\left( q^{2}-1\right) \sin 2E\right] \right. \nonumber \\&\left. +\frac{e^{2}}{18}q\left[ 9\left( q^{2}-7\right) \sin E+\left( q^{2}-3\right) \sin 3E\right] \right\} \end{aligned}$$

(45c)

$$\begin{aligned} W_{4}^{\mathbf {II}}= & {} K_{0}\frac{e}{n}\left[ \left( q+3\right) \sin E+\frac{ e}{8}p_{1}\left( 2E+\sin 2E\right) +\frac{e^{2}}{72}p_{2}\left( 9\sin E+\sin 3E\right) \right] \end{aligned}$$

(45d)

$$\begin{aligned} W_{5}^{\mathbf {II}}= & {} K_{0}\frac{1}{2n\sqrt{G}}\left\{ 4\sin \left( E+\varpi \right) +e\left[ \left( 2q+3\right) E\cos \varpi +\left( q+1\right) \sin \left( 2E+\varpi \right) \right] +e^{2}\gamma _{2}\right\} \nonumber \\ \end{aligned}$$

(45e)

$$\begin{aligned} W_{6}^{\mathbf {II}}= & {} K_{0}\frac{e}{4n\sqrt{G}}\cos h\sin \dfrac{i}{2} \left\{ 4\left( 1+q\right) \sin E+\frac{e}{2}\left[ 2\left( q^{2}-3\right) E+\left( q^{2}-1\right) \sin 2E\right] \right. \nonumber \\&\left. +\frac{e^{2}}{18}q\left[ 9\left( q^{2}-7\right) \sin E+\left( q^{2}-3\right) \sin 3E\right] \right\} \end{aligned}$$

(45f)

3.3.3 Full direct and inverse transformations

The direct transformation follows the same rules as in the canonical case, and it provides the expressions of the “old” variables with respect to the “new” ones, as follows (Barrio and Palácian 1997):

$$\begin{aligned} {\mathbf {X}}_{\mathcal {P}}={\mathcal {T}}\left( {\mathbf {X}}_{\mathcal {P}}^{*}\right) ={\mathbf {X}}_{\mathcal {P}}^{*}+\mathcal {I}\frac{\partial {\mathcal {W}}^{\mathbf {I}}\left( {\mathbf {X}}_{\mathcal {P}}^{*}\right) }{ {\mathbf {X}}_{\mathcal {P}}^{*}}+{\mathbf {W}}^{\mathbf {II}}\left( {\mathbf {X}}_{ \mathcal {P}}^{*}\right) \end{aligned}$$

(46)

The gradient of ${\mathcal {W}}^{\mathbf {I}}$ is performed with respect to the Poincaré canonical variables, and it is given in Eq. (38), while ${\mathbf {W}}^{\mathbf {II}}$ is expressed in Eq. (43). For the numerical implementation of Eq. (46), a series expansion with respect to the powers of the eccentricity e should be performed, and the terms up to ${\mathcal {O}}\left( e^{3}\right) \simeq 0$ are given in Eq. (45).

At first order, the inverse of the transformation from Eq. (46) is:

$$\begin{aligned} {\mathbf {X}}_{\mathcal {P}}^{*}={\mathcal {T}}^{-1}\left( {\mathbf {X}}_{\mathcal { P}}\right) ={\mathbf {X}}_{\mathcal {P}}-\mathcal {I}\frac{\partial {\mathcal {W}}^{ \mathbf {I}}\left( {\mathbf {X}}_{\mathcal {P}}\right) }{{\mathbf {X}}_{\mathcal {P}}} -{\mathbf {W}}^{\mathbf {II}}\left( {\mathbf {X}}_{\mathcal {P}}\right) \end{aligned}$$

(47)

and it can be simply put as the same as the direct transformation, but for $J_{2}\rightarrow -J_{2}$ and $\rho _{0}\rightarrow -\rho _{0}.$ The aforementioned inverting method injects uncertainties with respect to the initial conditions (both expressions are truncations of infinite Lie series), in the sense that, in practice, ${\mathcal {T}}\circ {\mathcal {T}}^{-1}$ is not the identity transformation (but is acceptably close to it). The error in the initial conditions will be of order 2 with respect to the small perturbation parameters, namely:

$$\begin{aligned} \text {d}\left( {\mathcal {T}}^{-1}\left( {\mathcal {T}}\left( {\mathbf {X}}^{*}\right) \right) -{\mathbf {X}}^{*}\right) \simeq \varepsilon ^{2}+\delta ^{2} \end{aligned}$$

where $\varepsilon$ is the small parameter of the conservative perturbation ($J_{2}$ in our case), while $\delta$ is the small parameter associated to the non-conservative term. Here d denotes some adequately chosen metric in the associated phase space. It may be assumed that $\varepsilon \sim \delta$ .

Equations (46) and (47) give the explicit transformation between the new and the original variables, approximated at first order.

4 Numerical validation

4.1 Algorithm for orbit propagation

The position and the velocity of a satellite at each moment of time will be analytically evaluated as follows. Consider ${\mathbf {r}}_{0}$ and ${\mathbf {v}} _{0}$ the initial (osculating) position and velocity vectors, respectively, at $t=t_{0}$. Since the equations of motion, as well as the transformation between the new and the old variables, are in the phase space, before proceeding to the propagation itself, the state vector $\left[ {\mathbf {r}} _{0},{\mathbf {v}}_{0}\right] ^{T}$ is transformed into Poincaré variables ${\mathbf {X}}_{\mathcal {P},0}=\left[ \mathbf {Q}_{0},\mathbf {P}_{0}\right] ^{T}.$ The three main steps of the orbit propagation are depicted below.⁸

• 1. Apply the inverse transformation ${\mathcal {T}}^{-1}$ from Eq. (47) to obtain the “new” state vector ${\mathbf {X}}_{ \mathcal {P},0}^{*}={\mathcal {T}}^{-1}\left( {\mathbf {X}}_{\mathcal {P} ,0}\right) .$

• 2. Determine the “new” state vector ${\mathbf {X}}_{ \mathcal {P}}^{*}$ at any moment of time $t\ge t_{0}$ by using Eq. (17).

• 3. Apply the direct contact transformation ${\mathcal {T}}$ from Eq. (46) to obtain the original state vector ${\mathbf {X}}_{\mathcal {P}}= {\mathcal {T}}\left( {\mathbf {X}}_{\mathcal {P}}^{*}\right) .$

The Cartesian position and velocity vectors are finally obtained by elementary geometric transformations.

4.2 Numerical simulation

The previous developments are now validated for a LEO satellite with an initial altitude $h_0$ = 350 km and with a slightly eccentric orbit. The initial conditions are:

$$\begin{aligned} a_{0}=6728.137~\text {km};\quad e_{0}=0.015;\quad i_{0}=71^{\circ };\quad \omega _{0}=0^{\circ };\quad \varOmega _{0}=0^{\circ };\quad M_{0}=0^{\circ } \end{aligned}$$

(48)

and they are given in classical orbital elements for purely geometrical reasons.

The following values for the various parameters involved are used:⁹

Mean equatorial radius	$r_{e}=6378.137\, \hbox {km}$
Gravitational parameter	$\mu =3.986004418\times 10^{14}\, \hbox {m}^{3}/\hbox {s}^{2}$
Second zonal harmonic	$J_{2}=0.00108263$
Drag coefficient	$C_{D}=2.2$
Cross-sectional surface	$S_{ref}=0.03\, \hbox {m}^{2}$
Satellite mass	$m=3\, \hbox {kg}$
Atmospheric density at $h_{0}$	$\rho _{0}=10^{-11}\, \hbox {kg/m}^{3}$
Density scale factor	$\alpha =50\, \hbox {km}$

The simulation is performed for a time interval of 2 days.

Figure 1 represents the magnitude of the errors of the position vectors, calculated between three different analytic propagations and the reference solution which is generated by the direct numerical integration of the equations of motion using Runge Kutta 4–5. Our previous analytic propagator Martinusi et al. (2015) which assumes constant atmospheric distribution and the conservative Brouwer–Lyddane contact transformation exhibits a large error after two days, i.e., 180 km. For a propagation with an exponential atmosphere and the classic Brouwer transformation, the error drops down to 50 km. Finally, the propagation error can be reduced down to 10 km for an exponential atmosphere coupled with the proposed contact transformation (Eqs. (46–47)).

Figure 2 depicts the drifts in four “slow” variables, namely $a,e,i,\varOmega$.¹⁰ It may be seen that the use of the non-conservative CT reduces the error propagation amplitude for all elements, but still exhibits the same average drift for the eccentricity.

Figure 2c depicts the errors in the argument of latitude $\theta$. This is the main source of error in Fig. 1, but the use of the drag-augmented CT is seen to reduce the errors in $\theta$ by a factor of 7.

The use of the non-conservative CT also leads to a much simpler frequency content in the error, as clearly shown in Fig. 2a–c. This can be explained by the presence of terms containing sines and cosines of integer multiples of the eccentric anomaly in the non-conservative part of the CT.

Fig. 1

Comparison between three different analytic propagations and the reference solution for a LEO satellite ($J_2$ + exponential atmosphere)

Fig. 2

Absolute errors for semimajor axis, eccentricity and argument of latitude a errors in semimajor axis, b errors in eccentricity, c errors in argument of latitude

5 Conclusions

This paper offers a first-order approximate time-explicit solution for the motion of a satellite under the combined influence of the $J_2$ perturbation and an exponential atmosphere. Targeting increased accuracy, an infinitesimal contact transformation that allows to navigate between the original and averaged variables is also proposed herein. The comparison against direct numerical simulations for a satellite with an altitude of 350 km shows an error on the order of 10 km after two days of propagation. Part of this error is explained by the first-order truncation of the near-identity transformation between the original and averaged variables, which leads to an approximation of the actual initial conditions. Obviously, a second-order transformation would reduce these errors, and this will be considered in our future investigations.

Our future research will also progress toward more complex atmospheric models including the atmospheric bulge and the day-night variations as well as the influence of other non-conservative perturbations such as the solar radiation pressure.

Appendix

1.1 Lie series approximation for $\overline{L}$

Although the variable $\overline{L}$ has an explicit expression, depicted in Eq. (10a), the numerical implementation of the complex error function, as well as its inverse, rise the problem of dealing with differences of very large numbers. It would be much more convenient to have an accurate approximation for $\overline{L}$, and this is obtained by writing the solution to Eq. (8d) with the help of Lie series. For a complete description of the expansion mechanism, see Steinberg (1984).

Denote:

$$\begin{aligned} \lambda =\sqrt{\mu \alpha };\quad \beta =\frac{\lambda }{\overline{L}_{0}} \end{aligned}$$

The IVP to solve is rewritten as:

$$\begin{aligned} \dot{\overline{L}}=-\mu C_{0}\exp \left( \frac{\overline{L}_{0}-\mu r_{0}}{ \mu \alpha }\right) \exp \left( -\frac{\overline{L}^{2}-\overline{L}_{0}^{2} }{\lambda ^{2}}\right) ,\quad \overline{L}\left( t_{0}\right) =\overline{L}_{0} \end{aligned}$$

and the change of variable:

$$\begin{aligned} z=\frac{\overline{L}^{2}-\overline{L}_{0}^{2}}{\lambda ^{2}} \end{aligned}$$

(49)

is performed. Denote

$$\begin{aligned} \xi _{0}=\overline{L}_{0}\frac{2\mu }{\lambda ^{2}}C_{0}\exp \left( \frac{ \overline{L}_{0}-\mu r_{0}}{\mu \alpha }\right) \end{aligned}$$

The IVP in z is:

$$\begin{aligned} \dot{z}=-\xi _{0}\sqrt{z\beta ^{2}+1}\exp \left( -z\right) ,~z\left( t_{0}\right) =0 \end{aligned}$$

(50)

Consider D to be the differential operator, defined for any arbitrary function $\phi$:

$$\begin{aligned} D\phi =-\xi _{0}\sqrt{z\beta ^{2}+1}\exp \left( -z\right) \frac{\partial \phi }{\partial z} \end{aligned}$$

(51)

and define its formal powers as:

$$\begin{aligned} D^{k+1}\phi =D\left( D^{k}\phi \right) ,\;k\ge 1 \end{aligned}$$

Consider the formal exponential operator:

$$\begin{aligned} e^{\left( t-t_{0}\right) D}\phi =\phi +\sum _{k=1}^{\infty }\frac{\left( t-t_{0}\right) ^{k}}{k!}\left( D^{k}\phi \right) \end{aligned}$$

(52)

Then the solution to IVP (50) is expressed as:

$$\begin{aligned} z\left( t\right) =\left. e^{\left( t-t_{0}\right) D}z\right| _{z=0}, \end{aligned}$$

(53)

and explicitely:

$$\begin{aligned} z\left( t\right) =\sum _{k=1}^{\infty }\frac{\left( t-t_{0}\right) ^{k}}{k!} \left( \left. D^{k}z\right| _{z=0}\right) \end{aligned}$$

(54)

By taking into account the expression in Eq. (51) of the operator D,  the formal powers $\left. D^{k}z\right| _{z=0}$ are expressed as:

$$\begin{aligned} \left. D^{1}z\right| _{z=0}= & {} -\xi _{0} \\ \left. D^{2}z\right| _{z=0}= & {} \xi _{0}^{2}\left( \frac{1}{2}\beta ^{2}-1\right) \\ \left. D^{3}z\right| _{z=0}= & {} \xi _{0}^{3}\left( 2\beta ^{2}-2\right) \\ \left. D^{4}z\right| _{z=0}= & {} \xi _{0}^{4}\left( -\beta ^{4}+9\beta ^{2}-6\right) \\ \left. D^{5}z\right| _{z=0}= & {} \xi _{0}^{5}\left( -13\beta ^{4}+48\beta ^{2}-24\right) \\ \left. D^{6}z\right| _{z=0}= & {} \xi _{0}^{6}\left( \frac{13}{2}\beta ^{6}-137\beta ^{4}+300\beta ^{2}-120\right) \\ \left. D^{7}z\right| _{z=0}= & {} \xi _{0}^{7}\left( 176\beta ^{6}-1422\beta ^{4}+2160\beta ^{2}-720\right) \\ \left. D^{8}z\right| _{z=0}= & {} \xi _{0}^{8}\left( -88\beta ^{8}+3365\beta ^{6}-15354\beta ^{4}+17640\beta ^{2}-5040\right) \\ \left. D^{9}z\right| _{z=0}= & {} \xi _{0}^{9}\left( -4069\beta ^{8}+57628\beta ^{6}-175752\beta ^{4}+161280\beta ^{2}-40320\right) \end{aligned}$$

Then $\overline{L}=\overline{L}\left( t\right)$ is evaluated based on Eq. ( 49):

$$\begin{aligned} \overline{L}\left( t\right) =\overline{L}_{0}\sqrt{\beta ^{2}z\left( t\right) +1} \end{aligned}$$

1.2 Evaluation of $I_{1,2,3}$ integrals

In the form they are written in Eq. (13), the integrals $I_{1,2,3}$ are not suitable for an efficient series expansion approximation, given the considerable length of the interval on which the integration is performed (i.e., for a good approximation, a large number of terms are required in the truncated series expansion). For a rapid convergence, and also to avoid differences between very large numbers (since $L=\sqrt{\mu \alpha }$ has the same order of magnitude of the angular momentum). It would therefore be ideal to transform them to integrals from 0 to some value z that has the smallest possible absolute value, so that the accuracy of the series expansion is maximum.

First, note that $I_{1,2,3}$ may be rewritten as:

$$\begin{aligned} I_{k}=\exp \left( \frac{\overline{a}_{0}-r_{0}}{\alpha }\right) \int \limits _{ \overline{L}_{0}}^{\overline{L}}q_{k}\left( u\right) \exp \left( \frac{u^{2}- \overline{L}_{0}^{2}}{\mu \alpha }\right) \text {d}u,\quad k=1,2,3 \end{aligned}$$

where

$$\begin{aligned} q_{1}\left( u\right) =u^{-3},\quad q_{2}\left( u\right) =\left( u+\overline{G} _{0}-\overline{L}_{0}\right) ^{-3}u^{-4},\quad q_{3}\left( u\right) =\left( u+ \overline{G}_{0}-\overline{L}_{0}\right) ^{-4}u^{-3} \end{aligned}$$

To this end, denote

$$\begin{aligned} \lambda =\sqrt{\mu \alpha },\quad z=\frac{\overline{L}^{2}-\overline{L}_{0}^{2} }{\lambda ^{2}},\quad w_{k}\left( y\right) =\frac{q_{k}\left( \sqrt{\lambda ^{2}y+\overline{L}_{0}^{2}}\right) }{\sqrt{\lambda ^{2}y+\overline{L}_{0}^{2} }} \end{aligned}$$

and perform the change of variable:

$$\begin{aligned} y=\frac{u^{2}-\overline{L}_{0}^{2}}{\lambda ^{2}}\Rightarrow \text {d}u=\frac{ \lambda ^{2}}{2}\frac{\text {d}y}{\sqrt{\lambda ^{2}y+\overline{L}_{0}^{2}}} \end{aligned}$$

The integrals become:

$$\begin{aligned} I_{k}=\frac{\lambda ^{2}}{2}\exp \left( \frac{\overline{a}_{0}-r_{0}}{\alpha }\right) \int \limits _{0}^{z}w_{k}\left( y\right) \exp \left( y\right) \text {d}y \end{aligned}$$

By performing a Taylor series expansion for $\exp \left( y\right) ,$ the integrals become:

$$\begin{aligned} I_{k}=\frac{\lambda ^{2}}{2}\exp \left( \frac{\overline{a}_{0}-r_{0}}{\alpha }\right) \sum \limits _{N=0}^{\infty }\left[ \frac{1}{N!}\int \limits _{0}^{z}y^{N}w_{k}\left( y\right) \text {d}y\right] \end{aligned}$$

and written separately:

$$\begin{aligned} I_{1}= & {} \frac{\lambda ^{2}}{2}\exp \left( \frac{\overline{a}_{0}-r_{0}}{ \alpha }\right) \sum \limits _{N=0}^{\infty }\left[ \frac{1}{N!} \int \limits _{0}^{z}\frac{y^{N}}{\left( \lambda ^{2}y+\overline{L} _{0}^{2}\right) ^{2}}\text {d}y\right] \\ I_{2}= & {} \frac{\lambda ^{2}}{2}\exp \left( \frac{\overline{a}_{0}-r_{0}}{ \alpha }\right) \sum \limits _{N=0}^{\infty }\left[ \frac{1}{N!} \int \limits _{0}^{z}\frac{y^{N}}{\left[ \sqrt{\lambda ^{2}y+\overline{L} _{0}^{2}}+\overline{G}_{0}-\overline{L}_{0}\right] ^{3}\left( \lambda ^{2}y+ \overline{L}_{0}^{2}\right) ^{\frac{5}{2}}}\text {d}y\right] \\ I_{3}= & {} \frac{\lambda ^{2}}{2}\exp \left( \frac{\overline{a}_{0}-r_{0}}{ \alpha }\right) \sum \limits _{N=0}^{\infty }\left[ \frac{1}{N!} \int \limits _{0}^{z}\frac{y^{N}}{\left[ \sqrt{\lambda ^{2}y+\overline{L} _{0}^{2}}+\overline{G}_{0}-\overline{L}_{0}\right] ^{4}\left( \lambda ^{2}y+ \overline{L}_{0}^{2}\right) ^{3}}\text {d}y\right] \end{aligned}$$

The evaluation of $I_{1,2,3}$ has been simplified to definite integrals that may be expressed explicitly through elementary functions.

1.3 Jacobian for coordinate transformations

The Jacobian of the transformation from Delaunay to Whittaker elements is:

$$\begin{aligned} {\mathcal {J}}_{\mathcal {D}}^{{\mathcal {W}}}=\frac{\partial \left( r,\theta ,\nu ,R,\varTheta ,N\right) }{\partial \left( l,g,h,L,G,H\right) }=\left[ \begin{array}{cccccc} \dfrac{p\sigma }{\eta ^{3}} &{} 0 &{} 0 &{} \dfrac{r\left( \kappa ^{2}+\kappa -2e^{2}\right) }{Le^{2}} &{} \dfrac{\eta p\kappa }{Le^{2}} &{} 0 \\ &{} &{} &{} &{} &{} \\ \dfrac{\left( 1+\kappa \right) ^{2}}{\eta ^{3}} &{} 1 &{} 0 &{} \dfrac{\sigma \left( 2+\kappa \right) }{Le^{2}} &{} -\dfrac{\eta \sigma \left( 2+\kappa \right) }{Le^{2}} &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} \\ \dfrac{L\kappa \left( 1+\kappa \right) ^{2}}{\eta ^{2}p} &{} 0 &{} 0 &{} \dfrac{ \eta \sigma }{pe^{2}}\left[ 1+2\kappa -\sigma ^{2}\right] &{} -\dfrac{\sigma \left( 1+\kappa \right) ^{2}}{pe^{2}} &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$

The Jacobian of the transformation from Poincaré to Delaunay variables is:

$$\begin{aligned} {\mathcal {J}}_{\mathcal {P}}^{\mathcal {D}}= & {} \frac{\partial \left( l,g,h,L,G,H\right) }{\partial \left( Q_{1},Q_{2},Q_{3},P_{1},P_{2},P_{3}\right) }\\= & {} \left[ \begin{array}{cccccc} 1 &{} \dfrac{P_{2}}{Q_{2}^{2}+P_{2}^{2}} &{} 0 &{} 0 &{} -\dfrac{Q_{2}}{ Q_{2}^{2}+P_{2}^{2}} &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} -\dfrac{P_{2}}{Q_{2}^{2}+P_{2}^{2}} &{} \dfrac{P_{3}}{Q_{3}^{2}+P_{3}^{2}} &{} 0 &{} \dfrac{Q_{2}}{Q_{2}^{2}+P_{2}^{2}} &{} -\dfrac{Q_{3}}{Q_{3}^{2}+P_{3}^{2} } \\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} -\dfrac{P_{3}}{Q_{3}^{2}+P_{3}^{2}} &{} 0 &{} 0 &{} \dfrac{Q_{3}}{ Q_{3}^{2}+P_{3}^{2}} \\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} -Q_{2} &{} 0 &{} 1 &{} -P_{2} &{} 0 \\ &{} &{} &{} &{} &{} \\ 0 &{} -Q_{2} &{} -Q_{3} &{} 1 &{} -P_{2} &{} -P_{3} \end{array} \right] \end{aligned}$$

The Jacobian of the transformation from Whittaker to Poincaré elements may now be explicitly derived as:

$$\begin{aligned} {\mathcal {J}}_{\mathcal {P}}^{{\mathcal {W}}}=\frac{\partial \left( r,\theta ,\nu ,R,\varTheta ,N\right) }{\partial \left( Q_{1},Q_{2},Q_{3},P_{1},P_{2},P_{3}\right) }={\mathcal {J}}_{\mathcal {D}}^{ {\mathcal {W}}}{\mathcal {J}}_{\mathcal {P}}^{\mathcal {D}} \end{aligned}$$

Since it involves only elementary computations, that are nevertheless leading to relatively long expressions, the full matrix form of ${\mathcal {J}} _{\mathcal {P}}^{{\mathcal {W}}}$ will not be displayed. In any case, it is obtained by the multiplication of two explicit matrices.

1.4 Transformation from Poincaré to Cartesian coordinates

The Poincaré canonical variables are mentioned and used in very few Astrodynamics/Orbital Mechanics textbooks, but they lack a comprehensive approach, and to our knowledge, a straightforward transformation from these variables to Cartesian is absent from the literature. The closest approach is found in Battin (1999), but it is made for the equinoctial variables, that are nonsingular but not canonical.

The transformation is determined here in the most direct way possible. It is known that the inertial position and velocity vectors are expressed in the perifocal frame $\left\{ P\right\}$ as:

$$\begin{aligned} {\mathbf {r}}^{\left\{ P\right\} }=r\left[ \begin{array}{c} \cos f \\ \sin f \\ 0 \end{array} \right] ;\quad {\mathbf {v}}^{\left\{ P\right\} }=\frac{\mu }{G}\left[ \begin{array}{c} -\sin f \\ e+\cos f \\ 0 \end{array} \right] \end{aligned}$$

and their corresponding column matrices in the inertial frame originated in the attraction center are:

$$\begin{aligned} {\mathbf {r}}^{\left\{ IN\right\} }= & {} {\mathbf {R}}\left( {\mathbf {i}}_{3},h\right) {\mathbf {R}}\left( {\mathbf {i}}_{1},i\right) {\mathbf {R}}\left( {\mathbf {i}} _{3},g\right) {\mathbf {r}}^{\left\{ P\right\} } \\ {\mathbf {v}}^{\left\{ IN\right\} }= & {} {\mathbf {R}}\left( {\mathbf {i}}_{3},h\right) {\mathbf {R}}\left( {\mathbf {i}}_{1},i\right) {\mathbf {R}}\left( {\mathbf {i}} _{3},g\right) {\mathbf {v}}^{\left\{ P\right\} } \end{aligned}$$

where the orthogonal matrices ${\mathbf {R}}_{h},$ ${\mathbf {R}}_{i},$ ${\mathbf {R}} _{g}$ are:

$$\begin{aligned} {\mathbf {R}}\left( {\mathbf {i}}_{3},h\right)= & {} \left[ \begin{array}{ccc} \cos h &{} -\sin h &{} 0 \\ \sin h &{} \cos h &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] ,\quad {\mathbf {R}}\left( {\mathbf {i}}_{1},i\right) =\left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos i &{} -\sin i \\ 0 &{} \sin i &{} \cos i \end{array} \right] ,\\ {\mathbf {R}}\left( {\mathbf {i}}_{3},g\right)= & {} \left[ \begin{array}{ccc} \cos g &{} -\sin g &{} 0 \\ \sin g &{} \cos g &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$

If a new fixed frame $\left\{ \mathcal {P}\right\}$ is defined such that the position vector has the expression:

$$\begin{aligned} {\mathbf {r}}^{\left\{ \mathcal {P}\right\} }=r\left[ \begin{array}{c} \cos \left( f+g+h\right) \\ \sin \left( f+g+h\right) \\ 0 \end{array} \right] =r\left[ \begin{array}{c} \cos \left( Q_{1}+f-l\right) \\ \sin \left( Q_{1}+f-l\right) \\ 0 \end{array} \right] , \end{aligned}$$

it will follow (by elementary computations) that the velocity in the same frame $\left\{ \mathcal {P}\right\}$ is:

$$\begin{aligned} {\mathbf {v}}^{\left\{ \mathcal {P}\right\} }=\frac{2\mu }{\sqrt{4P_{1}-2\left( Q_{2}^{2}+P_{2}^{2}\right) }}\left[ \begin{array}{c} \dfrac{Q_{2}}{2P_{1}}\sqrt{4P_{1}-\left( Q_{2}^{2}+P_{2}^{2}\right) }-\sin \left( Q_{1}+f-l\right) \\ \dfrac{P_{2}}{2P_{1}}\sqrt{4P_{1}-\left( Q_{2}^{2}+P_{2}^{2}\right) }+\cos \left( Q_{1}+f-l\right) \\ 0 \end{array} \right] \end{aligned}$$

Consequently, the inertial counterparts of ${\mathbf {r}}^{\left\{ \mathcal {P} \right\} },$ ${\mathbf {v}}^{\left\{ \mathcal {P}\right\} }$ are:

$$\begin{aligned} {\mathbf {r}}^{\left\{ IN\right\} }= & {} \mathbf {Ar}^{\left\{ \mathcal {P}\right\} } \\ {\mathbf {v}}^{\left\{ IN\right\} }= & {} \mathbf {Av}^{\left\{ \mathcal {P}\right\} } \end{aligned}$$

The matrix $\mathbf {A}$ is found to be¹¹:

$$\begin{aligned} \mathbf {A}={\mathbf {R}}\left( {\mathbf {i}}_{3},h\right) {\mathbf {R}}\left( \mathbf { i}_{1},i\right) {\mathbf {R}}\left( {\mathbf {i}}_{3},-h\right) \end{aligned}$$

Define U such that:

$$\begin{aligned} U=\sqrt{4P_{1}-2\left( Q_{2}^{2}+P_{2}^{2}\right) -\left( Q_{3}^{2}+P_{3}^{2}\right) }=\sqrt{2G\left( 1+\cos i\right) } \end{aligned}$$

Then the explicit expression of matrix $\mathbf {A,}$ in Poincaré variables, is:

$$\begin{aligned} \mathbf {A}=\frac{1}{U^{2}+Q_{3}^{2}+P_{3}^{2}}\left[ \begin{array}{ccc} U^{2}-Q_{3}^{2}+P_{3}^{2} &{} -2P_{3}Q_{3} &{} -2{{ UQ}}_{3} \\ -2P_{3}Q_{3} &{} U^{2}+Q_{3}^{2}-P_{3}^{2} &{} -2{{ UP}}_{3} \\ 2{{ UQ}}_{3} &{} 2{{ UP}}_{3} &{} U^{2}-Q_{3}^{2}-P_{3}^{2} \end{array} \right] \end{aligned}$$