1 Introduction

Second order leapfrog or splitting methods are a class of widely used time-symmetric, explicit and symplectic integration algorithms for Hamiltonian systems. These characteristics make them a standard tool for very long integrations, as they preserve the phase space structure and first integrals of the system. Being time-symmetric, second order leapfrog algorithms have an error expansion that only contains even powers of the timestep. This fact makes them convenient for use within extrapolation schemes, such as the Gragg–Bulirsch–Stoer (GBS) method (Gragg 1965; Bulirsch and Stoer 1966), which are often used when very high accuracy is required (Deuflhard and Bornemann 2002).

The main problem with leapfrog methods is the fact that they can only be constructed for systems where the Hamiltonian separates into two or more parts, where the flow of each part can be separately integrated (McLachlan and Quispel 2002). A solution to this problem for partitioned systems of the type

$$\begin{aligned} \dot{\mathbf {x}}&= \mathbf {v}\nonumber \\ \dot{\mathbf {v}}&= \mathbf {f}(\mathbf {x}, \mathbf {v}) \end{aligned}$$
(1)

was presented in Hellström and Mikkola (2010). By means of auxiliary velocity coordinates, the equations of motion were transformed into a separable form and thus amenable for integration with a leapfrog method. The method, called auxiliary velocity algorithm (AVA), can also be used for nonconservative systems as well.

In this paper we propose an improved extension of the AVA method, applicable for Hamiltonian and non-Hamiltonian cases where all equations of motion depend on both coordinates and momenta in general. We first briefly introduce leapfrog integration methods, and outline their properties. Next, we demonstrate how the phase space of general Hamiltonian systems can be extended and a new Hamiltonian constructed so that the equations of motion are brought into a separated form. We then construct symmetric leapfrog integrators for the equations. These include maps that mix the extended phase space, which we find to be a requirement for good long term behaviour. Finally, we investigate how the extended phase space can be projected back to the original number of dimensions so that extra accuracy can be gained in the process. We then show how the same principle can be applied to nonconservative systems as well. We apply the obtained leapfrog methods to illustrative example cases: Hamiltonian geodesic flow, and a forced van der Pol oscillator.

2 Leapfrog integration

In many applications to classical physics, such as gravitational interaction of point masses, the Hamiltonian function \(H:\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}\) of the system can be separated into two parts

$$\begin{aligned} H(\mathbf {q}, \mathbf {p}) = T(\mathbf {p}) + V(\mathbf {q}), \end{aligned}$$
(2)

where \(T:\mathbb {R}^n\rightarrow \mathbb {R}\) is the kinetic energy, and \(V:\mathbb {R}^n\rightarrow \mathbb {R}\) is the potential energy. In these cases, the Hamiltonian equations of motion read

$$\begin{aligned} \dot{\mathbf {q}}&= \nabla _\mathbf {p}H(\mathbf {q},\mathbf {p}) = \nabla _\mathbf {p}T(\mathbf {p}) \end{aligned}$$
(3)
$$\begin{aligned} \dot{\mathbf {p}}&= -\nabla _\mathbf {q}H(\mathbf {q},\mathbf {p}) = -\nabla _\mathbf {q}V(\mathbf {q}), \end{aligned}$$
(4)

where \(\nabla _\mathbf {x} = (\partial /\partial x_1, \ldots , \partial /\partial x_n)\). The equations for coordinates can then be directly integrated, if the momenta are kept constant, and vice versa. The solutions can be combined in a time-symmetric manner to obtain the two forms of the archetypal second order leapfrog, also known as the Störmer–Verlet method, or Strang splitting (Strang 1968):

$$\begin{aligned} \mathbf {q}_{n+\frac{1}{2}}&= \mathbf {q}_n + \frac{h}{2} \nabla _\mathbf {p}T(\mathbf {p}_n) \end{aligned}$$
(5a)
$$\begin{aligned} \mathbf {p}_{n+1}&= \mathbf {p}_n - h \nabla _\mathbf {\mathbf {q}}V(\mathbf {q}_{n+\frac{1}{2}}) \end{aligned}$$
(5b)
$$\begin{aligned} \mathbf {q}_{n+1}&= \mathbf {q}_{n+\frac{1}{2}} + \frac{h}{2} \nabla _\mathbf {p}T(\mathbf {p}_{n+1}) \end{aligned}$$
(5c)

and

$$\begin{aligned} \mathbf {p}_{n+\frac{1}{2}}&= \mathbf {p}_n- \frac{h}{2} \nabla _\mathbf {q}V(\mathbf {q}_n)\end{aligned}$$
(6a)
$$\begin{aligned} \mathbf {q}_{n+1}&= \mathbf {q}_n+ h \nabla _\mathbf {\mathbf {p}}T(\mathbf {p}_{n+\frac{1}{2}}) \end{aligned}$$
(6b)
$$\begin{aligned} \mathbf {p}_{n+1}&= \mathbf {p}_{n+\frac{1}{2}} - \frac{h}{2} \nabla _\mathbf {q}V(\mathbf {q}_{n+1}), \end{aligned}$$
(6c)

where \(\mathbf {q}_n = \mathbf {q}(nh), \,\mathbf {p}_n = \mathbf {p}(nh), \,n\in \mathbb {Z}\) and \(h\in \mathbb {R}\) is the timestep.

Equations (5) and (6) can also be written as

$$\begin{aligned} \begin{aligned} \mathbf {z}_{n+1}&= \left( \varphi ^{X_T}_{h/2} \circ \varphi ^{X_V}_h \circ \varphi ^{X_T}_{h/2}\right) (\mathbf {z}_n) \\&= \exp \left( \frac{h}{2}T\right) \exp \left( hV\right) \exp \left( \frac{h}{2}T\right) \mathbf {z}_n \end{aligned} \end{aligned}$$
(7)

and

$$\begin{aligned} \begin{aligned} \mathbf {z}_{n+1}&= \left( \varphi ^{X_V}_{h/2} \circ \varphi ^{X_T}_h \circ \varphi ^{X_V}_{h/2}\right) (\mathbf {z}_n) \\&= \exp \left( \frac{h}{2}V\right) \exp \left( hT\right) \exp \left( \frac{h}{2}V\right) \mathbf {z}_n, \end{aligned} \end{aligned}$$
(8)

where \(\mathbf {z}=(\mathbf {q},\mathbf {p}), \,X_T = \mathbf {J}^{-1}\nabla T\) and \(X_V = \mathbf {J}^{-1}\nabla V\) are the Hamiltonian vector fields of \(T\) and \(V, \,\varphi ^X_t:\mathbb {R}^{2n}\rightarrow \mathbb {R}^{2n}\) is the phase space flow along the vector field \(X\),

$$\begin{aligned} \mathbf {J}= \begin{pmatrix} \mathbf {0} &{} -\mathbf {I}_n \\ \mathbf {I}_n &{} \mathbf {0} \end{pmatrix}, \end{aligned}$$
(9)

is the symplectic form given in local coordinates, \(\mathbf {I}_n\) is the \(n\times n\) identity matrix and \(\exp :\mathfrak {g}\rightarrow G\) is the exponential mapping from a Lie algebra \(\mathfrak {g}\) to the corresponding Lie group. Here the Lie algebra is the algebra of smooth, real-valued functions on the phase space, with the Lie product given by the Poisson brackets \(\{f,g\} = \nabla g \mathbf {J}(\nabla f)^T\). The group action (written multiplicatively in Eqs. (7) and (8)) on the phase space manifold of the corresponding Lie group is the phase space flow of the associated vector field.

Now, a reverse application of the Baker–Campbell–Hausdorff (BCH) formula on equation (7) yields

$$\begin{aligned} \begin{aligned}&\exp \left( \frac{h}{2}T\right) \exp \left( hV\right) \exp \left( \frac{h}{2}T\right) \\&\quad \quad =\exp \left[ h(T + V) + h^3\left( -\frac{1}{24}\{\{V,T\},T\} + \frac{1}{12}\{ \{T,V\}, V\}\right) + \fancyscript{O}(h^4)\right] \\&\quad \quad = \exp (h\widehat{H}), \end{aligned} \end{aligned}$$
(10)

where then

$$\begin{aligned} \widehat{H}= T + V + h^2\left( -\frac{1}{24}\{\{V,T\},T\} + \frac{1}{12}\{ \{T,V\}, V\}\right) + \fancyscript{O}(h^3), \end{aligned}$$
(11)

and similarly for (8) with \(T\leftrightarrow V\). Equations (7)–(11) are of interest for a number of reasons. First, the flows of Hamiltonian vector fields \(X_f\) are symplectic transformations for smooth functions \(f\) (Hairer et al. 2006), and thus preserve the geometric structure of the phase space, and all first integrals. Since \(T\) and \(V\) are smooth, the leapfrog method has these properties as well. Equation (11) shows on the other hand that leapfrog integrators exactly solve a Hamiltonian problem that is asymptotically related to the original one, with a perturbed Hamiltonian \(\widehat{H}\).

Another desirable property of the second order leapfrogs is (relatively) easy composition of the basic second order method to yield methods of higher order (Yoshida 1990). If \(\varphi _h\) is the numerical flow of a time-symmetric second order leapfrog, then

$$\begin{aligned} \widetilde{\varphi }_h = \varphi _{\gamma _{s}h}\circ \varphi _{\gamma _{s-1}h}\circ \cdots \circ \varphi _{\gamma _{1}h}, \end{aligned}$$
(12)

can be shown to be a method of higher order for certain choices of \(s\) and \(\gamma _i\in \mathbb {R}\), with \(\gamma _{s+1-i} = \gamma _i\) for time-symmetric methods such as the second order leapfrog (Hairer et al. 2006). One particular example is the sixth order composition

$$\begin{aligned} \begin{aligned} \gamma _{1} = \gamma _{9}&= 0.39216144400731413928 \\ \gamma _{2} = \gamma _{8}&= 0.33259913678935943860 \\ \gamma _{3} = \gamma _{7}&= -0.70624617255763935981 \\ \gamma _{4} = \gamma _{6}&= 0.082213596293550800230 \\ \gamma _{5}&= 0.79854399093482996340, \end{aligned} \end{aligned}$$
(13)

from Kahan and Li (1997) (composition s9odr6a in the paper), which we will use in Sect. 5.2. The second order leapfrog is also useful when used within an extrapolation scheme, such as the GBS scheme (Mikkola and Aarseth 2002; Hellström and Mikkola 2010). Using an extrapolation scheme does in principle destroy the desirable properties of the leapfrog, since the substeps require a change in timestep which destroys symplecticity, and the final linear combination of the symplectic maps is also not symplectic in general. In practice, the increase in accuracy per computational work spent often offsets this. For a comprehensive review of splitting methods in contexts not limited to Hamiltonian ordinary differential equations (ODEs), see McLachlan and Quispel (2002), for geometric integration methods in general, see Hairer et al. (2006), and for extrapolation and other conventional methods for general ODEs, see Deuflhard and Bornemann (2002).

3 A splitting method for an extended inseparable Hamiltonian problem

In the general case, the Hamiltonian \(H(\mathbf {q}, \mathbf {p})\) does not separate into additive parts, and the approach of the previous section cannot be used. We can partially circumvent this problem in the following manner. We first extend the phase space \(S\) (essentially \(\mathbb {R}^{2n}\), when always operating in local coordinates) by joining it with another identical copy, giving an extended phase space \(S^2= S\times S\). In local coordinates \((\mathbf {q}, \widetilde{\mathbf {q}}, \mathbf {p}, \widetilde{\mathbf {p}})\), the symplectic form \(\mathbf {J}_{S^2}\) on this phase space is

$$\begin{aligned} \mathbf {J}_{S^2} = \begin{pmatrix} \mathbf {0} &{} -\mathbf {I}_{2n} \\ \mathbf {I}_{2n} &{} \mathbf {0} \end{pmatrix} = \mathbf {J}_{S} \otimes \mathbf {I}_2, \end{aligned}$$
(14)

where \(\mathbf {J}_{S}\) is the symplectic form on \(S\) and \(\otimes \) is the Kronecker product. We then introduce a new Hamiltonian \(\widetilde{H}:S^2\rightarrow \mathbb {R}\) on this extended phase space with

$$\begin{aligned} \widetilde{H}(\mathbf {q}, \widetilde{\mathbf {q}}, \mathbf {p}, \widetilde{\mathbf {p}}) = H_1(\mathbf {q}, \widetilde{\mathbf {p}}) + H_2(\widetilde{\mathbf {q}}, \mathbf {p}), \end{aligned}$$
(15)

where now \(H_1 = H_2 = H\), equal to the Hamiltonian function of the original system. Hamilton’s equations for the two parts of this split Hamiltonian are then

$$\begin{aligned} \dot{\widetilde{\mathbf {q}}}&= \nabla _{\widetilde{\mathbf {p}}} H_1 \end{aligned}$$
(16a)
$$\begin{aligned} \dot{\mathbf {p}}&= -\nabla _{\mathbf {q}} H_1 \end{aligned}$$
(16b)

and

$$\begin{aligned} \dot{\mathbf {q}}&= \nabla _{\mathbf {p}} H_2 \end{aligned}$$
(17a)
$$\begin{aligned} \dot{\widetilde{\mathbf {p}}}&= -\nabla _{\widetilde{\mathbf {q}}} H_2. \end{aligned}$$
(17b)

We see that the derivatives of \(\widetilde{\mathbf {q}}\) and \(\mathbf {p}\) depend only on \(\mathbf {q}\) and \(\widetilde{\mathbf {p}}\) and vice versa, and the equations can be integrated to yield the actions of \(\exp (tH_1)\) and \(\exp (tH_2)\). We can now apply the results from the previous section to find

$$\begin{aligned} \begin{aligned} \exp (h\widetilde{H})&= \exp \left( \frac{h}{2}H_1\right) \exp \left( h H_2\right) \exp \left( \frac{h}{2}H_1\right) + \fancyscript{O}(h^3) \\&= \exp \left( \frac{h}{2}H_2\right) \exp \left( h H_1\right) \exp \left( \frac{h}{2}H_2\right) + \fancyscript{O}(h^3), \end{aligned} \end{aligned}$$
(18)

where \(h\in \mathbb {R}\), which gives the leapfrog algorithms

$$\begin{aligned} \mathbf {q}_{n+\frac{1}{2}}&= \mathbf {q}_n + \frac{h}{2} \nabla _{\mathbf {p}} H_2(\widetilde{\mathbf {q}}_n, \mathbf {p}_n) \end{aligned}$$
(19a)
$$\begin{aligned} \widetilde{\mathbf {p}}_{n+\frac{1}{2}}&= \widetilde{\mathbf {p}}_n - \frac{h}{2} \nabla _{\widetilde{\mathbf {q}}} H_2(\widetilde{\mathbf {q}}_n, \mathbf {p}_n) \end{aligned}$$
(19b)
$$\begin{aligned} \widetilde{\mathbf {q}}_{n+1}&= \widetilde{\mathbf {q}}_n + h \nabla _{\widetilde{\mathbf {p}}} H_1(\mathbf {q}_{n+\frac{1}{2}}, \widetilde{\mathbf {p}}_{n+\frac{1}{2}}) \end{aligned}$$
(19c)
$$\begin{aligned} \mathbf {p}_{n+1}&= \mathbf {p}_n - h \nabla _{\mathbf {q}} H_1(\mathbf {q}_{n+\frac{1}{2}}, \widetilde{\mathbf {p}}_{n+\frac{1}{2}}) \end{aligned}$$
(19d)
$$\begin{aligned} \mathbf {q}_{n+1}&= \mathbf {q}_{n+\frac{1}{2}} + \frac{h}{2} \nabla _{\mathbf {p}} H_2(\widetilde{\mathbf {q}}_{n+1}, \mathbf {p}_{n+1}) \end{aligned}$$
(19e)
$$\begin{aligned} \widetilde{\mathbf {p}}_{n+1}&= \widetilde{\mathbf {p}}_{n+\frac{1}{2}} - \frac{h}{2} \nabla _{\widetilde{\mathbf {q}}} H_2(\widetilde{\mathbf {q}}_{n+1}, \mathbf {p}_{n+1}) \end{aligned}$$
(19f)

and

$$\begin{aligned} \widetilde{\mathbf {q}}_{n+\frac{1}{2}}&= \widetilde{\mathbf {q}}_n + \frac{h}{2} \nabla _{\widetilde{\mathbf {p}}} H_1(\mathbf {q}_n, \widetilde{\mathbf {p}}_n) \end{aligned}$$
(20a)
$$\begin{aligned} \mathbf {p}_{n+\frac{1}{2}}&= \mathbf {p}_n - \frac{h}{2} \nabla _{\mathbf {q}} H_1(\mathbf {q}_n, \widetilde{\mathbf {p}}_n) \end{aligned}$$
(20b)
$$\begin{aligned} \mathbf {q}_{n+1}&= \mathbf {q}_n + h \nabla _{\mathbf {p}} H_2(\widetilde{\mathbf {q}}_{n+\frac{1}{2}}, \mathbf {p}_{n+\frac{1}{2}}) \end{aligned}$$
(20c)
$$\begin{aligned} \widetilde{\mathbf {p}}_{n+1}&= \widetilde{\mathbf {p}}_n - h \nabla _{\widetilde{\mathbf {q}}} H_2(\widetilde{\mathbf {q}}_{n+\frac{1}{2}}, \mathbf {p}_{n+\frac{1}{2}}) \end{aligned}$$
(20d)
$$\begin{aligned} \widetilde{\mathbf {q}}_{n+1}&= \widetilde{\mathbf {q}}_{n+\frac{1}{2}} + \frac{h}{2} \nabla _{\widetilde{\mathbf {p}}} H_1(\mathbf {q}_{n+1}, \widetilde{\mathbf {p}}_{n+1}) \end{aligned}$$
(20e)
$$\begin{aligned} \mathbf {p}_{n+1}&= \mathbf {p}_{n+\frac{1}{2}} - \frac{h}{2} \nabla _{\mathbf {q}} H_1(\mathbf {q}_{n+1}, \widetilde{\mathbf {p}}_{n+1}) \end{aligned}$$
(20f)

over one timestep \(h\). The leapfrog methods (19) and (20) then exactly solve the Hamiltonian flows of the related Hamiltonians

$$\begin{aligned} \widehat{H}_{212} = H_1 + H_2 + h^2\left( -\frac{1}{24}\{\{H_2,H_1\},H_1\} + \frac{1}{12}\{\{H_1,H_2\},H_2\}\right) + \fancyscript{O}(h^3) \end{aligned}$$
(21)

and

$$\begin{aligned} \widehat{H}_{121} = H_1 + H_2 + h^2\left( -\frac{1}{24}\{\{H_1,H_2\},H_2\} + \frac{1}{12}\{\{H_2,H_1\},H_1\}\right) + \fancyscript{O}(h^3). \end{aligned}$$
(22)

If we now consider a Hamiltonian initial value problem, with the initial values \((\mathbf {q}_0, \mathbf {p}_0)\) and set \(\widetilde{\mathbf {q}}_0 = \mathbf {q}_0, \,\widetilde{\mathbf {p}}_0 = \mathbf {p}_0\), we see that the Eqs. (16) and (17) give identical derivatives and identical evolution for both pairs \((\mathbf {q}(t), \widetilde{\mathbf {p}}(t))\) and \((\widetilde{\mathbf {q}}(t), \mathbf {p}(t))\), equal to the flow of the original Hamiltonian system \((\mathbf {q}(t),\mathbf {p}(t))\). The numerical leapfrog solutions (19) and (20) then solve closely related Hamiltonian problems given by (21) and (22).

We can write the problem in the form

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \dot{\mathbf {q}} \\ \dot{\widetilde{\mathbf {q}}}\\ \dot{\mathbf {p}} \\ \dot{\widetilde{\mathbf {p}}} \end{pmatrix}&= \begin{pmatrix} \nabla _{\mathbf {p}}H_2 \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ \nabla _{\widetilde{\mathbf {p}}}H_1 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ -\nabla _{\mathbf {q}}H_1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ -\nabla _{\widetilde{\mathbf {q}}}H_2 \end{pmatrix} \\&= f_{\mathbf {q}}(\widetilde{\mathbf {q}},\mathbf {p}) + f_{\widetilde{\mathbf {q}}}(\mathbf {q},\widetilde{\mathbf {p}}) + f_{\mathbf {p}}(\mathbf {q},\widetilde{\mathbf {p}}) + f_{\widetilde{\mathbf {p}}}(\widetilde{\mathbf {q}},\mathbf {p}), \end{aligned} \end{aligned}$$
(23)

where the component vector fields \(f_{i}\) are Hamiltonian. We also define operators \(\mathbf {Q}(h) = \exp (hf_{\mathbf {q}}), \,\widetilde{\mathbf {Q}}(h) = \exp (hf_{\widetilde{\mathbf {q}}})\), and similarly for \(\mathbf {P}\) and \(\widetilde{\mathbf {P}}\), where \(\exp (hf)\mathbf {z}= \varphi ^{f}_h(\mathbf {z})\) is a translation along the vector field \(f\). From this we see that we can also construct split solutions like

$$\begin{aligned} \begin{aligned} \exp (h\widetilde{H})&= \mathbf {Q}(h/2)\widetilde{\mathbf {Q}}(h/2)\mathbf {P}(h/2)\widetilde{\mathbf {P}}(h)\mathbf {P}(h/2)\widetilde{\mathbf {Q}}(h/2)\mathbf {Q}(h/2) + \fancyscript{O}(h^3) \\&= \mathbf {Q}\widetilde{\mathbf {Q}}\mathbf {P}\widetilde{\mathbf {P}}(h) + \fancyscript{O}(h^3), \end{aligned} \end{aligned}$$
(24)

where the last equality defines a shorthand notation based on the symmetry of the operator. Pairs \(\mathbf {Q},\widetilde{\mathbf {P}}\) and \(\widetilde{\mathbf {Q}},\mathbf {P}\) commute, so e.g. \(\mathbf {H}_1(h)=\exp (hH_1) = \widetilde{\mathbf {Q}}(h)\mathbf {P}(h)=\mathbf {P}(h)\widetilde{\mathbf {Q}}(h)\). Original and auxiliary variables are also interchangeable, since they initially have the same values. As such, the only unique symmetric second order leapfrog compositions are (with the above shorthand)

$$\begin{aligned}&\displaystyle \widetilde{\mathbf {Q}}\mathbf {P}\mathbf {Q}\widetilde{\mathbf {P}}= \mathbf {H}_1(h/2)\mathbf {H}_2(h)\mathbf {H}_1(h/2) \end{aligned}$$
(25a)
$$\begin{aligned}&\displaystyle \mathbf {Q}\widetilde{\mathbf {Q}}\mathbf {P}\widetilde{\mathbf {P}}\end{aligned}$$
(25b)
$$\begin{aligned}&\displaystyle \mathbf {Q}\widetilde{\mathbf {Q}}\widetilde{\mathbf {P}}\mathbf {P}\end{aligned}$$
(25c)
$$\begin{aligned}&\displaystyle \mathbf {P}\widetilde{\mathbf {P}}\mathbf {Q}\widetilde{\mathbf {Q}}\end{aligned}$$
(25d)
$$\begin{aligned}&\displaystyle \mathbf {P}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {Q}\end{aligned}$$
(25e)

up to a reordering of commuting operators, and switching \((\mathbf {Q},\mathbf {P})\leftrightarrow (\widetilde{\mathbf {Q}},\widetilde{\mathbf {P}})\).

From the leapfrogs (25), the only one symplectic in the extended phase space is (25a), as well as its conjugate method \(\mathbf {H}_2(h/2)\mathbf {H}_1(h)\mathbf {H}_2(h/2)\). It is not, however symplectic as a mapping \(M\ni (\mathbf {q},\mathbf {p})\mapsto (\mathbf {q}',\mathbf {p}')\in M\) within the original phase space if the final \((\mathbf {q}',\mathbf {p}')\) are obtained from \(\widetilde{\mathbf {Q}}\mathbf {P}\mathbf {Q}\widetilde{\mathbf {P}}(h)(\mathbf {q}, \widetilde{\mathbf {q}},\mathbf {p},\widetilde{\mathbf {p}})\) by any pairwise choice. However, operating in the extended phase space and projecting only to obtain outputs, without altering the state in the extended phase space, leads to an algorithm that preserves the original Hamiltonian with no secular growth in the error. This is not entirely surprising, since the algorithms (25) have similarities with partitioned multistep methods, which can exhibit good long term behaviour despite a formal lack of symplecticity (Hairer et al. 2006). By virtue of being leapfrogs, the algorithms are also explicit, time-symmetric, have error expansions that contain only even powers of the timestep and can be sequentially applied to form higher order methods.

The idea behind Eq. (15) can be generalised further. Introducing yet another copy of the phase space with coordinates \((\widehat{\mathbf {q}}, \widehat{\mathbf {p}})\) leads to a Hamiltonian of the form

$$\begin{aligned} \widetilde{H}\left( \mathbf {q},\widetilde{\mathbf {q}},\widehat{\mathbf {q}},\mathbf {p},\widetilde{\mathbf {p}},\widehat{\mathbf {p}}\right)&= \frac{1}{2}\left[ H\left( \mathbf {q},\widetilde{\mathbf {p}}\right) + H\left( \mathbf {q},\widehat{\mathbf {p}}\right) + H\left( \widetilde{\mathbf {q}},\mathbf {p}\right) + H\left( \widetilde{\mathbf {q}},\widehat{\mathbf {p}}\right) + H\left( \widehat{\mathbf {q}},\mathbf {p}\right) \right. \nonumber \\&\quad \left. + H\left( \widehat{\mathbf {q}},\widetilde{\mathbf {p}}\right) \right] . \end{aligned}$$
(26)

The Hamiltonian (26) gives three sets of separable equations of motion that can be integrated with a leapfrog method. As with the leapfrogs (25), only the leapfrogs obtained from sequential applications of the flows of the different Hamiltonians in Eq. (26) give a method symplectic in the extended phase space. Again, no simple pairwise choice of the extended phase space variables leads to a method that is symplectic in the original phase space.

In general, using \(N>1\) sets of variables in total, with a phase space \(S^N\), one can use a Hamiltonian of the form

$$\begin{aligned} \begin{aligned} \widetilde{H}\left( \mathbf {q}^1,\ldots \mathbf {q}^N,\mathbf {p}^1,\ldots ,\mathbf {p}^N\right)&= \frac{1}{N-1}\sum _{i=1}^N \sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^N H\left( \mathbf {q}^i,\mathbf {p}^j\right) \\&= \frac{1}{N-1} \sum _{i=1}^{N-1} H_i\left( \mathbf {q}^1,\ldots \mathbf {q}^N,\mathbf {p}^1,\ldots ,\mathbf {p}^N\right) , \end{aligned} \end{aligned}$$
(27)

where

$$\begin{aligned} H_i(\mathbf {q}^1,\ldots \mathbf {q}^N,\mathbf {p}^1,\ldots ,\mathbf {p}^N) = \sum _{j=1}^{N} H(\mathbf {q}^j,\mathbf {p}^{\sigma _i(j)}). \end{aligned}$$
(28)

where \(\sigma _i(j) = (j+i-1\mod N)+1\) is a cyclic permutation of the indexes of the momenta. The equations of motion of any \(H_i\) can be integrated with a leapfrog, as is the case for their symmetric combination \(\widetilde{H}\). However, we will not investigate this general case in the paper.

3.1 Phase space mixing and projection

While Eqs. (16) and (17) can be integrated with a leapfrog, the fact that they are coupled only through the derivatives is a problem. The Hamiltonian vector field of one solution at a point depends on the other and vice versa, but not on the solution itself. Since the two numerical flows will not in general agree with each other or the exact flow, the derivative function for one numerical flow at one point will end up depending on a different point of the other solution, and both solutions may diverge with time. This problem is quickly confirmed by numerical experiments.

A seemingly straightforward solution for this problem would be to introduce feedback between the two solutions, in the form of mixing maps \(\mathbf {M}_i:S^2\rightarrow S^2, \,i=1,2\). We now amend the leapfrogs (25) to obtain, e.g.

$$\begin{aligned} \begin{aligned}&\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\mathbf {M}(h) = \mathbf {Q}(h/2)\widetilde{\mathbf {P}}(h/2)\widetilde{\mathbf {Q}}(h/2)\mathbf {P}(h/2)\mathbf {M}_1 \mathbf {P}(h/2)\widetilde{\mathbf {Q}}(h/2)\widetilde{\mathbf {P}}(h/2)\mathbf {Q}(h/2)\mathbf {M}_2, \end{aligned} \end{aligned}$$
(29)

so that the resulting algorithm is still symmetric, since at the last step, \(\mathbf {M}_2\) can be subsumed into the projection map described below. If \(\mathbf {M}_i\) are symplectic, then the leapfrogs that are symplectic on the extended phase space, i.e. (25a), retain this character. There is no need to restrict \(\mathbf {M}_i\) to strictly symplectic maps, however, since the extended phase space leapfrogs are not symplectic when restricted to the original phase space in any case. Without this restriction, potentially attractive candidates might stem from e.g. symmetries of the extended Hamiltonian (15) and its exact solution. For example, for (15), permutations of coordinates, \(\mathbf {q}\leftrightarrow \widetilde{\mathbf {q}}\), or momenta, \(\mathbf {p}\leftrightarrow \widetilde{\mathbf {p}}\), do not change the exact solution for given (equal) initial conditions. Permuting both switches the component Hamiltonians, but since they are equal, this has no effect for the exact solution. We will find that for the numerical method, the permutations can be beneficial.

A related problem is how to project a vector in extended phase space back to the dimension of the original. This should be done in a manner that minimizes the error in the obtained coordinates, momenta and original Hamiltonian. In addition, the final algorithm should be symplectic, or as close to symplectic as possible. To this end, we introduce a projection map \(\mathbf {P}:S^2\rightarrow S^2\). In principle, the projection map could be used in two different ways. The first is to obtain formal outputs at desired intervals, while the algorithm always runs in the extended phase space. The second is to use the projection map after each step, and then copy the projected values to create the extended set of variables for the next step. The final algorithm \(\psi \) over \(k\) steps would then be either of

$$\begin{aligned} \psi ^k&= \mathbf {P}\circ (\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\mathbf {M})^k\circ \mathbf {C} \end{aligned}$$
(30)
$$\begin{aligned} \psi ^k&= (\mathbf {P}\circ \mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\mathbf {M}\circ \mathbf {C})^k, \end{aligned}$$
(31)

where \(\circ \) is function composition, and \(\mathbf {C}:S\rightarrow S^2\) is the cloning map \(\mathbf {C}(\mathbf {q},\mathbf {p}) = (\mathbf {q},\mathbf {q},\mathbf {p},\mathbf {p})\).

It should be emphasized that in Eq. (30), the projection map is included only to obtain the formal output after \(k\) steps, while the current state \((\mathbf {q}_k,\widetilde{\mathbf {q}}_k,\mathbf {p}_k,\widetilde{\mathbf {p}}_k)\) is preserved, and used to continue the integration. In contrast, the algorithm (31) can evidently be considered as a mapping \(S\rightarrow S\) in the original phase space, and as such represents a conventional method such as a partitioned Runge–Kutta method, as seen in Sect. 3.3. Unfortunately, for Hamiltonian problems, it leads to secular increase of the error in the original Hamiltonian. In the Hamiltonian case, it seems that operating in the extended phase space is necessary, and as such, (30) is to be used.

To take a first stab at determining a suitable choice for \(\mathbf {M}_i\) and \(\mathbf {P}\), we turn to analyzing the error in the Hamiltonian function and deviations from symplecticity.

3.2 Error analysis

We start the search of suitable candidates for \(\mathbf {M}_i\) and \(\mathbf {P}\) from symmetric linear maps of the form

$$\begin{aligned} \begin{pmatrix} \mathbf {q}' \\ \widetilde{\mathbf {q}}' \\ \mathbf {p}' \\ \widetilde{\mathbf {p}}' \end{pmatrix} = \begin{pmatrix} {\alpha } _{M_i}&{}\quad \! {\widetilde{\alpha }}_{M_i} &{}\quad \! 0 &{}\quad \! 0 \\ {\widetilde{\alpha }}_{M_i} &{}\quad \! {\alpha } _{M_i}&{}\quad \! 0 &{}\quad \! 0 \\ 0 &{}\quad \! 0 &{}\quad \! {\beta } _{M_i}&{}\quad \! {\widetilde{\beta }} _{M_i}\\ 0 &{}\quad \! 0 &{}\quad \! {\widetilde{\beta }} _{M_i} &{}\quad \! {\beta } _{M_i} \end{pmatrix} \otimes I_n \quad \begin{pmatrix} \mathbf {q}\\ \widetilde{\mathbf {q}}\\ \mathbf {p}\\ \widetilde{\mathbf {p}}\end{pmatrix}, \end{aligned}$$
(32)

and

$$\begin{aligned} \begin{pmatrix} \mathbf {q}' \\ \mathbf {p}' \end{pmatrix} = \begin{pmatrix} {\alpha } _{P}&{}\quad \! {\widetilde{\alpha }}_{P} &{}\quad \! 0 &{}\quad \! 0 \\ 0 &{}\quad \! 0 &{}\quad \! {\beta } _{P}&{}\quad \! {\widetilde{\beta }} _{P}\\ \end{pmatrix} \otimes I_n \quad \begin{pmatrix} \mathbf {q}\\ \widetilde{\mathbf {q}}\\ \mathbf {p}\\ \widetilde{\mathbf {p}}\end{pmatrix}, \end{aligned}$$
(33)

where \(i=1,2\), and all matrix elements are real. We then look for the coefficients that give the best results according to conservation of Hamiltonian function or symplecticity. We can thus use, say,

$$\begin{aligned} \psi ^{k}=(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\mathbf {M})^{k}\circ \mathbf {C}, \end{aligned}$$
(34)

take two steps to make \(\mathbf {M}_2\) and \(\mathbf {P}\) independent, and expand

$$\begin{aligned} \Delta \widetilde{H}&= \widetilde{H}\left( \psi ^{2}(h)(\mathbf {z}_0)\right) - \widetilde{H}(\mathbf {C}(\mathbf {z}_0)) \end{aligned}$$
(35)
$$\begin{aligned} \Delta H&= H\left( (\mathbf {P}\circ \psi ^{2}(h))(\mathbf {z}_0)\right) - H(\mathbf {z}_0) \end{aligned}$$
(36)

in terms of \(h\), where \(\mathbf {z}_0=(\mathbf {q}_0,\mathbf {p}_0)\), and look at the coefficients. In this example case, the zeroth order coefficient of (36) reads

$$\begin{aligned} h^0: \quad H(C_1\mathbf {q}_0, C_2\mathbf {p}_0) - H(\mathbf {q}_0,\mathbf {p}_0), \end{aligned}$$
(37)

with

$$\begin{aligned} C_1&= ( {\alpha } _{M_1}+{\widetilde{\alpha }}_{M_1})^2( {\alpha } _{M_2}+{\widetilde{\alpha }}_{M_2})^2( {\alpha } _{P}+{\widetilde{\alpha }}_{P})\end{aligned}$$
(38)
$$\begin{aligned} C_2&=( {\beta } _{M_1}+{\widetilde{\beta }} _{M_1})^2( {\beta } _{M_2}+{\widetilde{\beta }} _{M_2})^2( {\beta } _{P}+{\widetilde{\beta }} _{P}). \end{aligned}$$
(39)

To make the cofficient identically zero, we need to have

$$\begin{aligned} {\widetilde{\alpha }}_{M} = 1- {\alpha } _{M}, \quad {\widetilde{\beta }} _{M} = 1 - {\beta } _{M} \end{aligned}$$
(40)

for all the maps \(\mathbf {M}_i\) and \(\mathbf {P}\), which makes them linear interpolations between the original and auxiliary coordinates and momenta. With the substitutions (40), also the first order coefficient of (36) becomes identically zero. The same substitution zeroes the coefficients of (35) up to and including the second order. The third order coefficient of (35) becomes independent of the map matrix elements, and as such we will focus on the expansion of (36).

The second order coefficient is

$$\begin{aligned} h^2: \quad -\frac{1}{2}\left[ C_1 \nabla _{\mathbf {p}}^2 H (\nabla _{\mathbf {q}}H)^2 + C_2 \nabla _{\mathbf {q}}\nabla _{\mathbf {p}}H \nabla _{\mathbf {q}}H \nabla _{\mathbf {p}}H + C_3 \nabla _{\mathbf {q}}^2 H (\nabla _{\mathbf {p}}H)^2 \right] , \end{aligned}$$
(41)

where

$$\begin{aligned} C_1&= (1 - 2 {\alpha } _{P})(1 - {\alpha } _{M_1})(1 - 2 {\alpha } _{M_2})(1 - {\alpha } _{M_1} - {\alpha } _{M_2} + 2 {\alpha } _{M_1} {\alpha } _{M_2}) \end{aligned}$$
(42)
$$\begin{aligned} C_2&= 2 {\alpha } _{M_1} + 3 {\alpha } _{M_2} - {\alpha } _{M_1}^2 - 7 {\alpha } _{M_1} {\alpha } _{M_2} - 2 {\alpha } _{M_2}^2 \nonumber \\&\quad +\, 4 {\alpha } _{M_1}^2 {\alpha } _{M_2} + 6 {\alpha } _{M_1} {\alpha } _{M_2}^2 - 4 {\alpha } _{M_1}^2 {\alpha } _{M_2}^2 \nonumber \\&\quad +\, 2 {\alpha } _{P}(1 - {\alpha } _{M_1})(1 - 2 {\alpha } _{M_2})(1 - {\alpha } _{M_2} - {\alpha } _{M_1} + 2 {\alpha } _{M_1} {\alpha } _{M_2}) \end{aligned}$$
(43)
$$\begin{aligned}&\quad -\,2 {\beta } _{M_1} - 3 {\beta } _{M_2} + {\beta } _{M_1}^2 + 7 {\beta } _{M_1} {\beta } _{M_2} + 2 {\beta } _{M_2}^2 \nonumber \\&\quad -\, 4 {\beta } _{M_1}^2 {\beta } _{M_2} - 6 {\beta } _{M_1} {\beta } _{M_2}^2 + 4 {\beta } _{M_1}^2 {\beta } _{M_2}^2 \nonumber \\&\quad -\,2 {\beta } _{P}(1 - {\beta } _{M_1})(1 - 2 {\beta } _{M_2})(1 - {\beta } _{M_2} - {\beta } _{M_1} + 2 {\beta } _{M_1} {\beta } _{M_2})\nonumber \\ C_3&= (1 - 2 {\beta } _{P})(1 - {\beta } _{M_1})(1 - 2 {\beta } _{M_2})(1 - {\beta } _{M_1} - {\beta } _{M_2} + 2 {\beta } _{M_1} {\beta } _{M_2}), \end{aligned}$$
(44)

and the derivatives \(\nabla _{\mathbf {q}}^k\nabla _{\mathbf {p}}^lH:\mathbb {R}^{(k+l)n}\rightarrow \mathbb {R}\) are \(k+l\)-linear operators

$$\begin{aligned} \begin{aligned}&\nabla _{\mathbf {q}}^k\nabla _{\mathbf {p}}^lH(\mathbf {v}_1,\ldots ,\mathbf {v}_k,\mathbf {v}_{k+1}, \ldots ,\mathbf {v}_{k+l})\\&\quad = \sum _{i_1,\ldots ,i_k,j_1,\ldots ,j_k}\frac{\partial ^{k+l}H}{ \partial q^{i_1}\cdots \partial q^{i_k} \partial p^{j_1}\cdots \partial q^{j_l}} v_1^{i_1}\cdots v_k^{i_k}v_{k+1}^{j_1}\cdots v_{k+l}^{j_l}, \end{aligned} \end{aligned}$$
(45)

where \(i_n\in \{1,\ldots ,k\}, \,j_n\in \{1,\ldots ,l\}\), and juxtaposition in (41) implies contraction.

From here, there are several choices available. We will consider some interesting combinations. Choosing \( {\alpha } _{M_1}= {\beta } _{M_1} = {\alpha } _{M_2}= {\beta } _{M_2} = 1\) makes the second order term identically zero. Taking \( {\alpha } _{P}=1/3\) and \( {\beta } _{P}=2/3\) then makes also the third order term be identically zero, and as such apparently gives an additional order of accuracy compared to the standard leaprog. However, despite this, these choices lead to poor long term behaviour, which numerically is quickly apparent. If \( {\alpha } _{M_1} = 1\) and \( {\beta } _{M_1}=0\), so that the momenta are permuted, then choosing \( {\beta } _{M_2}=1\) will also identically zero the second order coefficient. In this case, the third order coefficient can’t be brought to zero, but the numerical long term behaviour found in the problem of Sect. 5.1 is good, if \( {\alpha } _{M_2}=0\) is chosen so that there is a permutation symmetry between coordinates and momenta. Numerically, the best results were obtained with a choice \( {\alpha } _{M_1} = {\alpha } _{M_2} = 1, \, {\beta } _{M_1}= {\beta } _{M_2}=0\) and \( {\alpha } _{P}=1, \, {\beta } _{P} = 0\). This necessitates \( {\beta } _{P}= 1/2\) to zero the second order coefficient. We conclude that the long term behaviour of the method is not evident from considering the conservation of the Hamiltonian alone.

In addition to the conservation of the Hamiltonian, we are interested in the conservation of the symplectic form, or the symplecticity of the method. In local coordinates, the condition for symplecticity of an integration method \(\varphi _h:S\rightarrow S\) over one step \(h\) is

$$\begin{aligned} ( D\varphi _h )^T \mathbf {J}\left( D\varphi _h \right) - \mathbf {J}= 0, \end{aligned}$$
(46)

where \(D\varphi _h\) is the Jacobian of the map \(\varphi _h\) (Hairer et al. 2006).

We consider first symplecticity in the extended phase space \(S^2\). It is clear that if \(\mathbf {M}_1\) and \(\mathbf {M}_2\) are identity maps, then the method is symplectic. However, we know that this does not lead to good numerical results in the long term. To investigate other possibilities, we again apply the method (34) for two steps and expand the left side of Eq. (46) in terms of \(h\). The first order term gives two independent conditions

$$\begin{aligned} \begin{aligned}&4\left[ -( {\alpha } _{M_1}(1 - 2 {\alpha } _{M_2})^2) + {\alpha } _{M_1}^2(1 - 2 {\alpha } _{M_2})^2 + (-1 + {\alpha } _{M_2}) {\alpha } _{M_2}\right] \\&\quad \times \left[ -( {\beta } _{M_1}(1 - 2 {\beta } _{M_2})^2) + {\beta } _{M_1}^2(1 - 2 {\beta } _{M_2})^2 + (-1 + {\beta } _{M_2}) {\beta } _{M_2}\right] \\&\quad +\, \left[ 1 - 2 {\alpha } _{M_1}(1 - 2 {\alpha } _{M_2})^2 + 2 {\alpha } _{M_1}^2(1 - 2 {\alpha } _{M_2})^2 - 2 {\alpha } _{M_2} + 2 {\alpha } _{M_2}^2\right] \\&\quad \times \left[ 1 - 2 {\beta } _{M_1}(1 - 2 {\beta } _{M_2})^2 + 2 {\beta } _{M_1}^2(1 - 2 {\beta } _{M_2})^2 - 2 {\beta } _{M_2} + 2 {\beta } _{M_2}^2\right] = 1 \end{aligned} \end{aligned}$$
(47)
$$\begin{aligned} \begin{aligned}&2\left[ 1 - 2 {\alpha } _{M_1}(1 - 2 {\alpha } _{M_2})^2 + 2 {\alpha } _{M_1}^2(1 - 2 {\alpha } _{M_2})^2 - 2 {\alpha } _{M_2} + 2 {\alpha } _{M_2}^2\right] \\&\quad \times \left[ -( {\beta } _{M_1}(1 - 2 {\beta } _{M_2})^2) + {\beta } _{M_1}^2(1 - 2 {\beta } _{M_2})^2 + (-1 + {\beta } _{M_2}) {\beta } _{M_2}\right] \\&\quad +\, 2\left[ -( {\alpha } _{M_1}(1 - 2 {\alpha } _{M_2})^2) + {\alpha } _{M_1}^2(1 - 2 {\alpha } _{M_2})^2 + (-1 + {\alpha } _{M_2}) {\alpha } _{M_2}\right] \\&\quad \times \left[ 1 - 2 {\beta } _{M_1}(1 - 2 {\beta } _{M_2})^2 + 2 {\beta } _{M_1}^2(1 - 2 {\beta } _{M_2})^2 - 2 {\beta } _{M_2} + 2 {\beta } _{M_2}^2\right] = 0. \end{aligned} \end{aligned}$$
(48)

Solving any coefficient from these requires that none of the others is \(1/2\). As such, simply averaging the extended variable pairs leads to destruction of symplecticity in the extended phase space already in the zeroth order. On the other hand, any combination of \( {\alpha } _{M_i}, {\beta } _{M_i}\in \{0,1\}\) makes Eqs.  (47) and (48) identically true. Of these, combinations with \( {\alpha } _{M_i} = {\beta } _{M_i}\) are exactly symplectic, since the corresponding maps \(\mathbf {M}_i\) are. Other combinations give a non-zero coefficient at second order.

To investigate symplecticity in the original phase space \(S\), we append the projection map \(\mathbf {P}\). In this case, the zeroth and first order terms are zero independely of the coefficients of the maps \(\mathbf {M}_i\) and \(\mathbf {P}\). The second order term is a cumbersomely lengthy function of the map components and derivatives of the Hamiltonian. However, it is reduced to zero by those substitutions from \( {\alpha } _{M_i}, {\beta } _{M_i}\in \{0,1\}\) that have \( {\alpha } _{M_1}\ne {\alpha } _{M_2}\) or \( {\beta } _{M_1}\ne {\beta } _{M_2}\). In this case, if we also put \( {\alpha } _{P} = {\beta } _{P} = 1/2\), the first non-zero term is of the fifth order. In the case that \( {\alpha } _{M_1}= {\alpha } _{M_2}\) or \( {\beta } _{M_1}= {\beta } _{M_2}\), setting \( {\alpha } _{P} = {\beta } _{P} = 1/2\) does zero out the second order term, as well as the third order term, but not the fourth. The combination of identity maps \(\mathbf {M}_i\) with \( {\alpha } _{P}=1/3\) and \( {\beta } _{P}=2/3\), shown above to conserve Hamiltonian to an extra order of accuracy, leads to a non-zero error already in the third order. The method, which gives the best results for the application in Sect. 5.1 in both accuracy and long term behaviour, is the one with \( {\alpha } _{M_1}= {\alpha } _{M_2}=1, \, {\beta } _{M_1}= {\beta } _{M_2}=0\) and \( {\alpha } _{P}= {\beta } _{P}=1\). Interestingly, these choices give a non-zero contribution already at second order, and this is not affected by subsituting in the specific choice of Hamiltonian for the problem.

3.3 Relation to partitioned Runge–Kutta methods

Many common integration methods can be written in some general formulation as well, which can give additional insight to the numerical behaviour of the algorithm. Here, we will consider partitioned Runge–Kutta (PRK) methods. PRK methods form a very general class of algorithms for solving a partitioned system of differential equations

$$\begin{aligned} \begin{aligned} \dot{x}&= f(x,y) \\ \dot{y}&= g(x,y), \end{aligned} \end{aligned}$$
(49)

where \(x, \,y, \,f\) and \(g\) may be vector valued. A partitioned Runge–Kutta algorithm for system (49) can be written as

$$\begin{aligned} \begin{aligned} k_i&= f\left( x_0 + h\sum _{j=1}^{s}a^{(1)}_{ij} k_j, y_0 + h\sum _{j=1}^s a^{(2)}_{ij} l_j\right) \\ l_i&= g\left( x_0 + h\sum _{j=1}^{s}a^{(1)}_{ij} k_j, y_0 + h\sum _{j=1}^s a^{(2)}_{ij} l_j\right) \\ x_1&= x_0 + \sum _{i=1}^s b^{(1)}_i k_i \quad \quad y_1 = y_0 + \sum _{i=1}^s b^{(2)}_i l_i, \end{aligned} \end{aligned}$$
(50)

where \(a^{(1)}_{ij}, \,b^{(1)}_i\) and \(a^{(2)}_{ij}, \,b^{(2)}_i\) are the coefficients of two (possibly different) Runge–Kutta methods, respectively.

The second order leapfrog can be written as a PRK algorithm using the coefficients in Table 1. If \(f(x,y)\) and \(g(x,y)\) are functions of only \(y\) and \(x\), respectively, the resulting algorithm is explicit. In the extended phase space the equations of motion (16) and (17) can be written as

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \mathbf {f}(\mathbf {y}) \\ \dot{\mathbf {y}}&= \mathbf {f}(\mathbf {x}), \end{aligned} \end{aligned}$$
(51)

with \(\mathbf {x}= (\mathbf {q}, \widetilde{\mathbf {p}}), \,\mathbf {y}= (\widetilde{\mathbf {q}},\mathbf {p})\) and \(\mathbf {f}(\mathbf {x}) = J^{-1}\nabla H(\mathbf {x})\). If the maps \(\mathbf {M}_i\) are identity maps, the leapfrogs (19) and (20) can be written as PRK algorithms with coefficients from Table 1 as well. If this is not the case, the final result for \(\mathbf {x}_1\) will involve both \(\mathbf {x}_0\) and \(\mathbf {y}_0\), and similarly for \(\mathbf {y}_1\), but in general during the integration, \(\mathbf {x}_0\ne \mathbf {y}_0\) at the beginning of any given step. The resulting \(\mathbf {x}_1\) and \(\mathbf {y}_1\) will both also involve a mix of \(k^{(1)}_i\) and \(k^{(2)}_i\), as well. This cannot be obtained with a PRK scheme. If, however, \( {\beta } _{M_i} = {\alpha } _{M_i}\), we can write a PRK scheme for the first step, where \(\mathbf {x}_0=\mathbf {y}_0\), and also \(k^{(1)}_i = k^{(2)}_j\). The resulting coefficients are listed in Table 2.

Table 1 The Butcher tableaux for the second order leapfrog as a partitioned Runge–Kutta system
Full size table
Table 2 The Butcher tableaux for the extended phase space leapfrog with mixing as a partitioned Runge–Kutta system
Full size table

In this light, the algorithm (31) could be written as a PRK method on the original phase space if both \( {\beta } _{M_i} = {\alpha } _{M_i}\) and \( {\beta } _{P} = {\alpha } _{P}\). In this case, due to the continuous application of the cloning and projection maps \(\mathbf {C}\) and \(\mathbf {P}\), the conditions \(\mathbf {x}_i = \mathbf {y}_i\) and \(b^{(1)}_i=b^{(2)}_i\) hold at the beginning of each step. This method is unfortunately not very interesting for Hamiltonian systems, since it leads to secular growth in the energy error. In principle, the algorithm (30) could be written as a PRK method as well, but due to the points made above, we would need \(4k\) stages for \(k\) steps, effectively producing one huge and convoluted PRK step. This is due to the fact that the propagation needs to start from the initial point where \(\mathbf {x}_0=\mathbf {y}_0\).

4 Application to non-Hamiltonian systems

The idea of the previous section can be extended to general coupled systems of time dependent differential equations that can be reduced to a form

$$\begin{aligned} \dot{\mathbf {x}} = f(\mathbf {x},t), \end{aligned}$$
(52)

where \(\mathbf {x}\in \mathbb {R}^n, \,f:\mathbb {R}^n\times \mathbb {R}\rightarrow \mathbb {R}^n\) and \(\dot{\mathbf {x}} = \mathrm {d}\mathbf {x}/\mathrm {d}t\). The requirement is not severe, since all high order systems of differential equations, where the highest order derivatives can be explicitly solved for, can be written in this form.

In general, the Eq. (52) cannot be solved in closed form, but if \(f(\mathbf {x},t) = \sum _i f^i(\mathbf {x}, t)\), where the flows \(\varphi ^i\) of the parts \(f^i\) can be solved separately, a scheme equivalent to the operator splitting in (10) can be used. If \(f = f^1+f^2\), then in this scheme our numerical flow is either of

$$\begin{aligned} \varphi ^{S1} = \varphi ^1_{h/2} \circ \varphi ^2_h \circ \varphi ^1_{h/2} \end{aligned}$$
(53)

or

$$\begin{aligned} \varphi ^{S2} = \varphi ^2_{h/2} \circ \varphi ^1_h \circ \varphi ^2_{h/2}, \end{aligned}$$
(54)

a method known as Strang splitting (Strang 1968). Unfortunately, this approach does not work when either \(f\) cannot be split into additive parts, or the flows of the component parts cannot be solved.

However, having an equation of form (52), we can apply the idea of the previous chapter, and introduce auxiliary variables \(\widetilde{\mathbf {x}}\), an auxiliary time \(\widetilde{t}\), and an extended system of equations

$$\begin{aligned} \dot{\mathbf {x}}&= f(\widetilde{\mathbf {x}},\widetilde{t})\end{aligned}$$
(55a)
$$\begin{aligned} \dot{t}&= 1 \end{aligned}$$
(55b)
$$\begin{aligned} \dot{\widetilde{\mathbf {x}}}&= f(\mathbf {x},t) \end{aligned}$$
(55c)
$$\begin{aligned} \dot{\widetilde{t}}&= 1, \end{aligned}$$
(55d)

where the derivative is now taken with respect to a new independent variable. In the system of Eq. (55), the original independent variable (time) is now relegated to the role of another pair of coordinates. This corresponds to the usual extension of the phase space of a Hamiltonian system, where the canonical conjugate momenta of time \(p_0\) is added to the Hamiltonian and time \(t\) considered as an additional canonical coordinate (Hairer et al. 2006). In essence, the Eq. (52) splits to

$$\begin{aligned} \dot{\mathbf {z}} = f^1(\mathbf {z}) + f^2(\mathbf {z}), \end{aligned}$$
(56)

where \(\mathbf {z} = (\mathbf {x},\widetilde{\mathbf {x}},t,\widetilde{t})\in \mathbb {R}^{2n+2}, \,f^1(\mathbf {z}) = (f(\mathbf {x},\widetilde{t}),\mathbf {0},1,0), \,f^2(\mathbf {z}) = (\mathbf {0}, f(\widetilde{\mathbf {x}},t),0,1)\) and the derivative is taken with respect to a new independent variable. The flows of \(f^i\)’s can now be directly integrated, and Strang splitting can be used to derive a second order leapfrog of a form

$$\begin{aligned} \mathbf {x}_{n+\frac{1}{2}}&= \mathbf {x}_n + \frac{h}{2}f(\widetilde{\mathbf {x}}_n, \widetilde{t}_n) \end{aligned}$$
(57a)
$$\begin{aligned} t_{n+\frac{1}{2}}&= t_n + \frac{h}{2} \end{aligned}$$
(57b)
$$\begin{aligned} \widetilde{\mathbf {x}}_{n+1}&= \widetilde{\mathbf {x}}_n + h f(\mathbf {x}_{n+\frac{1}{2}}, t_{n+\frac{1}{2}}) \end{aligned}$$
(57c)
$$\begin{aligned} \widetilde{t}_{n+1}&= \widetilde{t}_n + h \end{aligned}$$
(57d)
$$\begin{aligned} \mathbf {x}_{n+1}&= \mathbf {x}_{n+\frac{1}{2}} + \frac{h}{2}f(\widetilde{\mathbf {x}}_{n+1}, \widetilde{t}_{n+1}) \end{aligned}$$
(57e)
$$\begin{aligned} t_{n+1}&= t_{n+\frac{1}{2}} + \frac{h}{2}, \end{aligned}$$
(57f)

or its adjoint, by exchanging the flows used for propagation.

Moreover, the problem (52) can also be split arbitrarily into a coupled form

$$\begin{aligned} \dot{\mathbf {x}}&= f(\mathbf {x}, \mathbf {y}, t) \end{aligned}$$
(58a)
$$\begin{aligned} \dot{\mathbf {y}}&= g(\mathbf {x}, \mathbf {y}, t), \end{aligned}$$
(58b)

where now \(\mathbf {x}\in \mathbb {R}^{n-k}, \,\mathbf {y}\in \mathbb {R}^k, \,f=(f_1,\ldots ,f_{n-k})\) and \(g=(f_{n-k+1},\ldots ,f_n)\), where \(f_i\) are the component functions of the original \(f\) in Eq. (52). The above approach could naturally be used here as well after introducing further auxiliary variables \(\widetilde{\mathbf {y}}\). However, we can now mix the auxiliary and original variables as in the previous section, to obtain a different system of equations

$$\begin{aligned} \dot{\mathbf {x}}&= f(\widetilde{\mathbf {x}}, \mathbf {y}, \widetilde{t}) \end{aligned}$$
(59a)
$$\begin{aligned} \dot{\widetilde{\mathbf {y}}}&= g(\widetilde{\mathbf {x}}, \mathbf {y}, \widetilde{t}) \end{aligned}$$
(59b)
$$\begin{aligned} \dot{t}&= 1 \end{aligned}$$
(59c)
$$\begin{aligned} \dot{\widetilde{\mathbf {x}}}&= f(\mathbf {x}, \widetilde{\mathbf {y}}, t) \end{aligned}$$
(59d)
$$\begin{aligned} \dot{\mathbf {y}}&= g(\mathbf {x}, \widetilde{\mathbf {y}}, t) \end{aligned}$$
(59e)
$$\begin{aligned} \dot{\widetilde{t}}&= 1. \end{aligned}$$
(59f)

These equations can be directly integrated as well, to produce a different second order leapfrog method with

$$\begin{aligned} \mathbf {x}_{n+\frac{1}{2}}&= \mathbf {x}_n + \frac{h}{2} f(\widetilde{\mathbf {x}}_n, \mathbf {y}_n, \widetilde{t}_n) \end{aligned}$$
(60a)
$$\begin{aligned} \widetilde{\mathbf {y}}_{n+\frac{1}{2}}&= \widetilde{\mathbf {y}}_n + \frac{h}{2} g(\widetilde{\mathbf {x}}_n, \mathbf {y}_n, \widetilde{t}_n) \end{aligned}$$
(60b)
$$\begin{aligned} t_{n+\frac{1}{2}}&= t_n + \frac{h}{2} \end{aligned}$$
(60c)
$$\begin{aligned} \widetilde{\mathbf {x}}_{n+1}&= \widetilde{\mathbf {x}}_n + h f(\mathbf {x}_{n+\frac{1}{2}}, \widetilde{\mathbf {y}}_{n+\frac{1}{2}}, t_{n+\frac{1}{2}}) \end{aligned}$$
(60d)
$$\begin{aligned} \mathbf {y}_{n+1}&= \mathbf {y}_n + h g(\mathbf {x}_{n+\frac{1}{2}}, \widetilde{\mathbf {y}}_{n+\frac{1}{2}}, t_{n+\frac{1}{2}}) \end{aligned}$$
(60e)
$$\begin{aligned} \widetilde{t}_{n+1}&= \widetilde{t}_n + h \end{aligned}$$
(60f)
$$\begin{aligned} \mathbf {x}_{n+1}&= \mathbf {x}_{n+\frac{1}{2}} + \frac{h}{2}f(\widetilde{\mathbf {x}}_{n+1}, \mathbf {y}_{n+1}, \widetilde{t}_{n+1}) \end{aligned}$$
(60g)
$$\begin{aligned} \widetilde{\mathbf {y}}_{n+1}&= \widetilde{\mathbf {y}}_{n+\frac{1}{2}} + \frac{h}{2}g(\widetilde{\mathbf {x}}_{n+1}, \mathbf {y}_{n+1}, \widetilde{t}_{n+1}) \end{aligned}$$
(60h)
$$\begin{aligned} t_{n+1}&= t_{n+\frac{1}{2}} + \frac{h}{2}. \end{aligned}$$
(60i)

In this manner, a system like (52) can be split into as many component parts as desired, down to single variables.

The propagation can be split further by using the individual vector fields in (59). Similarly to Sect. 3, these then give rise to propagation operators \(\mathbf {X}(h) = \exp (hD_f), \,\mathbf {Y}(h)=\exp (hD_g), \,\mathbf {T}=\exp (hD_1)\) and likewise for \(\widetilde{\mathbf {X}}, \,\widetilde{\mathbf {Y}}, \,\widetilde{\mathbf {T}}\), where \(D_f h(\mathbf {z}) = \nabla h(\mathbf {z})^T f(\mathbf {z})\) is the Lie derivative of \(h\) on the vector field \(f\), which reduces to a directional derivative in this case (Hairer et al. 2006). This then leads to various possibilities of splitting the propagation, as in (25), with several equivalent combinations due to the commutation relations

$$\begin{aligned}{}[\mathbf {X}, \widetilde{\mathbf {Y}}] = [\widetilde{\mathbf {X}},\mathbf {Y}] = [\mathbf {T},\mathbf {X}] = [\mathbf {T}, \mathbf {Y}] = [\widetilde{\mathbf {T}}, \widetilde{\mathbf {X}}] = [\widetilde{\mathbf {T}},\widetilde{\mathbf {Y}}] = [\widetilde{\mathbf {T}},\mathbf {T}] = 0, \end{aligned}$$
(61)

where for example

$$\begin{aligned}{}[\mathbf {X}, \mathbf {Y}](h)\mathbf {x}= \mathbf {X}(h)\mathbf {Y}(h)\mathbf {x}- \mathbf {Y}(h)\mathbf {X}(h)\mathbf {x}, \end{aligned}$$
(62)

for \(\mathbf {x}\in \mathbb {R}^n\).

Similarly to the Hamiltonian case, a combination of the maps \(\mathbf {M}_i\) and \(\mathbf {P}\) is to be used here as well. They generalize the leapfrogs (57) and (60), which otherwise represent known algorithms. For example, if we use identity maps for \(\mathbf {M}_i\) and set \( {\alpha } _{\mathbf {P}}=1\) and \( {\beta } _{\mathbf {P}}=0\), the leapfrog (57) is equivalent to the modified midpoint method (Mikkola and Merritt 2006). However, the modified midpoint method and its generalization in Mikkola and Merritt (2006) and Mikkola and Merritt (2008) as well as the AVA method in Hellström and Mikkola (2010) discard the auxiliary variables after integration. In general, this need not be done, though whether a measurable benefit can be obtained is harder to quantify than in the Hamiltonian case.

4.1 Error analysis

A backward error analysis on Eq. (56) can be done in a similar way as in the previous section (for details, see e.g. Hairer et al. 2006), yielding the modified differential equation

$$\begin{aligned} \dot{\mathbf {x}} = \tilde{f}(\mathbf {x}), \end{aligned}$$
(63)

which the discretization (57) solves exactly. Here

$$\begin{aligned} \tilde{f}&= f + h^2\Big \{ \frac{1}{12}\Big [ D^2f^1(f^2,f^2) + Df^1(Df^2(f^2)) \nonumber \\&\quad -\,D^2f^2(f^1,f^2)-Df^2\left( Df^1(f^2)\right) \Big ] \nonumber \\&\quad -\,\frac{1}{24}\Big [ D^2f^2\left( f^1,f^1\right) + Df^2(Df^1(f^1)) \nonumber \\&\quad - D^2f^1(f^2,f^1)-Df^1\left( Df^2(f^1)\right) \Big ] \Big \} + \fancyscript{O}(h^4), \end{aligned}$$
(64)

where \(D^kf:\mathbb {R}^{kn}\rightarrow \mathbb {R}^n\) is the \(k\)’th order derivative of \(f\), written as a \(k\)-linear operator in the usual way, so that

$$\begin{aligned} D^kf(\mathbf {v}_1,\ldots ,\mathbf {v}_k) = \sum _{i_1,\ldots ,i_k}\frac{\partial ^kf}{\partial x^{i_1}\cdots \partial x^{i_k}} v_1^{i_1}\cdots v_k^{i_k}, \end{aligned}$$
(65)

where \(i_j \in \{1,2,\ldots ,k\}\). Equation (64) is essentially the same as Eq. (22), but written with vector fields.

The problem of how to choose the mixing and projection maps \(\mathbf {M}_i\) and \(\mathbf {P}\) remains. In the context of general problems we have no invariants to guide us in choosing a suitable transformation. Numerical experiments indicate that averaging the auxiliary and original variables (\( {\alpha } _{M_i}= {\beta } _{M_i}=1/2\), and similarly for \(\mathbf {P}\)) leads to good results, but this matter should be investigated more thoroughly in a future work.

5 Applications

In the following, we call the methods of the two previous sections by the common name extended phase space methods. To rudimentarily explore their numerical behaviour, we test them with physically relevant non-linear and inseparable problems, both of Hamiltonian and non-Hamiltonian type.

5.1 Geodesic equation

The equation of a geodesic of a massive test particle in a pseudo-Riemannian spacetime with a metric \(g_{\mu \nu }(\mathbf {x})\), where \(\mathbf {x}\) are the coordinates and \(\mu ,\nu \in \{0,1,2,3\}\) index the components of the metric, can be written in a Hamiltonian form (Lanczos 1966)

$$\begin{aligned} H = \frac{1}{2}g^{\alpha \beta }(\mathbf {x})p_\alpha p_\beta = \frac{1}{2}m^2, \end{aligned}$$
(66)

\(g^{\mu \nu }\) is the inverse of the metric, \(m\) is the mass of the test particle, and the Einstein summation convection is used. The generalized momenta, \(p_\mu \), are

$$\begin{aligned} p_\mu = g_{\mu \alpha }(\mathbf {x})\dot{x}^{\alpha }, \end{aligned}$$
(67)

where \(\dot{x}^\alpha =\mathrm {d}x^{\alpha }/\mathrm {d}\tau \), and \(\tau \) is the parametrization of the geodesic.

For our test scenario, we take the Schwarzschild metric (in units where \(G=c=1\))

$$\begin{aligned} g_{\alpha \beta }\mathrm {d}x^\alpha \mathrm {d}x^\beta = \left( 1 - \frac{2M}{r}\right) \mathrm {d}t^2 - \left( 1-\frac{2M}{r}\right) ^{-1}\mathrm {d}r^2 - r^2\left( \sin ^2\theta \mathrm {d}\phi ^2 + \mathrm {d}\theta ^2\right) , \end{aligned}$$
(68)

where \(M\) is the central mass, so that Schwarzschild radius \(r_S=2M\), and \(\mathbf {x} = (t, r, \phi , \theta )\). We set \(\theta = \pi /2\) so that the motion is constrained to the equatorial plane, which leads to a Hamiltonian of the form

$$\begin{aligned} H = \left( 1 - \frac{2M}{r}\right) ^{-1}p_t^2 -\left( 1 - \frac{2M}{r}\right) p_r^2 - r^2 p_\phi ^2 = \frac{1}{2}m^2, \end{aligned}$$
(69)

where we have used the variable names in place of the corresponding numerical subscript. The Hamiltonian (69) evidently does not separate into additive parts dependent only on coordinates or momenta.

For the initial values, we set \(m=M=1, \,t_0=0\) and \(\phi _0 = 0\). To draw parallels with a classical Keplerian situation, we take \(\tau = t\) (i.e. the coordinate time), and demand that \(r_0\) corresponds to the apocentre of the orbit so that \(\dot{r}_0=0\) and \(r_0 = a_0(1+e)\), where \(a_0=14 \cdot 2M\) is the semi-major axis and \(e\) the eccentricity of the (classical) orbit, which we set to \(e=0.5\). From this the initial velocity \(v_0=\sqrt{(1-e)/[a(1+e)]}=\sqrt{(1-e)/r_0}\approx 0.109\) and \(\dot{\phi }_0 = v_0/r_0\approx 2.60\times 10^{-3}\). For the momenta we have then \(p_{r,0} = 0, \,p_{\phi ,0} = -r^2\dot{\phi }_0\approx -4.58\). The conjugate momentum of time must then be solved from the equality \(H = m^2/2\) in (69), to get \(p_{t,0}\approx 0.982\). The final initial conditions are then \(\mathbf {x} = (0, 42, 0), \,\mathbf {p} \approx (0.982, 0, -4.58)\). It should be noted that for these choices the first order estimate for pericenter precession \(\Delta \omega \) is (Lanczos 1966)

$$\begin{aligned} \Delta \omega = 6\pi M/[(1-e^2)a] = \pi /2. \end{aligned}$$
(70)

We simulate the system with three methods: \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\), implicit midpoint method, and the LSODE solver (Hindmarsh 1980) used from the SciPy Python environment (Jones et al. 2001). The LSODE solver internally uses either a high order Adams–Moulton method or a backwards differentiation formula, and automatically switches between them. It also includes a timestep control scheme (Radhakrishnan and Hindmarsh 1993). For the method \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\), we use the mixing maps with \( {\alpha } _{M_1} = {\alpha } _{M_2} = 1\) and \( {\beta } _{M_1} = {\beta } _{M_2} = 0\). These values were chosen after numerous experiments, since they yielded the best results for this particular problem by a wide margin. During the propagation, we obtained the physical outputs after each step using two different projection maps, either with \( {\alpha } _{P_1} = 1\) and \( {\beta } _{P_1}=0\), which yielded the best results, and with \( {\alpha } _{P_2} = 1\) and \( {\beta } _{P_2}=0\) for comparison.

The implicit midpoint method was chosen for comparison since it is symplectic and well-behaved (Hairer et al. 2006). For a differential equation

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}), \end{aligned}$$
(71)

the method is given by

$$\begin{aligned} \mathbf {x}_{n+1} = \mathbf {x}_n + h\mathbf {f}\left( \frac{\mathbf {x}_{n+1}+\mathbf {x}_{n}}{2}\right) . \end{aligned}$$
(72)

We applied the method to the equations of motion in the original phase space, and at each step solved the implicit Eq. (72) iteratively until a relative error of less than \(10^{-15}\) was achieved. As a truth model, we used the LSODE solver, which was run with a relative accuracy parameter of \(10^{-13}\) and absolute accuracy parameter of \(10^{-15}\). The simulations were first run for 10 orbital periods, with a timestep set to \(h=0.02P\), where \(P=2\pi \sqrt{a^3/M}\) is the orbital period. The LSODE method has internal stepsize control, so for this method \(h\) controlled only the initial trial timestep and output sampling.

Figure 1 shows the resulting orbits shown in \(xy\)-coordinates, with \((x,y)=(r\cos \phi ,r\sin \phi )\), as well as the relative errors in the coordinates when compared to the LSODE result. Table 3 shows the amount of vector field evaluations for the different methods, which is a rough estimate of the computing power required for each solution. The fourfold symmetry of the orbit is evident from the figure, as well as the fact that the methods show some precession. This precession is worst for the implicit midpoint method and less for the extended phase space method with \(\mathbf {P}_2\). The method with \(\mathbf {P}_1\) is nearly indistinguishable from the LSODE solution. From the figure we also see that the errors are mainly accumulated near the pericenter, as expected. For all the methods, there is a secular drift in the mean error for \(t\) and \(\phi \) coordinates, with the implicit midpoint method having the worst behaviour, followed by \(\mathbf {P}_2\) and \(\mathbf {P}_1\). The drift in \(\phi \) causes the observed precession. It should be noted that this precession is not reflected in the conservation of the Hamiltonian, since it is invariant for translations of \(t\) and \(\phi \). In this manner, the situation is analogous to the Keplerian problem.

Fig. 1
figure 1

Left The orbits \((r\cos (\phi ),r\sin (\phi ))\) of the \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\) method with \(\mathbf {P}_1\) (solid line) and \(\mathbf {P}_2\) (dotted line), implicit midpoint method (dashed line), and the LSODE method (dash-dotted line). Right The errors in the coordinates \(t, \,r\) and \(\phi \) with respect to the LSODE solution, relative to the orbital period \(P\), maximum radius \((1+e)a\) and \(2\pi \), respectively. The line styles are the same as in the figure on the left

Full size image
Table 3 The total number of evaluations of vector fields \(\dot{\mathbf {q}}\) and \(\dot{\mathbf {p}}\), including \(\dot{\widetilde{\mathbf {q}}}\) and \(\dot{\widetilde{\mathbf {p}}}\) for the extended phase space methods
Full size table

To assess the long term behaviour of the methods, we did another integration for 3000 orbital periods, and investigated the error in the conservation of the Hamiltonian. Figure 2 shows the absolute error for the first 10 orbits and the maximum error up to a given time during the integration for the whole run. While the LSODE method is very accurate, we see that it eventually displays a secular power law increase in the maximum error with time, typical for nonsymplectic algorithms. The symplectic implicit midpoint method shows no secular growth in the error, and neither does the method \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\) with either projection \(\mathbf {P}_i\). This result is not completely unexpected, since symmetric non-symplectic methods can also display behaviour similar to symplectic ones, particularly for quadratic Hamiltonians, such as in this case (Hairer et al. 2006).

Fig. 2
figure 2

The error in \(H\) for the \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\) method with \(\mathbf {P}_1\) (solid line) and \(\mathbf {P}_2\) (dotted line), implicit midpoint method (dashed line), and the LSODE method (dash-dotted line). Left Absolute error, for \(10\) first orbits. Right Maximum absolute error up to given time during integration. Note the different \(x\)-axis scaling

Full size image

For this particular problem, the method \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\) with \(\mathbf {P}_1\) produces excellent results. The resulting orbit is much more closely aligned with the LSODE solution than the orbit given by a basic symplectic integrator, the implicit midpoint method, and there is no secular growth in the error of the Hamiltonian. It is notable also that since the method is explicit, the number of vector field evaluations required and thereby the computing time used is much less than for the implicit midpoint method, or the LSODE method. As such, the \(\mathbf {Q}\widetilde{\mathbf {P}}\widetilde{\mathbf {Q}}\mathbf {P}\) could be used with a smaller timestep to obtain even better results relative to the other methods.

5.2 Forced van der Pol oscillator

We test the extended phase space method also on a non-conservative system, the forced van der Pol oscillator (van der Pol 1927)

$$\begin{aligned} \ddot{x} -\mu (1-x^2) + x = A\cos (2\pi t/P), \end{aligned}$$
(73)

which can be written in the equivalent form

$$\begin{aligned} \begin{array}{l} \dot{x} = y \\ \dot{y} = \mu (1-x^2) - x + A\cos (2\pi t/P), \end{array} \end{aligned}$$
(74)

where \(\mu \in \mathbb {R}\) parametrizes the non-linearity of the system, and \(A,P\in \mathbb {R}\) are the amplitude and period of the sinusoidal forcing. The van der Pol oscillator is essentially a damped non-linear oscillator that exhibits a limit cycle. For our test, we set \(\mu = 5, \,A=5\) and \(P=2\pi /2.463\); a choice for which the oscillator is known to exhibit chaotic behaviour (Parlitz and Lauterborn 1987). As initial conditions, we take \(x = y = 2\).

To integrate the system, we use split systems of types \(\mathbf {X}\mathbf {Y}\widetilde{\mathbf {T}}\widetilde{\mathbf {X}}\widetilde{\mathbf {Y}}\mathbf {T}\) (Method 1 in the following) \(\widetilde{\mathbf {X}}\widetilde{\mathbf {T}}\mathbf {X}\mathbf {Y}\widetilde{\mathbf {T}}\widetilde{\mathbf {Y}}\) (Method 2), in the same symmetric shorthand as in Eq. (25). Method 1 is of type (57) while Method 2 is of type (60). For both methods, we employ the 6th order composition coefficients from (13) to yield a 6th order method. In this case, we use the method (31), and set \( {\alpha } _{P}= {\beta } _{P}=1/2\) so that after one composited step, the original and auxiliary variables are averaged. For the mixing maps, we take \( {\alpha } _{M_1}= {\beta } _{M_1}=1\) and \( {\alpha } _{M_2}= {\beta } _{M_2}=0\). As in the previous section, we compare these methods to the implicit midpoint method (72), iterated to \(10^{-15}\) precision in relative error, and the LSODE solver with a relative accuracy parameter of \(10^{-13}\) and absolute accuracy parameter of \(10^{-15}\). We propagate the system until \(t = 500\) using a timestep \(h=0.02\).

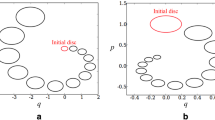
Figure 3 shows the numerical orbits of the four methods in the phase space \((x,y)\). The behaviour of the system is characterized by slow dwell near points \(x\approx \pm 1\), and quick progression along the curved paths when not. In Fig. 4 we have plotted the maximum absolute errors in \(x\) and \(y\) up to given time with respect to the LSODE method. We find that all the methods display a secular growth in the coordinate errors, with Method 1 performing best, followed by Method 2 and the implicit midpoint method. Methods 1 and 2 show similar qualitative behaviour as the LSODE solution, while the midpoint method shows a clear divergence. These results needs to be contrasted with the amounts of vector field evaluations, which are \(0.7 \times 10^{6}\) (Method 1), \(1.3 \times 10^{6}\) (Method 2), \(1.3 \times 10^{6}\) (implicit midpoint) and \(1.4 \times 10^{6}\) (LSODE). The number of evaluations is roughly similar for each method, and as such Method 1 is rather clearly the best of the constant timestep methods, with LSODE likely the best overall.

Fig. 3
figure 3

Numerical orbits of the van der Pol system (74) with \(\mu = 5\), \(A=5\) and \(P=2\pi /2.463\), integrated until \(t = 500\), with Method 1 (solid line, top left), Method 2 (dotted line, top right), the LSODE method (dash-dotted line, bottom left), and the implicit midpoint method (dashed line, bottom right)

Full size image
Fig. 4
figure 4

Maximum absolute errors in \(x\) and \(y\) up to given time, for Method 1 (solid line), Method 2 (dotted line) and the implicit midpoint method (dashed line), compared to the LSODE method along orbit in Fig. 3

Full size image

6 Discussion

Perhaps the most obvious benefit of splitting methods is that they’re explicit, which eliminates all problems inherent in having to find iterative solutions. Specifically, if evaluating the vector field, or parts of it, is very computationally intensive, then explicit methods are to be preferred, as they only require a single evaluation of the vector field for each step of the algorithm. Leapfrog methods can also be composited with large degrees of freedom, making it possible to optimize the method used for the specific task at hand. More subtly, when the problem separates to asymmetric kinetic and potential parts, different algorithmic regularization schemes can be used to yield very powerful (even exact), yet simple integrators (Mikkola and Tanikawa 1999a, b; Preto and Tremaine 1999).

However, for the case when the Hamiltonian remains unspecified, algorithmic regularization seems to yield little benefit, since both parts of the new Hamiltonian (15) are essentially identical. This is problematic, since the leapfrog integration of an inseparable Hamiltonian typically leads to wrong results only when the system is in “difficult” regions of the phase space, such as near the Schwarzschild radius for the case in Sect. 5.1, where the derivatives have very large numerical values and the expansions (21)–(22) may not converge for the chosen value of timestep. This is exactly the problem that algorithmic regularization solves, and it would be greatly beneficial if such a scheme could be employed even for the artificial splitting of the Hamiltonian in (15).

Despite the lack of algorithmic regularization, the extended phase space methods seem promising. The results in Sect. 5.1 demonstrate that the extended phase space methods can give results comparable to an established differential equation solver, LSODE, but with less computational work. More importantly, the results are superior to a known symplectic method, the implicit midpoint method. The results in Sect. 5.2 are less conclusive with respect to the LSODE method, but clear superiority versus the implicit midpoint method is still evident. We find this encouraging, and believe that the extended phase space methods should be investigated further. Obvious candidate for further research is the best possible form and use of the mixing and projection maps. The optimal result is likely problem dependent. Another issue that would benefit from investigation is how to find algorithmic regularization schemes for the split (15), preferably with as loose constraints on the form of the original Hamiltonian as possible. Finally, whether useful integrators can be obtained from the splits of types (26)–(28) should be investigated.

7 Conclusions

We have presented a way to construct splitting method integrators for Hamiltonian problems where the Hamiltonian is inseparable, by introducing a copy of the original phase space, and a new Hamiltonian which leads to equations of motion that can be directly integrated. We have also shown how the phase space extension can be used to construct similar leapfrogs for general problems that can be reduced to a system of first order differential equations. We have then implemented various examples of the new leapfrogs, including a higher order composition. These methods have then been applied to the problem of geodesics in a curved space and a non-linear, non-conservative forced oscillator. With these examples, we have demonstrated that utilizing both the auxiliary and original variables in deriving the final result, via the mixing and projection maps, instead of discarding one pair as is done in Mikkola and Merritt (2006) and Hellström and Mikkola (2010), can yield better results than established methods, such as the implicit midpoint method.

The new methods share some of the benefits of the standard leapfrog methods in that they’re explicit, time-symmetric and only depend on the state of the system during the previous step. For a Hamiltonian problem of the type in Sect. 5.1 they also have no secular growth in the error in the Hamiltonian. However, the extended phase space methods leave large degrees of freedom in how to mix the variables in the extended phase space, and how to project them back to the original dimension. As such, there is likely room for further improvement in this direction, as well as in the possibility of deriving a working algorithmic regularization scheme for these methods. In conclusion, we find the extended phase space methods to be an interesting class of numerical integrators, especially for Hamiltonian problems.