Sun–Earth $L_{1}$ and $L_{2}$ to Moon transfers exploiting natural dynamics

Abstract

This paper examines the design of transfers from the Sun–Earth libration orbits, at the $L_{1}$ and $L_{2}$ points, towards the Moon using natural dynamics in order to assess the feasibility of future disposal or lifetime extension operations. With an eye to the probably small quantity of propellant left when its operational life has ended, the spacecraft leaves the libration point orbit on an unstable invariant manifold to bring itself closer to the Earth and Moon. The total trajectory is modeled in the coupled circular restricted three-body problem, and some preliminary study of the use of solar radiation pressure is also provided. The concept of survivability and event maps is introduced to obtain suitable conditions that can be targeted such that the spacecraft impacts, or is weakly captured by, the Moon. Weak capture at the Moon is studied by method of these maps. Some results for planar Lyapunov orbits at $L_{1}$ and $L_{2}$ are given, as well as some results for the operational orbit of SOHO.

1 Introduction

It has become increasingly accepted by the space community that once a spacecraft has reached an end to its nominal mission lifetime it should be safely disposed of such that future missions are not jeopardized. While this holds especially true for particularly busy orbits around the Earth, such as low Earth and geosynchronous orbits, there is also a case to make for safely controlling the disposal of spacecraft in libration point orbits (LPOs) at the Sun–Earth $L_{1}$ and $L_{2}$ libration points. Often these spacecraft will still have propellant left after their mission has been completed, and it is therefore interesting to see what could be done with these spacecraft in terms of disposal or mission extension. In this work we study the disposal options towards the Moon from both Sun–Earth $L_{1}$ and $L_{2}$ libration points within the framework of the coupled circular restricted three-body problem, or coupled CR3BP (Koon et al. 2001a, b). This methodology has been used in the past to study trajectories between the Sun–Earth libration points and the vicinity of the Earth and Moon, where a connection is made using the unstable manifold flowing from the Sun–Earth libration point (within the Sun–Earth CR3BP) and the stable manifold flowing towards the Moon $L_{2}$ point (within the Earth–Moon CR3BP) at low $\Delta v$ cost. Examples include the work done by Koon et al. (2001a, b), Gómez et al. (2001), Canalias and Masdemont (2008) and Fantino et al. (2010).

This work introduces the concept of survivability map and event map to find target conditions, in the vicinity of the Moon, that lead to lunar impact or lunar weak capture. These maps aid in the design of trajectories and effectively replace the use of the stable manifold to design the trajectory arc incoming towards the Moon in the Earth–Moon CR3BP. This approach enables a very simple transfer design where one directly targets a state on the map in order to get the desired capture orbit or impact. In the past, Poincaré maps at the pericentre have been used to find useful target conditions that lead to a capture around a body (Villac and Scheeres 2003; Haapala and Howell 2014). Here we look at finding target states further away from the celestial body, using either variable or constant energy level, that give long permanence within a given region in the configuration space. In doing so we identify also possible capture, impact and escape states. Weak capture (or temporary ballistic capture) is typically defined as a spacecraft moving to within the vicinity of the planet (in this case the Moon) and staying there for some minimum period of time, or by performing at least a single revolution about the planet. There is extensive work in the literature on weak capture in particular to design transfers to the Moon with a reduced propellant cost with respect to a more traditional Hohmann transfer. An algorithmic definition of the weak stability boundary is given by Belbruno (2004), and later expanded upon by García and Gómez (2007). A quite complete overview of the existing literature can be found in the work of Silva and Terra (2012), and a clear definition of weak capture is given by Topputo et al. (2008).

This paper begins with a brief overview of the CR3BP, and the method of connecting (often referred to as patching) multiple CR3BPs, in Sect. 2. Then, Sect. 3 introduces the concept of the survival and event maps, which are used to acquire initial conditions (named lunar target states) that lead to lunar impact or capture. Section 4 describes the overall process used to find, and further optimize, transfers. The process of Sect. 4 is used to arrive at some results for a planar Lyapunov orbit at $L_{2}$, which are presented in Sect. 5. An initial study of the use of solar radiation pressure to aid the design is given in Sect. 6, with an eye towards future possibilities where smaller spacecraft with deployable structures may be disposed of from (perhaps displaced) libration point orbits. Finally, a description of future efforts and some concluding remarks are offered in Sect. 7.

2 Properties of the coupled CR3BP

The process of connecting (or patching together) three-body problems has been used successfully in the past to obtain suitable results that aid in the creation of transfers in a full ephemeris model. For instance, the methodology has been employed in the study of multi-moon tours (Koon et al. 2001a, b; Lantoine et al. 2011; Campagnola and Russell 2010) and in the context of the CR3BP (Koon et al. 2001a, b; Gómez et al. 2001; Marsden and Ross 2006; Canalias and Masdemont 2008; Fantino et al. 2010). The definition and equations of motion of the CR3BP (Sect. 2.1), its equilibrium points (Sect. 2.2), the flow near these equilibrium points (Sect. 2.3), and the method of connecting two CR3BPs (Sect. 2.4) provide the background theory from existing literature on which the subsequent sections (use of the survival maps and the design of the transfers) rely.

The motion of a spacecraft from a Sun–Earth $L_{1}/L_{2}$ libration point orbit towards the Moon is modelled in this work by using two coupled CR3BP models. This effectively divides a trajectory into two separate segments, each using a different gravitational model, where the initial segment is modelled within the framework of the Sun–Earth CR3BP while the second is modelled within the framework of the Earth–Moon CR3BP. The partial trajectories from both CR3BP models are connected at a specified point, via coordinate system conversion, to create a single trajectory that would approximate the trajectory in the actual four-body dynamics. The Sun–Earth CR3BP has as primary masses the Sun and the Earth–Moon barycentre (the mass of the Earth–Moon barycentre is considered here to be the combined mass of the Earth and the Moon).

2.1 Definition of the CR3BP

The circular restricted three-body problem (CR3BP) is a particular case of the three-body problem (being in itself a special case of the more general n-body problem). The restricted problem has been studied extensively in the past, and can be described as two masses (or primaries) of symmetric mass distribution (i.e. they may be considered as point masses) that revolve around their centre of mass in a circular motion. A third massless particle moves within the system of the two revolving primaries without influencing their motion (thus the problem is considered restricted). The CR3BP describes the motion of this third body. The equations of motion of the CR3BP can be derived in several ways, and many reference texts provide a detailed description of the problem formulation. A comprehensive Newtonian approach may be found in the book of Szebehely (1967), and a Lagrangian approach can be found in the book of Meyer et al. (2009). It is convenient to make the system non-dimensional by giving the system a unit of mass (or $m_1+m_2=1$), by choosing the distance between the primaries to be a unit of length, and by choosing the unit of time such that one full orbital period of both primaries is $2\pi$. As a result of this last choice the angular velocity of the two primaries about the barycentre is $\omega =1$ (thus making the gravitational constant unity due to this fact and the fact that the total mass is 1). The masses are made dimensionless by dividing each mass by the total system mass. If we assume that $m_1>m_2$ we may write for the dimensionless masses $\mu _1=1-\mu$ and $\mu _2=\mu$. The system is now solely defined by the mass ratio of the primaries $\mu$. Due to the rotation of primaries the equations of motion contain the time explicitly in the inertial system. The explicit appearance of time in the equations of motion is commonly eliminated by using a suitable rotating system (non-inertial) where the more massive primary is placed along the $x$ axis at $({-\mu ,0,0})$ and the less massive primary is placed at $({1-\mu ,0,0})$. The resulting equations can be written in vectorial form as

$$\begin{aligned} \frac{d^{2}\mathbf{r}}{dt^{2}}+2\varvec{\upomega }\times \frac{d\mathbf{r}}{dt}+\nabla U(\mathbf{r})=0, \end{aligned}$$

(1)

where $\mathbf{r}$ is the position vector of the massless third body. The angular velocity vector $\varvec{\upomega }$ of the rotating frame is defined as

$$\begin{aligned} \varvec{\upomega }=\omega \mathbf{e}_z, \end{aligned}$$

(2)

where $\mathbf{e}_z$ is the positive unit vector along the z axis (as stated above, the magnitude of the angular velocity is $\omega =1$ in the non-dimensional problem). The three-body gravitational potential is defined by

$$\begin{aligned} U(\mathbf{r})=-\left( {\frac{1}{2}\left| {\varvec{\upomega }\times \mathbf{r}} \right| ^{2}+\frac{1-\mu }{\mathbf{r}_1 }+\frac{\mu }{\mathbf{r}_2 }} \right) . \end{aligned}$$

(3)

In this work, a mass ratio of $\mu _{ EM } = 1.2150587\times 10^{-2}$ is used for the Earth–Moon set of primaries, and a mass ratio of $\mu _{ SE } = 3.0404234 \times 10^{-6}$ is used for the Sun–Earth set (here the smaller primary is considered to be the summed mass of the Earth and Moon). The positions of the third body (i.e. the spacecraft) w.r.t. the primary ${\mathbf{r}_\mathbf{1}}$ and primary ${\mathbf{r}_\mathbf{2}}$ are

$$\begin{aligned} \mathbf{r}_1&= \left[ {x+\mu ,y,z}\right] , \nonumber \\ \mathbf{r}_2&= \left[ {x+\mu -1,y,z}\right] . \end{aligned}$$

(4)

This system of equations has a first integral, named the Jacobi integral, which relates the value of the Jacobi constant with the gravitational potential and the velocity components of the massless particle. The integral is given by

$$\begin{aligned} J=-\left( \dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}\right) +2U(x,y,z). \end{aligned}$$

(5)

2.2 Equilibrium points and Hill’s region

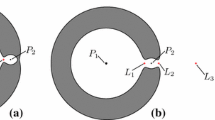
The CR3BP is known to have five equilibrium points; three unstable collinear points are located along the $x$ axis (named $L_{1}, \,L_{2}, \,L_{3})$ and two equilateral points (named $L_{4}$ and $L_{5})$, which are stable for the mass ratios considered here. All five equilibrium points lie in the plane of rotation of both primaries (see Fig. 1 for a plot of their locations). These can be found by solving $\nabla U(\mathbf{r})=0$ under the assumption of a planar configuration (i.e. all out-of-plane $z$ components are equal to zero). For a particular energy level of the system (by setting a constant value for the Jacobi constant) the regions around the primary can be divided into a region where the particle may travel (known as the Hill’s region) and a forbidden region (shown for an example energy level as the grey area in Fig. 1) which the particle may not access for the given value of the Jacobi constant.

Fig. 1

Diagram showing the equilibrium points in the CR3BP in the rotating frame (with the barycentre being the origin of the axes x and y) and the forbidden region (shown in grey) for a particular value of the Jacobi constant

2.3 Periodic orbits and their flow

As we are studying the departure of spacecraft from periodic orbits at Sun–Earth $L_{1}$ and $L_{2}$ and their arrival towards the Moon via $L_{2}$ from the exterior region in the Earth–Moon system we restrict our discussion to the motion about $L_{1}$ and $L_{2}$. There are four possible motions (Conley 1968) near each of these two equilibrium points: transit orbits that allow passage between the exterior and the interior regions, non-transit orbits where the particle approaches the equilibrium region but returns back into the region the particle came from, and unstable periodic orbits where the particle remains in the vicinity of the equilibrium point. The 4th type is the particle asymptotically joining or leaving the periodic orbit. These asymptotic orbits are part of a larger structure of invariant manifold ‘tubes’ (McGehee 1969; Gómez et al. 2001). The borders of these tubes form the boundary between the transit (inside the tube) and non-transit orbits (outside the tube). There are four manifold ‘tubes’; two stable manifolds where the particle flows towards the equilibrium region and two unstable manifolds where the particle flows away from the equilibrium region. These are shown in Fig. 2 for an example periodic orbit at the $L_{1}$ libration point in the Earth–Moon system. There exist a number of periodic orbits near the collinear libration points; for instance horizontal Lyapunov orbits (in the plane of the primaries), vertical Lyapunov orbits (figure eight shape where the orbit intersects the plane of the primaries in a single location in the rotating reference frame), and three-dimensional halo orbits. The existence of quasi-periodic orbits has also been shown: the Lissajous family of orbits that are around the vertical Lyapunov orbits, as well as the quasi-halo orbits that are around the halo orbits (Gómez et al. 2000a, b).

Fig. 2

Illustration of the unstable (red) and stable (blue) invariant manifolds, and their direction of flow, associated to a periodic orbit at $\hbox {L}_{1}$ in the Earth–Moon system

2.4 Connecting the CR3BPs

Connection between the two CR3BPs is accomplished by converting coordinates from one system to the other. This conversion occurs when the spacecraft, on its way from the Sun–Earth $L_{1}/L_{2}$ equilibrium region, crosses the $x$ location of the second primary (the combined mass of the Earth and Moon) in the Sun–Earth synodical system. Here it is assumed that both systems are coplanar and that both pairs of primaries are in circular orbits around another. To convert the position from Earth–Moon to Sun–Earth reference frame the relation

$$\begin{aligned} \eta _{ SE } =\frac{l_{ EM }}{l_{ SE }}e^{i\alpha }\eta _{ EM } +1-\mu _{ SE }, \end{aligned}$$

(6)

where complex notation is used, where the $x$ and $y$ components are given by

$$\begin{aligned} \eta _{ SE } =x_{SE} +iy_{ SE } ,\quad \eta _{ EM } =x_{EM} +iy_{ EM }. \end{aligned}$$

(7)

The distances between the Sun and Earth and Earth and Moon are given by $l_{ SE } =1.495979\times 10^{8}$ km and $l_{ EM } =384{,}400$ km. The mass parameter $\mu _{ SE }$ that defines the Sun–Earth system is computed by

$$\begin{aligned} \mu _{ SE } =\frac{m_E +m_M }{m_E +m_M +m_S}. \end{aligned}$$

(8)

The masses are given for the Earth as $m_E =5.973699\times 10^{24}$ kg, for the Moon as $m_M =7.347673\times 10^{22}$ kg, and for the Sun $m_S =5.973699\times 10^{30}$ kg. The angle $\alpha$ representing the relative geometry of both systems (i.e. the angle between the axes spanned along both sets of primaries) is computed using

$$\begin{aligned} \alpha =\alpha _0 +\left( {\omega _{ EM } -\omega _{ SE } }\right) \frac{t_{ EM } }{\omega _{ EM } }, \end{aligned}$$

(9)

where $\alpha _0$ is the initial relative geometry of the system. The angular velocities for both systems are given by Kepler’s third law as

$$\begin{aligned} \omega _{ EM } =\sqrt{\frac{G({m_E +m_M})}{l_{ EM }^{3}}} \end{aligned}$$

(10)

for the Earth–Moon system, and for the Sun–Earth system as

$$\begin{aligned} \omega _{ SE } =\sqrt{\frac{G({m_E +m_M +m_S})}{l_{ SE } ^{3}}}. \end{aligned}$$

(11)

This gives an angular velocity of $\omega _{ EM } =2.66531437\times 10^{-6}$ and $\omega _{ SE } =1.99098670\times 10^{-7}$ rad/s. The velocity from Earth–Moon rotating frame can be converted to Sun–Earth rotating frame by

$$\begin{aligned} \frac{d\eta _{ SE } }{dt_{ SE } }=\frac{l_{ EM } }{l_{ SE } }\frac{\omega _{ EM } }{\omega _{ SE } }e^{i\alpha }\left( {i\left( {1-\frac{\omega _{ SE } }{\omega _{ EM } }} \right) \eta _{ EM } +\frac{d\eta _{ EM } }{dt_{ EM } }}\right) \!. \end{aligned}$$

(12)

Because is it assumed that both rotating frames lie in the same plane (both systems are coplanar) the conversion for any out-of-plane conversion is straightforward. The position is converted using the relation

$$\begin{aligned} z_{ SE } =z_{ EM } \frac{l_{ EM } }{l_{ SE }}, \end{aligned}$$

(13)

and the velocity is converted using the relation

$$\begin{aligned} \dot{z}_{ SE } =\dot{z}_{ EM } \frac{l_{ EM } }{l_{ SE } } \frac{\omega _{ EM } }{\omega _{ SE }}. \end{aligned}$$

(14)

For a comprehensive description of the conversion process (including details on the conversion to and from the inertial reference frame, and from the Earth–Moon to Sun–Earth synodical system) the reader is referred to the work of Castelli (2011).

3 Survival and event maps

Regardless of the application, one can be interested in what kind of conditions near the $L_{2}$ libration point would be beneficial for establishing a long duration quasi-periodic orbit about the Moon, and what conditions would lead to an impact on the lunar surface. To this end, one can analyse the case of a family of virtual spacecraft placed at $x={x}_{{L}_{2}}$ and at interspaced points along $-0.25<y<0.25$ within the Earth–Moon CR3BP. These spacecraft can then be assigned a velocity, for which two methods are provided in this paper. The first assumes a parallel flow along the $x$ axis, and the second derives the velocity for each point on the basis of a specified value of the Jacobi constant. In the first method, the spacecraft are then given initial velocity components $\dot{y}=0$ and $\dot{x}$ sampled uniformly from the domain $-0.2<\dot{x}<0.2$ (all values in the non-dimensional system) such that the initial flow at $x={x}_{{L}_{2}}$ is always parallel to the $x$ axis within the Earth–Moon rotating frame. Without loss of generality one can start by restricting the analysis to the planar case so that the position and velocity along the $z$ axis are neglected. This leads to a group of initial states where $x$ and $\dot{y}$ are constant, and $y$ and $\dot{x}$ are varied. The state of the spacecraft can be generally written as

$$\begin{aligned} \mathbf{x}_{SC} =\left[ {x_{L_2 }},\quad {y}, \quad {0}, \quad {\dot{x}}, \quad 0, \quad 0 \right] ^\mathrm{T}. \end{aligned}$$

(15)

This group of states (henceforth referred to as lunar arrival states in this work) is then individually propagated forward in time until the orbit is no longer deemed stable or until the maximum propagation time of 3 months is met. In the framework of this discussion an orbit is considered stable when the spacecraft remains between the locations of the $L_{1}$ and $L_{2}$ points along the $x$ axis, and does not impact upon the Moon, i.e. when a set of coordinates $({x,y})$ fulfils

$$\begin{aligned} x_{L_1 } <x<x_{L_2 } \end{aligned}$$

(16)

and

$$\begin{aligned} \sqrt{x^{2}+y^{2}}>R_{ Moon }. \end{aligned}$$

(17)

The result of this propagation can be seen in the survival map shown in Fig. 3.

Fig. 3

a Lunar survival map and b corresponding lunar propagation event map with constant $x$ and $\dot{y}$ and $y$ and $\dot{x}$ varied along axes

It can be seen in Fig. 3a that large swaths of the map are accompanied by a low lifetime. Naturally those areas where the value of $\dot{x}$ are positive correspond to a low orbit lifetime as the initial condition will tend to cause the spacecraft to immediately exit the Earth–Moon system past $x_{L_2}$. The central area in Fig. 3a, however, shows promising areas where the orbit duration is higher. Note that the reason why the areas with positive $\dot{x}$ as initial condition have a non-zero lifetime is because the limit at which the propagation is halted is slightly further out from the Moon than $x_{L_2}$. This is to allow for a degree of flexibility where the spacecraft may initially move in the opposite direction before moving towards the Moon. Additionally, there is the practical consideration of preventing the propagation from already ceasing at the initial point. To understand which areas of initial conditions are suitable for lunar impact, and which are suitable for lunar capture, the cause of propagation termination is also recorded. This is shown in the event map in Fig. 3b. The possible outcomes are stability (shown in white) as defined previously in Eqs. (16) and (17) for the propagation duration of 90 days, impact on the lunar surface (shown in light grey), passing outside the lunar region via $x_{L_1}$ (shown in dark grey), and passing outside the lunar region via $x_{L_2 }$ (shown in black).

The map in Fig. 3a provides an indication of which initial conditions are suitable to achieve a lunar capture or a lunar impact, but provides no information about the feasibility of reaching the desired initial condition from a Sun–Earth libration point orbit. This is addressed by propagating backwards in time the same set of initial conditions that was used to construct the survivability map in order to ascertain which regions of the map are reachable from Sun–Earth libration point orbit. This process is relatively quick as the propagation from an initial state is immediately halted when the arc passes $x=x_{L_1}$. The value of $y$ at $x_{L_1}$ is checked when this occurs, to verify that the state is now in the exterior region (i.e. outside the surfaces of Hill) of the Earth–Moon system. Conversely, states that are inside the Earth–Moon system have originated from within the interior region of the surfaces of Hill. These states are unreachable from Sun–Earth libration point orbit and thus are filtered out of the set of valid initial conditions. A graphical representation of this is shown in Fig. 4, where the unreachable initial conditions are set to a lifetime of zero (indicated in Fig. 4 by a shade of dark red). It can be seen that the regions of interest are not adversely affected in this case. One can observe a central symmetry here (due to the symmetric properties of the CR3BP), where the states leading to exit via $L_{1}$, lunar impact, and 90 days stability are point reflected via the centre of the plot to the filtered out regions on the map. To illustrate this, a state $(-\dot{x},+y)$ on the map with positive survival time leads to motion about the Moon and has originated from the exterior region. This point is reflected to become $(+\dot{x},-y)$, and will now show opposite behaviour; the spacecraft immediately leaves the lunar vicinity. It can be seen that those states leading to exit via $L_{2}$ (as indicated by Fig. 3b) are generally not reflected onto the filtered part of the map. This stands to reason as any state leading to immediate exit towards the exterior region would, when point reflected, lead to movement towards the Moon and thus a non-zero lifetime.

Fig. 4

Lunar survival map with constant $x$ and $\dot{y}$ and $y$ and $\dot{x}$ varied along axes with filtering of unreachable initial conditions

In addition to the first method of specifying velocity one may also create a survival map by setting an energy level of the system, or in other words choosing a value of the Jacobi constant of motion

$$\begin{aligned} J=-\left( {\dot{x}^2}+{\dot{y}^2}+{\dot{z}^2}\right) +{{x}^2} + {{y}^2}+2 \left( \frac{1-\mu }{r_1}+\frac{\mu }{r_2} \right) , \end{aligned}$$

(18)

obtained from the Jacobi integral of the three-body problem (Szebehely 1967) where $r_{1}$ and $r_{2}$ are the scalar lengths of the vectors given by Eq. 4. Since this paper focuses only on the use of two dimensional maps, the $z$ components will be disregarded ($z=\dot{z}=0$). By choosing a value of the Jacobi constant, assuming a value of $x=x_{L_2}$, and given a mesh of values of $y$ and $\dot{x}$, the corresponding value of $\dot{y}$ (and $-\dot{y})$ can be computed. Then, as for the previous map the entire set of initial conditions can be propagated forwards in time to study the behaviour. The resulting maps for the set of Jacobi constants $J = [3.00,\,3.05,\,3.10,\,3.15]$ is given in Fig. 5a, along with the corresponding event map in Fig. 5b. The plots contain empty regions, due to no valid real value of $\dot{y}$ existing for particular combinations of the Jacobi constant and the other state parameters. The states that are stable for at least 90 days are only found for $J = 3.00$ and for clarity’s sake are marked in the event map in Fig. 5b as green dots on the event map. As the Jacobi constant increases the forbidden zone of the Hill’s regions increases, and thus the region of interest on the maps becomes smaller and smaller. As a result, increased resolution is generally needed to reveal the structures on the map. This increased resolution comes at an additional computational cost, which is offset by the fact that the region of interest on the maps has also shrunk.

Fig. 5

a Set of four lunar survival maps and b corresponding set of four lunar propagation event maps with constant $J$ and $y$ and $\dot{x}$ varied along axes

An example lunar target state from each category of event is taken from the survival map shown in Fig. 3 and propagated both forwards and backwards in time. The results are shown in Fig. 6 for a lunar target state leading to weak capture, impact, and exit from the vicinity of the Moon via $L_{1}$ and $L_{2}$.

Fig. 6

Example lunar target states (left four subplots) in the Earth–Moon rotating reference frame leading to a weak capture, b impact, c leaving the vicinity of the Moon towards the interior region, and d leaving the vicinity of the Moon towards the exterior region. Right Plots e through h are the corresponding plots in the inertial reference frame centred at the Earth

Note that the methodology used to create these maps can also be used for non-planar problems by extending the maps with the addition of the $z$ components for position and velocity. Keeping in mind that the maps define a set of target states with associated survivability, one possible extension features the definition of a plane normal to the $x$ axis vector. Points are sampled on this plane, providing a set of positions $(x,\,y,\,z)$ where $x$ is fixed. By assuming a value of the Jacobi constant the velocity components ($\dot{x},\dot{y},\dot{z}$) can be computed using two free angles. For every pair of coordinates in the y–z plane one can select the optimal velocity components that maximise survivability. This extension merely requires a more involved initial computation to generate the map. Other extensions are possible but require additional assumptions on the velocity components. These extensions, however, are not required to complete the analyses in this paper and are left for future work. Finally, it should also be noted that these maps can be constructed for transfers entirely within one CR3BP, for example interior transfers between the Earth and Moon (Van der Weg and Vasile 2012). The resulting set of initial conditions, their corresponding orbit lifetime, and their category of decay (impact or exit via libration points) can now serve as the basis for the design of transfers from Sun–Earth libration point orbits towards the Moon.

4 Transfer design using the maps

As described briefly in Sect. 2, the transfer between Sun–Earth libration point orbit and Moon is modelled in two parts: the initial leg in the Sun–Earth CR3BP and the leg describing the motion nearer to the Earth and Moon in the Earth–Moon CR3BP. The transfer from Sun–Earth $L_{1}/L_{2}$ libration point orbit (which defining parameters are given) to the Moon consists initially of following the branch of the unstable manifold, generated from the periodic orbit, towards the Earth–Moon barycentre in the Sun–Earth CR3BP. Instead of utilizing the stable manifold branch (originating from a libration point orbit at $L_{2}$ in the Earth–Moon system) in the Earth–Moon CR3BP to bring the spacecraft towards the Moon (as would be typical for a WSB transfer, see Koon et al. 2001a, b), use is made of the lunar arrival states on the survival map to directly target desired conditions near the Moon (such as weak capture or impact). The procedure outlined in this section is usable for both planar as well as non-planar cases. However, the results generated in the following section assume the two connected CR3BPs to be coplanar and make use of planar survival maps. The procedure remains unchanged; merely $z$ and $\dot{z}$ are always equal to zero for this case. Both individual transfer legs are described here by their position ($x,y,z$) and their velocity ($\dot{x},\dot{y},\dot{z})$ along a discretized period of time, effectively giving two $6\times N$ matrices (where $N$ differs for both legs due to numerical integration and the period of time thereof). The initial leg modelled in the Sun–Earth CR3BP is denoted by ${\varvec{s}}_{lpo}$, and the second leg modelled in the Earth–Moon CR3BP is denoted by ${\varvec{\sigma }}_m$. An example of a stable branch of an invariant manifold in the Earth–Moon CR3BP, as well as a subset of arcs leading to lunar capture and impact, is shown in Fig. 7. The stable branch denoting the flow towards the Moon from the exterior regions is shown in black, whereas the weak capture (shown in blue) and impact (shown in red) arcs are obtained from a representative sampling of the survival map in Fig. 3. Figure 7 illustrates that the collection of capture and impact arcs show the same behaviour as the manifold structure flowing towards its associated libration point orbit.

Fig. 7

Stable manifold branch flowing towards the Moon from the exterior of the Earth–Moon system (shown in black), the flow towards the Moon based on a representative selection of lunar arrival states targeting weak capture selected from Fig. 3 (shown in blue), and the flow towards the Moon based on a representative selection of lunar arrival states targeting lunar impact selected from Fig. 3 (shown in red)

A connection between the arcs ${\varvec{s}}_{lpo}$ and $\varvec{\sigma }_m$ from both Sun–Earth and Earth–Moon CR3BPs can be made by transforming one set of states into the reference frame of the other $\varvec{\sigma }_m ({\alpha _0})\rightarrow {\varvec{s}}_m$, and subsequently searching for intersections on a given Poincaré section. The initial orbital phases $\alpha _0^{SE}$ and $\alpha _0^{EM}$ of both CR3BPs control the geometry of the connection, but this is reduced to a single parameter $\alpha _0 \,\, ({=}\alpha _0^{EM} -\alpha _0^{SE} )$ as only the relative phasing between Sun–Earth and Earth–Moon systems is necessary (Fantino et al. 2010). The concept is illustrated in Fig. 8a, where a segment of arcs in the Earth–Moon system (shown in blue) has been converted into the Sun–Earth barycentric synodical reference frame.

Fig. 8

a Both unstable manifold from Sun–Earth $\hbox {L}_{1}$ (black) and stable manifold from Earth–Moon $\hbox {L}_{2}$ (blue) shown in Sun–Earth synodical barycentric reference frame, b unstable manifold from Sun–Earth $\hbox {L}_{1}$ LPO (black) and initial states leading to lunar impact (blue) shown in Sun–Earth synodical barycentric reference frame, and c unstable manifold from Sun–Earth $\hbox {L}_{1}$ LPO (black) and initial states leading to lunar quasi-capture (blue) shown in Sun–Earth synodical barycentric reference frame

A wide selection of lunar arrival states from the lunar survival map that lead to successful capture and to lunar impact are propagated backwards in time and the obtained arcs are translated into the Sun–Earth CR3BP. The resulting plot of lunar arrival states resulting in impact are shown in Fig. 8b, and for capture in Fig. 8c, for an initial orbit phasing of $\alpha _0 =0$. In both figures, these arcs (a group of arcs ${\varvec{s}}_m )$ are shown in blue while a segment (a group of arcs ${\varvec{s}}_{lpo})$ of an unstable invariant manifold is plotted in black for the sake of comparison.

The connection between the trajectory arcs from both CR3BPs is made on a plane ${\varvec{P}}$ at $x=1-\mu$ in the Sun–Earth CR3BP (the barycentre of the Earth–Moon system) whose normal vector is ${\varvec{e}}_x =\left[ {1,0,0} \right]$. An arc $\varvec{\sigma }_m$ flowing towards the Moon—after having its states converted $\varvec{\sigma }_m \left( {\alpha _0 } \right) \rightarrow {\varvec{s}}_m$ from Earth–Moon to Sun–Earth reference frame—thus has a certain position and velocity ${\varvec{s}}_m^{1-\mu }$ when it intersects the plane ${\varvec{P}}$. This arc must then be connected to an arc ${\varvec{s}}_{lpo}$ on the unstable manifold leading away from the Sun–Earth system libration point. This second arc also intersects plane ${\varvec{P}}$, but at ${\varvec{s}}_{lpo}^{1-\mu }$. For the matching of the arcs to be correct the $y$ and $z$ (if the problem is entirely planar $z$ components can be disregarded) position components of ${\varvec{s}}_m^{1-\mu }$ should be equal to those of ${\varvec{s}}_{lpo}^{1-\mu }$. The two connecting arcs will have a certain disparity in velocity, which is corrected for by manoeuvre. Poincaré sections at $x=1-\mu$ (the barycentre of the Earth–Moon system) in the Sun–Earth CR3BP for velocity components $\dot{x}$ and $\dot{y}$ illustrate this in Fig. 9, which shows the intersection of the unstable manifold from the Sun–Earth libration point orbit in black and the intersecting points of the flow leading towards selected lunar impact states in blue for the case of an initial orbit phasing of $\alpha _0 =0$. The insets show the (exaggerated in this case for the sake of clarity) velocity change of $\dot{x}$ and $\dot{y}$ to jump from the Sun–Earth CR3BP unstable manifold unto a selected arc intersection ${\varvec{s}}_m^{1-\mu }$. Figure 10 shows the same intersections as in Fig. 9, but for selected lunar capture, instead of impact, states.

Fig. 9

Poincaré sections of $\dot{y}-y$ (left) and $\dot{x}-y$ (right) phase space at $x=1-\mu$ in the Sun–Earth CR3BP, showing the intersections from the unstable manifold from the $\hbox {L}_{1}$ LPO (black line) and the intersections from the initial states leading to lunar impact (blue points)

Fig. 10

Poincaré sections of $\dot{y}-y$ (left) and $\dot{x}-y$ (right) phase space at $x=1-\mu$ in the Sun–Earth CR3BP, showing the intersections from the unstable manifold from the $\hbox {L}_{1}$ LPO (black) and the intersections from the initial states leading to lunar capture (blue)

If the arcs ${\varvec{s}}_m$ leading towards the Moon are numerically integrated for a sufficiently long period of time, they will cross the intersection plane multiple times. For each of these intersections a connection can be attempted with the unstable manifold. Naturally, transfer duration will increase when the connection is made at a later intersection (the increase in transfer time is dependent on the specific arc). Another consideration for a trajectory where the connection is delayed until a later intersection is the gravitational influence of the Sun. As the arc leading from the intersection plane towards the Moon takes more and more time (and also generally starts further out on plane ${\varvec{P}}$) the ability of the Earth–Moon CR3BP to approximate the full body dynamics degrades.

The general solution space for a set of lunar arrival states and a particular libration point orbit can be effectively and quickly mapped by computing and storing the unstable manifold trajectory arcs ${\varvec{s}}_{lpo}$ from the Sun–Earth libration point orbit and the trajectory arcs $\varvec{\sigma }_m$ flowing towards the lunar target states. Once this is computed, the transformation of the lunar target state arcs from Earth–Moon to Sun–Earth synodical barycentric reference frame ($\varvec{\sigma }_m ({\alpha _0} )\rightarrow {\varvec{s}}_m )$ can be performed for a range of values of the orbital phasing angle $\alpha _0$. For each lunar target state trajectory arc and value of orbital phasing angle $\alpha _0$ the best matching arc flowing from the Sun–Earth libration point orbit can be found. The criterion is the lowest $\Delta v$ to connect both arcs, which at the same time satisfies the positional difference on the Poincaré section (on plane ${\varvec{P}}$) to within set tolerance. Promising pairs of intersections can then be refined further by way of an optimization process. A number of matching pairs can be found based on ranking, which then serve as initial guesses for an optimization process using an SQP gradient solver (Nocedal and Wright 2006). The optimization initially only accounts for two design parameters $\alpha _0$ and $\beta$. This can be expressed as the design variable vector

$$\begin{aligned} \mathbf{x}=\left[ {\alpha _0 } \quad \beta \right] \!, \end{aligned}$$

(19)

where $\alpha _0$ is the initial orbit phasing and $\beta$ is the position along the Sun–Earth libration point orbit expressed as a curvilinear coordinate within the domain of $\left[ {0,2\pi } \right]$ where 0 is chosen as the position on the libration point orbit at $y=0$ and with the smallest value for $x$. The same position along the circuit of the libration point orbit is reached at $2\pi$ after clockwise rotation. Note that for initial optimization both parameters are assumed to be independent of each other. When translating this problem to a full ephemeris model an initial time will both proscribe the geometry of the planets $\alpha _0$ as well as the position of the spacecraft on the LPO $\beta$, reducing the number of variables to 1. The state of the arc ${\varvec{s}}_{lpo}$ flowing from the libration point orbit at the intersection with plane ${\varvec{P}}$ at $x=1-\mu$ is denoted as ${\varvec{s}}_{lpo}^{1-\mu } =\left[ {\mathbf{p}_{lpo} ,\dot{\mathbf{p}}_{lpo}} \right]$, where $\mathbf{p}_{lpo}$ and $\dot{\mathbf{p}}_{lpo}$ are the three element position and velocity vectors at plane ${\varvec{P}}$ in the Cartesian coordinate system in the Sun–Earth synodical reference frame, respectively. In a similar fashion, the state from the arc ${\varvec{s}}_m$ flowing towards the lunar vicinity at the intersection with the plane ${\varvec{P}}$ is denoted as ${\varvec{s}}_m^{1-\mu } =\left[ {\mathbf{p}_m ,\dot{\mathbf{p}}_m} \right]$. The objective of the optimization is to minimize the velocity change necessary to change the velocity at the intersection such that the velocity is matched between ${\varvec{s}}_{lpo}^{1-\mu }$ and ${\varvec{s}}_m^{1-\mu }$. This can be expressed as

$$\begin{aligned} f\left( {\varvec{x}} \right) =\Delta v={\vert }{\vert }\dot{\mathbf{p}}_{lpo}-\dot{\mathbf{p}}_{m}{\vert }{\vert }. \end{aligned}$$

(20)

The positional difference between the two arcs as they meet at plane ${\varvec{P}}$ is added as an equality constraint

$$\begin{aligned} c(x)={\vert }{\vert }\mathbf{p}_{lpo} -\mathbf{p}_m{\vert }{\vert } \end{aligned}$$

(21)

to the optimization process. This ensures any remaining gap between the arcs meeting at plane ${\varvec{P}}$ is closed. Once a single optimization pass has been completed (after having either satisfied constraint tolerances or having reached the maximum number of evaluations) the design variable vector is expanded to

$$\begin{aligned} \mathbf{x}=\left[ {\alpha _0 }\quad \beta \quad {\Delta v_{lpo}}\quad {\gamma _{lpo}}\quad {\delta _{lpo}}\quad {\Delta v_m } \quad {\gamma _m }\quad {\delta _m } \right] \!, \end{aligned}$$

(22)

where two manoeuvres are introduced at departure from the libration point orbit and at arrival near the Moon (at the position of the chosen lunar target state). $\Delta v_{lpo}$ and $\Delta v_m$ are the magnitudes of the manoeuvres, $\gamma _{lpo}$ and $\gamma _m$ are the respective in-plane right ascensions of the manoeuvres (counted from the tangential direction of the velocity change vector to its projection on the orbital plane), and $\delta _{lpo}$ and $\delta _m$ are the respective out-of-plane declinations of the manoeuvres (the angle between projection of the velocity change vector on the orbital plane and the velocity change vector itself). In the case of a planar transfer from a planar Lyapunov orbit the out-of-plane declinations for both manoeuvres are zero. The optimization process is now repeated with the same objective and constraints.

5 Disposal results for an $\hbox {L}_{2}$ Lyapunov orbit

As a case study, the prior described algorithm, lunar survival map, and event map are now used to generate $\Delta v$ maps for both capture and impact transfers from an initial libration orbit (in this case a planar Lyapunov orbit) at $L_{2}$ that shares the in-plane amplitude characteristics of the Herschel spacecraft (ESA 2013). Both of these orbits are shown in Fig. 11. The orbit is defined in the Sun–Earth CR3BP by a Jacobi constant of $J=3.00080469$, an $x$ amplitude of $3.2816\times 10^{-3}$ and a $y$ amplitude of $1.03808\times 10^{-2}$ (non-dimensional units).

Fig. 11

Representation of Herschel orbit in the CR3BP (back) and a planar Lyapunov orbit (blue) sharing the same amplitude along x and y axes

An online supplement is available separately, which also includes two further test cases: a second planar Lyapunov orbit representing a planar image of the operational orbit of the SOHO spacecraft (Felici 1995) at $L_{1}$ and a full CR3BP representation of the operational orbit of SOHO (with out-of-plane $z$ component) to test the sensitivity of the procedure (using planar lunar arrival states from the survival map) to non-planar transfers.

Given the libration orbit defined above, a subset of lunar arrival states is selected for the generation of the results. In the case of capture, states with an excellent survival time of at least 65 days are selected from the map (regardless of whether the orbit deteriorates by impacting the Moon, or escaping past $L_{1}$ or $L_{2})$. For the case of impact, only those states that impact the Moon, and with a not too long survival time ($<$30 days) are selected.

The results for lunar capture are provided in Figs. 12 and 13. These results were created by sampling the initial orbital phasing angle values $\alpha _0$ at $1^{\circ }$ intervals. The results presented in the figures are before optimization but fulfil relatively strict constraints on the distance between the meeting points ${\varvec{s}}_{lpo}^{1-\mu }$ and ${\varvec{s}}_m^{1-\mu }$ of the arcs at plane ${\varvec{P}}$. In the worst case the constraint violation at plane ${\varvec{P}}$ may be up to 1500 km, but most transfers have a difference of a few 100 km. These constraint violations can be reduced by using the optimization process in Sect. 4. Figure 12 shows the $\Delta v$ cost in m/s (ranging from 0 to 100 m/s) for each selected lunar arrival state for the very first intersection that occurs at the intersection plane ${\varvec{P}}$. Figure 13a shows the $\Delta v$ cost in m/s for the first six intersections of each arc ${\varvec{s}}_m$ with the intersection plane. Multiple crossings are achieved by increasing the numerical integration time for each arc; instead of halting propagation after the first intersection it is halted after a number of successive intersections with plane ${\varvec{P}}$. A plot showing the best $\Delta v$ value found from among all first six intersections per lunar arrival state is given in Fig. 13b.

The lower area of Fig. 12 for the $L_{2}$ ranges from near-zero to ca. 30 m/s $\Delta v$ cost. The lowest value found in the first intersection is 1.526 m/s (before optimization). $\Delta v$ cost is not substantially improved in the second intersection (Fig. 13a) with the lowest value being 1.424 m/s. Sampling further sections provides no performance benefit in this case.

Fig. 12

$\Delta v$ map of the 1st intersection for lunar capture from Lyapunov orbit at $\hbox {L}_{2}$

Fig. 13

a $\Delta v$ maps of the first six intersections for lunar capture from Lyapunov orbit at $\hbox {L}_{2}$ and b $\Delta v$ map of the best results from the first six intersection for lunar capture from Lyapunov orbit at $\hbox {L}_{2}$

The results for lunar impact are given in Figs. 14 and 15. As was the case for lunar capture, the results were created by sampling the initial orbital phasing angle values $\alpha _0$ at $1^{\circ }$ intervals. The results presented in the figures are before optimization but fulfil the same constraints on the distance between the meeting points ${\varvec{s}}_{lpo}^{1-\mu }$ and ${\varvec{s}}_m^{1-\mu }$ of the arcs at plane ${\varvec{P}}$ as was the case for lunar capture. Figure 14 shows the $\Delta v$ cost in m/s (ranging from 0 to 150 m/s) for each selected lunar arrival state for the very first intersection that occurs at the intersection plane ${\varvec{P}}$. Figure 15a shows the $\Delta v$ cost in m/s for the first six intersections of each arc ${\varvec{s}}_m$ with the intersection plane. Multiple intersections are achieved by increasing the numerical integration time for each arc; instead of halting propagation after the first intersection it is halted after a number of successive crossings with plane ${\varvec{P}}$. A plot showing the best $\Delta v$ value found from among all first six intersections per lunar arrival state is given in Fig. 15b.

Fig. 14

$\Delta v$ map of the 1st intersection for lunar impact from Lyapunov orbit at $\hbox {L}_{2}$

As can be seen from the figures the selected lunar arrival states that lead to impact cover a much wider portion of the generated survival map than those states that lead to capture. Connections between the libration point orbit and lunar impact can be achieved for a number of lunar arrival states at near-zero $\Delta v$ cost within the first intersection, before optimization. The lowest value found in the first intersection is 2.19 m/s. The $\Delta v$ cost remains between 1 and 3 m/s for succeeding intersections (Fig. 15a).

Fig. 15

a $\Delta v$ maps of the first six intersections for lunar impact from Lyapunov orbit at $\hbox {L}_{2}$ and b $\Delta v$ map of the best results from the first 6 intersection for lunar impact from Lyapunov orbit at $\hbox {L}_{2}$

Four example trajectories, after optimization, are plotted in Fig. 16, where the libration orbits are shown in red, the segments after the transfer has reached its lunar arrival state are shown in blue, and the connection manoeuvres for the trajectories are shown as stars. The first trajectory (a) is a planar trajectory from the libration point orbit at $L_{1}$ that leads to impact upon the lunar surface, costing slightly $<$1 m/s to connect the two legs. The second trajectory (b) is a planar trajectory from the libration point orbit at $L_{2}$ that is captured by the Moon for at least 3 months before the spacecraft exits the lunar vicinity via $L_{1}$ in the Earth–Moon system. This connection manoeuvre cost 1.6 m/s. The third trajectory (c) shows a capture trajectory from $L_{1}$ where two intersections occur before the Sun–Earth and Earth–Moon legs are connected, costing 12 m/s. The fourth trajectory (d) shows a non-planar example (costing 142 m/s to connect) of a lunar capture, including a side view of the trajectory.

Fig. 16

Plots of example trajectories: a $\hbox {L}_{1}$ lunar impact, b $\hbox {L}_{2}$ temporary lunar capture, c $\hbox {L}_{1}$ temporary lunar capture with two intersections, and d non-planar $\hbox {L}_{1}$ capture in the Sun–Earth synodic reference frame

6 Redesign of the transfer using solar radiation pressure

This section investigates the use of a hybrid propulsion system, combining solar radiation pressure and impulsive maneuvers, to complete the transfer. Alongside the classical definition of the CR3BP, a modified version, adding solar radiation pressure (Simo and McInnes 2009), is employed to study the trajectory in the Earth–Moon CR3BP. The larger primary $m_{1}$ is the Earth and the smaller primary $m_{2}$ is the Moon. The two primaries move about their centre of mass in a circular orbit while the third body is of negligible mass such that it is unable to influence the movement of the two primaries (cf. Fig. 17).

Fig. 17

Schematic geometry of circular restricted three-body problem (z-axis pointing out from paper)

The equations of motion now change from those given in Eq. (1) to

$$\begin{aligned} \frac{d^{2}\mathbf{r}}{dt^{2}}+2\varvec{\upomega }\times \frac{d\mathbf{r}}{dt}+\nabla U (\mathbf{r})={\varvec{a}}, \end{aligned}$$

(23)

where ${\varvec{a}}$ is the introduced acceleration of the solar radiation pressure. When the solar radiation pressure is taken into account for the Earth–Moon set of primaries, the acceleration due to the solar radiation pressure is defined as

$$\begin{aligned} {\varvec{a}}=a_0 \left( {\mathbf{S}\cdot {\varvec{n}}} \right) ^{2}{\varvec{n}}, \end{aligned}$$

(24)

where $a_0$ is the magnitude of the solar radiation pressure acceleration, $\mathbf{n}$ is the unit vector normal to the surface of the reflective surface of the spacecraft, and $\mathbf{S}$ is the direction vector of sunlight given by

$$\begin{aligned} \mathbf{S}=\left[ {\cos \left( {w_s t+S_0 } \right) } \quad {-\sin \left( {w_s t+S_0 } \right) }\quad 0 \right] \!, \end{aligned}$$

(25)

where $w_s$ is the angular rate of the sunlight vector in the synodic reference frame. $S_{0}$ represents the initial direction of the sunlight at $t_{0}$ (if this term is omitted the direction of sunlight is initially directly along the axis of the primaries from the larger primary Earth to the smaller primary). The angular rate of the sunlight vector $w_s$ can be determined by subtracting the dimensionless value of the rotation rate of the Earth about the Sun from the rotation rate of the Moon about the Earth (equal to unity in the dimensionless system), obtaining $w_s = 0.923$ as the angular rate of the sunlight in the dimensionless synodic reference frame.

The magnitude of the solar radiation pressure $a_0$ within the dimensionless Earth–Moon system is chosen based on the lightness number $\lambda$, which is a dimensionless parameter defined by the ratio of the acceleration experienced by the reflective surface normal to the Sun line and the Sun’s local gravity field. At 1 AU this is defined as

$$\begin{aligned} \lambda =\frac{a_c }{5.93\times 10^{3}\,\hbox {m/s}^{2}}, \end{aligned}$$

(26)

(from Dachwald et al. 2002) where $a_c$ is the characteristic acceleration given by

$$\begin{aligned} a_c =P_{ eff _{1\mathrm{AU}} } \frac{A}{m}=2\eta P_{0_{1\mathrm{AU}} } \frac{A}{m}. \end{aligned}$$

(27)

Here the area to mass ratio $A/m$ is a parameter of the spacecraft and $P_{eff_{1AU} }$ is the effective pressure acting upon the reflective surface at 1 AU distance from the Sun. An aluminium coated plastic film with an efficiency of 85 % ($\eta =0.85)$ is assumed. The solar radiation pressure at 1 AU is $P_{0_{1\mathrm{AU}}} =4.4563 \times 10^{-6}\,\hbox {N/m}^{2}$. With these parameters and an assumed value for the spacecraft’s area to mass ratio the lightness number can be computed and used to serve as the acceleration magnitude $a_0$. While the spacecraft moves within the Earth–Moon CR3BP the distance from the Sun is considered to remain constant at 1 AU such that the scalar magnitude of the solar radiation pressure remains constant throughout the trajectory arc.

The reflective surface can be controlled passively such that the spacecraft is generally always facing the Sun via the use of particular shapes (e.g. a cone). A more active control is considered here, where the reflective surface is controlled using a locally optimal control law obtained from maximising the change in velocity (in order to increase or decrease the energy) along the velocity vector of the spacecraft. This is derived from studying the geometry of the surface and incoming sunlight vector (McInnes 2004), and can be written as

$$\begin{aligned} \gamma =\hbox {atan}\left( {\frac{3\tan \alpha }{4}+\frac{\sqrt{9\tan ^{2}\alpha +8}}{4}} \right) . \end{aligned}$$

(28)

The angle $\alpha$ is defined as

$$\begin{aligned} \alpha =-\hbox {asin} ({\mathbf{e}_v \cdot \mathbf{S}}), \end{aligned}$$

(29)

where $\mathbf{e}_v$ and $\mathbf{S}$ represent the unit vector of velocity of the spacecraft and the unit vector of the sunlight direction (see Eq. 25), respectively. The angle $\gamma$ is the angle between sunlight unit vector $\mathbf{S}$ and the unit vector ${\varvec{n}}$, which defines the spacecraft’s surface pointing direction. This angle $\gamma$ is measured in the plane spanned by $\mathbf{S}$ and $\mathbf{e}_v$. To locally maximize the increase of energy the rotation is positive, while for local maximization of the decrease of energy the rotation is in the opposite direction ($-\gamma )$. If $\mathbf{S}=\langle x,y,z \rangle$ and $\mathbf{S}\times \mathbf{e}_v =\langle u,v,w \rangle$ then the rotation can be written as

$$\begin{aligned} {\varvec{n}}=\left[ {{\begin{array}{l} {-u\left( {-ux-vy-wz} \right) \left( {1-\cos \gamma } \right) +x\cos \gamma +\left( {-wy+vz} \right) \sin \gamma } \\ {-v\left( {-ux-vy-wz} \right) \left( {1-\cos \gamma } \right) +y\cos \gamma +\left( {wx-uz} \right) \sin \gamma } \\ {-w\left( {-ux-vy-wz} \right) \left( {1-\cos \gamma } \right) +z\cos \gamma +\left( {-vx+uy} \right) \sin \gamma } \\ \end{array} }} \right] \!. \end{aligned}$$

(30)

Once the unit vector ${\varvec{n}}$ is known the acceleration is known and the equations of motion can be numerically solved. In essence, this control aims to close the gap in energy level between the starting point at the LPO and the finishing point at the lunar target state. In both the Sun–Earth and Earth–Moon problems the velocity of the spacecraft is changed locally in an attempt to change the energy level (or Jacobi constant).

As a first indication of the influence of the solar radiation pressure and control law, transfers are generated (as described in Sect. 4) for a set of lunar target states leading to weak capture. This set is acquired by evenly sampling 1,000 times across the region of $-0.05<\dot{x}<0$ and $-0.05<y<0$ in Fig. 4, and selecting only those states leading to a survival time $>$2 months. An attempt is made to generate a valid transfer for each of the 1,000 lunar target states across the range of possible orbital phasing angle $\alpha _0$ at increments of $1^{\circ }$ (thus in effect producing a theoretical maximum of 359,000 transfers). Each transfer consists of the most suitable arc ${\varvec{s}}_{lpo}$ flowing from the LPO and the arc ${\varvec{s}}_m$ flowing towards the selected lunar target state. If the positional distance between the arcs at plane ${\varvec{P}}$ is $>$1 km it is discarded. This analysis is performed with and without the effect of solar radiation pressure (assuming an area-to-mass ratio of 4). The plot in Fig. 18 shows the areas where improvement was able to be made using a solar sail. Empty areas on the plot represent cases where either no improvement was found, or no transfer was found with a position mismatch at plane ${\varvec{P}}$ smaller than 1 km. Note that the points (which size on the plot have been exaggerated for legibility) showing a maximal (100 m/s) improvement are those where a transfer without solar pressure could not be found for $<$100 m/s cost.

Fig. 18

Solution space mapping of the lunar target states leading to weak capture showing the $\Delta {v}$ improvement of using a sail as a function of lunar target state and the initial orbital phasing angle $\alpha _0$

The computation with solar radiation pressure is unfortunately more involved than without, as the initial orbital phasing angle $\alpha _0$ controls the initial direction of sunlight in the Earth–Moon system. Thus, to accurately account for the acceleration due to solar radiation pressure one must numerically integrate the arcs leading to the lunar arrival states for each particular value of the phasing angle $\alpha _0$, effectively multiplying computation time by the number of initial angles used. Using the simple control law in Eq. (28) it is already possible to achieve a less costly connection for some—but not all—of the lunar target states. From the 1,000 states in Fig. 18 44.3 % of them scored a better $\Delta v$ cost at the first crossing with plane ${\varvec{P}}$, and 56.3 % if further crossings are taken into account (all values of phasing angle are taken into account per target state). Additionally, the better connections occur at different values of the initial phasing angle $\alpha _0$. Although the phasing angle is effectively a selectable parameter in the CR3BP it has an important effect when a transfer is translated into a full dynamic model using actual ephemeris, where the phasing angle controls what dates a particular transfer can be flown. This means that the use of the reflective surface can improve the launch window of spacecraft by allowing for departure from the periodic orbit on more dates in a particular month.

Corresponding Poincaré sections (at the previously defined plane ${\varvec{P}}$) for a spacecraft with an area to mass ratio of 4 are shown in Fig. 19a for the $y-\dot{x}$ phase space and in Fig. 19b for the $y-\dot{y}$ phase space for the case of an initial orbital phasing $\alpha _0 =0$. The colouring from light blue to purple in both figures indicates further intersections at a prior date (as the numerical integration proceeds backwards in time). As can be seen, despite a fixed initial orbital phasing, use of a sail can decrease the cost to connect arcs by bringing intersection points closer to the unstable manifold flowing from the Sun–Earth libration point orbit on the phase space.

Fig. 19

Poincaré sections of (a) $\dot{x}-y$ and (b) $\dot{y}-y$ phase space at plane ${\varvec{P}}$ in the Sun–Earth CR3BP, showing the intersections from the unstable manifold from the $\hbox {L}_{1}$ LPO (black) and the successive intersections from the initial states at the Moon for a spacecraft with area to mass ratio 4

7 Conclusions

An algorithm has been presented that efficiently generates transfers from Sun–Earth libration point orbit to the Moon. These transfers can then serve as the basis for further optimization or as the starting point for a transfer in a full ephemeris model. It has been shown that by using the presented survival and event maps lunar impact or weak capture can be directly targeted at low cost in the planar problem. The computational intensive parts of the algorithm have to be computed once; the maps are not linked to the particular problem and thus can be stored for future use. Numerical propagation for the arcs from a particular LPO have to be performed only once and then stored. Due to these facts, the entire search space (across the range of orbital phasing) can be quickly scanned in order to locate where promising initial guesses to generate trajectories lie. Using a basic control law it has been shown that the use of solar radiation pressure can be used to improve transfer cost to achieve connection to particular regions of the survival maps. Future work will include the generation and study of survival maps with differing Jacobi constant (for instance matching the energy of the map and the LPO) and extending the maps to include a non-planar $(z)$ component.