The Atmospheric Boundary Layer Over Urban-Like Terrain: Influence of the Plan Density on Roughness Sublayer Dynamics

Abstract

We investigate the effect of the packing density of cubical roughness elements on the characteristics of both the roughness sublayer and the overlying turbulent boundary layer, in the context of atmospheric flow over urban areas. This is based on detailed wind-tunnel hot-wire measurements of the streamwise velocity component with three wall-roughness configurations and two freestream flow speeds. The packing densities are chosen so as to obtain the three near-wall flow regimes observed in urban canopy flows, namely isolated-wake, wake-interference and skimming-flow regimes. Investigation of the wall-normal profiles of the one-point statistics up to third order demonstrates the impossibility of finding a unique set of parameters enabling the collapse of all configurations, except for the mean streamwise velocity component. However, spectral analysis of the streamwise velocity component provides insightful information. Using the temporal frequency corresponding to the peak in the pre-multiplied energy spectrum as an indicator of the most energetic flow structures at each wall-normal location, it is shown that three main regions exist, in which different scaling applies. Finally, scale decomposition reveals that the flow in the roughness sublayer results from a large-scale intrinsic component of the boundary layer combined with canopy-induced dynamics. Their relative importance plays a key role in the energy distribution and influences the near-canopy flow regime and its dynamics, therefore suggesting complex interactions between the near-wall scales and those from the overlying boundary layer.

1 Introduction

Understanding and modelling the flow dynamics over urban terrain still represent a challenge due to the high geometrical complexity of built areas, the existence of numerous interacting thermodynamic processes that take place in the urban canopy, and the mutual influence of atmospheric processes. In particular, the wind field and turbulence play a crucial role in the instantaneous exchanges of quantities such as momentum, heat and particle mass. From a purely aerodynamic point of view, the atmospheric flow over the urban canopy can be considered as a high Reynolds number boundary-layer flow developing over a heterogeneous and multi-scale surface. This flow has therefore an important multi-scale character in both space and time with strong and complex inter-scale interactions. The resulting high complexity limits our ability both to understand the dynamics of urban flows and to model these flows. This is due to the prohibitive computational cost of performing obstacle resolving simulations at the district or city scale that would be necessary to take into account the whole range of dynamical phenomena.

1.1 Background Literature

Despite the above mentioned challenges, several recent studies have investigated the spatio-temporal organization and characteristics of boundary-layer flow over rough walls in general (see Jimenez 2004, for a review) and over urban-like terrain in particular. In the latter case the terrain morphology, which is characterized by its plan area density $\lambda _{{p}}$, frontal density $\lambda _{{f}}$ and mean building height h, is a key property that controls the aerodynamic characteristics of the lower atmospheric boundary layer (ABL), namely the friction velocity $u_*$, the zero-plane displacement or displacement height d and the aerodynamic roughness length $z_0$, which characterizes the absorption of flow momentum by the underlying rough wall. In their effort to provide a general parametrization of d and $z_0$ based on an extensive survey of the existing literature on both wind-tunnel and field measurements, Grimmond and Oke (1999) have shown that the terrain morphology strongly influences both the aerodynamic characteristics of the boundary layer and the flow regime of the lower part of the boundary layer, that is in the roughness sublayer (RSL). They distinguished three flow regimes in this lower portion of the flow: the isolated-wake flow, the wake-interference and the skimming-flow regime, corresponding to the lowest to the highest packing density, respectively. Although not mentioned at the time, such a classification implies that the roughness morphology has a direct impact on the flow dynamics in the RSL and its characteristic scales, whose crucial role in the exchange of momentum and scalar between the canopy and the lower atmosphere is now well recognized.

Decades of research on the turbulent boundary layer that develops over a flat smooth wall has brought general consensus across the scientific community regarding its organization (Marusic et al. 2010; Smits et al. 2011): the turbulent structures existing in such a flow are the well-known near-wall streaks and hairpin vortices, the latter assembling into vortex packets to form a third type of coherent structures, the large-scale motions (LSMs). The fourth type of structures has been identified as very large-scale motions (VLSMs) consisting of narrow low-momentum regions meandering in the horizontal plane and flanked by regions of high momentum (Hutchins and Marusic 2007). While smaller structures such as streaks and hairpin vortices scale in wall units, LSMs and VLSMs are found to scale with $\delta$, the thickness of the boundary layer. Despite the total destruction of the near-wall turbulent cycle by the roughness elements in flow over very rough surfaces similar to urban terrain, similar types of coherent structures have been shown to exist in direct numerical simulation (DNS) (Coceal et al. 2007; Lee et al. 2011, 2012; Ahn et al. 2013), large-eddy simulation (LES) (Kanda et al. 2004; Kanda 2006; Anderson et al. 2015), wind-tunnel experiments (Castro et al. 2006; Takimoto et al. 2013), and field experiments (Inagaki and Kanda 2008, 2010). In their DNS study of flow over a staggered array of cubes, Coceal et al. (2007) showed the presence of hairpin vortices in the flow above the canopy consisting of cubical roughness elements, organized along low-momentum regions and associated with sweeps and ejections of fluid. Using DNS to investigate the structure of a spatially-developing turbulent boundary layer over cubic or two-dimensional (2D) bars, Lee et al. (2011) revealed the impact of the 2D or three-dimensional (3D) character of the roughness elements on both the one-point statistics and the coherent structures in the near-wall and in the outer regions of the boundary layer. In particular, they demonstrated that the streaky structures in the near-wall and low-momentum regions, along with hairpin packets in the outer layer, are the dominant features, the characteristics of which are strongly dependent on the nature of the roughness elements. Near-wall low- and high-momentum regions were found to be of smaller longitudinal extent in the flow over the cubic canopy compared to the case containing 2D bars, which were themselves considerably smaller in longitudinal extent than were the structures observed in smooth-wall boundary layers. Conversely, in the outer region, low-momentum regions were found to be independent of the roughness geometry, and again, smaller than in the smooth-wall case. Finally, they showed that the model of hairpin vortex packets holds in flow over a rough wall, with hairpin vortices organized into inclined LSM structures whose length scaled with $\delta$. Lee et al. (2012) extended this study by varying the packing density, or spacing, of roughness elements, and showed that flow properties such as form drag and friction velocity were strongly dependent on the streamwise spacing in the case of 2D bars whereas the dependence was weaker for cubic roughness. Examining profiles of Reynolds stresses, they demonstrated the lack of outer-layer similarity of boundary layers developing over cubes or bars, attributing this to the particular geometric shape of the roughness elements when compared to the properties of the flow developing over irregular 3D roughness such as mesh or sandpaper, more widely investigated for engineering applications (Schultz and Flack 2007). Ahn et al. (2013) used DNS to investigate boundary-layer flow over an array of cubes with constant streamwise spacing but varying spanwise distance between the obstacles. They found that the form drag and friction velocity peaked for a spanwise spacing of 3h, with a similar behaviour found when considering the evolution of these parameters as a function of the roughness density $\lambda _{{p}}$.

Using numerical approaches, higher Reynolds number flows have been investigated via LES. Kanda et al. (2004) investigated the boundary-layer flow developing over an aligned (or square) array of cubes with plan area density $\lambda _{{p}}$ from zero to 44%, and confirmed the existence of the three flow regimes suggested by Grimmond and Oke (1999) and the presence of turbulent organized structures consisting of streamwise elongated regions of low momentum. Due to the specific array configuration, these structures were found to be aligned with streets or roof lines. Finally, they showed that the turbulent statistical properties were strongly influenced by the recirculation motions existing within the canopy. Recently, Kanda (2006) extended this study to the investigation of both square and staggered arrays of cubes using LES; the drag coefficient of the roughness array was found to be dependent on the density $\lambda _{{p}}$, the strongest dependence being for the staggered configuration with a maximum for $\lambda _{{p}} = 20\%$. The roughness-element arrangement had no influence on the presence of low-speed streaks that were found in all the flow configurations. He also confirmed that turbulent organized structures, namely low-speed regions and vortex packets, in flow over urban-like terrain, strongly resemble, at least qualitatively, those found in flows over a smooth surface. Anderson et al. (2015) confirmed the presence of hairpin vortices arranged in packets along low-momentum regions in their LES of the boundary layer developing over a staggered cube array with $\lambda _{{p}} = 25\%$. By investigating the temporal relationship between low- or high-momentum regions present in the inertial layer and cube-scale vortices existing in the RSL, they showed that an excess (deficit) of the streamwise velocity component in the inertial layer precedes the excitation (reduction) of RSL turbulence.

Urban-like canopy flows at high Reynolds numbers have also been achieved experimentally through wind-tunnel experiments, based on the use of thermal anemometry (or hot-wire anemometry, HWA), laser Doppler anemometry (LDA) or particle image velocimetry (PIV). One of the most extensive studies of the flow developing over canopies made of cubical elements was conducted by Cheng and Castro (2002), Castro et al. (2006) and Reynolds and Castro (2008). Using both HWA and LDA methods, Cheng and Castro (2002) investigated the flow developing over an array of cubes with $\lambda _{{p}} = 25\%$, either in aligned or staggered configurations. The 3D nature of the flow in the RSL was clearly evident, with the RSL itself found between 1.8h and 1.85h. Staggered arrays of cubic roughness elements were shown to produce more drag than for aligned arrays. The authors pointed out the necessity of independent measurements of the drag and d with which to identify the presence of a logarithmic region and thus to estimate $z_0$. Measurements performed with an array where the obstacle height was varied randomly while keeping $\lambda _{{p}}$ constant showed that the extent of the inertial layer was greatly affected, suggesting that the use of an array of obstacles of uniform height could not be representative of highly complex real urban configurations (such as city centres, for instance). Castro et al. (2006) extended this investigation to the analysis of the turbulence characteristics of the flow developing over a staggered array of cubes of uniform height (with $\lambda _{{p}} = 25\%$), focusing on energy spectra, two-point correlations, length and time scales and the turbulent kinetic energy budget. They showed that, in the RSL, the dominant scale of the turbulence is of the same order as the height of the obstacles but showed a two-scale behaviour close to the top of the roughness elements. They attributed this to the existence of separated shear layers forming around the cubes, containing vortices of typical size smaller than the obstacle height interacting with much larger scales. They also confirmed that the near-surface characteristics and dynamics of the eddy structures are significantly different from those in smooth-wall flows or in flows developing over 2D obstacles. These differences were further confirmed by Reynolds and Castro (2008), who investigated the same flow configuration using PIV techniques. Takimoto et al. (2013) also used the PIV technique to study boundary-layer flows developing over cubical or 2D roughness elements. Through an analysis of the integral scales in the streamwise and spanwise directions conducted at different heights, they showed that the large-scale structures were highly correlated with the boundary-layer thickness $\delta$ and the gradient of the mean streamwise velocity component along the wall-normal direction, in contrast to the smaller scales. Once scaled with the gradient of the streamwise velocity component, the characteristics of the turbulent coherent structures were found to be independent of the wall roughness.

Inagaki and Kanda (2010) used a horizontal array of aligned cubes with $\lambda _{{p}} = 25\%$ to investigate the characteristics of the coherent structures in the lower regions of the near-neutral ABL developing over a rough surface representative of an urban terrain. Using spatial filtering in the spanwise direction or in time, they separated the turbulence into active and inactive motions (where active motion refers to that responsible for wall-normal momentum transfer), and found that the characteristics of the active turbulence were similar to that educed from other flow and surface configurations. The active coherent structures were found to be consistent with very large streaks of low-momentum fluid elongated in the streamwise direction, containing smaller structures responsible for ejections of fluid, thereby contributing to the wall-normal momentum transfer.

1.2 Need for Representative Experiments at High Reynolds Numbers

Past investigations of the turbulent smooth-wall boundary layer have demonstrated the influence of the boundary-layer Reynolds number $\delta ^+=\delta u_*/\nu$ and the so-called low-Reynolds number effect. The recognition of this called for experiments and numerical simulations performed at higher Reynolds numbers (the highest having been obtained through field experiments over hydrodynamically smooth flat terrain, Hutchins et al. 2012). Recent experimental wind-tunnel studies of flow over urban-like rough walls have been performed at a Reynolds number $\delta ^+$$\sim$ 5000 to 7000 (Castro et al. 2006; Cheng and Castro 2002; Placidi and Ganapathisubramani 2015, 2017; Takimoto et al. 2013), which can be considered to be in the low-Reynolds number range for turbulent boundary layers (Smits et al. 2011). It is important to note that, not only must the obstacle height Reynolds number $h^+$ be high enough to ensure that the flow is in the fully rough regime, but so must $\delta ^+$ to account for the Reynolds number effect on the boundary-layer flow. This point is further discussed in the last section.

Furthermore, when modelling flows over urban terrain, one must also ensure that the ratio of the boundary-layer thickness $\delta$ and the building height h lies in a realistic range, which corresponds to rather low values when compared to those for flows over rough walls in engineering applications, as pointed out by Castro et al. (2006) and Jimenez (2004). In near-neutral atmospheric flow over urban canopies the typical ratio $\delta /h \approx$ 10–20, while the mean velocity profile can be described with the classical logarithmic law, viz

$$\begin{aligned} \overline{u}(z)=\frac{u_*}{\kappa } \ln \left( \frac{z-d}{z_0}\right) , \end{aligned}$$

(1)

where $\overline{u}(z)$ is the mean streamwise velocity component at height z and $\kappa = 0.4$ is the von Kármán constant. The ratio $z_0/h$ is typically $\approx \,0.1$ in flow over urban terrain (Grimmond and Oke 1999). Extending the validity of the logarithmic law up to $z=\delta$, one obtains a rough estimate of the ratio between the typical temporal scales $T_\delta =\delta /U_\delta$ and $T_h=h/u_*$ (where $U_\delta$ is the integral velocity scale related to the largest scales) associated with the large-scale structures existing in the boundary layer and the obstacle-wake structures generated in and near the canopy, respectively, as,

$$\begin{aligned} \frac{T_\delta }{T_h} = \frac{\delta }{U_\delta } \frac{u_*}{h} = \frac{\delta }{h} \left[ \frac{1}{\kappa } \ln \left( \frac{\delta }{h}\frac{h}{z_0}\right) \right] ^{-1}. \end{aligned}$$

(2)

With typical values of $\delta /h$ and $z_0/h$ given above, this ratio is found to be close to unity, noting here that this appears to be an intrinsic characteristic of atmospheric flows over urban canopies. When modelling this type of flow at smaller scales in the wind tunnel, correct scaling is assured by achieving similarity between model and full scale of, e.g., the ratio $\delta /h$ and the Jensen number $z_0/h$ (Savory et al. 2013). A lack of separation in the spectral domain between the most energetic scales from the boundary layer and those existing near the canopy can therefore be expected.

1.3 Objectives

Three configurations of urban-like terrain have been investigated, based on measurements of the instantaneous streamwise velocity component at several heights throughout the entire boundary layer via the HWA method. The three urban-canopy configurations consist of staggered arrays of cubes, with three values of $\lambda _{{p}} =$ 6.25, 25 and 44.4%, chosen to cover the isolated-wake, wake-interference and skimming-flow regimes, as identified by Grimmond and Oke (1999). The objectives are to build upon the previous studies performed in flows over urban-like canopies in the neutral regime in order to

• 1. Provide a detailed analysis of the characteristics of the streamwise velocity component in the ABL developing over large roughness obstacles in three distinct flow regimes;

• 2. Investigate the scaling of the most energetic structures depending on the considered flow region;

• 3. Analyse the influence of the change of RSL flow regime on the boundary-layer-canopy-scale interaction mechanism.

The experimental set-up and methodologies are detailed in Sect. 2, while Sect. 3 is devoted to the presentation of the results, including a detailed characterization of the streamwise velocity component and an investigation of the presence of scale interaction. Discussion and conclusions are presented in the Sect. 4.

2 Experimental Details

A description of the experimental apparatus and procedures together with a presentation of the global characteristics of the generated boundary layers are provided below. In the following, x, y and z denote the streamwise, spanwise and wall-normal directions, respectively (Fig. 1), and u, v, w the streamwise, spanwise and wall-normal velocity components, respectively. Using the Reynolds decomposition, an instantaneous quantity $\alpha (t)$ can be decomposed as $\alpha = \overline{\alpha } + \alpha '$ where $\overline{\alpha }$ denotes the ensemble average (equivalent to a time average) of $\alpha$ and $\alpha '$ is its fluctuating part. The standard deviation $\sqrt{\overline{\alpha '^2}}$ of $\alpha$ is denoted as $\sigma _\alpha$.

2.1 Introductory remarks

In order to fulfil our objectives and considering the remarks made in Sect. 1.2, special care is paid to the representativity of the results regarding the choice of the atmospheric urban configuration. Experiments were therefore performed at two high Reynolds numbers: Reynolds number $\delta ^+$ based on the boundary-layer thickness $\delta$ and the friction velocity $u_*$ of the order 27,000 and 41,000, while the Reynolds number $h^+$ based on the height of the obstacles h and $u_*$ is close to 1300 and 2100. The latter ensures that the near-surface flow is in the fully-rough regime from an hydrodynamical point of view and therefore free of any Reynolds number effect. The obtained ratio $\delta / h \approx \,20$ for all the configurations, a value in the typical range for the near-neutral ABL developing over urban or suburban terrain (Jimenez 2004), and ensuring the representativity of the results regarding the atmospheric urban configuration under investigation. Special attention is also devoted to the quality of the acquired database via the choice of an adequate measurement duration, the independent measurement of aerodynamic characteristics such as the form drag and the intercomparison of independent streamwise-velocity-component measurements. As detailed below, the statistical convergence criteria chosen resulted, for the lowest Reynolds number of 27,000, in a measurement duration of 1 h 20 min at each wall-normal location (1 h for $\delta ^+=41{,}000$). Finally, the vast majority of studies existing in the literature makes use of spatial averaging in the horizontal plan to account for the spatial heterogennity of the flow induced by the canopy in the RSL. Profiles of the flow characteristics along the wall-normal direction are measured at only one location relative to a cube ($x/h=1$ downstream of a roughness element) to capture the roughness-element statistical signature in the flow. This particular choice does not account for the spatial heterogeneities of the flow in the wall-parallel plane, but due to experimental constraints, it was not possible to cover several locations relative to an obstacle. Rather than sacrificing data quality, preliminary experiments are performed to identify the location in the RSL at which the canopy-flow signature would be clearly captured, allowing for the identification of the interaction mechanism at play. Recent studies (Blackman and Perret 2016; Blackman et al. 2018) showed that the imprint of the large scales always exists in the near-wall region, with some dependencies on the actual location within the RSL where the strength of this mechanism is estimated.

These conclusions are in agreement with Anderson (2016) obtained from LES of flow over an array of cubic obstacles. Therefore, if it is likely that varying the near-wall location leads to a change of the quantitative results presented here, the general conclusions and the qualitative trends remain valid.

Fig. 1

Wind-tunnel set-up (sketch not to scale). Close-up shows the two-probe arrangement used in the region $1.25< z/h < 5$

2.2 Wind-Tunnel and Canopy Configurations

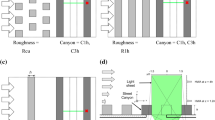
Experiments were conducted in the boundary-layer wind tunnel of the Laboratoire de recherche en Hydrodynamique, Energétique et Environnement Atmosphérique of Ecole Centrale de Nantes (LHEEA, Nantes, France), which has test-section dimensions of $24\,\hbox {m}\times 2\,\hbox {m}\times 2\,\hbox {m}$. A reproduction of the lower part of a suburban-type ABL developing over an idealized urban canopy model was achieved by using five vertical, tapered spires of height of 800 mm and width of 134 mm at their base, a 200 mm high solid fence across the working section located 0.75 m downstream of the inlet, followed by a 22 m fetch of staggered cubic roughness elements. The cube height was $h=50$ mm. Extensive details on this facility and set-up can be found in Rivet (2014), Blackman and Perret (2016) and Blackman et al. (2017). Three different rough walls of plan area density (i.e. the ratio between $A_{{p}}$ the area of the surface occupied by the roughness elements and that of the total surface $A_{{T}}$) of 6.25%, 25% and 44.4% were studied (Fig. 2). Experiments were systematically run at two nominal freestream flow speeds $U_{{e}}$ of 5.7 and 8.8 $\hbox {m s}^{-1}$, resulting in a total of six different flow configurations. The non-dimensional pressure gradient $K=({\nu }/{\rho U_{{e}}^3}){\hbox {d}P}/{\hbox {d}x}$ along the wind tunnel in the measurement cross-section was found to be $< -2.9\times 10^{-8}$ for all the configurations (Table 2), which indicates a negligible influence of the pressure gradient on the streamwise boundary-layer development (DeGraaff and Eaton 2000).

Fig. 2

Investigated canopy configurations with (left) $\lambda _{{p}} = 6.25\%$, (centre) $\lambda _{{p}} = 25\%$ and (right) $\lambda _{{p}} = 44.4$%. Red cross ($\times$): location of the hot-wire wall-normal profile kept constant relative to the upstream cube (1h downstream of the downstream edge)

2.3 Hot-Wire Measurements

The experiments were performed at a streamwise location of 19.5 m after the end of the contraction. They consisted in single hot-wire measurements performed along a wall-normal profile across the boundary layer. Accuracy of the HWA method was assessed by performing an a priori analysis in the case of $\lambda _{{p}} = 25\%$ using stereoscopic PIV combined with the use of the concept of effective cooling velocities (Perret and Rivet 2018). A good accuracy was observed on the streamwise velocity component using either a single or a cross hot-wire probe whereas the wall-normal component measured by the latter was biased by the non-measured component and therefore unreliable. The relative error on the variance of the streamwise velocity component resulting from the use of a single-wire probe has been estimated to be always smaller than 5% for $z/h > 1.25$. In order to investigate the structure of the lower part of the boundary layer and its link with the logarithmic region, a fixed hot-wire probe was set at $z_{{f}}/h=5$ and employed simultaneously with the moving probe so that two-point measurements were conducted in the lower part of the profiles ($1.25< z/h < 5$, i.e. the for lowest 13 locations of the wall-normal profiles). The location of the reference probe at $z_{{f}}/h=5$ has been chosen based on earlier studies performed in a $\lambda _{{p}}=25\%$ density cube array by Perret and Rivet (2013), Blackman and Perret (2016) and Basley et al. (2018) focusing on the analysis of the interaction between the canopy flow and the overlying boundary layer and the existence of a non-linear amplitude modulation mechanism, as found by Mathis et al. (2009) in smooth-wall boundary layers. These studies demonstrated that locating the reference point in the range $3h-5h$ enables the detection of the aforementioned mechanism, the reference point being above the RSL (the targeted flow) and well within the logarithmic layer (and still within the constant-flux region). This mild sensitivity regarding the choice of the reference-point wall-normal location is in agreement with Mathis et al. (2009).

Two Disa 55M01 electronics associated with Dantec 55P11 single hot-wire probes (Dantec Dynamics, Skovlunde, Denmark) with a wire length of 1.25 mm corresponding to $l^+=30{-}56$ wall units were used with an overheat ratio set to 1.8. While these wire length are in the upper range of advised length to avoid attenuation of the fluctuations of the streamwise velocity component and underestimation of the variance in the near-wall region of flat-plate boundary-layer flows (Hutchins et al. 2009), this possible bias is not present in the current case as the presence of large roughness elements in the near-wall region shifts the whole spectral content toward larger scales. Near the top of the $\lambda _{{p}} = 25\%$ canopy, the Kolmogorov scale and Taylor microscale have been estimated, in wall units, to be $\eta ^+ \approx \, 6$ and $\lambda ^+_{{T}} = 270$ (Blackman et al. 2017) and the most energetic scales are of the order of $\lambda ^+_{{ max}} = 1500$ (see Sect. 3.4). This ensures that, even if present, attenuation of the smaller scales remains marginal. At each wall-normal location in the profile, hot-wire signals were sampled at 10 kHz over a period of at least 24,000 $\delta / U_{{e}}$, and an eighth-order anti-aliasing linear phase elliptic low-pass filter was employed prior to signal digitization. A total of 39 logarithmically distributed wall-normal locations between 1.25h and $1.3\delta$ was investigated. Calibration of the hot-wire probes was performed at the beginning of each profiles by placing the probes in the free-stream flow. The calibration procedure was based on King’s law and accounts for temperature correction using the method proposed by Hultmark and Smits (2010). Static pressure, relative humidity and temperature in the wind tunnel were systematically recorded during the entire measurement period.

Conducting measurements with a fixed probe at $z/h=5$ for the 13 lowest wall-normal locations of the moving probe in each flow configuration allows for the estimation of accuracy of the measurements associated with the repeatability of the experiments at the fixed point. The relative error for the mean, variance, third- and fourth-order moments of the streamwise-velocity-component are reported in Table 1. Statistical error of convergence estimated as the standard deviation of these statistics at the same height ($z/h=5$) are also shown.

Table 1 Repeatability and statistical convergence error of hot-wire measurements estimated at $z/h=5$ as the standard deviation of the first four moments of the streamwise velocity component (%)

2.4 Wall-Pressure Measurements

As detailed in the next section, direct estimations of both the friction velocity and the displacement height were made using pressure measurements on a roughness obstacle (Cheng and Castro 2002). Distribution of the wall-pressure on the back and front faces of a cube obstacle was therefore measured for the six configurations. To this end, a cube face was equipped with 36 pressure ports to measure the pressure difference between the wall pressure on the cube and the static pressure in the freestream. The cube was rotated to access the pressure distribution on both faces successively. Two differential pressure transmitters Furness Control FCO 332 (Furness Controls Ltd., Bexhill-on-Sea, UK) with a range of $\pm \,50$ Pa were employed simultaneously to measure wall pressure on the cube, with a multi-channel scanner Furness Control FCS 421 (Furness Controls Ltd., Bexhill-on-Sea, UK) used to scan the pressure ports.

Table 2 Characteristics of the boundary layer

2.5 Boundary-Layer Characteristics

The main characteristics of the six boundary-layer configurations are shown in Table 2, and in the following the superscript $+$ denotes inner normalization based on the friction velocity $u_*$ and length scale $\nu /u_*$. In the case of a turbulent rough-wall boundary layer, the wall-normal profile of the mean streamwise velocity component in the logarithmic region reads

$$\begin{aligned} \overline{u}^+(z) = \frac{\overline{u}(z)}{u_*}= & {} \frac{1}{\kappa }\ln \left( \frac{z-d}{z_0} \right) ,\end{aligned}$$

(3)

$$\begin{aligned}= & {} \frac{1}{\kappa }\ln (z-d)^+ + B - \Delta U^+, \end{aligned}$$

(4)

where, $B=5$ is the smooth-wall intercept and $\Delta U^+$ is the streamwise-velocity-component deficit, the equivalent in the engineering community of $z_0^+$, these two being related by

$$\begin{aligned} \frac{1}{\kappa }\ln z_0^+ = - B +\Delta U^+. \end{aligned}$$

(5)

Combining the above with the relationship between $\Delta U$ and the sand-grain roughness $k_{{s}}$,

$$\begin{aligned} \Delta U^+ = \kappa ^{-1} \ln k_{{s}}^+ + B - C, \end{aligned}$$

(6)

where C is the roughness function intercept for uniform sand-grain roughness equal to 8.5, where it is straightforward to show that $k_{{s}} = z_0 \exp (C\kappa )$. Besides the friction velocity, d and $z_0$ are therefore key parameters that describe the influence of the rough wall on boundary-layer flow from an aerodynamic point of view.

As proposed by Jackson (1981), the zero-plane displacement is interpreted as the height at which the drag on the roughness elements is exerted. In the case of large roughness elements, the contribution of the viscous force to the drag is negligible with the form drag D being the major contributor (Cheng and Castro 2002). The zero-plane displacement can therefore be estimated directly from the calculation of the moment of the pressure forces on a roughness element about its base:

$$\begin{aligned} d\cdot D_{{p}} = \int _{A_{{f}}}z(P_{{f}}-P_{{b}}) \hbox {d}S, \end{aligned}$$

(7)

where $A_{{f}}$ is the frontal area of the cube, $P_{{f}}$ and $P_{{b}}$ are the local pressures on the front and back of the cube, respectively, and $D_{{p}}$ is the pressure drag calculated as

$$\begin{aligned} D_{{p}} = \int _{A_{{f}}}(P_{{f}}-P_{{b}}) \hbox {d}S. \end{aligned}$$

(8)

Being the velocity scale formed from the wall stress, the friction velocity can also be estimated from the form drag as

$$\begin{aligned} u_* = \sqrt{\frac{1}{\rho }\frac{D_{{p}}}{A_{{T}}}}. \end{aligned}$$

(9)

An alternative approach is to perform a fitting procedure of the wall-normal profile of the streamwise velocity component in the logarithmic region with Eq. 4 and estimate both $u_*$ and $z_0$ (Cheng and Castro 2002). In the present case, d and $u_*$ were estimated from the pressure measurements and $z_0$ from the fit of the wall-normal profile of the streamwise velocity component in the logarithmic region (Table 2). The average relative error over the complete set of experiments is estimated as 1% and 3% for $u_*$ and d, respectively. The boundary-layer thickness $\delta$, defined as the height where the mean streamwise velocity component is equal to 99% of the freestream velocity $U_{{e}}$, and the upper limit of the RSL $z_\text {RSL}$, are also shown in Table 2. For details regarding the estimation of $z_\text {RSL}$, see Sect. 3.3.

Fig. 3

Values of d / h and $z_0/h$ as a function of $\lambda _{{p}}$ of (coloured symbols, as in Table 2) the present configurations and (solid and open black circles) from the compilation of wind-tunnel studies performed by Grimmond and Oke (1999). Models for d / h and $z_0/h$ proposed by MacDonald et al. (1998) are shown in black solid lines. Dashed lines defining the plan-area-density range of real cities and the corresponding flow regimes are taken from Grimmond and Oke (1999). Note that both Reynolds numbers are shown for each $\lambda _{{p}}$ but barely distinguishable due to Reynolds number independence of d and $z_0$ (Table 2)

3 Results

3.1 Data Validation: Aerodynamics Parameters and Diagnostic Plot

Aerodynamics parameters d and $z_0$ estimated from the drag measurement and the wall-normal profile of the mean streamwise velocity component (discussed latter in Fig. 5a) are compared in Fig. 3 to both the models derived by MacDonald et al. (1998) and the data compiled by Grimmond and Oke (1999). The three chosen configurations are representative of the three different near-wall flow regimes identified in the literature (6.25%: isolated-wake flow, 25%: wake-interference flow, 44.4%: skimming flow). One therefore can expect differences in flow dynamics in the near-wall region when the roughness morphology is varied. It should be noted that only wind-tunnel data from the review of Grimmond and Oke (1999) are considered here and that they include configurations with different plan or frontal area densities, $\lambda _{{p}}$ and $\lambda _{{f}}$, respectively. The use of cubic obstacles implies that both parameters are equal. The wide spread of the data reflects the difficulty in both obtaining accurate aerodynamic parameters and deriving relationships between them and simple morphologic parameters such as $\lambda _{{p}}$. In the present case, when scaled with inner variables, the roughness length shows a lowest value of $z_0^+=47$ while $h^+>1170$, therefore ensuring that the flow configurations are all in the fully rough regime (Snyder and Castro 2002).

Recently, Alfredsson and Örlü (2010) have suggested to use the so-called diagnostic plot, an alternative way to plot the data of the mean and the standard deviation of the streamwise velocity component in wall-bounded flows, in order to assess the quality of the data. The strength of this representation, that consists in plotting $\sigma _u/\overline{u}$ as a function of $\overline{u}/U_{{e}}$, is that it does not rely on the use of parameters sometimes difficult to estimate such $u_*$, d, $z_0$ or the distance to the wall. They showed that in smooth-wall flows, $\sigma _u/\overline{u}$ and $\overline{u}/U_{{e}}$ are linearly related in the outer layer. Castro et al. (2013) extended these findings to rough-wall configurations for which a similar linear relationship was found between the turbulence intensity and the mean streamwise velocity component but with a different slope. These authors attributed the lack of agreement of certain datasets, with one or the other slope, to their transitionally rough character. Therefore, they introduced a modified form of the scaling using the mean streamwise-velocity-component deficit (or roughness parameter) $\Delta U^+$ normalized by $U_{{e}}$ that enables all the data, from smooth or rough walls, to be fitted empirically. There is still no clear physical foundation for the linear relationship between the streamwise turbulence intensity and the mean streamwise velocity component (Castro et al. 2015), but this peculiar behaviour is tied to the structure of the flow in the outer-layer region (Castro et al. 2015; Ebner et al. 2016). Therefore, the agreement with the diagnostic plot must be viewed rather as a necessary condition than a sufficient one to validate the characteristics of the flow. The original diagnostic plot, shown in Fig. 4a, depicts a good collapse of the six configurations onto the fitted linear relationship from Castro et al. (2013). The modified diagnostic plot, shown in Fig. 4b, leads to a good agreement of the present data with the smooth-wall asymptote in the outer layer, as demonstrated by Castro et al. (2013). It confirms that the investigated flows are in the fully rough regime and that they exhibit outer-layer similarity. Therefore, despite the wide range of planar density $\lambda _{{p}}$ investigated, the outer flow becomes insensitive to the roughness configuration. The different conclusions drawn by Placidi and Ganapathisubramani (2017) suggest a possible influence of the Reynolds number $\delta ^+$, the study of which is briefly discussed in Sect. 4.

Fig. 4

Diagnostic plot a as proposed originally by Alfredsson and Örlü (2010) and b modified by Castro et al. (2013) to include the roughness effect via the use of the mean streamwise-velocity-component deficit $\Delta U$. Symbols as in Table 2. The dashed and solid black lines show the asymptotes for the smooth and rough wall configurations, respectively, as in Castro et al. (2013)

Fig. 5

Wall-normal profile of the normalized mean streamwise velocity component $\overline{u}(z) / u_*$ as a function of a$(z-d)/z_0$ and b$(z-d)^+$. Symbols as in Table 2; black solid lines: logarithmic law a from Eq. 4 and b for smooth-wall boundary layers

3.2 Mean Flow

Figure 5a shows the wall-normal profile of the mean streamwise velocity component plotted using d and $z_0$ as scaling parameters. For all the configurations, a large portion of the profiles follows the logarithmic law. With this representation, no Reynolds number effect is visible. When scaling the wall-normal coordinate z with inner scales (Fig. 5b), the wall-normal profile of the mean streamwise velocity component still exhibits a well-defined logarithmic region but also clearly shows the influence of the roughness density. The roughness is responsible for a downward shift of the logarithmic-law region, and the higher $z_0$, the higher the velocity deficit $\Delta U^+$ (defined here as the difference between the smooth-wall logarithmic law and mean streamwise-velocity-component wall profile in the logarithmic region), implying the breakdown of the classical representation in inner scales if the velocity deficit is not accounted for (i.e. the lack of universality of the wall-normal profile of the mean streamwise velocity component when Reynolds number and wall geometry are varied).

Fig. 6

Wall-normal evolution of the a–d normalized variance and e–h skewness profiles of the streamwise velocity component; a, e in outer variables, b, f inner variables, c, g normalized using $z_0$ and d, h using the obstacle height h as the reference length scale. Symbols as in Table 2. The solid black line in a shows the logarithmic law for the variance with a slope $A_1=1.26$ (Eq. 10) while the dashed black lines show a range $\sigma _u^2/u_*^2 \pm 0.2$ as in Squire et al. (2016)

3.3 Variance and Skewness Profiles of the Streamwise Velocity Component

In this section, different scalings are tested to account for the influence of both Reynolds numbers and canopy configurations on the variance and skewness profiles of u, as shown in Fig. 6.

As found by Flack et al. (2007) in their study of various rough walls at lower Reynolds numbers, a good collapse of the wall-normal profiles is obtained in the outer region when outer variables are used, i.e. for $(z-d)/\delta >0.1$ (Fig. 6a, e). The inner variables do not provide a good scaling, even close to the roughness elements (Fig. 6b, f). In the outer layer, this scaling fails at collapsing the different Reynolds numbers while a good match is observed between the canopy configurations, which was to be expected as the flow far from the wall becomes insensitive to the influence of wall boundary conditions. Using $z_0$ and d as a length scale for the wall-normal location (Fig. 6c, g) also fails at collapsing the variance and skewness wall-normal profiles. It should be noted however that the skewness profiles of $\lambda _{{p}} = 6.25\%$ and $\lambda _{{p}} = 44.4\%$ collapse very well for a limited range of height, i.e. $15< (z-d)/z_0 < 35$. Finally, using h as a scaling parameter, and not taking into account the zero-plane displacement d, leads to a good agreement in the outer region, consistently with the very close ratio $\delta /h$ shown by the six configurations. However, it fails at collapsing the profiles close to the canopy top (Fig. 6d, h). Overall, no set of scaling variables has been found to satisfactorily collapse the wall-normal profile of the variance and skewness to account for both Reynolds numbers and canopy geometry in the vicinity of the canopy.

Despite this lack of scaling variable, the good agreement between the wall-normal profiles and the logarithmic law for the variance of the streamwise velocity component proposed by Marusic et al. (2013), namely

$$\begin{aligned} \frac{\sigma _u^2}{u_*^2} = B_1 - A_1\ln \left( \frac{z-d}{\delta }\right) , \end{aligned}$$

(10)

(where $B_1$ is a constant that depends on the flow geometry and wake parameter and $A_1=1.26$ is the slope constant proposed by Marusic et al. 2013) is remarkable (Fig. 6a). This logarithmic wall-normal evolution of the variance of the streamwise velocity component, combined with that of the mean streamwise velocity component (Eq. 4) has been originally shown by Townsend (1976) to be a consequence of the presence of self-similar wall-attached eddies in the inertial layer located above the RSL. The good collapse of the results with this theoretical prediction has several consequences. It first confirms the well-developed high-Reynolds number character of the investigated flows, with no visible influence of the spires on the variance wall-normal evolution. Secondly, it shows that the structure of the flow can be expected to match that of conventionally developing flows. Thirdly, the departure from this logarithmic law in the region close to the canopy top can serve as an estimate for the bottom limit of the inertial layer, or equivalently for the upper limit of the RSL $z_\text {RSL}$. Squire et al. (2016) recently demonstrated experimentally the good agreement between the location of the above mentioned departure and the wall-normal location of the onset of inertial dynamics predicted by Mehdi et al. (2013) based on their analysis of the scaling of the mean force structure in rough-wall boundary layers. To account for the possible scatter of experimental data and the error in estimating $B_1$ , a range of validity of $\sigma _u^2/u_*^2 \pm \,0.2$ is employed here as in Squire et al. (2016) (an example is provided in Fig. 6a for $\lambda _{{p}} = 44\%$). The estimated values of $z_\text {RSL}$ show the expected increase of the RSL depth with decreasing $\lambda _{{p}}$ (Table 2). It should be noted here that they are larger than those of 1.8h and 1.85h reported by Cheng and Castro (2002) who defined $z_\text {RSL}$ as the location above which the one-point statistics of the flow showed negligible variation in the horizontal plane. Lastly, analyzing both Fig. 6a, e shows that the wall-normal location of the zero crossing of the skewness of the streamwise velocity component matches quite well the estimated value of $z_\text {RSL}$, indicating that the change of sign of the skewness might mark the wall-normal location above which the inertial layer starts. This last point remains to be thoroughly analyzed and therefore requires further investigation.

3.4 Energy Spectrum of the Streamwise Velocity Component

In order to study the relevant scales of the most energetic structures, evolution with distance to the wall of the pre-multiplied energy spectra of the streamwise velocity component is presented in Fig. 7. In the outer region, the most energetic scales asymptotically tend to the same normalized frequency, for the three canopy configurations and both Reynolds numbers. It is observed that the region of energetically dominating large scales extends further to the wall with increasing canopy density. Below that region, an increase of the frequency of the most energetic scales is observed, and a good collapse is achieved when temporal frequencies are scaled using h and $u_*$ (not shown). One can also note the difference in shape of the energy spectra at higher frequency close to the canopy top, $(z-d)/\delta < 0.06h$, suggesting a change in flow dynamics in the near-wall region. The evolution of the frequency $f_{{ max}}$ corresponding to the maximum in the pre-multiplied energy spectrum is analysed in more detail below, in terms of the relevant scaling variables for both the wall-normal location and the frequency $f_{{ max}}$.

Fig. 7

Wall-normal evolution (in outer variables) of the pre-multiplied energy spectrum of the streamwise velocity component normalized by $u_*^2$ for a, b$\lambda _{{p}} = 6.25\%$, c, d$\lambda _{{p}} = 25\%$ and e, f$\lambda _{{p}} = 44.4\%$ for both (left-hand side column) the lowest and (right-hand side column) the highest Reynolds numbers. The temporal frequency f is normalized by the boundary-layer thickness $\delta$ and the local mean streamwise velocity component $\overline{u}(z)$ as $f \delta / \overline{u}(z)$. Symbols (as in Table 2) show the location of the maximum of the pre-multiplied energy spectrum at each wall-normal position

Fig. 8

Wall-normal evolution of the frequency $f_{{ max}}$ corresponding to the maximum of the pre-multiplied energy spectra of the streamwise velocity component as shown in Fig. 7, using different length and velocity scales. Symbols as in Table 2. The solid green line in a, c corresponds to a value of $f_{{ max}}\delta /\overline{u}(z)=0.3$, the orange dash-dotted line in b to $f_{{ max}}(z-d)/u_*=0.28$, the grey dashed line in a, c to $f_{{ max}}(z-d)/\overline{u}(z)=1/22$. The vertical solid lines indicate the normalized wall-normal location $z=h$ for each canopy density, the width of the lines accounts for the Reynolds number dependence of the normalized quantity

An attempt at finding the relevant length and velocity scales corresponding to the frequency of the maximum observed in the energy spectra in Fig. 7 is presented in Fig. 8. Different regions of the flow are considered. In the outer region of the boundary layer $(z-d)/\delta > 0.2$, scaling is achieved with outer variables $\delta$ and the local mean streamwise velocity component $\overline{u}(z)$ (Fig. 8a), showing that in the logarithmic and the outer regions, the most energetic scales have a non-dimensional frequency $f_{{ max}} \delta / \overline{u}(z) = 0.3$ (solid green line in Fig. 8a and c). This corresponds to a streamwise wavelength $\lambda _x=\overline{u}(z)/f~\approx ~3.3\delta$, characteristic of LSMs often reported in the literature (Hutchins and Marusic 2007; Inagaki and Kanda 2010; Dennis and Nickels 2011). This confirms the existence of large-scale structures whose streamwise extent scales with $\delta$ and who occupy most of the upper part of the boundary layer. The shape of the energy spectra of the streamwise velocity component in the surface layer of the ABL over flat uniform terrain has been extensively studied (Kaimal and Finnigan 1994). Depending on the stability regime of the atmosphere, expressions have been derived to model the pre-multiplied energy spectrum $f S_u(f)$ as a function of the non-dimensional frequency $n = f (z-d)/\overline{u}(z)$. The scaling of $f S_u(f)/u_*^2$ when plotted against n found by Kaimal and Finnigan (1994) implies that in the surface layer, the energy spectrum and the most energetic structures scale with the wall-normal distance. The most commonly used scaling for describing the energy spectra of the streamwise velocity component in a neutrally-stable boundary layer reads as (Kaimal and Finnigan 1994)

$$\begin{aligned} f S_u(f)/u_*^2 = 102 n (1+33n)^{-5/3} \end{aligned}$$

(11)

and it can be shown that the modelled energy spectrum reaches its maximum for $n=1/22$. This asymptotic value is represented by the grey dashed line in Fig. 8a and c. It can be seen (Fig. 8) that the agreement with the surface-layer value $f(z-d)/\overline{u}(z)=1/22$ is good for a limited range of heights centred around $(z-d)/\delta = 0.1$, for the canopies with $\lambda _{{p}}=$ 6.25% and 25%. In the near-wall region (Fig. 8b), the best collapse is achieved using $u_*$ and $(z-d)$ as velocity and length scales to normalize $f_{{ max}}$ and the obstacle height h for the wall-distance $(z-d)$. A good agreement between the configurations with $\lambda _{{p}} =$ 6.25% and 25% is obtained, resulting in a constant normalized frequency $f_{{ max}} (z-d)/u_* = 0.28$ in the region where $(z-d)/h < 1$ (orange dash-dotted line in Fig. 8b). This value has been estimated empirically from the present data and the link with relevant flow parameters is still to be made. A collapse for the configuration $\lambda _{{p}} =$ 44.4% is only achieved for the lowest three points, the evolution of $f_{{ max}}$ for this case being notably different, therefore suggesting a thinner RSL and flow dynamics drastically different from the two other configurations. This last finding gives evidence of a change in the flow regime, previously observed in the analysis of the mean flow (Fig. 5b), and qualitatively reported by Grimmond and Oke (1999). These three different scalings, corresponding to three distinct regions, are shown in Fig. 8c in which the line $f(z-d)/\overline{u}(z)=1/22$ is now horizontal (grey dashed line) and scaling $f_{{ max}}$ with $(z-d)$ and $\overline{u}(z)$ transforms the unique asymptote $f_{{ max}}(z-d)/u_*=0.28$ in the near-wall region in three different curves because of the dependence of $u_*$ with $\lambda _{{p}}$. The three distinct regions, namely the near-canopy top, an intermediate region and the outer region are clearly visible. It is worth noting here that the departure from the outer region asymptote with decreasing height corresponds to the point where the skewness of u switches from negative to positive values (Fig. 6e). Regarding the configuration with $\lambda _{{p}}=44.4\%$, this departure happens considerably lower than for the other two with a collapse onto the asymptote $f_{{ max}}(z-d)/u_*=0.28$ (purple dash–dotted line) of only the three lowest points in the near-canopy top region.

3.5 Spectral Correlation and Scale Decomposition

The above analysis evidences the existence of different regions in the flow, whose relevant scales and wall-normal extent depend on the planar density $\lambda _{{p}}$. In particular, the configuration with the highest density $\lambda _{{p}} = 44.4\%$ shows significant departure from the two others for height below $(z-d)/h \approx 2$. The results in Fig. 8 suggest that the most energetic structures in the boundary layer (scaling with $\delta$ and $\overline{u}(z)$) reach deeper into the RSL, masking those generated by the canopy (scaling with $(z-d)$ and $u_*$). To further investigate this point, two-point measurements are employed to separate the contribution of the boundary layer from that of the RSL, and a different scaling strategy is tested, the present data being based on temporal (pointwise) hot-wire measurements. As detailed below, instead of using velocity scales similar to that used in Taylor’s hypothesis, velocity scales directly linked to the most energetic streamwise-velocity-component fluctuations in the flow and based on the standard deviation of the streamwise velocity component $\sigma _u$ are preferred. The decomposition method is first presented, followed by the results using the alternative scaling.

The two-point measurements conducted in the lower part of the flow with a fixed probe at $z_{{f}}/h=5$ and a moving probe at $1.25< z_m/h < 5$ are first employed to estimate the degree of correlation between the inertial layer and the near-canopy region via the computation of the spectral coherence between the two points. The spectral coherence between $z_{{f}}$ and $z_m$ is defined as (Bendat and Piersol 2000)

$$\begin{aligned} \gamma ^2(f) = \frac{\left| \overline{U(f,z_{{f}})\hat{U}(f,z_m)}\right| ^2}{\overline{|U(f,z_{{f}})|^2} ~\overline{|U(f,z_m)|^2}} \end{aligned}$$

(12)

where U(f) is the Fourier transform of the fluctuating streamwise velocity component $u'(t)$, $\hat{U}(f)$ the complex conjugate of U(f) and |U(f)| its modulus. The spectral coherence $\gamma ^2(f)$ thus represents the correlation between the streamwise velocity components at the two locations for a particular frequency f. It lies between 0 (zero correlation) and 1 (perfect correlation).

Fig. 9

Spectral coherence $\gamma ^2(f)$ between the fixed probe at $z/h=5$ and the moving probe $1.25< z/h < 4.0$ for a$\lambda _{{p}} = 6.25\%$, b$\lambda _{{p}} = 25\%$ and c$\lambda _{{p}} = 44.4\%$, for both (solid line) lowest and (dashed line) highest Reynolds numbers. Lines are coloured using the height $(z-d)/\delta$ of the moving probe. Values of the wall-normal location of the fixed probe $(z_{{f}}-d)/\delta$ are provided in each plot based on parameter values obtained for the lowest Reynolds number

Results obtained for the six configurations are shown in Fig. 9. For all the configurations, the highest levels of correlation (which lie between 0.3 and 0.9 depending on $z_m$) are obtained for the lowest frequencies and the level of coherence decreases with increasing distance between the fixed and the moving point. When normalizing the frequency with $\delta$ and $\overline{u}(z_{{f}})$ (Fig. 9a–c) and taking into account the energy spectra in Fig. 7, high correlation levels are obtained for frequencies below the most energetic frequency of the streamwise velocity component existing at the fixed point $z_{{f}}/h=5$, i.e. $f\delta /\overline{u}(z_{{f}})<0.3$. When the wall-normal separation $z_{{f}}-z_m$ increases (i.e. when one considers a point closer to the canopy), the level of coherence at high frequency decreases, meaning that only the largest structures at $z_{{f}}/h=5$ reach that deep and maintain a significant imprint onto the near-canopy flow. This behaviour is consistently found for the three investigated densities $\lambda _{{p}}$. The only significant effect of $\lambda _{{p}}$ on the velocity coherence is a variation of the maximum level of coherence existing between the fixed point and the point closest to the canopy, the highest ($\gamma ^2=0.45$) being for $\lambda _{{p}} = 44.4\%$ while the lowest ($\gamma ^2=0.3$) is obtained for $\lambda _{{p}} = 25\%$. This suggests that at the particular location relative to a cube where the measurements were performed, the influence of the flow induced by the canopy elements is stronger for the case $\lambda _{{p}} = 25\%$ than for $\lambda _{{p}} = 44.4\%$, therefore slightly decreasing the relative importance of the boundary-layer imprint. This is consistent with the different known flow regimes.

Fig. 10

Modulus |H(f)| and phase $\arg (H(f))$ of the raw transfer function H(f) defined in Eq. 14 for (red) $\lambda _{{p}}=6.25\%$, (blue) $\lambda _{{p}}=25\%$ and (purple) $\lambda _{{p}}=44.4\%$. Only results for the lowest Reynolds number are shown, for the nearest location to the canopy top $z_m/h = 1.25$

Following Baars et al. (2016), the fact that a non-negligible coherence (or correlation) exists between the streamwise velocity component at two different heights at certain frequencies, serves here as the basis for the scale decomposition of the streamwise-velocity-component signal measured at $z_m$ in $u'(t,z_m)=\overline{u}(z_m)+u'_{{ LS}}(t,z_m)+u'_{{ SS}}(t,z_m)$, where $u'_{{ LS}}(z_m)$ is the fraction of $u'(z_m)$ correlated with $u'(z_{{f}})$ and $u_{{ SS}}(z_m)$ is the part uncorrelated with $u'(z_{{f}})$ (the dependence on time has been omitted for simplicity). As the correlation between $u'(z_m)$ and $u'(z_{{f}})$ is due to the largest scales (i.e. the lowest frequencies), the correlated part of $u'(z_m)$ with $u'(z_{{f}})$ is denoted $u'_{{ LS}}(z_m)$ and is referred to as its large-scale component, the remaining $u'_{{ SS}}(z_m)$ being the small-scale contribution. It must be noted here that the correlation $\overline{u'_{{ LS}}(z_m) u'_{{ SS}}(z_m)}$ is zero. The signal decomposition approach derived by Baars et al. (2016) is the spectral version of the multi-time delay linear stochastic estimation method employed by Blackman and Perret (2016). It is based on the use of the cross-spectrum between $u'(z_{{f}})$ and $u'(z_m)$ (as is the coherence $\gamma ^2(f)$ in Eq. 12) in order to derive a spectral transfer function that enables the extraction of $u'_{{ LS}}(z_m)$ from $u'(z_m)$. Only the basic principles of the spectral method are recalled here, the reader being referred for more details to the work of Baars et al. (2016) or that of Blackman and Perret (2016) for its time-domain version. Searching for the fraction of $u'(z_m)$ that is the most correlated with $u'(z_{{f}})$ is equivalent in the spectral domain to applying a transfer function onto $U(f,z_{{f}})$ (Baars et al. 2016)

$$\begin{aligned} U_{{ LS}}(f,z_m)= H(f)U(f,z_{{f}}) \end{aligned}$$

(13)

where H(f) accounts for the correlation level between $u'(z_m)$ and $u'(z_{{f}})$ at each frequency. It is calculated by multiplying both sides of the above equation by $\hat{U}(f,z_{{f}})$, taking the output of the filter $U_{{ LS}}(f,z_m)$ as the original signal $U(f,z_m)$ and ensemble averaging. It is therefore defined as

$$\begin{aligned} H(f) = \frac{\overline{U(f,z_m)\hat{U}(f,z_{{f}})}}{\overline{U(f,z_{{f}}) \hat{U}(f,z_{{f}})}} . \end{aligned}$$

(14)

It follows that the complex valued transfer function H(f) is the ratio between the cross-spectrum of $u'(z_m)$ and $u'(z_{{f}})$ and the auto-spectrum of $u'(z_{{f}})$. Its modulus |H(f)| is directly linked to the square root of coherence $\gamma ^2(f)$ (Baars et al. 2016). Examples of the modulus and the phase of H(f) calculated for $z_m/h=1.25$ (the nearest location to the canopy top) are presented in Fig. 10. The fact that only the largest scales are correlated between the two points $z_{{f}}$ and $z_m$ results in a low-pass filter effect clearly visible in |H(f)| while the non-zero phase of H(f) is directly linked to the forward inclined feature of the largest scales associated with the streamwise velocity component. Given the evolution of the coherence as a function of frequency, no correlation exists between the two signals beyond a certain frequency threshold $f_{{ th}}$. However, because of the presence of measurement noise, error in statistical convergence and the fact that ratios of very small values can be involved in the computation of H(f), non-physical but non-negligible levels of |H(f)| can be obtained at frequencies larger than $f_{{ th}}$. To avoid any contamination of the estimated signal $u'_{{ LS}}(z_m)$ from this non-physical part of H(f), the transfer function is set to zero at frequencies above $f_{{ th}}$. Following Baars et al. (2016), the frequency threshold $f_{{ th}}$ is defined as the frequency at which the coherence $\gamma ^2(f)$ falls below 0.05 and |H(f)| is smoothed in the range $0<f<f_{{ th}}$ to further limit the effect of noise. Once obtained from Eq. 14, H(f) is applied to $u'(z_{{f}})$ in the spectral domain via Eq. 13. The inverse Fourier transform of $U_{{ LS}}(f,z_m)$ gives access to $u'_{{ LS}}(z_m)$ in the time domain and its counterpart $u'_{{ SS}}(z_m)$ is calculated as $u'_{{ SS}}(z_m)= u^{\prime }(z_m)-u'_{{ LS}}(z_m)$.

Fig. 11

Pre-multiplied energy spectra of (grey) $u(z_{{f}}/h=5)$ at the fixed point, (black) the original streamwise velocity component $u(z_m/h=1.25)$ measured by the moving probe at the lowest location, (green) its fraction $u'_{{ LS}}(z_m)$ correlated with $u'(z_{{f}})$ and (orange) the complement $u'_{{ SS}}(z_m)$ uncorrelated with $u'(z_{{f}})$, for a$\lambda _{{p}}=6.25\%$, b$\lambda _{{p}}=25\%$ and c$\lambda _{{p}}=44.4\%$. Superimposed are presented the raw energy spectra and their smoothed versions used to detect the peak frequencies $f_{{ max}}$, $f_{{ max}}^{{ LS}}$ and $f_{{ max}}^{{ SS}}$. Only results for the lowest Reynolds number are shown for brevity. Evolution with $z_m$ of the spectra of (green) $u_m^{{ LS}}(z_m)$ and (orange) $u_m^{{ SS}}(z_m)$ is shown in d for $\lambda _{{p}}=44.4\%$ only (green and orange arrows show increasing height $z_m$ of the moving probe, darker colours corresponds to higher locations)

Results of the velocity decomposition on the pre-multiplied energy spectra of the streamwise velocity component are shown in Fig. 11 in which $z_m/h=1.25$ (the lowest wall-normal location investigated) and $z_{{f}}/h=5$. For the three canopy configurations, the low-pass filtering effect of H(f) is noticeable as well as the fact that the energy spectra of the small-scale $u'_{{ SS}}(z_m)$ (orange lines) and the large-scale $u'_{{ LS}}(z_m)$ (green lines) signals add up to give the energy spectra of the original signal $u'(z_m)$ (black lines), the uncorrelated part $u'_{{ SS}}(z_m)$ contributing the most to the total energy. The superimposition of the large scales measured at $z/h=5$ onto the flow close to the canopy top affects primarily the lowest frequencies and could go almost unnoticed for the lowest densities $\lambda _{{p}} = 6.25$ and 25% (Fig. 11a, b). However, in the case of $\lambda _{{p}} = 44.4\%$, the large-scale contribution has a clear impact on the spectral energy distribution. Due to the lower level of energy of the near-canopy flow relative to that of the flow at $z/h=5$, which can be attributed to the greater confinement of roughness-induced flow, the influence of $u'_{{ LS}}(z_m)$ results in a flattening of the pre-multiplied energy spectrum $f\cdot S_{uu}(z_m)$ while its global shape remains unchanged for $\lambda _{{p}} = 6.25$ and 25%. This is confirmed by the close inspection of all energy spectra obtained at different heights in the RSL shown here only for $\lambda _{{p}} = 44.4\%$ in Fig. 11d.

Fig. 12

Wall-normal evolution of a the scale-decomposed variances (lines) $(\sigma _{u}^{{ LS}})^2$ and (symbols) $(\sigma _{u}^{{ SS}})^2$ normalised by $u_*^2$ (dashed lines show results for the lowest Reynolds numbers) and b their ratio $\left( \sigma _{u}^{{ SS}}/\sigma _{u}^{{ LS}}\right) ^2$. The vertical solid lines indicate the normalized wall-normal location $z=h$ for each canopy density, the width of the lines accounts for the Reynolds number dependence of the normalized quantity. Symbols and colours as in Table 2

The global effect of the above scale-decomposition of the streamwise velocity component is shown in Fig. 12. The main differences observed in the variance profiles in Fig. 6 are in fact due to $u^\prime _{{ SS}}$ (symbols in Fig. 12a). Strikingly, the component $u^\prime _{{ LS}}$ correlated with the inertial layer is also affected by the change of roughness configuration, the densest canopy showing the highest variance. A plausible explanation is that, the canopy influence being weaker for $\lambda _{{p}}=44.4\%$, a stronger correlation exists between the inertial layer and the near-canopy top region, as visible on the spectral coherence or the transfer function gain (Figs. 9, 10, respectively). The contribution of the correlated component $u^\prime _{{ LS}}$ to the total variance is therefore greater in terms of magnitude. Again, no clear Reynolds number effect is visible, in any component. Analysis of the ratio of the scale-decomposed variances confirms the dominant contribution of the uncorrelated component $u^\prime _{{ SS}}$ close to the canopy, which decreases with height (by definition, the variance ratio tends to zero when $z_m$ approaches $z_{{f}}$) (Fig. 12b). It clearly exhibits the difference between the densest canopy configuration and the two others, the former showing a scale-decomposed variance ratio significantly lower. In the densest configuration, the close packing of roughness elements prevents the turbulent structures generated by the canopy elements from developing and being too energetic compared to those from the overlying boundary layer.

Fig. 13

Wall-normal evolution of the peak frequency of the pre-multiplied energy spectrum of the streamwise velocity component normalized by the length scale $(z-d)$ and the velocity scale $\sigma _u(z)$. Insets show the same evolution for (green) the large-scale correlated velocity component $f_{{ max}}^{{ LS}}$ and (orange) the fraction of the streamwise velocity component of the uncorrelated complement $f_{{ max}}^{{ SS}}$, using velocity scales $\sigma _{u}^{{ LS}}(z_m)$ and $\sigma _{u}^{{ SS}}(z_m)$, respectively, and the height of the moving probe $(z_m-d)$ as length scale. The solid black line in the green inset corresponds to a linear evolution of the normalized frequency with the wall-normal location, showing that $z_{{f}} f_{{ max}}^{{ LS}}/\sigma _{u}^{{ SS}}$ is almost constant with height. Note that in the three plots, lines correspond to frequencies normalized by $(z-d)$ and the standard deviation $\sigma _u(z)$ of the original streamwise velocity component. The vertical solid lines indicate the normalized wall-normal location $z=h$ for each canopy density, the width of the lines accounts for the Reynolds number dependence of the normalized quantity. The thick green line shows the wall-normal limit above which only one-point measurements are available. Symbols: scale-decomposed data, lines: non-decomposed streamwise velocity component. Symbols and colours as in Table 2

In order to further assess the influence of the larger scales from the boundary layer onto the RSL flow and the importance of the relative magnitude of energy contained in the structures from these two regions of the flow depending on the plan density, the wall-normal evolution of the peak frequency observed in the pre-multiplied energy spectra of the large and the small scale contributions to $u'(z_m)$ ($f_{{ max}}^{{ LS}}$ and $f_{{ max}}^{{ SS}}$, respectively) is investigated. Different spatial scalings have been tested using the obstacle height h, the height of the moving probe $z_m-d$, which is an estimate of the typical size of the eddies measured at $z_m$ when accounting for the canopy blockage, or $z_{{f}}-d$ which can be viewed as the largest size of the eddies measured at $z_{{f}}/h=5$ that extends into the RSL. For the sake of brevity, only the results obtained with $z_m-d$ are discussed in the following. As for the velocity scales, instead of employing the local mean streamwise velocity component generally used with Taylor’s hypothesis, turbulent velocity scales directly tied to the coherent structures of interest are defined based on the standard deviation of the large-scale and small-scale contributions $\sigma _{u}^{{ LS}}(z_m)$ and $\sigma _{u}^{{ SS}}(z_m)$, respectively, and that of the original streamwise velocity component $\sigma _u(z_m)$ (Tennekes and Lumley 1972). Scaling the most energetic frequencies of each contribution requires two different scale-dependent frequency scales (or temporal scales) that can be built by combining a length scale and a velocity scale. Several combinations have been tested, only the relevant one is presented in the subsequent analysis. Regarding the choice of the spatial scale, the distance from the wall has been chosen for the most energetics near-wall scales (the so-called small-scales) as their size is known to be height dependent whereas a fixed length scale has been retained for the most energetic scales in the outer logarithmic region (the large scales) as they are known to scale with the boundary-layer depth $\delta$, which is almost constant among all the investigated configurations. Using these length scales together with the local mean streamwise velocity component (as used in Taylor’s approach) did not enable to collapse the results. A scale-dependent velocity scale was therefore required. In their investigation of space–time correlation in isotropic turbulence, Comte-Bellot and Corrsin (1971) and references therein demonstrated that scale-dependent time scale can be estimated from the considered scale and either the energy at the considered scale or the global standard deviation (see Eqs. 76 and 78, respectively, in Comte-Bellot and Corrsin 1971). Following these ideas, the standard deviation of the scale-decomposed fluctuations of the streamwise velocity component proved to be a relevant scale-dependent parameter to collapse the wall-normal evolution of the most energetic frequency.

Results obtained at wall-normal distances $z_m < z_{{f}}$ are presented in Fig. 13. Profiles of $f_{{ max}}$ for the non-decomposed streamwise velocity component from Fig. 8 but normalized by the standard deviation of the local streamwise velocity component $\sigma _{u}(z)$ are also shown for comparison. When considering the evolution of $f_{{ max}}$ for the non-decomposed streamwise velocity component (lines in Fig. 13), using the standard deviation as a velocity scale does not lead to the collapse of the three canopy configurations, the discrepancy between $\lambda _{{p}} = 44.4\%$ and the two other densities in the lower region of the flow being unchanged. However, when considering the scale-decomposed streamwise velocity component, a good collapse of the profiles of the three canopy configurations is obtained, for both $f_{{ max}}^{{ LS}}$ and $f_{{ max}}^{{ SS}}$ (symbols in insets in Fig. 13). Furthermore, this behaviour is independent of scaling parameters and the Reynolds number (not shown here).

Comparing the profiles of either $f_{{ max}}^{{ LS}}$ or $f_{{ max}}^{{ SS}}$ to that of $f_{{ max}}$ from the original streamwise velocity component enables the elucidation of the dominant contribution to the flow in the RSL as a function of the density. In the region where the above mentioned discrepancy between $\lambda _{{p}} = 44.4\%$ and the two other densities exists, a good collapse between the profiles of $f_{{ max}}^{{ LS}}$ for $\lambda _{{p}} = 44.4\%$ and $f_{{ max}}$ is obtained when using $\sigma _{u_{{ LS}}}(z_m)$ as a velocity scale for $f_{{ max}}^{{ LS}}$ (bottom right green inset in Fig. 13). Very close to the canopy, no collapse was possible. Switching from $(z_m-d)$ to $(z_{{f}}-d)$ as a scaling length only modifies the global slope of the $f_{{ max}}^{{ LS}}$ profile (not shown here). It has also been found that the non-dimensional frequency $f_{{ max}}^{{ LS}}(z_{{f}}-d)/\sigma _{u_{{ LS}}}(z_m)$ is almost constant throughout the region $z/h < z_{{f}}$ (i.e. below the fixed probe). As for the evolution of $f_{{ max}}^{{ SS}}$, a good match with the wall-normal profile of $f_{{ max}}$ of the streamwise velocity component is visible in the region close to the canopy when using both $\sigma _{u_{{ SS}}}(z_m)$ and $\sigma _{u}(z_m)$ as a velocity scale and $(z_m-d)$ as a length scale (top left orange inset in Fig. 13). Above this region, the use of $\sigma _{u_{{ SS}}}(z_m)$ and h leads to a better agreement for all the density configurations but $\lambda _{{p}}~=~44.4\%$ for which the already noticed discrepancy appears again (not shown here).

The above analysis shows that for $\lambda _{{p}}~=~44.4\%$, the most energetic structures from the boundary layer have a strong influence on the RSL flow, confining the region where the structures from the canopy are dominating to the lowest investigated locations. Conversely, lowest densities $\lambda _{{p}}~=~6.25\%$ and $25\%$ show a region of large wall-normal extent where the most energetic structures seem to be associated with the canopy, progressively blending with those from the above boundary layer.

4 Discussion and Conclusions

The influence of roughness geometry on the characteristics of the ABL has been investigated via hot-wire measurements of the streamwise velocity component conducted in a wind tunnel. The flow configurations are representative of the lower atmosphere developing over urban-like terrain, for which the plan area density $\lambda _{{p}}$ has been varied so as to represent the three typical near-wall flow regimes (isolated-wake, wake-interference and skimming-flow regimes) (Grimmond and Oke 1999). We focussed on the identification of the relevant length and velocity scales that can be used to scale the characteristics of the streamwise velocity component depending on the considered flow region. Concerning the wall-normal profile of the streamwise velocity component, in agreement with previous work performed on similar flow configurations, $u_*$, d and $z_0$ have been found to be the optimum set of parameters with which to collapse all the flow configurations, taking into account both Reynolds number effects and the influence of $\lambda _{{p}}$. Conversely, when considering the profiles of the variance $\sigma _u^2$ and the skewness, none of the other tested scalings were able to provide a good match of all the configurations in the lowest region of the flow, providing only reasonable agreement in the outer region of the boundary layer. Investigation of the wall-normal evolution of the pre-multiplied energy spectra and that of the frequency $f_{{ max}}(z)$ of the local energy peak clearly revealed the existence of three distinct regions corresponding to three different sets of scaling variables. A link between the change in sign of the skewness and the transition between the outer region and the so-called intermediate region has also been found.

The effect of $\lambda _{{p}}$ on flow dynamics has been further investigated by using scale decomposition of the streamwise velocity component in the near-canopy top region into its mean value, a component correlated with the flow above (at $z/h=5$) and a third component viewed as being representative of the canopy induced flow. This spectral filtering was rendered possible through the choice of the measurement location, where the roughness element signature was strong enough to circumvent the fact that typical temporal scales from the canopy $h/u_*$ or from the boundary layer $\delta /U_{{e}}$ are of the same order. It has been demonstrated that the relative importance of the kinetic energy of the most energetic scales of both regions plays a key role in the emergence of characteristic frequencies and the footprint of the boundary layer on the near-canopy top flow. Despite the differences in the wall-normal profiles of the streamwise velocity component, spectral analysis and scale decomposition reveal dynamical similarities between the different density configurations. If defining the RSL as the region where the canopy-induced flow component exists, wake-isolated and wake-interference flow regimes lead to a thicker RSL with (at the Reynolds number) a flow dynamics dominated by the coherent structures generated by the roughness elements while the lower part of the flow in the skimming flow regime is under the influence of the most energetic structures of the overlying boundary layer. An attempt to summarize the flow organization and the relevant scales and to complete the typical representation of flow regimes as shown in Fig. 3 is proposed in Fig. 14: a change in flow regime leads to a variation of the wall-normal extent of the RSL and, as a consequence, that of the inertial layer. Large-scale structures from the overlying boundary layer are shown to superimpose onto those generated by the canopy elements with variable wall-normal overlap depending on the canopy flow regime. These conclusions are in line with Placidi and Ganapathisubramani (2015) who, through the use of proper orthogonal decomposition of PIV velocity fields, demonstrated that changing the plan density had no impact on the outer-layer structure of the flow and lead to a re-assignment of turbulent kinetic energy to smaller scales in the RSL. Therefore, the present results are likely to remain valid if the building geometry is changed, namely that, (i) large scales from the boundary layer leave their imprint deep within the RSL, (ii) sparse canopies allow the shear-layer developing from the roughness elements to develop more freely and therefore to have a stronger influence on the flow (leading to a thicker RSL) while (iii) dense canopies lead to a more confined flow and a greater relative influence of the large scales near canopy top, and (iv) no single scaling is valid for the mean flow and the other statistical properties. Therefore, switching from a staggered configuration to an aligned or more random arrangement is more likely to affect the local properties of the flow in the RSL than drastically change the main mechanisms. The same conclusions would be obtained with different building shapes.

Fig. 14

Schematic representation of the flow organization in (left) skimming flow and (right) isolated wake or wake-interference regimes. Solid and dashed green lines depict the high- and low-momentum large-scale regions in the boundary layer, orange lines and arrows correspond to the limit and flapping motion of canopy generated shear layers, respectively. Orange and green shaded areas show the limits of the RSL and the wake region, respectively. The white area corresponds to the inertial layer

Given the demonstrated influence of the most energetic structures of the overlying boundary layer, which can be characterized by the Reynolds number $\delta ^+$, the Reynolds numbers $h^+$ or $z_0^+$ cannot be the only criteria that characterize the flow dynamics and the validity of similarity law. Despite a high enough Reynolds number $h^+$ (or $z_0^+$) that stamps the flow as being in the fully rough regime from an hydrodynamical point of view, a too-small Reynolds number $\delta ^+$ may lead to an exaggerated footprint of the flow structures generated by the roughness elements and the failure of outer-layer similarity. Addressing this question therefore calls for new experiments performed at high Reynolds number $\delta ^+$ with similar $\delta /h$ ratio in the range 10 to 20, which are representative of typical flow over urban terrain, as in the present study or in Cheng and Castro (2002) and Placidi and Ganapathisubramani (2017). This question of the relative importance of the viscous scale $\nu /u_\tau$, roughness length $z_0$ (or the equivalent sand-grain roughness $k_{{s}}$) and outer scale $\delta$ on the structure of the near-wall region for rough-wall boundary layers has recently been investigated by Mehdi et al. (2013), with experimental support by Ebner et al. (2016) and Squire et al. (2016). These authors focussed their analysis on the combined influence of the wall roughness and the Reynolds number on the wall-normal onset $z_I$ of the region where “the leading order mean dynamics becomes described by a balance between the mean and turbulent inertia” and where Townsend’s attached eddy phenomenology should apply (i.e. where the wall-normal profiles of the mean and the variance of the streamwise velocity component follow a logarithmic law). One can therefore consider this wall-normal location as a limit below which roughness effects or viscous effects become predominant. Mehdi et al. (2013) showed that $z_I$ scales as $z_I = D(\nu /u_\tau )^a(z_0)^b(\delta )^c$ with D, a, b, c (such that $a+b+c=1$), four positive parameters whose values depend on the relative importance of $z_I$ and $z_0$ (smaller, of the order or larger than 1, see Mehdi et al. 2013 for the corresponding ranges and parameter values in terms of the ratio $z_I / k_{{s}}$). Dividing by h, this relatioship can be rewritten as $z_I/h = D(1/h^+)^a(z_0/h)^b(\delta /h)^c$. In the context of flows in the fully-rough regime over urban-like canopies, $z_0/h$ is constant with $\delta ^+$ for a given canopy configuration. The wall-normal location of the bottom limit (relative to the wall) of the inertial domain therefore depends on the ratio $\delta /h$ and the Reynolds number $h^+$. For a fixed $\delta /h$ ratio, increasing $h^+$ (and therefore $\delta ^+$ in the same proportion) decreases $z_I$. It shows that, in the same manner as for the smooth-wall flows, increasing the Reynolds number $\delta ^+$ increases the wall-normal extent of the inertial layer, physically toward the canopy top (its upper limit has been shown to vary proportionally to $\delta ^+$, Castro et al. 2013; Marusic et al. 2013; Mehdi et al. 2013). As a side note, it shows that an increase in $z_0$ (or $k_{{s}}$) leads to an increase of $z_I$, which can be interpreted as a thickening of the RSL (a trend observed by Placidi and Ganapathisubramani 2015).

Finally, thanks to an adequate choice of the roughness configurations, the change in the near-canopy flow regime has been quantified and observed to leave its imprint on most of the statistics of the streamwise velocity component, including the most energetic frequencies in the energy spectrum, resulting from the complex interaction between the most energetic scales generated close to the canopy and those existing in the overlying boundary layer, i.e. the large-scale logarithmic-region events. Several studies performed in boundary-layer flows over a smooth surface have demonstrated the existence of a non-linear mechanism between the large-scale structures in the inertial layer and the smaller scale near-wall turbulence (Hutchins and Marusic 2007; Mathis et al. 2009). The identified mechanism resembles an amplitude modulation process through which the large-scale turbulence leaves its imprint on the near-wall activity via the combination of both superposition and amplitude modulation. Recent studies performed in boundary-layer flows developing over sand-grain type rough wall (Squire et al. 2016) and urban-type roughness (Nadeem et al. 2015; Anderson 2016; Blackman and Perret 2016; Blackman et al. 2018; Basley et al. 2018) have demonstrated the existence of the same type of interaction between the near-surface turbulence and the large scales present in the inertial layer, confirming the influence of the outer flow on the roughness and canopy activity. Investigating this scale interplay and its dependence on the roughness density is the subject of ongoing research efforts.