1 Introduction

An inverse eigenvalue problem (IEP) aims to reconstruct a structured matrix from the prescribed spectral data. Inverse eigenvalue problems (IEPs) arise in various applications such as structural dynamics, vibration, inverse Sturm–Liouville problem, control design, geophysics, nuclear spectroscopy and molecular spectroscopy, etc. For the existence theory, numerical methods and applications of general IEPs, one may refer to [11, 13, 14, 20, 24, 25, 43] and references therein.

Recently, one may find some new applications and numerical methods of IEPs including the experiments for beaded strings [17], the inverse eigenvalue problem for graphs [5, 6, 31], the solvability condition and numerical algorithm for the parameterized generalized IEP [18], the weight optimization in a geodetic network [19], the IEP in wireless communications [40], the transcendental inverse eigenvalue problem in damage parameter estimation [36, 37], the IEP for quantum channels [42], and the IEP in microelectromechanical systems [38], etc. In many applications, the number of distributed parameters in the required structured matrix is often smaller than the number of measured eigenvalues (see for instance [9, 22, 39]). Thus it is desirable that one can find a least square solution to a structured IEP. Sparked by this, in this paper, we consider the following parameterized least squares inverse eigenvalue problem, which was originally given by Chen and Chu [10].

PLSIEP I

Given \(l+1\) real symmetric matrices \(A_0,A_1,\ldots ,A_l \in {\mathbb {R}}^{n\times n}\) and m real numbers \(\lambda ^*_1 \le \lambda ^*_2 \le \cdots \le \lambda ^*_m\ (m\le n)\), find a vector \(\mathbf {c}=(c_1,c_2,\ldots ,c_l)^T\in \mathbb {R}^{l}\) and a permutation \(\sigma =\{\sigma _1,\sigma _2,\ldots ,\sigma _m\}\) with \(1 \le \sigma _1< \sigma _2< \cdots < \sigma _m \le n\) to minimize the function

$$\begin{aligned} f(\mathbf {c},\sigma ) : = \frac{1}{2} \sum _{i=1}^m(\lambda _{\sigma _i}(\mathbf {c}) - \lambda _i^*)^2, \end{aligned}$$

where the real numbers \(\lambda _1(\mathbf {c})\le \lambda _2(\mathbf {c}) \le \cdots \le \lambda _n(\mathbf {c})\) are the eigenvalues of the matrix \(A(\mathbf {c})\) defined by

$$\begin{aligned} A(\mathbf {c}):= A_0 + \sum \limits _{i=1}^{l} c_i A_i. \end{aligned}$$

This is a nonlinear least-squares problem, where \(l\le m\le n\) and the cost function \(f(\mathbf {c},\sigma )\) is a function of a continuous variable \(\mathbf{c}\) and a discrete variable \(\sigma \). This is a special kind of mixed optimization problem, where the function \(f(\mathbf {c},\sigma )\) is nondifferentiable when the permutation \(\sigma \) is changed. For the PLSIEP I, there exists an equivalent least-squares problem defined on a product manifold. Let \(\mathscr {D}(m)\) and \(\mathscr {O}(n)\) denote the set of all real diagonal matrices of order m and the set of all real \(n\times n\) orthogonal matrices, respectively. Define \(\varLambda ^*_m := \mathrm{diag} (\lambda ^*_1, \lambda ^*_2, \ldots , \lambda ^*_m)\), where \(\mathrm{diag}(\mathbf{a})\) denotes a diagonal matrix with \(\mathbf{a}\) on its diagonal. Given a matrix \(\varLambda \in \mathscr {D}(n-m)\), \(\mathrm{blkdiag}\left( \varLambda ^*_m ,\; \varLambda \right) \) denotes the block diagonal matrix obtained from \(\varLambda ^*_m\) and \(\varLambda \). Based on Theorem 3.2 in [10], the PLSIEP I is equivalent to the following problem.

PLSIEP II

Given \(l+1\) real symmetric matrices \(A_0,A_1,\ldots ,A_l \in {\mathbb {R}}^{n\times n}\) and m real numbers \(\lambda ^*_1 \le \lambda ^*_2 \le \cdots \le \lambda ^*_m\ (m\le n)\), find a vector \(\mathbf {c}\in \mathbb {R}^{l}\), an orthogonal matrix \(Q\in \mathscr {O}(n)\), and a diagonal matrix \(\varLambda \in \mathscr {D}(n-m)\) to minimize the function

$$\begin{aligned} h(\mathbf {c},Q,\varLambda ) : = \frac{1}{2} \Vert A(\mathbf {c}) - Q\, \mathrm{blkdiag}\left( \varLambda ^*_m,\; \varLambda \right) Q^T \Vert _F^2, \end{aligned}$$

where \(\Vert \cdot \Vert _F\) denotes the Frobenius norm.

The PLSIEP II is a nonlinear least-squares problem defined on the product manifold \(\mathbb {R}^{l} \times \mathscr {O}(n) \times \mathscr {D}(n-m)\). To solve the PLSIEP II, Chen and Chu [10] proposed a lift and projection (LP) method. This method is a modification of the alternating projection method to an affine space and a Riemannian manifold. To solve the PLSIEP I, Chen and Chu [10] proposed a hybrid method called the LP-Newton method. The idea is that an initial guess of \((\mathbf{c}, \sigma )\) is obtained by using the LP method to the PLSIEP II, then the Newton method is applied to the PLSIEP I by fixing the value of \(\sigma \). As noted in [10], in spite of non-smoothness of f in \(\sigma \), one may still adopt the Newton method for solving the PLSIEP I, where the Hessian matrix of f can be explicitly derived. However, as the separation of eigenvalues decreases, the Hessian matrix becomes increasingly ill-conditioned. Also, as noted in [23], when \(l<m\), it is natural to consider the well-known techniques in [21, Chap. 10] (e.g., the Gauss–Newton method). Wang and Vong [41] proposed a Gauss–Newton-like method for a special case of \(m=n\).

Optimization methods on smooth manifolds have been widely studied and applied to various kinds of areas such as numerical linear algebra and dynamical systems (see for instance [1,2,3,4, 12, 15, 30, 35] and references therein). Recently, some Riemannian optimization methods were proposed for solving nonlinear eigenvalue problems and inverse eigenvalue problems [44,45,46,47]. In this paper, we propose a geometric inexact Gauss–Newton method for solving the PLSIEP II. Absil et al. [2] proposed a Riemannian Gauss–Newton method for solving nonlinear least squares problems defined between Riemannian manifold and Euclidean space, where the convergence analysis was not discussed. Gratton et al. [27] gave some approximate Gauss–Newton methods for solving nonlinear least squares problems defined on Euclidean space. Sparked by [2, 27], we present an efficient geometric inexact Gauss–Newton method for solving the PLSIEP II. The global convergence and local convergence rate are also derived under some assumptions. An effective preconditioner is proposed for solving the Riemannian Gauss–Newton equation via the conjugate gradient (CG) method [26]. Finally, some numerical experiments, including an application in the inverse Sturm–Liouville problem, are reported to show the efficiency of the proposed method for solving the PLSIEP II.

Throughout this paper, we use the following notation. The symbol \(A^T\) denotes the transpose of a matrix A. The symbol \(\mathrm{Diag}(M):= \mathrm{diag}(m_{11}, m_{22}, \ldots , m_{nn})\) denotes a diagonal matrix containing the diagonal elements of an \(n \times n\) matrix \(M = [ m_{ij} ]\). Let \(\mathbf {0}_{m\times n}\) be the \(m\times n\) zero matrix and \(\mathbf{e}_k\) be the kth column of the identity matrix \(I_n\) of order n. Let \({\mathbb {R}}^{n\times n}\) and \(\mathbb {SR}^{n\times n}\) be the set of all n-by-n real matrices and the set of all n-by-n real symmetric matrices, respectively. Denote by \(\mathrm{tr}(A)\) the trace of a square matrix A. For two matrices \(A,B\in {\mathbb {R}}^{n\times n}\), the Lie Bracket [A, B] of A and B is defined as the difference of the matrix products AB and BA, i.e., \([A,B]:=AB-BA\) [32, p. 512]. Let \(\mathrm{vec}(A)\) be the vectorization of a matrix A, i.e., a column vector obtained by stacking the columns of A on top of one another. For two finite-dimensional vector spaces \(\mathscr {X}\) and \(\mathscr {Y}\) equipped with a scalar inner product \(\langle \cdot ,\cdot \rangle \) and its induced norm \(\Vert \cdot \Vert \), let \(\mathscr {A}:\mathscr {X}\rightarrow \mathscr {Y}\) be a linear operator and the adjoint of \(\mathscr {A}\) be denoted by \(\mathscr {A}^*\). The operator norm of \(\mathscr {A}\) is defined by .

The remainder of this paper is organized as follows. In Sect. 2 we propose a geometric inexact Gauss–Newton method for solving the PLSIEP II. In Sect. 3 we establish the global convergence and local convergence rate of the proposed approach under some assumptions. A preconditioner is also proposed for solving the geometric Gauss–Newton equation. Finally, we report some numerical tests in Sect. 4 and give some concluding remarks in Sect. 5.

2 Geometric inexact Gauss–Newton method

In this section, we present a geometric inexact Gauss–Newton method for solving the PLSIEP II. Define an affine subspace and an isospectral manifold by

$$\begin{aligned} \mathscr {L}:= & {} \left\{ A_0 + \sum _{i=1}^{l} c_i A_i \ | \ c_i \in {\mathbb {R}}, i=1,2,\ldots ,l \right\} , \\ \mathscr {M}(\varLambda ^*_m):= & {} \big \{ X = Q\, \mathrm{blkdiag} \left( \varLambda ^*_m, \varLambda \right) Q^T \in \mathbb {SR}^{n\times n}\; | \; Q\in \mathscr {O}(n),\; \varLambda \in \mathscr {D}(n-m) \big \}. \end{aligned}$$

We see that \(\mathscr {M}(\varLambda ^*_m)\) is the set of all real \(n\times n\) symmetric matrices whose spectrum contains the m real numbers \(\lambda ^*_1, \lambda ^*_2, \ldots , \lambda ^*_m\). Thus, the PLSIEP II has a solution such that \(h(\mathbf {c},Q,\varLambda ) =0\) if and only if \(\mathscr {L}\cap \mathscr {M}(\varLambda ^*_m) \ne \emptyset \).

Denote

$$\begin{aligned} \mathscr {Z}:= \mathbb {R}^{l} \times \mathscr {O}(n) \times \mathscr {D}(n-m) \quad \hbox {and} \quad \overline{\varLambda } :=\mathrm{blkdiag} (\varLambda ^*_m ,\varLambda ). \end{aligned}$$
(2.1)

Let H be a nonlinear mapping between \(\mathscr {Z}\) and \(\mathbb {SR}^{n\times n}\) defined by

$$\begin{aligned} H(\mathbf {c}, Q, \varLambda ) := A(\mathbf {c}) -Q\overline{\varLambda }Q^T, \end{aligned}$$
(2.2)

for all \((\mathbf {c}, Q, \varLambda )\in \mathscr {Z}\). Then, the PLSIEP II can be written as the following minimization problem:

$$\begin{aligned} \begin{array}{ll} \min &{} \quad \displaystyle h(\mathbf {c}, Q, \varLambda ) :=\frac{1}{2} \Vert H(\mathbf {c}, Q, \varLambda )\Vert _F^2 \\ \hbox {subject to (s.t.)} &{} \quad (\mathbf {c}, Q, \varLambda )\in \mathscr {Z}. \end{array} \end{aligned}$$
(2.3)

Sparked by the ideas in [2, 27], we propose a geometric inexact Gauss–Newton method for solving Problem (2.3). We note that the dimension of the product manifold \(\mathscr {Z}\) is given by

$$\begin{aligned} \text {dim}(\mathscr {Z}) = l + \frac{n(n-1)}{2} + n-m. \end{aligned}$$

If \(l<m\), then

$$\begin{aligned} \text {dim}(\mathscr {Z}) < \text {dim}( \mathbb {SR}^{n\times n}). \end{aligned}$$

Therefore, the nonlinear equation \(H(\mathbf {c}, Q, \varLambda ) =\mathbf{0}_{n\times n}\) is an over-determined matrix equation defined on the product manifold \(\mathscr {Z}\).

Notice that \(\mathscr {Z}\) is an embedded submanifold of the Euclidean space \(\mathbb {R}^{l} \times {\mathbb {R}}^{n\times n}\times \mathscr {D}(n-m)\). One may equip \(\mathscr {Z}\) with the induced Riemannian metric:

$$\begin{aligned} g_{(\mathbf {c},Q,\varLambda )}\big ( (\xi _1, \eta _1, \tau _1), (\xi _2, \eta _2, \tau _2) \big ):=\mathrm{tr}(\xi _1^T\xi _2) +\mathrm{tr}(\eta _1^T\eta _2)+\mathrm{tr}(\tau _1^T\tau _2), \end{aligned}$$

for \((\mathbf {c},Q,\varLambda ) \in \mathscr {Z}\), and \((\xi _1, \eta _1, \tau _1), (\xi _2, \eta _2, \tau _2)\in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}\), and its induced norm \(\Vert \cdot \Vert \). The tangent space \(T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}\) of \(\mathscr {Z}\) at \((\mathbf {c},Q,\varLambda )\) is given by [2, p. 42]

$$\begin{aligned} T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}= \big \{(\mathbf {r}, Q\varOmega , U) \ | \ \varOmega ^T = -\,\varOmega , \;\mathbf {r}\in \mathbb {R}^{l}, \varOmega \in {\mathbb {R}}^{n\times n}, U\in \mathscr {D}(n-m)\big \}. \end{aligned}$$

Hence, \((\mathscr {Z},g)\) is a Riemannian product manifold.

For simplification, we use the following notation:

$$\begin{aligned} X_k: = (\mathbf {c}_k,Q_k,\varLambda _k)\in \mathscr {Z}\quad \hbox {and} \quad \varDelta X_k:=(\varDelta \mathbf {c}_k, \varDelta Q_k, \varDelta \varLambda _k) \in T_{X_k}\mathscr {Z}. \end{aligned}$$

A Riemannian Gauss–Newton method for solving Problem (2.3) can be stated as follows. Given the current iterate \(X_k\in \mathscr {Z}\), solve the normal equation

$$\begin{aligned} (\mathrm {D}H(X_k))^*\circ \mathrm {D} H(X_k)[\varDelta X_k] = -\,(\mathrm {D}H(X_k))^*[H(X_k)], \end{aligned}$$

for \(\varDelta X_k \in T_{X_k}\mathscr {Z}\). Here,

$$\begin{aligned} \mathrm {D}H(X_k): T_{X_k}\mathscr {Z}\rightarrow T_{H(X_k)} \mathbb {SR}^{n\times n}\end{aligned}$$

is the Riemannian differential of H at the point \(X_k\), which is given by

$$\begin{aligned} \mathrm {D}H(X_k) [\varDelta X_k]=(A(\varDelta \mathbf {c}_k)-A_0) +[ Q_k\overline{\varLambda }_k Q_k^T ,\varDelta Q_kQ_k^T ] -(Q_kP)\varDelta \varLambda _k (Q_kP)^T, \end{aligned}$$
(2.4)

where

$$\begin{aligned} \overline{\varLambda }_k :=\mathrm{blkdiag} (\varLambda ^*_m ,\varLambda _k) \quad \hbox {and} \quad P :=\left[ \begin{array}{c} \mathbf {0}_{m\times (n-m)} \\ I_{(n-m)\times (n-m)} \end{array}\right] . \end{aligned}$$
(2.5)

With respect to the Riemannian metric g, the adjoint

$$\begin{aligned} (\mathrm {D}H(X_k))^* : T_{H(X_k)} \mathbb {SR}^{n\times n}\rightarrow T_{X_k}\mathscr {Z}\end{aligned}$$

of \(\mathrm {D}H(X_k)\) is given by

$$\begin{aligned} (\mathrm {D}H(X_k))^*[\varDelta Z_k]=\big (\mathbf {v} (\varDelta Z_k), [ Q_k\overline{\varLambda }_k Q_k^T ,\varDelta Z_k ]Q_k, -\,\mathrm{Diag}\big ((Q_kP)^T\varDelta Z_k (Q_kP)\big )\big ), \end{aligned}$$
(2.6)

where

$$\begin{aligned} \mathbf {v}(\varDelta Z_k):= \big (\mathrm{tr}(A_1^T \varDelta Z_k), \mathrm{tr}(A_2^T \varDelta Z_k), \ldots , \mathrm{tr}(A_l^T \varDelta Z_k) \big )^T. \end{aligned}$$
(2.7)

For explicit derivation of (2.4) and (2.6), one may refer to Appendix A. Based on (2.6), the Riemannian gradient of h at a point \(X:=(\mathbf {c},Q,\varLambda )\in \mathscr {Z}\) is determined by [2, p. 185]:

$$\begin{aligned} \mathrm {grad}\;h(X)= & {} (\mathrm {D}H(X))^* [ H(X)] =\big (\mathbf {v}\big ( A(\mathbf {c}) -Q\overline{\varLambda } Q^T\big ), [Q\overline{\varLambda } Q^T, A(\mathbf {c}) - Q\overline{\varLambda } Q^T]Q, \nonumber \\&-\,\mathrm{Diag}\big ((QP)^T (A(\mathbf {c}) - Q\overline{\varLambda } Q^T) (QP)\big ) \big ). \end{aligned}$$
(2.8)

Let \(\nabla \) denote the Riemannian connection of \(\mathscr {Z}\). By using (8.31) in [2, p. 185] we obtain

$$\begin{aligned} \nabla ^2 h(X)[\xi _X,\eta _X] =\langle \mathrm{D} H(X)[\xi _X], \mathrm{D}H(X)[\eta _X]\rangle +\langle H(X),\nabla ^2 H(X)[\xi _X,\eta _X]\rangle , \end{aligned}$$
(2.9)

for all \(X:= (\mathbf {c},Q,\varLambda ) \in \mathscr {Z}\) and \(\xi _X, \eta _X \in T_{X}\mathscr {Z}\), where \(\nabla ^2 h\) is a (0, 2)-tensor field and \(\nabla ^2 H(X)[\cdot ,\cdot ]=\big [\nabla ^2 H_{ij}(X)[\cdot ,\cdot ] \big ]\in \mathbb {SR}^{n\times n}\) [2, p. 109]. The Riemannian Hessian \(\mathrm{Hess}\; h(X)\) at a point \(X\in \mathscr {Z}\) is determined by

$$\begin{aligned} \nabla ^2h(X)[\xi _X,\eta _X] =\langle \mathrm{Hess}\; h(X)[\xi _X], \eta _X \rangle , \end{aligned}$$
(2.10)

for all \(\xi _X, \eta _X \in T_{X}\mathscr {Z}\). In particular, if \(X_{*}\) is a solution of the equation \(H(X)=\mathbf {0}_{n\times n}\), then we can obtain

$$\begin{aligned} \mathrm{Hess}\; h(X_{*}) = (\mathrm{D} H(X_{*}))^*\circ \mathrm{D} H(X_{*}). \end{aligned}$$

Based on the above discussion, a geometric inexact Gauss–Newton method for solving Problem (2.3) can be described as follows.

Algorithm 1

A geometric inexact Gauss–Newton method

Step 0:

Choose an initial point \(X_0 \in \mathscr {Z}\), \(\beta , \eta _{\max }\in (0,1)\), \(\sigma \in (0,\frac{1}{2})\). Let \(k:=0\).

Step 1:

Apply the CG method to finding an approximate solution \(\varDelta X_k \in T_{X_k} \mathscr {Z}\) of

$$\begin{aligned} (\mathrm {D}H(X_k))^*\circ \mathrm {D}H(X_k)[\varDelta X_k] = - \, \mathrm{grad}\,h(X_k) \end{aligned}$$
(2.11)

such that

$$\begin{aligned} \Vert (\mathrm {D}H(X_k))^*\circ \mathrm {D}H(X_k)[\varDelta X_k] +(\mathrm {D}H(X_k))^*[H(X_k)]\Vert \le \eta _k\Vert \mathrm{grad}\,h(X_k)\Vert \end{aligned}$$
(2.12)

and

$$\begin{aligned} \langle \mathrm{grad}\,h(X_k) ,\varDelta X_k \rangle \le -\,\eta _k\langle \varDelta X_k ,\varDelta X_k\rangle , \end{aligned}$$
(2.13)

where \(\eta _k:=\min \{\eta _{\max }, \Vert \mathrm{grad}\,h(X_k)\Vert \}\). If (2.12) and (2.13) are not attainable, then let

$$\begin{aligned} \varDelta X_k:=-\,\mathrm{grad\,}h(X_k). \end{aligned}$$
Step 2:

Let \(l_k\) be the smallest nonnegative integer l such that

$$\begin{aligned} h\big (R_{X_k}(\beta ^{l} \varDelta X_k)\big )- h( X_k) \le \sigma \beta ^l\langle \mathrm{grad}\,h(X_k),\varDelta X_k\rangle . \end{aligned}$$
(2.14)

Set

$$\begin{aligned} X_{k+1}:= R_{X_k}(\beta ^{l_k} \varDelta X_k). \end{aligned}$$
Step 3:

Replace k by \(k+1\) and go to Step 1.

We point out that, in Step 2 of Algorithm 1, (2.14) is the Armijo condition (see [2, Definition 4.2.2]) and R is a retraction on \(\mathscr {Z}\), which takes the form of

$$\begin{aligned} R_{X_k}(\varDelta X_k) = \big (\mathbf {c}_k +\varDelta {\mathbf {c}_k}, R^o_{Q_k}( \varDelta Q_k), \varLambda _k +\varDelta \varLambda _k \big ), \end{aligned}$$
(2.15)

where \(R^o\) is a retraction on \(\mathscr {O}(n)\), which may be chosen as [2, p. 58]:

$$\begin{aligned} R^o_Q(\eta _Q) = \mathrm{qf} (Q + \eta _Q), \quad \eta _Q \in T_Q\mathscr {O}(n). \end{aligned}$$

Here, \(\mathrm{qf}(A)\) denotes the Q factor of the QR decomposition of an invertible matrix \(A\in \mathbb {R}^{n\times n}\) as \(A=Q\widehat{R}\), where Q belongs to \(\mathscr {O}(n)\) and \(\widehat{R}\) is an upper triangular matrix with strictly positive diagonal elements. For the retraction R defined by (2.15), there exist two scalars \(\nu >0\) and \(\mu _{\nu } >0\) such that [2, p. 149]

$$\begin{aligned} \nu \Vert \varDelta X \Vert \ge \mathrm{dist}\big (X,R_X (\varDelta X) \big ), \end{aligned}$$
(2.16)

for all \(X\in \mathscr {Z}\) and

$$\begin{aligned} \varDelta X \in T_X\mathscr {Z}\quad \hbox {with}\ \Vert \varDelta X \Vert \le \mu _{\nu }, \end{aligned}$$
(2.17)

where “\(\mathrm{dist}\)” means the Riemannian distance on the Riemannian product manifold \(( \mathscr {Z},g)\) [2, p. 46]. Of course, one may choose other retractions on \(\mathscr {O}(n)\) via the polar decomposition, Givens rotation, Cayley transform, exponential mapping, or singular value decomposition (see for instance [2, p. 58] and [45]).

3 Convergence analysis

In this section, we establish the global convergence and local convergence rate of Algorithm 1.

3.1 Global convergence

For the global convergence of Algorithm 1, we have the following result. The proof follows from Theorem 4.1 in [45]. Thus we omit it here.

Theorem 1

Any accumulation point \(X_*\) of the sequence \(\{X_k\}\) (if exists) generated by Algorithm 1 is a stationary point of the cost function h defined in Problem (2.3).

Remark 1

In Step 2 of Algorithm 1, the Armijo condition (2.14) guarantees that the objective function h is monotone decreasing. As in [2, Corollary 4.3.2], the sequence \(\{X_k\}\) generated by Algorithm 1 must have an accumulation point if the level set \(\mathscr {L}:=\{X\in \mathscr {Z}\ | \ h(X) \le h(X_0) \}\) is bounded. In particular, if \(m=n\) and the matrices \(A_1, A_2, \ldots , A_l\) are linearly independent, then it is easy to check that the level set \(\mathscr {L}\) is bounded for any initial point \(X_0\in \mathscr {Z}\) (see for instance [47, Lemma 3.1]).

The search directions \(\{\varDelta X_k\}\) generated by Algorithm 1 have the following property. The proof is similar to that of Lemma 4.3 in [45]. Thus we omit it here.

Lemma 1

Let \(X_*\) be an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. If \(\mathrm{D}H(X_{*}): T_{X_*}\mathscr {Z}\rightarrow T_{H(X_*)}\mathbb {SR}^{n\times n}\) is injective, then there exist five positive constants \(\bar{\rho }, \kappa _0,\kappa _1, d_1, d_2 > 0\) such that for all \(X_k\in B_{\bar{\rho }}(X_{*})\), the linear operator \((\mathrm{D}H(X_k))^*\circ \mathrm{D}H(X_k):T_{H(X_*)}\mathbb {SR}^{n\times n}\rightarrow T_{H(X_*)}\mathbb {SR}^{n\times n}\) is nonsingular,

(3.1)

and

$$\begin{aligned} d_1\, \Vert \mathrm{grad}\,h(X_k) \Vert \le \Vert \varDelta X_k \Vert \le d_2\, \Vert \mathrm{grad}\,h(X_k)\Vert , \end{aligned}$$
(3.2)

where \(B_{\bar{\rho }}(X_{*}):=\{X\in \mathscr {Z}\ | \ \mathrm{dist}(X,X_*)<\bar{\rho }\}\).

Next, we discuss the global convergence of Algorithm 1. We need the following assumption.

Assumption 1

Suppose the differential \(\mathrm{D}H(X_{*}): T_{X_*}\mathscr {Z}\rightarrow T_{H(X_*)}\mathbb {SR}^{n\times n}\) is injective and \(X_{*}\) is an isolated local minimizer of h defined in Problem (2.3), where \(X_{*}\) is an accumulation point of the sequence \(\{X_{k}\}\) generated by Algorithm 1.

For the global convergence of Algorithm 1 related to an isolated local minima of h, we have the following result. The proof follows from [8, Proposition 1.2.5].

Theorem 2

Let \(X_{*}\) be an accumulation point of the sequence \(\{X_{k}\}\) generated by Algorithm 1. Suppose that Assumption 1 holds, then \(\{X_{k}\}\) converges to \(X_{*}\).

Proof

By assumption, \(X_*\) is an isolated local minimizer of h. Thus there exists a parameter \(\hat{\rho }>0\) such that \(X_{*}\) is the only stationary point of h in the neighborhood \(B_{\hat{\rho }}(X_{*})\) and

$$\begin{aligned} h(X) > h(X_*), \quad \forall X\ne X_*,\ X \in B_{\hat{\rho }}(X_{*}). \end{aligned}$$

Since h is continuously differentiable and \(X_*\) is a stationary point of h, i.e., \(\mathrm{grad}\; h(X_{*}) = 0_{X_*}\), we obtain

$$\begin{aligned} \lim _{\mathrm{dist}(X,X_*) \rightarrow 0} \mathrm{grad}\, h(X) = 0_{X_*}. \end{aligned}$$
(3.3)

By using (3.3), the norm \(\Vert \mathrm{grad\,}h(X)\Vert \) can be as small as possible if X is sufficiently close to \(X_*\). Thus there exists a scalar \(0<\rho < \min \{\hat{\rho },\bar{\rho }\}\) such that

$$\begin{aligned} h\big (X_{*} \big ) \le h\big ( X \big ) \quad \hbox {and} \quad d_2\Vert \mathrm{grad\,}h(X)\Vert < \mu _{\nu }, \quad \forall X\in B_{\rho }(X_{*}), \end{aligned}$$
(3.4)

where \(\mu _{\nu }\) is defined in (2.17). By assumption, the differential \(\mathrm{D}H(X_{*})\) is injective. Thus, by Lemma 1 we know that (3.2) holds for \(X_k\in B_{\rho }(X_{*})\) since \(\rho \le \bar{\rho }\).

Let

$$\begin{aligned} \phi (t) := \min \limits _{ \{X | t\le \mathrm{dist}(X,X_{*}) \le \rho \} } \big \{ h(X) - h(X_{*}) \big \}, \quad \forall t\in [0,\rho ]. \end{aligned}$$

We note that \(\phi \) is a monotonically nondecreasing function of t and thus \(\phi (t) >0\) for all \(t\in (0,\rho ]\). Using (3.3), for any \( \varepsilon \in (0,\rho ]\), there exists a constant \(r \in (0,\varepsilon ]\) such that

$$\begin{aligned} \mathrm{dist} (X,X_{*}) + \nu d_2 \Vert \mathrm{grad}\, h(X)\Vert < \varepsilon , \end{aligned}$$
(3.5)

for all \(X\in B_{r}(X_{*})\), where \(\nu \) is defined in (2.16). Define the open set

$$\begin{aligned} S := \big \{ X \ | \ \mathrm{dist}(X,X_{*})< \varepsilon , \; h(X) < h(X_{*}) + \phi (r) \big \}. \end{aligned}$$

It is easy to see that \(S\subset B_{\rho }(X_{*})\) since \(\varepsilon \in (0,\rho ]\).

We claim that if \(X_k \in S\) for some k, then \(X_{k+1} \in S\). Indeed, by using the definitions of \(\phi \) and S, if \(X_k \in S\), then

$$\begin{aligned} \phi \big ( \mathrm{dist} (X_k,X_{*} ) \big ) \le h(X_k) - h(X_{*}) < \phi (r). \end{aligned}$$
(3.6)

Since \(\phi \) is monotonically nondecreasing we have \(\mathrm{dist}(X_k,X_{*}) < r\). This, together with (3.5), yields

$$\begin{aligned} \mathrm{dist} (X_k,X_{*} ) + \nu d_2 \Vert \mathrm{grad}\, h(X_k) \Vert < \varepsilon . \end{aligned}$$
(3.7)

Thus, (3.2) holds for \(X_k\) since \(X_k\in S\subset B_{\rho }(X_{*})\). Using (2.16), (3.2), and (3.4) we have

$$\begin{aligned} \mathrm{dist} (X_{k+1},X_{*} )\le & {} \mathrm{dist} (X_k,X_{*} ) + \mathrm{dist} \big ( X_{k+1} ,X_k \big ) \nonumber \\= & {} \mathrm{dist} (X_k,X_{*} ) + \mathrm{dist} \big ( R_{X_k} ( \rho ^{l_k} \varDelta X_k) ,X_k \big ) \nonumber \\\le & {} \mathrm{dist} (X_k,X_{*} ) + \nu \rho ^{l_k} \Vert \varDelta X_k \Vert \le \mathrm{dist} (X_k,X_{*} ) + \nu \Vert \varDelta X_k \Vert \nonumber \\\le & {} \mathrm{dist} (X_k,X_{*} ) + \nu d_2 \Vert \mathrm{grad}\, h(X_k) \Vert . \end{aligned}$$
(3.8)

Since \(h(X_{k+1}) \le h(X_k)\), it follows from (3.6), (3.7), and (3.8) that

$$\begin{aligned} \mathrm{dist}(X_{k+1},X_{*})< \varepsilon , \qquad h(X_{k+1})- h(X_{*}) < \phi (r). \end{aligned}$$

By the above inequalities and the definition of the set S we have \(X_{k+1} \in S\). This completes the proof of the claim. Also, By using induction to the claim we have \(X_i \in S\) for all \(i \ge k\) if \(X_{k} \in S\) for some k.

Since \(X_*\) is an accumulation point of the sequence \(\{X_k\}\), there exists a subsequence \(\{X_{k_j}\}\) such that \(\lim \nolimits _{j\rightarrow \infty }X_{k_j}=X_*\). Thus there exists an integer \(k_{\bar{l}}\) such that \(X_{k_{\bar{l}}}\in S\). By using the claim we have \(X_k\in S\) for all \(k \ge k_{\bar{l}}\). Since \(h(X_{k+1})<h(X_k)\) for all \(k \ge k_{\bar{l}}\) and \(\lim \nolimits _{k_j\rightarrow \infty }h(X_{k_j}) = h(X_*)\), it follows that

$$\begin{aligned} \lim _{k\rightarrow \infty }h(X_k) = h(X_*). \end{aligned}$$
(3.9)

Using (3.6), \(X_k\in S\) for all \(k \ge k_{\bar{l}}\), and (3.9) we have \(\lim \nolimits _{k\rightarrow \infty }\phi \big ( \mathrm{dist} (X_k,X_{*}) \big )=0\). Since \(\phi \) is monotone nondecreasing, it follows that \(\lim \nolimits _{k\rightarrow \infty } \mathrm{dist} (X_k,X_{*}) =0\) and thus \(X_k \rightarrow X_{*}\). The proof is complete. \(\square \)

3.2 Convergence rate

We discuss the local convergence rate of Algorithm 1. The pullbacks of H and h are defined as \(\widehat{H} := H\circ R\) and \(\widehat{h} := h\circ R\), where R is the retraction defined in (2.15). In addition, we use \(\widehat{H}_X := H\circ R_X\) and \(\widehat{h}_X := h\circ R_X\) to denote the restrictions of \(\widehat{H}\) and \(\widehat{h}\) to the tangent space \(T_X\mathscr {Z}\).

Since \(R_X(0_X) = X\) [2, Definition 4.1.1], the value of H at X is equal to the value of its pullback \(\widehat{H}_X\) at \(0_X\), i.e.,

$$\begin{aligned} H(X) = H(R_X(0_X)) = \widehat{H}_X(0_X). \end{aligned}$$
(3.10)

It follows from (2.3) and (3.10) that

$$\begin{aligned} h(X) = \widehat{h}_X(0_X). \end{aligned}$$
(3.11)

Let \(\mathrm{Id}_{T_X\mathscr {Z}}\) denote the identity mapping on \(T_X\mathscr {Z}\). Then one has \(\mathrm{D}R_X(0_X) = \mathrm{Id}_{T_X\mathscr {Z}}\) [2, (4.2)]. Thus the differential of H at X is equal to the differential of its pull back \(\widehat{H}_X\) at \(0_X\), i.e.,

$$\begin{aligned} \mathrm{D}\widehat{H}_X(0_X) = \mathrm{D}(H\circ R_X)(0_X) = \mathrm{D}H(R_X(0_X))\circ \mathrm{D}R_X(0_X)= \mathrm{D}H(X), \end{aligned}$$
(3.12)

for all \(X \in \mathscr {Z}\). Using (3.12) we have

$$\begin{aligned} (\mathrm{D}\widehat{H}_X(0_X))^* = (\mathrm{D}H(X))^*, \end{aligned}$$
(3.13)

for all \(X \in \mathscr {Z}\). For the Riemannian gradient of h and the gradient of its pull back \(\widehat{h}\), we have [2, p. 56]

$$\begin{aligned} \mathrm{grad}\, h(X) = \mathrm{grad}\, \widehat{h}_X(0_X), \end{aligned}$$
(3.14)

for all \(X \in \mathscr {Z}\).

Here, we need the following result on mean value inequality for differentiable mapping defined between normed vector spaces.

Lemma 2

[16, Corollary 3.3] Let V and W be normed vector spaces, U an open subset of V and \(F:U\rightarrow W\) differentiable on U. Given two vectors \(\mathbf{a},\mathbf{b}\in U\), if the segment between \(\mathbf{a}\) and \(\mathbf{b}\) is contained in U, then we have

where \(\Vert \cdot \Vert _V\) and \(\Vert \cdot \Vert _W\) denote the norms of V and W, respectively.

For the stepsize \(\beta ^{l_k}\) in (2.14), we have the following result [33].

Lemma 3

Let \(X_*\) be an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. Suppose that Assumption 1 holds and \(\Vert H(X_*)\Vert _F\) is sufficiently small, then for k sufficiently large, \(l_k = 0\) satisfies (2.14).

Proof

By hypothesis, Theorem 1, and Lemma 2 we have

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }X_k = X_* \quad \hbox {and} \quad \lim \limits _{k\rightarrow \infty }\mathrm{grad}\,h(X_k)=\mathrm{grad}\,h(X_*)=0_{X_*}. \end{aligned}$$
(3.15)

By the definition of \(\eta _k\) in Algorithm 1 and (3.15) we have

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\eta _k = \lim \limits _{k\rightarrow \infty } \min \{\eta _{\max }, \Vert \mathrm{grad}\,h(X_k)\Vert \} = \lim \limits _{k\rightarrow \infty }\Vert \mathrm{grad}\,h(X_k)\Vert =0. \end{aligned}$$
(3.16)

Since \(\mathrm{D}H(X_{*})\) is injective, it follows from (3.1) and (3.16) that the conditions (2.12) and (2.13) are satisfied for all k sufficiently large. Thus \(\varDelta X_k\) is an approximate solution to (2.11) for all k sufficiently large. Let \(\varDelta X_k^{GN}\) denote the exact solution to (2.11). Then we have

$$\begin{aligned} (\mathrm{D}H(X_k))^*\circ \mathrm{D}H(X_k)[ \varDelta X_k - \varDelta X_k^{GN}] =\mathrm{grad}\,h(X_k) + (\mathrm{D}H(X_k))^*\circ \mathrm{D}H(X_k)[ \varDelta X_k ]. \end{aligned}$$
(3.17)

From (2.11), (3.10), (3.12), and (3.13), it follows that

$$\begin{aligned} (\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*[\widehat{H}_{X_k}(0_{X_k})] + (\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*\circ \mathrm{D}\widehat{H}_{X_k} (0_{X_k}) [ \varDelta X_k^{GN} ] = 0_{X_k}. \end{aligned}$$
(3.18)

Using the definition of least-squares solution, (3.10), and (3.12) we find

$$\begin{aligned} \varDelta X_k^{GN}:=\mathop {\mathrm{argmin}}\limits _{\xi _{X_k} \in T_{X_k}\mathscr {Z}} \Vert \widehat{H}_{X_k}(0_{X_k}) + \mathrm{D}\widehat{H}_{X_k}(0_{X_k})[\xi _{X_k} ]\Vert _F. \end{aligned}$$

This implies that

$$\begin{aligned}&\Vert \widehat{H}_{X_k}(0_{X_k}) + \mathrm{D}\widehat{H}_{X_k} (0_{X_k})[ \varDelta X_k^{GN} ]\Vert _F \nonumber \\&\quad \le \Vert \widehat{H}_{X_k}(0_{X_k}) + \mathrm{D}\widehat{H}_{X_k} (0_{X_k})[ 0_{X_k} ]\Vert _F= \Vert \widehat{H}_{X_k}(0_{X_k})\Vert _F. \end{aligned}$$
(3.19)

By hypothesis, \(\mathrm{D}H(X_{*})\) is injective. Thus, by using Lemma 1, (2.12), (3.1), and (3.17), we have for all k sufficiently large,

(3.20)

In addition, the adjoint \((\mathrm{D}\widehat{H}_{X})^*\) of \(\mathrm{D}H_X\) is Lipschitz-continuous at \(0_X\) uniformly in a neighborhood of \(X_*\). That is, there exist three scalars \(\kappa _2, \delta _1, \delta _2 > 0\) such that

(3.21)

for all \(X\in B_{\delta _1}(X_*)\) and \(\xi _X \in B_{\delta _2}(0_X)\). Let

$$\begin{aligned} G(X_k) := \widehat{H}_{X_k}(\varDelta X_k) - \widehat{H}_{X_k}(0_{X_k}) -\mathrm {D}\widehat{H}_{X_k}(0_{X_k})[\varDelta X_k]. \end{aligned}$$
(3.22)

By using Lemma 2, (3.21), and (3.22), we have

(3.23)

for all k sufficiently large.

In the rest of the proof, for simplification, we drop the subindex k. Based on (3.11), (3.14), and (3.22), we have

$$\begin{aligned} h\big (R_{X}(\varDelta X)\big )= & {} \widehat{h}_{X}(\varDelta X) = \tfrac{1}{2} \Vert \widehat{H}_{X}(\varDelta X) \Vert _F^2\\= & {} \tfrac{1}{2} \Vert \widehat{H}_{X}(0_{X}) + \mathrm {D}\widehat{H}_{X}(0_{X})[\varDelta X] + G(X)\Vert _F^2\\= & {} \tfrac{1}{2} \Vert \widehat{H}_{X}(0_{X}) + \mathrm {D}\widehat{H}_{X}(0_{X})[\varDelta X] \Vert _F^2\\&+\, \big \langle \widehat{H}_{X}(0_{X}) + \mathrm {D}\widehat{H}_{X}(0_{X})[\varDelta X], G(X) \big \rangle + \tfrac{1}{2} \Vert G(X)\Vert _F^2\\= & {} \tfrac{1}{2} \Vert \widehat{H}_{X}(0_{X})\Vert _F^2 + \big \langle \widehat{H}_{X}(0_{X}), \mathrm {D} \widehat{H}_{X}(0_{X})[\varDelta X] \big \rangle + \tfrac{1}{2} \Vert G(X)\Vert _F^2\\&+ \,\tfrac{1}{2} \big \langle \mathrm {D} \widehat{H}_{X}(0_{X})[\varDelta X],\mathrm {D} \widehat{H}_{X}(0_{X})[\varDelta X_k] \big \rangle \\&+\, \big \langle \widehat{H}_{X}(0_{X}) + \mathrm {D} \widehat{H}_{X}(0_{X})[\varDelta X], G(X)\big \rangle \\= & {} h(X) + \tfrac{1}{2}\big \langle \mathrm{grad\,}h(X), \varDelta X\big \rangle + \tfrac{1}{2}\big \langle (\mathrm {D} \widehat{H}_{X}(0_{X}))^*[\widehat{H}_{X}(0_{X})],\varDelta X\big \rangle \\&+\, \tfrac{1}{2} \big \langle (\mathrm {D} \widehat{H}_{X}(0_{X}))^* \mathrm {D}\widehat{H}_{X} (0_{X})[\varDelta X], \varDelta X \big \rangle \\&+\, \big \langle \widehat{H}_{X}(0) +\mathrm {D}\widehat{H}_{X}(0_{X})[\varDelta X], G(X)\big \rangle + \tfrac{1}{2} \Vert G(X)\Vert _F^2. \end{aligned}$$

Using (3.1), (3.10), (3.18), (3.19), (3.20), (3.23), and the above equality, we have for all k sufficiently large,

Based on (3.15), if \(\Vert H(X_*)\Vert _F\) is sufficiently small, then \(\Vert H(X_k)\Vert _F\) is small enough for all k sufficiently large. By using the above inequality, (2.14) holds with \(l_k=0\) for all k sufficiently large. This completes the proof. \(\square \)

We now establish the local convergence rate of Algorithm 1.

Theorem 3

Let \(X_*\) be an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. Suppose that Assumption 1 holds and \(\Vert H(X_*)\Vert _F\) is sufficiently small, then the sequence \(\{X_k\}\) converges to \(X_*\) linearly. Furthermore, if \(H(X_*)=\mathbf {0}_{n\times n}\), then the sequence \(\{X_k\}\) converges to \(X_*\) quadratically.

Proof

By hypothesis and using Lemma 3 we have \(X_k\rightarrow X_*\) and \(X_{k+1} = R_{X_k}(\varDelta X_k)\) for all k sufficiently large. Using Lemma 7.4.8 and Lemma 7.4.9 in [2], there exist three scalars \(\tau _0,\tau _1,\tau _2>0\) such that for all k sufficiently large,

$$\begin{aligned} \left\{ \begin{array}{l} \tau _0\mathrm{dist}(X_k,X_*)\le \Vert \mathrm{grad}\, h(X_k) \Vert \le \tau _1\mathrm{dist}(X_k,X_*),\\ \Vert \mathrm{grad}\, h(X_{k+1}) \Vert = \Vert \mathrm{grad}\, h\big (R_{X_k}(\varDelta X_{k})\big ) \Vert \le \tau _2 \Vert \mathrm{grad}\, \widehat{h}_{X_k}(\varDelta X_{k}) \Vert . \end{array}\right. \end{aligned}$$
(3.24)

By using Taylor’s formula we have for all k sufficiently large,

$$\begin{aligned} \mathrm{grad}\, \widehat{h}_{X_k}(\varDelta X_k)= & {} \mathrm{grad}\, \widehat{h}_{X_k}(0_{X_k}) +(\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*\circ \mathrm{D}\widehat{H}_{X_k}(0_{X_k})[\varDelta X_k ]\nonumber \\&+\,\mathrm{Hess}\; \widehat{h}_{X_k}(0_{X_k})[ \varDelta X_k ] -(\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*\circ \mathrm{D} \widehat{H}_{X_k}(0_{X_k})[\varDelta X_k ]\nonumber \\&+ \,\int ^1_0 \big ( \mathrm{Hess}\; \widehat{h}_{X_k} (t\varDelta X_k ) - \mathrm{Hess}\; \widehat{h}_{X_k} (0_{X_k}) \big )[ \varDelta X_k ]\mathrm{d}t. \end{aligned}$$
(3.25)

Since H is twice continuously differentiable, it follows from (2.9) and (2.10) that there exist two scalars \(\kappa _3>0\) and \(\delta _3>0\) such that for all \(X\in B_{\delta _3}(X_*)\),

(3.26)

Furthermore, the Hessian operator \(\mathrm{Hess}\; \widehat{h}_{X}\) is Lipschitz-continuous at \(0_X\) uniformly in a neighborhood of \(X_*\), i.e., there exist three scalars \(\kappa _4>0\), \(\delta _4 >0\), and \(\delta _5 > 0\), such that for all \(X\in B_{\delta _4}(X_*)\) and \(\xi _X \in B_{\delta _5}(0_X)\), it holds that

(3.27)

In addition, H is Lipschitz-continuous in a neighborhood of \(X_*\), i.e., there exist two constants \(L>0\) and \(\delta _6 > 0\) such that for all \(X,Y\in B_{\delta _6}(X_*)\),

$$\begin{aligned} \Vert H(X) - H(Y) \Vert _F \le L\mathrm{dist}(X,Y). \end{aligned}$$
(3.28)

From Lemma 1, (2.12), (3.24), (3.25), (3.26), and (3.27), we have for k sufficiently large,

$$\begin{aligned}&\tfrac{\tau _0}{\tau _2}\, \mathrm{dist} (X_{k+1},X_*) \le \Vert \mathrm{grad}\, \widehat{h}_{X_k}(\varDelta X_k) \Vert \nonumber \\&\quad \le \big \Vert \mathrm{grad}\, \widehat{h}_{X_k}(0_{X_k}) + (\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*\circ \mathrm{D} \widehat{H}_{X_k}(0_{X_k})[\varDelta X_k ] \big \Vert \nonumber \\&\qquad +\, \big \Vert \mathrm{Hess}\; \widehat{h}_{X_k}(0_{X_k})[ \varDelta X_k ] -(\mathrm{D}\widehat{H}_{X_k}(0_{X_k}))^*\circ \mathrm{D}\widehat{H}_{X_k} (0_{X_k})[\varDelta X_k ] \big \Vert \nonumber \\&\qquad + \,\left\| \int ^1_0\big ( \mathrm{Hess}\; \widehat{h}_{X_k}(t\varDelta X_k ) -\mathrm{Hess}\; \widehat{h}_{X_k}(0_{X_k})\big )[ \varDelta X_k ] dt \right\| \nonumber \\&\quad \le \Vert \mathrm{grad}\,h(X_k)+(\mathrm{D}\widehat{H}_{X_k} (0_{X_k}))^*\circ \mathrm{D}\widehat{H}_{X_k}(0_{X_k})[\varDelta X_k ] \Vert \nonumber \\&\qquad + \,\kappa _3\Vert H(X_k)\Vert _F\cdot \Vert \varDelta X_k\Vert +\kappa _4 \Vert \varDelta X_k\Vert ^2 \nonumber \\&\quad \le \eta _k \Vert \mathrm{grad}\,h(X_k) \Vert + \kappa _3d_2 \Vert H(X_k)\Vert _F\cdot \Vert \mathrm{grad}\,h(X_k)\Vert + \kappa _4 d_2^2\Vert \mathrm{grad}\,h(X_k)\Vert ^2 \nonumber \\&\quad \le \kappa _3d_2\tau _1\Vert H(X_k)\Vert _F\mathrm{dist} (X_k,X_{*}) + (1+\kappa _4 d_2^2)\Vert \mathrm{grad}\,h(X_k) \Vert ^2 \nonumber \\&\quad \le \kappa _3d_2\tau _1\Vert H(X_k)\Vert _F\mathrm{dist} (X_k,X_{*}) + ( 1 + \kappa _4 d_2^2)\tau _1^2\big (\mathrm{dist}(X_k, X_*)\big )^2. \end{aligned}$$
(3.29)

Thus,

$$\begin{aligned} \mathrm{dist}(X_{k+1}, X_* )\le & {} \displaystyle \tfrac{\tau _1\tau _2}{\tau _0}\kappa _3d_2\Vert H(X_k)\Vert _F\mathrm{dist}(X_k,X_{*}) + \tfrac{\tau _1^2\tau _2}{\tau _0}( 1 + \kappa _4 d_2^2)\big (\mathrm{dist}(X_k, X_*)\big )^2\\= & {} c_1\Vert H(X_k)\Vert _F\mathrm{dist}(X_k,X_{*}) + c_2\big (\mathrm{dist}(X_k, X_*)\big )^2, \end{aligned}$$

where \(c_1:=\tfrac{\tau _1\tau _2}{\tau _0}\kappa _3d_2\) and \(c_2 :=\tfrac{\tau _1^2\tau _2}{\tau _0}( 1 + \kappa _4 d_2^2)\). If \(\Vert H(X_*)\Vert _F\) is sufficiently small, then \(\Vert H(X_k)\Vert _F\) is small enough such that \(c_1\Vert H(X_k)\Vert _F <1\) for all k sufficiently large. Thus if \(\Vert H(X_*)\Vert \) is sufficiently small, then\(\{X_k\}\) converges to \(X_*\) linearly.

If \(H(X_*)=\mathbf {0}_{n\times n}\), then we have from (3.28) for all k sufficiently large,

$$\begin{aligned} \Vert H(X_k) \Vert _F = \Vert H(X_k) - H(X_*)\Vert _F \le L \mathrm{dist}(X_k,X_*). \end{aligned}$$
(3.30)

Using (3.29) and (3.30), we have

$$\begin{aligned} \mathrm{dist}(X_{k+1}, X_* )\le \displaystyle \tfrac{\tau _1\tau _2}{\tau _0} \big (\kappa _3d_2L + ( 1 + \kappa _4 d_2^2)\tau _1\big )\big (\mathrm{dist}(X_k, X_*)\big )^2. \end{aligned}$$

Therefore, if \(H(X_*)=\mathbf {0}_{n\times n}\), then \(\{X_k\}\) converges to \(X_*\) quadratically. This completes the proof. \(\square \)

As a direct consequence of (3.24) and (3.29), we have the following result.

Corollary 1

Let \(X_*\) be an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. Suppose the assumptions in Theorem 3 are satisfied. Then there exist two constants \(\mu _1, \mu _2>0\) such that for all k sufficiently large,

$$\begin{aligned} \Vert \mathrm{grad}\, h(X_{k+1}) \Vert \le \mu _1\Vert H(X_k)\Vert _F \Vert \mathrm{grad}\, h(X_k) \Vert + \mu _2\Vert \mathrm{grad}\, h(X_k) \Vert ^2. \end{aligned}$$

Furthermore, if \(H(X_*)=\mathbf {0}_{n\times n}\), then there exists a scalar \(\bar{\nu }>0\) such that for all k sufficiently large,

$$\begin{aligned} \Vert \mathrm{grad}\, h(X_{k+1}) \Vert \le \bar{\nu }\Vert \mathrm{grad}\, h(X_k) \Vert ^2. \end{aligned}$$

3.3 Injectivity condition

We provide the injectivity condition of \(\mathrm {D} H(X_{*})\), where \(X_*=(\mathbf{c}_*,Q_*,\varLambda _*)\) is an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. Based on (2.4), \(\mathrm {D} H(X_*)\) is injective if and only if the following matrix equation

$$\begin{aligned} \left\{ \begin{array}{l} (A(\varDelta \mathbf {c})-A_0) + Q_*\overline{\varLambda }_* Q_*^T \varDelta QQ_*^T - \varDelta Q\overline{\varLambda }_* Q_*^T -(Q_*P) \varDelta \varLambda (Q_*P)^T = \mathbf {0}_{n\times n}, \\ \hbox {s.t.}\quad (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda ) \in T_{X_*}\mathscr {Z}, \end{array} \right. \end{aligned}$$
(3.31)

has a unique solution \((\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )=(\mathbf {0}_{l},\mathbf {0}_{n\times n}, \mathbf {0}_{(n-m)\times (n-m)})\in T_{X_*}\mathscr {Z}\), where \(\overline{\varLambda }_*:=\mathrm{blkdiag}\left( \varLambda ^*_m ,\varLambda _* \right) \) and P is defined in (2.5).

For \(W\in \mathbb {R}^{n\times n}\) define \(\widehat{\mathrm {vec}}(W) \in \mathbb {R}^{\frac{n(n-1)}{2}}\) by

$$\begin{aligned} \widehat{\mathrm {vec}}(W)_{{\frac{(j-1) (j-2)}{2}+i}} := W_{ij}, \quad 1\le i<j\le n. \end{aligned}$$

This shows that \(\widehat{\mathrm {vec}}(W)\) is a column vector obtained by stacking the strictly upper triangular part of W. For \(\mathbf {w}\in \mathbb {R}^{\frac{n(n-1)}{2}}\) define \(\widehat{\mathrm {skew}}(\mathbf {w}) \in \mathbb {R}^{n\times n}\) by

$$\begin{aligned} \widehat{\mathrm {vec}} \Big (\widehat{\mathrm {skew}}(\mathbf {w})\Big ) := \mathbf {w}, \qquad \widehat{\mathrm {vec}} \Big ( \big (\widehat{\mathrm {skew}}(\mathbf {w})\big )^T \Big ) := -\mathbf {w}, \end{aligned}$$

and

$$\begin{aligned} \big (\widehat{\mathrm {skew}}(\mathbf {w})\big )_{ii}=0, \quad i=1,2,\ldots ,n. \end{aligned}$$

We observe that \(\widehat{\mathrm {skew}}(\mathbf {w})\) is a skew-symmetric matrix constructed from \(\mathbf {w}\). Therefore, \(\widehat{\mathrm {vec}}\) and \(\widehat{\mathrm {skew}}\) are a pair of inverse operators. In addition, there exists a matrix \(\widehat{P}\in \mathbb {R}^{n^2\times \frac{n(n-1)}{2}}\) such that

$$\begin{aligned} \mathrm {vec}\big (\widehat{\mathrm {skew}}(\mathbf {w})\big ) = \widehat{P}\mathbf {w} \end{aligned}$$
(3.32)

for all \(\mathbf {w}\in \mathbb {R}^{\frac{n(n-1)}{2}}\). Since \(\varDelta Q\in T_{Q_*} \mathscr {O}(n)\), there exists a skew-symmetric matrix \(\varDelta \varOmega \in \mathbb {R}^{n\times n}\) such that \(\varDelta Q = Q_*\varDelta \varOmega \). For \(\varDelta \varOmega \in \mathbb {R}^{n\times n}\), it follows from (3.32) that there exists a vector \(\varDelta \mathbf {v}\in \mathbb {R}^{\frac{n(n-1)}{2}}\) such that \(\mathrm {vec}\big (\varDelta \varOmega \big ) = \widehat{P}\varDelta \mathbf {v}\). Thus, we have

$$\begin{aligned} \mathrm {vec}(\varDelta Q) = \mathrm {vec}(Q_*\varDelta \varOmega ) =(I_n \otimes Q_*) \mathrm {vec}(\varDelta \varOmega ) = (I_n \otimes Q_*)\widehat{P} \varDelta \mathbf {v}, \end{aligned}$$
(3.33)

where “\(\otimes \)” means the Kronecker product [7, Definition 7.1.2]. Let \(\widehat{A}\) be an \(n^2\times l\) matrix defined by

$$\begin{aligned} \widehat{A}:= \big [ \mathrm {vec}(A_1), \mathrm {vec}(A_2), \ldots , \mathrm {vec}(A_l) \big ]\in \mathbb {R}^{n^2\times l}. \end{aligned}$$
(3.34)

Since \(\varDelta \varLambda \in \mathscr {D}(n-m)\), there exists a matrix \(G\in {\mathbb {R}}^{(n-m)^2\times (n-m)}\) and a vector \(\varDelta \mathbf{w}\in {\mathbb {R}}^{n-m}\) such that

$$\begin{aligned} \mathrm{vec}(\varDelta \varLambda ) = G\varDelta \mathbf{w}. \end{aligned}$$
(3.35)

Based on (3.33), (3.34), and (3.35), the vectorization of the matrix equation (3.31) is given by

$$\begin{aligned} \Big [ \widehat{A},\; (Q_*\otimes Q_*)(I_n\otimes \overline{\varLambda }-\overline{\varLambda } \otimes I_n)\widehat{P},\;(Q_*P)\otimes (Q_*P)G \Big ] \left[ \begin{array}{c} \varDelta \mathbf {c}\\ \varDelta \mathbf {v}\\ \varDelta \mathbf{w}\end{array}\right] = \mathbf {0}_{n^2}. \end{aligned}$$

Based on the above analysis, we have the following injectivity condition of \(\mathrm {D} H(X_{*})\).

Theorem 4

Let \(X_*=(\mathbf{c}_*,Q_*,\varLambda _*)\) be an accumulation point of the sequence \(\{X_k\}\) generated by Algorithm 1. Then \(\mathrm{D}H(X_*)\) is injective if and only if the following matrix

$$\begin{aligned} \Big [ \widehat{A},\; (Q_*\otimes Q_*)(I_n\otimes \overline{\varLambda }_* -\overline{\varLambda }_*\otimes I_n)\widehat{P},\; (Q_*P)\otimes (Q_*P)G \Big ] \end{aligned}$$

is of full rank.

3.4 Preconditioning technique

We propose a preconditioner for solving (2.11). Here we adapt a centered preconditioner [34, p. 279]. For the CG method, instead of solving (2.11), we solve the following preconditioned linear system

$$\begin{aligned} \left\{ \begin{array}{l} (\mathrm {D}H(X_k))^*\circ M_k^{-1} \circ \mathrm {D}H (X_k)[\varDelta X_k ] =-(\mathrm {D}H(X_k))^*\circ M_k^{-1} [H(X_k)], \\ \text {s.t.} \quad \varDelta X_k \in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}, \end{array}\right. \end{aligned}$$

where \(M_k:T_{H(X_k)}\mathbb {SR}^{n\times n}\rightarrow T_{H(X_k)}\mathbb {SR}^{n\times n}\) is a self-adjoint and positive definite linear operator.

According to (2.4) and (2.6), for \(\varDelta Z_k\in T_{H(X_k)}\mathbb {SR}^{n\times n}\), we have

$$\begin{aligned}&\big (\mathrm {D}H(X_k)\circ (\mathrm {D}H(X_k))^*+ \hat{t}\mathrm {Id}_{T_{H(X_k)} \mathbb {SR}^{n\times n}}\big )[\varDelta Z_k ] \nonumber \\&\quad = (A(\mathbf {v}(\varDelta Z_k))-A_0) + \big [ Q_k\overline{\varLambda }_k Q_k^T,[ Q_k\overline{\varLambda } _kQ_k^T, \varDelta Z_k] \big ] \nonumber \\&\qquad +\, Q_kP\,\mathrm{Diag}\big (P^TQ_k^T \varDelta Z_k Q_kP\big )P^TQ_k^T + \hat{t} \varDelta Z_k, \end{aligned}$$
(3.36)

where \(\hat{t}>0\) is a given constant, and \(\mathrm {Id}_{T_{H(X_k)} \mathbb {SR}^{n\times n}}\) means the identity mapping on \(T_{H(X_k)} \mathbb {SR}^{n\times n}\). Replacing the matrix \(\mathrm{Diag}\big (P^TQ_k^T \varDelta Z_k Q_kP\big )\) in (3.36) by \(P^TQ_k^T \varDelta Z_k Q_kP\), we can construct a centered preconditioner \(M_k\) in the following form:

$$\begin{aligned} M_k[\varDelta Z_k]&:= (A(\mathbf {v}(\varDelta Z_k))-A_0) +(Q_k\overline{\varLambda }_k^2 Q_k^T)\varDelta Z_k -2(Q_k\overline{\varLambda }_k Q_k^T)\varDelta Z_k(Q_k\overline{\varLambda }_k Q_k^T)\nonumber \\&\quad +\, \varDelta Z_k (Q_k\overline{\varLambda }_k^2 Q_k^T) +Q_kPP^TQ_k^T \varDelta Z_k Q_kPP^TQ_k^T + \hat{t} \varDelta Z_k, \end{aligned}$$
(3.37)

for all \( \varDelta Z_k\in T_{H(X_k)}\mathbb {SR}^{n\times n}\). Based on (3.36) and (3.37), the constructed preconditioner \(M_k\) is an approximation of \(\mathrm {D}H(X_k)\circ (\mathrm {D}H(X_k))^*+ \hat{t}\mathrm {Id}_{T_{H(X_k)} \mathbb {SR}^{n\times n}}\).

Given four matrices \(A,B,C,D\in {\mathbb {R}}^{n\times n}\), we have the following properties of the Kronecker product [7, pp. 400–401]:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{vec}(ABC) = (C^T\otimes A)\mathrm{vec}(B), \quad (A\otimes B) (C\otimes D) = (AC)\otimes (BD),\\ (A+B)\otimes C = A\otimes C +B\otimes C, \quad C\otimes (A+B) = C\otimes A + C\otimes B,\\ (A\otimes B)\otimes C = A \otimes (B\otimes C). \end{array} \right. \end{aligned}$$
(3.38)

Using (3.34) we find

$$\begin{aligned} \widehat{A}\widehat{A}^T = \sum _{i=1}^{l} \mathrm {vec}(A_i)\mathrm {vec}(A_i)^T. \end{aligned}$$
(3.39)

From (2.7), (3.37), (3.38), (3.39) we have for any \( \varDelta Z_k\in T_{H(X_k)}\mathbb {SR}^{n\times n}\),

$$\begin{aligned}&\mathrm {vec}\big (M_k [\varDelta Z_k]\big )\nonumber \\&\quad = \mathrm {vec}\Big (\sum _{i=1}^l \mathrm{tr}(A_i^T\varDelta Z_k)\cdot A_i\Big ) +\big ((Q_k I_n Q_k^T)\otimes (Q_k\overline{\varLambda }_k^2 Q_k^T)\big ) \mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad -\,2\big ((Q_k \overline{\varLambda }_k Q_k^T)^T\otimes (Q_k\overline{\varLambda }_k Q_k^T)\big )\mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad +\big ((Q_k\overline{\varLambda }_k^2 Q_k^T)^T\otimes (Q_k I_n Q_k^T)\big ) \mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad +\, \big ( (Q_kPP^TQ_k^T)^T \otimes Q_kPP^TQ_k^T \big ) \mathrm {vec}(\varDelta Z_k) + \hat{t}I_{n^2}\mathrm {vec}(\varDelta Z_k)\nonumber \\&\quad = \sum _{i=1}^l \big (\mathrm {vec}(A_i)\mathrm {vec}(A_i)^T\big ) \mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad + \,\Big ((Q_k\otimes Q_k)\big (I_n \otimes \overline{\varLambda }_k^2 -2\overline{\varLambda }_k\otimes \overline{\varLambda }_k +\overline{\varLambda }_k^2\otimes I_n \big ) (Q_k^T\otimes Q_k^T)\Big )\mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad +\, \big ((Q_k\otimes Q_k)(PP^T\otimes PP^T)(Q_k^T\otimes Q_k^T)\big ) \mathrm {vec}(\varDelta Z_k)\nonumber \\&\qquad +\, \big ((Q_k\otimes Q_k)(\hat{t} I_{n^2}) (Q_k^T\otimes Q_k^T)\big )\mathrm {vec}(\varDelta Z_k)\nonumber \\&\quad = (Q_k \otimes Q_k) \big ( (I_n\otimes \overline{\varLambda }_k -\overline{\varLambda }_k \otimes I_n)^2 + (PP^T)\otimes (PP^T) \nonumber \\&\qquad +\,\hat{t}I_{n^2} \big )(Q_k^T \otimes Q_k^T)\mathrm {vec}(\varDelta Z_k) +\widehat{A}\widehat{A}^T\mathrm {vec}(\varDelta Z_k), \end{aligned}$$
(3.40)

where the equality \(I_n = Q_kI_nQ_k^T\) is used. Let

$$\begin{aligned} \widehat{B}_k : = (Q_k \otimes Q_k)\big ( (I_n \otimes \overline{\varLambda }_k - \overline{\varLambda }_k\otimes I_n)^2 + (PP^T)\otimes (PP^T)+\hat{t}I_{n^2} \big )(Q_k^T \otimes Q_k^T) \end{aligned}$$
(3.41)

and

$$\begin{aligned} \widehat{M}_k : = \widehat{B}_k + \widehat{A}\widehat{A}^T. \end{aligned}$$
(3.42)

From (3.40) and (3.42) we have for \(\varDelta Z_k\in T_{H(X_k)}\mathbb {SR}^{n\times n}\),

$$\begin{aligned} \mathrm {vec}\big (M_k [\varDelta Z_k]\big ) = \widehat{M}_k\mathrm {vec}(\varDelta Z_k) = \big (\widehat{B}_k + \widehat{A}\widehat{A}^T \big )\mathrm {vec}(\varDelta Z_k). \end{aligned}$$
(3.43)

Given two nonsingular matrices \(C_1\in {\mathbb {R}}^{n\times n}\) and \(C_2\in {\mathbb {R}}^{m\times m}\), we have

$$\begin{aligned} (C_1 \otimes C_2)^{-1} = C_1^{-1} \otimes C_2^{-1}. \end{aligned}$$
(3.44)

By using the definition of the matrix P in (2.4) we have

$$\begin{aligned} PP^T = \mathrm{blkdiag}(\mathrm{0}_{m}, I_{n-m}). \end{aligned}$$

Thus the matrix \((I_{n}\otimes \overline{\varLambda }_k -\overline{\varLambda }_k \otimes I_{n})^2 + (PP^T)\otimes (PP^T) +\widehat{t}I_{n^2}\) is a diagonal matrix with positive diagonal entries. Then it follows that the matrix \(\widehat{B}_k\) is invertible. Using (3.41), and (3.44) we have

$$\begin{aligned} \widehat{B}_k^{-1} =(Q_k \otimes Q_k)\big ((I_{n}\otimes \overline{\varLambda }_k - \overline{\varLambda }_k \otimes I_{n})^2 + (PP^T)\otimes (PP^T) +\widehat{t}I_{n^2}\big )^{-1}(Q_k^T \otimes Q_k^T). \end{aligned}$$

Thus \(\widehat{B}_k^{-1}\) can be easily computed.

By (3.39), the matrix \(\widehat{A}\widehat{A}^T\) is a low rank matrix, i.e., \(\mathrm {rank}(\widehat{A}\widehat{A}^T) \le l\). By assumption, \(l<m\le n<n^2\), thus \(\widehat{M}_k\) is a low rank perturbation of \(\widehat{B}_k\). By using the Sherman–Morrison–Woodbury formula [28] we find

$$\begin{aligned} \widehat{M}_k^{-1} = \big (\widehat{B}_k + \widehat{A}\widehat{A}^T\big )^{-1} = \widehat{B}_k^{-1} - \widehat{B}_k^{-1}\widehat{A} \big (I_l + \widehat{A}^T\widehat{B}_k^{-1}\widehat{A} \big )^{-1} \widehat{A}^T\widehat{B}_k^{-1}. \end{aligned}$$
(3.45)

We conclude from (3.45) that, for any vector \(\mathbf {x}\in \mathbb {R}^{n^2}\), the matrix-vector product \(\widehat{M}_k^{-1}\mathbf {x}\) can be computed efficiently, where the main computational cost is to calculate the inverse of \((I_l + \widehat{A}^T\widehat{B}_k^{-1}\widehat{A} )\in {\mathbb {R}}^{l\times l}\).

4 Numerical experiments

In this section we report the numerical performance of Algorithm 1 for solving the PLSIEP II. All the numerical tests are carried out by using MATLAB 7.1 running on a workstation with a Intel Xeon CPU E5-2687W at 3.10 GHz and 32 GB of RAM. To illustrate the efficiency of our algorithm, we compare Algorithm 1 with the LP method in [10].

In our numerical tests, we set \(\beta =0.5\), \(\eta _{\max }=0.01\), \(\sigma =10^{-4}\), and \(\hat{t}=10^{-5}\). The largest number of iterations in Algorithm 1 and the LP method is set to be 30000, and the largest number of iterations in the CG method is set to be \(n^3\). Let ‘CT.’, ‘IT.’, ‘NF.’, ‘NCG.’, ‘Res.’, ‘grad.’ , and ‘err-c.’ denote the averaged total computing time in seconds, the averaged number of outer Gauss–Newton iterations or LP iterations, the averaged number of function evaluations, the averaged total number of inner CG iterations, the averaged residual \(\Vert H(X_k)\Vert _F\), the averaged residual \(\Vert \mathrm{grad\,}h(X_k)\Vert \), and the averaged relative error \(\Vert \mathbf{c}_k-\widehat{\mathbf{c}}\Vert _\infty /\Vert \widehat{\mathbf{c}}\Vert _\infty \) at the final iterates of the corresponding algorithms, accordingly. Here, \(\Vert \cdot \Vert _\infty \) means the vector \(\infty \)-norm.

The stopping criterion for Algorithm 1 and the LP method is set to be

$$\begin{aligned} \Vert \mathrm{grad\,}h(X_k)\Vert < \zeta , \end{aligned}$$

where \(\zeta >0\) is the prescribed tolerance.

We consider the following two examples.

Example 1

We consider the Sturm–Liouville problem of the form:

$$\begin{aligned} -\frac{d^{2}y}{dx^{2}}+q(x)y=\lambda y,\quad 0\le x\le \pi , \end{aligned}$$
(4.1)

where q is a real, square-integrable function and the following Dirichlet boundary conditions are imposed

$$\begin{aligned} y(0)=y(\pi )=0. \end{aligned}$$

By using the Rayleigh–Ritz method in [29], the Rayleigh quotient of (4.1) is given by

$$\begin{aligned} R\big (y(x)\big ) = \frac{ \int ^{\pi }_0 \big ((y'(x))^2 +q(x)y(x)^2\big )\mathrm{d}x}{ \int ^{\pi }_0 y(x)^2 \mathrm{d}x}. \end{aligned}$$

Suppose that \(y(x) = \sum \nolimits _{j=1}^n w_j \sin (jx)\). By simple calculation, we have

$$\begin{aligned}&R\big (y(x)\big )\nonumber \\&\quad = \frac{\sum \nolimits _{i=1}^n \sum \nolimits _{j=1}^n i\cdot j \cdot w_i\cdot w_j \cdot \delta ^i_j {+} \frac{2}{\pi }\cdot \sum \nolimits _{i=1}^n \sum \nolimits _{j=1}^n w_i\cdot w_j \int ^{\pi }_0 q(x) \sin (ix) \sin (jx) \mathrm{d}x }{\sum \nolimits _{i=1}^n \sum \nolimits _{j=1}^n w_i\cdot w_j \cdot \delta ^i_j}, \end{aligned}$$

i.e.,

$$\begin{aligned} R\big (y(x)\big ) = \frac{ \mathbf{w}^T A \mathbf{w}}{\mathbf{w}^T\mathbf{w}}, \end{aligned}$$

where \(\mathbf{w}:= (w_1, w_2, \ldots , w_n)^T\) and the entries of the symmetric matrix \(A=[a_{ij}]\in {\mathbb {R}}^{n\times n}\) are given by

$$\begin{aligned} a_{ij}= & {} i\cdot j \cdot \delta ^i_j +\frac{2}{\pi }\cdot \int ^{\pi }_0 q(x) \sin (ix) \sin (jx) \mathrm{d}x\\= & {} i\cdot j \cdot \delta ^i_j +\frac{2}{\pi } \int ^{\pi }_0 q(x) \frac{\cos \big ((i-j)x\big ) - \cos \big ((i+j)x\big )}{2} \mathrm{d}x, \end{aligned}$$

for \(i,j=1,2,\ldots ,n\). If \(q(x)=2\sum \nolimits _{k=1}^l c_k \cos (2kx)\), then one has

$$\begin{aligned} a_{ij}= i\cdot j \cdot \delta ^i_j + \sum _{k=1}^l c_k \cdot \big (\delta ^{2k}_{|i-j|} -\delta ^{2k}_{i+j} \big ), \quad i,j=1,2,\ldots ,n. \end{aligned}$$

Let \(T_k\ (k=1,2,\ldots , n-1)\) and \(H_k\ (k=1,2, \ldots , 2n-1)\) be \(n\times n\) real matrices generated by the MATLAB built-in functions toeplitz and hankel:

$$\begin{aligned} T_k = \texttt {toeplitz}(\mathbf{e}_{k+1}),\quad k=1,2,\ldots , n-1 \end{aligned}$$

and

$$\begin{aligned} H_k = \left\{ \begin{array}{ll} \texttt {hankel}(\mathbf{e}_k,\mathbf{0}_n), &{} \quad k=1,2,\ldots , n,\\ \texttt {hankel}(\mathbf{0}_n,\mathbf{e}_{k-n+1}), &{}\quad k=n+1,n+2,\ldots ,2n-1. \end{array} \right. \end{aligned}$$

Define

$$\begin{aligned} A_0 = \mathrm{diag}(1,2^2, 3^2, \ldots , n^2), \quad A_k= \left\{ \begin{array}{ll} T_{2k} - H_{2k-1}, &{}\quad 1 \le k \le \min \Big \{l, \frac{n-1}{2}\Big \}, \\ -\,H_{2k-1}, &{} \quad \min \Big \{l, \frac{n-1}{2}\Big \} < k \le l. \end{array} \right. \end{aligned}$$

Then

$$\begin{aligned} A = A_0+\sum _{k=1}^l c_kA_k\equiv A(\mathbf{c}). \end{aligned}$$

To estimate the first l Fourier coefficients of the potential q(x) defined by [29]

$$\begin{aligned} q(x) = \sum _{k=1}^{\infty } \frac{192}{\pi ^4}\frac{1}{k^4}\cos (2kx), \end{aligned}$$

we consider the PLSIEP with above \(\{A_k\}\) and the n eigenvalues of \(A(\widehat{\mathbf{c}})\) as the prescribed spectrum for varying \(n=m\) and l, where the entries of \(\widehat{\mathbf{c}}\) are given by

$$\begin{aligned} \hat{c}_k= \frac{192}{\pi ^4}\frac{1}{k^4}, \quad k=1,2,\ldots ,l. \end{aligned}$$
Table 1 Comparison results for Example 1
Full size table
Table 2 Comparison results for Example 2
Full size table

Example 2

We consider the PLSIEP with varying n, l, and m. Let \(\widehat{\mathbf {c}}\in \mathbb {R}^{l}\) be a random vector and \(A_0,A_1,\ldots ,A_l \) be \(n\times n\) random symmetric matrices, which are generated by the MATLAB built-in function randn:

$$\begin{aligned} \widehat{\mathbf {c}} := \texttt {randn}(l,1),\quad B_k : = \texttt {randn} (n,n), \quad A_k = \frac{1}{2}(B_k + B_k^T), \quad k=0,1,\ldots ,l. \end{aligned}$$

We choose the m smallest eigenvalues of \(A(\widehat{\mathbf{c}})\) as the prescribed partial spectrum.

For Algorithm 1 and the LP method in [10], the starting points are generated by the MATLAB built-in function eig:

$$\begin{aligned} \big [ Q_0, \widetilde{\varLambda } \big ] = \texttt {eig} \,(A(\mathbf{c}_0),\mathrm{'real'}), \quad \varLambda _0 = \widetilde{\varLambda }(m+1:n). \end{aligned}$$

For Example 1, \(\mathbf{c}_0\) is set to be a zero vector. For Example 2, \(\mathbf{c}_0\) is formed by chopping the components of \(\widehat{\mathbf{c}}\) to two decimal places for \(n<100\) and to three decimal places for \(n\ge 100\).

We first apply the LP method and Algorithm 1 to Example 1 with \(\zeta =10^{-6}\). Table 1 displays numerical results for Example 1, where the symbol “*” means the largest number of iterations is reached. We observe that Algorithm 1 with PCG works much better than the LP method in terms of computing time.

Table 3 Numerical results for Example 1
Full size table
Table 4 Numerical results for Example 2
Full size table

Next, we apply the LP method and Algorithm 1 to Example 2 with \(\zeta =10^{-8}\). For comparison purposes, we repeat our experiments over 10 different problems. Table 2 shows numerical results for Example 2. We observe from Table 2 that Algorithm 1 is more effective than the LP method in terms of computing time. We also see that the proposed preconditioner can reduce the number of inner CG iterations effectively.

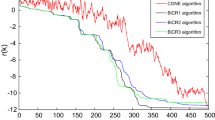
To further illustrate the efficiency of Algorithm 1, we apply Algorithm 1 with the proposed preconditioner to Examples 1 and 2 for varying n, l, m with \(\zeta =10^{-8}\). The corresponding numerical results are displayed in Tables 3 and 4. In Fig. 1, we give the convergence history of Algorithm 1 for two tests. Figure 1 depicts the logarithm of the residual versus the number of outer iterations. We see from Tables 3 and 4 that Algorithm 1 with the proposed preconditioner works very efficient for different values of n, l, m. Finally, the linear or quadratic convergence of Algorithm 1 is observed from Fig. 1, which agrees with our prediction.

Fig. 1
figure 1

Convergence history of two tests

Full size image

5 Conclusions

In this paper, we focus on the parameterized least squares inverse eigenvalue problem where the number of parameters is smaller than the number of given eigenvalues. We have proposed a geometric Gauss–Newton method for solving the problem. We have established the global and linear or quadratic convergence of the proposed method under the assumption that the Riemannian differential \(\mathrm{D}H(\cdot )\) is injective and the residual \(\Vert H(\cdot )\Vert _F\) is sufficiently small or equal to zero at an accumulation point \(X_*\) of the sequence \(\{X_k\}\) generated by our method.

In each outer iteration of the proposed method, the Riemannian Gauss–Newton equation is solved approximately by the CG method. However, the Riemannian Gauss–Newton equation is often ill-conditioned. To improve the efficiency of our method, we have constructed a preconditioner by investigating the special structure of the Riemannian Gauss–Newton equation. Numerical results show that the proposed preconditioner can reduce the number of inner CG iterations and the computational time very effectively. Thus our method can be applied to solve large-scale problems.

Finally, we should point out that the proposed method may not be effective as expected if the differential \(\mathrm{D}H(X_*)\) is not injective or the residual \(\Vert H(X_*)\Vert _F\) is not small enough. This needs further study.