1 Introduction

In this paper, we are concerned with numerical integration of ordinary differential equations with some invariants. For example, let us consider the Hamiltonian systems:

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t} = J \nabla H (y(t)) ,\quad y(0) = y_0 \in \mathbb {R}^N, \end{aligned}$$
(1.1)

where J is the symplectic matrix and \(H:\mathbb {R}^N \rightarrow \mathbb {R}^N\) is the Hamiltonian. We also call it an energy function. From the formulation (1.1), we see that the exact solution of the Hamiltonian system preserves the energy function H:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} H(y(t)) = \nabla H (y(t))^\top \frac{\mathrm{d}y}{\mathrm{d}t} =\nabla H(y(t))^\top J \nabla H (y(t)) = 0, \end{aligned}$$
(1.2)

where we used the chain rule and the skew symmetry of J. Such ODEs with (possibly multiple) invariants appear in wide range of modern science and engineering.

For such systems, we hope that numerical solutions preserve the invariants, but generally such expectation does not come true. In fact, Runge–Kutta (RK) methods cannot preserve energy function in general [7]. Hence, in these several decades, several invariants-preserving methods have been constructed (e.g. [1, 3, 9, 18, 20]). Then it has been proved that such methods are in fact stabler than general RK methods, and often well compare with other geometric numerical integration methods, such as symplectic methods for Hamiltonian systems [13].

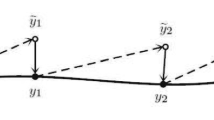
Energy-preserving methods for the Hamiltonian systems (1.1) (or more generally, systems with invariants) can be divided into two groups: (i) methods whose numerical solutions automatically satisfy \(H(y_{n+1}) = H(y_{n})\) without using H or \(\nabla H\) explicitly (e.g. [9, 17, 19]), and (ii) methods that first get a temporary solution \(\widetilde{y}_{n+1}\) by some method, and obtain the next solution \(y_{n+1}\) by projecting the temporary solution \(\widetilde{y}_{n+1}\) to some \(y_{n+1}\) satisfying \(H(y_{n+1}) = H(y_{n})\) (e.g. [2, 4, 8, 11]). Although methods in the first group generate stable numerical solutions, they demands the solution of at least N dimensional nonlinear system at every time step, thus demand much computation time when N is large. Even worse, most of them have only second order accuracy, and demand extra computational cost when further accuracy is necessary [12, 21]. In contrast to this, some methods in the second group only require the solution of a single nonlinear equation (instead of N) in every time step, while keeping the same accuracy as the base integrator. Therefore, from the view of actual computation, the second group seems more promising unless we can count on some fast nonlinear solvers.

Here we review typical methods of the second group. Orthogonal projection method (OPM) [13] projects \(\widetilde{y}_{n+1}\) along \(\nabla H(\widetilde{y}_{n+1})\) to obtain the next solution \(y_{n+1}\) satisfying \(H(y_{n+1}) = H(y_n)\). Calvo–Hernández-Abreu–Montijano–Rández [4] proposed a projection method called “incremental direction technique” (IDT) that searches the next solution along the direction \(\widetilde{y}_{n+1} - \overline{y}_{n+1}\), where \(\overline{y}_{n+1}\) is the solution by an embedded Runge–Kutta method. In contrast to these linear methods, recently a method called EQUIP method that searches for \(y_1\) nonlinearly has been proposed by Brugnano–Iavernaro–Trigiante [2]. The key of the method is the clever use of the W-transformation associated with collocation methods.

Next let us focus on their solvability and accuracy. The known results gave in the above mentioned studies can be reorganized in more general context as follows. Let us introduce the concept of “1-parameter projection method”: we first prepare a family of integrators \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) depending on 1-parameter \(\alpha \); then, in every time step, we adjust \(\alpha \) such that \(H(\varPhi _\alpha (y_0)) = H(y_0)\) holds. This concept includes the OPM, IDT and EQUIP, and forms a wider class of energy-preserving methods. By an obvious generalization of the result of [2], we can prove that “1-parameter projection method” is solvable and has the same order of accuracy as the base integrator \(\varPhi \) under quite reasonable assumptions (see Theorem 2). This implies, at least theoretically, that all 1-parameter projection methods achieve high accuracy with low computational cost.

Although this gives a clear support for all the 1-parameter projection methods, here a natural question arises from the viewpoint of actual computation: which method among all the “1-parameter projection methods” is actually the best in terms of stability and computational efficiency? Moreover, how can we construct it systematically? Theoretical results mentioned above are of course mathematically quite important, but do not answer these questions, because they hold only for sufficient small time step h, and thus do not necessarily provide information on the behavior under practical size of h. Some new perspective is needed to answer these questions. To this end, let us again review each existing 1-parameter projection method and consider whether it can be the ideal answer for the questions. OPM and IDT introduced before may be the answers, since they can be arbitrary accurate and only require the solution of a 1-dimensional nonlinear equation, i.e., they are highly efficient. Between these methods, IDT is generally considered to be better because it preserves linear invariants; thus let us below consider IDT with more details. IDT searches the next solution linearly along the difference of two numerical solutions constructed by an embedding Runge–Kutta method with no extra function evaluation. Thus this method needs surprisingly low computational costs while keeping the original high accuracy, as mentioned above. In this sense, IDT is quite a good method. However, it has a slight drawback that when the direction \(\widetilde{y}_{n+1} - \overline{y}_{n+1}\) happens to be almost orthogonal to \(\nabla H\), the projection can be quite unstable, i.e., the next solution might be far away from the exact solution. In other words, the correction of the projection can be huge, and that may lead to some instability. One way of working around this is to employ some adaptive step size technique. In this case, IDT is really a good method, and practical. Nevertheless, we feel that this observation reveals the possible essential limitation of the linear search methods—they can yield fatal projection steps when they fail to suggest good directions. This can happen in all linear search methods including OPM.

Another good candidate as the best 1-parameter projection method is EQUIP method. Since it is based on the W-transformation, its parameterization does not destroy the symplecticity of the Gauss method, which was the main subject in [2]. In the present paper, however, we like to see the method from a different perspective. In [2], the authors chose to discard linear search, and turn to a completely new idea of projection, where they introduced a clever, natural parameterization of the Gauss method. There, the “search” is no longer linear, but thanks to the new view as a parameterized Gauss method, the correction by the projection is expected to remain relatively small, avoiding possible fatal projections in linear search methods. In fact, in [2], numerical examples show that EQUIP runs stably with constant time steps. However, because the Gauss method is implicit, EQUIP method also demands the solution of high dimensional nonlinear equations in every time step. Therefore, although EQUIP method can generate much stabler numerical solutions, we like to continue the journey to “the best” method, unless the computational cost can be substantially decreased by, for example, the clever use of multiple core implementations.

From the discussion above, we are encouraged to construct 1-parameter projection methods based on explicit Runge–Kutta methods for low computational cost. At the same time, we hope to keep the good nature of EQUIP, i.e., the natural parameterization of such RK methods for their stability. If we succeed in this challenge, we expect that such methods can be the definitive answer for the questions.

The key idea for this challenge in the present paper is as follows. Recall that the natural parameterization in EQUIP was done by viewing the Gauss method as collocation method. But exactly this very trick implied the implicitness of the resulting schemes. Then, how can we do a similar thing based on explicit RK methods? The idea here is that we interpret explicit RK methods as perturbed collocation methods as proposed by Nørsett–Wanner [16]. With the aid of perturbation operators, perturbed collocation methods can express larger class of RK methods, including both explicit and implicit ones. Then we basically follow the strategy in EQUIP; we first consider a RK method and its perturbed collocation method representation. Then we try to find a natural way to parameterize the representation, so that the modification (which will result in the correction of the projection) remains as small as possible. The latter step is quite different from that of EQUIP. In EQUIP method, the small correction was made in terms of the W-transformed expression of the Gauss method. In the perturbed collocation method, however, no corresponding expression exists. Instead, in the present paper, we propose to introduce parameterization only in higher order perturbation terms. This sounds natural for achieving as small correction as possible. This task is, however, not straightforward as one would simply imagine. Since as described above the perturbed collocation method can express both explicit and implicit RK methods, inappropriate parameterization of explicit RK methods should destroy the explicitness and result in implicit schemes. This is not what we hope in terms of computational cost. In the present paper, we show that this difficulty can be worked around by using the characterization of explicitness obtained by Nørsett–Wanner [16]. We also would like to point out that the idea of perturbed collocation methods has not been intensively utilized recently, as far as the author understands—in this sense, the present work might be interesting for related researchers in that it breathes new life into perturbed collocation methods themselves.

This paper is organized as follows. In Sect. 2, we introduce perturbed collocation methods and the general theory for 1-parameter projection methods. In Sect. 3, we propose a new method via perturbed collocation methods. In Sect. 4, we test the proposed method and show its stability and efficiency comparing with existing methods. In Sect. 5, we give conclusions of this paper.

2 Preliminaries

2.1 Perturbed collocation methods

Here we give a brief review of perturbed collocation methods [16]. These methods are proposed mainly to expand the relation between the collocation methods and some implicit RK methods. In fact, perturbed collocation methods can express a larger class of RK methods, including some explicit RK methods.

First, we introduce the perturbation operator.

Definition 1

(Perturbation operator [16]) Let \({\varPi }_s\) be the linear space of s-degree polynomials. Then the perturbation operator \(P_{t_0,h} :{\varPi }_s \rightarrow {\varPi }_s\) is defined as below:

$$\begin{aligned} (P_{t_0,h} u) (t) := u(t) + \sum _{j=1}^s N_j\left( \frac{t-t_0}{h}\right) u^{(j)} (t_0) h^j, \end{aligned}$$
(2.1)

where \(N_j(t)\ (j=1,\ldots ,s)\) are s-degree polynomials defined as

$$\begin{aligned} N_j (t)&= \frac{1}{j!} \sum _{i=0}^s \left( p_{ij} - \delta _{ij} \right) t^i ,\end{aligned}$$
(2.2)
$$\begin{aligned} p_{ij}&\in \mathbb {R} \quad (i=0,1,\ldots ,s;\ j=1,2,\ldots ,s),\end{aligned}$$
(2.3)
$$\begin{aligned} \delta _{ij}&= \left\{ \begin{aligned}&1, \quad \mathrm{if}\ i=j,\\&0, \quad \mathrm{otherwise}. \end{aligned} \right. \end{aligned}$$
(2.4)

For convenience, \(t_0\) and h will be omitted when they are fixed. Using this perturbation operator, we define the perturbed collocation method.

Definition 2

(Perturbed collocation methods [16]) Let s be a positive integer and P a perturbation operator. There is an s-degree polynomial u(t) satisfying the following conditions:

$$\begin{aligned} u(t_0)&= y_0,\end{aligned}$$
(2.5)
$$\begin{aligned} \dot{u}(t_0 + c_i h)&= f(Pu(t_0 + c_i h)) \qquad (1 \le i \le s). \end{aligned}$$
(2.6)

Then the numerical solution of perturbed collocation methods is defined by \(y_1 := u(t_0 + h)\).

From these definitions, we see perturbed collocation methods are an extension of collocation methods in the sense that they reduce to collocation methods when P is the identity operator.

Next we review the relation between perturbed collocation methods and RK methods.

Proposition 1

[16] The perturbed collocation method defined by (2.5) and (2.6) is equivalent to a Runge–Kutta method whose coefficients are the entries of

$$\begin{aligned} A&= V_c \ P \ J \ V^{-1} , \end{aligned}$$
(2.7)
$$\begin{aligned} {\varvec{b}}&= (1,\ldots ,1)^\top J V^{-1}, \end{aligned}$$
(2.8)

where

$$\begin{aligned} V_c&= \begin{pmatrix} 1 &{}\quad c_1 &{}\quad \ldots &{}\quad {c_1}^{s} \\ \vdots &{}\quad &{}\quad &{}\quad \vdots \\ 1 &{}\quad c_s &{}\quad \ldots &{}\quad {c_s}^{s} \end{pmatrix} ,\quad P = \begin{pmatrix} 1 &{}\quad p_{01} &{}\quad \ldots &{}\quad p_{0s} \\ 0 &{}\quad \vdots &{}\quad &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \vdots \\ 0 &{}\quad p_{s1} &{}\quad \ldots &{}\quad p_{ss} \end{pmatrix} ,\end{aligned}$$
(2.9)
$$\begin{aligned} J&= \begin{pmatrix} 0 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad 1/2 &{}\quad \ldots &{}\quad 0 \\ \ldots &{}\quad \ldots &{}\quad \ldots &{}\quad \ldots \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad 1/s \end{pmatrix} , \quad V = \begin{pmatrix} 1 &{}\quad c_1 &{}\quad \ldots &{}\quad {c_1}^{s-1} \\ \vdots &{}\quad &{}\quad &{}\quad \vdots \\ 1 &{}\quad c_s &{}\quad \ldots &{}\quad {c_s}^{s-1} \end{pmatrix}. \end{aligned}$$
(2.10)

Conversely, a Runge–Kutta method that satisfies (2.8) and has distinct \(\{c_i\}_{1 \le i \le s}\) can be expressed by a perturbed collocation method.

Remark 1

It is not unique how to express a RK method by perturbed collocation methods. Let us consider polynomial \(M(t) = \prod _{i=1}^s (t-c_i)\). Adding this M to \(N_j\) (which compose the perturbation operator P) does not change the perturbed collocation method (see [16, Prop. 4]). From this observation, we see that we can always express a RK method by a perturbed collocation method whose perturbation operator is \(P :{\varPi }_s \rightarrow {\varPi }_{s-1}\); in other words, \(p_{sj} = 0\ (j=1,\ldots ,s)\). Hence we assume \(Pu \in {\varPi }_{s-1}\) in what follows.

This proposition shows that perturbed collocation methods form a subclass of RK methods. Moreover, in [16], a characterization for a perturbed collocation method being an explicit RK method was given. This characterization will play a key role in the clever parameterization of explicit RK methods in Sect. 3.

Proposition 2

[16] We consider a perturbed collocation method that satisfies \(Pu \in {\varPi }_{s-1}\) and define its RK coefficients triple by \((A,{\varvec{b}},{\varvec{c}})\). Then the entry \(a_{ij}\) is zero if and only if the vector

$$\begin{aligned} \left( (N_1 + t)(c_i),\ldots ,(s-1)!\left( N_s + \frac{t^s}{s!}\right) (c_i)\right) ^\top \end{aligned}$$
(2.11)

is a linear combination of

$$\begin{aligned} (1,\ldots ,{c_k}^{s-1})^\top \quad (k=1,\ldots ,j-1,j+1,\ldots ,s). \end{aligned}$$
(2.12)

Moreover, a perturbed collocation method which satisfies \(Pu \in {\varPi }_{s-1}\) corresponds with an explicit Runge–Kutta method if and only if the perturbation operator P satisfies (2.12) for \(1 \le i \le j \le s\).

2.2 A general theory for 1-parameter projection methods

As we mentioned in the introduction, we introduce a general theory for 1-parameter projection methods. This theory is easily obtained by extending the results of Brugnano–Iavernaro–Trigiante [2] (similar results can be found in Calvo–Hernández-Abreu–Montijano–Rández [4]). First we define a family of integrators.

Definition 3

We call \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) a family of integrators with order reduction r when each integrator \(\varPhi _\alpha \ (\alpha \ne 0)\) is well-defined and has order \(p-r\), where p is the order of the “base integrator” with \(\alpha =0\), i.e., \(\varPhi _0\). We also define the solution curve \(y_1(\alpha ,h) := \varPhi _\alpha (y_0)\).

In order to implement 1-parameter projection methods, we need to solve the following nonlinear equation in terms of \(\alpha \) with h fixed:

$$\begin{aligned} g(\alpha ,h) = H(y_1(\alpha ,h)) - H(y_0). \end{aligned}$$
(2.13)

Under this general setting, we can prove the existence of solutions of (2.13) and the recovery of the order. To prove them, we suppose that the following assumptions \(\mathscr {B}_1\) and \(\mathscr {B}_2\) hold for \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) for a fixed state \(y_0\).

  • \(\mathscr {B}_1^{}\): \(g(\alpha ,h)\) is analytic near the origin.

  • \(\mathscr {B}_2^{}\): Let d be the order of the error in the energy function H when the base method is applied:

    $$\begin{aligned} g(0,h) = H(y_1(0, h)) - H(y_0) = c_0 h^d + \mathscr {O} (h^{d+1}), \end{aligned}$$
    (2.14)

    where \(c_0 \ne 0\). Then, for any fixed \(\alpha \in \mathbb {R}\ (\alpha \ne 0)\),

    $$\begin{aligned} g(\alpha ,h) = c(\alpha ) h^{d-r} + \mathscr {O} (h^{d-r+1}) \end{aligned}$$
    (2.15)

    holds with \(c'(0) \ne 0\).

The above setting basically follows [2]. Here we rephrase the underlying idea. From the fact that the base integrator \(\varPhi \) has order p, it is obvious d is generally \(p+1\). But it can happen that \(d>p+1\) holds coincidentally, and we do not hope to exclude such cases. Thus we define d as the lowest integer with nonzero \(c_0\) and \(c'(0)\). The order \(p-r\) for \(g(\alpha ,h)\) comes from the fact that an integrator \(\varPhi \in \{\varPhi _{\alpha }\}_{\alpha \in {\mathbb R}}\) with a fixed \(\alpha \) has order \(p-r\).

Under these assumptions we prove the existence of the solution for (2.14). This is essentially by Brugnano–Iavernaro–Trigiante [2], although there they focused on EQUIP method.

Theorem 1

Let us assume \(\mathscr {B}_1\) and \(\mathscr {B}_2\). Then there exists a positive number \(h_0^*\) and a function \(\alpha ^* (h)\) s.t.

  1. (1)

    \(g(\alpha ^*(h),h) = 0 , \quad h \in (-h_0^*,h_0^*) ,\)

  2. (2)

    \(\alpha ^* (h) = \mathrm{const} \cdot h^r + \mathscr {O} (h^{r+1}).\)

Proof

The following proof is a straightforward extension of the proof in [2]. From the assumptions, \(g(\alpha ,h)\) can be expanded as

$$\begin{aligned} g(\alpha ,h) = \sum _{j=d}^{\infty } \frac{1}{j!} \frac{\partial ^j g}{\partial h^j}(0,0) h^j + \sum _{ i=1}^{\infty } \sum _{j=d-r}^{\infty } \frac{1}{i!j!} \frac{\partial ^{i+j} g}{\partial \alpha ^i \partial h^j} (0,0) \alpha ^i h^j. \end{aligned}$$
(2.16)

The first term comes from (2.14), and the second from (2.15). Then we hope to apply the implicit function theorem to search for a solution in the form of \(\alpha (h) = \eta (h) h^r\), where \(\eta (h)\) is a real-valued function of h. To this end, we consider the change of variable \(\alpha = \eta h^r\) and insert it into (2.16) to get

$$\begin{aligned} g(\alpha ,h)&= \frac{1}{d!} \frac{\partial ^d g}{\partial h^d} (0,0) h^d + \frac{1}{(d+1)!} \frac{\partial ^{d+1} g}{\partial h^{d+1}} (0,0) h^{d+1} \nonumber \\&\quad + \frac{1}{(d-r)!} \frac{\partial ^{d-r+1} g}{\partial \alpha \partial h^{d-r}} (0,0) h^d \eta +\frac{1}{(d-r+1)!} \frac{\partial ^{d-r+2} g}{\partial \alpha \partial h^{d-r+1}} (0,0) h^{d+1} \eta \nonumber \\&\quad + \mathscr {O}(h^{d+2}). \end{aligned}$$
(2.17)

Hence, for \(h \ne 0\), \(g(\alpha ,h) = 0\) if and only if

$$\begin{aligned} \widetilde{g} (\eta ,h) \!&=\! \frac{1}{(d-r\!+\!1)\cdots (d-1)d} \frac{\partial ^d g}{\partial h^d} (0,0) \!+\! \frac{1}{(d-r+1)\cdots d(d\!+\!1)} \frac{\partial ^{d+1} g}{\partial h^{d+1}}(0,0)h \nonumber \\&\quad + \frac{\partial ^{d-r+1} g}{\partial \alpha \partial h^{d-r}} (0,0) \eta +\frac{1}{d-r+1} \frac{\partial ^{d-r+2} g}{\partial \alpha \partial h^{d-r+1}} (0,0) h \eta \nonumber \\&\quad + \mathscr {O}(h^2), \end{aligned}$$
(2.18)

is zero. By the assumption \(\mathscr {B}_2\), \(\frac{\partial ^{d-r+1}g}{\partial \alpha \partial h^{d-r}} (0,0)\) is not zero, and we can apply the implicit function theorem which ensures that there is a real-valued function \(\eta (h)\) satisfying \(\widetilde{g}(\eta (h),h) = 0\). In addition, from (2.18), \(\eta (h)\) is calculated as follows. For sufficiently small h,

$$\begin{aligned} \eta (h)&= -\frac{\frac{1}{(d-r+1)\cdots (d-1)d} \frac{\partial ^d g}{\partial h^d} (0,0) + \frac{1}{(d-r+1)\cdots d(d+1)} \frac{\partial ^{d+1} g}{\partial h^{d+1}}(0,0)h + \mathscr {O}(h^2)}{\frac{\partial ^{d-r+1} g}{\partial \alpha \partial h^{d-r}} (0,0) + \frac{1}{d-r+1} \frac{\partial ^{d-r+2} g}{\partial \alpha \partial h^{d-r+1}} (0,0) h }\nonumber \\&=- \frac{1}{(d-r+1)\cdots (d-1)d} \frac{\frac{\partial ^d g}{\partial h^{d}}(0,0)}{\frac{\partial ^{d-r+1}g}{\partial \alpha \partial h^{d-r}} (0,0)} + \mathscr {O}(h). \end{aligned}$$
(2.19)

Note that \(\frac{\partial ^d g}{\partial h^{d}}(0,0)\) is not zero from \(\mathscr {B}_2\). This reveals that the solution of \(g(\alpha ,h) = 0\) for \(\alpha \) takes the form

$$\begin{aligned} \alpha ^* (h) = \eta (h) h^r = - \frac{1}{(d-r+1)\cdots (d-1)d} \frac{\frac{\partial ^d g}{\partial h^{d}}(0,0)}{\frac{\partial ^{d-r+1}g}{\partial \alpha \partial h^{d-r}} (0,0)} h^r + \mathscr {O} (h^{r+1}). \end{aligned}$$
(2.20)

This completes the proof.

From this theorem 1-parameter projection method recovers its order to the same order as the base integrator.

Theorem 2

Let us consider 1-parameter projection methods defined in Definition 3. These methods have the same order as the base integrator under the mild assumptions \(\mathscr {B}_1\) and \(\mathscr {B}_2\).

Proof

The following proof is also an obvious replication of the proof of [2]. Then we apply the mean value theorem to obtain

$$\begin{aligned} y_1(\alpha ,h) = y_1(0,h) + \alpha \int _0^1 \frac{\partial y_1}{\partial \alpha } (\tau \alpha ,h) \mathrm{d} \tau . \end{aligned}$$
(2.21)

When \(\alpha \) is fixed, the solution \(y_1(\alpha ,h) \) has the accuracy \(\mathscr {O} (h^{p+1-r})\) because of Definition 3. On the other hand, the solution \(y_1(0,h)\) provided by the base integrator is \(\mathscr {O} (h^{p+1})\). Therefore we see

$$\begin{aligned} \int _0^1 \frac{\partial y_1}{\partial \alpha } (\tau \alpha ,h) \mathrm{d} \tau = \mathscr {O} (h^{p+1-r}). \end{aligned}$$
(2.22)

If we define \(\alpha ^*\) as the solution of (2.14), then from Theorem 1, we have \(\alpha ^* = \mathscr {O}(h^r)\) thus

$$\begin{aligned} y_1(\alpha ^*,h) - y(t_0 +h)= y_1(0,h) - y(t_0+h) + \alpha ^* \int _0^1 \frac{\partial y_1}{\partial \alpha } (\tau \alpha ,h) \mathrm{d} \tau = \mathscr {O}(h^{p+1}). \end{aligned}$$
(2.23)

This completes the proof.

3 Construction of new schemes

The proposed method belongs to 1-parameter projection methods. Thus we begin with the construction of a family of integrators \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\).

3.1 Deriving a family of 1-parameter explicit Runge–Kutta methods

In what follows, we will propose how to construct a family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) of explicit RK methods. As we saw in Sect. 2, by perturbing classical collocation methods, we can express larger class of RK methods. Recall that EQUIP method aimed at a natural parameterization via collocation method which led to small correction. In the present explicit RK method context, we parameterize higher order terms of perturbation operators, hoping it leads to small correction in a similar manner. In this project, a special care is needed to keep the explicitness.

Our construction of a family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) of explicit RK methods consists of three steps.

Definition 4

We derive a family of explicit Runge–Kutta methods in the following three steps.

  • Step 1. Take an explicit RK method which can be expressed by a perturbed collocation method with \(\{ N_j\}_{1 \le j \le s} \) and \(c_i \ (i = 1,\ldots ,s)\).

  • Step 2. Calculate \(d_{s-1}, d_s\) by Gaussian elimination of the following matrix

    $$\begin{aligned} \begin{pmatrix} 1 &{} c_1 &{} \ldots &{} \ldots &{} {c_1}^{s-1} \\ \vdots &{} &{} &{} &{} \\ 1 &{} c_{s-1} &{} \ldots &{} \ldots &{} {c_{s-1}}^{s-1} \end{pmatrix} \rightarrow \begin{pmatrix} 1 &{} c_1 &{} \ldots &{} \ldots &{} {c_1}^{s-1} \\ \vdots &{} &{} &{} &{} \\ 0 &{} \cdots &{} 0 &{} \widehat{d}_{s-1} &{} \widehat{d}_s \end{pmatrix}. \end{aligned}$$
    (3.1)

    Then we take \(d_{s-1},d_s\) as

    $$\begin{aligned} d_{s-1} = \frac{1}{(s-2)!} \widehat{d}_{s-1}, \quad d_s = \frac{1}{(s-1)!} \widehat{d}_s. \end{aligned}$$
    (3.2)

  • Step 3. Make a family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) of perturbed collocation methods whose expressions are \(\{\widetilde{N}_j\}_{1 \le j \le s} \) and \(c_i \ (i = 1,\ldots ,s)\):

    $$\begin{aligned} \widetilde{N}_j&= N_j \quad (j=1,\ldots ,s-2) , \end{aligned}$$
    (3.3)
    $$\begin{aligned} \widetilde{N}_{j}&= N_j + \alpha d_{j} \prod _{k=1}^{s-1} (t-c_k)\quad (j=s-1,s). \end{aligned}$$
    (3.4)

    This family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) is in fact a family of explicit RK methods.

Here we illustrate these steps taking an example.

Example 1

(Based on the 3/8 formula) We consider the 3/8 formula which is a 4-stage explicit RK method.

Step 1. Take the 3/8 formula whose coefficient triple is \((A,{\varvec{b}},{\varvec{c}})\) shown in Table 1.

Table 1 Butcher Tableau of the 3/8 formula
Full size table

This method can be expressed as the perturbed collocation method with \((\{N_j\}_{1\le j \le s},\{c_i\}_{1 \le i \le s})\):

$$\begin{aligned}&N_1(t) = 0,\end{aligned}$$
(3.5)
$$\begin{aligned}&N_2(t) = - \frac{7}{6} t + 4 t^2 - 3t^3,&\end{aligned}$$
(3.6)
$$\begin{aligned}&N_3(t) = -\frac{1}{12} t + \frac{1}{4} t^2 - \frac{1}{6}t^3 ,\end{aligned}$$
(3.7)
$$\begin{aligned}&N_4(t) = \frac{5}{324} t - \frac{1}{12} t^2 + \frac{1}{9} t^3 -\frac{1}{24} t^4,&\end{aligned}$$
(3.8)
$$\begin{aligned}&c_1 = 0,\ c_2 = 1/3,\ c_3 = 2/3,\ c_4 = 1.&\end{aligned}$$
(3.9)

These can be calculated from the relation (2.7). Note that this expression satisfies \(Pu \in {\varPi }_{s-1}\) (\(p_{sj} = 0\ (j=1,\ldots ,s)\)).

Step 2. To calculate \(d_3,d_4\), the matrix is transformed into rank normal form.

$$\begin{aligned} \begin{pmatrix} 1 &{}\quad c_1 &{}\quad {c_1}^2 &{}\quad {c_1}^{3} \\ 1 &{}\quad c_2 &{}\quad {c_2}^2 &{}\quad {c_2}^3 \\ 1 &{}\quad c_3 &{}\quad {c_3}^2 &{}\quad {c_3}^{3} \end{pmatrix} = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 1/3 &{}\quad 1/9 &{}\quad 1/27 \\ 1 &{}\quad 2/3 &{}\quad 4/9 &{}\quad 8/27 \end{pmatrix}\nonumber \\ \overset{\mathrm{Gaussian\ elimination}}{\longrightarrow } \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1/3 &{}\quad 1/9 &{}\quad 1/27 \\ 0 &{}\quad 0 &{}\quad 2/9 &{}\quad 2/9 \end{pmatrix} \end{aligned}$$
(3.10)

Then we obtain \(d_3,d_4\) as those satisfying \((2! d_3, 3! d_4) = (2/9,2/9) \Leftrightarrow (d_3,d_4) = (1/9,1/27)\).

Step 3. Construct a family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) whose expressions are \((\{\widetilde{N}_j\}_{1\le j \le s},\{c_i\}_{1 \le i \le s})\):

$$\begin{aligned}&\widetilde{N}_1(t) = 0, \end{aligned}$$
(3.11)
$$\begin{aligned}&\widetilde{N}_2(t) = - \frac{7}{6} t + 4 t^2 - 3t^3,&\end{aligned}$$
(3.12)
$$\begin{aligned}&\widetilde{N}_3(t) = -\frac{1}{12} t + \frac{1}{4} t^2 - \frac{1}{6}t^3 + \frac{1}{9} \alpha t \left( t-\frac{1}{3}\right) \left( t-\frac{2}{3}\right) ,&\end{aligned}$$
(3.13)
$$\begin{aligned}&\widetilde{N}_4(t) = \frac{5}{324} t - \frac{1}{12} t^2 + \frac{1}{9} t^3 -\frac{1}{24} t^4 + \frac{1}{27} \alpha t \left( t-\frac{1}{3}\right) \left( t-\frac{2}{3}\right) ,&\end{aligned}$$
(3.14)
$$\begin{aligned}&c_1 = 0,\ c_2 = 1/3,\ c_3 = 2/3,\ c_4 = 1.&\end{aligned}$$
(3.15)

This family has the coefficients in Table 2 as RK methods. It is easy to see that the method has order 3 for all values of \(\alpha \) and has order 4 for \(\alpha = 0\).

Table 2 The family of the proposed explicit RK method based on the 3/8 formula
Full size table

Some comments on each step are in order.

Comment for Step 1. Recall the claim that RK methods satisfying (2.8) and having distinct \(c_i\)’s are equivalent to perturbed collocation methods. In addition, s must be greater than 3 for Step 1 to be well-defined.

Comment for Step 2. A crucial observation here is that this step is always feasible.

Lemma 1

Step 2 in Definition 4 is always feasible.

Proof

The base integrator chosen in Step 1 can be expressed as a perturbed collocation method, and thus \(c_i\)’s are distinct and a \((s-1) \times (s-1)\) sub-matrix of the left hand side matrix in (2.2) is a Vandermonde matrix. In other words, its rank is \(s-1\), and we can always transform the matrix into a ladder matrix whose bottom row has the form \((0,\ldots ,0,*,*)^\top \).

Comment for Step 3. This step does not destroy the characterization of explicit RK method. This is ensured by Theorem 3 below. Before its proof, we mention the idea of the parameterization. As we mentioned in the beginning of this section, we aim (i) to parameterize higher order terms of a perturbation operator and (ii) to construct a family \(\{\varPhi _\alpha \}_{\alpha \in \mathbb {R}}\) of explicit RK methods. The construction in Definition 4 is designed to achieve the above two goals.

For (i), recall (3.3) and (3.4). An important observation here is that parameterizing only \(N_s\) is not feasible as we can see in the proof of Theorem 3 and the characterization Proposition 2. The matrix (3.1) in Step 2 has \(s-1\) rank, and thus, in general, vectors of the forms \((0,0,\ldots ,0,*)^\top \) cannot be composed by linear combinations of (2.12). In other words, parameterizing only \(N_s\) leads to a family of implicit RK methods in general. This encourages us to employ the parameterization in Definition 4.

For (ii), the key idea is to add \(\prod _{k=1}^{s-1} (t-c_k)\) to \(N_j\ (j=s-1,s)\). Leaving its detail to the proof of Theorem 3, here we emphasize that the polynomial \(\prod _{k=1}^{s-1} (t-c_k)\) vanishes for \(t=c_j \ (j=1,\ldots ,s-1)\), which realizes (ii).

Theorem 3

The family of the perturbed collocation methods constructed in Definition 4 is actually a family of explicit RK methods.

Proof

Let \((A,{\varvec{b}},{\varvec{c}})\) be a coefficients triple of an explicit RK method in Step 1 and \((\{N_j\}_{1 \le j \le s},\{c_i\}_{1 \le i \le s})\) are the corresponding expression in terms of the perturbed collocation method. Also we define P as a perturbation operator composed by \(\{N_j\}_{1 \le j \le s}\), and assume P satisfies \(Pu \in {\varPi }_{s-1}\). And let \((\widetilde{A},{\varvec{b}},{\varvec{c}})\) be the RK family which is constructed in Step 3 and \((\{\widetilde{N}_j\}_{1 \le j \le s},\ \{c_i\}_{1 \le i \le s} )\) be the corresponding expressions of the family. Also we define \(\widetilde{P}\) as a perturbation operator composed by \(\{\widetilde{N}_j\}_{1 \le j \le s}\). Note that both \(\widetilde{A} = (\widetilde{a}_{ij})\) and \(\{\widetilde{N}_j\}_{1 \le j \le s}\) depend on \(\alpha \) linearly and the claim of this proposition is that \(\widetilde{a}_{ij}=0 \ (1\le i \le j \le s)\) hold.

To check \(\widetilde{a}_{ij} = 0 \ (1\le i \le j \le s)\), it is sufficient to show that

\((\{\widetilde{N}_j\}_{1 \le j \le s},\ \{c_i\}_{1 \le i \le s} )\) satisfies the assumption of Proposition 2. Here we define a vector space \(\mathbb {V}_k \ (k=1,\ldots ,s)\) to simplify notation.

$$\begin{aligned} \mathbb {V}_k&:= \{ {\varvec{v}}\in \mathbb {R}^s \ \mathrm{:}\ {\varvec{v}}\hbox { is a linear combination of } (1,c_l,\ldots ,{c_l}^{s-1})^\top \nonumber \\&\qquad \,\,\hbox {where } l=1,\ldots ,k-1,k+1,\ldots ,s \}. \end{aligned}$$
(3.16)

We first note that, by construction, the perturbation operator \(\widetilde{P}\) satisfies \(\widetilde{P}u \in {\varPi }_{s-1}\). From Proposition 2, for (i, j) in \(1\le i \le j \le s\), \(\widetilde{a}_{ij} = 0 \ (1\le i \le j \le s)\) if and only if

$$\begin{aligned} \left( (\widetilde{N}_1 + t)(c_i),\ldots ,(s-1)!\left( \widetilde{N}_s + \frac{t^s}{s!}\right) (c_i)\right) ^\top \in \mathbb {V}_j. \end{aligned}$$
(3.17)

Recall, by (3.3) and (3.4), this vector is equivalent to

$$\begin{aligned}&\left( (N_1 + t)(c_i),\ldots ,(s-1)!\left( N_s + \frac{t^s}{s!}\right) (c_i)\right) ^\top \nonumber \\&\quad +\alpha \left( \underbrace{0,\ldots ,0}_{s-2},\ (s-2)!d_{s-1}\prod _{k=1}^{s-1} (c_i-c_k), (s-1)!d_s\prod _{k=1}^{s-1} (c_i-c_k)\right) ^\top . \end{aligned}$$
(3.18)

The first term of this vector belongs to \(\mathbb {V}_j\) for all i, j in \(1 \le i \le j \le s\), since the base integrator is an explicit RK method. Note that the perturbation operator P satisfies \(Pu \in {\varPi }_{s-1}\).

For \(i \le s-1\), the second term of (3.18) trivially vanishes, and thus in total (3.17) holds. This good nature comes from the fact that the modification to \(N_j\ (j=s-1,s)\) takes the form of the polynomial \(\prod _{k=1}^{s-1} (t-c_k)\). For \(i=s\), the second term of (3.18) does not vanish, but from (3.1), (3.2), it is equivalent to

$$\begin{aligned} \alpha \prod _{k=1}^{s-1} (c_s - c_k) \left( 0,\ldots ,0,\widehat{d}_{s-1},\widehat{d}_s\right) ^\top , \end{aligned}$$
(3.19)

which belongs to \(\mathbb {V}_s\) by construction. This completes the proof.

Remark 2

Note that, from the proof in [16], we see that the upper \(s-1\) rows of \(\widetilde{A}\) coincide with those of A. Therefore, if an approximation \(\varPhi _\alpha \) is constructed for some \(\alpha \), we just need an additional evaluation of f for the computation of \(\varPhi _{\hat{\alpha }} \ (\hat{\alpha } \ne \alpha )\). Thus the proposed method does not need many evaluations f in solving \(H(\varPhi _\alpha (y_0)) = H(y_0)\). Note that IDT needs no evaluation f for the construction of another integrator \(\varPhi _{\hat{\alpha }} \ (\hat{\alpha } \ne \alpha )\). Therefore the proposed method demands a bit longer computation time than IDT.

Remark 3

From an easy calculation, for the family constructed in Definition 4, we see that we can take r to \(p-3\) in Definition 3, if the base integrator has order p. We can apply an adaptive step size control technique (see e.g. [14]), based on the two numerical integrators with order p and 3. This implementation requires one additional evaluation of f. A natural question here would be whether there exists a family whose r is independent of p or not. The present author has a pessimistic view on this point. Perturbed collocation methods were well investigated theoretically, in particular, in terms of their order of accuracy by Nørsett–Wanner [16]. The analysis was based on the nonlinear Variation-Of-Constants formula. However, it is difficult to use the formula for explicit RK methods because the derivative of the perturbed collocation polynomial (u in Definition 2) may diverge as Nørsett–Wanner [16] have already pointed out.

Remark 4

Another, simple way to parameterize explicit RK methods would be to consider parameterizations for each explicit RK method directly, carefully observing order conditions. Of course this approach makes sense, but in the present paper we did not employ it, since order conditions are generally quite complicated, and it seems difficult to discuss which conditions are important or safe to violate. Furthermore, even if we can do that for a specific explicit RK method, we should do the whole thing all over again from scratch when we move on to another RK method. The parameterization technique proposed in this paper is free from this difficulty. Because parameterizing RK coefficients matrix A is equivalent to adding parameterized polynomials to \(N_j\ \mathrm{(}1\le j\le s\mathrm{)}\) which compose the perturbation operator, we can intuitively say that a nice parameterization should be the one that changes the perturbation operator to a minimum degree. One way to realize this is to only allow the changes in \(N_j\) with higher indices. The following numerical experiments support this view.

3.2 Preserving multiple invariants

We can generalize the proposed method to preserve several invariants. We realize this by constructing a family of RK methods depending on a set of parameters. Namely we parameterize them with the same number of parameters as the number of the targeted invariants. For example, if two invariants are targeted, we should construct a family with two parameters \(\{\varPhi _{(\alpha ,\beta )}\}_{(\alpha ,\beta ) \in \mathbb {R}^2}\).

  • Step 1. Take an explicit RK method which can be expressed by a perturbed collocation method with \(\{ N_j\}_{1 \le j \le s} \) and \(\{c_i\}_{1\le i \le s}\).

  • Step 2. Calculate \(d^{(1)}_{s-2},d^{(1)}_{s-1},d^{(1)}_s\) and \(d^{(2)}_{s-1},d^{(2)}_{s}\) from the elementary row operations of the following matrix

    $$\begin{aligned} \begin{pmatrix} 1 &{} c_1 &{} \ldots &{} {c_1}^{s-1} \\ \vdots &{} &{} &{} \vdots \\ \vdots &{} &{} &{} \vdots \\ 1 &{} c_s &{} \ldots &{} {c_s}^{s-1} \end{pmatrix} \longrightarrow \begin{pmatrix} 1 &{} c_1 &{} \ldots &{}&{} {c_1}^{s-1} \\ \vdots &{} &{} &{}&{}\vdots \\ 0 &{} \cdots &{} \hat{d}^{(1)}_{s-2} &{}\hat{d}^{(1)}_{s-1} &{} \hat{d}^{(1)}_s \\ 0 &{} \cdots &{} 0&{}\hat{d}^{(2)}_{s-1} &{} \hat{d}^{(2)}_s \end{pmatrix}. \end{aligned}$$
    (3.20)

    Then we take \(d^{(1)}_{s-2},d^{(1)}_{s-1},d^{(1)}_s\) and \(d^{(2)}_{s-1},d^{(2)}_{s}\) as

    $$\begin{aligned} d^{(1)}_{s-2} = \frac{1}{(s-3)!} \hat{d}^{(1)}_{s-2}, \quad d^{(1)}_{s-1} = \frac{1}{(s-2)!} \hat{d}^{(1)}_{s-1}, \quad d^{(1)}_s = \frac{1}{(s-1)!} \hat{d}^{(1)}_s,\end{aligned}$$
    (3.21)
    $$\begin{aligned} d^{(2)}_{s-1} = \frac{1}{(s-2)!} \hat{d}^{(2)}_{s-1}, \quad d^{(2)}_s = \frac{1}{(s-1)!} \hat{d}^{(2)}_s. \end{aligned}$$
    (3.22)

  • Step 3. Make a family \(\{\varPhi _{(\alpha ,\beta )}\}_{(\alpha ,\beta ) \in \mathbb {R}^2}\) of the perturbed collocation methods whose expressions are \(\{\widetilde{N}_j\}_{1 \le j \le s} \) and\(\{c_i\}_{1\le i \le s}\):

    $$\begin{aligned} \widetilde{N}_j&= N_j \quad (j=1,\ldots ,s-3), \end{aligned}$$
    (3.23)
    $$\begin{aligned} \widetilde{N}_{s-2}&= N_{s-2} + \alpha d^{(1)}_{s-2} \prod _{k=1}^{s-1} (t-c_k), \end{aligned}$$
    (3.24)
    $$\begin{aligned} \widetilde{N}_{s-1}&= N_{s-1} + (\alpha d^{(1)}_{s-1} + \beta d^{(2)}_{s-1}) \prod _{k=1}^{s-1} (t-c_k), \end{aligned}$$
    (3.25)
    $$\begin{aligned} \widetilde{N}_{s}&= N_s + (\alpha d^{(1)}_{s} + \beta d^{(2)}_{s}) \prod _{k=1}^{s-1} (t-c_k). \end{aligned}$$
    (3.26)

    This family \(\{\varPhi _{(\alpha ,\beta )}\}_{(\alpha ,\beta ) \in \mathbb {R}^2}\) is in fact a family of explicit RK methods.

In a similar manner as above, we are able to construct a family of explicit RK methods with \(s-1\) parameters. The proof of the explicitness is similar to Theorem 3, and hence we omit it here.

4 Numerical tests

In this section we show numerical tests that confirm the efficiency of the proposed method. In particular, we focus on the consequences of the natural parameterization of our approach.

Fig. 1
figure 1

A reference solution (represented as a red line) by RK4 with sufficiently small step size \(h=2/300\) (color figure online)

Full size image
Fig. 2
figure 2

IDT34: top the numerical solution with \(h=2/3\), bottom left value of the corrections by projection (its label “projDistance” means the corrections by projection), bottom right value of the parameter

Full size image

We consider the Hénon–Heiles equation:

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}&= J \nabla H(y),\quad y \in \mathbb {R}^4,\quad J = \begin{pmatrix} 0 &{} I \\ -I &{} 0 \end{pmatrix} \in \mathbb {R}^{4\times 4},\end{aligned}$$
(4.1)
$$\begin{aligned} H(y)&= H(q_1,q_2,p_1,p_2) = \frac{1}{2} ({p_1}^2 + {p_2}^2) + U(q_1,q_2), \end{aligned}$$
(4.2)

where \(U(q_1,q_2)\) is called potential (also we denote it as U(y) to simplify notation). The Hénon–Heiles equation was derived to describe the stellar motion inside the (gravitational) potential \(U(y_0)\) for a very long time. The constant \(y_0\) denotes the initial state. See, e.g., [13]. In our experiment we set the potential to

$$\begin{aligned} U(q_1,q_2) = \frac{1}{2} ({q_1}^2 + {q_2}^2) + {q_1}^2 q_2 - \frac{1}{3} {q_2}^3. \end{aligned}$$
(4.3)
Fig. 3
figure 3

IDT14: top the numerical solution with \(h=2/3\), bottom left value of the corrections by projection (its label “projDistance” means the corrections by projection). The maximum value of projDistance is about \(1.7\times 10^{-3}\), bottom right value of the parameter. The maximum value of \(\alpha \) is about 0.01

Full size image
Fig. 4
figure 4

The proposed method: top the numerical solution with \(h=2/3\), bottom left value of the corrections by projection (its label “projDistance” means the corrections by projection). The maximum value of projDistance is about \(3.5\times 10^{-3}\), bottom right value of the parameter. The maximum value of \(\alpha \) is about 0.3

Full size image
Fig. 5
figure 5

Lines which display \(g(\alpha ,h) = 0, \ (h,\alpha ) \in [-0.9,0.9]\times [-9,9]\). Top shows lines of IDT34. Bottom shows lines of the proposed method

Full size image

We will compare the proposed method with IDT to show the naturalness and effectiveness of the proposed parameterization. We set the final time to \(T = 1000\) and the initial state to \(y_0 = (0,0,\sqrt{\frac{3}{10}},0)^\top \). For comparison, in Fig. 1 we show a reference solution constructed by the 3/8 RK4 with a sufficiently small step size \(h = 2/300\). For the proposed method and IDT, we take RK introduced in Example 1 as the base integrator. In addition, for IDT, the third order method introduced in [14] and the first order method (the Euler method) are taken as the embedded RK method. When we need to distinguish these two methods, we call the former IDT34 and the latter IDT14, clarifying the order of the embedded methods. Here IDT14 is considered in view of [4]. In what follows we set the step size h to 2 / 3. The reason we take such a large time step is that we aim to see how robust the methods are. Recall that, for sufficiently small step size, Theorem 2 can be applied to all 1-parameter projection methods; but that does not necessarily reflect actual behaviors. In addition we do not apply adaptive step size controls in our experiments because this technique may conceal the difference among the methods, although from a practical point of view, we do not doubt the effectiveness of the controls. Note that both the proposed method and IDT can utilize adaptive step size control (see Remark 4); however, the proposed method falls slightly behind IDT, because the proposed method needs one extra evaluation of f, unless some sophisticated technique such as FSAL is employed (see e.g. [13]).

In Figs. 2, 3 and 4 we show numerical solutions by IDT34, IDT14 and the proposed method respectively. All figures also include values of the parameter \(\alpha \) and the corrections by projection. Here we take the 2-norm of the differences between reference solutions and the numerical solutions as the values of the corrections.

To observe the consequences of the proposed parameterization, let us pay attention to the figures of the values of the parameter and the corrections by projection. From these figures, we find that the values of IDT34 are often large, while the values of the proposed method and IDT14 remain constantly small. At the occasions where IDT34 takes large parameter it seems that the search direction is almost perpendicular to \(\nabla H\) and ceases to work with the constant step size h. Accordingly, there the corrections made by projection also get large values. In contrast, the proposed method and IDT14 do not exhibit such a behavior even with this large time step \(h=2/3\), and consequently, the correction remains small. For IDT14, the search directions seem to be stabler than those of IDT34. However, these figures, in particular Fig. 2, indicate that linear search methods can yield fatal projection steps without the special technique argued in [6].

Comparing the numerical solutions, we find that the solution by the proposed method is closer to the reference solution than those by IDT34 and IDT14. In particular, we see that the solution by the proposed method generates an appropriate trajectory. This can be considered as a good consequence of the natural parameterization of the proposed method.

The naturalness of the proposed parameterization can be seen from another perspective on robustness; i.e., how large the step size h can be safely. Theorem 1 does not answer this because it is just a theoretical result in the limit of \(h\rightarrow 0\). However, in actual computation, it is expected that the theorem can hold for large step h. In Fig. 5, we show lines which denote zeros of \(g(\alpha ,h) = H(y_1(\alpha , h)) - H(y_0),\ (h,\alpha ) \in [-0.9,0.9]\times [-9,9]\) where \(y_0\) is a state vector which IDT34 takes large \(\alpha \) (\(t=8/3\)). The top of Fig. 5 is the contour of IDT34 and the bottom is that of the proposed method. The straight line on the axis \(h=0\) is obvious (since no evolution occurs), and thus should be ignored. Our attention should be paid to the horizontal curves that touch the origin. From these figures, we see the proposed method can provide appropriate parameters even for large h; in other words, the implicit function theorem employed in Theorem 1 keeps working. On the contrary, the curve of IDT34 sharply goes down near \(h=0.6\). This shows that Theorem 1 does not hold here, and in such a case, the parameter \(\alpha \) can be quite large, and the projection becomes fatal. Therefore we see the naturalness of the proposed parameterization. But again we would like to emphasize that this issue usually happens only occasionally (recall Fig. 2; in most time steps the corrections are small), and can be easily avoided by adaptive time stepping if necessary. What we like to state here is the better stability of the proposed method.

5 Conclusion

In this paper we gave a new strategy to parameterize explicit RK methods via the perturbed collocation method. One of the advantages of this strategy is that we can systematically parameterize explicit RK methods. Another advantage is that in the strategy, we can demand the parameterization is done only in higher order terms of the perturbation operators, in the hope of small projection correction. We showed that such a parameterization is always feasible without destroying the explicitness of the base explicit RK method. In addition we confirmed by numerical examples that the proposed strategy in fact results in small corrections in a robust manner.

We conclude this paper with some remarks. First, we can also apply the proposed method to other classes of ODEs, in particular, dissipative ODEs with a known Lyapunov function. This is an obvious extension of the results [5, 10]. Second, in this paper, we mainly investigated the robustness of the parameterization; however, the proposed method needs a bit longer computation time than IDT because the proposed method needs more evaluations of f in solving \(H(\varPhi _\alpha (y_0)) = H(y_0)\). This is a trade-off between the robustness and stability. When we can take sufficiently small step size h, IDT should beautifully work, and thus it might be sufficient. But if we hope to take larger time step sizes, for example when we are considering integration over long time, the proposed method can be a better solution since it works robustly even in such a circumstance. Finally, when the system is essentially highly unstable, projections based on explicit methods might not work well, and implicit projections such as EQUIP become necessary. Such trade-offs among methods should be more carefully investigated.

A possible future work is to develop a rigorous theoretical explanation on how the proposed parameterization, employed in higher order perturbations, results in the actual small corrections. And through such theoretical investigations, we hope the challenge for “the best 1-parameter projection method” continues. In this sense, we feel the proposed strategy via perturbed collocation methods is just a starting point of such a challenge, which reveals a certain aspect of good parameterization.