A normalized representation of super splines of arbitrary degree on Powell–Sabin triangulations

Abstract

In the paper, a family of bivariate super spline spaces of arbitrary degree defined on a triangulation with Powell–Sabin refinement is introduced. It includes known spaces of arbitrary smoothness r and degree $3r-1$ but provides also other choices of spline degree for the same r which, in particular, generalize a known space of $\mathscr {C}^{1}$ cubic super splines. Minimal determining sets of the proposed super spline spaces of arbitrary degree are presented, and the interpolation problems that uniquely specify their elements are provided. Furthermore, a normalized representation of the discussed splines is considered. It is based on the definition of basis functions that have local supports, are nonnegative, and form a partition of unity. The basis functions share numerous similarities with classical univariate B-splines.

1 Introduction

Despite extensive research, a natural generalization of univariate polynomial splines to bivariate and multivariate ones is far from being clear and complete (see e.g. [12] for discussion on this topic). Since the dimension of low degree spline spaces on triangulations depends substantially on the geometry of a particular triangulation, usually splines on refined triangulations are considered. The most common refinements are the Clough–Tocher and the Powell–Sabin split.

On a Powell–Sabin refinement quadratic splines were originally considered (see [13]). The so-called Powell–Sabin splines are characterized by the interpolation problem with values and derivatives prescribed at the vertices of the initial triangulation. In [3] a representation of Powell–Sabin splines in terms of a normalized basis was proposed, which led to many results and applications in different areas of numerical analysis (see e.g. [11, 16, 20–24]). Also, splines of higher degrees on Powell–Sabin triangulations were studied extensively. The problem of finding the spline spaces of arbitrary smoothness with degree as low as possible was addressed and solved in [1, 6, 7]. The spline spaces proposed therein have local and stable bases, but none of them forms a convex partition of unity. Recently, several papers have dealt with the construction of spline spaces on Powell–Sabin triangulations with bases possessing this property. Namely, a family of spline spaces of arbitrary smoothness was proposed in [17], and three different cubic spline spaces were studied in [5, 10, 19]. All of them have similar normalized representations that generalize the representation of the quadratic space.

In this paper, a family of super spline spaces of arbitrary degree on Powell–Sabin triangulations is introduced. It is a close extension of the family of super splines of arbitrary smoothness r and degree $3r-1$ analysed in [17, 18]. Additionally, it contains super spline spaces of degree $3r-2$ and 3r for every r. The spline spaces of degree 3r are a generalization of the cubic super spline space introduced in [2]. The paper also deals with a construction of normalized bases for the discussed family of spaces. The derived B-spline functions generalize the basis functions of degrees 3 and $3r-1$ provided in [10, 17, 18]. Since splines in a B-representation play an important role in approximation theory and computer aided geometric design, this result may be interesting from many applicative viewpoints.

The remaining of the paper is organized as follows. In Sect. 2, some preliminaries about representation of bivariate polynomials and splines in the Bézier form are reviewed. In Sect. 3, the definition of Powell–Sabin refinement is recalled, and super spline spaces of arbitrary degree on a Powell–Sabin refinement are introduced. In what follows, these spaces are characterized by minimal determining sets and interpolation problems. Section 4 is devoted to a normalized representation of the discussed splines. The Powell–Sabin B-splines of arbitrary degree are defined, and the associated representation of super splines on Powell–Sabin triangulations is provided. It is proved that B-splines have local supports, are nonnegative, and form a partition of unity. The paper concludes with some applications and remarks.

2 Preliminaries

2.1 Bivariate polynomials on triangles

Let $\mathbb P_d$ denote the space of bivariate polynomials of total degree less or equal to $d \in \mathbb N_0$. It is a well known fact that every $p \in \mathbb P_d$ can be uniquely represented in the Bézier form as

$$\begin{aligned} p = \sum _{|\mathbf {i}| = d} b_{\mathbf {i}} B_{\mathbf {i}}^{d}. \end{aligned}$$

(2.1)

In the expression above $B_{\mathbf {i}}^{d}$ denotes the Bernstein basis polynomial of degree d on a triangle ${\mathscr {T}} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$, defined as

$$\begin{aligned} B_{\mathbf {i}}^{d}(\mathbf {\tau }) = \frac{d!}{i_1! \, i_2! \, i_3!} \, \tau _1^{i_1} \tau _2^{i_2} \tau _3^{i_3}, \end{aligned}$$

where $\mathbf {i} = (i_1, i_2, i_3)$, and $\mathbf {\tau } = (\tau _1, \tau _2, \tau _3)$ are barycentric coordinates with respect to the triangle $\mathscr {T}$. The coefficients $b_{\mathbf {i}}$ are called the Bézier ordinates of p and are associated with the domain points $\mathbf {D}_{\mathbf {i}}$ determined by the barycentric coordinates $\left( \frac{i_1}{d}, \frac{i_2}{d}, \frac{i_3}{d} \right)$ with respect to the triangle $\mathscr {T}$. Let

$$\begin{aligned} {\varXi }_{d,\mathscr {T}} = \left\{ \mathbf {D}_{\mathbf {i}} \in \mathscr {T}; \ |\mathbf {i}| = d \right\} \end{aligned}$$

denote the set of all domain points in the triangle $\mathscr {T}$. To describe particular subsets of ${\varXi }_{d,\mathscr {T}}$, let us define the notions of a disk and a row. The disk of radius r around the vertex $\mathbf {V}_1$ is the set

$$\begin{aligned} D_{r,\mathscr {T}}(\mathbf {V}_1) := \left\{ \mathbf {D}_{i_1,i_2,i_3} \in {\varXi }_{d,\mathscr {T}}; \ i_1 \ge d-r \right\} . \end{aligned}$$

The convex hull of $D_{r,\mathscr {T}}(\mathbf {V}_1)$ is a triangle, which will be denoted by $\mathscr {D}_{r,\mathscr {T}}(\mathbf {V}_1)$. Moreover, the set

$$\begin{aligned} E_{r,\mathscr {T}}(\langle \mathbf {V}_1, \mathbf {V}_2 \rangle ) := \left\{ \mathbf {D}_{i_1,i_2,i_3} \in {\varXi }_{d,\mathscr {T}}; \ i_3 = r \right\} \end{aligned}$$

is the row at distance r parallel to the edge $\langle \mathbf {V}_1, \mathbf {V}_2 \rangle$.

The representation (2.1) has a number of advantages in comparison to the standard representation of p in terms of the power basis. Since Bernstein basis polynomials form a partition of unity and are nonnegative on $\mathscr {T}$, one can regard p on $\mathscr {T}$ as a convex combination of its Bézier ordinates. The polynomial p can be evaluated using the de Casteljau algorithm in a stable and efficient way. We refer to [4] for details.

The Bézier ordinates of $p \in \mathbb P_d$ can be expressed with its blossom. The blossom of p is a map $\mathscr {B}[p]: (\mathbb R^2)^d \rightarrow \mathbb R$ satisfying the following properties.

Property 2.1

(Symmetry) For any permutation $\pi$ of d arguments,

$$\begin{aligned} \mathscr {B}[p](\mathbf {P}_1, \ldots , \mathbf {P}_d) = \mathscr {B}[p](\pi (\mathbf {P}_1, \ldots , \mathbf {P}_d)). \end{aligned}$$

Property 2.2

(Multi-affinity) For any $a,b \in \mathbb R$ satisfying $a+b = 1$,

$$\begin{aligned} \mathscr {B}[p](a \mathbf {P} + b \mathbf {Q}, \mathbf {P}_2, \ldots , \mathbf {P}_d) = a \mathscr {B}[p](\mathbf {P}, \mathbf {P}_2, \ldots , \mathbf {P}_d) + b \mathscr {B}[p](\mathbf {Q}, \mathbf {P}_2, \ldots , \mathbf {P}_d). \end{aligned}$$

Property 2.3

(Diagonality) For any $\mathbf {P} \in \mathbb R^2$,

$$\begin{aligned} \mathscr {B}[p](\mathbf {P}, \ldots , \mathbf {P}) = p(\mathbf {P}). \end{aligned}$$

The Bézier ordinate $b_{\mathbf {i}}$, $\mathbf {i} = (i_1, i_2, i_3)$, of p can be expressed as

$$\begin{aligned} b_{\mathbf {i}} = \mathscr {B}[p](\mathbf {V}_1[i_1], \mathbf {V}_2[i_2], \mathbf {V}_3[i_3]), \end{aligned}$$

(2.2)

where $\mathbf {P}[r]$ means that the argument $\mathbf {P}$ is repeated r times.

If $\mathbf {\tau }^1, \ldots , \mathbf {\tau }^d$ are the barycentric coordinates of points $\mathbf {P}_1, \ldots , \mathbf {P}_d$ with respect to $\mathscr {T}$, the blossom of p may be written as

$$\begin{aligned} \mathscr {B}[p](\mathbf {P}_1, \ldots , \mathbf {P}_d) = \mathscr {B}[p, \mathscr {T}](\mathbf {\tau }^1, \ldots , \mathbf {\tau }^d). \end{aligned}$$

It can be evaluated using the multi-affine de Casteljau algorithm. This representation of the blossom becomes particularly useful when one subdivides p on $\mathscr {T}$. Let ${\mathscr {T}'} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$ be another (finer) triangle, and let $\mathbf {\sigma }^\ell$, $\ell = 1, 2, 3$, be the barycentric coordinates of $\mathbf {W}_\ell$ with respect to the triangle $\mathscr {T}$. Suppose that the Bézier ordinates of p expressed in the form (2.1) with respect to the triangle $\mathscr {T}'$ are denoted by $b_{\mathbf {i}}'$. By (2.2) and the defining properties of blossom, it follows that

$$\begin{aligned} b_{\mathbf {i}}' = \mathscr {B}[p, \mathscr {T}](\mathbf {\sigma }^1[i_1], \mathbf {\sigma }^2[i_2], \mathbf {\sigma }^3[i_3]). \end{aligned}$$

Notice an important property that in the case when the Bézier ordinates of p with respect to $\mathscr {T}$ are nonnegative, and the barycentric coordinates $\mathbf {\sigma }^\ell$, $\ell = 1, 2, 3$, are nonnegative, the ordinates $b_{\mathbf {i}}'$ are nonnegative, too. We refer to [4, 14, 15] for details on the blossoming principle.

2.2 Polynomial splines on triangulations

Let ${\varOmega }$ be a simply connected subset of $\mathbb R^2$ with a polygonal boundary, and let $\triangle$ be its regular triangulation. Denote by $\mathscr {V}$ the set of all vertices of $\triangle$ and by $\mathscr {E}$ the set of all edges of $\triangle$. Additionally, let the set $M_{\triangle }(\mathbf {V})$ of all triangles in $\triangle$ sharing the vertex $\mathbf {V} \in \mathscr {V}$ be called the molecule of $\mathbf {V}$ in $\triangle$.

The space of all polynomial splines of degree $d \in \mathbb N_0$ and smoothness $r \in \mathbb N_0$ on $\triangle$ is defined as

$$\begin{aligned} \mathscr {S}_{d}^{r}(\triangle ) := \left\{ s \in \mathscr {C}^{r}({\varOmega }); \ s|_{\mathscr {T}} \in \mathbb P_d, \ \mathscr {T} \in \triangle \right\} . \end{aligned}$$

The restriction of a spline $s \in \mathscr {S}_{d}^{r}(\triangle )$ to an arbitrary triangle of $\triangle$ can be represented in the Bézier form (2.1). In this way, the Bézier representation of s is obtained. As in the polynomial case, the Bézier ordinates of s are associated with the domain points

$$\begin{aligned} {\varXi }_{d,\triangle } := \bigcup _{\mathscr {T} \in \triangle } {\varXi }_{d,\mathscr {T}}. \end{aligned}$$

The Bézier ordinates of $s \in \mathscr {S}_{d}^{0}(\triangle )$ corresponding to ${\varXi }_{d,\triangle }$ uniquely specify s. The situation becomes more complicated when $r > 0$ since smoothness constraints imply relations between the Bézier ordinates of a spline. These relations are described in the following theorem. Its proof can be found in [8].

Theorem 2.1

Let p and $p'$ be polynomials of total degree d written in the form (2.1) on ${\mathscr {T}} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ and ${\mathscr {T}'} \langle \mathbf {V}_4, \mathbf {V}_3, \mathbf {V}_2 \rangle$ with Bézier ordinates $b_{\mathbf {i}}$ and $b_{\mathbf {i}}'$, respectively. Suppose that $\mathbf {V}_4$ lies outside of $\mathscr {T}$ and has barycentric coordinates $\mathbf {\sigma }$ with respect to $\mathscr {T}$. Then $D_x^a D_y^b p = D_x^a D_y^b p'$, $0 \le a + b \le \mu$, on $\langle \mathbf {V}_2, \mathbf {V}_3 \rangle$ if and only if

$$\begin{aligned} b_{m,i_2,i_3}' = \sum _{|\mathbf {j}| = m} b_{j_1, i_3+j_2, i_2+j_3} B_{\mathbf {j}}^{m}(\mathbf {\sigma }) \end{aligned}$$

(2.3)

for $m = 0, \ldots , \mu$ and $i_2 + i_3 = d-m$, where $\mathbf {i} = (i_1, i_2, i_3)$ and $\mathbf {j} = (j_1, j_2, j_3)$.

A subset $M_{d}^{r}(\triangle ) \subseteq {\varXi }_{d,\triangle }$ is called a minimal determining set of $\mathscr {S}_{d}^{r}(\triangle )$ if every $s \in \mathscr {S}_{d}^{r}(\triangle )$ is uniquely determined by the Bézier ordinates corresponding to the points in $M_{d}^{r}(\triangle )$. Consequently, the dimension of $\mathscr {S}_{d}^{r}(\triangle )$ is equal to the cardinality of $M_{d}^{r}(\triangle )$. For spline spaces $\mathscr {S}_{d}^{r}(\triangle )$ with $d \ge 3r+2$, an explicit construction of a minimal determining set is given in [8]. For spaces with $d < 3r+2$, among which are $\mathscr {S}_{2}^{1}(\triangle )$ and $\mathscr {S}_{3}^{1}(\triangle )$, the dimensions in most cases depend on the geometry of the underlying triangulations, and special classes of them must be considered.

When possible, the dimension of a spline space $\mathscr {S}_{d}^{r}(\triangle )$ is characterized by an interpolation problem. It is desirable that interpolation data are provided at the vertices of $\triangle$. Note that the values $D_{x}^{a} D_{y}^{b} p(\mathbf {V}_1)$, $0 \le a+b \le \rho \le d$, of a polynomial $p \in \mathbb P_d$ on ${\mathscr {T}} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ uniquely determine the Bézier ordinates of p corresponding to the domain points in the disk $D_{\rho ,\mathscr {T}}(\mathbf {V}_1)$, and vice versa. Suppose now that $s \in \mathscr {S}_{d}^{r}(\triangle ) \cap \mathscr {C}^{\rho }(\mathbf {V})$, $\mathbf {V} \in \mathscr {V}$, with $\rho \ge r$, and let

$$\begin{aligned} D_{\rho ,\triangle }(\mathbf {V}) := \bigcup _{\mathscr {T} \in M_{\triangle }(\mathbf {V})} D_{\rho ,\mathscr {T}}(\mathbf {V}) \end{aligned}$$

(2.4)

be the disk of radius $\rho$ around $\mathbf {V}$ in the triangulation $\triangle$. The Bézier ordinates of s corresponding to the domain points in $D_{\rho ,\triangle }(\mathbf {V})$ are then consistently determined by the values $D_{x}^{a} D_{y}^{b} s(\mathbf {V})$, $0 \le a+b \le \rho$. We refer to [8] for details.

3 Super splines on Powell–Sabin triangulations

3.1 Powell–Sabin refinement

The Powell–Sabin refinement $\triangle ^*$ of a triangulation $\triangle$ was introduced in [13]. It partitions each triangle of $\triangle$ into six smaller triangles and is obtained in the following way. First, an interior split point $\mathbf {Z}_m$ for every triangle $\mathscr {T}_m \in \triangle$ is chosen such that the line segment $\langle \mathbf {Z}_k, \mathbf {Z}_{k'} \rangle$ for any two neighbouring triangles ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ and ${\mathscr {T}_{k'}} \langle \mathbf {V}_4, \mathbf {V}_3, \mathbf {V}_2 \rangle$ intersects the interior of the common edge $\langle \mathbf {V}_2, \mathbf {V}_3 \rangle$ (see Fig. 1). The point of intersection is denoted by $\mathbf {R}_{23}$. Additionally, for every boundary edge $\langle \mathbf {V}_i, \mathbf {V}_j \rangle$ of $\triangle$, the point $\mathbf {R}_{ij}$ in its interior is chosen. The desired refinement is then acquired by connecting every interior split point with the vertices and the edge split points inside a particular triangle. For arbitrary $\triangle$, the Powell–Sabin refinement can always be realized by choosing the incenters of triangles in $\triangle$ to be the interior split points of $\triangle ^*$. In the remaining of the paper, the set of all interior split points of $\triangle ^*$ will be denoted by $\mathscr {Z}$. Furthermore, the set of all edges of $\triangle ^*$ that connect a triangle interior split point to an edge split point will be denoted by $\mathscr {E}^*$.

Fig. 1

A Powell–Sabin refinement of two neighbouring triangles

3.2 Super spline spaces on Powell–Sabin triangulations

The well known Powell–Sabin splines are the elements of $\mathscr {S}_{2}^{1}(\triangle ^*)$, namely the quadratic splines of smoothness order one defined on a triangulation $\triangle$ with a Powell–Sabin refinement $\triangle ^*$. As it was proved in [13], every $s \in \mathscr {S}_{2}^{1}(\triangle ^*)$ is uniquely determined by the values $D_{x}^{a} D_{y}^{b} s(\mathbf {V})$, $0 \le a+b \le 1$, at the vertices $\mathbf {V} \in \mathscr {V}$ of the initial triangulation $\triangle$. Therefore, the dimension of this spline space is equal to $3|\mathscr {V}|$, independently of the geometry of the triangulation $\triangle$.

Several authors considered splines of a higher smoothness on a Powell–Sabin refinement. In order to obtain a spline space for which the dimension is independent of the geometry of the triangulation, the degree of splines has to be increased. It also seems to be inevitable to impose certain additional smoothness constraints at particular vertices and edges of the refinement. Such splines spaces are, in general, denoted as super spline spaces. Among others, the super spline space

$$\begin{aligned} \mathscr {S}_{5}^{2, 3}(\triangle ^*) = \mathscr {S}_{5}^{2}(\triangle ^*) \cap \mathscr {C}^{3}(\mathscr {V}\cup \mathscr {Z}\cup \mathscr {E}^*) \end{aligned}$$

(3.1)

of quintic splines of smoothness order two on $\triangle ^*$ was introduced in [7]. It was proved therein that every $s \in \mathscr {S}_{5}^{2, 3}(\triangle ^*)$ is uniquely determined by the values $D_{x}^{a} D_{y}^{b} s(\mathbf {V})$, $0 \le a+b \le 3$, at the vertices $\mathbf {V} \in \mathscr {V}$ of the initial triangulation $\triangle$ and the values $s(\mathbf {Z})$ at the interior split points $\mathbf {Z} \in \mathscr {Z}$ of the refinement $\triangle ^*$. This result was extended in [17] to the spaces

$$\begin{aligned} \mathscr {S}_{3r-1}^{r, 2r-1}(\triangle ^*) = \mathscr {S}_{3r-1}^{r}(\triangle ^*) \cap \mathscr {C}^{2r-1}(\mathscr {V}\cup \mathscr {Z}\cup \mathscr {E}^*) \end{aligned}$$

(3.2)

for arbitrary $r \in \mathbb N$. This family also contains the standard space of Powell–Sabin splines, which is obtained by choosing $r = 1$. Every $s \in \mathscr {S}_{3r-1}^{r, 2r-1}(\triangle ^*)$ is uniquely determined by the values $D_{x}^{a} D_{y}^{b} s(\mathbf {V})$, $0 \le a+b \le 2r-1$, at the vertices $\mathbf {V} \in \mathscr {V}$ of $\triangle$ and the values $D_{x}^{a} D_{y}^{b} s(\mathbf {Z})$, $0 \le a+b \le r-2$, at the interior split points $\mathbf {Z} \in \mathscr {Z}$ of $\triangle ^*$. A particular super spline space,

$$\begin{aligned} \mathscr {S}_{3}^{1, 2}(\triangle ^*) = \mathscr {S}_{3}^{1}(\triangle ^*) \cap \mathscr {C}^{2}(\mathscr {V}), \end{aligned}$$

(3.3)

that does not fit into (3.2) was studied in [2], and it was shown therein that every $s \in \mathscr {S}_{3}^{1, 2}(\triangle ^*)$ is uniquely determined by the values $D_{x}^{a} D_{y}^{b} s(\mathbf {V})$, $0 \le a+b \le 2$, at the vertices $\mathbf {V} \in \mathscr {V}$ of $\triangle$.

In order to unify and to generalize the spaces in (3.1), (3.2), and (3.3), let us consider the spaces

$$\begin{aligned} \mathscr {S}_{d}^{r, \rho , \mu }(\triangle ^*) = \mathscr {S}_{d}^{r}(\triangle ^*) \cap \mathscr {C}^{\rho }(\mathscr {V}) \cap \mathscr {C}^{\mu }(\mathscr {Z}\cup \mathscr {E}^*) \end{aligned}$$

for different choices of d, r, $\rho$, and $\mu$. More precisely, our prime interest will be the spaces

$$\begin{aligned} \mathscr {S}_{d}(\triangle ^*):= \mathscr {S}_{d}^{r_d, \rho _d, \mu _d}(\triangle ^*) = {\left\{ \begin{array}{ll} \mathscr {S}_{d}^{r-1, 2r-2, 2r-1}(\triangle ^*); &{} d = 3r-2 \\ \mathscr {S}_{d}^{r, 2r-1, 2r-1}(\triangle ^*); &{} d = 3r-1 \\ \mathscr {S}_{d}^{r, 2r, 2r-1}(\triangle ^*); &{} d = 3r \end{array}\right. } \end{aligned}$$

(3.4)

for arbitrary degree $d \in \mathbb N$. Notice that $\mathscr {S}_{d}(\triangle ^*)$ for $d = 3r-1$ coincides with (3.2), and $\mathscr {S}_{3}(\triangle ^*)$ agrees with (3.3). The elements of $\mathscr {S}_{1}(\triangle ^*)$ are simply continuous linear splines on $\triangle$. Table 1 contains parameters defining $\mathscr {S}_{d}(\triangle ^*)$ for d up to 36. In the following theorem, a characterization of the spaces $\mathscr {S}_{d}(\triangle ^*)$ for arbitrary degree d is given in terms of interpolation problems.

Table 1 Parameters defining $\mathscr {S}_{d}(\triangle ^*)$ for $d = 1, \ldots , 36$

Theorem 3.1

For arbitrary $d \in \mathbb N$, consider the spline space $\mathscr {S}_{d}(\triangle ^*)$ defined in (3.4). There exists a unique spline $s \in \mathscr {S}_{d}(\triangle ^*)$ satisfying

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s(\mathbf {V}_\ell ) = f_{x^a y^b, \ell }, \quad 0 \le a+b \le \rho _d, \ \ell = 1, \ldots , |\mathscr {V}|, \end{aligned}$$

(3.5a)

and

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s(\mathbf {Z}_m) = g_{x^a y^b, m}, \quad 0 \le a+b \le r-2, \ m = 1, \ldots , |\triangle |, \end{aligned}$$

(3.5b)

for a given set of values $f_{x^a y^b, \ell }$ and $g_{x^a y^b, m}$.

Fig. 2

Macro-triangles of $\mathscr {S}_{d}(\triangle ^*)$ with domain points for $d \in \{ 3r-2, 3r-1, 3r \}$, $r = 4$. The black coloured points represent minimal determining sets

The proof of the correctness of the interpolation problem (3.5) for $d = 3r-1$, $r \in \mathbb N$, can be found in [17]. In principle, the statement for $d = 3r-2$ and $d = 3r$ can be verified in a very similar way. In order to make the proof shorter and less technical, let us pursue the idea that a single macro-triangle for $d = 3r-2$ can be viewed as an inscribed triangle in a macro-triangle for $d = 3r-1$. Similarly, a macro-triangle for $d = 3r$ is nothing else than an extension of a macro-triangle for $d = 3r-1$. See Fig. 2 for an illustration of this perspective. The following theorem restates Theorem 3.1 in terms of the theory of minimal determining sets.

Theorem 3.2

For any vertex $\mathbf {V}_\ell \in \mathscr {V}$, let us define $M_\ell ^v = D_{\rho _d,\triangle ^*}(\mathbf {V}_\ell ) \cap \mathscr {T}_\ell ^*$, where $\mathscr {T}_\ell ^*$ is an arbitrary triangle in $\triangle ^*$ with a vertex at $\mathbf {V}_\ell$. Similarly, for any macro-triangle $\mathscr {T}_m \in \triangle$, let us define $M_m^t = D_{r-2,\triangle ^*}(\mathbf {Z}_m) \cap \mathscr {T}_m^*$, where $\mathscr {T}_m^*$ is an arbitrary triangle in $\triangle ^*$ with a vertex at $\mathbf {Z}_m$. Then

$$\begin{aligned} M_{d}(\triangle ^*) := \bigcup _{\ell =1}^{|\mathscr {V}|} M_\ell ^v \cup \bigcup _{m=1}^{|\triangle |} M_m^t \end{aligned}$$

is a minimal determining set of $\mathscr {S}_{d}(\triangle ^*)$.

The proof of Theorem 3.2 will follow based on the next three lemmas. In the first two of them, Theorem 3.2 is verified on a single macro-triangle for the cases $d = 3r-2$ and $d = 3r$ by referring to the fact that Theorem 3.2 holds for $d = 3r-1$.

Lemma 3.1

Let ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$. Then $M_{3r-2}(\{ \mathscr {T}_k \}^*)$ is a minimal determining set of $\mathscr {S}_{3r-2}(\{ \mathscr {T}_k \}^*)$.

Proof

Consider the triangle $\mathscr {T}_k'$ with the vertices

$$\begin{aligned} \mathbf {V}_\ell ' = \left( 1 + \frac{1}{d} \right) \mathbf {V}_\ell - \frac{1}{d} \mathbf {Z}_k, \quad \ell = 1, 2, 3, \end{aligned}$$

and let $\{ \mathscr {T}_k' \}^*$ be derived from $\{ \mathscr {T}_k \}^*$ so that the domain points of both Powell–Sabin triangulations satisfy ${\varXi }_{3r-2,\{ \mathscr {T}_k \}^*} \subseteq {\varXi }_{3r-1,\{ \mathscr {T}_k' \}^*}$. Denote by $M'$ the set $M_{3r-1}(\{ \mathscr {T}_k' \}^*)$ defined in Theorem 3.2. As proved in [17], $M'$ is a minimal determining set of $\mathscr {S}_{3r-1}(\{ \mathscr {T}_k' \}^*)$. Let us show that $M = M' \cap {\varXi }_{3r-2,\{ \mathscr {T}_k \}^*}$ is a minimal determining set of $\mathscr {S}_{3r-2}(\{ \mathscr {T}_k \}^*)$. Associate with the points in M an arbitrary set of Bézier ordinates. Additionally, specify arbitrary Bézier ordinates for the points in $M' \backslash M$, and let $s'$ be the element of $\mathscr {S}_{3r-1}(\{ \mathscr {T}_k' \}^*)$ uniquely determined by the Bézier ordinates corresponding to the points in $M'$. The Bézier ordinates of $s'$ associated with the points in ${\varXi }_{3r-1,\{ \mathscr {T}_k' \}^*} \backslash M'$ are uniquely determined by smoothness constraints. Namely, by Theorem 2.1 they can be expressed as (2.3) with the Bézier ordinates corresponding to the points in ${\varXi }_{3r-1,\{ \mathscr {T}_k' \}^*}$ for particular pairs of triangles in $\{ \mathscr {T}_k' \}^*$. Notice that these expressions are completely independent of the degree of $s'$ and only depend on the smoothness constraints across the interior edges of $\{ \mathscr {T}_k' \}^*$. Since the smoothness constraints across the interior edges of $\{ \mathscr {T}_k' \}^*$ and $\{ \mathscr {T}_k \}^*$ are the same, it follows that the Bézier ordinates corresponding to the points in $M'$ uniquely define an element of $\mathscr {S}_{3r-2}(\{ \mathscr {T}_k \}^*)$. Moreover, none of the Bézier ordinates of $s'$ that belongs to a domain point in ${\varXi }_{3r-1,\{ \mathscr {T}_k' \}^*} \backslash {\varXi }_{3r-2,\{ \mathscr {T}_k \}^*}$ appears in the expression of the Bézier ordinate corresponding to a domain point in ${\varXi }_{3r-2,\{ \mathscr {T}_k \}^*} \backslash M$. This means that an element of $\mathscr {S}_{3r-2}(\{ \mathscr {T}_k \}^*)$ is completely determined by the Bézier ordinates associated with M, which in turn proves that M is a minimal determining set of $\mathscr {S}_{3r-2}(\{ \mathscr {T}_k \}^*)$. $\square$

Lemma 3.2

Let ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$. Then $M_{3r}(\{ \mathscr {T}_k \}^*)$ is a minimal determining set of $\mathscr {S}_{3r}(\{ \mathscr {T}_k \}^*)$.

Proof

The idea of the proof is similar to the proof of Lemma 3.1. In this case, consider the triangle $\mathscr {T}_k''$ with the vertices

$$\begin{aligned} \mathbf {V}_{\ell }'' = \left( 1-\frac{1}{d} \right) \mathbf {V}_\ell + \frac{1}{d} \mathbf {Z}_m, \quad \ell = 1, 2, 3, \end{aligned}$$

and let $\{ \mathscr {T}_k'' \}^*$ be derived from $\{ \mathscr {T}_k \}^*$ so that ${\varXi }_{3r-1,\{ \mathscr {T}_k'' \}^*} \subseteq {\varXi }_{3r,\{ \mathscr {T}_k \}^*}$. Denote by $M''$ the set $M_{3r-1}(\{ \mathscr {T}_k'' \}^*)$, which is known to be a minimal determining set of $\mathscr {S}_{3r-1}(\{ \mathscr {T}_k'' \}^*)$. Let $M = M_{3r}(\{ \mathscr {T}_k \}^*)$ be such that $M'' \subseteq M$. Suppose that a certain set of Bézier ordinates is associated with the points in M. The subset of these ordinates corresponding to the domain points in $M''$ uniquely specifies an element $s''$ from $\mathscr {S}_{3r-1}(\{ \mathscr {T}_k'' \}^*)$. The Bézier ordinates that belong to the domain points in ${\varXi }_{3r-1,\mathscr {T}_k''} \backslash M''$ are uniquely determined by the smoothness constraints across the interior edges of $\{ \mathscr {T}_k'' \}^*$. By the same line of arguments as in the proof of Lemma 3.1, it follows that the Bézier ordinates associated with $M''$ uniquely specify the Bézier ordinates of a spline in $\mathscr {S}_{3r}(\{ \mathscr {T}_k \}^*)$ that belong to the domain points in ${\varXi }_{3r-1,\{ \mathscr {T}_k'' \}^*} \backslash M''$. The remaining Bézier ordinates, i. e., the ordinates associated with the points in ${\varXi }_{3r,\{ \mathscr {T}_k \}^*} \backslash ({\varXi }_{3r-1,\{ \mathscr {T}_k'' \}^*} \cup M)$ located on the edges of $\mathscr {T}_k$, can be determined by the known ordinates as follows. The unknown ordinates corresponding to the points in disks $D_{3r,\{ \mathscr {T}_k \}^*}(\mathbf {V}_\ell )$, $\ell = 1, 2, 3$, are determined by the smoothness constraints across the edges $\langle \mathbf {V}_\ell , \mathbf {Z}_k \rangle$ that are implied by the smoothness at the vertices $\mathbf {V}_\ell$. The rest of them can be thought of as the Bézier ordinates (after subdivision) of a one-dimensional polynomial of degree $2r-1$ defined on the line segment $\langle \mathbf {W}_{ij}, \mathbf {W}_{ji} \rangle$, where

$$\begin{aligned} \mathbf {W}_{ij} = \frac{2r-1}{3r} \mathbf {V}_i + \left( \frac{r+1}{3r} \right) \mathbf {R}_{ij}, \quad \mathbf {W}_{ji} = \frac{2r-1}{3r} \mathbf {V}_j + \left( \frac{r+1}{3r} \right) \mathbf {R}_{ij}, \end{aligned}$$

and $\langle \mathbf {V}_i, \mathbf {V}_j \rangle$ is an edge of $\mathscr {T}_k$. This observation follows from the smoothness constraint of order $2r-1$ across the edge $\langle \mathbf {R}_{ij}, \mathbf {Z}_k \rangle$. Of these $4r-1$ ordinates, 2r are known, and they completely specify the polynomial. $\square$

Let us return to the statement of Theorem 3.2, which has to be proved for the cases $d = 3r-2$ and $d = 3r$. Suppose that a set of Bézier ordinates is assigned to the points in $M_{d}(\triangle ^*)$. By Lemma 3.1 and Lemma 3.2, these ordinates uniquely determine a spline on every single triangle of $\triangle$. In order to show that $M_{d}(\triangle ^*)$ is a minimal determining set of $\mathscr {S}_{d}(\triangle ^*)$, it has to be verified that any two such splines defined on neighbouring triangles of $\triangle$ admit the smoothness constraint of order $r_d$ across the common edge. The following lemma proves this fact by following the same reasoning as used in the last part of the proof of [17, Theorem 4].

Lemma 3.3

Let $\mathscr {T}_k$ and $\mathscr {T}_{k'}$ be triangles in $\triangle$ with a common edge $\langle \mathbf {V}_i, \mathbf {V}_j \rangle$, and let $\{ \mathscr {T}_k \}^*$ and $\{ \mathscr {T}_k' \}^*$ be parts of $\triangle ^*$. Let $s_k \in \mathscr {S}_{d}(\{ \mathscr {T}_k \}^*)$ and $s_{k'} \in \mathscr {S}_{d}(\{ \mathscr {T}_{k'} \}^*)$. If

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s_k(\mathbf {V}_\ell ) = D_{x}^{a} D_{y}^{b} s_{k'}(\mathbf {V}_\ell ), \quad \ell = i, j, \ 0 \le a+b \le \rho _d, \end{aligned}$$

then

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s_{k} = D_{x}^{a} D_{y}^{b} s_{k'}, \quad 0 \le a+b \le r_d, \end{aligned}$$

on $\langle \mathbf {V}_i, \mathbf {V}_j \rangle$.

Proof

Consider the triangles ${\mathscr {T}_{\ell ,m}^*} \langle \mathbf {V}_\ell , \mathbf {R}_{ij}, \mathbf {Z}_m \rangle$, $\ell = i,j$, $m = k,k'$, in $\triangle ^*$. Denote the Bézier ordinates corresponding to the points in ${\varXi }_{d,\mathscr {T}_{\ell ,m}^*}$ by $b_{\mathbf {i}}^{\ell ,m}$ with $\mathbf {i} = (i_1, i_2, i_3)$, $|\mathbf {i}| = d$. By Theorem 2.1, the smoothness constraints of order $r_d$ across $\langle \mathbf {V}_\ell , \mathbf {R}_{ij} \rangle$, $\ell = i,j$, are of the form

$$\begin{aligned} b_{\mathbf {i}}^{\ell ,k'} = \sum _{p=0}^{i_3} \alpha _p^{i_3} b_{i_1,d-p-i_1,p}^{\ell ,k}, \quad 0 \le i_3 \le r_d, \ |\mathbf {i}| = d, \end{aligned}$$

(3.6)

where the weights $\alpha _{p}^{i_3}$, given in (2.3), are the same for $\ell = i$ and $\ell = j$ since $\langle \mathbf {Z}_k, \mathbf {R}_{ij} \rangle$ and $\langle \mathbf {Z}_{k'}, \mathbf {R}_{ij} \rangle$ lie on the line segment $\langle \mathbf {Z}_k, \mathbf {Z}_{k'} \rangle$ by the definition of the Powell–Sabin refinement. The smoothness constraints at the vertices imply that conditions (3.6) are satisfied for $i_1 \ge r$. In order to prove that they are also satisfied for $i_1 < r$, consider the smoothness constraints of order $\mu _d$ across the edges $\langle \mathbf {Z}_m, \mathbf {R}_{ij} \rangle$, $m = k, k'$. The ordinates $b_{\mathbf {i}}^{i,m}$ for $0 \le i_1 < r$ and $0 \le i_3 \le r_d$ can be expressed as

$$\begin{aligned} b_{\mathbf {i}}^{i,m} = \sum _{q=0}^{r-1} \beta _q^{i_1} b_{r+q,d-r-q-i_3,i_3}^{i,m} + \sum _{q=0}^{r-1} \gamma _q^{i_1} b_{r+q,d-r-q-i_3,i_3}^{j,m}, \end{aligned}$$

where the weights $\beta _q^{i_1}$ and $\gamma _q^{i_1}$ are the same for $m = k$ and $m = k'$. Combining these observations leads to the conclusion that

$$\begin{aligned} b_{\mathbf {i}}^{i,k'}= & {} \sum _{q=0}^{r-1} \beta _q^{i_1} \left( \sum _{p=0}^{i_3} \alpha _p^{i_3} b_{r+q,d-r-p-q,p}^{i,k} \right) + \sum _{q=0}^{r-1} \gamma _q^{i_1} \left( \sum _{p=0}^{i_3} \alpha _p^{i_3} b_{r+q,d-r-p-q,p}^{j,k} \right) \\= & {} \sum _{p=0}^{i_3} \alpha _p^{i_3} \left( \sum _{q=0}^{r-1} \beta _q^{i_1} b_{r+q,d-r-p-q,p}^{i,k} + \sum _{q=0}^{r-1} \gamma _q^{i_1} b_{r+q,d-r-p-q,p}^{j,k} \right) \\= & {} \sum _{p=0}^{i_3} \alpha _p^{i_3} b_{i_1,d-p-i_1,p}^{i,k} \end{aligned}$$

for $i_1 < r$. It can be similarly verified that (3.6) holds for $\ell = j$, too.$\square$

Two additional observations can be made from the above discussion. It is easy to see that the restriction of $s \in \mathscr {S}_{3r-2}(\triangle ^*)$ to every triangle of $\triangle$ is of smoothness r. Moreover, every $s \in \mathscr {S}_{3r}(\triangle ^*)$ is of smoothness $r+1$ across the edges of $\triangle$. Note that these smoothness constraints are satisfied automatically by the prescribed constraints.

Corollary 3.1

The dimension of $\mathscr {S}_{d}(\triangle ^*)$ is given by

$$\begin{aligned} \dim \mathscr {S}_{d}(\triangle ^*)= \left( {\begin{array}{c}\rho _d + 2\\ 2\end{array}}\right) |\mathscr {V}| + \left( {\begin{array}{c}r\\ 2\end{array}}\right) |\triangle |. \end{aligned}$$

Proof

The proof follows directly from Theorem 3.2. $\square$

4 A normalized representation of super splines

As already mentioned, a normalized representation of elements of a spline space is of a particular interest in many areas of numerical analysis. In [17], a normalized representation for $\mathscr {S}_{3r-1}^{r, 2r-1}(\triangle ^*)$, $r \in \mathbb N$, was introduced. It extends the representation for $\mathscr {S}_{2}^{1}(\triangle ^*)$ given in [3] and the representation for $\mathscr {S}_{5}^{2, 3}(\triangle ^*)$ presented in [16]. Recently, a similar construction for $\mathscr {S}_{3}^{1, 2}(\triangle ^*)$ was derived in [10]. In this section, these results are extended to a normalized representation for $\mathscr {S}_{d}(\triangle ^*)$ with arbitrary $d \in \mathbb N$, and its main properties are proved. The notation and main ideas are adopted from [17, 18].

Fig. 3

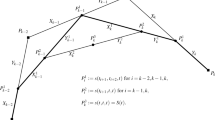
a A PS-triangle ${t_i} \langle \mathbf {Q}_{i,1}, \mathbf {Q}_{i,2}, \mathbf {Q}_{i,3} \rangle$ and PS-points associated with $\mathbf {V}_i$. b A macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ and its associated triangle ${\mathscr {W}_k} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$

4.1 Construction of Powell–Sabin B-splines

The construction of Powell–Sabin B-splines relies on the interpolation problems of the form (3.5). The goal is to choose suitable values for the interpolation data so that the resulting functions will form a basis and will possess desirable properties such as a partition of unity and a local support.

• 1. For each vertex $\mathbf {V}_i \in \mathscr {V}$, choose $\theta _i \in (0,1)$, and identify the PS-points associated with $\mathbf {V}_i$ as

  $$\begin{aligned} \mathbf {S}_{i \ell } = \left( 1 - \theta _i \right) \mathbf {V}_i + \theta _i \mathbf {V}_\ell \end{aligned}$$

  for all edges $\langle \mathbf {V}_i, \mathbf {V}_\ell \rangle$ of $\triangle$, together with the point $\mathbf {V}_i$ itself. Then choose a PS-triangle ${t_i} \langle \mathbf {Q}_{i,1}, \mathbf {Q}_{i,2}, \mathbf {Q}_{i,3} \rangle$, i. e., an arbitrary triangle that contains all the PS-points associated with the vertex $\mathbf {V}_i$. See Fig. 3a for a demonstration. Consider the Bernstein basis polynomials $B_{\mathbf {j}}^{\rho _d}$, $|\mathbf {j}| = \rho _d$, of degree $\rho _d$ on $t_i$, and define parameters

  $$\begin{aligned} \alpha _{i,\mathbf {j},d}^{ab} := \left( \theta _i \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\rho _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} B_{\mathbf {j}}^{\rho _d}(\mathbf {V}_i) \end{aligned}$$

  (4.1)

  for $0 \le a+b \le \rho _d$ and $\mathbf {j} \in \mathbb N_0^3$ with $|\mathbf {j}| = \rho _d$.

• 2. For each macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$, denote by $\mathscr {W}_k$ the triangle with vertices

  $$\begin{aligned} \mathbf {W}_\ell = \frac{\mu _d}{d} \mathbf {V}_\ell + \left( 1 - \frac{\mu _d}{d} \right) \mathbf {Z}_k, \quad \ell = 1, 2, 3. \end{aligned}$$

  See Fig. 3b. In this case, consider the Bernstein basis polynomials $B_{\mathbf {i}}^{\mu _d}$, $|\mathbf {i}| = \mu _d$, of degree $\mu _d$ on $\mathscr {W}_k$, and define parameters

  $$\begin{aligned} \beta _{k,\mathbf {j},d}^{ab} := \left( \frac{\mu _d}{d} \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\mu _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{x}^{b} B_{r-1-j_1, r-1-j_2, r-1-j_3}^{\mu _d}(\mathbf {Z}_k) \end{aligned}$$

  (4.2)

  for $0 \le a+b \le r-2$ and $\mathbf {j} = (j_1, j_2, j_3) \in \mathbb N_0^3$ with $|\mathbf {j}| = r-2$.

• 3. For each vertex $\mathbf {V}_1 \in \mathscr {V}$, each macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ with a vertex at $\mathbf {V}_1$, and each $\mathbf {j} \in \mathbb N_0^3$ with $|\mathbf {j}| = \rho _d$, denote by $p_{1,k,\mathbf {j}}^{d}$ the polynomial of degree $\mu _d$ defined as follows. Let $\mathscr {T}_k^* \in \triangle ^*$ be a triangle in $\mathscr {T}_k$ with a vertex at $\mathbf {V}_1$. Consider the polynomial q of degree $\rho _d$ on the triangle $\mathscr {D}_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1)$ that is completely specified by the interpolation conditions $D_{x}^{a} D_{y}^{b} q(\mathbf {V}_1) = \alpha _{1,\mathbf {j},d}^{ab}$, $0 \le a+b \le \rho _d$. Let its Bézier ordinates be denoted by $b_{\mathbf {\ell }}$, $|\mathbf {\ell }| = \rho _d$. Specify the polynomial $p_{1,k,\mathbf {j}}^{d}$ as

  $$\begin{aligned} p_{1,k,\mathbf {j}}^{d} = \sum _{|\mathbf {i}| = \mu _d} d_{\mathbf {i}} B_{\mathbf {i}}^{\mu _d} \end{aligned}$$

  with respect to the triangle ${\mathscr {W}_k} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$. Let $d_{\mathbf {i}}$, $\mathbf {i} = (i_1, i_2, i_3)$, with $i_1 < r$ be equal to 0, and let $d_{\mathbf {i}}$ with $i_1 \ge r$ be determined so that the ordinates of the subdivided polynomial $p_{1,k,\mathbf {j}}^{d}$ on $\mathscr {D}_{\mu _d,\mathscr {T}_k^*}(\mathbf {Z}_k)$ that correspond to the domain points in $D_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1) \cap D_{\mu _d,\mathscr {T}_k^*}(\mathbf {Z}_k)$ coincide with the ordinates $b_{\mathbf {\ell }}$ of q associated with the same domain points. For an illustration, see Fig. 4. With the help of $p_{1,k,\mathbf {j}}^{d}$, define parameters

  $$\begin{aligned} \gamma _{1,k,\mathbf {j},d}^{ab} := \left( \frac{\mu _d}{d} \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\mu _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} p_{1,k,\mathbf {j}}^{d}(\mathbf {Z}_k) \end{aligned}$$

  (4.3)

  for $0 \le a+b \le r-2$.

Fig. 4

Construction of the polynomial $p_{1,k,\mathbf {j}}^{d}$ associated with a vertex $\mathbf {V}_1$ and a macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ for $d = 12$. On the left-hand side, $p_{1,k,\mathbf {j}}^{d}$ is represented on the triangle $\mathscr {D}_{\mu _d,\mathscr {T}_k^*}(\mathbf {Z}_k)$, where $\mathscr {T}_k^*$ is the triangle with the vertices $\mathbf {V}_1$, $\mathbf {R}_{12}$, $\mathbf {Z}_k$. The black coloured points are associated with the Bézier ordinates determined by $\alpha _{i,\mathbf {j},d}^{ab}$. On the right-hand side, $p_{1,k,\mathbf {j}}^{d}$ is represented with respect to the triangle ${\mathscr {W}_k} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$. The Bézier ordinates corresponding to the uncoloured points are equal to 0

Let us use the parameters introduced in (4.1), (4.2), and (4.3) to define Powell–Sabin B-splines as unique solutions of interpolation problems of the form (3.5). For every $\mathbf {V}_i \in \mathscr {V}$ and $\mathbf {j} \in \mathbb N_0^3$ with $|\mathbf {j}| = \rho _d$, denote by $B_{i,\mathbf {j}}^{v,d}$ the unique solution of the interpolation problem with

$$\begin{aligned} f_{x^a y^b,\ell } = {\left\{ \begin{array}{ll} \alpha _{i,\mathbf {j},d}^{ab}; &{} \ell = i \\ 0; &{} \text {else} \end{array}\right. } \quad \text {and} \quad g_{x^a y^b, m} = {\left\{ \begin{array}{ll} \gamma _{i,m,\mathbf {j},d}^{ab}; &{} \mathscr {T}_m \in M_{\triangle }(\mathbf {V}_i) \\ 0; &{} \text {else} \end{array}\right. }. \end{aligned}$$

Furthermore, for every $\mathscr {T}_k \in \triangle$ and $\mathbf {j} \in \mathbb N_0^3$ with $|\mathbf {j}| = r-2$, define $B_{k,\mathbf {j}}^{t,d}$ as the unique solution of the interpolation problem with

$$\begin{aligned} f_{x^a y^b,\ell } = 0 \quad \text {and} \quad g_{x^a y^b, m} = {\left\{ \begin{array}{ll} \beta _{m,\mathbf {j},d}^{ab}; &{} m = k \\ 0; &{} \text {else} \end{array}\right. }. \end{aligned}$$

4.2 B-spline representation

To get an insight into the definition of Powell Sabin B-splines, the theorem proved in [18] is first considered.

Theorem 4.1

Let $p_{d_1}$ be a polynomial of degree $d_1$ that is defined on the triangle ${\mathscr {T}_1} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$, and let $p_{d_2}$ be a polynomial of degree $d_2$ (with $d_2 \le d_1$) that is defined on the triangle ${\mathscr {T}_2} \langle \mathbf {V}_1, \mathbf {U}_2, \mathbf {U}_3 \rangle$, where

$$\begin{aligned} \mathbf {U}_2 = (1-\theta ) \mathbf {V}_1 + \theta \mathbf {V}_2, \quad \mathbf {U}_3 = (1-\theta ) \mathbf {V}_1 + \theta \mathbf {V}_3 \end{aligned}$$

for some $\theta \in (0,1)$. Suppose that the Bézier ordinates of the polynomial $p_{d_1}$ are denoted by $b_{\mathbf {i}}$, $|\mathbf {i}| = d_1$, and the Bézier ordinates of the polynomial $p_{d_2}$ are denoted by $b_{\mathbf {i}}'$, $|\mathbf {i}| = d_2$. Then

$$\begin{aligned} D_{x}^{a} D_{y}^{b} p_{d_1}(\mathbf {V}_1) = \left( \theta \right) ^{a+b} \frac{\left( {\begin{array}{c}d_1\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}d_2\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} p_{d_2}(\mathbf {V}_1) \end{aligned}$$

for a given value $0 \le \nu \le d_2$ and all $0 \le a+b \le \nu$ if and only if

$$\begin{aligned} b_{d_1-\nu +i_1, i_2, i_3} = b_{d_2-\nu +i_1, i_2, i_3}' \end{aligned}$$

for all $\mathbf {i} = (i_1, i_2, i_3)$ with $|\mathbf {i}| = \nu$.

In what follows, two lemmas extending [18, Lemmas 1 and 2] are presented. They show how to describe an element of $\mathscr {S}_{d}(\triangle ^*)$ locally at the points of $\triangle$ and at the interior split points of $\triangle ^*$ in terms of polynomials.

Lemma 4.1

For $\mathbf {V}_i \in \mathscr {V}$ and parameter $\theta _i$, let

$$\begin{aligned} T_i^v = \sum _{|\mathbf {j}| = \rho _d} c_{i,\mathbf {j}}^{v,d} B_{\mathbf {j}}^{\rho _d} \end{aligned}$$

be a polynomial of degree $\rho _d$ with the Bernstein basis polynomials $B_{\mathbf {j}}^{\rho _d}$ defined on a PS-triangle ${t_i} \langle \mathbf {Q}_{i,1}, \mathbf {Q}_{i,2}, \mathbf {Q}_{i,3} \rangle$. Furthermore, let $s \in \mathscr {S}_{d}(\triangle ^*)$. Then

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s(\mathbf {V}_i) = \left( \theta _i \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\rho _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} T_i^v(\mathbf {V}_i) \end{aligned}$$

(4.4)

for all $0 \le a+b \le \rho _d$ if and only if the Bézier ordinates $c_{i,\mathbf {j}}^{v,d}$, $\mathbf {j} = (j_1, j_2, j_3)$, $|\mathbf {j}| = \rho _d$, of $T_i^v$ with respect to the PS-triangle $t_i$ are given by

$$\begin{aligned} c_{i,\mathbf {j}}^{v,d} = \mathscr {B}[s|_{\mathscr {T}_i^*}] \left( \mathbf {V}_i[r], \widehat{\mathbf {Q}}_{i,1}[j_1], \widehat{\mathbf {Q}}_{i,2}[j_2], \widehat{\mathbf {Q}}_{i,3}[j_3] \right) , \end{aligned}$$

(4.5)

where $\mathscr {T}_i^*$ is an arbitrary triangle in $\triangle ^*$ with a vertex at $\mathbf {V}_i$, and

$$\begin{aligned} \widehat{\mathbf {Q}}_{i,\ell } = \left( 1 - \frac{1}{\theta _i} \right) \mathbf {V}_i + \frac{1}{\theta _i} \mathbf {Q}_{i,\ell }, \qquad \ell = 1, 2, 3. \end{aligned}$$

Proof

Without loss of generality assume that $i = 1$, and let $\mathbf {V}_1$, $\mathbf {V}_2^*$, and $\mathbf {V}_3^*$ denote the vertices of $\mathscr {T}_1^*$. Let $\widehat{\mathscr {T}}_1^*$ be the triangle with the vertices $\mathbf {V}_1$ and

$$\begin{aligned} \mathbf {S}_{1\ell }^* = \left( 1 - \theta _1 \right) \mathbf {V}_1 + \theta _1 \mathbf {V}_\ell ^*, \quad \ell = 2,3. \end{aligned}$$

Suppose that $b_{\mathbf {i}}$, $|\mathbf {i}| = d$, are the Bézier ordinates of $s|_{\mathscr {T}_1^*}$ with respect to $\mathscr {T}_1^*$, and $d_{\mathbf {j}}$, $|\mathbf {j}| = \rho _d$, are the Bézier ordinates of $T_1^v$ with respect to $\widehat{\mathscr {T}}_1^*$. By Theorem 4.1, the equality (4.4) holds if and only if $d_{\mathbf {j}} = b_{r+j_1,j_2,j_3}$, $\mathbf {j} = (j_1, j_2, j_3)$. This is equivalent to the condition that

$$\begin{aligned} \mathscr {B}[T_1^v, \widehat{\mathscr {T}}_1^*] \left( \mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\rho _d} \right) = \mathscr {B}[s|_{\mathscr {T}_1^*}, \mathscr {T}_1^*] \left( \mathbf {e}^1[r], \mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\rho _d} \right) \end{aligned}$$

(4.6)

for any set of barycentric coordinates $\mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\rho _d}$, where $\mathbf {e}^1 = (1,0,0)$. It is known that

$$\begin{aligned} c_{1,\mathbf {j}}^{v,d} = \mathscr {B}[T_1^v] \left( \mathbf {Q}_{1,1}[j_1], \mathbf {Q}_{1,2}[j_2], \mathbf {Q}_{1,3}[j_3] \right) . \end{aligned}$$

Let $\mathbf {\sigma }^\ell = (\sigma _1^\ell , \sigma _2^\ell , \sigma _3^\ell )$, $\ell = 1, 2, 3$, denote the barycentric coordinates of $\mathbf {Q}_{1,\ell }$ with respect to $\widehat{\mathscr {T}}_1^*$, i. e.,

$$\begin{aligned} \mathbf {Q}_{1,\ell } = \sigma _1^\ell \mathbf {V}_1 + \sigma _2^\ell \mathbf {S}_{12}^* + \sigma _3^\ell \mathbf {S}_{13}^*. \end{aligned}$$

One can easily verify that

$$\begin{aligned} \widehat{\mathbf {Q}}_{1,\ell } = \sigma _1^\ell \mathbf {V}_1 + \sigma _2^\ell \mathbf {V}_2^* + \sigma _3^\ell \mathbf {V}_3^*, \quad \ell = 1, 2, 3. \end{aligned}$$

(4.7)

By (4.6), it follows that

$$\begin{aligned} c_{i,\mathbf {j}}^{v,d}= & {} \mathscr {B}[T_1^v, \widehat{\mathscr {T}}_1^*] \left( \mathbf {\sigma }^1[j_1], \mathbf {\sigma }^2[j_2], \mathbf {\sigma }^3[j_3] \right) \\= & {} \mathscr {B}[s|_{\mathscr {T}_1^*}, \mathscr {T}_1^*] \left( \mathbf {e}^1[r], \mathbf {\sigma }^1[j_1], \mathbf {\sigma }^2[j_2], \mathbf {\sigma }^3[j_3] \right) , \end{aligned}$$

which by (4.7) implies (4.5). $\square$

In case when the Bézier ordinates of $T_i^v$ are determined as in (4.5), the spline $s \in \mathscr {S}_{d}(\triangle ^*)$ and the polynomial $T_i^v$ have the same value at $\mathbf {V}_i$. Also, the first derivative values coincide if $\theta _i$ is chosen to be equal to $\frac{\rho _d}{d}$.

Lemma 4.2

For $s \in \mathscr {S}_{d}(\triangle ^*)$ and ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$, let

$$\begin{aligned} T_k^t = \sum _{\ell = 1}^3 \sum _{|\mathbf {j}| = \rho _d} c_{\ell ,\mathbf {j}}^{v,d} p_{\ell ,k,\mathbf {j}}^{d} + \sum _{\begin{array}{c} |\mathbf {j}| = r-2, \\ \mathbf {j} = (j_1,j_2,j_3) \end{array}} c_{k,\mathbf {j}}^{t,d} B_{r-1-j_1,r-1-j_2,r-1-j_3}^{\mu _d} \end{aligned}$$

be a polynomial of degree $\mu _d$, where the coefficients $c_{\ell ,\mathbf {j}}^{v,d}$ are given by (4.5), the polynomials $p_{\ell ,k,\mathbf {j}}^{d}$ are specified in the Sect. 4.1, and the Bernstein basis polynomials $B_{r-1-j_1,r-1-j_2,r-1-j_3}^{\mu _d}$ are defined on ${\mathscr {W}_k} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$. Then

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s(\mathbf {Z}_k) = \left( \frac{\mu _d}{d} \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\mu _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} T_k^t(\mathbf {Z}_k) \end{aligned}$$

for every $0 \le a+b \le \mu _d$ if and only if

$$\begin{aligned} c_{k,\mathbf {j}}^{t,d} = \mathscr {B}[s|_{\mathscr {T}_k^*}] \left( \mathbf {Z}_k[d-\mu _d], \mathbf {V}_1[r-1-j_1], \mathbf {V}_2[r-1-j_2], \mathbf {V}_3[r-1-j_3] \right) , \end{aligned}$$

(4.8)

where $\mathscr {T}_k^*$ is an arbitrary triangle in $\triangle ^*$ with a vertex at $\mathbf {Z}_k$.

Proof

The smoothness of order $\mu _d$ at the vertex $\mathbf {Z}_k$ implies that the Bézier ordinates of s corresponding to the domain points in $D_{\mu _d,\triangle ^*}(\mathbf {Z}_k)$ can be regarded as the Bézier ordinates (after subdivision) of a polynomial p of order $\mu _d$ on $\mathscr {W}_k$. Consider a triangle $\mathscr {T}_\ell ^* \in \triangle ^*$, $\ell \in \{ 1, 2, 3 \}$, with a vertex at $\mathbf {V}_\ell$. Since the Bézier ordinates of p on $\mathscr {D}_{\mu _d,\mathscr {T}_\ell ^*}(\mathbf {Z}_k)$ and $s|_{\mathscr {T}_\ell ^*}$ on $\mathscr {T}_\ell ^*$ associated with the domain points in $D_{\mu _d,\mathscr {T}_\ell ^*}(\mathbf {Z}_k)$ agree, Theorem 4.1 implies that the polynomial p satisfies the condition

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s(\mathbf {Z}_k) = D_{x}^{a} D_{y}^{b} s|_{\mathscr {T}_\ell ^*}(\mathbf {Z}_k) = \left( \frac{\mu _d}{d} \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\mu _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} p(\mathbf {Z}_k). \end{aligned}$$

By the same argument, the blossom of p on $\mathscr {D}_{\mu _d,\mathscr {T}_\ell ^*}(\mathbf {Z}_k)$ can be expressed as the blossom of $s|_{\mathscr {T}_\ell ^*}$ on $\mathscr {T}_\ell ^*$. With the help of the subdivision property of the blossom, it can be easily verified that the identity

$$\begin{aligned} \mathscr {B}[p, \mathscr {W}_k](\mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\mu _d}) = \mathscr {B}[s|_{\mathscr {T}_\ell ^*}, \mathscr {T}_k](\mathbf {z}[d-\mu _d], \mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\mu _d}) \end{aligned}$$

holds for any set of barycentric coordinates $\mathbf {\tau }^1, \ldots , \mathbf {\tau }^{\mu _d}$, where $\mathbf {z}$ denotes the barycentric coordinates of $\mathbf {Z}_k$ with respect to $\mathscr {T}_k$. This proves that the Bézier ordinates $b_{\mathbf {i}}$, $|\mathbf {i}| = \mu _d$, of p with respect to the triangle $\mathscr {W}_k$ can be expressed as

$$\begin{aligned} b_{\mathbf {i}} = \mathscr {B}[s|_{\mathscr {T}_\ell ^*}](\mathbf {Z}_k[d-\mu _d], \mathbf {V}_1[i_1], \mathbf {V}_2[i_2], \mathbf {V}_3[i_3]) \end{aligned}$$

for $\ell = 1, 2, 3$. Let us write the polynomial p in the form

$$\begin{aligned} p = \sum _{\ell = 1}^3 \sum _{\begin{array}{c} |\mathbf {i}| = \mu _d, \\ i_\ell \ge r \end{array}} b_{\mathbf {i}} B_{\mathbf {i}}^{\mu _d} + \sum _{\begin{array}{c} |\mathbf {i}| = \mu _d, \\ i_1, i_2, i_3 < r \end{array}} b_{\mathbf {i}} B_{\mathbf {i}}^{\mu _d}. \end{aligned}$$

To complete the proof, it remains to check that

$$\begin{aligned} \sum _{|\mathbf {j}| = \rho _d} c_{\ell ,\mathbf {j}}^{v,d} p_{\ell ,k,\mathbf {j}}^{d} = \sum _{\begin{array}{c} |\mathbf {i}| = \mu _d, \\ i_\ell \ge r \end{array}} b_{\mathbf {i}} B_{\mathbf {i}}^{\mu _d}, \qquad \ell = 1, 2, 3, \end{aligned}$$

since this implies that $T_k^t = p$ if and only if $c_{k,\mathbf {j}}^{t,d}$ is given as in (4.8). Consider the polynomials in the above identity on the triangle $\mathscr {D}_{\mu _d,\mathscr {T}_\ell ^*}(\mathbf {Z}_k)$. They are both uniquely determined by the Bézier ordinates corresponding to the domain points contained in $D_{\rho _d,\mathscr {T}_\ell ^*}(\mathbf {V}_\ell ) \cap D_{\mu _d,\mathscr {T}_\ell ^*}(\mathbf {Z}_k)$. The referring ordinates of the polynomial on the right-hand side are clearly equal to the ordinates of $s|_{\mathscr {T}_\ell ^*}$ on $\mathscr {T}_\ell ^*$. By Lemma 4.1, this also holds for the polynomial on the left-hand side since, by definition, the ordinates of $p_{\ell ,k,\mathbf {j}}^{d}$ agree with the ordinates of $B_{\ell ,\mathbf {j}}^{v,d}$ with respect to $\mathscr {T}_\ell ^*$. $\square$

Under the assumption that the Bézier ordinates of $T_k^t$ are equal to (4.8), the value and the first derivative values of $s \in \mathscr {S}_{d}(\triangle ^*)$ and $T_k^t$ at $\mathbf {Z}_k$ coincide. The following theorem is analogous to [18, Theorem 5] and justifies the representation of an arbitrary spline in $\mathscr {S}_{d}(\triangle ^*)$ in terms of B-splines.

Theorem 4.2

Every $s \in \mathscr {S}_{d}(\triangle ^*)$ can be expressed as

$$\begin{aligned} s = \sum _{\ell = 1}^{|\mathscr {V}|} \sum _{|\mathbf {j}| = \rho _d} c_{\ell ,\mathbf {j}}^{v,d} B_{\ell ,\mathbf {j}}^{v,d} + \sum _{m = 1}^{|\triangle |} \sum _{|\mathbf {j}| = r-2} c_{m,\mathbf {j}}^{t,d} B_{m,\mathbf {j}}^{t,d}, \end{aligned}$$

(4.9)

where $B_{\ell ,\mathbf {j}}^{v,d}$ and $B_{\ell ,\mathbf {j}}^{t,d}$ are Powell–Sabin B-splines defined in the Sect. 4.1, and the coefficients $c_{\ell ,\mathbf {j}}^{v,d}$ and $c_{m,\mathbf {j}}^{t,d}$ are given in (4.5) and (4.8), respectively.

Proof

Denote by $s'$ the right hand-side of the Eq. (4.9). In order to prove that $s = s'$, it is sufficient to check that s and $s'$ satisfy the same interpolation conditions in (3.5). The result then follows from Theorem 3.1.

Let $\mathbf {V}_i \in \mathscr {V}$ and $0 \le a+b \le \rho _d$. From definition of the B-splines and the parameters $\alpha _{\ell ,\mathbf {j},d}^{ab}$ in (4.1), it follows that

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s'(\mathbf {V}_i)= & {} \sum _{|\mathbf {j}| = \rho _d} c_{i,\mathbf {j}}^{v,d} D_{x}^{a} D_{y}^{b} B_{i,\mathbf {j}}^{v,d}(\mathbf {V}_i) \\= & {} \sum _{|\mathbf {j}| = \rho _d} c_{i,\mathbf {j}}^{v,d} \alpha _{i,\mathbf {j},d}^{ab} \\= & {} \left( \theta _i \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\rho _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} T_i^v(\mathbf {V}_i). \end{aligned}$$

By Lemma 4.1, this is equal to $D_{x}^{a} D_{y}^{b} s(\mathbf {V}_i)$. Similarly, let ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$ and $0 \le a+b \le r-2$. According to definition of the B-splines and the parameters $\beta _{m,\mathbf {j},d}^{ab}$ and $\gamma _{\ell ,m,\mathbf {j},d}^{ab}$ in (4.2) and (4.3),

$$\begin{aligned} D_{x}^{a} D_{y}^{b} s'(\mathbf {Z}_k)= & {} \sum _{\ell = 1}^3 \sum _{|\mathbf {j}| = \rho _d} c_{\ell ,\mathbf {j}}^{v,d} D_{x}^{a} D_{y}^{b} B_{\ell ,\mathbf {j}}^{v,d}(\mathbf {Z}_k) + \sum _{|\mathbf {j}| = r-2} c_{k,\mathbf {j}}^{t,d} D_{x}^{a} D_{y}^{b} B_{k,\mathbf {j}}^{t,d}(\mathbf {Z}_k) \\= & {} \sum _{\ell = 1}^3 \sum _{|\mathbf {j}| = \rho _d} c_{\ell ,\mathbf {j}}^{v,d} \gamma _{\ell ,k,\mathbf {j},d}^{ab} + \sum _{|\mathbf {j}| = r-2} c_{k,\mathbf {j}}^{t,d} \beta _{k,\mathbf {j},d}^{ab} \\= & {} \left( \frac{\mu _d}{d} \right) ^{a+b} \frac{\left( {\begin{array}{c}d\\ a+b\end{array}}\right) }{\left( {\begin{array}{c}\mu _d\\ a+b\end{array}}\right) } D_{x}^{a} D_{y}^{b} T_k^t(\mathbf {Z}_k). \end{aligned}$$

By Lemma 4.2, this is equal to $D_{x}^{a}D_{y}^{b}s(\mathbf {Z}_k)$, which completes the proof. $\square$

4.3 Bézier representation of B-splines

In the following remarks, the computation of the Bézier representation of Powell–Sabin B-splines is investigated. The remarks rephrase [17, Lemmas 1–4] in order to validate the results for an arbitrary degree. The goal is to express B-spline Bézier ordinates in terms of blossoms of Bernstein basis polynomials defined either on a PS-triangle or on a scaled triangle of a macro-triangle. The resulting observations can be rather easily extended to the instructions on computation of the Bézier representation of a spline given in the form (4.9), but most of all they will be of a great help in the proof of nonnegativity of the basis functions.

Fig. 5

Representation of Bézier ordinates of B-splines of degree 12 on a macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$. The uncoloured domain point indicates that the corresponding Bézier ordinate is equal to 0. a A B-spline associated with the vertex $\mathbf {V}_1$. b A B-spline associated with the triangle $\mathscr {T}_k$

First, let us examine a B-spline $B_{1,\mathbf {j}}^{v,d}$, $|\mathbf {j}| = \rho _d$, associated with the vertex $\mathbf {V}_1$ of $\triangle$ on a macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$. See Fig. 5a.

Remark 4.1

Consider the triangle ${\mathscr {T}_k^*} \langle \mathbf {V}_1, \mathbf {R}_{12}, \mathbf {Z}_k \rangle \in \triangle ^*$. By definition of the B-splines associated with the vertex and by Theorem 4.1, the Bézier ordinates $b_{r+j_1,j_2,j_3}$ of $B_{1,\mathbf {j}}^{v,d}$, $\mathbf {j} = (j_1, j_2, j_3)$, $|\mathbf {j}| = \rho _d$, corresponding to the domain points in $D_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1)$ can be regarded as the Bézier ordinates (after subdivision) of the Bernstein basis polynomial $B_{\mathbf {j}}^{\rho _d}$ defined on the PS-triangle $t_1$. Thus, they can be expressed in terms of blossom as

$$\begin{aligned} b_{r+j_1,j_2,j_3} = \mathscr {B}[B_{\mathbf {j}}^{\rho _d}, t_1] \left( \mathbf {\sigma }^1[j_1], \mathbf {\sigma }^2[j_2], \mathbf {\sigma }^3[j_3] \right) , \end{aligned}$$

(4.10)

where $\mathbf {\sigma }^1$, $\mathbf {\sigma }^2$, $\mathbf {\sigma }^3$ are the barycentric coordinates of the vertices of $\mathscr {D}_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1)$ with respect to $t_1$. Similarly, one can express the ordinates of $B_{1,\mathbf {j}}^{v,d}$ associated with the points in the disk of radius $\rho _d$ around $\mathbf {V}_1$ on the triangle determined by the vertices $\mathbf {V}_1$, $\mathbf {R}_{13}$, $\mathbf {Z}_k$.

In Remark 4.1, a compact representation of the ordinates of $B_{1,\mathbf {j}}^{v,d}$ corresponding to the points in $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_1)$ is derived. By definition of the B-spline, it is obvious that the ordinates associated with the points in disks $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_2)$ and $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_3)$ are equal to 0.

Remark 4.2

Consider the triangle ${\mathscr {T}_k^*} \langle \mathbf {V}_1, \mathbf {R}_{12}, \mathbf {Z}_k \rangle \in \triangle ^*$, and let $\mathscr {D}_{\mu _d,\mathscr {T}_k^*}(\mathbf {Z}_k)$ be denoted by ${\mathscr {W}_k^*} \langle \mathbf {W}_1, \mathbf {T}_{12}, \mathbf {Z}_k \rangle$, where $\mathbf {T}_{12}$ is the intersection point of $\langle \mathbf {W}_1, \mathbf {W}_2 \rangle$ and $\langle \mathbf {R}_{12}, \mathbf {Z}_k \rangle$. Let us specify a polynomial of degree $\mu _d$ on $\mathscr {W}_k^*$. Suppose that its Bézier ordinates are denoted by $b_{\mathbf {i}}$, $|\mathbf {i}| = \mu _d$, and let them be equal to the Bézier ordinates of the B-splines $B_{1,\mathbf {j}}^{v,d}$ with respect to $\mathscr {T}_k^*$ corresponding to the same domain points. Based on Remark 4.1, the ordinates $b_{\mathbf {i}}$, $\mathbf {i} = (i_1, i_2, i_3)$, with $i_1 \ge r$ can be expressed as

$$\begin{aligned} b_{\mathbf {i}} = \mathscr {B}[B_{\mathbf {j}}^{\rho _d}, t_1] \left( \mathbf {\sigma }^1[i_1 - r], \mathbf {\sigma }^2[i_2], \mathbf {\sigma }^3[i_3 + d - \mu _d] \right) \end{aligned}$$

(4.11)

under the assumption that $\mathbf {\sigma }^1$ corresponds to the vertex $\mathbf {V}_1$ and $\mathbf {\sigma }^3$ corresponds to the vertex of $\mathscr {D}_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1)$ located on the edge $\langle \mathbf {V}_1, \mathbf {Z}_k \rangle$. By construction, the ordinates $b_{\mathbf {i}}$ can be regarded as the Bézier ordinates (after subdivision) of the polynomial $p_{1,k,\mathbf {j}}^{d}$ of degree $\mu _d$ defined on ${\mathscr {W}_k} \langle \mathbf {W}_1, \mathbf {W}_2, \mathbf {W}_3 \rangle$. Let us denote by $d_{\mathbf {i}}$, $|\mathbf {i}| = \mu _d$, the Bézier ordinates of $p_{1,k,\mathbf {j}}^{d}$ with respect to the triangle $\mathscr {W}_k$. They can be expressed as

$$\begin{aligned} d_{\mathbf {i}} = \mathscr {B}[p_{1,k,\mathbf {j}}^{d}, \mathscr {W}_k^*] \left( \mathbf {\varrho }^1[i_1], \mathbf {\varrho }^2[i_2], \mathbf {\varrho }^3[i_3] \right) , \quad \mathbf {i} = (i_1, i_2, i_3), \end{aligned}$$

where $\rho ^\ell = (\rho _1^\ell , \rho _2^\ell , \rho _3^\ell )$, $\ell = 1, 2, 3$, are the barycentric coordinates of $\mathbf {W}_\ell$ with respect to the triangle $\mathscr {W}_k^*$. Note that $\rho ^1 = (1,0,0)$. The calculation of $d_{\mathbf {i}}$ with $i_1 \ge r$ can be carried out by the multi-affine de Casteljau algorithm. Suppose that the algorithm begins with the weight $\rho ^1$. After the first r steps, only the ordinates $b_{\mathbf {i}}$ with $i_1 \ge r$ are still involved in the calculation. If they are expressed as in (4.11), the remaining $\mu _d-r$ steps of the algorithm result in the identity

$$\begin{aligned} d_{\mathbf {i}} = \mathscr {B}[B_{\mathbf {j}}^{\rho _d}, t_1] \left( \mathbf {\sigma }^1[i_1-r], \mathbf {\sigma }^3[d-\mu _d], \sum _{\ell =1}^3 \varrho _\ell ^2 \mathbf {\sigma }^\ell [i_2], {\sum _{\ell =1}^3 \varrho _\ell ^3 \mathbf {\sigma }^\ell }[i_3] \right) \end{aligned}$$

(4.12)

for $i_1 \ge r$. The Bézier ordinates $d_{\mathbf {i}}$ with $i_1 < r$ are known to be 0. Using subdivision, one can explicitly compute the Bézier ordinates of $B_{1,\mathbf {j}}^{v,d}$ corresponding to the domain points in the disk $D_{\mu _d,\{ \mathscr {T}_k \}^*}(\mathbf {Z}_k)$.

The Bézier ordinates of $B_{1,\mathbf {j}}^{v,d}$ associated with the points in ${\varXi }_{d,\{ \mathscr {T}_k \}^*}$ that were not taken into the consideration in Remark 4.1 and Remark 4.2 all correspond to the points on the rows parallel to the edges of $\mathscr {T}_k$ at distance less than $d - \mu _d$. Clearly, the ordinates associated with the points in $E_{m,\{ \mathscr {T} \}^*}(\langle \mathbf {V}_2, \mathbf {V}_3 \rangle )$, $m = 0, \ldots , d-\mu _d-1$, are equal to 0. The ordinates in the rows parallel to $\langle \mathbf {V}_1, \mathbf {V}_2 \rangle$ are determined in the following remark. The ordinates in the rows parallel to $\langle \mathbf {V}_1, \mathbf {V}_3 \rangle$ can be treated in an analogue way.

Remark 4.3

For every $m \in \{ 0, \ldots , d-\mu _d-1 \}$, the Bézier ordinates of $B_{1,\mathbf {j}}^{v,d}$ associated with the points in the row $E_{m,\{ \mathscr {T}_k \}^*}(\langle \mathbf {V}_1, \mathbf {V}_2 \rangle )$ are partially determined since those corresponding to the points in $D_{\rho _d,\mathscr {T}_k^*}(\mathbf {V}_1)$ were expressed in Remark 4.1, and those corresponding to the points in $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_2)$ are equal to 0. The remaining ordinates can be obtained by using the assumption of $\mathscr {C}^{\mu _d}$-smoothness across the edge $\langle \mathbf {R}_{12}, \mathbf {Z}_k \rangle$. By this constraint, they can be regarded as the ordinates (after subdivision) of a one-dimensional polynomial of degree $\mu _d$. Let its Bézier ordinates with respect to the line segment $\langle \widetilde{\mathbf {W}}_1, \widetilde{\mathbf {W}}_2 \rangle$,

$$\begin{aligned} \widetilde{\mathbf {W}}_\ell = \frac{\mu _d}{d} \mathbf {V}_\ell + \frac{d-\mu _d-m}{d} \mathbf {R}_{12} + \frac{m}{d} \mathbf {Z}_k, \qquad \ell = 1, 2, \end{aligned}$$

be denoted by $d_{\mathbf {i}}$, $|\mathbf {i}| = \mu _d$. Similarly as in Remark 4.2, it can be derived that the ordinates $d_{\mathbf {i}}$, $\mathbf {i} = (i_1,i_2)$, with $i_1 \ge r$ can be expressed as

$$\begin{aligned} d_{\mathbf {i}} = \mathscr {B}[B_{\mathbf {j}}^{\rho _d}, t_1] \left( \mathbf {\sigma }^1[i_1-r], \mathbf {\sigma }^2[d-\mu _d-m], \mathbf {\sigma }^3[m], \sum _{\ell =1}^2 \varrho _\ell ^2 \mathbf {\sigma }^\ell [i_2] \right) , \end{aligned}$$

(4.13)

where $\rho ^2 = (\rho _1^2, \rho _2^2)$ denotes the barycentric coordinates of $\widetilde{\mathbf {W}}_2$ with respect to the line segment determined by $\widetilde{\mathbf {W}}_1$ and the intersection point between $\langle \mathbf {R}_{12}, \mathbf {Z}_k \rangle$ and $\langle \widetilde{\mathbf {W}}_1, \widetilde{\mathbf {W}}_2 \rangle$. The values $d_{\mathbf {i}}$ with $i_1 < r$ are equal to 0.

Consider now a B-spline $B_{k,\mathbf {j}}^{t,d}$, $|\mathbf {j}| = r-2$, associated with the macro-triangle ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle \in \triangle$. See Fig. 5b. By definition, its Bézier ordinates corresponding to the domain points in the disks $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_\ell )$, $\ell = 1, 2, 3$, are equal to 0. Consequently, all its Bézier ordinates corresponding to the points in the rows parallel to the edges of $\mathscr {T}_k$ at distance less or equal to $d-\mu _d$ are 0. The remaining ordinates can be expressed in a similar manner as the ordinates of a B-spline associated with a vertex in Remark 4.1.

Remark 4.4

Consider the Bézier ordinates of $B_{k,\mathbf {j}}^{t,d}$, $\mathbf {j} = (j_1,j_2,j_3)$, $|\mathbf {j}| = r-2$, with respect to ${\mathscr {T}_k^*} \langle \mathbf {V}_1, \mathbf {R}_{12}, \mathbf {Z}_k \rangle$ that are associated with the points in the disk $D_{\mu _d,\mathscr {T}_k^*}(\mathbf {Z}_k)$. Let them be denoted by $b_{i_1,i_2,d-\mu _d+i_3}$, where $i_1 + i_2 + i_3 = \mu _d$. From definition (4.2) and Theorem 4.1, it can be deduced that they can be regarded as the Bézier ordinates (after subdivision) of the Bernstein basis polynomial $B_{r-1-j_1, r-1-j_2, r-1-j_3}^{\mu _d}$ defined on $\mathscr {W}_k$. It then follows immediately that

$$\begin{aligned} b_{i_1,i_2,d-\mu _d+i_3} = \mathscr {B}[B_{r-1-j_1,r-1-j_2,r-1-j_3}^{\mu _d}, \mathscr {W}_k] \left( \mathbf {\lambda }^1[i_1], \mathbf {\lambda }^2[i_2], \mathbf {\lambda }^3[i_3] \right) , \end{aligned}$$

(4.14)

where $\mathbf {\lambda }^1$, $\mathbf {\lambda }^2$, $\mathbf {\lambda }^3$ denote the barycentric coordinates of $\mathbf {W}_1$, $\mathbf {T}_{12}$, $\mathbf {Z}_k$ with respect to the triangle $\mathscr {W}_k$.

4.4 Properties of B-splines

It remains us to prove the main properties of the derived Powell–Sabin B-splines $B_{i,\mathbf {j}}^{v,d}$, $i = 1, \ldots , |\mathscr {V}|$, $|\mathbf {j}| = \rho _d$, and $B_{k,\mathbf {j}}^{t,d}$, $k = 1, \ldots , |\triangle |$, $|\mathbf {j}| = r-2$. The following theorems are generalizations of [17, Theorems 7–9].

Theorem 4.3

The Powell–Sabin B-splines have local supports.

Proof

From the proof of Theorem 3.1 it follows that an element of $\mathscr {S}_{d}(\triangle ^*)$ is identically equal to zero on every macro-triangle with zero interpolation conditions at its vertices and at the interior split point of its Powell–Sabin refinement. Thus, by definition, every $B_{i,\mathbf {j}}^{v,d}$ is nonzero only on the molecule $M_{\triangle }(\mathbf {V}_i)$, and every $B_{k,\mathbf {j}}^{t,d}$ is nonzero only on the macro-triangle $\mathscr {T}_k \in \triangle$. $\square$

Theorem 4.4

The Powell–Sabin B-splines are nonnegative.

Proof

It is sufficient to show that Bézier ordinates of B-splines are nonnegative. For each $B_{i,\mathbf {j}}^{v,d}$, this needs to be verified on the molecule $M_{\triangle }(\mathbf {V}_i)$ since other ordinates are equal to 0 by Theorem 4.3. To simplify the notation, let $i = 1$, and let ${\mathscr {T}_k} \langle \mathbf {V}_1, \mathbf {V}_2, \mathbf {V}_3 \rangle$ be a triangle in $M_{\triangle }(\mathbf {V}_1)$. By Remark 4.1, the ordinates associated with the points in the disk $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_1)$ can be expressed in the form (4.10), i. e., as the blossom of Bernstein basis polynomials on the PS-triangle $t_1$ with nonnegative arguments, which confirms that they are nonnegative. The ordinates corresponding to the points in the disks $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_2)$ and $D_{\rho _d,\{ \mathscr {T}_k \}^*}(\mathbf {V}_3)$ are equal to 0. By Remark 4.2, the ordinates associated with the points in the disk $D_{\mu _d,\{ \mathscr {T}_k \}^*}(\mathbf {Z}_k)$ can be obtained from (4.12) by using subdivision. It can be easily verified that $\sum _{\ell = 1}^3 \varrho _\ell ^2 \mathbf {\sigma }^\ell$ and $\sum _{\ell = 1}^3 \varrho _\ell ^3 \mathbf {\sigma }^\ell$ are the barycentric coordinates of PS-points $\mathbf {S}_{12}$ and $\mathbf {S}_{13}$, respectively, and since these two are contained in the PS-triangle $t_1$, the arguments of expression (4.12) are nonnegative. After applying subdivision to a subtriangle, the sign of ordinates does not change. For the remaining ordinates, the nonnegativity follows from Remark 4.3 and expression (4.13) by similar arguments. The same result for each $B_{k,\mathbf {j}}^{t,d}$ can be obtained from the property of a local support proved in Theorem 4.3 and the expression (4.14) of its ordinates described in Remark 4.4. $\square$

Theorem 4.5

The Powell–Sabin B-splines form a partition of unity.

Proof

It needs to be shown that

$$\begin{aligned} \sum _{\ell = 1}^{|\mathscr {V}|} \sum _{|\mathbf {j}| = \rho _d} B_{\ell ,\mathbf {j}}^{v,d} + \sum _{m = 1}^{|\triangle |} \sum _{|\mathbf {j}| = r-2} B_{m,\mathbf {j}}^{t,d} = 1. \end{aligned}$$

The constant 1 is an element of $\mathscr {S}_{d}(\triangle ^*)$ so it can be expressed as (4.9). By Theorem 4.2, the coefficients can be expressed as the blossom of 1. Since the blossom of 1 is equal to one irrespective of the arguments, all coefficients are equal to one. $\square$

5 Conclusion

In this paper, super spline spaces on Powell–Sabin triangulations of arbitrary degree d were proposed. Their definition is inspired by the construction of super spline spaces of arbitrary smoothness r and degree $d = 3r-1$ introduced in [17]. The two additional families consist of spline spaces of degree $d = 3r - 2$ and $d = 3r$ with global smoothness $r-1$ and r, respectively. This means that within the considered spline spaces, the ones presented in [17] have the lowest degree for a certain smoothness. However, the accompanying families studied in this paper possess some additional super smoothness across certain edges and may thus be a relevant extension of the original family.

The main motivation to consider these splines is the ability to represent them in terms of nonnegative locally supported B-splines that form a partition of unity. It has been shown that the B-spline representation of $s \in \mathscr {S}_{d}(\triangle ^*)$ is uniquely determined by the choice of a PS-triangle $t_i$ and a parameter $\theta _i$ for every point $\mathbf {V}_i$ of the initial triangulation $\triangle$. If $\theta _i = \frac{\rho _d}{d}$, the polynomial $T_i^v$ introduced in Lemma 4.1 agree with s in the value and in the first derivative values at the point $\mathbf {V}_i$. Consequently, it might be an interesting geometric tool for modelling. By changing the shape of the polynomial patch on $t_i$, only the coefficients $c_{i,\mathbf {j}}^{v,d}$, $|\mathbf {j}| = \rho _d$, corresponding to $\mathbf {V}_i$ are modified, and the surface of s is changed locally due to Theorem 4.3. The polynomial $T_k^t$ proposed in Lemma 4.2 can be used in the same way, but only a certain subset of its Bézier ordinates may be modified. In order to obtain a meaningful tool, PS-triangles with small area should be considered. On the other hand, it is useful to choose the values of parameters $\theta _i$ independently of the degree d. This enables the choice of PS-triangles in advance, and the same PS-triangles can be used for the construction of splines of arbitrary degree. From this point of view, PS-triangles can be understood as an analogue of knots for univariate B-splines, and thus the parallel between the Powell–Sabin B-splines and the univariate B-splines is further improved.

Some additional properties and applications of the proposed family of super splines are straightforward. The Marsden’s identity can be simply derived as a corollary of Theorem 4.2 by taking $s \in \mathscr {S}_{d}(\triangle ^*)$ to be equal to a polynomial of degree d. Extension of functional splines to parametric splines can be carried out componentwise. Similarly as in [24] for $d = 2$, polynomial splines of arbitrary degree d can be generalized to rational splines. In [9, 10, 18] quasi-interpolants for splines of degrees 3 and $3r-1$, $r \in \mathbb N$, were studied. These results can also be adapted for general degree. Considering these options, super splines of arbitrary degree on Powell–Sabin triangulations might be a potentially interesting subject for a future research.