Fitting Procedures for Novel Gene-by-Measured Environment Interaction Models in Behavior Genetic Designs

Abstract

For quantitative behavior genetic (e.g., twin) studies, Purcell proposed a novel model for testing gene-by-measured environment (GxM) interactions while accounting for gene-by-environment correlation. Rathouz et al. expanded this model into a broader class of non-linear biometric models for quantifying and testing such interactions. In this work, we propose a novel factorization of the likelihood for this class of models, and adopt numerical integration techniques to achieve model estimation, especially for those without close-form likelihood. The validity of our procedures is established through numerical simulation studies. The new procedures are illustrated in a twin study analysis of the moderating effect of birth weight on the genetic influences on childhood anxiety. A second example is given in an online appendix. Both the extant GxM models and the new non-linear models critically assume normality of all structural components, which implies continuous, but not normal, manifest response variables.

Introduction

It is now well-established that genetic vulnerabilities are necessary but not sufficient for the expression of many health problems and most mental disorders, and that moderation of genetic influences by non-genetic factors plays an important role in the degree to which such disorders are expressed (Weaver et al. 2004; Rutter et al. 2006; Bennett 2008). Accurately identifying such gene-environment interactions, wherein genetic variation influencing the phenotype of interest is greater under certain environmental conditions than under others, is therefore of critical importance for mental health research (Eaves et al. 2003). To address this need, gene-environment interaction is now being regularly investigated using quantitative behavior genetic (BG) designs. In these designs, genotype is not observed directly; rather the genetic contribution to one or more phenotypes is inferred based on varying degrees of genetic relatedness among individuals such as twins. In contrast, a measured aspect of the environment, together with the phenotype of interest, is observed, and the measured environment is posited as a putative moderator of genetic influences on the phenotype. Models and methods of analysis for testing such gene-by-measured (GxM) environment interaction based on these designs are of great significance in furthering mental health research (Lahey and Waldman 2003).

Beginning with an article by Dick et al. (2001) and especially popularized by Purcell (2002), non-linear latent variable models have been intensively used for estimating GxM in quantitative BG designs. In Purcell’s paper, he proposed an important extension of the classic bivariate biometric model to allow quantifying and testing GxM between a measured environment and each of the classic biometric variance components, including additive genetic influences ($A$), and shared ($C$) and unshared ($E$) environmental factors. The importance and novelty of this work is that it also accounted for potential correlations between $M$ and those same $A$, $C$, or $E$ variance components. Rathouz et al. (2008) and Van Hulle et al. (2013) have examined statistical aspects of Purcell’s approach and found in preliminary studies that, under some plausible conditions, identification of GxM interaction in Purcell’s model is not fully convincing because models not including such interactions may explain the data as well as Purcell’s interaction model. In applied studies, however, such alternative models have not been regularly considered as explanations for the underlying biological mechanism.

A novel class of such models would greatly enlarge the available model space for the data to distinguish between GxM and equally parsimonious non-GxM mechanisms. The methodological hypothesis is that, in this broader class of models, findings of GxM would be more robust because the opportunity for alternative explanations of the data generating process—with different biologic interpretations—is greater. We describe their entire class of models in "Non-linear biometric models for GxM" section. To illustrate the importance of considering such models in real investigations of GxM, we present an analysis of the moderation of genetic influences on anxiety by birth weight in a community sample of twins in "Illustrative application: birth weight and anxiety" section. Different models from "Non-linear biometric models for GxM" section are fitted and compared. A second example is given in an online appendix and is also discussed briefly in "Non-linear biometric models for GxM" section.

Whereas the class of models posited by Rathouz et al. (2008) is biologically interesting, one of the main reasons up to now that some of these models have not been fully investigated is that an important subset of them cannot be estimated or tested in standard structural equation modeling software such as Mplus (Muthén and Muthén 1998–2012). To rectify this situation, the present article concerns new fitting algorithms for all of these proposed models. A major challenge is that some of the models contain latent multiplicative terms, leading to integrals which cannot be expressed analytically, and a likelihood which is inexpressible in closed-form.

Although the likelihood can be expressed in terms of a multiple integral, large dimensional integration is involved in its calculation, and direct application of numerical techniques to obtain an approximation is not feasible. To address this key issue, our strategy, elaborated in "Model testing and estimation" section, is to exploit the special structure of this class of models in order to re-express the likelihood via a novel factorization into a closed-form factor and a factor containing a low-dimensional integral, and then to apply high-accuracy numerical integration techniques to approximate the resulting low-dimensional integral. Technical details including adaptive Gauss–Hermite quadrature (AGHQ) and its specific application to our problem are covered in "Appendix 1" section. A common value of $k$ as the number of AGHQ nodes for each dimension of numerical integration is set to perform the calculation. Available routines of derivative-free optimization, implemented entirely in freely available packages in the ${\mathbf{R}}$ statistical software environment (R Core Team 2013), are employed for numerical maximization, and the inverse of the Hessian matrix, also obtained numerically, is used to estimate standard errors of the parameter estimates.

In "Numerical performance of model estimation" section, we first validate our model estimation and testing procedures via comparisons with those in Mplus for some models that are available in that environment. Expanding to models that are not available in Mplus, we examine the numerical accuracy and stability of our model estimates across varying numbers of integration nodes, with the goal of making recommendations on the required number of such nodes for computationally efficient yet accurate approximations. We note here that the aim of our empirical investigation is to examine the numerical—and not the statistical—performance of our proposed procedures. The final section contains conclusions and a discussion. Statistical operating characteristics are examined in a companion paper (Zheng et al. 2015), which also provides an overarching summary of our findings in the form of guidance to the worker using these models in applications.

Non-linear biometric models for GxM

In this section, we briefly revisit the proposed models from Rathouz et al. (2008) for testing and estimating GxM; complete explanation and interpretation of these models are available elsewhere (Rathouz et al. 2008; Van Hulle et al. 2013). We denote the measured—or putatively moderating—environmental variable by $M$, and the response variable by $P$ for phenotype. Both $M$ and $P$ are observable on each individual in a sample of relative pairs, and are modeled together in a joint bivariate latent structural equation model. Whereas variation in relatedness yields model identifiability, for the most part, we present models in terms of a single individual for compactness of exposition.

The standard biometric model for $M$ is given by

$$M = \mu _M + a_M A_M + c_M C_M + e_M E_M,$$

(1)

where $A_M$, $C_M$ and $E_M$ are latent variables representing additive genetic influences, and shared and unshared environmental influences on $M$ (Jinks and Fulker 1970; Neale and Cardon 1992). As is common in latent variable models, $A_M$, $C_M$ and $E_M$ are standard normal latent random variables, independent of one another. Parameter $\theta _M = (\mu _M,a_M,c_M,e_M)^{T}$ for $M$ contains the mean $\mu _M$ of $M$, and non-negative coefficients of $(a_M,c_M,e_M)$ of $(A_M,C_M,E_M)$. Thus, $a^2_M,c^2_M$ and $e^2_M$ are the additive genetic, shared, and non-shared environmental components of variance of $M$ respectively, with total ${\text {var}}(M) = a^2_M+c^2_M+e^2_M$.

When the data from a relative (e.g., twin) pair are combined, $M$, $A_M$, $C_M$ and $E_M$ become two-vectors. The model is therefore expressed more completely as:

$$\left( {\begin{array}{ll} {M_{1} } \\ {M_{2} } \\ \end{array} } \right) = \mu _{M} + a_{M} \left( {\begin{array}{ll} {A_{{M_{1} }} } \\ {A_{{M_{2} }} } \\ \end{array} } \right) + c_{M} \left( {\begin{array}{ll} {C_{{M_{1} }} } \\ {C_{{M_{2} }} } \\ \end{array} } \right) + e_{M} \left( {\begin{array}{ll} {E_{{M_{1} }} } \\ {E_{{M_{2} }} } \\ \end{array} } \right),$$

(1*)

where $M_j$, $A_{M_j}$, $C_{M_j}$ and $E_{M_j}$ represent the corresponding quantities on twin $j,j=1,2.$ In a twin study, the model is identified via extra constraints, specifically $A_{M_1}=A_{M_2}$ for monozygotic (MZ) twins, ${\text {corr}}(A_{M_1},A_{M_2})$ = 0.5 for dizygotic (DZ) twins, $C_{M_1}=C_{M_2}$, and ${\text {corr}}(E_{M_1},E_{M_2})$= 0 for all twin pairs. Other relationship pairs require different values of ${\text {corr}}(A_{M_1},A_{M_2})$.

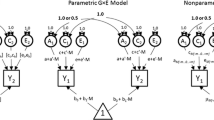
With the model for $M$ specified, GxM interactions are explored through various specifications for $P$. Purcell’s (Purcell 2002) Cholesky with GxM (CholGxM) model for phenotype $P$ specifies

$$\begin{aligned} P= \mu _P + (a_C+\alpha _C M)A_M + (c_C+\kappa _C M)C_M + (e_C+\varepsilon _C M)E_M \\ + (a_U+\alpha _U M)A_U + (c_U+\kappa _U M)C_U + (e_U+\varepsilon _U M)E_U, \end{aligned}$$

(2)

where $A_U$, $C_U$ and $E_U$ are also standard normal latent random variables, independent of each other and of $(A_M,C_M,E_M)$, and $\mu _P$ is the intercept for $P$. Coefficients $a_C$ and $\alpha _C$ quantify additive genetic effects on $P$ that are common with those on $M$, $c_C$ and $\kappa _C$ quantify additive shared environmental effects on $P$ that are common with those on $M$, and $e_C$ and $\varepsilon _C$ quantify additive non-shared environmental effects on $P$ that are common with those on $M$. In a parallel manner, $(a_U,\alpha _U)$, $(c_U,\kappa _U)$ and $(e_U,\varepsilon _U)$ quantify additive genetic, shared and non-shared environmental effects on $P$ that are unique to $P$. Coefficients $a_U$, $c_U$, and $e_U$ are assumed non-negative. Greek coefficients $\alpha _C$, $\kappa _C$, $\epsilon _C$, $\alpha _U$, $\kappa _U$ and $\varepsilon _U$ capture the interaction of moderator $M$ with the various genetic and environmental factors that act on $P$. In particular, the magnitude of $\alpha _C$ ($\alpha _U$) captures the GxM interaction of $M$ with common (unique) genetic factor $A_M$ ($A_U$) in determining $P$. Thus, GxM can be detected via the statistical hypothesis that $\alpha _C=\alpha _U=0$. Without interaction, Model (2) reduces to the classic bivariate Cholesky (Chol) model, specified as

$$P = \mu _P + a_C A_M + c_C C_M + e_C E_M + a_U A_U + c_U C_U + e_U E_U\, .$$

(3)

Rathouz et al. (2008) note that Model (2) does not explicitly contain a “main effect” of $M$ on $P$, but rather captures such effects indirectly through $a_C$, $c_C$ and $e_C$ on common genetic and environmental influences $A_M$, $C_M$ and $E_M$. Those authors have proposed an alternative, more parsimonious, model that does contain direct effects of $M$ on $P$. This non-linear main effects model with GxM (NLMainGxM), viz.

$$P = \mu _P + \beta _1 M + \beta _2 M^2 + (a_U+\alpha _U M)A_U + (c_U+\kappa _U M)C_U + (e_U+\varepsilon _U M)E_U,$$

(4)

is nested within Model (2) but yields a different interpretation in terms of GxM. In sub-model (4), the common factors $A_M$, $C_M$ and $E_M$ only operate through the manifest value $M$ to influence $P$. Because of that, genetic and environmental influences on $P$ are mediated through $M$. When $\alpha _U=0$ in Model (4), this model does not contain GxM. However, in that situation, Rathouz et al. (2008) and Van Hulle et al. (2013) have shown that if Model (2) is fitted to the data without considering Model (4) as an alternative, GxM may be artifactually detected as non-zero $\alpha _C$.

As indicated by the appearance of unique effects $A_U$, $C_U$ and $E_U$, Model (2), (3) and to a partial degree Model (4) are based on the bivariate Cholesky parameterization. As discussed by Johnson (2007), the Cholesky parameterization is more interpretable when there is a clear theoretical, causal, or temporal ordering of the variables $M$ and $P$ in the model. In situations without a clear causal ordering, Loehlin (1996) has suggested using either a “common factor” or a “correlated factors” model. These models, which treat $M$ and $P$ on equal footing, might be simpler and more defensible reference (null) models for analysis of GxM. Denoting by $A_P$, $C_P$, and $E_P$ the genetic and environmental influences on $P$, an alternative to Model (2) obtains by extending the correlated factors model to allow for GxM (CorrGxM), viz.,

$$\begin{aligned} P = \mu_P + (a_P + \alpha _P M) A_P + (c_P + \kappa _P M) C_P + (e_P + \varepsilon _P M) E_P\, , \\ r_a = {\text {corr}}(A_M,A_P)\, ,\; r_c = {\text {corr}}(C_M,C_P) \; {\text{and}} \; r_e = {\text {corr}}(E_M,E_P). \end{aligned}$$

(5)

Model (5) provides a more straightforward model for testing and quantifying GxM than does Model (2) when $M$ and $P$ do not have a clear causal ordering. Moreover, Model (5) allows for multiplicative effects with $M$ with three fewer parameters than Model (2), which may increase the power to detect GxM. We note that Model (5) is nested in Model (2), and that when $\alpha _P=\kappa _P=\varepsilon _P=0$, Model (5) reduces to Model (3).

The foregoing Cholesky and correlated factors models are available in Mplus and have been studied earlier by Van Hulle et al. (2013). There are, however, two important and novel variants on these models which are not available in standard software. These models have different biological interpretations that do not involve GxM in the sense of (2). Rather they posit that genetic and shared and non-shared environmental effects operate additively and independently—but not linearly—in the model for $P$. The non-linear Cholesky (CholNonLin) model is specified as:

$$\begin{aligned} P= \mu _P + a_C A_M + c_C C_M + e_C E_M + \gamma _1 A^2_M + \gamma _2 C^2_M + \gamma _3 E^2_M \\ + a_U A_U + c_U C_U + e_U E_U + \delta _1 A_M A_U + \delta _2 C_M C_U + \delta _3 E_M E_U\, . \end{aligned}$$

(6)

Unlike Model (2), the defining and unique feature of this model is that additive genetic ($A_M$, $A_U$), and shared ($C_M$, $C_U$) and unshared or ($E_M$, $E_U$) environmental influences do not interact or moderate one another, nor are they moderated by measured environment $M$, even while each of them does act non-linearly. Rather, like the classical ACE model, the three underlying sources of variation combine additively and independently to influence $P$. Such a model could arise because the genetic factors common to $M$ and $P$ (i.e. $A_M$) and the shared and non-shared environmental counterparts simply operate on a different scale for $M$ than for $P$. Alternatively, the model could arise out of gene-by-gene interaction of additive genetic effects—either of $A_M$ with itself or of $A_M$ with $A_U$, with similar terms for common and unique environmental effects.

In an analogous spirit, one can extend the classic bivariate correlated factors model to include non-linear but additive genetic and environmental influences, yielding the model (CorrNonLin):

$$\begin{aligned} P= \mu _P + a_P A_P + c_P C_P + e_P E_P + \lambda _1 A_M A_P + \lambda _2 C_M C_P + \lambda _3 E_M E_P\, , \\ r_a= {\text {corr}}(A_M,A_P)\, ,\; r_c = {\text{corr}}(C_M,C_P) \; {\text{and}} \; r_e = {\text{corr}}(E_M,E_P).\end{aligned}$$

(7)

In this model, the additive genetic effects $A_M$ on $M$ moderate the additive genetic effects $A_P$ on $P$. In the following we describe a likelihood factorization and numerical integration routine suitable for fitting and testing all of the foregoing models, including Models (6) and (7).

Illustrative application: birth weight and anxiety

Here we present a real data analysis to illustrate our approach. The data arise from a random sample of 6-17-year-old twin pairs born in Tennessee and living in one of the state’s five metropolitan statistical areas in 2000-2001 (Lahey et al. 2004). Twin pairs were selected stratified on age and geographic area, and psychopathology information was collected. One of the research interests is to examine the relationship between birth weight and childhood anxiety. In this illustration, we use a quantitative measure of twins’ anxiety symptoms and birth weight in ounces as reported by their biological mothers. The analysis presented here extends the results in Van Hulle et al. (2013) to include newly available models.

Our analysis comprises 541 MZ and 887 DZ twin pairs. Measured environment $M$ is the residual for birth weight after linear regression on gender and ethnicity. Similarly, phenotype $P$ is the residual anxiety measure after regression on gender, ethnicity and age. Models are fitted based on numerical likelihood calculation with $k$ = 8 AGHQ nodes. The definition of AGHQ nodes $k$ is covered in the "Model testing and estimation" section.

Model fit statistics, including Bayesian information criterion (BIC) (Schwarz 1978; Raftery 1995), are summarized in Table 1 in terms of differences relative to the basic Chol model; lower values of $-2\times$ log-likelihood or BIC imply a better fit to the data. Whereas we recognize there has been some criticism of the BIC for overly favoring simpler models (Weakliem 1999), there are several features in its favor in this setting. First, with our moderately large sample size, likelihood ratio tests will tend to detect effects that are statistically important, but not scientifically significant. Second, the BIC allows a basis for comparing non-nested models, which is of critical utility in this setting. Third, when examining a construct such as GxM, we seek results which are robust and replicable; it therefore behooves us to take a conservative stance and favor simpler models unless there is very strong evidence to the contrary.

Turning to Table 1, we note that the Chol model is nested in all other models except the NLMainGxM model. Additionally, the CorrGxM (CorrNonLin) model is nested in the CholGxM (CholNonLin) model. Based on likelihood ratio tests (LRT), CholGxM fits better than CorrGxM and Chol, and CorrGxM also fits better than Chol. Ignoring new models NLMainGxM, CholNonLin, and CorrNonLin, one might conclude that the data are supportive of a GxM effect. The new CorrNonLin model is, however, a strong competitor and also fits better than Chol. Based on LRT alone, one might conclude that CorrNonLin is the best fitting model; this model does not contain GxM. Incorporating BIC values, we would conclude that NLMainGxM and CorrNonLin are roughly equivalent in terms of model fit. However, we have previously shown (Van Hulle et al. 2013) that model NLMainGxM without the GxM effects provides a better fit to the data.

Table 1 Differences of degrees of freedom (df), $-2\times$ log-likelihood, and BIC of fitted models in Tennessee Twin Study relative to the fitted Chol model (terms of fitted Chol model serving as subtrahends)

Fitted individual models are shown in Table 2. We note that in the CholGxM model, the coefficient of $M\times A_M$ is significant, especially as compared to the coefficient of $A_M$, as are the coefficients of $M\times C_M$ and $M\times E_M$. Without considering other models, these effects might be scientifically compelling. The CorrNonLin model is notable in that all of its non-linear terms are significant, suggesting the model is well-suited to the data. In the NLMainGxM model, the coefficient −0.104 of $M\times A_U$ is found significant based on the standard error from inverting the hessian matrix. However, the entries related to $\mu _M$ in that hessian matrix are all very close to zero, which makes the inverse suffer numerical issues. The standard error from inverting the hessian matrix without those entries suggests an insignificant coefficient of $M\times A_U$. To resolve this issue, we turn to LRT, comparing models with and without $M\times A_U$, resulting in a $p$-value greater than 0.1 on 1 degree of freedom. As such, whether one concludes that the CorrNonLin or the NLMainGxM models is the best fitting, the evidence for GxM effects, including $M\times C_M$ and $M\times E_M$, is not greatly supported by the data. In contrast, analysis with only the CholGxM and Chol models from Purcell (2002) would have led to a conclusion of GxM in the Tennessee Twins sample.

Table 2 Fitted models for Tennessee Twins Study. Starred (${}^{*}$) coefficients are significant at the 0.05 level based on Wald tests using the inverse of the Hessian matrix to obtain standard errors

In a second example,¹ we analyzed the potential moderating effect of quality of infant and toddler family environment ($M$) on reading ability in middle childhood ($P$). This example illustrates use of our algorithm in a study wherein the relationships are primarily siblings and half-siblings. The analysis revealed very important non-linear effects which do not include GxM, highlighting the importance of considering alternative models to those containing GxM.

Model testing and estimation

We return to estimating models from Rathouz et al. (2008) in this section. The strategy is to exploit the special structure of this class of models in order to re-express the likelihood. Denote $\theta = (\theta ^T_M, \theta ^T_P)^T$, where $\theta _P$ is the parameter vector for the specified structural equation model for $P$. Likelihood $L$ for $\theta$ arising from data on a sample of relative pairs $i=1,\ldots ,n$, is given by $L(\theta ) = \prod _{i=1}^n f(M_i,P_i; \theta )$. This likelihood involves up to ten latent dimensions per relative pair. In what follows, we develop a decomposition to avoid integration over all but three of those dimensions.

The contribution from one individual pair can be written (suppressing subscripts $i$) using the factorization

$$f(M,P; \theta ) = f(M;\theta _M) \; f(P|M;\theta ).$$

(8)

The likelihood has two parts: the contribution from data $M$ and the contribution from $P$ given $M$. The first part, $f(M;\theta _M)$, is a bivariate normal density, expressible in closed-form, with mean $\mu _M$ and variance-covariance matrix based on $(a_M,c_M,e_M)$ and ${\text {corr}}(A_{M_1},A_{M_2})$. The second part, $f(P|M;\theta )$, is more complex, for it might involve non-linear terms and is not necessarily available in closed-form.

From Model (1), $(A_M,C_M,E_M)$ are jointly multivariate normal, and there is a linear relationship between $M$ and $(A_M,C_M,E_M)$. As such, $M$ is bivariate normal, and the conditional distribution of $(A_M,C_M|M)$ is multi(tri)variate normal as well. The variates are $A_{M_1}$, $A_{M_2}$ and $C_{M_1}$, since $C_{M_1}$ and $C_{M_2}$ are equal. Turning to the distribution of $(P|A_M,C_M,E_M)$, because $E_M$ is jointly determined by $(A_M,C_M,M)$, we have that $f(P|A_M,C_M,E_M; \theta )=f(P|A_M,C_M,M; \theta )$. Therefore,

$$\begin{aligned} f(P|M; \theta )&= \int _{R^3} \; f(P,A_M,C_M|M; \theta ) \; dA_M \, dC_M \\&= \int _{R^3} \; f(P|A_M,C_M,M; \theta ) \; f(A_M,C_M|M; \theta _M) \; dA_M \, dC_M \\&= \int _{R^3} \; f(P|A_M,C_M,E_M; \theta ) \; f(A_M,C_M|M; \theta _M) \; dA_M \, dC_M. \end{aligned}$$

(9)

Moreover, for Models (2)–(7) for $P$, $(P|A_M,C_M,E_M)$ is bivariate normal marginally over either $(A_U,C_U,E_U)$ or $(A_P,C_P,E_P)$; we do not need to explicitly integrate over $(A_U,C_U,E_U)$ or $(A_P,C_P,E_P)$ to obtain $(P|A_M,C_M,E_M)$. The reason for this is that, given $(A_M,C_M,E_M)$, $P$ is linear in $(A_U,C_U,E_U)$ or $(A_P,C_P,E_P)$, and either $(A_U,C_U,E_U)$ or $(A_P,C_P,E_P)$ is multivariate normal given $(A_M,C_M,E_M)$. We conclude that $f(P|M; \theta )$ reduces to a trivariate integral given on the right hand side of (9). du Toit and Cudeck (2009) use a similar method to calculate marginal distribution by separating random effects in random coefficient model estimation.

Based on considerations similar to those of Klein and Moosbrugger (2000) in estimating latent interaction effects, we turn to numerical integration techniques—specifically AGHQ—for evaluation of this integral. We show in "Appendix 1" section that the contribution to the likelihood from $(P | M)$ can be approximated for all proposed models in Rathouz et al. (2008). The procedure involves three-dimensional AGHQ. Even though each dimension can in theory have a different number of nodes for numerical integration, denoted using $k_1,k_2$ and $k_3$ in "Appendix 1" section, we fix $k_1=k_2=k_3=k$ in our algorithm, and refer to the value $k$ as the number of AGHQ nodes. Larger values of $k$ yield more accurate approximations, but are more computationally intensive. The choice of $k$ aims to balance accuracy and computational cost. In later simulation-based numerical analysis, we show that moderate values of $k$ (e.g., $k$ = 8) yield satisfactory results.

With both $f(M;\theta _M)$ and $f(P|M;\theta )$ available, individual likelihood contributions obtain through (8). With the aforementioned numerical integration approach, we use maximum likelihood for estimation and inferences in the class of models. Owing to the lack of a closed-form expression for the likelihood, however, analytic derivatives are especially difficult to obtain. We propose to use a derivative-free optimization technique, the BOBYQA algorithm for bound constrained optimization without derivatives (Powell 2009). This algorithm has been integrated into an ${\mathbf{R}}$ package minqa (Bates et al. 2012) and is directly available in the ${\mathbf{R}}$ environment.

A computational barrier in derivative-free optimization is that many more evaluations of the likelihood are required than when analytic derivatives are available. We alleviate this burden through parallel computing using the parallel facility in ${\mathbf{R}}$, distributing the likelihood calculation across observations at each step to as many cores as are available. We also provide a variety of options for obtaining initial values; these and other options are described in the documentation for our ${\mathbf{R}}$ package entitled GxM (Zheng and Rathouz 2013), and the package is available on CRAN.

Numerical performance of model estimation

Comparison of GxM package in R to Mplus

We conducted computational experiments comparing model estimation with our new ${\mathbf{R}}$ package GxM to that in Mplus using scripts from Van Hulle et al. (2013). As the current standard in structural equation modeling, Mplus can estimate a variety of latent variable models, including those with non-linearities. Models involving the product of latent terms—such as CholNonLin and CorrNonLin—are, however, not available in Mplus. As such, we compared fits for the CholGxM model in this investigation. With a moderate number of AGHQ nodes, we hypothesized that our model estimation results would match those from Mplus very closely.

We simulated data under two data generating mechanisms, labeled A and B:

$$\begin{aligned} M&= \sqrt{0.45} \, A_M + \sqrt{0.10} \, C_M + \sqrt{0.45} \, E_M, \\ P&= 0.5 \, A_M + 0.01 \, C_M + 0.1 \, E_M \\&\quad + \sqrt{0.9-0.5^2} \, A_U + \sqrt{0.2} \, C_U + \sqrt{0.9-0.1^2} \, E_U\, , \end{aligned}$$

(A)

and

$$\begin{aligned} M&= \sqrt{0.45} \, A_M + \sqrt{0.10} \, C_M + \sqrt{0.45} \, E_M, \\ P&= 0.1 \, A_M + 0.01 \, C_M + 0.5 \, E_M \\&\quad + \sqrt{0.9-0.1^2} \, A_U + \sqrt{0.2} \, C_U + \sqrt{0.9-0.5^2} \, E_U\, , \end{aligned}$$

(B)

wherein $A_{M_1}=A_{M_2}$ for MZ twins, ${\text {corr}}(A_{M_1},A_{M_2})$ = 0.5 for DZ twins, and $C_{M_1}=C_{M_2}$ and ${\text {corr}}(E_{M_1},E_{M_2})$ = 0 for all the twins. In each of 2,000 replicates, we simulated data either from 250 MZ twin pairs and 250 DZ twin pairs ($n$ = 500), or from 1,000 MZ pairs and 1,000 DZ pairs ($n$ = 2,000).

For each replicate, we applied both our ${\mathbf{R}}$ package GxM and Mplus to perform model estimation for CholGxM. Eight ($k$ = 8) AGHQ nodes were used in the numerical integration routine. Examining the standard deviation of the pair-wise differences, we see that the log-likelihood values from two approaches are almost identical, especially given the scale of the total log-likelihood (Table 3).

Table 3 Simulated means (standard deviations) of log-likelihood values comparing GxM in ${\mathbf{R}}$ to Mplus for 2,000 replicates for two sample sizes and two parameter specifications

To quantify accuracies of individual parameter estimates, we rely on the root-mean-square error (RMSE). For a given scalar element $\xi$ of parameter vector $\theta$, and letting $\hat{\xi }^{(s)}$ denote the estimate of $\xi$ in the $s$-th replicate from the total $S$ = 2,000 replicates, we compare the average performance of GxM to Mplus via what we refer to as RMSE “Ratio 1”:

$${\text {Ratio\,1}} = \sqrt{ \frac{ {\sum _{s=1}^S (\hat{\xi }^{(s)}_{R} - \xi )^2 }}{ {\sum _{s=1}^S (\hat{\xi }^{(s)}_{\text {Mplus}} - \xi )^2 }} }.$$

How close Ratio 1 is to unity indicates the accuracy of parameter estimation using GxM relative to that of Mplus. Results are in the first four columns of Table 4 for all four simulation conditions. The ratios for all parameters are very close to unity, strongly suggesting, together with the log-likelihood results (Table 3), that the two computational approaches are equally valid.

As with the likelihood values, it is also of interest to quantify the coherence of the two approaches, even as they provide similar results on average across replicates. For this purpose, we compare the RMSE of the pair-wise differences of estimates from Mplus and GxM, relative to ${\text{RMSE}}(\hat{\xi}_{\text{Mplus}})$, the reference variability of estimates from Mplus. This yields “Ratio 2”, viz.,

$${\text {Ratio\, 2}} = \sqrt{ \frac{ {\sum _{s=1}^S (\hat{\xi }^{(s)}_{R} - \hat{\xi }^{(s)}_{\text {Mplus}})^2 }}{ {\sum _{s=1}^S (\hat{\xi }^{(s)}_{\text {Mplus}} - \xi )^2 }} }.$$

The smaller the value of Ratio 2, the closer the results from the two computational approaches. Results are in the last four columns of Table 4. Values corresponding to intercepts and unshared environmental influences are satisfactorily small, suggesting the differences between fitting results for these parameters are negligible compared with the simulated sampling variabilities. Ratio 2 values corresponding to genetic influences and shared environmental influences are larger, suggesting some differences between GxM and Mplus in the optimization algorithm or in the nature of the likelihood surface near the maximum for these parameters. In conclusion, with a moderate number ($k$ = 8) of AGHQ nodes for the CholGxM model, some differences exist. Nevertheless, estimation based on numerical integration and optimization using GxM appears equally valid to that in Mplus. Further, in many settings, GxM and Mplus yield highly concordant results for specific data sets.

Stability and computational time of model estimation with respect to number of AGHQ nodes

To further assess the performance of our GxM procedure and to examine its performance in models CholNonLin and CorrNonLin models which are not available in standard structural equations modeling packages, we conducted an investigation of its numerical stability with respect to the number of AGHQ nodes. In this experiment, we fit all of the proposed models through maximization of the likelihood computed with numerical integration, with several choices of number $k$ of AGHQ nodes for each data set and model. We expected that, when the number of nodes is adequate, the fitted models will be close to each other. In addition, closed-form likelihood calculation is available for the Chol, NLMainGxM, CholGxM, and CorrGxM models, so for these models, we include results obtained through maximizing the closed-form likelihood in the pool of comparisons.

Table 4 Ratio 1 and 2 values (defined in text) for estimated parameters from 2,000 replicates for two sample sizes ($n$ = 500 and n = 2,000) and two parameter specifications (setting A and B)

We simulated 23 data sets corresponding to different scenarios. These scenarios follow the simulation specifications in Van Hulle et al. (2013), with additional scenarios based on the CholNonLin and CorrNonLin models. These scenarios are based on various combinations of factors with different biological meanings; the configurations are listed in "Appendix 2" section. For each configuration, we simulated data for 1,000 MZ twin pairs and 1,000 DZ twin pairs. When numerical integration is used, $k$ = 8, 10, and 15 AGHQ nodes are employed to provide estimates for the parameter vector. When $k$ = 15, computations become very time-consuming, but are feasible for a small number (e.g., 23) cases. A possible fourth estimate results from maximizing the closed-form likelihood when it is available. Hence, the likelihood and parameter vector in the CholGxM, Chol, NLMainGxM, and CorrGxM model have 4 estimates, and those in the CholNonLin and CorrNonLin models have 3 estimates. Variation among the three or four estimates is an index of the stability of our model estimation across $k$.

We first compare the log-likelihood values across different values of $k$. For each data set and fitted model, the three or four log-likelihood values yield an interval covering these values; the range of this interval provides a direct measure of the dispersion of log-likelihood values. For each model, we calculated individual ranges for all 23 data sets, and summarize them in Table 5 via the median, the 3rd largest (21st out of 23), and the largest range. Whereas the ranges for fitted CholGxM, Chol, NLMainGxM and CorrGxM models are uniformly close to zero, those for the new CholNonLin and CorrNonLin models are relatively larger. The differences, however, remain small in an absolute sense. Multiplying by two puts the differences on a comparable scale as the chi-square statistic for comparing two nested models. We see that whereas using numeric integration could occasionally yield different conclusions in a statistical hypothesis test, this is likely a rare event.

Table 5 Summaries of fitting results using median values from 23 data sets

For each data set and fitted model, we also compare fitted parameter vectors across values of $k$ via the maximum norm distance. For two parameter vectors ${\varvec{a}}=(a_1,...,a_p)$ and ${\varvec{b}}=(b_1,...,b_p)$, the maximum norm distance from ${\mathbf{a}}$ to ${\mathbf{b}}$ is defined as $\Vert {\varvec{a}}-{\varvec{b}}\Vert _{\infty } = \text {max}(|a_1-b_1|,...,|a_p-b_p|).$ The pairwise combinations of model estimates provide a set of distance vectors. For instance, in fitting the CholGxM model, 4 parameter vector estimates are available, and thus, 6 difference vectors and their corresponding maximum norm values (distances) are produced; we computed the maximum of these pairwise distances, and summaries of these maxima are reported in Table 5 as well; there we report the median, the 3rd largest (21st out of 23), and the largest of the maximum pairwise distances across the 23 data generation conditions. Given the foregoing likelihood results, it is not surprising that the difference values from fitting model CholNonLin and CorrNonLin are larger than others. Yet for most cases, differences are quite modest and acceptable.

The computational time of fitting these models with $k$ = 8, 10, and 15 AGHQ nodes is shown in the bottom panel of Table 5. The median values of time cost across 23 conditions using our package GxM with a single 2.4 GHz CPU are listed. The time cost increases with $k$, but the increase is slower than cubic growth.

Discussion and conclusion

This paper continues the work of Rathouz et al. (2008) and Van Hulle et al. (2013) by developing computational algorithms and associated code to fit alternative non-linear behavior genetic models to twin data as competitors to a now-classic GxM model proposed by Purcell (2002). The focus here is on numerical implementation of models not available in standard structural equation modeling software. To illustrate our approach, we presented an analysis of the putative moderation of genetic influences on anxiety by birth weight in a community sample of twin children. The implementation of new non-linear latent variable models provides alternative interpretations of the underlying biological relationships. Had these models not been considered, a researcher might have concluded that GxM was an important feature in the structural model for anxiety.

We achieved our model estimation via a novel factorization of likelihood and implementation of AGHQ, and maximized the likelihood using derivative-free optimization. We showed via numerical simulation that our fitting algorithm is equally valid to that of standard software, and is stable for a moderate number integration nodes.

The problem addressed by our novel class of models is related but not equivalent to that of scaling issues leading to loss of power to, or false detection of, gene-by-environment interaction. A comprehensive review is beyond the scope of this paper, but some key references include the compelling work by Eaves et al. (1977), Eaves (2006), Molenaar and Dolan (2014). That work for the most part deals with unmeasured environments versus our measured $M$. It also deals with problems of the scale of the response variable. In this and our prior work, we raise a different problem, namely that alternative latent non-linear structural models could be misinterpreted as GxM. Should scaling problems overlay our latent structural models, additional problems could arise. This is an issue which we will address in future work.

A few comments about the numerical results and future work. First, in numerical experiments, the accuracy of our numerical algorithm was very high for models admitting a closed-form likelihood (even with numerical integration in lieu of the closed-form objective function); corresponding results for models CorrNonLin or CholNonLin were not quite as strong, although it appears acceptable. We note, however, that the data used in these studies was generated from mechanisms involving fairly strong departures from the global null Chol model. Our experience thus far is that all of the fitting algorithms perform more accurately and more efficiently when departures from the Chol model are more modest. Second, we note that the GxM package cannot currently handle missing data. For small amounts of missing data, we recommend using an imputation routine.

Finally, the statistical—as differentiated from the numerical—operating characteristics of these new model fitting algorithms are presented in a companion paper in this same issue of Behavior Genetics (Zheng et al. 2015). To briefly summarize, in that paper, Type I error analysis suggests conservative behavior for models based on the bivariate Cholesky behavior genetic model, and liberal behavior for models based on the bivariate correlated factors models; for some models comparisons, asymptotic convergence to the correct Type I error rate is very slow. Simulations of the bias in parameter recovery are very encouraging as, by and large, maximum likelihood parameters estimators exhibit very little bias. In examination of the ability of the data to discriminate among alternative models with and without GxM, we found that it can be difficult to distinguish GxM from other non-linear effects. Please see (Zheng et al. 2015) for full details; in that work, we also provide some practical comments and guidance to applied researchers based on the present work. In addition, taking a longer view, we also summarize all of our results to date on these GxM methods in a technical report on “Lessons Learned”, again with the researcher using these methods in applied work as the intended audience.²

Appendices

Appendix 1: Likelihood calculation through numerical integration

Adaptive Gauss–Hermite quadrature

In the calculation of a definite integral, even when the formula for the integrand is known, it may be difficult to find an antiderivative which has a closed-form expression. In such circumstances, numerical integration methods are often applied to obtain approximate results. The Gaussian quadrature rule is one of the most widely used numerical integration techniques to approximate the integral of a function $g(x)$ over a specified domain ${\mathcal {D}}$ with a known weighting kernel $\phi (x)$. If the integrand $g(x)$ can be well approximated by a polynomial of order $2k-1$ or less, then a quadrature with $k$ nodes suffices for a good estimate of the integral,

$$\int _{{\mathcal {D}}} g(x)\phi (x)dx \approx \sum _{i=1}^{k} w_i g(x_i).$$

The nodes $x_i$ and weights $w_i$, $i=1,\ldots ,k$, are uniquely determined by the domain ${\mathcal {D}}$ and the weighting kernel $\phi (x)$ (Stroud and Secrest 1966). In the case wherein the integration domain is the real line and the integration kernel is $\phi (x)=e^{-x^2}$, the resulting quadrature rule is known as Gauss–Hermite quadrature (GHQ).

Because of its close relationship to the normal distribution, GHQ is widely used in statistics. Adaptive GHQ (AGHQ) (Liu and Pierce 1994; Naylor and Smith 1982) arises by shifting and scaling the kernel for greater numerical accuracy, strategically placing the nodes $x_i$ to emphasize the areas of greatest mass in the integrand function. The advantages of AGHQ over traditional GHQ are shown in the estimation of latent models with nonlinear random effects by Pinheiro and Bates (1995) and Rabe-Hesketh et al. (2005). In this work, we relocate the nodes according to the easily obtainable location and scale of the normal density. Specifically, if $Y\sim {\mathcal {N}}(m, \sigma ^2)$ and $g$ is a known but complicated function, the expectation of $g(Y)$ can be calculated approximately as

$$\begin{aligned} {\mathbf{E}}(g(Y))&= \int _{-\infty }^{+\infty } g(y) \frac{1}{\sqrt{2\pi }\, \sigma } \exp \left\{ -\frac{(y-m)^2}{2\sigma ^2}\right\} dy \\&= \int _{-\infty }^{+\infty } \frac{g(m+\sqrt{2}\,\sigma x)}{\sqrt{\pi }} e^{-x^2} dx\; \approx \; \sum _{i=1}^k \frac{ w_i \, g(m+\sqrt{2}\,\sigma x_i)}{\sqrt{\pi }}\; , \end{aligned}$$

(10)

using $x=(y-m)/\sqrt{2}\sigma$. Whereas this is not “adaptive” in the strictest sense of Liu and Pierce (1994), we still use AGHQ to represent this technique because of the application of the relocation of nodes.

With regard to numerical evaluation of a multiple integral, a natural way forward is to decompose it into a sequence of nested one-dimensional quadratures and to repeatedly apply (10). Taking integration over domain ${R^p}$, we could use $k_j$ points in the $j$th dimension, $j=1,\ldots ,p$, and obtain a multi-dimensional version of AGHQ. Specifically, if ${\varvec{Y}}$ is a $p$-dimensional random vector which follows a multivariate normal distribution with mean vector $\mathbf{m}$ and covariance matrix $\Sigma$, the expectation of $g({\varvec{Y}})$, where $g(\cdot )$ is now a multivariate function, obtains approximately as

$$\begin{aligned} {\mathbf{E}}(g({\varvec{Y}}))&= \int _{R^p} g({\varvec{y}}) \; \frac{1}{(\sqrt{2\pi })^p \, |\Sigma |^{1/2}} \exp \left\{ -\frac{1}{2}({\varvec{y}}-{\mathbf{m}})^{T}\Sigma ^{-1}({\varvec{y}}-{\mathbf{m}})\right\} \; d{\varvec{y}} \\&= \int _{R^p} \frac{g({\mathbf{m}}+\sqrt{2} \, {\Sigma }^{1/2} \, {\varvec{x}})}{{\pi }^{p/2}} \exp \{-{\varvec{x}}^{T}{\varvec{x}}\} \; d{\varvec{x}} \qquad \quad \Big ( \text {with}\; {\varvec{x}} = \frac{1}{\sqrt{2}} \Sigma ^{-1/2} ({\varvec{y}}-{\mathbf{m}}) \Big ) \\&\approx \sum _{i_1=1}^{k_1} \cdots \sum _{i_p=1}^{k_p} w_{i_1} \cdots w_{i_p} \frac{g({\mathbf{m}}+\sqrt{2}\,{\Sigma }^{1/2}\,{\varvec{x_{(i)}}})}{{\pi }^{p/2}}, \end{aligned}$$

(11)

where ${\varvec{x_{(i)}}} = (x_{1i_1}, \ldots , x_{p\,i_p})^T$; $x_{j1},\ldots ,x_{jk_j}$ are the nodes for the $j$th dimension; and the product $w_{i_1} \cdots w_{i_p}$ is the corresponding weight for node ${\varvec{x_{(i)}}}$.

AGHQ in likelihood calculation

In the application of AGHQ to approximation of likelihood $f(P|M;\theta )$, we incorporate distribution functions from specific models into the integration. We denote ${\varvec{y}} = (A_M,C_M)^T$ to simplify the notation. Because $f(A_M,C_M|M)$ is a multivariate normal density function, we set ${\mathbf{m}}= \text {E}({\varvec{y}}|M;\theta _M)$ and $\Sigma = \text {Cov}({\varvec{y}}|M;\theta _M)$, so that the function specified by $f(P|{\varvec{y}},M)=f(P|A_m,C_M,M)$ plays the role of $g({\varvec{y}})$ in (11). Therefore, we have

$$\begin{aligned} f(P|M; \theta )&= \int _{R^3} \; f(P|{\varvec{x}},M; \theta ) \, \frac{1}{\pi ^{3/2} } \exp \{-{\varvec{x}}^T{\varvec{x}} \} \; d{\varvec{x}} \\&\approx \sum _{i_1=1}^{k_1} \sum _{i_2=1}^{k_2} \sum _{i_3=1}^{k_3} w_{i_1} w_{i_2} w_{i_3} \frac{f(P| {\varvec{x_{(i)}}},M;\theta )}{{\pi }^{3/2}} \ , \end{aligned}$$

where conditional distribution function $f(P|{\varvec{x_{(i)}}},M;\theta )$ is computable for all proposed models from Rathouz et al. (2008).

Appendix 2: Argument options in R package GxM

Model option

We consider both bivariate Cholesky models and bivariate correlated factors models, including Chol, CholGxM, NLMainGxM, CorrGxM, CholNonLin and CorrNonLin. The routines for fitting these models are provided in our ${\mathbf{R}}$ package, GxM. For models that do not admit a closed-form likelihood, we apply numerical integration techniques; for models that have closed-form likelihood, both fitting with closed formula and numerical techniques are provided. All models exploit derivative-free optimization.

Zero set option

This option provides for constraining some parameters to zero, greatly expanding the number of nested sub-models that are available, and allowing testing of specific parameters via likelihood ratio tests or by comparing BIC values. As explained in the Model section, GxM can be detected by testing statistical hypothesis under which certain parameters are zero. We supply an option named “zeroset” to enable users to fit models with chosen parameter(s) constrained to zero.

Initialization and priority option

For optimization problem with high dimensional parameters and non-concave surfaces, it is important to have reasonable and multiple starting points. By setting the non-linear latent terms to zero, all of our proposed models except Model (4) reduce to a common trivial model, and direct parameter estimation such as a method of moment estimator can be applied. This set of estimates serves as a desirable starting point. For Model (4), we use polynomial regression technique to eliminate the main effect of $M$ on $P$. After replacing the original $P$ with regression residuals, the modified model can also be viewed as a case of the common trivial model. For non-linear models, we further add an intermediate update using a small number ($k$ = 3) of AGHQ nodes. Lastly, we provide for the option of leaving the initialization to potential users. With priority level equal to 1, the user-specified initialization would be updated in the intermediate stage. By increasing priority level from 1 to 2, the manually specified initialization would ignore the intermediate update.

AGHQ nodes number option

We provide this option to allow a tradeoff between accuracy and computational intensity. As one may expect, a larger number of AGHQ nodes produces more accurate likelihood values. On the other hand, because the integration is 3-dimensional, the computation cost increases fast.

Parallel computing option

As an interpreted language, the performance of ${\mathbf{R}}$ in terms of computational speed is not as satisfactory as that for compiled languages. This issue is of concern when using computationally intensive numerical integration and derivative-free optimization techniques. Therefore, we embed parallel processing technique in response to the challenge.

Parallel computing with ${\mathbf{R}}$ is directly supported beginning with release 2.14.0. The package parallel provides convenient functions to perform parallel computing in both explicit and implicit modes. For instance, in the calculation of log-likelihood for GxM models, because of the summation over individual observations as $l(\theta ) = \log L(\theta ) = \sum _{i} \log f(M_i,P_i;\theta )$, the global log-likelihood computation can be performed in a parallel manner. Users are provided the option to use parallel computation, and if so the number of CPU cores to allocate the computations.

Appendix 3: Configurations for 23 scenarios

The configurations of simulation settings for 23 scenarios in numerical analysis is shown in Table 6.

Table 6 Configurations of model settings and data generation for 23 scenarios in numerical analysis