A Bayesian update of Kotha et al. (2020) ground-motion model using Résif dataset

Abstract

Recent updates of pan-European seismic hazard and risk maps adopted the partially non-ergodic Kotha et al. (Bull Earthq Eng 18:4091–4125, 2020) ground-motion model. This model was regressed from the Engineering Strong Motion dataset, containing ground-motion data of ${M}_{W}\ge 3$ events mostly from Italy, Turkey, Greece, and in smaller fractions from rest of the active shallow crustal tectonic regions of Europe. Through mixed-effects regressions, the non-ergodic model partially resolved the spatial variability of attenuation characteristics across most of seismically active Europe, but not in France due to the then lack of a regional dataset. With the availability of a manually processed dataset from Résif network, and a computationally viable Bayesian inferencing algorithm, this study aims to extend the non-ergodic applicability of the model to ${M}_{W}<3$ earthquakes, attenuating regions, tectonic localities, and sites located in France. In process, a few important decisions had to be made concerning the updating methodology, and the interpretation of spatial variability of attenuation—specifically, that of the tectonic localities producing earthquakes. The methodology and results are discussed, emphasising the need to revise the current ground-motion regionalisation approach, and to tailor the updating procedure to be application specific. This study anticipates and supports a shift from frequentist to Bayesian approach of ground-motion modelling, in order to maintain continuity of knowledge regressed from various ground-motion datasets.

1 Introduction

The European Seismic Hazard Maps of 2020 (ESHM20) have adopted new strategies in developing harmonised hazard assessments across the geological and tectonically diverse environments of Euro-Mediterranean region (Danciu et al. 2021). Among these is the shift towards a more data-driven representation of ground-motion epistemic uncertainties (Weatherill et al. 2023a, b), as a variation of the ‘scaled backbone’ ground-motion model (GMM) logic-tree approach of Bommer (2012) and Douglas (2018). The backbone approach ensures transparency on the level of uncertainty implied by the GMM, a clearer description of logic-tree branch weights, and the flexibility to make the logic-tree specific for a given region. One of the main challenges of regionally scaling and adapting the ESHM20 backbone GMM logic-tree is to ensure that its calibration captures the appropriate level of ground-motion epistemic uncertainty (e.g., Kowsari et al. 2023); which is particularly difficult for regions with limited ground-motion data, and hence is the interest of this study.

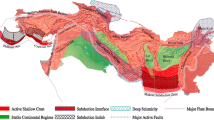
The ESHM20 GMM logic-tree for active shallow crustal earthquakes (Weatherill, Kotha and Cotton 2020) is an application driven implementation of the Kotha et al. (2020a, b) and Kotha et al. (2022) GMMs. Together, these GMMs together will be referred to as K20 from hereon. The K20 models were regressed from the Engineering Strong Motion (ESM) dataset developed and validated by Lanzano et al. (2018) and Bindi et al. (2018). The ESM dataset featured ground-motions recorded in several seismically active Euro-Mediterranean regions hypothesised to exhibit strong spatial variability of attenuation characteristics. To quantify the spatial (or regional) variability of ground-motion attenuation characteristics, K20 relied on geology and tectonics based regionalisation models of Basili et al. (2019) and Danciu et al. (2021).

Figure 1 shows a partially non-ergodic region-specific application of K20 GMM as a logic-tree with two branching levels: level 1 to account for variability and uncertainty in far-source attenuation ($>80$km) depending on the receiving site location, and level 2 to account for variability and uncertainty in at-source attenuation ($\sim 1$km) depending on the event location. Note that, at-source attenuation introduced in this study is an alternative interpretation/hypothesis on the tectonic-locality random-effects group elaborated in K20 development (see Kotha et al. 2022), and will be detailed in later sections. The two branching levels adjust specific coefficients of K20 to predict Gaussian distributions of ground-motions best representing the site and event location dependent attenuation characteristics in a region. In level 1 of the logic-tree shown in Fig. 1, ${\delta c}_{3,r}$ is the adjustment to the ‘apparent anelastic attenuation’ coefficient (${c}_{3}$ in K20) specific to the region $r$ hosting the site, and $SE(\delta {c}_{3,r})$ is the uncertainty on ${\delta c}_{3,r}$. In level 2, ${\delta L2L}_{l}$ is the adjustment to the ‘offset/bias/intercept’ coefficient (${e}_{1}$ in K20) specific to the tectonic locality $l$ hosting the event, and $SE(\delta L2{L}_{l})$ is the uncertainty on ${\delta L2L}_{l}$. To ensure that the resulting ground-motions follow a Gaussian distribution, one may set $\eta =1.732$ with branch weights ${W}_{1,j}$ = 0.167, 0.666, 0.167 for $j=1, 2, 3$ (Miller III and Rice 1983)—similar to those in ESHM20 GMM logic-tree. The logic-tree is cast as such so that [${\delta c}_{3,r}$, $SE(\delta {c}_{3,r})$], [$\delta L2{L}_{l}$, $SE(\delta L2{L}_{l})$], $\eta$, and the branch weights can be modified and adapted to new regions when and where new ground-motion datasets beyond ESM become available.

Fig. 1

Partially non-ergodic region-specific GMM logic-tree proposed in Kotha et al. (2020a, b)

In K20, $\delta {c}_{3,r}$ and $\delta {L2L}_{l}$ were treated as statistical estimates, while Kotha et al. (2022) evaluated the physical meaning of these random-effects and their spatial variabilities. Subsequently, it was argued that the regionally-adaptable scaled GMM logic-tree reflects, for example, weaker far-source attenuation in Pyrenees compared to French Alps, weaker far-source attenuation in French Alps compared to Apennines in Italy, weaker far-source attenuation towards east of Apennines compared to the west of Apennines in central Italy, etc. However, ESM contained very few ground-motion records from France (~ 300) compared to Italy (~ 10,000), while several densely populated regions in France (e.g., Parisian basin) are still barely sampled from lack of seismic activity. Since $\delta {c}_{3,r}$ and $\delta {L2L}_{l}$ were inestimable for most regions in France, the ESHM20 backbone GMM logic-tree could only use the pan-European averages with large uncertainties in these regions; resulting in hazard estimates with large uncertainties as well. As a follow-up to ESHM20, this study explores a methodology to update, in a Bayesian framework, the existing K20 GMM using a new dataset of ground-motions recorded in France—the Résif (1996–2019) dataset by Traversa et al. (2020), recently extended to include data until end of 2021 by Buscetti et al., (in-prep.). As such, this study is an intermediary step towards updating the K20 GMM and adapting the Fig. 1 backbone logic-tree to France.

A modest updating procedure would be to compare the ground-motion distributions from the GMM logic-tree against the new data from a region, and iteratively—and exclusively—modify the $\delta {c}_{3,r}$, $\delta {L2L}_{l}$, or other GMM coefficients. There are at least three problems that deter such a simplified approach: (1) GMM fixed-effect coefficients are often correlated—this challenges exclusively adjusting any coefficient while leaving the rest unchanged; (2) the new dataset may have sampled $[{M}_{W}, {R}_{JB}]$ ranges beyond the GMM’s applicability—this may require evaluating first and then recalibrating the GMM to extend its usability; (3) the new dataset may have sampled $[{M}_{W}, {R}_{JB}]$ scenarios well within GMM’s applicability, but the event-, path-, and site-effects, and their combinations may be rather peculiar—this may lead to misattributing, for example, systematically strong site-effects as event- and path-effects. In combination, these three issues may render iterative estimation of physically meaningful $\delta {c}_{3,r}$ and $\delta {L2L}_{l}$ rather challenging, and possibly unreliable. Incidentally, this was the case with the Résif dataset of French ground-motions. It is impossible to guess via residual analyses, for example, if the French earthquakes are systematically stronger, if the French site amplifications are stronger, or if the French regional crust attenuates ground-motions rather weakly compared to the pan-European average of K20. Therefore, this study explores an approach to overcome these issues by shifting from classical or frequentist mixed-effects regressions to Bayesian mixed-effects GMM regressions (Samaniego 2010).

Essentially, this study first recasts the K20 GMM in a Bayesian framework. Following an implementation and evaluation of the new regression approach, the K20 model is updated using the French dataset. The changes to K20 GMM, the relevant technical issues in Bayesian updating, and the apparent causes for the most remarkable changes in the GMM are discussed. This study does not propose an application-ready update to ESHM20 logic-tree for France, but is intended as a reference to any future attempts to scale and adapt the K20 GMM to new regions.

2 Datasets

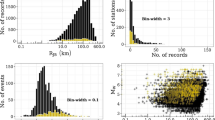
The pan-European dataset (ESM, yellow markers and histograms in Fig. 2) was used in conjunction with the regionalisation model of Basili et al. (2019) and tectonic localisation model of Danciu et al. (2021) in deriving the K20 GMMs. Details on each of these are available in their respective publications, and will be skipped here. The data selection procedure for the robust linear mixed-effects regression (RLMM; robustlmm by Koller 2016) of K20 is also described in Kotha et al. (2020a, b). The companion dataset from France by Traversa et al. (2020) contains ground-motion data recorded by Résif network (Résif, blue markers and histograms in Fig. 2). The key features of the datasets relevant to this study are:

• (1) The pan-European ESM dataset contains ground-motion recordings made over the period 1969–2016, while the Résif dataset used here covers the period 1996–2021.

• (2) Prior to data selection procedure based on usable frequency range with good signal-to-noise ratio, while ESM contains data from $3<{M}_{W}<8$ events, Résif dataset contains data from a largely disjoint range $2<{M}_{W}<5$. This means that, the new data is well beyond the applicability range of K20, particularly towards lower ${M}_{W}$.

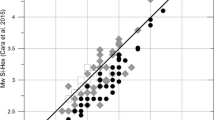
• (3) The preferred ${M}_{W}$ of events in ESM dataset are those from the EMEC catalogue (Grünthal and Wahlström 2012) revised by Weatherill and Lammers (GeoForschungsZentrum, GFZ Potsdam) during ESHM20 development. The ${M}_{W}$ estimates of Résif events are derived predominantly from the SIHEX-BCSF-RENASS catalogue (Cara et al. 2015) and from conversions from local-magnitude estimates. In this study, the ${M}_{W}$ provided in the Résif dataset are preferred even if EMEC values are available for some of the events.

• (4) Résif dataset contains data from broadband seismometers, structure-related, and borehole sensors as well. There are 98 stations common to both the datasets. These stations are retained in the analyses, because many of them have recorded several small ${M}_{W}$ events in Résif dataset that were absent in ESM. Only data from the sea-bottom station “FR.ASEAF” was removed from the analyses.

• (5) Laurendeau, Clément and Scotti (2022) identified 11 events common to both ESM and Résif datasets. Associated to these events, there are 270 records common to both the datasets. Following the data selection procedure described in Kotha et al. (2020a, b), K20 GMM was derived using 18,222 records in ESM. Following an identical data selection procedure, 15,586 Résif records were available for the Bayesian update in this study. As shown in Fig. 3, the number of usable records in Résif dataset decreases rapidly towards longer periods due to limited usable frequency range with signal-to-ratio $\ge 3$ (details in Traversa et al. 2020). At short periods, the relatively small fraction of common records did not alter the key outcomes of this study. At long periods, removing these common records further reduced the available Résif records. Therefore, in this study, the common events, stations, and their associated ground-motion records are all retained in the analyses.

• (6) The Résif ground-motion data is regionalised with the same models as the ESM dataset in Kotha et al. (2020a, b). As in, ground-motion records are assigned into different attenuating regions based on site locations, and into different tectonic localities based on event locations. Regions that were very poorly sampled in ESM are now populated with several tens of recordings in a few cases (Fig. 4).

Fig. 2

Comparison of ESM (yellow) and Résif (blue) ground-motion datasets

Fig. 3

Comparison of number of usable records passing the low-pass and high-pass filter criteria in ESM and Résif datasets

Fig. 4

Distribution of Résif ground-motion data among the attenuation regions (right panel) of Basili et al. (2019) and tectonic localities (left panel) of Danciu et al. (2021)

3 Method

The published K20 GMM was derived using a robust linear mixed-effects regression (RLMM) algorithm of the robustlmm package in R (R-Core-Team 2000; RStudio-Team 2022). The robust regressions were necessary to identify and down-weight possible outlier ESM data from biasing the fixed-effects median and random-effect variances of the mixed-effects K20 GMM. Although RLMM regressions could provide the maximum-likelihood estimates of GMM fixed-effects coefficients and random-effects variances (or standard-deviations), they do not inform on uncertainties of these quantities. Uncertainties are joint distributions of GMM mixed-effects estimates that could allow a modeller understand which components are relatively better constrained, and which ranges of the dataset may require better sampling. In addition, the customary practice has been to derive a completely new maximum-likelihood based GMM every few years when new datasets become available; while ignoring the knowledge regressed from existing datasets via GMMs. With ground-motion datasets growing exponentially large every year, this practice could soon become computationally intense, and the number of GMMs may become too numerous and incongruent to choose from (see Douglas and Edwards 2016).

Bayesian approach to ground-motion modelling overcomes most of the above issues. A Bayesian regression yields joint distributions of the mixed-effects parameters of a GMM. These joint distributions help in assessing the strengths and weaknesses of the GMM; but more importantly, instead of performing a new regression on a new and extended dataset, these joint distributions of mixed-effects can be used as informative priors in developing a new GMM or updating an existing GMM. Several authors have argued for the need and advantages of Bayesian approach in ground-motion modelling (e.g., Kowsari et al. 2020, 2019; Stafford 2019; Kuehn and Scherbaum 2016; Arroyo and Ordaz 2010; Wang and Takada 2009). Moreover, with the recent developments in approximate Bayesian inferencing using Integrated Nested Laplace Approximation (INLA; Rue et al. 2009), Bayesian GMM regressions have become computationally much more viable (e.g. Kuehn 2021; Gómez-Rubio 2020). Therefore, in this study, the first step is to recast the ESM based frequentist K20 GMM in a Bayesian framework (Samaniego 2010), and then perform a Bayesian update using the Résif dataset using the R-INLA package (Lindgren and Rue 2015).

3.1 Bayesian inference of K20 GMM from ESM dataset

The functional form of K20 GMM is shown in Eqs. (1–4). The purpose of its fixed-effects (${e}_{1},{b}_{1},{b}_{2},{b}_{3},{c}_{1},{c}_{2},{c}_{3}$), random-effects ($\Delta {{\text{c}}}_{3,{\text{r}}},\Delta {{\text{L}}2{\text{L}}}_{{\text{l}}},\Delta {{\text{B}}}_{{\text{e}},{\text{l}}}^{0},\Delta {{\text{S}}2{\text{S}}}_{{\text{s}}}$), and residuals ($\mathrm{\rm E}$) are explained in Kotha et al. (2020a, b), Kotha et al. (2022), Kotha et al. (2022), and will be skipped here.

$${\text{Ln}}\left(\upmu \right)={{\text{e}}}_{1}+{{\text{f}}}_{{\text{R}},{\text{g}}}\left({M}_{W},{R}_{JB}\right)+{{\text{f}}}_{{\text{R}},{\text{a}}}\left({R}_{JB}\right)+{{\text{f}}}_{{\text{M}}}\left({M}_{W}\right)+\Delta {{\text{L}}2{\text{L}}}_{{\text{l}}}+\Delta {{\text{B}}}_{{\text{e}},{\text{l}}}^{0}+\Delta {{\text{S}}2{\text{S}}}_{{\text{s}}}+\mathrm{\rm E}$$

(1)

$${{\text{f}}}_{{\text{R}},{\text{g}}}= {({\text{c}}}_{1 }+{{\text{c}}}_{2}.({M}_{W}-{{\text{M}}}_{{\text{ref}}})).{\text{ln}}\sqrt{{(R}_{JB}^{2}+{{\text{h}}}_{{\text{D}}}^{2})/({{\text{R}}}_{{\text{ref}}}^{2}+{{\text{h}}}_{{\text{D}}}^{2})}$$

(2)

$${{\text{f}}}_{{\text{R}},{\text{a}}}=\frac{{{\text{c}}}_{3}+\Delta {{\text{c}}}_{3,{\text{r}}}}{100} .(\sqrt{{R}_{JB}^{2}+{{\text{h}}}_{{\text{D}}}^{2} }-\sqrt{{{\text{R}}}_{{\text{ref}}}^{2}+{{\text{h}}}_{{\text{D}}}^{2} })$$

(3)

$${{\text{f}}}_{{\text{M}}}= \left\{\begin{array}{c}{{\text{b}}}_{1}.\left({M}_{W}-{{\text{M}}}_{{\text{h}}}\right) {+{{\text{b}}}_{2}{.\left({M}_{W}-{{\text{M}}}_{{\text{h}}}\right)}^{2}}\quad M_{W} \le {{\text{M}}}_{{\text{h}}}\\ \\ {{{\text{b}}}_{3}.\left({M}_{W}-{{\text{M}}}_{{\text{h}}}\right)\quad {\mathrm{ M}}_{{\text{h}}}<M}_{W}\end{array}\right.$$

(4)

The exact same subset of ESM dataset used in deriving the K20 model is used in this study. Through Eqs. (1–4), and at all periods T = 0.01–8 s, the ${M}_{ref}=4.5$, ${h}_{D}$ = 4, 8, 12 km depending on hypocentral depths, ${R}_{ref}=30\,{\rm km}$, and ${M}_{h}=5.7$ are a priori values, and remain unaltered in this study. The robust estimates of K20 GMM fixed-effects published in Kotha et al. (2022) are used as means of the log-gamma informative priors with a precision of 0.1. The robust standard-deviations of random-effect groups ∆c₃,r = Ɲ(0, τc₃), ∆L₂L_l = Ɲ(0, τL₂L), $\Delta {B}_{e,l}^{0}$ = Ɲ(0, τ₀), and $\Delta S2S$ = Ɲ(0, ϕ_S2S) were published and detailed in Kotha et al. (2022). The informative priors of these quantities in the Bayesian regression are input as typical log-gamma distributions with $1/{\tau }_{L2L}^{2}$,$1/{\tau }_{0}^{2}$, and $1/{\phi }_{S2S}^{2}$ as scale parameters and 1 as the rate parameter. Following a few trials, the rate parameter of log-gamma distribution with scale parameter 1$/{\tau }_{c3}^{2}$ is changed to 0.5 (instead of 1) to bring the INLA estimates of ${\tau }_{c3}$ closer to its RLMM counterpart. With these settings, the GMM is regressed using the inla function of R-INLA package.

Kotha et al. (2020a, b) derived two sets of K20 mixed-effects estimates: robust approach (RLMM) where random-effects and residuals follow a Huber loss distribution (Huber 1992), and a classical approach (LME) where random-effects and residuals follow a Gaussian distribution (lme4 by Bates et al. 2015). At the time of this study, the inla function of R-INLA package failed to converge for any error distribution (e.g., student-t) other than the Gaussian. Consequently, the INLA mixed-effects estimates cannot be expected to coincide with RLMM estimates, but perhaps be closer to LME estimates.

Figure 5 shows the fixed-effects (${e}_{1},{b}_{1},{b}_{2},{b}_{3},{c}_{1},{c}_{2},{c}_{3}$) estimates from multiple regressions: the black solid lines are robust RLMM estimates, the black dashed lines are the ordinary-least square LME estimates, and the yellow curves are the joint distributions estimated in the Bayesian regression of K20 GMM (assuming Gaussian errors). The blue curves are those from the Bayesian update of K20 with Résif dataset, and will be discussed in the Results section. Figure 5 indicates that the RLMM, LME, INLA fixed-effects estimates from ESM dataset are in reasonably good agreement, with the maximum likelihood estimates of LME (dashed lines) falling closer to the medians of INLA joint distributions (yellow curves) than those of RLMM (solid lines). This confirms that, at least the fixed-effects estimates from INLA can be used as reliable priors in the subsequent Bayesian update. In addition, although not shown here, the fixed-effects variance–covariance matrices were almost identical; which means, the within-model epistemic uncertainty (${\sigma }_{\mu }$, Atik and Youngs 2014) from RLMM and INLA can be used interchangeably.

Fig. 5

Joint distributions of Kotha et al. (2020a, b) GMM fixed-effects coefficients at ${\varvec{T}} = 0.01, 0.1, 1{\varvec{s}}$ (top—to—bottom). The black solid lines are robust (RLMM) estimates, the black dashed lines are classical (LME) estimates, the yellow curves are the joint distributions estimated in the Bayesian (INLA) regression of K20 GMM with ESM, and the blue curves are the joint distributions from the Bayesian (INLA) update of K20 using Résif dataset

Figure 6 is similar to Fig. 5 but shows instead the residual and random-effects standard-deviations (${\phi }_{0},{\tau }_{c3},{\tau }_{0}, {\phi }_{S2S}, {\tau }_{L2L}$) from RLMM (solid black lines), LME (dashed black lines), and INLA (yellow curves) approaches to inferring K20 from ESM. The difference in RLMM and LME standard-deviations are clearer in Fig. 6, where the former are often smaller than the latter as a consequence of down-weighting outlier data from their estimations. The INLA estimates of ${\phi }_{0}$ and ${\phi }_{S2S}$ match remarkably well with LME estimates while being very different from RLMM estimates, indicating possibly a large number of outlier records and sites in ESM dataset—those the LME is unable to identify. Such differences can be expected between different regression algorithms due to the various underlying assumptions and approximations (also remarked in Stafford 2019). For the purpose of this study, however, they are considered reasonably similar and interchangeable. The INLA mixed-effects joint distributions obtained for ESM dataset will be used as informative priors in Bayesian update of K20 using Résif dataset.

Fig. 6

Joint distributions of Kotha et al. (2020a, b) GMM random-effects standard-deviations at ${\varvec{T}} = 0.01, 0.1, 1{\varvec{s}}$ (top-to-bottom). The black solid lines are robust (RLMM) estimates, the black dashed lines are classical (LME) estimates, the yellow curves are the joint distributions estimated in the Bayesian (INLA) regression of K20 GMM with ESM, and the blue curves are the joint distributions from the Bayesian (INLA) update of K20 using Résif dataset

3.2 Bayesian update of K20 GMM with Résif dataset

The data selection procedure described in the Datasets section resulted in 15,586 records in Résif dataset available for the Bayesian update at $T=0.01s$; which falls to 10,450 at $T=1s$, and 3558 at $T=2s.$ The marginal distributions of K20 mixed-effects—the yellow curves in Figs. 5 and 6—can be used as informative priors in the Bayesian update using Résif dataset.

Initial attempts with the inla function allowed simply updating the K20 mixed-effects with the natural-log of ground-motion values in Résif dataset as likelihoods. Following the INLA package update (version 23.04.24) the regressions have become unstable and produced nonsensical GMM coefficients. To remedy this, the Bayesian update is performed on the $Residuals$ obtained by subtracting K20 fixed-effects (median, Eqs. 2–4) prediction from natural-log of Résif ground-motions (${\text{ln}}(GM)$), as in Eq. (5). Accordingly, the priors for the fixed-effects are those shown in Fig. 5 but instead centred on zero, because the fixed-effects trends are already removed from the Résif data via Eq. (5). Therefore, the $Residuals$ regressed in Eq. (6) produce $\delta$ estimates of the fixed-effects. The $\delta$ estimates are then added to the K20 median of priors of fixed-effects to obtain their conjugate posteriors.

$$ Residuals = ln\left( {GM} \right) - \left( {e_{1} + f_{{R,g}} \left( {M_{W} ,R_{{JB}} } \right) + f_{{R,a}} \left( {R_{{JB}} } \right) + f_{M} \left( {M_{W} } \right)} \right) $$

(5)

$$Residuals={\delta e}_{1}+{\delta b}_{1}+{\delta b}_{2}+{\delta b}_{3}+{\delta c}_{1}+{\delta c}_{2}+{\delta c}_{3}+\Delta {c}_{3,r} +\Delta {L2L}_{l}+ \Delta {B}_{e,l}^{0}+\Delta {S2S}_{s}+\epsilon $$

(6)

Through several trials it is understood that the Bayesian updates (of GMMs) are rather sensitive to the priors and the restrains placed on them. The effect of restrains, i.e., to allow random-effects parameter to be updated or to remain fixed, will be shown in the Discussion section. Only the trial considered to be producing the most defensible GMM update is discussed here. These restrains were placed on specific fixed-effects; meaning, certain coefficients among (${e}_{1},{b}_{1},{b}_{2},{b}_{3},{c}_{1},{c}_{2},{c}_{3}$) were restrained from being updated:

• ${e}_{1}$ is the offset, bias or intercept of the GMM median (Eq. 1). This fixed-effects coefficient is indispensable in a GMM regression, but has no strict physical meaning. A positive ${\delta e}_{1}$ (Eq. 6) following the update would shift the GMM median to higher values for all $[{M}_{W},{R}_{JB}]$ combinations—both ergodic and non-ergodic predictions. This can be considered indefensible because the Résif dataset does not have the same $[{M}_{W},{R}_{JB}]$ range as ESM, and the updated coefficients should (preferably) not effect predictions beyond the $\left[{M}_{W},{R}_{JB}\right]$ range of the new dataset.In addition, the ${\delta L2L}_{l}$ values are added to ${e}_{1}$ to obtain partially non-ergodic predictions via the GMM logic-tree (level 2 in Fig. 1). Since, the K20 estimate of ${e}_{1}$ is a pan-European average, modifying ${e}_{1}$ may render the ESM estimates of ${\delta L2L}_{l}$ incompatible with K20. In order to be able to compare ${\delta L2L}_{l}$ of the new Résif tectonic localities (in left panel of Fig. 4) to those estimated using ESM, it was deemed necessary to restrain ${e}_{1}$ from updating. Therefore, ${e}_{1}$ is not updated by fixing ${\delta e}_{1}=0$ in Eq. (6).

• ${b}_{1},{b}_{2}$ fixed-effects coefficients control the scaling of ground-motions with ${M}_{W}$ (Eq. 4) for events with ${M}_{W}\le {M}_{h}=5.7$. Since Résif dataset contains data from events with ${2<M}_{W}<5$, it is necessary to allow ${b}_{1},{b}_{2}$ to be updated. It is important to note that, ${e}_{1}$ is positively correlated to ${b}_{1},{b}_{2}$ (discussed in Kotha et al. 2022). Therefore, constraining ${\delta e}_{1}=0$ or not strongly effects the update of ${b}_{1},{b}_{2}$. In this study, ${\delta b}_{1},\delta {b}_{2}$ in Eq. (6) are allowed to take non-zero values.

• ${b}_{3}$ fixed-effects coefficient controls the scaling of ground-motions with ${M}_{W}$ (Eq. 5) for events with ${M}_{W}>{M}_{h}=5.7$. Although ${b}_{3}$ is allowed to be updated, the $[{M}_{W},{R}_{JB}]$ range of the Résif dataset should not affect it. In this study, $\delta {b}_{3}$ in Eq. (6) is allowed to obtain non-zero values.

• ${c}_{1},{c}_{2}$ fixed-effects coefficients control the linear-decay of ground-motions with ${R}_{JB}$ and $[{M}_{W},{R}_{JB}]$, respectively. Equation (2) models the geometric attenuation of ground-motions via weakly correlated ${c}_{1},{c}_{2}$ (discussed in Kotha et al. 2022). Bindi and Kotha (2020) observed that geometric spreading could be region-specific due to regional differences in near-surface crustal structure, and seismogenic depths. Since the hypocentral depth of small events are often poorly constrained, there was no concrete reason to restrict these coefficients from updating. Therefore, ${\delta c}_{1},\delta {c}_{2}$ are allowed to obtain non-zero values.

• ${c}_{3}$ fixed-effects coefficient controls the exponential-decay of ground-motions with ${R}_{JB}$. Equation (3) models the so-called ‘apparent anelastic’ attenuation of ground-motions at far-source distances. This parameter is regionalised via ${\delta c}_{3,r}$ in Eq. (3). The ${c}_{3}$ estimated from ESM are the pan-European averages, to which region-specific ${\delta c}_{3,r}$ values can be added (level 1 in Fig. 1) to obtain region-specific predictions. ${\delta c}_{3,r}$ values are estimated for new Résif regions beyond the ESM coverage (Fig. 4). In this study, similar to argument made against updating ${e}_{1}$, in order to main the compatibility of ESM based ${c}_{3}$ and ${\delta c}_{3,r}$ values, and to evaluate ${\delta c}_{3,r}$ values of new Résif regions against those from ESM, ${c}_{3}$ is not allowed to change during the Bayesian update by constraining ${\delta c}_{3}=0$ in Eq. (6).

• The marginals of all random-effects groups $\Delta {{\text{c}}}_{3,{\text{r}}}$ = Ɲ(0,τ_c3), $\Delta L2{L}_{l}$ = Ɲ(0,τ_L2L), $\Delta {B}_{e,l}^{0}$ = Ɲ(0,τ₀), and $\Delta S2S$ = Ɲ(0,ϕ_S2S) are restricted from being updated. The random-effect values of the levels within each group—say, the $\updelta {{\text{c}}}_{3,{\text{r}}}$ of a region $r$ in $\Delta {{\text{c}}}_{3,{\text{r}}}$ = Ɲ(0,τ_c3) group—are estimated with respect to their group variance. In doing so, for example, the $\updelta {{\text{c}}}_{3,{\text{r}}}$ values of regions common to both datasets are not updated but re-estimated using the new Résif data; and are compared to their ESM based estimates in Supplementary Figures. This has been decided after several trials, but there is no clear reason as to whether they should be or not. The only justification is that, allowing one or more of these parameters to update led to instabilities in regression across the spectral period range. This study discusses the results of the trial where none of the random-effects are allowed to update, but this issue will be revisited in the Discussion section.

4 Results

Bayesian inference of K20 from ESM and subsequent update using Résif data were performed for $RotD50$ combination of horizontal spectral accelerations at periods $T=0.01-8s$, $PGA$ and $PGV$. Figure 7 compares the fixed-effects (left panel) and random-effects (right panel) values inferred from ESM (dashed lines) and updated using Résif (solid lines) datasets.

Fig. 7

Comparison of ESM (dashed lines) inferred and Résif (solid lines) updated GMM fixed-effects coefficients (left panel), random-effects and residual standard-deviations (right panel)

4.1 Fixed-effects

Figure 5 and the left panel of Fig. 7 show the behaviour of the fixed-effects coefficients following the Bayesian update. Coefficients ${e}_{1}$ and ${c}_{3}$ are restricted from updating, so there is not much to discuss except for a remark that: ${\delta L2L}_{l}$ and ${\delta c}_{3,r}$ values estimated from ESM—for regions not present in Résif—will remain usable even after the update. Regarding the other coefficients:

• ${b}_{1},{b}_{2}$ fixed-effects coefficients exhibit the largest changes. The blue curves in Fig. 5 suggest that both these coefficients have lower uncertainty following the update, as indicated by the posteriors (blue curves) narrower than the priors (yellow curves). Figure 7 suggests that at short-periods both coefficients have updated values (solid lines) smaller than those of K20 (dashed lines); although the changes are less significant for ${b}_{1}$. The effect of these changes in GMM median predictions can be observed in Fig. 8. In the lower panels of Fig. 8 showing the scaling of spectral accelerations at $T=0.01, 0.1, 1s$ (left-to-right) with ${M}_{W}$, the faded lines correspond to ESM based K20 predictions, overlain by solid lines from updated predictions. The updated predictions are lower than K20 predictions at ${M}_{W}\le 4$ at all distance ranges. However, the smallest events considered hazard relevant in most PSHA studies, even in low seismicity regions, are of ${M}_{W}\ge 4.5$. Therefore, changes in ${b}_{2}$ shown here do not affect the ESHM20.

Fig. 8

Comparison of ESM inferred (faded lines) and Résif updated (strong lines) scaling of spectral accelerations at ${\varvec{T}} = 0.01{\varvec{s}},0.1{\varvec{s}},1{\varvec{s}}$ (left-to-right columns) with distance metric ${\varvec{R}}_{{{\varvec{JB}}}}$ (top panels) and with ${\varvec{M}}_{{\varvec{W}}}$ (bottom panels). The curves are colour coded according to the hypocentral depth-bin of the event, and the curves’ line-type changes with attenuation region—details in Kotha et al. (2020a, b, 2022)

A more interesting aspect of this update is that ${b}_{2}$ values are now close-to-zero as opposed to being positive in K20. While discussing the purpose of various fixed-effects coefficients, Kotha et al. (2022) acknowledged that while empirically ${b}_{2}$ takes positive values in K20, theoretically it should take non-positive values as proposed by Fukushima (1996) and Douglas and Jousset (2011). Kotha et al. (2022) argued that the uncertainty on ${b}_{2}$ and K20 predictions at ${M}_{W}\le 4$ is large due to sparse calibration data in ESM, and the errors in ${M}_{W}$ of small events. Although errors in ${M}_{W}$ of small French events persist in Résif, the 10,000 + records from ${M}_{W}\le 4$ have worked in favour of reducing the uncertainty in ${b}_{2}$ values.

• ${b}_{3}$ fixed-effects coefficient controls the scaling of ground-motions at ${M}_{W}>5.7$. Since the $[{M}_{W},{R}_{JB}]$ range of Résif dataset falls short, ${b}_{3}$ has remained the same.

• ${c}_{1},{c}_{2}$ fixed-effect coefficients controlling the geometric attenuation exhibit only marginal changes in their median values (Fig. 5 and left panel of Fig. 7) but have lower uncertainties than in K20. The update has mostly unnoticeable impact on predictions at near-source distances (e.g., $\le 30\,{\rm km})$.

In summary, the only remarkable changes following the update are the lower uncertainties on the fixed-effects coefficients that were allowed to be updated, and ${b}_{2}$ values that better confirm with analytical expectations. The impact on median predictions is largely unnoticeable, and may even be irrelevant to most PSHA studies. However, prospective PSHA studies in low-moderate seismicity regions such as France, Germany, United Kingdom, and regions effected by local induced seismicity composed of small events, this Bayesian update of K20 may be more appropriate with its improved predictions at ${M}_{W}\le 4$.

As a side note, a trial regression where ${e}_{1}$ was allowed to update had increased its value ($\delta {e}_{1}>0$) at short-periods, which traded-off with a stronger decrease in ${b}_{2}$ on to negative values. This increase in ${e}_{1}$ combined with decrease in ${b}_{2}$ rendered only minor changes in predictions in the range $3.5<{M}_{W}<4.5$, but led to an increase in GMM median predictions by up to 50% at ${M}_{W}>5.7$. Since that would be an update difficult to substantiate, the decision to restrain ${e}_{1}$ from updating was considered more defensible. Similarly, allowing ${c}_{3}$ to update also increased its values. However, the updated (less negative) ${c}_{3}$ in combination with ESM based ${\delta c}_{3,r}$ values would have suggested anelastic amplification at far-source distances in a few ESM regions. Therefore, not allowing ${c}_{3}$ to update was considered appropriate. It is important to note again that, the restrains chosen in this study are appropriate for this dataset, but may need revision for other datasets.

4.2 Random-effects

Figure 6 and the right panel of Fig. 7 show the behaviour of the random-effects standard-deviations following the Bayesian update. Since all the random-effect variances are restricted from updating, neither of these plots show curves corresponding to the Résif update—except ${\phi }_{0}$. The random-effects (variability) components of a mixed-effects GMM are as important as the fixed-effects (median) component. Higher random-effects standard-deviations, if treated as aleatory variabilities, contribute to the total ground-motion aleatory variability ($\sigma$ in Fig. 7)—which in-turn yield conservative hazard estimates with extreme ground-motions becoming more likely (e.g., Bommer and Abrahamson 2006). When instead treated as epistemic uncertainties, the random-effects standard-deviations can be discounted from the total ground-motion variability, and used in GMM logic-tree. For example, Weatherill, Kotha and Cotton (2020) used ${\tau }_{c3}$ and ${\tau }_{L2L}$ to define the attenuation uncertainties in the ESHM20 shallow crustal GMM logic-tree. Since neither of ${\tau }_{c3}$ and ${\tau }_{L2L}$ is changed in this update, the ESHM20 logic-tree is not impacted.

In this study, as important as the random-effects groups’ standard-deviations (${\tau }_{c3},{\tau }_{0}, {\phi }_{S2S}, {\tau }_{L2L}$) themselves, are the random-effects values ($\delta {c}_{3,r}$, $\delta {B}_{e,l}^{0}, \delta S2{S}_{s}$, $\delta L2{L}_{l}$) of the levels within the groups. For instance, ${\tau }_{c3}$ is a quantification of spatial variability of far-source attenuation in ESM ground-motion data, when regionalised using Basili et al. (2019). The group in this case is ‘far-source attenuation regions’, and the levels are the ‘far-source attenuating regions’ within Basili et al. (2019) regionalisation model. When ${\tau }_{c3}$ is the (group) standard-deviation, $\Delta {c}_{3,r}$ = Ɲ(0,τ_c3) is the Gaussian random-variable with unique $\delta {c}_{3,r}$ values for each (level) region $r$. Figure 1 is a logic-tree using region-specific $\delta {c}_{3,r}$ and $\delta L2{L}_{l}$ values from Kotha et al. (2020a, b), and is different from that of Weatherill, Kotha and Cotton (2020) using ${\tau }_{c3}$ and ${\tau }_{L2L}$ values. Similarly, $\Delta {S2S}_{s}$ = Ɲ(0,ϕ_S2S) can be used to make site-specific hazard and risk assessments as demonstrated in, e.g., Kotha et al. (2017), and Kohrangi, Kotha and Bazzurro (2020), respectively.

It is important to note also that, the random-effects level values ($\delta {c}_{3,r}$, $\delta {B}_{e,l}^{0}, \delta S2{S}_{s}$, $\delta L2{L}_{l}$) are estimated from the group standard-deviations (${\tau }_{c3},{\tau }_{0}, {\phi }_{S2S}, {\tau }_{L2L}$), respectively. This means that, the ($\delta {c}_{3,r}$, $\delta {B}_{e,l}^{0}, \delta S2{S}_{s}$, $\delta L2{L}_{l}$) and their standard-errors (e.g., the $SE$ in Fig. 1) are sensitive to (${\tau }_{c3},{\tau }_{0}, {\phi }_{S2S}, {\tau }_{L2L}$) values being updated or not. The methods to estimate $\delta {B}_{e,l}^{0}$ (or $\delta {B}_{e}$) and $\delta S2{S}_{s}$ using ${\tau }_{0}$ (or $\tau$) and ${\phi }_{S2S}$, respectively, were already presented in earlier studies (e.g., Abrahamson and Youngs 1992; Stafford 2014; Bradley 2015, etc.). In this study, (${\tau }_{c3},{\tau }_{0}, {\phi }_{S2S}, {\tau }_{L2L}$) are restrained from being updated. The following subsections discuss the ($\delta {c}_{3,r}$, $\delta {B}_{e,l}^{0}, \delta S2{S}_{s}$, $\delta L2{L}_{l}$) estimated under these restrains.

4.2.1 Attenuation variability: $\Delta {{\varvec{c}}}_{3,{\varvec{r}}}$ = Ɲ(0,τ_c3)

Figure 9 shows the $\delta {c}_{3,r}$ values of the various far-source attenuation regions estimated using ESM (top panels) and Résif (bottom panels) datasets at spectral periods $T=0.01, 0.1, 1s$ (left-to-right). Clearly, the regions newly populated with Résif data (right panel of Fig. 4) now have region-specific $\delta {c}_{3,r}$ values; which were to be otherwise assigned the pan-European average ${c}_{3}$ values with $\delta {c}_{3,r}$ = 0 in Eq. (3).

Fig. 9

Comparison of ESM inferred (top) and Résif inferred (bottom) region-to-region variability of apparent far-source anelastic attenuation random-effects group $\boldsymbol{ }\Delta {{\varvec{c}}}_{3,{\varvec{r}}}$ = Ɲ(0,τ_c3)

The ‘red regions’ in Fig. 9 are those with $\delta {c}_{3,r}>0$ values, and are supposed to exhibit weaker/slower far-source attenuation than the pan-European average with $\delta {c}_{3,r}=0$. Partially non-ergodic region-specific ground-motion predictions (from level 1 of Fig. 1) for these red regions would therefore be larger than those predicted for ‘white/grey’ and ‘blue’ regions, with pan-European average $\delta {c}_{3,r}=0$ and stronger/faster attenuation characteristics with $\delta {c}_{3,r}<0$, respectively. However, despite the surplus of Résif data in France, since the regionalisation model itself does not distinguish regions within France, there is not much to infer from these maps regarding the variability of far-source attenuation. The crustal tomography maps of Mayor et al. (2018) image France as multiple regions with distinct intrinsic absorption ${Q}_{i}/{Q}_{m}$ characteristics in different frequency bands—except the Parisian basin with no data (0^o–5^o East and 47^o–50^oNorth). The Basili et al. (2019) model did not adopt the Mayor et al. (2018) findings in their regionalisation of France, because neither were specifically designed for GMM attenuation regionalisation.

Supplementing Fig. 9, Fig. S1 shows that the $\delta {c}_{3,r}$ values for some of the regions common to both ESM and Résif datasets are rather similar, and with lower uncertainty following the update. However, there are as well regions with very different values estimated from ESM and Résif datasets, e.g., Pyrenees (−5^o–2^oEast and 42^o–45^oNorth) and Corsica Sardinia (10^oE and 38^o–43^oN). The latter contains only about a dozen ground-motion records in Résif dataset and will be ignored for the time being. The Pyrenees region however, has a few 100 s of new Résif records that were absent in ESM, and now is assigned a less extreme positive $\delta {c}_{3,r}$ value. The tomography maps of Mayor et al. (2018) showed that the Pyrenees region has an intrinsic absorption ${Q}_{i}$ close to the French national average ${Q}_{m}$, and lower than Brittany region to its north-west (−5^o–0^oE and 46^o–50^oN)—suggesting that attenuation in Pyrenees could be stronger (less positive $\delta {c}_{3,r}$) than in Brittany. However, none of these features could be captured with the current Basili et al. (2019) regionalisation model used in K20. Therefore, recognising the need for better refinement on regionalisation of France, this study will be followed-up by an evaluation and redesign of the regionalisation models used in K20. Meanwhile, this update suggests that far-source attenuation in France is on average always weaker/slower than elsewhere in pan-European region covered by ESM, and especially, in comparison to the stronger/faster attenuation inferred for the highly active regions of Central Italy. Consequently, ergodic GMMs developed using ground-motions recorded primarily at stations located in Italy may severely under-predict far-source ground-motions observable in France.

4.2.2 Tectonic variability: $\Delta {{\varvec{L}}2{\varvec{L}}}_{{\varvec{l}}}$ = Ɲ(0,τ_L2L)

Figure 10 shows the $\delta L2{L}_{l}$ values of the various tectonic localities estimated using ESM (top panels) and Résif (bottom panels) datasets at spectral periods $T=0.01, 0.1, 1s$ (left-to-right). Similar to Fig. 9, the localities newly populated with Résif data (right panel of Fig. 4) now have locality-specific $\delta L2{L}_{l}$ values; which were to be otherwise assigned average pan-European ${e}_{1}$ values in Eq. (1).

Fig. 10

Comparison of ESM inferred (top) and Résif inferred (bottom) tectonic locality-to-locality variability of at-source attenuation random-effects group $\boldsymbol{ }\Delta {\varvec{L}}2$ = Ɲ(0,τ_L2L)

The ‘red regions’ in Fig. 10 are those with $\delta L2{L}_{l} >0$ values, and are supposed to exhibit lower at-source attenuation than the pan-European average with $\delta L2{L}_{l}=0$. Partially non-ergodic locality-specific ground-motions (from level 2 of Fig. 1) for these red localities would therefore be larger than those predicted for ‘white/grey’ and ‘blue’ localities, with pan-European average with $\delta L2{L}_{l}=0$ and stronger at-source attenuation characteristics with $\delta L2{L}_{l} <0$, respectively. Unlike the far-source attenuation regionalisation in Fig. 9, the at-source attenuation regionalisation in Fig. 10 appears to capture a greater spatial variability within France. For instance, tectonic localities in Fig. 10 are distinct for the Pyrenees (−5^o–2^oE and 42^o–45^oN), the Parisian basin (0^o–5^oE and 47^o–50^oN), and the Brittany regions (−5^o–0^oE and 46^o–50^oN)—the latter two were merged into one far-source attenuation region in Fig. 9. In this study, it is important to reintroduce and clarify the meaning of at-source attenuation.

Both K20 and Kotha et al. (2022) adopted the tectonic localities of Danciu et al. (2021) (left panel of Fig. 4) to regionalise (or localise) ground-motion data and quantify source related attenuation characteristics in the ESM dataset. In those studies, the ${\tau }_{L2L}$ took larger values—indicating a greater regional variability—at short spectral periods ($T<1s$) and high frequencies ($f>1Hz$). However, random-effects and residual analyses showed that the $\Delta {L2L}_{l}$ = Ɲ(0,τ_L2L) were poorly correlated to any available physical parameters at that time. For instance, $\Delta {L2L}_{l}$ showed no correlation with Brune (1970) stress-drop estimated by Bindi and Kotha (2020) of events originating the tectonic localities. $\Delta {L2L}_{l}$ showed some negative correlation to Activity Index ($AIx$) of Chen et al. (2018), which in-turn is a fuzzy combination of 1 Hz coda Q, crustal shear-wave velocity at 175 km, and seismic moment rate density parameters. Meaning, tectonic localities with higher $AIx$ had on-average lower δ ${L2L}_{l}$ values (and the other way), but it was inconclusive which of the three Chen et al. (2018) crustal parameters are responsible for the correlation. Essentially, δ ${L2L}_{l}$ was assigned no physical meaning in Kotha et al. (2022).

In this study, upon comparing the crustal tomography maps of Mayor et al. (2018) with the $\Delta {L2L}_{l}$ spatial variability in Fig. 10, it becomes evident that the regions with higher ${Q}_{i}/{Q}_{m}$ often coincide with tectonic localities with $\delta L2{L}_{l} >0$ (e.g., the Brittany region), and those with lower ${Q}_{i}/{Q}_{m}$ coincide with tectonic localities with $\delta L2{L}_{l}<0$ (e.g. the Pyrenees region). Note that a higher intrinsic absorption quality-factor ${Q}_{i}/{Q}_{m}$ implies lower attenuation. Based on this observation, this study hypothesises that the regional variability of source-effects captured by $\Delta {L2L}_{l}$ = Ɲ(0,τ_L2L)—via the tectonic localities of Danciu et al. (2021)—could in fact be related to intrinsic absorption quality-factor ${Q}_{i}/{Q}_{m}$ at the earthquake source location and the Earth’s crust immediately around its hypocentre. Therefore, in this study, the tectonic localities random-effects group is hypothesised to be capturing the at-source attenuation characteristics. Based on this hypothesis, evidently, the earthquakes originating in the Brittany region with $\delta L2{L}_{l}>0$ suffered weaker at-source attenuation by virtue of the region’s lower intrinsic absorption as indicated by its higher ${Q}_{i}/{Q}_{m}$. Supplementary to Fig. 10, Fig. S2 shows that the $\delta L2{L}_{l}$ values for the tectonic localities common to both ESM and Résif datasets are rather similar at short periods $T<1s$, and with lower uncertainty following the update.

4.2.3 Between-event variability: $\boldsymbol{\Delta }{{\varvec{B}}}_{{\varvec{e}},{\varvec{l}}}^{0}$ = Ɲ(0,τ₀)

Figure 11 shows the trend of $\delta {B}_{e,l}^{0}$ with ${M}_{W}$ of ESM events (yellow markers) and Résif events (blue markers) at spectral periods $T=0.01, 0.1, 1s$ (left-to-right). The $\delta {B}_{e,l}^{0}$ versus ${M}_{W}$ plots are customarily used to verify if the ${M}_{W}$-scaling component of GMM (Eq. 4) is appropriate for the dataset. Absence of any systematic trends confirm that the Bayesian update efficiently removed ${M}_{W}$-scaling from Résif ground-motion data. However, it appears that the scatter of $\delta {B}_{e,l}^{0}$ of ${M}_{W}<4$ Résif events is rather narrow, suggesting that the between-event variability of such small events is in fact lower than that of $4<{M}_{W}<5.7$ events in ESM dataset. This observation is counter to the general consensus on heteroskedastic ${M}_{W}$-dependent between-event variability ${\tau }_{0}\left({M}_{W}\right)$ (e.g., Youngs et al. 1995).

Fig. 11

Comparison of $\delta B_{e,l}^{0}$ trends versus $M_{W}$ of ESM events (yellow) and Résif-RAP events (blue), at $T = 0.01, 0.1, 1s$ (left-to-right)

K20 proposed a heteroskedastic model with a large ${\tau }_{0}\left({M}_{W}\right)$ at ${M}_{W}<5$, decreasing linear with ${M}_{W}$ and reaching about a 20% smaller ${\tau }_{0}\left({M}_{W}\right)$ at ${M}_{W}\ge 6.5$. The heteroskedastic model used in ESHM20 is a Weatherill, Kotha and Cotton (2020) adoption of the Al Atik (2015) proposal. Figure 11 suggests that either of the above-mentioned heteroskedastic ${\tau }_{0}\left({M}_{W}\right)$ models can be used with this Bayesian update. However, it is important to recall that the Bayesian update trial being discussed here is the one with all random-effects group variances restrained from changing, and that the $\delta {B}_{e,l}^{0}$ are estimated directly from the unchanged ${\tau }_{0}$. If the between-event variability ${\tau }_{0}$ is allowed to change, the consequent $\delta {B}_{e,l}^{0}$ of the Résif events will necessarily change. This issue will be revisited in the Discussion section.

Supplementing Fig. 11, Fig. S3 compares $\delta {B}_{e,l}^{0}$ of the events identified by Laurendeau, Clément and Scotti (2022) as common to both datasets. While majority of events have similar $\delta {B}_{e,l}^{0}$ values inferred from the two datasets, the events with largest differences in their $M_{W}$ sourced from EMEC in ESM and Si-HEX in Résif datasets also show the largest differences in their $\delta B_{e,l}^{0}$ values. In addition, there appears also an inverse relation, wherein ESM inferred $\delta B_{e,l}^{0}$ values are larger than Résif inferred $\delta B_{e,l}^{0}$ when ESM assigned $M_{W}$ are lower than Résif assigned $M_{W}$—although not strictly. Laurendeau and Kotha (2023) analysed in detail the impact of $M_{W}$ homogenisation/unification on the between-event variability of Kotha et al. (2022) Fourier GMM derived from ESM, and discussed the sources of such $M_{W}$ and $\delta B_{e,l}^{0}$. discrepancies. Such analyses have not yet been performed on the K20 response spectra GMMs, and are among the planned activities to follow-up this study.

4.2.4 Between-station variability: $\Delta S2{S}_{s}$ = Ɲ(0,ϕ _S2S)

Figure 12 shows the trend of $\delta S2S_{s}$ versus $V_{s30}$ of ESM stations (yellow markersand Résif stations (blue markers) at spectral periods $T = 0.01, 0.1, 1s$ (left-to-right). The plot offers not much insight except that the Résif stations with $V_{s30} > 800m/s$ are more numerous. Figure 4 supplements Fig. 12 by comparing the $\delta S2S_{s}$ of stations common to both datasets at spectral periods $T = 0.01, 0.1, 1s$ (left-to-right). Most sites with $\delta S2S_{s}$ values around the zero-median of Ɲ(0,ϕ_S2S) distributions appear to have similar values across datasets, while those at the extremes of the random-distributions are very different. Once again, note that restraining $\Phi_{S2S}$ from updating also effects the $\Delta S2S_{s}$ estimates. Although not shown here, in trials where $\Phi_{S2S}$ is allowed to update, the between-dataset coherence of $\delta S2S_{s}$ of common stations noticeably improves. It is not clear yet whether s $\Phi_{S2S}$ should be updated or not, but this issue is briefly revisited in the Discussion section.

Fig. 12

Comparison of $\delta S2S_{s}$ trends versus measured $V_{s30}$ of ESM stations (yellow) and Résif stations (blue) at $T = 0.01, 0.1, 1s$ (left-to-right)

4.3 Residuals: $\boldsymbol{\rm E}$ = Ɲ(0,ϕ ₀)

Figures 6 and 7 compare the standard-deviation of ‘left-over’ residuals $\phi_{0}$ from ESM and Résif datasets. Despite all the random-effects and residual standard-deviations being restrained from updating, $\phi_{0}$ becomes larger following the update. This is because, unlike with the random-fects where level-specific values are estimated from group variances, residual variance is estimated from record-specific residuals obtained after removing mixed-effects values from the ground-motion observations. The hypothesis in this study is that the random-effect and residual variances trade-off depending on whether their priors are restrained from updating or not. Here, the additional variability of Résif ground-motion data appears to be absorbed into the residuals and their larger standard-deviation $\phi_{0}$.

Figure 13 visualises the $M_{W} - R_{JB}$ dependence of Résif record-to-record variability $\phi_{0,M,R}$ at $T = 0.01, 0.1, 1$ s. Here, $\phi_{0,M,R}$ is the standard-deviation of residuals in the 900 evenly spaced $M_{W} - R_{JB}$ bins defined solely for visualisation and discussion purpose. The numerous $M_{W} - R_{JB}$ bins with grey colour are those where $\phi_{0,M,R}$ is equal to the generic $\phi_{0}$ for that specific period. Moderate deviations of $\phi_{0,M,R}$ from $\phi_{0}$ appear at $30 < R_{JB} < 100\,{\rm km}$, where the Résif dataset is densely sampled. Stronger deviations appear at $0 < R_{JB} < 30\,{\rm km}$, where the dataset is poorly sampled. However, at this resolution of $M_{W} - R_{JB}$ binning, the deviations are rather irregular between adjacent cells, with steep changes in $\phi_{0,M,R}$; plus, choosing larger $M_{W} - R_{JB}$ bins show similar trends with no additional insights. An $M_{W} - R_{JB}$ dependent heteroskedastic $\phi_{0,M,R}$ is an option for this update, but perhaps after first evaluating their physical causes. Since both $\tau_{0}$ and $\Phi_{S2S}$ are restricted from updating, it is likely that the event- and site-dependent variabilities have been absorbed by the event- and site-specific residuals; which can be captured by period-dependent event-specific residual standard-deviation $\Phi_{0,e}$ and station-specific residual standard-deviation $\Phi_{0,s}$.

Fig. 13

${\varvec{M}}_{{\varvec{W}}} - {\varvec{R}}_{{{\varvec{JB}}}}$ dependence of residual variability $\phi_{{0,{\varvec{M}},{\varvec{R}}}}$ at ${\varvec{T}} = 0.01, 0.1, 1{\varvec{s}}$ (left-to-right columns). Note that the colour scale is centred (grey) on the $\phi_{0}$ at that specific period

Figure 14 shows the event-specific residual variabilities $\phi_{0,e}$ at $T = 0.01, 0.1, 1s;$ in top panels at event locations, and in bottom panels as histograms. The histograms suggest that a majority of events have $\phi_{0,e}$ lower than the updated Résif $\phi_{0}$; which means, the larger Résif $\phi_{0}$ could have been biased by a few extreme $\phi_{0,e}$ values. Therefore, it is worth analysing ground-motions of (these few) individual events for an explanation. An immediately noticeable feature in the maps (top panels) is that $\phi_{0,e}$ are systematically larger (in red) than $\phi_{0}$ for events located at the Italy-France-Switzerland frontier [45^oN, 7.5^oE] compared to elsewhere; especially compared to events more eastward in Italy [45^oN, 10^oE]. The Alpine region on the Italy-France-Switzerland frontier is geologically a very complex region, which can be hypothesised to have caused stronger azimuthal variability in propagation effects (e.g., Causse et al. 2021, Laurendeau et al. 2023). It could also be due to the anisotropy in shear-wave radiation pattern of small, point-source approximal, $M_{W} < 3$ events in this region (e.g., Dujardin et al. 2018, Kotha, Cotton and Bindi 2019, Trugman, Chu and Tsai 2021). The deterministic radiation pattern effects can be empirically modelled provided reliable event hypocentral depth and centroid-moment-tensor solutions are available, and the large $\phi_{0,e}$ can be resolved. However, the crustal heterogeneities around event locations may rapidly render the radiation patterns stochastic, making it impossible to resolve the large $\phi_{0,e}$ in this region. Another option is a regionally varying $\phi_{0}$, but only following an evaluation of its physical meaning. Moreover, such analyses are more sensible in the Fourier domain than with the response spectra here.

Fig. 14

Spatial distribution (top) and histogram (bottom) of event-specific residual variability $\phi_{{0,{\varvec{e}}}}$ at ${\varvec{T}} = 0.01, 0.1, 1{\varvec{s}}$ (left-to-right). The map colour scales are centred on $\phi_{0}$ (grey) at respective periods, with events of $\phi_{{0,{\varvec{e}}}} > \phi_{0}$ coloured in red, and vice-versa for blue. The histograms are overlain with vertical lines at $\phi_{0}$ of ESM (yellow) and of Résif (blue)

Figure 15 shows the station-specific residual variabilities $\phi_{0,s}$ at $T = 0.01, 0.1, 1s;$ in top panels at station locations, and in bottom panels as histograms. The histograms suggest that a majority of stations have $\phi_{0,s}$ lower than the updated Résif $\phi_{0}$. As with the events, it is worth analysing ground-motions of individual stations for an explanation. The maps (top panels) show that a few stations in the Pyrenees region (−5^o–2^oE and 42^o–45^oN) show systematically larger $\phi_{0,s}$ (in red) compared to stations elsewhere in France. Site-responses can become extremely complex, especially at the numerous Résif stations located in basins and valley. Results from this study can help in selecting sites with large $\phi_{0,s}$ for site characterisation missions (e.g., Hollender et al. 2021), to identify reference sites with small $\phi_{0,s}$ (e.g., Pilz, Cotton and Kotha 2020, Lanzano et al. 2020, Thompson et al. 2012), and to improve regional site-response maps (e.g., Weatherill et al. 2023a, b, Parker and Baltay 2022).

Fig. 15

Spatial distribution (top) and histogram (bottom) of station-specific residual variability $\phi_{{0,{\varvec{s}}}}$ at ${\varvec{T}} = 0.01, 0.1, 1{\varvec{s}}$ (left-to-right). The map colour scales are centred on $\phi_{0}$ (grey) at respective periods, with stations of $\phi_{{0,{\varvec{s}}}} > \phi_{0}$ coloured in red, and vice-versa for blue. The histograms are overlain with vertical lines at $\phi_{0}$ of ESM (yellow) and of Résif (blue)

5 Discussion

The parametric K20 ground-motion models were developed from the pan-European ESM dataset, quantifying various repeatable physical phenomena as mixed-effects. These models were intended to be evaluated, updated and adapted to new regions as and when new ground-motion datasets become available. Regression of a dataset is essentially a condensation of the knowledge it provides, into an interaction of a few predictable physical parameters. This condensed knowledge can be used as prior information that can be validated and updated with new data as likelihoods. Such an approach to ground-motion prediction is more aptly handled via a Bayesian framework. The aim of this study was to develop an approach and explore the feasibility of updating the pan-European K20 GMM in a Bayesian framework using a dataset of ground-motions recorded in France. In process, the first step was to recast the regression of ESM based K20 GMMs in a Bayesian framework; in order to validate the knowledge gained from regression of ESM against Résif ground-motion data, and update as necessary.

The Bayesian linear mixed-effects regression of ESM dataset yielded a version of K20 that can be used interchangeably with the published version. While the fixed-effects components of the two versions produce identical median ground-motion predictions, the random-effects and residual components (standard-deviations) are not identical. The published random-effects estimates were from a computationally intense robust regression that iteratively down-weight outlier data, but were not replicable with current capabilities of the INLA algorithm—although this may change in the near future. For the time being, the marginal distributions of mixed-effects inferred from ESM dataset were used as priors to update the K20 with Résif ground-motion data. In process, a few major assumptions had to be made.

There are events, stations, and associated ground-motion records common to both datasets. These were few in number, and were retained in the update process. The $M_{W}$ of events in ESM and Résif datasets are sourced from different catalogues, and are based on different selection criteria. It is unreasonable to expect that newer datasets will share the same preferred $M_{W}$ selection criteria as ESM. Therefore, $M_{W}$ reported in Résif dataset were used as they are. Among the planned activities is a unification/homogenisation of $M_{W}$ across datasets, and advance this study into Fourier domain as well.

ESM dataset regression considered only the surface strong-motion sensors, while all Résif stations were used, irrespective of their installation conditions, to enhance the spatial coverage. The resulting site-specific random-effects can be investigated if this selection criteria can be justified. In this study, there is no such detailed analysis because nothing remarkable was noticed. However, the outcomes from this study can be used to develop a more application-ready version of the GMM; with revised decisions on which sites should be retained in, for example, developing a companion empirical site-response model for France.

Multiple trial regressions were made with various restrains on the mixed-effects, allowing them to be updated or not. Ultimately, a rather restrained approach was chosen wherein some of the fixed-effects known to be strongly correlated are locked to their prior values, allowing the others to absorb the possible differences in physical process across the two datasets. The first important outcome, in this approach, is a large correction to the quadratic scaling of ground-motions with $M_{W}$. While the model inferred from ESM suggested a counter-intuitive scaling towards small $M_{W}$, the Résif update rectified it to a more analytically agreeable scaling. With this update, the K20 model becomes slightly more appropriate for small $M_{W}$ ground-motion predictions, e.g., those likely to be critical in PSHA of regions with low-moderate tectonic and induced seismicity.

The second, equally important outcome, are the regional variabilities of at-source and far-source attenuations connected to event and station locations. The far-source attenuation variability is governed by station location, and can be used to adjust the ‘apparent anelastic’ exponential decay of ground-motions with $R_{JB}$ to be specific to a far-source attenuating region hosting the station. The at-source attenuation variability is governed by the event location. In this study, the at-source attenuation is hypothesised as an intrinsic absorption–scattering process that occurs around the events’ hypocentres, and therefore, effects ground-motion predictions at all distances. ESM dataset had barely enough data to quantify these well-known regional variabilities in attenuation within France. Résif dataset can tremendously increase the capability of K20 to make partially non-ergodic region-specific ground-motions in France; and not-to-mention, site-specific predictions are now possible at several dozen new locations all over France.

The maps showing spatial variabilities of far-source and at-source attenuation are interesting but offer little insight on the underlying physical processes. Particularly, the attenuation regionalisation model used to quantify far-source attenuation variabilities are in urgent need of refinement. The model used to quantify at-source attenuation variabilities are at-times consistent with crustal tomography maps available for France. This means that, the hypothesis on at-source attenuation may hold– but further investigation is necessary. These crustal tomography models will come handy in refining the regionalisation models.

Random-effects quantifying event- and site-specific ground-motion variabilities did not offer much insight into how French events and stations are systematically different from the pan-European sample in ESM. This could be partly because these random-effects priors were restrained from updating, and hence being validated with Résif data. These restrains however appear to have forced the ‘left-over’ residuals to accommodate the additional ground-motion variability. This brings to scrutiny the approach of restraining all random-effects variabilities from updating.

Figure 16 shows partial results from three distinct Bayesian update trials: Trial 1 is one where all the random-effects group variances were unrestrained from updating; Trial 2 is where only the far-source and at-source attenuation random-effects were restrained from updating, leaving the rest unrestrained from updating; Trial 3 is the one presented in this study, with all random-effects variances being restrained to their prior ESM inferred values. The impact of these methodical assumptions is evident in the top panels of Fig. 16. Trial 1 suggested that the Résif updated far-source ($\tau_{c3}$) and at-source ($\tau_{L2L}$) attenuation group variabilities coincide with those inferred from ESM, at short periods. At long periods, the updated values become negligibly small and unstable across periods. In turn, the random-effects values for their levels—estimated from their small group variances—were close to zero. Trial 1 outcome was considered unpromising, and needed a remedy—therefore, trial 2.

Fig. 16

Comparison of three trial regressions with selective restraining of ESM inferred prior random-effects group variances from being updated with Résif data. In the top panel, ESM inferred estimates are in dashed lines, overlain with Résif estimates in solid lines. In the two middle rows, $\varvec{\delta B}_{{{\varvec{e}},{\varvec{l}}}}^{0} \left( {{\varvec{T}} = 0{\varvec{s}}} \right)$ versus ${\varvec{M}}_{{\varvec{W}}}$ and $\varvec{\delta S}2{\varvec{S}}_{{\varvec{s}}} \left( {{\varvec{T}} = 0{\varvec{s}}} \right)$ versus ${\varvec{V}}_{{{\varvec{s}}30}}$ plots show ESM estimates in yellow and Résif estimates in blue. The bottom panels show ‘left-over’ residual variabilities estimated for several ${\varvec{M}}_{{\varvec{W}}} - {\varvec{R}}_{{{\varvec{JB}}}}$ bins (${\varvec{\varPhi}}_{{0,{\varvec{M}},{\varvec{R}}}}$), with the colour scale centred at ${\varvec{\varPhi}}_{0} { }\left( {{\mathbf{grey}}} \right){ }$. ${\varvec{T}} = 0{\varvec{s}}$ in these plots implies ${\varvec{PGA}}$

Instead of restraining the priors from updating at specific periods, trial 2 superseded trial 1 by simply restraining far-source ($\tau_{c3}$) and at-source ($\tau_{L2L}$) attenuation group variabilities from being updated at all spectral periods. The resulting outcomes on regional variabilities of far-source and at-source attenuations were similar to those from trial 3 presented in Figs. 9 and 10. This brings to emphasis the very large between-event group variabilities ($\tau_{0}$) estimated in trial 2. The $\delta B_{e,l}^{0} \left( {T = 0s} \right)$ versus $M_{W}$ plots under trial 1 and trial 2 are quite similar; with the scatter at $M_{W} < 4$ being as large as at $4 < M_{W} < 5.5$. The $M_{W}$—dependent heteroskedastic models either of K20 or ESHM20 can be used as is with this update. The large $\delta B_{e,l}^{0} \left( {T = 0s} \right)$ versus $M_{W}$ in trial 1 and 2 may be indicative of the well-known uncertainties and regional variabilities in $M_{W}$ estimation procedures of Résif events. At the time of this study, there was no remedy for this issue. A similar analysis in Fourier domain may offer more insights on trial 2.

The usable Résif ground-motion data with good signal-to-noise ratio falls rapidly at $T > 0.3s$. The sudden changes in the dataset composition may have caused convergence issues, leading to the instabilities in random-effects standard-deviations around $T = 1s$; otherwise, trial 2 would be as acceptable as the preferred trial 3 in this study—if not more. However, it is the $\delta S2S_{s} \left( {T = 0s} \right)$ versus $V_{s30}$ plots from trial 2 that dissuaded from it being preferred over trial 3. This plot shows that the variability in site-response of Résif stations with $V_{s30} > 1800m/s$ to be rather large. At the time of the study, the inexplicably high variability of high-frequency site-response has already been a key issue in ground-motion analyses—and it was not clear if there is supposed to be an upper or lower limit to site-response variability $\Phi_{S2S}$. Bayesian frameworks are quite convenient in setting up prior constrains, which in this case is to use the ESM inferred knowledge of $\Phi_{S2S}$ to be undisputed and thus, not updated. With these assumptions regarding both $\tau_{0}$ and $\Phi_{S2S}$, and other random-effects groups, trial 3 is presented as the preferred approach. However, it is to be noted that if the Bayesian regression algorithm becomes capable of robust regressions, it is worth repeating the analyses presented in this study.

Restraining all the random-effects variances to their ESM inferred priors led to trial 3, which clearly shows the largest ‘left-over’ residual variabilities $\Phi_{0}$ at all spectral periods. The running hypothesis, in this study, is that the additional Résif ground-motion variability is absorbed into residual variability $\Phi_{0}$, suggesting a high record-to-record variability for a few events and stations. The bottom panels of Fig. 16 show $\Phi_{0,M,R}$ across the three trials at $T = 0s$, which is essentially the $M_{W} - R_{JB}$ dependent residual variability of $PGAs$ in Résif dataset. The redistribution of residual ground-motion variability—from trial 1 to 3—appears to have accumulated in $30 < R_{JB} < 100$ km range across the entire $M_{W}$ range. Further investigation showed that the record-to-record variabilities are systematically larger for events located in the complex tectonic environment of the Alps mountain ranges, and for stations located in the Pyrenees mountain ranges. There are a few options to reduce or remodel the residual variability $\Phi_{0}$, in order to mitigate its impact as a component of aleatory variability ($\sigma$) in PSHA. But these options will be explored in a more application-oriented manner; similar to the implementation of K20 GMMs in ESHM20.

This study presents the K20 GMMs in a Bayesian framework, with a more formalised updating procedure. New ground-motion datasets are steadily becoming more available following the demonstration of impact of GMM uncertainties in ESHM20, especially for low-moderate seismicity regions of pan-Europe. These new datasets can serve to extend the non-ergodic application of K20 GMMs to newer regions; but more significantly, in validating and improving existing ground-motion models themselves. It has often been the case that, numerous new GMMs supersede earlier models derived from older, more limited datasets. The newer models also often predict median ground-motions incongruent with their superseded versions, and quite often with larger aleatory variability. Bayesian frameworks may offer a connectivity between various versions of a GMM, and ensure a continuity of knowledge inferred from across various ground-motion datasets. This study concludes with the outlook that: Ground-motion analyses should benefit from advances in Bayesian regressions, by bringing in more data-driven transparency to their development, and in producing application-oriented GMMs for seismic hazard and risk assessments.