1 Introduction

A reinforcement with a yield strength of 500 MPa or greater is defined as high-strength (HS) reinforcement (NEHRP 2014). High-strength steel bars can be used to reduce the reinforcement ratios for concrete structures, reduce the processing and transportation costs of steel bars, and improve the mechanical performance of reinforced concrete members. Meanwhile, high-strength steel bars can solve the problem of steel bar congestion in construction to improve the construction quality. Therefore, the application of high-strength reinforcement in concrete structures is beneficial for energy savings and emission reduction and has good economic, environmental and social benefits. Reinforced concrete columns are the main vertical bearing members of overall structures and are also used to resist horizontal loads generated by earthquakes or wind, so the safety of column members is important for such structures. HS reinforcement can take the form of longitudinal steel bars and stirrups for concrete column members. However, the permissible maximum strength grade for longitudinal reinforcement in the Chinese code is HRB500 with a nominal yield strength of 500 MPa, and HRB600 is expected to be approved in Chinese codes in the next few years. Consequently, more studies should be conducted to promote the application of HRB600 reinforcement in concrete structures.

Many types of high-strength reinforcement have been developed worldwide, including America Grade 550 MPa (80 psi) and 690 MPa (100 psi) (Li et al., 2019), Japan USD 685 MPa (Hwang et al., 2014), Korea SD600 MPa (Ousalem et al. 2009), and China HRB600 MPa. Figure 1 shows the strain‒stress curves for the above types of high-strength reinforcement. High-strength reinforcing bars have a similar elasticity modulus. HRB600, SD600, and USD685 reinforcing bars show yield plateaus and considerable elongation, which are different from that for Grade 550 MPa and 690 MPa reinforcement (America). From a comparison of the strain–stress curves obtained for HRB600 and SD600 with the same nominal yield strength of 600 MPa, the SD600 reinforcement shows a longer yield plateau, larger yield strength, and similar elongation. Therefore, the mechanical properties of HRB600 reinforcement are different from that of other types of high-strength reinforcement. On the other hand, the key performance specifications of HRB600, such as yield strength, yield plateau, and ultimate strain, can meet the engineering requirements of other countries, so such reinforcement can be used for civil engineering in other countries. HRB600 is a new type of high-strength reinforcing bar developed in China, but the current design specifications do not cover such steel bars, mainly due to the lack of relevant experimental and theoretical research.

Fig. 1
figure 1

Stress‒strain curves for high-strength reinforcing bars

Full size image

HS steel bars can be used as longitudinal bars and stirrups for concrete members, and the application of HS steel bars in columns has been experimentally investigated in depth. Restrepo et al. (2006), Matsumoto et al. (2008), Ousalem et al. (2009), Rautenberg et al. (2011), Su et al. (2014a, b), Legage et al. (2012), Link et al. (2014), Ou et al. (2015), Sokoli et al. (2014), Ibarra et al. (2016), Trejo et al. (2016), Lim et al. (2017), Aboukifa et al. (2021), Ding et al. (2021), He et al. (2020), and Zhang et al. (2020) have conducted cyclic loading tests on column specimens with high-strength longitudinal bars. The test results show that compared with normal strength bar reinforced concrete columns, HS longitudinal bar reinforced concrete columns show similar ductility and reduced energy dissipation capacity, which indicates that HS longitudinal reinforcement can solve the problem of reinforcement congestion and save reinforcement ratios without affecting the seismic performance of the columns. The test results also found that the bond-slip failure phenomenon occurs between HS longitudinal steel bars and normal strength concrete, while the bond-slip failure phenomenon does not occur between HS longitudinal steel bars and ultra high-performance fiber concrete. Thomsen et al. (1994), Xiao-Martirossyan et al. (1998), Paultre et al. (2001), Shi et al. (2011), and Hwang et al. (2005) have experimentally investigated the influence of HS stirrups on the seismic performance of columns. The test results indicate that HS stirrups can develop a strong confinement on the concrete columns under high axial compression. HS stirrups can save reinforcement ratios without reducing the seismic performance of the columns and can help the columns obtain satisfactory ductility. HS stirrups have little effect on the strength of the columns under small axial loading ratios, while they can significantly increase the strength of the columns with high axial compression ratios. The above studies also find that HS stirrups can be used to significantly improve the postpeak deformation and ductility of columns. For the failure of column specimens in shear, high-strength stirrups cannot significantly improve the shear strength of column specimens, and HS stirrups generally stay in an elastic state, but the deformation and energy dissipation capacity of the column specimens can be increased with such reinforcement.

The above experimental studies have demonstrated that the application of high-strength steel bars in concrete columns has high feasibility and can be used to effectively reduce the reinforcement ratios in concrete columns. Then solve the problem of reinforcement congestion. To promote the application of HS steel bars in concrete columns, more theoretical research is needed, but related studies are limited at present (Ni et al. 2019). The flexure strength of normal strength bar reinforced concrete columns can be accurately predicted using the theory of the Bernoulli–Euler assumption, but for high-strength steel bars, the stress‒strain characteristics are quite different from those of normal strength steel bars, especially large yield strain, so it is necessary to study the applicability of the Bernoulli–Euler assumption to high-strength bar reinforced concrete columns. The nonlinear deformation of columns under cyclic loading is commonly calculated by plastic hinge theory (Thomsen et al. 2004), and the adaptability of this theory to high-strength reinforced concrete columns needs to be investigated. The above experimental studies have found that bond-slip failure can occur between a HS longitudinal bar and concrete and can lead to an increase in the lateral deformation of the column, so the deformation caused by bond-slip cannot be ignored. Bond-slip deformation is, currently, a difficult research point. Many studies have been conducted on the hysteretic models of concrete columns built with normal strength reinforcement, but due to the application of high-strength steel bars in columns, the hysteretic characteristics of such columns are quite different from those of normal strength bar reinforced concrete columns, especially in terms of unloading stiffness and pinch effect. In conclusion, the deficiencies of the present study can be summarized as follows:

  1. (1)

    The mechanical property of HRB600 reinforcement newly developed in China show some differences in material properties compared with existing high-strength steel bars, while previous research into HS steel bars in concrete structures has mainly focused on a yield strength of 500 MPa and below or 900 MPa and above, and the experimental research into the application of HRB600 reinforcement in columns remains limited.

  2. (2)

    The hysteretic behavior of HS bar reinforced concrete columns has been experimentally investigated in depth, but few theoretical studies have been conducted. A hysteretic model can be used to predict the hysteretic response of the columns under cyclic loading, which can also be used for the nonlinear analysis of the column members in the whole structure. The hysteretic performance of concrete columns built with HS reinforcement is different than that of columns with normal strength reinforcement. However, studies based on hysteretic models of concrete columns built with HS reinforcement are scarce.

  3. (3)

    Owing to the application of HS reinforcement in concrete columns, the applicability of the Bernoulli–Euler assumption and plastic hinge theory for such columns needs to be investigated. The bond-slip between HS longitudinal bars and concrete is complex, and the deformation caused by bond-slip should be considered and mathematized. However, few related studies have been conducted.

To address the above research gaps, a cyclic loading test is first carried out for column specimens built with HRB600 reinforcement to examine the influence of stirrup spacing and axial compression ratio on the hysteretic performance. Then, a simplified calculation method for hysteretic curves is proposed by combining the skeleton curve and hysteretic rule. Finally, the proposed model is used to predict the hysteretic curves for the column specimens, and the prediction accuracy is evaluated based on the test data.

2 Test program

2.1 Column specimens

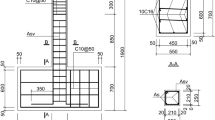
Figure 2 depicts the geometric dimensions and reinforcing arrangement of the specimens. To research the effect of stirrup spacing and axial compression ratio on hysteretic behavior, four RC cantilever column specimens were tested under cyclic loading. The specimens' precise design specifications can be obtained in a prior study (Li et al. 2018). The longitudinal bars of the column specimens adopted HRB600 reinforcement with a diameter of 16 mm (fy = 615 MPa) and HRB400 reinforcement with a diameter of 16 mm (fy = 471 MPa). Every specimen was given a unique name that could be used to identify the study parameters. The nomenclature is described as follows: the first two numerals denote longitudinal and stirrup reinforcing types, respectively, H signifies HRB600 reinforcement, and N signifies HRB400 reinforcement. The second numeral denotes the axial compression ratios for the specimens: 0.2, 0.4, and 0.5, and the axial compression ratios can be obtained by Eq. (1). The concrete utilized for the sample had a C50 strength rating (the measured value is 47.4 MPa). The column's longitudinal bars comprised 12 steel bars with a diameter of 16 mm, with a longitudinal bar ratio of 1.97 percent. The stirrup was constructed of an HRB400/600 steel bar with a diameter of 8 mm and yield strengths of 437 MPa and 629 MPa, respectively, and a well-shaped compound stirrup form. Stirrup spacings of 70 mm and 105 mm stirrup spacing were available, with volume stirrup ratios of 1.91% and 1.28%, respectively. Table 1 lists the details for the above six specimens.

$$n = \frac{N}{{f_{c} A}}$$
(1)

where N is the axial load applied on the wall, fc is the strength of the concrete on the test day, and A is the wall cross-sectional area.

Fig. 2
figure 2

Dimensions and reinforcement

Full size image
Table 1 Design parameters
Full size table

2.2 Hysteretic response

The hysteresis responses of the specimen are generally in the shape of a plump shuttle, indicating that the specimen has good seismic performance (Fig. 3). During the initial stage, the hysteresis loop areas are very small. With increasing loading displacement, the surrounding area of the hysteretic loops continuously increases, and an obvious residual deformation occurs after unloading; when the specimen reaches the peak force, the deformation accelerates. Under the same displacement, the peak load and the slope of the curve decrease with increasing cycle number, which indicates that the specimen shows strength attenuation and stiffness attenuation under cyclic loading. Due to failure of the bond between the HRB600 reinforcement and concrete, the plumpness of the hysteresis curves becomes significantly worse, and the curve develops into an inverse S-shape in the later stage, indicating that the configuration of the HRB600 longitudinal reinforcement can reduce the hysteretic performance of the specimen in the later stage.

Fig. 3
figure 3

Hysteretic curves

Full size image

Table 2 summarizes the detailed experimental results obtained for the hysteretic curves of the above column specimens. Compared to Specimen NN-0.2–1 built with HRB400, the specimens built with HRB600 longitudinal reinforcement have a larger yield displacement owing to the larger yield strain of HRB600 reinforcement. Compared to Specimen NN-0.2–1 with a HRB400 stirrup, Specimen NH-0.2–1 with a HRB600 stirrup (stirrup strength is increased by 43.9%) shows a larger lateral strength (↑ 15%) and drift ratio capacity (↑ 12%) but smaller ductility ratio (↓8.28%). Compared to Specimen NH-0.2–2 with a HRB400 stirrup, Specimen HH-0.2–4 built using a HRB600 stirrup has a larger peak strength (↑ 29.3%) and a similar drift ratio capacity but a reduced ductility ratio (↓29.6%).

Table 2 Detailed experimental results obtained for the hysteretic curves
Full size table

3 Simplified calculation method

3.1 Hysteretic model

The hysteretic model for HS bar reinforced columns is composed of a skeleton curve and hysteretic rule.

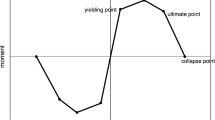
3.1.1 By analyzing the above hysteretic curves, the force process for the above column specimens can be roughly divided into three stages, including the elastic stage, elastic‒plastic stage from yielding to the peak point, and failure stage from Skeleton curve

the peak point to failure, as shown in Fig. 4. Therefore, the skeleton curve is simplified into a trilinear model that can be determined using three characteristic points, namely, Y, M and U, corresponding to the yield, peak and failure points, respectively. Therefore, six parameters need to be determined to establish the skeleton curve model, which are the preyield stiffness k1, yield load Py and displacement Δy; stiffness k2, peak load Pm and displacement Δm; stiffness k3, ultimate load Pu and displacement Δu. The skeleton curve can be expressed as Eq. (2).

$$P = \left\{ \begin{array}{ll} \frac{{P_{y} }}{{\Delta_{y} }} \cdot \Delta &\quad 0 \le \Delta < \Delta_{y} \hfill \\ \frac{{P_{m} - P_{y} }}{{\Delta_{m} - \Delta_{y} }} \cdot (\Delta - \Delta_{y} ) + P_{y} &\quad \Delta_{y} \le \Delta < \Delta_{m} \hfill \\ \frac{{P_{u} - P_{m} }}{{\Delta_{u} - \Delta_{m} }} \cdot (\Delta - \Delta_{m} ) + P_{m} &\quad \Delta_{m} \le \Delta < \Delta_{u} \\ \end{array}\right.$$
(2)
Fig. 4
figure 4

Trilinear model for the skeleton curve

Full size image

3.1.2 Hysteretic rule

With increasing loading displacement (especially after yield displacement), both the loading and unloading stiffnesses of the columns degrade. The line between the unloading point and point where the force is unloaded to 0 is the unloading line, and the slope represents the unloading stiffness ku. ku changes with increasing loading displacement, and the axial ratios have a significant influence on the unloading stiffness attenuation. Li et al. (2014) reported that the unloading stiffness of an HS concrete column confined by an HS stirrup is related to the volume ratio of the stirrups and axial loading ratios, and they obtained the formula for unloading stiffness by regression. Guo et al. (2004) studied the variation law for unloading stiffness of concrete columns under different axial compression ratios and considered that the axial loading ratio is a critical parameter that can influence unloading stiffness. Meanwhile, a regression formula for unloading stiffness is proposed. Figure 5 presents the variation in unloading stiffness attenuation rates (ku/k1) with ductility ratios for the above column specimens. The unloading stiffness formula can be obtained from regression analysis and is expressed as Eq. (3):

$$k_{u} = 1.061k_{1} \left( {\frac{{\Delta_{i} }}{{\Delta_{y} }}} \right)^{ - 0.733n - 0.361}$$
(3)

where k1 is the equivalent elastic stiffness, k1 = Py/Δy; Δi is the maximum displacement experienced by the specimen before unloading; and n is the axial compression ratio.

Fig. 5
figure 5

Unloading stiffness of the columns

Full size image

Based on the above experimental hysteretic curves, the hysteretic rule for the hysteretic model of concrete columns can be summarized as shown in Fig. 6, and its hysteresis rules are described as follows:

  1. (1)

    Points A and A′ are yield points, B and B′ are peak points, and C and C′ are failure points.

  2. (2)

    The load‒displacement curve moves along Path O-A from the beginning to the yield point, and the loading stiffness is k1 (the equivalent elastic stiffness before yielding). If an unloading curve is performed by following Path O-A, the unloading path returns along the original loading path. When unloading to the origin, reverse loading is carried out along Path O-A′.

  3. (3)

    After yielding, the loading stiffness changes to k2, and the loading path goes along Path A-B. At this point, if the unloading is carried out in Section A-B, the unloading path is carried out along Line 1–2, and the unloading stiffness ku can be calculated according to Eq. (3). After unloading to Point 2, if the specimen fails to yield in the reverse direction, the path points to the reverse yield Point A', that is, reverse loading is carried out along Path 2-A′-B′; if the specimen has yielded in the reverse direction, the maximum point pointing principle is adopted to point to the maximum displacement (Point 3) experienced in the previous loading, that is, reverse loading is carried out along Path 2–3-B′. When reverse unloading is carried out in Section A'-B', unloading is carried out along Path 3–4, and the unloading stiffness ku can be calculated according to Eq. (3). For the case of reverse unloading to 0 followed by forward loading, the loading path points to the maximum displacement (Point 1) experienced at the previous loading, that is, along Path 4–1-B.

  4. (4)

    After the specimen reaches peak point B (B′), the loading stiffness changes to k3, and the loading path proceeds along Path B-C. At this point, if the unloading is carried out in Section B-C, the unloading path is carried out along Path 5–6, and the unloading stiffness ku is calculated according to Eq. (3). If the reverse load does not reach the peak load point (point B′), the path points to the reverse peak point B′, that is, along Path 6-B′-C′. If the reverse load reaches the peak load, the loading path points to the maximum displacement (Point 7) in the previous loading, that is, to proceed along Path 6–7-C ′. For the case of reverse unloading in Section B'-C', unloading is carried out along Paths 7–8, and the unloading stiffness is calculated according to Eq. (3). For reverse unloading to 0 (Point 8) and forward loading, the loading path follows Path 8–5. Other loading and unloading paths are the same as that for the preceding rules.

Fig. 6
figure 6

Hysteresis rules

Full size image

3.2 Lateral deformation

The lateral displacement is composed of three parts: flexure deformation (Δf), shear deformation (Δv) and deformation (Δs) caused by the bond-slip, as shown in Fig. 7. Before yielding, the curvature formed by the bending moment and the shear deformation is linearly distributed along the column height. After yielding, a plastic hinge forms at the column bottom. The curvature formed by the bending moment in the plastic hinge region is obviously larger than that of the elastic segment. The shear displacement of the column is composed of shear deformation in the plastic hinge zone and elastic zone. The deformation caused by the bond-slip is generally small before the specimen yields. After the specimen yields, bond slip causes the column to rotate around the bottom of the column. Therefore, the lateral displacement can be expressed as follows (Wang et al. 2019a):

$$\Delta = \Delta_{f} + \Delta_{v} + \Delta_{s}$$
(4)
Fig. 7
figure 7

Lateral deformation

Full size image

3.3 Yield point

3.3.1 Yield force

For the flexural-dominated member, it is generally assumed that the yield load (Py) and displacement (Δy) are the load and displacement when the outermost longitudinal bars yield in the tensile direction. The stress‒strain formula for compressive concrete is expressed as follows (GB 50,010–2010 2011):

$$\sigma = \left\{ {\begin{array}{*{20}c} {f_{c} \left( {1 - \left( {1 - \frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{{2}} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon \le \varepsilon_{0} } \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f_{c} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon_{0} < \varepsilon \le \varepsilon_{cu} } \\ \end{array} } \right.$$
(5)

where fc is the axial compressive strength of concrete; ε0 is the peak strain, generally, ε0 is taken to be equal to 0.002; and εcu is the ultimate compressive strain, generally, εcu is taken to be equal to 0.0033 (GB 50,010–2010 2011).

According to the assumption of a flat section, the force state of the critical cross-section at the point of yielding is shown in Fig. 8. According to the balance condition of the force, the following formulas can be obtained:

$$\sum {\sigma_{si} } A_{si} + N = \int_{0}^{{x_{c} }} {\sigma_{x} } bdx$$
(6)
$$M_{y} + \sum {\sigma_{si} } A_{si} x_{i} + N\left( {h_{0} - \frac{h}{2}} \right) = \int_{0}^{{x_{c} }} {\sigma_{x} } \left( {h_{0} - x_{c} + x} \right)bdx$$
(7)
Fig. 8
figure 8

Force state of the critical cross-section at the yield point of the columns

Full size image

With

$$\sigma_{si} = E_{s} \varepsilon_{si} = E_{s} \left( {h_{0} - x_{c} - x_{i} } \right)\frac{{\varepsilon_{y} }}{{h_{0} - x_{c} }} \le f_{y}$$
(8)
$$\varepsilon_{x} = x\frac{{\varepsilon_{y} }}{{h_{0} - x_{c} }}$$
(9)

where b is the width of the cross-section and h and h0 are the height and effective height of the cross-section, respectively, where Es is the elastic modulus of the longitudinal reinforcement, N is the axial load, My is the yield bending moment of the critical cross-section when the specimen yields, xc is the height of the concrete compression zone, fy is the tensile yield strength of the longitudinal reinforcement, and εy is the tensile yield strain of the outermost longitudinal reinforcement. σsi and εsi are the stress and strain for the ith longitudinal reinforcing bar (positive in tension and negative in compression), respectively. xi is the distance from the ith longitudinal reinforcing bar to the outermost tensile longitudinal reinforcing bar; x is the distance for any position along the neutral axis; and σx and εx are the compressive stress and strain of compressive concrete, respectively, at the distance of x to the neutral axis of the cross-section.

3.3.2 Yield displacement

The yield curvature of the critical section is \(\phi_{y}\), and the curvatures generated by the bending moment are linearly distributed along the column height (Fig. 9(a)).

Fig. 9
figure 9

Curvature distribution

Full size image
  1. (1)

    Flexure displacement Δyf.

    Based on Bernoulli's assumption, the displacement caused by bending deformation can be obtained from

    $$\Delta_{yf} = \frac{{Vl^{3} }}{{3E_{c} I}} = \frac{1}{3}\phi_{y} l^{2}$$
    (10)

    With

    $$\phi_{y} = \frac{{\varepsilon_{y} }}{{h_{0} - x_{c} }}$$
    (11)

    where V is the lateral force, I is the inertia moment of the cross-section, and Ec is the elastic modulus of concrete.

  2. (2)

    Shear displacement Δyv.

    The shear displacement can be obtained from

    $$\Delta_{yv} = \mu \frac{Vl}{{G_{c} A}}$$
    (12)

    where Gc is the shear modulus of concrete, Ec/Gc = 2.5; A is the total area of the cross-section; and μ is the nonuniform coefficient of the shear stress distribution of the rectangular section, which is equal to 1.2.

  3. (3)

    Lateral displacement caused by bond-slip Δys.

    Sezen-Setzler (2008) proposed a formula for calculating the bond slip based on experimental and theoretical analysis:

    $$\Delta_{ys} = \theta_{s} l = \frac{{\varepsilon_{y} f_{y} d_{b} l}}{{8\mu_{e} \left( {h_{0} - x_{c} } \right)}}$$
    (13)

    where θs is the rotation angle of the rigid body generated by bond-slip, db is the diameter of the longitudinal reinforcing bars, μe is the uniform elastic bond stress, and the other parameters have the same meanings as above.

3.4 Peak point

3.4.1 Peak force

The peak point of the columns corresponds to the ultimate state of the bearing capacity, which is controlled by the maximum normal stress of the critical cross-section, and when the concrete at the compression edge reaches the ultimate compressive strain, the columns enter the peak point. The stress and strain distribution of the critical cross-section at the peak point is shown in Fig. 10, where the concrete at the compression edge reaches the ultimate compressive strain. From the force balance condition for the cross-section, it can be determined that

$$N = \alpha_{1} f_{c} bx - \sum {\sigma_{si} } A_{si}$$
(14)
$$M_{{\text{u}}} = \alpha_{1} f_{c} bx\left( {h_{0} - \frac{x}{2}} \right) - \sum {\sigma_{si} } A_{si} x_{i} - N\left( {h_{0} - \frac{h}{2}} \right)$$
(15)
Fig. 10
figure 10

Force state of the critical cross-section of the peak point

Full size image

where

$$\sigma_{si} = E_{s} \varepsilon_{si} = E_{s} \left( {h_{0} - x_{c} - x_{i} } \right)\frac{{\varepsilon_{cu} }}{{x_{c} }} \le f_{y}$$
(16)
$$x_{c} = \frac{x}{{\beta_{1} }}$$
(17)

where α1 and β1 are the characteristic coefficients of the equivalent rectangular stress graph for the concrete stress distribution of the cross-section, which are adopted according to GB50010-2010 (2011), α1 = 1.0, and β1 = 0.8. Mu is the maximum bending moment; x is the height of the equivalent rectangular stress diagram in the concrete compression zone; and σsi and εsi are the stress and strain of the ith longitudinal reinforcement (positive in tension and negative in pressure), respectively. xi is the distance from the ith longitudinal reinforcement to the outermost tensile longitudinal reinforcement.

3.4.2 Peak displacement

At the peak point, the concrete strain at the edge of the compressive zone of the critical cross-section reaches the ultimate strain εcu, and, at this time, the curvature is the ultimate curvature ϕu, and a plastic hinge is formed with a height of lp. The area outside of the plastic hinge area is still in the elastic stage. The curvature distribution for the specimen is shown in Fig. 11. The lateral displacement of the specimen is composed of the displacement generated by the upper elastic segment and that of the plastic hinge region. The displacements of the upper elastic segment and plastic hinge region are all composed of flexure, shear, and bond-slip displacements (Wang et al. 2019a), as expressed by Eq. (18):

$$\Delta_{{\text{m}}} = \Delta_{{{\text{mf}}}} + \Delta_{{{\text{mv}}}} + \Delta_{{{\text{ms}}}}$$
(18)

where Δmf, Δmv, and Δms are the peak flexure, shear and bond-slip deformation, respectively.

Fig. 11
figure 11

Shear displacement

Full size image
  1. (1)

    Flexure displacement Δmf.

    The flexure displacement is composed of the displacement Δmf1 of the upper elastic segment and Δmf2 of the plastic hinge region, i.e., Δmf = Δmf1 + Δmf2. The displacement Δmf1 can be calculated using Eqs. (10–11). The column height l in the formula should be replaced by the height le of the upper elastic segment. The height lp of the plastic hinge region can be calculated according to Eq. (19):

    $$l_{p} = 0.08l + 0.022f_{y} d_{b}$$
    (19)
    $$l_{e} = l - l_{p}$$
    (20)

    The displacement Δmf2 can be obtained from

    $$\Delta_{mf2} = \int_{{l_{e} }}^{{l_{e} + l_{p} }} {x\phi \left( x \right)} dx$$
    (21)
    $$\phi \left( x \right) = \frac{\phi \left( u \right) - \phi \left( y \right)}{{l_{p} }}\left( {x - l_{p} } \right) + \phi \left( y \right)$$
    (22)

    Combining Eqs. (21) and (22), the displacement Δmf2 can be obtained as follows:

    $$\Delta_{mf2} = \frac{1}{2}l_{e} l_{p} \phi_{y} + \frac{1}{2}l_{e} l_{p} \phi_{u} + \frac{1}{6}l_{p}^{2} \phi_{y} + \frac{1}{3}l_{p}^{2} \phi_{u}$$
    (23)

    With

    $$\phi_{u} = \frac{{\varepsilon_{cu} }}{{x_{c} }}$$
    (24)
  2. (2)

    Shear displacement Δmv.

    As shown in Fig. 12, the shear deformation is composed of Δmv1 for the upper elastic section and Δmv2 for the plastic hinge region, i.e., Δmv = Δmv1 + Δmv2. The displacement Δmv1 can be calculated using Eq. (12), and the column height l given in the equation is replaced by the upper elastic section height le. The shear force V is replaced by the peak load. The shear displacement Δmv2 can be calculated according to the shear strain ductility coefficient μγ proposed by Gerin-Adebar (2004). The empirical formula for μγ can be obtained from

    $$\mu_{\gamma } = \frac{{\gamma_{u} }}{{\gamma_{y} }} = 4 - 12\frac{{v_{y} }}{{f_{c} }}$$
    (25)
    Fig. 12
    figure 12

    Bond strain and stress distribution for longitudinal bars

    Full size image

    It is assumed that the shear strain in the plastic hinge region is a trapezoidal distribution, in which the shear strain in the upper part of the plastic hinge region is the yield shear strain, and the shear strain at the bottom of the plastic hinge region reaches the limit shear strain. Therefore, the shear displacement Δmv2 can be expressed as follows:

    $$\Delta_{mv2} = \frac{1}{2}\left( {\gamma_{y} + \gamma_{u} } \right)l_{p} = \frac{1}{2}\left( {\gamma_{y} + \mu_{\gamma } \gamma_{y} } \right)l_{p} = \frac{1}{2}\left( {5 - 12\frac{{v_{y} }}{{f_{c} }}} \right)\gamma_{y} l_{p}$$
    (26)

    where

    $$v_{y} = 0.25\sqrt {f_{c} } + \rho_{h} f_{yh} \le 0.25f_{c}$$
    (27)
    $$\gamma_{y} = \frac{{f_{yh} }}{{E_{s} }} + \frac{{v_{y} - n}}{{\rho_{v} E_{s} }} + \frac{{4v_{y} }}{{E_{c} }},0 \le \frac{{v_{y} - n}}{{\rho_{v} E_{s} }} \le \frac{{f_{yh} }}{{E_{s} }}$$
    (28)

    where μγ is the shear strain ductility coefficient; γy is the yield shear strain; γu is the ultimate shear strain; vy is the yield shear stress; ρh is the ratio of stirrup reinforcement; ρv is the longitudinal reinforcement ratio; and fyv is the stirrup yield strength.

  3. (3)

    Lateral displacement caused by bond-slip Δms.

    As shown in Fig. 12, the bond-slip between the longitudinal bars and concrete consists of the slip displacement generated in the upper elastic segment and the plastic hinge region. The rotation angle (θs1) of the rigid body due to bond-slip in the upper elastic segment can also be calculated by using the model proposed by Sezen-Setzler (2008). The rigid body rotation angle (θs2) due to the slip of longitudinal bars in the plastic hinge region is mainly related to the plastic hinge length and the strain in longitudinal bars. The bond strain and stress distribution for the longitudinal bars in the slip region are shown in Fig. 12. Δms can be obtained from

    $$\Delta_{ms} = \left( {\theta_{s1} + \theta_{s2} } \right)l$$
    (29)

    where

    $$\theta_{s1} = \frac{{\varepsilon_{y} f_{y} d_{b} }}{{8\mu_{e} \left( {h_{0} - x_{c} } \right)}}$$
    (30)
    $$\theta_{s2} = \frac{{l_{p} \left( {\varepsilon_{y} + \varepsilon_{s} } \right)}}{{2\left( {h_{0} - x_{c} } \right)}}$$
    (31)

3.5 Ultimate point

3.5.1 Ultimate force

The failure force is taken as 0.85 times the previous peak load (JGJ3-20102010): \(P_{u} = 0.85P_{m}\) (32).

3.5.2 Ultimate displacement

When the failure is closed, the concrete in the plastic hinge area is seriously damaged, buckling of the longitudinal bars occurs, and the concrete out of the core area is crushed. The cross-section curvature distribution of the specimen at this point is shown in Fig. 12. The height of the plastic hinge area at the bottom of the specimen is still lp, the outside plastic hinge area is still in the elastic stage, and the cross-section curvature of the plastic hinge area reaches the ultimate curvature. The lateral displacement of the specimen is mainly divided into the displacements generated by the upper elastic segment and the plastic hinge region. Among them, the displacements are all composed of the displacements generated by flexure, shear and reinforcing bar slip, as shown in Eq. (33).

$$\Delta_{{\text{u}}} = \Delta_{{{\text{uf}}}} + \Delta_{{{\text{uv}}}} + \Delta_{{{\text{us}}}}$$
(33)

where Δuf, Δuv and Δus are the flexure, shear and bond slip displacements at the ultimate point, respectively.

  1. (1)

    Flexure displacement Δuf.

    The flexure displacement is composed of the displacement Δuf1 of the upper elastic segment and the displacement Δuf2 of the plastic hinge region. Δuf = Δuf1 + Δuf2. The displacement Δuf1 can be calculated by Eqs. (10–11). The displacement Δuf2 can be obtained from

    $$\Delta_{{{\text{u}}f2}} = \int_{{l_{e} }}^{{l_{e} + l_{p} }} {\phi \left( u \right)} xdx = \frac{1}{2}\phi \left( u \right)l_{p}^{2} + \phi \left( u \right)l_{e} l_{p}$$
    (34)
  2. (2)

    Shear displacement Δuv.

    The ultimate displacement caused by shear is composed of displacement Δuv1 of the upper elastic section and displacement Δuv2 of the plastic hinge region: Δmv = Δuv1 + Δuv2. The displacement Δuv1 can be calculated from Eq. (12), and the column height l in the equation is replaced by the upper elastic section height le. The shear force V is replaced by the ultimate load. Δmv2 can be obtained from the shear strain ductility coefficient μγ proposed by Gerin-Adebar (2004). The displacement Δuv2 can be expressed as follows:

    $$\Delta_{uv2} = \gamma_{u} l_{p} = \mu_{\gamma } \gamma_{y} l_{p} = \left( {4 - 12\frac{{v_{y} }}{{f_{c} }}} \right)\gamma_{y} l_{p}$$
    (35)
  3. (3)

    Lateral displacement caused by bond-slip Δus.

    The rotation angle (θs1) of the rigid body due to bond-slip in the upper elastic segment can also be calculated by the method proposed by Sezen-Setzler (2008). The displacement due to bond slip can be obtained from

    $$\Delta_{{{\text{us}}}} = \left( {\theta_{s1} + \theta_{s2} } \right)l$$
    (36)

    where

    $$\theta_{s2} = \frac{{l_{p} \left( {\varepsilon_{y} + \varepsilon_{s} } \right)}}{{2\left( {h_{0} - x_{c} } \right)}}$$
    (37)

    where εs is the strain when the tensile longitudinal reinforcement reaches the ultimate tensile strength. According to previous low-cycle reciprocating fatigue performance tests for high-strength reinforcement (Li et al. 2005), εs is taken to be equal to 0.035.

4 Discussion

4.1 Prediction of the characteristic points

Table 3 summarizes a comparison of the analytical and experimental values obtained for the yield force for the above four column specimens. The mean value for the analytical to experimental yield force ratio is 1.0, and the coefficient of variation is 0.06, so it can be seen that the proposed model can well predict the yield force for concrete columns built with HRB600 steel bars.

Table 3 Analytical and experimental values for the yield force
Full size table

Table 4 lists the analytical and experimental values for the yield displacements of the above column specimens. The mean value for the analytical to experimental yield displacement ratio is 1.03, and the coefficient of variation is 0.11, so it can be seen that the proposed method has reasonable accuracy. The yield displacement is mainly caused by the bending moment, and the shear displacement is very small and can be ignored.

Table 4 Analytical and experimental values for the yield displacement
Full size table

Table 5 lists the analytical and experimental values for the peak load of the above four column specimens. The height values for the equivalent rectangular stress diagrams of specimens HH-0.2–3, HH-0.2–4 and HH-0.4–5 are 90.7 mm, 90.7 mm and 121.1 mm, respectively, which are all less than ξbh0. For specimen HH-0.5–6, due to the larger axial load, x = 135.2 mm, which is greater than ξbh0 = 130.1 mm, the specimen suffers a small eccentric compression failure, which is consistent with the test results. Mu can be calculated according to Eq. (15), and then the peak load Pm can be obtained from Pm = Mu/(l-υh). υ is the influence of the upward movement of the plastic hinge position due to the restriction of the foundation beam on the column bottom. υ is considered to range between 0.2 and 0.5, and a value of υ = 0.3 is adopted in this paper. The mean value for the analytical to experimental peak force ratio is 0.88, and the coefficient of variation is 0.08, so it can be seen that the proposed method can well predict the peak force for the columns.

Table 5 Comparison of the analytical and experimental values obtained for the peak force
Full size table

The displacements (Δmf, Δmv, Δms) at the peak point can be obtained from the above equations. Table 6 lists the analytical and experimental values for the peak displacements of the above column specimens. The mean value for the analytical to experimental peak displacement ratio is 0.99, and the coefficient of variation is 0.06, so it can be seen that the proposed method has a reasonable prediction accuracy.

Table 6 Analytical and experimental values for the peak displacement
Full size table

Table 7 lists the analytical and experimental values for the ultimate displacement, and the proportion of the displacement caused by the bond-slip is the largest. The mean value for the analytical to experimental ultimate displacement ratio is 0.92, and the coefficient of variation is 0.17. Due to the large axial compression ratio of HH-0.5–6, the P-Δ effect is obvious, which leads to a reduction in the deformation capacity and a small ultimate displacement in the specimens.

Table 7 The analytical and experimental values for ultimate displacement
Full size table

4.2 Predicted hysteretic curves

The above simplified method and finite element modeling are used to model the mechanical behavior of HRB600 bar reinforced concrete column specimens under cyclic loading, and the obtained analytical results are compared with the test results. OpenSees was used to model the hysteretic behavior of HRB600 bar reinforced concrete columns. To accurately simulate the hysteretic performance of the columns built with HRB600 reinforcement, the fibers of the cross-section are divided into reinforcement bars and concrete fibers depending on the material types, as shown in Fig. 13. According to the different confinement conditions of concrete at the cross-section, concrete fibers can be divided into two areas: concrete fibers in the cover area and confinement concrete fibers in the core area. Figure 14 presents a comparison of the analytical, simulated, and experimental hysteretic curves obtained for the HRB600 longitudinal bar reinforced concrete column specimen. To evaluate the accuracy of the predicted hysteretic curves, the analytical skeleton curves and energy dissipation were compared with the simulated and experimental curves. Figure 15 presents a comparison of the skeleton curves obtained using the analytical, simulated, and experimental hysteretic curves shown in Fig. 14. The error range for the predicted to experimental strength is 4% ~ 26%, and the error range for the predicted to experimental deformation capacity is 0 ~ 19%. Therefore, the proposed model can be used to well predict the strength and deformation of HRB600 longitudinal bar reinforced concrete columns. The energy dissipation capacity is an important index for the seismic performance of RC members. (Fig. 15) The energy dissipated by the members is indicated by the area surrounded by the hysteresis loops. Figure 16 shows a comparison of the variation in the experimental, simulated and analytical dissipated energy with increasing lateral displacement. The maximum error in the predicted to experimental dissipated energy is 20%, with both values showing a reasonable agreement.

Fig. 13
figure 13

Fiber element arrangement of the finite model (OpenSees)

Full size image
Fig. 14
figure 14

Comparison of the hysteresis curves

Full size image
Fig. 15
figure 15

Comparison for the skeleton curves

Full size image
Fig. 16
figure 16

Comparison for the energy dissipation

Full size image

In conclusion, the analytical and simulated hysteresis curves are in reasonable agreement with the experimental hysteretic curves in terms of energy dissipation, strength, and deformation capacity, indicating that the proposed hysteretic model can be used to well predict the hysteresis performance of HS bar reinforced concrete columns under cyclic loading. It also shows that the proposed model can achieve a prediction accuracy similar to that of the finite element software OpenSees.

5 Conclusions

In this paper, cyclic tests were conducted to examine the effect of the reinforcement strength, axial load ratio and stirrup spacing on the seismic performance of concrete columns built with HRB600 reinforcement. A hysteretic model for HS bar reinforced columns is proposed, and its prediction accuracy is evaluated based on the test data. The following conclusions can be drawn:

  1. (1)

    The skeleton curve and hysteretic rule can be combined to establish a calculation model for concrete columns built with HS and normal strength reinforcement. The skeleton curve is simplified as a trilinear model represented by yield, peak and ultimate points. By deriving the formulas for yield, peak and ultimate force and displacement, a method can be obtained for determining the skeleton curve. A hysteretic rule is established based on the experimental hysteretic curves shown in this paper.

  2. (2)

    The equations for the flexure strength are derived based on the theory of the Bernoulli–Euler assumption. The lateral deformation is assumed to be composed of flexure, shear, and bond-slip deformations. The equations for the flexure deformation are derived based on plastic hinge theory, the equations for shear deformation are derived based on elastic mechanics, and bond-slip deformations are calculated according to the actual contact stress between HS longitudinal bars and concrete. These studies demonstrate that the proposed equations have reasonable accuracy.

  3. (3)

    The proposed model is used to calculate the hysteretic curves for HS and normal-strength bar reinforced concrete columns, which are compared with the experimental curves. The research results show that the analytical hysteresis curves are in good agreement with the experimental hysteretic curves in terms of strength, deformation and energy dissipation.