Effects of various modeling uncertainty parameters on the seismic response and seismic fragility estimates of the aging highway bridges

Abstract

This paper proposes an alternative time-dependent seismic fragility assessment framework for aging highway bridges considering the non-uniform chloride-induced corrosion and various modeling uncertainty parameters. Firstly, sensitivity analysis with the tornado diagram technique is performed to determine the sensitivity of some typical bridge engineering demand parameters (EDPs) to 22 modeling related uncertain parameters, and then 10 critical parameters are identified. Subsequently, based on a series of nonlinear time history analyses (NLTHAs) on the sample models generated by using the Latin hypercube sampling (LHS) method, comparative studies for the time-invariant and time-evolving seismic response, as well as the time-dependent seismic fragility estimates incorporating different levels of uncertainty are performed, respectively. It is concluded that (1) the uncertainty of the modeling related uncertain parameters may lead to the difference in the trajectory of seismic hysteretic response for a given bridge member, whereas the variation of the peak value of seismic response may result from the couple contributions of the uncertainty of ground motions and modeling related parameters; (2) the inclusion of only ground motion uncertainty is inadequate and inappropriate, and the proper way is to incorporate the uncertainty of the identified critical modeling parameters and ground motions into the time-evolving seismic response and the time-dependent seismic fragility assessment of the deteriorating highway bridges.

1 Introduction

In the probabilistic seismic risk and fragility analysis framework, it is highly likely that various sources of uncertainty such as structural geometric, material and boundary conditions related parameters exist due to the structure-to-structure (STS) variation in the development of seismic fragility curves, particularly when the generated vulnerability curves are utilized for the regional seismic risk assessment of highway bridges (Padgett and DesRoches 2007; Mangalathu and Jeon 2018). According to Kiureghian and Ditlevsen (2009), all sources of uncertainty can be categorized into either aleatory uncertainty or epistemic uncertainty. The former mainly stems from the intrinsic randomness of ground motions, material, structural properties, static or dynamic loading, and geometric parameters, whereas the latter may derive from the incomplete of statistic data, the lack of human knowledge, and several modeling assumptions. One may either ignore the critical uncertain parameters which could result in unreliable seismic fragility estimates; or conversely may devote efforts unnecessarily to the time-consuming and computationally expensive simulations which have minimal effects on the seismic response and seismic vulnerability assessment of highway bridges (Padgett and DesRoches 2007). Thus, there is a need for a schematic sensitivity study to investigate the effects of the input uncertain parameters and identify the significant parameters on the seismic response and seismic fragility estimates of bridge structures.

Significant research efforts have been devoted to investigating the sensitivity of seismic responses or evaluating seismic fragility to parameter uncertainty. For instance, Padgett and DesRoches (2007) evaluated the sensitivity of seismic responses for some critical bridge components to the uncertainty in the modeling parameters, structural geometries, and ground motions by an analysis of variance (ANOVA) technique. Their studies suggested that the seismic fragility curves generated with the critical parameters identified from the sensitivity analysis are nearly identical to those developed with all of the input uncertain parameters. Their work also indicated that savings in the computational efforts in the seismic fragility estimates may be achieved through a preliminary screening of parameters. Likewise, the sensitivity study was further extended by Padgett et al. (2010) to investigate and evaluate the relative importance of 13 random variables that reflected the variation in structural and liquefiable soil modeling parameters on the seismic reliability of critical structural components for steel bridges. Tubaldi et al. (2012) investigated the sensitivity of seismic response and seismic vulnerability assessment of steel–concrete composite (SCC) bridges with a dual load path to the uncertainty in the seismic inputs and 23 modeling related uncertain parameters. Their studies highlighted that it is significant to take into account the influence of the variability in modeling parameters on the safety of the typology of SCC bridges. Pang et al. (2014) studied the influence of different sources of uncertainty on the seismic fragility estimates of a cable-stayed bridge by the uniform design (UD) method, and they found that the vulnerability of the cable-stayed bridge considering the uncertainty in ground motions, structural geometry, and material is more severe than that considering only the uncertainty in ground motions. Similarly, Mangalathu and Jeon (2018) proposed a multiparameter fragility model using the Lasso regression technique and utilized it to explore the relative influence of each uncertain variable and level of uncertainty treatment needed for these variables on the assessment of seismic demand models and seismic fragility curves. They found that ignoring the uncertainty in the critical parameters identified from sensitivity analysis may lead to inaccurate estimates of seismic demand models and seismic vulnerabilities. Similarly, by considering a total of 26 modeling uncertain parameters that were related to the material, boundary conditions and structural properties, Wu et al. (2018) identified 13 significant modeling parameters through the sensitivity analysis with the tornado diagram technique, and they also suggested that without considering the uncertainty in these significant parameters may result in inaccurate estimates for different bridge engineering demand models (EDPs). In summary, all of the above-mentioned studies highlight the importance of sensitivity study of the time-invariant seismic response and seismic fragility estimates of highway bridges to the uncertainty in modeling related uncertain parameters. However, there is still a lack of overall understanding of the influence of various modeling uncertainty parameters on the time-variant seismic response and time-dependent seismic fragility estimates of the aging highway bridges. Thus, it is necessary to investigate whether the variability of modeling related uncertain parameters and the ground motion uncertainty may have significant effects on the time-variant seismic response as well as the time-dependent seismic vulnerability estimates of the deteriorating bridges, and how to treat different levels of uncertainty can be more appropriate and reliable within the time-dependent seismic fragility assessment framework.

In the last two decades, significant efforts focused on the quantification of the seismic fragility of RC bridges have been made (Nielson 2005; Pan et al. 2007; Pang et al. 2014; Wu et al. 2016; Chen 2020; Li et al. 2020). However, during their service life, highway bridges can be attacked by various deterioration mechanisms due to harsh environment, such as erosion, fatigue, sulfate and acid attacks on concrete, carbonation and chloride-induced corrosion of steel members, etc. (Enright and Frangopol 1998a, b; Ghosh and Padgett 2013; Ghosh and Sood 2016; Cheng et al. 2019). Among these, corrosion deterioration (particularly induced by chloride ions) has been regarded as one of the primary factors and has received considerable attention concerning the seismic vulnerability quantification of the aging highway bridges (Cheng et al. 2019). Chloride-induced corrosion is a significant hazard to the serviceability and durability of RC structures and increases their vulnerability to seismic events (Ge et al. 2020). This is especially the case for those highway bridges either in the marine environment or the regions that are exposed to de-icing salt (Chiu et al. 2015; Ge et al. 2020). Many experimental and analytical studies have been performed to investigate the effects of chloride-induced corrosion on the structural performance of corroded RC structures (Ma et al. 2012; Meda et al. 2014; Guo et al. 2015; Rao et al. 2017; Ge et al. 2020). These studies suggested that the chloride-induced corrosion may lead to the degradation of material and mechanical properties, low-cycle fatigue life, and the reduction of bond strength between steel and concrete interface (Dizaj and Kashani 2020). Since the degradation of material and mechanical properties occurs due to the deterioration events, a number of researches that are related to the chloride-induced corrosion on the time-varying seismic response and the time-dependent seismic fragility estimates of the aging highway bridges have been carried out (Choe et al. 2009; Ghosh and Padgett 2010; Simon et al. 2010; Guo et al. 2015; Ghosh and Sood 2016; Li et al. 2016; Rao et al. 2017; Cui et al. 2018; Cheng et al. 2019; Li and Li 2019).

Numerous modeling techniques are available in the literature to consider the influence of chloride-induced corrosion on the structural performance of corroded RC structures (Dizaj and Kashani 2020). Most of these models are generally based on the reduced cross-sectional area of corroded bars under the uniform chloride-induced corrosion (Choe et al. 2009; Ghosh and Padgett 2010; Simon et al. 2010; Li et al. 2016; Li and Li 2019). However, a number of previous studies demonstrated that pitting corrosion is the primary chloride-induced deterioration form in the field situations (Melchers and Frangopol 2008; Stewart and Al-Harthy 2008; Darmawan 2010; Ghosh and Sood 2016; Cui et al. 2018; Shekhar et al. 2018; Ge et al. 2020). According to a number of previous studies, non-uniform pitting corrosion along the bar is widely suggested as one of the critical factors influencing the stress–strain behaviour of corroded reinforcing bars under both the monotonic and cyclic loading (Almusallam 2001; Kashani et al. 2013a, b; Fernandez et al. 2015, 2016; Balestra et al. 2016; Zhu et al. 2017; Dizaj and Kashani 2020). In addition, distribution of pitting also affects the inelastic buckling mechanism of the bars in compression (Kashani 2017), and the non-uniform residual cross-section is more vulnerable to tensile loading compared with the general symmetrical residual cross-section for RC columns (Zhu and Francois 2014). Therefore, pitting corrosion may further lead to the localized weakening and remarkable reduction in the load-carrying capacity of RC columns under the seismic events. It tends to under-predict significantly the vulnerability of deteriorating highway bridges by ignoring pitting corrosion in the time-dependent seismic fragility analysis. Then, such an underestimation of seismic fragility is also likely to be propagated as performing the life-cycle loss and reliability evaluation of deteriorating RC highway bridges (Deco and Frangopol 2013; Ghosh and Sood 2016; Shekhar et al. 2018). Hence, this paper intends to investigate the effects of various modeling related parameter variability and ground motion uncertainty on the time-variant seismic response and the time-dependent seismic fragility estimates of the aging highway bridges under the non-uniform chloride-induced corrosion, and finally find a more appropriate and reliable method to include different levels of uncertainty in the time-dependent seismic fragility assessment framework for the aging highway bridges.

The main objectives of the present study are to (i) identify the critical modeling parameters that impose relative significant effects on the seismic demand models of some typical bridge components through the sensitivity analysis; (ii) investigate the relative influence of different levels of uncertainty on the time-variant seismic response and the time-dependent seismic fragility estimates; and (iii) suggest a proper and reliable approach to treat the uncertainty of ground motions and different modeling related uncertain parameters in evaluating the time-dependent seismic fragilities of the aging highway bridges. Therefore, the current study is organized into several sections. Following this introduction, Sect. 2 mainly elaborates on the non-uniform chloride-induced deterioration modeling and the corresponding degradation mechanisms of steel bars and concrete. Section 3 focuses on the introduction of the proposed time-dependent seismic fragility assessment framework considering various modeling related uncertain parameters and the non-uniform chloride-induced deterioration. Then, Sect. 4 presents the basic information regarding the numerical modeling of the case-study bridge and summarizes the probabilistic information of 22 modeling related uncertain parameters from three aspects, i.e., material, structural geometries, and boundary conditions. Subsequently, based on some previous literature, the critical modeling parameters are identified through the sensitivity analysis with the tornado diagram technique in Sect. 5. Then, Sect. 6 and Sect. 7 investigate the effects of different levels of uncertainty impose on the time-invariant and time-evolving seismic responses, as well as the time-dependent seismic fragilities both at bridge component and system level of the case-study bridge, respectively. Finally, this study ends with a summary of conclusions and possible future work in Sect. 8.

2 Modeling of non-uniform chloride-induced deterioration

2.1 Chloride-induced corrosion modeling

It is widely recognized that the diffusion process of chloride ion ingresses through the RC structures can be simulated by the Fick’s second law. According to the previous literature (Duracrete 2000; Shin 2002), the most acceptable chloride-induced corrosion model is Duracrete model, which can be represented as

$$ C(x,t) = C_{0} \left[ {1 - erf(\frac{x}{{2\sqrt {k_{e} k_{t} k_{c} D_{0} (t_{0} )^{n} (t)^{1 - n} } }})} \right] $$

(1)

where C₀ is the chloride concentration on the concrete surface, D₀ is the diffusion coefficient at the reference period t₀ (i.e., 28 days), n is the aging factor, k_e is the environmental factor, k_t is the testing method factor, k_c is the curing time correction factor, and erf (·) is the Gaussian error function. Equation (1) can be used to determine the chloride concentration C(x, t) of the concrete at the depth of x at an arbitrary time t. Besides, the chloride concentration C₀ on the concrete surface can be obtained as

$$ C_{0} = A_{cs} ({w \mathord{\left/ {\vphantom {w b}} \right. \kern-\nulldelimiterspace} b}) + \varepsilon_{cs} $$

(2)

where w/b represents the water-to-blinder ratio. A_cs and ε_cs are the modeling parameters that are related to the environmental conditions. It has been demonstrated that the initial corrosion tends to happen when C(x, t) reaches a critical value C_critical (Yu and Hartt 2007; Guo et al. 2015). This specific time point is termed as the corrosion initiation time T_corr, which can be expressed by the following equation (Duracrete 2000).

$$ T_{corr} = \left\{ {\frac{{d_{c}^{2} }}{{4k_{e} k_{t} k_{c} D_{0} (t_{0} )^{n} }}\left[ {erf^{ - 1} \left( {\frac{{C_{0} - C_{critical} }}{{C_{0} }}} \right)} \right]^{ - 2} } \right\}^{{\frac{1}{1 - n}}} $$

(3)

where d_c is the thickness of the cover concrete protective layer. Additionally, according to Duracrete (2000), the chloride exposure conditions can be divided into four categories, such as (i) marine submerged, (ii) marine tidal, (iii) marine splash, and (iv) marine atmospheric zone exposure conditions. Based on the experimental work done by Duracrete (2000), the statistical distributions of these parameters that could be used to estimate the corrosion initiation time of steel rebar under different chloride exposure conditions are presented in Table 1.

Table 1 Random parameters used to estimate the corrosion initiation time of steel bars under different marine exposure scenarios

After the corrosion initiation time, T_corr is reached, based on the previous researches, the chloride-induced corrosion mainly has two distinct corrosion forms, such as uniform corrosion and pitting corrosion (Thoft-Christensen 2003; Melchers 2004; Stewart and Al-Harthy 2008; Darmawan, 2010; Ghosh and Sood 2016). Generally, uniform corrosion model assumes that a continued equally area loss of the cross-section of steel bars, and the corresponding residual cross-sectional area can be computed as (Ghosh and Sood 2016)

$$ A_{r}^{{{\text{Uniform}}}} (t) = \frac{{\pi \left[ {d_{0} - 2\int_{{T_{corr} }}^{t} {\lambda (t)\,{\text{dt}}} } \right]^{2} }}{4} $$

(4)

where d₀ is the initial diameter of the steel bars before the corrosion initiation, and λ(t) is the time-dependent corrosion rate at t years, which can be calculated as (Stewart and Al-Harthy 2008)

$$ \lambda (t) = 0.0116i_{corr} (t) $$

(5)

where the time-variant corrosion current density, i_corr can be expressed as

$$ i_{corr} (t) = 0.85 \times \frac{{37.8(1 - {w \mathord{\left/ {\vphantom {w b}} \right. \kern-\nulldelimiterspace} b})^{ - 1.64} }}{{d_{c} }} \times (t - T_{corr} )^{ - 0.29} $$

(6)

Similarly, according to Val and Melchers (1997), pitting corrosion can be assumed to simulate by using a hemispherical form to approximate estimate the section area loss. The pitting depth p(t) can be expressed as

$$ p(t) = R\int_{{T_{corr} }}^{t} {\lambda (t)\,{\text{dt}}} $$

(7)

where R represents the pitting factor. The corresponding time-variant residual cross-sectional area of steel bars subject to pitting corrosion can be represented by the following equation (Val and Melchers 1997; Stewart and Al-Harthy 2008; Ghosh and Sood 2016).

$$ A_{r}^{{{\text{Pitting}}}} (t) = \left\{ {\begin{array}{ll} {A_{1} + A_{2} \begin{array}{*{20}l} {\begin{array}{*{20}l} {} & {} \\ \end{array} } & {{\text{when}}\begin{array}{*{20}l} {p(t) \le \frac{\sqrt 2 }{2}d_{0} } \\ \end{array} } \\ \end{array} } \\ {\frac{{\pi d_{0}^{2} }}{4} - (A_{1} - A_{2} )\begin{array}{*{20}l} {} & {{\text{when}}\begin{array}{*{20}l} {\frac{\sqrt 2 }{2}d_{0} < p(t) < d_{0} } \\ \end{array} } \\ \end{array} } \\ {\frac{{\pi d_{0}^{2} }}{4}\begin{array}{*{20}l} {} & {} & {{\text{when}}\begin{array}{*{20}c} {p(t) \ge d_{0} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right. $$

(8)

where the areas A₁ and A₂ can be calculated as

$$ A_{1} = \frac{1}{2}\left[ {\theta_{1} (\frac{1}{2}d_{0} )^{2} - a\left| {\frac{{d_{0} }}{2} - \frac{{p(t)^{2} }}{{d_{0} }}} \right|} \right] $$

(9)

$$ A_{2} = \frac{1}{2}\left[ {\theta_{2} p(t)^{2} - a\frac{{p(t)^{2} }}{{d_{0} }}} \right] $$

(10)

where the model parameters a, θ₁ and θ₂ can be computed as

$$ \begin{gathered} a = 2p(t)\sqrt {1 - \left[ {\frac{p(t)}{{d_{0} }}} \right]^{2} } \hfill \\ \theta_{1} = 2\sin^{ - 1} (\frac{a}{{d_{0} }})\begin{array}{*{20}c} , \\ \end{array} \theta_{2} = 2\sin^{ - 1} \left[ {\frac{a}{2p(t)}} \right] \hfill \\ \end{gathered}. $$

(11)

2.2 Secondary effects caused by the chloride-induced corrosion in RC structures

Secondary effects due to the chloride-induced deterioration in RC structures mainly include three aspects, such as (i) degradation of the mechanical characteristics of reinforcement, (ii) loss of unconfined concrete strength, and (iii) loss of confined concrete strength result from the corrosion of reinforcing hoops or ties (Shekhar et al. 2018). The following sections briefly introduce these secondary effects in RC structures due to the chloride-induced corrosion.

Firstly, based on the previous experimental tests performed by Du et al. (2005), the reduction of the reinforcing steel yield and ultimate strengths can be calculated as

$$ \begin{gathered} f_{y} (t) = \left[ {1 - 0.005Q_{corr} (t)} \right]f_{y0} \hfill \\ f_{u} (t) = \left[ {1 - 0.005Q_{corr} (t)} \right]f_{u0} \hfill \\ \end{gathered} $$

(12)

where f_y0 and f_u0 represent the initial yield and ultimate stress of pristine reinforcing bars, while f_y (t) and f_u (t) denote the corresponding strengths of corroding rebar at time t. Q_corr (t) is the time-dependent corrosion percentage of reinforcement in terms of area loss, which can be expressed as

$$ Q_{corr} (t) = \frac{{A_{0} - A_{r} (t)}}{{A_{0} }} \times 100 $$

(13)

where A₀ is the initial area of reinforcement, which can be calculated from A₀ = πd₀²/4. A_r(t) represents the time-variant residual cross-sectional area of reinforcement due to uniform corrosion and pitting corrosion, which can be expressed as

$$ A_{r} (t) = A_{r}^{{{\text{Uniform}}}} (t) + A_{r}^{{{\text{Pitting}}}} (t) $$

(14)

where the residual cross-sectional area of reinforcement A_r^Uniform (t) and A_r^Pitting (t) can be determined by Eq. (4) and Eq. (8), respectively. Thus, according to Eq. (13) and Eq. (14), based on the developed residual cross-sectional area of steel bars for uniform corrosion and pitting corrosion from Eq. (4) and Eq. (8), the corrosion percentage of reinforcement Q_corr (t) can be determined. Then the reduction of the reinforcing steel yield and ultimate strengths can be determined by Eq. (12). Similarly to some previous studies (Du et al. 2005; Kashani et al. 2015, Shekhar et al. 2018), this paper herein does not consider the degradation of the ultimate strains of steel rebar that is caused by pitting corrosion.

Secondly, according to the recommendations suggested by Coronelli and Gambarova (2004), the reduction in the unconfined concrete compressive strength can be determined by

$$ f_{{c,{\text{cover}}}} (t) = \frac{{f_{{c,{\text{cover}}}} }}{{1 + k\left[ {{{\varepsilon^{ * } (t)} \mathord{\left/ {\vphantom {{\varepsilon^{ * } (t)} {\varepsilon_{{c,{\text{cover}}}} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{{c,{\text{cover}}}} }}} \right]}} $$

(15)

where f_c,cover (t) is the time-dependent compressive strength of unconfined concrete at any time t, f_c,cover is the corresponding peak strength of cover concrete for the pristine column. k is a parameter that depends on diameter and roughness of the steel rebar, which is generally assumed to be 0.1 for medium diameter ribbed reinforcement (Vecchio and Collins 1986). ε_c,cover is the cover concrete compressive strain corresponding to the peak strength and ε^*(t) is the average tensile strain in the transverse direction that leads to the development of micro-cracks, which can be expressed as

$$ \varepsilon^{ * } (t) = \frac{{N_{{{\text{bars}}}} w_{cr} (t)}}{{D_{{{\text{column}}}} }} $$

(16)

where N_bar represents the number of the corroded steel bars and D_column is the diameter of the pristine column. w_cr (t) is the total crack width at time t for a specific corrosion level, which can be determined by the following formula (Molina et al. 1993; Rao et al. 2017).

$$ w_{cr} (t) = 4\pi (\nu_{rs} - 1)d_{rs} (t) $$

(17)

where v_rs represents the ratio of volumetric expansion of rust products to the volume of pristine steel rebar, which is typically assumed to be 2. d_rs (t) is the corrosion depth due to separately from uniform corrosion.

Furthermore, for the circular RC columns, as the case-study bridge used in this study, the degradation of compressive strength of confined concrete can be simulated by using the theoretical stress–strain model proposed by Mander et al. (1988) as

$$ f_{{c,{\text{core}}}} (t) = f_{{c,{\text{cover}}}} \left[ {2.254\sqrt {1 + \frac{{7.94f_{le} (t)}}{{f_{{c,{\text{cover}}}} }}} - \frac{{2f_{le} (t)}}{{f_{{c,{\text{cover}}}} }} - 1.254} \right] $$

(18)

where f_c,core (t) is the time-dependent compressive strength of confined concrete, f_c,cover is the compressive strength of cover concrete, and f_le (t) is the time-variant effective lateral confining pressure assumed to be uniformly distributed over the surface of confined concrete. After the secondary effects caused by the non-uniform chloride-induced corrosion are determined, the time-dependent material and cross-sectional properties of bridge piers of the case-study bridge can be determined. Thus, the nonlinear FE models of the case-study bridge can be further updated and the corresponding seismic response and seismic fragility of the bridge can be developed.

3 Time-dependent seismic fragility analysis considering various modeling uncertainty parameters

Seismic fragility can be defined as the conditional probability of the structural seismic demand (D) reaching or exceeding the structural seismic capacity (C) under the given intensity measure (IM) level, which can be written as (Li et al. 2020)

$$ P_{f} = P(D \ge C|IM = x) $$

(19)

From Eq. (19), the seismic fragility analysis framework mainly has two crucial parts, such as (i) probabilistic seismic capacity analysis (PSCA) and (ii) probabilistic seismic demand analysis (PSDA) (Li and Li 2019). The former can be used to obtain the structural capacity damage model to determine the relationship between the seismic capacity and the ground motion intensity measures (IMs), while the latter can be utilized to determine the relationship between the seismic demand and the IMs, which can be represented by the probabilistic seismic demand models (PSDMs). Currently, two methods, such as the “cloud” approach and the scaling approach are the most frequently used methods to develop the PSDMs of bridge structural components (Billah et. al 2013; Wu et al. 2016; Chen 2020). Compared to the “cloud” approach, although the scaling approach is relatively accurate, the involved computational effort makes it too complicated for practical applications (Wu et al. 2016). Thus, this paper uses the “cloud” approach for the development of PSDMs and the seismic fragility functions.

In the “cloud” approach, the structural seismic demand and seismic capacity of bridge members are generally assumed to follow the lognormal distributions (Wu et al. 2016; Li and Li 2019; Chen 2020), and the median structural seismic demand (S_d) and the given ground motion intensity measures (IMs) are assumed to follow a lognormal correlation according to the power-law function (Cornell et al. 2002; Wu et al. 2016; Li and Li 2019; Chen 2020), which can be expressed as

$$ S_{d} = a \cdot IM^{b} \begin{array}{*{20}c} {} & {{\text{or}}} & {\ln (S_{d} )} \\ \end{array} = \ln (a) + \ln (IM) $$

(20)

where a and b are the unknown regression coefficients, which can be determined by regression analysis. Based on some previous studies (Cornell et al. 2002; Wu et al. 2016; Chen 2020), by assuming that S_d follows a lognormal distribution and to consider the uncertainty of the developed PSDMs, the dispersion of the structural seismic demand, β_D|IM, can be computed by

$$ \beta_{D|IM} = \sqrt {\frac{{\sum\nolimits_{i}^{N} {\ln (D_{i} ) - \ln (S_{d} )^{2} } }}{N - 2}} = \sqrt {\frac{{\sum\nolimits_{i}^{N} {\ln (D_{i} ) - \ln (a \cdot IM^{b} )^{2} } }}{N - 2}} $$

(21)

where N is the number of the selected ground motions, and D_i represents the structural seismic demand at ith (i equals 1, 2, 3, and 4) damage state. Based on the work done by Chen (2020), assuming that the defined damage states follow the lognormal distributions as well, then the seismic fragility function can be written as

$$ P_{f} (DS_{i} |IM) = {\varPhi} \left\{ {\frac{{\ln (S_{d} ) - \ln (S_{ci} )}}{{\sqrt {\beta_{D|IM}^{2} + \beta_{ci}^{2} } }}} \right\} = {\varPhi} \left\{ {\frac{{[\ln (a) + b \cdot \ln (IM)] - \ln (S_{ci} )}}{{\sqrt {\beta_{D|IM}^{2} + \beta_{ci}^{2} } }}} \right\} $$

(22)

where S_ci and β_ci is the median structural seismic capacity and the logarithmic standard deviation of seismic capacity at ith (i equals 1, 2, 3, and 4) limit state, respectively. Φ{·} is the standard normal cumulative distribution function. Generally, Eq. (22) represents the traditional time-invariant seismic fragility function, which is often used to evaluate the vulnerability of highway bridges at several specific time points (Li and Li 2019). However, in the realistic engineering fields, due to the chloride-induced corrosion, material and cross-sectional properties should be gradually degraded. This leads to structural seismic demand and seismic capacity varies at different time points within the bridge service life range. Thus, the time-dependent seismic demand and seismic capacity should be functions of time, and the relevant time-dependent seismic fragility function can be expressed as

$$ P_{f} (DS_{i} |IM) = {\varPhi} \left\{ {\frac{{\ln [S_{d} (t)] - \ln [S_{ci} (t)]}}{{\sqrt {\beta_{D|IM} (t)^{2} + \beta_{ci} (t)^{2} } }}} \right\} = {\varPhi}\left\{ {\frac{{\ln [a(t)] + b(t) \cdot \ln (IM) - \ln [S_{ci} (t)]}}{{\sqrt {\beta_{D|IM} (t)^{2} + \beta_{ci} (t)^{2} } }}} \right\} $$

(23)

To simplify the seismic fragility function, Eq. (23) can be further written as

$$ P_{f} (DS_{i} |IM) = {\varPhi} \left\{ {\frac{{\ln (IM) - {{[\ln S_{ci} (t) - a(t)]} \mathord{\left/ {\vphantom {{[\ln S_{ci} (t) - a(t)]} {b(t)}}} \right. \kern-\nulldelimiterspace} {b(t)}}}}{{{{\sqrt {\beta_{D|IM} (t)^{2} + \beta_{ci} (t)^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\beta_{D|IM} (t)^{2} + \beta_{ci} (t)^{2} } } {b(t)}}} \right. \kern-\nulldelimiterspace} {b(t)}}}}} \right\} = {\varPhi} \left\{ {\frac{\ln (IM) - \ln [\mu (t)]}{{\xi (t)}}} \right\} $$

(24)

where μ(t) represents the median intensity measure and ξ(t) is the logarithmic standard deviation of fragility function at different time points, respectively. Thus, μ(t) and ξ(t) can be used as the seismic fragility parameters to assess the seismic fragility of bridge structures, which can be represented as

$$ \begin{gathered} \mu (t) = e^{{[\ln (S_{ci} (t)) - a(t)]/b(t)}} \hfill \\ \xi (t) = {{\sqrt {\beta_{D|IM}^{2} (t) + \, \beta_{ci}^{2} (t)} } \mathord{\left/ {\vphantom {{\sqrt {\beta_{D|IM}^{2} (t) + \, \beta_{ci}^{2} (t)} } b}} \right. \kern-\nulldelimiterspace} b}(t) \hfill \\ \end{gathered} $$

(25)

According to the recommendations suggested by Wen et al. (2004), Pang et al. (2014), and Mangalathu and Jeon (2018), it tends to underestimate the structural seismic fragility by ignoring the modeling uncertainty and the ground motion variability. Thus, to incorporate the uncertainty of modeling related uncertain parameters and ground motions within the seismic fragility assessment framework, β_D|IM (t) can be further expressed as

$$ \beta_{D|IM} (t) = \sqrt {\beta_{RTR}^{2} (t) + \beta_{Model}^{2} (t)} $$

(26)

where β_D|IM (t) can be determined by the PSDA; β_RTR (t) and β_Model (t) is the deviation due to the uncertainty in ground motions and modeling related uncertain parameters, respectively. Thus, the logarithmic standard deviation of seismic fragility function can be further transformed as

$$ \xi (t) = {{\sqrt {\beta_{RTR}^{2} (t) + \beta_{Model}^{2} (t) + \beta_{ci}^{2} (t)} } \mathord{\left/ {\vphantom {{\sqrt {\beta_{RTR}^{2} (t) + \beta_{Model}^{2} (t) + \beta_{ci}^{2} (t)} } {b(t)}}} \right. \kern-\nulldelimiterspace} {b(t)}} $$

(27)

Based on the time-dependent seismic fragility functions, the non-uniform chloride-induced deterioration modeling, and the sensitivity analysis with tornado diagram technique (Celik and Ellingwood 2010; Zhong et al. 2018; Wu et al. 2018), Fig. 1 presents the proposed schematic time-dependent seismic fragility assessment framework considering various modeling related uncertain parameters for the aging highway bridges.

Fig. 1

Time-dependent seismic fragility assessment framework considering various modeling related uncertain parameters: part A modeling uncertainty parameter sensitivity analysis, part B chloride-induced deterioration analysis, and part C time-dependent seismic fragility analysis

As shown in Fig. 1, the proposed framework can be mainly divided into three different parts. For instance, in part (A), three aspects of modeling related uncertain parameters, such as structural, material, and boundary conditions related parameters, are first determined and then utilized to yield the strip analysis through the median-valued OpenSEES model. Based on the strip analysis, some specific tornado diagrams based sensitivity analyses of some bridge typical EDPs to the uncertain modeling parameters are performed, and the critical modeling parameters can be determined. Subsequently, to incorporate the record to record (RTR) variability in ground motions, the sample structures are randomly paired with the selected seismic records for the seismic fragility analysis by using the Latin hypercube sampling (LHS) method, and a series of “bridge-ground motion” samples are generated for the following time-dependent seismic fragility analysis. Following the section in part (B), according to the time-dependent material and cross-sectional degradation mechanisms under some specific chloride-induced exposure conditions, the corresponding chloride-induced deterioration analysis for the RC columns is conducted. In part (C), based on the time-evolving sectional and material mechanical properties, the updated bridge OpenSEES finite element (FE) model and the RC column sectional model are developed to obtain the time-variant seismic demand and seismic capacity by the nonlinear time history and nonlinear sectional moment–curvature analysis. Finally, the time-dependent seismic fragility curves and corresponding seismic fragility parameters are developed for deriving practical estimates of seismic vulnerability of the aging highway bridges.

4 Bridge characteristics and the modeling related uncertain parameters

4.1 Case-study bridge and numerical modeling

The case-study bridge shown in Fig. 2 is a typical multi-span reinforced concrete continuous girder (MSRCCG) bridge, which consists of five spans, 30 m each, and a 16 m wide deck supported by four RC circular piers and two RC abutments. The superstructure consists of a 1.8 m high box girder and a cap beam. The height of each pier is 10 m. According to the guidelines for seismic design of Chinese highway bridges (JTG/TB02-01 2008), each pier is reinforced by longitudinal bars and transverse spiral hoops at a reinforcing ratio of 1.08% and 0.58%, respectively. The case-study bridge also utilizes the plate-type elastomeric bearing (PTEB) and the lead rubber bearing (LRB) to transfer the loading from the superstructure to substructure through the piers and abutments, respectively. The foundation of each pier consists of nine RC piles with a diameter of 1.5 m and a length of 30 m, and the soil condition belongs to the medium-hard soil profiles.

Fig. 2

Nonlinear dynamic finite element model of the case-study offshore bridge

With the aid of the OpenSEES software, a three-dimensional nonlinear FE model is developed to simulate the seismic response of the case-study bridge. A general overview of the simulations of some critical bridge components in the OpenSEES database (Manual 2009) is provided herein. For instance, the composite action of the deck and cap beam is modeled using the linear elastic beam-column elements since their damages are not expected in the bridge superstructure during the seismic shaking events. Bridge piers are modeled using nonlinear beam-column elements with fiber defined cross-sections considering the axial force-moment interaction and material nonlinearities. For the fiber-element model of RC piers, the stress–strain relationship of the confined and unconfined concrete is modeled as Concrete 04 material, whereas the longitudinal steel bars, as well as the transverse spiral hoops, are simulated using the Steel 02 material, both of which are available material models in the OpenSEES database (Manual 2009). Linear translational and rotational springs are utilized to simulate the pile foundations under the piers to capture the translation and rotation behaviors of the foundation system. The stiffness of these springs is determined by the “m” method according to the guidelines for the seismic design of Chinese highway bridges (JTG/TB02-01 2008). In addition, the PTEB and LRB bearings are simulated by using the elastomeric bearing (plasticity) element, and the behavior of abutments is considered by incorporating the contribution of back-fill soil and piles, which can be modeled by using the hyperbolic material and the hysteretic material in the OpenSEES database (Manual 2009), respectively. Furthermore, the transverse concrete stoppers are simulated by the hysteretic material and elastic-perfectly plastic gap elements. The pounding effect between the deck and abutments can be simulated using the contact element (i.e., nonlinear translational springs) considering the effects of hysteretic energy loss, which can be simulated by impact materials in the OpenSEES database (Manual 2009). The three-dimensional nonlinear dynamic FE model of the case-study bridge and the force–deformation backbone curves of all critical bridge components are summarized in Fig. 2.

4.2 Modeling related uncertain parameters

The modeling related uncertain parameters considered in this paper mainly include three different aspects, such as (i) structurally related uncertainty (SU) parameters, (ii) material related uncertainty (MU) parameters, and (iii) boundary conditions related uncertainty (BU) parameters. Firstly, SU parameters mainly affect the global dynamic characteristics of the bridge structures. From the perspective of structural dynamics, these uncertainties associated with mass, stiffness, and damping matrix can be attributed to this category, but this paper mainly considers the uncertain parameters that are related to the geometric dimensions of the bridge components and the damping ratio. Similarly, MU parameters mainly affect the nonlinear response of bridge columns under the earthquake actions. Since the bridge superstructure and the cap beam are simulated by the elastic beam-column element, this paper mainly considers the material related uncertain parameters of the RC columns. Moreover, the case-study bridge considers the complicated nonlinear mechanical properties of bearings (i.e., LRB and PTEB), abutments, and pounding between the girder and the abutments. These nonlinear features are of great importance to the seismic analysis of bridge structures. Therefore, it is necessary to take into account the BU parameters. To investigate and quantify the significance of different modeling related uncertain parameters, Table 2 summarizes the associated probability distributions of various modeling uncertainty parameters based on some previous studies.

Table 2 Statistical information on the modeling related uncertainty parameters

Firstly, for the SU parameters, based on the specification of Chinese General Code for Design of Highway Bridges and Culverts (JTG-D60 2004), the concrete volume mass (m) should follow a normal distribution and the specification suggests the value of m should range as 25 to 26 kN/m³. Thus, the concrete weight coefficient (λ_w) of the girder and piers are assumed to follow a normal distribution, the mean value is set as 1.04, and the coefficient of variation (COV) is set as 10% (Wu et al. 2018; Ma et al. 2019). According to the work done by Padgett et al. (2008) and Ma et al. (2019), the pier diameter (D), the concrete cover thickness (c), and the longitudinal reinforcement diameter (φ) are suggested to follow the normal distribution. The mean values are selected from their original designed values, while the COV of these three parameters is set as 5%. Similarly, the damping ratio (ξ) is defined to consider the energy dissipation mechanism. According to the guidelines for the seismic design of Chinese highway bridges (JTG/TB02-01 2008), ξ is suggested as 0.05 for concrete structures. During the FE modeling of the case-study bridge, the Rayleigh damping is defined, and based on the research of Nielson (2005) and Ma et al. (2019), ξ is assumed following a normal distribution with a 30% of COV.

Secondly, for the MU parameters, a total of 10 material related parameters are selected. For instance, for the nonlinear modeling of RC piers using the Concrete 04 and Steel 02 material in the OpenSEES database (Manual 2009), three parameters need to be defined for the confined concrete (i.e., core concrete) (f_{c, core} = peak strength; ε_{c, core} = strain at the peak strength; and ε_{cu, core} = strain at the ultimate strength), three parameters for the unconfined concrete (i.e., cover concrete) (f_{c, cover}, ε_{c, cover}, ε_{cu, cover}), and three parameters for the reinforcing steel (E_s = Young’s modulus; f_y = yield strength; and γ = post-yield to initial stiffness ratio). Based on the research done by Barbato et al. (2010) and Pang et al. (2014), all of these 10 material parameters are assumed following lognormal distribution, and their related distribution details are shown in Table 2. In addition, for Young’s modulus of concrete (E_c), it is assumed as lognormally distributed with 30% of COV (Wu et al. 2018).

Furthermore, for the BU parameters, a total of 7 parameters are selected to treat as random variables to consider the nonlinear features of the PTEB, LRB, and abutments of the case-study bridge. As seen from Fig. 2, the mechanical model of PTEB is determined by the shear stiffness (K) and the critical friction force (F_y). The former can be determined by the shear modulus of rubber material used in PTEB, whereas the latter can be determined by the friction coefficient. According to the previous work done by (Wu et al. 2018), the shear modulus of PTEB (G_PTEB) was suggested as normally distributed with a 14% of COV, and its mean value was set as the designed value. Since the PTEB of the case-study bridge in this paper is similar to that in Wu et al. (2018), the friction coefficient of PTEB (μ_PTEB) is selected as uniformly distributed with a lower and upper bound equal to 0.15 and 0.25, respectively. Likewise, the post-yield stiffness of LRB (K_P-LRB) can be also determined by the shear modulus of rubber material. Similar to G_PTEB, K_P-LRB is selected as a random variable that follows a normal distribution with 14% of COV. As shown in Fig. 2, the mechanical model of the abutment of the case-study bridge incorporates the couple contributions of backfill soils and piles. This shows that the stiffness of abutment includes two different parts, such as the passive stiffness support by the abutment backfill soils and the active stiffness contribute by the pile foundation system. For the contribution of backfill soils, it can be simulated by using the Hyperbolic Force–Displacement (HFD) model proposed by Shamsabadi et al. (2007). In the OpenSEES database, the Hyperbolic Gap Material can be used to simulate the HFD model, and the critical input parameter is defined as the abutment passive stiffness (K_passive) (Wilson and Elgamal 2010). Meanwhile, this paper uses the Hysteresis Material in the OpenSEES database (Manual 2009) to consider the active stiffness provide by the pile foundation system. Thus, according to previous studies (Nielson 2005; Wu et al. 2018), to consider the nonlinear modeling of abutments, the abutment ultimate capacity (P_ult), the abutment passive stiffness (K_passive), and the abutment active stiffness (K_active) are assumed as random variables that follow the uniform distribution as U(0.5R, 1.5R), where R represents their design value computed by using the mechanical model suggested by Shamsabadi et al. (2007) and Wilson and Elgamal 2010, respectively. Moreover, this paper uses the Impact Material that is available in the OpenSEES database (Manual 2009) to simulate the pounding between the girder and the abutments. The pounding effective stiffness (K_eff) can be simply set as the axial stiffness of the girder, which can be expressed as

$$ K_{eff} = \frac{{E_{c} A}}{L} $$

(28)

where E_c is the Young’s modulus of concrete, A is the cross-sectional area the girder, and L is the length of the girder. Thus, similar to E_c, K_eff is also selected as a random variable that lognormally distributed with 30% of COV.

5 Sensitivity analysis of seismic responses of the case-study bridge to the modeling uncertainty parameters

5.1 Ground motions used for the sensitivity analysis

According to the guidelines for the seismic design of Chinese highway bridges (JTG/TB02-01 2008), the case-study bridge requires two probabilistic seismic design levels of E1 and E2. In which, E1 and E2 seismic design levels need the frequent earthquake evaluation and the rare earthquake evaluation. According to the seismic design of Chinese highway bridges (JTG/TB02-01 2008), the E1 level of seismic design corresponds to the earthquake with a return period of 475 years, while the E2 level corresponds to the earthquake with a return period of 2500 years. For the ground motions used for the sensitivity analysis in this section, this paper selects 22 pairs of far-field strong earthquake records recommended by the US Federal Emergency Management Agency FEMA-P695 Research Report (FEMA 2009) as the input seismic records. These far-field ground motions were originated from the measured records of 14 major earthquakes that occurred between 1971 and 1999. The detailed information for these ground motions can be found in the report (FEMA 2009). According to the given requirements in the report (FEMA 2009), the original ground motions should be first normalized based on the peak ground velocity (PGV) before using these original records. This is because such a standardized process is of great importance to reduce the effects of uncertainty in ground motions derived from the magnitude, the epicenter distance, and the site categories. Meanwhile, this normalized procedure can still keep the inherent uncertainty of the selected seismic records. Figure 3 displays the scaling of the selected ground motions under the probabilistic seismic design levels of E1 and E2 in the guidelines for seismic design of Chinese highway bridges (JTG/TB02-01 2008).

Fig. 3

Response spectra of ground motions for sensitivity analysis: a E1 level and b E2 level

As shown in Fig. 3, corresponding to the case-study bridge fundamental period of T₁ = 1.33 s, the spectral acceleration (SA) values of the selected 22 pairs of ground motions after scaling are matching well with the standard spectral acceleration. It should be mentioned herein that the recommended seismic records in the report (FEMA 2009) are derived from the strong earthquake database of the Pacific Earthquake Engineering Research Centre Ground Motion Database (PEER Ground Motion Database 2015) and each pair of seismic record contains both FP (Fault Parallel) and FN (Fault Normal) directions. Furthermore, since there are differences in spectral characteristics for each pair of seismic record, the corresponding PGA, PGV, and SA are inconsistent and varied. Thus, each pair of the seismic record should be considered as two independent ground motions, a total of 44 ground motions are employed for the following sensitivity analysis in this paper.

5.2 Sensitivity analysis of seismic responses to different modeling uncertainty parameters

In the probabilistic seismic demand analysis (PSDA) of bridge structures, it is necessary to investigate the effects of various uncertain parameters on some typical bridge EDPs (as presented in Table 3) of the case-study bridge, and based on a series of previous studies (Porter et al 2002; Celik and Ellingwood 2010; Zhong et al. 2018; Wu et al. 2018), the sensitivity analyses of seismic responses for different bridge components to the modeling related uncertain parameters are performed herein through the tornado diagram technique.

Table 3 Bridge engineering demand parameters (EDPs)

According to the work done by Celik and Ellingwood 2010, Zhong et al. (2018), and Wu et al. (2018), the sensitivity analysis with the tornado diagram technique can be carried out as follows. Firstly, all of the considered modeling related uncertain parameters listed in Table 2 are set equal to their respective median values, and then 44 nonlinear time history analyses (NLTHAs) are conducted to develop the median-value model for the critical EDPs listed in Table 3. Subsequently, this procedure is carried out repeatedly for each of the 22 modeling related uncertain parameters, in turn, varying only one at a time and setting each parameter to its lower bound (5th percentile) and upper bound (95th percentile) while holding the remaining parameters at their median values. Furthermore, after a number of NLTHAs are performed, the variation in median values of the seismic responses with each modeling uncertain parameter can be displayed through a tornado diagram (Porter et al 2002; Celik and Ellingwood 2010; Zhong et al 2018). For example, Figs. 4, 5, 6 ,7 and 8 illustrate the tornado diagram for the seismic responses, Φ_L, δ_{LRB_L}, δ_{PTEB_L}, Δ_{Abut_active}, and Δ_{Abut_passive}, under E1 and E2 designed levels of ground motions. However, it should be noted that the NLTHAs may fail to converge for some ground motions when they are scaled to a higher seismic hazard event (i.e., E2 design level). For such cases, the maximum likelihood function can be used to estimate the parameters of the lognormal probability distribution (Celik and Ellingwood 2010). This paper presents only a brief introduction of the sensitivity analysis using the tornado diagram technique, interested readers can refer to more relevant works (Celik and Ellingwood 2010; Zhong et al. 2018; Wu et al. 2018).

Fig. 4

Tornado diagrams for pier curvature (Φ_L) under different levels of ground motions

Fig. 5

Tornado diagrams for the displacement of LRB (δ_{LRB_L}) under different levels of ground motions

Fig. 6

Tornado diagrams for the displacement of PTEB (δ_{PTEB_L}) under different levels of ground motions

Fig. 7

Tornado diagrams for the displacement of abutment-active (Δ_{Abut_active}) under different levels of ground motions

Fig. 8

Tornado diagrams for the displacement of abutment-passive (Δ_{Abut_passive}) under different levels of ground motions

As seen from Figs. 4, 5, 6 ,7 and 8, for a specific tornado diagram, the longer the histogram is the higher the sensitivity of this modeling uncertain parameter is (Celik and Ellingwood 2010). In other words, the length of the histogram in a tornado diagram identifies the influential effect of the modeling related uncertain parameter, and the longer the histogram is the more significant of the modeling uncertain parameter is. It can be observed from Figs. 4, 5, 6 ,7 and 8 that the effects of different modeling related uncertain parameters impose on the seismic responses of different bridge members are significantly varied. Thus, it is necessary to consider the influence of various modeling uncertainty parameters. Sensitivity analysis through the tornado diagram technique provides new insight into the identification of the critical modeling parameters. By counting the total number of times each modeling parameter has been ranked in the top ten, we can obtain the corresponding critical parameters as summarized in Table 4, while the rest of the random parameters have much smaller or no discernible effects on the seismic responses of the given bridge components. Thus, these 10 identified critical parameters are suggested to be regarded as random variables, while the uncertainty in the other 12 remaining parameters can be neglected without resulting in a significant loss of accuracy. Hence, these 12 remaining parameters can be set to their median values (deterministic) in the FE models used for the following time-dependent seismic fragility analysis.

Table 4 Critical modeling uncertain parameters obtained from the sensitivity analysis

6 Effects of modeling uncertainty parameters on the seismic responses of the case-study bridge

6.1 Seismic responses of the pristine bridge

To qualitatively investigate the influence of modeling uncertainty parameters on the dynamic seismic responses of the case-study bridge, Fig. 9 shows a comparative study of the nonlinear dynamic seismic responses for different pristine bridge components, such as RC pier, LRB, PTEB, and abutment, obtained from the NLTHAs by using the seismic record of Northridge. The acceleration time history of Northridge ground motion is shown in Fig. 10a. As shown in Fig. 9, the given nonlinear seismic hysteretic curves with three different levels of uncertainty are developed under the Northridge ground motion. In which, uncertainty case 1, case 2, and case 3 can be referred to as “RTR Only”, “RTR + Critical”, and “RTR + All”, respectively. In specific, case 1 (“RTR only”) incorporates only the uncertainty in the ground motion and all the modeling related uncertain parameters listed in Table 2 are set equal to their median values to achieve the median-valued FE model of the case-study bridge. Similarly, case 2 (“RTR + Critical”) considers both the uncertainty of ground motion and the variability of the identified 10 critical modeling parameters by the sensitivity analysis in the previous section listed in Table 4, while case 3 (“RTR + All”) accounts for both the uncertainty of ground motion and all modeling parameters as displayed in Table 2.

Fig. 9

Seismic responses for different bridge components of the pristine case-study bridge under the Northridge ground motion: a pier, b LRB, c PTEB, and d abutment

Fig. 10

Acceleration time history curve for a ground motion #1: Northridge and b ground motion #2: Kobe seismic record

As seen from Fig. 9, after considering the uncertainty in the modeling parameters, the seismic responses of bridge components are varied significantly. The seismic response of the pristine pier tends to have a certain reduction, while that for the abutment and bearings (i.e., PTEB and LRB) have a certain increase after considering part or all of the modeling parameter variability. For example, for case 1 (“RTR Only”), when the median-valued FE model of the case-study bridge is used to perform the nonlinear time history analysis, the maximum ductility ratio of the pier bottom section (i.e., pier #1) is 2.81, whereas that for case 3 (“RTR + All”) is 2.16, which shows a reduction ratio up to 23%. Also, according to the defined damage indexes for pier under different limit states as shown in Table 6, the pristine pier tends to have slight damage for case 1 (“RTR Only”) as the median-valued FE model is employed, while it may have moderate damage for case 3 (“RTR + All”). However, the maximum relative displacement for the pristine PTEB and the abutment is 0.095 m and 0.042 m for case 1 (“RTR Only”) respectively, while it increases to 0.122 m and 0.057 m for case 3 (“RTR + All”) respectively after considering the uncertainty in all modeling parameters. The ratio of increase for the relative displacement of PTEB and the abutment is up to 28% and 36%, respectively. Thus, the effects of the variability in modeling parameters impose on different bridge members are significantly different, and this highlights the importance of modeling uncertainty parameters in evaluating the nonlinear dynamic seismic responses of highway bridges. Meanwhile, it should be mentioned herein that the effects of modeling parameter uncertainty on different bridge components’ seismic responses are random due to the combination of different uncertain parameters in generating the test sample models by using the LHS method (part (A) in Fig. 1) is a highly random process. In other words, the nonlinear seismic responses for different bridge members as shown in Fig. 9 for the cases of “RTR + Critical” and “RTR + All” are also random. Thus, Fig. 9 only shows one specific case from these infinity random cases to illustrate the influence of the modeling parameter uncertainty on the nonlinear dynamic seismic responses of the case-study bridge.

Moreover, Fig. 11 presents the nonlinear seismic responses for different critical bridge components obtained by using the NLTHAs under two different ground motions (i.e., Northridge and Kobe). The acceleration time histories for these two seismic records are shown in Fig. 10. Since all of the modeling uncertainty parameters in case 1 (“RTR Only”) equal to their respective median values (deterministic), this case can be defined as the “Deterministic model”, which only considers the uncertainty in the earthquake records, and the median-valued FE model for the case-study bridge is used to perform the NLTHAs. However, all modeling parameters in case 3 (“RTR + All”) are treated as random variables, case 3 can be defined as the “Stochastic model”, which considers both the uncertainty in ground motions and all modeling uncertain parameters. As seen from Fig. 11 (a1), (b1), (c1) and (d1), for the “Deterministic model”, due to the uncertainty of seismic records, the peak value of nonlinear seismic hysteretic curve for each component of the pristine bridge is different, while the trajectory of the seismic hysteretic curve is almost the same under the action of Northridge and Kobe seismic records. However, as it can be observed from Fig. 11 (a2), (b2), (c2) and (d2), for the “Stochastic model”, under the impact caused by the uncertainty both of the ground motions and all modeling parameters, not only the peak value but also the trajectory of seismic hysteretic response for each given bridge member may vary with the input ground motions. In addition, compared to the pier and LRB, the differences of the trajectory of seismic hysteretic response curves for PTEB and abutment are more significant due to more uncertain parameters that are related to their mechanical models are considered in this paper. Thus, these findings indicate that the difference of the trajectory of seismic hysteretic response for a specific bridge component may result from the uncertainty of modeling parameters, while the variation of the peak seismic response is caused by the joint contributions of the uncertainty of ground motions and the variability of modeling related uncertain parameters.

Fig. 11

Seismic responses for different components of the pristine case-study bridge under two different ground motions: a pier, b LRB, c PTEB, and d abutment

6.2 Seismic responses of the corroded RC columns

The proposed framework is applied to investigate the time-varying seismic response and the time-dependent seismic fragility of the case study bridge. Firstly, to determine the corrosion initiation time of steel rebars of RC columns (i.e., RC column #1 as shown in Fig. 2) under different marine exposure conditions, the Monte-Carlo simulation (MCS) method is employed to generate 10,000 samples considering the random parameters as shown in Table 1 by Eq. (3). Based on the samples generated by the MCS method, the statistical parameters of initial corrosion time for the portions of RC column #1 of the case-study bridge in different chloride exposure conditions can be obtained. Thus, detailed information concerning the statistical parameters of steel corrosion initial time estimated by using the lognormal distribution under different marine conditions is presented in Table 5.

Table 5 Statistical parameters for steel corrosion initial time under different marine conditions

As it is observed from Table 5, among these investigated marine exposure conditions, since the marine tidal zone is always evolved in a state of dry and wet alternation environment with relatively higher humidity, chloride ion content and sufficient oxygen, the corrosion initial time for both the longitudinal bars and spiral hoops in this exposure zone are less than that in other three marine environments. In addition, as seen in Table 5, the initial corrosion time of spiral hoops is less than that of longitudinal reinforcement as expected. This is because the diameter of spiral hoops and the thickness of the concrete protective layer are smaller than that of longitudinal reinforcement. Moreover, the initial corrosion time of steel bars in different marine conditions may have a significant difference up to several decades. Such a significant difference would lead to a great deviation in the degree of steel rebar corrosion in different locations of RC columns, which makes the degradation mechanism of bridge piers more complicated. Thus, it is necessary to account for the influence of inconsistent corrosion initiation time of steel bars for RC columns that are prone to the non-uniform chloride-induced corrosion attacks.

Then, according to the non-uniform chloride-induced deterioration modeling in Sect. 2, Fig. 12 shows the corresponding time-dependent material properties of RC column #1 of the case-study bridge. As observed from Fig. 12, it can be seen that the chloride-induced deterioration has a great influence on the degradation of materials. Compared with the other three different exposure conditions, the degradation of the mechanical properties of each material at the marine tidal zone is the most severe. This is consistent with the trend of the corrosion initiation time of steel bars under different chloride exposure conditions as presented in Table 5. Thus, based on the nonlinear sectional moment–curvature analysis, Fig. 13 compares the bending moment–curvature curves and the moment–curvature hysteretic curves of the bottom section for the pristine RC column 1# and the corroded columns towards 50 years and 100 years of service life for the marine tidal exposure scenario under uniform and pitting corrosion attacks.

Fig. 12

Time-dependent material properties for RC column #1: a the yield and ultimate stress of the longitudinal reinforcement, b the yield and ultimate stress of the spiral hoops, c the compressive strength of the confined and unconfined concrete, and d the ultimate strain of the confined concrete

Fig. 13

Effects of chloride ion induced corrosion on the seismic capacity and demand of RC column #1: a the bending moment–curvature curves and b the moment–curvature hysteretic response curves

As seen from Fig. 13a, due to the effect of chloride-induced corrosion, both the flexural capacity and curvature ductility of RC columns under uniform and pitting corrosion reduce significantly with the increase of service time. Furthermore, the degradation of flexural capacity and curvature ductility for pitting corrosion is generally more severe than that for uniform corrosion. For example, compare to the pristine column, there is an approximately 6.54% and 14.01% reduction in ultimate flexural capacity for uniform and pitting corrosion case at 50 years, respectively. However, the change ratio of curvature ductility reduces by 10.71% and 24.99% under uniform and pitting corrosion cases, respectively. This underlines the complexity of pitting corrosion deterioration may lead to a remarkable stress concentration and local weakening at multiple locations along the length of steel rebar. Similarly, as observed from Fig. 13b, compared to the uncorroded column, the 50-year-old corroded column reveals a 14.20% and 49.32% increase in the curvature ductility demand (calculated by φ) for uniform and pitting corrosion case respectively. In which, φ is the curvature ductility demand ratio that represents the ratio of peak curvature φ_max to the yield curvature φ_y. At the end of service life (100 years), pitting corrosion results in a 65.88% increase in peak column curvature demand compared to the pristine column, while uniform corrosion leads to only a 27.70%. These findings demonstrate that the uniform corrosion model used in most of the existing literature may underestimate the impact of chloride-induced corrosion on the seismic responses of aging highway bridges, and it indicates the significance of the non-uniform chloride-induced corrosion modeling within the time-dependent seismic fragility assessment framework for the deteriorating highway bridges.

Furthermore, although the PTEB and LRB bearings of the case-study bridge may also prone to chloride-induced corrosion attacks, bearing deterioration problems are not the focus of this paper. This paper focuses on the impacts caused by the chloride-induced deterioration on the time-variant seismic responses of the RC piers. Thus, Fig. 14 presents the comparative sectional moment–curvature hysteretic curves of 50 and 100-year-old piers under the pitting corrosion at the marine tidal zone with three different levels of uncertainty. As shown in Fig. 14, compared to hysteretic response considering only the uncertainty in the ground motions (case “RTR only”), there is a relatively significant difference from those considering the additional uncertainty of critical or all modeling parameters, and the difference tends to increase with the service life. However, the difference between the set of seismic hysteretic responses incorporating the uncertainty in ground motions as well as the critical parameters (case “RTR + Critical”) and those with the additional uncertainty in the other remaining 12 parameters (case “RTR + All”) are minimal. This indicates that the seismic hysteretic responses of RC columns are sensitive to these 10 critical parameters identified in the preceding sensitivity analysis but much less sensitive to the remaining 12 modeling related parameters.

Fig. 14

Time-variant seismic responses of RC columns under pitting corrosion with different levels of uncertainty: a 50 years and b 100 years

7 Effects of modeling uncertainty parameters on the time-dependent seismic fragility estimates of the case-study bridge

7.1 Ground motions and limit states

The selection of ground motions is critical to provide a good prediction of seismic response for the bridge structures. Based on the regional site conditions of the case-study bridge, this paper selects 50 pairs of seismic records from the PEER Centre Ground Motion Database (PEER Ground Motion Database 2015) as the input ground motions used for the time-dependent seismic fragility analysis. Figure 15a shows the response spectra of the selected ground motions. It is observed that the mean value of acceleration spectra of the selected seismic records is well consistent with the design spectrum for the case study bridge that designed according to the guidelines for seismic design of Chinese highway bridges (JTG/TB02-01 2008). The selection of an optimal intensity measure (IM) is a crucial task within the seismic fragility assessment framework, and the corresponding metrics, such as practically, efficiency, sufficiency, and hazard computability (Padgett et al. 2008; Zhou et al. 2018). For the regular RC girder bridges that are similar to the case-study bridge, the seismic response is mainly dominated by the first mode of dynamic analysis. As a consequence, the 5% damped first-mode spectral acceleration (SA) is employed as the IM for the seismic fragility analysis in this study (Li et al. 2020). Figure 15b shows the distribution of SA values for the selected ground motions. Thus, it can be observed that the selected seismic records cover a relatively broad range of SA values. For the selected ground motions, their moment magnitudes vary from 6.5 to 7.5 and their hypo-central distances range from 15 and 100 km. This shows that the selected ground motions can represent both small and large earthquakes with different epicentral distances.

Fig. 15

Response spectrum of the selected ground motions used for the time-dependent seismic fragility analysis of the case-study bridge

Within the performance-based earthquake engineering (PBEE) framework, the most widely accepted limit state definitions are proposed by HAZUS (1999), which defines four damage states, such as slight (SL), moderate (MO), extensive (EX) and complete (CO) damage states. In the seismic fragility assessment framework, structural failure or damage under a given ground motion can be generally represented in terms of the damage index (DI). According to several previous studies (Nielson 2005; Pan et al. 2007), the ductility factor can be utilized as the DI of concrete components, whereas for other bridge components, such as abutments and bearings can be indicated by the relative displacement or shear strain. This study considers the damage of RC pier, LRB, PTEB, and abutment. In addition, it should be mentioned herein that the seismic capacity of the RC column, LRB, PTEB, and abutment can be influenced by the chloride-induced corrosion attacks. This leads to the relevant damage indexes of these critical bridge members under different damage states should be time-variant. However, since the estimates of these time-dependent damage states are beyond the scope of this study, the corresponding damage indexes are considered to remain constants over time herein (Cui et al. 2018). Hence, based on the studies of Nielson (2005), the defined damage indexes under different limit states for different bridge components are summarized in Table 6, where μ_Φ is the curvature ductility at the base section of the columns, μ_z is the displacement ductility of PTEB, γ_a is the allowable shear strain of LRB, δ_active and δ_passive is the active and passive displacement of the abutment, respectively.

Table 6 Damage indexes of different bridge components under different damage states

7.2 Bridge component seismic fragilities

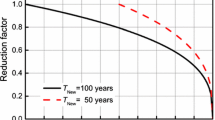
Generally, both the seismic fragility curves and fragility parameters (μ and ξ in Eq. (24)) can be utilized to assess the seismic vulnerabilities of bridges. Thus, to investigate the effects of incorporating different levels of uncertainty in the modeling parameters on the time-variant seismic fragility estimates of the case-study bridge, three cases of uncertainty treatment mentioned in Sect. 6 (“RTR only”, “RTR + All” and “RTR + Critical”) are taken into consideration herein. Due to the failure probabilities for bridge piers under the EX and CO damage states are relatively small, Fig. 16 only compares the median SA (corresponding to 50% failure probability) of RC column #1 under the SL and MO limit states. As shown in Fig. 16, compared to the median SA in case “RTR only”, there is a relatively significant difference from those in case “RTR + Critical” and “RTR + All”, and the difference tends to increase with the severity of damage states. However, the difference between the set of seismic fragility parameters (median SA) in case “RTR + Critical” and “RTR + All” are minimal. Thus, this indicates that the sensitivity of these 10 critical modeling related parameters identified in proceeding sensitivity analysis has a significant influence on the time-dependent seismic vulnerability of RC columns. However, the importance of other remaining 12 modeling parameters is negligible.

Fig. 16

Time-dependent seismic fragility parameter (median SA) of the column with different levels of uncertainty: a SL and b MO damage state

7.3 Bridge system seismic fragilities

Likewise, to investigate the effects of the modeling related uncertain parameters on the time-dependent seismic vulnerability at the bridge system level, Fig. 17 and Fig. 18 compares the system time-dependent seismic fragility curves at 50 years and 100 years of service life and median SA with three different levels of uncertainty, respectively. As observed from Fig. 17 and Fig. 18, the influences generated by different levels of uncertainty in the modeling related uncertain parameters on the system level time-variant fragility can be found similar to that on the seismic vulnerabilities at bridge component level. Thus, the results suggest that the inclusion of only the uncertainty derived from ground motions (case “RTR only”) may not adequate to evaluate the time-dependent seismic vulnerabilities of the aging highway bridges, and it is necessary to take into account the uncertainty of different modeling parameters. The results also indicate that one can reduce the number of NLHTAs and metamodel (i.e., RSM) simulations for PSDA and thereby save time as well as the computational efforts by considering the uncertainty in ground motions and the critical modeling parameters identified through the sensitivity analysis with the tornado diagram technique in the future time-dependent seismic fragility assessment for the aging highway bridges. Such an identification of significant modeling parameters by using the sensitivity analysis through the tornado diagram technique helps bridge owners and design engineers to identify the critical variables to pay attention to the design and the corresponding seismic performance evaluation of bridge structures.

Fig. 17

System time-dependent seismic fragility curves with different levels of uncertainty: a 50 years; b 100 years

Fig. 18

System time-dependent seismic fragility parameter (median SA) with different levels of uncertainty: a SL; b MO; c EX and d CO damage state

8 Conclusions and future work

This paper proposes a schematic time-dependent seismic fragility assessment framework for the aging highway bridges considering various modeling uncertainty parameters and the non-uniform chloride-induced deterioration. A total of 22 modeling uncertain parameters from three aspects are probabilistically characterized. A variety of bridge EDPs such as the column curvature, displacement of LRB, and PTEB in the longitudinal direction, as well as the abutment deformation both in the active and passive directions are utilized as the measures to investigate the sensitivity of the seismic responses to these modeling uncertainty parameters. Then, 10 critical parameters are identified via the sensitivity analysis with the tornado diagram technique, and we suggest that these identified critical parameters should be treated as random variables, while the remaining 12 parameters can be regarded as deterministic by setting equal to their respective median values. Then, the findings of the sensitivity analysis are extended to investigate the influence of incorporating different levels of uncertainty on the seismic responses of the pristine and corroded case-study bridge, as well as the time-dependent seismic fragility estimates both at the bridge component and system level. Finally, the following conclusions can be summarized as.

• (1) The difference of the trajectory of seismic hysteretic response for a given bridge member may vary due to the uncertainty of modeling parameters, whereas the variation of the peak seismic response may vary due to the joint contributions of the ground motion uncertainty and modeling parameters variability.

• (2) It is essential to consider the variability of these identified critical parameters because their uncertainty has considerable effects on the seismic demand models, seismic responses, and time-dependent seismic fragility estimates of highway bridges.

• (3) The differences of the developed time-dependent seismic fragilities between the case of “RTR + Critical” and “RTR + All” are negligible. In which, case “RTR + Critical” considers the uncertainty in ground motions and the variability of the identified critical parameters, while the case “RTR + All” incorporates the uncertainty in seismic records and all modeling parameters. Thus, sensitivity analysis with the tornado diagram technique is an ideal candidate approach to identify the critical parameters, and it helps reduce the number of nonlinear simulations and minimizing the computational efforts in the time-dependent seismic fragility estimates of the aging highway bridges.

While this paper proposes an alternative time-dependent seismic fragility assessment framework incorporating the influence of non-uniform chloride-induced corrosion and various modeling related uncertain parameters, the present study only focused on the deterioration of RC columns. Future work will consider the realistic deterioration modeling of other critical bridge components (such as bridge bearings and the abutments), and the time-variant damage indexes for these bridge components should be further defined. In addition, this paper only performs the sensitivity analyses to identify some critical parameters from various aspects of modeling uncertainty parameters. However, the deterioration parameters that are related to the non-uniform chloride-induced corrosion to different bridge members (i.e., RC piers, bearings, and abutments) should be incorporated in the range of the investigated uncertain parameters to determine the critical parameters. Thus, a more coherent and extensive sensitivity analysis approach to identify the critical parameters from various modeling and deterioration related uncertain parameters can be incorporated in the future time-dependent seismic fragility and life-cycle loss assessment framework of the deteriorating highway bridges. Furthermore, a more complete and meticulous study should be performed in the future to investigate several problems such as how to set and determine the appropriate threshold value in determining the critical parameters identified from for a set of random variables by using the sensitivity analyses with the tornado diagram technique.