Coherency model for translational and rotational ground motions

Abstract

Spatial variability of the translational ground motion may influence the seismic design of certain civil engineering structures with spatially extended foundations. Lagged coherency is usually considered to be the best descriptor of the spatial variability. Most coherency models developed to date do not consider the spatial variability of the spectral shape of auto-spectral density (ASD), which is expected to be critical. This paper proposes a coherency model that accounts for the variability in spectral shape of ASD. Numerical results illustrate that the effect is not that critical for a dense array but can be significant in case of large array. Rotational ground motions on the other hand are not measured by the accelerograph deployed in the free-field owing to the unavailability of appropriate instruments and rather extracted from the recorded three-component translational data. Previous studies [e.g., Basu et al. (Eng Struct 99:685–707, 2015)] reported the spatial variability of extracted rotational components, even over a dimension within the span of most civil engineering structures, for example, tens of metres. Since rotation does not propagate like a plane wave, coherency model based on plane wave propagation does not apply to address the spatial variability of rotational components. This paper also proposes an alternative to address the spatial variability of rotational components. Illustrations based on relatively short separation distance confirm the expectation.

1 Introduction

Spatial variability of ground motion is primarily contributed from four distinct effects, namely, the incoherence effect, wave passage effect, attenuation effect and site-response effect. Spatial variability of free-field translational ground motion could be significant within the dimension of a typical engineered structure (Schneider et al. 1992; Vanmarcke 1992; Harichandran 1991; Zerva and Zervas 2002) and seismic array provides a unique opportunity to study the spatial variability. This has led to considerable research in the last two decades on modelling the spatially varying horizontal and vertical ground motions. Coherency and some of its variants are generally used as a measure of the spatial variability. Denoting f as the frequency in Hz, coherency between two time series x₁(t) and x₂(t) is given by the ratio of cross-spectral density (CSD) to auto-spectral density (ASD) and hence, can be expressed mathematically as

$$ \gamma (f) = \frac{{S_{{x_{1} x_{2} }} \left( f \right)}}{{\sqrt {S_{{x_{1} x_{1} }} \left( f \right)S_{{x_{2} x_{2} }} \left( f \right)} }}{\text{ where}}\,S_{{x_{1} x_{2} }} \,{\text{is}}\,{\text{the}}\,CSD\,{\text{between}}\,x_{1} (t)\,{\text{and}}\,x_{2} (t) $$

(1)

Lagged coherency is defined as the absolute value of coherency (|γ(f)|) and often used to describe the spatial variability instead the true coherency. In that case, it is obvious that |γ(f)| = 1 at all frequencies and hence, spectral densities (ASD and CSD) are smoothed (for example, using Hamming window) before computing the lagged coherency.

Usually, one seismic event recorded over the footprint of an array is considered and lagged coherency is numerically computed for all possible station-pairs. Since the station-pairs are characterized by their separation distance, under the assumption of rotational invariance and spatial uniformity of earthquake field, lagged coherency is assumed to be dependent on separation distance and frequency contents. An appropriate functional form is then assumed and the associated constants are evaluated in a best-fit sense through the numerical coherency data. A number of researchers have studied the characteristics of translational ground motion and its spatial variability, and lagged coherency was reported to be reducing with the increasing separation distance and frequency.

For example, Harichandran and Vanmarcke (1986) reported an empirical coherency form which is a sum of two exponential forms and given by

$$ \left| {\gamma (\nu ,f)} \right| = A\exp \left[ { - \frac{2\nu }{\alpha \theta (f)}(1 - A + \alpha A)} \right] \, + (1 - A)\exp \left[ { - \frac{2\nu }{\theta (f)}(1 - A + \alpha A)} \right] $$

(2)

Here, θ(f) = k(1 + (f/f _o )^b)^−1/2 is a frequency dependent spatial scale of fluctuation; ν is the distance and all other parameters ($A,\alpha ,f_{o} ,b\,{\text{and}}\,k$) will have to be estimated by the regression analysis. Hao (1996) reported another coherency model, which is given by

$$ \begin{aligned} \gamma (x,y,\omega ) = \exp \left( {\left( { - \alpha_{1} (\omega )x^{2} - \alpha_{2} (\omega )y^{2} } \right)\omega } \right)*\exp \left( { - \frac{i\omega x}{{v_{a} }}} \right) \, \hfill \\ \alpha_{i} (\omega ) = \frac{{a_{i} }}{{b_{i} + \ln (\omega )}}, \, \omega \ge 0.314{\text{ rad/sec}}, \quad\, i = 1,2 \hfill \\ \end{aligned} $$

(3)

where ω is the circular frequency, v _a is the apparent propagation velocity, x and y are distances between stations along and perpendicular to the wave propagation, respectively, a _i and b _i are to be determined by regression analysis. Besides, among many others, Loh (1985) studied the spatial variability over the SMART1 array and Ye et al. (2011) reported the coherency model for the vertical ground motion. Most coherency models are proposed targeting the seismic arrays, where stations are separated in the range of a few hundred meters to a few kilometers. Such a large civil engineering structures where these models can be applied include bridges, dams etc. Most civil engineering structures are of spatial dimensions less than 100 m and in such cases, effect of spatial variability should be assessed using a coherency model developed based on data recorded over the footprint of dense array with station separation of the order of a few or tens of meters. Abrahamson et al. (1991) reported such a coherency model, which is of the form

$$ \tanh^{ - 1} \left| {\gamma \left( {f,\xi } \right)} \right| = \left( {a_{1} + a_{2} \xi } \right)\left[ {\exp \left\{ {\left( {b_{1} + b_{2} \xi } \right)} \right\} + \frac{1}{3}f^{c} } \right] + k $$

(4)

where $a_{1} ,a_{2} ,k,b_{1} ,b_{2} \,{\text{and}}\,c$ are model parameters, ω is frequency in Hz and ξ is the separation distance in meters. Even though the fitting might be satisfactory in inverse hyperbolic form, deviation can be significant once model is compared with numerical coherency in normal scale. Further, most of the coherency model proposed to date are empirical in nature. Most researchers prefer developing empirical coherency models over semi-empirical and analytical because of (1) large scatter in data; (2) variability in data recorded at different sites and different events; and (3) differences in numerical processing of the data. Zerva (2016) has discussed this issue in details. One of the objectives of present paper is to develop a unified coherency model from the first principle that can be applied to both large and dense seismic arrays, and in other words, can be used to address the spatial variability in civil engineering structures regardless of spatial dimension.

Rotational ground motion may contribute significantly to the response of certain structures but their effects are generally ignored in seismic design partly because these components are not measured by the accelerographs deployed in the free-field owing to the non-availability of appropriate instruments (Basu et al. 2012). A number of researchers reported the effect of rotational ground motion on structural response including Newmark (1969), Hart et al. (1975), Bycroft (1980), Wolf et al. (1983), De La Llera and Chopra (1994), Zembaty and Boffi (1994), Zembaty (2009), Politopoulos (2010), Ghafory-Ashtiany and Falamarz-Sheikhabadi (2010), Falamarz-Sheikhabadi and Ghafory-Ashtiany (2012, 2015), Basu et al. (2014), Falamarz-Sheikhabadi (2014), Basu and Giri (2015), Basu et al. (2015), and Falamarz-Sheikhabadi et al. (2016). Despite these studies, the lack of consensus about the effect of rotational ground motions can be attributed to the use of different interpretations of rotation, namely, the free-field or point rotation, chord rotation and averaged rotation. Free-field rotation is defined as the spatial derivative of the displacement field at that instant; chord rotation is the ratio of the difference in displacements between two closely spaced, adjacent stations measured along a direction perpendicular to the line joining the two stations; and average rotation is the average of chord rotations of several station pairs with one common station. Luco and Wong (1986) studied the effect of spatially random ground motion on a rigid foundation. A rigid foundation will filter the high frequency components of free-field motion although foundations are never infinitely stiff (Basu et al. 2013). Accordingly, average rotation may be the best choice because chord rotation is usually sensitive to separation distance and point rotation ignores the presence of a foundation. Regardless of the choice of rotation, free-field ground motions are in general preferred in seismic design and effect of foundation flexibility is separately accounted for in a case-by-case.

Many attempts have been made to date on measuring the rotational ground motion in free-field (Yin et al. 2016; Liu et al. 2009; Nigbor et al. 2009) and a comprehensive list of literature up to 2009 was reported in the special publication of Bulletin of the Seismological Society of America (BSSA), 99(2B). Nevertheless, direct recording of rotational ground motion in free-field is still at the research level and it will take, perhaps, a long time before achieving a general agreement for its deployment with desired confidence level on the expected outcome. Owing to the challenges associated with direct recording of rotational motion, a number of indirect methods on extracting the same using the three-component translational acceleration data have been reported. These indirect methods are of two types: (1) one uses the translational data recorded over a footprint of array and referred to multiple station procedures (MSP), and Basu et al. (2013) provides a review of available MSPs; and (2) the other type uses the data recorded at one single station and referred to single station procedure (SSP). Basu et al. (2012) reviewed the available SSPs and reported a robust framework.

Theoretically, rotation doesn’t propagate in the form of plane waves like translation, and hence, it may be inappropriate to estimate the spatial variation of rotational motion using coherency models. But, if the rotational motion is estimated in terms of temporal derivative of a translational motion with due scaling and the focus is limited to a functional form analogous to lagged coherency, it is possible to estimate the spatial variability of rotational motion completely in terms of spatial variability of the respective translational motion. Rodda and Basu (2017a) defined such apparent translational component (ATC) for the torsional and rocking motions under suitable assumptions and the resulting rotational components are in well agreement with more rigorous approach reported by Basu et al. (2012). One of the objectives of present paper is to extend the coherency model to rotational ground motion using the analogy of ATC.

This paper first presents the theoretical development of a unified coherency model for the translational ground motion under suitable assumptions. The proposed model is then compared with three well-known coherency models (Harichandran and Vanmarcke 1986; Hao 1996; Abrahamson et al. 1991) and recording over a dense array (Large Scale Seismic Testing (LSST) array) is used for this comparison. Proposed coherency model is then verified against recording over a large seismic array (SMART1 array in Lotung, Taiwan). Both horizontal and vertical lagged coherency are used in these illustrations. Next the (lagged) coherency model is extended to rotational ground motion and its performance is demonstrated with the help of dense array recording. Note that rotational motion considered here is not recorded and rather extracted through the recorded translational motion over the footprint of a dense array.

Proposed coherency model is then used to study the event-to-event variability of lagged coherency as a function of frequency and separation distance. LSST array is chosen to study the variation against small separation distance whereas SMART1 array is considered for the larger separation distance. Station-pairs were divided into different bins and the numerical coherency in a specific bin at each frequency is sorted from the smallest to largest values to get the “median coherency”. The calculated median coherency is regressed thorough the proposed coherency model to estimate the theoretical coherency, which is used to study the event-to-event of variability. This study is further extended to rotational components at LSST array. Also, spatial coherency loss is studied at some discrete frequencies: translational ground motions are studied at both the arrays whereas rotational motions are considered only at the LSST array.

The notation of the parameters/variables given up to this point is limited to the introductory part only. The symbols will be redefined in the remaining part of this paper as and when necessary.

2 Formulation of translational acceleration field for coherency model

Let j and k be two surface stations, separated by some distance with a vector representation of $\bar{u}$ and plane wave propagating over the ground surface is given by its velocity vector $\bar{c}$. Further arrival time at station k is assumed to be delayed by t _o when compared to that at the station j. Now representing the change in acceleration at station k with respect to station j (as the wave propagates from j to k) as h(t, u), the recorded acceleration time series at the both the stations may be related as

$$ x_{k} \left( {t,u} \right) = h\left( {t,u} \right) * x_{j} \left( {t - t_{o} } \right) + r\left( {t,u} \right)\,{\text{where}}\,t_{o} = \frac{{\bar{c} \times \bar{u}}}{{\left| {\bar{c}} \right|^{2} }} $$

(5)

Here, * indicates convolution. Further, r(t, u) is a random component contributed from several sources of uncertainty, and is assumed to be of zero mean and uncorrelated with the signals at recording stations. Employing the shift theorem, Fourier transform of Eq. (5) may be written as

$$ X_{k} \left( {f,u} \right) = H\left( {f,u} \right)e^{{ - i2\pi ft_{o} }} X_{j} \left( f \right) + R\left( {f,u} \right) $$

(6)

where f is the frequency, X _j , X _k and Rare the Fourier transforms of the recorded motions at stations j and k, and the random motion, respectively. The function H(f, u) describes the amplitude decay of each frequency with respect to distance. The function H(f, u) in the proposed model accounts for not only the attenuation effect of wave amplitude but also the effect due to incoherence. This illustrated in what follows through comparing the acceleration field in proposed model with that considered in Der Kiureghian (1996).

2.1 Comparison of acceleration field with Der Kiureghian (1996)

Der Kiureghian (1996) proposed a theoretical coherency model characterizing the distinct effects of spatial variability, namely, the incoherence effect, wave passage effect, attenuation effect and site-response effect. In absence of site response effect, then acceleration assumed by Der Kiureghian (1996) at stations j and k (x _j and x _k , respectively) are given by

$$ \begin{aligned} &x_{j} \left( t \right) = \sum\limits_{i = 1}^{i = n} {A_{i} F\left( {f_{i} ,r_{j} } \right)\cos \left( {2\pi f_{i} t + \varphi_{i} } \right)} \hfill \\ &x_{k} \left( t \right) = \sum\limits_{i = 1}^{i = n} {\left( {p_{jk,i} A_{i} + q_{jk,i} B_{i} } \right)F\left( {f_{i} ,r_{k} } \right)\cos \left( {2\pi f_{i} \left( {t - \tau_{jk,i} } \right) + \varphi_{i} + \varepsilon_{jk,i} } \right)} \hfill \\ \end{aligned} $$

(7)

Here, i stands for the harmonic; A _i is the amplitude of ground acceleration in absence of wave amplitude attenuation; ϕ _i is the phase; function F(f _i , r _j ) is the wave amplitude attenuation for a station with epicentral distance r _j ; B _i represents the incoherent portion of the amplitudes; ɛ_jk,i is the random phase difference with variance α ²_jk,i ; τ_jk,i is the travel time for wave to reach station k from j; and p_jk,i and q_jk,i are deterministic coefficients defined in the interval (0, 1). If the attenuation function F(f, r) is assumed to be deterministic, corresponding coherency model is given by

$$ \gamma \left( {f,u} \right) = \cos \left( {\beta \left( {f,u} \right)} \right)e^{{\left[ { - 0.5\alpha^{2} \left( {f,u} \right)} \right]}} e^{{i\theta \left( {f,u} \right)^{wave \, passage} }} $$

(8)

where β(f, u) = cos⁻¹p _jk .

Re-writing the Eq. (7) in frequency domain, Fourier transforms of accelerations at stations j and k are given by

$$ X_{j} \left( f \right) = A\left( f \right)F\left( {f,r_{j} } \right)e^{ - i\varphi } $$

(9)

$$ X_{k} \left( f \right) = \left( {p_{jk} \left( f \right)A\left( f \right) + q_{jk} \left( f \right)B\left( f \right)} \right)F\left( {f,r_{k} } \right)e^{{ - i\left( {2\pi f\tau_{jk} + \varphi_{i} + \varepsilon_{jk} } \right)}} $$

(10)

Here, f is the frequency, X _j and X _k are the Fourier transforms of the recorded motions at stations j and k. Substitution of Eq. (9) into Eq. (10) leads to the following relation between the Fourier transforms of accelerations at stations j and k

$$ X_{k} \left( f \right) = p_{jk} \left( f \right)\frac{{F\left( {f,r_{k} } \right)}}{{F\left( {f,r_{j} } \right)}}e^{{ - i\varepsilon_{jk} }} e^{{ - i2\pi f\tau_{jk} }} X_{j} \left( f \right) + q_{jk} \left( f \right)B\left( f \right)F\left( {f,r_{k} } \right)e^{{ - i\left( {2\pi f\tau_{jk} + \varphi + \varepsilon_{jk} } \right)}} $$

(11)

Equation (11) can be compared with the acceleration filed of the proposed method per Eq. (6), where,

$$ \begin{aligned} H\left( {f,u} \right) = p_{jk} \left( f \right)\frac{{F\left( {f,r_{k} } \right)}}{{F\left( {f,r_{j} } \right)}}e^{{ - i\varepsilon_{jk} }} \hfill \\ R\left( {f,u} \right) = q_{jk} \left( f \right)B\left( f \right)F\left( {f,r_{k} } \right)e^{{ - i\left( {2\pi f\tau_{jk} + \varphi + \varepsilon_{jk} } \right)}} \hfill \\ \end{aligned} $$

(12)

Therefore, acceleration field assumed in both proposed and Der Kiureghian (1996) models are consistent. Despite the similarity in assumed acceleration fields, it is instructive to point out the differences in two coherency models as explained below.

Equation (12) shows that the amplitude decay function H(f, u) in proposed model accounts for the incoherent effect through p _jk (f)and the attenuation effect through F(f, r). Similarly, R(f, u) in the proposed model accounts for the attenuation effect and randomness in ground motion through F(f, r)and q _jk (f)B(f), respectively. Therefore, all the three effects, namely, incoherence, wave passage and attenuation are considered in the proposed model but not their mutual independence, as opposed to Der Kiureghian (1996).

This completes the discussion on comparison of acceleration fields of proposed method and Der Kiureghian (1996).

2.2 Formulation of coherency model for translational ground motions

According to Eq. (6), auto-spectral density (ASD) functions at the station k is given by

$$ \begin{aligned} S_{kk} \left( {f,u} \right)& = \frac{1}{T}X_{k}^{*} \left( {f,u} \right)X_{k} \left( {f,u} \right) \hfill \\ &= \frac{1}{T}\left( {H^{*} \left( {f,u} \right)e^{{i2\pi ft_{o} }} X_{j}^{*} \left( f \right) + R^{*} \left( {f,u} \right)} \right)\left( {H\left( {f,u} \right)e^{{ - i2\pi ft_{o} }} X_{j} \left( f \right) + R\left( {f,u} \right)} \right) \hfill \\ \end{aligned} $$

(13)

Since the random component is uncorrelated with the recorded signals, Eq. (13) may be further simplified to

$$ S_{kk} \left( {f,u} \right) = \left( {\left| {H\left( {f,u} \right)} \right|^{2} S_{jj} \left( f \right) + S_{rr} \left( {f,u} \right)} \right) $$

(14)

Similarly, the cross-spectral density between the ground motions at stations j and k is given by

$$ S_{jk} \left( {f,u} \right) = \frac{1}{T}X_{j}^{*} \left( f \right)\left( {H\left( {f,u} \right)e^{{ - i2\pi ft_{o} }} X_{j} \left( f \right) + R\left( {f,u} \right)} \right) $$

(15)

Thereafter, utilizing the assumption of uncorrelated signal(s) and random components,

$$ S_{jk} \left( {f,u} \right) = H\left( {f,u} \right)e^{{ - i2\pi ft_{o} }} S_{jj} \left( f \right) $$

(16)

Resulting coherency is then given by

$$ \gamma_{jk} \left( {f,u} \right) = \frac{{S_{jk} \left( {f,u} \right)}}{{\sqrt {S_{jj} \left( f \right)S_{kk} \left( {f,u} \right)} }} = \frac{{H\left( {f,u} \right)e^{{ - i2\pi ft_{o} }} S_{jj} \left( f \right)}}{{\sqrt {S_{jj} \left( f \right)\left( {\left| {H\left( {f,u} \right)} \right|^{2} S_{jj} \left( f \right) + S_{rr} \left( {f,u} \right)} \right)} }} $$

(17)

2.3 Functional form for ASD of random component (S _rr (f, u))

Now, two extreme cases are considered: (1) no change in amplitude (H(f, u) ≈ 1) with random motion ceases to exist (S _rr  ≈ 0 & S _kk  ≈ S _jj ) when the separation distance is close to zero and ii) significant change in amplitude (H(f, u) ≈ 0) with maximum random motion contribution to auto-spectral density at station k(S _kk  ≈ S _rr  = S _o ) when the stations are infinitely/well separated. In compliance with these two scenario, auto-spectral density of random motion is assumed to be a product of functions of both the amplitude decay and the frequency. Hence, following functional from for ASD of random component is assumed in this paper:

$$ S_{rr} \left( {f,u} \right) = \ell \left( {H\left( {f,u} \right)} \right)S_{o} \left( f \right) $$

(18)

Note (1) Amplitude decay is a function of frequency and separation distance; (2) S _o is the ASD at an infinitely away station and function of frequency only; and (3) Limits of amplitude decay vary from one (for the station pair close to each other) to zero (for an infinitely away pair). Hence,

$$ \begin{aligned} H\left( {f,u} \right) \approx 1 \Rightarrow S_{rr} \approx 0 \Rightarrow S_{kk} \approx S_{jj} \& \ell \left( {H\left( {f,u} \right)} \right) \approx 0 \hfill \\ H\left( {f,u} \right) \approx 0 \Rightarrow S_{rr} \approx S_{o} \Rightarrow S_{kk} \approx S_{o} \& \ell \left( {H\left( {f,u} \right)} \right) \approx 1 \hfill \\ \end{aligned} $$

(19)

In compliance with the two scenario shown in Eq. (19), ASD of ground motion at station k, which is at a distance $u \, ({\text{somewhere}}\,{\text{between}}\,0\,{\text{and}}\,\infty )$ from station j can be assumed as the weighted average of ASD of ground motion at station $j \, \left( {S_{jj} } \right)$ and ASD of ground motion at an infinitely away station (S _o ).

From Eq. (14), it can be seen that weight of S _jj is |H(f, u)|², hence, weight for $S_{rr} \left( {f,u} \right), \, \ell \left( {H\left( {f,u} \right)} \right),$ is 1 − |H(f, u)|²

$$ \begin{aligned} \ell \left( {H\left( {f,u} \right)} \right) &= 1 - \left| {H\left( {f,u} \right)} \right|^{2} \hfill \\ S_{rr} \left( {f,u} \right) &= \left( {1 - \left| {H\left( {f,u} \right)} \right|^{2} } \right)S_{o} \left( f \right) \hfill \\ \end{aligned} $$

(20)

Substituting the Eq. (20) into Eq. (14)

$$ S_{kk} \left( {f,u} \right) = \left| {H\left( {f,u} \right)} \right|^{2} S_{jj} \left( f \right) + \left( {1 - \left| {H\left( {f,u} \right)} \right|^{2} } \right)S_{o} \left( f \right) $$

(21)

Utilizing Eqs. (20), (17) may be simplified to

$$ \begin{aligned} \gamma_{jk} \left( {f,u} \right) = \frac{{H\left( {f,u} \right)e^{{ - j2\pi ft_{o} }} S_{jj} \left( f \right)}}{{\sqrt {S_{jj} \left( f \right)\left( {\left| {H\left( {f,u} \right)} \right|^{2} S_{jj} \left( f \right) + \left( {1 - \left| {H\left( {f,u} \right)} \right|^{2} } \right)S_{o} \left( f \right)} \right)} }} \hfill \\ \, = e^{{ - j2\pi ft_{o} }} \left( {1 + \left( {\frac{1}{{\left| {H\left( {f,u} \right)} \right|^{2} }} - 1} \right)\frac{{S_{o} \left( f \right)}}{{S_{jj} \left( f \right)}}} \right)^{ - 0.5} \hfill \\ \end{aligned} $$

(22)

The associated lagged coherency is given by

$$ \begin{aligned} &\left| {\gamma_{jk} \left( {f,u} \right)} \right| = \left( {1 + \left( {\frac{1}{{\left| {H\left( {f,u} \right)} \right|^{2} }} - 1} \right)\frac{{S_{o} \left( f \right)}}{{S_{jj} \left( f \right)}}} \right)^{ - 0.5} = \left( {1 + g_{1} \left( {f,u} \right)g_{2} \left( f \right)} \right)^{ - 0.5} \hfill \\ &g_{1} \left( {f,u} \right) = \frac{1}{{\left| {H\left( {f,u} \right)} \right|^{2} }} - 1 \hfill \\ &g_{2} \left( f \right) = \frac{{S_{o} \left( f \right)}}{{S_{jj} \left( f \right)}} \hfill \\ \end{aligned} $$

(23)

2.4 Functional forms for H(f, u)

Even though the amplitude decay H(f, u) (incoherence effect as well as attenuation effect) depends on both frequency and distance, for the sake of simplicity, the amplitude decay is henceforth assumed to be frequency independent. One may argue that the change in the wave amplitude mostly depends on the frequency rather than distance at short separation distances. However, this is significant at frequencies higher than the range of interest to the most civil engineering structures. Hence, the amplitude decay may be assumed to be frequency independent without losing generality. In other words, this paper deals with the amplitude decay as a function of only distance. Further, if the contribution of random component to the ground motion is ignored, H(u)describes how the amplitude of each Fourier coefficient attenuates with respect to distance. This is analogous to the median estimates of Ground Motion Prediction Equations (GMPEs) for intensity measures like PGA and PGV against the epicentral distance Margaris et al. (2004). This paper proposes two alternatives for the amplitude decay.

One possible functional form for the amplitude decay may be considered as exponential and hence,

$$ \left| {H\left( u \right)} \right| = e^{ - \beta u} , \, \beta > 0 $$

(24)

Accordingly, from Eq. (23),

$$ g_{1} \left( u \right) = \left( {\frac{1}{{\left| {H\left( {f,u} \right)} \right|^{2} }} - 1} \right) = \left( {e^{2\beta u} - 1} \right) $$

(25)

Another possible functional form for amplitude decay can be considered as the

$$ \left| {H\left( u \right)} \right| = \left( {1 + a_{1} u} \right)^{{ - a_{2} }} , \quad a_{1} ,a_{2} > 0 $$

(26)

Accordingly, from Eq. (23), another possible functional form for g₁(u)is

$$ g_{1} \left( u \right) = \left( {\left( {1 + a_{1} u} \right)^{{2a_{2} }} - 1} \right) $$

(27)

2.5 Functional form for g ₂(f)

The only function left to be estimated is g₂(f) = S _o (f)/S _o (f)S _jj (f) × S _jj (f). Recently, the authors have reported a parametric form for ASD of ground motion S(f) as follows (Rodda and Basu 2017b):

$$ S(f) = \sum\limits_{i = 1}^{n} {\frac{{A_{i} }}{f}\exp \left( { - \frac{{(\log (f) - \mu_{\log f,i} )^{2} }}{{2\sigma_{\log f,i}^{2} }}} \right)} , \, n{\text{ is the number of modes}} $$

(28)

Here, μ_logf and σ_logf are related to the central frequency (f _c ) and the frequency spread (f _s ) as

$$ \mu_{\log f} = \log \left( {{{f_{c} } \mathord{\left/ {\vphantom {{f_{c} } {\sqrt {1 + {\raise0.7ex\hbox{${f_{s}^{2} }$} \!\mathord{\left/ {\vphantom {{f_{s}^{2} } {f_{c}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{c}^{2} }$}}} }}} \right. \kern-0pt} {\sqrt {1 + {\raise0.7ex\hbox{${f_{s}^{2} }$} \!\mathord{\left/ {\vphantom {{f_{s}^{2} } {f_{c}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${f_{c}^{2} }$}}} }}} \right), \, \sigma_{\log f}^{{}} = \sqrt {\log \left( {1 + \frac{{f_{s}^{2} }}{{f_{c}^{2} }}} \right)} $$

(29)

Theoretically, both S _jj (f)and S _o (f)are expected to be parameterized by Eq. (28) with some of the high frequency modes attenuated/suppressed in the latter. However, the ratio S _o (f)/S _o (f)S _jj (f) × S _jj (f)is difficult to parameterized using Eq. (28) and instead, hypothesized as

$$ g_{2} \left( f \right) = \sum\limits_{i = 1}^{n} {A_{i} e^{{ - \, \frac{{\left( {f - \mu_{i} } \right)^{2} }}{{2\sigma_{i}^{2} }}}} } $$

(30)

The resulting coherency model is

$$ \gamma_{jk} \left( {f,u} \right) = \left| {\gamma_{jk} \left( {f,u} \right)} \right|e^{{ - j2\pi ft_{o} }} {\text{ and }}\left| {\gamma_{jk} \left( {f,u} \right)} \right| = \left( {1 + g_{1} \left( u \right)\sum\limits_{i = 1}^{n} {A_{i} e^{{ - \, \frac{{\left( {f - \mu_{i} } \right)^{2} }}{{2\sigma_{i}^{2} }}}} } } \right)^{ - 0.5} $$

(31)

Note that any functional form of g₁(u) [from Eqs. (25) and (27)] can be substituted in Eq. (31) to define the coherency model. Since the proposed coherency model is regressed over the frequency for a particular distance u, the choice of functional form for g₁(u) will not affect the results that are going to be presented in the following sections. This is because g₁(u) will be absorbed into the parameter A _i and will produce the same results. However, the choice of functional form for g₁(u) may affect the results slightly if the proposed coherency model is regressed over the footprint of array (along the distance) for a particular frequency, which is not discussed in the present paper. The hypothesis of Eq. (30) will be verified while presenting the illustration on proposed coherency model.

The parameters of the coherency model are to be calculated from the numerical data through regression analysis and the number of modes, n, is to be selected/assessed a priori. Towards this, a recursive procedure is recommended: (1) start with single mode and estimate the model parameters in a best-fit sense; (2) extract the residue and repeat the first step; (3) continue first two steps until the amplitude of the extracted mode is less than 1/10th of that of the first mode. This completes the description of the proposed coherency model.

3 Illustrations on translational coherency model

Proposed coherency model will now be evaluated with respect to the recorded ground motion. Two different seismic arrays are considered for this purpose, namely, Large Scale Seismic Testing (LSST) array and SMART1 array in Lotung, Taiwan. Description of the arrays and the considered seismic events are presented next.

3.1 Description of seismic array and events considered

3.1.1 LSST array, Lotung

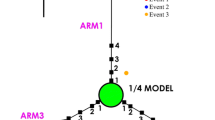
The Large Scale Seismic Test (LSST) array in Lotung, Taiwan is a part of the much larger SMART1 array. Figure 1 shows the layout of the surface stations: three arms at an interval of approximately 120 ° with five stations each. Length of each arm is about 50 m and the spacing between the surface stations is in the range of 3–90 m. The stations in each arm are numbered from 1 to 5, starting at the centre of the array. For example, FA2_5 denotes the outermost station (station 5) located on arm 2. The average wave velocities at the surface of the recording site are: 595 and 140 m/sec for the P and S waves, respectively (Wen and Yeh 1984). Further details on the site characteristics, instrumentation and recorded seismic events are available at the following website: http://www.earth.sinica.edu.tw/~smdmc/llsst/llsst.

Fig. 1

LSST array, Lotung (http://www.earth.sinica.edu.tw/~smdmc/llsst/llsstfs.htm)

Ground motion was recorded in LSST array along the East-West (EW), North-South (NS) and vertical directions. Defining the vertical plane comprising of the epicentre and the recording station as the principal plane, most of the energy is reported to be travelling on this principal plane to the station and the three rotated components along and normal to the principal plane are uncorrelated (Penzien and Watabe 1974). The recorded horizontal accelerations (EW and NS) are rotated along and normal to the principal plane to enable extraction of the rotational components, which will be explored in later part of this paper. The rotated horizontal components along and normal to the principal planes are denoted in this paper as a_g1 and a_g3, respectively, and the vertical acceleration is a_g2. Three strong motions events recorded at the LSST array are considered for illustration in this paper and a brief description of each event is presented in Table 1. Event-3 may exhibit some near-field characteristics as the epicentral distance is approximately 24 km. Only surface stations are considered in the analysis and out of 15, usually, 11–14 actually functioned during the events. Hence, number of surface stations analysed here varies from one event to another.

Table 1 Strong motion events considered—LSST array

3.1.2 SMART1 array, Lotung

SMART1 is a Strong Motion array located in Lotung, in the north-east corner of Taiwan. It consists of 37 force-balanced tri-axial accelerometers arranged on three concentric circles and one central station. Radii of inner, middle and outer circles are 0.2, 1 and 2 km, respectively. The inner ring is denoted by I, the middle by M, and the outer by O. Twelve uniformly spaced stations, are located on each ring and numbered 1–12 and station C00 is located at the centre of the array (Fig. 2).

Fig. 2

SMART1 array, Lotung (Zerva and Zervas 2002)

Ground motion was recorded in SMART1 array along the EW, NS and vertical directions. Five strong motions events recorded at the SMART1 array (ground motions taken from PEER database—http://ngawest2.berkley.edu/) are considered for illustration in this paper and a brief description of three of the events is presented in Table 2. The data recorded during Events 1 and 2 (described in Table 1) at SMART1 array is also considered for analysis. Further information about the events can be found at the following website: http://www.earth.sinica.edu.tw/~smdmc/smart1/smart1.

Table 2 Strong motion events considered—SMART1 array

3.2 Verification of hypothesis

Event-4 (Table 2) recorded over the SMART1 array is considered for this purpose. Due to the non-availability of ground motion at two infinitely away stations, two farthest stations O06 and O12 (Fig. 2) are chosen and numerical ASDs (S_O06 and S_O12) are computed. Direction of arrival for this event is from O06 to O12 and hence, as per the hypothesis, the ratio S_O12/S_O06 is calculated as a function of frequency. Such a variation is presented in Fig. 3a–c for the EW, NS and Vertical directions, respectively. Also included in these panels are the best-fit per Eq. (30). The resemblance may be acceptable for all practical purposes. Further, in order to verify the importance of direction of arrival (DOA), the same data are presented in Fig. 3d–f but for the ratio S_O06/S_O12 along with the respective best-fit. Clearly, the comparison is not as good as before. This completes the verification of hypothesis.

Fig. 3

Verification of hypothesis (Event-4 in SMART1 array). a S_O12/S_O06 in EW direction (Event 4), b S_O12/S_O06 in NS direction (Event 4), c S_O12/S_O06 in vertical direction (Event 4), d S_O06/S_O12 in EW direction (Event 4), e S_O06/S_O12 in NS direction (Event 4), f S_O06/S_O12 in vertical direction (Event 4)

3.3 Assessment of proposed coherency model

Numerical coherency between the stations pairs is calculated using data recorded at LSST array and SMART1 array. The numerical coherency is regressed thorough the proposed coherency model for the estimation of parameters. Also included are three well known coherency models, namely, Harichandran and Vanmarcke (1986), Hao (1996) and Abrahamson et al. (1991) for the purpose of comparison.

3.4 Performance of the coherency models

All the four coherency models are compared with numerical lagged coherency for three events (Table 1) recorded over the LSST array. All three translational components are included in this comparison (Fig. 4) for all three events. All coherency models perform nearly the same in tracing the numerical lagged coherency in an average sense but the proposed model shows a relatively better trace in terms of changing the curvature. Although the coherency model by Abrahamson et al. (1991) was aimed to address specifically the short distance lagged coherency, in present illustration that appears no way better than the others.

Fig. 4

Comparison of different coherency models—LSST array. a Lagged coherency between FA1_1 and FA1_4 in Event 2—a_g1, b lagged coherency between FA1_1 and FA2_2 in Event 1—a_g2, c lagged coherency between FA1_1 and FA1_4 in Event 3—a_g3

SMART1 array is next considered for the purpose of performance comparison of different coherency models. Figure 5 presents some sample illustrations. In all cases, the proposed model represents the pattern of numerical coherency much better as compared to others. This may be attribited to the spatial variability of the spectral shape of ASD over the footprint of an array. Such a variability was not significant in LSST (dense array) but plays the pivotal role in large arrays, like SMART1.

Fig. 5

Comparison of different coherency models—SMART1 array. a Coherency between C00-I06 at Event 4—EW, b coherency between C00-I07 at Event 1—NS, c coherency between C00-O07 at Event 6—V, d coherency between C00-I07 at Event 1—EW, e coherency between C00-O04 at Event 2—NS, f Coherency between I01-M03 at Event 5—V

4 Coherency model for rotational ground motions

4.1 Background

Theoretically, rotation does not propagate in the form of plane waves (unlike translation). For illustration, consider the one-dimensional wave equation

$$ \frac{{\partial^{2} u\left( {x,t} \right)}}{{\partial x^{2} }} = \frac{1}{{c^{2} }}\frac{{\partial^{2} u\left( {x,t} \right)}}{{\partial t^{2} }} $$

(32)

Here, u(x, t) is the translational field and c is wave velocity of the medium. Rotational motion can be represented as the spatial derivative of the translational filed:

$$ \theta \left( {x,t} \right) = \frac{{\partial u\left( {x,t} \right)}}{\partial x} \approx \frac{1}{v}\frac{{\partial u\left( {x,t} \right)}}{\partial t} $$

(33)

Here, θ(x, t) is the rotational field and v is the associated apparent wave velocity. Substituting the Eq. (33) into Eq. (32), one may write

$$ \frac{{\partial \theta \left( {x,t} \right)}}{\partial x} = \frac{v}{{c^{2} }}\frac{{\partial \theta \left( {x,t} \right)}}{\partial t} $$

(34)

Clearly Eq. (34) does not satisfy the one-dimensional wave equation. Hence, the assumption of plane wave propagation is not valid for rotational components of ground motion. Hence, the coherency model does not exist theoretically for the rotational ground motion. However, treating the rotation as a mere time series, numerical lagged coherency between two stations can be calculated in a similar way as that of the translational components. This lagged coherency is defined throughout the manuscript in describing the spatial variability of rotational ground motion. If the rotational component can be expressed as a spatial derivative of one translational component at any station with due scaling through apparent velocity, which however, is not the case in general, one may prove that the lagged coherency model for the translational motion will also apply to describe that of the associated rotational motion. However, such assumption of frequency independent of apparent velocities is possible only in body waves, but not in surface waves. Castellani and Boffi (1989) demonstrated that the contribution of the surface waves to the rotational components for epicentral distances more than 20 km is negligible at frequencies greater than 1 Hz. Rotational components, being the time derivative of translational components followed by scaling with the apparent velocity, have frequency content generally on higher side of the frequency band. Hence, neglecting the surface wave contribution to the rotational components is a reasonable assumption. Neglecting the surface wave contribution to the rotational excitation, Rodda and Basu (2017a) explored the possibility of existence of ATC and derived the torsional and rocking accelerations under suitable assumptions as follows:

$$ \begin{gathered} \ddot{\theta }_{{x_{1} x_{3} }} (t) = \frac{1}{{2C_{3} }}\dot{a}_{{g3}} (t) \hfill \\ \left. \begin{aligned} \mathop \theta \limits^{{..}} _{{x_{1} x_{2} }} (t) & = - \frac{1}{{C_{2} }}\left[ {\dot{a}_{{g2}} (t)} \right]^{{if}} + \frac{1}{{C_{1} }}\left[ {\dot{a}_{{g1}} (t)} \right]^{{if}} \\ {\text{ }} = & - \frac{1}{{C_{1} }}\left\{ {\frac{1}{\alpha }\left[ {\dot{a}_{{g2}} (t)} \right]^{{if}} - \left[ {\dot{a}_{{g1}} (t)} \right]^{{if}} } \right\} \\ \end{aligned} \right|\,{\text{ and}}\,\alpha = \frac{{C_{2} }}{{C_{1} }} \hfill \\ \end{gathered} $$

(35)

In other words, ATC (a) for the torsional and rocking motions are given by

$$ \dot{a}(t) = \dot{a}_{g3} (t)\,{\text{for}}\,{\text{Torsion}}\,{\text{and}}\,\left. {\dot{a}(t) = - \left\{ {\frac{1}{\alpha }\left[ {\dot{a}_{g2} (t)} \right]^{if} - \left[ {\dot{a}_{g1} (t)} \right]^{if} } \right\}} \right|\,{\text{for}}\,{\text{Rocking}} $$

(36)

Here the superscript ‘if’ denotes appropriate filter and α is a parameter that can be approximated with the knowledge of three-component translational accelerations using an empirical procedure (Rodda and Basu 2017a). The constants C₃ and C₁ may be considered as the apparent velocities for extracting torsional and rocking acceleration, respectively. Rodda and Basu (2016) reported an empirical rotational window for extracting the apparent velocities from the three-component recorded translational accelerations. Overall, the simplified framework leads to rotational components comparable to those extracted using more rigorous approach such as Basu et al. (2012). Figure 6 presents a sample comparison for the torsional and rocking spectra; Simplified and rigorous frameworks are denoted as ‘derived’ and ‘original’, respectively.

Fig. 6

Comparison of rotational ground motions—simplified and rigorous framework. a Torsional spectra comparison at station FA2_1 for Event 3, b rocking spectra comparison at station FA3_5 for Event 2

4.2 Formulation

Per the definition offered by Rodda and Basu (2017a), relation between rotational motion and its ATC can be written as

$$ \ddot{\theta }(t) = \frac{1}{v}\dot{a}(t) $$

(37)

Here, a denotes the ATC, θ is the rotational motion and v is the corresponding apparent velocity. Note that rotational motion can be estimated from spatial derivative of only ATC and not from any arbitrary translational component.

Equation (37) in frequency domain can be written as

$$ X_{\theta } \left( f \right) = \frac{i2\pi f}{v}X_{a} \left( f \right) $$

(38)

Here, X _θ and X _a represent the Fourier transforms of rotational motion and corresponding ATC, respectively. Using Eq. (38), ASD and CSD of rotational ground motion at two stations can be expressed as

$$ \begin{aligned} S_{\theta ,jj} = \frac{{\left( {2\pi f} \right)^{2} }}{{v_{j}^{2} }}S_{a,jj} \hfill \\ S_{\theta ,kk} = \frac{{\left( {2\pi f} \right)^{2} }}{{v_{k}^{2} }}S_{a,kk} \hfill \\ S_{\theta ,jk} = \frac{{\left( {2\pi f} \right)^{2} }}{{v_{j} v_{k} }}S_{a,jk} \hfill \\ \end{aligned} $$

(39)

Here, $S_{\theta ,jj} {\text{ and }}S_{a,jj}$ represents ASD of rotational motion and translational motion, respectively, at station j. Consequently, lagged coherency of rotational motion (|γ_θ,jk(f)|) is given by

$$ \left| {\gamma_{\theta ,jk}^{{}} \left( f \right)} \right| = \left| {\frac{{S_{\theta ,jk}^{{}} \left( f \right)}}{{\sqrt {S_{\theta ,jj}^{{}} \left( f \right)S_{\theta ,kk}^{{}} \left( f \right)} }}} \right| = \left| {\frac{{\left( {\frac{{\left( {2\pi f} \right)^{2} }}{{v_{j} v_{k} }}} \right)S_{a,jk}^{{}} \left( f \right)}}{{\sqrt {\left( {\frac{2\pi f}{{v_{j} }}} \right)^{2} S_{a,jj}^{{}} \left( f \right)\left( {\frac{2\pi f}{{v_{k} }}} \right)^{2} S_{a,kk}^{{}} \left( f \right)} }}} \right|{ = }\left| {\frac{{S_{a,jk}^{{}} \left( f \right)}}{{\sqrt {S_{a,jj}^{{}} \left( f \right)S_{a,kk}^{{}} \left( f \right)} }}} \right| = \left| {\gamma_{a,jk}^{{}} \left( f \right)} \right| $$

(40)

Equation (40) shows that the lagged coherency of the rotational motion is identical to that of its ATC.

Per the definition offered by Rodda and Basu (2017a), ATC is a linear combination of recorded translational components at one single station. Hence, ATC propagates like a plane wave and the proposed coherency model will hold. The same functional form as developed for the translational motion may therefore be used with extracted rotational motion while estimating the parameters of lagged coherency model.

5 Illustrations on rotational coherency model

LSST array at Lotung has been specifically selected to study the lagged coherency of rotational components. Rotational ground motions are first extracted using the SSP reported by Basu et al. (2012) at all surface stations over the footprint of LSST array. Three events reported in Table 1 are considered for this purpose. Lagged coherency between the stations pairs is calculated numerically and it is regressed thorough the proposed coherency model for the estimation of parameters.

Figure 7 presents some sample comparisons of proposed coherency model against the numerical lagged coherency. In all cases, proposed model is able to reasonably capture the average trend of numerical lagged coherency. Therefore, the proposed coherency model may be used to capture the spatial variability of rotational motion over the footprint of a dense array.

Fig. 7

Lagged coherency of rotational ground motions at LSST array. a Lagged coherency between FA1_1 and FA2_2 in Event 1—torsional motion, b lagged coherency between FA1_1 and FA2_2 in Event 1—rocking motion, c lagged coherency between FA1_1 and FA1_4 in Event 2—torsional motion, d lagged coherency between FA1_1 and FA1_4 in Event 2—rocking motion, e lagged coherency between FA1_2 and FA2_5 in Event 3—torsional motion, f lagged coherency between FA1_2 and FA2_5 in Event 3—rocking motion

6 Results and discussions

Proposed coherency model is used to study the event-to-event variability of lagged coherency as a function of frequency and separation distance. LSST array is considered to study the variation against small separation distance whereas SMART1 array is chosen for the larger separation distance. In case of LSST array, span of the footprint of array is negligible as compared to the epicentral distance of the recorded events and hence, principal plane for each station remains the same. Orientation of the principal plane is considered as the direction of arrival (DOA) and the separation distance along the DOA is computed for all possible station-pairs. Numerical coherency is then calculated for all possible station-pairs. Separation distance (along the DOA) between the station-pair is divided into a bin of 10 m and the numerical coherency in a specific bin at each frequency is sorted from smallest to largest values. Coherency corresponding to 50% percentile value, in other words median numerical coherency at each frequency is estimated and regressed thorough the proposed coherency model for the estimation of parameters and theoretical coherency. Figure 8 presents some sample results for the three translational components recorded over the footprint of LSST array. It is interesting to note that coherency model for two horizontal components does not show significant event-to-event variability although the source-to-site travel paths are quite different in the three seismic events studied. However, coherency model for vertical motion exhibits relatively high variability from one event to another. Similar studies are carried out for the rotational ground motions and Fig. 9 presents some sample illustrations. Coherency model for torsional component shows much lesser variability from one event to another when compared with that of the rocking motion. This is expected as the torsional component is contributed from the SH wave field, which is approximately the horizontal motion normal to the principal plane. On the other hand, rocking motion is contributed from both P and SV-wave fields which constitute the horizontal motion along the principal plane and vertical component.

Fig. 8

Event-to-Event variability of coherency model for translational ground motions at LSST array. a Distance range 0–10 m—a_g1, b distance range 20–30 m—a_g2, c distance range 10–20 m—a_g3

Fig. 9

Event-to-Event variability of coherency model for rotational ground motions at LSST array. a Distance range 0–10 m—rocking motion, b distance range 20–30 m—torsional motion

Spatial coherency loss is then studied at some discrete frequencies for the translational ground motions. Figure 10 presents some sample illustrations. Coherency loss of a particular frequency over the spatial dimension of a dense array is not significant and the associated event-to-event variability is also minimum. Similar study is extended to the rotational components also and Fig. 11 presents some sample illustrations. As expected, rocking components show significant sensitivity while the torsional components exhibit similar variability as that of the horizontal components.

Fig. 10

Coherency loss with spatial attenuation for translational ground motions at LSST array. a Coherency against distance at 1 Hz—a_g1, b coherency against distance at 2 Hz—a_g2, c coherency against distance at 4 Hz—a_g3

Fig. 11

Coherency loss with spatial attenuation for rotational ground motions at LSST array. a Coherency against distance at 1 Hz—torsion, b coherency against distance at 2 Hz—rocking

The study of event-to-event variability of ground motion is further extended to large distances using the translational data recorded at SMART1 array. Numerical coherency is then calculated for all possible station-pairs. Separation distance (along the line joining epicenter and C00) between the station-pair is divided into a bin of 100 m and the numerical coherency in a specific bin at each frequency is sorted from the smallest to the largest values. Median numerical coherency at each frequency is estimated and regressed thorough the proposed coherency model for the estimation of parameters and theoretical coherency. Similar to the observations noted at LSST array, coherency for all three translational motions did not show significant event-to-event variability for the far-field events (4 events). The coherency for the near-field event (Event 4) is significantly different than the other four far-field events. This may be attributed to (1) array size is comparable to the epicentral distance; (2) the assumption of plane wave propagation of seismic waves may not hold; and (3) definition of principal plane may not be correct. However, the coherency from one near-field event is not expected to show significant variability when compared with the other near-field events. This, however, is not verified in this paper due to non-availability of translational records for additional near-field events at SMART1 array. Further studies are required to draw meaningful conclusions regarding near-field events. Figure 12 presents some sample illustrations.

Fig. 12

Event-to-Event variability of coherency model for translational ground motions at SMART1 array. a Distance range 0–100 m—EW, b distance range 800–900 m—NS, c distance range 200–300 m—vertical

For a particular frequency, theoretical coherency was observed to be decreasing with the distance for all 3 directions as expected. This is shown in Fig. 13 for some of the frequencies. Also it is observed that the coherency loss against distance for both the horizontal directions is very close. This may be due to considering coherency of EW and NS components, which are not completely uncorrelated like the rotated components with respect to principal plane.

Fig. 13

Coherency loss with spatial attenuation for translational ground motions at SMART1 array. a Coherency against distance at 1 Hz—Event 5, b coherency against distance at 4 Hz—Event 4, c coherency against distance at 2 Hz—Event 6, d coherency against distance at 2 Hz—Event 1, e coherency against distance at 4 Hz—Event 2, f coherency against distance at 3 Hz—Event 6

Therefore, coherency model arrived at on the basis of past events can be used to generate the spatially varying ground motions around a site but within the dimension of a dense array. This is particularly true for the horizontal components but extended to vertical component, as well. Torsional component may also be treated likewise whereas the rocking components need special attention.

7 Conclusions

A new coherency model is developed to describe the spatial variability of translational ground motions. Unlike the currently available models, proposed coherency model accounts for the spatial variability in the spectral shape of auto-spectral density (ASD) functions. Results on the ground motions recorded over LSST (dense) array indicates that the coherency model is not significantly affected by the spectral shape of ASD. However, this is seen to be critical over SMART1 (large) array.

Spatial variability of the rotational ground motions (theoretically) cannot be addressed through coherency function as the rotation does not propagate like a plane wave. However, rotational motions can be shown as the time derivative of a derived translational component, also known as the apparent translational component (ATC) with due scaling through apparent velocity. Under this condition, spatial variability of the rotational motion can be completely described by that of the ATC. In other words, the same functional from of the (lagged) coherency model developed for the translational ground motions can be used to describe the spatial variability of rotational components. Results on LSST array indicates significant spatial variability for the rocking motion while that of the torsional motion is comparable with the horizontal components.

Coherency model does not show significant variability from one event to another, provided recorded at the same site. Parameters of the coherency model estimated using past seismic events are expected to be valid for any future events also and hence, can be used to generate the spatially varying ground motions for seismic design but within the dimension of a dense array. This is particularly true in case of far-field events for the horizontal components but can be extended to the vertical component, as well. In contrast, the coherency of near-field event exhibits significant variability when compared with that of other far-field events, especially in SMART1 array. Further studies are required to draw meaningful conclusions on the event-to-event variability of near-field coherency. Torsional component may also be treated in a way similar to the translational motions (but not near-filed) whereas the rocking components need special attention. Results of the SMART1 array exhibit similar loss of spatial coherency for both horizontal components (EW–NS and not along and normal to the principal plane). This may be attributed to the correlation of orthogonal (lateral) components.

Finally, the conclusions arrived at in this paper is specific to the seismic events and arrays considered. Further studies are required to confirm the expectations.