Apparent translational component for rotational ground motions

Abstract

Even though the rotational ground motion may contribute significantly to the response of certain structures, their effects are generally ignored in seismic design, because of non-availability of appropriate instruments for direct recording of the rotational components. Like many others, a simplified framework was proposed by the authors elsewhere (Rodda and Basu in Int J Earthq Impact Eng 1(3):253–288, 2016) to extract the rotational motion as a temporal derivative of an apparent translational component (ATC) followed by scaling with an apparent velocity. ATC was defined such that its time derivative is closely correlated with the respective rotational motion. But the a priori knowledge of rotational motion is required in estimating the ATC for rocking component. An empirical procedure has been proposed here to bypass the requirement of rotational motion a priori. This paper also assesses the definition of ATC through examining the similitude between the time derivative of ATC and the respective rotational motion (benchmark) quantitatively. Similitude is assessed on smoothened response spectra (by Hamming window) of the time derivative of ATC and that of rotational motion. A new definition of spectral contrast angle (SCA) based on distance correlation has been proposed to assess the spectral similitude. To differentiate the similar from non-similar spectra, SCA corresponding to an acceptable degree of similarity is proposed by studying a large ensemble of ground motions from the PEER database. This similitude study is further extended using relative energy build up and energy spectra.

1 Introduction

Studies on the effect of rotational ground motion on structural response dates back to 1960s (Newmark 1969). A number of researchers later reported the effect of rotational components on response of various types of structures (Basu et al. 2014, 2015; Falamarz-Sheikhabadi 2014; Basu and Giri 2015; Falamarz-Sheikhabadi and Ghafory-Ashtiany 2015; Falamarz-Sheikhabadi et al. 2016; and more related references can be found therein). Several attempts have been made till date on measuring the rotational excitation (Yin et al. 2016; Nigbor et al. 2009) and a comprehensive list of literature up to 2009 was reported in the special publication of Bulletin of the Seismological Society of America (BSSA), 99(2B). Even after all these efforts, the direct recording of rotational excitation is still at the research level and it will take, perhaps, a long time before achieving a general agreement for its deployment with desired confidence level on the expected outcome. Therefore, engineers will have to rely on the theoretical extraction (indirect methods) of rotational motion in order to incorporate its effect on structural response.

Indirect methods, such as multiple station procedure (MSP) and single station procedure (SSP) are used to extract the rotational motion from the recorded three-component translational data. While MSP requires the translational data recorded at a dense array, data recorded at a single station is sufficient for SSP. Rotational ground motions obtained using MSPs have been reported by a number of researchers including Basu et al. (2013, 2015); and more related references can be found therein. Generally, SSP is a more common choice in extracting the rotational component as the availability of dense array recordings is scarce in most parts of the world. SSP approximates the rotational motion, a spatial derivative of the translational motion, by the time derivative of the translational motion with due scaling through apparent velocity. Defining the vertical plane comprising of the epicentre and the recording station as the principal plane, most of the energy is reported to be travelling on this principal plane to the station and the three rotated components along and normal to the principal plane are uncorrelated (Penzien and Watabe 1974). A number of researchers have used the definition offered by Penzien and Watabe to extract rotational time series from the translational recordings at a single station (for example, Basu et al. 2012; Falamarz-Sheikhabadi and Ghafory-Ashtiany 2012 and the references cited therein). The available SSPs involve a number of assumptions, including the plane wave propagation, a frequency-dependent angle of incidence, lateral homogeneity of the soil medium, the effect of dispersion and a number of other simplified scenarios to bypass the indeterminacy involved in deconstruction of the recorded translational ground motion into contributions from different types of surface and body waves. One such SSP proposed by Basu et al. (2012) is described here to enable the further description of the framework presented in this paper.

Salient features of the SSP reported in Basu et al. (2012)

Rotational components at any surface station are extracted from the three-component translational data recorded/rotated at the same station. Extracted rotational motion has two components, namely, torsional motion perpendicular to the principal plane and rocking motion on the principal plane. The procedure allows simultaneous incidence of P- and S-waves with frequency dependent incident angles. Neglecting the contribution from surface waves and assuming the plane wave propagation, horizontal motion normal to the principal plane is contributed from the SH wave only while that along the principal plane and vertical motion are due to both P and SV waves. Therefore, torsional component is extracted from the spatial derivative of the horizontal motion normal to the principal plane (in absence of Love wave) while rocking motion can be extracted from the spatial derivative of either vertical motion or horizontal motion along principal plane. Hence, extraction of rocking motion requires the P and SV wave decomposition of recorded/rotated ground motion. Under suitable assumptions, body wave decomposition of vertical motion and horizontal motion along principal plane are carried out and rocking component is extracted from the contribution of P and SV-waves to the respective translational components through respective spatial derivatives followed by a linear superposition, which is computationally rigorous. This completes the description of the SSP presented in Basu et al. ( 2012 ).

Attempts have been made (for example, Trifunac 1982; Li et al. 2004; Zembaty 2009) on extracting the rotational motion without body-wave decomposition but assuming single wave incidence (P or S) that seems to be overly simplistic. Hence, there is a scope of including simultaneous incidence of P and S waves but without requiring the body wave decomposition to retain simplicity. In other words, there is a scope to extract the rotational motion as a temporal derivative of translational components followed by scaling with the apparent velocity associated with that component. However, this is possible provided the associated translational component is contributed from a single (type) wave field and the apparent velocity belongs to the associated wave field. One such simplified framework was proposed by Rodda and Basu (2016) and description of which is given here for the ready reference.

Description of the Simplified Framework proposed in Rodda and Basu (2016)

Proposed simplified framework to extract the rotational components from the three-component translational data comprises of two steps: First step is to seek the existence of an apparent translational component (ATC) for each rotational component and the next step involves scaling the time series or spectra of ATC through appropriate apparent velocity.

ATC was defined such that its time derivative is closely correlated with the respective rotational motion. Under the assumption of principal plane (and in absence of surface waves), existence of ATC is apparent for the torsional component as it is contributed only from the SH wave field (when the surface wave contribution is neglected). This, however, is not the case with the rocking motion (on the principal plane): even if the surface wave contribution is negligible, P and SV waves both contribute. Hence, a seemingly hypothetical translational motion, which is a linear combination of both, the horizontal motion along the principal plane and the vertical motion, was considered to be a possible candidate of ATC for rocking motion. ATC for rocking motion also involves a parameter $\alpha$ that depends on the actual rocking motion.

Next, apparent velocity was defined such that peak spectral ordinate of time derivative of the ATC matches with that of the respective rotational motions. Note that, a priori knowledge of actual rotational (rocking and torsion, as the case may be) components is required in estimating these apparent velocities.

The framework was focused on developing an empirical procedure of estimating the required apparent velocities without the knowledge of actual rotational motions. This was accomplished through defining a rotational window as the ratio of spectra of actual rotational component to that of its ATC, and identifying a set of invariant characteristics. However, the simplified framework still requires the a priori knowledge of actual rocking motion owing to the parameter $\alpha$.

Rotational spectra obtained from this framework were compared with more rigorous treatment offered by Basu et al. (2012) for assessment through visual inspection. This completes the description of the simplified framework presented in Rodda and Basu ( 2016 ).

Given that the ATC was defined in Rodda and Basu (2016), the first objective of the present paper is to develop an empirical procedure for estimating the parameter $\alpha$ without a priori knowledge of actual rocking motion. This will enable the simplified framework estimating the rotational components without a priori knowledge of actual rotational motion. Final objective of the present paper is to assess the definition of ATC by quantitatively measuring the spectral similitude between the time derivative of ATC and its respective rotational component using the measures such as ‘distance correlation’ (Szekely and Rizzo 2014) and ‘spectral contrast angle’ (Wan et al. 2002). Owing to the challenges in recording rotational component through the accelerometers deployed in free-field, SSP described in Basu et al. (2012) is taken as the reference in this paper for benchmark and referred to ‘original’ henceforth. Note that the spectral similitude depends only on the spectral shape and is independent of the scaling of spectra. Hence, calculation of apparent velocities is not required in this similitude study. This similitude study is further extended using the energy spectra, relative energy build-up etc.

Before assessing the definition of ATC with respect to the original rotational motion, it would be wise to briefly describe the dense array and recorded events considered in this paper and background of the various tools employed for comparison of the ground motion characteristics for ready reference.

2 Description of seismic array and events considered

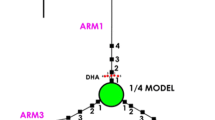
The Large Scale Seismic Test (LSST) array in Lotung, Taiwan is a part of the much larger SMART1 array. Figure 1 shows the layout of the surface stations: three arms at an interval of approximately 120° with five stations each. Length of each arm is about 50 m and the spacing between the stations varies from 3 to 90 m. The stations in each arm are numbered from 1 to 5, starting at the centre of the array. For example, FA3_5 denotes the outermost station (station 5) located on arm 3. The average wave velocities at the surface of the recording site are: 595 and 140 m/s for the P and S waves, respectively (Wen and Yeh 1984).

Fig. 1

Location of free surface stations (relative locations of epicentres not to scale) (http://www.earth.sinica.edu.tw/~smdmc/llsst/llsstfs.htm)

Ground motion is recorded in LSST array along the east–west (EW), north–south (NS) and vertical directions. But the recorded horizontal accelerations (EW and NS) are rotated along and normal to the principal plane to enable extraction of the rotational components. The rotated horizontal components along and normal to the principal planes are denoted in this paper as $a_{g1}$ and $a_{g3}$, respectively, and the vertical acceleration is $a_{g2}$. Three strong motions events recorded at the LSST array are considered for illustration in this paper and a brief description of each event is presented in Table 1. Event-3 may exhibit some near-field characteristics as the epicentral distance is approximately 24 km. Only surface stations are considered in the analysis and out of 15, usually, 11–14 actually functioned during the events. Hence, number of surface stations analysed here varies from one event to another.

Table 1 Strong motion events considered

3 Tools considered for comparing the characteristics of ground motion

3.1 Spectral representation

Owing to the difficulty in extracting any meaningful conclusion from the time series, correlation between the time derivative of ATC and the rotational motion is studied through response spectrum here. Response spectra for time derivative of ATC and rotational motion are calculated separately for comparison. Spectral ordinate of the time derivative of ground acceleration stands for the peak (absolute maxima) response of a single degree of freedom system subjected to the derivative time series as input acceleration. Similarly, response spectra of rotational motion is computed from the peak rotational response of a rotational oscillator subjected to the rotational ground motion. Figure 2a presents the response spectrum of $a_{g1}$ at station FA1_1 in Event-1. A sample rotational spectrum (torsional) is included in Fig. 2b (the same station and the same event). Unless otherwise stated, all the spectra considered in this paper are 5% damped.

Fig. 2

Spectral acceleration plot for Event 1 at station FA1_1. a Response spectrum for a_g1 and b response spectrum for torsion

3.2 Smoothening with Hamming window

Response spectrum of one ground motion is usually sporadic in nature and hence, of no specific importance in seismic design/performance assessment, which uses the design spectrum instead. Design spectrum, an appropriate fractile of response spectra of an ensemble of consistent ground motions, after some processing exhibits a smoother spectral shape. Measuring the similitude between the spectra of rotational motion and that of derivative of ATC is more relevant in terms of design spectrum rather than individual spectrum. Non-availability of sufficient number of recordings for ensembles poses a serious challenge to the construction of smoothened design spectra. Another way of smoothening involves the use of Hamming window that consists of a set of weights, which are used to average the spectral ordinate around a point. The weights $w\left( m \right)$ of a $M$-point symmetric window are given by

$$ w(m) = \frac{{\left[ {0.54 - 0.46\cos \frac{\pi (m + M)}{M}} \right]}}{1.08M},\quad {\text{For}}\;m \, = \, - M, \, - M + 1, \, \ldots , \, M{-}1, \, M $$

(1)

Resulting smoothened spectral ordinate is given by the weighted average of all the surrounding points within the window:

$$ SA_{smooth} (T_{i} ) = \sum\limits_{j = - M}^{j = + M} {SA} (T_{i} + j\Delta T)w(j) $$

(2)

Mean spectrum, an ensemble average of consistent ground motions, conditioned to a specific spectral ordinate (say, PGA) is considered here as a variant of design spectrum in a crude sense. It has been observed in this study that the smoothening of a response spectrum with a moving window closely resembles the mean spectrum calculated from the ensemble average. In order to illustrate this application, an ensemble comprising of ground motion recordings (Table 1) along EW direction over the footprint of the LSST array is considered. Mean spectrum, conditioned to Peak Ground Acceleration (PGA) of 1 g is computed through ensemble average. Also computed are the spectra with bounds $\mu + 1.67\sigma$ and $\mu - 1.67\sigma$, with $\mu$ and $\sigma$ denoting the ensemble mean and standard deviation, respectively. Next, a moving Hamming window (20 points @ 0.005 s) on the individual response spectrum is applied followed by scaling of resulting spectrum to a PGA of 1 g. Mean spectra, $\mu + 1.67\sigma$ and $\mu - 1.67\sigma$ spectra are then computed. The smoothening operation did not significantly affect the spatial variability of individual spectra as both the mean spectra [smoothened (SM) and unsmoothed (US)] are remarkably similar to each other (Fig. 3). Also shown in Fig. 3 are similar comparison for $\mu + 1.67\sigma$ and $\mu - 1.67\sigma$ spectra. Close resemblance of these spectra indicates that smoothening does not alter the statistical properties of ensemble.

Fig. 3

Mean spectra in EW direction conditioned at period of 0 s

Similar observation is noted along other recording directions also. Even though, the smoothened spectrum of individual record does not exactly match the shape of mean spectrum, it is wise to measure the spectral similarity in terms of smoothened spectra (with Hamming window) in case of insufficient recordings for computation of mean spectrum. Therefore, smoothened spectra using Hamming window (instead of unsmoothed) are used for comparison in the remainder of this paper.

3.3 Distance correlation as a measure of the similitude of spectral shape

Distance correlation is chosen here to measure the resemblance between the shapes of two response spectra. Note that correlation being zero does not imply the independence while the distance correlation being zero does imply the independence. Calculation of distance correlation is reviewed below for the ready reference (Szekely and Rizzo 2014).

Let $X_{k} ,Y_{k}$, $k = 1,2, \ldots ,n$ be two vectors, whose distance correlation is to be determined. First, compute all possible pairwise distances, as follows,

$$ a_{j,k} = \left\| {X_{j} - X_{k} } \right\|,\quad b_{j,k} = \left\| {Y_{j} - Y_{k} } \right\|,\quad \, j,k \, = \, 1, \, 2, \, \ldots , \, n $$

(3)

where ||·|| denotes the Euclidean norm. Next, compute the matrices A and B, as follows,

$$ \begin{aligned} A_{j,k} & = a_{j,k} - \tilde{a}_{j} - \hat{a}_{k} + \bar{a} \\ B_{j,k} & = b_{j,k} - \tilde{b}_{j} - \hat{b}_{k} + \bar{b} \\ \end{aligned} $$

(4)

where $\tilde{a}_{j}$ and $\hat{a}_{k}$ are the mean of $j$th row and $k$th column, respectively, and $\bar{a}$ is the grand mean of the matrix $[a]$. Analogous notations are used for $[b]$. The squared sample distance covariance is given by the average of the products $A_{j,k}$ and $B_{j,k}$, as follows:

$$ \begin{aligned} dCov_{n}^{2} (X,Y) & = \frac{1}{{n^{2} }}\sum\limits_{j,k = 1}^{n} {A_{j,k} B_{j,k} } \\ dCor(X,Y) & = \frac{{dCov_{n} (X,Y)}}{{\sqrt {dVar_{n} (X,X)dVar_{n} (Y,Y)} }} \\ \end{aligned} $$

(5)

The distance correlation of two random variables is obtained through dividing their distance covariance by the product of their distance standard deviations.

3.4 Spectral contrast angle as a measure of the similitude of spectral shape

3.4.1 Spectral contrast angle based on correlation

Another useful tool to measure similitude of two spectra is the spectral contrast angle (SCA), calculation of which is reviewed below for the ready reference.

Let $X_{k} ,Y_{k}$, $k = 1,2,..,n$ be two spectra with spectral contrast angle (SCA-$\theta$), cosine of which is given by Wan et al. (2002)

$$ \cos \left( {{\text{SCA-}}\theta } \right) = \frac{{\sum\nolimits_{i = 1}^{n} {X_{i} Y} }}{{\sqrt {\sum\nolimits_{j = 1}^{n} {X_{j} X_{j} } \sum\nolimits_{k = 1}^{n} {Y_{k} Y_{k} } } }} $$

(6)

Therefore, an angle close to zero degrees indicates two nearly identical spectra, while an angle of 90 degrees indicates no spectral similarity.

3.4.2 Spectral contrast angle based on distance correlation

A new definition is also explored here by replacing the correlation between the spectra with the distance correlation, which is expected to show better sensitivity against the change in spectral shape:

$$ \cos \left( {{\text{SCA-}}\theta^{\prime}} \right) = \frac{{dCov_{n} (X,Y)}}{{\sqrt {dVar_{n} (X,X)dVar_{n} (Y,Y)} }} $$

(7)

3.4.3 Sensitivity of proposed and existing spectral contrast angles

Three ground motions from PEER database (http://ngawest2.berkeley.edu/) have been selected (Table 2) and termed as GM_1, GM_2 and GM_3 here for identification purpose. Three different levels of Gaussian white noise (SNR 30, 1 and 0.1) are added to the GM_1 in order to simulate the spectra with various degrees of similitude. SCA-$\theta$ and SCA-$\theta^{\prime}$ between spectra of GM_1 and GM_1 with noise are computed and compared (Table 2; Fig. 4). Proposed SCA-$\theta^{\prime}$ clearly shows more sensitivity (4°–23°) as compared to existing SCA-$\theta$ (3°–15°). The SCA-$\theta^{\prime}$ is also observed to be decreasing with the increase in SNR.

Table 2 Comparison of spectral contrast angles

Fig. 4

Comparison of proposed and existing spectral contrast angles. a GM_1 against GM_1 with SNR of 30, b GM_1 against GM_1 with SNR of 1, c GM_1 against GM_1 with SNR of 0.1, d GM_1 against GM_2 and e GM_1 against GM_3

Next, the similitude between the spectra of GM_2 and GM_3 with GM_1 is calculated (Table 2; Fig. 4) and the resulting SCA-$\theta^{\prime}$ (>40°) is much greater compared to the previous set of observations (<23°). This is expected as the ground motions considered are independent. These observations are based on the limited data considered and hence, cannot be generalised.

In order to study the sensitivity of SCA-$\theta$ and SCA-$\theta^{\prime}$, similar study has been done with a larger database of events with magnitudes ranging from 6 to 7 and shear wave velocities with 200–400 m/s (from PEER database, described in “Appendix”: Table 4). Mean spectrum is computed for the ensemble, conditioned to the PGA of 1 g. SCA-$\theta$ and SCA-$\theta^{\prime}$ have been calculated between the mean spectrum and the individual spectra. Again it is observed that the SCA-$\theta^{\prime}$ is more sensitive to the change in spectral shape in most of the cases. Range of values of SCA-$\theta^{\prime}$ between mean spectrum (smoothened because of ensemble averaging) and individual spectrum varies from 14° to 65°, whereas for SCA-$\theta$ it is 9°–59°. Once again SCA-$\theta^{\prime}$ shows better sensitivity as compared to SCA-$\theta$ as expected. In view of these observations, SCA-$\theta^{\prime}$ is used as a measure of spectral similitude in the remainder of this paper.

3.4.4 SCA-$\theta^{\prime}$ for acceptable degree of similarity

Rigid boundary does not exist to differentiate the similar spectra from the non-similar spectra. Because of large variation in SCA, average (50 percentile) value cannot be taken as the suitable limit. In order to select an SCA for acceptable degree of similarity, SCA-$\theta^{\prime}$ between mean spectrum and individual spectrum from a larger ensemble is studied and an acceptable limit is chosen corresponding to the 10% non-exceedance probability. This is done in two steps. First step involves assumption of a particular probability distribution and parameters of which are estimated from the observed sample space. This distribution with estimated parameters is defined here as the theoretical probability distribution. Several such theoretical distributions are selected for the Chi squared goodness-of-fit test against the observed sample and the distribution with least $\chi^{2}$ value at the 5% significance level is accepted. Burr distribution qualifies in the present case with $\chi^{2}$ score = 7.7 against $\chi_{5, \, 0.05}^{2} = 11.1$ (the degrees of freedom five was calculated as 9 (no of bins in histogram)—3 (no of parameters in distribution)—1 = 5). The distribution was compared against the numerical data in the form of histogram (Fig. 5) and the cumulative distribution function (Fig. 6). Next step involves the calculation of SCA-$\theta^{\prime}$ using the theoretical cumulative distribution function. The SCA-$\theta^{\prime}$ corresponding to 10% non-exceedance is found to be around 20°, which is considered in the remainder of this paper for an acceptable degree of similarity.

Fig. 5

Burr fitting (theoretical distribution) for the histogram

Fig. 6

Cumulative distribution function

4 Apparent translational component (ATC)

An apparent translational component (ATC) is defined such that time derivative of which is closely correlated to the associated rotational component. Consider the simplified procedure reported by Rodda and Basu (2016) and the existence of ATC for both torsional and rocking motions is explored below, but one at a time.

4.1 ATC for torsional ground motion

Under the assumption of negligible surface wave contribution, torsional ground motion is contributed from the SH wave component of the body wave field. SH wave component can be extracted through rotating the recorded ground motion normal to the principal plane. Assuming the plane wave propagation, torsional component contributed from the $r^{th}$ harmonic is given by Basu et al. (2012)

$$ {}_{r}^{sh} \ddot{\theta }_{{x_{1} x_{3} }} (t) = \frac{1}{2}\frac{{\sin \theta_{0} }}{{c_{T} }}{}_{r}^{sh} \dot{a}_{g3} (t) $$

(8)

Here, left superscript $sh$ denotes the contribution from the SH wave, $c_{T}$ is the SH-wave velocity and $\theta_{o}$ is the angle of incidence, which are frequency dependent. Torsional component is calculated in this paper (following Basu et al. 2012) by the spatial derivative of $a_{g3}$ in frequency domain. In other words, even if the SH-wave velocity is assumed to be frequency independent, linearity between the torsional motion and temporal derivative of $a_{g3}$ is not warranted owing to the frequency dependent incident angles. Nevertheless, one may start with $a_{g3}$ while seeking the ATC for torsional ground motion:

$$ \ddot{\theta }_{{x_{1} x_{3} }} (t) = \frac{1}{{2C_{3} }}\dot{a}_{g3} (t) $$

(9)

where $C_{3}$ may be considered as the proportionality constant representing some form of frequency independent apparent velocity. The next task is to investigate the similarity in spectral shapes as presented below.

Torsional (original) spectrum is first smoothened (20-point Hamming window @0.005 s) and compared with that of $\dot{a}_{g3}$ (unsmoothed) for the spectral contrast angle. Resulting SCA-$\theta^{\prime}$ (Fig. 7a) is noted to be varying within a range space of 6° to 12°, which is within the acceptable limit of similarity (20°). This comparison is analogous to that presented in Sect. 3.4.4 between the mean and individual spectra in an ensemble. However, comparison of spectral shape between smoothened spectra is more meaningful and hence, $\dot{a}_{g3}$ spectrum is smoothened (20-point Hamming window @0.005 s) and similar comparison is repeated. Resulting SCA-$\theta^{\prime}$ (Fig. 7b) resembles better similarity with a range space of 2° to 11°. Hence, torsional spectra based on the proposed ATC may be considered of similar shape as that of the original.

Fig. 7

Proposed spectral contrast angle between spectra of torsional motion and that of its derivative of ATC. a SCA-proposed between smoothed original torsional spectra and that of unsmoothed time derivative of ATC and b SCA-proposed between smoothed original torsional spectra and that of smoothed time derivative of ATC

Therefore, despite the dependency through frequency dependent incident angle, torsional acceleration (time series) can be well characterized through $\dot{a}_{g3}$ and hence, $a_{g3}$ component may be identified as the ATC for torsional ground motion.

4.2 ATC for rocking ground motion

Even though torsional motion is fully described by a single translational component, $a_{g3}$, rocking motion is contributed from the both $a_{g1}$ and $a_{g2}$. Therefore, ATC for rocking motion is not intuitive and needs an approach to be derived from the first principles under suitable assumptions which is given in Rodda and Basu (2016).

Based on the assumption of near vertical incidence of incident waves and existence of cut-off frequency, rocking component can be written as (Rodda and Basu 2016)

$$ \mathop \theta \limits^{..}_{{x_{1} x_{2} }} (t) = - \frac{{\sin \theta_{0p} }}{{c_{L} }}\left[ {\dot{a}_{g2} (t)} \right]^{if} + \frac{{2\sin^{2} \theta_{0s} }}{{\beta c_{T} }}\frac{{(1 - \beta^{2} \sin^{2} \theta_{0s} )^{0.5} }}{{1 - 2\sin^{2} \theta_{0s} }}\left[ {\dot{a}_{g1} (t)} \right]^{if} $$

(10)

Here, $\theta_{0p}$ and $\theta_{0s}$ denotes the angle of incidence of P and S waves respectively, and $\beta = {{c_{L} } \mathord{\left/ {\vphantom {{c_{L} } {c_{T} }}} \right. \kern-0pt} {c_{T} }}$ is the ratio of P to S wave velocity. Denoting the filter by $\left[ \,\,\right]^{if}$,$\left[ {\dot{a}_{g2} (t)} \right]^{if}$ denotes the component of $\dot{a}_{g2}$ passed through a high-pass filter of frequency $f_{c}$ and $\left[ {\dot{a}_{g1} (t)} \right]^{if}$ denotes the component of $\dot{a}_{g1}$ passed through a low-pass filter of frequency $f_{c}$.

Defining the following two constants,

$$ C_{2} = \frac{{c_{L} }}{{\sin \theta_{0p} }}\;{\text{and}}\;C_{1} { = }\frac{{c_{T} }}{{\left[ {\frac{{2\sin^{2} \theta_{0s} }}{\beta }\frac{{\left( {1 - \beta^{2} \sin^{2} \theta_{0s} } \right)^{0.5} }}{{1 - 2\sin^{2} \theta_{0s} }}} \right]}} $$

(11)

rocking component can be re-written as

$$ \left. \begin{aligned} \mathop \theta \limits^{..}_{{x_{1} x_{2} }} (t) & = - \frac{1}{{C_{2} }}\left[ {\dot{a}_{g2} (t)} \right]^{if} + \frac{1}{{C_{1} }}\left[ {\dot{a}_{g1} (t)} \right]^{if} \\ & = - \frac{1}{{C_{1} }}\left\{ {\frac{1}{\alpha }\left[ {\dot{a}_{g2} (t)} \right]^{if} - \left[ {\dot{a}_{g1} (t)} \right]^{if} } \right\} \\ \end{aligned} \right|\;{\text{and}}\;\alpha = \frac{{C_{2} }}{{C_{1} }} $$

(12)

Denoting the ATC for the rocking motion as ‘$a$’, its time derivative may be defined as

$$ \dot{a} = - \left( {\frac{1}{\alpha }\left[ {\dot{a}_{g2} (t)} \right]^{if} - \left[ {\dot{a}_{g1} (t)} \right]^{if} } \right) $$

(13)

Next, task is to explore the possible linearity between the rocking component and $\dot{a}$. Such a linearity may be considerably influenced by the parameter $\alpha$ and hence, it is mandatory to seek for the best possible estimate of $\alpha$.

4.2.1 Best estimate of alpha

Best estimate of $\alpha$ may be defined as the one that exhibits best resemblance between the spectra of rocking ground motion and that of the time derivative of ATC. One way of measuring the similitude is through using the smoothened spectra. However, a deviation spectrum is next defined as the square of difference between the spectral ordinates of unsmoothed and smoothened response spectra. Finally, the resemblance is measured using both, the distance correlation of the smoothened spectra and that of the deviation spectra. For example, the distance correlation coefficients computed between deviation spectra is plotted against that of smoothed spectra in Fig. 8a for Event-2 at some of the stations. Smoothened and deviation spectra do not necessarily yield the same $\alpha$ at respective maximum correlations (Fig. 9a). Hence, total distance correlation, defined by SRSS of distance correlation of smoothed spectra and deviation spectra, is now considered as the measure of resemblance and $\alpha$ associated with the maximum total distance correlation is considered as the best estimate. Following step-by-step procedure is adopted in this paper: (1) assume a possible estimate for $\alpha$ and calculate the ATC; (2) plot the response spectra of rocking motion and $\dot{a}$, and smooth each spectrum using a Hamming window (20 points @0.005 s in this paper); (3) compute the distance correlation coefficient between these smoothen spectral-pair; (4) calculate the deviation spectra for rocking and $\dot{a}$, and compute the distance correlation coefficient for these deviation spectral-pair; (5) calculate the total distance correlation as the SRSS of distance correlations computed in steps-3 and -4; (6) repeat these steps for a range of assumed $\alpha$ (0.1–20 @ 0.1 in this paper), (7) plot the total distance correlation as a function of assumed $\alpha$ and pick the estimate associated with the maximum total distance correlation.

Fig. 8

Variation of distance correlation for Event 2. a Distance correlation of deviation spectra against that of smoothed spectra and b total distance correlation against alpha

Fig. 9

Variation of distance correlation for Event 2 at station FA1_3. a Distance correlation of deviation spectra against that of smoothed spectra and b total distance correlation against alpha

For example, Fig. 8b presents the total distance correlation against the parameter $\alpha$ for Event-2. Even though the best estimate of $\alpha$ differs from one station to another (for the same seismic event), the variation of total correlation with respect to $\alpha$ is reasonably flat around the peak. This is observed in all three events analysed in this paper. Resulting best estimate of $\alpha$ are presented in Table 3. However, owing to the flat plateau around the peak, it may be sufficient to work with any $\alpha$ around the peak without losing the correlation significantly.

Table 3 Comparison of estimated $\alpha$ with the bounds of 90% maximum total distance correlation

4.2.2 Empirical prediction of the best estimate of alpha

The procedure described above for the best estimate of $\alpha$ requires the rotational ground motion to be known a priori, which is usually not the case. The objective here is to explore the possibility of predicting the best estimate of $\alpha$ empirically, without using the knowledge of rotational component. If such a prediction is possible, which is close to the best if not the best, but without sacrificing total distance correlation significantly, it would enable the computation of ATC completely based on the information of translational ground motion. Following step-by-step empirical procedure is proposed and illustrated for the Event 1 recorded at FA1_4 (Fig. 10):

Fig. 10

GM of spectral ordinates against alpha at FA1_4 for Event 1

(1) Normalize the translational motions $a_{g1}$, $a_{g2}$ and ATC (a) with respect to acceleration due to gravity, g and term $\bar{a}_{g1}$, $\bar{a}_{g2}$ and $\bar{a}$, respectively; (2) consider two limiting cases of $\dot{\bar{a}}$ (time derivative of $\bar{a}$), namely, the $\left[ {\dot{\bar{a}}_{g1} (t)} \right]^{if}$ and $\frac{1}{\alpha }\left[ {\dot{\bar{a}}_{g2} (t)} \right]^{if}$, and plot the respective response spectra [it is apparent from Eq. (13) that when $\alpha$ is close to zero, $\dot{\bar{a}} \to \frac{1}{\alpha }\left[ {\dot{\bar{a}}_{g2} (t)} \right]^{if}$ and when $\alpha$ is large, $\dot{\bar{a}} \to \left[ {\dot{\bar{a}}_{g1} (t)} \right]^{if}$]; (3) note the time periods associated with the peak spectral ordinates, say, $T_{1}$ and $T_{2}$ respectively; (4) assume any value for $\alpha$ close to zero, say 0.1 and plot the response spectrum for $\dot{\bar{a}}$; (5) compute the geometric mean $SA_{GM}$ of the spectral ordinates at $T_{1}$ and $T_{2}$; (6) repeat steps-4 and -5 for a wide range of $\alpha$ (for example, 0.1–15 @ 0.1 in this paper) and plot the $SA_{GM}$ against $\alpha$ (see Fig. 10, for example); (7) resulting plot will be always asymptotic to the horizontal axis and identify the least $\alpha$ beyond which it can be considered horizontal for all practical purpose and hence, for the best empirical estimate.

Table 3 summarises the empirically estimates for all three events recorded over the footprint of the array.

4.2.3 Comparison of alpha: best and empirical estimates

It is instructive to compare the empirical estimates (Table 3) with the associated best estimates furnished in Table 3. The bounds on $\alpha$ for 90% of maximum total correlation are also noted (see for example, Fig. 9b) and presented in Table 3. Empirical estimates are mostly within these bounds.

4.2.4 Results and discussions

Rocking (original) spectrum is first smoothened (20-point Hamming window @0.005 s) and compared with that of $\dot{a}$(unsmoothed). Resulting SCA-$\theta^{\prime}$ (Fig. 11a) is noted to be varying within a range space of 12°–24°, which is within the acceptable limit of similarity (20°) at most of the stations; even in remaining stations, it is noted as close to the limit. This comparison is analogous to that presented in Sect. 3.4.4 between the mean and individual spectra in an ensemble. However, comparison of spectral shape between mean spectra is more meaningful and hence, $\dot{a}$ spectrum is smoothened (20-point Hamming window @0.005 s) and similar comparison is repeated. Resulting SCA-$\theta^{\prime}$ (Fig. 11b) resembles better similarity with a range space of 8° to 22°. Hence, rocking spectra based on the proposed ATC may be considered of similar shape as that of the original.

Fig. 11

Proposed spectral contrast angle between spectra of rocking motion and that of its derivative of ATC. a SCA-proposed between smoothed original rocking spectra and that of unsmoothed time derivative of ATC and b SCA-proposed between smoothed original rocking spectra and that of smoothed time derivative of ATC

Based on these observed results, the component $a$, defined per Eq. (13), may be considered as the ATC for rocking motion.

5 Assessment of ATC through energy considerations

Energy measures are also used as alternative indices to the response quantities such as forces or displacements and thereby, enabling the direct inclusion of duration-related seismic damage. Hence, definition of ATC for rotational motion has been assessed through two energy considerations, namely, relative energy build-up and energy spectra in the following sections. Energy based method has the merit of replacing a vector quantity by a scalar energy parameter. Let one SDOF moves through an increment of displacement $du$ at any instant under a seismic excitation $\ddot{u}_{g}$. Relative energy input $\left( {E\left( t \right)} \right)$ by the effective force $p_{eff} (t) = - m\ddot{u}_{g} (t)$ is given by

$$ E(t) = - \int\limits_{0}^{t} {m\ddot{u}_{g} (t)du} = - \int\limits_{0}^{t} {m\ddot{u}_{g} (t)\dot{u}dt} \Rightarrow \frac{E(t)}{m} = - \sum\limits_{0}^{t} {\ddot{u}_{g} (t)\dot{u}\Delta t} $$

(14)

Here, $\dot{u}$ is the relative velocity with respect to ground. Relative energy imparted per unit mass is often used to characterize the structural response and is generally believed to be an indicator of the damage potential of a ground motion. Note that rigid body movement of the oscillator is not included in the formulation of cumulative relative energy build up [Eq. (14)]. Figure 12 presents an illustration for a 5% damped oscillator with natural period 1 s and subjected to the ground motion recorded along $a_{g1}$ at station FA1_1 during Event-1. Note that Eq. (14) is specific to the oscillator chosen and hence, to enable a comparative description over a band of natural periods, energy spectrum is often used: A plot of maximum cumulative relative energy imparted to a spectrum of SDOFs with constant damping ratio. A sample illustration of 5% damped energy spectrum is shown in Fig. 13 for $a_{g1}$ at FA1_1 in Event-1.

Fig. 12

Relative energy time history for Event 1 at FA1_1 for a_g1 for T = 1 s

Fig. 13

Relative energy spectra for Event 1 at FA1_1 for $a_{g1}$

5.1 Energy time history

Cumulative relative energy build-up (in %) over time is considered for comparing the rotational motion and derivative of ATC, and the sample data are presented in Figs. 14 (torsional motion and $\dot{a}_{g3}$) and 15 (rocking motion and $\dot{a}$). In order to measure the degree of similitude, the SCA-$\theta^{\prime}$ has been calculated between the rotational motion and derivative of ATC (Fig. 16a, b) and a strong resemblence has been observed between rotational motion and the derivative of ATC.

Fig. 14

Comparison of energy build-up for torsional motion and $\dot{a}_{g3}$ for Event 1 at FA1_1 for T = 1 s

Fig. 15

Comparison of energy build-up for rocking motion and $\dot{a}$ for Event 1 at FA1_1 for T = 1 s

Fig. 16

Proposed spectral contrast angle between energy considerations of rotational motion and that of its derivative of ATC. a SCA-proposed between relative energy build-up of original torsional motion and that of time derivative of its ATC, b SCA-proposed between relative energy build-up of original rocking motion and that of time derivative of its ATC, c SCA-proposed between energy spectra of original torsional motion and that of time derivative of its ATC and d SCA-proposed between energy spectra of original rocking motion and that of time derivative of its ATC

5.2 Energy spectra

Percentage energy build up compared above reflects the behaviour of one oscillator ($T = 1\;\text{s}$ in this case). Such comparison is further extended by considering a spectrum of oscillators and the obtained energy spectra are used to study the similitude between the rotational motion and derivative of the ATC. In order to study the similitude, energy spectra is first smoothened with a Hamming window and the resulting SCA-$\theta^{\prime}$ calculated between the smoothened energy spectra of rotational motion and that of time derivative of ATC is given in Fig. 16c, d and a strong resemblance is noted.

6 Conclusions

This paper makes use of the definition of ATC offered by Rodda and Basu (2016) and aims to develop an empirical procedure for estimating the parameter $\alpha$ without a priori knowledge of actual rocking motion. Another aim is to study the similitude between the derivative of ATC and original rotational motion (both rocking and torsion). Following conclusions may be arrived at based on the results of this paper:

• 1. An apparent translational component (ATC), time derivative of which is closely related with the respective rotational motion, has been assessed through various representations including the response spectra, energy spectra, relative energy build-up etc. to study the similitude between the time derivative of ATC and the respective rotational motion.

• 2. Smoothening of spectral shape using Hamming window is shown to be not altering the statistical properties of ensemble. Hence, similitude is assessed on smoothened (by Hamming window) spectra.

• 3. A new definition of ‘spectral contrast angle (SCA)’ based on ‘distance correlation’ is proposed and noted to be more sensitive to the change in spectral shape as compared to the existing definition. Proposed definition is used throughout this paper for assessing the spectral similitude.

• 4. Rigid boundary does not exist to differentiate the similar from non-similar spectra. SCA corresponding to an acceptable degree of similarity is proposed (20°) by studying a large ensemble of ground motions from the PEER database.

• 5. ATC for the torsional component is horizontal ground motion normal to the principal plane, owing to the contribution from only SH wave field (in absence of surface wave).

• 6. Rocking motion has contributions from both P and SV waves (even if surface wave is neglected), and hence, a seemingly hypothetical translational motion, which is a combination of both the horizontal motion along the principal plane and the vertical motion is considered as the ATC for rocking motion. This involves estimation of a parameter called $\alpha$ and an empirical procedure is also proposed for the same.

Both rocking and torsional components are found to be reasonably well described by the respective ATC. The rotational motions considered as ‘original’ here are not recorded from the accelerographs deployed in the free field. Instead, one of the various available methods is used to extract these components from the recorded translational motion and hence, the conclusions drawn in this paper is likely to be biased of the method of extraction. Nevertheless, the framework presented in this paper will still be applicable if any other method is used for extracting the rotational motion and it will be interesting to explore some of these methods.

Appendix

See Table 4.

Table 4 Record sequence numbers (RSN) of the ground motions used from PEER database