Exploring the impact of spatial correlations and uncertainties for portfolio analysis in probabilistic seismic loss estimation

Abstract

The significant potential for human and economic losses arising from earthquakes affecting urban infrastructure has been demonstrated by many recent events such as, for example, L’Aquila (2009), Christchurch (2011) and Tohoku (2012). Within the current practice of seismic loss estimation in both academic and industry models, the modelling of spatial variability of the earthquake ground motion input across a region, and its corresponding influence upon portfolios of heterogeneous building types, may be oversimplified. In particular, the correlation properties that are well-known in observations of ground motion intensity measures (IMs) may not always be fully represented within the probabilistic modelling of seismic loss. Using a case study based on the Tuscany region of Italy, the impacts of including spatially cross-correlated random fields of different ground motion IMs are appraised at varying spatial resolutions. This case study illustrates the impact on the resulting seismic loss when considering synthetic aggregated portfolios over different spatial scales. Inclusion of spatial cross-correlation of IMs into the seismic risk analysis may often result in the likelihood of observing larger (and in certain cases smaller) losses for a portfolio distributed over a typical city scale, when compared against simulations in which the cross-correlation is neglected. It can also be seen that the degree to which the spatial correlations and cross-correlations can impact upon the loss estimates is sensitive to the conditions of the portfolio, particularly with respect to the spatial scale, the engineering properties of the different building types within the portfolio and the heterogeneity of the portfolio with respect to the types.

1 Introduction

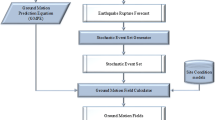
The process of analysing risk to a spatially distributed portfolio of assets is a central tenet of catastrophe modelling in both academic research and in industry. A typical portfolio will often consist of assets that are heterogeneous in terms of structure type, usage, seismic code design and age (Crowley et al. 2009). The derivation of fragility models for different structures often defines the ground motion intensity measure (IM) in terms of metrics that are most efficient in characterising the resulting damage to the structure. This may typically be the spectral acceleration or displacement at the fundamental elastic period of the structure ($S_a \left( {T_0} \right) , S_d \left( {T_0} \right)$). The requirements to define the seismic input in a manner that is most consistent with the fragility models for each structure type, present challenges to the seismic risk modeller. The generation of spatial random fields of a ground motion intensity measure (IM), either for a single scenario event or for a set of stochastic events with a given probability of occurrence, is a critical step in the loss estimation process.

The analysis of a spatially distributed set of elements, be it a portfolio of buildings, such as the case here, or an infrastructure system such as utility networks (e.g., water, electrical power, communications etc.), presents risk modellers with further challenges in the characterisation of the ground motion. For a probabilistic seismic risk analysis to a single structure, the aleatory variability in the ground motion is a critical parameter in controlling the losses. When considering multiple structures it is insufficient to treat the ground motion IMs at all structures sites as independent variables if the structures themselves can be affected by the same earthquake and, especially, if they are located closely in space. Therefore, such probabilistic seismic risk analyses need to consider the spatial correlation properties of the ground motion IMs.

It is well-established that observations of strong ground motion IMs resulting from the same earthquake may display correlations over distance (e.g. Boore et al. 2003; Wang and Takada 2005; Sokolov et al. 2010), and that the distances over which the correlations may be significant are generally greater for the long period characteristics of the ground motion (Jayaram and Baker 2009). In recent years these observations have proceeded to form the basis for the development of models of spatial cross-correlation to describe the correlation between different ground motion IMs across sites separated over a distance (e.g. Goda and Hong 2008; Goda and Atkinson 2009; Loth and Baker 2013). In the analysis considered here, the focus is primarily upon seismic risk analysis to building portfolios. It should be recognised, however, that the same requirements to consider spatially correlated and spatially cross-correlated fields of ground motion also apply, and may indeed be even more critical, when considering seismic risk to urban infrastructure. Recent developments in the European SYNER-G project (Franchin et al. 2011) have considered the use of spatial cross-correlation in the generation of ground motion fields of IMs for use in multi-system infrastructure analysis. The development of a computationally efficient methodology for spatial co-simulation of cross-correlated ground motion fields of IMs, and the need to understand its impact in a seismic risk context has been an important motivation for the current work.

The objective of the current paper is to explore, and illustrate with realistic examples, the effects of spatial correlation in seismic risk analysis for portfolios of heterogeneous building types. Assessment of risk to heterogeneous portfolios requires the use of different IMs to define the vulnerability of different building types. Heterogeneous portfolios can be seen as a generalisation of the homogeneous case, in which the same IM is used for all buildings. Therefore,, for heterogeneous portfolios the correlation between the IMs is more complex than in the homogeneous case. Yet even for heterogeneous portfolios the incorporation of spatial correlation of IMs into the risk analysis may be done via simulation of correlated (in this case jointly normally distributed) random variates. The subsequent analysis is intended to demonstrate, however, the manner in which the correlation matrix is constructed using available models of correlation in the published literature, and the means by which the correlations are simulated in the analysis impact upon the resulting estimates of seismic losses, and to consider the potential conditions under which such impacts may be of relevance to the risk modeller.

2 Modelling spatial correlation and cross-correlation of ground motion intensity measures in seismic risk analysis

Empirical models of both spatial correlation and between-IM cross-correlation of ground motion IMs generally capture the phenomenon within the aleatory variability of the ground motion prediction equation (GMPE), which takes the form:

$$\begin{aligned} \log \left( {IM_{ij}} \right) = f \left( {M_i, R_{ij}, \mathbf {\theta }_{ij}} \right) + \tau \nu _i + \sigma \epsilon _{ij} \end{aligned}$$

(1)

where IM $_{ij}$ denotes the value of the ground motion IM of interest at site $j$ located at a distance $R_{ij}$ from the source of an earthquake of magnitude $M_i$. The parameters $\mathbf {\theta _{ij}}$ account for terms related to style-of-faulting and site effects. Aleatory variability in the ground motion model is separated into an inter-event ($\tau \nu _i$) and an intra-event ($\sigma \epsilon _{ij}$) term, the inter-event term representing the variability of the median IM from one earthquake to another earthquake of the same magnitude and rupture mechanism and the intra-event term representing the variability of the ground motion value from one site to another at the same distance with the same site characterisation (Bommer and Crowley 2006). The terms $\tau _i$ and $\epsilon _{ij}$ are standard normally distributed random variables, and the constants $\tau$ and $\sigma$ are the standard deviations of the inter- and intra-event variability.

Observations of ground motion from densely recorded earthquakes have shown that the intra-event residual term ($\epsilon _{ij}$) is found to be spatially correlated, such that the coefficient of correlation ($\rho _h$) between the intra-event residuals observed at two sites separated by a distance, $h$, will decrease with increasing separation distance. In the majority of spatial correlation models (e.g. Wang and Takada 2005; Goda and Hong 2008; Goda and Atkinson 2009; Jayaram and Baker 2009; Esposito and Iervolino 2011, 2012) an exponential function form has been preferred:

$$\begin{aligned} \rho _h \left( T \right) = \exp \left[ {a\left( T \right) h^{b \left( T \right) }}\right] \end{aligned}$$

(2)

where $a\left( T \right)$ and $b\left( T \right)$ are period-dependent coefficients describing the strength of attenuation of spatial correlation with distance. The distance over which the correlation may be considered significant, termed “correlation length” in geostatistical analysis, is also known to be greater for IMs that characterise the lower frequency content of the ground motion (e.g. long period spectral acceleration/displacement) (e.g. Jayaram and Baker 2009; Esposito and Iervolino 2012). In adopting the exponential model, of the form shown in Eq. 2, as a basis for simulating spatially correlated fields of ground motions several assumptions are made. The first is that the ground motion residuals for a set of spatially distributed points can be considered joint normally distributed, and that therefore the simulation of the residuals need only consider a multivariate Gaussian distribution. The assumption of multivariate normality in spatially distributed ground motion residuals has been shown to be appropriate by Jayaram and Baker (2008). The second assumption underlying this model is that the fields are isotropic and homogeneous; isotropy indicates that no azimuthal trend is visible in the correlation, as shown by Jayaram and Baker (2009), while the homogeneity indicates that the mean and auto-covariance of the field are not dependent on the location, as shown by Wang and Takada (2005).

It is also well-established from observed ground motion records, that the intra-event ground motion residual term for two different periods of spectral acceleration at the same site are cross-correlated, with the coefficient of correlation decreasing in accordance with an increase in the spacing between periods (Inoue and Cornell 1990; Baker and Cornell 2006; Jayaram and Baker 2008). When considering the seismic risk to a heterogeneous type of buildings, utilising fragility models that are functions of the fundamental period of response of each building type, it is desirable, even necessary, that the ground motion fields preserve all three facets of correlation within the ground motion IMs generated by the same earthquake: the correlation between the intra-event residuals of different ground motion IMs for the same site, the spatial correlation between the intra-event residuals of the same IM for sites separated by a distance $h$, and the spatial cross-correlation between the intra-event residuals of different ground motion IMs for sites separated by a distance $h$.

2.1 Simulating spatially correlated ground motion fields

The simplest methodology for simulation of spatially correlated random fields of GMPE residual values that are not conditioned to any observation comes from the classical decomposition approach. Under the assumption of joint log-normality in the GMPE residuals, a multivariate Gaussian distributed random field ($\mathbf {Y}$) is defined as a set of $y_1, y_2, \ldots y_N$ ground motion residual values for $N$ sites, generated from the following function:

$$\begin{aligned} \mathbf {Y} = \mathbf {\mu } + \mathbf {LZ} \end{aligned}$$

(3)

where $\mathbf {Z}$ is a vector of independent Gaussian distributed random variates that take on the values $z_1, z_2, \dots z_N, \mathbf {\mu }$ is a zero-valued vector of length $N, \mathbf {L}$ the lower triangular matrix, obtained using Cholesky factorisation, such that $\mathbf {LL^T} = \mathbf {C}$, where $\mathbf {C}$ is the positive-definite correlation matrix:

$$\begin{aligned} \mathbf {C} = \begin{bmatrix} 1&\quad \! \rho \left( {h_{1,2}} \right)&\quad \! \cdots&\quad \! \rho \left( {h_{1,N}} \right) \\&\quad \! 1&\quad \! \cdots&\quad \! \rho \left( {h_{2,N}} \right) \\ \quad \!&\quad \!&\quad \! \ddots&\quad \! \vdots \\ sym&\quad \!&\quad \!&\quad \! 1 \end{bmatrix} \end{aligned}$$

(4)

and $\rho \left( {h_{i,j}} \right)$ is the coefficient of correlation between ground motion residuals for two locations separated by a distance of $h_{i,j}$. For spatially distributed portfolios of a homogeneous building type, requiring only one IM (often a spectral acceleration at a given period), Eq. 3 is sufficient to characterise the spatial correlation of the IM at different sites. To retrieve the resulting logarithmic ground motion values for the set of sites, the residual values are multiplied by the aleatory variability term ($\sigma$) of the GMPE and added to the expected, or median, ground motion defined by the GMPE $(f \left( {M_i, R_{ij}, \mathbf {\theta }_{ij}} \right)$ in Eq. 1).

For heterogeneous portfolios considering multiple intensity measure types the problem is more complex as the coefficient of correlation in GMPE residuals between two different intensity measures $\rho _{IM_k, IM_l} \left( {h_{ij}} \right)$ is not equal to unity in the case that $IM_k \ne IM_l$. Nevertheless, it is still necessary to co-simulate multiple fields of ground motion IMs whilst preserving their spatial cross-correlation structure. To undertake this, the several different approaches are presented below.

2.2 Conditional hazard (“Markov-type” approach)

The conditional hazard approach (Iervolino et al. 2010) one method by which fields of ground motion residuals for different IMs can be generated at multiple sites, taking into account the spatial correlation. Assuming a spatially correlated field of ground motion residuals for $IM_1$ generated using Eq. 3, and defining $\rho _{IM_k, IM_l}$ equivalent to $\rho _{IM_k, IM_l} \left( {h = 0} \right)$, the distribution of each additional intensity measure $IM_k$ is described via:

$$\begin{aligned} \mu _{IM_k | IM_1, M, R}&= \mu _{IM_k | M, R} + \rho _{IM_1, IM_k}\sigma _{IM_k} \frac{z - \mu _{IM_1, M, R}}{\sigma _{IM_1}} \end{aligned}$$

(5)

$$\begin{aligned} \sigma _{IM_k | IM_1}&= \sigma _{IM_k} \sqrt{1 - \rho _{IM_1, IM_k}^{2}} \end{aligned}$$

(6)

where $\mu _{IM_k | IM_1, M, R}$ and $\sigma _{IM_k | IM_1}$ are the mean and total standard deviation of the logarithmic ground motion for intensity measure $k, \mu _{IM_k | M, R}$ and $\sigma _{IM_k}$ the corresponding unconditional mean and standard deviation, and $z$ is the random variate corresponding to the total aleatory variability term, simulated for the primary IM using Eq. 3. Therefore at each site, the ground motion residuals at each intensity measure are conditioned upon that of the primary intensity measure. This approach is equivalent to the “Markov-type” approach described in Loth and Baker (2013) and Journel (1999).

The conditional hazard approach implicitly assumes that the distribution of the ground motion residual for each secondary intensity measure IM $_k$ is conditional only upon the primary intensity measure at the site. This makes it an approximate method, by which the spatial correlations in the secondary intensity measures are inferred from the spatial correlation of the primary IM. In the case where multiple secondary intensity measures are being considered, correlations between the secondary IMs are not directly modelled, or are only implicit via the correlation with the primary IM. Furthermore, the spatial correlation structure of each the secondary IMs is not faithfully reproduced. As the correlation length of longer period motion is greater than that of short period motion it is preferable to adopt the longer period IM as the primary IM in practice (e.g. Goda and Hong 2008) so as to better ensure that the conditions of the screening hypothesis assumed by the “Markov-type” approach are met (Journel 1999). The reader is referred to Loth and Baker (2013) for further discussion of this issue; however, later subsequent analysis in this paper will illustrate the impact of selection of the primary IM in practice.

2.3 Full-block cross-correlation

A method for co-simulation of multiple cross-correlated fields is demonstrated by Oliver (2003), who extends the classical matrix decomposition approach to separate the co-simulation of the random fields $\mathbf {Y_k}$ and $\mathbf {Y_l}$ into the following matrix formulation:

$$\begin{aligned} \begin{bmatrix} \mathbf {Y}_k \\ \mathbf {Y}_l \end{bmatrix} = \begin{bmatrix} \mathbf {\mu }_{IM_k} \\ \mathbf {\mu }_{IM_l} \end{bmatrix} + \begin{bmatrix} \mathbf {L}_{IM_k}&\mathbf {0} \\ \rho _{IM_k,IM_l}\mathbf {L}_{IM_l}&\sqrt{1 - \rho _{IM_k,IM_l}^2}\mathbf {L}_{IM_l} \end{bmatrix} \begin{bmatrix} \mathbf {Z}_{IM_k} \\ \mathbf {Z}_{IM_l} \end{bmatrix} \end{aligned}$$

(7)

where $\mathbf {L}_{IM_k} \mathbf {L}_{IM_k} ^T = \mathbf {C}_{IM_k,IM_k}, \mathbf {L}_{IM_l} \mathbf {L}_{IM_l} ^T = \mathbf {C}_{IM_l, IM_l}$ are the auto-covariance matrices of fields $\mathbf {Y}_{IM_k}$ and $\mathbf {Y}_{IM_l}$ respectively. This relatively simple formulation therefore allows for the definition of the cross-covariance matrix:

$$\begin{aligned} \mathbf {LL}^T&= \begin{bmatrix} \mathbf {L}_{IM_k}&\mathbf {0} \\ \rho _{IM_k,IM_l}\mathbf {L}_{IM_l}&\sqrt{1 - \rho _{IM_k, IM_l}^2}\mathbf {L}_{IM_l} \end{bmatrix}\begin{bmatrix} \mathbf {L}_{IM_k}^T&\rho _{IM_k,IM_l} \mathbf {L}_{IM_l}^T\\ \mathbf {0}&\sqrt{1 - \rho _{IM_k,IM_l}^2}\mathbf {L}_{IM_l}^T \end{bmatrix}\nonumber \\&=\begin{bmatrix} \mathbf {L}_{IM_k} \mathbf {L}_{IM_k}^T&\rho _{IM_k,IM_l} \mathbf {L}_{IM_k}\mathbf {L}_{IM_l}^T\\ \rho _{IM_k,IM_l}\mathbf {L}_{IM_l} \mathbf {L}_{IM_k}^T&\mathbf {L}_{IM_l} \mathbf {L}_{IM_l}^T \end{bmatrix} \end{aligned}$$

(8)

It follows that this formulation can be extended to an arbitrary number ($k$) of IMs in the following manner:

$$\begin{aligned} \mathbf {LL^T} = \begin{bmatrix} \mathbf {L}_{IM_1} \mathbf {L}_{IM_1}^T&\rho _{IM_1,IM_2}\mathbf {L}_{IM_1} \mathbf {L}_{IM_2}^T&\cdots&\rho _{IM_1,IM_k}\mathbf {L}_{IM_1} \mathbf {L}_{IM_k} ^ T \\ \rho _{IM_1,IM_2}\mathbf {L}_{IM_2} \mathbf {L}_{IM_1}^T&\mathbf {L}_{IM_2} \mathbf {L}_{IM_2}^T&\cdots&\rho _{IM_2,IM_k}\mathbf {L}_{IM_2}, \mathbf {L}_{IM_k}^T \\ \vdots&\vdots&\ddots&\vdots \\ \rho _{IM_1,IM_k}\mathbf {L}_{IM_k} \mathbf {L}_{IM_1}^T&\rho _{IM_2, IM_k}\mathbf {L}_{IM_k} \mathbf {L}_{IM_2}^T&\cdots&\mathbf {L}_{IM_k} \mathbf {L}_{IM_k}^T \end{bmatrix} \end{aligned}$$

(9)

definition of the full cross-correlation matrix, co-simulation of all the corresponding parameter fields is simply undertaken in the same manner as in Eq. 3. It is also the case that if the spatial correlation matrices for each IM $\mathbf {C}_{IM_k, IM_k}$ are each positive-definite, and the correlation matrix describing the IM to IM correlations is positive-definite, then the resulting full-block cross-correlation matrix $\mathbf {C} = \mathbf {LL}^T$ will be positive-definite.

This approach to deriving the cross-correlation matrix ensures that not only are the spatial correlation properties within each intensity measure preserved. This allows for the distance-dependent correlation length of each IM to be modelled (as $\mathbf {L}_{IM_k} \mathbf {L}_{IM_l}^T$ is equivalent to $\mathbf {LL}^T$ in the case that $k = l$), whilst the IM to IM correlation will reduce to the cross-correlation matrix in the case that $N = 1$, thus rendering the correlation between IMs independent of the distance scaling of the correlation. This is in contrast to the conditional hazard approach in which the spatial correlation structures of the ground motion residuals within each IM are not explicitly retained. It also permits for the construction of the spatial cross-correlation model using separate correlation models for the spatial correlation and the IM-to-IM correlation, provided that the correlation matrices for both are positive-definite. This allows for greater flexibility in adopting correlation models, particularly spatial correlation models, that may reflect more the local characteristics of a region.

2.4 Linear model of coregionalisation (LMCR)

The third approach to modelling the cross-correlation between fields of ground motion at different spectral periods is via the linear model of coregionalisation, which is fit to a set of experimental semi-variograms and cross-variograms of observed GMPE residuals from well-recorded events by Loth and Baker (2013). The authors propose an appropriate functional form of the LMCR for this purpose to be:

$$\begin{aligned} \mathbf {C} \left( h \right) = \mathbf {B^1} \exp \left( {\frac{-3h}{20}} \right) + \mathbf {B^2} \exp \left( {\frac{-3h}{70}} \right) + \mathbf {B^3}I_{h=0} \end{aligned}$$

(10)

where $\mathbf {B^1}, \mathbf {B^2}$ and $\mathbf {B^3}$ are the coregionalisation matrices for short-range, long-range and zero-separation, respectively. $I_{h=0}$ is an indicator function taking the value of 1 for $h = 0$, and zero otherwise. The coefficients of the coregionalisation matrices are given in Loth and Baker (2013). As the correlation model is fit directly to the variograms, positive-definiteness can largely be ensured in the resulting cross-covariance matrix. Therefore the model does not separate the spatial correlation and inter-IM correlation models, but instead fits a single model capturing both characteristics. This may mean that if regional differences, or even inter-event differences, in the correlation structure exist it may be necessary to determine different coregionalisation matrices more suitable for local application.

2.5 A note on the residual terms

A new question that arises when transitioning from consideration of single intensity measures to co-simulation of multiple correlated intensity measures is the role of the inter-event residual. Both the conditional hazard and LMCR approaches define the spatial correlation and cross-correlation using the inter-event residual, whilst the full-block cross-correlation models can be constructed using correlation models from intra-event residuals where such models are available. In the derivation of existing spatial correlation models, both Park et al. (2007) and Jayaram and Baker (2009) demonstrate that if the inter-event variability is assumed to be constant, then the coefficient of correlation for the intra-event residual can be derived from the total residual term. This assumption is not necessarily valid in many cases that are relevant here. Recent developments in the modelling of nonlinear site response in modern GMPEs, such as Abrahamson and Silva (2008), now incorporate magnitude and site dependence into the inter-event residual term, though notably not in Boore and Atkinson (2008) as used by Loth and Baker (2013) for the derivation of the LMCR. This would prevent the inter-event residual term from being considered constant for a single period. Secondly, and more importantly for the current analysis, it is known that the coefficient of correlation in the inter-event residual term between two different IMs is less than unity(Goda and Atkinson 2009), thus for a given event the inter-event residual is not constant across multiple period. In deriving the linear model of co-regionalisation, Loth and Baker (2013) use the total residual, thus aggregating the inter-event correlation into the cross-correlation model. It may be the case, therefore, that when implementing the LMCR in a co-simulation it may be inconsistent to separate the inter- and intra-event residuals. The impact of modelling inter-event correlation versus simply modelling the total residual when applying the LCMR approach is considered subsequently.

3 Case study application to synthetic portfolios derived from Italian data

To demonstrate the influence of spatial cross-correlation on the risk analysis of a heterogeneous portfolio of buildings, we consider a case study from the Tuscany region of Italy. Seismic risk analysis is carried out for portfolios aggregated over different spatial scales. To generate the ground motion fields for the Tuscany region, the stochastic seismic hazard analysis is undertaken using the SHARE area source model for Italy (Woessner et al. 2012). In the current example, 129 uniform area sources are considered within Italy and the surrounding Mediterranean region, of which 78 are found within a distance of 250 km from Tuscany. For each source the magnitude frequency distribution is characterised by a doubly-truncated exponential model, consistent with the Gutenberg-Richter earthquake recurrence model. The focal mechanism and earthquake depth distributions are defined for each zone allowing for the characterisation of a finite pseudo-rupture plane for each stochastically generated earthquake. In the present example only the Akkar and Bommer (2010) GMPE is considered. The influence of the choice of GMPE, and other epistemic uncertainties, on the final loss estimates is not within the scope of this study. As suggested previously the choice of GMPE may influence upon the results depending on whether the inter- and intra-event components of the aleatory variability are homo- or hetero-skedastic, or due to the manner in which soil nonlinearity is accounted for in the functional form. In this particular case the GMPE in question assumes a relatively simple functional form in which nonlinear site response is not considered and inter-event variance is constant for each period. No spatial correlation in the ground motion residual terms was considered in the fitting of this GMPE to data, though subsequent analysis of the European strong motion data set by Esposito and Iervolino (2012) identifies clear evidence of spatial correlation in the strong motion records.

The hazard is rendered for the “rock” site condition (in this case NEHRP class B). Application to real portfolios should require detailed microzonation of the exposure region in order to constrain the spatial distribution of site conditions. In this analysis we simulated the occurrence of more than 120,000 earthquakes corresponding to 100,000 realisations of one-year seismicity in the region. For each earthquake one realisation of the cross-correlated random fields of the selected ground motion IMs is generated.

3.1 Correlation models

With the exception of the LMCR methodology, the cross-correlation methods described in Sect. 2 require the definition of both a spatial correlation model, and a spectral cross-correlation model. In the current analysis the spectral cross-correlation model of Baker and Cornell (2006) is preferred, and the period-dependent spatial correlation model of Jayaram and Baker (2009) is adopted:

(11)

where $b$ denotes the spatial length scale of the correlation, namely the distance at which the correlation coefficient is found to fall below 0.05, and is a property of the frequency of the ground motion IM. The two cases presented in this formulation refer to a model in which no clustering in site condition ($V_{S30}$) is expected (“Case 1”) and when clustering is believed to be observed (“Case 2”).

In this analysis, spectral correlation in the inter-event residual is incorporated using the model of Goda and Atkinson (2009):

$$\begin{aligned} \rho _{\tau } \left( {T_1, T_2} \right) =&\frac{1}{3} \left( 1 - \cos \left\{ \frac{\pi }{2} - \left[ \theta _1 + \theta _2 I_{T_{\min } < 0.25} \right. \right. \right. \nonumber \\&\left. \left. \left. \times \left( {\frac{T_{\min }}{T_{\max }}} \right) ^{\theta _3} \log _{10} \left( {\frac{T_{\min }}{0.25}} \right) \right] \log _{10} \left( {\frac{T_{\max }}{T_{\min }}} \right) \right\} \right) \nonumber \\&+ \frac{1}{3} \left\{ {1 + \cos \left[ {-1.5 \log _{10} \left( {\frac{T_{\min }}{T_{\max }}} \right) }\right] }\right\} \end{aligned}$$

(12)

where $T_{\max }$ and $T_{\min }$ are the maximum and minimum of the two periods, $I_{T_{\min } < 0.25}$ takes the value of $1$ if $T_{\min } < 0.25$ and $0$ otherwise, and $\theta _1, \theta _2$ and $\theta _3$ are coefficients taking the values of $1.374, 5.586$ and $0.728$ respectively. For clarity we note that the inter-event residual correlation model presented by Goda and Atkinson (2009) is applied to the geometric mean of the horizontal components, whilst that of Jayaram and Baker (2009) is fit to the rotationally independent geometric mean.

As discussed in Sect. 2.5, many spatial correlation models available in peer-reviewed literature, including that selected here, are fit to the total residual term, rather than the inter-event residual. Whereas in the current simulation method we are separating the simulation of the aleatory variability into the inter- and intra-event components. This creates an inconsistency between the manner in which the correlation models are constructed and the manner in which they are applied. This inconsistency may only be resolved by defining correlation models for the full-block cross-correlation and LMCR methodologies that explicitly separate the inter- and inter-event terms. Construction of such models is beyond the scope of this paper, but differences in the resulting loss curves should be interpreted taking into consideration this issue.

3.2 Exposure model

An exposure model capable of providing the spatial distribution of each building type, along with its structural replacement cost, throughout the region of Tuscany has been developed (Fig. 1), mostly based on information from the Italian Building Census Survey of 1991. In this source, buildings are organised according to the predominant construction material [reinforced concrete, masonry, other (i.e., wood and steel) and unknown], age of construction and number of storeys. For the sake of simplicity buildings from the category “other” and “unknown” have been ignored as there was insufficient information available regarding their seismic vulnerability and, moreover, these categories represent only 1 % of the buildings in the region of interest. To take into account the age of construction, two sub-classes have been considered: Pre-code (buildings constructed prior to the 1974 design code, which endorsed the consideration of a horizontal lateral load equal to 2 % of the total weight) and Post-code (buildings constructed according to the 2003 design code, which establishes a horizontal lateral load depending on the seismic zone, taken as 7 % of the total weight in our case). All of the masonry buildings were assumed to have no seismic design. Regarding the number of storeys, three sub-classes have been considered: low-rise (1–3 storeys), mid-rise (4–6 storeys) and high-rise (7 storeys or greater). This information was available at the level of the third Italian administrative unit (i.e., “comune”). The spatial extent of these regions can vary from 5 to $470\,\mathrm {km}^2$, with an average area of $80\,\hbox {km}^2$. The organisation of the exposure model and the percentage of each building type within the building portfolio are described in Table 1.

Fig. 1

Aggregated value of exposure data for the Tuscany province, with SHARE area sources delineated by black lines. Florence administrative district and city district are highlighted in pink and yellow, respectively

Table 1 Characteristics of the building portfolio

The assumption that all the buildings are located at the centroid of the associated “comune” would not allow for consideration of the variation of the seismic hazard within each region, and also would essentially induce an artificial perfect correlation of the ground motion IM, since each building belonging to a given type would experience the same shaking. Furthermore, the distance between the centroids of each “comune” is often larger than typical correlation lengths, which would impede an adequate evaluation of the various methodologies described herein. In order to overcome these issues, the original exposure model was spatially disaggregated according to a 30 arc-second grid (approximately 0.9 km at the latitude considered here). To this end, the LandScan dataset (Dobson et al. 2000) that provides population count for a grid with the aforementioned resolution was used. For each “comune”, the number of buildings was distributed throughout the grid cells based on the population in each cell. Thus, in grid cells with a high population count a large number of buildings was assigned, whilst in cells with zero population count no buildings were allocated. In this process, the fraction of each building class was retained, thus not favouring any particular typology depending on the size of the population. Both the original and disaggregated models are shown in Fig. 2.

Fig. 2

Exposure model following an unevenly spaced (commune) resolution (top) and according to the 30 arc-second grid (bottom)

It should be noted that in the current approach there may exist an artificial bias in the correlation due to the aggregation of the assets from within a cell such that the input ground motion is taken from a single point at the centroid of the cell (Bazzurro and Luco 2005). This is demonstrated by Stafford (2012), who propose an adaptation to the conditional simulation procedure in the case of aggregated portfolios. To demonstrate that the trends seen in the results can not be attributable to this aggregation bias on the mean loss estimates, a second set of synthetic portfolios are generated in which a set of heterogeneous assets are sampled from within each cell (weighted according to the total aggregated value of the cells) and distributed randomly within the cell. Two sample portfolios, one for the Firenze (Florence) administrative province, and one for the Firenze (Florence) city district, are shown in Fig. 3.

Fig. 3

Synthetic heterogeneous portfolio of single assets for the Firenze administrative province (main) and city district (inset)

The estimation of the structural replacement cost of each building was performed based on information regarding the average number of dwellings per building type, average building year per dwelling and average replacement cost per area, taken from the Italian Statistical Office database.¹

3.3 Vulnerability model

In order to fully explore the various methodologies for spatial correlation and cross-correlation modelling of ground motion IMs in seismic risk, the loss estimation for the different building types was performed using a new set of vulnerability functions (i.e. loss ratio distribution for a set of intensity measure levels). This vulnerability model was developed based on a methodology proposed by Silva et al. (2013), and using the material and geometrical properties for Italian buildings defined in Borzi et al. (2008) for reinforced concrete types and in Binda et al. (1999) for the masonry classes. Each vulnerability function is expressed in terms of spectral acceleration for the yielding period of vibration (see Table 1), which was calculated using the simplified period-height relationships proposed by Crowley et al. (2004) and Bal et al. (2010).

The vulnerability methodology consists in generating thousands of synthetic buildings considering the variability in the geometrical and material properties, whose nonlinear capacity is estimated using the displacement-based earthquake loss assessment (DBELA) concept (Crowley et al. 2004), against a large set of ground motion records compatible with the seismogenic environment around the region of interest (Barani et al. 2009). The respective fundamental periods o the buildings remain constant, however. Global limit states are used to estimate the damage distribution for different levels of ground motion, and a regression algorithm is applied to derive fragility functions (i.e., probability of exceeding different limit states for given intensity measure levels). Then, the resulting fragility functions are combined with a damage-to-loss model (Di Pasquale and Goretti 2001) to derive a vulnerability function for each building type, as illustrated in Fig. 4. It is pertinent to mention that this vulnerability methodology allows for the propagation of a large spectrum of uncertainties (e.g. variability in the geometric and material properties, uncertainty in the damage definition, record-to-record variability) into the final vulnerability curves, which may result not in a single loss ratio per intensity measure level, but rather in a probabilistic distribution of loss ratio, usually characterised by a lognormal distribution with an associated mean and standard deviation. However, in order to decrease the computational burden of the calculations and to reduce the number of variables affecting the final results, a decision was made to consider only the mean loss ratio at each IM.

Fig. 4

Vulnerability model for the Italian building portfolio. Type acronyms are shown in Table 1

4 Impact of Cross-correlation on analyses of seismic loss at an urban scale

4.1 Loss analysis at urban scale

To understand the role that spatial cross-correlation plays in modelling earthquake losses, the analysis is initially limited to the smallest spatial scale. In this current study for this scale we considered the Florence (Firenze) city district and the wider Florence administrative district. To give a clearer perspective on the spatial scale, the greatest site-to-site distance within the Firenze city district is approximately 15 km, compared to 100 km for the Florence administrative district and more than 250 km for the Tuscany region as a whole. These parameters are relevant as it will be seen in due course that the comparative influence of spatial correlation and cross-correlation on an exposure portfolio is strongly dependent on the relative density of site-to-site distances within the portfolio. This is intuitive as more spatially constrained portfolios are more likely affected in their entirety by the same earthquakes than more widely dispersed ones are. For the Florence city and administrative districts a comparison of the annual exceedance probability loss curves is made considering seven IM correlation modelling options:

• 1. No spatial correlation or spatial cross-correlation is considered, and inter-event residuals are sampled independently for each period.

• 2. Spatial correlation is considered separately for each spectral quantity and the inter-event residuals are independent for each period.

• 3. Spatial correlation and cross correlation are modelled using a conditional hazard approach (Sect. 2.2), with the shortest period represented in the portfolio ($S_a \left( {0.2 s} \right)$) selected as the primary IM for modelling the spatial correlation.

• 4. Spatial correlation and cross correlation are modelled using a conditional hazard approach (Sect. 2.2), with the longest period represented in the portfolio ($S_a \left( {1.2 s} \right)$) selected as the primary IM for modelling the spatial correlation.

• 5. Spatial correlation and cross-correlation are included and modelled using the full-block cross correlation methodology (Sect. 2.3). Spectral correlation in the inter-event residual is simulated using the model of Goda and Atkinson (2009).

• 6. Spatial correlation and cross-correlation are included and modelled using the LMCR methodology (Sect. 2.4). Spectral correlation in the inter-event residual is also simulated using the model of Goda and Atkinson (2009).

• 7. Spatial correlation and cross-correlation are included and modelled using the LMCR methodology (Sect. 2.4) with uncertainty represented using only the total $\sigma$ term.

To initially verify that spatial correlation is influencing the analysis for a homogenous portfolio, an initial analysis is undertaken using a single type of building, which in this case the masonry wall, mid-rise, pre-code type (see Table 1) with a corresponding fundamental period of 0.5 s. Figure 5 demonstrates the impact upon the aggregated loss analysis when including spatial correlation for the Firenze Administrative Province (with a typical footprint diameter on the order of approximately 100 km) and for the Firenze City District (with a typical footprint diameter on the order of 15 km) respectively. The loss curves indicate that when spatial correlation is included in the model greater losses are observed at lower annual probabilities of exceedance. Furthermore, the impact that inclusion of spatial correlation has on the loss analysis is relatively greater for the portfolio with the smaller “footprint”. This observation is consistent with the trends observed by Park et al. (2007) and Silva et al. (2014). It can also be observed that for higher annual probabilities the inclusion of spatial correlation will often reduce the loss estimates. This trend can be explained by the considering how inclusion of correlation increases variability in the losses for a single scenario. Neglect of correlation narrows the tails of the distribution, meaning that for each event the probability of sampling low values in the left tail is reduced, therefore the losses are higher. Equally, however, the probabilities of sampling the very high values in the right tail are also reduced, thus leading to lower losses. However, even at the $5 \times 10^{-3}$ annual probability it may be the case that spatial correlation may still result in higher losses in other portfolios if the assets are more spatially clustered than is the case here. The noise in the curves at low probabilities (less than $10^{-3}$) is due to the occurrence of rare high-impact events, which due to their very low likelihood may be under- or over-sampled in the synthetic catalogue with respect to their long-term occurrence rate. Extension of the synthetic catalogue length would ensure a more stable sample of the larger events, which control the extreme losses at the lowest probabilities.

Fig. 5

Aggregated Loss Curves for the masonry-wall, mid-rise, low-code type (M-MR-PC) for the Firenze Administrative Province (top), containing 2591 assets over 1192 locations, and the Firenze (Florence) City District (bottom), containing 168 assets over 166 locations

The loss analyses for the heterogeneous portfolio (Figs. 6 and 7) illustrates the impact of considering spatial correlation and spatial cross-correlation. For both the Florence city portfolio and the administrative district portfolios, the inclusion of spatial cross-correlation results in greater losses at lower annual probabilities (typically less than $10^{-3}$), with the trend seen more clearly for the smaller scale city portfolio. The full-block cross-correlation methodology and the LMCR methodology provides generally similar results for the case when inter- and intra-event residuals are separated, suggesting that the method by which spatial cross-correlation is modelled has a relatively small impact on the loss analysis. In comparison, the similarity in the loss curves when considering spatial correlation for each individual period without cross-correlation, and when neglecting correlation altogether, shows that for a heterogeneous portfolio the neglect of the cross-correlation drastically erodes the total influence of correlation on the loss estimation. This is to be expected given that neglecting cross-correlation in a given simulation of random fields of different IMs for a given earthquake generates completely different spatial patterns of high and low values for each specific IM. It is the statistical correlation of these patterns of high and low values of different IMs that causes the unusually high losses (and low as well but of less importance here) that would make the curve greatly differ at lower annual probabilities for a heterogeneous portfolio. Using this approach for assessing losses to heterogeneous portfolios, therefore, leads to estimates of large losses that are not particularly accurate.

Fig. 6

Aggregated Loss Curves for Firenze (Florence) Administrative Province for a heterogeneous portfolio containing 21,151 assets at 1192 locations

Fig. 7

Aggregated Loss Curves for Firenze (Florence) City District for a heterogeneous portfolio containing 2,082 assets at 168 locations

The loss curves derived using the conditional hazard methodology require careful interpretation. In the case when the shorter period spectral acceleration (0.2 s) is used as the primary IM, at the provincial scale the loss curves tend strongly toward the “no-correlation” case, whilst at the city scale these curves tend more strongly toward the “spatial only” case.. When conditioning on the longer period (1.2 s) spectral acceleration, however, we see the trend in the loss curves following more closely those of the LMCR and full-block cross-correlation case, though with a tendency more toward the middle (i.e. with less extremes) than in the cases when correlation is fully considered. When using the shorter-period as the primary IM the correlation length of the spatial field is shorter,thus when combined with the smaller cross-correlation between longer and shorter period IMs the spatial correlation for the longer period IMs is significantly underestimated. Conversely, when using the longer period IM as the conditioning IM, the mid- and long-period IMs the spatial correlation is being over-estimated. For the short period IMs, however, the effect of overestimation in the spatial correlation is eroded by the smaller cross-correlation between IMs. Ultimately, the competing influence of spatial correlation and IM to IM cross-correlation on the resulting loss curves will depend on the composition of the portfolio, which may be very difficult to anticipate prior to the analysis. This condition may be one compelling argument against the use of this particular methodology. Or else, if adopting the conditional hazard approach it is strongly recommended to use the longer period IM for generating the spatially correlated fields, as will be pursued in the subsequent comparisons.

Focusing specifically on the full spatial cross-correlation methodologies, all three methods (full-block cross-correlation, LMCR and LMCR using total $\sigma$) result in higher losses at lower annual probabilities of exceedance, and lower losses at higher annual probabilities, when compared with those from methods in which spatial cross-correlation is neglected. For the portfolio with the larger “footprint” (Fig. 6) all three methods provide curves that are in close agreement even at low annual probabilities of exceedance. For the city-district (Fig. 7) it is relevant to note that whilst the full-block cross-correlation and LMCR methods are in close agreement, in the case that only the total $\sigma$ term is modelled with the LMCR the losses are lower than in the cases where the inter- and intra-event variability are separated. From these trends it could be inferred that the means by which the full cross-covariance matrix is defined, be it by full-block cross-correlation or LMCR, is of less significance than the manner in which the inter- and inter-event correlations are modelled. In this respect there may be further work needed to develop an additional LMCR derived specifically for the intra-event term, thus allowing the correlations in the inter- and intra-event residuals to be separated in the modelling process.

An additional observation from the loss curves in Figs. 6 and 7 are the close correspondence between the losses when only spatial correlation is considered (i.e. the ground motion fields for each IM are each spatially correlated, but no cross-correlation is considered) and the case when correlation is neglected. As it is demonstrated in Fig. 5 that for a single type within the portfolio the inclusion of spatial correlation increases the losses, it is clear that when considering a heterogenous portfolio the neglect of spatial cross-correlation can erode the influence of spatial correlation. This may not be so unexpected if one considers that for a single realisation of ground motion fields, it is possible, common even, to expect that without the inclusion of cross-correlation an asset of a particular type my be subject to weaker than expected ground motion (a strong negative residual) whilst a co-located asset of a different type may be subject to stronger than expected ground motion (a strong positive residual). Without the inclusion of spatial cross-correlation to connect the different fields of IMs for a single realisation then the total effects of the correlation on a heterogenous portfolio are minimised.

Whilst the impact of the both the spatial correlation and spatial cross-correlation can be seen, it is also necessary to expand upon the role that the spatial dispersion, or spatial “footprint” as it is referred to in Park et al. (2007), of the portfolio plays in elucidating the differences between the methodologies. Recalling that the portfolio itself is rendered here onto an evenly spaced 30 arc-second grid, the distance between neighbouring assets is the same regardless of the size of the footprint. For the Florence city portfolio, however, as the assets are limited to only the city district itself the largest site to site distance is approximately 20 km, and the majority of site-to-site distances are less than 10 km. Conversely the administrative district spans over 100 km and the typical site-to-site distances are on the order of 20–30 km, which is beyond the correlation lengths for the spectral accelerations at the periods under consideration. This drastically reduces the impact of the spatial correlation. It remains pertinent, however, that for portfolios with a larger footprint the impact of the spatial cross-correlation remains visible. The portfolio footprint is therefore of great significance. The impact of spatial correlation and spatial cross-correlation on the loss analysis will depend on both the degree of spatial clustering within the portfolio, or even just the degree of spatial clustering of the highest value assets, and on the spatial footprint of the portfolio. This is not a trivial outcome as many real portfolios will contain assets distributed over a relatively small spatial scale, such as city or district, which will experience similar levels of ground shaking in an earthquake, and will therefore likely result in similar levels of damage.

An alternative approach for assessing losses to heterogeneous portfolios can be devised when cross-correlation of IMs cannot be modelled correctly, as it is in the approach above. Loss estimation for a heterogeneous portfolio does not necessarily require co-simulation of spatially cross-correlated ground motions, so long as the risk modeller accepts to derive fragility models for all structure types within the portfolio using a single intensity measure. Of course, this alternative approach comes at a price, as the selected IM will likely not be an efficient predictor of structural response, i.e. an IM that results in a smaller variability of the structural demand given the ground motion intensity (Luco and Cornell 2007), and may therefore lead to less accurate building response estimates. This reduction in structural response efficiency means that greater uncertainty in the vulnerability model will be transferred to the loss curve, which may potentially affect the loss estimates. Which one of the two alternative methods is preferable in these circumstances depends, to a certain extent, on the degree of heterogeneity in the portfolio.

To illustrate whether the spatial aggregation of the portfolio is biasing the trends, the loss curves for simpler distributed portfolios of unique assets (Fig. 3) are shown in Fig. 8. The same trends in the results from the different methodologies are visible as for the fully aggregated portfolio. In this particular case, however, the impact of the spatial cross-correlation is not quite so large, indicating that whilst the aggregation may be introducing a degree of artificially high correlation the overall results are persistent. Of course, it is still important to note that the degree of divergence between the loss curves derived using methodologies that neglect spatial cross-correlation and those that include it will depend heavily on the properties of the portfolio, and in this case in the period range of the IMs being considered in the risk analysis.

Fig. 8

Aggregated Loss Curves for Firenze (Florence) Administrative Province (top) Firenze (Florence) City District (bottom) for the sample portfolios shown in Fig. 3

4.2 Sensitivity to portfolio weighting

The examples demonstrate that the inclusion of spatial cross-correlation may impact upon the resulting estimates of seismic losses, it follows that the scale of this impact may depend not only upon the “footprint” of the portfolio but also upon the range of periods considered and the weighting of the exposure in different building types. This can be demonstrated by considering a slightly simplified example in which the spatial distribution of the assets, and therefore the “footprint”, remain the same as before. A simplification is made in the portfolio in that building types are limited only to the three low-code reinforced concrete classes: RC_LR_PC, RC_MR_PC and RC_HR_PC. Figures 9 and 10 demonstrate the impact upon the loss curves when the portfolios are weighted more in the low-rise, mid-rise and high-rise types, for the province and city areas respectively. In each of the three portfolios two-thirds of the assets are assigned to the corresponding LR, MR and HR types, and the remaining third of the assets divided evenly between the other types.

The loss curves from the different methodologies that are displayed in Figs. 9 and 10 show, to some extent, a greater degree of convergence than those derived for the more evenly distributed portfolio. As expected, this case demonstrates quite clearly that when weighted predominantly toward a single asset type, the impact of considering spatial cross-correlation on the loss curves is relatively minimal. At the level of the city scale (Fig. 10) loss curves generated using cross-correlation still give noticeably higher values at lower annual probabilities, albeit this effect is somewhat reduced in comparison with those from the more evenly distributed portfolios.

Fig. 9

Sensitivity of the loss curves for the Firenze Province to different weightings of the portfolio in the low-rise (top), mid-rise (middle) and high-rise (bottom) type

Fig. 10

Sensitivity of the loss curves for Firenze City to different weightings of the portfolio in the low-rise (top), mid-rise (middle) and high-rise (bottom) type

A second effect that is visible within these analyses is that there is greater convergence amongst the curves when the portfolio is weighted more with building type that consist of longer-period (mid-rise and high-rise) structures. This trend is again more evident in the city-scale portfolio than in the provincial scale portfolio. This would seem to indicate the influence of the correlation length in the analysis, as in the case of the high-rise building types the fundamental period is greater and the correlation between sites for these buildings assumes a greater role in the modelling than the cross-correlation between types. This essentially minimises the impact of cross-correlation, thus the full-block and LMCR methods produce similar results to that of the case when cross-correlation is neglected.

5 Conclusions

This loss estimation exercise for an aggregated, synthetic, heterogeneous portfolio for the Tuscany region of Italy demonstrates that the inclusion of spatial cross-correlation is important for estimating accurately the likelihood of observing large, infrequent losses. This impact remains visible, albeit diminished, when considering losses for portfolios spread over larger spatial scales, even at scales where the influence of ordinary spatial correlation might be seen to be negligible. It is emphasised, however, that for heterogeneous portfolios of any spatial scale modelling spatial cross correlation is always important, as loss estimates are also routinely needed for subsets of the portfolios that are limited geographically (e.g., into a zipcode or a commune).

The analyses presented herein also highlight the influence of the portfolio composition, in terms of period range of the IMs and proportions of the building types, when incorporating spatial cross-correlation of the ground motion variability into the risk analyses. It is evident from the sensitivity studies that there are many possible conditions under which the impact of spatial cross-correlation is negligible. Certainly the influence diminishes when the portfolios are more spatially dispersed (i.e. with a larger “footprint”), or are dominated by a particular building type.

These results also show, for the first time, a side-by-side comparison of loss curves computed by different methodologies use for the generation of spatially cross-correlated random fields of ground motion intensity measures. It can be seen clearly that the loss curves may be sensitive to the choice of methodology, albeit we noted similar (but not identical) losses in the two methodologies that include both full spatial cross-correlation and inter-event residual correlation, i.e. the full-block cross-correlation and the LMCR approach. From an implementation perspective the two methodologies are similar in terms of computational demand and should both ensure positive-definiteness in the spatial covariance matrix, thus there is not necessarily a clear case for adopting one over the other in application. It is recommended, however, that if wishing to represent the full spatial cross-correlation structure of the ground motion intensity measures that these particular methodologies are adopted in favour of the others considered within this study.

The potential influence of the spatial cross-correlation is dependent on a balance between the spatial, spectral (or IM-dependent) and compositional properties of the portfolio, such as the proportion of different types and/or the form of the vulnerability models, for example. The balance of the influencing factors may be hard to predict prior to the analysis. Therefore the most prudent approach to follow when undertaking an analysis of seismic risk to heterogeneous portfolios would be one in which the spatial cross-correlation in the ground motion IMs is included in the modelling process, or at least until it can be established by sensitivity studies that the effects of the spatial cross-correlation are negligible for the portfolio in question.

The inferences made from this analysis, and the possible applications in seismic loss modelling for both research and industry, necessitate further investigation into conditions in which the spatial cross-correlation may be seen to impact the loss estimates. In particular, the artificial correlations introduced by aggregating assets within a geospatial region, such as a grid-cell, zip/postal code or electoral district, need to be compensated for within the risk analysis. Stafford (2012) describe the process by which this may be undertaken for a single IM in a post-disaster assessment, demonstrating that when considering the aggregated assets the standard deviation $\sigma$ of the IM at the aggregation site generated by a given earthquake must be reduced as a result of the fact that assets are averaged within the spatially extended region. This can be readily incorporated into analyses of the sort demonstrated here. Similarly, the application of spatial cross-correlation to simulations of ground motion conditioned upon a set of observations would enhance the characterisation of uncertainty in real-time post-event modelling of earthquake losses.