1 Introduction

Unmanned Surface Vehicles (USVs) are becoming more common in military and civilian applications. Such operations include port security, oceanic surveying, and reconnaissance. With this increased use also comes an increased need for efficient path planning strategies that can safely route the USV through the operating environment.

While path planning is a term used to refer to wide range of navigational algorithms, this paper will focus on developing a spatial plan between two vehicle states for a single agent. Thus, this paper does not consider time-varying trajectories, or multi-agent scenarios. Like many unmanned systems, USVs generally have a well-defined operating area, such as a specific waterway. The set of all vehicle states within this operating area is generally referred to as the configuration space, while the set of vehicle states that avoid obstacle collisions is called the traversable space or free space. However, each vehicle has different motion characteristics. Thus, paths are sought that are both fully within the free space and considered dynamically-feasible or kinematically-feasible. It is also often desired to achieve an optimal plan subject to a cost function, such as minimum distance or minimum time.

While USVs have recently increased in use, unmanned ground vehicles (UGVs) have been in use for a longer period of time and are more common due to the introduction of driverless car technologies. Since both UGVs and USVs can be assumed to be operating on a horizontal plane, planning algorithms are often presented as being applicable to both modalities. However, in practice there are several factors that complicate directly translating UGV planners to USVs. First, generating feasible paths is exceptionally difficult. While there is well-established literature on developing kinematic and dynamic models for UGVs, there is a large amount of uncertainty in how to model USVs and by extension low reliability of these models Fossen (2011); Schoener (2019); Mask (2011). Second, there are often significant errors in the knowledge of the vehicle free space. The lack of infrastructure, the unstructured nature of obstacles (sandbars, floating obstacles, etc.), sensing errors and the non-planar elements of vehicle motion all contribute to this uncertainty. Third, USVs have limited obstacle avoidance capability due to low maneuverability and long stopping distances.

The combination of these factors means that USV path planning should minimize the potential risk of collisions. However, reducing risk comes at the expense of lower quality vehicle paths (as measured by cost). That is, increasing safety leads to staying further from objects, which in turn leads to paths that are longer, take more time to complete, and consume more energy. Thus, this paper presents a novel USV path planning approach for obtaining feasible paths, while allowing the user to tune path optimality and path safety in the presence of model and environmental uncertainties. This method is based on a Visibility–Voronoi (V–V) diagram roadmap, which have recently been suggested for USV path planning Niu et al. (2016), and can be searched by traditional graph search algorithms. V–V diagrams are roadmaps where a Visibility graph is created from inflated objects and a Voronoi graph is created inside the inflated objects. The approach presented in this paper improves on existing USV planning and V–V methodologies in the following ways:

Contributions

  1. 1.

    Introduces a new anytime process for generating V–V diagrams and suggests a heuristic for anytime path planning using a V–V diagram

    • Thus the algorithm finds a valid solution as quickly as possible and uses the remaining time to optimize the solution

    • The anytime strategy makes it suitable for online local USV planning, while previous V–V were used for offline global planning

  2. 2.

    Feasible paths are generated for even under-actuated systems, as edges are generated and smoothed using motion curves

  3. 3.

    Each path node now includes position and heading, while prior USV approaches were based only on position

  4. 4.

    Unlike many approaches, results are presented from maritime maps generated on-board a USV through perception techniques

A literature review is presented in Sect. 2, which begins with a general discussion of path planning algorithms and considerations, followed by the techniques that have been presented for generating feasible USV paths. The proposed roadmap generation method is presented in Sect. 3, along with its anytime variant in Sect. 4. Section 5 presents sample results for a specific case study vehicle, and analyzes real-time performance. Concluding remarks and suggested future work are presented in Sect. 6.

2 Literature review

This literature review will begin with a discussion of general practices for spatial path planning to provide breadth to the techniques used as well as their benefits and challenges for use on USVs. This discussion is organized by the categorizations of path planning algorithms: Roadmaps and Graph Search Theory, Potential Fields, and Sampling-Based Planning (SBP). The general path planning discussion is then followed by the presentation of techniques that have been specifically proposed for USV path planning and a discussion of USV motion modeling.

2.1 Roadmaps and graph search theory

One of the most common approaches to path planning for unmanned systems is to cast the problem in the form of a graph. This approach begins by decomposing the free space into a finite set of vehicle states, called vertices or nodes. Edges between nodes are then generated subject to the requirement that the edges themselves must also lie inside the vehicle’s free space. Such graphs are traditionally generated using a Visibility Graph Lozano-Pérez and Wesley (1979), Voronoi Diagram Bhattacharya and Gavrilova (2008), or grid partitioning of the configuration space. However, more advanced techniques generate vertices and edges through sampling-based methods Dunlap et al. (2011); Barraquand and Latombe (1991), (discussed in Sect. 2.3) or attempt to optimize node and edge generation Kumar et al. (2019). The generated graphs are commonly referred to as a roadmap.

Once a roadmap through the vehicle’s free space has been obtained, the path planning problem is reduced to searching the graph for the best series of edges to follow from the start to goal node. Traditional graph-search algorithms include the Dijkstra algorithm, originally proposed in Dijkstra (1959), and the A* (pronounced “A-star”) algorithm, presented in Hart et al. (1968). Both approaches return optimal results (subject to the graph and measured by a cost function), but A* attempts to reduce search time by the introduction of an admissible heuristic. Furthermore, graph search algorithms are considered resolution complete, meaning a solution will be found if one exists as long as the free space is discretized with enough resolution.

The more recent focus of graph search theory has been on improving graph search efficiency. The D* algorithm, presented in Stentz (1995), showed how to efficiently re-plan to a goal state when node costs are changed. A faster alternative to D*, the D* Lite algorithm, was later presented in Koenig and Likhachev (2005), which incrementally repairs solution paths through a priority queue of nodes where changes occur, referred to as inconsistent nodes. The Anytime Repairing A* (ARA*) algorithm presented in Likhachev et al. (2004), also shows how to use the repairing nature of D* to implement anytime graph searches for path planning applications. ARA* is able to quickly find a valid, often sub-optimal solution, but any remaining time is used to incrementally improve path quality until the optimal solution has been found. Furthermore, the Lifelong Planning A* (LPA*) algorithm presented in Koenig et al. (2004) is able to re-use parts of previous searches regardless of the choice of start and goal states. While searching the graph can be relatively efficient using these approaches, when navigating cluttered environments and accounting for vehicle dynamics Omar et al. (2015), generating the graph itself is often the more computationally expensive task.

2.2 Potential fields

Another class of algorithms used for path planning and navigation are based on Artificial Potential Fields (also called APFs or Potential Fields), which have been implemented on mobile robots since the 1980s Koren and Borenstein (1991). The basic principle of Potential Fields is that a net field is created by a goal that attracts and obstacles that repel the unmanned system. For path planning, the minimum potential route to the goal provides a safe route to the goal state Hwang and Ahuja (1992). However, potential fields are also used for obstacle avoidance where the resultant force magnitude and direction are used to select vehicle direction and speed. One of the better properties about potential fields is the ability to tune the level of safety it provides. To increase safety, an obstacle’s repulsive force can be increased, resulting in a vehicle path that will typically move farther from the obstacle and yield longer paths. Conversely, reducing the repulsive force of obstacles will typically decrease the safety distance and yield shorter paths. However, the relationship is not fully deterministic since the net repulsive force depends on object density. Thus settings that work in an object sparse environments are less effective in object dense areas.

Potential fields have also been shown to exhibit a number of undesirable attributes. First, zero resultant force locations other than the goal are difficult for the system to handle natively, sometimes referred to as the local minimum problem. This has been addressed by later works that modify the potential field based on the relationship between the vehicle and obstacle Zhou and Li (2014). Second, the vehicle’s path or behavior can be highly oscillatory in cluttered environments, though researchers have presented mitigating strategies to this issue Sfeir et al. (2011). Third, the resulting path is not guaranteed to be feasible according to a vehicle model. While researchers have shown that pairing potential fields with an optimal controller can allow for planning feasible paths Rasekhipour et al. (2017), accurate vehicles models needed for this appraoch are difficult to derive for USVs and this work has not been proved experimentally. Additionally, the literature is yet to show how to simultaneously address the local minimum, oscillation, and feasibility concerns of potential field planners.

2.3 Sampling-based planning

Sampling-Based Planning (SBP) reduces the portion of the configuration space considered for planning through sampling the space or control inputs Elbanhawi and Simic (2014). While sampling-based methods have the ability to quickly find solutions to complex planning scenarios, the solutions themselves are generally sub-optimal. Additionally, SBP algorithms do not ensure a solution and are typically only probabilistic complete and/or resolution complete.

One of the first SBP approaches, and one that is still popular today, is a Probabilistic Roadmap (PRM) Barraquand and Latombe (1991). A PRM generates random samples in the configuration space and connects the random samples to the nearest neighbor in the existing roadmap as long as it will not create a collision. While this approach is effective for holonomic vehicles, the paths generated are not guaranteed to be feasible for non-holonomic vehicles such as USVs.

Perhaps the most powerful SBP algorithm in use today is that of a rapidly exploring random tree (RRT), which was originally proposed in LaValle (1998). RRTs begin in a similar fashion to PRMs, by selecting a random sample in the configuration space and and finding a nearest neighbor from the existing tree. Rather than creating an edge between these samples, edges are “grown” from the nearest neighbor toward the randomly generated sample. This results in fast exploration of the space and these edges can be grown based on a motion model including motion constraints Kim and Ostrowski (2003), effectively avoiding the problem that PRMs have with non-holonomic vehicles. RRTs are used to directly solve path planning problems by growing separate RRTs between the start and goal states, which when connected contain a valid solution. Efficient re-planning of RRTS has also been studied by Ferguson et al. (2006), where trees are trimmed and reconnected due to changes in the search. While RRTs can efficiently explore the configuration space, the result can be highly sub-optimal. This led to the introduction of the RRT* Karaman and Frazzoli (2011) and anytime RRT* algorithms Karaman et al. (2011) which typically converge toward an optimal solution.

Sampling-Based Model Predictive Control Optimization (SBMPO) also addresses the optimality issue Dunlap et al. (2011); Caldwell et al. (2010). SBMPO differs from RRTs by sampling the control inputs to the vehicle’s motion model, which also eliminates the two-point boundary value problem (BVP) of connecting one state to a future state Dunlap et al. (2011). SBMPO is then paired with the A* graph-search algorithm Hart et al. (1968) to determine node suitability for expansion via additional control input sampling and integration. Additionally, an implicit state grid is used to avoid the local minimum problem that can arise when selecting nodes for expansion based on cost Ericson (2004). Like RRTs, SBMPO is able to generate feasible paths due to its use of a kinematic or dynamic model, though it lacks the time efficiency of RRTs.

2.4 USV path planning

There are significantly fewer path planning methods designed for USVs than ground vehicles. However, USV methods have been proposed from each of the aforementioned path planning categories: graph search algorithms, potential fields, and sampling-based methods. USV algorithms are generally categorized into global and local algorithms Peralta et al. (2020). Global algorithms refer to planning strategies used when complete knowledge of the environment is known, such as areas with known landmasses and few other vessels, and time efficiency is less of a concern. Local algorithms apply when sensors are needed to discover the environmental hazards during navigation.

For global planning, the use of visibility graphs and voronoi diagrams have already been proposed Niu et al. (2016). However, Niu et al. (2019) later showed that a Visibility–Voronoi (V–V) diagram has several advantages over the traditional roadmap approaches. The V–V diagram separates the configuration space into areas close to hazards, where voronoi diagram edges are used, and the remaining area is navigated through visibility diagram edges. The resulting roadmap is able to ensure a tunable level of safety, while optimizing the distance traveled in areas where safety is not a concern. However, this approach does not directly address feasibility. Potential fields have also been shown to have safety benefits Manzini (2017) for global planning in sparse areas, but may have issues with local minimum in obstacle dense environments. The Fast Marching Method (FMM) has been used with USVs to avoid the local minima issue while improving smoothness and safety over global graph search approaches Liu et al. (2015), but the required tuning and computational efficiency is not well-suited for local planning.

In terms of local planning, the work of Chiang and Tapia (2018) attempts to develop a sampling-based path planning algorithm that complies with the rules for maritime vessels developed in the 1972 Convention on the International Regulations for Preventing Collisions, better known as COLREGs. The proposed method is based on a modification of the RRT* algorithm and can avoid stationary and moving objects. The work of Peralta et al. (2020) compared the USV local planning methods of A*, Potential Fields, RRT*, the Fast Marching Method Sethian (1996) and an updated Fast Marching method on a lake navigation case study. This work concluded that A* should be chosen when optimality is the primary concern and the updated Fast Marching method provided the highest level of security, as determined by author observation on feasibility and safety.

2.4.1 Dynamic modelling of USVs

In order to understand the difficulty in ensuring path feasibility, it is important to briefly discuss the issues associated with dynamic modeling of USVs. It has been shown that obtaining an accurate dynamic model of a boat is a highly complex process, with separate strategies for calm waters and rougher seas (where wave excitation is more significant) Fossen (2011). However, even when focusing on calm waters obtaining an accurate model is challenging. The work of Fossen Fossen (2011) is currently viewed by many as the signature resource for such modeling efforts. This work suggests finding the six degree of freedom model using a 3rd-order, truncated Taylor series in order to capture the Hydrodynamic drag and Coriolis effect with a rigid-body ship. The parameters of this model must be experimentally generated by executing a set of predetermined maneuvers, which can be expensive and time consuming. Thus, these modeling efforts are generally best reserved for larger, more expensive vessels or those that will be mass-produced.

There have been works that specifically sought to simplify the modeling process for USVs using a parametric identification approach Mask (2011); Schoener (2019). The work of Mask (2011) used a diagonal 2nd-order, 3 degree of freedom model to capture the primary effects of the control forces of the vehicle. This gave a baseline for control-aided modelling of Surge, Sway and Yaw. The primary disadvantage of this model is there are no cross-coupling effects between these degrees of freedom. For instance, there are no additive drag effects on surge drag from both forward and turning motion, which can be significant when one realizes the difference in side and forward surface area. The work of Schoener (2019) uses a Genetic Algorithm to solve for the high number of model coefficients in its proposed 2nd-order model. In essence, this attempt addresses the issue of accurately determining the highly cross-coupled model coefficients through optimization. While this process was able to capture forward motion and cross-correlated effects, the results were noted to be less accurate than desired and appeared to be on the border of stability due to 2nd order curve-fitting of the coefficients.

In addition to the parametric approaches, researchers have more recently investigated learning methods for USV dynamic modeling Wang et al. (2016); Ensemble (2020). The work of Ensemble (2020) attempts to learn the dynamics directly through an ensemble learning approach, which combines the benefits of multiple weaker learners. The work of Wang et al. (2016) avoids the issues of disturbances and unknown dynamics altogether by using a single-hidden-layer feedforward network to determine control effort and minimize error.

2.4.2 Feasibility through motion curves and smoothing

When an accurate dynamic model is unknown, which is in general true of USVs, a simpler representation of vehicle motion could be sought to ensure feasibility. In ground vehicles, a kinematic model may suffice, but USVs do not have meaningful kinematic models due to the significant effects of vehicle drag. Another approach is to leverage segments of feasible motion, called motion curves, to construct more complex vehicle paths. As long as the transition between the segments is also feasible, then the path itself must be feasible. One such approach is Dubins curves, presented in Dubins (1957), where the shortest path trajectory between two planar vehicle states is found for a vehicle with a minimum turn radius. The resulting paths include only arcs with this minimum turn radius and straight line segments. This work was later extended to include reversing motion by Reeds and Shepp Reeds and Shepp (1990). A similar approach has also been proposed for vehicles that are capable of zero-radius turns Chitsaz et al. (2009). However, these motion curve approaches do not directly show how to avoid collisions and ensure vehicle safety.

Curve interpolation, also known as path smoothing, modifies an existing path to ensure compliance with a set of pre-defined motion constraints. Typical constraints include bounds on vehicle motion (e.g. linear/angular velocity and acceleration) or requiring path velocities and accelerations to be continuous. Smoothing algorithms have been proposed based on Bezier curves Choi et al. (2008), Clothoids Silva and Grassi (2018), and splines Lau et al. (2009). In addition to these approaches, smoothing techniques have also been proposed that avoid collisions with stationary Zhu et al. (2015) or moving obstacles Keller et al. (2014).

3 Primary methodology

3.1 Overview

The USV path planning problem considered in this paper is to generate a local USV path, p, defined by a series of nodes \(n=\{x, y, \psi \}\) consisting of a 2D location (x, y) and orientation \(\psi \). The path p must also satisfy the following constraints:

  1. 1.

    p is feasible subject to a model of vehicle motion

  2. 2.

    p should be contained in the free space of the vehicle operating environment OE

  3. 3.

    p should maintain a distance from marine objects of more than \(d_{thresh}\). (Mathematically this is defined as \({{\,\mathrm{dist}\,}}(p, \mathbf {O}) > d_{thresh}\), where \({{\,\mathrm{dist}\,}}(p, \mathbf {O})\) returns the minimum distance between p and the set of object boundaries, \(\mathbf {O}\)).

Traditionally, the distance \(d_{thresh}\) is chosen to satisfy \(d_{thresh} = r_{min} + e_{max}\) where \(r_{min}\) is the radius of the minimum area bounding circle of the vehicle’s 2D geometry and \(e_{max}\) is the maximum expected error in the vehicle’s ability to follow p. But as \(e_{max}\) can be quite large with USVs, this leads to longer paths and can even close off all routes to the goal. Instead, the method presented here uses a roadmap based on a modified V–V diagram to balance the need for appropriate levels of safety with the need to take efficient routes. Unlike other V–V diagram approaches to USV path planning, path feasibility is ensured by generating edges using motion curves and path smoothing. It is also shown that building the roadmap is suitable for local path planning through the use of an anytime variant of roadmap generation.

3.2 Roadmap generation and search

A roadmap R can be viewed as consisting of a set of nodes, and edges between these nodes. Thus

$$\begin{aligned} R = \{\mathbf {n},\mathbf {e}\} \end{aligned}$$
(1)

where \(\mathbf {n}\) is the set of all nodes and \(\mathbf {e}\) is the set of all edges in R.

Building the modified V–V roadmap used in this paper, requires the user to specify the operating environment of the vehicle, OE, the objects \(\mathbf {O}\) contained in OE, and two user-selected distances, \(d_{safe}\) and \(d_{min}\). These distances are expected to follow the relationship

$$\begin{aligned} r_{min} + e_{max} \ge d_{safe} > d_{min} \ge r_{min}. \end{aligned}$$
(2)

Based on (2), paths that ensure \({{\,\mathrm{dist}\,}}(p, \mathbf {O}) > d_{min}\) avoid static collisions and have a minimum level of safety, while paths that ensure \({{\,\mathrm{dist}\,}}(p, \mathbf {O}) > d_{safe}\) are not expected to cause collision due to uncertainties and have the maximum desired level of safety.

The steps needed to generate the modified V–V diagram R are then given by Algorithm 1, where \(n_s\) and \(n_g\) are nodes that defined the start and goal state respectively.

figure d

Algorithm 1 uses three subroutines. The first is \({{\,\mathrm{buffer}\,}}(\mathbf {O}, d)\), which grows the objects \(\mathbf {O}\) by a distance d, resulting in a new set of non-overlapping polygon objects. The second is \({{\,\mathrm{Voronoi}\,}}(OE, \mathbf {K})\), which computes the voronoi roadmap of OE, given object definitions \(\mathbf {K}\) based on the method presented in Fortune (1986). Lastly, the function \({{\,\mathrm{edge}\,}}({\mathbf {n}}_{\mathbf {1}},{\mathbf {n}}_{\mathbf {2}},\mathbf {B})\) grows dynamically feasible edges between the nodes in \({\mathbf {n}}_{\mathbf {1}}\) and those in \({\mathbf {n}}_{\mathbf {2}}\) and returns all edges that do not intersect \(\mathbf {B}\). When Algorithm 1 completes, finding p is simply reduced to an A* graph search on R. As such, p is optimal subject to R and the cost function criteria.

While Algorithm 1 is generalized to use any method of dynamically feasible edge generation, the results presented in this paper will use Dubins curves Dubins (1957), which, as noted in Sect. 2.4.2, finds the shortest path between two states for a vehicle with a minimum turn radius r. Thus, we can effectively replace \({{\,\mathrm{edge}\,}}({\mathbf {n}}_{\mathbf {1}}, {\mathbf {n}}_{\mathbf {2}}, \mathbf {B})\) with dubins curve edge generation subroutine \({{\,\mathrm{Dubins}\,}}({\mathbf {n}}_{\mathbf {1}}, {\mathbf {n}}_{\mathbf {2}}, \mathbf {B}, r)\).

While \({{\,\mathrm{Dubins}\,}}({\mathbf {n}}_{\mathbf {B}}, {\mathbf {n}}_{\mathbf {B}}, \mathbf {B}, r)\) would generate feasible edges between grown objects \(\mathbf {B}\), it has quadratic computational complexity and requires the complex process of checking each generated curve for collision with \(\mathbf {B}\). Thus, a more efficient alternative to \({{\,\mathrm{Dubins}\,}}({\mathbf {n}}_{\mathbf {B}}, {\mathbf {n}}_{\mathbf {B}}, \mathbf {B}, r)\) should be considered. The work of Niu et al. (2016), which used linear edges for V–V diagram generation, suggests only generating the edges that are considered tangent to an object in \(\mathbf {B}\). However, this concept must be re-considered for Dubins edge generation.

To find a more efficient alternative to generating all Dubins edges, realize the edges within \(\mathbf {e}_{\mathbf {B}}\) that are part of the distance-optimal path p will satisfy one of four cases:

  1. 1.

    \(e \in \mathbf {e}_{\mathbf {B}}\) connects adjacent nodes on the boundary of a grown object in \(\mathbf {B}\).

  2. 2.

    \(e \in \mathbf {e}_{\mathbf {B}}\) is linear and tangent to the bounds of an object in \(\mathbf {B}\) at both endpoints.

  3. 3.

    \(e \in \mathbf {e}_{\mathbf {B}}\) connects two nodes \(n_1\) and \(n_2\), where \(n_1, n_2 \in \mathbf {n_{B}}\) and \(n_1, n_2 \in n_{V^\prime }\), denoted \(\mathbf {n_{B,{V^\prime }}} = {\mathbf {n}}_{\mathbf {B}} \cap \mathbf {n}_{V^\prime }\)

  4. 4.

    \(e \in \mathbf {e}_{\mathbf {B}}\) is tangent to a boundary in \(\mathbf {B}\) at one end and connected to a node in \(\mathbf {n_{B,{V^\prime }}}\) at the other end

All four of these cases are illustrated in the scenario of Fig. 1.

Fig. 1
figure 1

Roadmap R and resulting distance optimal path p, showing the edges that will be generated by new functions \({{\,\mathrm{tangents}\,}}\) (Case 1 and 2) and \({{\,\mathrm{VoronoiTangents}\,}}\) (Case 3 and 4). Edges not highlighted are generated by Voronoi segments, or Dubins curves involving \(n_s\) or \(n_g\)

Full size image
Fig. 2
figure 2

Steps toward building the Visibility–Voronoi and dubins motion curve roadmap

Full size image

Recognition of these cases allows \({{\,\mathrm{Dubins}\,}}({\mathbf {n}}_{\mathbf {1}}, {\mathbf {n}}_{\mathbf {2}}, \mathbf {B}, r)\) to be replaced with two more efficient routines. The first of these is \({{\,\mathrm{tangents}\,}}({\mathbf {n}}_{\mathbf {B}}, \mathbf {B})\), which generates tangential edges for the objects in \(\mathbf {B}\) (Cases 1 & 2 above). The second routine is \({{\,\mathrm{VoronoiTangents}\,}}({\mathbf {n}}_{\mathbf {B}},\mathbf {n}_{V^\prime })\), which generates tangent edges between the nodes in \({\mathbf {n}}_{\mathbf {B}}\) and \(\mathbf {n_{B,{V^\prime }}}\), as well as edges from nodes in \(\mathbf {n_{B,{V^\prime }}}\) to different nodes in \(\mathbf {n_{B,{V^\prime }}}\) (Cases 3 & 4 above). While the Dubins routine would generate an edge to be checked for possible collision between every pair of input nodes, there are significantly fewer tangential edges. Since every edge is checked for collision before returning the final set of edges, the tangent functions are significantly more computationally efficient. With the introduction of these tangent functions, the resulting vehicle roadmap R can then be found using Algorithm 2, and finding p is again reduced to an A* graph search on R.

figure e
Fig. 3
figure 3

The final Roadmap R and path p generated by Algorithm 2 for the same scenario as Fig. 2

Full size image
Fig. 4
figure 4

Left: Example roadmap that requires smoothing of Voronoi edges \(\mathbf {e_{V^\prime }}\) for feasibility. Scenario uses settings of \(d_{safe} = 7.5\) m, \(d_{min} = 1.5\) m, and \(r = 5\) m. Right: Original path p from roadmap compared to smooth path \(p_{smooth}\) that results from Dubins Curve smoothing of p

Full size image

To better illustrate the steps of Algorithm 1, consider the scenario of Fig. 2a where the operating environment OE, obstacles \(\mathbf {O}\), starting node \(n_s=\{5, 5, 90^\circ \}\) and goal node \(n_g=\{90, 50 ,90^\circ \}\) are as shown. Using values of \(d_{min}=1.5\) and \(d_{safe}=5\) the set of polygon objects \(\mathbf {K}\) and \(\mathbf {B}\) are found and shown in Fig. 2b (Steps 1 & 2). The voronoi diagram V is then generated based on the limits of the environment OE and \(\mathbf {K}\), as shown in Fig. 2c (Step 3). The intersection of V and \(\mathbf {B}\) then yields \(V^{\prime }\) as shown in Fig. 2d (Step 4). Tangent and voronoi tangent edges are then generated and shown in Fig. 2e (Steps 5 & 6). Next, dubins curves are generated from the start node to the nodes of \({\mathbf {n}}_{\mathbf {B}}\) and from the nodes of \({\mathbf {n}}_{\mathbf {B}}\) to the goal node as shown in Fig. 2f (Steps 7 & 8). The roadmap R (returned in Step 9), as well as the distance optimal path p from \(n_s\) to \(n_g\), is then given in Fig. 3.

3.3 Path smoothing to ensure feasibility

The set of edges found in \(\mathbf {e}_{{\mathbf {B},{\mathbf {V}^\prime }}}, \mathbf {e}_{start}, \mathbf {e}_{goal}\) are all dynamically feasible according to Dubins curves, as are the tangent edges that are a subset of \(\mathbf {e}_{\mathbf {B}}\). However, the rest of the edges in \(\mathbf {e}_{\mathbf {B}}\) (which lie on the boundaries of \(\mathbf {B}\), and the edges in \(\mathbf {e}_{V^\prime }\) are not guaranteed to be feasible. In fact, when more than two edges in \(\mathbf {e}_{V^\prime }\) share a common node \(n_i \in n_{V^\prime }\) sharp angles are created by consecutive adjacent voronoi edges as shown in Fig. 4. To address this concern it is suggested that a smoothing function be used to ensure feasibility. While a smoothing function could be used on the entire roadmap, here only p is smoothed to improve efficiency. As Algorithm 2 is based on a vehicle with a minimum turn radius, a minimum curvature smoothing function, such as the one presented in Parlangeli and Indiveri (2010) is suggested (see Fig. 4).

3.4 Planning close to objects

While Algorithm 1 or Algorithm 2 is effective when \(n_s\) and \(n_g\) are far from objects, if \(n_s\) or \(n_g\) are inside \(\mathbf {B}\), there will be no valid edges connecting to these nodes. Similarly, if \(n_s\) or \(n_g\) is close to \(\mathbf {B}\) there may be no Dubins curve involving these states that does not intersect \(\mathbf {B}\). Realize that \(n_s\) and \(n_g\) will in general be inside or close to \(\mathbf {B}\) whenever the vehicle needs to dock, or a new plan is requested while navigating an edge shared with \(\mathbf {B}\).

To address this issue, it is suggested that the boundary used to check collisions of edges be based on \(\mathbf {B}^{\prime } = (\mathbf {B} - \mathbf {SG}) \cup \mathbf {K}\) rather than \(\mathbf {B}\), where \(\mathbf {SG}\) is area to be removed from \(\mathbf {B}\). The choice of \(\mathbf {SG}\) should be dependent on the chosen motion curve. Here \(\mathbf {SG}\) is chosen as two circular regions with diameter \(d_{SG}\) centered on \(n_s\) and \(n_g\), where \(d_{SG}\) is the larger value of \(3*r\) (three times the minimum turn radius of the USV) and \(d_{safe}\). This ensures \(n_s\) and \(n_g\) can be connected to the rest of the roadmap as long as it is dynamically feasible to do so without collision. Note that \(\mathbf {SG}\) can be viewed as a algorithm parameter, which may need to be tuned when using motion curves other than Dubins. An example calculation of \(\mathbf {B}^{\prime }\) is found in Fig. 5.

Fig. 5
figure 5

Visual representation of computing \(\mathbf {B}^{\prime } = (\mathbf {B} - \mathbf {SG}) \cup \mathbf {K}\) when the start and/or goal are close to an object. Here \(d_{safe} = 5\) m, \(d_{min} = 1.5\) m, and \(r=2.5\) m

Full size image

4 Anytime methodology

While the roadmaps produced by Algorithm 2 satisfy the need for feasible and safe USV paths, generating the roadmap has the potential to be computationally intensive if OE encompasses a large number of objects or highly complex objects. Thus, generating the full USV roadmap may require more time than the USV can allow before needing to act on a plan. One way to address this issue is to alter roadmap generation to be an anytime process.

Generating R as an anytime process is based on a few key insights about the relationship between the roadmap R and optimal path p generated in Algorithm 2.

  1. 1.

    R could be built incrementally by adding objects in \(\mathbf {O}\) to R sequentially rather than as a single batch

  2. 2.

    The distance optimal path p is more likely to contain edges and nodes generated from objects close to the most direct route from \(n_s\) to \(n_g\).

  3. 3.

    During the building process, there is no value in adding an object in \(\mathbf {O}\) to R unless it has the potential to result in a lower cost path than current best path from \(n_s\) to \(n_g\) found in R.

The first insight may at first imply the roadmap can be built one object \(o \in \mathbf {O}\) at a time, but in actuality R should be built one safety boundary \(b \in \mathbf {B}\) at a time. This is because a given b may contain any number of objects in \(\mathbf {O}\) and it is the multiple nature of these objects that leads to adding voronoi edges between objects to the roadmap. The second insight suggests that a priority queue can be established which determines the order in which objects in \(\mathbf {O}\) should be added to R based on the distance to the line segment connecting \(n_s\) to \(n_g\). Based on the third insight, the cost of the best path in R should be monitored and an admissible heuristic established for determining which objects should remain in the priority queue during the building process. When using a distance-based cost function, the path length forms this cost bound and the sum of the minimum distance from \(n_s\) and \(n_g\) to the object’s safety boundary forms an admissible heuristic.

Before presenting the anytime V–V Roadmap generation algorithm, consider that collision detection in Algorithm 2 requires the potentially complex batch process \(\mathbf {B} = {{\,\mathrm{buffer}\,}}(\mathbf {O}, d_{safe})\). However, in the field of collision detection, the use of shape primitives, such as axis-aligned bounding boxes (AABBs), is often suggested to efficiently rule out collisions before conducting the more complex process of intersection with polygon bounds such as those found in \(\mathbf {B}\) Cai et al. (2014). Thus for anytime roadmap generation a list of collision detection geometries \(\mathbf {CD}\) will be maintained, which will initially be composed of the AABB of each object \(o_i\) in \(\mathbf {O}\) grown by a distance \(d_{safe}\). During algorithm execution if the AABB of an object \(o_i\) causes a collision with a roadmap edge or \(o_i\) is selected to generate roadmap nodes and edges, the function \({{\,\mathrm{overlaps}\,}}(o_i,\mathbf {o},d_{safe})\) is used to generate the the list of all objects in \(\mathbf {O}\), denoted \(\mathbf {o}_i\), that are \(2d_{safe}\) distance-reachable from \(o_i\). An object \(o_j\) is \(2d_{safe}\) distance-reachable from \(o_i\) if an ordered set of objects from \(o_i\) to \(o_j\) exists such that adjacent objects in the set are never separated by a distance of more than \(2d_{safe}\). The AABB of each object in the set \(\mathbf {o}_i\) is then removed from \(\mathbf {CD}\) and replaced by \(B_i={{\,\mathrm{buffer}\,}}(\mathbf {o}_i,d_{safe})\), where \(B_i\) will be a single polygon boundary.

Based on the presented insights and collision detection strategy, the anytime procedure for roadmap generation is defined by Algorithm 3, where \(q = {{\,\mathrm{sort}\,}}(\mathbf {O})\) sorts the objects starting with the object closest to the line segment from \(n_s\) to \(n_g\). Collision checks utilize the full set of collision detection geometries \(\mathbf {CD}\), and not just the collision detection geometries corresponding to objects currently in the roadmap.

figure f

If Algorithm 3 is interrupted, then \(\hat{p}\) contains the best path currently found in the roadmap. If the algorithm is allowed to finish, \(\hat{p}\) will be equivalent to the optimal path p. While Algorithm 3 is presented as a sequential algorithm, the architecture lends itself to parallelization of the main loop and parallel computations within each loop iteration through the use of queues for generating edges and check generated edges for collisions before adding them to the roadmap. Only sequential processing is considered in this paper however, and an example Anytime V–V Roadmap Generation is shown in Fig. 6.

Fig. 6
figure 6

Progression of Anytime V–V Roadmap building using example scenario with \(n_s = \{-20m, 50m, 0^\circ \}\) to \(n_s = \{120m, 50m, 0^\circ \}\), \(d_{min} = 1.5\) m, \(d_{safe} = 5\) m, and \(r=2.5\) m

Full size image

From Fig. 6 it can be seen that after the first iteration of the main loop from Algorithm 3, edges have been generated due to the selection of only a single object and added to R. Furthermore, there is no path within R between \(n_s\) and \(n_g\) until the fourth algorithm iteration. It can also be seen after the 4th iteration that all objects chosen for edge generation are close to the line between \(n_s\) and \(n_g\), which is the dubins curve heuristic for this case. Thus, if the algorithm was interrupted at any point after the completion of iteration 4, then a valid path would be returned. However, by giving the algorithm more time, it is able to improve the path quality in iteration 5 and again in iteration 7. Once iteration 8 is completed, the algorithm is completes due to an empty queue q, and the \(\hat{p}\) can now be assured to be the optimal path p.

5 Results

As previously discussed, the V–V work of Niu et al. (2019) is the most closely related published work to the method presented in this paper, but its authors state it is intended for global planning. The results shown below, which are broken into two studies of algorithm performance, are intended to show the method presented in this paper is suitable for local planning. The first is a case study of paths obtained when avoiding real marine objects and algorithm parameters consistent with a medium-sized (16-foot long) USV. The case study is discussed in Sect. 5.1. The second study uses randomly generated scenarios to analyze the computational complexity of the presented algorithm and applicability to local planning where plans are obtained in real-time. These simulation results are presented in Sect. 5.2. The computer used to produce the processing times noted in Sects. 5.1 and 5.2 has a Intel i7-8650U CPU @ 1.9 GHz and 16 GB of RAM. All timing results are for single-threaded performance.

Fig. 7
figure 7

The Minion Research Platform is a 16-foot long USV that is equipped with a high fidelity GPS/INS and four multi-beam Lidar sensors

Full size image

5.1 Case study: Maritime RobotX Challenge

The case study presented here is based on the Maritime RobotX Challenge, which is an international, university-level student competition designed to foster student interest in autonomous and robotic systems operating in the maritime domain, with an emphasis on the science and engineering of cooperative autonomy. This competition involves tasks derived from existing Naval operations and challenges, such as USV docking, complex navigation, and environmental perception. All competing USVs are based on the Marine Advanced Research 16-foot WAM-V platform, which is the vessel studied in Schoener (2019) and Mask (2011). This competition motivated the development of the path planning algorithm presented in this paper due to tasks that require navigation close to obstacles, but a need to handle uncertainties in vehicle model and environment.

The ERAU-owned WAM-V USV, named Minion (see Fig. 7), is designed to allow the operator to select vehicle control by either differential thrust or azimuth control of the propulsion motors. However, both control schemes result in under-actuated systems, yielding a minimum turn radius that varies with vehicle speed. This means Dubins curve edge generation is appropriate when Minion operates at a pre-defined vehicle speed. As an under-actuated system, the USV has an inability to compensate for some unknown disturbances or modeling errors. The vehicle is also equipped with four Lidar sensors for environmental perception, which map objects using the scheme defined in Thompson et al. (2019). Thus, the V–V path planning scheme proposed in this paper is appropriate for this USV and its perception suite. Minion is just under 3 m wide, so \(d_{min} = 1.5\) m is chosen. Also, Minion’s typical operational speed is 1.5 m/s, which corresponds to a minimum turn radius of just under 2.5 m, thus \(d_{safe} = 5\) m and \(r=2.5\) m are chosen.

The results presented in this paper will utilize planning scenarios Minion encountered when attempting the docking and obstacle field navigation tasks at the 2018 Maritime RobotX Challenge. During competition, the vehicle state and Lidar measurements were recorded. By replaying these logs and executing the perception algorithm presented in Thompson et al. (2019), the originally perceived environment can be re-created, as seen in Figs. 8a and 9a.

Fig. 8
figure 8

A docking scenario from the 2018 Maritime RobotX Competition. In this scenario \(n_s = \{90m, -405m, 6^\circ \}\) and \(n_g = \{68.25m, -342.5m, 73^\circ \}\) and all obstacles are created from empirical data. Algorithm 3 is implemented using settings of \(d_{safe} = 5\) m, \(d_{safe} = 1.5\) m, and \(r = 2.5\) m

Full size image
Fig. 9
figure 9

A obstacle field scenario from the 2018 Maritime RobotX Competition using empirical data. Algorithm 3 is implemented using settings of \(d_{safe} = 5\) m, \(d_{safe} = 1.5\) m, and \(r = 2.5\) m over a series of waypoints

Full size image

During the docking scenario, the vehicle must navigate into one of two docking bays on a H-shaped, moored, floating dock. Given that Minion is just under 3 m wide and the docking bays are only 3.2 m wide, this is a scenario where the planning algorithm must plan close to an object (the dock) but stay as far from the object as it can and still succeed at the task. After identifying the docking bay and its orientation using the methodology presented in Barnes et al. (2018), Algorithm 3 produces the plan shown in Fig. 8b. The plan first navigates between the two buoys located at approximately \((84E, -394N)\) and \((93E, -389.5N)\) while following the voronoi edges to maximize safety. The path then connects to the voronoi edges to lead it into the center of the bay, which maximizes safety and likelihood of success when entering the dock. The optimal vehicle path is returned in 114msecs in this scenario.

The RobotX Challenge’s obstacle field scenario requires the vehicle to make several “lawn-mower” style passes through an obstacle field marked by four cylindrical, white buoys. The obstacles within the field are spherical in nature and vary from 0.5 to 1.2 m in diameter. Figure 8a shows the perceived objects, outlines the area marked by the four cylindrical buoys, and shows the 10 target waypoints for completing the lawnmower pattern.

Algorithm 3 is applied to each consecutive pair of waypoints, and the path between each pair of waypoints is concatenated to give a complete “lawn-mower” pattern p as shown in Fig. 9b. It can be seen that the final vehicle path p closely mirrors the originally designated pattern, but deviates in order to maintain safety. This is understandable considering the waypoints were assigned manually without consideration of the objects inside the obstacle field. When p is less than \(d_{safe} = 5\) m from an object, p follows the voronoi edges between the objects. However, the path is never less than \(d_{min} = 1.5\) m from an object. Algorithm 3 returned the Fig. 9b result, which consists of 9 separate paths (one path between each consecutive pair of the 10 waypoints), in a total of 451 msecs.

5.2 Simulated environment

Given the need to consider edges between each node pair in R, it is reasonable to assume the order of complexity is \(O(N^2)\) for Algorithm 1, where N is the number of nodes used in R. If each object \(o \in \mathbf {O}\) has a nearly equivalent number of nodes, it can be further assumed that Algorithm 2 would have a complexity of \(O(m^2)\), where m is the number of objects in \(\mathbf {O}\). However, since Algorithm 3 only adds nodes and vertices to R for objects likely to influence the optimal path p, Algorithm 3 is expected to have a complexity of \(O(\tilde{m}^2)\), where \(\tilde{m}\) is the number of objects for which nodes are added to R before the optimal path is found. Thus, \(\tilde{m} \le {m}\). Furthermore, if Algorithm 3 returns before completion, then an estimate of the optimal path \(\hat{p}\) may be found which required \(\hat{m}\) objects to be added to the roadmap, where \(\hat{m} \le \tilde{m}\). So, it is theorized in order to return a non-empty path \(\hat{p}\) the complexity is quadratic (\(O(\hat{m}^2)\)), but the quadratic complexity results in significantly slow execution only when the local environment is highly complex.

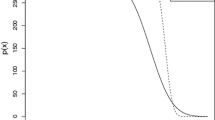
To test the theorized complexity of Algorithm 3, and determine if the algorithm is efficient enough for local planning, a series of simulations are conducted. These simulations are based on a 500 m \(\times \) 500 m operating area OE, with random starting state, \(n_s\), and random goal state, \(n_g\). A thousand random scenarios are then generated for the case where OE contains 0, 25, 50, 100, 200, 250, 300, 400, and 500 obstacles. Objects are non-overlapping regular hexadecagons (16-sided polygon) circumscribed by a circle with radius between 0.5m and 2m and the object location within OE is random. For each scenario the algorithm completion time and time to find the first path estimate \(\hat{p}\) is recorded. The completed simulations are then sorted based on if a solution exists. The average algorithm completion time for all scenarios and scenarios where a solution does not exist is shown in Fig. 10. Furthermore, when a solution does exist, Fig. 10 shows both the average time to find the the first path estimate \(\hat{p}\), and the time to find the optimal path p.

Fig. 10
figure 10

Average timing for 1000 random scenarios of non-overlapping 16-sided objects

Full size image

Figure 10 is strong evidence that the Algorithm 3 has a quadratic complexity of \(O(\tilde{m}^2)\). The completion time of all scenarios (Blue line), in fact has a coefficient of determination \(r^2=0.998\) for a quadratic fit. Furthermore, there is also a strong quadratic relationship when looking at the time to find the first estimate of the optimal path (Red line) and the time to find the optimal path (Orange Line), with coefficients of determination of 0.996, and 0.998 respectively. However, the benefits of the anytime approach are clearly shown as well, as the first path is in on average returned much faster than the time it takes to return the known optimal path.

The one surprising result of Fig. 10 is the algorithm complexity when a valid path does not exist appears to be linear instead of quadratic with a coefficient of determination of 0.916. To explain this phenomenon, consider that a path will not exist if and only if \(n_s\) or \(n_g\) is so close to objects that feasible edges cannot be created from \(n_s\) or to \(n_g\) without collision. Recall that Algorithm 3 prioritizes adding objects to R based on distance to \(n_s\) and \(n_g\). Thus, if there are objects within a 2r distance of \(n_s\) or \(n_g\), then they will be added to R first. Furthermore, once these objects are added to R a edge involving \(n_s\) and \(n_g\) should exist if it will ever exist. If it does not exist at that time, the algorithm can terminate. As there is a physical limit to how many objects can be within 2r of \(n_s\) and \(n_g\), the complexity is not quadratic or linear based on the number of objects, but bounded when a path will not exist. However, the complexity will still be quadratic based with respect to the total number of nodes on the objects within 2r of \(n_s\) and \(n_g\).

While algorithm complexity is important to understanding performance, the time required to obtain a path in real-world scenarios is often a more practical measure for determining applicability to local planning. Additionally, returning a valid path is often a higher priority than returning an optimal path. Thus, Fig. 11 presents the worst-case completion time for obtaining an optimal path and obtaining any path among all randomly generated scenarios.

Fig. 11
figure 11

Worst case timing results from 1000 random scenarios of non-overlapping 16-sided objects

Full size image

The results of Fig. 11 indicate that even in a worst-case scenario, the proposed algorithm can be effective for local planning. To understand this, consider that a USV will often move at a slow rate of speed. For example, the Minion USV, for which this algorithm was originally developed, typically operates at 1.5 m/s. While finding the optimal path was shown to take up to 6.27 s in the most obstacle dense environment, finding a valid solution only requires 1.17 s. This worst case time corresponds to traveling 1.8 m while moving at 1.5 m/s and the results of Fig. 10 indicates that this distance will typically be much shorter with a 250 ms average time yielding a travel distance of 0.375m. However, if the algorithm chose to wait on the optimal path, then it could travel close to 10m while waiting on a solution. So there is tremendous value in the anytime approach.

While the results shown here are based on the number of obstacles, increasing the number of nodes should also yield a quadratic complexity. This is due to the original hypothesis of \(O(N^2)\) complexity, where N is the number of nodes used in R. More obstacles means more nodes, but more complex obstacle geometries also increases the total number of nodes. Thus, a decimation algorithm such as the Douglas-Peucker algorithm Douglas and Peucker (1973) or Visvalingam algorithm Visvalingam and Whyatt (1993) is highly recommended for use with this algorithm to decrease the complexity of the obstacles themselves.

6 Conclusion

This paper builds on existing USV path planning and Visibility–Voronoi (V–V) diagram approaches in several key ways. First, the presented approach is presented as an anytime process. This anytime approach prioritizes node and edge generation in areas where the optimal path is expected to lie, as defined by a heuristic. This often enables the algorithm to return a feasible, near-optimal path even when interrupted before completion due to the relatively sparse nature of the USV environment. Second, the presented method differs from existing USV and V–V approaches by using motion curves and path smoothing to ensure path feasibility subject to a simplistic vehicle model. This is especially important for USVs, which are primarily under-actuated systems. Third, unlike prior V–V approaches, all roadmap nodes include a definition of vehicle heading, which improves complex maneuvering capabilities. Lastly, it is shown that this new V–V planning approach allows the user to balance uncertainties in the vehicle model and environment with the need for better paths (as measured by a cost function). This is done through the use of two safety boundaries, one that ensures a minimum level of safety at all times, and a second that is only violated when necessary to find a solution or achieve a significantly better path in terms of cost. Furthermore, it is shown that the algorithm has a quadratic complexity when a valid path exists and a near-linear complexity when a valid path does not exist. Unlike many prior approaches that are validated using only simulated scenarios, real-time maps from a USV perception suite are used in addition to random simulations to prove the effectiveness of the presented approach.

6.1 Future work

Several efficiency-based improvements should considered in future work. First, the authors believe significant computational improvements can be achieved through parallelization of the presented algorithm, both in how objects are added to the roadmap and in how edges are generated and subsequently checked for collision. Second, future work should also consider methods to reduce the number of edges generated, as most motion curve generated edges involving the start and goal node are thrown out due to object collision. Third, treating collision detection as a 3D problem could lead to improvements in path safety and cost. Lastly, efficient methods of re-planning should be investigated.

Future work should also consider the use of other motion curves. While the general approach presented here is agnostic to the choice of motion curve, several of the efficiency-based improvements used in the anytime version of the algorithm are based on Dubins curves. As a result, the use of other motion curves may require new assumptions, simplifications, and heuristics. The use of other motion curves will also required the use of a different smoothing function.