Robust circumnavigation of a heterogeneous multi-agent system

Abstract

This paper focuses on the design of robust control laws for a heterogeneous multi-agent system composed of omnidirectional and differential-drive mobile robots under the leader–follower scheme and considering the distance and orientation measurements. It is assume that the agent leader is an omnidirectional mobile robot moving freely in the plane while the rest of the agents are the followers. The control laws are designed by means of the Backstepping approach. It is proved that, although the control laws do not need information about the velocity of the leader, the followers will circumnavigate the leader. Numerical simulations and real-time experiments exhibit the performance of the proposed control strategy.

1 Introduction

In the last decade, the research on multi-agent systems has increased due to the improvement in efficiency, scope and robustness in its objectives. Within the different topologies in the literature, the leader–follower scheme is the mainly used to model the flow of information from one agent to another. The most basic configuration consists of two agents, where one of them is the leader who follows a trajectory, while the follower must satisfy a relative posture with respect to the leader. In that sense, different communities have developed special emphasis on circumnavigation. This means that the follower agents move in a circular trajectory, surrounding the leader (or target agent), which can be static or in constant motion. This technique is commonly applied in missions of security and surveillance in robotics applications to detect, locate and follow targets. These problems have been studied by different researchers, proposing distinct hypotheses, topologies and approaches.

In Deghat et al. (2014), Shames et al. (2012), Shao and Tian (2017) and Zhong et al. (2019) can be found works related with the leader–follower formation control of first or second order agents. Specifically, in Deghat et al. (2014), an estimator is proposed to locate the target and a robust control law is designed allowing to the agent to maintain a distance and circumnavigate the target. It is assumed that the target moves slowly with an unknown speed and the agent can only measure the angle towards the target. In a similiar manner, in Shames et al. (2012) a control law is designed such that an agent keeps a desired distance with respect to a target while circumnavigate him. This approach is not robust with respect to the measurement noise. Furthermore, unlike the velocity of the objective is unknown, it has to be very small. It is worth mentioning that in Deghat et al. (2014) and Shames et al. (2012), even though the control strategy is robust, there are oscillations between the distance of the agent and the target. On the other hand, if there is noise in the measurement, the distance between the agent and the target starts to oscillate. In Shao and Tian (2017), an estimator is designed in order to know the position of the targets, and therefore, each agent circumnavigate them. The problem of progressively deploying a set of robots to a formation defined as a point cloud, in a decentralized manner, is described in Li et al. (2018), where the authors have proved that for a 2D shape it is sufficient for a free robot to compute its distance from two robots in the formation to achieve this objective. Furthermore, a distributed control is designed in Bechliouli et al. (2018) for uncertain homogeneous Lagrangian nonlinear multi-agent systems in a leader–follower scheme, that achieves and maintains a rigid formation. In Lopez-Gonzalez et al. (2016) a formation scheme, using Lyapunov techniques, and considering that the local controllers of the agents can be equipped with distance and orientation sensors, is proposed. Finally, in Zhong et al. (2019), a control law, based on gradients, is proposed to avoid inter-robot collisions and circumnavigate a dynamic target. The consensus problem of Lipschitz non-linear multi-agent systems with higher-order dynamics has been addressed in Li et al. (2020), where the Backstepping method, feedback domination technique and sliding-mode control approach were used to design a control strategy that guarantees that the leader–follower multi-agent systems reach global consensus asymptotically.

The works Boccia et al. (2017), DongBin et al. (2014), Zhao et al. (2019) and Zheng et al. (2013), address the problem of leader–follower formation control for differential-drive robots. Particularly, in Boccia et al. (2017), is proposed a control in which the follower agents circumnavigate an objective with bounded velocity while in Zheng et al. (2013), a proportional control is designed to circumnavigate a static objective. In DongBin et al. (2014), the formation control problem is addressed considering two differential mobile robots without direct measurement of the leader robot’s linear velocity. The nonlinear strategies are based on the adaptive dynamic feedback and Immersion and Invariance estimation based second order sliding mode control technologies, which are continuous and robust against unknown bounded uncertainties. However, the main disadvantages are that the linear velocity of the leader has to be constant and the distance and formation angle are constants. In a similar way, in Zhao et al. (2019), a control strategy is proposed by means of a kinematic controller based on Lyapunov theory with dynamic controller using the Sliding Mode technique. As well as in the previous case, the linear velocity of the leader has to be constant. Finally, in Robin and Lacroix (2016), the authors analyse the different approaches that are recurrent through the target detection and tracking for multi-agent systems.

It is worth pointing out that most of the works, consider only two agents with the same dynamic model. Furthermore, in Shao and Tian (2017) and Zheng et al. (2013) the target does not move and do not consider perturbations. On the other hand, in Boccia et al. (2017), Deghat et al. (2014), DongBin et al. (2014), Shames et al. (2012) and Zhao et al. (2019) it is assumed that the target’s velocity is constant or it moves with a slow velocity.

Motivated by the aforementioned drawbacks and inspired by the works (Deghat et al. 2014; Shames et al. 2012), the main contributions of this work are:

• 1. A group of heterogeneous multi-agent system composed by differential-drive and omnidirectional mobile robots is considered to perform the circumnavigation task.

• 2. Different communication topologies can be used in the proposed approach, i.e., leader-follower, leader centered, or considering a spanning tree with root in the leader agent.

• 3. Unlike the works (Deghat et al. 2014; Shames et al. 2012), the circumnavigation velocity of the follower agent can be determined in the proposed approach.

• 4. It is proved that the distance between the follower and the leader has oscillations of smaller amplitude than the works (Deghat et al. 2014; Shames et al. 2012).

• 5. The leader’s velocity can be either constant or time-varying.

• 6. The control strategy does not need information of the leader’s velocity.

The outline of this work is as follows. The problem statement and the kinematic model, based on distance and orientation between agents, is described in Sect. 2. Section 3 presents the main contribution of this work related to the circumnavigation control problem, while Sect. 4 illustrates the numerical simulations and real-time experiments. Finally, the conclusions are presented in Sect. 5.

2 Problem statement

• Let $N=N_\mathcal {O} \cup N_\mathcal {D}=\left\{ R_1,...,R_n\right\}$ be a group of n mobile robots where $N_\mathcal {O} \subset N$ is the group of all the omnidirectional mobile robots while $N_\mathcal {D}\subset N$ is the set of all the differential-drive robots, and assume that the agent $R_n$ is the target which is going to be circumnavigated by the follower agents $R_1,...,R_{n-1}$.

• Let $N_i \subset N$ be the set of those agents that can be detected by $R_i$, $i=1,...,n-1$, and there exists a spanning directed tree with root in $R_n$, i.e. $N_i=\left\{ \forall R_j \mid j>i\right\}$.

• The leader agent $R_n$ is an omnidirectional mobile robot moving freely in the plane while the followers can be either differential or omnidirectional robots.

• The follower agents do not have information about the velocity of $R_n$.

• It is assumed that the maximum velocity of the leader is less or equal than the maximum velocity of the followers.

The objective is to design a robust control law such that the followers keep a certain distance and orientation with respect to their own leader while circumnavigating the agent $R_n$. Furthermore, due to the capability of omnidirectional mobile robots to orientate, the omnidirectional mobile robots will keep looking straight at $R_n$, i.e. the formation angle is zero.

2.1 Kinematic model

The kinematic model for the omnidirectional mobile robot is given as

$$\begin{aligned} \dot{\varvec{\xi }}_p=R(\theta _p) \mathbf {u}_p, \end{aligned}$$

(1)

for all $p \in N_\mathcal {O}$, where $R(\theta _p)$ is the rotation matrix defined as

$$\begin{aligned} R(\theta _p)=\begin{bmatrix} \cos \theta _p &{} -\sin \theta _p &{} 0 \\ \sin \theta _p &{} \cos \theta _p &{} 0 \\ 0 &{} 0&{} 1 \end{bmatrix}, \end{aligned}$$

$\varvec{\xi }_p=\begin{bmatrix} x_p&y_p&\theta _p \end{bmatrix}^\top \in \mathbb {R}^3$ is the state vector with $x_p$, $y_p \in \mathbb {R}$ as the position in the plane of each agent, $\theta _p \in \mathbb {R}$ is the orientation with respect to the horizontal axis X and $\mathbf {u}_p=\begin{bmatrix} v_{x_p}&v_{y_p}&w_p \end{bmatrix}^\top \in \mathbb {R}^3$ is the input control with $v_{x_p} \in \mathbb {R}$ as the linear velocity, $v_{y_p} \in \mathbb {R}$ is the lateral velocity and $w_p \in \mathbb {R}$ is the angular velocity.

Note that if the lateral velocity is cancelled, i.e., $v_{y_p}=0$, then, it is possible to obtain the kinematic model of the differential-drive mobile robot, given by

$$\begin{aligned} \dot{x}_\ell= & {} v_{x_\ell } \cos \theta _\ell , \end{aligned}$$

(2a)

$$\begin{aligned} \dot{y}_\ell= & {} v_{x_\ell } \sin \theta _\ell , \end{aligned}$$

(2b)

$$\begin{aligned} \dot{\theta }_\ell= & {} w_\ell , \end{aligned}$$

(2c)

for all $\ell \in N_\mathcal {D}$. It is worth mentioning that system (2) is underactuated and satisfies the following non-holonomic restriction $\dot{x}_{\ell }\sin \theta _\ell -\dot{y}_{\ell }\cos \theta _\ell =0$.

2.2 Kinematic model based on distance and orientation between agents

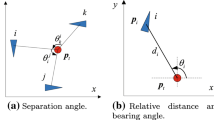
Let us recall the dynamic model, based on distance and orientation, between two mobile robots (González-Sierra et al. 2018; Paniagua-Contro et al. 2019), defined as (Fig. 1)

Fig. 1

Leader–follower scheme

$$\begin{aligned} \dot{\varvec{\eta }}_{ji}=f_{\eta _{ji}}(\varvec{\eta }_{ji})\mathbf {u}_j+g_{\eta _{ji}}(\varvec{\eta }_{ji})\mathbf {u}_{i}, \quad i\ne j, \quad i,j\in N, \end{aligned}$$

(3)

where $\varvec{\eta }_{ji}=\begin{bmatrix} d_{ji}&\alpha _{ji}&\theta _i \end{bmatrix}^\top \in \mathbb {R}^3$ is the state vector, $d_{ji} \in \mathbb {R}_+$ is the distance measured from the geometrical center of agent $R_j$ to the geometrical center of the agent $R_i$, with $\mathbb {R}_+$ as the set of all positive real numbers, $d_{{ji}_{x}}$ and $d_{{ji}_{y}} \in \mathbb {R}_+$ are the components of the distance vector $\mathbf {d}_{ji}$ with respect to a global frame and $\alpha _{ji} \in \mathbb {R}$ is the formation angle measured from the distance vector $\mathbf {d}_{ji}$ to a local frame attached to the agent $R_i$. The functions $f_{\eta _{ji}}$ and $g_{\eta _{ji}}$ are determined depending on the type of robot which is being used. Specifically, in Paniagua-Contro et al. (2019) four dynamic models are proposed

• $\mathcal {O}$–$\mathcal {O}$ Leader–follower scheme,

• $\mathcal {D}$–$\mathcal {O}$ Leader–follower scheme,

• $\mathcal {D}$–$\mathcal {D}$ Leader–follower scheme,

• $\mathcal {O}$–$\mathcal {D}$ Leader–follower scheme,

where $\mathcal {O}$ means an omnidirectional robot while $\mathcal {D}$ is a differential robot.

2.3 $\mathcal {O}$–$\mathcal {O}$ leader–follower scheme

In this scheme, both agents $R_j$ and $R_i$ are omnidirectional mobile robots, hence (3) is rewritten as

$$\begin{aligned} \dot{\varvec{\eta }}_{{ji}_{\mathcal {O}\mathcal {O}}}=f_{{ji}_{\mathcal {O}\mathcal {O}}}(\varvec{\eta }_{{ji}_{\mathcal {O}\mathcal {O}}})\mathbf {u}_{j_\mathcal {O}}+g_{{ji}_{\mathcal {O}\mathcal {O}}}(\varvec{\eta }_{{ji}_{\mathcal {O}\mathcal {O}}})\mathbf {u}_{i_\mathcal {O}}, \end{aligned}$$

(4)

where

$$\begin{aligned} f_{{ji}_{\mathcal {O}\mathcal {O}}}= & {} \begin{bmatrix} \cos (\theta _j-\theta _i + \alpha _{ji}) &{} -\sin (\theta _j-\theta _i + \alpha _{ji}) &{} 0 \\ -\frac{\sin (\theta _j-\theta _i + \alpha _{ji})}{d_{ji}} &{} -\frac{\cos (\theta _j-\theta _i + \alpha _{ji}) }{d_{ji}}&{} 0 \\ 0 &{} 0 &{}0 \end{bmatrix},\nonumber \\ \end{aligned}$$

(5a)

$$\begin{aligned} g_{{ji}_{\mathcal {O}\mathcal {O}}}= & {} \begin{bmatrix} -\cos \alpha _{ji} &{} \sin \alpha _{ji} &{} 0\\ \frac{\sin \alpha _{ji}}{d_{ji}} &{} \frac{\cos \alpha _{ji}}{d_{ji}} &{} 1\\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(5b)

while the vector control inputs are defined as $\mathbf {u}_{j_\mathcal {O}}=\begin{bmatrix}v_{x_j}&v_{y_j}&w_j \end{bmatrix}^\top \in \mathbb {R}^3$ and $\mathbf {u}_{i_\mathcal {O}}=\begin{bmatrix}v_{x_i}&v_{y_i}&w_i \end{bmatrix}^\top \in \mathbb {R}^3$. Note that $\mathbf {u}_{i_\mathcal {O}}$ refers to the control inputs for the omnidirectional robot while $\mathbf {u}_{i_\mathcal {D}}$ refers to the control inputs for the differential-drive robots.

2.4 $\mathcal {D}$–$\mathcal {O}$ leader–follower scheme

In this scheme, agent $R_j$ is a differential-drive robot while agent $R_i$ is an omnidirectional mobile robot. In this sense, (3) is rewritten as

$$\begin{aligned} \dot{\varvec{\eta }}_{{ji}_{\mathcal {D}\mathcal {O}}}=f_{{ji}_{\mathcal {D}\mathcal {O}}}(\varvec{\eta }_{{ji}_{\mathcal {D}\mathcal {O}}})\mathbf {u}_{j_\mathcal {D}}+g_{{ji}_{\mathcal {D}\mathcal {O}}}(\varvec{\eta }_{{ji}_{\mathcal {D}\mathcal {O}}})\mathbf {u}_{i_\mathcal {O}}, \end{aligned}$$

(6)

where $\mathbf {u}_{j_\mathcal {D}}=\begin{bmatrix}v_{x_j}&w_j \end{bmatrix}^\top \in \mathbb {R}^2$, $g_{{ji}_{\mathcal {D}\mathcal {O}}}=g_{{ji}_{\mathcal {O}\mathcal {O}}}$, while

$$\begin{aligned} f_{{ji}_{\mathcal {D}\mathcal {O}}}=\begin{bmatrix} \cos (\theta _j-\theta _i+ \alpha _{ji}) &{} 0\\ -\frac{\sin (\theta _j-\theta _i + \alpha _{ji})}{d_{ji}} &{} 0\\ 0 &{} 0 \end{bmatrix}. \end{aligned}$$

(7)

2.5 $\mathcal {D}$–$\mathcal {D}$ leader–follower scheme

Both agents are differential-drive mobile robots, therefore, (3) is rewritten as

$$\begin{aligned} \dot{\varvec{\eta }}_{{ji}_{\mathcal {D}\mathcal {D}}}=f_{{ji}_{\mathcal {D}\mathcal {D}}}(\varvec{\eta }_{{ji}_{\mathcal {D}\mathcal {D}}})\mathbf {u}_{j_\mathcal {D}}+g_{{ji}_{\mathcal {D}\mathcal {D}}}(\varvec{\eta }_{{ji}_{\mathcal {D}\mathcal {D}}})\mathbf {u}_{i_\mathcal {D}}, \end{aligned}$$

(8)

where $f_{{ji}_{\mathcal {D}\mathcal {D}}}=f_{{ji}_{\mathcal {D}\mathcal {O}}}$, while

$$\begin{aligned} g_{{ji}_{\mathcal {D}\mathcal {D}}}=\begin{bmatrix} -\cos \alpha _{ji} &{} 0\\ \frac{\sin \alpha _{ji}}{d_{ji}} &{} 1\\ 0 &{} 1 \end{bmatrix}. \end{aligned}$$

(9)

Considering the output function $\mathbf {h}_{{ji}_{\mathcal {D}\mathcal {D}}}=\begin{bmatrix} d_{ji}&\alpha _{ji} \end{bmatrix}^\top$, then, the dynamics of this output is simply given as

$$\begin{aligned} \dot{\mathbf {h}}_{{ji}_{\mathcal {D}\mathcal {D}}}=\bar{f}_{{ji}_{\mathcal {D}\mathcal {D}}}(\mathbf {h}_{{ji}_{\mathcal {D}\mathcal {D}}},\theta _j,\theta _i)\mathbf {u}_{j_\mathcal {D}}+\bar{g}_{{ji}_{\mathcal {D}\mathcal {D}}}(\mathbf {h}_{{ji}_{\mathcal {D}\mathcal {D}}})\mathbf {u}_{i_\mathcal {D}}, \end{aligned}$$

(10)

where

$$\begin{aligned} \bar{f}_{{ji}_{\mathcal {D}\mathcal {D}}}= & {} \begin{bmatrix} \cos (\theta _j-\theta _i+ \alpha _{ji}) &{} 0\\ -\frac{\sin (\theta _j-\theta _i + \alpha _{ji})}{d_{ji}} &{} 0 \end{bmatrix},\\ \bar{g}_{{ji}_{\mathcal {D}\mathcal {D}}}= & {} \begin{bmatrix} -\cos \alpha _{ji} &{} 0\\ \frac{\sin \alpha _{ji}}{d_{ji}} &{} 1 \end{bmatrix}. \end{aligned}$$

2.6 $\mathcal {O}$–$\mathcal {D}$ leader–follower scheme

Finally, in this scheme, agent $R_j$ is an omnidirectional mobile robot while $R_i$ is a differential-drive robot, thus, (3) is rewritten as

$$\begin{aligned} \dot{\varvec{\eta }}_{{ji}_{\mathcal {O}\mathcal {D}}}=f_{{ji}_{\mathcal {O}\mathcal {D}}}(\varvec{\eta }_{{ji}_{\mathcal {O}\mathcal {D}}})\mathbf {u}_{j_\mathcal {O}}+g_{{ji}_{\mathcal {O}\mathcal {D}}}(\varvec{\eta }_{{ji}_{\mathcal {O}\mathcal {D}}})\mathbf {u}_{i_\mathcal {D}}, \end{aligned}$$

(11)

where $f_{{ji}_{\mathcal {O}\mathcal {D}}}=f_{{ji}_{\mathcal {O}\mathcal {O}}}$, $g_{{ji}_{\mathcal {O}\mathcal {D}}}=g_{{ji}_{\mathcal {D}\mathcal {D}}}$. Taking into account the output function $\mathbf {h}_{{ji}_{\mathcal {O}\mathcal {D}}}=\begin{bmatrix} d_{ji}&\alpha _{ji} \end{bmatrix}^\top$, then, the dynamics of this output is simply given as

$$\begin{aligned} \dot{\mathbf {h}}_{{ji}_{\mathcal {O}\mathcal {D}}}=\bar{f}_{{ji}_{\mathcal {O}\mathcal {D}}}(\mathbf {h}_{{ji}_{\mathcal {O}\mathcal {D}}},\theta _j,\theta _i)\mathbf {u}_{j_\mathcal {O}}+\bar{g}_{{ji}_{\mathcal {O}\mathcal {D}}}(\mathbf {h}_{{ji}_{\mathcal {O}\mathcal {D}}})\mathbf {u}_{i_\mathcal {D}}, \end{aligned}$$

(12)

where

$$\begin{aligned} \bar{f}_{{ji}_{\mathcal {O}\mathcal {D}}}= & {} \begin{bmatrix} \cos (\theta _j-\theta _i+ \alpha _{ji}) &{} -\sin (\theta _j-\theta _i+ \alpha _{ji}) &{} 0\\ -\frac{\sin (\theta _j-\theta _i + \alpha _{ji})}{d_{ji}} &{} -\frac{\cos (\theta _j-\theta _i + \alpha _{ji})}{d_{ji}} &{} 0 \end{bmatrix}, \\ \bar{g}_{{ji}_{\mathcal {O}\mathcal {D}}}= & {} \begin{bmatrix} -\cos \alpha _{ji} &{} 0\\ \frac{\sin \alpha _{ji}}{d_{ji}} &{} 1 \end{bmatrix}. \end{aligned}$$

2.7 Complete model

Without loss of generality, take into account that the agents are arrange as follows $N=\left\{ \mathcal {N}_1, \mathcal {N}_2,...,\mathcal {N}_q \right\}$, where $\mathcal {N}_r=\left\{ \mathcal {O}, \mathcal {D}, \mathcal {D}, \mathcal {O}\right\}$, for $r=1,...,q-1$ and $\mathcal {N}_q=\left\{ \mathcal {O}, \mathcal {D}, \mathcal {D}, \mathcal {O}, \mathcal {O}\right\}$. Assume that the agents are under the directed open-chain formation, then, the complete dynamic model is given as

$$\begin{aligned} \dot{\varvec{\zeta }}=\mathcal {A}(\varvec{\zeta })\mathbb {U}, \end{aligned}$$

(13)

where

$$\begin{aligned} \varvec{\zeta }= & {} \begin{bmatrix}\varvec{\eta }_{{21}_{\mathcal {D}\mathcal {O}}}\\ \mathbf {h}_{{32}_{\mathcal {D}\mathcal {D}}}\\ \mathbf {h}_{{43}_{\mathcal {O}\mathcal {D}}}\\ \varvec{\eta }_{{54}_{\mathcal {O}\mathcal {O}}}\\ \vdots \\ \varvec{\eta }_{{(n-3)(n-4)}_{\mathcal {D}\mathcal {D}}}\\ \mathbf {h}_{{(n-2)(n-3)}_{\mathcal {D}\mathcal {D}}}\\ \mathbf {h}_{{(n-1)(n-2)}_{\mathcal {O}\mathcal {D}}}\\ \varvec{\eta }_{{N(n-1)}_{\mathcal {O}\mathcal {O}}} \\ \varvec{\xi }_n \end{bmatrix}, \quad \mathbb {U}=\begin{bmatrix} \mathbf {u}_{1_{\mathcal {O}}}\\ \mathbf {u}_{2_{\mathcal {D}}}\\ \mathbf {u}_{3_{\mathcal {D}}}\\ \mathbf {u}_{4_{\mathcal {O}}} \\ \mathbf {u}_{5_{\mathcal {O}}}\\ \vdots \\ \mathbf {u}_{{n-4}_{\mathcal {O}}}\\ \mathbf {u}_{{n-3}_{\mathcal {D}}}\\ \mathbf {u}_{{n-2}_{\mathcal {D}}} \\ \mathbf {u}_{{n-1}_{\mathcal {O}}} \\ \mathbf {u}_{{n}_{\mathcal {O}}} \end{bmatrix},\\ \end{aligned}$$

$$\begin{aligned} \mathcal {A}= & {} \left[ \begin{array}{ccccccccccc} g_{{21}_{\mathcal {D}\mathcal {O}}}&{} f_{{21}_{\mathcal {D}\mathcal {O}}} &{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{}... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3}\\ 0_{2\times 3} &{} \bar{g}_{{32}_{\mathcal {D}\mathcal {D}}} &{} \bar{f}_{{32}_{\mathcal {D}\mathcal {D}}} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{}0_{2\times 3}&{}0_{2\times 2}&{}0_{2\times 2}&{}0_{2\times 3}&{}0_{2\times 3}\\ 0_{2\times 3} &{} 0_{2\times 2} &{} \bar{g}_{{43}_{\mathcal {O}\mathcal {D}}} &{} \bar{f}_{{43}_{\mathcal {O}\mathcal {D}}} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{}0_{2\times 3} &{} 0_{2\times 3} \\ 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} g_{{54}_{\mathcal {O}\mathcal {O}}} &{} f_{{54}_{\mathcal {O}\mathcal {O}}} &{} ... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3}\\ \vdots &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} &{} \vdots \\ 0_{3\times 3} &{} 0_{3\times 2}&{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{} ... &{} g_{{(n-3)(n-4)}_{\mathcal {D}\mathcal {O}}}&{} f_{{(n-3)(n-4)}_{\mathcal {D}\mathcal {O}}} &{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3}\\ 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} \bar{g}_{{(n-2)(n-3)}_{\mathcal {D}\mathcal {D}}} &{} \bar{f}_{{(n-2)(n-3)}_{\mathcal {D}\mathcal {D}}} &{} 0_{2\times 3} &{} 0_{2\times 3} \\ 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} 0_{2\times 2} &{} \bar{g}_{{(n-1)(n-2)}_{\mathcal {O}\mathcal {D}}} &{} \bar{f}_{{(n-1)(n-2)}_{\mathcal {O}\mathcal {D}}} &{} 0_{2\times 3}\\ 0_{3\times 3} &{} 0_{3\times 2}&{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{} ... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} g_{{n(n-1)}_{\mathcal {O}\mathcal {O}}} &{} f_{{n(n-1)}_{\mathcal {O}\mathcal {O}}}\\ 0_{3\times 3} &{} 0_{3\times 2}&{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{} ... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{}0_{3\times 3} &{} R(\theta _n) \end{array} \right] , \end{aligned}$$

with $0_{a \times b}$ as an $a \times b$ zero matrix.

Remark 1

Because the leader agent is moving freely in the plane, therefore a control law is not needed. Furthermore, it is considered that the velocities of the leader act as a perturbation.

3 Control strategy

In this section, a control strategy, based on the Backstepping approach (Khalil 2002), is used to solve the circumnavigation problem.

3.1 Heading angle control

For the heading angle control, only the omnidirectional mobile robots will be taken into account.

Remark 2

Note that the omnidirectional robot model is fully actuated, therefore, it is possible to design a control law for its orientation angle. Contrary to the differential-drive robot, where it has 3 outputs and only two control inputs.

Recall that $N_\mathcal {O} \subset N$, then, one can define $S_\mathcal {O}=\mathrm {card} ({N}_{\mathcal {O}})$. In this sense, let us define the orientation error as

$$\begin{aligned} \mathbf {e}_\theta =\varvec{\theta }-\varvec{\theta }^*+\varvec{\varsigma }(t), \quad \bar{\mathbf {e}}_\theta =\int _0 ^t \mathbf {e}_\theta (\tau )d\tau . \end{aligned}$$

(14)

where $\varvec{\varsigma }\in \mathbb {R}^{S_{\mathcal {O}}}$ is a time-varying disturbances vector which is bounded, $\mathbf {e}_\theta =\begin{bmatrix}e_{\theta _1}&e_{\theta _4}&...&e_{\theta _{n-4}}&e_{\theta _{n-1}} \end{bmatrix}^\top \in \mathbb {R}^{S_{\mathcal {O}}}$ is the orientation error vector, the vector $\varvec{\theta }=\begin{bmatrix}\theta _1&\theta _4&...&\theta _{n-4}&\theta _{n-1} \end{bmatrix}^\top \in \mathbb {R}^{S_{\mathcal {O}}}$ while the desired orientation vector is given by $\varvec{\theta }^*=\begin{bmatrix}\theta _1^*&\theta _4^*&...&\theta _{n-4}^*&\theta _{n-1}^* \end{bmatrix}^\top \in \mathbb {R}^{S_{\mathcal {O}}}$. Based on (13), the dynamics of (14) is given by

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_\theta= & {} \mathbf {e}_\theta , \end{aligned}$$

(15a)

$$\begin{aligned} \dot{\mathbf {e}}_\theta= & {} \mathbf {w}-\dot{\varvec{\theta }}^*+\varvec{\delta }_{\theta }(\mathbf {e}_\theta ), \end{aligned}$$

(15b)

where $\varvec{\delta }_{\theta }=\begin{bmatrix}\delta _{\theta _1}&\delta _{\theta _4}&...&\delta _{\theta _{n-4}}&\delta _{\theta _{n-1}}\end{bmatrix}^\top \in \mathbb {R}^{S_{\mathcal {O}}}$ is the time-derivative of $\varvec{\varsigma }$ which satisfies one of the following restrictions

$$\begin{aligned} \Vert \varvec{\delta }_{\theta } \Vert\le & {} \alpha _{\theta }\Vert \mathbf {e}_\theta \Vert , \end{aligned}$$

(16a)

$$\begin{aligned} \Vert \varvec{\delta }_{\theta } \Vert\le & {} \varDelta _\theta , \end{aligned}$$

(16b)

with $\alpha _{\theta }$, $\varDelta _\theta >0$. Using the backstepping approach, one proceeds to stabilize system (15a) with function $\phi (\bar{\mathbf {e}}_\theta )$, i.e., system (15a) is rewritten as

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_\theta =\phi (\bar{\mathbf {e}}_\theta ). \end{aligned}$$

(17)

Let us propose the following Lyapunov candidate function $V_{\theta _1}=\frac{1}{2}\bar{\mathbf {e}}_\theta ^\top \bar{\mathbf {e}}_\theta$. Calculating the time-derivative along the trajectories (17) with $\phi (\bar{\mathbf {e}}_\theta )=-K_{\theta _1} \bar{\mathbf {e}}_\theta$ and $K_{\theta _1} \in \mathbb {R}^{S_{\mathcal {O}} \times S_{\mathcal {O}}}$ is a positive definite matrix, one has

$$\begin{aligned} \dot{V}_{\theta _1}=-\bar{\mathbf {e}}_\theta ^\top K_{\theta _1}\bar{\mathbf {e}}_\theta , \end{aligned}$$

and, applying (16a), hence, $\dot{V}_{\theta _1}$, has an upper bound given by

$$\begin{aligned} \dot{V}_{\theta _1}\le - \lambda _{\min }( K_{\theta _1} ) \Vert \bar{\mathbf {e}}_\theta \Vert ^2, \end{aligned}$$

which is negative definite, with $\lambda _{\min }( K_{\theta _1} )>0$. Now, defining a new variable $\mathbf {z}_\theta =\mathbf {e}_\theta -\phi (\bar{\mathbf {e}}_\theta )$, the system (15) is rewritten as

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_\theta= & {} \mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta , \end{aligned}$$

(18a)

$$\begin{aligned} \dot{\mathbf {z}}_\theta= & {} \mathbf {w}-\dot{\varvec{\theta }}^*+K_{\theta _1}(\mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta )+\varvec{\delta }_{\theta }. \end{aligned}$$

(18b)

Proposing the following Lyapunov candidate function

$$\begin{aligned} V_{\theta _2}=V_{\theta _1}+\frac{1}{2}\mathbf {z}_\theta ^\top \mathbf {z}_\theta , \end{aligned}$$

(19)

and, calculating the time-derivative along the trajectories (18), one has

$$\begin{aligned} \dot{V}_{\theta _2}= & {} \dot{V}_{\theta _1}+\mathbf {z}_\theta ^\top \dot{\mathbf {z}}_\theta =\bar{\mathbf {e}}_\theta ^\top \dot{\bar{\mathbf {e}}}_\theta +\mathbf {z}_\theta ^\top \dot{\mathbf {z}}_\theta ,\\= & {} \bar{\mathbf {e}}_\theta ^\top \left( \mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta \right) \\&+\mathbf {z}_\theta ^\top \left[ \mathbf {w}-\dot{\varvec{\theta }}^*+K_{\theta _1}(\mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta )+\varvec{\delta }_{\theta }\right] ,\\= & {} \mathbf {z}_\theta ^\top \left[ \bar{\mathbf {e}}_\theta +\mathbf {w}-\dot{\varvec{\theta }}^*+K_{\theta _1}(\mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta )+\varvec{\delta }_{\theta } \right] \\&-\bar{\mathbf {e}}_\theta ^\top K_{\theta _1}\bar{\mathbf {e}}_\theta . \end{aligned}$$

If the control input is defined as

$$\begin{aligned} \mathbf {w}=\dot{\varvec{\theta }}^*-\bar{\mathbf {e}}_\theta -K_{\theta _1}(\mathbf {z}_\theta -K_{\theta _1}\bar{\mathbf {e}}_\theta )-K_{\theta _2}\mathbf {z}_\theta , \end{aligned}$$

(20)

with $K_{\theta _2} \in \mathbb {R}^{S_{\mathcal {O}} \times S_{\mathcal {O}}}$ as a positive definite matrix, then, $\dot{V}_{\theta _2}$ simplifies to

$$\begin{aligned} \dot{V}_{\theta _2}= & {} -\bar{\mathbf {e}}_\theta ^\top K_{\theta _1}\bar{\mathbf {e}}_\theta -\mathbf {z}_\theta ^\top K_{\theta _2}\mathbf {z}_\theta +\mathbf {z}_\theta ^\top \varvec{\delta }_{\theta },\\ \dot{V}_{\theta _2}\le & {} -\lambda _{\min }( K_{\theta _1} ) \Vert \bar{\mathbf {e}}_\theta \Vert ^2-\left[ \lambda _{\min }( K_{\theta _2} ) -\alpha _{\theta } \right] \Vert \mathbf {z}_\theta \Vert ^2\\&+ 2\lambda _{\max }(K_{\theta _1})\Vert \mathbf {z}_\theta \Vert \Vert \bar{\mathbf {e}}_\theta \Vert \alpha _\theta ,\\ \dot{V}_{\theta _2}\le & {} - \begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert&\Vert \mathbf {z}_\theta \Vert \end{bmatrix} Q_\theta \begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert \\ \Vert \mathbf {z}_\theta \Vert \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} Q_\theta =\begin{bmatrix} \lambda _{\min }(K_{\theta _1}) &{} &{} &{} -\lambda _{\max }(K_{\theta _1})\alpha _\theta \\ lambda_{\max }(K_{\theta _1})\alpha _\theta &{} &{} &{} \lambda _{\min }(K_{\theta _2})-\alpha _{\theta } \end{bmatrix}, \end{aligned}$$

therefore $\dot{V}_{\theta _2}$ has an upper bound given by

$$\begin{aligned} \dot{V}_{\theta _2}\le -\sigma _\theta \left[ \Vert \bar{\mathbf {e}}_\theta \Vert ^2 + \Vert \mathbf {z}_\theta \Vert ^2 \right] , \end{aligned}$$

(21)

with $\sigma _\theta >0$. Due to $\lambda _{\min }( K_{\theta _1} )>0$, and, with the assumption $\lambda _{\min }(K_{\theta _2}) \ge \frac{(\lambda _{\max }(K_{\theta _1})\alpha _\theta )^2}{\lambda _{\min }(K_{\theta _1})}+\alpha _{\theta }$, guarantees that matrix $Q_\theta$ is definite positive. Based on this, the following Proposition is stated.

Proposition 1

Let the system (18) with the control law (20) and consider that the perturbation satisfies the restriction (16a), then, if the design parameters satisfy

$$\begin{aligned} \lambda _{\min }( K_{\theta _1} )> & {} 0,\\ \lambda _{\min }(K_{\theta _2})\ge & {} \frac{\left[ \lambda _{\max }(K_{\theta _1})\alpha _\theta \right] ^2}{\lambda _{\min }(K_{\theta _1})}+\alpha _{\theta }, \end{aligned}$$

then, the orientation error will converge asymptotically to zero, i.e., $\lim \limits _{t \rightarrow \infty }\bar{\mathbf {e}}_\theta =\lim \limits _{t \rightarrow \infty }\mathbf {e}_\theta =0$.

Proof

It becomes evident that (21) is definite negative, hence $\lim \limits _{t \rightarrow \infty }\bar{\mathbf {e}}_\theta =\lim \limits _{t \rightarrow \infty }\mathbf {z}_\theta =0$. Because $\mathbf {z}_\theta =\mathbf {e}_\theta +K_{\theta _1}\bar{\mathbf {e}}_\theta$ and $\lim \limits _{t \rightarrow \infty }\bar{\mathbf {e}}_\theta =0$, then $\lim \limits _{t \rightarrow \infty }\mathbf {z}_\theta =\lim \limits _{t \rightarrow \infty }\mathbf {e}_\theta =0$.

$\square$

Proposition 2

Let the system (18) with the control law (20) and consider that $\varvec{\delta }_\theta$ is a non-vanishing perturbation with the upper bound given in (16b), then, if the design parameters satisfy

$$\begin{aligned} \lambda _{\min }( K_{\theta _1} )> & {} 0,\\ \lambda _{\min }(K_{\theta _2})\ge & {} \frac{\left[ \lambda _{\max }(K_{\theta _1})\right] ^2}{\lambda _{\min }(K_{\theta _1})}, \end{aligned}$$

hence, system (18) is input-to-state stable with respect to the perturbation $\varvec{\delta }_\theta$.

Proof

Considering the same Lyapunov candidate function $V_{\theta _2}$ given in (19), therefore, its time-derivative along the trajectories (18) with control (20) is reduced to

$$\begin{aligned} \dot{V}_{\theta _2}= & {} -\bar{\mathbf {e}}_\theta ^\top K_{\theta _1}\bar{\mathbf {e}}_\theta -\mathbf {z}_\theta ^\top K_{\theta _2}\mathbf {z}_\theta +\mathbf {z}_\theta ^\top \varvec{\delta }_{\theta },\\ \dot{V}_{\theta _2}\le & {} -\lambda _{\min }( K_{\theta _1} ) \Vert \bar{\mathbf {e}}_\theta \Vert ^2- \lambda _{\min }( K_{\theta _2} ) \Vert \mathbf {z}_\theta \Vert ^2\\&+ 2\lambda _{\max }(K_{\theta _1})\Vert \mathbf {z}_\theta \Vert \Vert \bar{\mathbf {e}}_\theta \Vert +\Vert \varvec{\delta }_\theta \Vert (\Vert {\mathbf {z}}_\theta \Vert + \Vert \bar{\mathbf {e}}_\theta \Vert ),\\ {\dot{V}}_{\theta _2}\le & {} - \begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert&\Vert \mathbf {z}_\theta \Vert \end{bmatrix} \bar{Q}_\theta \begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert \\ \Vert \mathbf {z}_\theta \Vert \end{bmatrix}+\begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert&\Vert \mathbf {z}_\theta \Vert \end{bmatrix} \varDelta , \end{aligned}$$

where $\varDelta =\begin{bmatrix} \Vert \varvec{\delta }_\theta \Vert&\Vert \varvec{\delta }_\theta \Vert \end{bmatrix}^\top$ and

$$\begin{aligned} \bar{Q}_\theta =\begin{bmatrix} \lambda _{\min }(K_{\theta _1}) &{} -\lambda _{\max }(K_{\theta _1})\\ -\lambda _{\max }(K_{\theta _1}) &{} \lambda _{\min }(K_{\theta _2}) \end{bmatrix}, \end{aligned}$$

where $K_{\theta _1}$, $K_{\theta _2}$, $\bar{Q}_\theta$ are positive definite matrices. Now, defining $\varvec{\epsilon }=\begin{bmatrix} \Vert \bar{\mathbf {e}}_\theta \Vert&\Vert \mathbf {z}_\theta \Vert \end{bmatrix}^\top$, one has

$$\begin{aligned} \dot{V}_{\theta _2}\le & {} -(1-\kappa ) \lambda _{\min } (\bar{Q}_\theta ) \Vert \varvec{\epsilon }\Vert ^2+\sqrt{2}\Vert \varvec{\delta }_\theta \Vert \Vert \varvec{\epsilon }\Vert \nonumber \\&- \kappa \lambda _{\min }(\bar{Q}_\theta ) \Vert \varvec{\epsilon }\Vert ^2 \end{aligned}$$

(22)

with $\kappa \in (0,1)$. Note that $\dot{V}_{\theta _2}$ will be definite negative if $\sqrt{2}\varvec{\delta }_\theta \Vert \Vert \varvec{\epsilon }\Vert - \kappa \lambda _{\min }(\bar{Q}_\theta ) \Vert \varvec{\epsilon }\Vert ^2 \le 0$, therefore it is possible to define the following region

$$\begin{aligned} \Vert \varvec{\epsilon } \Vert \ge \frac{\sqrt{2}\Vert \varvec{\delta }_\theta \Vert }{\kappa \lambda _{\min }(\bar{Q}_\theta )}. \end{aligned}$$

Finally, one has

$$\begin{aligned} \dot{V}_2\le & {} -(1-\kappa )\lambda _{\min }(\bar{Q}_\theta )\Vert \varvec{\epsilon }\Vert ^2 , \quad \forall \Vert \varvec{\epsilon }\Vert \ge \frac{\sqrt{2} \Vert \varvec{\delta }_\theta \Vert }{\kappa \lambda _{\min }(\bar{Q}_\theta )}, \end{aligned}$$

and one can conclude that system (18) is input-to-state stable with respect to the perturbation $\varvec{\delta }_\theta$. $\square$

Remark 3

It is worth mentioning that Proposition 1 states that the orientation errors will converge asymptotically to zero, while Proposition 2 states that system (18) is input-to-state stable with respect to the perturbation $\varvec{\delta }_\theta$.

3.2 Distance and formation angle control

In a similar manner, let us define the distance error and the formation angle error vector as

$$\begin{aligned} \mathbf {e}_{d \alpha }=\begin{bmatrix} e_{d_{21}}&e_{\alpha _{21}}&...&e_{d_{n(n-1)}}&e_{\alpha _{n(n-1)}}\end{bmatrix}^\top \in \mathbb {R}^{2(n-1)}, \end{aligned}$$

(23a)

$$\begin{aligned} \bar{\mathbf {e}}_{d \alpha }=\begin{bmatrix} \bar{e}_{d_{21}}&\bar{e}_{\alpha _{21}}&...&\bar{e}_{d_{n(n-1)}}&\bar{e}_{\alpha _{n(n-1)}} \end{bmatrix}^\top \in \mathbb {R}^{2(n-1)}, \end{aligned}$$

(23b)

where $e_{d_{ji}}=d_{ji}-d_{ji}^*$ is the distance error, $e_{\alpha _{ji}}=\alpha _{ji}-\alpha _{ji}^*$ is the formation angle error, $\bar{e}_{d_{ji}}=\int _0^t e_{d_{ji}}(\tau )d\tau$, $\bar{e}_{\alpha _{ji}}=\int _0^t e_{\alpha _{ji}}(\tau )d\tau$, with $d_{ji}^*(t)$ as the desired time-varying distance between agent $R_j$ and $R_i$; and $\alpha _{ji}^*(t)$ as the desired time-varying formation angle between agent $R_j$ and $R_i$. From (13), the dynamics of (23) is given as follows

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_{d\alpha }= & {} \mathbf {e}_{d\alpha }, \end{aligned}$$

(24a)

$$\begin{aligned} \dot{\mathbf {e}}_{d\alpha }= & {} \mathcal {L}(\mathbf {e}_{d\alpha })\mathbf {v}_F+\mathbf {p}^*(\dot{d}_{ji}^*,\dot{\alpha }_{ji}^*,\mathbf {w}) \nonumber \\&+\varvec{\delta }_{e}(\mathbf {e}_{d\alpha },\mathbf {e}_\theta , v_{x_n},v_{y_n}), \end{aligned}$$

(24b)

where $\mathbf {v}_F=\begin{bmatrix} v_{x_1}&v_{y_1}&v_{x_2}&w_2&v_{x_3}&w_3&...&v_{x_{n-1}}&v_{y_{n-1}} \end{bmatrix}^\top \in \mathbb {R}^{2(n-1)}$ is the vector control input;

$$\begin{aligned} \mathbf {p}^*=\begin{bmatrix} -\dot{d}^*_{21} \\ w_1-\dot{\alpha }^*_{21} \\ -\dot{d}^*_{32} \\ -\dot{\alpha }^*_{32} \\ -\dot{d}^*_{43} \\ -\dot{\alpha }^*_{43} \\ -\dot{d}^*_{54} \\ w_4-\dot{\alpha }^*_{54} \\ \vdots \\ -\dot{d}^*_{(n-1)(n-2)} \\ -\dot{\alpha }^*_{(n-1)(n-2)} \\ -\dot{d}^*_{n(n-1)} \\ w_{n-1}-\dot{\alpha }^*_{n(n-1)}\end{bmatrix}, \end{aligned}$$

is a vector that contains the desired time-varying distances and formation angles as well as the angular velocity of those agents that are omnidirectional mobile robots; matrix $\mathcal {L}$ is similar to (14) and is given as follows

$$\begin{aligned} \mathcal {L}=\left[ \begin{array}{ccccccccccc} \mathcal {G}_{{21}_{\mathcal {D}\mathcal {O}}}&{} \mathcal {F}_{{21}_{\mathcal {D}\mathcal {O}}} &{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{}... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} 0_{3\times 3} \\ 0_{2\times 3} &{} \bar{g}_{{32}_{\mathcal {D}\mathcal {D}}} &{} \bar{f}_{{32}_{\mathcal {D}\mathcal {D}}} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{}0_{2\times 3}&{}0_{2\times 2}&{}0_{2\times 2}&{}0_{2\times 3}\\ 0_{2\times 3} &{} 0_{2\times 2} &{} \bar{g}_{{43}_{\mathcal {O}\mathcal {D}}} &{} \bar{f}_{{43}_{\mathcal {O}\mathcal {D}}} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{}0_{2\times 3} \\ 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} \mathcal {G}_{{54}_{\mathcal {O}\mathcal {O}}} &{} \mathcal {F}_{{54}_{\mathcal {O}\mathcal {O}}} &{} ... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} 0_{3\times 3} \\ \vdots &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} \vdots \\ 0_{3\times 3} &{} 0_{3\times 2}&{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{} ... &{} \mathcal {G}_{{(n-3)(n-4)}_{\mathcal {D}\mathcal {O}}}&{} \mathcal {F}_{{(n-3)(n-4)}_{\mathcal {D}\mathcal {O}}} &{} 0_{3\times 2} &{} 0_{3\times 3} \\ 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} \bar{g}_{{(n-2)(n-3)}_{\mathcal {D}\mathcal {D}}} &{} \bar{f}_{{(n-2)(n-3)}_{\mathcal {D}\mathcal {D}}} &{} 0_{2\times 3} \\ 0_{2\times 3} &{} 0_{2\times 2}&{} 0_{2\times 2} &{} 0_{2\times 3} &{} 0_{2\times 3} &{} ... &{} 0_{2\times 3} &{} 0_{2\times 2} &{} \bar{g}_{{(n-1)(n-2)}_{\mathcal {O}\mathcal {D}}} &{} \bar{f}_{{(n-1)(n-2)}_{\mathcal {O}\mathcal {D}}}\\ 0_{3\times 3} &{} 0_{3\times 2}&{} 0_{3\times 2} &{} 0_{3\times 3} &{} 0_{3\times 3} &{} ... &{} 0_{3\times 3} &{} 0_{3\times 2} &{} 0_{3\times 2} &{} \mathcal {G}_{{n(n-1)}_{\mathcal {O}\mathcal {O}}} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} \mathcal {G}_{{ji}_{\mathcal {D}\mathcal {O}}}= & {} \mathcal {G}_{{ji}_{\mathcal {O}\mathcal {O}}}=\begin{bmatrix} -\cos (e_{\alpha _{ji}}+\alpha ^*_{ji}) &{} &{} \sin (e_{\alpha _{ji}}+\alpha ^*_{ji})\\ \frac{\sin (e_{\alpha _{ji}}+\alpha ^*_{ji})}{e_{d_{ji}}+d^*_{ji}} &{} &{} \frac{\cos (e_{\alpha _{ji}}+\alpha ^*_{ji})}{e_{d_{ji}}+d^*_{ji}} \end{bmatrix},\\ \mathcal {F}_{{ji}_{\mathcal {D}\mathcal {O}}}= & {} \begin{bmatrix} -\cos \beta _{ji} &{} &{} 0\\ -\frac{\sin \beta _{ji}}{e_{d_{ji}}+d^*_{ji}} &{} &{} 0 \end{bmatrix},\\ \mathcal {F}_{{ji}_{\mathcal {O}\mathcal {O}}}= & {} \begin{bmatrix} \cos \beta _{ji} &{} -\sin \beta _{ji} \\ -\frac{\sin \beta _{ji}}{e_{d_{ji}}+d^*_{ji}} &{} -\frac{\cos \beta _{ji}}{e_{d_{ji}}+d^*_{ji}} \end{bmatrix}, \end{aligned}$$

with $\beta _{ji}=e_{\theta _j} +\theta _j^*-e_{\theta _i}-\theta _i^*+e_{\alpha _{ji}}+\alpha ^*_{ji}$ and $\varvec{\delta }_{e}$ is a vector that contains the lineal and lateral velocities of the leader agent, i.e.,

$$\begin{aligned} \varvec{\delta }_{e}=\begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ v_{x_n}\cos \gamma -v_{y_n}\sin \gamma \\ -v_{x_n}\frac{\sin \gamma }{e_{d_{n(n-1)}}+d^*_{n(n-1)}} -v_{y_n}\frac{\cos \gamma }{e_{d_{n(n-1)}}+d^*_{n(n-1)}} \end{bmatrix}, \end{aligned}$$

with $\gamma =\theta _n-e_{\theta _{n-1}}-\theta _{n-1}^* + e_{\alpha _{n(n-1)}}+\alpha ^*_{n(n-1)}$.

Remark 4

It is assume that the information of vector $\varvec{\delta }_{e}$ is unknown and acts as a perturbation for the system (24). However, it is possible to show that $\varvec{\delta }_{e}$ satisfies the following bounds

$$\begin{aligned} \Vert \varvec{\delta }_{e}\Vert \le \varDelta _e, \end{aligned}$$

(25)

with $\varDelta _e=\max \left( \sqrt{v_{x_n}^2+v_{y_n}^2} \right) \max \left( 1,\frac{1}{d_{n(n-1)}} \right)$. In this sense, the maximum velocity of the leader agent is boun-ded.

Proposition 3

Consider that $\varvec{\delta }_e$ is a non-vanishing perturbation of system (24b), thus, $\varvec{\delta }_e$ has the following upper bound

$$\begin{aligned} \Vert \varvec{\delta }_e \Vert \le \varDelta _e, \end{aligned}$$

with $\varDelta _e=\max \left( \sqrt{v_{x_n}^2+v_{y_n}^2} \right) \max \left( 1,\frac{1}{d_{n(n-1)}} \right)$.

Proof

Applying the norm operator to $\varvec{\delta }_e$ one has

$$\begin{aligned} \Vert \varvec{\delta }_e\Vert= & {} \left\| \begin{bmatrix} \cos \gamma &{} -\sin \gamma \\ -\frac{\sin \gamma }{d_{n(n-1)}} &{} -\frac{\cos \gamma }{d_{n(n-1)}} \end{bmatrix} \begin{bmatrix} v_{x_n}\\ v_{y_n}\end{bmatrix}\right\| , \\\le & {} \Vert \varGamma \Vert \sqrt{v_{x_n}^2+v_{y_n}^2}. \end{aligned}$$

The norm of $\varGamma$ is given by $\Vert \varGamma \Vert =\sqrt{\lambda _{\max } (\varGamma ^\top \varGamma )}$. Simple calculations show that $\Vert \varGamma \Vert =\max (1,\frac{1}{d})$. Finally, one has

$$\begin{aligned} \Vert \varvec{\delta }_e \Vert \le \varDelta _e, \end{aligned}$$

where $\varDelta _e=\max \left( \sqrt{v_{x_n}^2+v_{y_n}^2} \right) \max \left( 1,\frac{1}{d_{n(n-1)}} \right)$. $\square$

From the Backstepping approach, one proceeds to stabilize system (24a) with function $\phi (\bar{\mathbf {e}}_{d\alpha })$, i.e., system (24a) is rewritten as

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_{d\alpha }=\phi (\bar{\mathbf {e}}_{d\alpha }). \end{aligned}$$

(26)

Let us propose the following Lyapunov candidate function $V_{d\alpha _1}=\frac{1}{2}\bar{\mathbf {e}}_{d\alpha }^\top \bar{\mathbf {e}}_{d\alpha }$ and, calculating the time-derivative along the trajectories (26) with $\phi (\bar{\mathbf {e}}_{d\alpha })=-K_{d\alpha _1} \bar{\mathbf {e}}_{d\alpha }$ and $K_{d\alpha _1}\in \mathbb {R}^{2(n-1) \times 2(n-1)}$ is a positive definite matrix, one has

$$\begin{aligned} \dot{V}_{d\alpha _1}\le -\lambda _{\min } \left\{ K_{d\alpha _1} \right\} \Vert \bar{\mathbf {e}}_{d\alpha }\Vert ^2, \end{aligned}$$

which is negative definite if $\lambda _{\min } \left\{ K_{d\alpha _1} \right\} >0$. Now, proposing a new variable $\mathbf {z}_{d\alpha }=\mathbf {e}_{d\alpha }-\phi (\bar{\mathbf {e}}_{d\alpha })$, system (24) is rewritten as

$$\begin{aligned} \dot{\bar{\mathbf {e}}}_{d\alpha }= & {} \mathbf {z}_{d\alpha }-K_{d\alpha _1} \bar{\mathbf {e}}_{d\alpha }, \end{aligned}$$

(27a)

$$\begin{aligned} \dot{\mathbf {z}}_{d\alpha }= & {} \mathcal {L}\mathbf {v}_F+\varvec{\delta }_{e}+\mathbf {p}^* +K_{d\alpha _1}(\mathbf {z}_{d\alpha }-K_{d\alpha _1} \bar{\mathbf {e}}_{d\alpha }). \end{aligned}$$

(27b)

Defining the Lyapunov candidate function $V_{d\alpha _2}=V_{d\alpha _1}+\frac{1}{2}\mathbf {z}_{d\alpha }^\top \mathbf {z}_{d\alpha }$, and, calculating the time-derivative along the trajectories (27), one has

$$\begin{aligned} \dot{V}_{d\alpha _2}= & {} \mathbf {z}_{d\alpha }^\top \left[ \bar{\mathbf {e}}_{d\alpha }+\mathcal {L}\mathbf {v}_F+\varvec{\delta }_{e}+\mathbf {p}^*+K_{d\alpha _1}\mathbf {e}_{d\alpha } \right] \\&-\bar{\mathbf {e}}_{d\alpha }^\top K_{d\alpha _1}\bar{\mathbf {e}}_{d\alpha }. \end{aligned}$$

If the control input is defined as

$$\begin{aligned} \mathbf {v}_F=\mathcal {L}^{-1}\left[ -K_{d\alpha _1}\mathbf {e}_{d\alpha }-\bar{\mathbf {e}}_{d\alpha }-K_{d\alpha _2}\mathbf {z}_{d\alpha }-\mathbf {p}^* \right] , \end{aligned}$$

(28)

with $K_{d\alpha _2}\in \mathbb {R}^{2(n-1) \times 2(n-1)}$ as a positive definite matrix. Before proceeding, the following Lemma is defined

Lemma 1

Matrix $\mathcal {L}$ is always invertible for all $\alpha _{ji} \ne \pm \frac{\pi }{2}$ and $j\ne i$.

Proof

Since matrix $\mathcal {L}$ is an upper triangular block matrix, hence, the determinant is given by the product of the determinants of the diagonal matrices. Specifically, for $n=2$, the determinant of matrix $\mathcal {L}$ is defined as

$$\begin{aligned} \mathrm {det}(\mathcal {L})=\frac{1}{d_{21}}, \end{aligned}$$

while for $n \ge 3$, the determinant of matrix $\mathcal {L}$ is obtained as

$$\begin{aligned} \mathrm {det}(\mathcal {L})=r \mathop {\prod }\limits _{p,q} \limits ^n \frac{\cos \alpha _{q(q-1)}}{d_{p(p-1)}}, \end{aligned}$$

where $p=2,5,6,9,10...,n$, $q=3,4,7,8,11...,n$ and

$$\begin{aligned} r={\left\{ \begin{array}{ll} -1, &{}\hbox {if } n=3,7,11,... \\ 1, &{} \hbox {otherwise.} \end{array}\right. } \end{aligned}$$

$\square$

Remark 5

Recall that the angle $\alpha _{ji}$ is the angle measured from the distance vector $\mathbf {d}_{ji}$ to a local frame attached to the agent $R_i$. In this sense, an angle $\alpha _{ji}= \pm \frac{\pi }{2}$ means that the component of the velocity perpendicular to the wheels of the differential-drive mobile robots is aligned to the distance vector $\mathbf {d}_{ji}$ , and, due to the nonholonomic restriction of this kind of vehicles, given by $\dot{x}_i\sin \theta _i - \dot{y}_i \cos \theta _i=0$, then the motion, perpendicular to the linear velocity, is zero. Therefore, the restriction of $\alpha _{ji}= \pm \frac{\pi }{2}$ implies the nonholonomic restriction of the differential-drive mobile robots.

Substituting (28) into $\dot{V}_{d\alpha _2}$, one has

$$\begin{aligned} \dot{V}_{d\alpha _2}= & {} -\bar{\mathbf {e}}_{d\alpha }^\top K_{d\alpha _1}\bar{\mathbf {e}}_{d\alpha }-\mathbf {z}_{d\alpha }^\top K_{d\alpha _2}\mathbf {z}_{d\alpha }+\mathbf {z}_{d\alpha }^\top \varvec{\delta }_{e} ,\\ \dot{V}_{d\alpha _2}\le & {} -\lambda _{\min }(K_{d\alpha _1}) \Vert \bar{\mathbf {e}}_{d\alpha }\Vert ^2- \lambda _{\min }(K_{d\alpha _2})\Vert \mathbf {z}_{d\alpha } \Vert ^2\\&+2 \lambda _{\max }(K_{d\alpha _1})\Vert \bar{\mathbf {e}}_{d\alpha }\Vert \Vert \mathbf {z}_{d\alpha } \Vert \\&+ \Vert \varvec{\delta }_e\Vert (\Vert \mathbf {z}_{d\alpha } \Vert +\Vert \bar{\mathbf {e}}_{d\alpha }\Vert ),\\ \dot{V}_{d\alpha _2}\le & {} - \begin{bmatrix} \Vert \bar{\mathbf {e}}_{d\alpha }\Vert&\Vert \mathbf {z}_{d\alpha } \Vert \end{bmatrix}Q_{d\alpha } \begin{bmatrix} \Vert \bar{\mathbf {e}}_{d\alpha }\Vert \\ \Vert \mathbf {z}_{d\alpha } \Vert \end{bmatrix}\\&+ \begin{bmatrix} \Vert \bar{\mathbf {e}}_{d\alpha }\Vert&\Vert \mathbf {z}_{d\alpha } \Vert \end{bmatrix} \begin{bmatrix} \Vert \varvec{\delta }_e\Vert \\ \Vert \varvec{\delta }_e\Vert \end{bmatrix} \end{aligned}$$

where

$$\begin{aligned} Q_{d\alpha }=\begin{bmatrix} \lambda _{\min }( K_{d\alpha _1}) &{} -\lambda _{\max }( K_{d\alpha _1} ) \\ -\lambda _{\max }( K_{d\alpha _1} ) &{} \lambda _{\min }( K_{d\alpha _2}) \end{bmatrix}. \end{aligned}$$

Defining $\varvec{\epsilon }_{d\alpha }=\begin{bmatrix} \Vert \bar{\mathbf {e}}_{d\alpha } \Vert&\Vert \mathbf {z}_{d\alpha } \Vert \end{bmatrix}^\top$, one has

$$\begin{aligned} \dot{V}_{d\alpha _2}\le & {} -(1-\kappa ) \lambda _{\min } (Q_{d\alpha }) \Vert \varvec{\epsilon }_{d \alpha }\Vert ^2+\sqrt{2}\Vert \varvec{\delta }_e\Vert \Vert \varvec{\epsilon }_{d\alpha }\Vert \nonumber \\&- \kappa \lambda _{\min }(Q_{d\alpha }) \Vert \varvec{\epsilon }_{d\alpha }\Vert ^2, \end{aligned}$$

(29)

with $\kappa \in (0,1)$. Note that $\dot{V}_{d\alpha _2}$ will be definite negative if $\sqrt{2}\Vert \varvec{\delta }_e\Vert \Vert \varvec{\epsilon }_{d\alpha }\Vert - \kappa \lambda _{\min }(Q_{d\alpha }) \Vert \varvec{\epsilon }_{d\alpha }\Vert ^2 \le 0$, therefore it is possible to define the following region given by

$$\begin{aligned} \Vert \varvec{\epsilon }_{d\alpha } \Vert \ge \frac{\sqrt{2}\Vert \varvec{\delta }_e\Vert }{\kappa \lambda _{\min }(Q_{d \alpha })}. \end{aligned}$$

Finally, one has

$$\begin{aligned} \dot{V}_{d\alpha _2}\le & {} -(1-\kappa )\lambda _{\min }(Q_{d\alpha })\Vert \varvec{\epsilon }_{d\alpha }\Vert ^2,\ \end{aligned}$$

(30a)

$$\begin{aligned}&\forall \Vert \varvec{\epsilon }_{d\alpha }\Vert \ge \frac{\sqrt{2} \Vert \varvec{\delta }_e\Vert }{\kappa \lambda _{\min }(Q_{d\alpha })} , \end{aligned}$$

(30b)

and, one can conclude that system (27) is input-to-state stable with respect to the perturbation $\varvec{\delta }_e$. Based on this, the following Proposition is stated.

Proposition 4

Let the system (27) with the control law (28), and consider that $\varvec{\delta }_e$ is a non-vanishing perturbation with the upper bound given in (25), then, if the design parameters satisfy

$$\begin{aligned} \lambda _{\min }( K_{{d\alpha }_1} )> & {} 0,\\ \lambda _{\min }(K_{{d\alpha }_2})\ge & {} \frac{\left[ \lambda _{\max }(K_{{d\alpha }_1})\right] ^2}{\lambda _{\min }(K_{{d\alpha }_1})}, \end{aligned}$$

thus, system (27) is input-to-state stable with respect to the perturbation $\varvec{\delta }_e$.

Table 1 Initial conditions for the agents

Note that if the leader’s velocity is greater than the followers’ velocity, then, the region given by (30b) will increase and, therefore, the distance and formation angle errors will also increase. In this sense, it is considered that the difference between the norm of the maximum velocity of the followers $\mathbf {v}_{\max _i}$, for $i=1,...,n-1$, and the maximum velocity of the leader $\mathbf {v}_n$ must be bounded and this bound must be small enough, i.e. $\Vert \mathbf {v}_{\max _i} - \mathbf {v}_n\Vert \le \nu$, where $\nu \ge 0$. This means that even though we do not explicitly know the velocity of the leader, it is known that the difference between the norm of the maximum velocity of the followers and the maximum velocity of the leader is bounded.

4 Numerical simulations and real-time experiments

4.1 Numerical simulations

For the first numerical simulation, it is considered that the set $N_\mathcal {O}$ is given by $N_\mathcal {O}=\lbrace \mathcal {O}_1, \mathcal {O}_2, \mathcal {O}_5, \mathcal {O}_6, \mathcal {O}_9, \mathcal {O}_{10} \rbrace$, while the set $N_\mathcal {D}$ is given by $N_\mathcal {D}=\lbrace \mathcal {D}_3, \mathcal {D}_4, \mathcal {D}_7, \mathcal {D}_8, \rbrace$ and $N=N_\mathcal {O} \cup N_\mathcal {D}$. For this case, the leader–follower scheme is used, in this sense, $N_1=\lbrace \mathcal {O}_2\rbrace$, $N_2=\lbrace \mathcal {D}_3\rbrace$, $N_3=\lbrace \mathcal {D}_4\rbrace$, $N_4=\lbrace \mathcal {O}_5\rbrace$, $N_5=\lbrace \mathcal {O}_6\rbrace$, $N_6=\lbrace \mathcal {D}_7\rbrace$, $N_7=\lbrace \mathcal {D}_8\rbrace$, $N_8=\lbrace \mathcal {O}_9\rbrace$ and $N_9=\lbrace \mathcal {O}_{10}\rbrace$. The motion of the leader is given by the following equations

$$\begin{aligned} \begin{bmatrix} v_{x_{10}}\\ v_{y_{10}} \\ w_{10} \end{bmatrix}=R^{-1} (\theta _{10}) \begin{bmatrix} \dot{x}_d\\ \dot{y}_d \\ \dot{\theta }_d \end{bmatrix}, \end{aligned}$$

where $\dot{x}_d=0.5$, $\dot{y}_d=0.5\cos (0.5t)+0.5$ and $\theta _d=\tan ^{-1}\frac{\dot{y}_d}{\dot{y}_d}$. The initial conditions for the agents are given in Table 1. The desired distances between agents are given by $d_{109}^*=3$[m], $d_{98}^*=0.5$ [m], $d_{87}^*=0.6$ [m], $d_{76}^*=0.52$[m], $d_{65}^*=0.55$ [m], $d_{54}^*=0.7$ [m], $d_{43}^*=0.58$[m], $d_{32}^*=0.65$ [m] and $d_{21}^*=0.53$ [m]; while the desired formation angles are $\alpha _{109}^*=\alpha _{98}^*=\alpha _{87}^*=\alpha _{76}^*=\alpha _{65}^*=\alpha _{54}^*=\alpha _{43}^*=\alpha _{32}^*=\alpha _{21}^*=0$; the desired orientations for the omnidirectional mobile robots are $\theta _1^*=\theta _2$, $\theta _2^*=\theta _3$, $\theta _5^*=\theta _6$, $\theta _6^*=\theta _7$ and $\theta _9^*=-2.535t$, and the time-varying disturbance vector $\varvec{\varsigma }$ is given by the Band-Limited White Noise block form Simulink/Matlab with noise power of 0.00001. The design parameters are given by $K_{{d\alpha }_1}=\mathrm {diag}\lbrace 4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2\rbrace$, $K_{{d\alpha }_2}=8K_{{d\alpha }_1}$, $K_{{\theta }_1}=\mathrm {diag}\lbrace 1,2,1,2,1\rbrace$ and $K_{{\theta }_2}=21.2K_{{\theta }_1}$.

Fig. 2

Trajectory in the plane of the multi-agent system for different time instants where $\mathcal {O}_p$ is the omnidirectional robot while $\mathcal {D}_{\ell }$ is the differential-drive robot

For the first simulation, Fig. 2 describes the trajectory in the plane of the agents for different time instants, using control law (20) and (28), where the follower agents are circumnavigating the leader. The distance among the agents is shown in Fig. 3. Note that the distances $d_{98}$, $d_{87}$, $d_{76}$, $d_{65}$, $d_{54}$, $d_{43}$, $d_{32}$ and $d_{21}$ converge to the desired distance, while the distance $d_{109}$ is oscillating around 3[m]. This is because agent $\mathcal {O}_9$ is the only agent that it is being perturbed by the velocities of the leader. Therefore, based on Proposition 4, the distance error is input-to-state stable with respect to the perturbation $\varvec{\delta }_e$. The formation angle and the orientation error are shown in Fig. 4, where the formation angle $\alpha _{109}$ is oscillating around zero while $\alpha _{98}$, $\alpha _{87}$, $\alpha _{76}$, $\alpha _{65}$, $\alpha _{54}$, $\alpha _{43}$, $\alpha _{32}$ and $\alpha _{21}$ converge to zero. Again, this is because agent $\mathcal {O}_9$ is the only agent that it is being perturbed by the velocities of the leader. On the other hand, the orientation errors $e_{\theta _9}$, $e_{\theta _6}$, $e_{\theta _5}$, $e_{\theta _2}$ and $e_{\theta _1}$ are also oscillating around zero. Figure 5 presents the control inputs for the follower agents, the linear velocity, the lateral velocity and the angular velocity, respectively. Finally, Fig. 6, displays the magnitude of the velocity of each agent. It becomes evident that, to accomplish the circumnavigation task, the followers’ velocity has to be greater than the leaders’ velocity.

Fig. 3

Distance between the leader and the follower agents

Fig. 4

Formation angle and orientation error

Fig. 5

Control inputs for the followers

Fig. 6

Magnitude of the velocity of each agent

For the second simulation, a comparison is made among the proposed Backstepping approach and the approach given by Deghat et al. (2014) and the approach given by Shames et al. (2012). For this case, it is considered that $N=\lbrace \mathcal {O}_1,\mathcal {O}_2\rbrace$. The motion of the leader is the same as in the previous simulation, while the desired distance is $d_{21}^*=2$[m], the desired formation angle is $\alpha _{21}^*=0$ and the desired orientation $\theta _2^*=-2.535t$. Furthermore, the initial conditions for the leader is the same as in the previous case and for the follower are $\begin{bmatrix} x_1(0)&y_1(0)&\theta _1(0)\end{bmatrix}^\top =\begin{bmatrix} -0.65&0&0\end{bmatrix}^\top$. Figure 7 displays the trajectory in the plane of the follower agent circumnavigating the leader agent in different time instants for the three approaches. Note that, while the leader is moving, the follower circumnavigates him. Furthermore, it is important to point out that, when using the Backstepping approach, the follower keeps facing the leader. On the other hand, Fig. 8 illustrates the distance between the leader and the follower using the three approaches. It becomes evident that, when using the proposed Backstepping approach, the distance between agents has oscillations of smaller amplitude compared to the other two approaches. This comes from the fact that when the velocity of the leader increases, the Deghat and Shames approaches failed. Figure 9 shows the orientation error which converge to zero while the formation angle is oscillating around zero as it is stated in Proposition 4. On the other hand, Fig. 10 depicts a comparison of the control inputs for each approach. Finally, Fig. 11 displays the average RMS value of the distance error between the follower and the leader over a suitable receding-horizon time interval of finite length, i.e.

$$\begin{aligned} e_{RMS}(t)=\left( \frac{1}{\varDelta T} \int _{t-\varDelta T} ^t \Vert e_d (\tau ) \Vert ^2 d\tau \right) ^\frac{1}{2}, \end{aligned}$$

where $\varDelta T=2$ is a time window width in which the corresponding signal is evaluated. It becomes clear that the error index for the proposed Backstepping approach decreases to zero faster than the Deghat and Shames approaches.

Based on the previous simulations, it is worth mentioning the following aspects:

• Using the proposed approach, it is easy to add or subtract agents (differential or omnidirectional mobile robots).

• Different communication topologies can be used, i.e. leader–follower, leader centered, or considering a spanning directed tree with root in $R_n$, for all $j>i$.

• Unlike Shames and Deghat approaches, the circumnavigation velocity of the follower agent can be determined in the proposed approach.

• It becomes evident that, when using the proposed approach, the distance between the follower and the leader has oscillations of smaller amplitude than the Deghat and Shames approaches.

• The omnidirectional follower agent keeps looking straight at the leader while circumnavigating him.

Fig. 7

Trajectory in the plane for different time instants

Fig. 8

Distance between the leader and the follower agent

Fig. 9

Orientation error and formation angle

Fig. 10

Control inputs for the follower

Fig. 11

Error index performance

4.2 Real-time experiments

4.2.1 Experimental set-up

The approach is tested using two omnidirectional robots with three omnidirectional wheels and one omnidirectional robot acting as as a differential-drive robot (Fig. 12). The robots are actuated by servomotors Dynamixel^®$\mathrm {AX-12W}$, and controlled by a microcontroller NXP^® model LPC 1768 with Bluetooth communication to a PC computer using the module $HC-05$. In a first step, the position and orientation of the robots are measured by a Vicon^® motion capture system composed by 6 cameras model Bonita^® and 4 cameras model Vero^®. The motion capture measures within an available workspace area of $8 \times 8$ [m]. The control algorithm runs at 117 ms rate with a resolution of $\pm 0.5$ [mm].

Fig. 12

Omnidirectional robots

4.2.2 Leader’s circular trajectory

For the first experiment, a group of three agents is considered, where the leader and the first follower are omnidirectional robots, i.e. $\mathcal {O}_3$ and $\mathcal {O}_2$, respectively, while the second follower is a differential-drive robot $\mathcal {D}_1$. The leader is moving in a circular trajectory with radius of 0.5 [m]. On the other hand, the desired distance between the leader $\mathcal {O}_3$ and the follower $\mathcal {O}_2$ is $d_{32}^*=0.5$ [m], the desired distance between the follower $\mathcal {O}_2$ and the follower $\mathcal {O}_1$ is $d_{21}^*=0.3$ [m]; the desired formation angles are $\alpha _{32}^*=\alpha _{21}^*=0$ and the desired orientation is $\theta _1^*=-t$. The initial conditions for the followers are $\begin{bmatrix} x_1(0)&y_1(0)&\theta _1(0)\end{bmatrix}^\top$ $=$ $\begin{bmatrix} -0.32&0.74&-1.42\end{bmatrix}^\top$ and $\begin{bmatrix} x_2(0)&y_2(0)&\theta _2(0)\end{bmatrix}^\top$ $=$ $\begin{bmatrix} -0.06&0.87&2.44\end{bmatrix}^\top$. The design parameters are given by $K_{\theta _1}=50$, $K_{\theta _2}=0.3$, $K_{{d\alpha }_1}=\mathrm {diag}\lbrace 50,40,50,40\rbrace$ and $K_{{d\alpha }_2}=\mathrm {diag}\lbrace 0.5,0.4,0.5,0.4\rbrace$. The trajectory in the plane of the agents, at different time instants, is described in Fig. 13 where the followers are circumnavigating the leader and taking into account that the followers do not know the leader’s velocities. It is worth mentioning that the transient response from Fig. 13a is omitted to a better visualization of the trajectory. One can watch the video¹ corresponding to this experiment in the link given below. The video shows the performance of two follower robots circumnavigating a leader. The three agents are omnidirectional robots, however, the second follower behaves as a differential-drive robot by cancelling the lateral velocity (Paniagua-Contro et al. 2019). At the beginning, the transient-response becomes evident, nevertheless, the followers are able to reach the steady-state and achieve the circumnavigation task. From Fig. 14 it can be noticed that the distance between $\mathcal {O}_3$ and $\mathcal {O}_2$, and the distance between $\mathcal {O}_2$ and $\mathcal {D}_1$ is oscillating around 0.5[m] and 0.3[m], respectively, as expected by Proposition 4. Furthermore, Fig. 15 displays the formation angles $\alpha _{32}$ and $\alpha _{31}$ as well as the orientation error $e_\theta$, which are oscillating around zero. Finally, the control inputs for the followers are presented in Fig. 16. It becomes evident that in the transient response the control inputs have a high amplitude. Nevertheless, after 40 seconds the system reaches the steady-state.

Fig. 13

Trajectory in the plane of the multi-agent system for different time instants

Fig. 14

Distance between the leader and the follower agent

Fig. 15

Formation angle and orientation error

Fig. 16

Control inputs for the followers

4.2.3 Leader’s free trajectory

In order to prove the effectiveness of our approach, for the second experiment, the leader is moving in a free and random trajectory. The initial conditions are $\begin{bmatrix} x_1(0)&y_1(0)&\theta _1(0)\end{bmatrix}^\top =\begin{bmatrix} -2.35&-0.23&-1.51\end{bmatrix}^\top$. The desired distance, the desired formation angle, the desired orientation and the design parameters are the same as in the previous case. The trajectory in the plane of the agents is shown in Fig. 17. Note that while the leader is moving, the follower is circumnavigating it taking into account that the follower does not know the leader’s velocities. From Fig. 18 it worth noting that the distance between the agents is oscillating around 0.5 [m] as expected by Proposition 4. On the other hand, Fig. 19 illustrates the formation angle and the orientation error which are oscillating around zero. Finally, the control inputs for the follower are presented in Fig. 20.

Remark 6

Recall that there is a singularity when $\alpha _{ji}=\pm \frac{\pi }{2}$. This singularity is avoided in the initial conditions for each robot. However, during the course of the experiment it may pass through that point, but do not stay there.

Fig. 17

Trajectory in the plane of the multi-agent system for different time instants

Fig. 18

Distance between the leader and the follower agent

Fig. 19

Formation angle and orientation error

Fig. 20

Control inputs for the followers

5 Conclusions

This work contributes with the design of a robust control strategy to solve the circumnavigation problem for a heterogeneous multi-agent system composed by omnidirectional and differential-drive mobile robots. The control strategy is designed by means of the Backstepping approach and the kinematic model based on distance and orientation angle between agents. Furthermore, it is worth mentioning the following aspects

• 1. It was proved that the orientation error is input-to-state stable with respect some bounded perturbations.

• 2. The distance error and the formation angle error are also input-to-state stable with respect to the leader’s velocities.

• 3. The proposed control strategy was compared with other similar approaches through numerical simulations. In this sense it is important pointing out the following aspects

  • Using the proposed approach, it is easy to add or subtract agents due to the mathematical analysis is based on matrices.

  • Different communication topologies can be used i.e., leader–follower, leader centered, or considering a spanning tree with root in the leader agent.

  • The circumnavigation velocity of the follower agent can be determined.

  • It is proved that when the velocity of the leader increases, the distance between the follower(s) and the leader has oscillations of smaller amplitude than the Shames and Deghat approaches.

• 4. Real-time experiments, taking into account both omnidirectional and differential-drive robots, exhibit the performance of the proposed approach considering that the leader is moving in a circular trajectory and, then, that is moving in a free random trajectory.

For future work, an observer will be designed to estimate some states of the system as well as implement sensors into the mobile robots. Furthermore, the collision avoidance with Repulsive Vector Fields approach is being studied as well as a control strategy law that switches to avoid singularity $\alpha _{ji}=\pm \frac{\pi }{2}$.