1 Introduction

In a number of practical applications, one or more moving entities need to be continually tracked or kept under a more or less constant observation. For instance, in the case of a search and rescue mission, keeping under observation the rescue agents can help to guarantee their safety and can allow to locally interact with them for coordination purposes. Similarly, in the case of an unwanted intrusion in a surveilled area, once detected, it is necessary to keep the intruders under constant observation in order to effectively trigger and coordinate response actions. In all these cases, using a team of mobile autonomous robots to perform the observation of the moving targets has been shown to be a viable option (Robin and Lacroix 2016; Khan et al. 2016). However, since the robots have limited-range observation sensors and might be less in number compared to the moving targets, they need to implement some form of implicit or explicit coordination in order to effectively perform the observation task. The use of robot teams for multi-target observation has been formalized first by Parker and Emmons (1997), who defined the NP-hard class of problems termed Cooperative Multi-Robot Observation of Multiple Moving Targets (CMOMMT).

In the CMOMMT scenarios studied in the literature, targets are commonly assumed as being evasive or moving according to random patterns. The average number of targets covered by at least one robot during the time span of the mission has been the reference performance metric used to direct the behavior of the robots. Since no distinction is made among the targets being observed, the optimization of this metric can easily result in lack of fairness of monitoring among the different targets, with some targets being observed much more than others.Footnote 1 However, in most of the applications of practical interest, ensuring a balanced coverage among all targets is an important requirement. For instance, in a battle field, all ground troops would equally need to receive aerial support and defense by a team of flying drones. When communication between ground and aerial agents is not permitted, the flying drones have to coordinate to ensure an overall fair monitoring. Similarly, during a search and rescue mission, all the deployed human/animal rescuers would need to be equally covered by a (smaller) team of autonomous robots (e.g., flying or ground ones) employed to both monitor rescuers’ safety status and act as communication relays for them.

In these examples, the provisioning of a fair monitoring among the whole set of targets is an important objective to set over the mission’s time span. In order to effectively achieve such an objective, the motion of the targets needs to be predictable, to some extent. This is to allow the robots to make decisions aimed to intercept a target along its trajectory even when the target does not currently fall under the observation range of any robot. The possibility of obtaining relatively long-term predictions about targets’ future positions is realistic in many scenarios, even if the predictions would be necessarily affected by errors. For instance, in the two examples above, some planning authority needs to be in place to assign the paths to follow and/or the areas to cover for the troops or the rescuers. Even in the case of tracking intruders, who cannot be explicitly controlled, a good guess of where they will move next to could be derived, especially in structured environments. In general, estimates about future target positions can be exploited to obtain an effective and uniform/fair coverage of the targets by the robots. When a completely random motion is assumed, this objective could be difficult or impossible to achieve.

Fig. 1
figure 1

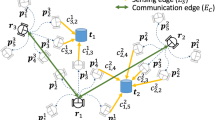
The scenario considered in this paper. Targets and robots move in a bounded environment S, discretized into a set C of cells; \(c_t(a)\) and \(c_t(\omega )\) denote, respectively, the cell in which robot a and target \(\omega \) lie at step t, while \(R(c_t(a))\) denotes the cells currently observed by a. The objective is to compute robots’ paths to ensure a comparable amount of observations among the targets, by leveraging a (generally uncertain) knowledge of their future movements

Full size image

The original contribution of this paper precisely consists in addressing the fairness issue in CMOMMT scenarios (see Fig. 1), providing a mathematical optimization model that extends the original CMOMMT formulation explicitly including the notion of fairness for monitoring the different targets (Sect. 3). For dealing with this new problem, which we refer to as Cooperative Multi-Robot Fair Multi-Target Tracking (CMFMT), the model exploits some knowledge about targets’ motion patterns and accounts for sensing errors in target detection. It employs a Bayesian framework to keep continually up-to-date spatial maps associating to each portion of the environment the probability of being occupied by a moving target in future times (Sect. 6). While the model explicitly exploits the ability to make predictions about targets’ motion, it could be equally employed when the motion is a random walk. The mathematical model is in the form of a multi-objective integer linear program (ILP) (Sect. 4), which is reduced to a single-objective problem whose solution is used to iteratively plan robots’ paths according to a receding horizon approach. The proposed ILP model extends the formulation of the NP-hard Team Orienteering Problem (TOP) (Vansteenwegen et al. 2011).

Both a centralized and a distributed architecture are proposed (Sect. 5). In the first case, all robots send out their status and information about sensed targets to a common data aggregation point, where the path planning problem is solved for the team as a whole. In the distributed case, the robots exchange data over their multi-hop network, and locally use the available information to autonomously solve their own path planning problems, which are computationally much lighter than in the centralized case. Behavior and performance of both the architectures are studied in simulation under a variety of different conditions and constraints (Sect. 7.1). Simulations also show that the proposed approach can outperform other methods, selected from the literature, that explicitly account for fairness in target monitoring. Finally, the approach is validated in a realistic setting using a multirobot system, that confirms the good results obtained in simulation (Sect. 7.2).

An early version of this work has appeared in Banfi et al. (2015). This paper significantly extends those preliminary results with a revised ILP model (now allowing to specify an arbitrary replanning time), a more in-depth discussion of the CMFMT performance metrics and of their correlation with the ILP model, new simulation results and analyses, comparisons with other methods, scenarios with obstacles, and experiments with real robots.

2 Related work

The proposed solution to the CMFMT problem extends existing approaches for CMOMMT, which all derive from the mentioned work by Parker and Emmons (1997). This work can be considered as the forefather of a whole family of highly distributed, highly reactive solutions, where it is possible to rely at most on very short-term predictions of targets’ paths, since they are assumed to move evasively or randomly. Parker (2002) extends her initial work with a new approach called A-CMOMMT, which is based on the use of weighted local force vectors. In Kolling and Carpin (2006), the authors propose a behavioral solution with an algorithm, called B-CMOMMT, that is further improved by Kolling and Carpin (2007). More recently, Elmogy et al. (2012) replace the use of local force vectors with the introduction of a tracking algorithm based on unsupervised extended Kohonen maps. In all these works, the robots keep under observation as many targets as possible, according to their sensing range and to avoid situations where two or more robots remain focused on following the same target. Instead, the approach by Ding et al. (2006) considers uniformity of coverage among the performance metrics, stated in terms of the information entropy of targets’ observations: the algorithm, called P-CMOMMT, heuristically takes into account how much time can be spent in monitoring the same target before a robot may decide to leave it to go in search of another one, but does not exploit possibly available knowledge of targets’ motion patterns, and no belief is maintained about the positions of the last observed targets, which makes it very difficult to perform an effective tracking. We explicitly compare our principled approach for fairness based on ILP against the more heuristic one represented by P-CMOMMT in Sect. 7. In the same section, we also compare our approach to A-CMOMMT.

From a more general perspective, target tracking problems are not limited to CMOMMT scenarios and approaches. For instance, in (Jung and Sukhatme 2006) robots exploit localization algorithms to build probability density functions representing the spatial positions of targets and of their teammates, and move towards regions displaying the lowest ratio between targets and robots. In Luke et al. (2005), the assumption of the limited field of view is relaxed (assuming all the targets’ positions known), and a “tunable” class of tracking algorithms is presented to test the effect of various degrees of decentralization. In Capitan et al. (2013), a scalable multi-agent distributed POMDP (Partially Observable Markov Decision Process) decision framework is introduced and tested in a single-target tracking problem scenario.

Finally, target monitoring problems can also be seen as a special class of task assignment problems, where the goal is to allocate a target to each robot in order to maximize some monitoring performance measure. In this context, Bertuccelli and How (2011) present a multi-objective optimization framework which allows to find the best robot-target allocation according to an uncertain score associated to each target, while, at the same time, reducing the score uncertainty by exploring the environment. While such formulation seems appealing for missions where the score associated to each target is not precisely known but fixed (e.g., the objectives of an aerial strike), it fails to capture the fact that in a uniform target tracking problem each target may have a different score across the time span of the mission, according to how much coverage has already been provided to it.

In order to provide the targets with a balanced coverage, our work requires from the robots the ability of obtaining and maintaining a belief about the targets’ positions in environment, and the capacity to propagate this knowledge among all their teammates involved in the monitoring mission. This, in fact, can be considered an autonomous area of study, whose most recent advances are due to works in the field of probabilistic target search (Bertuccelli and How 2006, 2005; Hu et al. 2013). In general, a common approach is to resort to Bayesian filtering (Thrun et al. 2005) to maintain up-to-date a probability map obtained by the discretization of the environment in cells, while accounting for false-positive and false-negative detection probabilities. We choose to keep the problem of the belief update separate from the CMFMT problem, which is the main focus of our work: our model requires the current targets’ probability maps as parameters, but it can be agnostic about how such maps are actually obtained.

3 Problem formulation

3.1 The original CMOMMT problem

In order to introduce the CMFMT problem, we start by describing a discrete version of the CMOMMT problem based on its continuous version as introduced by Kolling and Carpin (2007) which will be useful in the design of our tracking algorithms. The following set of elements characterize a CMOMMT problem (refer to Fig. 1):

  • A bounded region of interest S (for sake of simplicity, we focus on the 2D case). S is discretized into a set C of equally sized square cells.

  • A mission time duration T, partitioned into a sequence of discrete time steps indexed by \(t=1,\ldots ,T\).

  • A set \(\varOmega \) of targets moving in S, that have to be kept under observation. The cell where target \(\omega \in \varOmega \) lies at time step t is denoted by \(c_{t}(\omega ) \in C\).

  • A set A of robotic agents, that are deployed in S to observe the targets. \(c_{t}(a) \in C\) is the cell where robot \(a \in A\) lies at time step t. C is known to the robots. During each time step, a robot moves within a cell or between adjacent cells, and makes observations. The robots are assumed to be cooperative, meaning that they act as a team, sharing information and possibly coordinating with each other for the achievement of a common utility. This assumes that some communication mechanism is in place. The maximal speed of the robots is higher than that of the targets, to balance the limitation that the targets can outnumber the robots.

  • Each robot is equipped with an omnidirectional sensor for target observation: the sensor serves to detect the presence/absence of a target. The output of the sensor is potentially noisy. When a robot is located at cell c, its sensor range covers an approximately circular subset \(R(c) \subset C\) of the cells, centered in c. A target \(\omega \) is monitored at time t if it lies inside the sensing range of at least one robot. Note that a robot a is aware of monitoring target \(\omega \) at time t if \(c_t(\omega ) \in R(c_t(a))\) and the sensor correctly detects the target.

    At each time step t, the indicator function \(\theta _t\) keeps track of which targets are monitored:

    $$\begin{aligned} \theta _t(\omega )={\left\{ \begin{array}{ll} 1 &{} \text {if } \omega \text { is monitored at } t,\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
    (1)

  • For each target \(\omega \), its detection rate\(\mu (\omega )\) quantifies the fraction of time elapsed under the observation of at least one robot during the mission:

    $$\begin{aligned} \mu (\omega )= \frac{1}{T}\sum _{t=1}^{T} \theta _t(\omega ). \end{aligned}$$
    (2)

  • The objective for the robot team consists in maximizing the average \(\bar{\mu }\) of the detection rate for all targets in \(\varOmega \):

    $$\begin{aligned} \bar{\mu } = \frac{1}{|\varOmega |} \sum _{\omega \in \varOmega } \mu (\omega ). \end{aligned}$$
    (3)

Note that, contrarily to the original (continuous) problem formulation which assumes S to be obstacle-free, in our discrete version the CMOMMT problem we are not making assumptions about the presence/absence of obstacles. Indeed, the presence of obstacles can be modeled in a straightforward way by setting some cells of the set C as obstacles and limiting the robots’ movements and perceptions accordingly, as it is shown in Sect. 4. This allows to flexibly describe real-world scenarios, as well as other scenarios, like pursuit-evasion (Thunberg and Ögren 2011) ones, that are related to CMOMMT.

The discrete problem version just introduced still does not capture the fact that a mission planner may be interested in providing a fair monitoring over the set of the targets. The issues related to the addition of the notion of fairness to the CMOMMT model are discussed in the next two sections, while the formulation of the new CMFMT problem, that addresses the fairness limitation of the original CMOMMT problem, is introduced in Sect. 3.4.

3.2 The need for a predictive model

The CMOMMT model does not assume any knowledge about the number of targets and/or their motion patterns. The robot team is somehow deployed blindly. This is a reasonable assumption for the scenarios in which the CMOMMT problem has been mostly framed so far, in which the targets are considered to be moving evasively or randomly (Ding et al. 2006; Elmogy et al. 2012; Kolling and Carpin 2007, 2006; Parker 2002; Parker and Emmons 1997). In these cases, when a robot detects a target, it tends to keep following it, except when the robot executes stochastic exploration moves or when a new target falls within its sensing range (then the robot can decide which one to keep following). Otherwise, the robot has little incentives to leave the currently observed target to go (blindly) searching for a different, possibly less monitored target to observe. In fact, the robot neither knows whether such a target exists nor where it could be located. However, if we want to enforce a fair monitoring of all targets, a robot needs some reliable information about how many targets are in the field, about their monitoring status, and about where they could be intercepted in the near future. Therefore, in this work we assume that robots have access to such information. More precisely, since in general targets’ motion dynamics can hardly be known with precision, for issuing predictions we assume a probabilistic knowldge. This is in the form of Bayesian belief functions describing current and future positions of the targets. Beliefs are based on some a priori knowldge regarding the motion patterns of the targets and are kept continually updated based on online robot observations, as described in Sect. 6.

3.3 Measuring fairness

In order to quantify how fair is the monitoring performed by the robot team, a number of different choices are possible. In the following we discuss a few of them and provide the rationale behind the specific choice that we adopt in this paper.

The so-called max-min criterion has been employed as a metric to measure fairness in a large number of applications including, for example, communication networks design (Pióro and Medhi 2004). In the CMOMMT scenario, this performance metric would be translated in measuring the minimum detection rate \(\mu (\omega )\) among all targets at the end of the mission: maximizing such value would implicitly results in favoring a solution that balances the detection rate of each target. However, the minimum \(\mu (\omega )\) could be a far too pessimistic indicator for describing the performance of a system encompassing a large number of targets.

Another way of measuring fairness comes from the observation that, if \(|A|<|\varOmega |\), the optimal way of distributing the monitoring effort over the targets would consist in a uniform allocation of the total coverage effort. That is, each target gets monitored for a fraction \(|A|/|\varOmega |\) of time steps of the mission length T. Therefore, the deviation \(|\mu (\omega ) - |A|/|\varOmega ||\) could be used to measure the fairness of coverage of target \(\omega \), upon which deriving classical statistical indicators (average, standard deviation, etc.). However, there are some cases in which the minimization of this performance metric would fail to capture the idea of fairness. This happens, for instance, if some targets are moving close to each other, so that they could fall in the sensing range of a single robot for a number of consecutive time steps. In this case, the optimal way of distributing the monitoring effort should be corrected to take into account such a group of targets. Given the uncertainty about the targets’ motion, this would be a difficult task.

A perhaps more natural fairness performance metric is the standard deviation\(\sigma _\mu \) of the detection rate \(\mu (\omega )\), since a low value of \(\sigma _\mu \) at the end of the mission would imply that all the targets have received a comparably equal amount of observations. However, also the minimization of this performance metric is not completely free from drawbacks since all the solutions in which \(\mu (\omega )\) is the same for each target would be considered optimal. These include also the case where \(\mu (\omega ) = 0, \ \forall \omega \in \varOmega \). This example also points out the need for using a multi-objective approach, to maximize both the fairness measure and the total amount of monitoring.

Similar considerations would hold if, for instance, the information entropy of targets’ observations is used instead of the standard deviation as fairness performance metrics.

Since no fairness performance metric seems to be free from issues, in this work, we choose to use the standard deviation of the detection rate, for its generality and immediateness of interpretation. At the same time, in order to avoid the issues just described above, in the problem formulation we embed the concept of optimizing multiple objectives and the concept of eliminating degenerate optimal solutions, where robots are purposely avoiding targets in order to decrease the standard deviation of targets’ observation rates.

3.4 The CMFMT problem formalized

The Cooperative Multirobot Fair Multitarget Tracking (CMFMT) problem can now be formalized according to what discussed above. We take all the elements listed in Sect. 3.1, and add the following:

  • The number of targets \(|\varOmega |\) is known, and their motion in terms of future positions is known to the robots according to some given uncertainty model.

  • Another objective for the robot team consists in minimizing the fairness\(\sigma _\mu \) of the distribution of the monitoring effort over the targets, which we define as the standard deviation of \(\mu (\omega )\):

    $$\begin{aligned} \sigma _\mu = \sqrt{\frac{1}{|\varOmega |} \sum _{\omega \in \varOmega } \left( \mu (\omega )-\bar{\mu } \right) ^2}\ . \end{aligned}$$
    (4)

    A low value of \(\sigma _{\mu }\) indicates that the monitoring performance is quite equally distributed among the robots, meaning that all targets receive a comparably equal amount of coverage between \(t=1\) and \(t=T\).

The resulting CMFMT optimization problem is a multi-objective problem where the robot team should optimize both \(\bar{\mu }\) (maximize) and \(\sigma _\mu \) (minimize). The goal is thus to maximize the overall monitoring performed while ensuring at the same time that all targets receive a similar (high) amount of monitoring.

4 Optimization model

Tackling a CMFMT problem requires that the plans for the robot team are continually updated or recomputed to account for the movements of both robots and targets, as well as for the uncertainty of the robots observations about the targets. For the moment, let us assume that a centralized entity is in charge of periodically computing a global plan using the most recent observations sent by robots on a perfect (error-free) communication channel. This planning entity has access to a probabilistic model of targets’ motion and, therefore, is able to predict the targets’ future positions in the environment within some level of uncertainty. The aim of this section is to describe how to compute a single team plan: we take a “snapshot” of a generic mission scenario and show how to obtain a new plan for the next h time steps by means of our optimization model. We discuss how the process is iterated over time to make planning happening in stages, as well as the issues of practical implementations of centralized and distributed systems in Sect. 5.

We model the CMFMT problem using an ILP formulation which extends the one of the Team Orienteering Problem (TOP) (Vansteenwegen et al. 2011), a well known NP-hard problem. However, while the TOP features a single problem objective, we employ the linear combination of two objectives, which are potentially conflicting with each other. Moreover, while in classical TOPs the agents are supposed to visit each cell only once to collect the related reward, in our case we must consider the possibility for robots to come back to cells already visited. In fact, a target could walk through a closed-loop path, or could be in a cell previously occupied by a different target. An additional difference is that we associate a time-varying reward to each cell based on probabilistic predictions for targets’ mobility.

A team plan is computed on a directed graph \(G=(N,E)\) encoding the feasible movements of the robots in the environment S according to the cell partitionC: each cell is associated to a node in N, and, in absence of blocked cells representing obstacles, each node is connected to each one of its neighbor cells—4 (Banfi et al. 2017) or 8 (Standley and Korf 2011) according to the chosen multiagent path planning model— by a directed arc in E representing a feasible move. The size of a cell mapped to N is chosen such that the robots are able to traverse an edge in one time step when moving at their typical speed. A team plan is built for a temporal horizon of h steps. A plan for a robot corresponds to a walk on the graph: a sequence of h contiguous cells (including self-loops), that are assumed to be handled as waypoint commands by a lower level navigation controller also in charge of performing reactive collision avoidance.

As introduced in Sect. 3, CMFMT’s goal is to maximize the average cumulative monitoring performance while evenly distributing it among the targets. We propose a planner that considers a finite planning horizon and that uses an objective function consisting of two terms that are defined as linear expressions and that are related to the reference metrics \(\bar{\mu }\) (Eq. (3)) and \(\sigma _\mu \) (Eq. (4)), respectively:

  1. 1.

    A monitoring term M(), that rewards the individual robots for each target they monitor at each time step.

  2. 2.

    A fairness term F(), that rewards the whole team for the number of different targets they monitor for enough time steps: the more different targets monitored for a sufficiently long time, the higher the reward.

The objective function of the proposed ILP will combine these two objectives into a single-objective scalar function of the form \(\alpha M() + (1 - \alpha )F()\), with \(0 \le \alpha \le 1\). Being a linear combination, at the optimum, the two objective values will be located on the Pareto frontier for each value of the parameter \(\alpha \) (Branke et al. 2008).

The notion of “sufficiently long time” for F() is quantified based on the information about the number of targets, \(|\varOmega |\), and the fact that, in general, targets are supposed to be evenly spatially distributed: as introduced in Sect. 3.3, robots are expected to monitor each target for a fraction \(|A|/|\varOmega |\) of the total time when distributing optimally the effort. We consider that a target is monitored long enough if the actual fraction of time steps at which it is monitored is greater than \(\epsilon |A|/|\varOmega |\), where \(\epsilon \ge 0\) sets a threshold value. The threshold \(\epsilon \) needs to be used to adapt the ideal model to account for the following three issues:

  • Traveling times between targets must be taken into account: since robots cannot move instantaneously between two locations, some fraction of the time \(|A|/|\varOmega |\) will be “wasted” while traveling.

  • Predictions of targets’ future positions are in general imperfect: when searching for a currently unseen target, robots may be driven by their beliefs to a region where the target is not present.

  • The typical planning horizonh is shorter than the total mission length T: due to the growth of the complexity of the optimization model, \(|A|/|\varOmega |\) must also be adapted to match the actual number of time steps in which targets are expected to be seen.

By rewarding the team for having different targets monitored for sufficiently long time, we are able to avoid the degenerate optimal solutions described in Sect. 3.3 from the optimal plans. In order to be able to express the fairness objective in the ILP, the minimization of \(\sigma _\mu \), a quadratic function, will be converted in the minimization of a related linear function F().

According to what stated above, let us assume that a centralized entity is computing a global team plan with horizon h at a generic mission time step \(\tau \).Footnote 2 In order to define robots’ legal moves on G in a more rigorous and non-redundant way, we will exploit a support graph \(\widehat{G}=(\widehat{N},\widehat{E})\) built as follows. The set \(\widehat{N}\) is obtained from the original N by removing all the vertices that cannot be reached by any robot within the planning horizon h, while the set \(\widehat{E}\) is given by the set of arcs belonging to the subgraph of G induced by \(\widehat{N}\) augmented with all the possible self-loops. Upon the support graph \(\widehat{G}\), we define the following notation: \(\mathcal {E^\pm }(n)\) are the edges entering(−)/leaving(+) node \(n \in \widehat{N}\); \(N_{t}(a)\) is the subset of nodes reachable by robot a within time t starting from cell \(c_{\tau }(a)\); \(N_{t}\) is the subset of nodes reachable by at least one robot at time t; \(A_{t;n}\) is the subset of robots that can reach node n at time t.

We can now define the first two sets of ILP decision variables:

  • \(x_{t;ij}^a\): binary variables defined for nodes \(i \in N_{t}(a)\) whose value is 1 if and only if (i) robot a goes from node i to node j, with \((i,j) \in \widehat{E}\), between time steps t and \(t+1\), or (ii) robot a goes from node i to node \(j=c_{\tau }(a)\) at \(t=\tau +h\) (these last “virtual arcs” will not be actually traveled by the robots).

  • \(y_{t;n}\): binary variables defined for nodes \(n \in N_{t}\) equal to the number of robots placed at node n at time t, defined for \(t > \tau \). By defining binary variables, we implicitly impose that robots do not share the same cells. A non-zero \(y_{t;n}\) variable allows the team of robots to collect some reward if a target is visible from n at time t.

In the following, we will use \(\mathbf {x},\mathbf {y}\) to denote the sets containing all the corresponding variables. Clearly, we have that \(|\mathbf {x}|=O(h|A||C|)\) and \(|\mathbf {y}|=O(h|C|)\).

Two sets of model parameters are used to guide the robots towards the most promising targets’ locations:

  • \(\pi _{t;n}(\omega )\): this parameter is equal to the probability of seeing target \(\omega \) from node n at time t. For \(t=\tau \), its value can be obtained directly from the current belief, while for \(\tau <t\le \tau + h\) it can be obtained by applying a prediction model on the current belief.

  • \(r_{t;n}\): this parameter is directly proportional to the probability of seeing any target from node n at time t. It can be obtained by collapsing all the \(\pi _{t;n}(\omega )\) in a single parameter.

In Sect. 6 we discuss how we use a Bayesian framework to maintain an up-to-date belief about the targets’ future positions and to make predictions, and, consequently, how to obtain the above parameters for any generic time step t.

To define the last ingredient of our ILP, we introduce two additional sets: \(\varOmega _l^{\tau }(a) \subseteq \varOmega \) and \(\varOmega _{p>0} \subseteq \varOmega \). The first set, \(\varOmega _l^{\tau }(a)\), is composed of those targets that are the last observed ones by robot a at time \(\tau \) (if sensing is not perfect, it is sufficient to check that the probability of having the target within robot a’s sensing range is above a high threshold at \(\tau \)). The second set, \(\varOmega _{p>0}\), contains all the targets for which a non-zero observation probability can be collected (by any robot) along the planning horizon h. We can now define the set \(\varOmega _{\tau } \subseteq \varOmega \) as:

$$\begin{aligned} \varOmega _{\tau } = \varOmega _{p>0}{\setminus }\cup _{a \in A}\varOmega _l^{\tau }(a). \end{aligned}$$
(5)

Intuitively, \(\varOmega _{\tau }\) represents the set of all the targets that will be able to contribute to the optimization of the fairness term in the objective function if observed in the new plan. For each target \(\omega \) in \(\varOmega _{\tau }\), we define \(\mu _{\tau }(\omega )\) as its detection rate up to time \(\tau \), and introduce a new binary variable \(u^{\omega }\) taking value 1 if and only if \(\omega \) is expected to be monitored for enough time steps (at least \(\epsilon |A|/|\varOmega _{\tau }|\)) during the plan execution.

Based on all the above definitions, the two components of the objective function are defined as follows:

$$\begin{aligned}&M(\tau ,h,\mathbf {y})=\frac{1-\gamma }{1-\gamma ^h}\frac{1}{|A|}\sum _{t=\tau +1}^{\tau +h} \left( \gamma ^{t-\tau -1} \sum _{n\in N_{t}}r_{t;n}y_{t;n} \right) \nonumber \\ \end{aligned}$$
(6)
$$\begin{aligned}&F(\tau ,h,\mathbf {u})=\frac{\sum _{\omega \in \varOmega _\tau } \left( 1- \mu _{\tau }(\omega ) \right) u^{\omega } }{\sum _{\omega \in \varOmega _\tau }(1- \mu _{\tau }(\omega ))}, \end{aligned}$$
(7)

where each term is normalized to have a value in [0, 1]. \(M(\tau ,h,\mathbf {y})\) and \(F(\tau ,h,\mathbf {u})\) are, respectively, the monitoring performance and the fairness performance collected between \(t=\tau \) and \(t=\tau +h\). In Eq. (6), \(\gamma \in (0,1)\) is a discount factor that confers greater importance to decisions happening earlier in the plan because of the increasing uncertainty of future events. In Eq. (7), since plans are issued over a limited time horizon \(h < T\), the terms are weighted by \(1- \mu _{\tau }(\omega )\) to take into account the history and give more reward to the monitoring of targets that have been monitored less in the past. Without it, when the path horizon is short, i.e., \(h\ll T\), it would not be possible to obtain an even distribution of the monitoring performance over \(\{1,2,\ldots ,T\}\).

The complete ILP model for the CMFMT problem at time \(\tau \) and for a time horizon of h steps is the following:

$$\begin{aligned}&\displaystyle \text {maximize}_{\mathbf {x},\mathbf {y},\mathbf {u}} \quad \alpha M(\tau ,h,\mathbf {y}) + (1-\alpha ) F(\tau ,h,\mathbf {u}) \end{aligned}$$
(8)
$$\begin{aligned}&\begin{array}{ll} \text {subject to } &{} \\ \displaystyle \sum _{\begin{array}{c} (i,j)\in \mathcal {E}^{-}(n) \text { s.t.} \\ i \in N_{t-1}(a) \end{array}} x_{t-1;ij}^a = \sum _{(i,j)\in \mathcal {E}^{+}(n)} x_{t;ij}^a \\ \qquad \forall \, a\in A,\quad n\in N_{t}(a), \quad \tau < t \le \tau +h \end{array} \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \sum _{(i,j)\in \mathcal {E}^{+}(c_\tau (a))} x_{\tau ;ij}^a = \sum _{(i,j)\in \mathcal {E}^{-}(c_\tau (a))} x_{\tau +h;ij}^a=1 \qquad \qquad \forall \, a\in A \end{aligned}$$
(10)
$$\begin{aligned}&\begin{array}{ll} \displaystyle \sum _{a \in A_{t;n}} \sum _{(i,j)\in \mathcal {E}^{+}(n)} x_{t;ij}^a = y_{t;n}&\qquad \qquad \forall n \in N_{t},\quad \tau < t \le \tau +h \end{array} \end{aligned}$$
(11)
$$\begin{aligned}&\displaystyle \sum \limits _{{t=\tau +1}}^{\tau +h}\gamma ^{t-\tau -1}\sum \limits _{{n\in N_{t}}} y_{t;n} \pi _{t;n}(\omega ) \ge \epsilon \frac{|A| (1-\gamma ^h)}{|\varOmega _{\tau }|(1-\gamma )} u^{\omega } \qquad \quad \forall \, \omega \in \varOmega _{\tau } \end{aligned}$$
(12)

where \(\alpha \in [0,1], \gamma \in (0,1), \epsilon \in (0,\infty )\), \(h\in \{1,2,\ldots ,T\}\) are parameters.

For each robot a, constraints (9) ensure path feasibility. The robots travel along one edge at a time, therefore, for each time step t there can be only a single variable \(x_{t;ij}^a\) set to 1 among all the possible (a, ij) combinations (the number of these constraints is bounded by O(h|A||C|)). Constraints (10) enforce that a path starts at the current robot’s position and forms a closed loop (as typically done in expressing the TOP, see Vansteenwegen et al. 2011). Constraints (11) define the relationship between \(y_{t;n}\) and \(x_{t;ij}^a\) variables: the number of robots at a node equals the number of robots that have been traveling to it from the previous time step (the number of these constraints is bounded by O(h|C|)). Constraints (12), along with the maximization of the objective function, activate the \(u^{\omega }\) variables when the corresponding target \(\omega \) is receiving an adequate monitoring during the current plan. The amount of expected monitoring of a target is defined as the sum of the probabilities of seeing target \(\omega \). Once it goes over the assigned threshold \(\{\epsilon |A|(1-\gamma ^h)\}/\{(1-\gamma )|\varOmega _\tau |\}\), the corresponding variable \(u^\omega \) is allowed to be 1 and increases the objective in Eq. (7). Note, in the fraction on the right-hand side of Eq. (12), the use of \(\varOmega _\tau \) instead of \(\varOmega \) to accommodate the model with a planning horizon \(h<T\). Parameter \(\epsilon \) regulates which fraction of the expected maximal monitoring time is needed to consider that the target got enough attention. We account for the uncertainty of future events by discounting future terms with \(\gamma \).

The objective function in Eq. (8) is a weighted sum of two terms. The first term pushes the robots towards cells that have higher probability of hosting targets. The second term adds a reward for each newly monitored target, pushing the system to evenly distribute the monitoring effort over them. From this second term, we exclude the additional reward for the last monitored targets (recall Eq. (5)) for the following reason. Consider a situation in which a new plan is computed at a time \(\tau \) at which a robot is in the middle of a travel between two different targets with no “memory” of the last monitored target: the optimal solution could push the robot to return to the same target it was trying to leave, thus obtaining undesired “cyclic” behaviors.

The trade-off between the two objectives should be tuned according to the mission goal: provide a continuous monitoring of the currently located targets (\(\alpha \rightarrow 1\)), or prefer a more exploratory strategy that could allow to monitor more targets, equally distributing the observations among them (\(\alpha \rightarrow 0\)).

Finally, note that a variation of the above ILP model could in principle be able to take collision avoidance constraints into account, but at the expenses of an increase in the model complexity; see Yu and LaValle (2016), Banfi et al. (2017).

5 CMFMT: system implementation

In the previous section, we have presented an optimization model for the CMFMT problem. In order to ease the presentation, we assumed the presence of a centralized entity capable of coordinating the team actions. However, its operational model was left unspecified. The aim of this section is to present a centralized and a distributed architecture of a fair multitarget tracking system making use of the ILP above, by first discussing how, in general, plans can be operatively devised, executed, and iteratively adapted according to the most recent observations.

5.1 General operational model

Regardless of the particular architecture (i.e., centralized or distributed), the overall operational model of the robot system can be described in terms of the four high-level macro-steps depicted in Fig. 2.

Fig. 2
figure 2

Image taken from Banfi et al. (2015)

The operational model of the robot system 

Full size image

The first notion to introduce regards how the robots can issue predictions about targets’ positions in order to effectively intercept them. As pointed out in the previous sections, we assume that the robots have at hand some probabilistic model of targets’ motions. Therefore, based on actual targets’ observations obtained through on-board sensors and on messages exchanged with other robots and/or a centralized entity, each robot \(a\in A\) has access to a probabilistic belief about the expected positions of all the targets.

Given that the overall CMFMT mission starts at time 1 and ends at time T, periodically, at time steps \(\tau =1,1+\varDelta ,1+2\varDelta , \ldots \), the probabilistic knowledge from the belief functions is used by the planner to plan the movements of the robots for the next \(h\ge \varDelta \) steps. Planning, therefore, happens in stages, where, at each stage, the assigned time horizon for planning corresponds to h time steps, implementing in this way a receding horizon control. While executing a plan, a robot makes observations about the targets. These observations are used to update the beliefs about targets’ positions. In turn, the new beliefs are used to make predictions about future positions of targets, which are needed for planning. In general, in presence of errors and uncertainty, new plans should be computed at each time step (\(\varDelta =1\)), to continuously adapt the plan to the most recent observations made by the robots. However, in practice, such a high replanning frequency could not be affordable, due to, e.g., timing constraints (like when in the time discretization of the mission a time step corresponds only to a fraction of a second), or power-consumption constraints. As we show in Sect. 7, a high replanning frequency might not actually be needed when in presence of moderate uncertainty. Also different solutions, not investigated in this paper, could be devised if needed to adapt the current plan to the most recent observations. For instance, new plans could be computed only every \(\varDelta =h\) steps, while suitable ad hoc behaviors would be in charge of taking over when the computed plan shows too many discrepancies w.r.t. the observed events.

5.2 Centralized planner

The operational mechanisms described in the previous section have been implemented first according to a centralized computational architecture, and then a distributed model has been derived. In the centralized case, a single planner jointly computes the paths for all the robots of the team. The robots share with the planner all their observations. The planner fuses them together to keep up-to-date an aggregated belief. For sake of simplicity, communications between planner and robots are assumed to be lossless and instantaneous. Specifically, the information that robots send to the centralized planner comprises the observations they take at each time step t and their current locations at t.

The computation to obtain the optimal solution, or even a solution with a few percent of ILP gap from the optimal solution, can require a large amount of time in large scenarios. Therefore, the centralized model mainly serves to provide an optimal performance baseline to evaluate distributed solutions for more realistic real-time implementations.

5.3 Distributed independent planners

Following a top-down approach, the distributed architecture is derived directly from the centralized one, by devising a simple yet effective distribution design of the system. In this case, each robot maintains its own belief about the targets’ positions, and plans its own path independently. We assume that neighboring robots are able to reliably communicate within a given communication range \(r_c\), but that no global coordination and communication infrastructure is present.

Robots exchange information about their recent history of observations and their current path plans. More precisely, robots receive both the information sent by direct neighbors (i.e., those within the communication range) and that relayed through the multi-hop network formed by a chain of neighboring robots. Observations are exchanged in the form of time-stamped sensor readings (discussed Sect. 6), so that each robot can keep up-to-date its own belief based not only on its own observations, but also on those of its teammates, in a transparent manner.

For what concerns planning, each robot, according to a fixed priority, computes a plan for itself. The main difference against the centralized approach is that each robot uses the information about the current plan of other robots \(\bar{a}\) that have already computed their new plans to fix the related variables in the ILP (i.e., their \(x_{ij t}^{\bar{a}}\) variables become constants). Robots within communication range, but that have not yet computed a new plan, are momentarily assumed to remain still at their current positions. In this way, the robot takes into account future movements of robots in the surroundings, but it does not plan for them. This dramatically reduces the complexity of the ILP to solve, since in each ILP model to solve we have now that \(|\mathbf {x}|=O(h|C|)\). Note that this planning scheme requires that the computation of new plans and their execution is synchronized at each step.

The distributed model requires less communication infrastructure and solves the ILP much faster. We compare computational costs and performance of the central and distributed architectures in Sect. 7, and we empirically show that the advantages of the distributed approach come at the expenses of only a small decrease in performance. This is related to the fact that, in general, the impact of long-distance interactions is expected to be relatively small in the considered scenarios (as it often happens in cooperative multiagent pathfinding problems; see, e.g., Silver 2005).

6 Update the belief about targets’ positions

In this section, we discuss the robots’ sensing model and the Bayesian framework used for updating the belief and predicting future targets’ positions. Without loss of generality, we focus on the distributed case.

For each robot \(a\in A\), the sensor output, \(z_{t}^{a}(\omega )\), is represented as a binary array: for each cell in the field of view \(R(c_t(a))\) the sensor output contains a Boolean value indicating whether target \(\omega \) was detected or not at time t. As said, in presence of obstacles, the field of view excludes cells that are occluded and, thus, not visible. This sensing information is used by the robots to continuously update their beliefs about targets’ positions. In particular, for each different target \(\omega \in \varOmega \), the belief function \(b(t, c;\omega )\) quantifies the probability that the robot assigns to the event that \(\omega \) is in cell c at time t after having taken into account \(\omega \)’s observation history from the beginning of the mission. For simplicity, we consider a synchronous setting, where the sensing events of each member of the team take place at the same discrete time step t.

To consistently maintain up-to-date the targets’ belief functions (also taking into account possible false positives and/or negatives in the sensor outputs \(z_{t}^{a}(\omega )\)), we employ standard Bayesian filtering (e.g., see Thrun et al. 2005). In particular, the prior about the targets’ motion is modeled as a Markov chain, where the state transition matrix expresses the probability that a given target will move from one cell to another during one time step. The robots integrate such a prior with their observations and, possibly, with those received from their teammates currently in communication.

At each step, the robots can use the targets’ belief functions to obtain the model parameters \(\pi _{t;n}(w)\) and \(r_{t;n}\) (introduced in Sect. 4) as follows. At any planning step, a robot uses its current beliefs to predict the future positions of all targets over the time horizon \(\{\tau +1,\ldots ,\tau +h\}\) by recursively applying the targets’ motion model prior. In particular, a robot a estimates the probability \(\pi \) that, if it would move to node n at time t, target \(\omega \) would fall within its field of view:

$$\begin{aligned} \pi _{t;n}(\omega )=\sum \limits _{{c \in R(n)}} b(t,c;\omega ). \end{aligned}$$

Since the planner aims at selecting paths that let the robots intercept targets, it is necessary to express how good, in terms of optimizing system’s monitoring and fairness performance, it would be for a robot a to be in a specific node n at a future time t. Based on the current beliefs, we quantify this by defining the total expected reward \(r_{t;n}\) that a robot would collect at node n at time t for monitoring the targets:

$$\begin{aligned} r_{t;n}=\sum _{\omega \in \varOmega } \frac{ \sum _{c \in R(n)} \rho (c,n) b(t,c;\omega ) }{\sum _{c \in R(n)} \rho (c,n)}. \end{aligned}$$

In the equation, the cells c are those that belong to the field of view R(n) of the robot once in n. The reward is additively computed over all these cells based on the strength of the belief that a target would be located in any of these cells. A sum over all the elements in \(\varOmega \) is performed to account for the presence of any of the targets. Since a robot with a realistic sensor benefits by getting closer to a target, even if the target is already visible, the weights \(\rho (c,n)\) are introduced to reward such proximity. In practice the weights \(\rho \) are an assigned convolution mask that depends on the distance between c and n and that increases the rewards collected at cells close to the believed target position. The introduction of such weights makes it possible to avoid situations where the same target is followed by two or more robots, since every robot except that closest to the target is penalized by not following it from the optimal position.

7 Experimental results

7.1 Experiments in simulation

In order to perform replicable tests under controlled conditions, as well as to study the behavior of the proposed planning approach independently of any particular robotic platform, we start by evaluating the performance of our multirobot system in simulation. Here, robots and targets can move in a square gridworld of a given number of cells at each (discrete) time step. Paths are planned on 8-connected grid graphs.

At the start of each simulation run, we randomly choose a different piecewise-linear closed path (having width of a single cell) for each target to follow during the run. Targets are initially randomly positioned along their trajectories and move at constant speed. Robots use target motion predictors that assign non-zero probability to contain the target to the “nominal” cell along the target path (that is, the cell that the target would reach when moving at its nominal speed) and to its neighbors. In practice, this means that a convolution along the target path with a 3-cell long convolutional kernel is performed. Clearly, in case of perfect prediction, we put probability 1 on a single cell.

All the ILP models have been solved using the GUROBI solver (v.6.0.5)  (Gurobi Optimization 2014). In order to cope with possible “difficult” models resulting from the centralized implementation, we consider the models to be solved optimally with a relative MIP gap tolerance of \(3\%\) and, in any case, after a 20 minutes deadline. Due to the online nature of the problem, we argue that the performance resulting from these approximations would be in line with that obtained with smaller gaps. We use 8 Intel Xeon e312xx processors and 8 GB of RAM.

We start by evaluating the performance of the centralized implementation. Then, we compare the centralized implementation, the distributed implementation, the A-CMOMMT algorithm (Parker 2002), and the P-CMOMMT algorithm (Ding et al. 2006). The last two strategies are both based on local force vectors, but only with P-CMOMMT a robot may decide to leave a currently observed target if the latter has been continuously observed for too many steps. In this sense, P-CMOMMT represents a heuristic way to introduce fairness in cooperative target tracking. Finally, we test the distributed implementation in realistic scenarios with limited communication range, uncertain predictions, and the possibility of sensing affected by false negatives, also against A-CMOMMT.

Fig. 3
figure 3

Monitoring \(\bar{\mu }\) (red) and fairness \(\sigma _\mu \) (blue) performance of the centralized approach as a function of the main ILP parameters. a Varying \(\epsilon \), \(\alpha =0.5\), b varying \(\alpha \), \(\epsilon =0.3\) (Color figure online)

Full size image

The following parameters are kept fixed in all experiments: environment dimension (C is composed of 80 cells \(\times \) 80 cells); target speed (1 cell/time step), number of targets (15), robot speed (2 cells/time step), robot sensing range (6 cells \(\times \) 6 cells), robot sensing rate (1 observation/time step), planning horizon \(h = 10\) time steps, duration of a run T (300 time steps), number of runs for each scenario (5), \(\gamma \) (0.99). The size of the environment is about half of the one used by Kolling and Carpin (2007), in order to be able to achieve a significant planning horizon even in the centralized case; the robot/target ratios are comparable to the majority of the experiments reported in the literature.

Fig. 4
figure 4

Comparison of the four algorithms (ILP-Centralized, ILP-Distributed, A-CMOMMT, P-CMOMMT) with perfect sensing and prediction. a Monitoring performance, b fairness performance, c planning time

Full size image

Performance of the ILP planning model We study the effectiveness of the ILP planning model in terms of monitoring and fairness by considering a centralized implementation and a team of 5 robots. We assume global perfect sensing, full communication, and perfect predictions of the targets future positions. Therefore, we can safely set \(\varDelta =h\). Considering a balanced setting in which \(\alpha =0.5\), we examine in Fig. 3a the impact of choosing different values for \(\epsilon \) (the parameter that controls the fraction of the time needed to consider that the target got enough attention). We discover that good values lie in the range between 0.1 and 1.0, since with \(\epsilon =0.0\) robots receive the fairness reward for a target even without observing it, while larger values impose an excessive effort for collecting such a reward. Fixing \(\epsilon \) to 0.3, Fig. 3b shows how our ILP model can be effectively used to plan tracking missions capable of trading off between the monitoring and the fairness performance. For \(\alpha =0.0\) the highest fairness is achieved, but at the expenses of poor tracking performance. This is due to the fact that each optimal set of paths could prescribe to visit as many targets as possible, but possibly for a single time step, since we are completely neglecting the optimization of the monitoring performance. With \(0.1 \le \alpha < 1\), instead, we see how no solution fully dominates the other, and that the region of values 0.5–1.0 seems more sensitive to parameter changes as far as the fairness performance is concerned. In the following experiments, we keep fixed \(\alpha =0.5\) and \(\epsilon =0.3\), which represent a balanced trade-off that guarantees a fair coverage with a nearly optimal monitoring performance, and that showed to perform well in preliminary experiments also considering uncertainty in predictions and sensing errors.

Centralized versus distributed implementation We compare the centralized and the distributed implementations to quantify the performance loss when distributing the planning. These two strategies are compared against A-CMOMMT and P-CMOMMT. Again, we assume perfect sensing, full communication, and perfect prediction of targets’ future positions. Fig. 4a–b show, respectively, the monitoring and fairness performance of the four tracking strategies for a varying number of robots. While the monitoring performance is always close to the optimal one except for P-CMOMMT, the fairness performance is better optimized by the latter and by our approach. This suggests that our principled approach is more effective in trading-off between monitoring and fairness than heuristic approaches. In particular, the centralized planner outperforms the distributed one (according to both metrics) only for a large number of robots. This is easily explained by observing that, with a low number of robots, the impact of locally sub-optimal decisions is mitigated by the fact that, in a single planning horizon, robots are expected to display only a few conflicts on the responsibility of optimally tracking a given target. Also, note that even the distributed planner outperforms P-CMOMMT in both the performance metrics (except for 13 robots). Fig. 4c compares the time required by the solver to obtain a plan when using the centralized and the distributed version of the ILP model. It is clear that the computational cost of the distributed planner is much lower (and manageable on real robots) than the cost required by the centralized planner, which also shows a very high variability. Overall, the distributed approach performs close to the centralized one, but with a lower computational effort.

Real-world limitations In the final set of experiments, we move to more realistic practical settings in which the robots have to deal with limited communication ranges, uncertainty in the prediction of targets’ motion, sensing errors, and the presence of obstacles. Recall that we specify uncertainty in terms of a 3-cells long convolutional kernel that spreads the current probability of seeing the target along its predefined trajectory. In this set of experiments, we define the kernel to be a vector of the type \(\langle \nu , 1-2\nu ,\nu \rangle \), where \(1 - 2\nu \) represents the probability that the target will move in the “nominal” cell of the corresponding motion model, and \(\nu \) represents the probability of moving in the cell before or after the nominal one. The number of robots is kept fixed to 5.

Fig. 5
figure 5

Performance of the distributed approach for varying replanning time and communication range. a Varying \(\varDelta \), \(\nu =0.2\), range 20 cells; b varying range, \(\varDelta =3\), \(\nu =0.2\); c varying range, \(\varDelta =5\), \(\nu =0.2\); d varying range, A-CMOMMT and P-CMOMMT. Note that the graphs in b–d have the same scale on y-axis to ease comparison between our distributed approach, A-CMOMMT, and P-CMOMMT

Full size image
Fig. 6
figure 6

Performance of the distributed approach under uncertainty and sensing errors. a Varying uncertainty \(\nu \), perfect sensing; b varying false negative probability, \(\nu =0.2\); c varying uncertainty \(\nu \) with high false negative probability (0.9); d varying number of obstacles, \(\nu =0.2\), perfect sensing (but limited by obstacles)

Full size image

First, we study the effect of choosing different replanning times and the impact of larger communication ranges on the performance of our distributed approach. Fig. 5a shows the results obtained while varying the replanning time \(\varDelta \) while keeping fixed a medium communication range (20 cells), a medium degree of uncertainty (\(\nu =0.2\)), and perfect sensing. We observe that the impact of choosing a high replanning time is modest in the considered scenario: the monitoring performance decreases slightly, due to the fact that robots are not updating their plans according to their most recent observations. However, even with \(\varDelta =10\), we can obtain good performance. This is explained by the moderate source of uncertainty of the current setting, combined with perfect sensing. In Fig. 5b, c we investigate now the impact of adopting different communication ranges for \(\varDelta =3\) and \(\varDelta =5\), respectively (again, with \(\nu =0.2\)). In both cases, we observe that a communication range able to span the whole planning horizon (recall that \(h=10\) with robot speed of 2 cells/time step) is enough to ensure the best performance. Indeed, shorter communication ranges can easily lead to suboptimal solutions where two different robots decide to go after the same target at the last time steps of the plan. The impact of a larger communication range, instead, is effectively reduced by constant multi-hop information sharing. It is clear that, compared against A-CMOMMT and P-CMOMMT (Fig. 5d), our approach offers dramatically better fairness performance against the former, and moderately, but still significant, better performance than the latter.

Then, we consider scenarios with varying uncertainty and false negative probability in the sensing events. In particular, we assume perfect sensing while varying the former, and fix \(\nu =0.2\) while varying the latter. We fix the communication range to 20 cells and \(\varDelta =3\). The results are shown in Fig. 6a–c. In Fig. 6a, we notice that the increase in uncertainty does not have a strong impact on any of the performance metrics for our distributed approach. While the monitoring performance remains substantially similar, we can start to observe a significant variation in the fairness performance only for high values of \(\nu \) (0.3,0.4). Such a good behavior of our approach is easily explained by the combination of multiple factors: a sufficient communication range, frequent replanning, perfect sensing, and a low value for \(\epsilon \) (a value too high would excessively constrain robots’ paths to remain focused on searching a target in the wrong place). Similarly, a moderate source of uncertainty gives rise to a similar performance trend while varying the probability of false negatives (see Fig. 6b). In Fig. 6c we show the results obtained while keeping fixed a high false negative probability (0.9) and varying the uncertainty. This time, we observe that the tracking performance significantly decreases for high values of \(\nu \). Indeed, when uncertainty is high, only a sufficient sensing detection rate would allow a robot that has located a target to keep it under its sensing range.

Finally, we consider more complex environments in which the presence of obstacles constrains robots’ movements and sensing. In particular, we run experiments with a varying number of rectangular obstacles with size \(4 \times 20\) cells (randomly distributed in the environment), assuming that sensing has no errors, but is limited by obstacles, and setting \(\nu =0.2\) for the uncertainty. The results for different numbers of obstacles are shown in Fig. 6d. We can notice that, while the monitoring performance remains substantially the same, an increasing number of obstacles negatively impacts on the variability of the fairness performance. Since paths are more constrained, the robots may not find anymore convenient to leave the currently monitored target, because the planning horizon may not be large enough to allow to collect the fairness bonus in the ILP model.

7.2 Experiments with real robots

We have set up a small-scale indoor scenario to study the behavior of the developed distributed model under the effect of real multi-hop communications and real robot mobility. As robotic platform we have used the foot-bot, a small differential drive robot (about 15 cm wide and 20 cm high). A total of 9 foot-bots have been placed in a test arena of \(7\times 7\) m\(^2\), with some of the foot-bots playing the role of targets and others playing the role of trackers.

Fig. 7
figure 7

The foot-bot robotic platform. Note the wireless interface card with the signal attenuator used for experiments with multi-hop data transmission

Full size image

Since the foot-bots have minimal on-board processing power, plan computation is performed at a central desktop computer according to the distributed model described before and based on local robot data. To this aim, each foot-bot is equipped with two radio interfaces. An 802.11 based network operating on the 5 GHz band allows the communication between the desktop computer and the foot-bots. Each robot uses this network to request the solution to its ILP model and to obtain back the new plan. A second wireless interface is used as data network, to exchange data among the robots in a multi-hop way as described in Sect. 5.3. The data network operates in the 2.4 GHz band and its transmission power is artificially constrained in order to enforce the use of multi-hop routes in the used indoor arena. To this end, we use TL-WN722N Wi-Fi adapters with attenuators attached between the adapter and their external antennas. Setting a transmission power of 1 mW, a bit rate of 54 Mbps, and a signal attenuator of 20 dBm, the resulting wireless transmission range is approximately 1.5 m. This implies a maximum of about 5 hops in the robot mobile ad hoc network. A picture of one of the foot-bot robots used in the experiments is shown in Fig. 7. The robots can move at a maximum speed of 0.3 m/s. For each robot, an on-board controller enables it to navigate autonomously towards any point in the area (according to the plan) while avoiding collisions (Guzzi et al. 2013). An OptiTrack motion capture system provides the low level controllers with positional information (the 5 GHz network is used to broadcast robot positions).

We ran a limited set of experiments, following the general settings of the more extensive experimental campaign performed in simulation. In this case, we discretized the environment in cells of 15 cm \(\times 15\) cm, and chose 5 seconds as basic time step unit. (Robot and targets’ speeds are again set to 2 and 1 cell/step, respectively.) For what concerns the motion model, compared with the simulations, we had to take into account also the source of uncertainty given by the fact that the targets cannot be anymore expected to move along the nominal cells of their predefined trajectory. Therefore, motion prediction happens now in two stages. First, we use the same three-cells long convolutional kernel to obtain a “nominal” prediction (with \(\nu =0.2\)); then, we “smooth” the obtained probability density function so that a small fraction of the probability is assigned to the neighboring cells of the nominal trajectory. For what concerns the remaining parameters, we set \(h=7\) and \(\varDelta =4\).

We considered two scenarios: in one case there are 2 trackers and 5 targets, while the other case features 6 targets and 3 trackers. Fig. 8 shows the results obtained for both the tested configurations while varying the \(\alpha \) parameter of the model objective function. The results confirm what has been observed in simulation, that our ILP-based approach is effectively able to offer a good trade-off between monitoring and fairness by a suitable choice of the \(\alpha \) parameter.

Compared to the simulation results, we observe a higher variability in the two performance metrics, especially in the fairness one. This is explained by the fact that, in our small-scale environment, the robots have to deviate very frequently from the “nominal” high-level plans computed by the ILP model, which does not take into account low-level collision avoidance constraints. For the same reason, the monitoring performance in a run with \(\alpha =1.0\) can be slightly less than the ideal one (\(|A|/|\varOmega |\)). In particular, we noticed that, quite frequently, two robots might start to follow the same target after having remained “stuck” in a particularly congested situation with the two targets that the robots were initially trying to follow. In this case, the first target able to leave the congestion and go back to its original path is often able to “escape” from both the robots’ field of view.

Fig. 8
figure 8

Performance obtained in real robots experiments by varying the \(\alpha \) parameter. a 2 robots, 5 targets, b 3 robots, 6 targets

Full size image

8 Conclusions and future work

We presented an extension of the Cooperative Multi-Robot Observation of Multiple Moving Targets problem which includes the notion of fairness for monitoring the different targets. The proposed solution for this new problem, which we called the Cooperative Multirobot Fair Multitarget Tracking problem, is based on the formulation and use of an ILP model to iteratively plan the robots’ paths, and has been implemented following both a centralized and a distributed approach according to a receding horizon model.

Simulations have shown that our model is able to guarantee a tunable monitoring strategy (i.e., in which robots stay focused on their current targets or exhibit a more exploratory behavior) and to obtain a uniform monitoring of the targets by exploiting different degrees of knowledge of the targets’ motion patterns. With respect to the centralized system, the distributed one shows very limited reduction in performance, while it brings significant advantages, dramatically reducing the needs for computational and communication resources. Moreover, our approach reaches a better balance between monitoring and fairness than heuristic approaches from the literature. The experimental validation on real robots confirmed the good results obtained in simulation.

Since the proposed strategy is based on an ILP model, in general we cannot expect that the (centralized) approach is able to scale to very large environments and/or arbitrary long planning horizons. However, the distributed version is expected to really suffer from these issues only in “extreme” scenarios. In the perspective of supporting scalability also in such challenging situations, as a future research we envision the study of behavioral strategies, possibly coupled with a smart partitioning of the environment between robots. The goal will be to guarantee good performance with short/bounded planning times. It would be also interesting to investigate alternative formulations for fair multitarget tracking based on Partially Observable Markov Decision Processes and to study more complex models for the behavior of the targets and for dealing with them, for instance using anticipatory planning (Mercier and Van Hentenryck 2007).