Retrograde co-orbital orbits in the Earth–Moon system: planar stability region under solar gravitational perturbation

Abstract

This paper explores a stability region near the $1:1$ retrograde resonance with the Moon in the planar bicircular restricted four-body problem. We find, in addition to lunar distant retrograde orbits and Trojan orbits around the triangular equilibria, another co-orbital stability region in the Earth–Moon system under solar gravitational perturbations. We identify three families of periodic orbits that could be the possible origin of the stability region. As an application, ballistic capture trajectories into the stability region from the vicinity of the Earth or interplanetary space are computed with the aid of the symmetry of the model. We reveal trade-offs among time-of-flights, characteristic energies, and lunar flyby altitudes for the ballistic capture trajectories.

1 Introduction

Long-term stability regions in space have attracted interests due to their importance in celestial mechanics and astrodynamics. Stability regions are natural candidates for holding small objects such as asteroids, comets, meteoroids, and dust particles. The triangular libration points possess Trojan asteroids widely in the Solar System (Murray and Dermott 1999; Stacey and Connors 2008; Connors et al. 2011), and may trap dust particles even in the Earth–Moon system (Kordylewski 1961; Slíz-Balogh et al. 2018, 2019). Distant retrograde orbits (or quasi-satellite orbits, DRO/QSOs) also offer stability regions capturing small objects (Mikkola et al. 2006; Kinoshita and Nakai 2007; Kortenkamp 2013). Trojan orbits and DRO/QSOs can be useful for engineering purposes including the robust parking of a spacecraft around planetary moons (Lam and Whiffen 2005; Lara et al. 2007) and the long-term storage of natural objects for subsequent explorations (Strange et al. 2013; Bezrouk and Parker 2017; Tan et al. 2017). Trojan orbits and DRO/QSOs are in the $1:1$ resonance with the secondary moving on prograde co-orbital orbits around the primary in the restricted three-body problem (Morais and Namouni 2017).

Recent discoveries of retrograde co-orbital objects around the Sun (Wiegert et al. 2017; Li et al. 2018, 2019) may indicate the existence of a novel co-orbital stability region in the Earth–Moon system. However, the substantial gravitational perturbations of the Sun can alter the linear stability of periodic orbits computed in the Earth–Moon system (Boudad et al. 2020). Although triangular libration points are linearly stable for a small mass ratio in the restricted three-body problem (Murray and Dermott 1999), Gómez et al. (2001) has found that planar stability regions around them in the Earth–Moon system disappear due to solar gravitational perturbations, whereas spatial stability regions survive. The previous works have indicated that long-term stable regions around DRO/QSOs exist under solar gravitational perturbations both in the planar (Minghu et al. 2014) and spatial (Oshima and Yanao 2019) dynamics. Since the qualitative effect is various depending on families of orbits, the inclusion of solar gravitational perturbations would be necessary to assess long-term stabilities in the Earth–Moon system.

The present paper globally searches for a stability region near the $1:1$ retrograde resonance with the Moon in the planar bicircular restricted four-body problem including solar gravitational perturbations. The broad search via parallel computing reveals a stability region consisting of orbits persistent for longer than one year near the $1:1$ retrograde resonance. Special stability islands independent of solar phase angles exist, which could be potential locations to search for natural objects in the Earth–Moon system. We find that the location of the stability region qualitatively agrees with phase-space structures in the planar circular restricted three-body problem. Based on the comparison, we identify three families of periodic orbits that could be the possible origin of the stability region. As an application, we explore ballistic capture trajectories into the stability region. The symmetry of the bicircular model enables an efficient search from the dataset of the stability region for ballistic capture trajectories into one-year stable orbits from the vicinity of the Earth or interplanetary space. We find a variety of ballistic capture trajectories and reveal trade-offs among time-of-flights, characteristic energies, and lunar flyby altitudes.

The remainder of the present paper is organized as follows. Section 2 introduces mathematical models. Section 3 summarizes a grid search procedure. Section 4 presents results including stability regions, families of periodic orbits, and ballistic capture trajectories. Section 5 summarizes concluding remarks.

2 Mathematical models

2.1 Planar circular restricted three-body problem

2.1.1 Equations of motion

The planar circular restricted three-body problem (CR3BP) models the motion of a massless particle $P_{3}$ under the gravitational influences of two bodies $P_{1}$ and $P_{2}$ of masses $m_{1}$, and $m_{2}$ ($m_{1} > m_{2}$), respectively. The planar CR3BP assumes that $P_{1}$ and $P_{2}$ move on circular orbits around their barycenter and the bodies and $P_{3}$ move on the same orbital plane. In this paper, $P_{1}$ and $P_{2}$ correspond to the Earth and the Moon, respectively. The non-dimensional equations of motion in the Earth–Moon rotating frame (EMrf) are (Szebehely 1967)

$$ \begin{gathered} {\mathrm{d}}x / {\mathrm{d}}t = v_{x}, \\ {\mathrm{d}}y / {\mathrm{d}}t = v_{y}, \\ {\mathrm{d}}v_{x} / {\mathrm{d}}t = 2 v_{y} - \partial \bar{U} / \partial x, \\ {\mathrm{d}}v_{y} / {\mathrm{d}}t = -2 v_{x} - \partial \bar{U} / \partial y, \end{gathered} $$

(1)

where

$$\begin{aligned} &\bar{U} = -\frac{1}{2}(x^{2}+y^{2})-\frac{1-\mu }{r_{1}}- \frac{\mu }{r_{2}}-\frac{1}{2} \mu (1-\mu ), \end{aligned}$$

(2)

$$\begin{aligned} &r_{1} = \sqrt{{(x+\mu )}^{2}+y^{2}}, \end{aligned}$$

(3)

$$\begin{aligned} &r_{2} = \sqrt{{(x-1+\mu )}^{2}+y^{2}}, \end{aligned}$$

(4)

and $\mu = m_{2} / (m_{1}+m_{2})$.

In the planar CR3BP, the Jacobi energy

$$ C = -({v_{x}}^{2}+{v_{y}}^{2})-2\bar{U} $$

(5)

is a constant of motion, which indicates the energy level of trajectories (smaller $C$ corresponds to higher energy).

2.1.2 Symmetry

The planar CR3BP possesses the symmetry

$$ \left (x, y, v_{x}, v_{y}, t \right ) \rightarrow \left (x, -y, -v_{x}, v_{y}, -t \right ), $$

(6)

which does not alter Eq. (1).

Therefore, once an initial condition $\left (x_{0}, y_{0}, v_{x0}, v_{y0}, t \right )$ is propagated forward in time, its symmetric counterpart with respect to the $x$-axis coincides with a result of propagating an initial condition $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -t \right )$ backward in time. This property indicates that a symmetric periodic orbit passes through $y=v_{x}=0$.

2.2 Planar bicircular restricted four-body problem

2.2.1 Equations of motion

The planar bicircular restricted four-body problem (BCR4BP) describes the motion of a massless particle $P_{3}$ under the gravitational influences of three bodies $P_{0}$, $P_{1}$, and $P_{2}$ of masses $m_{0}$, $m_{1}$, and $m_{2}$ ($m_{0} > m_{1} > m_{2}$), respectively. The model assumes that $P_{1}$ and $P_{2}$ move on circular orbits around their barycenter and $P_{0}$ moves on a circular orbit around the $P_{1}$–$P_{2}$ barycenter. The bodies and $P_{3}$ move on the same orbital plane. In this paper, $P_{0}$, $P_{1}$, and $P_{2}$ correspond to the Sun, the Earth and the Moon, respectively. The non-dimensional equations of motion in the EMrf are (Koon et al. 2011)

$$\begin{aligned} \begin{gathered} {\mathrm{d}}x / {\mathrm{d}}t = v_{x},\\ {\mathrm{d}}y / {\mathrm{d}}t = v_{y},\\ {\mathrm{d}}v_{x} / {\mathrm{d}}t = 2 v_{y} - \partial \bar{U}_{4BP} /\partial x,\\ {\mathrm{d}}v_{y} / {\mathrm{d}}t = -2 v_{x} - \partial \bar{U}_{4BP} /\partial y, \end{gathered} \end{aligned}$$

(7)

where

$$ \bar{U}_{4BP} = \bar{U} - \dfrac{m_{S}}{r_{3}} + \dfrac{m_{S}}{a_{S}^{2}} (x \cos {\theta _{S}} + y \sin {\theta _{S}}), $$

(8)

$$ r_{3} = \sqrt{(x - a_{S} \cos {\theta _{S}})^{2} + (y - a_{S} \sin {\theta _{S}})^{2}}, $$

(9)

$$ \theta _{S} = \theta _{S0} + \omega _{S} t, $$

(10)

and $t$ is time, $\theta _{S0}$ is the Sun’s phase angle at $t=0$, $\omega _{S}$ is the Sun’s relative angular velocity in the EMrf, $a_{S}$ is the distance from the Sun to the Earth–Moon barycenter, and $m_{S} = m_{0} / (m_{1}+m_{2})$. The values of these parameters used in the present paper can be found in Topputo (2013).

The planar BCR4BP is a non-autonomous system due to the motion of the Sun in the EMrf and thus the Jacobi energy in Eq. (5) is no longer a constant of motion. Although the Jacobi energy varies with time in the planar BCR4BP, it is still an instructive energy-like quantity and thus we use it to set initial conditions for the grid search in Sect. 3. This model coincides with the planar CR3BP in the limit of $m_{S} \rightarrow 0$.

2.2.2 Symmetry

The planar BCR4BP has the symmetry

$$ \left (x, y, v_{x}, v_{y}, t, \theta _{S} \right ) \rightarrow \left (x, -y, -v_{x}, v_{y}, -t, -\theta _{S} \right ), $$

(11)

which does not alter Eq. (7). Therefore, once an initial condition $\left (x_{0}, y_{0}, v_{x0}, v_{y0}, t, \theta _{S0} \right )$ is propagated forward in time, its symmetric counterpart with respect to the $x$-axis coincides with a result of propagating an initial condition $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -t, -\theta _{S0} \right )$ backward in time. This symmetric property in the planar BCR4BP is useful for reducing computational costs in Sect. 4.3.

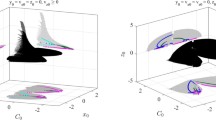
Figure 1 illustrates this symmetric property. The dark star indicates an initial condition $\left (x_{0}, y_{0}, v_{x0}, v_{y0}, t, \theta _{S0} \right )$ for the forward propagation, while the light star represents an initial condition $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -t, -\theta _{S0} \right )$ for the backward propagation. The trajectories propagated forward (dark curve) and backward (light curve) in time, respectively, are symmetric with respect to the $x$-axis.

Fig. 1

The trajectories propagated forward (dark curve) and backward (light curve) in time from initial conditions $\left (x_{0}, y_{0}, v_{x0}, v_{y0}, t, \theta _{S0} \right )$ (dark star) and $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -t, -\theta _{S0} \right )$ (light star), respectively, in the planar BCR4BP

Note that the symmetry also holds true for quantities such as the Kepler energy around the Earth

$$ H_{1} = \frac{(v_{x} - y)^{2} + (v_{y} + x + \mu )^{2}}{2} - \frac{1-\mu }{r_{1}}, $$

(12)

the angular momentum around the Earth

$$ h_{1} = (x + \mu ) (v_{y} + x + \mu ) - y (v_{x} - y), $$

(13)

and the distance from the Moon $r_{2}$. Figure 2 highlights symmetric time histories of these quantities for the trajectory in Fig. 1. The sharp peaks in the Earth-centered two-body quantities $H_{1}$ and $h_{1}$ correspond to the local minima in $r_{2}$.

Fig. 2

Forward (dark) and backward (light) time evolutions of (a) the Kepler energy around the Earth $H_{1}$, (b) the angular momentum around the Earth $h_{1}$, and (c) the distance from the Moon $r_{2}$ for the trajectory in Fig. 1

3 Grid search

The present study searches for initial conditions of trajectories persistent in the vicinity of the $1:1$ retrograde resonance with the Moon for longer than one year in the planar BCR4BP dynamics. Although the definition of the long-term stability varies depending on the scope of each work, the one-year stability region would be useful for many engineering applications and could become good starting points for exploring longer-term stability regions. Throughout the paper, we define the vicinity of the $1:1$ retrograde condition as $-0.6 < H_{1} < -0.4$ and $h_{1} < 0$.

Four parameters $\left (x_{0}, y_{0}, C_{0}, \theta _{S0} \right )$ determine initial conditions for propagations with $v_{x0} = 0$ and $x_{0} < 0$ adopted in the present search. Using the initial Jacobi energy $C_{0}$ yields

$$ v_{y0} = \pm \sqrt{-{v_{x0}}^{2} - C_{0} - 2\bar{U}(x_{0}, y_{0})}, $$

(14)

where only the positive sign satisfies the retrograde condition $h_{1} < 0$. Table 1 summarizes the search condition in the four-dimensional parameter space.

Table 1 The search conditions in the $x_{0}$–$y_{0}$–$C_{0}$–$\theta _{S0}$ parameter space

Figure 3 shows the distribution of the grid points symmetric about the origin on the $y_{0}$–$\theta _{S0}$ plane. Since $v_{x0} = 0$, there is always one pair of initial conditions $(x_{0}, y_{0}, v_{x0}, v_{y0}, \theta _{S0} )$ and $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -\theta _{S0} \right )$. This origin symmetry of the grid points is useful for exploiting the symmetry in the planar BCR4BP in Eq. (11) to efficiently find ballistic capture trajectories in Sect. 4.3.

Fig. 3

The distribution of the grid points near the origin on the $y_{0}$–$\theta _{S0}$ plane. The arrow indicates an example of a pair of grid points exhibiting the origin symmetry

The selection of negative $x_{0}$ leads to initial positions far from the Moon enabling immediate scanning in terms of the Earth-centered two-body quantities. We only propagate initial conditions satisfying $-0.6 < H_{1} < -0.4$ and $h_{1} < 0$. However, trajectories can temporarily violate this condition when they are near the Moon as indicated in Fig. 2. Therefore, during propagations, we evaluate $H_{1}$ and $h_{1}$ only when a trajectory is far from the Moon satisfying $r_{2}>0.5$. We stop propagations if one of the following conditions is satisfied: propagation time exceeds one year; a trajectory violates $-0.6 < H_{1} < -0.4$ or $h_{1} < 0$ when $r_{2}>0.5$; a trajectory collides with the surface of the Earth or the Moon.

4 Results

4.1 Stability region

Figure 4 presents initial conditions (light dots) of trajectories persistent for longer than one year near the $1:1$ retrograde resonance with the Moon under solar gravitational perturbations. It is notable that another broad stability region in the Earth–Moon system exists around the $1:1$ resonance with the Moon, in addition to lunar distant retrograde orbits and Trojan orbits around the triangular libration points. Note that the retrograde motion around the Earth causes high relative velocities with the Moon and thus the Jacobi energies are much smaller than typical prograde orbits.

Fig. 4

Initial conditions (light dots) of trajectories with $v_{x}=0$ and $v_{y}>0$ persistent for longer than one year near the $1:1$ retrograde resonance with the Moon. Datasets of $\left ( x_{0}, y_{0}, C_{0} \right )$ exhibiting the one-year stability independent of $\theta _{S0}$ are shown in dark dots

The dark dots represent special datasets of $\left ( x_{0}, y_{0}, C_{0} \right )$ exhibiting the one-year stability independent of $\theta _{S0}$. They could be potential locations to search for natural objects in the Earth–Moon system because of their capability of capturing small objects with less dependency on epoch.

The isolate stability islands (the dark dots) in Fig. 4 indicate the existence of different families of one-year stable orbits. Figure 5 exhibits examples of the two different families propagated for one year from (a) the larger stability island and (b) the smaller stability island. We set $\theta _{S0}=0$ for both trajectories because the one-year stability of the datasets are independent from $\theta _{S0}$. See the caption for the initial conditions. The crossing points of the trajectory in the panel (a) with $v_{x}=0$ and $v_{y}>0$ qualitatively explain the two nearly symmetric stability islands about $y=0$ in Fig. 4(a).

Fig. 5

Trajectories propagated for one year from (a) $\left ( x_{0}, y_{0}, C_{0}, \theta _{S0} \right ) = \left ( -1, -0.4, -0.4, 0 \right )$ and (b) $\left ( x_{0}, y_{0}, C_{0}, \theta _{S0} \right ) = \left ( -1, 0, -1.2, 0 \right )$. The arrow indicates the direction of motion

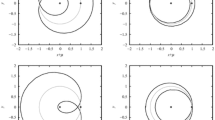
The high dimensionality of the phase space in the planar BCR4BP causes difficulties in visualizing fates of the initial conditions due to the possibility of overlapping each other in a single figure. However, it is still possible to visualize a unique set of initial conditions on a surface of section with prescribed $C_{0}$ and $\theta _{S0}$ owing to the constraints $v_{x0}=0$ and $v_{y0}>0$. This approach enables detailed classifications of the initial conditions according to their fates at the expense of limited information for $C_{0}$ and $\theta _{S0}$. Figure 6 classifies fates of the initial conditions into one-year capture, escape from the $1:1$ retrograde resonance, Earth collision, and Moon collision on the $x$–$y$ plane with the prescribed values of $C_{0}$ and $\theta _{S0}$ indicated at the top of each panel. The emergence of the stability island in the vicinity of $y=0$ in Fig. 6(b) may indicate the occurrence of a bifurcation. The possible origin of this phenomenon will be investigated in Sect. 4.2. These slices of the phase space indicate that the boundaries of the stability regions closely correlate with the initial conditions of lunar collision orbits. This is one of the reasons we will take care of lunar flyby altitudes in Sect. 4.3. In the restricted three-body problem, stability boundaries of long-term stable orbits have been also associated with unstable periodic orbits and their stable and unstable manifolds (Gómez et al. 2001; Ross and Scheeres 2007; Scott and Spencer 2010; Ren et al. 2012; Oshima and Yanao 2015). It would be interesting to investigate the stability region from this perspective, though which is beyond the scope of the present paper.

Fig. 6

Classifications of fates of the initial conditions defined in Table 1 with $v_{x}=0$ and $v_{y}>0$ into one-year capture (light dots), escape from the $1:1$ retrograde resonance (dark dots), Earth collision (dark asterisks), and Moon collision (light asterisks) on the $x$–$y$ plane with the prescribed values of $C_{0}$ and $\theta _{S0}$ indicated at the top of each panel. There is no Earth collision orbit in this figure

4.2 Families of periodic orbits

This section explores the origin of the stability region visualized in the previous section. Although solar gravitational perturbations can alter the linear stability of periodic orbits (Boudad et al. 2020), the broad stability region of the retrograde co-orbital orbits around the Earth in Fig. 4 may indicate that linearly stable periodic orbits in the Earth–Moon planar CR3BP are still responsible for long-term stable orbits under solar gravitational perturbations.

Figure 7 confirms this expectation by comparing the one-year stability region in Fig. 4 (light dots) with phase-space structures (dark dots) in the Earth–Moon planar CR3BP with several energy levels. The stability islands in the CR3BP are qualitatively in good agreement with the stability region in the BCR4BP. Thus, we explore families of linearly stable periodic orbits in the CR3BP as the possible origin of the stability region near the $1:1$ retrograde resonance with the Moon under solar gravitational perturbations.

Fig. 7

The one-year stability region in the BCR4BP (light dots) shown in Fig. 4 and phase-space structures (dark dots) in the CR3BP with $v_{x}=0$ and $v_{y}>0$ in the $x$–$y$–$C$ space

Figure 8 shows an example of generating an initial guess for a linearly stable periodic orbit from the vicinity of the resonance island surrounded by the invariant curves. The nearly periodic initial guess is converged into a periodic orbit via the multiple shooting scheme (Betts 1998) and its continuous family is generated via the continuation procedure (Keller 1977).

Fig. 8

Phase-space structures (small dots) with $v_{x}=0$, $v_{y}>0$, and $C=-0.9$ visualized in the $x$–$y$–$v_{x}$ space. The initial guess for a periodic orbit (curve) is propagated from the vicinity of the center of the resonance island and divided into 4 segments by 5 nodes (large dots). The panel (a) is the amplification of the panel (b)

Figure 9 presents three families of periodic orbits $\mathrm{{I}}$, $\mathrm{{II}}$, and $\mathrm{{III}}$ superimposed on the phase-space structures in the CR3BP. These families have been found in Broucke (1968), Morais and Namouni (2013), Huang et al. (2018). See the caption for the color code distinguishing the linear stability of each of the families. The linearly stable ranges (darker curves) of each of the families penetrate the centers of the resonance islands and thus play the role of backbone structures for the stability regions. Especially, the linearly stable range of the family $\mathrm{{II}}$ (dark green curve) are responsible for stability regions of the broad energy levels. On the other hand, the linearly stable range of the family $\mathrm{{I}}$ (red curve) is narrow in terms of the energy level as shown in the panel (b). The panel (b) also highlights the connection between the families $\mathrm{{I}}$ and $\mathrm{{III}}$, where a period-doubling bifurcation doubling the period of the family $\mathrm{{III}}$ at the bifurcation point occurs. The linearly stable range of the family $\mathrm{{III}}$ (blue curve) could be the origin of the emergence of the stability island in the vicinity of $y=0$ in Fig. 6(b).

Fig. 9

Three families of periodic orbits $\mathrm{{I}}$, $\mathrm{{II}}$, and $\mathrm{{III}}$ and the phase-space structures (dark dots) in the CR3BP shown in Fig. 7 with $v_{x}=0$ and $v_{y}>0$ in the $x$–$y$–$C$ space. The darker curves (red, dark green, and blue) indicate the linearly stable ranges of the families $\mathrm{{I}}$, $\mathrm{{II}}$, and $\mathrm{{III}}$, respectively, whereas the lighter curves (magenta, light green, and cyan) correspond to the unstable ranges of the same families. The panel (b) is the amplification of the panel (a)

Figure 10 exhibits examples of the linearly stable periodic orbits of the families (a) $\mathrm{{I}}$, (b) $\mathrm{{II}}$, and (c) $\mathrm{{III}}$. Note the similarities in appearance between the panel (b) and Fig. 5(a), and between the panel (c) and Fig. 5(b), which also indicate the significance of the families of the periodic orbits for long-term stable orbits under solar gravitational perturbations. The geometries of the orbits in the panels (a) and (b) intersecting $v_{x}=0$ and $v_{y}>0$ twice explain the existence of the two curves for each of the families $\mathrm{{I}}$ and $\mathrm{{II}}$ in Fig. 9. At the period-doubling bifurcation point, the single-revolutional orbit of the family $\mathrm{{III}}$ connects with the double-revolutional orbit of the family $\mathrm{{I}}$.

Fig. 10

Examples of the linearly stable periodic orbits of the families (a) $\mathrm{{I}}$ with $C=-1.1$, (b) $\mathrm{{II}}$ with $C=-1$, and (c) $\mathrm{{III}}$ with $C=-1.2$. The arrow indicates the direction of motion

4.3 Ballistic capture

The present study investigates a ballistic capture scenario such that the forward propagation from one initial point results in a one-year capture trajectory, while the backward propagation from the same point leads to a non-capture trajectory. The overall trajectory thus achieves ballistic capture into the one-year persistent orbit near the $1:1$ retrograde resonance with the Moon far from the stable orbit. The symmetric distribution of the grid points enables efficient scanning of the ballistic capture solutions.

The origin symmetry of the grid points on the $y_{0}$–$\theta _{S0}$ plane illustrated in Fig. 3 indicates that a result of propagating one initial point forward in time, which is classified according to the end of Sect. 3 into one-year capture, escape from the $1:1$ retrograde resonance, Earth collision, or Moon collision, coincides with a result of propagating the other symmetric initial point backward in time. This is because the time-reversal symmetry in Eq. (11) holds true for the quantities $H_{1}$, $h_{1}$, $r_{2}$ (and also $r_{1}$) used in the classification as highlighted in Fig. 2.

Therefore, we first extract initial conditions that lead to escape from the $1:1$ retrograde resonance or a collision with the surface of the Earth. Note that Earth collision orbits can be useful as initial guesses for transfers from low Earth orbits. We then flip the sign of $\left ( y_{0}, \theta _{S0} \right )$ of the initial conditions. As noted in Sect. 3, there always exists one pair of initial conditions $\left (x_{0}, y_{0}, v_{x0}, v_{y0}, \theta _{S0} \right )$ and $\left (x_{0}, -y_{0}, -v_{x0}, v_{y0}, -\theta _{S0} \right )$ with $v_{x0}=0$ in this computational setting. If the flipped initial condition is destined to exhibit one-year capture in the forward propagation, which has been already computed, then the flipped initial condition is a patch point of a ballistic capture trajectory.

We then propagate from the patch point backward in time and stop propagation if one of the following conditions is satisfied: propagation time exceeds 1 year; a trajectory reaches $10{,}000$ [km] altitude from the Earth; a trajectory reaches $r_{1}=5$; a trajectory collides with the surface of the Moon. The cases reaching $10{,}000$ [km] altitude from the Earth and $r_{1}=5$ correspond to ballistic capture trajectories from the vicinity of the Earth and interplanetary space, respectively.

Figure 11(a) shows time-of-flights (TOFs) and launch energies $C_{3}=2H_{1}$ at $10{,}000$ [km] altitude from the Earth for ballistic capture trajectories into the retrograde one-year stable orbits. The color indicates prograde ($h_{1}>0$, dark dots) and retrograde ($h_{1}<0$, light dots) orbits, respectively, at $10{,}000$ [km] altitude from the Earth. Although retrograde launches are more advantageous for transferring into the retrograde one-year stable orbits, Fig. 11(b) extracts the solutions of typical prograde launches. The color indicates the minimum altitude from the lunar surface, small values of which may lead to critical events during the transfers. The orbital characteristics of the sample solutions indicated in the figure are presented next.

Fig. 11

TOF and $C_{3}$ of ballistic capture trajectories from $10{,}000$ [km] altitude from the Earth to the retrograde one-year stable orbits. (a) The color denotes prograde ($h_{1}>0$, dark) and retrograde ($h_{1}<0$, light) orbits, respectively, at $10{,}000$ [km] altitude from the Earth. (b) The color indicates the minimum altitude from the lunar surface for initially prograde solutions. Four sample solutions (i)–(iv) are indicated

Figure 12 exhibits the ballistic capture trajectories of the samples (i)–(iv) in the Earth–Moon and Sun–Earth rotating frames, respectively. The sample (i) is a fast solution immediately jumping into the one-year stable orbit. The sample (ii) experiences one lunar flyby before the ballistic capture. In addition to lunar flybys, the sample (iii) exploits solar gravitational perturbations, which cause the small $C_{3}$ (Belbruno and Miller 1993). The sample (iv) resembles the sample (iii), but it also experiences a high-altitude lunar flyby soon after the launch to further reduce $C_{3}$ (Oshima et al. 2019). These ballistic capture trajectories do not require insertion maneuvers and may be useful for in-situ detections of natural objects such as meteoroids and dust particles near the $1:1$ retrograde resonance with the Moon. The quasi-periodic nature of the long-term stable orbits would also be advantageous due to multiple chances for detections as compared with a single-loop trajectory around a stable region (Uesugi 1996).

Fig. 12

Ballistic capture trajectories (dark curve) from $10{,}000$ [km] altitude from the Earth into one-year stable orbits near the $1:1$ retrograde resonance with the Moon (light curve) in the Earth–Moon and Sun–Earth rotating frames (EMrf and SErf), respectively. The sample numbers are indicated at the upper-left corner of each panel. In the SErf, the light circle represents the lunar orbit and the left and right crosses denote the Sun–Earth $L_{1}$ and $L_{2}$ libration points, respectively

Figure 13 presents ballistic capture solutions from interplanetary space into the retrograde one-year stable orbits in terms of TOF and $C_{3}$ at $r_{1} = 5$ colored according to the minimum altitude from the lunar surface. Note that Eq. (12) suggests the lower limit of $H_{1}$ at $r_{1} = 5$ as approximately −0.2, which corresponds to the lower limit of $C_{3}\approx -0.4$ in the figure. The sample solutions (i)–(iv) indicated in the figure are detailed next.

Fig. 13

TOF and $C_{3}$ of ballistic capture trajectories from $r_{1} = 5$ to the retrograde one-year stable orbits. The color indicates the minimum altitude from the lunar surface. The upper limit of the color bar is smaller than that in Fig. 11(b). Four sample solutions (i)–(iv) are indicated

Figure 14 exhibits the ballistic capture trajectories of the samples (i)–(iv). The two consecutive lunar flybys in the samples (i) and (ii) enable ballistic captures of energetic particles from interplanetary space. A less critical single lunar flyby in the samples (iii) and (iv) is also useful for capturing less energetic particles. Such ballistic capture trajectories from interplanetary space into long-term stable orbits may be useful for Asteroid Redirect Robotic Mission (Strange et al. 2013)—like missions cheaply bringing and storing natural objects in the Earth–Moon system. This result also indicates that interplanetary objects experiencing lunar flybys can be captured into the long-term stable retrograde orbits around the Earth.

Fig. 14

Ballistic capture trajectories (dark curve) from $r_{1} = 5$ into one-year stable orbits (light curve) near the $1:1$ retrograde resonance with the Moon in the Earth–Moon and Sun–Earth rotating frames (EMrf and SErf), respectively. The sample numbers are indicated at the upper-left corner of each panel. In the SErf, the light circle represents the lunar orbit and the left and right crosses denote the Sun–Earth $L_{1}$ and $L_{2}$ libration points, respectively

5 Conclusion

The present paper has found a novel stability region in the Earth–Moon system near the $1:1$ retrograde resonance with the Moon under solar gravitational perturbations. The broad search via parallel computing has globally explored the phase space in the planar bicircular restricted four-body problem. Three families of periodic orbits in the planar circular restricted three-body problem have been identified as the possible origin of the stability region. As an application, a variety of ballistic capture trajectories into the stability region from the vicinity of the Earth and interplanetary space has been computed and orbital characteristics of sample solutions have been presented.