Overview and comparison of approaches towards the planar restricted five-body problem with primaries forming an axisymmetric four-body central configuration

Abstract

The aim of this paper is to present recent results on the restricted five-body problem where the primaries are located at a known central configuration having the $x$-axis as symmetry axis, so that two bodies with equal masses are situated symmetrically with respect to this axis. We firstly give an overview of the axisymmetric central configurations computed by Érdi and Czirják (2016), as well as that where three bodies with equal masses are situated at the vertices of an equilateral triangle, while the fourth body lies at the center of the triangle. This last one bridges the gap between convex and concave four-body central configurations. After that, the characterization of the geometry of the restricted five-body problem families with these configurations are described, and the number and the evolution positions of equilibrium points, which depend on the mass parameters of the primaries, are compared.

1 Introduction

From ancient times, the motion of heavenly bodies has attracted the attention of all cultures, western and eastern civilizations dedicated their attention to understand the universe, this fascination still remains. At present times, one of the tools that permits to understand the motion of some subsystems in the Solar system is the one known as the few-body problem, which has been widely used by mathematicians, astronomers as well as astrophysicists (Murray and Dermott 1999). In the Milky Way galaxy, it is known that more than the 60% of its stars belongs to a system that can be seen as a few-body system. There exist millions of systems in our galaxy that are formed by four and five stars, this is a reason why the interest of studying the four-body and five-body problem has heightened in recent years. By using few-body problems as models it is possible to understand the complex behavior as well as the dynamics that is seen in the Solar system and to grasp that of exoplanetary systems that have been discovered by astronomers. Lately, stellar systems of five stars have also been located. See Koo et al. (2014) and Rappaport et al. (2016) for more detail.

The planar $n$-body problem describes the dynamics of $n\geq 2$ particles with masses $m_{k}$, $k = 1,\dots , n$ moving in the plane $\mathbb{R}^{2}$, and is governed by the Newtonian force law of inverse square distance. Let $\mathbf{r}_{i}\in \mathbb{R}^{2}$ the vector position of the body with mass $m_{i}$. The equations which describe the motion of the masses are

$$ \frac{d^{2}\mathbf{r}_{i}}{dt^{2}} = \sum_{\stackrel{j=1}{j\neq i}}^{n} \frac{ m_{j} (\mathbf{r}_{j}-\mathbf{r}_{i})}{|\mathbf{r}_{i}-\mathbf{r}_{j}|^{3}} = \frac{\partial U}{\partial \mathbf{r}_{i}}, \quad i=1,\dots , n $$

(1)

where $U$ is the Newtomian potential given by

$$ U(\mathbf{r}) = \sum_{1\leq i < j \leq n} \frac{m_{i}m_{j}}{|\mathbf{r}_{i}-\mathbf{r}_{j}|} $$

and $|\cdot |$ denotes the Euclidean norm and the gravitational constant is normalized to $G= 1$.

A solution of a system of differential equations, as the given above, is said to experience a singularity at time $t^{*} < \infty$ if the solution cannot be analytically extended beyond $t^{*}$. Note that Eqs. (1) are defined everywhere and are real analytic except at points in the physical space that are occupied by at least two bodies. In order to be more precise, by defining the sets $\Delta _{ij}= \{ (\mathbf{r}_{1},\dots , \mathbf{r}_{n})\in \mathbb{R}^{2n} \, | \; \mathbf{r}_{i}= \mathbf{r}_{j} \}$ and $\Delta =\bigcup_{i< j} \Delta _{ij}$, we see that the potential $U$ is a real analytical function in $\mathbb{R}^{2n}\setminus \Delta$.

This paper is inscribed in the realm of the restricted$n$-body problems, whose importance has increasingly grown in recent years. A planar restricted $n$-body problem consists of describing the motion of $n$ bodies with masses $m_{1}, \dots ,m_{n-1}$ attracting each other according to the Newtonian gravitational law, where $m_{0}$ is an infinitesimal mass and $m_{1},\dots , m_{n-1}$ are positive (usually called primaries). We assume that $m_{0}$ is so small that it does not influence the motion of the primaries, and these are moving following a known solution of the ($n-1$)-body problem. It is further assumed that the motion of $m_{0}$ takes place in the same plane where the primaries move.

In the case of the planar restricted three-body problem, the primaries move in Keplerian orbits which are not affected by the infinitesimal mass. The most extensively studied restricted problem has been the planar circular restricted three-body problem, where the primaries move in fixed circular orbits around their common center mass. It is of practical interest as well since it accurately describes many real-world problems, an important example being the Sun, Jupiter and an asteroid system, see Szebehely (1967).

We denote by the vector $\mathbf{r}=(\mathbf{r}_{1}, \dots , \mathbf{r}_{n})\in \mathbb{R}^{2n}$ a configuration formed by $n$ bodies. A central configuration in the $n$-body problem is a special position of the bodies where the position and the acceleration vectors are proportional and the constant of proportionality is the same for all $n$ bodies. The acceleration vectors of the bodies satisfy the equations

$$ \sum_{\stackrel{j=1}{j\ne i}}^{n} \frac{m_{j}(\mathbf{r}_{j}-\mathbf{r}_{i})}{r_{ij}^{3}} = \lambda ( \mathbf{r}_{i} - \mathbf{c}_{m}), \quad \text{for} \ i=1,\dots , n $$

where $\lambda$ is a constant, $r_{ij}= |\mathbf{r}_{i}-\mathbf{r}_{j} |$ and

$$ {\mathbf{c}}_{m}= \frac{m_{1} \mathbf{r}_{1} + \cdots + m_{n} \mathbf{r}_{n}}{ m_{1} + \cdots + m_{n}} $$

is the position vector of the center of mass of the $n$ bodies (see, for example, Wintner 1941).

A central configuration $\mathbf{r}=(\mathbf{r}_{1}, \dots , \mathbf{r}_{n})$ is convex if the $\mathbf{r}_{i}$’s are at the vertices of a convex polygon; ${\mathbf{r}}$ is concave if one particle is located in the interior of the convex hull of the other $n-1$ vertices.

The central configurations allow to obtain the homographic solutions of the $n$-body problem, which are the unique explicit solutions in function of the time known until now of that problem, for such solutions the ratios of the mutual distances between the bodies remain constant. In the three-body problem the collinear configurations and the equilateral triangle for any choice of positive masses are the only central configurations, for further details see Wintner (1941).

Now, we provide a brief summary of some results known so far about the axisymmetric central configuration of four bodies. Long and Sun (2002) proved that a convex non-collinear planar four-body central configuration with three equal masses must be a kite. They also proved the existence of the two types of concave central configurations, in which three equal masses are at the vertices of an equilateral triangle and the fourth one with any given mass at its geometric center, or three equal masses are at the vertices of an isosceles triangle and the fourth one on the symmetry axis.

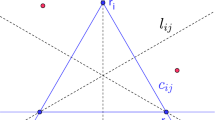
Later on, in a seminal paper, Érdi and Czirják (2016) classified a broad class of central configurations for the four-body problem in which two of the bodies lie along an axis of symmetry, and the other two bodies with equal masses are situated symmetrically with respect to this axis of symmetry. They found three types of central configurations where the four-sided polygon formed by connecting the on-axis masses to the off-axis masses. The first family corresponds to convex central configurations and it is shown in Fig. 1(a), and the other two families are concave central configurations, see Figs. 1(b) and 1(c).

Fig. 1

The Érdi and Czirják’s class of symmetric four-body central configuration having one pair of equal masses located symmetrically with respect to the $x$-axis, where the center of mass is at origin. The two off-axis masses are fixed by the angles $\alpha$ and $\beta$, whereas the positions of the masses $m_{1}$ and $m_{2}$ are defined using rectangular coordinates

The two concave subclasses are different depending on whether the center of mass of the system excluding $m_{2}$ is enclosed by the polygon or not.

The goal of this paper is to perform an analysis of the planar symmetric restricted five-body problem in such a way that the four primaries are arranged in a symmetric central configuration forming a convex or concave four-sided polygon obtained in Érdi and Czirják (2016). Moreover, we will consider the configuration of equilateral triangle so that a fourth mass is at its geometric center. This special four-body central configuration was called as a singular case in Érdi and Czirják (2016). Our review is mainly based on previous results obtained by Ollöngren (1988), Gao et al. (2017), Zotos and Sanam Suraj (2018), and Zotos and Papadakis (2019).

The main contributions of this paper are as follows: A comprehensive survey of the restricted five-body problem approaches when the primaries form a four-body central configuration computed by Érdi and Czirják’s is given. A comparison on the number of equilibrium points for the restricted five-body problem is shown, with focus on the results obtained by Ollöngren (1988), Gao et al. (2017), Zotos and Sanam Suraj (2018), and Zotos and Papadakis (2019). Connections between unconnected research about the restricted five-body problem in the different descriptions are shown, which can provide guidance both to the development of novel formulations and to the use of the existing ones.

This paper is organized as follows. In Sect. 2, we set the symmetric restricted five-body problem in a general frame. Also, the equations of motion for the particular case studied in this work are introduced. Section 3 is dedicated to give a brief description of Érdi and Czirják’s axisymmetric four-body configurations, that are used in Sect. 4 to introduce planar restricted symmetric five-body problems with primaries in central configuration of the four-body problem. Section 5 deals to describe how do the number and location of the equilibrium points vary when the angular coordinates change in the allowed domain. Finally, in Sect. 6 concluding remarks are given.

2 The planar symmetric restricted five-body problem

Let $(x,y)$ be a synodic reference frame with origin at the center of mass of the primaries $\mathbf{c}_{m}$. We consider the restricted symmetric five-body problem where the primaries form a symmetric four-body central configuration, with $m_{1}$ and $m_{2}$, ordered from right to left, are collinear on the $x$-axis, while the other two bodies $m_{3}=m_{4}=m$ are placed symmetrically with respect to the line containing the two collinear bodies.

In order to maintain the central configuration of the primaries, the sum of the gravity forces exerted by $m_{2}$, $m_{3}$ and $m_{4}$ on $m_{1}$ must be equal to the centrifugal force. Hence the angular velocity of the synodal frame is

$$ \omega ^{2} = \varLambda = \displaystyle { \frac{(m_{2}/|AB|^{2}+ 2m \sin \alpha / |AE|^{2})}{|AO|}} $$

(2)

where the gravitational constant $G=1$, the angle $\alpha$ is formed by the lines connecting $m_{1}$ with $m_{3}$, and $m_{3}$ with $m_{4}$, while $|AO|$, $|AB|$ and $|AE|$ are the relative distances from $m_{1}$ to ${\mathbf{c}}_{m}$, $m_{2}$ and $m_{3}$, respectively. We stress the fact that this expression was derived by Gao et al. (2017).

If we assume that the rotating coordinate system $(x,y)$ rotates with the angular velocity of the primaries given by (2), then the primaries are fixed in the $(x,y)$ plane. We take the primary of mass $m_{1}$ located on the positive $x$-axis at $(x_{1},0)=(a,0)$, as well as $m_{2}$ at $(x_{2},0)=(b,0)$, while the other two primaries $m_{3}$ and $m_{4}$ are placed at $(x_{3},y_{3})=(c,1)$ and $(x_{4},y_{4})=(c,-1)$.

The differential equations describing the motion of the infinitesimal mass of the restricted symmetric five-body problem, in the usual dimensionless rectangular rotating coordinate system are written as

$$ \textstyle\begin{array}{c} \ddot{x} - 2 \dot{y} = \displaystyle { \frac{\partial \varOmega }{\partial x}}, \\ \ddot{y} +2 \dot{x} = \displaystyle { \frac{\partial \varOmega }{\partial y}} \end{array} $$

(3)

where dots denote time derivatives while the gravitational potential $\varOmega$ is defined as

$$ \varOmega = \varOmega (x,y) = \frac{1}{2} \bigl(x^{2}+y^{2}\bigr) + \frac{1}{\varLambda } \biggl( \frac{m_{1}}{r_{1}}+\frac{m_{2}}{r_{2}}+ \frac{m_{3}}{r_{3}}+ \frac{m_{4}}{r_{4}} \biggr), $$

(4)

and

$$ r_{i}^{2}=(x-x_{i})^{2}+(y-y_{i})^{2}, \quad i=1,2,3,4. $$

Note that Eq. (3) are invariant under the following symmetry:

$$ (x,y,\dot{x},\dot{y},t) \to (x,-y,-\dot{x},\dot{y},-t). $$

The system (3) has a first integral given by

$$ C_{J} = 2 \varOmega (x,y) - \dot{x}^{2} - \dot{y}^{2}. $$

(5)

We remark that this expression bears resemblance to the first integral of the circular restricted three-body problem, called Jacobi’s constant, differing only in the expression of the function $\varOmega$.

3 Some geometrical scenarios for the planar four-body central configuration having an axis of symmetry

From now on, we will consider that in the restricted five-body problem the configuration of the four primaries is a non-collinear central configuration with a symmetry axis given by the $x$-axis. Furthermore, the bodies $m_{1}$ and $m_{2}$ are placed on the $x$-axis, ordered from right to left, while the other two, $m_{3}$ and $m_{4}$, are placed symmetrically with respect to the line of symmetry. Hence, by using the symmetry, we get that $m_{3}=m_{4}$.

It is known that when three particles in a four-body central configuration have equal masses, the configuration possesses a symmetry, see Albouy (1996). In Shi and Xie (2010), the authors discovered two families of central configurations of the planar four-body problem, depending on whether the unequal mass is inside or outside of the triangle formed by the three equal masses. For the concave family the bodies of equal mass lie at the vertices of the isosceles triangle, while the fourth particle is on the interior symmetric axis of the triangle. In the convex family the three equal masses form an isosceles triangle, where the fourth mass is located on the exterior symmetric axis of the triangle.

3.1 Érdi and Czirják’s central configurations

Érdi and Czirják (2016) carried out an extensive and complete study of the central configurations of the four bodies, when two bodies have equal masses and are situated symmetrically with respect to the axis of symmetry, and the other two bodies are on this axis of symmetry. They studied in detail the cases of concave and convex central configurations, so that the masses can be determined, and described the geometry of the configurations in terms of two angles, namely, $\alpha$ and $\beta$, and the positions of the masses $m_{1}$ and $m_{2}$ are defined using rectangular coordinates. The angle $\alpha$ is between the lines joining the masses $m_{3}$ and $m_{1}$ and the line joining the masses $m_{3}$ and $m_{4}$, while $\beta$ is the angle between the line joining mass $m_{3}$ with $m_{4}$ and the line joining $m_{3}$ and $m_{2}$, see Fig. 1.

The masses and positions of the particles are obtained from the angles $\alpha$ and $\beta$. In the case of convex central configurations we have that the values of the angles $\alpha$ and $\beta$ are bounded on the $(\alpha ,\beta )$ plane by the lines $\alpha +2\beta =90^{\circ }$, $\alpha =60^{\circ }$ and $\alpha =\beta$. For the first case of concave central configurations, the angles satisfy the restrictions $\beta \in [0,30^{\circ }]$ and $\frac{\beta }{2}+45^{\circ }\leq \alpha \leq 60^{\circ }$, while for the second case of the concave central configurations, $\beta \in [30^{\circ },60^{\circ }]$ and $60^{\circ }\leq \alpha \leq \frac{\beta }{2}+45^{\circ }$. It is worthwhile to observe that the equilateral triangle with the fourth mass placed at the geometric center of the triangle corresponds to the singular case $\alpha =60^{\circ }$ and $\beta = 30^{\circ }$. These angle coordinates appertain to the shared vertex of the two regions associated to the concave central configurations.

According to Érdi and Czirják (2016), to make the convex or concave central configurations possible, the parameters of positions and masses in terms of the angles $\alpha$ and $\beta$ should satisfy some conditions respectively as follows.

• 1. Convex central configurations,

  $$\begin{aligned} a_{0} =& \biggl(\cos ^{3}\alpha -\frac{1}{8} \biggr)\tan \alpha , \\ a_{1} =&\frac{1}{ (\tan \alpha +\tan \beta )^{2}}+ \biggl( \frac{1}{8}-\cos ^{3}\alpha -\cos ^{3}\beta \biggr)\tan \beta \\ & - \frac{1}{8}\tan \alpha , \\ b_{0} =& \biggl(\cos ^{3}\beta -\frac{1}{8} \biggr)\tan \beta , \\ b_{1} =& \frac{1}{ (\tan \alpha +\tan \beta )^{2}}+ \biggl( \frac{1}{8}-\cos ^{3}\alpha -\cos ^{3}\beta \biggr)\tan \beta \\ & - \frac{1}{8}\tan \beta . \end{aligned}$$

  The ordinates $a$, $-b$ and $c$ of the masses $m_{1}$, $m_{2}$ and $m_{3}$ (which is the same as that of $m_{4}$) are given through

  $$\begin{aligned} a =& (1-m_{1} )\tan \alpha +m_{2}\tan \beta , \\ b =&m_{1}\tan \alpha + (1-m_{2} )\tan \beta , \\ c =&-\frac{m_{1} a-m_{2} b}{1-m_{1}-m_{2}}. \end{aligned}$$

• 2. Concave central configurations

  $$\begin{aligned} a_{0} =& \biggl(\cos ^{3}\alpha -\frac{1}{8} \biggr)\tan \alpha , \\ a_{1} =&\frac{1}{ (\tan \alpha +\tan \beta )^{2}}+ \biggl( \frac{1}{8}-\cos ^{3}\alpha -\cos ^{3}\beta \biggr)\tan \beta \\ & - \frac{1}{8}\tan \alpha , \\ b_{0} =& \biggl(\cos ^{3}\beta -\frac{1}{8} \biggr)\tan \beta , \\ b_{1} =& \frac{1}{ (\tan \alpha +\tan \beta )^{2}}+ \biggl( \frac{1}{8}-\cos ^{3}\alpha -\cos ^{3}\beta \biggr)\tan \beta \\ & - \frac{1}{8}\tan \beta . \end{aligned}$$

  The values of the ordinates $a$, $-b$ (first concave case) or $b$ (second concave case) and $c$ of masses $m_{1}$, $m_{2}$ and $m_{3}$ (which is the same ordinate for $m_{4}$) reduce to

  $$\begin{aligned} a =& (1-m_{1} )\tan \alpha -m_{2}\tan \beta , \\ b =&m_{1}\tan \alpha - (1-m_{2} )\tan \beta , \\ c =&-\frac{m_{1} a-m_{2} b}{1-m_{1}-m_{2}} \quad \text{(first concave case)}, \\ c =&-\frac{m_{1} a+m_{2} b}{1-m_{1}-m_{2}} \quad \text{(second concave case)}. \end{aligned}$$

  Observe that the value $c$ changes depending on the choice of the concave case.

For all considered central configurations, either convex or concave, the values of the masses of the particles are obtained by using

$$ m_{1}= \frac{ (b_{1}+a_{0}-b_{0} )b_{0}}{a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}}, \qquad m_{2}= \frac{ (a_{1}+b_{0}-a_{0} )a_{0}}{a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}} $$

(6)

and

$$ m=\frac{1}{2}(1-m_{1}-m_{2}). $$

(7)

3.2 The case $\alpha = 60^{\circ }$ and $\beta =30^{\circ }$

Long and Sun (2002) proved that three equal masses forming an equilateral triangle with a fourth mass located at the center of the triangle is a concave central configuration of the four body problem. In Érdi and Czirják (2016), the authors called it as a singular case because it is associated to the limit values of the angles $\alpha = 60^{\circ }$ and $\beta =30^{\circ }$.

Then, one finds that the parameters of the positions are given explicitly by

$$ a_{0}=0, \qquad a_{1}= \frac{9-\sqrt{3}}{8}, \qquad b_{0}=b_{1}= \frac{9-\sqrt{3}}{8}, $$

while the masses satisfy $m_{2}= 1-3m_{1}$. Since $m_{3}=m_{4}=m$ where $m= \frac{1}{2} (1-m_{1}-m_{2})$, it arises to $m=m_{1}$. Hence, the masses lying at the vertices of the equilateral triangle are equal. Furthermore, according to what is said in Long and Sun (2002), the fourth mass must be placed at the geometric center of the triangle, which coincides with the center of mass of the bodies forming the triangle.

4 The planar symmetric restricted five-body problem endowed with an axisymmetric four-body central configuration

This section is addressed to describe planar symmetric restricted five-body problems with primaries in central configurations of the four-body problem, as was described in the last section, and that have been studied so far. It would seem that the main differences in the corresponding effective potential that characterize each problem are, the angular velocity $\varLambda$ and the relative distances between the primaries.

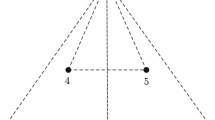
Firstly, we consider the restricted five-body problem introduced by Ollöngren (1988), who supposed that the three bodies with equal masses $m$ revolve in the same plane forming an equilateral triangle (for which the lengths of the sides are equal to unity), and they move around their center in circular orbits under the influence of their mutual gravitational attraction. At the center of the triangle a mass $\tilde{\beta }m$ is present, where $\tilde{\beta }\geq 0$. We recall that this corresponds to $\alpha = 60^{\circ }$ and $\beta =30^{\circ }$.

Note that for an equilateral triangle in which all three sides are equal to $a$ and the radius of the circle containing the vertices of the triangle is given by $r$, we have that $\sqrt{3}r=a$, see Fig. 2. So, for $a=1$, we get $r=\frac{\sqrt{3}}{3}$ and the angle $\alpha$ formed by the segments joining particles $m_{3}$ with $m_{4}$ and $m_{3}$ with $m_{1}$ is equal to $\pi /3$, $|AE|=1$, $|AO|=|AB|=r=\frac{\sqrt{3}}{3}$. So, the angular velocity (2) yields

$$ \omega ^{2} = \varLambda = \displaystyle { \frac{(\tilde{\beta }/|AB|^{2}+ 2 \sin (\pi /3))}{|AO|}=3(1+ \tilde{ \beta } \sqrt{3})}. $$

This is just the $1/k$ described in Ollöngren (1988), and has been used afterwards.

Fig. 2

Equilateral triangle configuration having the body $m_{2}= m\tilde{\beta }$ at its geometric center, where $\alpha =60^{\circ }$ and $\beta =30^{\circ }$

Before continuing, let us make some comments involving the different notations used along (Ollöngren 1988; Zotos and Sanam Suraj 2018) and compare them with the ones we use. In both papers, the authors enumerate the primaries at the vertices of the equilateral triangle in an increasing way, starting at the mass at the right of the configuration and use counterclockwise sense. While in Ollöngren (1988) the author use as notation $m_{1}$, $m_{2}$ and $m_{3}$, in Zotos and Sanam Suraj (2018) the authors use $P_{1}$, $P_{2}$ and $P_{3}$ to refer to the same. Finally, the mass inside the equilateral triangle is denoted as $m_{0}$ in Ollöngren (1988), and by $P_{0}$ in Zotos and Sanam Suraj (2018). In Érdi and Czirják (2016), Gao et al. (2017) and this paper, $m_{1}$, $m_{3}$ and $m_{4}$ denote $m_{1} (P_{1})$, $m_{2} (P_{2})$ and $m_{3} (P_{3})$, respectively, while the mass inside the triangle is named $m_{2}$, that corresponds to $m_{0} (P_{0})$ in Ollöngren (1988) and Zotos and Sanam Suraj (2018), respectively.

By taking dimensionless masses of the primaries $m_{1}=m_{2}=m_{3}=m=1$ and $m_{4}=\tilde{\beta } m$, Ollöngren (1988) used analytical methods to compute equilibrium points. He obtained 9 points in total, 3 of them become stable when $\tilde{\beta } > 43.18$, while for smaller values all the equilibrium points are linearly unstable. Later on, the same problem was studied by Zotos and Sanam Suraj (2018), who explored from a numerical point of view the basins of convergence of the equilibrium points. They defined a mass parameter $\mu = 1/(1+\tilde{\beta })$, similar to the mass parameter of the classical restricted three-body problem, in such a way that $\mu \in (0,1]$ when $\tilde{\beta }\in [0,\infty )$. They concluded that the total number of equilibrium points is as follows: for $\mu \in (0, 0.98617275]$ there are 9 points: 3 collinear and 6 non-collinear; if $\mu \in [0.98617276, 1)$ there exits 15 points: 5 collinear and 10 non-collinear. They are shown in Fig. 3. More recently, Zotos and Papadakis (2019) made a numerical study of the orbital dynamics for the same restricted five-body problem. In order to classify the possible types of orbits, they carried out a numerical integration of several large sets of initial conditions of orbits, and found three main categories: (i) close encounter orbits, (ii) bounded (chaotic or regular) and (iii) escaping. In addition, the authors verified that when $\tilde{\beta }$ lies in the interval $(0,0.01402112)$ there are only 15 equilibrium points, while when $\tilde{\beta }\in (0.01402113,\infty )$ there are only 9 equilibrium points.

Fig. 3

The parametric evolution of the position of the equilibrium points $L_{j}$, $j=1,\dots , 15$ in the Ollöngren problem, when $\mu \in (0, 1]$ or equivalently $\tilde{\beta }\in (0,0.01402112)\cup (0.01402113,\infty )$. The arrows indicate the evolution direction of the equilibrium points as the mass parameter increases. The points $P_{1}$, $P_{2}$, and $P_{3}$ denote the three primaries forming an equilateral triangle with the fourth body at its geometric center. The big black dots pinpoint the fixed centers of the primaries, whereas the small black dots $A$, $B$ and $C$ correspond to $\mu \to 0$, $\mu =0.98617276$ and $\mu =1$, respectively. The figure was taken from Zotos and Sanam Suraj (2018)

At this point, it is worth noting that we have a wide family of the symmetric restricted five-body problem, where the four primaries are maintaining four-body central configurations given in Érdi and Czirják (2016), which have been described in Sect. 3. Taking into account that the angular velocity $\varLambda$ depends on each specific central configuration and the masses involved, Gao et al. (2017) got families of restricted five-body problems, one for each of the configurations that have been chosen. In particular, they computed the number and placement of the equilibrium points, from a numerical perspective, when varying the angles $\alpha$ and $\beta$ that are used as a coordinate system.

5 Analysis of the number of the equilibrium points

In this section, we include a description of the number of collinear and non-collinear equilibrium points of the restricted five-problem and the bifurcations depending on the angle coordinates.

In order to present the results, we have chosen different values of the angles $\alpha$ and $\beta$, each pair corresponding to a different scenario with respect to convex and concave configurations, and consequently the number of equilibrium points will vary.

At this stage, we make an account of the numerical results obtained by Gao et al. (2017), who considered the axisymmetric central configurations studied by Érdi and Czirják (2016). Gao et al. showed how the number and location of the equilibrium points change when the angular coordinates $\alpha$ and $\beta$ are modified inside the permitted regions. To do so, they fix the angle $\alpha$ and take a value for $\beta$ and proceed to compute where the equilibrium points are placed and determine the number of collinear and non-collinear equilibrium points, then increase values for $\beta$ and continue their calculations.

Below we summarize the numerical results that appear spread over several plots and tables in Gao et al. (2017) about the number of the equilibrium points for some pairs of the angles $\alpha$ and $\beta$.

• 1. Equilibrium points in convex configurations

  • (i) The equilibrium points in convex configurations with $\alpha = 52.5^{\circ }$.

    When $\beta$ increasing, the number of the non-collinear equilibrium points jumps to 12 at $26^{\circ }$ and then decreases to 10 quickly. In the process of jumping to 12 from 8, a critical solution should exist where the number of the non-collinear equilibrium points equals to 10 at some value of $\beta$ near $26^{\circ }$. When the number of the non-collinear equilibrium points decreases to 10, at $\beta =27.5^{\circ }$, it does not change anymore. However, when $\beta$ reaches $52^{\circ }$, the combination of the angle coordinates gets close to $\alpha =\beta$, and two more collinear equilibrium points appear between the masses $m_{1}$ and $m_{2}$.

  • (ii) For $\alpha >52.5^{\circ }$.

    The same behavior as in the previous case is observed for $\alpha >52.5^{\circ }$. A critical situation comes up in the process of increasing $\beta$ from $50^{\circ }$ to $52.5^{\circ }$, when there exist simultaneously only 2 collinear equilibrium points between $m_{1}$ and $m_{2}$.

  • (iii) The value for $\alpha$ is taken as $50^{\circ }$.

    The same changing behavior occurs as $\beta$ increases, but the number of the collinear equilibrium points is 3, and it remains fixed.

  • (iv) Fix $\alpha =35^{\circ }$.

    There are 3 collinear equilibria for all the values of $\beta$ considered. What changes is the number of the non-collinear equilibrium points; as $\beta =28^{\circ }$ there are 8 non-collinear equilibria, and when $\beta$ is increased to $\beta =33^{\circ }, 34^{\circ }$ and $34.9^{\circ }$, in these cases the number of non-collinear equilibrium points is equal to 12, and this number does not decrease to 10 as $\beta$ increases.

• 2. Equilibrium points in concave configurations, first case.

  There are some regularities in the number of the equilibrium points, there exist 3 collinear equilibrium points that are separated by the primaries $m_{1}$ and $m_{2}$ and there is no variation in this number for all combinations of the angle coordinates that belong to the region which define the first concave case. For angular combinations near $\beta =0^{\circ }$ there are 6 axisymmetric equilibrium points.

  • (i) For $\alpha$ as large as $57.5^{\circ }$ or $59.5^{\circ }$, there is some pattern in the way how the number of the non-collinear equilibrium points changes as angle $\beta$ increases. By taking $\alpha =59.5^{\circ }$ as $\beta$ grows from $0.5^{\circ }$ there appear two new more collinear equilibrium points for $\beta =2^{\circ }$. For $\beta =18^{\circ }$, there are 10 non-collinear equilibrium points and then this number decreases to 6. Another critical situation arises where the number of the non-collinear critical points is equal to 8 between $\beta =18^{\circ }$ and $\beta =25^{\circ }$.

  • (ii) If $\alpha =65^{\circ }$ or any value below this, no matter what value is assigned to $\beta$, there are always 6 non-collinear equilibrium points. So, it is likely to expect that there must be a value for $\alpha$ between $57.5^{\circ }$ and $55.0^{\circ }$ which determines whether the number of the non-collinear equilibrium points jumps from 8 to 6 or not.

• 3. Equilibrium points in concave configurations, second case.

  • (i) If $\alpha =60.5^{\circ }$ is fixed, by beginning with $\beta =59.5^{\circ }$ there exist 9 equilibrium points, 5 are collinear while the other 4 are non-collinear. When decreasing $\beta$, there appear 2 more non-collinear equilibria at $\beta =40^{\circ }$. By dropping to $\beta =35^{\circ }$, that is, the angular combination getting close to $2\alpha -\beta =90^{\circ }$, two collinear equilibria disappear and only one is left. For a value of $\beta$ between $40^{\circ }$ and $35^{\circ }$, there are three collinear equilibrium points, two placed to the left of $m_{2}$, but for the authors it was difficult to find it in an accurate way.

  • (ii) For $\alpha =65^{\circ }$, $\beta <60^{\circ }$ and $2\alpha -\beta <90^{\circ }$, some changing trend appears. The larger $\alpha$ the larger is $\beta$, where the number of the non-collinear equilibria is equal to 4.

  • (iii) For $\alpha =70^{\circ }$ and $\beta =59.9^{\circ }$ the non-collinear equilibria is 6.

  • (iv) As for the concave cases there are two allowed regions in the plane $(\beta ,\alpha )$, bounded by two right triangles defined by the lines $\alpha =60^{\circ }$, $\beta =0^{\circ }$ and $2\alpha -\beta =90^{\circ }$ (first triangle), and by the lines $\alpha =60^{\circ }$, $\beta =60^{\circ }$ and $2\alpha -\beta =90^{\circ }$ (second triangle), respectively. The last triangular region corresponds to the second concave case. When the combination of angles is inside the second triangle and it is near the vertical and the horizontal sides of the triangle, there are 5 collinear and 4 non-collinear equilibrium points. As the value of $\alpha$ is increased and kept fixed, and those of $\beta$ are decreased, at some point, 2 collinear equilibria to the left of mass $m_{2}$ disappear and there will appear 2 non-collinear equilibrium points.

  It is worth noting the following. In the convex case, for most combinations of $\alpha$ and $\beta$, there exist 3 collinear equilibrium points that are separated by $m_{1}$ and $m_{2}$, but as the combination gets close to $\alpha =\beta$ two new equilibrium points emerge between $m_{1}$ and $m_{2}$. There exist 8 non-collinear equilibrium points when the combination of angles is near to $\alpha +2\beta =90^{\circ }$ and their number will change regularly as $\beta$ increases, once $\alpha$ has been fixed. In general, for the first concave case there are always 3 collinear equilibrium points and 6 non-collinear for most combinations of the angular variables. For the second concave case, the changing pattern and distribution of the equilibrium points is relatively simple when compared to the other two types of configurations.

From the information already described we see that the distribution of equilibrium points and the way they behave is more complex than the one that appears in the different types of the restricted four-body problem studied so far. The authors found that there exist many critical situations during the process of change of the angle combination.

5.1 Equilibrium points for the problem close to Ollöngren problem

In this section we analyze two Ollöngren restricted five-body problems for different values of the mass parameter $\tilde{\beta }$ and we compare them with some cases obtained by Gao et al. (2017) that are close to them.

First, we consider configurations with $\alpha =60^{\circ }$ and $\beta =30^{\circ }$, see Fig. 4, which have equilateral triangles. For the parameter $\tilde{\beta }=1$, 0.00502513, their corresponding systems have 9 and 15 equilibrium points, respectively, where 5 of them are collinear.

Fig. 4

The equilibrium points and zero velocity curves for values of $\alpha =60^{\circ }$, $\beta =30^{\circ }$, $m_{1}=m_{3}=m_{4}=1$ for $m_{2}=\tilde{\beta }=1$, 0.00502513 with 9 (left plot) and 15 (right plot) equilibrium points, respectively. The figure was taken from Zotos and Sanam Suraj (2018)

Now, look into concave or convex central configurations that are close to the one considered by Ollöngren. Consider the second concave case with central configuration with $\alpha =60.5^{\circ }$ and $\beta =31.5^{\circ }$, the configuration formed by $m_{1}$, $m_{3}$ and $m_{4}$ is very near to equilateral, see Fig. 5. Observe that the masses take values $m_{1}=0.277665$, $m_{2}=0.161854$, $m_{3}=m_{4}=0.280241$, and except for $m_{2}$, the other three masses are almost equal. For this, the number of equilibrium points is equal to 9, where 3 are collinear.

Fig. 5

The left picture represents the restricted five-body problem with primaries in a concave four-body central configuration. The right picture contains the zero velocity curves and 9 equilibrium points. It was taken from Gao et al. (2017). The parameter values are $\alpha =60.5^{\circ }$, $\beta =31.5^{\circ }$, $m_{1}=0.277665$, $m_{2}=0.161854$, $m_{3}=m_{4}=0.280241$, $a=1.17754$, $b=0.0228463$, $c=-0.589955$

In Fig. 6, the configuration belongs to the first concave case with $\alpha =59.5^{\circ }$ and $\beta =18^{\circ }$ then, as in the previous case, the configuration formed by $m_{1}$, $m_{3}$ and $m_{4}$ is almost an equilateral triangle. Also, this is close to the one in Ollöngren problem, and the masses are given by $m_{1}=0.401265$, $m_{2}=0.00883964$, $m_{3}=m_{4}=0.294947$. Here the total number of equilibria is 13 and 3 of them are collinear.

Fig. 6

The left picture represents the restricted five-body problem with primaries in a first concave four central configuration. The right picture contains zero velocity curves and the 13 equilibrium points. The right picture was taken from Gao et al. (2017). The parameter values are $\alpha =59.5^{\circ }$, $\beta =18^{\circ }$, $m_{1}=0.401265$, $m_{2}=0.00883964$, $m_{3}=m_{4}=0.294947$, $a=1.01358$, $b=0.359166$, $c=-0.684086$

The convex case is more sensitive to small changes in the angle parameters as we shall see through two configurations. The angle $\alpha$ is fixed to $\alpha =52.5^{\circ }$ and $\beta$ takes values $\beta =26^{\circ }$ (see Fig. 7), $\beta =27.5^{\circ }$ refers to Fig. 8, and $\beta =2^{\circ }$ is shown in Fig. 9. In the first one, the number of equilibrium points is 15, while in the second one is equal to 13 and for the last one there are 11 equilibria.

Fig. 7

The left picture represents the restricted five-body problem with primaries in a convex four-body central configuration, where the parameter values are $\alpha =52.5^{\circ }$, $\beta =26^{\circ }$, with 15 equilibrium points. $m_{1}=0.73719$, $m_{2}=0.0307723$, $m_{3}=m_{4}=0.116019$, $a=0.357509$, $b=1.43345$, $c=-0.945716$. The right picture was taken from Gao et al. (2017)

Fig. 8

The left picture represents the restricted five-body problem with primaries in a convex four-body central configuration, where the parameter values are $\alpha =52.5^{\circ }$, $\beta =27.5^{\circ }$ giving rise to 13 equilibrium points. $m_{1}=0.703401$, $m_{2}=0.03524$, $m_{3}=m_{4}=0.1306769$, $a=0.404883$, $b=1.41891$, $c=-0.898343$. The right picture was taken from Gao et al. (2017)

Fig. 9

The left picture represents the restricted five-body problem with primaries in a convex four-body central configuration, where the parameter values are $\alpha =59.5^{\circ }$, $\beta =2^{\circ }$ giving rise to 11 equilibrium points. $m_{1}=0.173357$, $m_{2}=0.00615907$, $m_{3}=m_{4}= 0.410242$, $a=1.40315$, $b=0.259596$, $c=-0.294517$. The right picture was taken from Gao et al. (2017)

From the information in the previous paragraphs we get that in the two configurations with three primaries close to an equilateral triangle configuration there are 9, 11, 13 or 15 equilibrium points, unlike the Ollöngren problem, where there are only 9, 10 or 15 equilibrium points. It seems that this fact is “hidden” in existing symmetries, which will be broken when the primary bodies reach unequal masses.

6 Concluding remarks

As we have seen, Zotos and Sanam Suraj (2018) studied the restricted five-body problem where three primaries with unit masses from an equilateral configuration, and a body of mass $\tilde{\beta }$ is placed at their center of mass, as introduced by Ollöngren (1988). The authors reparametrized the mass parameter to $\mu ={\frac{1}{1+\tilde{\beta }}}$ and showed, in a numerical fashion, that for $\mu =0.5$ the exist 9 equilibrium points, 3 collinear and 6 non-collinear, while for $\mu =0.995$ there are 15 equilibria, where 5 are collinear and 10 non-collinear. From a numerical point of view these are the only generic cases.

For several restricted five-body problems where the primaries form Érdi-Czirják’s configurations that are close to the Ollöngren problem, the number of the equilibrium points are 9, 11, 13 or 15, but in all these examples the number of the collinear equilibria are different from 5. In none of the cases for the convex or concave Érdi-Czirják’s configurations is recovered this number of collinear equilibria found in the Ollömgren problem. This means that, for any of the considered slight modifications of the Ollöngren problem there is a variation on the number of equilibria and even more, the number of collinear equilibria in it is altered and not retrieved.

It is a hard task to establish a comparison between the numerical studies done in Gao et al. (2017), Zotos and Sanam Suraj (2018), and Zotos and Papadakis (2019), in relation to the number and the evolution of the positions of the equilibrium points, since the symmetries imposed in the Ollöngren problem are very restrictive, as we have seen in the last section. As a matter of fact, for each fixed central configuration one could perform numerical exploration of the basins of attraction for the equilibrium points, but this is not enough. The idea should be to apply technique of the bifurcation theory, to prove the existence and the number of equilibrium points as the parameters are varied. Nevertheless, we have not been able to address this satisfactorily so far.