1 Introduction

Galaxies have various shapes, sizes and colors. To understand how the morphologies of galaxies relate to the physics that create them, galaxies need to be classified. Thus galaxy morphology classification is a key step in studying galaxy formation and evolution. In 1926, Edwin Hubble first proposed the “Hubble Sequence” using visual inspection with fewer than 400 galaxy images (also called the “Hubble Tuning Fork”), and classified galaxies into three basic types: elliptical, spiral and irregular (Hubble 1926; Sandage 2005). The “Hubble Sequence” is still in use today. For a long time, astronomers have used the visual inspection to classify galaxies and update the Hubble’ classification scheme. During recent decades, large scale surveys such as the Sloan Digital Sky Survey (SDSS) have resulted in a tremendous amount of galaxy images. The classification of this enormous quantity of images by astronomers is not only time consuming but also an impossible mission.

Then, the Galaxy Zoo project, which attempted to solve the problem, was launched (Lintott et al. 2008, 2010). Galaxy Zoo 1 with a dataset comprising one million SDSS galaxy images, invited a large number of citizen scientists to provide basic morphological information and identify if a galaxy was ‘‘spiral’’, ‘‘elliptical’’, ‘‘a merger’’or ‘‘star/don’t know’’ (Lintott et al. 2008). The project was a huge success, and the million galaxy images were annotated within several months. Then, Galaxy Zoo 2 (Willett et al. 2013), Galaxy Zoo: Hubble (Willett et al. 2016), and Galaxy Zoo: Cosmic Assembly Near-Infrared Deep Extragalactic Legacy Survey (CANDELS) (Simmons et al. 2016) were launched. Unfortunately, these approaches cannot keep up with the pace of data growth. Thus, astronomers have turned their sights to an automatic classification method.

Galaxy morphology classification using machine learning methods has played an important role in the past 20 years. Artificial neural networks (ANNs), Naive Bayers, decision tree and locally weighted regression have been applied in galaxy classification on relatively small datasets in early work (Naim et al. 1995; Owens et al. 1996; Bazell and Aha 2001; De La Calleja and Fuentes 2004). De La Calleja and Fuentes (2004) found that the accuracy dropped from 95.66% to 56.33% when classifying galaxies into 2 classes to 5 classes, respectively. Banerji et al. (2010) used ANNs to assign galaxies to 3 classes with several input parameters, e.g., colors, shapes, concentration and texture. Gauci et al. (2010) used decision tree and fuzzy logic algorithms to classify galaxy morphology based on the designed photometric parameters and spectral parameters. Ferrari et al. (2015) measured galaxy morphological parameters, including concentration, asymmetry, smoothness, the Gini coefficient, moment, entropy and spirality to automatically classify galaxies using linear discriminant analysis (LDA). Other recent galaxy classification methods (Orlov et al. 2008; Huertas-Company et al. 2011; Polsterer et al. 2012) all require feature extraction, which requires careful human design. It is well known that the performance of classification depends on the choice of data representation, called feature engineering (LeCun et al. 2015). Feature engineering needs domain expertise and is time-consuming.

During the past three years, galaxy morphology classification using deep learning algorithms has received increasingly more attention. Deep learning models are composed of multiple nonlinear layers to learn data representations, these layers are directly fed with raw data and automatically learn the data representations (Bengio et al. 2013; LeCun et al. 2015). After multiple nonlinear transformations, the representations of the higher layers are abstract and beneficial for discrimination and classification. Deep convolutional neural networks (CNNs) have become the dominant approach for image classification tasks. With the availability of a large number of Galaxy Zoo labelled dataset, some studies have yielded good results. For the first time, Dieleman et al. (2015) used a 7-layer CNN to classify galaxy morphology classification, exploiting the translation of galaxy images and rotation invariance. Then, Huertas-Company et al. (2015) used the Dieleman model to classify high redshift galaxies in the 5 CANDELS fields. Hoyle (2016) used CNNs to estimate the photometric redshift of galaxies. Kim and Brunner (2016) presented a star-galaxy classification framework similar to VGG (Simonyan and Zisserman 2014). Recently, CNNs have been applied to find strong gravitational lenses in the Kilo Degree Survey (Petrillo et al. 2017). In addition, Aniyan and Thorat (2017) used CNNs to classify radio galaxies into Fanaro-Riley Class I (FRI), Fanaro-Riley Class II (FRII) and bent-tailed radio galaxies.

In this study, we propose a modified residual network (ResNet) for galaxy morphology classification. We selected 28790 galaxy images from the Galaxy Zoo 2 dataset and used five forms of data augmentation to enlarge the number of our training samples in data preprocessing to avoid overfitting. The variant we proposed combines the advantages of the Dieleman model (Dieleman et al. 2015) and residual networks. In addition, we implemented several other popular CNN models, including Dieleman, AlexNet (Krizhevsky et al. 2012), VGG (Simonyan and Zisserman 2014), Inception (Szegedy et al. 2015; Ioffe and Szegedy 2015; Szegedy et al. 2016, 2017) and ResNets (He et al. 2016a,b) and systematically compared the classification performance of our model with these CNN models. As expected, we demonstrate that our model achieves state-of-the-art performance. Furthermore, to understand what the CNNs learn, we visualized the filter weights and feature maps to provide a qualitative empirical analysis.

This paper is organized as follows. We introduce the dataset selection in Sect. 2. Section 3 describes deep learning models and CNNs. Section 4 contains the data preprocessing pipeline, data augmentation, the proposed ResNet and training tips. Section 5 presents the results and analysis of our network and other CNN models. Finally, we draw conclusions and future work in Sect. 6.

2 Dataset

The galaxy images in this study are drawn from Galaxy Zoo-the Galaxy Challenge,Footnote 1 which contain 61578 JPG color galaxy images with probabilities such that each galaxy is classified into different morphologies. Each image is \(424\times 424\times 3 \) pixels in size taken from the Galaxy Zoo 2 main spectroscopic samples from SDSS DR7.Footnote 2 The morphological classification vote fractions are a modified version of the weighted vote fractions in the Galaxy Zoo 2 project.Footnote 3 The classification vote fractions have a high level of agreement and an authoritative basis with professional astronomers (Willett et al. 2013), and the data have been used in studies of galaxy formation and evolution (Land et al. 2008; Schawinski et al. 2009; Bamford et al. 2009; Willett et al. 2015).

In this study, clean samples are selected that match a specific morphology category with an appropriate threshold (Willett et al. 2013), which depends on the number of votes for a classification task considered to be sufficient. For example, to select the spiral, the cuts are the combination of \(f_{\text{features/disk}} \geq 0.430\), \(f_{\text{edge-on,no}} \geq 0.715\), and \(f_{\text{spiral,yes}} \geq 0.619\). These thresholds are considered conservative for the selection of clean samples in Willett et al. (2013). By this means, we assign galaxy images to five classes, i.e., completely round smooth, in-between smooth (between completely round and cigar-shaped), cigar-shaped smooth, edge-on and spiral. In practice, all thresholds are derived from Willett et al. (2013) except that the thresholds of smooth galaxies are relaxed from 0.8 to 0.5, and for full details refer to Willett et al. (2013). Table 1 shows the clean sample selection criterion for every class. The 5 classes of galaxies are referred to as 0, 1, 2, 3 and 4, each containing a sample of 8434, 8069, 578, 3903 and 7806 images, respectively. Figure 1 shows the galaxy images randomly selected from the dataset, and each row represents a class. From top to bottom, their labels are 0, 1, 2, 3 and 4.

Fig. 1
figure 1

Example galaxy images from the dataset. Each row represents a class. From top to bottom, their Galaxy Zoo 2 labels are completely round smooth, in-between smooth, cigar-shaped smooth, edge-on and spiral. They are referred to as 0, 1, 2, 3 and 4

Full size image
Table 1 Clean samples selection in Galaxy Zoo 2. The clean galaxy images are selected from Galaxy Zoo 2 data release (Willett et al. 2013), in which thresholds determine well-sampled galaxies. Moreover, for Table 1 they are called clean samples. Thresholds depend on the number of votes for a classification task considered to be sufficient. As an example, to select the spiral, cuts are the combination of \(f_{\text{features/disk}} \geq 0.430\), \(f_{\text{edge-on,no}} \geq 0.715\) and \(f_{\text{spiral,yes}} \geq 0.619\)
Full size table

The dataset reduces to 28790 images after filtering and is then divided into a training set and a testing set at a ratio of 9:1. Thus, there are 25911 images for the training set to train our model, and the remaining 2879 images are used for the testing set to evaluate our model. The training and testing sets have the same distribution. Table 2 gives the number of galaxy images in each morphological class of the training and testing sets, and Fig. 2 reproduces the dataset graphically.

Fig. 2
figure 2

Galaxy samples counts

Full size image
Table 2 Number of galaxy images in each morphological class in each set. The numbers 0, 1, 2, 3 and 4 represent completely round, in-between, cigar-shaped, edge-on and spiral, galaxy classes, respectively
Full size table

3 Deep convolutional neural networks

Deep learning models are composed of multiple layers to automatically learn data representations from the raw data, which are capital for classification, localization, detection, and segmentation without feature extraction (LeCun et al. 2015). Deep CNNs have played an important role in deep learning (Goodfellow et al. 2016) and have become the dominant approach in image classification. In this section, we briefly introduce ANNs and CNNs, especially ResNets.

3.1 Artificial neural networks

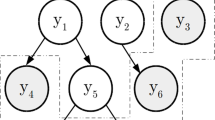
ANNs are composed of simple adaptive interconnected units that can simulate biological nervous systems as interactions in response to real-world objects (Kohonen 1988). Figure 3 shows a simple feedforward neural network, which is composed of an input layer, a hidden layer and an output layer. Formally, \(x_{i}^{l}\), \(x_{j}^{l+1}\) are defined as the \(i\)-th neuron of \(l\)-th layer and the \(j\)-th neuron of \((l+1)\)-th layer, and \(w_{ij}^{l}\), \(b_{j}^{l}\) are defined as weights and the bias of the \(l\)-th layer, respectively. Then, the outputs of the \(l\)-th layer are \(x_{j}^{l+1} \):

$$ x_{j}^{l+1}=f\biggl(\sum _{i\in N^{l}}\bigl(w_{ij}^{l}x_{i}^{l}+b_{j}^{l} \bigr)\biggr) $$
(1)

where \(N^{l}\) is the number of \(l\)-th layers and \(f \) is the activation function. Activation functions have many types, such as the popular rectified linear unit (ReLU) (Nair and Hinton 2010), \(f=\max (0,x)\), sigmoid, tanh, leaky ReLU, and exponential linear unit (ELU).

Fig. 3
figure 3

Schematic of a feed forward neural network

Full size image

Then, we let \(\hat{y}=( \hat{y_{1}},\hat{y_{2}} , \ldots , \hat{y_{k}}, \ldots , \hat{y_{m}})\) be the output of the network and \(y=( y_{1}, y_{2}, \ldots , y_{k}, \ldots y_{m} ) \) be the desired output and we define a cost function \(\ell ( \hat{y},y)\). In the classification task, cross entrophy can be selected as the cost function. In particular, in binary classification, the cross entropy can be defined as

$$ \ell (\hat{y},y)=-y\log \hat{y} -(1-y)\log (1-\hat{y}) $$
(2)

where \(y\in \{0, 1\}\), \(\hat{y}\in [0, 1] \). Then, we compute the cross entropy of all training data. To minimize the cross entropy, we use stochastic gradient descent (SGD) to update the weights and bias until the loss function converges:

$$ w_{n+1}^{l}=w_{n}^{l}-\eta \frac{\partial \ell }{\partial w_{n}^{l}} $$
(3)
$$ b_{n+1}^{l}=b_{n}^{l}-\eta \frac{\partial \ell }{\partial b_{n}^{l}} $$
(4)

where \(\eta \) is the learning rate. Of course, in practice, we use minibatch SGD instead of all data SGD to save training time when seeking a local optimal solution.

3.2 Convolutional neural networks

CNNs or ConvNets (Cun et al. 1989) are designed to process multiple arrays data, for example, image data. CNNs have been very successful in practical applications. A classical layer of a CNN consists of three stages. In the first stage, the layer performs several convolutions. Then, a nonlinear activation function such as ReLU is applied. Finally, a pooling function modifies the output of the layer (Goodfellow et al. 2016). CNNs generally contain convolutional layers, pooling layers and fully connected layers.

Convolutional layers

Convolution is a specialized type of linear operation. Discrete convolution can be viewed as multiplication by a matrix. Convolutional layers can be computed by

$$ x_{j}^{l}=f(\Sigma _{i\in M_{j}}x_{i}^{l-1}\times k_{ij}^{l}+b_{j}^{l}) $$
(5)

where \(l\) is the number of layers, \(f\) is the activation function, usually ReLU, \(k\) represents the convolutional kernel, \(M_{j}\) represents the receptive field and \(b\) is the bias.

Pooling layers (also called subsampling)

Pooling can be achieved by taking the average (average pooling) or the maximum (max pooling) value within a rectangular neighbourhood of pixels. For an image, subsampling can reduce the image sizes.

Fully connected layers

Fully connected layers are usually followed by the last pooling layer or the convolutional layer, and every neuron in fully connected layers is connected to all the neurons in the upper layers.

Generally, CNNs have sparse connectivity, parameter sharing and equivariant representation, which represent three important ideas.

Deep CNNs have brought about a series of breakthroughs in image classification. CNNs are becoming increasingly deeper, from 8 layers (Krizhevsky et al. 2012), 16/19 layers (Simonyan and Zisserman 2014), 42 layers (Szegedy et al. 2016), to 152 layers (He et al. 2016a). In order to train deeper networks, some new techniques have been adopted, such as ReLU (Nair and Hinton 2010), dropout (Srivastava et al. 2014), graphics processing units (GPUs), data augmentation (Krizhevsky et al. 2012), and batch normalization (BN) (Ioffe and Szegedy 2015). Currently, CNN models have developed several versions, primarily including AlexNet (Krizhevsky et al. 2012), VGG (Simonyan and Zisserman 2014), Inception (Szegedy et al. 2015; Ioffe and Szegedy 2015; Szegedy et al. 2016, 2017), ResNets (He et al. 2016a,b) and DenseNet (Huang et al. 2016).

3.3 Residual Networks

Deep ResNets are reported in He et al. (2016a,b), which can deepen the networks up to thousands of layers and can achieve state-of-the-art performance. In this section, we provide a brief description of ResNets.

He et al. (2016a) proposed a deep residual learning framework: let the layers try to learn a residual mapping instead of the directly desired underlying mapping of a few stacked layers. Figure 4 shows a residual building block. Let the desired underlying mapping be \(H(x_{l}) \), and let the stacked nonlinear layers fit the mapping of \(F(x_{l})=H(x_{l})-x_{l} \). This is a residual framework. The formulation \(F(x_{l})=H(x_{l})-x_{l} \) can be written as \(H(x_{l})=F(x _{l})+ x_{l} \), and \(F(x_{l})+ x_{l} \) can be realized by feeding forward the neural networks with a “short connection” (Fig. 4); this process skips one or more layers and performs identity mapping. Finally, their outputs are added to the outputs of the stacked layers. A residual unit can be expressed as follows:

$$ x_{l+1}=f\bigl(h(x_{l})+F(x_{l},W_{l}) \bigr) $$
(6)

where \(x_{l} \) and \(x_{l+1} \) are the input and output of the \(l\)-th unit, respectively. In addition, \(F \) is a residual function. For example, Fig. 4 has two layers, \(F=W_{2}\sigma (W _{1}x) \) in which \(\sigma \) denotes ReLU and the biases are omitted to simplify the notation. Additionally, \(h(x_{l})=x_{l} \) and \(f \) is a ReLU function.

Fig. 4
figure 4

Residual learning: a building block

Full size image

There are two types of residual building blocks in He et al. (2016a) as shown in Fig. 5. The basic residual unit (Fig. 5, left) contains two layers, namely, \(3\times 3\), \(3 \times 3 \) convolutions. To decrease the training time and network parameters, a modified residual unit is presented as Fig. 5 (right), which is called a “bottleneck” building block. The “bottleneck” building block uses 3 layers instead of 2 layers and they are \(1 \times 1\), \(3\times 3\), \(1 \times 1 \) convolutions, where the \(1 \times 1 \) convolutional layers can both decrease and increase the dimensions.

Fig. 5
figure 5

A deeper residual function F. Left: a building block as in Fig. 4 for ResNet-34. Right: a “bottleneck” building block for ResNet-50/101/152/200. Reproduced from Fig. 5 in He et al. (2016a)

Full size image

In He et al. (2016b), both \(h(x_{l}) \) and \(f \) are identity mapping functions, where the signal could be directly propagated from one unit to other units, in both forward and backward passes. The residual unit can be redefined as:

$$ x_{l+1}=x_{l}+F(x_{l},W_{l}) $$
(7)

He et al. (2016b) also adopted ‘‘preactivation’’, where “BN-ReLU-Conv” replaced the traditional ‘‘Conv-BN-ReLU’’. This is called ResNet V2, which is much easier to train and exhibits better performance than ResNet V1 (He et al. 2016a). ResNets have many versions, such as ResNet-50/101/152/200 with, deeper layers up to 1001 layers.

4 Approach

In the previous section, we introduced the theory of ResNets. In this section, we describe our framework including data preprocessing, data augmentation, scale jittering, network architecture, and implementation details.

4.1 Preprocessing

From the dataset, the images are composed of large fields of view with the galaxy of interest in the center. Therefore, it is necessary to crop the image in the first step. In practice, we crop from the center of the image to a range scale \(S=[170,240]\) in the training set for every image (as explained later). This strategy allows all the main information to be contained in the center of the image, eliminates considerable noise, such as other secondary objects, and reduces the dimensions of the images by almost a quarter for faster training. The complete preprocessing procedure is illustrated in Fig. 6.

Fig. 6
figure 6

Preprocessing procedure. The original image is first center cropped to a range scale \(S=[170,240]\) in training set (\(Q=\{ 180,200,220,240\} \)in testing set). For example, the spiral galaxy (GalaxyID: 237308) is cropped to \(220 \times 220 \times 3 \) pixels, then resized to \(80 \times 80 \times 3 \) pixels, randomly cropped to \(64 \times 64 \times 3 \) pixels, randomly rotated \(0^{\circ }\), \(90^{\circ }\), \(180^{\circ }\), \(270^{\circ }\), and randomly horizontally flipped. After optical distorting and image whitening, it (\(64 \times 64 \times 3 \) pixels) becomes the input of networks

Full size image

Then, the image is resized to \(80 \times 80 \times 3 \) pixels, which is just dimension reduction and is easy to compute using a limited computing source. Next, a random cropping operation is carried out, which increases the size of the training set by a factor of 256. The size of the image drops to \(64 \times 64 \times 3 \) pixels. Next, the image is randomly rotated by \(0^{\circ }\), \(90^{\circ }\), \(180^{\circ }\), and \(270^{\circ } \) because of the rotation invariance of galaxy images and then is randomly horizontally flipped. Brightness, contrast, saturation and hue adjustments are applied to the image and the last step is image whitening. The abovementioned process describes the whole preprocessing pipeline in training. After those steps, images (\(64 \times 64 \times 3 \) pixels) will be used as input to the network when training.

At testing time, the preprocessing procedure does not include random cropping, rotation, horizontal flipping and optical distortion. After center cropping to a fixed value \(Q=\{ 180,200,220,240\} \) (as explained later), the image is resized to \(80 \times 80 \times 3 \) pixels and then center cropping is performed again, thus, the size of the image is \(64 \times 64 \times 3 \) pixels. The last step is still image whitening, and the images will be used as input to the networks when testing.

4.2 Data augmentation

To avoid overfitting, data augmentation is a common and effective way to reduce overfitting. Because of our limited training data, data augmentation can enlarge the number of training images. We use five different forms of data augmentation.

Scale jittering is the first form of data augmentation. During the training time, we crop the images to a range scale \(S=[170,240]\), which is called multi-scale training images because of the \(S \) random value. Because different images can be cropped to different sizes and even the same images can be cropped to different sizes at different iterations, it is beneficial to consider data augmentation during training. This approach can be seen as training set augmentation by scale jittering.

Random cropping is carried out from \(80 \times 80 \times 3 \) pixels to \(64 \times 64 \times 3 \) pixels, which increases the size of the training set by a factor of 256. Rotating training images by \(0^{\circ }\), \(90^{\circ }\), \(180^{\circ }\), and \(270^{\circ } \) can enlarge the size of the training set by a factor of 4. A horizontal flipping is a doubling of training images.

The first four forms of data augmentation are affine transformations, which entail very little computation and these transformations are completed on the CPU before training on the central processing unit (CPU). Brightness, contrast, saturation and hue adjustment are the same in Krizhevsky et al. (2012), which are optical distortion for data augmentation.

4.3 Scale jittering

Scale jittering is derived from Simonyan and Zisserman (2014), in which the images of the input are cropped from multiscale training images and fixed multiscale testing images.

Training scale jittering

Let set \(S \) be multiscale training (we also refer to \(S \) as the training scale), where each training image is individually rescaled by randomly sampling \(S \) from a certain range \([S_{\min}, S_{\max}] \) (we use \(S_{\min}=170\) and \(S_{\max}=240 \)). Thus, different images can be cropped to different sizes, and even the same images can be cropped to different sizes at different iterations, which greatly enlarge the number of training sets and effectively avoid overfitting. This process can be seen as training set augmentation by scale jittering.

Testing scale jittering

Let set \(Q \) be fixed multiscale testing (we also refer to \(Q \) as the testing scale). In practice, we use \(Q=\{ 180,200,220,240\} \) when testing, which makes our models achieve better performance.

4.4 Network architecture

Our model is a variant of ResNets V2 (He et al. 2016b). As Sect. 3.3 describes, deep ResNets always seek increasingly deeper layers. Therefore, ResNets are very thin and high. Recent research shows that such deep ResNets encounter the risk of diminishing feature reuse, which train very slowly and need too much time (Zagoruyko and Komodakis 2016). We propose a network specially designed for a galaxy by trying to decrease the depth and widen the ResNets. Our overall architecture of the network is depicted in Fig. 8 and Table 3.

Table 3 Architecture of our model for galaxy in this study. Residual units are shown in brackets. where \(k \) is the widening factor, and \(N \) denotes the number of blocks in the group (We use \(k=2\), \(N=2\), which means our network is 26 layers in total). Downsampling is performed by the last layers in groups conv2, conv3 and conv4 with a stride of 2
Full size table

We adopt full preactivation residual units, as shown in Fig. 7. A “bottleneck” building block (Fig. 5, right) presented in He et al. (2016a) is used, namely, a combination of \(1 \times 1\), \(3\times 3\), and \(1 \times 1\) convolutions, for example, \(1 \times 1\), \(m \times k \) convolution, \(3\times 3\), \(m \times k\) convolution, \(1 \times 1\), \(n \times k\) convolution, where \(m\), \(n \) denotes the number of channels and \(k \) is the widening factor. The full preactivation includes the standard ‘‘BN-ReLU-Conv’’operation. In addition, we add a dropout after the \(3\times 3\) convolution whereas ResNet V2 (He et al. 2016b) did not use a dropout to prevent coadaptation and overfitting. The residual unit is defined as

$$ x_{l+1}=x_{l}+W_{3}\sigma \bigl(W_{2}\sigma \bigl(W_{1}\sigma (x_{l}) \bigr)\bigr). $$
(8)

Here, \(x_{l} \) and \(x_{l+1} \) are the input to and output of the \(l\)-th unit, respectively; \(\sigma \) denotes the BN and ReLU; and \(W_{1}\), \(W_{2}\), \(W_{2}\) represent 3 convolutional kernels. The dropout is placed after the \(W_{2} \) operation and the biases are omitted to simplify the notations.

Fig. 7
figure 7

Full preactivation residual unit in our study. \(m\), \(n \) denotes the number of channel, \(k \) is the widening factor. We use \(1 \times 1\), \(3\times 3\), and \(1 \times 1\) convolutions and the standard “BN-ReLU-Conv”

Full size image

Then, considering our network architecture (Fig. 8 and Table 3), the size of the input to the network is \(64 \times 64 \times 3 \) pixels. First, 64 kernels of size \(6 \times 6 \times 3\) with a stride of 1 are implemented, which is derived from Dieleman et al. (2015) and proven to be optimal. After the first convolutional layer, a maximum pooling of size \(2\times 2\) with a stride of 2 is connected. The size of the output of the image becomes \(32 \times 32 \times 64 \).

Fig. 8
figure 8

Our network architecture for Galaxy in this study. where \(k \) is the widening factor. The dashed shortcuts decrease dimensions. Table 3 shows more details

Full size image

The output of maximum pooling is fed to 4 convolutional groups: conv2, conv3, conv4 and conv5. Each group has 2 residual blocks. For example, in convolutional group 2, there are 2 residual blocks: \(1 \times 1\), \(64 \times 2 \) (128 channels) convolution, \(3\times 3,64 \times 2\) (128 channels) convolution, \(1 \times 1\), \(256\times 2 \) (512 channels) convolution; \(1 \times 1, 64 \times 2 \) (128 channels) convolution, \(3\times 3\), \(64 \times 2\) (128 channels) convolution, \(1 \times 1\), \(256 \times 2 \) (512 channels) convolution with a stride of 2, which perform downsampling. Group3, group4 and group 5 are the same, except for the last layer of group 5, which does not perform downsampling. Downsampling is performed in the last layers in groups conv2, conv3 and conv4 with a stride of 2.

The dashed shortcuts of Fig. 8 decrease the dimensions. The contributions of \(1\times 1\) convolutional layers are reducing the dimensions at first and then increasing dimensions to reduce the parameters of the model and speed up training. The last layer is the global average-pooling layer with a \(4 \times 4 \) kernel, and the size of the output of average pooling is \(1 \times 1 \times 4096 \). Finally, a 5-way fully connected layer is implemented with softmax.

where \(k \) is the widening factor and \(N \) denotes the number of blocks in the group. After hundreds of attempts, we finally use \(k=2\), \(N=2\) in practice. Therefore, our network includes 26 layers, including 26.3 M parameters. The 26-layer network achieves the best performance regarding accuracy and other metrics.

From our network architecture, some tips are concluded: the first convolutional layer adopts a relatively large convolution filter of \(6 \times 6 \); the convolutional layers mostly have \(1 \times 1\) and \(3\times 3 \) convolutions. The advantages of \(1 \times 1\) convolutions have been described. The advantages of small \(3\times 3 \) filters were demonstrated in (Simonyan and Zisserman 2014), which can decrease the number of parameters of the model and achieve a better performance. The feature maps in each group are the same except for the last layer of each convolutional group (conv2, conv3 and conv4). The feature map size is halved, and the number of filters is doubled.

4.5 Implementation details

We use minibatch gradient descent with a batch size of 128 and a Nesterov momentum of 0.9. The initial learning rate is set to 0.1, then decreases by a factor of 10 at 30k and 60k iterations, and we stop training after 72k iterations. The weight decay is 0.0001, the dropout probability value is 0.8 and the weights are initialized as in He et al. (2015). We adopt BN before activation and convolution, following He et al. (2016b).

Our implementation is based on Python, Pandas, scikit-learn (Pedregosa et al. 2012) and scikit-image (Van Walt et al. 2014), and TensorFlow (Abadi et al. 2016). It takes approximately 31.5 hours to train a single network with an NVIDIA Tesla K80 GPU. Our code is available at https://github.com/Adaydl/GalaxyClassification.

5 Results and discussion

In this section, we describe 7 types of classification performance metrics: accuracy, precision, recall, F1, confusion matrix (CM), receiver operating characteristic (ROC) and area under an ROC curve (AUC). Then, we show the results of our model and systematically compare the performance of our model with other popular CNN models, such as Dieleman, AlexNet, VGG, Inception and ResNets. Ultimately, we visualize the filters and feature maps.

5.1 Classification performance metrics

To assess the performance of our classification models, we present 7 types of classification performance metrics: accuracy, precision, recall, F1, CM, ROC and AUC. They are defined as follows:

Accuracy

\(\hat{y_{i}}\) is the predicted value of the \(i\)-th sample and \(y_{i}\) is the corresponding true value. Then, the fraction of correct predictions over \(n_{samples}\) is defined as:

$$ Accuracy(y_{i},\hat{y_{i}})=\frac{1}{n_{\mathrm{samples}}}\sum _{i=0}^{n_{\mathrm{samples}}-1}1( \hat{y_{i}}=y_{i}). $$
(9)

Precision, recall and & F1

(Ceri et al. 2013) Given the number of true positive (TP), false positive (FP), true negative (TN) and false negative (FN), we define the following:

$$\begin{aligned} &P=\frac{TP}{TP+FP}. \end{aligned}$$
(10)
$$\begin{aligned} &R=\frac{TP}{TP+FN}, \end{aligned}$$
(11)
$$\begin{aligned} &F1=\frac{2PR}{P+R}. \end{aligned}$$
(12)

Confusion matrix (CM)

An entry \(CM_{ij}\) \(( i,j=1,2, \ldots , n_{\mathrm{samples}}) \) is defined as the number of the true class \(i \),that is predicted to class \(j \).

ROC & AUC

A ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) for every possible classification threshold. AUC is the area under the ROC curve. The closer the AUC is to 1, the better the classification performance is.

5.2 Classification results and discussion

In this section, we summarize the results of our models on 7 types of classification performance metrics and compare the results of our model with other popular CNNs.

Table 4 shows precision, recall and F1 values of our model for each class on testing set. The numbers 0, 1, 2, 3 and 4 represent completely round, in-between, cigar-shaped, edge-on and spiral galaxy classes, respectively. The average precision, recall and F1 of the 5 galaxy classes of our model are 0.9512, 0.9521 and 0.9515. respectively. The completely round achieves the best precision of 0.9611. The spiral achieves the best recall of 0.9782 and the best F1 value of 0.9677. On the whole, the results for the completely round, the in-between, the edge-on and the spiral are excellent. Those for the cigar-shaped images are not excellent. This result is due to the small number of cigar-shaped images for training.

Table 4 Precision, Recall and F1 of our model for each class on testing set
Full size table

The CM of our model for each class on the testing set is shown in Table 5. The column represents the true label and the row represents the prediction label. Consequently,815 completely round, 762 in-between, 34 cigar-shaped, 368 edge-on and 763 spiral are classified correctly. Therefore, the accuracies of the 5 galaxy types are as follows: completely round, 96.6785%; in-between, 94.4238%; cigar-shaped, 58.6207%; edge-on, 94.3590% and spiral, 97.6953%. For teh completely round, 29 are incorrectly classified as in-between. Obviously, intuition suggestions that since completely round and in-between classes are similar, they are easily misclassified. Notably, 4 completely round are misclassified as spiral, perhaps due to faint images photographed from far distances. Additionally, 12 cigar-shaped classes are misclassified as edge-on and 18 edge-on classes are misclassified as cigar-shaped, where the number of misclassifications is greater than that of the others. We presume that this behaviour occurs due to the similarity of the cigar-shaped and edge-on classes, which is very surprising.

Table 5 Confusion matrix of our model for each class on testing set. The column represents true label and row represents prediction label
Full size table

Figure 9 shows the ROC curve of our model for the 5 classes of galaxies in the testing set. Each color represents a class. The closer the TPR is to 1 and the FPR is to 0, the better the curve prediction, namely, the closer the curve is to the upper left corner, the better it predicts. From Fig. 9, the ROC curve of each class performs well, and the edge-on demonstrates the best predictions and the cigar-shaped exhibits a relatively poorer prediction, which occurs due to the small number of cigar-shaped images. The average AUC of our model is 0.9823, which shows that the overall prediction performance of our model is excellent.

Fig. 9
figure 9

ROC curve of our model for 5 classes galaxies on testing set. Each color represents a class

Full size image

Table 6 summarizes the test accuracy of different methods at multiple test scales. Our results are based on average values of the maximum values of 10 runs at each test scale. Recent research shows that scale jittering at testing time can obtain a better performance (Simonyan and Zisserman 2014). Our model obtains the best results with a 94.6875% accuracy. Table 6 shows that the Dieleman model works well with a 93.8800% accuracy, although only a 7-layer CNN was used. Clearly, our model designed specifically for galaxy images while the other networks, such as AlexNet, VGG, Inception, and ResNets, are designed for ImageNet, however, they demonstrate excellent performance because of their good generalization performance. For example, AlexNet is an 8-layer CNN that won first place in the ImageNet LSVRC-2012. Here, it achieves a 91.8230% accuracy due to its use of a relatively large filter (\(11\times 11 \) convolution). VGG-16 achieves a 93.1336% accuracy and uses many small \(3 \times 3 \) filters. Inception implemented here is Inception V3, which includes 42 layers with carefully designed inception modules, and achieves a 94.2014% accuracy. ResNet-50 is implemented as pre-act-ResNets and obtains a 94.0972% accuracy.

Table 6 Test accuracy of different methods at multiple testing scales. Our results are based on average values of the maximum values of 10-time runs of each testing scale. The bold entries highlight the best results
Full size table

Table 7 summarizes the test accuracy, precision, recall, F1 and AUC of different methods. Our results are based on the maximum values of 10 runs of each testing scale. Notably, the accuracy results are better than the results indicated in Table 6 because they are obtained by selecting the maximum values of 10 runs of each testing scale instead of the average values of the maximum values of 10 runs of each testing scale. Our model achieves the best accuracy of 95.2083% at a single testing scale. Because the fatal flaw of accuracy as a measure in a multiclass task is that it depends on the number of samples in the majority class, we also adopt average precision, recall, F1 and AUC to measure the classification performance. Our model obtains the best average precision of 0.9512, the best average recall of 0.9521 and the best average F1 of 0.9515. Inception achieves the best average AUC of 0.9852. On the whole, our model is excellent and achieves state-of-the-art performance.

Table 7 Test accuracy, precision, recall, F1 and AUC of different methods. Our results are based on the maximum values of 10-time runs of each testing scale. The bold entries highlight the best results within each column
Full size table

5.3 Filters and feature maps visualization

Neural networks are always known as ‘‘black boxes’’. Since we want to visualize what the CNN learns, we visualize filter weights and feature maps and then provide a qualitative empirical analysis (Zeiler and Fergus 2014; Yosinski et al. 2015). For easy understanding, we visualize a simple CNN, 7 layers in total, including 4 convolutional layers (\(6\times 6 \), 32 filters, \(5\times 5\), 64 filters, \(3 \times 3 \), 128 filters, and \(3\times 3 \), 128 filters, respectively) and 3 fully connected layers.

Figure 10 shows the features that the filter weights learn in every convolutional layer. The first layer filters detect the different galaxy edges, corners, etc. from the original pixels, abd then the edge are used to detect simple shapes, such as a bar or an ellipse, in second layer filters. Next these shapes are used to detect more advanced features in high-level layer filters. More invariant representations are learned with increasing layers. From Fig. 10, different filters also learn different color information, mainly red and blue that might correspond to the color of galaxy itself, such as a red elliptical galaxy and or a blue spiral galaxy.

Fig. 10
figure 10

Filter weights learned on every convolutional layer. From top to bottom, they are filter weights of 4 convolutional layers. From left to right, they are filter weights visualization of different channels on certain convolutional layer. Brackets show the number of filters, the size of filters and channels visualized

Full size image

Figure 11 shows the activation of each layer on a smooth galaxy (GalaxyID: 909652). In the first layer, some feature maps recognize the intermediate core of the galaxy, and some recognize the background. In high layers, feature maps recognize the abstract blobs with a combination of high-level features, e.g., in the fourth convolutional layer. After pooling layers, the differentiability of each feature map is stronger, which is the exact expectation of the classification model. These interesting phenomena can also be found in Fig. 12 and Fig. 13.

Fig. 11
figure 11

Activations of each layer on a smooth galaxy (GalaxyID: 909652). From top to bottom, left to right, they are: input image after whitening; activations on the Conv 1, Pooling 1, Conv 2, Pooling 2, Conv 3, Conv 4 and Pooling 4. Brackets show the number of feature maps and the size of feature maps

Full size image
Fig. 12
figure 12

Similar to Fig. 11 but for an edge-on galaxy (GalaxyID: 416412)

Full size image
Fig. 13
figure 13

Similar to Fig. 11 but for a spiral galaxy (GalaxyID: 237308)

Full size image

6 Conclusions

In this paper, we propose a variant of ResNets for galaxy morphology classification. We classify 28790 galaxies into 5 classes, namely, completely round smooth, in-between smooth (between completely round and cigar-shaped), cigar-shaped smooth, edge-on and spiral using the Galaxy Zoo 2 dataset. In data preprocessing, a complete preprocessing pipeline is presented and five forms of data augmentation are adopted to avoid overfitting, especially the scale jittering approach that vastly enlarges the number of training images.

The advantage of our network is combining the Dieleman model with ResNets, in which we try to decrease the depth and widen the ResNet. We use a “bottleneck” residual unit with full preactivation “BN-ReLU-Conv”. To avoid overfitting, we use dropout after a \(3\times 3\) convolution. Our network has 26 layers with 26.3 M parameters. We perform a systematic comparison between our model and other popular CNNs in deep learning, such as Dieleman, AlexNet, VGG, Inception and ResNets. Our model achieves the best classification performance, with an overall accuracy on the testing set of 95.2083% , while the accuracies of the 5 galaxy types are completely round, 96.6785%; in-between, 94.4238%; cigar-shaped, 58.6207%; edge-on, 94.3590% and spiral, 97.6953%. The average precision, recall, F1 and AUC of our model are 0.9512, 0.9521, 0.9515 and 0.9823, respectively. From the CM, we find that 12 cigar-shaped classes are misclassified as edge-on and 18 edge-on are misclassified as cigar-shaped, where the number of misclassifications is greater than that of others. We believe that this occurs due to the similarity of cigar-shaped and edge-on classes, which is very surprising. The Dieleman model also works well, and the average accuracy is 94.6528% because it is specially designed for galaxy images. Although AlexNet, VGG, Inception and ResNets are designed for ImageNet, they all achieve excellent performance with accuracies of 92.2569%, 93.6458%, 94.5139% and 94.6857%, respectively, because of their good generalization.

By visualizing filter weights and feature maps, we attempt to understand what the CNN model learns. For instance, the first layer filters detect the different galaxy edges, corners, etc., from the original pixels, and then edges are used to detect simple shapes, such as a bar or an ellipse, in the second layer filters. Next these shapes are utilized to detect more advanced features in the high-level layer filters. We also find that different filters also learn different color information, mainly red and blue, which might correspond to the color of the galaxy itself, such as a red elliptical galaxy or a blue spiral galaxy. Regarding the activations of each layer on a galaxy image, some feature maps recognize the intermediate core, some recognize the background part in the first layer, and feature maps recognize the abstract blobs with a combination of high-level features in the higher layers. Additionally, after pooling layers, the differentiability of each feature map is stronger, which is the exact expectation of the classification medel.

In the future, large-scale surveys, such as the Dark Energy Survey (DES) and the LSST survey, billions of galaxy images will be obtained, and our algorithms can be applied to automatically classify galaxies and achieve state-of-the-art performance.

In future work, we focus on a much more fine-grained galaxy morphology classification. We plan to train our model on a larger and higher quality galaxy dataset. Ultimately, more advanced algorithms in deep learning will merge with galaxy morphology classification.