1 Introduction

Asteroids, considered to be remnant material from the early solar system, have become desirable destinations for deep space exploration in recent years. Valuable information from asteroids about the evolution of the solar system, the formation of planets and the source of life, as well as their potential for human exploration missions, attracts both scientists and engineers. However, missions to asteroids face significant dynamical problems. One of the major challenges to probes is the strong gravitational perturbations caused by the irregular shapes of asteroids. Lack of familiarity with the dynamics of the environment in the vicinity of an asteroid makes it difficult to keep a spacecraft safe around a small body.

To overcome this difficulty, several studies have been conducted in the past. Different asteroid models have been proposed to approximate the gravity field caused by the irregular shape of an asteroid, including but not limited to a tri-axial ellipsoid (Scheeres 1994), a homogeneous cube (Liu et al. 2011a,b), an annular disk (Alberti and Vidal 2007), an elongated segment (Riaguas et al. 2001), a dumbbell-shaped body (Li et al. 2013), a combination of a sphere and an ellipsoid (Feng et al. 2015, 2016), a rotating mass dipole (Zeng et al. 2015) and a polyhedron model (Hudson and Ostro 1994; Yu and Baoyin 2012b; Wang et al. 2015). Of these, the dumbbell-shaped body is an ideal model, consisting of two incomplete spheres and one optional cylinder. By varying the relative position and the size of spheres, this model has the ability to simulate an elongated asteroid, a contact binary or more complicated asteroids, which are suitable approximations for a number of real celestial bodies in the solar system.

Based on the above gravitational models, the motion of a particle in the vicinity of an asteroid has been investigated. The equilibrium points and stability, periodic orbits (Scheeres et al. 1996; Yu and Baoyin 2013; Wang et al. 2014) and topological structure of motion (Lara and Scheeres 2002; Jiang and Baoyin 2014; Jiang et al. 2014; Feng et al. 2016) around the asteroid have been studied. In particular, based on the dumbbell-shaped model, Li analyzed the equilibrium points and their linear stability for different length-diameter ratios. Additionally, planar periodic orbits around equilibrium points were found.

In this paper, we further investigate the motion around dumbbell-shaped bodies. In particular, we extend the research from local motion around equilibrium points to global motion in the vicinity of a dumbbell-shaped body. The local motion in space is discussed, and additional families of periodic orbits around equilibria are generated by bifurcation theory. Moreover, the invariant manifold associated with orbits is analyzed, which may help to study the low-energy connections between equilibria. With the help of manifolds and Poincaré sections, potential global transfer trajectories around a dumbbell-shaped body are designed. The study of local and global motion can provide a reference to select proper transfer and reconnaissance orbits around small celestial bodies, which is essential to future exploration mission design.

This paper is organized as follows. In Sect. 2, the dumbbell-shaped model is established, the equilibria are calculated, and the critical angular speed is investigated. In Sect. 3, we treat the local motion around equilibria. With the continuation method and bifurcation theory, several families of periodic orbits are generated. The global motion in the vicinity of a dumbbell-shaped body is discussed in Sect. 4. The invariant manifolds associated with periodic orbits are calculated for different extended length-diameter ratios and orbit amplitudes. By introducing the Poincaré section, the heteroclinic connections around dumbbell-shaped bodies are analyzed. Finally, several global transfer trajectories are designed to demonstrate the potential application to small-body exploration.

2 Dynamic equation in dumbbell-shaped model

2.1 The dumbbell-shaped model

In this paper, a dumbbell-shaped body is employed for dynamic research. The model is the combination of two incomplete spheres and an optional cylinder, as shown in Fig. 1.

Fig. 1
figure 1

The dumbbell-shaped model

Full size image

For simplicity, the radii of the two spheres are the same, denoted as \(R\). The radius of the cylinder is half that of the sphere, \({R_{c}} = {R/2}\). There is one additional important parameter that describes the shape of the model: the length-diameter ratio \(m=L/2R\), where \(L\) is distance between the centers of the two spheres. It is easy to show that \(m\leq\sqrt{3}/2\) describes two spheres in contact, which is analogous to a contact binary asteroid. The cylinder is used when \(m>\sqrt{3}/2\); the height of cylinder is \(H = L - 2\sqrt {{R^{2}} - R_{c}^{2}} \). The special case of \(m = 0\) represents a single sphere.

2.2 Gravitational potential

We assume that the dumbbell-shaped body is homogeneous. The gravitational potential of a dumbbell-shaped body can be calculated by the polyhedron method (Werner and Scheeres 1996). The incomplete spheres and cylinder are meshed into a set of tetrahedrons. The gravitational potential at an external point \(P\) due to each part can be calculated by Eq. (1).

$$ U=\frac{1}{2}G\sigma \sum _{e\in{\mathit{edges}}} \mathbf{r}_{e}\cdot\mathbf{E}_{e}\cdot\mathbf{r}_{e} \cdot L_{e}- \frac{1}{2}G\sigma \sum _{f\in{\mathit{faces}}} \mathbf{r}_{f}\cdot\mathbf{F}_{f}\cdot\mathbf{r}_{f} \cdot\omega_{f} $$
(1)

where \(L_{e}\) and \(\omega _{f}\) represent the line factor and the face factor, respectively. \({\mathbf{{r}}_{e}}\) is a vector from a point on edge \(e\) to \(P\). \({\mathbf{{E}}_{e}}\) and \({\mathbf{{F}}_{f}}\) are the direction matrices of edge \(e\) and the embodied face \(f\). The potential of the dumbbell-shaped body at point \(P\) can be obtained by summing the potentials of the three parts. The attraction and gravity gradient of the polyhedron can also be obtained by Eqs. (2) and (3), which are applied in the following sections.

$$\begin{aligned}& \nabla U=-G\sigma \sum _{e\in{\mathit{edges}}}\mathbf{E}_{e} \cdot\mathbf{r}_{e}\cdot L_{e}+ G\sigma\sum _{f\in{\mathit{faces}}}\mathbf{F}_{f}\cdot\mathbf{r}_{f} \cdot\omega_{f} \end{aligned}$$
(2)
$$\begin{aligned}& \nabla\nabla U=G\sigma \sum _{e\in{\mathit{edges}}} \mathbf{E}_{e}\cdot L_{e}- G\sigma\sum _{f\in{\mathit{faces}}} \mathbf{F}_{f}\cdot\omega_{f} \end{aligned}$$
(3)

2.3 The equilibria and their stability

The dumbbell-shaped body is assumed to be rotating uniformly around its maximum moment-of-inertia axis with angular velocity \(\omega \). Normally, the motion of a third particle is established in the body-fixed frame whose \(Z\)-axis is aligned with the rotation axis, and whose \(X\)- and \(Y\)-axes coincide with two other symmetrical axes of the body. The centers of the two spheres are located at the \(X\)-axis.

In the rotating frame, the equation of motion of a particle is given as,

$$\begin{aligned}& \begin{aligned} &\ddot{x}-2\omega\dot{y}=\omega^{2}x+U_{x}\\ &\ddot{y}+2\omega\dot{x}=\omega^{2}y+U_{y}\\ &\ddot{z}=U_{z} \end{aligned} \end{aligned}$$
(4)

where \({U_{x}}, {U_{y}}, {U_{z}}\) are components of Eq. (1) along the respective axes. The results of Eq. (4) are related only to the ratio between the square of the rotational speed and the density of the body: \(\tau = {{{\omega ^{2}}} / \rho }\). Therefore, we define a normalized angular speed \(\omega ' = \sqrt {{{{\omega ^{2}}} / {G\rho }}}\). In the new system, the gravity constant \(G'\) and the density \(\rho '\) of the model are equal to 1. That is, any property of motion in the system \(S' = \{ \omega ',G',\rho ',R\} \) is equivalent to the original system \(S = \{ \omega,G,\rho,R\} \). The radii of sphere \(R\) is taken as the length unit. The normalized equation can be written as,

$$\begin{aligned}& \begin{aligned} &\ddot{x}-2\omega'\dot{y}= \omega^{\prime\,2}x+U_{x}\\ &\ddot{y}+2\omega'\dot{x}= \omega^{\prime\,2}y+U_{y}\\ &\ddot{z}= U_{z} \end{aligned} \end{aligned}$$
(5)

Setting \(\dot{x} = \ddot{x} = \ddot{y} = \dot{y} = \dot{z} = \ddot{z} = 0\), the equilibrium points of the dumbbell-shaped body can be obtained. Their stability can be determined by the eigenvalues of the characteristic equation. The equilibrium is stable if no eigenvalue has a positive real part; otherwise, the equilibrium is unstable. According to a previous study (Li et al. 2013), an equilibrium along the \(X\)-axis is always unstable, while equilibrium points along the \(Y\)-axis are conditionally stable. The stability at a certain angular speed has been investigated and the corresponding critical length-diameter ratio \({m_{cr}}\) was found. Here, we focus on determining the critical length-diameter ratio \({m_{cr}}\) with different angular velocities.

The normalized angular velocity \(\omega '\) is allowed to change from 0.1 to 1. For each \(\omega '\), the critical length-diameter ratio is calculated that satisfies the multiple eigenvalues in the characteristic equation. The result is shown in Fig. 2.

Fig. 2
figure 2

The relation between normalized angular velocity \(\omega '\) and critical length-diameter ratio \({m_{cr}}\)

Full size image

As shown in Fig. 2, the curve divides the region into two parts. In the upper region, the equilibria along the \(Y\)-axis are unstable, while the lower region is the stable area. It is clear that the critical length-diameter ratio decreases as the normalized angular speed increases. Considering the definition of normalized angular speed, it is concluded that an equilibrium with a high spin speed or low-density body is usually unstable unless the body is close to a sphere.

To systematically discuss the motion in the vicinity of a dumbbell-shaped model, four models are analyzed below: I. \(\omega ' = 0.63,m = 0.3\), II. \(\omega ' = 0.63,m = 0.8\), III. \(\omega ' = 0.63,m = 2\), IV. \(\omega ' = 0.22,m = 0.8\). From Fig. 2, models II and III are larger than the corresponding critical length-diameter ratio \({m_{cr}}\), while I and IV are smaller than \({m_{cr}}\). Hence, the equilibrium points along the \(Y\)-axis are unstable for II and III and stable for I and IV. The position and linear stability of equilibrium for each situation are listed in Table 1.

Table 1 Location, existence and stabilities of periodic orbits for the equilibrium points
Full size table

3 Local motion around the equilibria of a dumbbell-shaped body

If we put the center of a frame at any equilibrium and perform a small perturbation \((\xi ,\eta ,\zeta )\), the linear perturbation equation can be written as:

$$\begin{aligned}& \begin{aligned} &\ddot{\xi}- 2\omega '\dot{\eta}= U_{xx}^{E}\xi + U_{xy}^{E}\eta + U_{xz}^{E}\zeta \\ &\ddot{\eta}+ 2\omega '\dot{\xi}= U_{yx}^{E}\xi + U_{yy}^{E}\eta + U_{yz}^{E}\zeta \\ &\ddot{\zeta}= U_{zx}^{E}\xi + U_{zy}^{E} \eta + U_{zz}^{E}\zeta \end{aligned} \end{aligned}$$
(6)

The characteristic equation of Eq. (6) can be written in the following form:

$$ \left| \textstyle\begin{array}{c@{\quad}c@{\quad}c} {{\lambda ^{2}} - U_{xx}^{E}} & { - 2\omega '\lambda - U_{xy}^{E}} & {U_{xz}^{E}} \\ {2\omega '\lambda - U_{xy}^{E}} & {{\lambda ^{2}} - U_{yy}^{E}} & {U_{yz}^{E}} \\ {U_{xz}^{E}} & {U_{yz}^{E}} & {{\lambda ^{2}} - U_{zz}^{E}} \end{array}\displaystyle \right| = 0 $$
(7)

Due to the symmetry of the model, \(U_{xy}^{E}=U_{yx}^{E}=0, U_{yz}^{E}=U_{zy}^{E}=0, and U_{xz}^{E}=U_{zx}^{E}=0\). Equation (7) can be simplified as:

$$\begin{aligned} \bigl({\lambda ^{2}} - U_{zz}^{E} \bigr)\bigl[{\lambda ^{4}} + \bigl(4{\omega ^{\prime\,2}} - U_{xx}^{E} - U_{yy}^{E}\bigr){\lambda ^{2}} + U_{xx}^{E}U_{yy}^{E} \bigr] = 0 \end{aligned}$$
(8)

where \(\lambda \) denotes the eigenvalues of Eq. (6). The value of \(\lambda \) not only defines the stability of equilibrium points but also determines the mode of perturbation motion around equilibria. Planar periodic orbits around equilibria have been investigated previously (Li et al. 2013). Here, we extend them to the spatial situation.

3.1 Local motion around an equilibrium

Case 1. Local motion around an equilibrium along the X-axis

The eigenvalues for \({E_{x}}\) in a dumbbell-shaped body have the form \(\pm \alpha, \pm i{\beta _{j}}\ (j = 1,2)\). Hence, the general solution of the linearized equation can be expressed as (Wang et al. 2014):

$$\begin{aligned}& \begin{aligned} &\xi = {d_{1}}{e^{\alpha t}} + {d_{2}}{e^{ - \alpha t}} + {d_{3}}\cos {\beta _{1}}t + {d_{4}}\sin {\beta _{1}}t\\ &\eta = {\kappa _{1}}\bigl({d_{1}}{e^{\alpha t}} - {d_{2}}{e^{ - \alpha t}}\bigr) - {\kappa _{2}}({d_{3}}\sin {\beta _{1}}t - {d_{4}}\cos {\beta _{1}}t)\\ &\zeta = {d_{5}}\cos {\beta _{2}}t + {d_{6}}\sin {\beta _{2}}t \end{aligned} \end{aligned}$$
(9)

where \({\kappa _{1}} = \frac{1}{{2\omega '}}(\alpha - \frac{{U_{xx}^{E}}}{{{\alpha _{1}}}})\), \({\kappa _{2}} = \frac{1}{{2\omega '}}({\beta _{1}} + \frac{{U_{xx}^{E}}}{{{\beta _{1}}}})\). Motion along the z-axis is decoupled from motion in the xy-plane. Therefore, two types of periodic orbits can be found near \({E_{x}}\). One is in the xy-plane with period \({T_{1}} = {{2\pi } / {{\beta _{1}}}}\) as discussed previously; the other is the out-of-plane motion with period \({T_{2}} = {{2\pi } / {{\beta _{2}}}}\). Equation (9) provides a proper initial guess for periodic orbits. Based on a differential correction, the accurate result can be obtained as shown in Fig. 3.

Fig. 3
figure 3

Periodic orbits around \({E_{x}}\) in model II

Full size image

The perturbation motion around equilibria can also be described in matrix form,

$$ X(t) = \varPhi (t,{t_{0}})X({t_{0}}) $$
(10)

where \(X({t_{0}})\) and \(X(t)\) are the perturbations at the initial time \(t_{0}\) and time \(t\), respectively. \(\varPhi (t,{t_{0}})\) is the state transition matrix. In particular, the periodic orbit satisfies \(X(T) = X({t_{0}})\). The state transition matrix for a periodic orbit is called Monodromy matrix \(M = \varPhi (T,{t_{0}})\). Normally, the stability of an orbit is defined by a stability index,

$$ \upsilon = \frac{1}{2}\biggl(\vert {{\lambda _{\max }}} \vert + \frac{1}{{\vert {{\lambda _{\max }}} \vert }}\biggr) $$
(11)

where \({\lambda _{\max }}\) is the maximum eigenvalue of the monodromy matrix. If \(\upsilon > 1\), the period orbit is unstable. The larger the value of \(\upsilon \), the more easily the orbit diverges. Periodic orbits were investigated for the dumbbell-shape models with different parameters. Table 2 lists the stabilities and periods of orbits with the same amplitude (\(\Delta \xi (\zeta ) = 0.1\)).

Table 2 Stabilities and periods of orbits around \(E_{x}\)
Full size table

As shown in Table 2, the periods and stabilities of periodic orbits around \({E_{x}}\) are influenced by both the angular speed \(\omega '\) and length-diameter ratio \(m\). Two types of periodic orbits are unstable under all circumstances. On one hand, when increasing the length-diameter \(m\), the orbital periods of planar and spatial orbits decrease slowly but the stability indexes increase rapidly. On the other hand, the orbital periods and stability of an orbit increase with the decrease of the angular velocity. Additionally, the spatial orbit is more unstable than the planar orbit in the same model.

Case 2. Local motion around an equilibrium along the Y-axis

The local motion around equilibrium \({E_{y}}\) of a dumb-bell-shaped body depends on the stability of \({E_{y}}\). If the length-diameter ratio \(m\) is smaller than \(m_{cr}\), the equilibrium is stable. The eigenvalues for \({E_{y}}\) have the form \(\pm i{\beta _{j}}\ (j = 1,2,3)\). Hence, the general solution of the linearized equation can be written as

$$\begin{aligned}& \begin{aligned} &\xi = {d_{1}}\sin ({\beta _{1}}t + {\varphi _{1}}) + {d_{2}}\sin ({\beta _{2}}t + {\varphi _{2}})\\ &\eta = {\kappa _{1}}{d_{1}}\cos ({\beta _{1}}t + {\varphi _{1}}) + {\kappa _{2}}{d_{2}}\cos ({\beta _{2}}t + {\varphi _{2}})\\ &\zeta = {d_{3}}\cos ({\beta _{3}}t + {\varphi _{3}}) \end{aligned} \end{aligned}$$
(12)

where \({\kappa _{1}} = \frac{1}{{2\omega '}}({\beta _{1}} + \frac{{U_{xx}^{E}}}{{{\beta _{1}}}})\), \({\kappa _{2}} = \frac{1}{{2\omega '}}({\beta _{2}} + \frac{{U_{xx}^{E}}}{{{\beta _{2}}}})\). Three types of periodic orbits can be found near equilibria. Two are in the \(xy\)-plane and the other is out-of-plane. Their periods are \({T_{j}} = {{2\pi } / {{\beta _{j}}(j = 1,2,3)}}\), respectively. The numerical results of periodic orbits are shown in Fig. 4.

Fig. 4
figure 4

Periodic orbits around \({E_{y}}\) in model IV

Full size image

For a dumbbell-shaped body with a length-diameter ratio larger than \({m_{cr}}\), \({E_{y}}\) becomes unstable. The forms of the eigenvalues are \(\pm \alpha \pm i{\beta _{1}}\) and \(\pm {\beta _{2}}\). The linearized equations of motion near equilibria are

$$\begin{aligned}& \begin{aligned} & \xi = {e^{\alpha t}}({C_{1}}\cos {\beta _{1}}t + {C_{2}}\sin {\beta _{1}}t) \\ &\phantom{\xi =\,\,}{} + {e^{ - \alpha t}}({C_{3}}\cos {\beta _{1}}t + {C_{4}}\sin {\beta _{1}}t)\\ &\eta = {e^{\alpha t}}({D_{1}}\cos {\beta _{1}}t + {D_{2}}\sin {\beta _{1}}t) \\ &\phantom{\eta =\,\,}{}+ {e^{ - \alpha t}}({D_{3}}\cos {\beta _{1}}t + {D_{4}}\sin {\beta _{1}}t) \\ &\zeta = {C_{5}}\cos {\beta _{2}}t + {C_{6}}\sin {\beta _{2}}t \end{aligned} \end{aligned}$$
(13)

where \({D_{i}}\) are functions of \({C_{i}}\ (i = 1,2,3,4)\). Only one type of periodic orbit exists, as shown in Fig. 5.

Fig. 5
figure 5

Periodic orbits around \({E_{y}}\) in model II

Full size image

The periods and stabilities of periodic orbits in different models are listed in Table 3 (\(\Delta \xi (\zeta ) = 0.1\)).

Table 3 Stabilities and periods of orbits around \(E_{y}\)
Full size table

As shown in Table 3, the stable equilibria have stable periodic orbits in both the planar and spatial dimensions. Similar to orbits around \({E_{x}}\), the stability indices of spatial orbits increase as \(m\) increases, but the periods remain nearly unchanged.

3.2 Continuation method for orbit families

The linearized equation can provide initial guesses for orbits close to the equilibria. However, it fails when the perturbation is large. In that case, the continuation method is adopted to generate a family of orbits. In this paper, the pseudo-arc-length continuation is employed (Doedel et al. 2007). A new member of the family \({X_{i}}\) is generated from the previous converged solution \({X_{i - 1}}\) with a step along the characteristic direction \(\Delta X\).

Taking the periodic orbit along the \(X\)-axis as an example, according to symmetry, the converged solution satisfies

$$ X_{i - 1}^{\eta}\biggl(\frac{T}{2}\biggr) = 0,\quad\quad X_{i - 1}^{\dot{\xi}}\biggl(\frac{T}{2}\biggr) = 0,\quad\quad X_{i - 1}^{\dot{\zeta}}\biggl(\frac{T}{2}\biggr) = 0 $$
(14)

The characteristic direction \(\Delta {X_{i}}\) should satisfy

$$\begin{aligned}& \begin{aligned} &X_{i}^{\eta}\biggl(\frac{T}{2} + \Delta {t_{i}}\biggr) = 0,\quad\quad X_{i}^{\dot{\xi}}\biggl( \frac{T}{2} + \Delta {t_{i}}\biggr) = 0,\\ &X_{i}^{\dot{\zeta}} \biggl(\frac{T}{2} + \Delta {t_{i}}\biggr) = 0 \end{aligned} \end{aligned}$$
(15)

where \(\Delta {t_{i}}\) is the half value of the period, and

$$\Delta {X_{i}} = [ {\Delta \xi }\quad 0\quad {\Delta \zeta }\quad 0\quad {\Delta \dot{\eta}}\quad 0 ]. $$

Equation (15) can be written in matrix form as

$$ {{\frac{{\partial X}}{{\partial {X_{0}}}}} \bigg| _{T/2}}\Delta {X_{i}} + { {\frac{{\partial X}}{{\partial t}}} \bigg| _{T/2}}\Delta {t_{i}} = 0 $$
(16)

An additional constraint, \({\vert {\Delta {X_{i}}} \vert ^{2}} + {\vert {\Delta {t_{i}}} \vert ^{2}} = 1\), is added to keep the solution unique. A step size \(\Delta s\) is chosen to generate a new guess for a differential correction:

$$ {X_{i}} = {X_{i - 1}} + \Delta {X_{i}}\Delta s $$
(17)

The pseudo-arc-length continuation provides a better initial guess than the traditional continuation method and increases the convergence. Based on the continuation, a family of periodic orbits are produced as shown in Fig. 6.

Fig. 6
figure 6

Orbit Families around equilibria in Model IV (a) \({E_{x}}\) planar orbits (b) \({E_{x}}\) vertical orbits (c) \({E_{y}}\) short-period orbits (d) \({E_{y}}\) long-period orbits (e) \({E_{y}}\) vertical orbits

Full size image

All orbits can extend to the surface of the dumbbell-shaped body except the long-period orbit around stable \({E_{y}}\), where the orbit suddenly disappears in space. Figure 6(d) shows the terminal orbit.

3.3 Periodic orbits via bifurcation

Based on the linear perturbation equations above, several types of periodic orbits can be found and orbit families generated. However, more complex periodic orbits such as the “Halo” type orbit in the Circular Restricted Three Body Problem (CRTBP) cannot be found by such methods. Three methods have been used to search for periodic orbits. One is the grid search, in which six-dimensional states \((x,y,z,\dot{x},\dot{y},\dot{z})\) and the period \(T\) are regarded as searching parameters in a meshed grid to find a periodic solution. Yu has used this to find 29 families of periodic orbits around 216 Kleopatra (Yu and Baoyin 2012a). This method can search for orbits systematically, but it is time-consuming, especially for polyhedron models. The second method requires a high-order analytical solution as in the CRTBP. However, it is difficult to obtain a high-order derivate by the polyhedron method. Therefore, the third method, bifurcation, is employed to find additional periodic orbits in the vicinity of a dumbbell-shaped model.

Bifurcation is a common phenomenon in nonlinear dynamic systems. In the context of periodic orbits, bifurcation means a change in stability of orbits or the location of eigenvalues in the complex plane (Chappaz 2015). One of the characteristics of bifurcation is the existence of a new family of orbits that intersects the known family at the bifurcation point; this facilitates the search for periodic orbit families. Bifurcation has been studied analytically for asteroids by Yu and applied to asteroid 216 Kleopatra (Jiang et al. 2015). Here, we extend it to search for periodic orbits for a singular polyhedron body.

Based on continuation, the motion of an eigenvalue for planar orbits around \({E_{x}}\) is shown in Fig. 7.

Fig. 7
figure 7

Motion of characteristic value for planar orbits around \({E_{x}}\) (model II)

Full size image

As shown in Fig. 7, initially, the original orbit has two eigenvalues equal to 1, and two of the eigenvalues lie on the unit circle. Two other eigenvalues are located on the real axis. As the orbit amplitude increases, two complex eigenvalues converge at 1 and split on the real axis into a real reciprocal pair, which indicates a tangent bifurcation (Campbell 1999). By bisection and the continuation method, the accuracy of the bifurcation orbit can be calculated numerically. If we denote the bifurcation eigenvalue \({\lambda _{bi}} = - 1\) and the corresponding eigenvector as \(V({\lambda _{bi}})\) and \(V(\lambda _{bi}^{*} )\), the average eigenvector is defined as

$$ V = \bigl[V({\lambda _{bi}}) + V\bigl(\lambda _{bi}^{*}\bigr)\bigr]/ 2 $$
(18)

The initial guess of a new orbit family can be obtained as \({X^{new}} = {X_{bi}} + \Delta s \cdot V\), where \({X_{bi}}\) is the initial state of the periodic orbit at bifurcation points, and \(\Delta s\) is an arbitrary step size. Once the first orbit of a new type is generated, the continuation method is used to fill up the whole family. By bifurcation, two types of periodic orbits are found around \({E_{x}}\), as shown in Fig. 8.

Fig. 8
figure 8

Two types of periodic orbits around \({E_{x}}\) from the bifurcation (model II)

Full size image

Figure 9 marks the bifurcation orbits from the original orbit family. Those two types of orbits are analogous to axial orbits and Halo orbits in the CRTBP.

Fig. 9
figure 9

Bifurcation orbits in the original orbit family

Full size image

The eigenvalues of vertical orbits in \({E_{x}}\) have also been investigated. The location of eigenvalues is the same as for a planar orbit. However, no bifurcation occurs when we increase the \(Z\)-axis amplitude.

The same process is applied to periodic orbits around \({E_{y}}\). The eigenvalues of a vertical periodic orbit around stable and unstable equilibria are shown in Fig. 10. The vertical orbits around stable equilibria have 2 pairs of complex eigenvalues lying on the unit circle and one pair of unity, while orbits around unstable equilibria have two pairs of eigenvalues in the complex plane. For both types of orbits, no bifurcation occurs even if the amplitude \(\zeta \) is as large as 3. Therefore, no new orbit family is generated from vertical orbits.

Fig. 10
figure 10

Characteristic values for vertical orbits around \({E_{y}}\) (a) Stable equilibrium point (model IV) (b) Unstable equilibrium point (model II)

Full size image

For stable \({E_{y}}\), the bifurcation in two types of planar orbits is discussed further. The long-period orbits occur in secondary Hopf-bifurcation, in which two pairs of complex eigenvalues converge on the unit circle and split into the complex plane, as shown in Fig. 11. The secondary Hopf-bifurcation changes the stability of motion, which results in the disappearance of the long-period orbit (Fig. 6(d)).

Fig. 11
figure 11

Hopf-bifurcation for long period orbits (model IV)

Full size image

The bifurcation for a short-period orbit is complicated. With increasing amplitude, the eigenvalue successively incurs period-doubling bifurcation (the eigenvalue converges to −1) and tangent bifurcation (the eigenvalue converges to 1). The motion of characteristic value for model IV is shown in Fig. 12.

Fig. 12
figure 12

Motion of characteristic value for short orbits around \(E_{y}\) (model IV)

Full size image

According to bifurcation theory, the doubling bifurcation will generate a new orbit family possessing a period double that of the original family (Iooss and Joseph 1977). Based on new initial guesses, multiple-cycle orbits are found near \({E_{y}}\), as shown in Fig. 13(a) and (b). Additionally, the tangent bifurcation for a short-period orbit produces a new kind of asymmetrical period orbit. Asymmetrical correction schemes are adopted to find the numerical result (Grebow 2006), as shown in Fig. 13(c). For both long- and short-period orbits around \({E_{y}}\), no spatial orbits are generated from planar orbits as in \({E_{x}}\).

Fig. 13
figure 13

Three types of periodic orbits around \(E_{y}\) from bifurcation (model IV) (a) Multiple-cycle orbit (b) Multiple-cycle orbit (c) Asymmetrical period orbit

Full size image

4 Global motion in the vicinity of a dumbbell-shaped body

4.1 Invariant manifolds associated with periodic orbits for a dumbbell-shaped body

The invariant manifold is an important property for periodic orbits around equilibria, especially for unstable periodic orbits. An invariant manifold can be defined as an \(m\) -dimensional surface embedded in \(\mathbb{R}^{n}\) \({{(m< n)}}\). From nonlinear dynamics theory, there are two types of invariant manifolds: unstable manifolds and stable manifolds. The unstable manifold includes the set of all possible trajectories that diverge from a nominal orbit if it was perturbed in an unstable direction of orbits, while the stable manifold is the set of all possible trajectories that asymptotically approach the orbit along a stable direction. The stable and unstable directions can be determined by the Monodromy matrix of a periodic orbit.

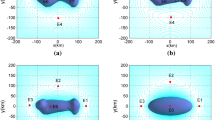
Here, we analyze the manifold of an unstable orbit around \({E_{x}}\) in the vicinity of a dumbbell-shaped body. The manifold picks up 100 points uniformly from a periodic orbit and generates stable and unstable manifolds forward or backward to the plane \(X = 0\). The invariant manifold associated with planar and spatial orbits is shown in Fig. 14.

Fig. 14
figure 14

Invariant manifold associated with periodic orbit for dumbbell-shaped body (a) Planar orbit in model I (b) Vertical orbit in model II

Full size image

As illustrated in Fig. 14, there are two branches of stable manifolds (red) and two branches of unstable manifolds (blue). One branch of the stable (unstable) manifolds extends along the positive \(y\)-direction and the other stretches to the negative \(y\)-direction. The stable and unstable manifolds are symmetric with respect to the \(X\)-axis. Moreover, manifolds from \({E_{ - x}}\) are anti-symmetric to manifolds from \({E_{x}}\). In that case, the stable and unstable manifolds are calculated for one quadrant, and the other part can be obtained by symmetry and anti-symmetry. For convenience, the closer branch is called the inner manifold and the branch away from the body is called the outer manifold. The impacts of the orbit amplitude and the length-diameter ratio are investigated as follows.

4.2 Parametric analysis for invariant manifolds

To systematically understand the global motion near the equilibria, the influence of orbit amplitude \(\xi \) and length-diameter ratio \(m\) on invariant manifolds is investigated. Here, we take a planar orbit as example. Relevant results are shown in Fig. 15.

Fig. 15
figure 15

Invariant manifold with different orbit amplitudes (model I) (a) \(\xi = 0.2\) (b) \(\xi = 0.4\) (c) \(\xi = 0.6\) (d) \(\xi = 0.8\)

Full size image

As shown in Fig. 15, the orbit amplitude \(\xi \) has a great impact on the size and direction of the manifold. With the increase of amplitude, the size of the manifold tube increases. Inner and outer manifolds may overlap with each other. Unlike in the CRTBP, the manifold near a dumbbell-shaped body system has nearly the same size as the center body (seen in Fig. 14 and 15). Therefore, the inner manifold may touch the surface of a dumbbell-shaped body when the amplitude is large.

Increasing the length-diameter ratio \(m\) has the same effect as the amplitude, as shown in Fig. 16, where models II and III are shown with particular cases \(\xi = 0.2\). The inner manifold comes close to the center body as the relative distance between the two spheres increases. In particular, only the outer manifold exists for model III; the inner manifold totally intersects with the model before it crosses the plane \(x = 0\).

Fig. 16
figure 16

Invariant manifold with different length-diameter ratios (a) Model II (b) Model III

Full size image

4.3 Heteroclinic connection between \({E_{x}}\) and \({E_{ - x}}\)

As discussed above, there are two branches of stable and unstable manifolds for each orbit around equilibria \({E_{x}}\). That is, at most four heteroclinic connections exist between two equilibria. Each direction has two channels. Spacecraft in periodic orbits can transfer from one equilibrium to the other with limited energy and achieve global exploration of the small body.

To study the low-energy transfer, two Poincaré sections are set as:

$$ \left \{ \textstyle\begin{array}{l} {{U_{1}}:x = 0,\quad y > 0,\ \dot{x} > 0}\\ {{U_{2}}:x = 0,\quad y > 0,\ \dot{x} < 0} \end{array}\displaystyle \right . $$
(19)

The black lines in Fig. 15(a) show the sections. The projections for stable and unstable manifolds in these sections are shown in Figs. 17 and 18 for models I and II. The manifolds for different amplitudes are investigated separately.

Fig. 17
figure 17

Poincaré section for model I

Full size image
Fig. 18
figure 18

Poincaré section for model II

Full size image

It is clear that the projection of some stable manifolds overlap with the projection of unstable manifolds on the Poincaré section, which means there are heteroclinic connections between two equilibria points. In particular, if the point of intersection corresponds to an equal-amplitude orbit with the same orbital energy, the connection is a zero-energy transfer. Otherwise, a small energy increment is needed at the intersection point to accommodate the change in velocity.

Comparing models I and II, with the increase of \(m\), the projections of the stable and unstable manifolds in the Poincaré section gradually separate, which means a velocity increment is needed to complete the transfer. Low-energy transfers exist only in large-amplitude manifolds.

Based on the Poincaré section, heteroclinic transfers between two equilibria along the \(X\)-axis are shown in Fig. 19. In Fig. 19(a), the transfer is between equal-amplitude orbits. The outer heteroclinic connection is applied from \({E_{ - x}}\) to \({E_{x}}\). No extra velocity is needed at the intersection point (\(x=0\)). In Fig. 19(b), the spacecraft transfers from a large-amplitude orbit around \({E_{x}}\) to a small one around \({E_{ - x}}\). The velocity increment is only 0.02 on a normalized scale.

Fig. 19
figure 19

Heteroclinic connection between \(E_{x}\) (a) Equal-amplitude transfer in model I (b) Transfer between different amplitudes in model II

Full size image

Moreover, through two heteroclinic connections, it is possible to transfer the spacecraft between different amplitude orbits around the same equilibria, as shown in Fig. 20. The spacecraft transfers from a small-amplitude orbit to a large-amplitude large-amplitude orbit around \({E_{ - x}}\). At least one impulse is required during the transfer.

Fig. 20
figure 20

Transfer between different amplitude orbits (model II)

Full size image

4.4 Heteroclinic connection between \({E_{x}}\) and \({E_{y}}\)

The above connections focus on the transfer between equilibria along the \(X\)-axis. Here, we discuss the transfer between \({E_{x}}\) and \({E_{y}}\). Due to the stability of \({E_{y}}\), the invariant manifold cannot be employed to heteroclinic connections for stable periodic orbits. In that case, one-impulse transfers are investigated between a periodic orbit around \({E_{y}}\) and a stable or unstable manifold from a periodic orbit around \({E_{x}}\). The Poincaré map for a periodic orbit and invariant manifold is shown in Fig. 21.

Fig. 21
figure 21

Poincaré section for \(E_{y}\) periodic orbit

Full size image

As shown in Fig. 21, the projection of a periodic orbit in the Poincaré section \(Y - {V_{y}}\) is a line that coincides with the \(X\)-axis. Therefore, the invariant manifold that satisfies \({V_{y}} = 0\) is selected as a candidate. The spacecraft will execute one impulse when it crosses the \(X = 0\) plane to complete the transfer. Figure 22 shows one of the examples in model I. Generally, the heteroclinic connection between \({E_{x}}\) and \({E_{y}}\) costs a larger velocity increment than the heteroclinic connection between \({E_{x}}\). However, velocity is not the key factor for a small celestial body. The transfer in Fig. 22 requires a normalized velocity maneuver change of 0.17, which is small on a real scale.

Fig. 22
figure 22

Heteroclinic connection between \(E_{x}\) and \(E_{y}\)

Full size image

The periodic orbit around \({E_{y}}\) can connect with two periodic orbits simultaneously. In that case, the spacecraft can also achieve transfer between different amplitudes by the path of unstable manifold-periodic orbit to stable manifold. Figure 23 shows an example.

Fig. 23
figure 23

Transfer between different amplitude orbits by the \(E_{y}\) periodic orbit

Full size image

4.5 Global transfer around a dumbbell-shaped body

Taking advantage of heteroclinic transfer between \({E_{x}}\) and \({E_{y}}\), it is possible to complete the global transfer around a dumbbell-shaped body. Here, we design a series of reference transfer trajectories that can achieve transfers between different equilibria, and make a global observation about dumbbell-shaped bodies. The reference trajectories are shown in Fig. 24. Such trajectories consist of two periodic orbits around \({E_{x}}\) and \({E_{ - x}}\), denoted as \({P_{1}}\) and \({P_{2}}\), their associated invariant manifolds, denoted \({S_{1}},{S_{2}},{S_{3}},{S_{4}}\) and \({U_{1}},{U_{2}},{U_{3}},{U_{4}}\), and four periodic orbits around \({E_{y}}\) and \({E_{ - y}}\), denoted \({Q_{1}},{Q_{2}},{Q_{3}},{Q_{4}}\). The stable and unstable manifolds connect with \({Q_{1}},{Q_{2}},{Q_{3}},{Q_{4}}\) in the plane \(X = 0\), respectively.

Fig. 24
figure 24

Reference global transfer trajectory around a dumbbell-shaped body

Full size image

Based on a reference transfer trajectory, several types of scenarios can be designed, including global mapping, a heteroclinic connection between \({E_{ - y}}\) and \({E_{y}}\), and a homoclinic connection for \({E_{x}}\), as shown in Fig. 25.

Fig. 25
figure 25

Different transfer scenarios: (a) Transfer between orbits around \(E_{y}\) with different amplitudes; (b) Heteroclinic connection for \(E_{y}\); (c) Global mapping by inner heteroclinic connection; (d) Global mapping by outer heteroclinic connection; (e) Homoclinic connection for \(E_{x}\)

Full size image

Figure 25(a) shows the transfer between \(Q_{1}\) and \(Q_{2}\); the transfer sequence is \(Q_{1}\)–\(S_{3}\)–\(P_{2}\)–\(U_{3}\)–\(Q_{2}\). The reverse transfer is also available, but the transfer sequence becomes \(Q_{2}\)–\(S_{1}\)–\(P_{1}\)–\(U_{1}\)–\(Q_{1}\). Figure 25(b) shows the transfer from \(Q_{3}\) to \(Q_{1}\); the spacecraft travels along \(Q_{3}\)–\(S_{2}\)–\(P_{1}\)–\(U_{1}\)–\(Q_{1}\). Two impulses are required at the intersections of \(Q_{3}\) and \(S_{2}\) and \(U_{1}\) and \(Q_{1}\).

Figure 25(c) and (d) show two types of global mapping trajectories. The first uses the inner heteroclinic connection. The transfer sequence is \(P_{1}\)–\(U_{1}\)–\(Q_{1}\)–\(S_{3}\)–\(P_{2}\)–\(U_{4}\)–\(Q_{3}\)–\(S_{2}\)–\(P_{1}\). The second uses the outer heteroclinic connection with sequence \(P_{1}\)–\(U_{2}\)–\(Q_{4}\)–\(S_{4}\)–\(P_{2}\)–\(U_{3}\)–\(Q_{2}\)–\(S_{1}\)–\(P_{1}\). Both need four impulses at the intersections.

Figure 25(e) demonstrates the homoclinic connection for \(P_{1}\), \(P_{1}\)–\(U_{1}\)–\(S_{3}\)–\(P_{2}\)–\(U_{3}\)–\(S_{1}\)–\(P_{1}\). It can in fact be considered as two heteroclinic connections between \({E_{x}}\) and \({E_{ - x}}\). Taking advantage of the invariant manifolds, almost no energy is required during the transfer. Table 4 shows the velocity increment for each scenario. The parameter of the dumbbell-shaped body is assumed to be \(R = 10~\mbox{km}\), the spin period is 6 h and the asteroid density is \(3200~\mbox{kg/m}^{3}\).

Table 4 Transfer sequence and velocity increment for each scenario
Full size table

As shown in Table 4, due to the property of invariant manifolds, the total velocity increment for transfer is less than 5 m/s. These trajectories can be applied to future small-body exploration and provide references for design of reconnaissance orbits.

5 Conclusions

This paper investigates local and global motion in the vicinity of a rotating dumbbell-shaped body. Based on the polyhedron method, a geometrical model of a dumbbell-shaped body is established, and the stability of equilibria are investigated with different parameters. The critical length-diameter ratios \({m_{cr}}\) are calculated. Local motion around equilibria is analyzed. Based on linear perturbation equations, two, one and three types of periodic orbits are found around \(X\)-axis equilibria, unstable \(Y\)-axis equilibria and stable \(Y\)-axis equilibria, respectively. Using pseudo-arc-length continuation, a family of periodic orbits is generated. By introducing the bifurcation method, more types of orbits are found around equilibria, such as ‘Halo’ orbits, ‘Axial’ orbits and multi-revolution orbits. Then, on the basis of invariant manifolds and Poincaré sections, global motion around the dumbbell-shaped body is studied. Four heteroclinic connections are found for equilibria along the \(X\)-axis. Low-energy transfers between different periodic orbits are constructed. Finally, several applications of global transfer trajectories are discussed that offer good options for reconnaissance orbits for future small-body exploration missions.