1 Introduction

It is seen that the cases of the early time inflation and the late time acceleration of the universe have been supported by the recent observational researches (Ade et al. 2014a, 2014b, 2015). In particular, it has been considered the concept of the dark energy which has a repulsive impact that causes the current acceleration. However, the observations show that the structure of the universe consists of 68.3 %’s dark energy, 26.8 %’s dark matter, and also it spatially is flat. The remaining 4 % component of the universe consists of the normal matter. To explain the dark energy paradigm, Einstein equation which includes the cosmological constant has been taken into consideration. However, this approach is not so sufficient to explain the case because the magnitude of this constant does not coincide with observation data. Therefore, the scalar field descriptions have been made by researchers. Here, while the quintessence phase region of the universe is defined by a normal scalar field (equation of state parameter (EOS) is in the range \(- 1< w < \frac{- 1}{3}\)) (Caldwell et al. 1998; Peebles and Vilenkin 1999) the scalar field that has a negative sign describes the phantom case \(( w < - 1)\) (Caldwell 2002; Nojiri and Odintsov 2003; Cline et al. 2004; Wei and Cai 2006). In the case \(w = - 1\) shows the cosmological constant where the expansion of the universe is a de Sitter type expansion. The early time inflation of the universe is also explained by defining the scalar field, in which it is constructed a mechanism that requires a scalar field. This mechanism tells that the inflation drives from a false vacuum rolling slowly to a true vacuum. Namely, after the beginning singularity, this mechanism remarks that the inflation of the universe is de Sitter type till the radiation era. This picture of the early universe resembles to the late time cosmic acceleration of the universe. On the other hand, there are also other alternative approaches to explain the cosmic acceleration that one of these is the modified gravitational theory. One can show the unification of the early time inflation and the late time acceleration of the universe by this way. For example, the \(f ( R )\) gravity, which a functional form of the Einstein’s term, can describe this unification. One can take its simplest model such as \(f ( R ) = R + R^{n}\) that shows the cosmic inflation if \(n >1\) or the cosmic acceleration if \(n <0\) (Nojiri and Odintsov 2003, 2011; Carroll et al. 2004; Sotiriou 2007; Faraoni 2008; De Felice and Tsujikawa 2010). Transition from the matter dominant epoch into the late time cosmic acceleration in \(f(R)\) gravity has been shown by Nojiri and Odintsov (2006) where several realistic models obtained from the theory produce this transition compatible with the solar system tests. The unification of the early time inflation with the late time acceleration of the universe has been studied by Cognola et al. (2008), where the realistic \(f(R)\) models are considered. The model produces inflation at the large curvature where the model behaves as the cosmological constant. Whereas with the small curvature late time acceleration is shown besides to intermediate universe (deceleration phase regions). Other candidate of the dark energy sector is the modified Gauss-Bonnet gravity, i.e. \(R+f ( G )\). The authors have shown that the late time acceleration of the universe could be explained by this gravity theory and by a deceleration phase case as well (Nojiri et al. 2006; Nojiri and Odintsov 2011), in which it was considered the power form of the function, i.e. \(f ( G ) = G^{\sigma}\). Furthermore the \(\varLambda\mathrm{CDM}\) model in this gravity was studied by Myrzakulov et al. 2011. It has been also shown the late time cosmic acceleration in non-minimial coupling scalar field lagrangian with the \(f ( G )\) (Sadeghi et al. 2009). Further, the exact scale factor power-law phantom solutions could be seen in the literature (Rastkar et al. 2012). Unification of both the decelerated and accelerated expansion of the universe was also shown by Goheer et al. (2009) in this gravity theory. In the modified teleparallel gravity including torsion tensor in the functional form \(f ( T )\), the exact scale factor power-law solutions were studied by Setare and Darabi (2012), and also early time inflationary cases as well (Ferraro and Fiorini 2007; Bengochea and Ferraro 2009). On the other hand, a more general approach in gravity theories is the \(f ( R, G )\) gravity theory that includes the curvature scalar and the Gauss-Bonnet term in the functional form (Cognola et al. 2006). The some cosmological applications on this gravity were done by (Alimohammadi and Ghalee 2009; Makarenko et al. 2013; Álvaro and Saez-Gomez 2012), and the future time singularities were studied by (Bamba et al. 2010; Nojiri and Odintsov 2011), and cosmic acceleration, as well (Bamba et al. 2013). Furthermore, the unification of stages of the universe can be realized in a single form by proposing realistic \(f(R)\) and \(f(G)\) models consistent with the local tests and cosmological bounds (Nojiri and Odintsov 2007a). It is proposed some different \(f(R)\), \(f(G)\) and \(f(R,G)\) models to show the unification of the early time inflation with the late time acceleration or the transition from the deceleration to the acceleration (Nojiri and Odintsov 2007b), where these models are considered as the models that verified by the solar system tests. These theories are candidates for explaining the dark energy paradigm and the other stages of the universe. In the present work, we have a model that shows this unification via solving the field equations of \(f(R,G)\) theory in the cases of the phantom and the non-phantom phase.

In this study, we considered extended Gauss Bonnet gravity, namely \(f ( R, G )\) gravity theory. We take the \(F ( R, G ) =f ( G ) + R + \alpha R^{2}\) model that is an extended version of the modified Gauss Bonnet gravity, i.e. \(f ( G ) + R\) where \(\alpha\) is a small constant (Nojiri and Odintsov 2009; Hussain et al. 2012). We constructed the Friedmann equation corresponding to the gravity and obtained the real valued of our model by considering scale factor power-law solutions for the both phantom and non-phantom phase cases. It is seen that this model defines mathematically three stages of evolution of the universe in a unified form: inflation, deceleration and the late time cosmic acceleration. Furthermore, without using scalar field we obtained an inflation model according to \(\alpha\) parameter in this unified solution, and also we verified our early time inflationary scenario using observational parameters, i.e. \(n_{s}\), \(r\). The paper is organized as follow: In Sect. 2 we constructed the Friedmann equation of the extended Gauss Bonnet gravity for spatial FRW geometry; in Sect. 3 we performed the power-law solution of the equation and obtained the real valued of our model which describes three stages of the universe in a unified form; in Sect. 4 we demonstrated that our model has a solution when the universe is in the phantom region. Finally, in Sect. 5 we summarized our results.

2 Friedmann equations for \(F(R,G)\) gravity

The action integral of the extended Gauss Bonnet gravity is given as the following (Cognola et al. 2006):

$$ S = \int d^{4} x \sqrt{- g} \biggl[ \frac{1}{2 k^{2}} F ( R, G ) + L_{m} \biggr]. $$
(1)

Here, \(L_{m}\) is lagrangian density of the matter, \(\sqrt{- g}\) is the determinant of the metric tensor \(g^{\mu\nu}\). We will use the FRW metric with the scale factor \(a\):

$$ d s^{2} = - d t^{2} + a^{2} ( t ) \bigl[ d x^{2} + d y^{2} + d z^{2} \bigr]. $$
(2)

The Ricci scalar and the Gauss Bonnet term are given as

$$ R =6 \bigl[ \dot{H} +2 H^{2} \bigr],\qquad G =24 H^{2} \bigl( \dot{H} + H^{2}\bigr), $$
(3)

respectively, where \(H = \frac{\dot{a}}{a}\) is the Hubble parameter and over dot represents the time derivative. Varying the action (1) with respect to the metric tensor the field equations are obtained as the following:

$$\begin{aligned} &\frac{1}{2} g^{\mu \nu} F ( R, G ) + \nabla^{\mu} \nabla^{\nu} F_{R} - g^{\mu \nu} \bigl( \nabla^{2} F_{R} \bigr) - R^{\mu \nu} F_{R} \\ &\qquad{}- 2 R R^{\mu \nu} F_{G} - 4 F_{G} R^{\mu \beta\sigma\nu} R_{\beta\sigma} +4 F_{G} R_{ \rho}^{\mu} R^{\nu\rho} \\ &\qquad{}- 2 F_{G} R_{ \rho\varepsilon\sigma}^{\mu} R^{\nu\rho\varepsilon\sigma} +2 R \bigl( \nabla^{\mu} \nabla^{\nu} F_{G} \bigr) \\ &\qquad{} - 2 g^{\mu \nu} R \bigl( \nabla^{2} F_{G} \bigr)- 4 R^{\beta \mu} \bigl( \nabla_{\beta} \nabla^{\nu} F_{G} \bigr) \\ &\qquad{} - 4 R^{\nu\beta} \bigl( \nabla_{\beta} \nabla^{\mu} F_{G} \bigr) +4 R^{\mu \nu} \bigl( \nabla^{2} F_{G} \bigr) \\ &\qquad{}+4 g^{\mu \nu} R^{\rho\beta} ( \nabla_{\rho} \nabla_{\beta} F_{G} )- 4 R^{\mu \rho\nu\tau} ( \nabla_{\rho} \nabla_{\tau} F_{G} ) \\ &\quad{}= - k^{2} T^{\mu \nu} \end{aligned}$$
(4)

where \(F_{G} = \frac{\partial f ( R, G )}{\partial G}\), \(F_{R} = \frac{\partial f ( R, G )}{\partial R}\), and \(T^{\mu \nu}\) is the energy-momentum tensor of matter. We have the Friedmann equations from (4) as

$$\begin{aligned} &- 12 H^{3} \dot{F}_{G} + \frac{G}{2} F_{G} - \frac{F ( R, G )}{2} \\ &\quad{}+3 \bigl( \dot{H} + H^{2} \bigr) F_{R} - 3 H \dot{F}_{R} = - k^{2} \rho, \end{aligned}$$
(5)
$$\begin{aligned} &\frac{F ( R, G )}{2} - \frac{1}{2} ( R F_{R} + G F_{G} ) + \ddot{F}_{R} +2 H \dot{F}_{R} \\ &\qquad{}+4 H^{2} \ddot{F}_{G} +8 H \dot{H} \dot{F}_{G} +8 H^{3} \dot{F}_{G} + \bigl( 2 \dot{H} +3 H^{2} \bigr) F_{R} \\ &\quad{}= - k^{2} p. \end{aligned}$$
(6)

We can write the above equations in the standard Einstein equations form without cosmological constant (Bamba et al. 2010):

$$\begin{aligned} &\rho_{e} k^{2} =3 H^{2}, \end{aligned}$$
(7)
$$\begin{aligned} &p_{e} k^{2} = - \bigl(2 \dot{H} +3 H^{2} \bigr), \end{aligned}$$
(8)

where,

$$\begin{aligned} \rho_{e} =& \frac{1}{F_{R}} \biggl\{ \rho + \frac{1}{2 k^{2}} \bigl[ 12 H^{2} F_{R} - f ( R, G ) - 6 H \dot{F}_{R} \\ &{}+6 \dot{H} F_{R} - 24 H^{3} \dot{F}_{G} + G F_{G} \bigr] \biggr\} , \end{aligned}$$
(9)
$$\begin{aligned} p_{e} =& \frac{1}{F_{R}} \biggl\{ p + \frac{1}{2 k^{2}} \bigl[ - 12 H^{2} F_{R} + f ( R, G ) +4 H \dot{F}_{R} \\ &{} - 6 \dot{H} F_{R} + 2 \ddot{F}_{R} -G F_{G} +16 H \dot{H} \dot{F}_{G} +16 H^{3} \dot{F}_{G} \\ &{} +8 H^{2} \ddot{F}_{G} \bigr] \biggr\} \end{aligned}$$
(10)

are the effective energy density and pressure, respectively, that satisfy the conservation law in the FRW universe:

$$ \dot{\rho} +3 H ( \rho + p ) =0,\qquad \dot{\rho}_{e} +3 H ( \rho_{e} + p_{e} ) =0. $$
(11)

One should note that, when \(f ( R, G ) =R\), \(\rho_{e} =\rho\) and \(p_{e} = p\) Eqs. (9) and (10) reduce the standard Einstein equations.

3 Scale factor power law solutions

In this section, we will construct the Friedmann equation. Next we will realize the scale factor power-law solution of it. For this purpose when we use the relationship

$$ Z = \bigl[ k^{2} ( p_{e} - w \rho_{e} )+2 \dot{H} +3 H^{2} (1+ w ) \bigr] F_{R}, $$
(12)

with \(w_{e} = w = - 1 - \frac{2 \dot{H}}{3 H^{2}}\), and obtain the following equation:

$$\begin{aligned} &4 H^{2} \ddot{F}_{G} +8 H \dot{H} \dot{F}_{G} +4 H^{3} \dot{F}_{G} ( 2+3 w ) - \frac{G}{2} F_{G} ( 1+ w ) \\ &\quad{}+ \frac{F ( R, G )}{2} ( 1+ w ) + \ddot{F}_{R} + H \dot{F}_{R} ( 2+3 w ) \\ &\quad{}- \dot{H} F_{R} ( 1+3 w ) - 3 H^{2} F_{R} ( 1+ w ) =Z=0. \end{aligned}$$
(13)

Here, we used the definition of the equation of the state parameter \(w= \frac{p}{\rho}\) which equals to the effective one. This means that the \(w\) parameter behaves as dark energy when the universe is in the early time or the late time.

Now, we examine the solutions of Eq. (13). Taking the lagrangian density as sum of two functions

$$ F ( R, G ) = f_{1} ( G ) + f_{2} ( R ), $$
(14)

and inserting it into Eq. (13) we have

$$\begin{aligned} &4 H^{2} \ddot{f}_{1 G} +8 H \dot{H} \dot{f}_{1 G} +4 H^{3} \dot{f}_{1 G} ( 2+3 w ) - \frac{G}{2} f_{1 G} ( 1+ w ) \\ &\quad{}+ \biggl[ \frac{f_{1} ( G )}{2} + \frac{f_{2} ( R )}{2} \biggr] ( 1+ w ) + \ddot{f}_{2 R} + H \dot{f}_{2 R} ( 2+3 w ) \\ &\quad{}- \dot{H} f_{2 R} ( 1+3 w ) - 3 H^{2} f_{2 R} ( 1+ w ) =0 \end{aligned}$$
(15)

for a specific case, this equation can be split into two equations as (Makarenko et al. 2013; Álvaro and Saez-Gomez 2012)

$$\begin{aligned} &4 H^{2} \ddot{f}_{1 G} +8 H \dot{H} \dot{f}_{1 G} +4 H^{3} \dot{f}_{1 G} ( 2+3 w ) \\ &\quad{}+ \biggl[ \frac{f_{1} ( G )}{2} - \frac{G}{ 2} f_{1 G} \biggr] ( 1+ w ) =0, \end{aligned}$$
(16)
$$\begin{aligned} &\ddot{f}_{2 R} + H \dot{f}_{2 R} ( 2+3 w ) - \dot{H} f_{2 R} ( 1+3 w ) \\ &\quad{}- 3 H^{2} f_{2 R} ( 1+ w ) + \frac{f_{2} ( R )}{2} ( 1+ w ) =0. \end{aligned}$$
(17)

The lagrangian (14) is generally found by the solutions of Eqs. (16) and (17). But, since we consider \(F ( R, G ) = f_{1} ( G ) + R + \alpha R^{2}\) model where the function \(f_{2} ( R )\) is clear, we will only solve Eq. (16) and investigate \(f_{2} ( R )\) into Eq. (17) that includes quadratic term (which is known as Staronbinsky model [Starobinsky 1980]). However the \(R + \alpha R^{2}\) model is in agreement with the Planck data, and the inflationary cosmology is perfectly realized by this model (Ade et al. 2014b). In brief, the lagrangian (14) will be determined by \(f_{1} ( G )\).

Finding an exact solution of Eq. (16) is very difficult since it includes some higher derivative terms of functions and Hubble parameter. Therefore, we focus on the scale factor power-law solutions that given as

$$ a ( t ) = a_{0} t^{h},\qquad H = \frac{h}{t}, $$
(18)

where the \(\ddot{a} >0\) denotes acceleration and \(\ddot{a} <0\) denotes deceleration. Using the solution (18) Eq. (16) can be written in terms of cosmic time as

$$\begin{aligned} &4 \frac{d}{dt} \bigl( g ( t ) \bigr) - 4 \frac{h}{t} g ( t ) \\ &\quad{}= N t^{- 3 h (1+ w )} - 54 h^{2} ( 2 h - 1 ) \alpha ( 1+ w ) t^{- 4} \\ &\qquad{}+3 h^{2} (1+ w ) t^{- 2}, \end{aligned}$$
(19)

where \(N = - k^{2} \rho_{0} a_{0}^{- 3(1+ w )}\) and \(g ( t )= H^{2} \dot{f}_{1 G}\). The solution of this differential equation is

$$\begin{aligned} g ( t ) =& - \frac{N t^{- 3 h ( 1+ w ) +3}}{4 h^{2} [ 4 h +3 h w - 1 ]} + \frac{54 ( 2 h - 1 ) \alpha (1+ w )}{4( h +3)} t^{- 1} \\ &{}- \frac{3(1+ w )}{4( h +1)} t + \frac{c_{1}}{ h^{2}} t^{h +2}. \end{aligned}$$
(20)

Using the relation \(G = \beta t^{- 4} =24 h^{3} ( h - 1) t^{- 4}\), it is obtained the following equation in terms of Gauss Bonnet invariant:

$$\begin{aligned} f_{1} ( G ) =& A \biggl( \frac{G}{\beta} \biggr)^{\frac{3 h (1+ w )}{4}} + B \biggl[ G \ln \frac{G}{\beta} - G \biggr] + F \biggl( \frac{G}{ \beta} \biggr)^{\frac{1}{2}} \\ &{}+ D G^{\frac{- h +1}{4}} + c_{2} G, \end{aligned}$$
(21)

where, \(A = \frac{k^{2} \rho_{0} ( 1+ w ) \beta}{h^{2} [ 4 h +3 h w - 1 ] [ - 3 h ( 1+ w ) +4 ] [ 3 h (1+ w ) ]}\), \(B = - \frac{27 ( 2 h - 1 ) \alpha (1+ w )}{ 8( h +3)}\), \(F = - \frac{3(1+ w ) \beta}{4( h +1)}\) and \(D = \frac{4 c_{1} \beta^{\frac{h +3}{4}}}{h^{2} ( h +3 ) (1 - h )}\). Furthermore, it is known that the linear \(c_{2}\) term does not contribute to the field equations, and therefore \(c_{2} =0\) (Goheer et al. 2009). As we mentioned before that the lagrangian (14) was found by obtaining \(f_{1} ( G )\). However, we will search the case of \(f_{2} ( R ) = R + \alpha R^{2}\) function in Eq. (17). In line with this, using \(f_{2} ( R ) = R + \alpha R^{2}\) and Eq. (17) we obtain

$$ X t^{- 4} + Y t^{- 2} =0, $$
(22)

with \(X =18 \alpha h (2 h - 1) [ 4 - 3 h - 3 h w ]\) and \(Y = h [ - 2+3 h +3 h w ]\). This equation has a trivial solution given as following:

$$\begin{aligned} &h_{1} = \frac{2}{3(1+ w )}, \end{aligned}$$
(23)
$$\begin{aligned} &h_{2} = \frac{4}{3(1+ w )}. \end{aligned}$$
(24)

While the solution given by (23) denotes the FRW solution, the other one satisfies super acceleration one (Elizalde and Saez-Gomez 2009). Note that the EOS parameter obtained from (12) matches with the solution (23).

Hence the lagrangian (14) is constructed as

$$\begin{aligned} F ( R, G ) =& B \biggl[ G \ln \frac{G}{\beta} - G \biggr] + A \biggl( \frac{G}{\beta} \biggr)^{\frac{3 h (1+ w )}{4}} + F \biggl( \frac{G}{ \beta} \biggr)^{\frac{1}{2}} \\ &{}+ D G^{\frac{- h +1}{4}} + R + \alpha R^{2}. \end{aligned}$$
(25)

This solution is more general a unified solution comparing to the solution of the modified Gauss Bonnet gravity (Goheer et al. 2009). To illiterate this for instance,

1. To show Einstein approach in modified Gauss Bonnet gravity the authors have taken \(k^{2} \rho_{0} =3 h^{2}\) and \(h = \frac{2}{3(1+ w )}\), and concluded that \(c_{1} =0\) to make \(f ( G ) =0\) (Goheer et al. 2009). Similarly by using (23) and \(k^{2} \rho_{0} =3 h^{2}\) with \(\alpha =0\) the expression (25) reduces to \(F ( R, G ) = D G^{\frac{- h +1}{4}} + R\) under the requirement \(c_{1} =0\) for the Einstein approach. Thereafter, when this lagrangian is inserted into Eq. (15) the solution (23) will be found, so that the deceleration phase regions are seen: the radiation (with \(w= \frac{1}{3}\)) and the dust (with \(w=0\)).

2. If \(c_{1} \neq 0\) and \(\alpha =0\) the real value of \(D G^{\frac{- h +1}{4}}\) term can be obtained by using values (23), (24) as \(f_{1} ( G ) = D G^{\frac{3 w +1}{12(1+ w )}}\) or \(D G^{\frac{3 w - 1}{12(1+ w )}}\), respectively. But, using the value (24) in (25) brings an uncertainty in the A term. That is why we use the value in (23). When \(\sigma = \frac{3 w +1}{12(1+ w )}\), and \(\sigma <0\), the late time acceleration of the universe (\(- 1< w < \frac{- 1}{3}\)) is exhibited. As a result, the lagrangian function can be written the form \(F ( R, G ) = D G^{\sigma} + R\), with \(\alpha =0\).

3. If \(c_{1} =0\) and \(\alpha \neq 0\) or the first term dominates the other terms the solution is reduced to the super accelerated expansion case, in which the dark energy term is \(F ( R, G ) = B [ G \ln \frac{G}{\beta} - G ]\). To illustrate this one can put this term Eq. (16) and obtains

$$ \frac{27 h^{2} ( 2 h - 1 ) \alpha (1+ w )(3 h w +3 h - 4)}{2 t^{4}} =0. $$
(26)

For real value of \(h\) with \(w\) we have only one solution of the above equation: \(h_{2} = \frac{4}{3(1+ w )}\). So, the function \(f_{1} ( G ) = B [ G \ln \frac{G}{\beta} - G ]\) produces the super accelerated expansion. However, when the function \(f_{2} ( R ) = R + \alpha R^{2}\) is inserted into Eq. (17), Eq. (22) will be found. When the value obtained from (26) is written in (22) the following result will be obtained:

$$ \frac{8}{3(1+ w )} t^{- 2} =0. $$
(27)

There is one solution of this equation in the FRW universe which indicates the big bang singularity as \(w \rightarrow\infty\). As a result, after the singularity at the beginning one can have the early time super accelerated inflation model with \(f_{1} ( G ) = B [ G \ln \frac{G}{ \beta} - G ]\).

Hence in general the real value of the lagrangian function should be as follows

$$ F ( R, G ) = B \biggl[ G \ln \frac{G}{\beta} - G \biggr] + D G^{\sigma} + R + \alpha R^{2}, $$
(28)

with the FRW value. This lagrangian provides a transition mechanism among the three evolution stages of the universe in unified way:

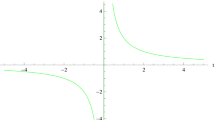
(\(i\)). In the early time universe, the first term dominates to the other terms where we fixed \(\sigma<0\). At the limit \(t \rightarrow 0\) the \(F ( R, G )\) has a singularity as \(F ( R, G ) \rightarrow-\infty\). If \(\alpha >0\). Here it should be noted that \((1+w)>0\). When \(t >0\) this term increases with time as given in Fig. 1 that corresponding to the inflation.

Fig. 1
figure 1

Evolution of \(F ( R, G )\) versus cosmic time where we fixed \(h=3\) and taken \(0< t<1\) and \(\alpha= 10^{-2}\). Also, for any value of \(h\) in the range \(1< h< 2\) the figure exhibits a similar form due to the evolution of the function relating directly to the cosmic time

Full size image

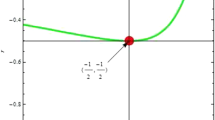
As we explained in (26) and (27) previously this term in the function produces a super accelerated expansion. In this regard (see Fig. 2), for \(h>2\) the EOS parameter is in the range \(-1< w< \frac{-1}{3}\) that there is a quintessence type expansion after the singularity. For \(1< h< 2\) the EOS parameter is in the range of \(\frac{-1}{3} < w< \frac{1}{3}\). Here, we conclude that the quintessence type-energy should evolve into the known normal matter-energy form or the known normal matter-energy should be made from a part of dark energy during the inflation.

Fig. 2
figure 2

Evolution of \(F ( R, G )\) versus \(t\) and the EOS parameter. The time and the EOS parameter are in the range of \(0< t<1\) and \(-1< w< \frac{1}{3}\), respectively

Full size image

Since the EOS parameter is \(w< \frac{1}{3}\) for \(h>1\) the inflation continues till the radiation era (\(h = \frac{1}{2}, w= \frac{1}{3}\)) where the \(B\) term is zero. Therefore, the universe should pass to a new phase in this point and the FRW solution is valid in this point only. Here we did not use any inflationary scalar field (Ferraro and Fiorini 2007) or any scalar field description.

On the other hand, we have clarified our approach using the slow-roll parameters, i.e., \(\epsilon = - \frac{\dot{H}}{H^{2}}\), \(\eta= - \frac{\ddot{H}}{2H \dot{H}}\) which satisfy the following conditions during inflation (Bamba et al. 2014; De Laurentis et al. 2015):

$$ \biggl\vert \frac{\dot{H}}{H^{2}} \biggr\vert \ll 1,\qquad \biggl\vert \frac{\ddot{H}}{H \dot{H}} \biggr\vert \ll 1, $$
(29)

where \(\epsilon=- \frac{\dot{H}}{H^{2}}\) and \(\eta= - \frac{\ddot{H}}{H \dot{H}}\) are positive due to \(\dot{H} <0\) and must be very small during the inflation process. Using Eqs. (9), (10) one can arrive at the following result:

$$\begin{aligned} &\rho_{e} ( 1+ w_{e} ) f_{R} - \rho (1+w) \\ &\quad{}= \frac{1}{2 k^{2}} \bigl( - 2 H \dot{F}_{R} + 2 \ddot{F}_{R} +16H \dot{H} \dot{F}_{G} \\ &\qquad{}- 8 H^{3} \dot{F}_{G} +8 H^{2} \ddot{F}_{G} \bigr). \end{aligned}$$
(30)

Inserting the function into the equation above and using the definition of the EOS parameter from \(Z\) relation we obtain the slow-roll parameters as

$$ \epsilon = \frac{2}{h},\qquad \eta= \frac{4}{h}, $$
(31)

where we take \(w \sim w_{e}\) for \(h \gg 2\) (where the EOS parameter behaves as the dark energy). The slow-roll conditions given by (29) are satisfied when \(h \gg 2\). Furthermore, the spectral index \(n_{s}\) and the tensor scalar ratio \(r\), which are the observational parameters, are given as follows (Bamba et al. 2014):

$$ n_{s} - 1\sim - 6 \epsilon +2\eta,\qquad r=16 \epsilon. $$
(32)

Using the values in (31) one obtains

$$ n_{s} \sim1 - \frac{4}{h},\qquad r= \frac{32}{h}. $$
(33)

For the very large values of \(h\), namely when \(h \gg 2\), it can be obtained the realistic values coming from the observational data given by the spectral index and the tensor scalar ratio \(n_{s} =0.9603 \pm 0.0073 (68\%CL)\) and \(r<0.11 (95\%CL)\), respectively (Ade et al. 2014a, 2014b). However, for the very large values of \(h\) both the spectral index and the tensor scalar ratio dominate during the inflation stage, but for \(1< h <2\) the inflation is driven by \(n_{s}\) only. To show this cases we will use the number of e-folds \(N\) (because of our inflation model relating to the cosmic time (see Fig. 1)) given as

$$ N(t)= \int_{t_{i}}^{t_{e}} H dt, $$
(34)

where \(t_{i}\) and \(t_{e}\) denote the time at the beginning and ending of the inflation, respectively. When we use the Hubble parameter given by (18) the number of e-folds is found as

$$ N ( t ) =h(\ln t_{e} -\ln t_{i} ). $$
(35)

The expression given by (33) can be written in the terms of e-folds as

$$ n_{s} \sim1 - \frac{4 (\ln t_{e} -\ln t_{i} )}{N},\qquad r= \frac{32 (\ln t_{e} -\ln t_{i} )}{N}. $$
(36)

We define \(t_{e} = 10^{-m}\), \(t_{i} = 10^{-n}\) and two regions in the inflation process, i.e. \(h>2\) and \(1< h <2\). We also define two slow-roll parameters corresponding to the regions \(\epsilon_{1}\) and \(\epsilon_{2}\). When the range of \(h\) is evolved from \(h>2\) into \(1< h <2\) the slow-roll parameter is evolved from \(\epsilon_{1}\) into \(\epsilon_{2}\).

For the first region \(h>2\), the condition \(r<0.11\) shows that \(n-m<0.0901\) when \(N=60\). The spectral index \(n_{s}\) is approximately equal to 0.98 when \(n-m=0.09\), where we have chosen the initial time of the inflation as \(10^{-3}\) to compatible with Fig. 1.

On the other hand, for the second region when we use Eq. (30) the effective EOS is obtained as \(w_{e} =-1+ \frac{4}{3 h}\). Using \(\epsilon\), which equals to \(\epsilon_{1}\) we obtain \(\epsilon_{1} = \frac{3( w_{e} +1)}{ 2}\). As we expressed before (\(w_{e} =w\)), we expect evolving of \(w_{e}\) into \(w\), i.e. \(w_{e} \sim w\) after the first region so that \(\epsilon_{1} \sim \epsilon_{2}\) showing the creation of the normal matter. Using the FRW value given by (23) and \(\epsilon_{2} = \frac{3(w+1)}{2}\), the slow-roll parameters of the second region are found as \(\epsilon_{2} = \frac{1}{h}\), \(\eta= \frac{2}{h}\), and are obtained in the terms of \(N\) the spectral index and the tensor scalar ratio as \(n_{s} \sim1 - \frac{2(\ln t_{e_{2}} -\ln t_{i_{2}} )}{N}\) and \(r= \frac{16 (\ln t_{e_{2}} -\ln t_{i_{2}} )}{N}\), respectively, where \(t_{e_{2}} =1\) and \(t_{i_{2}} = 10^{-m}. m =2.91\) is the beginning time of the second region in the inflation process. When \(N\sim 50 n_{s}\) and \(r\) are found as \({\sim}0.74\) and \({\sim}2.14\), respectively, and the slow-roll parameters as \(\epsilon_{2} \sim0.13\), \(\eta \sim 0.26\). However, it is known that when the values in (33) equal to or larger than unity, and \(N\gtrsim 50\) the inflation stops (Bamba et al. 2014). Therefore the inflation in the second region is driven by \(n_{s}\).

Hence it is provided that the first term given by (28) describes the inflationary universe in the two regions by the observables parameters \(n_{s}\) and \(r\).

On the other hand, some authors argued that for the disappearing of the anti-gravity (namely ghost field) in the early time universe, it should be \(\alpha>0\) in the \(f ( R ) = \alpha R^{m}\) model (Nojiri and Odintsov 2009, 2011) that coincides with our approach. After the inflation they used \(\alpha<0\). In this study, we similarly take \(\alpha<0\) after the inflation.

(\(\mathit{ii}\)). Next, the radiation type expansion occurs with the Einstein term due to \(B=0\). However, for dust region \(h= \frac{2}{3}\) there is not a physical meaning of the second term, and therefore it has not any impact on this region so \(c_{1} =0\). In this case the Einstein term again dominates to the first term. Further, for \(h=1\) the universe is at beginning of acceleration but the acceleration has not started yet. The EOS parameter is \(w= \frac{-1}{3}\), and the lagrangian function is still defined by the Einstein term. So, the expansion of the universe continues with this term.

(\(\mathit{iii}\)). If \(\alpha <0\) and when \(w< \frac{-1}{3}\), the late time acceleration of the universe occurs with the second term because we fixed \(\sigma< 0\).

Hence, we shown that the lagrangian function (28) is a unified solution which describes transitions between the phases from the early time inflation to the deceleration and also the late time cosmic acceleration without using a scalar field.

4 Phantom solutions

The scale factor and Hubble parameter in this region are given as follows (Nojiri and Odintsov 2005):

$$ a = a_{0} ( t_{s} - t )^{- h}, \qquad H = \frac{h}{t_{s} - t}\quad (h>0), $$
(37)

where \(t_{s}\) indicates Rip time singularity at \(t_{s} = t\) (Nojiri and Odintsov 2005; Bamba et al. 2010). From (3) Ricci scalar and its derivative and from (11) the energy density are

$$ \begin{aligned} &R = \frac{6 h (2 h +1)}{ ( t_{s} - t )^{2}},\qquad \dot{R} = \frac{12 h (2 h +1)}{ ( t_{s} - t )^{3}},\\ &\rho = \rho_{0} a_{0}^{- 3(1+ w )} ( t_{s} - t )^{3 h (1+ w )}. \end{aligned} $$
(38)

By following a similar way as we did in the previous section and by taking \(h \rightarrow- h\) we obtain

$$\begin{aligned} f_{1} ( G ) =& \check{A} \biggl( \frac{G}{\beta} \biggr)^{\frac{- 3 h (1+ w )}{4}} + \check{B} \biggl[ G \ln \frac{G}{\beta} - G \biggr] + \check{D} \biggl( \frac{G}{\beta} \biggr)^{\frac{1}{2}} \\ &{}+ \check{F} G^{\frac{h +1}{4}} + c_{2} G, \end{aligned}$$
(39)

finally the lagrangian (14) will be found as

$$\begin{aligned} F ( R, G ) =& \check{A} \biggl( \frac{G}{\beta} \biggr)^{\frac{- 3 h (1+ w )}{4}} + \check{B} \biggl[ G \ln \frac{G}{\beta} - G \biggr] + \check{D} \biggl( \frac{G}{\beta} \biggr)^{\frac{1}{2}} \\ &{}+ \check{F} G^{\frac{h +1}{4}} + R + \alpha R^{2}, \end{aligned}$$
(40)

with \(c_{2} =0\). Here \(\check{A} = \frac{k^{2} \rho_{0} a_{0}^{- 3(1+ w )} ( 1+ w ) \beta}{h^{2} [ 4 h +3 h w +1 ] [ 3 h ( 1+ w ) +4 ] [ 3 h (1+ w ) ]}\), \(\check{B} = - \frac{27 ( 2 h +1 ) \alpha (1+ w )}{8( h - 3)}\), \(\check{D} = \frac{3(1+ w ) \beta}{4( h - 1)}\) and \(\check{F} = \frac{4 c_{1} \beta^{\frac{- h +3}{4}}}{h^{2} ( h - 3 ) (1+ h )}\). The \(h\) values are found from Eq. (17):

$$\begin{aligned} &h_{1} = - \frac{2}{3(1+ w )}, \end{aligned}$$
(41)
$$\begin{aligned} &h_{2} = - \frac{4}{3(1+ w )}. \end{aligned}$$
(42)

One can write the real value of the lagrangian (40) as the following:

$$\begin{aligned} F ( R, G ) =& \check{B} \biggl[ G \ln \frac{G}{\beta} - G \biggr] + \check{F} G^{\frac{3w+1}{12(1+w)}} \\ &{}+ R + \alpha R^{2}, \end{aligned}$$
(43)

this is the solution of our model in the phantom phase. This lagrangian specifies that the acceleration of the universe is in two regions:

  1. 1.

    The range \(- \frac{11}{9} < w < - 1\) is described by the second term.

  2. 2.

    The case \(w < - \frac{11}{9}\) is defined by the first term.

Other terms produce the FRW and the super accelerated values, in which one can investigate the expansion of the universe in the phase by using these values.

5 Concluding remarks

In this study, we have considered the extended Gauss Bonnet gravity that its lagrangian is given by \(F ( R, G ) =f ( G ) + R + \alpha R^{2}\). This model is a modification including \(R^{2}\)-term comparing with the modified Gauss Bonnet lagrangian density i.e., \(f ( G ) + R\). We have constructed the Friedmann equation corresponding to the gravity (given in (12)). This equation is appeared as a differential equation which relates to the time (given in (19)) with the solution (18). Next, we discussed the power-law solutions of the equation. By this way, we have realized the unified solution of our model, which describes a mechanism that provides transitions between three stages of the universe (in given (28)). In particular, in this solution we have obtained an inflation model that continues into two phase regions;

1. In initial part the universe should completely be filled with dark energy.

2. During the process it is appearing that a part of this energy evolves to the normal matter-energy form.

Here, we did not use a scalar field, and the inflation of the universe is an expansion out of de Sitter type. The function approaches to zero at the end point of the inflation for any values of the EOS parameter in the range \(\frac{1}{3} >w>-1\), because the evolution of the function depends only on cosmic time. However, when the universe passes in the radiation region the term is zero due to \(B=0\). Further, we have shown that our approach for the inflation is realistic by finding \(n_{s}\), \(r\) indexes. Here, the inflation in the initial part is driven by the both indexes whereas the second region is driven by \(n_{s}\) only.

It should be noted that, when \(\alpha>0\) we have obtained the inflation stage, in which any ghost field (the case of negative energy density) does not exist, because \(\rho>0\), \(p<0\) from Eqs. (5), (6), where the EOS behaves as the quintessence type dark energy. In the range of \(1< h< \frac{4}{3}\) the pressure is greater than zero, so that in this point a part of dark energy evolves into the normal matter-energy form where the inflation is driven by the spectral index parameter \(n_{s}\). Although the first term given in (28) contains the ghosts in the stages out of the inflation it does not affect these stages. Therefore it does not cause any instability in the space-time.

Next, the universe passes to a new phase where the Einstein term is trivial, so the radiation and dust regions, and also beginning of the acceleration case are expressed by this term.

Next, with the real value of the Gauss Bonnet term we have shown the late time accelerated expansion case if \(\sigma<0\). In other words, the value (23) which is produced by Eq. (17) tells us that it is necessarily to be a real value of \(D G^{\frac{-h +1}{4}}\) term to find the real valued of \(F ( R, G )\) for quintessence type acceleration.

Finally, we have demonstrated the solution of our model if the universe crosses the \(w=-1\) barrier, and in a similar way as we did previously for non-phantom case, we have found the real valued of our \(F ( R, G )\) model with the value (43) that shows accelerating universe in two regions:

  1. 1.

    \(- \frac{11}{9} < w < - 1\),

  2. 2.

    \(w < - \frac{11}{9}\),

that coincides with recent cosmological observations (Ade et al. 2014a). However, in both cases, the type I (Big Rip) singularity can occur at \(t_{s} =t\), where \(a\rightarrow\infty\), \(\rho\rightarrow\infty\) and \(p\rightarrow\infty\) (Nojiri and Odintsov 2005, 2011; Nojiri at al. 2005; Bamba et al. 2010).