Half space albedo problem for the nonconservative vector equation of transfer with a combination of Rayleigh and isotropic scattering

Abstract

The half-space albedo problem has been solved for a combination of Rayleigh and isotropic scattering using $H_{N}$ method which is developed for the neutron transport studies. The numerical results are compared with exact values obtained using variational method and Chandrasekhar’s equation for the $\mathbf{H}$-matrix. The analytical solutions of $H_{N}$ method are easy to handle in comparison with the other methods. The numerical results are in good agreement with previous works in literature.

1 Introduction

The equations of transfer for the two components $I_{\ell } \mathbf{(\tau ,\mu )}$ and $I_{r}\mathbf{(\tau ,\mu )}$ of the polarized radiation field in a free-electron stellar atmospheres are formulated by Chandrasekhar (1946). Viik (1989) solved the vector equation of radiative transfer both for conservative and non-conservative planetary atmospheres by using discrete ordinates method. Siewert and Fraley (1967) used the singular eigenfunction expansion technique developed by Case (1960) to construct rigorous analytical solutions for the half-space problems. Similar methods have been used to establish full range completeness and orthogonality theorems to the normal mode approach for a conservative combination of Rayleigh and isotropic scattering (Mourad and Siewert 1969). This method was applied to establish full range completeness and orthogonality theorems for the general Rayleigh-scattering problem by Schnatz and Siewert (1970). They obtained the solutions of the half-space albedo and Milne problems in terms of normal modes and got the all unknown expansion coefficients in terms of the H-matrix (Schnatz and Siewert 1971). Pomraning (1970) described the half-space albedo problem by the Rayleigh scattering law averaged over polarization and used variational method for this problem. Here, the half-space albedo problem has been solved for a combination of Rayleigh and isotropic scattering using $H_{N}$ method (Tezcan et al. 2003). This method was also used for nonconservative Milne problem (Karahasanoğlu Şenyığıt and Kaşkaş 2007).

We consider the vector equation of transfer

$$ \mu \frac{\partial \mathbf{I}(\tau ,\mu )}{\partial \tau }+\mathbf{I}( \tau ,\mu )=\frac{1}{2}\omega \mathbf{Q}(\mu ) \int_{-1}^{+1} \mathbf{Q}^{T}\bigl( \mu^{\prime }\bigr)\mathbf{I}\bigl(\tau ,\mu^{\prime }\bigr)d \mu^{\prime }, $$

(1)

where

$$ \mathbf{Q}(\mu )=\frac{3}{2}(c+2)^{-1/2} \begin{pmatrix} c\mu^{2}+\frac{2}{3}(1-c) & (2c)^{\frac{1}{2}}(1-\mu^{2}) \\ \frac{1}{3}(c+2) & 0 \end{pmatrix} . $$

(2)

Here, $\tau$ is the optical variable, $\mu$ is the direction cosine of the propagating radiation (as measured from the positive $\tau$-axis) and $\omega \in {}[ 0,1]$ is the single-scattering albedo. $\mathbf{I(\tau ,\mu )}$ is a vector whose two components $I_{\ell }\mathbf{(\tau ,\mu )}$ and $I_{r}\mathbf{(\tau ,\mu )}$ are the angular intensities in the two states of polarization. $\mathbf{Q}^{T}(\mu )$ denotes the transpose of $\mathbf{Q}(\mu )$. The parameter $c$ is a measure of the Rayleigh component of scattering law: $c=1$ and $w=1$ would yield Chandrasekhar’s conservative Rayleigh-scattering case, $w=1$ and $c\in [ 0,1]$ is Chandrasekhar’s conservative case for a mixture of Rayleigh and isotropic scattering laws. $c=1$ and $w\in [ 0,1]$ yields the general Rayleigh scattering (Siewert 1999).

We consider boundary conditions of the form (Majorino and Siewert 1980; Pomraning 1970)

$$ \mathbf{I}(0,-\mu )=\mathbf{Q}(\mu )\sum_{i=0}^{N} \mathbf{a} _{i}\mu^{i}, \quad \mu >0 , $$

(3)

and

$$ \mathbf{I}(0,\mu )=\mathbf{F}, \quad \mu >0 , $$

(4)

where the $\mathbf{a}_{i}$ coefficients are $2\times 1$ matrices and $\mathbf{F}$ is a constant vector. This vector represents the three states of degree of the polarization for isotropic incident radiation: $\delta =1$, $\delta =0$ and $\delta =-1$ and they can be written alternatively with (Schnatz and Siewert 1971; Pomraning 1970)

$$ \mathbf{I}(0,\mu ) = \begin{pmatrix} 0 \\ 1 \end{pmatrix} , \qquad \mathbf{I}(0,\mu ) = \begin{pmatrix} 1 \\ 1 \end{pmatrix} , \qquad \mathbf{I}(0,\mu ) = \begin{pmatrix} 1 \\ 0 \end{pmatrix} . $$

(5)

The general solution of (1) is

$$\begin{aligned} \mathbf{I}(\tau ,\mu ) =& A(\eta_{0})\mathbf{\varPhi }( \eta_{0},\mu )e ^{-\tau /\eta_{0}} \\ &{} +A(-\eta_{0})\mathbf{\varPhi }(-\eta_{0},\mu )e^{ \tau /\eta_{0}} \\ &{}\times\int_{-1}^{+1}\mathbf{\varPsi }(\eta , \mu ) \mathbf{A}(\eta )e^{-\tau /\eta }d\eta , \end{aligned}$$

(6)

where $A(\pm \eta_{0})$ and the vector $\mathbf{A}(\eta )$, are the arbitrary expansion coefficients determined by using appropriate boundary conditions (Burniston and Siewert 1970). $\mathbf{\varPsi }( \eta ,\mu )$ denotes the $2\times 2$ matrix,

$$ \mathbf{\varPsi }(\eta ,\mu )= \begin{pmatrix} \mathbf{\varPhi }_{1}(\eta ,\mu ) & \mathbf{\varPhi }_{2}(\eta ,\mu ) \end{pmatrix} , $$

(7)

and

$$ \mathbf{A }(\eta )= \begin{pmatrix} A_{1}(\eta ) \\ A_{2}(\eta ) \end{pmatrix}. $$

(8)

The discrete eigenvector corresponding to the eigenvalue $\eta_{0}$ is

$$\begin{aligned} \mathbf{\varPhi }(\pm \eta_{0},\mu ) =&\frac{3}{2}\omega \eta_{0}\biggl(\frac{1}{ \eta_{0}\mp \mu }\biggr) \\ &{}\times \begin{pmatrix} c(1-\mu^{2})\varLambda_{2}(\eta_{0})+\omega_{2}(\eta_{0}) & \\ \omega_{2}(\eta_{0}) & \end{pmatrix} , \end{aligned}$$

(9)

where

$$\begin{aligned} &\varLambda_{i}(z)=(-1)^{i}+3\bigl(1-z^{2}\bigr) \varLambda_{0}(z)-(-1)^{i}3(1-\omega )z ^{2}, \\ &\quad i=1\text{ or }2, \end{aligned}$$

(10)

and

$$ \varLambda_{0}(z)=1+\frac{1}{2}\omega z \int_{-1}^{+1}\frac{d \mu }{\mu -z}. $$

(11)

The continuum eigenvectors can be written as (Burniston and Siewert 1970),

$$\begin{aligned} \!\begin{aligned} &\mathbf{\varPhi }_{1}(\eta ,\mu ) \\ &\quad=\begin{pmatrix} \frac{3}{2}\omega c\eta (1-\eta^{2})(1-\mu^{2})\frac{P}{\eta -\mu }+ \omega_{1}(\eta )\delta (\eta -\mu ) \\ -\omega_{2}(\eta )\delta (\eta -\mu ) \end{pmatrix} , \\ &\mathbf{\varPhi }_{2}(\eta ,\mu ) =\begin{pmatrix} \frac{3}{2}\omega \eta (1-\eta^{2})\frac{P}{\eta -\mu }+\lambda_{1}( \eta )\delta (\eta -\mu ) \\ \frac{3}{2}\omega \eta (1-\eta^{2})\frac{P}{\eta -\mu }+\lambda_{2}( \eta )\delta (\eta -\mu ) \end{pmatrix}, \\ &\quad \eta \in ({-}1,1) , \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} \!\begin{aligned} &\lambda_{i}(\eta ) = (-1)^{i}+3\bigl(1-\eta^{2} \bigr)\lambda_{0}(\eta ) -(-1)^{i}3 \eta^{2}(1- \omega ),\\ &\quad i= 1 \ \text{or} \ 2, \\ &\lambda_{0}(\eta ) =1-\omega \eta \tanh^{-1}\eta , \\ &\omega_{1}(\eta ) =c\bigl(1-\eta^{2}\bigr) \lambda_{1}(\eta )+\omega_{2}(\eta ), \\ &\omega_{2}(\eta ) =\frac{4}{3}(1-c)+2c(1-\omega ) \eta^{2} . \end{aligned} \end{aligned}$$

(13)

The orthogonality condition of the discrete eigenvectors is

$$ \int_{-1}^{+1}\mu \mathbf{\varPhi }^{T} \bigl(\eta_{0}^{\prime }, \mu \bigr)\mathbf{\varPhi }( \eta_{0},\mu )d\mu =0, \qquad \eta_{0}^{\prime }\neq \eta_{0}, $$

(14)

and the associated full-range discrete normalization integrals may be evaluated to yield

$$ N(\pm \eta_{0})= \int_{-1}^{ +1}\mu \mathbf{\varPhi }^{T}( \pm \eta_{0},\mu )\mathbf{\varPhi }(\pm \eta_{0},\mu )d\mu , $$

(15)

with

$$\begin{aligned} \mathbf{N}(\pm \eta_{0}) =&\pm 12\omega \eta_{0}^{2} \bigl[c\bigl(1- \eta_{0}^{2}\bigr) \varLambda_{2}(\eta_{0})+\omega_{2}( \eta_{0})\bigr] \\ &{}\times \frac{ d}{dz}\varLambda (z) \biggm|_{z=\eta_{0}} . \end{aligned}$$

(16)

The orthogonality relation of the continuum eigenfunctions are given by the following equation (Schnatz and Siewert 1970)

$$ \langle i| j \rangle {=} \int^{ +1}_{-1} \mu \mathbf{\varPhi }_{i}^{T\dagger }(\eta ,\mu )\mathbf{\varPhi }_{j}( \eta ,\mu )d\mu , \quad i,j=1 \ \text{and} \ 2 . $$

(17)

The adjoint vectors are defined as

$$\begin{aligned} \!\begin{aligned} \mathbf{\varPhi }_{1}^{\dagger }(\eta ,\mu ) =N_{22}( \eta ) \mathbf{\varPhi } _{1}(\eta ,\mu )-N_{12}(\eta ) \mathbf{\varPhi }_{2}( \eta ,\mu ), \\ \mathbf{\varPhi }_{2}^{\dagger }(\eta ,\mu ) =N_{11}( \eta ) \mathbf{\varPhi } _{2}(\eta ,\mu )-N_{21}(\eta ) \mathbf{\varPhi }_{1}(\eta ,\mu ) , \end{aligned} \end{aligned}$$

(18)

with

$$\begin{aligned} \!\begin{aligned} &\langle i| j \rangle =0,\quad i\neq j, \\ &\langle 1| 1 \rangle = \langle 2| 2 \rangle =N( \eta )\delta \bigl(\eta -\eta^{\prime }\bigr). \end{aligned} \end{aligned}$$

(19)

Here

$$ N(\eta )=\eta \bigl[N_{11}(\eta )N_{22}(\eta )-N_{12}( \eta )N_{21}(\eta )\bigr], $$

(20)

and

$$\begin{aligned} N_{11}(\eta ) =& c^{2}\bigl(1-\eta^{2} \bigr)^{2} \biggl[ \lambda_{1}^{2}(\eta )+ \frac{9}{4}\omega^{2}\eta^{2}\bigl(1-\eta^{2} \bigr)^{2}\pi^{2} \biggr] \\ &{}+ 2\omega _{2}(\eta ) \bigl[ c\bigl(1-\eta^{2}\bigr)\lambda_{1}(\eta )+ \omega_{2}(\eta ) \bigr] , \\ N_{12}(\eta ) =& N_{12}(\eta ) \\ =&c\bigl(1-\eta^{2} \bigr) \biggl[ \lambda_{1}^{2}( \eta )+\frac{9}{4} \omega^{2}\eta^{2}\bigl(1-\eta^{2} \bigr)^{2}\pi^{2} \biggr] \\ &{}-2 \omega_{2}(\eta ) \bigl[ 1-3(1-\omega )\eta^{2} \bigr] , \\ N_{22}(\eta ) =& 2 \bigl[ 1-3(1-\omega )\eta^{2} \bigr] ^{2} \\ &{} +18\bigl(1-\eta ^{2}\bigr)^{2} \biggl[ \lambda_{0}^{2}(\eta )+\frac{1}{4}\omega^{2} \eta^{2}\pi ^{2} \biggr] . \end{aligned}$$

(21)

2 Analysis

For the half space albedo problem, we seek solution of (1) for $\tau \epsilon (0,\infty )$ which satisfies the boundary conditions

$$ \lim_{\tau \rightarrow \infty } \mathbf{I}(\tau ,\mu )< \infty . $$

(22)

This condition requires that $A(-\eta_{0})$ and $\mathbf{A}(\eta )$ are to be zero in (6) for $\eta <0$ . Then the solution is

$$\begin{aligned} \mathbf{I}(\tau ,\mu ) =&A(\eta_{0})\mathbf{\varPhi }( \eta_{0},\mu )e^{- \tau /\eta_{0}} \\ &{}+ \int_{0}^{+1}\mathbf{\varPsi }(\eta ,\mu ) \mathbf{A}(\eta )e^{-\tau /\eta }d\eta . \end{aligned}$$

(23)

The general solution using (7) and (8) for $\tau =0$ is

$$\begin{aligned} \mathbf{I}(0,\mu ) =&A(\eta_{0})\mathbf{\varPhi }(\eta_{0}, \mu ) \\ &{}+ \int _{0}^{+1}\bigl[ A_{1}(\eta ) \mathbf{\varPhi }_{1}(\eta ,\mu )+A_{2}(\eta )\mathbf{\varPhi }_{2}(\eta , \mu )\bigr]d\eta . \end{aligned}$$

(24)

To get the unknown coefficients $A(\eta_{0})$, $A_{1}(\eta )$ and $A_{2}(\eta )$, Eq. (24) is multiplied by $\mu \varPhi^{T}(\eta_{0}, \mu )$ and $\mu \varPhi_{i}^{T^{\dagger }}(\eta ,\mu )$ respectively and integrated over $\mu$, $\mu \in (-1,1)$. Here we use the boundary conditions in Eqs. (3–4) and the orthogonality relations for the discrete and continuum modes. Then

$$\begin{aligned} &\!\begin{aligned}[b] A(\eta_{0})&=\frac{1}{N(\eta_{0})} \Biggl[-\sum _{i=0} ^{N} \mathbf{\varGamma }_{i}( \eta_{0})\mathbf{a}_{i}\\ &\quad{}+ \int_{0}^{ +1}\mu \mathbf{\varPhi }^{T}( \eta_{0},\mu )\mathbf{F}d\mu \Biggr] , \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned} &\!\begin{aligned}[b] A_{1}(\eta ) &= \frac{1}{N(\eta )} \Biggl\{ -\sum _{i=0}^{N}\bigl[ -N_{22}(\eta ) \mathbf{\varGamma }_{i}^{1}(\eta )+N_{12}(\eta )\mathbf{\varGamma } _{i} ^{2}(\eta ) \bigr] \mathbf{a}_{i} \\ &\quad{}+ \int_{0}^{ +1}\mu \bigl[N_{22}( \eta ) \mathbf{\varPhi }_{1}^{T}(\eta ,\mu )\\ &\quad{}-N_{12}(\eta )\mathbf{\varPhi }_{2} ^{T}(\eta ,\mu ) \bigr]\mathbf{F}d\mu \Biggr\} , \end{aligned} \end{aligned}$$

(26)

and

$$\begin{aligned} A_{2}(\eta ) =& \frac{1}{N(\eta )}\Biggl\{ -\sum _{i=0}^{N} \bigl[ N_{21}(\eta ) \mathbf{\varGamma }_{i}^{1}(\eta )-N_{11}(\eta )\mathbf{\varGamma } _{i} ^{2}(\eta ) \bigr] \mathbf{a}_{i} \\ &{}+ \int_{0}^{+1}\mu \bigl[N_{11}( \eta ) \mathbf{\varPhi }_{2}^{T}(\eta ,\mu ) \\ &{}-N_{21}( \eta )\mathbf{\varPhi }_{1} ^{T}(\eta ,\mu ) \bigr]\mathbf{F}d\mu \Biggr\} , \end{aligned}$$

(27)

where

$$\begin{aligned} \!\begin{aligned} &\mathbf{\varGamma }_{i}(\eta_{0}) = \frac{2}{\omega \eta_{0}} \int _{0}^{1}\mu^{i+1}\mathbf{\varPhi }^{T}(\eta_{0},-\mu )\mathbf{Q} ( \mu )d\mu , \\ &\mathbf{\varGamma }_{i}^{j}(\eta ) =\frac{2}{\omega \eta } \int _{0}^{1} \mu^{i+1}\mathbf{\varPhi }_{j}^{T}(\eta ,-\mu )\mathbf{Q}( \mu )d\mu ,\quad j=1,2 , \end{aligned} \end{aligned}$$

(28)

Now, multiplying the exit radiation, $\mathbf{I}(0,-\mu )$, by $\mu^{m+1}$, integrating over $\mu \in (0,1)$, using Eqs. (3–4) and Eqs. (25–28) we obtain

$$\begin{aligned} &\sum_{i=0}^{N} \biggl\{ \int_{0}^{+1} \mu^{m+i+1}\mathbf{Q}(\mu )d\mu +\frac{1}{N(\eta_{0})}\mathbf{D} _{m}( \eta_{0})\mathbf{ \varGamma }_{i}(\eta_{0}) \\ &\qquad{}+ \int_{0}^{ +1}\frac{1}{N( \eta )}\mathbf{D}_{m}^{1}( \eta )\bigl[N_{22}(\eta ) \mathbf{\varGamma }_{i}^{1}(\eta ) \\ &\qquad{}-N_{12}(\eta )\mathbf{\varGamma } _{i} ^{2}(\eta ) \bigr]d\eta \\ &\qquad{}+ \int_{0}^{ +1}\frac{1}{N(\eta )}\mathbf{D}_{m}^{2}( \eta )\bigl[-N_{21}(\eta )\mathbf{\varGamma } _{i}^{1}( \eta ) \\ &\qquad{}+N_{11}(\eta )\mathbf{\varGamma }_{i}^{2}(\eta )\bigr]d\eta \biggr\} \mathbf{a}_{i} \\ &\quad{}= \int_{0}^{\quad +1}\mu \mathbf{\varPhi }^{T}( \eta_{0},\mu )\mathbf{F}d\mu \\ &\qquad{}+ \int_{0}^{+1}\mu \bigl[N_{22}( \eta ) \mathbf{\varPhi }_{1}^{T}(\eta ,\mu )-N_{12}(\eta )\mathbf{\varPhi }_{2} ^{T}(\eta ,\mu ) \bigr]\mathbf{F}d\mu \\ &\qquad{}+ \int _{0}^{ +1}\mu \bigl[N_{11}(\eta )\mathbf{\varPhi } _{2}^{T}(\eta ,\mu )-N_{21}(\eta )\mathbf{\varPhi }_{1}^{T}(\eta ,\mu ) \bigr]\mathbf{F}d\mu , \end{aligned}$$

(29)

where

$$\begin{aligned} \!\begin{aligned} &\mathbf{D}_{i}(\eta_{0})= \int_{0}^{ +1}\mu^{i+1} \mathbf{\varPhi }(- \eta_{0},\mu )d\mu , \\ &\mathbf{D}_{i}^{j}(\eta ) = \int_{0}^{+1}\mu^{i+1} \mathbf{\varPhi }_{j}(-\eta ,\mu )d\mu . \end{aligned} \end{aligned}$$

(30)

The half-space albedo values are computed for the three states of polarization from the following equation

$$ \beta =\frac{ \int_{0}^{1}\Bigl(\begin{matrix} 1 \\ 1 \end{matrix} \Bigr)^{T}\mathbf{I}(0,-\mu )\mu d\mu } { \int_{0}^{ 1}\Bigl(\begin{matrix} 1 \\ 1 \end{matrix}\Bigr) ^{T}\mathbf{I}(0,\mu )\mu d\mu } . $$

(31)

The unknown $\mathbf{a}_{i}$ coefficients in (31) can be obtained from Eq. (29) for three states of polarization in Eq. (5) which are the scalar system of $2N+2$ linear algebraic equations.

3 Conclusions

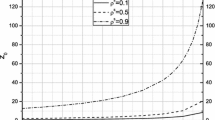
The half-space albedo problem is solved by using $H_{N}$ method for mixture of isotropic and Rayleigh scattering case. The albedo values for $c=1$ for isotropic incident radiation in the three states of polarization with increasing $N$ are given in Tables 1, 2 and 3. Here, $N$ shows the order of approximations. The numerical results are compared with Schnatz and Siewert’s values (Schnatz and Siewert 1971). In general, it is clearly seen that the exact results are obtained in the lowest order approximations. In Tables 4, 5 and 6, the albedo values are given for combination of $c\> \epsilon \> (0,1]$ and different values of $\omega$ in the three states of polarization for $N=10$. Some values are compared with literature (Bond and Siewert 1971). They are good agreement with this reference’s results. Figure 1 shows the half-space albedo versus $\omega$-single scattering albedo graph for $c=0.5$ and $\delta =0$. Albedo increases with increasing the single scattering albedo values and same effect can be shown for different values of $c$ and $\delta =-1$ and $\delta =1$.

Fig. 1

The half-space albedo versus $\omega$-single scattering albedo for $c=0.5$ and the incident radiation in the state of $\delta =0$

Table 1 The half-space albedo for isotropic incident radiation, $c=1$, in the state of $\delta =1$ for selected values of $\omega$

Table 2 The half-space albedo for isotropic incident radiation, $c=1$, in the state of $\delta =0$ for selected values of $\omega$

Table 3 The half-space albedo for isotropic incident radiation, $c=1$, in the state of $\delta =-1$ for selected values of $\omega$

Table 4 The half-space albedo for the incident radiation in the state of $\delta =1$ for selected values of $\omega$ and $c$ for $N=10$

Table 5 The half-space albedo for the incident radiation in the state of $\delta =0$ for selected values of $\omega$ and $c$ for $N=10$

Table 6 The half-space albedo for the incident radiation in the state of $\delta =-1$ for selected values of $\omega$ and $c$ for $N=10$