1 Introduction

Lifshitz spacetimes have received considerable attention from the condensed matter point of view due to the AdS/CFT correspondence, i.e., searching for gravity duals of Lifshitz fixed points for condensed matter physics and quantum chromodynamics (Kachru et al. 2008). From the quantum field theory point of view, there are many invariant scale theories of interest when studying such critical points. Such theories exhibit the anisotropic scale invariance \(t\rightarrow\chi^{z}t\), \(x\rightarrow\chi x\), with \(z\neq1\), where \(z\) is the relative scale dimension of time and space, and these are of particular interest in studies of critical exponent theory and phase transitions. Systems with such behavior appear, for instance, in the description of strongly correlated electrons. The importance of possessing a tool to study strongly correlated condensed matter systems is beyond question, and consequently much attention has focused on this area in recent years.

One of the most well studied systems in the context of gauge/gravity duality is the holographic superconductor. In its simplest form, the gravity sector is a gravitating system with a cosmological constant, a gauge field and a charged scalar field with a potential. The dynamics of the system defines a critical temperature above which the system finds itself in its normal phase and the scalar field does not have any dynamics. Below the critical temperature the system undergoes a phase transition to a new configuration. From the gravity side this is interpreted as a black hole acquiring hair, while from boundary conformal field theory site this is interpreted as a condensation of the scalar field, and the system enters a superconducting phase. In this sense, Lifshitz holographic superconductivity has been a topic of numerous studies, and interesting properties are found when one generalizes the gauge/gravity duality to non-relativistic situations (Hartnoll et al. 2010; Brynjolfsson et al. 2010; Sin et al. 2011; Schaposnik and Tallarita 2013; Momeni et al. 2015; Bu 2012; Keranen and Thorlacius 2012; Zhao et al. 2014; Lu et al. 2014; Tallarita 2014).

The Lifshitz spacetimes are described by the metrics

$$ ds^{2}=- \frac{r^{2z}}{\ell^{2z}}\,dt^{2}+\frac{\ell^{2}}{r^{2}}\,dr^{2}+ \frac{r^{2}}{\ell^{2}} \,d\vec{x}^{2}, $$
(1)

where \(\vec{x}\) represents a \((D-2)\)-dimensional spatial vector, \(D\) is the spacetime dimension, and \(\ell\) denotes the length scale in the geometry. If \(z=1\), the spacetime is the usual anti-de Sitter metric in Poincaré coordinates. Furthermore, all scalar curvature invariants are constant, and these spacetimes have a null curvature singularity at \(r\rightarrow0\) for \(z\neq1\), which can be seen by computing the tidal forces between infalling particles. This singularity is reached in finite proper time by infalling observers, so the spacetime is geodesically incomplete (Horowitz and Way 2012). The metrics of Lifshitz black holes asymptotically have the form (1); however, obtaining analytical solutions does not seem to be a trivial task, and therefore constructing finite temperature gravity duals requires the introduction of strange matter content with a theoretical motivation that is not clear. Another way of finding such a Lifshitz black hole solution is by considering carefully-tuned higher-curvature modifications to the Hilbert–Einstein action, as in new massive gravity (NMG) in 3-dimensions or \(R^{2}\) corrections to general relativity. This has been done, for instance, in Ayon-Beato et al. (2009, 2010), Cai et al. (2009), Dehghani and Mann (2010). A 4-dimensional topological black hole with \(z=2\) was found in Mann (2009), Balasubramanian and McGreevy (2009) and a set of analytic Lifshitz black holes in higher dimensions for arbitrary \(z\) in Bertoldi et al. (2009). Lifshitz black holes with arbitrary dynamical exponent in Horndeski theory were found in Bravo-Gaete and Hassaine (2014) and nonlinearly charged Lifshitz black holes for any exponent \(z>1\) in Alvarez et al. (2014). Thermodynamically, it is difficult to compute conserved quantities for Lifshitz black holes; however, progress was made on the computation of mass and related thermodynamic quantities by using the ADT method (Devecioglu and Sarioglu 2011a, 2011b) as well as the Euclidean action approach (Gonzalez et al. 2011; Myung and Moon 2012). Also, phase transitions between Lifshitz black holes and other configurations with different asymptotes have been studied in Myung (2012). However, due to their different asymptotes these phases transitions do not occur.

Conformal gravity is a four-derivative theory and is perturbatively renormalizable (Stelle 1977, 1978). Also, it contains ghost-like modes in the form of massive spin-2 excitations. However, a solution to the ghost problem in fourth order derivative theories was shown in Mannheim (2007) by using the method of Dirac constraints (Dirac 1964) to quantize the Pais–Uhlenbeck fourth order oscillator model (Pais and Uhlenbeck 1950). In this work, we consider a matter distribution outside the event horizon of the Lifshitz black hole in 4-dimensions in conformal gravity with a spherical transverse section and dynamical exponent \(z=0\). It is worth mentioning that for \(z=0\) the previously mentioned anisotropic scale invariance corresponds to space-like scale invariance with no transformation of time. The matter is parameterized by scalar fields minimally and conformally coupled to gravity. Then, we obtain analytically and numerically the quasinormal frequencies (QNFs) (Regge and Wheeler 1957; Zerilli 1970a, 1970b; Kokkotas and Schmidt 1999; Nollert 1999; Konoplya and Zhidenko 2011) for scalar fields, after which we study their stability under scalar perturbations. Also, we compute the reflection and transmission coefficients and the absorption cross-section.

The study of the QNFs gives information about the stability of black holes under matter fields that evolve perturbatively in their exterior region, without backreacting on the metric. In general, the oscillation frequencies are complex, where the real part represents the oscillation frequency and the imaginary part describes the rate at which this oscillation is damped, with the stability of the black hole being guaranteed if the imaginary part is negative. The QNFs are independent of the initial conditions and depend only on the parameters of the black hole (mass, charge and angular momentum) and the fundamental constants (Newton constant and cosmological constant) that describe a black hole, just like the parameters that define the test field. On the other hand, the QNFs determine how fast a thermal state in the boundary theory will reach thermal equilibrium according to the AdS/CFT correspondence (Maldacena 1998), where the relaxation time of a thermal state is proportional to the inverse of the imaginary part of the QNFs of the dual gravity background, which was established due to the QNFs of the black hole being related to the poles of the retarded correlation function of the corresponding perturbations of the dual conformal field theory (Birmingham et al. 2002). Fermions on a Lifshitz background were studied in Alishahiha et al. (2012) by using the fermionic Green’s function in 4-dimensional Lifshitz spacetime with \(z=2\); the authors considered a non-relativistic (mixed) boundary condition for fermions and showed that the spectrum has a flat band. Also, the Dirac quasinormal modes (QNMs) for a 4-dimensional Lifshitz black hole were studied in Catalan et al. (2014). Generally, the Lifshitz black holes are stable under scalar perturbations, and the QNFs show the absence of a real part (Cuadros-Melgar et al. 2012; Gonzalez et al. 2012a, 2012b; Myung and Moon 2012; Becar et al. 2013; Giacomini et al. 2012). The QNFs have been calculated by means of numerical and analytical techniques, some remarkably numerical methods are: the Mashhoon method, Chandrasekhar–Detweiler, WKB method, Frobenius method, method of continued fractions, Nollert, asymptotic iteration method (AIM) and improved AIM, among others. In the context of black hole thermodynamics, QNMs allow the quantum area spectrum of the black hole horizon, as well as the mass and the entropy spectrum, to be studied (Cuadros-Melgar et al. 2012).

On the other hand, knowledge of black holes’ perturbations is also useful for studying the Hawking radiation, which is a semiclassical effect and gives the thermal radiation emitted by a black hole. At the event horizon, the Hawking radiation is, in fact, blackbody radiation. However, this radiation still has to traverse a non-trivial curved spacetime geometry before reaching a distant observer that can detect it. The surrounding spacetime thus works as a potential barrier for the radiation, giving a deviation from the blackbody radiation spectrum, seen by an asymptotic observer (Maldacena and Strominger 1997). Thus the total flux observed at infinity is that of a \(D\)-dimensional greybody at the Hawking temperature. The factors that modify the spectrum emitted by a black hole are known as greybody factors and can be obtained through the classical scattering (for a review, see Harmark et al. 2010). In this sense, the scalar greybody factors for an asymptotically Lifshitz black hole were studied in Gonzalez et al. (2012b), Lepe et al. (2012), and particle motion on these geometries in Olivares et al. (2014, 2013), Villanueva and Vasquez (2013).

The paper is organized as follows. In Sect. 2, we give a brief review of the 4-dimensional Lifshitz black hole in conformal gravity. In Sect. 3, we calculate the QNFs of scalar perturbations for the 4-dimensional Lifshitz black hole with spherical topology and \(z=0\) for some special cases analytically and numerically by using the improved AIM. Then, in Sect. 4, we study the reflection and transmission coefficients and the absorption cross section. Finally, our conclusions are in Sect. 5.

2 4-Dimensional asymptotically Lifshitz black hole in conformal gravity

In this work, we consider a matter distribution described by a scalar field outside the event horizon of a 4-dimensional asymptotically Lifshitz black hole in conformal gravity with \(z=0\) and spherical topology for the transverse section (Lu et al. 2012). Conformal gravity is a limit case of Einstein–Weyl gravity. The action of Einstein–Weyl gravity is given by

$$ S=\frac{1}{2k^{2}} \int{\sqrt{-g}\,d^{4}x} \biggl( {\mathcal{R}-2\varLambda+ \frac{1}{2}\alpha|\mathit{Weyl}|^{2}} \biggr) , $$
(2)

where

$$ |\mathit{Weyl}|^{2}=\mathcal{R}^{\mu\nu\rho\sigma}\mathcal{R}_{\mu\nu\rho \sigma}-2 \mathcal{R}^{\mu\nu }\mathcal{R}_{\mu\nu}+\frac{1}{3} \mathcal{R}^{2}, $$
(3)

ℛ is the Ricci scalar and \(\varLambda\) is the cosmological constant. When \(\alpha\) goes to infinity, we have the special case of conformal gravity, and the field equations in vacuum are given by \(B_{\mu\nu}=0\), where \(B_{\mu\nu}\) is the Bach tensor defined by

$$ B_{\mu\nu}=\biggl(\nabla^{\rho}\nabla^{\sigma}+ \frac{1}{2}\mathcal{R}^{\rho\sigma}\biggr)C_{\mu\nu\rho\sigma}, $$
(4)

where \(C_{\mu\nu\rho\sigma}\) is the Weyl tensor. The following metric solves the field equations (Lu et al. 2012):

$$\begin{aligned} &{ds^{2} =-f\,dt^{2}+\frac{4\ell^{2}\,dr^{2}}{r^{2}f}+r^{2}\,d \varOmega_{2,k}^{2}, } \end{aligned}$$
(5)
$$\begin{aligned} &{f =1+\frac{\lambda}{r^{2}}+\frac{\lambda^{2}-k^{2}\ell^{4}}{3r^{4}}.} \end{aligned}$$
(6)

For \(k=\pm1\), there is an event horizon at the largest root of \(f\), given by

$$ r_{+}^{2}=\frac{1}{6} \Bigl( \sqrt{3\bigl(4 \ell^{4}-\lambda^{2}\bigr)}-3\lambda\Bigr) , $$
(7)

and for \(k=0\) the singularity is naked. Note that the requirement \(r_{+}^{2}>0\) implies that \(-2\ell^{2}\leq\lambda<\ell^{2}\). When \(\lambda =-2\ell^{2}\) the solution becomes extremal, and for \(k=1\) the entropy vanishes. The Kretschmann scalar (for \(k=1\)) is given by

$$ \mathcal{R}_{\mu\nu\rho\sigma} \mathcal{R}^{\mu\nu\rho\sigma }=\frac{9r^{8}+6(\lambda-4\ell^{2})r^{6}+(50\ell^{4}+\lambda(19 \lambda -24\ell^{2}))r^{4}+2(\lambda^{2}-\ell^{4})(21 \lambda-4\ell^{2})r^{2}+25(\lambda ^{2}-\ell^{4})^{2}}{12\ell^{4}r^{8}}, $$
(8)

therefore, there is a curvature singularity at \(r=0\). In the next section, we determine the QNFs by considering the Klein–Gordon equation in this background and by establishing the boundary conditions on the scalar field at the horizon and at spatial infinity.

3 Quasinormal modes of a 4-dimensional Lifshitz black hole

The QNMs of scalar perturbations in the background of a 4-dimensional asymptotically Lifshitz black hole in conformal gravity with dynamical exponent \(z=0\) are given by the scalar field solution of Klein–Gordon equation with suitable boundary conditions. This means there are only ingoing waves on the event horizon and we consider that the scalar field vanishes at spatial infinity, known as Dirichlet boundary conditions. These fields are considered as mere test fields, without backreaction over the spacetime itself. Therefore, it is not necessary for such fields to have the same symmetries as the background spacetime. On the other hand, if one considers the backreaction of the matter fields over the spacetime, in order to look for exact solutions to the field equations, the relation between symmetries of the spacetime and the matter fields is not trivial; for a recent study about symmetry inheritance of scalar fields, see Smolić (2015) and references therein. In the case considered here, the gravitational field equations imply that the trace of the stress-energy tensor must vanish, due to the fact that the Bach tensor is traceless; therefore, if one goes beyond the probe-field approximation, this implies that the stress-energy tensor of the matter fields must be traceless. Based on these arguments, we will first consider a test scalar field minimally coupled to curvature, then we will consider a test scalar field conformally coupled to curvature, which have a traceless stress-energy tensor, and we will find analytically and numerically the quasinormal frequencies for scalar fields for some special cases.

3.1 Scalar field minimally coupled to gravity

In this section, we calculate the QNMs of the \(z=0\) Lifshitz black hole for a test scalar field minimally coupled to gravity. The Klein–Gordon equation in curved spacetime is

$$ \frac{1}{\sqrt{-g}}\partial_{\mu} \bigl( \sqrt{-g}g^{\mu\nu} \partial_{\nu} \bigr) \psi=m^{2}\psi, $$
(9)

where \(m\) is the mass of the scalar field \(\psi\) which is minimally coupled to curvature. By means of the following ansatz

$$ \psi=e^{-i\omega t}R(r)Y(\theta,\phi), $$
(10)

where \(Y(\theta,\phi)\) is a normalizable harmonic function on the two-sphere which satisfies

$$ \nabla^{2}Y=-\kappa Y, $$
(11)

with \(\kappa=l ( l+1 )\) being the eigenvalues for the spheric manifold, with \(l=0,1,2,\dots{}\), the Klein–Gordon equation reduces to

$$ \frac{1}{4r}\partial_{r} \bigl( r^{3}f ( r ) \partial_{r}R \bigr) + \biggl( \frac{\omega^{2} \ell^{2}}{f ( r ) }- \frac{\kappa\ell^{2} }{r^{2}}-m^{2} \ell^{2} \biggr) R ( r ) =0. $$
(12)

Now, by considering \(R(r)=K(r)/r\) and by introducing the tortoise coordinate \(r_{\ast}\), given by \(dr_{\ast}=\frac{2 \ell \,dr}{rf(r)}\), the latter equation can be rewritten as a one-dimensional Schrödinger equation

$$ \bigl[ \partial_{r_{\ast}}^{2}+\omega^{2}-V_{\mathit{eff}}(r) \bigr] K(r_{\ast })=0, $$
(13)

where the effective potential is given by

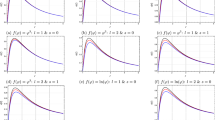
$$ V_{\mathit{eff}}(r)=\frac{f(r)}{4} \biggl[ \frac{f(r)}{\ell^{2}}+ \frac{rf^{\prime}(r)}{\ell^{2}}+\frac{4\kappa}{r^{2}}+4m^{2} \biggr] . $$
(14)

In Figs. 1 and 2, we respectively plot the effective potential for \(\kappa=2\) and \(\kappa=0\), using different values of the parameter \(\lambda\). Note that when \(r\rightarrow\infty \), the effective potential goes to \(1/(4\ell^{2})+m^{2}\).

Fig. 1
figure 1

The effective potential as a function of \(r\), for \(m=1\), \(\ell =1\) and \(\kappa=2\)

Full size image
Fig. 2
figure 2

The effective potential as a function of \(r\), for \(m=1\), \(\ell =1\) and \(\kappa=0\)

Full size image

3.1.1 Case \(\kappa=0\)

In order to find analytical solutions to the radial equation (12), we perform the change of variables \(y=r^{2}\) and get the following equation:

$$ \begin{aligned}[b] & y ( y-y_{+} ) ( y-y_{-} ) R^{\prime\prime} ( y ) +y ( 2y+\lambda) R^{\prime} ( y ) \\ &\quad {} + \biggl( \frac{\omega^{2} \ell ^{2}y^{3}}{ ( y-y_{+} ) ( y-y_{-} ) }-\kappa \ell^{2} -m^{2} \ell^{2} y \biggr) R ( y ) =0, \end{aligned} $$
(15)

where the prime denotes the derivative with respect to \(y\), and \(y_{+}\) and \(y_{-}\) are the roots of

$$ f ( y ) =1+\frac{\lambda}{y}+\frac{\lambda^{2}-\ell^{4}}{3y^{2}}, $$
(16)

given by

$$ y_{\pm}=-\frac{\lambda}{2}\pm\sqrt{-\frac{\lambda^{2}}{12}+ \frac{\ell^{4}}{3}}. $$
(17)

Additionally, performing another change of variable \(z=1-\frac{y_{+}}{y}\) and noting that \(\lambda=- ( y_{+}+y_{-} ) \), we arrive at the following expression:

$$ \begin{aligned}[b] & z ( z-1 ) \bigl( z- ( 1-Q ) \bigr) R^{\prime\prime } ( z ) - ( z-1 ) ( 1-Q-2z ) R^{\prime} ( z ) \\ &\qquad {}+ \biggl( \frac{\omega^{2} \ell^{2}Q^{2}}{z ( z-1 ) ( z- (1-Q ) ) }+\frac{\kappa\ell^{2} }{y_{-}}- \frac{m^{2} \ell^{2} Q}{z-1} \biggr) R ( z ) \\ &\quad =0, \end{aligned} $$
(18)

where we have defined \(Q=y_{+}/y_{-}\), and now prime means a derivative with respect to \(z\). In Fig. 3, we plot \(Q\) as a function of \(\lambda / \ell^{2}\) and we observe that \(Q\) can be positive or negative depending on the values of the parameter \(\lambda\):

$$\begin{aligned} Q >&1\quad\text{for }-2\ell^{2}\leq\lambda< -\ell^{2}, \end{aligned}$$
(19)
$$\begin{aligned} Q < &0\quad\text{for }-\ell^{2}< \lambda< \ell^{2}. \end{aligned}$$
(20)

On the other hand, Eq. (18) can be manipulated and put into the following form:

$$\begin{aligned} &{ R^{\prime\prime} ( z ) + \biggl( \frac{1}{z}+ \frac{1}{z- ( 1-Q ) } \biggr) R^{\prime} ( z ) } \\ &{\quad {}+ \biggl( \frac{\omega^{2} \ell^{2}Q^{2}/(1-Q)}{z}+\frac{Q ( \omega ^{2} \ell^{2}-m^{2}\ell^{2} ) }{z-1} +\frac{\kappa\ell^{2} }{y_{-}} } \\ &{\quad {}- \frac{Q\omega^{2} \ell^{2}/(1-Q)}{z- ( 1-Q ) } \biggr) \frac{1}{z ( z-1 ) ( z- ( 1-Q ) ) }R ( z ) =0. } \end{aligned}$$
(21)

We note that for \(\kappa=0\) this equation corresponds to a Riemann differential equation, whose general form is (Abramowitz and Stegun 1970)

$$\begin{aligned} &{\frac{d^{2}w}{dz^{2}}+ \biggl( \frac{1-\alpha-\alpha^{\prime }}{z-a}+\frac{1-\beta-\beta^{\prime}}{z-b}+ \frac{1-\gamma-\gamma^{\prime}}{z-c}\biggr) \,\frac{dw}{dz} } \\ &{ \quad {}+\biggl( \frac{\alpha\alpha^{\prime} ( a-b ) ( a-c ) }{z-a}+\frac{\beta\beta^{\prime} ( b-c ) ( b-a ) }{z-b} } \\ &{\quad {}+\frac{\gamma\gamma^{\prime} ( c-a ) ( c-b ) }{z-c}\biggr) \frac{w}{ ( z-a ) ( z-b ) ( z-c ) }=0,} \end{aligned}$$
(22)

where \(a,b\) and \(c\) are the singular points, and the exponents \(\alpha ,\alpha ^{\prime},\beta,\beta^{\prime},\gamma\) and \(\gamma^{\prime}\) are subject to the condition

$$ \alpha+\alpha^{\prime}+\beta+\beta^{\prime}+\gamma+\gamma ^{\prime}=1. $$
(23)

The complete solution is denoted by the symbol

$$ w=P\left \{ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} a & b & c & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\displaystyle \right \}, $$
(24)

and the Riemann \(P\) function can be reduced to the hypergeometric function through

$$ \begin{aligned}[b] w & = \biggl( \frac{z-a}{z-b} \biggr) ^{\alpha} \biggl( \frac{z-c}{z-b} \biggr) ^{\gamma} \\ &\quad {}\times P\left \{ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & \infty& 1 & \\ 0 & \alpha+\beta+\gamma& 0 & \frac{ ( z-a ) ( c-b ) }{( z-b ) ( c-a ) } \\ \alpha^{\prime}-\alpha& \alpha+\beta^{\prime}+\gamma& \gamma ^{\prime }-\gamma& \end{array}\displaystyle \right \}, \end{aligned} $$
(25)

where the \(P\) function is now Gauss hypergeometric function (Abramowitz and Stegun 1970). We observe that, in the radial equation (21), the regular singular points \(a,b\) and \(c\) have the values

$$ a=0,\qquad b=1-Q,\qquad c=1, $$
(26)

and the exponents are given by

$$\begin{aligned} &{\alpha=\pm\frac{i\omega\ell y_{+}}{y_{+}-y_{-}},\qquad\alpha^{\prime} =\mp \frac{i\omega\ell y_{+}}{y_{+}-y_{-}},} \end{aligned}$$
(27)
$$\begin{aligned} &{\beta=\pm\frac{i\omega\ell \vert y_{-}\vert }{y_{+}-y_{-} },\qquad \beta^{\prime} =\mp \frac{i\omega\ell \vert y_{-}\vert }{y_{+}-y_{-} },} \end{aligned}$$
(28)
$$\begin{aligned} &{ \begin{aligned}[c] & \gamma = \frac{1}{2}\pm\sqrt{ \frac{1}{4} - \bigl(\omega ^{2}-m^{2} \bigr) \ell^{2} }, \\ & \gamma^{\prime} =\frac{1}{2}\mp\sqrt{ \frac{1}{4} - \bigl(\omega ^{2}-m^{2} \bigr) \ell^{2} }. \end{aligned} } \end{aligned}$$
(29)

Therefore, the solution to (21) can be written as

$$\begin{aligned} R ( z ) =&C_{1} \biggl( \frac{z}{z-1+Q} \biggr) ^{\alpha} \biggl( \frac{z-1}{z-1+Q} \biggr) ^{\gamma} \\ &{}\times {}_{2}F_{1} \biggl( A,B,C,\frac{Qz}{z-(1-Q)} \biggr) \\ &{}+ C_{2} \biggl( \frac{z}{z-1+Q} \biggr) ^{\alpha^{\prime}} \biggl( \frac{z-1}{z-1+Q} \biggr) ^{\gamma} \\ &{}\times {}_{2}F_{1}\biggl( A-C+1,B-C+1,2-C, \\ &\phantom{{}\times {}_{2}F_{1}\biggl(} \frac{Qz}{z-(1-Q)} \biggr), \end{aligned}$$
(30)

where we have defined the constants \(A\), \(B\) and \(C\) as

$$\begin{aligned} \begin{aligned}[c] A &=\alpha+\beta+\gamma, \\ B &=\alpha+\beta^{\prime}+\gamma, \\ C &=1+\alpha-\alpha^{\prime}. \end{aligned} \end{aligned}$$
(31)

In the near-horizon limit, the above expression behaves as

$$ R ( z\rightarrow0 ) =\frac{(-1)^{\gamma}C_{1}}{(-1+Q)^{\alpha +\gamma}}z^{\alpha}+ \frac{(-1)^{\gamma}C_{2}}{(-1+Q)^{\alpha^{\prime}+\gamma}}z^{\alpha ^{\prime}}. $$
(32)

Now, we impose as a boundary condition that classically nothing can escape from the event horizon. So, choosing the exponent \(\alpha\) as

$$ \alpha=-\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}, $$
(33)

implies that we must take \(C_{2}=0\) in order to have only ingoing waves at the horizon. Therefore, our solution simplifies to

$$ \begin{aligned}[b] R ( z ) &=C_{1} \biggl( \frac{z}{z-1+Q} \biggr) ^{\alpha} \biggl( \frac{z-1}{z-1+Q} \biggr) ^{\gamma} \\ &\quad {}\times {}_{2}F_{1} \biggl( A,B,C,\frac{Qz}{z-(1-Q)} \biggr). \end{aligned} $$
(34)

Now, we implement boundary conditions at spatial infinity. In order to do so, we employ the Kummer relations (Abramowitz and Stegun 1970), and write the solution as

$$\begin{aligned} R ( z ) =&C_{1} \biggl( \frac{z}{z-1+Q} \biggr) ^{\alpha} \biggl( \frac{z-1}{z-1+Q} \biggr) ^{\gamma} \\ &{}\times \frac{\varGamma ( C ) \varGamma ( C-A-B ) }{\varGamma ( C-A ) \varGamma ( C-B ) } \\ &{}\times{}_{2}F_{1}\biggl( A,B,A+B-C,1-\frac{Qz}{z- ( 1-Q ) } \biggr) \\ &{}+ C_{1} ( 1-Q ) ^{\gamma^{\prime}-\gamma} \biggl( \frac{z}{z-1+Q}\biggr) ^{\alpha} \biggl( \frac{z-1}{z-1+Q} \biggr) ^{\gamma^{\prime}} \\ &{}\times \frac{\varGamma ( C ) \varGamma ( A+B-C ) }{\varGamma ( A ) \varGamma ( B ) } \\ &{}\times {}_{2}F_{1}\biggl( C-A,C-B,C-A-B+1, \\ &\phantom{ {}\times {}_{2}F_{1}\biggl(} 1-\frac{Qz}{z- ( 1-Q ) } \biggr). \end{aligned}$$
(35)

At the limit \(z\rightarrow1\), the above solution becomes

$$\begin{aligned} R ( z\rightarrow1 ) =&\frac{C_{1}}{Q^{\alpha+\gamma}} ( z-1 ) ^{\gamma} \frac{\varGamma ( C ) \varGamma ( C-A-B ) }{\varGamma ( C-A ) \varGamma ( C-B ) } \\ &{}+\frac{C_{1} ( 1-Q )^{\gamma^{\prime}-\gamma }}{Q^{\alpha+\gamma^{\prime}}} ( z-1 ) ^{\gamma^{\prime}} \\ &{}\times \frac{\varGamma ( C ) \varGamma ( A+B-C ) }{\varGamma ( A ) \varGamma ( B ) }. \end{aligned}$$
(36)

Now, we choose the exponents \(\gamma\) and \(\gamma^{\prime}\) as follows:

$$\begin{aligned} \begin{aligned}[c] &\gamma=\frac{1}{2}+ \sqrt{ \frac{1}{4} - \bigl(\omega ^{2}-m^{2} \bigr) \ell^{2} }, \\ &\gamma^{\prime} =\frac{1}{2}- \sqrt{ \frac{1}{4} - \bigl( \omega^{2}-m^{2} \bigr) \ell^{2} }. \end{aligned} \end{aligned}$$
(37)

So, imposing the condition that the scalar field be null at spatial infinity, we can determine the QNFs. The second term of (36) blows up when \(z\rightarrow1\), unless we impose the condition \(A=-n\) or \(B=-n\); therefore, we obtain the following set of QNFs:

$$ \omega\ell=\frac{i (m^{2} \ell^{2} -n(1+n) )}{1+2n}. $$
(38)

These QNFs are purely imaginary and negative for \(m=0\), which guarantees that the Lifshitz black hole is stable under massless scalar field perturbations for the mode with the lowest angular momentum. For \(m>0\) there are QNFs with imaginary and positive value, and the Lifshitz black hole is unstable under scalar field perturbations. Also, we note that if we interchange the values of the exponents in Eq. (37), the same QNFs are obtained. It is worth mentioning that Eq. (15) with \(\kappa=0\) can be written as

$$ \begin{aligned}[b] & z(1-z)R''(z)+(1-z)R'(z) \\ &\quad {}+ \biggl( \frac{\omega^{2} \ell^{2}(z y_{-} - y_{+})^{2}}{(y_{+}-y_{-})^{2}z(1-z)}-\frac{m^{2} \ell ^{2} }{1-z} \biggr)R(z)=0, \end{aligned} $$
(39)

under the change of variable \(z=\frac{y-y_{+}}{y-y_{-}}\), and if we define \(R(z)=z^{\alpha}(1-z)^{\beta}F(z)\), the above equation leads to the hypergeometric equation

$$ z(1-z)F''(z)+ \bigl[c-(1+a+b)z \bigr]F'(z)-ab F(z)=0, $$
(40)

where

$$\begin{aligned} &{\alpha= \pm\frac{i\omega\ell y_{+}}{y_{+}-y_{-}},} \end{aligned}$$
(41)
$$\begin{aligned} &{\beta= \frac{1}{2} \Bigl(1\pm\sqrt{1+4 \bigl( m^{2} - \omega^{2} \bigr) \ell^{2} } \,\Bigr),} \end{aligned}$$
(42)

and the constants are given by

$$\begin{aligned} &{ a=\alpha+\beta- \frac{i\omega\ell \vert y_{-}\vert }{(y_{+} - y_{-})},} \end{aligned}$$
(43)
$$\begin{aligned} &{b=\alpha+\beta+ \frac{i\omega\ell \vert y_{-}\vert }{(y_{+} - y_{-})},} \end{aligned}$$
(44)
$$\begin{aligned} &{c=1+2\alpha.} \end{aligned}$$
(45)

The general solution of the hypergeometric equation (40) is

$$ \begin{aligned}[b] F(z)&=c_{1}{}_{2}F_{1}(a,b,c;z) \\ &\quad {}+c_{2}z^{1-c}{}_{2}F_{1}(a-c+1,b-c+1,2-c;z), \end{aligned} $$
(46)

and it has three regular singular points at \(z=0\), \(z=1\), and \(z=\infty\). \({}_{2}F_{1}(a,b,c;z)\) is a hypergeometric function, and \(c_{1}\) and \(c_{2}\) are integration constants. Note that the above QNFs could be computed using the solution (46).

Fig. 3
figure 3

\(Q\) as a function of \(\lambda/ \ell^{2}\)

Full size image

3.1.2 Case \(Q=\pm\infty\)

In this case, it is possible to obtain an analytical solution for all values of the angular momentum \(\kappa\). Thus, for \(\lambda=-\ell^{2}\), or equivalently \(Q=\pm\infty\), the radial equation (12) can be written as

$$ \begin{aligned}[b] & z (1-z )\partial_{z}^{2}R(z)+ (1-z ) \partial_{z}R(z) \\ &\quad {}+ \biggl[\frac{\omega^{2} \ell^{2}}{z(1-z)}-\frac{m^{2} \ell ^{2} }{1-z}-\kappa \biggr]R(z)=0, \end{aligned} $$
(47)

where we have considered \(z=1-\ell^{2}/r^{2}\). Using the decomposition \(R(z)=z^{\alpha}(1-z)^{\beta}K(z)\) with

$$\begin{aligned} &{ \alpha_{\pm}=\pm i \omega\ell,} \end{aligned}$$
(48)
$$\begin{aligned} &{ \beta_{\pm}= \frac{1}{2} \bigl(1\pm\sqrt{1+4 \bigl(m^{2}-\omega^{2}\bigr) \ell^{2}} \bigr),} \end{aligned}$$
(49)

we can write (47) as a hypergeometric equation for \(K\)

$$ z(1-z)K''(z)+ \bigl[c-(1+a+b)z \bigr]K'(z)-ab K(z)=0, $$
(50)

where the coefficients are given by

$$\begin{aligned} &{ a=\alpha+\beta\mp\sqrt{-\kappa},} \end{aligned}$$
(51)
$$\begin{aligned} &{b=\alpha+\beta\pm\sqrt{-\kappa},} \end{aligned}$$
(52)
$$\begin{aligned} &{ c=1+2\alpha.} \end{aligned}$$
(53)

The general solution of the hypergeometric equation (50) is

$$ \begin{aligned}[b] K&=C_{1}{}_{2}F_{1}(a,b,c;z) \\ &\quad {}+C_{2}z^{1-c}{}_{2}F_{1}(a-c+1,b-c+1,2-c;z), \end{aligned} $$
(54)

and it has three regular singular points at \(z=0\), \(z=1\), and \(z=\infty\). \({}_{2}F_{1}(a,b,c;z)\) is a hypergeometric function and \(C_{1}\) and \(C_{2}\) are constants. Thus, the solution for the radial function \(R(z)\) is

$$ \begin{aligned}[b] R(z)&=C_{1}z^{\alpha}(1-z)^{\beta}{}_{2}F_{1}(a,b,c;z) \\ &\quad {}+C_{2}z^{-\alpha}(1-z)^{\beta}\\ &\quad {}\times {}_{2}F_{1}(a-c+1,b-c+1,2-c;z). \end{aligned} $$
(55)

So, in the vicinity of the horizon, \(z=0\) and, using the property \(F(a,b,c,0)=1\), the function \(R(z)\) behaves as

$$ R(z)=C_{1} e^{\alpha\ln z}+C_{2} e^{-\alpha\ln z}, $$
(56)

and the scalar field \(\psi\), for \(\alpha=\alpha_{-}\), can be written as follows:

$$ \psi\sim C_{1} e^{-i\omega\ell(t+ \ln z)}+C_{2} e^{-i\omega\ell(t-\ln z)}, $$
(57)

in which the first term represents an ingoing wave and the second an outgoing wave in the black hole. So, by imposing that only ingoing waves existing at the horizon, this fixes \(C_{2}=0\). The radial solution then becomes

$$ \begin{aligned}[b] R(z)&=C_{1} e^{\alpha\ln z}(1-z)^{\beta}{}_{2}F_{1}(a,b,c;z) \\ &=C_{1}e^{-i\omega\ell\ln z}(1-z)^{\beta}{}_{2}F_{1}(a,b,c;z). \end{aligned} $$
(58)

To implement boundary conditions at infinity (\(z=1\)), we apply Kummer’s formula for the hypergeometric function (Abramowitz and Stegun 1970),

$$ \begin{aligned}[b] {}_{2}F_{1}(a,b,c;z)&=\frac{\varGamma(c)\varGamma (c-a-b)}{\varGamma(c-a)\varGamma(c-b)}F_{1} \\ &\quad {}+(1-z)^{c-a-b} \frac{\varGamma(c)\varGamma(a+b-c)}{\varGamma(a)\varGamma(b)}F_{2}, \end{aligned} $$
(59)

where

$$\begin{aligned} &{F_{1}={}_{2}F_{1}(a,b,a+b-c,1-z),} \end{aligned}$$
(60)
$$\begin{aligned} &{F_{2}={}_{2}F_{1}(c-a,c-b,c-a-b+1,1-z).} \end{aligned}$$
(61)

With this expression, the radial function (58) reads

$$ \begin{aligned}[b] R(z) & = C_{1} e^{-i\omega\ell\ln z}(1-z)^{\beta}\frac{\varGamma(c)\varGamma(c-a-b)}{\varGamma(c-a)\varGamma(c-b)} F_{1} \\ &\quad {}+C_{1} e^{-i\omega\ell \ln z}(1-z)^{c-a-b+\beta} \\ &\quad {}\times \frac{\varGamma(c)\varGamma(a+b-c)}{\varGamma(a)\varGamma(b)}F_{2}, \end{aligned} $$
(62)

and at infinity it can be written as

$$ \begin{aligned}[b] R_{\mathit{asymp}.}(z) & = C_{1} (1-z)^{\beta}\frac{\varGamma(c)\varGamma(c-a-b)}{\varGamma(c-a)\varGamma(c-b)} \\ &\quad {}+C_{1} (1-z)^{1-\beta}\frac{\varGamma(c)\varGamma(a+b-c)}{\varGamma(a)\varGamma(b)}. \end{aligned} $$
(63)

So for \(\beta_{+}>1\), the field at infinity vanishes if \((a)|_{\beta_{+}}=-n\) or \((b)|_{\beta_{+}}=-n\) for \(n=0,1,2,\dots{}\), and for \(\beta_{-}<0\), the field at infinity vanishes if \((c-a)|_{\beta_{-}}=-n\) or \((c-b)|_{\beta_{-}}=-n\). Therefore, the QNFs are given by

$$ \omega\ell=-i \frac{-m^{2} \ell^{2} + n + n^{2} +\kappa\mp\sqrt {-\kappa} (1+2n)}{ 1 + 2 n \mp2 \sqrt{-\kappa}}, $$
(64)

where \(\sqrt{-\kappa}=i\sqrt{l(l+1)}\). This expression can be written asFootnote 1

$$ \begin{aligned}[b] \omega\ell&=\pm\frac{ \sqrt{\kappa} ( -(1+2n)^{2}+2(-m^{2} \ell ^{2}+n+n^{2}-\kappa) )}{(1+2n)^{2}+4\kappa} \\ &\quad {}-i \frac{(1+2n)(-m^{2} \ell ^{2}+n+n^{2}+\kappa)}{(1+2n)^{2}+4\kappa}. \end{aligned} $$
(65)

Because not all the QNFs have a negative imaginary part, we conclude that this black hole is not stable under scalar field perturbations for the case when \(Q=\pm\infty\).

3.1.3 Case \(Q=1\)

In the extremal case \(\lambda=-2\ell^{2}\), or equivalently \(Q=1\), the radial equation (18) reads

$$ \begin{aligned}[b] & z ( z-1 ) R^{\prime\prime} ( z ) +2 ( z-1 ) R^{\prime} ( z ) \\ &\quad {}+ \biggl( \frac{\omega^{2} \ell^{2}}{z^{3} ( z-1 ) }+\frac{\kappa}{z}-\frac{m^{2} \ell^{2}}{z ( z-1 ) } \biggr) R ( z ) =0, \end{aligned} $$
(66)

and its solution is given by

$$\begin{aligned} R ( z ) =&C_{1}e^{\frac{i\omega\ell}{z}}\mathit{Heun}_{C} \biggl( -2i\omega\ell,\sqrt{1-4 \bigl( \omega^{2} -m^{2} \bigr) \ell^{2} },1, \\ &\phantom{C_{1}e^{\frac{i\omega\ell}{z}}\mathit{Heun}_{C} \biggl(} {-}2\omega^{2} \ell^{2},-\kappa+\frac{1}{2}+2\omega^{2} \ell^{2},\frac{z-1}{z} \biggr) \\ &{}\times z^{-\frac{3}{2}-\frac{1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell^{2} }} ( z-1 ) ^{\frac{1}{2}+\frac{1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell ^{2} }} \\ &{}+ C_{2}e^{\frac{i\omega\ell}{z}} \\ &{}\times \mathit{Heun}_{C} \biggl( -2i \omega\ell,-\sqrt{1-4 \bigl( \omega^{2} -m^{2} \bigr) \ell^{2} }, \\ &\phantom{{}\times \mathit{Heun}_{C} \biggl(} 1,-2\omega^{2} \ell^{2},-\kappa+ \frac{1}{2}+2\omega^{2} \ell^{2},\frac{z-1}{z} \biggr) \\ &{}\times z^{-\frac{3}{2}+\frac{1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell^{2} }} ( z-1 ) ^{\frac{1}{2}-\frac{1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell ^{2} }}, \end{aligned}$$
(67)

where \(\mathit{Heun}_{C}\) is the confluent Heun function. Thus, when \(z\rightarrow1\), and in order to have a regular scalar field at spatial infinity, we must set \(C_{2}=0\); therefore, the solution reduces to

$$\begin{aligned} R ( z ) =& C_{1}e^{\frac{i\omega\ell}{z}}\mathit{Heun}_{C}\biggl( -2i\omega\ell,\sqrt{1-4 \bigl( \omega^{2} -m^{2} \bigr) \ell^{2}},1, \\ &\phantom{ C_{1}e^{\frac{i\omega\ell}{z}}\mathit{Heun}_{C}\biggl(} {-}2\omega^{2} \ell^{2},-\kappa+\frac{1}{2}+2\omega^{2} \ell^{2}, \frac{z-1}{z} \biggr) \\ & {}\times z^{-\frac{3}{2}-\frac{1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell^{2}}} ( z-1 ) ^{\frac{1}{2}+\frac {1}{2}\sqrt{1-4 ( \omega^{2} -m^{2} ) \ell^{2}}}, \end{aligned}$$
(68)

where the property \(\mathit{Heun}_{C}(a,b,c,d,e,0)=1\) was used (Fiziev 2010). However, we observe that when \(z\rightarrow1\), the scalar field is null \(R(z) \rightarrow0\); therefore, there are no QNMs in this case.

3.1.4 Numerical analysis

Now, we will perform numerical studies by using the improved AIM (Cho et al. 2010), which is an improved version of the method proposed in Ciftci et al. (2003, 2005) and has been successfully applied in the context of QNMs for different black holes’ geometries; see, for instance, Cho et al. (2010, 2012), Catalan et al. (2014), Zhang et al. (2015), Barakat (2006). So, in order to implement the improved AIM, we make the consecutive change of variables \(y=r^{2}\) and \(z=\frac{y-y+}{y-y-}\) to Eq. (12). Then, the Klein–Gordon equation yields

$$ \begin{aligned}[b] & z(1-z )R''(z)+(1-z)R'(z) \\ &\qquad {}+\biggl( \frac{\omega^{2} \ell^{2} (zy_{-}-y_{+})^{2}}{(y_{+}-y_{-})^{2}z(1-z)}+\frac {\kappa\ell^{2}}{zy_{-}-y_{+}}-\frac{m^{2}\ell^{2}}{1-z} \biggr)R(z) \\ &\quad =0. \end{aligned} $$
(69)

Now, we must consider the behavior of the scalar field on the event horizon and at spatial infinity. Accordingly, on the horizon, \(z\rightarrow0\), the behavior of the scalar field is given by

$$ R ( z\rightarrow0 ) \sim C_{1}z^{-\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}}+C_{2}y^{\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}}. $$
(70)

So, if we consider only ingoing waves on the horizon, we must impose \(C_{2}=0\). Asymptotically, from Eq. (69), the scalar field behaves as

$$ \begin{aligned}[b] R ( z\rightarrow1 ) \sim {}& D_{1} ( 1-z ) ^{\frac{1}{2}-\frac{1}{2}\sqrt {1-4(\omega^{2}-m^{2})\ell^{2}}} \\ & {}+D_{2} ( 1-z ) ^{\frac{1}{2}+\frac{1}{2}\sqrt{1-4(\omega^{2}-m^{2})\ell^{2}}}. \end{aligned} $$
(71)

So, in order to have only outgoing waves at infinity, we must impose \(D_{2}=0 \). Therefore, taking into account these behaviors, we define

$$ R ( z ) =z^{-\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}} ( 1-z ) ^{\frac {1}{2}-\frac{1}{2}\sqrt{1-4(\omega^{2}-m^{2})\ell^{2}}} \chi( z ). $$
(72)

Then, by inserting these fields into Eq. (69), we obtain the homogeneous linear second-order differential equation for the function \(\chi(z)\)

$$ \chi^{\prime\prime}=\lambda_{0}(z)\chi^{\prime}+s_{0}(z) \chi, $$
(73)

where

$$\begin{aligned} \lambda_{0}(z) =& -\frac{2i\omega\ell y_{+}}{z(y_{-} - y_{+})} \\ &{}+\frac {1+z(-2+\sqrt{1-4\ell^{2}(\omega^{2} -m^{2})})}{z(z-1)}, \\ s_{0}(z) =& -\frac{1}{2z(z-1)} \biggl(1+2 \ell^{2} \biggl(m^{2}+\frac{\kappa}{y_{+} - y_{-} z} \\ &{}+\frac{2y_{+}\omega^{2}}{y_{-} - y_{+}} \biggr)-\sqrt{1-4\ell^{2}\bigl(\omega^{2}-m^{2} \bigr)} \\ &{}-\frac{2i\omega\ell y_{+}(-1+\sqrt{1-4\ell^{2}(\omega^{2}-m^{2})})}{y_{-} - y_{+}} \biggr). \end{aligned}$$
(74)

Then, in order to implement the improved AIM, it is necessary to differentiate Eq. (73) \(n\) times with respect to \(z\), which yields the following equation:

$$ \chi^{n+2}=\lambda_{n}(z)\chi^{\prime}+s_{n}(z) \chi, $$
(75)

where

$$\begin{aligned} &{\lambda_{n}(z)=\lambda_{n-1}^{\prime}(z)+s_{n-1}(z)+ \lambda_{0}(z)\lambda_{n-1}(z), } \end{aligned}$$
(76)
$$\begin{aligned} &{s_{n}(z)=s_{n-1}^{\prime}(z)+s_{0}(z) \lambda_{n-1}(z). } \end{aligned}$$
(77)

Then, by expanding the \(\lambda_{n}\) and \(s_{n}\) in a Taylor series around the point \(\delta\), at which the improved AIM is performed,

$$\begin{aligned} &{\lambda_{n}(\delta)=\sum_{i=0}^{\infty}c_{n}^{i}(z- \delta)^{i},} \end{aligned}$$
(78)
$$\begin{aligned} &{s_{n}(\delta)=\sum_{i=0}^{\infty}d_{n}^{i}(z- \delta)^{i},} \end{aligned}$$
(79)

where the \(c_{n}^{i}\) and \(d_{n}^{i}\) are the \(i\)th Taylor coefficients of \(\lambda_{n}(\delta)\) and \(s_{n}(\delta)\), respectively, and by replacing the above expansions in Eqs. (76) and (77), the following set of recursion relations for the coefficients are obtained:

$$\begin{aligned} &{c_{n}^{i}=(i+1)c_{n-1}^{i+1}+d_{n-1}^{i}+\sum_{k=0}^{i}c_{0}^{k}c_{n-1}^{i-k},} \end{aligned}$$
(80)
$$\begin{aligned} &{d_{n}^{i}=(i+1)d_{n-1}^{i+1}+\sum _{k=0}^{i}d_{0}^{k}c_{n-1}^{i-k}.} \end{aligned}$$
(81)

In this manner, the authors of the improved AIM have avoided the derivatives that contain the AIM in Cho et al. (2010, 2012), and the quantization condition, which is equivalent to imposing a termination to the number of iterations and given by

$$ d_{n}^{0}c_{n-1}^{0}-d_{n-1}^{0}c_{n}^{0}=0. $$
(82)

We solve this equation numerically to find the QNFs. In Table 1, we show several first QNFs for a scalar field minimally coupled to curvature with \(\kappa= 2\), \(\ell=1\), \(m=0, 1, 2\), and different values of \(\lambda\). We observe that the imaginary part of the QNFs is always negative for massless scalar field, whereas for a massive scalar field there are some QNFs with a positive imaginary part.

Table 1 First quasinormal frequencies (\(n= 0\)), \(\ell=1\), \(\kappa= 2\), \(m=0, 1, 2\), and different values of \(\lambda\)
Full size table

3.2 Scalar field conformally coupled to gravity

In this section, we calculate the QNMs of the \(z=0\) Lifshitz black hole for a test scalar field conformally coupled to gravity. The Klein–Gordon equation for a scalar field non-minimally coupled to curvature is

$$ \frac{1}{\sqrt{-g}}\partial_{\mu} \bigl( \sqrt{-g}g^{\mu\nu} \partial_{\nu} \bigr) \psi-\xi\mathcal{R} \psi=m^{2}\psi, $$
(83)

where \(m\) is the mass of the scalar field \(\psi\), \(\xi\) is the non-minimal coupling parameter, and ℛ is the Ricci scalar which reads

$$ \mathcal{R}=\frac{\ell^{4}-\lambda^{2}}{2\ell^{2} r^{4}}+\frac{4\ell^{2}-\lambda }{2\ell^{2} r^{2}}-\frac{3}{2\ell^{2}}. $$
(84)

For a conformally coupled scalar field case, we must take \(m=0\) and \(\xi =1/6\). Now, by means of the following ansatz

$$ \psi=e^{-i\omega t}R(r)Y(\theta,\phi), $$
(85)

where \(Y(\theta,\phi)\) is a normalizable harmonic function on the two-sphere which satisfies Eq. (11), the Klein–Gordon equation reduces to

$$ \begin{aligned}[b] & \frac{1}{4r}\partial_{r} \bigl( r^{3}f ( r ) \partial_{r}R \bigr) + \biggl( \frac{\omega^{2} \ell^{2}}{f ( r ) }- \frac{\kappa\ell^{2}}{r^{2}}-m^{2}\ell^{2}-\xi \ell^{2}\mathcal{R} \biggr) R ( r ) \\ &\quad =0, \end{aligned} $$
(86)

which can be written as a 1-dimensional Schrödinger equation with an effective potential that vanishes at spatial infinity. Therefore, we will consider only outgoing waves at the asymptotic region as boundary condition. It is worth mentioning that Eq. (86) has an analytical solution only for \(\lambda=-1\) as we will show below. Therefore, we will perform numerical studies for \(\lambda\neq-1\) by using the improved AIM (Cho et al. 2010).

3.2.1 Numerical analysis

In order to implement the improved AIM, we make the consecutive change of variables \(y=r^{2}\) and \(z=\frac{y-y+}{y-y-}\) to Eq. (86), as we did in the previous sections. Then, the Klein–Gordon equation yields

$$\begin{aligned} &{ z(1-z )R''(z)+(1-z)R'(z)+ \biggl( \frac{\omega^{2} \ell^{2} (zy_{-}-y_{+})^{2}}{(y_{+}-y_{-})^{2}z(1-z)} } \\ &{\quad {} +\frac {\kappa\ell^{2}}{zy_{-}-y_{+}} -\frac{\xi(\ell^{4}-\lambda^{2})(1-z)}{2 (zy_{-}-y_{+})^{2}}+\frac{\xi(4\ell ^{2}-\lambda)}{2(zy_{-}-y_{+})} } \\ &{\quad {}+\frac{3 \xi}{2(1-z)} \biggr)R(z)=0. } \end{aligned}$$
(87)

Now, the behavior of the scalar field on the event horizon (\(z\rightarrow0\)) is given by

$$ R ( z\rightarrow0 ) \sim F_{1}z^{-\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}}+F_{2}y^{\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}}. $$
(88)

So, if we consider only ingoing waves at the horizon, we must impose \(F_{2}=0\). Asymptotically (\(z\rightarrow1\)), from Eq. (87), the scalar field behaves as

$$ R ( z\rightarrow1 ) \sim G_{1} ( 1-z ) ^{1/2-i \omega\ell}+G_{2} ( 1-z ) ^{1/2+i \omega\ell}. $$
(89)

So, in order to have only outgoing waves at infinity, we must impose \(G_{2}=0 \). Therefore, taking into account these behaviors, we define

$$ R ( z ) =z^{-\frac{i\omega\ell y_{+}}{y_{+}-y_{-}}} ( 1-z ) ^{1/2-i \omega \ell} \chi( z ). $$
(90)

Then, by inserting these fields into Eq. (87), we obtain the following homogeneous linear second-order differential equation for the function \(\eta(z)\):

$$ \eta^{\prime\prime}=\lambda_{0}(z)\eta^{\prime}+s_{0}(z) \eta, $$
(91)

where

$$ \begin{aligned}[c] & \lambda_{0}(z) = -\frac{(y_{+}-y_{-})(1-2z)-2i \omega\ell (y_{+}+y_{-}z-2y_{+}z)}{(y_{+}-y_{-})z(1-z)}, \\ & \begin{aligned}[b] s_{0}(z) &= \frac{\ell^{4}+3y_{+}^{2}+z(-\ell^{4}+y_{-} (-4\ell^{2}+3y_{-}z-12\kappa \ell^{2}))+\lambda y_{-}z-\lambda^{2} (1-z) -y_{-} (-4\ell^{2}+6y_{-}z-12 \kappa \ell^{2} +\lambda)}{12z(1-z)(y_{+}-y_{-}z)^{2}} \\ & \quad {}+ \frac{12 i \omega\ell(y_{-}-2y_{+})(y_{+}-y_{-}z)^{2}-48 \omega^{2} \ell^{2} y_{+}(y_{+}-y_{-}z)^{2}}{12z(1-z)(y_{+}-y_{-})(y_{+}-y_{-}z)^{2}}. \end{aligned} \end{aligned} $$
(92)

Thus, by performing the improved AIM method, we find several lowest QNFs, for a scalar field conformally coupled to curvature with \(\kappa= 0\), \(\ell=1\) and different values of \(\lambda\); see Table 2. Then, in Table 3, we show some fundamental QNFs for a scalar field conformally coupled to curvature with \(\kappa= 0, 2, 6, 12\), \(\ell =1\), and different values of \(\lambda\). We observe that the QNFs have real and imaginary parts, with an imaginary part that is negative, which ensures the stability of the 4-dimensional Lifshitz black hole under scalar perturbations.

Table 2 Quasinormal frequencies for \(\kappa= 0\), \(\ell=1\) and different values of \(\lambda\)
Full size table
Table 3 Fundamentals quasinormal frequencies (\(n= 0\)), \(\ell=1\) and different values of \(\kappa\) and \(\lambda\)
Full size table

3.2.2 Case \(Q=\pm\infty\)

In this case (\(\lambda=-\ell^{2}\)), due to the simplicity of the Ricci scalar, it is possible to obtain an analytical solution. The radial equation (86) reads

$$ \begin{aligned}[b] & \frac{1}{4r}\partial_{r} \bigl( r^{3}f ( r ) \partial_{r}R \bigr) + \biggl( \frac{\omega^{2} \ell^{2}}{f ( r ) }-\frac{\kappa\ell^{2}+5 \xi\ell^{2} /2 }{r^{2}}\\ &\quad {}-m^{2} \ell^{2}+\frac{3 \xi}{2} \biggr) R ( r ) =0. \end{aligned} $$
(93)

So, if we compare this equation with the analogous equation of the minimal case (Eq. (12)), we see that is possible to obtain (93) by means of the following substitutions in Eq. (12):

$$\begin{aligned} \begin{aligned}[c] & \kappa \rightarrow \kappa+\frac{5 \xi}{2}, \\ & m^{2} \rightarrow m^{2}-\frac{3 \xi}{2 \ell^{2}}. \end{aligned} \end{aligned}$$
(94)

Thus, using the above substitutions in the QNFs (65), we find

$$ \begin{aligned}[b] \omega\ell& =\pm \frac{ \sqrt{\kappa+\frac{5 \xi}{2}} ( -(1+2n)^{2}+2(-m^{2} \ell^{2}+n+n^{2}-\kappa-\xi) )}{(1+2n)^{2}+4\kappa+10\xi} \\ &\quad {}-i \frac{(1+2n)(-m^{2} \ell^{2}+n+n^{2}+\kappa+4\xi)}{(1+2n)^{2}+4\kappa+10\xi}, \end{aligned} $$
(95)

and for a conformal scalar field (\(m=0\), \(\xi=1/6\)) this equation yields

$$ \begin{aligned}[b] \omega\ell&=\pm\frac{1}{2} \sqrt{\kappa+\frac{5}{12}} \\ &\quad {}-\frac{i}{4} \frac{1+6n+12n^{2}+8n^{3}+4(\kappa +5/12)(1+2n)}{1+4n+4n^{2}+4(\kappa+5/12)}, \end{aligned} $$
(96)

implying that there are only outgoing waves at the asymptotic region; see footnote 1. Clearly, the imaginary part of the QNFs is negative, which ensures the stability of this black hole under conformally coupled scalar field perturbations. These QNFs agree with the numerical results for \(\lambda =-1\), \(\kappa=0\) and \(\ell=1\) showed in Table 2.

4 Reflection and transmission coefficients and absorption cross-section

In this section, we focus our attention to the minimally coupled scalar field case. However, a similar analysis can be performed for scalar fields conformally coupled to gravity, and for \(\lambda=-\ell^{2}\) the results are straightforwardly obtained from the minimal case by using the substitutions (94) and taking \(m=0\), \(\xi=1/6\). The reflection and the transmission coefficients are defined by

$$ \Re:=\biggl\vert \frac{F_{\mathrm{asymp}}^{\mathrm{out}}}{F_{\mathrm{asymp}}^{\mathrm{in}}}\biggr\vert \quad \mbox{and} \quad\mathfrak{T}:=\biggl\vert \frac{F_{\mathrm{hor}}^{\mathrm{in}}}{F_{\mathrm{asymp}}^{\mathrm{in}}}\biggr\vert , $$
(97)

where \(F\) is the flux given by

$$ F=\frac{1}{2i}\sqrt{-g}g^{rr} \bigl(R^{\ast}\partial_{r}R-R\partial_{r}R^{\ast} \bigr). $$
(98)

So, in order to calculate the above coefficients, we need to know the behavior of the radial function both on the horizon and at asymptotic infinity.

4.1 Case \(\kappa= 0\)

In this case, the behavior at the horizon is given by Eq. (46) with \(c_{2}=0\), and choosing the negative value of \(\alpha\) and using Eq. (98), we get the following flux on the horizon:

$$ F _{\mathit{hor}}^{\mathit{in}}=-\omega\sin\theta \vert c_{1}\vert ^{2} y_{+}. $$
(99)

On the other hand, by applying Kummer’s formula (59) for the hypergeometric function in Eq. (46), the asymptotic behavior of \(R(z)\) can be written as

$$ R ( z \rightarrow1 ) = \bar{c}_{1} (z-1)^{\beta}+ \bar{c}_{2} (z-1)^{1-\beta}, $$
(100)

where

$$\begin{aligned} \begin{aligned}[c] & \bar{c}_{1} = c_{1}\frac{\varGamma ( c ) \varGamma ( c-a-b ) }{\varGamma ( c-a ) \varGamma ( c-b ) }, \\ & \bar{c}_{2} = c_{1}\frac{\varGamma ( c ) \varGamma ( a+b-c ) }{\varGamma ( a ) \varGamma ( b ) }. \end{aligned} \end{aligned}$$
(101)

Thus, using Eq. (98), we obtain the flux

$$ \begin{aligned}[b] F_{\mathit{asymp}.}&=\frac{\sin\theta}{\ell} (y_{+}-y_{-}) \sqrt{ \bigl( \omega^{2} -m^{2} \bigr) \ell^{2}- \frac{1}{4}} \\ &\quad {}\times \bigl(\vert \bar{c}_{2}\vert ^{2}- \vert \bar{c}_{1}\vert ^{2} \bigr), \end{aligned} $$
(102)

for \(\beta=\beta_{+}\), the reflection and transmission coefficients are given by

$$\begin{aligned} &{ \Re=\frac{\vert \bar{c}_{2}\vert ^{2}}{\vert \bar {c}_{1}\vert ^{2}},} \end{aligned}$$
(103)
$$\begin{aligned} &{ \mathfrak{T}=\frac{\omega\ell \vert c_{1}\vert ^{2} y_{+}}{(y_{+} - y_{-})\vert \bar{c}_{1}\vert ^{2}\sqrt{ ( \omega^{2} -m^{2} ) \ell ^{2}-\frac{1}{4}}},} \end{aligned}$$
(104)

and the absorption cross-section, \(\sigma_{\mathit{abs}}\), is given by

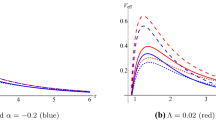
$$ \sigma_{\mathit{abs}}=\frac{\ell \vert c_{1}\vert ^{2} y_{+}}{(y_{+} - y_{-})\vert \bar{c}_{1}\vert ^{2}\sqrt{ ( \omega^{2} -m^{2} ) \ell^{2}-\frac{1}{4}}}. $$
(105)

Interestingly, the poles of the transmission coefficient yield the same set of QNFs found in the previous section, which is equivalent to imposing as a boundary condition that only outgoing waves exist at asymptotic infinity. Now, we perform a numerical analysis of the reflection coefficient (103), transmission coefficient (104) and absorption cross-section (105) of the 4-dimensional Lifshitz black hole with \(z=0\) for scalar fields. So, we plot the reflection and transmission coefficients and the absorption cross-section in Fig. 4 for scalar fields with \(m=1\). Essentially, we found that the reflection coefficient is 1 at low frequency limit, and for high frequency limit this coefficient is null, with the behavior of the transmission coefficient being opposite with \(R+T = 1\). In addition, the absorption cross-section is null in the low and high-frequency limit, but there is a range of frequencies for which the absorption cross-section is not null, and it also has a maximum value in the low-frequency limit (see Fig. 5). Furthermore, we observe that the absorption cross-section can take higher values when the mass of the scalar field decreases (Fig. 5) in the low frequency limit. However, beyond a certain value of the frequency, the absorption cross-section does not depend on the mass of the scalar field.

Fig. 4
figure 4

The reflection coefficient \(R\) (solid curve), the transmission coefficient \(T\) (dashed curve), \(R+T\) (thick curve) and the absorption cross-section \(\sigma_{\mathit{abs}}\) (dotted curve) as a function of \(\omega\), for \(m=1\), \(\ell=1\), and \(\lambda=-1.9\)

Full size image
Fig. 5
figure 5

The behavior of \(\sigma_{\mathit{abs}}\) as a function of \(\omega\), for \(\lambda=-1.9\), \(\ell=1\), and \(m = 1, 1.5, 2\)

Full size image

4.2 Case \(Q=\pm\infty\)

In this case, the behavior at the horizon is given by Eq. (56), with \(C_{2}=0\), and using Eq. (98), we get the flux at the horizon

$$ F _{\mathit{hor}}^{\mathit{in}}=-\omega\ell^{2} \sin \theta \vert C_{1}\vert ^{2}. $$
(106)

On the other hand, the asymptotic behavior of \(R(z)\) is given by Eq. (63), which can be written as

$$ R ( z \rightarrow1 ) = B_{1} (z-1)^{\beta}+B_{2} (z-1)^{1-\beta}, $$
(107)

where

$$\begin{aligned} \begin{aligned}[c] B_{1} & = C_{1}\frac{\varGamma ( c ) \varGamma ( c-a-b ) }{\varGamma ( c-a ) \varGamma ( c-b ) }, \\ B_{2} & = C_{1}\frac{\varGamma ( c ) \varGamma ( a+b-c ) }{\varGamma ( a ) \varGamma ( b ) }. \end{aligned} \end{aligned}$$
(108)

Thus, using Eq. (98), we get the flux

$$ F_{\mathit{asymp}.}=\ell\sin\theta\sqrt{ \bigl( \omega^{2} -m^{2} \bigr) \ell^{2}- \frac{1}{4}} \bigl(\vert B_{2}\vert ^{2}-\vert B_{1}\vert ^{2} \bigr) . $$
(109)

Therefore, the reflection and transmission coefficients are given by

$$\begin{aligned} &{ \Re=\frac{\vert B_{2}\vert ^{2}}{\vert B_{1}\vert ^{2}},} \end{aligned}$$
(110)
$$\begin{aligned} &{ \mathfrak{T}=\frac{\omega\ell \vert C_{1}\vert ^{2}}{\sqrt { ( \omega^{2} -m^{2} ) \ell^{2}-\frac{1}{4}}\vert B_{1}\vert ^{2}},} \end{aligned}$$
(111)

and the absorption cross-section, \(\sigma_{\mathit{abs}}\), is given by

$$ \sigma_{\mathit{abs}}=\frac{\mathfrak{T}}{\omega }=\frac{\ell \vert C_{1}\vert ^{2}}{\sqrt{ ( \omega^{2} -m^{2} ) \ell ^{2}-\frac{1}{4}}\vert B_{1}\vert ^{2}}. $$
(112)

As in the previous case, the poles of the transmission coefficient yield the same set of QNFs found in the previous section. Also, we observe the same behavior described in the previous case for the reflection coefficient (110), transmission coefficient (111), and absorption cross-section (112), i.e., we have found that the reflection coefficient is 1 at the low frequency limit, and for the high frequency limit this coefficient is null, with the behavior of the transmission coefficient being opposite with \(R+T = 1\) (see Fig. 6). Also, the absorption cross-section is null in the low and high frequency limits, but there is a range of frequencies for which the absorption cross-section is not null, and it also has a maximum value in the low frequency limit (see Fig. 7). Furthermore, we observe that the absorption cross-section can take higher values when the mass of the scalar field decreases (Fig. 7) in the low frequency limit. However, beyond a certain value of the frequency the absorption cross-section does not depend on the mass of the scalar field. It is worth noting that the absorption cross-section does not depend on the angular momentum of the scalar field, being the same for every value of \(\kappa\).

Fig. 6
figure 6

The reflection coefficient \(R\) (solid curve), the transmission coefficient \(T\) (dashed curve), \(R+T\) (thick curve) and the absorption cross-section \(\sigma_{\mathit{abs}}\) (dotted curve) as a function of \(\omega\), for \(m=1\), \(\ell=1\) and \(\kappa=0\)

Full size image
Fig. 7
figure 7

The behavior of \(\sigma_{\mathit{abs}}\) as a function of \(\omega\), for \(\kappa=0\), \(\ell=1\) and \(m = 1, 1.5, 2\)

Full size image

5 Conclusions

In this work, we calculated the QNFs of scalar field perturbations for the 4-dimensional asymptotically Lifshitz black hole in conformal gravity with a spherical topology and dynamical exponent \(z=0\), where the anisotropic scale invariance corresponds to a space-like scale invariance with no transformation of time, for some special cases that depend on \(Q\), and by imposing suitable boundary conditions at spatial infinity. These scalar fields are considered as mere test fields, without backreaction over the spacetime itself. Therefore, it is not necessary for such fields to have the same symmetries as the background spacetime. However, if one considers the backreaction of the matter fields over the spacetime, the relation between the symmetries of the spacetime and the matter fields is not trivial. For conformal gravity the gravitational field equations imply that the trace of the stress-energy tensor must vanish due to the fact that the Bach tensor is traceless.

First, we analyzed massive scalar field perturbations minimally coupled to curvature, which does not have the same symmetries as the background spacetime due to the trace of stress-energy tensor being not null. The first case studied corresponds to a scalar field without angular momentum (\(\kappa=0\)), and we found that there is a spectrum of quasinormal frequencies for which the scalar field becomes null at spatial infinity. These frequencies are purely imaginary and negative for \(m=0\); however, for \(m \neq0\) some QNFs are imaginary and positive. Another case we analyzed corresponds to \(Q=\pm\infty\), where we found a spectrum of QNFs that respect the Dirichlet boundary condition; however, some of them have a positive imaginary part. Therefore, the black hole is unstable under massive scalar field perturbations and stable under massless scalar field perturbations. Also, we analyzed the extremal case \(Q=1\), for which we found that there are no QNMs as in Crisostomo et al. (2004), where the authors demonstrated the absence of QNMs in the extremal BTZ black hole. However, it was shown that it is possible to construct the QNMs of 3-dimensional extremal black holes algebraically as the descendants of the highest weight modes (Chen and Zhang 2011), with hidden conformal symmetry being an intrinsic property of the extremal black hole. Also, it is worth mentioning that QNMs for extremal black holes are not always absent, for instance, see Afshar et al. (2010), where the authors reported the presence of QNMs for extremal BTZ black holes in topologically massive gravity. Additionally, for different values of \(Q\) we have found the QNFs numerically and observed that the imaginary part of the QNFs is always negative for massless scalar field, whereas for massive scalar field there are some QNFs with a positive imaginary part; see Table 1.

On the other hand, because the gravitational field equations imply that the trace of the stress-energy tensor must vanish, we also considered scalar field perturbations conformally coupled to curvature which have a traceless stress-energy tensor, and we showed that the imaginary part of the QNFs calculated is negative, which guaranties the stability of the Lifshitz black hole under conformally coupled scalar field perturbations, this was shown by using the improved AIM and analytical solutions. This behavior is similar to the studied in Catalán and Vásquez (2014) for a 3-dimensional Lifshitz black hole in conformal gravity with null dynamical exponent. This is due to the effective potentials having a similar behavior, that is, for a minimally coupled scalar field both potentials go to \(1/(4 \ell^{2}) + m^{2}\), and for a conformally coupled scalar field both potentials vanish asymptotically. Also, the real part of the QNFs does not depend on \(n\) for a conformally coupled scalar field and \(Q=\pm\infty\), for both dimensions. On the other hand, the QNFs of three-dimensional case (Eq. (49) of Catalán and Vásquez 2014) can be obtained from the 4-dimensional case, for a conformally coupled scalar field and \(Q=\pm \infty\), by doing the redefinitions \(\ell\rightarrow\ell/2\) and \(\sqrt{\kappa+5/2} \rightarrow\frac{\kappa}{2\sqrt{M}}\) in Eq. (96). It is worth mentioning that for other theories with a non-fixed dynamical exponent, the behavior of the QNFs depends on the dimension of the spacetime as well as on the dynamical exponent (see Sybesma and Vandoren 2015), where the authors have found that for \(D\leq z+2\) the QNFs are always overdamped, that is, the QNF has no real part so there is no oscillatory behavior of the perturbation, only exponential decay, whereas for \(D > z + 2\) the system is not overdamped. This is consistent with our results for a conformally coupled scalar field and for a massless scalar field minimally coupled to gravity. Additionally, it was shown that for the Lifshitz black holes with hyperscaling violating factor, the hyperscaling exponent modifies the above expression (Bécar et al. 2015; González and Vásquez 2015).

According to the gauge/gravity duality, the relaxation time \(\tau\) for a thermal state to reach thermal equilibrium in the boundary conformal field theory is \(\tau=1/\omega_{I}\), where \(\omega_{I}\) is the imaginary part of the fundamental QNF. For stable configurations it is possible to reach thermal equilibrium and, as can be deduced from the tables, the relaxation time decreases when \(\lambda\) increases for all the cases analyzed, except for a minimally coupled scalar field with \(\kappa=0\), where the relaxation time is independent of \(\lambda\).

Finally, we focused our attention on the minimally coupled scalar field case, and we computed the reflection and transmission coefficients and the absorption cross-section. We showed numerically that the absorption cross-section vanishes at the low and high frequency limits. Therefore, a wave emitted from the horizon, with low or high frequency, does not reach the spatial infinity and is totally reflected because the fraction of particles penetrating the potential barrier vanishes. However, we have shown that there is a range of frequencies where the absorption cross-section is not null. The reflection coefficient is 1 at the low frequency limit, and for the high frequency limit this coefficient is null, with the behavior of the transmission coefficient being opposite with \(R+T=1\). Also, we have shown that the absorption cross-section increases if the mass of the scalar field decreases in the low frequency limit; however, beyond a certain value of the frequency the absorption cross-section does not depend on the mass of the scalar field. Furthermore, we have shown that the absorption cross-section does not depend on the angular momentum.