1 Introduction

The spectacular discoveries made in the past few decades shown that Relativity is a necessary feature for describing astrophysical phenomena involving compact objects in contemporary cosmology and astrophysics. Recent observations have shown that some of the phenomena are core collapse supernovae, X-ray binaries, pulsars, coalescing neutron stars, formation of black holes, micro-quasars, active galactic nuclei, superluminal jets and gamma-ray bursts. A number of promising developments of astronomical instrumentation in the last decade such as gravitational wave detectors LIGO, LISA, VIRGO and Geo-600 currently under mission will improve significant detection of gravitational waves emitted from compact stellar objects such as compact astrophysical objects and black holes. The Einstein equations for the structure of space-time theory is essential in describing phenomena such as black holes, compact objects, supernovae, and the formation of structure in the universe.

In general, gravitational self-collapsing body cannot be properly explained by any post-Newtonian approximation because their character is basically controlled by strong gravity. These include the imploding cores of supernovae, hybrid compact objects, the quasinormal-mode vibrations of neutron stars and black holes and formation structure in the universe. Phenomena such as these must be analyzed using different techniques. Einstein numerical models are a useful framework for analyzing astrophysical phenomena around compact objects such as black holes and neutron stars. Compact stars with a core consisting of quark matter are dubbed hybrid stars. The physical basis for understanding hybrid stars containing both the hadrons and quarks has been described with great clarity and a great detail by many authors (Glendenning 1997; Steiner et al. 2000; Hanauske et al. 2001; Schaffner-Bielich et al. 2002; Burgio et al. 2002). Compact stars which are entirely made a mixture of free Fermi gases of \(u\), \(d\), \(s\) quarks, besides may be a small layer of a crust of nuclei, are so called strange stars which have been usually modeled by using the MIT bag model and Nambu–Jona–Lasinio (NJL) model. In both the hadronic and quark phases their contributions to energy density and pressure are given by the well-known formulae of ideal Fermi gas. The system is supposed to be an uncharged mixture nuclear matter containing nucleons, leptons, and hyperons.

The physical properties of matter at ultrahigh densities are highly uncertain and the modes derived for the equation of state of such matter differs considerably with respect to the function dependence of pressure and density. The frame work to the study nature of ultra-high nuclear density is made by heavy-ion collision experiments which provide a unique way to compress and heat up nuclear matter, and to prove the existence of an exotic state of ultra-compressed nuclear matter, called quark-gluon plasma, which is described by the theory of strong nuclear interactions. They recreate, within a tiny region of space, conditions similar to those under which matter existed in the early universe, fractions of a second after the big bang. Astrophysical compact objects as the neutron stars and black holes may conceal the quark-gluon nuggets in their dense centers.

The fabric of space-time of compact star may also change depending on the inhomogeneity of matter distribution and its evolution and development of anisotropy. At interior of compact star two different kinds of pressure exists i.e., radial and tangential pressure. In order to understand the dynamics and evolution of such compact object system, astrophysicists usually resort to mathematical models which incorporate anisotropic matter distribution as a key building block.

The possible causes of anisotropy may be due to phase transitions in dense nuclear matter such as pion, kaon and hyperon condensation, super fluidity and quark matter. Kaplan and Nelson (1986) studied the Kaon condensation in dense matter, and have been discussed in many recent publications (Brown et al., 1994; Waas et al., 1997).

The objective of present study the ways of incorporating anisotropy in stellar matter. Rather, we are interested in constructing models for relativistic anisotropic fluid spheres of Mattese and Whiteman solution. Consenza et al. (1981), Bayin (1982), Krori et al. (1984), Maharaj and Maarten (1989) and Gokhroo and Mehra (1993), Maurya and Gupta (2012a), Maurya et al. (2015a, 2015b, 2015c, 2015d, 2016), Malaver (2014, 2015a, 2015b), Pant et al. (2015) have obtained different exact solutions of the Einstein field equations describing the interior gravitational fields of anisotropic fluid spheres. This solution can be used as models of massive compact objects.

Motivated by the earlier work of Maurya and Gupta (2012b), in this present paper we have developed a new anisotropic strange star model by using the Matese and Whitman (1980) interior solution. The paper has been organized as follows: In Sect. 2, we mentioned the Einstein’s field equation for anisotropic star and Matese and Whiteman transformations. However the solutions for anisotropic compact star models and measure of anisotropy factor are given in Sect. 3. In Sect. 4, we determined the arbitrary constants by joining our metric with Schwarzschild’s metric at the boundary of the star. The physical features of the models like regularity at center, generalized TOV equation, energy conditions, speed of sound and stability analysis of the star are given in Sect. 5. The effective mass to radius ratio and surface red-shift are present in Sect. 5.5. At last, we have written the conclusion of the paper in Sect. 6.

2 Field equations and transformations

2.1 Einstein’s field equation

We assume the static spherically symmetric metric to describe the charged fluid spheres as

$$ ds^{2} = - e^{\lambda} dr^{2} - r^{2}\bigl(d \theta^{2} + \sin^{2}\theta d \phi^{2}\bigr) + e^{\nu} dt^{2} $$
(1)

where the functions \(\lambda(r)\) and \(\nu(r)\) satisfy the Einstein–Maxwell equations

$$ - \kappa G^{i}_{j} = R_{j}^{i} - \frac{1}{2}R\delta_{j}^{i} = - \kappa \bigl(T_{j}^{i} + E_{j}^{i}\bigr) $$
(2)

where

$$\begin{aligned} &{T_{j}^{i} = \bigl(c^{2}\rho+ p \bigr)v^{i}v_{j} - p\delta_{j}^{i},} \end{aligned}$$
(3)
$$\begin{aligned} &{E_{j}^{i} = \frac{1}{4\pi} \biggl( - F^{im}F_{jm} + \frac{1}{4}\delta_{j} ^{i} F_{mn}F^{mn}\biggr)} \end{aligned}$$
(4)

with \(\kappa= \frac{8\pi G}{c^{4}}\) while \(\rho, p, v^{i}, F_{i j}\) denote energy density, fluid pressure, flow vector and skew-symmetric electromagnetic field tensor respectively. \(F_{i j}\) further satisfies the Maxwell equations

$$ F_{ik,j} + F_{k j,i} + F{}_{ji.k} = 0 $$
(5)

In view of the metric (1), the field equation (2) gives (Dionysiou 1982)

$$\begin{aligned} &{\frac{v'}{r}e^{ - \lambda} - \frac{(1 - e^{ - \lambda} )}{r^{2}} = \kappa p - \frac{q^{2}}{r^{4}}} \end{aligned}$$
(6)
$$\begin{aligned} &{ \biggl[ \frac{v''}{2} - \frac{\lambda'v'}{4} + \frac{v^{\prime\,2}}{4} + \frac{v' - \lambda'}{2r} \biggr] e^{ - \lambda} = \kappa p + \frac{q ^{2}}{r^{4}}} \end{aligned}$$
(7)
$$\begin{aligned} &{\frac{\lambda'}{r}e^{ - \lambda} + \frac{(1 - e^{ - \lambda} )}{r ^{2}} = \kappa c^{2}\rho+ \frac{q^{2}}{r^{4}}} \end{aligned}$$
(8)

where, prime denotes the differentiation with respect to \(r\).

On substituting \(e^{ - \lambda} = Z\), \(e^{\nu} = y^{2}\) and \(x = r^{2}\) in (6)–(8), we get

$$\begin{aligned} &{\kappa c^{2}\rho= \frac{1 - Z}{x} - 2\frac{dZ}{dx}} \end{aligned}$$
(9)
$$\begin{aligned} &{\kappa p_{r} = \frac{4Z}{y}\frac{dy}{dx} - \frac{1 - Z}{x}} \end{aligned}$$
(10)
$$\begin{aligned} &{\kappa p_{t} = \frac{4 x Z}{y}\frac{d^{2}y}{dx^{2}} + 2 \frac{x}{y} \frac{dZ}{dx}\frac{dy}{dx} + 4\frac{Z}{y} \frac{dy}{dx} + \frac{dZ}{dx}} \end{aligned}$$
(11)

Pressure isotropy condition gives:

$$\begin{aligned} \Delta =& (p_{t} - p_{r}) \\ =& \frac{1}{\kappa} \biggl[ \frac{4 x Z}{y}\frac{d ^{2}y}{dx^{2}} + 2\frac{x}{y}\frac{dZ}{dx} \frac{dy}{dx} + \frac{dZ}{dx} + \frac{1 - Z}{x} \biggr] \end{aligned}$$
(12)

2.2 Matese and Whitman (1980) transformation

Let us introduce the Matese and Whitman (1980) transformation as:

$$ y = \sqrt{1 + ax} Y $$
(13)

The Eq. (12) reduces as:

$$ \frac{d^{2}Y}{dx^{2}} + f(x)\frac{dY}{dx} + g(x) Y = 0; $$
(14)

where,

$$\begin{aligned} &{f(x) = \frac{1}{2}\frac{d}{dx}\log\bigl[(1 + ax)^{2}Z \vert g \vert \bigr]} \end{aligned}$$
(15)
$$\begin{aligned} &{\begin{aligned}[b] g(x) &= \biggl[ \frac{(1 + 2ax)}{2 xZ (1 + ax)}\frac{dZ}{dx} + \frac{1}{4xZ} \biggl( \frac{1 - Z}{x} - \kappa\Delta \biggr) \\ &\quad {}- \frac{a ^{2}}{4 (1 + ax)^{2}} \biggr]. \end{aligned}} \end{aligned}$$
(16)

Now introduce new independent variable

$$ t = \int \vert g \vert ^{1/2}dx $$
(17)

Then Eq. (8) read as:

$$ \frac{d^{2}Y}{dt^{2}} + \frac{1}{2}\frac{d}{dt}\log \bigl[ (1 + ax)^{2}Z \vert g \vert \bigr] \frac{dY}{dt} + \frac{g}{\vert g \vert } Y = 0 $$
(18)

For solving the Eq. (18) we put

$$ (1 + ax)^{2}Z g = K $$
(19)

By using the Eq. (17) and (19), we get

$$ t = \vert K \vert ^{1/2} \int\frac{1}{(1 + ax)\sqrt{Z}} dx $$
(20)

By using Eqs. (19), the Eq. (16) can be read as:

$$ \begin{aligned}[b] &\frac{dZ}{dx} - \frac{1 + 2ax + 2a^{2}x^{2}}{x (1 + ax) (1 + 2ax)}Z \\ &\quad {}= \frac{4x(1 + ax)}{(1 + 2ax)} \biggl[ \frac{K}{(1 + ax)^{2}} - \frac{1}{4x ^{2}} + \frac{k \Delta}{4x} \biggr] . \end{aligned} $$
(21)

3 New solutions for anisotropic compact star models

After solving the Eq. (21), we get

$$ Z = \frac{x (1 + ax)}{(1 + 2ax)} \int \biggl( \frac{4K}{(1 + ax)^{2}} - \frac{1}{x^{2}} + \frac{k \Delta}{x} \biggr) dx $$
(22)

In order to integrate Eq. (22), we suppose the anisotropy factor of the form

$$ \Delta= \frac{\beta a^{2}x}{k (1 + ax)^{2}},\quad\mbox{where } \beta\ge0 $$
(23)

It is observed from Fig. 1, the pressure anisotropy \(\Delta\) is regular and positive inside the star. However it is monotonically increasing with fractional radius \(r/R\).

Fig. 1
figure 1

Variation of anisotropy factor (\(\Delta_{i} = \frac{\Delta}{a}\)) with respect to fractional radius \((r/R)\) for case-1. For the purpose of plotting this graph, we have employed the data set of values as: (i) \(k=0.90\), \(a=4.7385\times10^{ - 13}\) for Her X-1, (ii) \(k=0.60\), \(a=7.2057\times10^{ - 13}\) for RXJ 1856-37, (iii) \(k=0.99\), \(a=8.7354\times10^{ - 13}\) for SAX J1808.4-3658(SS2), (iv) \(k=0.953\), \(a=6.8093\times10^{ - 13}\) SAX J1808.4-3658(SS1)

Full size image

Using Eq. (22) and Eq. (23), we get:

$$ Z = \frac{ [a (1 + ax) - 4K x - \beta a^{2} x]}{a (1 + 2ax)}; $$
(24)

There are three cases: (i) \(K>0\) , (ii) \(K=0\) , (iii) \(K<0\) .

Case 1: \(K\) is positive. Take \(K = \frac{a^{2}}{4}\).

The Eqs. (24), (18) and (20) give respectively

$$\begin{aligned} &{Z = \frac{1 - \beta ax}{1 + 2ax}} \end{aligned}$$
(25)
$$\begin{aligned} &{y = \sqrt{(1 + ax)} (A\sin t + B\cos t)} \end{aligned}$$
(26)
$$\begin{aligned} &{\begin{aligned}[b] t &= \frac{1}{\sqrt{2\beta}} \sin^{ - 1} \biggl[ \frac{\beta(1 + 4ax) - 2}{(2 + \beta)} \biggr]\\ &\quad {} - \frac{1}{2\sqrt{1 + \beta}} \cos^{ - 1} \biggl[ \frac{ - \beta- (2 + 3\beta)ax}{(1 + ax) (2 + \beta)} \biggr] ; \end{aligned}} \end{aligned}$$
(27)

where \(A\) and \(B\) are arbitrary constants of integration.

The expressions for pressure and energy density can be read as

$$\begin{aligned} &{\begin{aligned}[b] p_{r} &= \frac{a}{8\pi} \biggl[ - \frac{(\beta+ 2ax + 3\beta ax)}{(1 + 3a x + 2a^{2}x^{2})}\\ &\quad {} + \frac{2}{(1 + ax)}\sqrt{\frac{(1 - \beta ax)}{(1 + 2a x)}} \frac{(A\cos t - B\sin t)}{(A\sin t + B\cos t)} \biggr] , \end{aligned}} \end{aligned}$$
(28)
$$\begin{aligned} &{\rho= \frac{a}{8\pi} \biggl[ \frac{ (2 + \beta) (3 + 2a x)}{(1 + 2ax)^{2}} \biggr] ,} \end{aligned}$$
(29)

Case 2: \(K=0\).

The Eqs. (24), (18) and (20) give respectively

$$\begin{aligned} &{Z = \frac{1 + ax - \beta ax}{1 + 2ax},} \end{aligned}$$
(30)
$$\begin{aligned} &{y = \sqrt{(1 + a x)} \bigl[C F(x) + D\bigr]} \end{aligned}$$
(31)
$$\begin{aligned} &{\begin{aligned}[b] F(x) &= \sqrt{\frac{2}{(1 - \beta)}} \log \biggl[ a x + \frac{(3 - \beta)}{4 (1 - \beta)} + \frac{f_{1}(x)}{\sqrt{2 (1 - \beta)}} \biggr] \\ &\quad {}+ \frac{1}{\sqrt{\beta}} \sin^{ - 1} \biggl[ \frac{1 - \beta+ (1 - 3 \beta) a x}{(1 + a x)f_{2}(x)} \biggr]; \end{aligned}} \end{aligned}$$
(32)

where, \(C\) and \(D\) are arbitrary constants of integrations and

$$\begin{aligned} &{f_{1}(x) = \sqrt{1 + (3 - \beta) a x + 2(1 - \beta)a^{2}x^{2}},} \\ &{f_{2}(x) = \sqrt{1 + 2\beta+ 17\beta^{2}}.} \end{aligned}$$

The following expressions for pressure and energy density as

$$\begin{aligned} &{\begin{aligned}[b] p_{r} &= \frac{a}{8\pi} \biggl[ \frac{1 - \beta+ ax - 3\beta ax}{(1 + 3ax + 2a^{2}x^{2})} \\ &\quad {}+ \frac{4 C\sqrt{1 + (1 - \alpha) ax}}{ [C F(x) + D] (1 + ax) \sqrt{1 + 2ax}} \biggr]; \end{aligned}} \end{aligned}$$
(33)
$$\begin{aligned} &{\rho= \frac{a}{8\pi} \biggl[ \frac{ (1 + \beta) (3 + 2ax)}{(1 + 2ax)^{2}} \biggr].} \end{aligned}$$
(34)

Case 3: \(K < 0\) .

The relation between the pressure and the energy density depends on the microscopic properties of matter and the equation of state of the star. This case gives the unphysical solution i.e. pressure or density is negative.

4 Matching conditions

Besides the above, the anisotropic fluid solution is expected to join smoothly with Schwarzschild exterior solution:

$$ \begin{aligned}[b] ds^{2} &= \biggl( 1 - \frac{2m}{r} \biggr) dt^{2} - r^{2}\bigl(d\theta^{2} + \sin^{2}\theta d \phi^{2}\bigr) \\ &\quad {}- \biggl( 1 - \frac{2m}{r} \biggr) ^{ - 1}dr ^{2}, \end{aligned} $$
(35)

which requires the continuity of \(e^{\lambda}\) and \(e^{\nu}\) across the boundary \(r = R\) (Misner and Sharp 1964).

Einstein’s field equation (32) yields the following set of differential equations for the functions \(v(R)\) and \(\lambda(R)\):

$$\begin{aligned} &{e^{ - \lambda(R)} = 1 - \frac{2M}{R},} \end{aligned}$$
(36)
$$\begin{aligned} &{e^{\nu(R)} = 1 - \frac{2M}{R} = y_{r = R}^{2}} \end{aligned}$$
(37)
$$\begin{aligned} &{p_{r}(r = R) = 0.} \end{aligned}$$
(38)

The conditions (36) and (38) give respectively the arbitrary conditions as:

Case 1:

$$\begin{aligned} &{B = \frac{\sqrt{ (1 - \beta aX)}}{ ( \frac{A}{B}\sin T + \cos T ) \sqrt{(1 + aX) (1 + 2aX)}}} \end{aligned}$$
(39)
$$\begin{aligned} &{\frac{A}{B} = \frac{2\tan T\sqrt{(1 + 2aX) (1 - \beta aX)} + ( \beta+ 2aX + 3\beta aX)}{2\sqrt{(1 + 2aX) (1 - \beta aX)} - \tan T (\beta+ 2aX + 3\beta aX)},} \end{aligned}$$
(40)

where,

$$\begin{aligned}[c] T &= \frac{1}{\sqrt{2 \beta}} \sin^{ - 1} \biggl[ \frac{\beta(1 + 4aX) - 2}{\sqrt{4 + 6 \beta- \beta^{2}}} \biggr] \\ &\quad {}- \frac{1}{2\sqrt{1 + \beta}} \cos^{ - 1} \biggl[ \frac{ - 2aX - \beta(1 + 3aX)}{(1 + aX)\sqrt{4 + 4 \beta+ 9\beta^{2}}} \biggr] \end{aligned} $$

Case 2:

$$\begin{aligned} &{D = \sqrt{\frac{1 + aX - \beta aX}{1 + 3aX + 2a^{2}X^{2}}} \biggl[ 1 + \frac{C}{D}F(X) \biggr] ^{ - 1},} \end{aligned}$$
(41)
$$\begin{aligned} &{\frac{C}{D} = \frac{3\beta a X - aX + \beta- 1}{4\sqrt{(1 + 2aX) (1 - \beta aX)} + F(X) (1 - \beta+ aX - 3\beta a X)},} \end{aligned}$$
(42)

where,

$$ \begin{aligned}[b] F(X) &= \sqrt{\frac{2}{(1 - \beta)}} \log \biggl[ a X + \frac{(3 - \beta)}{4 (1 - \beta)} + \frac{f_{1}(X)}{\sqrt{2 (1 - \beta)}} \biggr] \\ &\quad {}+ \frac{1}{\sqrt{\beta}} \sin^{ - 1} \biggl[ \frac{1 - \beta+ (1 - 3 \beta) a X}{(1 + a X)f_{2}(\beta)} \biggr] ; \end{aligned} $$
(43)

with \(f_{1}(X) = \sqrt{1 + (3 - \beta) a X + 2(1 - \beta)a^{2}X ^{2}}\), \(f_{2}(\beta) = \sqrt{1 + 2\beta+ 17\beta^{2}}\).

5 Physical features of anisotropic models

5.1 Regularity conditions

(A) The metric potentials \(e^{\lambda(r)}\) and \(e^{\nu(r)}\)must be positive and finite at the center.

Case (i): From Eqs. (25) and (26), we obtain that \(e^{\lambda(0)} = 1\) and \(e^{\nu(0)} = [A\sin(t_{r = 0}) + B\cos(t_{r = 0})]^{2}\).

Case (ii): From Eqs. (30) and (31), we obtain that \(e^{\lambda(0)} = 1\) and \(e^{\nu(0)} = [C F(0) + D]^{2}\).

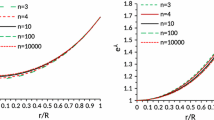
We observe from above these cases that the metric potentials are positive and finite at the center. The behavior can see in Fig. 2.

Fig. 2
figure 2

Variation of metric potentials \(e^{\lambda}\) and \(e^{\nu}\) with respect to fractional radius (\(r/R\)) for case-1. The data values used in this figure is same as of Fig. 1

Full size image
Fig. 3
figure 3

Variation of radial pressure (left panel) and transverse pressure (right panel) with respect to fractional radius (\(r/R\)) for case-1. The data values used in this figure is same as of Figs. 1 and 2

Full size image
Fig. 4
figure 4

Variation of energy density with respect to fractional radius (\(r/R\)) for case-1. For the purpose of plotting this graph, we have employed the data set of values as: (i) \(k=0.90\), \(a=4.7385\times10^{ - 13}\) for Her X-1, (ii) \(k=0.60\), \(a=7.2057\times10^{ - 13}\) for RXJ 1856-37, (iii) \(k=0.99\), \(a=8.7354\times10^{ - 13}\) for SAX J1808.4-3658(SS2), (iv) \(k=0.953\), \(a=6.8093\times10^{ - 13}\) SAX J1808.4-3658(SS1)

Full size image

(B) Density at center:

Case (i): \(\rho_{0} = \frac{3a (2 + \beta)}{8\pi}\), Case (ii): \(\rho_{0} = \frac{3a (1 + \beta)}{8\pi}\). Since \(\beta\) is positive, this implies that \(a\) is also positive.

5.2 Generalized Tolman–Oppenheimer–Volkoff (TOV) equation

The general-relativistic hydrostatic equations were derived and applied to models of neutron stars already in 1939 by Tolman (1939), Oppenheimer and Volkoff (1939). These equations are derived from Einstein’s field equation under the assumptions that the metric is static and isotropic, and that matter is a perfect fluid. The latter assumption is expected to be a good approximation for the extremely dense interior of a static compact star, because the strong gravitational force is balanced by a huge pressure and rigid-body forces have a negligible effect on the structure. In combination with the expression for the mass and a microscopic theory for the relation between the pressure and the energy density, this equation gives the equilibrium solution for the pressure in a compact star. These equations are the generalizations of the Newtonian hydrostatic equations for anisotropic fluid distribution is given by

$$ \frac{M_{G}(\rho+ p_{r})}{r^{2}}e^{\frac{\lambda- \nu}{2}} + \frac{dp _{r}}{dr} + \frac{2}{r}(p_{r} - p_{t}) = 0. $$
(44)

We can write the above TOV equation as Varela et al. (2010):

$$ - \frac{1}{2}v'(\rho+ p_{r}) - \frac{dp_{r}}{dr} + \frac{2}{r}(p_{t} - p_{r}) = 0; $$
(45)

where \(M_{G}\) is the effective gravitational mass given by

$$ M_{G}(r) = \frac{1}{2}r^{2}e^{\frac{\nu- \lambda}{2}} \nu' $$
(46)

The Eq. (44) describes the equilibrium condition for an anisotropic fluid distribution subject to gravitational force (\(F_{g}\)), hydrostatic force (\(F_{h}\)), anisotropic stress (\(F_{a}\)) such that:

$$ F_{g} + F_{h} + F_{a} = 0, $$
(47)

where,

$$\begin{aligned} &{F_{g} = - \frac{1}{2}v'(\rho+ p_{r}),} \end{aligned}$$
(48)
$$\begin{aligned} &{F_{h} = - \frac{dp_{r}}{dr},} \end{aligned}$$
(49)
$$\begin{aligned} &{F_{a} = \frac{2}{r}(p_{t} - p_{r}).} \end{aligned}$$
(50)

The explicit form these forces can be expressed as:

Case (1)

$$\begin{aligned} &{\begin{aligned}[b] F_{g} &= - \frac{a^{2}r}{16\pi(1 + ax)} \biggl[ 1 + \sqrt{ \frac{1 + 2ax}{1 - \beta ax}} F_{1}(t) \biggr] \\ &\quad {}\times\biggl[ \frac{F_{2}(x)}{(1 + ax)(1 + 2ax)^{2}} \\ &\quad {}+ \frac{2}{(1 + ax)}\sqrt{\frac{(1 - \beta ax)}{(1 + 2a x)}} F_{1}(t) \biggr] \end{aligned}} \end{aligned}$$
(51)
$$\begin{aligned} &{F_{h} = - \frac{dp_{r}}{dr};} \end{aligned}$$
(52)
$$\begin{aligned} &{F_{a} = \frac{\beta a^{2}r}{4\pi(1 + ax)^{2}}} \end{aligned}$$
(53)

where, \(F_{1}(t) = \frac{A\cos t - B\sin t}{A\sin t + B\cos t}\), \(F_{2}(x) = 6 + 8ax - 3\beta ax (1 + 2ax) + \beta(2 + 3ax + 2a^{2}x ^{2})\).

We plotted the graph for generalized Tolman–Openheimer–Volkoff equations in Fig. 5. Form this figure, we observe that the system is counter balance under the different forces, i.e. the gravitational force, hydrostatic force and anisotropic stress. Also the system attains a static equilibrium. However hydrostatic force is dominated by gravitational force and it is balanced by the joint action of anisotropic stress and hydrostatic force. As we can see from Fig. 5, the anisotropic stress has a less role to the action of equilibrium condition. These physical features represents that our compact star models are stable.

Fig. 5
figure 5

Variation of different forces with respect to fractional radius \((r/R)\). (i) RXJ 1856-37 (top left), (ii) Her X-1 (top right), (iii) SAX-1 (bottom left), (iv) SAX-2 (bottom right) for case-1. The data set of values \(a\) and \(k\) are used in this figure same as in Fig. 4

Full size image

Case (2):

$$\begin{aligned} &{\begin{aligned}[b] F_{g} &= - \frac{a^{2}r}{16\pi(1 + ax)} \biggl[ 1 + \frac{2C}{[C F(x) + D]F_{5}(x)} \biggr]\\ &\quad {}\times \biggl[ \frac{F_{3}(x)}{F_{4}(x)} + \frac{4C F_{5}(x)}{[C F(x) + D](1 + ax)\sqrt{1 + 2ax}} \biggr] \end{aligned}} \end{aligned}$$
(54)
$$\begin{aligned} &{F_{h} = - \frac{dp_{r}}{dr};} \end{aligned}$$
(55)
$$\begin{aligned} &{F_{a} = \frac{\beta a^{2}r}{4\pi(1 + ax)^{2}};} \end{aligned}$$
(56)

where, \(F_{3}(x) = 4(1 + ax)^{2} + \beta(2 - 4a^{2}x^{2})\), \(F_{4}(x) = (1 + ax)(1 + 2ax)^{2}\), \(F_{5}(x) = \sqrt{1 + (1 - \beta)a x}\).

5.3 Energy conditions

For physically valid models, the following energy conditions must be satisfied at each point inside the anisotropic stars:

  • Null energy condition (NEC): \(\rho\ge0\)

  • Weak energy condition (\(\mathrm{WEC}_{r}\)): \(\rho- p_{r} \ge0\)

  • Weak energy condition (\(\mathrm{WEC}_{t}\)): \(\rho- p_{t} \ge0\)

  • Strong energy condition (SEC): \(\rho- p_{r} - 2p_{t} \ge0\).

5.4 Speed of sound and stability analysis of the models

In addition to the positivity of density and pressures profiles, we shall pay special and particular attention to the conditions bounding sound speeds (radial and tangential) within the matter configuration. The speed of sound of the compact star should be less that speed of light i.e. \(dp_{i}/d\rho\) should lies between 0 and 1. From Fig. 7, it is clear that speed of sound is monotonically decreasing and less than speed of light.

The stability of the models with internal pressure anisotropy was also probed by Herrera (1992) and collaborators. They have shown that, for particular dependent perturbations, potentially stable regions within anisotropic matter configurations could occur when there is no change in sign of \(V_{t}^{2} - V_{r}^{2}\) and \(V_{r}^{2} - V_{t}^{2}\) i.e. radial velocity of sound should always greater than the tangential velocity. It is also well understood that stability of particular anisotropic configurations is independent perturbation. We can observe from Fig. 8 that our models are stable.

The radial and tangential sound speeds are calculated and its difference is evaluated as shown below:

Case-1

$$ \bigl\vert V_{t}^{2} - V_{r}^{2} \bigr\vert = \frac{\beta}{(2 + \beta)}\frac{(1 + 2ax)^{3}}{(1 + ax)^{3}}.\frac{1}{(5 + 2ax)} , $$
(57)

Case-2

$$ \bigl\vert V_{t}^{2} - V_{r}^{2} \bigr\vert = \frac{\beta}{(1 + \beta)}\frac{(1 + 2ax)^{3}}{(1 + ax)^{3}}.\frac{1}{(5 + 2ax)}. $$
(58)

5.5 The effective mass and surface red-shift

The effective mass and surface red-shift of the compact star is defined as:

Case-1:

$$ M_{\mathrm{eff}} = \frac{R}{2} \biggl[ \frac{(2 + \beta)a R^{2}}{1 + 2aR^{2}} \biggr],\qquad Z = \sqrt{\frac{1 - \beta aR^{2}}{1 + 2aR^{2}}} - 1 $$
(59)

Case-2:

$$ \begin{aligned}[c] &M_{\mathrm{eff}} = \frac{R}{2} \biggl[ \frac{(1 + \beta)a R^{2}}{1 + 2aR^{2}} \biggr],\\ &Z = \sqrt{\frac{1 + aR^{2} - \beta aR^{2}}{1 + 2aR ^{2}}} - 1. \end{aligned} $$
(60)

The red-shift is a consequence of gravitational time dilation. Time moves slowly in a strong gravitational field, as measured by a remote observer. Redshift measurements of neutron stars provide information about \(M / R\). In combination with other observational techniques used to deduce \(M\) and/or \(R\), this information can be used to pinpoint the physical compact star sequence in the \(M\)–\(R\) plane. In addition, high redshifts are difficult to explain with compact star models based on soft EOS. A measurement of a star with high surface redshift would therefore rule out some microscopic models.

We can determine the maximum mass for the models of compact stars and realize that the differences between the models are not negligible. All the static solutions displayed have radius and total masses, \(M_{\odot}\) (in terms of solar mass \(M\)) central density, surface density and central pressure that correspond to typical values for expected astrophysical compact objects. The boundary redshifts, surface and central densities, pressure and density emerge from our theoretical model fit the typical values for these objects.

6 Physical analysis and conclusions

Our theoretical model shows a stability behavior in many aspects similar that of present studies have done by a large group workers (Mak and Harko 2003; Dev and Gleiser 2002). By suitably choosing values of the unknown parameters, it is possible to show that our model can describe realistic compact stellar objects (Tables 1 and 2). The behavior of the energy density, two pressures and anisotropic parameter, metric potential, red-shift, forces, energy conditions and velocity of sound are shown in Figs. 1–9. We start with Matese–Whiteman transformation and introduce anisotropic factor \(\Delta\). After that we obtained three distinct classes of solutions are given by the following three cases. As case 1 and 2 are physically accepted however case 3 is unphysical. By imposing an energy condition, the value for the maximum possible redshift at the surface of the star can be obtained. The stability of the models with internal pressure anisotropy was also probed by Herrera and collaborators. They have shown that, for particular dependent perturbations, potentially stable regions within anisotropic matter configurations could occur when the radial speed of sound, is greater than tangential speed of sound. It is also well understood that stability of particular anisotropic configurations is well behaved condition i.e., the velocity of sound is monotonically decreasing away from the center and it is increasing with the increase of density. These features can be seen in Fig. 7 and Fig. 8. Also our obtained are satisfying the various energy conditions everywhere inside the stars (Fig. 6).

Fig. 6
figure 6

Variation of energy conditions with respect to fractional radius \((r/R)\) for case-1. The data set of values \(a\) and \(k\) are used in this figure same as in Figs. 4 and 5

Full size image
Fig. 7
figure 7

Variation of radial speed of sound (left panel) and transverse speed of sound (right panel) with respect to fractional radius \((r/R)\). For the purpose of plotting this graph, we have employed the data set of values as: (i) \(k=0.90\), \(a=4.7385\times10^{ - 13}\) for Her X-1, (ii) \(k=0.60\), \(a=7.2057\times10^{ - 13}\) for RXJ 1856-37, (iii) \(k=0.99\), \(a=8.7354\times10^{ - 13}\) for SAX J1808.4-3658(SS2), (iv) \(k=0.953\), \(a=6.8093\times10^{ - 13}\) SAX J1808.4-3658(SS1)

Full size image
Fig. 8
figure 8

Variation of absolute value of square velocity with respect to fractional radius \((r/R)\) for case-1. For the purpose of plotting this graph, we have employed same data values as in Fig. 7

Full size image
Table 1 Values of the model parameters of case (1) for different values of \(a R^{2}\) and \(K\)
Full size table
Table 2 Energy densities, central pressure and \(a\) for different strange star candidates for the above parameter values of Table 1 (Case-1)
Full size table

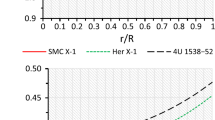
On the ground of regular Oppenheimer–Volkoff solution the three important astrophysical concepts are based: the Oppenheimer limit (1939) for the object mass, Buchdal (1959) for mass to the radius ratio and the Bondi limit for gravitational redshift. Bohmer and Harko (2006) provided an exhaustive review on the subject of red-shift (\(Z\leq5\)) in the presence of cosmological constant. More recently a comprehensive work on surface redshift (\(Z\leq5.21\)) of compact object has been studied by Ivanov (2002). In our present models, the obtained red-shift is good agreement (Fig. 9).

Fig. 9
figure 9

Variation of red shift with respect to fractional radius \((r/R)\) for case-1. For the purpose of plotting this graph, we have employed the data set of values as: (i) \(k=0.90\), \(a=4.7385\times10^{ - 13}\) for Her X-1, (ii) \(k=0.60\), \(a=7.2057\times10^{ - 13}\) for RXJ 1856-37, (iii) \(k=0.99\), \(a=8.7354\times10^{ - 13}\) for SAX J1808.4-3658(SS2), (iv) \(k=0.953\), \(a=6.8093\times10^{- 13}\) SAX J1808.4-3658(SS1)

Full size image

A necessary, but not sufficient, condition for stability of a compact star is that the total mass is an increasing function of the central density \(dM/d\rho_{c} > 0\) (Glendenning 1997). This condition implies that a slight compression or expansion of a star will result in a less favorable state, with higher total energy. The features seem physically not realistic when the anisotropic conditions are relaxed. Within our generalized theoretical model with Matese & Whitman solution the maximum mass of anisotropic compact star is in the range \(0.98M_{\odot}\)–\(1.4 M_{\odot}\) for different strange star candidates for the above parameter. In our present models, the comprehensive physical analysis through graphical approach suggests that the model for the compact star like Her. X-1, RXJ 1856-37, SAX J1808.4-3658(SS2) and SAX J1808.4-3658(SS1) are well behaved.