1 Introduction

In astrophysics and cosmology, visibility of singularity remains as one of the open problems so far as collapse of a self-gravitating system is concerned. In astrophysical context, the final stage of a collapsing star has long been very much speculative in nature (Chandrasekhar 1934). In the absence of any physical or mathematical theory governing gravitational collapse, development of realistic collapsing models is expected to provide valuable information about the factors that might effect the evolution and subsequent end stage of a collapsing star. However, due to highly non-linear nature of the field equations, it has always been a difficult task to generate solutions of self-gravitating astrophysical systems. In order to reduce mathematical complexity, various simplifying methods are often adopted. The seminal work of Oppenheimer and Snyder (1939) was a first step in this direction who studied the collapse of a highly idealized spherically symmetric dust cloud. Later, Vaidya (1951) obtained a solution describing the exterior gravitational field of a radiating star and Santos (1985) presented the junction conditions joining smoothly the interior spacetime of the collapsing object to the Vaidya exterior metric. Subsequently, many realistic stellar models have been constructed to investigate critically the effects of various factors such as shear, density inhomogeneity, local anisotropy, electromagnetic field, viscosity and many other factors, on the gross physical behaviour of collapsing systems (see for example, Joshi and Malafarina 2011; Sharma and Das 2013; Sharma and Tikekar 2012a, 2012b; Sharma et al. 2015; Naidu et al. 2006; de Oliveira and Santos 1987, 1988; de Oliveira et al. 1988; Herrera et al. 2008, 1998; di Prisco et al. 2007; Pinheiro and Chan 2010; Chan 2001; Chan et al. 1994 and references therein).

The main objective of the current investigation is to develop a simple technique to analyze the effects of anisotropy on the evolution of a star collapsing non-adiabatically under the influence of its own gravity and dissipating energy in the form of radial heat flow. Amongst others, Herrera et al. (1998) have made in depth analyses of impacts of anisotropic stresses on gravitational collapse of fluid distributions. Recently, on a shearing background spacetime, Reddy et al. (2015) have analyzed impacts of anisotropic stresses onto the collapse by adopting a perturbative scheme where the initial static configuration was assumed to be described by Bowers and Liang (1974) static stellar solution. Since our primary objective is to analyze impacts of anisotropy onto the collapse, we develop the model under shear-free condition and retain bulk viscosity term only in the energy-momentum tensor describing the anisotropic fluid distribution. The possible role of bulk viscosity on the evolution of a collapsing matter distribution has been dealt in with details (see Chan 2001 and references therein) in the past. In our study, we would like to examine the possible role of bulk viscosity in the absence of shear.

One of the key techniques that is often adopted to generate a collapsing model is to assume that the metric functions are separable in its variables. The method allows one to choose a suitable static seed solution from which the collapse begins. Although, thousands of relativistic static stellar solutions are available in the literature, only a few of them are physically well-behaved and satisfy all the requirements of a realistic star (Delgaty and Lake 1998). The static stellar solution of Pant and Sah (1985) is one such class which has been shown to be relevant for the description of cold compact stars like neutron stars. For a perfect fluid with isotropic pressure, the model allows a maximum permissible mass \(\sim4~M_{\odot}\). Recently, a new class of solutions describing the spacetime of a static spherically symmetric anisotropic star has been obtained by Paul and Deb (2014) which reduces to Pant and Sah (1985) solution if one sets the anisotropic parameter \(n=0\) in their paper. It is to be stressed that pressure anisotropy plays an important role in the studies of self-gravitating objects. Anisotropic stresses might occur due to phase transitions (Sokolov 1980) and/or pion condensation (Sawyer 1972) during stellar collapse. Presence of strong electromagnetic field (Usov 2004) may also give rise to anisotropy. In fact, in the studies of gravitationally self-bound systems, shear and electromagnetic field have an anisotropic interpretation as pointed out by Ivanov (2010). Similarly, null fluid admixed perfect fluid spheres too may be represented by an effective anisotropic fluid model (Letelier 1980). Strong magnetic fields can also generate anisotropic stresses inside a compact sphere (Weber 1999). Kippenhahn and Weigert (1990) have shown that in stellar interiors anisotropy might develop in the presence of a solid core or type \(3A\) super-fluid. Amongst many others, Ruderman (1972), Bowers and Liang (1974) and Herrera and Santos (1997) have extensively discussed the underlying causes that generate anisotropy at stellar interiors. In our work, without going into the microscopic origin of anisotropic stress, we develop a model of a collapsing star whose initial configuration is assumed to be described by the anisotropic static fluid solution obtained by Paul and Deb (2014). Since Paul and Deb (2014) solution has an isotropic limit, it provides a simple platform to analyze the effects of anisotropy on the evolution of the collapsing system.

Our paper has been organized as follows. In Sect. 2, the Einstein field equations for an anisotropic matter distribution collapsing under the influence of its own gravity and dissipating energy in the form of radial heat flux have been laid down. The exterior spacetime of the collapsing matter is appropriately described by the Vaidya (1951) metric. In Sect. 3, we have laid down the main results of the junction conditions joining smoothly the interior (\(r < r_{\varSigma}\)) and the exterior (\(r > r_{\varSigma}\)) spacetimes across the boundary surface \(\varSigma\) separating the two regions. Making use of the junction conditions and a static seed solution, we have developed our collapsing model in Sect. 4. In Sect. 5, we have analyzed the effects of pressure anisotropy based on the developed model.

2 Einstein field equations

We write the interior spacetime of a gravitationally collapsing star in isotropic coordinates as

$$\begin{aligned} ds_{-}^{2} =& -A^{2}(r,t)dt^{2} + B^{2}(r,t) \\ &{}\times \bigl[dr^{2}+r^{2} \bigl(d \theta^{2} + \sin ^{2}\theta d\phi^{2} \bigr) \bigr], \end{aligned}$$
(1)

where \(A(r,t)\) and \(B(r,t)\) are yet to be specified. The choice of shear-free spacetime makes our model suitable for slowly collapsing objects (de Oliveira et al. 1988). We assume the matter composition of the collapsing star to be an imperfect fluid with anisotropic stresses undergoing dissipation in the form of radial heat flow. Accordingly, energy-momentum tensor of the collapsing fluid is written in the form

$$\begin{aligned} T_{ij} =& (\rho+ p_{t})u_{i} u_{j} + p_{t} g_{ij} + (p-p_{t})X_{i}X_{j} \\ &{} + q_{i} u_{j} + q_{j} u_{i}-\zeta \varTheta(g_{ij}+u_{i} u_{j}), \end{aligned}$$
(2)

where \(\rho\) is the energy density of the fluid, \(p\) is the radial pressure, \(p_{t}\) is the tangential pressure, \(q^{i}=q\;\delta_{1}^{i}\) is the radial heat flux vector, \(X^{i}\) is an unit 4-vector along the radial direction and \(u^{i}\) is the 4-velocity of the fluid. The quantities obey the following relations: \(u^{i} q_{i} = 0\), \(X_{i} X^{i} = 1\), \(X_{i} u^{i} = 0\). In Eq. (2), \(\zeta> 0\) is the coefficient of bulk viscosity.

The Einstein field equations for the line element (1) are obtained as

$$\begin{aligned} &{k\rho = -\frac{1}{B^{2}} \biggl(\frac{2B''}{B}+\frac{4B'}{rB}- \frac{B^{\prime 2}}{B^{2}} \biggr)+\frac{3\dot{B}^{2}}{ A^{2} B^{2}},} \end{aligned}$$
(3)
$$\begin{aligned} &{ \begin{aligned}[b] k(p-\zeta\varTheta) &= \frac{1}{B^{2}} \biggl(\frac{B^{\prime 2}}{B^{2}}+ \frac {2B'}{rB}+\frac{2A'B'}{AB}+\frac{2A'}{rA} \biggr) \\ &\quad {}+\frac{1}{A^{2}} \biggl(-\frac{2\ddot{B}}{B}-\frac{\dot{B}^{2}}{B^{2}}+ \frac{2\dot{A}\dot {B}}{AB} \biggr), \end{aligned}} \end{aligned}$$
(4)
$$\begin{aligned} &{ \begin{aligned}[b] k(p_{t}-\zeta\varTheta) &= - \frac{2\ddot{B}}{A^{2} B}+\frac{2\dot{A}\dot {B}}{A^{3} B}- \frac{\dot{B}^{2}}{A^{2} B^{2}}+\frac{A'}{r A B^{2}} \\ &\quad {}+\frac{B'}{r B^{3}}+\frac{A''}{A B^{2}}- \frac{B^{\prime 2}}{B^{4}}+ \frac{B''}{B^{3}}, \end{aligned}} \end{aligned}$$
(5)
$$\begin{aligned} &{k q = -\frac{2}{A B^{2}} \biggl(-\frac{\dot{B}'}{B}+ \frac{\dot {B}B'}{B^{2}}+ \frac{A'\dot{B}}{AB} \biggr),} \end{aligned}$$
(6)

where, we have set \(c=1\) and \(8\pi G = k\). Note that a prime (′) and an overhead dot (.) denote differentiation with respect to \(r\) and \(t\), respectively.

3 Exterior space-time and junction conditions

The space-time exterior to the radiating star is appropriately described by the Vaidya (1951) metric

$$\begin{aligned} ds_{+}^{2} =& - \biggl(1-\frac{2m(v)}{\mathsf{r}} \biggr)dv^{2} - 2dv d\mathsf{r} \\ &{}+ \mathsf{r}^{2} \bigl[d \theta^{2} + \sin^{2} \theta d\phi^{2} \bigr], \end{aligned}$$
(7)

where the mass function \(m(v)\) is a function of retarded time \(v\). The junction conditions joining smoothly the interior (1) and exterior (7) spacetimes are obtained by assuming a time-like 3-surface \(\varSigma\) which separates the interior and the exterior manifolds (Santos 1985). Continuity of metric functions (\((ds_{-}^{2})_{\varSigma} = (ds_{+}^{2})_{\varSigma} = ds_{\varSigma}^{2}\)) and extrinsic curvatures (\(K_{ij}^{-} = K_{ij}^{+}\)) across the surface \(\varSigma\), then yield the following matching conditions linking smoothly the interior (\(r \leq r_{\varSigma}\)) and the exterior (\(r \geq r_{\varSigma}\)) space-times across the boundary:

$$\begin{aligned} &{m(v) = \biggl(\frac{r^{3} B \dot{B}^{2}}{2 A^{2}}-r^{2} B' - \frac{r^{3} B^{\prime 2}}{2 B} \biggr)_{\varSigma},} \end{aligned}$$
(8)
$$\begin{aligned} &{(p-\zeta\varTheta)_{\varSigma}=(q B)_{\varSigma}.} \end{aligned}$$
(9)

Consequently, using Eq. (8), we write the mass of the evolving star at any instant \(t\) within a radius \(r < r_{\varSigma}\) as

$$ m(r,t) \stackrel{\varSigma}{=} \biggl(\frac{r^{3} B \dot{B}^{2}}{2 A^{2}}-r^{2} B' -\frac{r^{3} B^{\prime 2}}{2 B} \biggr). $$
(10)

To understand behaviour of the physical quantities, we need to solve the system which will be taken up in the following sections.

4 A particular model

By combining Eqs. (4) and (5), we write

$$\begin{aligned} &{\Delta(r,t)=\frac{1}{B^{2}} \biggl[\frac{B''}{B}+ \frac{A''}{A}- \frac{2 B^{\prime 2}}{B^{2}}-\frac{B'}{r B}-\frac{2 A' B'}{A B}- \frac{A'}{r A} \biggr],} \end{aligned}$$
(11)

where, \(\Delta(r,t) = k(p_{t}-p)\) is the measure of anisotropy of the collapsing matter. Now, to make Eq. (11) tractable, we assume that the metric potentials \(A(r,t)\), \(B(r,t)\) are separable in their variables and accordingly we write

$$\begin{aligned} A(r,t) =& A_{0}(r), \end{aligned}$$
(12)
$$\begin{aligned} B(r,t) =& B_{0}(r) h(t). \end{aligned}$$
(13)

If we further assume

$$ \Delta(r,t) = \frac{\Delta_{s}(r)}{h^{2}(t)}. $$
(14)

Equation (11) takes the form

$$\begin{aligned} &{\Delta_{s}(r) = \frac{1}{B_{0}^{2}} \biggl[ \frac{B_{0}''}{B_{0}}+ \frac {A_{0}''}{A_{0}}-\frac{2 B_{0}^{\prime 2}}{B_{0}^{2}}-\frac{2 A_{0}' B_{0}'}{A_{0} B_{0}}- \frac {A_{0}'}{r A_{0}}- \frac{B_{0}'}{B_{0} r} \biggr],} \end{aligned}$$
(15)

which is independent of \(t\). One, therefore, is free to choose any physically reasonable static anisotropic stellar solution (\(A_{0}(r), B_{0}(r)\)) satisfying Eq. (15). Subsequently, the field equations (3)–(6) can be rewritten as

$$\begin{aligned} &{\rho = \frac{\rho_{0}}{h^{2}}+\frac{3 \dot{h}}{k h^{2} A_{0}^{2}},} \end{aligned}$$
(16)
$$\begin{aligned} &{p = \frac{p_{0}}{h^{2}}-\frac{1}{k A^{2}_{0}} \biggl(\frac{2\ddot{h}}{h}+ \frac {\dot{h}^{2}}{h^{2}} \biggr)+\frac{3\dot{h} \zeta}{A_{0} h},} \end{aligned}$$
(17)
$$\begin{aligned} &{p_{t} = \frac{p_{t0}}{h^{2}}-\frac{1}{k A^{2}_{0}} \biggl( \frac{2\ddot {h}}{h}+\frac{\dot{h}^{2}}{h^{2}} \biggr)+\frac{3\dot{h} \zeta}{A_{0} h},} \end{aligned}$$
(18)
$$\begin{aligned} &{q = -\frac{2A'_{0}\dot{h}}{k A^{2}_{0} B^{2}_{0} h^{3}},} \end{aligned}$$
(19)

where,

$$\begin{aligned} &{\rho_{0} = -\frac{1}{k B_{0}^{2}} \biggl[\frac{2B_{0}''}{B_{0}}+ \frac {4B_{0}'}{rB_{0}}-\frac{{B_{0}'}^{2}}{B_{0}^{2}} \biggr],} \end{aligned}$$
(20)
$$\begin{aligned} &{p_{0} = \frac{1}{k B_{0}^{2}} \biggl[\frac{B_{0}^{\prime 2}}{B_{0}^{2}}+ \frac{2B_{0}'}{rB_{0}}+\frac{2A'_{0} B'_{0}}{A_{0} B_{0}}+\frac{2A'_{0}}{rA_{0}} \biggr],} \end{aligned}$$
(21)
$$\begin{aligned} &{p_{t0} = \frac{1}{k B^{2}_{0} r^{4}} \biggl[\frac{B_{O}''}{B_{0}}+ \frac{B_{O}'}{r B_{0}}+\frac{A_{0}''}{A_{0}}+\frac{A_{0}'}{r A_{0}}-\frac{B_{0}^{\prime 2}}{B_{0}^{2}} \biggr].} \end{aligned}$$
(22)

In our formulation, we assume that the collapse begins from an initial anisotropic distribution of matter described by the Paul and Deb (2014) solution:

$$\begin{aligned} A_{0}(r) =& a \biggl(\frac{1-k \alpha+n\frac{r^{2}}{R^{2}}}{1+k\alpha} \biggr), \end{aligned}$$
(23)
$$\begin{aligned} B_{0}(r) =& \frac{(1+k \alpha)^{2}}{1+\frac{r^{2}}{R^{2}}}, \end{aligned}$$
(24)

with

$$ \alpha(r) = \sqrt{\frac{1+\frac{r^{2}}{R^{2}}}{1+\frac{\lambda r^{2}}{R^{2}}}}. $$
(25)

The model has four parameters \(\lambda\), \(k\), \(n\) and \(R\). For a given mass and radius, the parameters can be fixed by using of the appropriate boundary conditions. Details of numerical procedure to evaluate values of the constants and physical viability of the model are discussed in Paul and Deb (2014) paper. For appropriate choices of the model parameters, the solution has been shown to satisfy the causality condition as well as strong energy condition and has also been shown to be capable of describing realistic stars. It is, therefore, fair to say that the collapse in our construction is initiated from the state of a star with reasonable initial conditions which begins collapsing when the equilibrium is lost.

The dynamical quantities of the initial configuration have the following explicit expressions:

$$\begin{aligned} &{\rho_{0} = \frac{12(1+ k \alpha^{5} \lambda)}{k R^{2}(1+k \alpha)^{5}},} \end{aligned}$$
(26)
$$\begin{aligned} &{p_{0} =\frac{2(2 x^{2}(k^{2} \alpha^{6} \lambda-1)+n(2-\alpha^{2} z))}{x R^{2} (1+k\alpha)^{5}(n(\alpha^{2}-1)+(1-k\alpha)x)},} \end{aligned}$$
(27)
$$\begin{aligned} &{p_{t0} = \frac{x(4 x^{2}(k^{2} \alpha^{6} \lambda-1)+n y)}{R^{6}(1+k\alpha )^{5}(\alpha^{2}-1)^{2}(n(\alpha^{2}-1)+(1-k \alpha)x)},} \\ \end{aligned}$$
(28)
$$\begin{aligned} &{\begin{aligned}[b] \Delta_{s} &= n \alpha\bigl(1- \alpha^{2}\bigr) \bigl(-8\alpha(\lambda-1)+k\bigl(-3+\alpha ^{2}\bigl(-1 \\ &\quad {}+\lambda\bigl(10+3\alpha^{2}\bigl(2+\bigl(-5+ \alpha^{2}\bigr)\lambda\bigr)\bigr)\bigr)\bigr)\bigr)\\ &\quad {}\times\bigl[R^{2}(1+k \alpha )^{5}\bigl(\alpha^{2} \lambda-1\bigr) \bigl(n\bigl(\alpha^{2}-1\bigr)\\ &\quad {}+(k\alpha-1) \bigl( \alpha^{2} \lambda -1\bigr)\bigr)\bigr]^{-1}, \end{aligned}} \end{aligned}$$
(29)

where, we have defined

$$\begin{aligned} x =& \bigl(1-\alpha^{2} \lambda \bigr), \end{aligned}$$
(30)
$$\begin{aligned} y =& \bigl(4 + \alpha \bigl(4 \alpha \bigl(\alpha^{2} -1 \bigr) + k \bigl(3 + \alpha^{4} \bigr) - 4 \alpha \bigl(1 + 2 k \alpha+ \alpha^{2} \bigr) \lambda \\ &{} + \alpha^{3} \bigl(4 + k \alpha \bigl(9 - 8 \alpha^{2} + 3 \alpha^{4} \bigr) \lambda^{2} \bigr) \bigr) \bigr) , \end{aligned}$$
(31)
$$\begin{aligned} z =& \bigl(-2 +6 \lambda+\alpha \bigl(-2\alpha \bigl(-1+\lambda+ \lambda^{2} \bigr) \\ &{}-k \bigl(1+\lambda+\alpha^{2} \bigl(1+\lambda^{2} \bigl(5 \alpha^{2}-3 \bigr) \\ &{}-\lambda \bigl(2+3 \alpha ^{2} \bigr) \bigr) \bigr) \bigr) \bigr). \end{aligned}$$
(32)

Using Eq. (9) together with the condition that pressure of the initial static configuration must vanish at the surface, i.e., \(p_{0}(r = r_{\varSigma}) = 0\), we obtain

$$ 2h\ddot{h}+\dot{h}^{2}-2 \gamma\dot{h} =0, $$
(33)

where,

$$ \gamma= \biggl[\frac{A_{0}'}{B_{0}} \biggr]_{\varSigma}. $$
(34)

Note that for a given initial static configuration \(\gamma\) is a constant. Solution of Eq. (33) governs the overall temporal behaviour of the collapsing star. Following Bonnor et al. (1989), we express the second order differential equation into a first order differential equation

$$ \dot{h} = -\frac{2\gamma}{\sqrt{h}}(1-\sqrt{h}), $$
(35)

which admits a solution

$$ t = \frac{1}{\gamma} \biggl[\frac{h}{2}+\sqrt{h}+\ln(1-\sqrt{h}) \biggr]. $$
(36)

Obviously, at \(t \rightarrow- \infty\), \(h = 1\) and \(\dot{h} =0\) when \(h =1\). Thus, in this construction, the collapse begins in the remote past \(t \rightarrow- \infty\) when \(h = 1\) and it continues till the black hole is formed.

Using Eq. (10), we write the mass of the evolving star at any instant \(t\) within a radius \(r\) as

$$ m(r,t) \stackrel{\varSigma}{=} \biggl[m_{0} h(t)+\frac{2 \gamma^{2} r^{3} B_{0}^{3}(1-\sqrt{h})^{2}}{A_{0} ^{2}} \biggr], $$
(37)

where,

$$ m_{0} \stackrel{\varSigma}{=} -\frac{r^{2} B_{0}'}{2} \biggl(2+ \frac{B_{0}' r}{B_{0}} \biggr), $$
(38)

is the mass of the initial static star. We assume that at \(t= - \infty\) (i.e., when \(h(t) = 1\)), the collapsing star had an initial mass \(m_{0}\) within a boundary surface \(r_{0}\). The star continues to collapse until its shrinking radius reaches its horizon \([r h (t_{\mathit{bh}})]_{\varSigma}=r_{0} h(t_{\mathit{bh}}) = 2m(v)\), where \(t= t_{\mathit{bh}}\) is the time of formation of the black hole (de Oliveira and Santos 1988). The condition yields

$$ h(t)= \biggl[\frac{\frac{2 r \gamma B_{0}}{A_{0}}}{\frac{2 r \gamma B_{0}}{A_{0}}+\sqrt{1-\frac{2 m_{0}}{r B_{0}}}} \biggr]^{2}_{\varSigma}, $$
(39)

which takes the value \(h_{\mathit{bh}}\) at a time

$$ t_{\mathit{bh}} = \frac{1}{\gamma} \biggl[\frac{h_{\mathit{bh}}}{2}+ \sqrt{h_{\mathit{bh}}}+\ln (1-\sqrt{h_{\mathit{bh}}}) \biggr], $$
(40)

where \(h(t_{\mathit{bh}}) = h_{\mathit{bh}}\).

5 Physical analysis

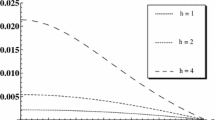
To examine the effects of anisotropy, we have considered a star having initial mass \(m_{0} = 3.5~M_{\odot}\) and radius \(r_{0} = 20~\mbox{km}\) which could be either isotropic (\(n=0\)) or anisotropic (\(n \neq0\)) in nature. Once the star departs from equilibrium, it starts collapsing until the black hole is formed. For different choices of the anisotropic parameter \(n\), the values of the model parameters including the mass (\(m_{\mathit{bh}}\)) of the black hole and corresponding horizon radius (\(r_{\mathit{bh}}\)) are given in Table 1. Of particular interest is the time of formation of black hole (\(t_{\mathit{bh}}\)) for different choices of the anisotropic parameter \(n\). Based on the calculations, the following comments may be made:

  • If tangential pressure of the initial configuration is greater than the radial pressure (\(p_{t} > p\)), i.e., \(n > 0\), the horizon is formed at an earlier epoch as compared to an isotopic star (\(n=0\)). However, if \(p > p_{t}\), i.e., \(n < 0\), the horizon is formed at a later stage as compared to an isotropic (\(n=0\)) star.

  • Although we have considered bulk viscosity in our model construction, it seems to have no effect on the collapse as it gets absorbed in the pressure term. This conclusion is in agreement with an earlier observation made by Chan (2001).

Table 1 Dynamical variables for different anisotropy. (We have assumed, \(m_{0} = 3.5~M_{\odot}\), \(r_{0} = 20~\mbox{km}\) and \(k= 0.23\).)
Full size table

To conclude, our model provides a simple mechanism to investigate the effects of anisotropy on gravitational collapse and validates some of the earlier findings. Consequences of our findings on the cosmic censorship conjecture is beyond the scope of this article and will be taken up elsewhere.