1 Introduction

One of the biggest cosmological mysteries is the accelerating cosmic expansion which was discovered by the observations of Type Ia supernovae (SNIa) starting from more than 10 years ago. The cosmological observations of Type Ia supernovae (SNeIa) (Riess et al. 1998; Perlmutter et al. 1999) and Bennett et al. (2003) indicate that the universe is currently accelerating. When these results combined with the observations of cosmic microwave background (CMB) (Bennett et al. 2003; Spergel et al. 2003) and large scale structure (LSS) (Tegmark et al. 2004a, 2004b), strongly suggest that the universe is spatially flat and dominated by an exotic component with large negative pressure called as dark energy (DE) (Weinberg 1989; Carroll 2001; Peebles and Ratra 2003; Padmanabhan 2003). Wilkinson Microwave Anisotropy Probe (WMAP) shows that Dark energy occupies 73 % of the energy of our universe. Dark matter occupies 23 % and rest 4 % energy is baryonic matter (ordinary matter) in the universe.

An approach to the problem of DE arises from holographic principle that states that the number of degrees of freedom related directly to entropy scales with the enclosing area of the system. The holographic DE models are originated from some considerable features of the quantum theory of gravity. The holographic principle was first put forward by ’t Hooft (2009) in the context of black- hole physics. According to this principle, the entropy of a system scales not with its volume, but also with its surface area (Li 2004). A special class of models in which holographic DE is allowed to interact with DM have been studied by several researchers are Carvalho and Saa (2004), Pavón and Zimdahl (2005), Wang et al. (2005, 2006), Perivolaropoulos (2005), Gong and Zhang (2005), Guberina et al. (2005, 2006), Guo et al. (2005, 2007a), Hu and Ling (2006), Nojiri and Odintsov (2006), Li et al. (2006), Kim et al. (2006), Banerjee and Pavón (2007), Zimdahl and Pavón (2007), Setare (2007a, 2007b, 2007c, 2007d) studied the correspondence between the holographic dark energy and each one of tachyon, phantom, Chaplygin gas and generalized Chaplygin gas in FRW universe.

Fischler and Susskind (1998) have proposed a new version of the holographic principle, viz. at any time during cosmological evolution, the gravitational entropy within a closed surface should not be always larger than the particle entropy that passes through the past light-cone of that surface. Recently, Bamba et al. (2012) have studied modified theory like \(f(R)\) gravity, \(f(R,T)\) gravity, \(f(T)\) gravity, scalar field theory Holographic dark energy, Coupled dark energy and \(\varLambda \mathrm{CDM}\) cosmological models representing the accelerating expansion with the quintessence/phantom nature in details along with cosmography tests.

In the context of the DE problem, though the holographic principle proposes a relation between the holographic DE density \(\rho_{\mathit{DE}}\) and the Hubble parameter \(H\) as \(\rho_{\mathit{DE}} = H^{2}\), this is does not contribute to the present accelerated expansion of the universe. Granda and Oliveros (2008) proposed a holographic density of the form \(\rho_{\mathit{DE}} \approx ( \alpha_{1} H^{2} + \beta_{1} \dot{H} )\) where \(H\) is the Hubble parameter and \(\alpha_{1},\beta_{1}\) are constants which must satisfy the restrictions imposed by the current observational data. They have been showed that this new model of DE represents the accelerated expansion of the universe and is consistent with the current observational data. Granda and Oliveros (2009) also studied the quintessence, tachyon, k-essence and dilaton DE models with this holographic DE model in the flat FRW universe. Karami and Fehri (2010) have reconstructed models of holographic quintessence, holographic tachyon and new holographic quintessence, tachyon, k-essence scalar field of DE. Ma et al. (2010) have considered the interaction between dark matter and dark energy in the framework of holographic dark energy, and proposed a natural and physically plausible form of interaction, in which the interacting term is proportional to the product of the powers of the dark matter and dark energy densities. Sarkar (2014a, 2014b, 2014c), Debnath (2014), Borah and Ansari (2014) have been studied the Bianchi type space-times in the context of holographic dark energy. Sadeghi and Farahani (2014) have studied dark energy and tachyon field in Bianchi type-V universe and they have obtained results for non-interacting models with three different kinds of matters such as pressureless matter, barotropic matter and modified Chaplygin gas. Adhav et al. (2014) have studied interacting dark matter and holographic dark energy in an anisotropic universe. Som and Sil (2014) have discussed general approach of interacting holographic dark energy models.

Motivated by the above investigations, in this paper, we have studied spatially homogeneous and anisotropic Bianchi type-V universe filled with interacting Dark matter and Holographic dark energy. The exact solutions of Einstein’s field equations have been obtained by (i) applying the special law of variation of Hubble parameter that yields constant values of the deceleration parameter and (ii) using a special form of deceleration parameter. It has been observed that for suitable choice of interaction between dark matter and holographic dark energy there is no coincidence problem (unlike \(\varLambda \mathrm{CDM}\)). In all the resulting models the anisotropy of expansion dies out after some finite time and subsequently the models approach to isotropy. The physical and geometrical aspects of the models are also discussed.

2 Metric and field equations

The Bianchi type-V line element can be written as

$$\begin{aligned} ds^{2} = dt^{2} - a_{1}^{2}(t)dx^{2} - a_{2}^{2}(t)e^{ - 2\alpha x}dy^{2} - a_{3}^{2}(t)e^{ - 2\alpha x}dz^{2}, \end{aligned}$$
(2.1)

where \(a_{1}(t)\), \(a_{2}(t)\) and \(a_{3}(t)\) are the cosmic scale factors and \(\alpha \ne 0\) is an arbitrary constant.

The Einstein’s field equations, in natural limits (\(8\pi G = 1\) and \(c = 1\)) are

$$ R_{ij} - \frac{1}{2}g_{ij}R = - \bigl( {}^{\mathit{DM}}T_{ij} + {}^{\mathit{DE}}T_{ij} \bigr), $$
(2.2)

where

$$\begin{aligned} \textstyle\begin{array}{@{}l} {}^{\mathit{DM}}T_{ij} = \rho_{\mathit{DM}}u_{i}u_{j} \quad \mbox{and} \\ {}^{\mathit{DE}}T_{ij} = ( \rho_{\mathit{DE}} + p_{\mathit{DE}} ) u_{i}u_{j} - g_{ij}p_{\mathit{DE}} \end{array}\displaystyle \end{aligned}$$
(2.3)

are energy-momentum tensors for dark matter (pressureless i.e. \(w_{\mathit{DM}} = 0\)) and holographic dark energy respectively. Here \(\rho_{\mathit{DM}}\) is the energy density of dark matter \(\rho_{\mathit{DE}}\) and \(p_{\mathit{DE}}\) are the energy density and pressure of holographic dark energy.

In comoving coordinate systems, the Einstein’s field Eqs. (2.2) for the metric (2.1) with the help of Eq. (2.3) can be written as

$$ \frac{\dot{a}_{1}\dot{a}_{2}}{a_{1}a_{2}} + \frac{\dot{a}_{2}\dot{a}_{3}}{a_{2}a_{3}} + \frac{\dot{a}_{3}\dot{a}_{1}}{a_{3}a_{1}} - \frac{3\alpha^{2}}{a_{1}^{2}} = \rho_{\mathit{DM}} + \rho_{\mathit{DE}}, $$
(2.4)
$$ \frac{\ddot{a}_{2}}{a_{2}} + \frac{\ddot{a}_{3}}{a_{3}} + \frac{\dot{a}_{2}\dot{a}_{3}}{a_{2}a_{3}} - \frac{\alpha^{2}}{a_{1}^{2}} = - p_{\mathit{DE}}, $$
(2.5)
$$ \frac{\ddot{a}_{1}}{a_{1}} + \frac{\ddot{a}_{3}}{a_{3}} + \frac{\dot{a}_{1}\dot{a}_{3}}{a_{1}a_{3}} - \frac{\alpha^{2}}{a_{1}^{2}} = - p_{\mathit{DE}}, $$
(2.6)
$$ \frac{\ddot{a}_{1}}{a_{1}} + \frac{\ddot{a}_{2}}{a_{2}} + \frac{\dot{a}_{1}\dot{a}_{2}}{a_{1}a_{2}} - \frac{\alpha^{2}}{a_{1}^{2}} = - p_{\mathit{DE}}, $$
(2.7)
$$ \frac{\dot{a}_{2}}{a_{2}} + \frac{\dot{a}_{3}}{a_{3}} = 2\frac{\dot{a}_{1}}{a_{1}}, $$
(2.8)

where an overhead dot (.) represents derivative with respect to time \(t\).

Integration on Eq. (2.8), we get

$$ a_{1}^{2} = \lambda a_{2}a_{3}, $$
(2.9)

where \(\lambda\) is an integration constants. Without loss of generality we can take \(\lambda = 1\).

The volume scale factor \(V\) and average scale factor \(a\) are given by

$$ V = a^{3} = a_{1}a_{2}a_{3}. $$
(2.10)

The mean Hubble parameter \(H\) is defined as

$$ H = \frac{\dot{a}}{a} = \frac{1}{3} ( H_{x} + H_{y} + H_{z} ), $$
(2.11)

where \(H_{x} = \frac{\dot{a}_{1}}{a_{1}}\), \(H_{y} = \frac{\dot{a}_{2}}{a_{2}}\), \(H_{z} = \frac{\dot{a}_{3}}{a_{3}}\) are the directional Hubble parameters in the directions of \(x\), \(y\) and \(z\) axes respectively.

The deceleration parameter \(q(t)\) is defined by

$$ q = - \frac{a \ddot{a}}{\dot{a}^{2}}. $$
(2.12)

The mean anisotropy parameter of expansion (\(\Delta\)) is defined by

$$ \Delta = \frac{1}{3}\sum_{i = 1}^{3} \biggl( \frac{H_{i} - H}{H} \biggr)^{2}. $$
(2.13)

Subtracting Eq. (2.5) from Eq. (2.6), Eq. (2.6) from Eq. (2.7), Eq. (2.5) from Eq. (2.7) and using Eq. (2.10), we get

$$ \frac{d}{dt} \biggl( \frac{\dot{a}_{1}}{a_{1}} - \frac{\dot{a}_{2}}{a_{2}} \biggr) + \biggl( \frac{\dot{a}_{1}}{a_{1}} - \frac{\dot{a}_{2}}{a_{2}} \biggr)\frac{\dot{V}}{V} = 0, $$
(2.14a)
$$ \frac{d}{dt} \biggl( \frac{\dot{a}_{2}}{a_{2}} - \frac{\dot{a}_{3}}{a_{3}} \biggr) + \biggl( \frac{\dot{a}_{2}}{a_{2}} - \frac{\dot{a}_{3}}{a_{3}} \biggr)\frac{\dot{V}}{V} = 0, $$
(2.14b)
$$ \frac{d}{dt} \biggl( \frac{\dot{a}_{1}}{a_{1}} - \frac{\dot{a}_{3}}{a_{3}} \biggr) + \biggl( \frac{\dot{a}_{1}}{a_{1}} - \frac{\dot{a}_{3}}{a_{3}} \biggr)\frac{\dot{V}}{V} = 0. $$
(2.14c)

On integrating Eqs. (2.14a)–(2.14c) and using Eqs. (2.9) and (2.10), the scale factors \(a_{1}(t),a_{2}(t)\) and \(a_{3}(t)\) can be written explicitly as

$$ a_{1}(t) = V^{\frac{1}{3}}, $$
(2.15a)
$$ a_{2}(t) = DV^{\frac{1}{3}}\exp \biggl( X\int \frac{dt}{V} \biggr), $$
(2.15b)
$$ a_{3}(t) = D^{ - 1}V^{\frac{1}{3}}\exp \biggl( - X\int \frac{dt}{V} \biggr), $$
(2.15c)

where \(X\) and \(D\) are constants of integration. The holographic dark energy density is given by

$$ \rho_{\mathit{DE}} = 3 \bigl( \alpha_{1} H^{2} + \beta_{1} \dot{H} \bigr), $$
(2.16)

i.e. \(\rho_{\mathit{DE}} = 3 ( \alpha_{1} H^{2} + \beta_{1} \dot{H} )\) with \(M_{p}^{ - 2} = 8 \pi G = 1\) (Granda and Oliveros 2008).

For the universe, where dark energy and dark matter are interacting to each other the total energy density (\(\rho = \rho_{\mathit{DM}} + \rho_{\mathit{DE}}\)) satisfies the equation of continuity as

$$ \dot{\rho}_{\mathit{DM}} + \dot{\rho}_{\mathit{DE}} + 3H(\rho_{\mathit{DM}} + \rho_{\mathit{DE}} + p_{\mathit{DE}}) = 0. $$
(2.17)

Assuming that the dark matter component is interacting with the dark energy component through an interaction term \(Q\), the continuity equation of matter and dark energy can be obtained as

$$ \dot{\rho}_{\mathit{DM}} + \biggl( \frac{\dot{V}}{V} \biggr) \rho_{\mathit{DM}} = Q, $$
(2.18)
$$ \dot{\rho}_{\mathit{DE}} + \biggl( \frac{\dot{V}}{V} \biggr) (1 + \omega_{\mathit{DE}})\rho_{\mathit{DE}} = - Q, $$
(2.19)

where \(\omega_{\mathit{DE}} = \frac{p_{\mathit{DE}}}{\rho_{\mathit{DE}}}\) is the equation of state parameter for holographic dark energy and \(Q > 0\) measures the strength of the interaction. A vanishing \(Q\) implies that dark matter and dark energy are separately conserved. In view of continuity equations, the interaction between dark energy and dark matter must be a function of the energy density multiplied by a quantity with units of inverse of time, which can be chosen as the Hubble parameter \(H\). There is freedom to choose the form of the energy density, which can be any combination of dark energy and dark matter. Thus, the interaction between dark energy and dark matter could be expressed phenomenologically in the forms as (Guo et al. 2007a, 2007b; Amendola et al. 2007)

$$ Q = 3b^{2}H\rho_{\mathit{DM}} = b^{2}\frac{\dot{V}}{V} \rho_{\mathit{DM}}, $$
(2.20)

where \(b^{2}\) is coupling constant.

Cai and Wang (2005) have taken same relation for interacting dark matter and phantom dark energy in order to avoid the coincidence problem.

Using Eqs. (2.18) and (2.20), we get the energy density of dark matter as

$$ \rho_{\mathit{DM}} = \rho_{0}V^{ ( b^{2} - 1 )}, $$
(2.21)

where \(\rho_{0} > 0\) is real constant of integration.

Using Eqs. (2.20) and (2.21), we get the interacting term \(Q\) as

$$ Q = 3\rho_{0}b^{2}HV^{ ( b^{2} - 1 )}. $$
(2.22)

3 Cosmological solutions for constant deceleration parameter

In order to obtain the solutions of Eqs. (2.4)–(2.8), we assume the special law of variation for the Hubble parameter which yields the constant value of deceleration parameter (Berman 1983). According to this law the variation of the mean Hubble parameter is given by

$$ H = k a^{ - n}, $$
(3.1)

where \(k > 0\) and \(n \ge 0\).

Here we obtain two cosmological models (i) Model for \(n = 0\) and (ii) Model for \(n \ne 0\).

  1. (i)

    Model for \(n = 0\) [Exponential Volumetric Expansion Model]

For \(n = 0\), Eq. (3.1) gives the volume scale factor as

$$ V = c_{1}e^{3kt}, $$
(3.2)

where \(c_{1} > 0\) is a constant of integration.

Using Eq. (3.2) in Eqs. (2.15a)–(2.15c), we obtain the exact values of scale factors as

$$ a_{1}(t) = (c_{1})^{1/3}e^{kt}, $$
(3.3a)
$$ a_{2}(t) = D(c_{1})^{1/3}\exp \biggl( kt - \frac{X}{3c_{1}k}e^{ - 3kt} \biggr), $$
(3.3b)
$$ a_{3}(t) = D^{ - 1}(c_{1})^{1/3}\exp \biggl( kt + \frac{X}{3c_{1}k}e^{ - 3kt} \biggr). $$
(3.3c)

Using Eq. (3.2) in Eqs. (2.21) and (2.22), we get

$$ \rho_{\mathit{DM}} = \rho_{0}(c_{1})^{b^{2} - 1} e^{3k(b^{2} - 1)t}, $$
(3.4)
$$ Q = 3kb^{2}\rho_{0}(c_{1})^{b^{2} - 1} e^{3k(b^{2} - 1)t}. $$
(3.5)

Using Eqs. (3.3a)–(3.3c) and (3.4) in Eq. (2.4), we obtain the energy density of holographic dark energy as

$$\begin{aligned} \rho_{\mathit{DE}} =& 3k^{2} - \biggl( \frac{X}{c_{1}} \biggr)^{2}e^{ - 6kt} - \frac{3\alpha^{2}}{(c_{1})^{2/3}e^{2kt}} \\ &{} - \rho_{0}(c_{1})^{(b^{2} - 1)}e^{3k(b^{2} - 1)t}. \end{aligned}$$
(3.6)

Using Eqs. (3.2), (3.4) and (3.6) in Eqs. (2.4)–(2.8), we obtain the pressure of holographic dark energy as

$$ p_{\mathit{DE}} = - 3k^{2} - \biggl( \frac{X}{c_{1}} \biggr)^{2}e^{ - 6kt} + \frac{\alpha^{2}}{(c_{1})^{2/3}e^{2kt}}. $$
(3.7)

The EoS parameter of holographic dark energy is given by

$$\begin{aligned} w_{\mathit{DE}} = \mbox{$ \dfrac{ - ( 3k^{2} + ( \frac{X}{c_{1}} )^{2}e^{ - 6kt} - \frac{\alpha^{2}}{(c_{1})^{2/3}e^{2kt}} )}{3k^{2} - ( \frac{X}{c_{1}} )^{2}e^{ - 6kt} - \frac{3\alpha^{2}}{(c_{1})^{2/3}e^{2kt}} - \rho_{0}(c_{1})^{(b^{2} - 1)}e^{3k(b^{2} - 1)t}}$}. \end{aligned}$$
(3.8)

Using Eqs. (3.3a)–(3.3c) in Eqs. (2.11), (2.12) and (2.13), we get the mean Hubble parameter \(H\), deceleration parameter \(q\) and mean anisotropy parameter of expansion \(\Delta\) are given by respectively

$$ H = k, $$
(3.9)
$$ q = - 1, $$
(3.10)
$$ \Delta = \frac{2 X^{2}}{3 c_{1}^{2}k^{2}}e^{ - 6kt}. $$
(3.11)

The coincidence parameter \(r = \rho_{\mathit{DM}}/\rho_{\mathit{DE}}\) i.e. the ratio of dark energy densities of dark matter and dark energy is given by

$$\begin{aligned} r = \mbox{$ \dfrac{\rho_{0}(c_{1})^{b^{2} - 1}e^{3k(b^{2} - 1)t}}{3k^{2} - ( \frac{X}{c_{1}} )^{2}e^{ - 6kt} - \frac{3\alpha^{2}}{(c_{1})^{2/3}e^{2kt}} - \rho_{0}(c_{1})^{(b^{2} - 1)}e^{3k(b^{2} - 1)t}}$}. \end{aligned}$$
(3.12)
  1. (ii)

    Model for \(n \ne 0\) [Power-law Volumetric Expansion Model]

For \(n \ne 0\), Eq. (3.1) gives the volume scale factor as

$$ V = (nkt + c_{2})^{3/n}, $$
(3.13)

where \(c_{2}\) is a arbitrary constant of integration.

Using Eq. (3.13) in Eqs. (2.15a)–(2.15c), we obtain the exact solution of the scale factors as

$$\begin{aligned} a_{1}(t) = (nkt + c_{2})^{1/n}, \end{aligned}$$
(3.14a)
$$\begin{aligned} a_{2}(t) =& D (nkt + c_{2})^{1/n} \\ &{}\times \exp \biggl( \frac{X}{k(n - 3)}(nkt + c_{2})^{(n - 3)/n} \biggr), \end{aligned}$$
(3.14b)
$$\begin{aligned} a_{3}(t) =& D^{ - 1}(nkt + c_{2})^{1/n} \\ &{}\times\exp \biggl( \frac{ - X}{k(n - 3)}(nkt + c_{2})^{(n - 3)/n} \biggr). \end{aligned}$$
(3.14c)

Using Eq. (3.13) in Eqs. (2.21) and (2.22), we get

$$ \rho_{\mathit{DM}} = \rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n}}, $$
(3.15)
$$ Q = 3kb^{2}\rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n} - 1}. $$
(3.16)

Using Eqs. (3.14a)–(3.14c) and (3.15) in Eq. (2.4), we obtain the energy density of holographic dark energy as

$$\begin{aligned} \rho_{\mathit{DE}} =& 3k^{2}(nkt + c_{2})^{ - 2} - X^{2}(nkt + c_{2})^{\frac{ - 6}{n}} \\ &{}- \frac{3\alpha^{2}}{(nkt + c_{2})^{2/n}} - \rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n}}. \end{aligned}$$
(3.17)

Using Eqs. (3.13), (3.15) and (3.17) in the linear combination of Eqs. (2.4)–(2.7), we obtain the pressure of holographic dark energy as

$$\begin{aligned} p_{\mathit{DE}} =& - k^{2}(nkt + c_{2})^{ - 2} - X^{2}(nkt + c_{2})^{\frac{ - 6}{n}} \\ &{} + \frac{\alpha^{2}}{(nkt + c_{2})^{2/n}}. \end{aligned}$$
(3.18)

The EoS parameter of holographic dark energy is given by

$$\begin{aligned} \omega_{\mathit{DE}} = \frac{ - k^{2}(nkt + c_{2})^{ - 2} - X^{2}(nkt + c_{2})^{\frac{ - 6}{n}} + \frac{\alpha^{2}}{(nkt + c_{2})^{2/n}}}{3k^{2}(nkt + c_{2})^{ - 2} - X^{2}(nkt + c_{2})^{\frac{ - 6}{n}} - \frac{3\alpha^{2}}{(nkt + c_{2})^{2/n}} - \rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n}}}. \end{aligned}$$
(3.19)

Using Eqs. (3.14a)–(3.14c) in Eqs. (2.11), (2.12) and (2.13), we get the mean Hubble parameter \(H\), deceleration parameter \(q\) and mean anisotropy parameter of expansion \(\Delta\) are given by respectively

$$ H = k (nkt + c_{2})^{ - 1}, $$
(3.20)
$$ q = n - 1, $$
(3.21)
$$ \Delta = \frac{2X^{2}}{3k^{2}} ( nkt + c_{2} )^{\frac{2(n - 3)}{n}}. $$
(3.22)

The coincidence parameter \(r\) i.e. the ratio of dark energy densities of dark matter and dark energy is given by

$$ r = \dfrac{\rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n}}}{3k^{2}(nkt + c_{2})^{ - 2} - X^{2}(nkt + c_{2})^{\frac{ - 6}{n}} - \frac{3\alpha^{2}}{(nkt + c_{2})^{2/n}} - \rho_{0}(nkt + c_{2})^{\frac{3(b^{2} - 1)}{n}}}. $$
(3.23)

4 Cosmological solution for special form of deceleration parameter

The exponential volumetric expansion and power-law volumetric expansion models are either accelerating (\(n = 0\) and \(0 < n < 1\)) or decelerating (\(n > 1\)). In order to obtain the solutions of the field Eqs. (2.4)–(2.8), we assume a mathematical condition which is a special form of deceleration parameter. Singha and Debnath (2009) have defined a special form of deceleration parameter for FRW model as

$$ q = - \frac{\ddot{a}a}{\dot{a}^{2}} = - 1 + \frac{\beta}{1 + a^{\beta}}, $$
(4.1)

where \(\beta > 0\) is a constant and \(a\) is mean scale factor of the universe.

Solving Eq. (4.1), we obtain the mean Hubble parameter \(H\) as

$$ H = \frac{\dot{a}}{a} = \gamma \bigl(1 + a^{ - \beta} \bigr), $$
(4.2)

where \(\gamma\) is constant of integration.

On integrating Eq. (4.2), we obtain the mean scale factor as

$$ a = V^{1/3} = \bigl(e^{\gamma \beta t} - 1\bigr)^{1/\beta}. $$
(4.3)

Using Eq. (4.3) for \(\gamma = 1\) in Eqs. (2.15a) to (2.15c), we obtain exact value of scale factor as

$$ a_{1}(t) = \bigl(e^{\beta t} - 1\bigr)^{1/\beta}, $$
(4.4a)
$$\begin{aligned} a_{2}(t) =& D\bigl(e^{\beta t} - 1\bigr)^{1/\beta} \exp \biggl\{ X\biggl[ - \frac{1}{3} \bigl(e^{\beta t} - 1 \bigr)^{3/\beta} \\ &{}\times \bigl(e^{\beta t} - 1\bigr)^{ - 3/\beta} {}_{2}F_{1} \biggl(\frac{3}{\beta},\frac{3}{\beta};\frac{\beta + 3}{\beta};e^{ - \beta t} \biggr) \biggr] \biggr\} , \end{aligned}$$
(4.4b)
$$\begin{aligned} a_{3}(t) =& D^{ - 1}\bigl(e^{\beta t} - 1 \bigr)^{1/\beta} \exp \biggl\{ - X\biggl[ - \frac{1}{3} \bigl(e^{\beta t} - 1\bigr)^{3/\beta} \\ &{}\times \bigl(e^{\beta t} - 1\bigr)^{ - 3/\beta} {}_{2}F_{1} \biggl( \frac{3}{\beta},\frac{3}{\beta};\frac{\beta + 3}{\beta};e^{ - \beta t} \biggr) \biggr] \biggr\} , \end{aligned}$$
(4.4c)

where \({}_{2}F_{1}(l,m;n;t)\) is hypergeometric function.

Using Eq. (4.3) in Eqs. (2.21) and (2.22), we get

$$ \rho_{\mathit{DM}} = \rho_{0}\bigl(e^{\beta t} - 1 \bigr)^{\frac{3(b^{2} - 1)}{\beta}}, $$
(4.5)
$$ Q = 3\rho_{0}b^{2}e^{\beta t}\bigl(e^{\beta t} - 1\bigr)^{\frac{3(b^{2} - 1)}{\beta} - 1}. $$
(4.6)

Using Eqs. (4.4a)–(4.4c) and (4.5) in Eq. (2.4), we obtain the energy density of holographic dark energy as

$$\begin{aligned} \rho_{\mathit{DE}} =& 3e^{2\beta t}\bigl(e^{\beta t} - 1 \bigr)^{ - 2} - X^{2}\bigl(e^{\beta t} - 1 \bigr)^{ - 6/\beta} \\ &{}- \frac{3\alpha^{2}}{(e^{\beta t} - 1)^{1/2\beta}} - \rho_{0} \bigl(e^{\beta t} - 1\bigr)^{\frac{3(b^{2} - 1)}{\beta}}. \end{aligned}$$
(4.7)

Using Eqs. (4.3), (4.5) and (4.7) in Eqs. (2.4)–(2.7), we obtain the pressure of holographic dark energy as

$$\begin{aligned} p_{\mathit{DE}} =& 3e^{2\beta t}\bigl(e^{\beta t} - 1 \bigr)^{ - 2} - X^{2}\bigl(e^{\beta t} - 1 \bigr)^{ - 6/\beta} \\ &{}+ \frac{\alpha^{2}}{(e^{\beta t} - 1)^{1/2\beta}} - 2 \biggl[ \frac{\beta e^{\beta t}}{(e^{\beta t} - 1)} + \frac{(3 - \beta )e^{\beta t}}{(e^{\beta t} - 1)^{2}} \biggr]. \end{aligned}$$
(4.8)

The EoS parameter of holographic dark energy is given by

$$ \omega_{\mathit{DE}} = \frac{3e^{2\beta t}(e^{\beta t} - 1)^{ - 2} - X^{2}(e^{\beta t} - 1)^{ - 6/\beta} + \frac{\alpha^{2}}{(e^{\beta t} - 1)^{1/2\beta}} - 2 [ \frac{\beta e^{\beta t}}{(e^{\beta t} - 1)} + \frac{(3 - \beta )e^{\beta t}}{(e^{\beta t} - 1)^{2}} ]}{3e^{2\beta t}(e^{\beta t} - 1)^{ - 2} - X^{2}(e^{\beta t} - 1)^{ - 6/\beta} - \frac{3\alpha^{2}}{(e^{\beta t} - 1)^{1/2\beta}} - \rho_{0}(e^{\beta t} - 1)^{\frac{3(b^{2} - 1)}{\beta}}}. $$
(4.9)

The mean anisotropy parameter \(\Delta\) is given by

$$ \Delta = \frac{2}{3}X^{2}\bigl(e^{\beta t} - 1 \bigr)^{\frac{2(\beta - 3)}{\beta}}. $$
(4.10)

The coincidence parameter \(r\) i.e. the ratio of dark energy densities of dark matter and dark energy is given by

$$ r = \frac{\rho_{0}(e^{\beta t} - 1)^{\frac{3(b^{2} - 1)}{\beta}}}{ 3e^{2\beta t}(e^{\beta t} - 1)^{ - 2} - X^{2}(e^{\beta t} - 1)^{ - 6/\beta} - \frac{3\alpha^{2}}{(e^{\beta t} - 1)^{1/2\beta}} - \rho_{0}(e^{\beta t} - 1)^{\frac{3(b^{2} - 1)}{\beta}}}. $$
(4.11)

5 Discussion

The physical and geometrical behaviors of the cosmological models are as follows:

  1. (i)

    The deceleration parameter \((q)\)

For the models presented in Sect. 3, from Eqs. (3.10), (3.21) it is observed that the deceleration parameter \(q\) is negative for \(n = 0\) and \(0 < n < 1\). This indicates that the universe is accelerating as shown in Fig. 1. For the model presented in Sect. 4, the deceleration parameter \(q\) varies from \(+ 1\) to −1 as shown in Fig. 1. It shows that the value of \(q\) is positive at the early stage of the universe and becomes negative at late time. For \(\beta = 3/2\) the deceleration parameter \(q\) is in the range \(- 1 \le q \le 0.5\) (shaded region in Fig. 1) which is consistent with the observations made by Perlmutter et al. (1998, 1999) and Riess et al. (1998) and the present day universe is undergoing accelerated expansion.

Fig. 1
figure 1

The variation of \(q\) vs. time (\(t\))

Full size image

In other words, the sign of \(q\) indicates whether the models inflates or not. A positive sign of \(q\) indicates decelerating model whereas negative sign of \(q\) indicates inflation.

In our exponential volumetric expansion model [from Eq. (3.10)], we can say that the model inflates. Further, this value of deceleration parameter leads to \(dH/dt = 0\) implying the greatest value of Hubble’s parameter and fastest rate of expansion of universe.

Whereas, in the power-law volumetric expansion model [from Eq. (3.21)], we can say that a positive sign of \(q\) [i.e. for \(n > 1\)] correspond to the standard decelerating model whereas the negative sign of \(q\) [i.e. \(0 < n <1\)] indicate inflation.

Thus our derived model is suitable to describe the late time evolution of the universe.

  1. (ii)

    The anisotropy parameter of expansion (\(\Delta\))

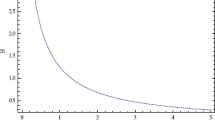
In Fig. 2, we plotted an anisotropy parameter of expansion (\(\Delta\)) for Eqs. (3.11), (3.22) and (4.11) against cosmic time \(t\) for (i) exponential volumetric expansion model (ii) power-law volumetric expansion model and (iii) model for special form of deceleration parameter respectively. It is observed that in these three models anisotropy decreases as time increases and then becomes zero after some time and remains zero after some finite time. Hence, the models are approaches to isotropy after some finite time which matches with the recent observation as the universe is isotropic at large scale.

  1. (iii)

    The equation of state parameter (\(\omega_{\mathit{DE}}\))

Figure 3 shows the variation of EoS parameter (\(\omega_{\mathit{DE}}\)) with cosmic time \(t\) for constant deceleration parameter models and special form of deceleration parameter model.

Fig. 2
figure 2

Evolution of anisotropy parameter of expansion (\(\Delta\)) vs. time (\(t\)) for \(k = 1\), \(X^{2} = 1\), \(n = 0.5\)

Full size image
Fig. 3
figure 3

Evolution of EoS parameter (\(\omega_{\mathit{DE}}\)) vs. time (\(t\)) for \(k = 1\), \(X^{2} = 1\), \(n = 0.5\), \(\beta = 1.5\)

Full size image

For the models presented in Sect. 3, from Eqs. (3.8) and (3.19), it is observed that the parameter \(\omega_{\mathit{DE}}\) starts from phantom region (\(\omega_{\mathit{DE}} < - 1\)) and attains the value \(\omega_{\mathit{DE}} = - 1\) after some finite \(t\) i.e. the model approaches to \(\varLambda\mathrm{CDM}\) model after some finite \(t\). Spergel et al. (2003), Riess et al. (2004, 2007), Eisenstein et al. (2005), Astier et al. (2006), Bamba et al. (2012) all indicate that the \(\varLambda \mathrm{CDM}\) model or the model that reduces to \(\varLambda \mathrm{CDM}\) are served as an excellent models to describe the cosmological evolution. From Eq. (4.9), we observed that for a special form of deceleration parameter model, the parameter \(\omega_{\mathit{DE}}\) starts from quintessence (\(- 1 < \omega_{\mathit{DE}}\)) for particular value of \(n (n \ne 0)\) and converges in the phantom region as model presented in Sect. 3, It has been argued that the interacting holographic dark energy model can accommodate the transition of the dark energy equation of state (\(\omega_{\mathit{DE}}\)) from (\(\omega_{\mathit{DE}} > - 1\) and \(\omega_{\mathit{DE}} < - 1\)) (Wang et al. 2005, 2006).

  1. (iv)

    Coincidence Parameter (\(r\))

The recent observations demands that the ratio of two energy densities \(r = \rho_{\mathit{DM}}/\rho_{\mathit{DE}}\) i.e. the coincidence parameter stays constant or varies very slowly, around the present time, with respect to the universe expansion. But, the leading candidate for dark energy, the popular \(\varLambda \mathrm{CDM}\) model is not consistent with this observation. This coincidence problem has led numerous authors to consider alternatives to \(\varLambda \mathrm{CDM}\) which preserve its stunning successes (Type Ia SNe, CMB anisotropies, large-scale structure) but avoid the above difficulty. To avoid the coincidence problem, matter and dark energy must scale each other over a considerably long period of time during the later stage of evolution of the universe. In other words, the ratio of two energy densities \(r = \rho_{\mathit{DM}}/\rho_{\mathit{DE}}\) remains constant in spite of their different rates of time evolution. The variation of coincidence parameter \(r\) with respect to cosmic time \(t\) is as shown in Fig. 4. From Eq. (3.12), we observed that coincidence parameter \(r\) at very early stage of evolution varies, but after some finite time \(t\) it converges to a constant value and remains constant throughout the evolution in exponential volumetric expansion models provided that \(b^{2} = 1\). From Eq. (3.23), it is observed that, \(r\) increases linearly throughout the evolution of the universe in power-law model. From Eq. (4.11), the coincidence parameter \(r\) vanishes at very early stage of evolution. It is also observed that parameter \(r\) increases as time increases but after some finite time it decreases and converges to a constant value and remains constant throughout the evolution in a special form of deceleration parameter model. Thus, a suitable kind of interaction between holographic dark energy and dark matter can make the ratio of their densities possible to attain a stationary value during the course of evolution and consequently can help alleviating the coincidence problem which appears in the \(\varLambda \mathrm{CDM}\) models.

Fig. 4
figure 4

Coincidence parameter \(r\) vs. cosmic time (\(t\))

Full size image

6 Conclusion

We have studied the anisotropic and homogeneous Bianchi type-V cosmological model filled with interacting Dark matter and Holographic dark energy. The solutions of the Einstein’s field equations are obtained under the assumption of constant value of deceleration parameter and special form of deceleration parameter. We have noted that

  1. (i)

    In our exponential volumetric expansion model [from Eq. (3.10)], we can say that the model inflates. Further, this value of deceleration parameter leads to \(dH/dt = 0\) implying the greatest value of Hubble’s parameter and fastest rate of expansion of universe.

    Whereas, in the power-law volumetric expansion model [from Eq. (3.21)], we can say that a positive sign of \(q\) [i.e. for \(n > 1\)] correspond to the standard decelerating model whereas the negative sign of \(q\) [i.e. \(0 < n <1\)] indicate inflation.

    Thus our derived model is suitable to describe the late time evolution of the universe.

  2. (ii)

    From Eq. (2.20), it is observed that for suitable choice of interaction between dark matter and holographic dark energy with \(b^{2} = 1\), there is no coincidence problem in case of exponential volumetric expansion model and in the model with special form of deceleration parameter. This result matches with the present observations as we live in the stationary coincidence state of the universe. Whereas, there is coincidence problem in case of power-law volumetric expansion model [i.e. model for \(n \ne 0\)].

  3. (iii)

    One should note that for \(b^{2} = 0\) [in Eq. (2.20)], it represents the non-interacting Bianchi type-V model while \(b^{2} = 1\) yields complete transfer of energy from dark energy to dark matter. Recently, it has been reported that such interaction is observed in the Abell cluster \(\mathrm{A}586\) showing a transition of dark energy into dark matter and vice versa [Bertolami et al. 2007; Jamil and Rashid 2008].

  4. (iv)

    In the power-law volumetric expansion model, we have observed that at \(t = - c_{2}/nk\), the spatial volume vanishes and other parameter \(H\), \(p_{\mathit{DE}}\), \(\rho_{\mathit{DE}}\) diverges. Therefore, the model has a big bang singularity at \(t = - c_{2}/nk\), which can be shifted to \(t = 0\) by choosing \(c_{2} = 0\). The singularity is point type as the directional scale factors \(a_{1}(t)\), \(a_{2}(t)\) and \(a_{3}(t)\) vanish at the initial moment (Maccallum 1971).

  5. (v)

    For \(Q = 0\) (non interacting case) the models with constant deceleration parameter reduce to the particular models of Samanta (2013), Sarkar (2014b) (with \(k = 0\) their in) and Sadeghi and Farahani (2014).

  6. (vi)

    For \(Q \ne 0\) (i.e. interacting case) and \(\alpha = 0\) the model with constant deceleration parameter reduces to Bianchi type-I model obtained by Adhav et al. (2014).

  7. (vii)

    Also, in all three models the anisotropy of expansion dies out very quickly and attains isotropy after some finite time. In other words, we can say that the Bianchi type-V model reduces to flat FRW soon after inflation.